Chapter 2 Simple random sampling

2.1 Definition

Simple random sampling (SRS) is a method of selecting n units out of N such that each sample s of size n has the same probability of selection:

\[\begin{equation} Pr\left(S=s\right) = 1 / \binom{N}{n} \tag{2.1} \end{equation}\]

Where \(\binom{N}{n}\) denotes the total number of possible samples of size \(n\) from \(N\) units.

Basically, SRS is what we do when \(n\) balls are selected in a lottery:

• First draw: a unit is selected with probability \(1/N\)
• Second draw: a unit is selected with probability \(1/N-1\) …
• \(n^{th}\) draw: one unit is selected with probability \(1/N-(n-1)\)

Thus, the probability of selecting \(s \in \mathcal{S}\) is given by:

\[\begin{equation} \begin{array}{lcl} Pr\left(S=s\right) & = & n! \times \frac{1}{N} \times \frac{1}{N} \times \cdots \frac{1}{N-(n-1)} \\ & = & n! \times \frac{(N-n)!}{N!} \\ & = & 1 / \binom{N}{n} \\ \end{array} \tag{2.2} \end{equation}\]

Simple random sampling is the simplest form of sampling scheme, requiring no auxiliary information to be implemented.

2.2 Inclusion probabilities

Inclusion probabilities are key concepts in survey sampling. Basically, they are defined as the probability for a unit (simple inclusion probability) or a couple of units (double inclusion probability) to appear in the sample.

The simple inclusion probability of \(i \in U\) is given by:

\[\begin{equation} \pi_{i} = Pr\left(i \in S\right) = \sum_{\substack {s \in \mathcal{S} \\ s \ni i}} Pr\left(S = s\right) = \frac{\binom{N-1}{n-1}}{\binom{N}{n}} = \frac{n}{N} \tag{2.3} \end{equation}\]

The double inclusion probability of \(i\) and \(j \in U\) \(\left(i \neq j\right)\) is given by:

\[\begin{equation} \pi_{ij} = Pr\left(i,j \in S\right) = \sum_{\substack {s \in \mathcal{S} \\ s \ni i,j}} Pr\left(S = s\right) = \frac{\binom{N-2}{n-2}}{\binom{N}{n}} = \frac{n}{N} \frac{n-1}{N-1} \tag{2.4} \end{equation}\]

2.3 Estimating population totals and means

Suppose we wish to estimate the total \(Y\) of a study variable \(y\) over the target population \(U\): \[\begin{equation} Y = \sum_{k \in U} y_k \tag{2.5} \end{equation}\]

Assuming the size \(N\) of the population is known, the mean of a variable can be regarded as a particular case of a total: \[\begin{equation} \bar{Y} = (1/N) \sum_{k \in U} y_k = \sum_{k \in U} \left(y_k / N\right) = \sum_{k \in U} z_k \tag{2.6} \end{equation}\]

In the absence of any additional information, we are going to use the sample mean \(\bar{y}\) of the study variable \(\mathbf{y}\) as an estimator of \(\bar{Y}\): \[\begin{equation} \hat{\bar{Y}}_{SRS} = \bar{y} \tag{2.7} \end{equation}\]

Hence, the population total \(Y = N\bar{Y}\) is estimated by: \[\begin{equation} \hat{Y}_{SRS} = N\bar{y} \tag{2.8} \end{equation}\]

Result 1: The sample mean \(\bar{y}\) is an unbiased estimator of the population mean \(\bar{Y}\)

Proof: \[E\left(\bar{y}\right) = \sum_{s \in \mathcal S} Pr\left(S=s\right) \displaystyle{\frac{\sum_{i \in s} y_i}{n}} = \displaystyle{\frac{1}{n\binom{N}{n}}}\sum_{s \in \mathcal S} \displaystyle{\sum_{i \in s} y_i}= \displaystyle{\frac{\binom{N-1}{n-1}}{n\binom{N}{n}}}\displaystyle{\sum_{i \in U} y_i} = \bar{Y}\]

Result 2: The variance of \(\bar{y}\) is given by: \[\begin{equation} V\left(\bar{y}\right) = \left(1-\frac{n}{N}\right)\frac{S^2_y}{n} = \left(1-f\right)\frac{S^2_y}{n} \tag{2.9} \end{equation}\]

where

• \(S^2_y\) is the dispersion of the study variable \(y\) over the population \(U\): \(S^2_y = \frac{1}{N-1}\sum_{i \in U} \left(y_i - \bar{Y}\right)^2\)
• \(f=n/N\) is the sampling rate or sampling fraction
• \(1-f=1-n/N\) is the finite population correction factor

Proof:

\(E\left(\bar{y}^2\right) = \sum_{s \in \mathcal S} Pr\left(S=s\right) \displaystyle{\left(\frac{\sum_{i \in s} y_i}{n}\right)^2} = \displaystyle{\frac{1}{n^2\binom{N}{n}}}\sum_{s \in \mathcal S} \displaystyle{\left(\sum_{i \in s} y_i\right)^2}\)

\(= \displaystyle{\frac{1}{n^2\binom{N}{n}}}\sum_{s \in \mathcal S} \displaystyle{\sum_{i \in s} y^2_i}+ \displaystyle{\frac{1}{n^2\binom{N}{n}}}\sum_{s \in \mathcal S} \displaystyle{\sum_{i \in s , j \in s j \neq i} y_i y_j}\)

\(= \displaystyle{\frac{\binom{N-1}{n-1}}{n^2\binom{N}{n}}}\displaystyle{\sum_{i \in U} y^2_i}+ \displaystyle{\frac{\binom{N-2}{n-2}}{n^2\binom{N}{n}}} \displaystyle{\sum_{i \in U , j \in U j \neq i} y_i y_j}\)

\(= \displaystyle{\frac{1}{nN}}\displaystyle{\sum_{i \in U} y^2_i}+ \displaystyle{\frac{\left(n-1\right)}{nN\left(N-1\right)}} \left[ \displaystyle{\left(\sum_{i \in U} y_i\right)^2 - \sum_{i \in U} y^2_i} \right]\)

\(= \displaystyle{\frac{1}{nN}\left(1-\frac{n-1}{N-1}\right)\sum_{i \in U} y^2_i + \frac{N^2\left(n-1\right)}{nN\left(N-1\right)} \left(\frac{\sum_{i \in U} y_i}{N}\right)^2}\)

Hence the variance of \(\bar{y}\) is:

\(V\left(\bar{y}\right) = E\left(\bar{y}^2\right) - \bar{Y}^2 = \displaystyle{\frac{1}{nN}\frac{N-n}{N-1}}\displaystyle{\sum_{i \in U} y^2_i} \displaystyle{-\left[1-\frac{N\left(n-1\right)}{n\left(N-1\right)}\right]\bar{Y}^2}\)

\(=\displaystyle{\frac{1}{n}\frac{N-n}{N-1}\left(\frac{1}{N}\sum_{i \in U} y^2_i - \bar{Y}^2\right) = \frac{1}{n}\frac{N-n}{N}S^2_y = \frac{1-f}{n}S^2_y}\)

Result 3: The variance of the estimator \(\hat{Y}_{SRS} = N\bar{y}\) is: \[\begin{equation} V\left(\hat{Y}_{SRS}\right) = N^2\left(1-f\right)\frac{S^2_y}{n} \tag{2.10} \end{equation}\]

Result 4: An unbiased estimator of the variance of \(\bar{y}\) is: \[\begin{equation} \hat{V}\left(\bar{y}\right) = \left(1-f\right)\frac{s^2_y}{n} \tag{2.11} \end{equation}\]

where \(s^2_y\) is the dispersion of the study variable \(y\) over the sample values: \(s^2_y = \frac{1}{n-1}\sum_{i \in s} \left(y_i - \bar{y}\right)^2\).

Proof: Through expanding the sample dispersion, we have: \[\begin{equation} \begin{array}{rcl} s^2_y & = & \displaystyle{\frac{1}{n-1}\sum_{i \in s} \left(y_i - \bar{y}\right)^2} \\ & = & \displaystyle{\frac{1}{n-1}\sum_{i \in s} \left(y^2_i - 2 y_i \bar{y} + \bar{y}^2\right)} \\ & = & \displaystyle{\frac{1}{n-1}\sum_{i \in s} y^2_i} - 2 \displaystyle{\frac{1}{n-1} \left(\sum_{i \in s} y_i\right) \bar{y}} + \displaystyle{\frac{n}{n-1}\bar{y}^2} \\ & = & \displaystyle{\frac{n}{n-1}\frac{1}{n}\sum_{i \in s} y^2_i} - \displaystyle{\frac{n}{n-1}\bar{y}^2} \end{array} \end{equation}\]

By taking the expectation of the previous expression, and by using (2.9), we obtain the following:

\[\begin{equation} \begin{array}{rcl} E\left(s^2_y\right) & = & \displaystyle{\frac{n}{n-1}\frac{1}{N}\sum_{i \in U} y^2_i} - \displaystyle{\frac{n}{n-1}E\left(\bar{y}^2\right)} \\ & = & \displaystyle{\frac{n}{n-1}\frac{1}{N}\sum_{i \in U} y^2_i} - \displaystyle{\frac{n}{n-1}\left[V\left(\bar{y}\right) + E^2\left(\bar{y}\right) \right]} \\ & = & \displaystyle{\frac{n}{n-1}\left(\frac{1}{N}\sum_{i \in U} y^2_i - \bar{Y}^2\right)}- \displaystyle{\frac{n}{n-1}\left[\left(1-f\right)\frac{S_y^2}{n}\right]} \\ & = & \displaystyle{\frac{n}{n-1}\frac{N-1}{N}S_y^2} - \displaystyle{\frac{n}{n-1}\left[\left(1-f\right)\frac{S_y^2}{n}\right]} \\ & = & \displaystyle{S_y^2~\frac{n}{n-1}\left[\frac{N-1}{N}-\left(1-f\right)\frac{1}{n}\right]} \\ & = & \displaystyle{S_y^2~\frac{n}{n-1}\left[\frac{N-1}{N}-\frac{N-n}{Nn}\right]} = S^2_y \end{array} \end{equation}\]

The main lessons to be drawn from (2.9), (2.10) and (2.11) are as follows:

• The variance is directly related to the size \(n\) of the sample: the larger the size, the smaller the variance.
• The variance depends on the dispersion \(S^2_y\) of the study variable: given the sample size, the smaller the dispersion \(S^2_y\), the smaller the variance.
• Since the finite population factor \(1-f \approx 1\), the effect of the population size \(N\) on the variance is often negligible⁹. This means that interviewing 1,000 individuals from a population of 600,000 (such as Luxembourg) will produce results that are as statistically accurate as interviewing the same number of individuals from a population of over 1 billion people (such as China)¹⁰.

2.4 Estimating population counts and proportions

A typical category of population parameter that one might wish to estimate is the size of a sub-population of interest. For example, we may wish to estimate the total number of males/females in a population, the number of elderly people aged over 65, or the total number of establishments with more than 50 employees in a particular geographical region or industry.

By introducing the dummy membership variables, the size \(N_A\) of a subpopulation \(U_A \subseteq U\) is actually a particular example of a population total over the whole population \(U\). Further, assuming that the size \(N\) of the population \(U\) is known, the proportion \(P_A = N_A/N\) of \(U_A\) is a particular case of a mean:

• \(N_A = \sum_{k \in U_A} 1 = \sum_{k \in U} 1^A_k\)
• \(P_A = \left(1/N\right) \sum_{k \in U_A} 1 = \sum_{k \in U} \left(1^A_k / N\right)\)

where \(1^A_k = \begin{cases} 1 & \text{if $k \in U_A$}\\ 0 & \text{otherwise.} \end{cases}\). Hence, by using the results from the previous section, we obtain the following:

Result 1: The size \(N_A\) of \(U_A\) is estimated by: \[\begin{equation} \hat{N}_A = N p_A \tag{2.12} \end{equation}\]

where \(p_A\) is the sample proportion of units from \(U_A\)

Result 2: Assuming the size \(N\) of the population is large enough and the sampling fraction is close to 0, the variance of the estimator \(N p_A\) is given by:

\[\begin{equation} \begin{array}{lcl} V\left(N p_A\right) & = & N^2\left(1-f\right){\displaystyle \frac{N}{N-1}} {\displaystyle \frac{P_A\left(1-P_A\right)}{n}} \\ & \approx & N^2{\displaystyle \frac{P_A\left(1-P_A\right)}{n}} \\ \end{array} \tag{2.13} \end{equation}\]

Proof: The dispersion of the dummy variable \(1^A\) is given by: \[\begin{equation} \begin{array}{rcl} S^2 & = & \displaystyle{\frac{1}{N-1} \sum_{i \in U} \left(1_i^A - P_A\right)^2} \\ & = & \displaystyle{\frac{1}{N-1} \left[\sum_{i \in U_A} \left(1 - P_A\right)^2 +\sum_{i \notin U_A} \left(0 - P_A\right)^2 \right]} \\ & = & \displaystyle{\frac{1}{N-1} \left[ NP_A\left(1 - P_A\right)^2 + \left(N-NP_A\right) P^2_A \right]} \\ & = & \displaystyle{\frac{N}{N-1} P_A\left(1 - P_A\right) \left(1-P_A+P_A\right)} \\ & = & \displaystyle{\frac{N}{N-1} P_A\left(1 - P_A\right)} \end{array} \end{equation}\]

Result 3: The variance of the estimated proportion \(p_A\) is given by: \[\begin{equation} V\left(p_A\right) \approx \frac{P_A\left(1-P_A\right)}{n} \tag{2.14} \end{equation}\]

Result 4: The variance of \(p_A\) is estimated by: \[\begin{equation} \hat{V}\left(p_A\right) = \frac{p_A\left(1-p_A\right)}{n} \tag{2.15} \end{equation}\]

2.5 Domain estimation

Domain estimation refers to the estimation of population parameters for subpopulations of interest, called domains. For example, one might want to estimate average household disposable income broken down by personal characteristics such as age, gender, or nationality. In the case of business surveys, we may want to compare company profits or IT investments across industries or company sizes.

By introducing dummy membership variables the total \(Y_D\) of a study variable \(y\) over a domain \(U_D \subseteq U\) of size \(N_D \leq N\) is a particular example of a total for the whole population \(U\):

• \(Y_D = \sum_{k \in U_D} y_k = \sum_{k \in U} y_k 1^D_k = \sum_{k \in U} z^D_k\)
• \(\hat{Y}_D = \left(N/n\right) \sum_{k \in s} z^D_k = \left(N/n\right) \sum_{k \in s \cap U_D} y_k = \left(Nn_D/n\right) \bar{y}_D\)

where \(\bar{y}_D\) is the mean of \(y\) within the domain \(U_D\) and \(n_D\) is the total number of sample units falling into the domain \(U_D\). The sample size \(n_D\) is a random variable of mean \(\bar{n}_D = n P_D\), where \(P_D = N_D / N\).

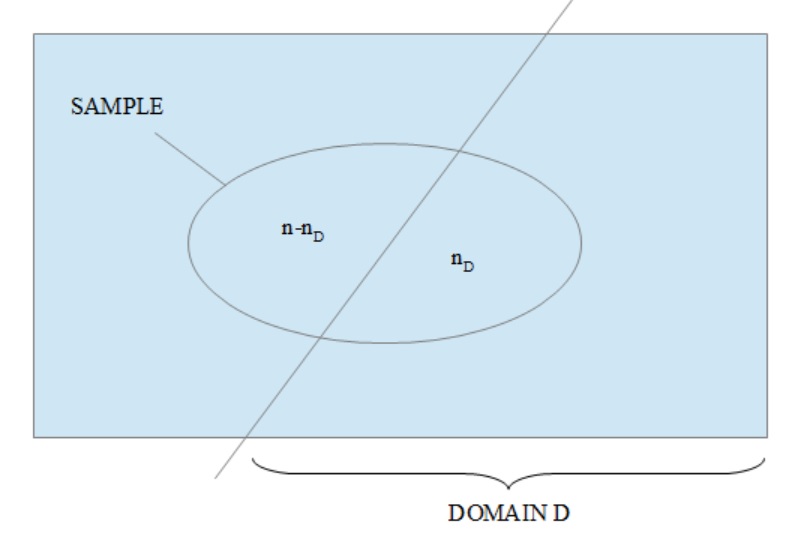
Figure 2.1: Domain estimation

Thus \(\hat{Y}_D = \left(Nn_D/n\right) \bar{y}_D = \hat{N}_D \bar{y}_D\) is an unbiased estimator of the total \(Y_D\), where \(\hat{N}_D = \left(Nn_D/n\right)\) is the estimated size of the domain. \(\hat{N}_D\) is generally random.

However, when the size \(N_D\) of \(U_D\) is known, we can use the following formula as an alternative to \(\hat{Y}_D\): \[\begin{equation} \hat{Y}_{D,alt} = N_D \bar{y}_D \tag{2.16} \end{equation}\]

Using the main results for simple random sampling, we obtain the following:

• Result 1: Assuming the population sizes \(N\) and \(N_D\) are large enough, the variance of the domain estimator \(\hat{Y}_D\) is given by: \[\begin{equation} V\left(\hat{Y}_D\right) \approx N^2_D \left(1/\bar{n}_D-1/N_D\right)S_D^2\left(1 + \frac{1-P_D}{CV^2_D}\right) \tag{2.17} \end{equation}\]

where:

\(S_D^2 = \sum_{k \in U_D} \left(y_k - \bar{Y}_D\right)^2 / \left(N_D-1\right)\)

\(CV_D = S_D / \bar{Y}_D\)

• Result 2: Assuming the sample size \(n_D\) is large enough, the variance of \(\hat{Y}_{D,alt}\) is given by: \[\begin{equation} V\left(\hat{Y}_{D,alt}\right) \approx N^2_D \left(1/\bar{n}_D-1/N_D\right)S_D^2 \tag{2.18} \end{equation}\]

• Result 3: The variance of \(\hat{Y}_{D,alt}\) is lower than that of \(\hat{Y}_{D}\): \[\begin{equation} \begin{array}{lcl} V\left(\hat{Y}_{D,alt}\right) / V\left(\hat{Y}_D\right) & \approx & 1 / \left(1 + {\displaystyle \frac{1-P_D}{CV^2_D}}\right) \\ & = & CV^2_D / \left(CV^2_D + Q_D\right) \end{array} \tag{2.19} \end{equation}\]

where \(Q_D = 1 - P_D\).

This ratio accounts for the additional variability introduced by the fact that the domain size \(N_D\) is generally random and unknown in advance.

---

9. Though correct in case of household or individual samples, this assumption may be violated in case of business samples, where the population size may happen to be small in certain specific sectors of activity↩︎

10. This result only relates to sampling errors and assumes all other things being equal. However, the magnitude of non-sampling errors is expected to be higher in China than in Luxembourg↩︎