8 Series Temporales

8.1 Introducción

El presente epígrafe pretende ser una breve introducción al estudio de las series temporales, las cuales poseen una gran importancia en el campo de la Economía dada la abundancia de este tipo de observaciones; de hecho, las series temporales constituyen la mayor parte del material estadístico con el que trabajan los economistas.

Pero, ¿qué es una serie temporal? Por definición, una serie temporal es una sucesión de observaciones de una variable realizadas a intervalos regulares de tiempo. Según realicemos la medida de la variable considerada podemos distinguir distintos tipos de series temporales:

Discretas o Continuas, en base al intervalo de tiempo considerado para su medición.
Flujo o Stock. En Economía, se dice que una serie de datos es de tipo flujo si está referida a un período determinado de tiempo (un día, un mes, un año, etc.). Por su parte, se dice que una serie de datos es de tipo stock si está referida a una fecha determinada (por ejemplo, el 31 de Diciembre de cada año). Un ejemplo de datos de tipo flujo serían las ventas de una empresa ya que éstas tendrán un valor distinto si se obtiene el dato al cabo de una semana, un mes ó un año; por su parte, la cotización de cierre de las acciones de esa misma empresa sería una variable de tipo stock, ya que sólo puede ser registrado a una fecha y hora determinadas. Obsérvese que existe relación entre ambos tipos de variables, pues la cotización al cierre de las acciones no es más que el precio de cierre del día anterior más, o menos, el flujo de precios de la sesión considerada.
Dependiendo de la unidad de medida, podemos encontrar series temporales en euros o en diversas magnitudes físicas (kilogramos, litros, millas, etc.)
En base a la periodicidad de los datos, podemos distinguir series temporales de datos diarios, semanales, mensuales, trimestrales, anuales, etc.

Antes de profundizar en el análisis de las series temporales es necesario señalar que, para llevarlo a cabo, hay que tener en cuenta los siguientes supuestos:

Se considera que existe una cierta estabilidad en la estructura del fenómeno estudiado. Para que se cumpla este supuesto será necesario estudiar períodos lo más homogéneos posibles.
Los datos deben ser homogéneos en el tiempo, o lo que es lo mismo, se debe mantener la definición y la medición de la magnitud objeto de estudio. Este supuesto no se da en muchas de las series económicas, ya que es frecuente que las estadísticas se perfeccionen con el paso del tiempo, produciéndose saltos en la serie debidos a un cambio en la medición de la magnitud estudiada. Un caso particularmente frecuente es el cambio de base en los índices de precios, de producción, etc. Tales cambios de base implican cambios en los productos y las ponderaciones que entran en la elaboración del índice que repercuten considerablemente en la comparabilidad de la serie en el tiempo.

El objetivo fundamental del estudio de las series temporales es el conocimiento del comportamiento de una variable a través del tiempo para, a partir de dicho conocimiento, y bajo el supuesto de que no van a producirse cambios estructurales, poder realizar predicciones, es decir, determinar qué valor tomará la variable objeto de estudio en uno o más períodos de tiempo situados en el futuro, mediante la aplicación de un determinado modelo calculado previamente.

Dado que en la mayor parte de los problemas económicos, los agentes se enfrentan a una toma de decisiones bajo un contexto de incertidumbre, la predicción de una variable reviste una importancia notoria pues supone, para el agente que la realiza, una reducción de la incertidumbre y, por ende, una mejora de sus resultados.

Las técnicas de predicción basadas en series temporales se pueden agrupar en dos grandes bloques:

Métodos cualitativos, en los que el pasado no proporciona una información directa sobre el fenómeno considerado, como ocurre con la aparición de nuevos productos en el mercado. Así, por ejemplo, si se pretende efectuar un estudio del comportamiento de una acción en Bolsa, y la sociedad acaba de salir a cotizar al mercado, no se puede acudir a la información del pasado ya que ésta no existe.
Métodos cuantitativos, en los que se extrae toda la información posible contenida en los datos y, en base al patrón de conducta seguida en el pasado, realizar predicciones sobre el futuro.

Indudablemente, la calidad de las previsiones realizadas dependerán, en buena medida, del proceso generador de la serie: así, si la variable observada sigue algún tipo de esquema o patrón de comportamiento más o menos fijo (serie determinista) seguramente obtengamos predicciones más o menos fiables, con un grado de error bajo. Por el contrario, si la serie no sigue ningún patrón de comportamiento específico (serie aleatoria), seguramente nuestras predicciones carecerán de validez por completo.

Generalmente, en el caso de las series económicas no existen variables deterministas o aleatorias puras, sino que contienen ambos tipos de elementos. El propósito de los métodos de previsión cuantitativos es conocer los componentes subyacentes de una serie y su forma de integración, con objeto de realizar predicciones de su evolución futura.

Dentro de los métodos de predicción cuantitativos, se pueden distinguir dos grandes enfoques alternativos:

Por un lado, el análisis univariante de series temporales mediante el cual se intenta realizar previsiones de valores futuros de una variable, utilizando como información la contenida en los valores pasados de la propia serie temporal. Dentro de esta metodología se incluyen los métodos de descomposición y la familia de modelos ARIMA univariantes que veremos más adelante.
El otro gran bloque dentro de los métodos cuantitativos estaría integrado por el análisis multivariante o de tipo causal, denominado así porque en la explicación de la variable o variables objeto de estudio intervienen otras adicionales a ella o ellas mismas.

En el tratamiento de series temporales que vamos a abordar, únicamente se considerará la información presente y pasada de la variable investigada. Si la variable investigada es $Y$ y se dispone de los valores que toma dicha variable desde el momento 1 hasta $T$, el conjunto de información disponible vendrá dado por: $Y_1, Y_2, Y_3, …, Y_{T-1}, Y_T$.

Dada esa información, la predicción de la variable $Y$ para el período $T+1$ la podemos expresar como $\hat Y_{T+1/T}$.

Con esta notación queremos indicar que la predicción para el periodo $T+1$ se hace condicionada a la información disponible en el momento $T$. El acento circunflejo sobre la Y nos indica que esa predicción se ha obtenido a partir de un modelo estimado. Conviene también hacer notar que $T+1$ significa que se está haciendo la predicción para un período hacia delante, es decir, con la información disponible en t hacemos una predicción para el período siguiente.

Análogamente, la predicción para el período $T+2$ y para el período $T+m$, con la información disponible en $T$, vendrá dada, respectivamente, por $\hat Y_{T+2/T},...,\hat Y_{T+m/T}$, que serán predicciones de 2 y m períodos hacia adelante.

Si, genéricamente, para el período t se efectúa una predicción con la información disponible en t–1, y a la que designamos por $\hat Y_{t/t-1}$, para el período t podemos hacer una comparación de este valor con el que realmente observemos ($Y_t$). La diferencia entre ambos valores será el error de predicción de un período hacia adelante y vendrá dado por:

\[e_{t/t-1}=Y_t-\hat Y_{t/t-1}\]

Cuando un fenómeno es determinista y se conoce la ley que lo determina, las predicciones son exactas, verificándose que $e_{t/t-1}=0$. Por el contrario, si el fenómeno es poco sistemático o el modelo es inadecuado, entonces los errores de predicción que se vayan obteniendo serán grandes.

Para cuantificar globalmente los errores de predicción se utilizan los siguientes estadísticos: la Raíz del Error Cuadrático Medio (RECM) y el Error Absoluto Medio (EAM).

En el caso de que se disponga de $T$ observaciones y se hayan hecho predicciones a partir de la observación 2, las fórmulas para la obtención de la RECM y el EAM son las siguientes:

\[RECM=\sqrt{\frac{\sum_{t=2}^T (Y_t-\hat Y_{t/t-1})^2}{T-1}}\]

\[EAM=\frac{\sum_{t=2}^T (Y_t-\hat Y_{t/t-1})^2}{T-1}\]

De forma análoga, se pueden aplicar la RECM y el EAM en predicciones de $2, 3, …, m$ períodos hacia adelante.

En el análisis de series temporales se aplican, en general, métodos alternativos a unos mismos datos, seleccionando aquel modelo o aquel método que, en la predicción de períodos presentes y pasados, arroje errores de predicción menores, es decir, arroje una RECM o un EAM menor.

En R “ts” es la función genérica para que los datos tengan forma de serie temporal. Su sintaxis es la siguiente:

ts(data = NA, start = 1, end = numeric(), frequency = 1, deltat = 1, ts.eps = getOption(“ts.eps”), class = , names = )

De esta sintaxis hay que tener presentes los siguiente argumentos:

data: Vector, “data frame” o matriz de datos.
start: Referencia de la primera observacion, es un vector con dos valores numéricos, el primero relativo al año y el segundo relativo al trimestre y mes de inicio (1 para el primer trimestre y 1 para enero en series de datos mensuales).
end: Referencia de la ultima observación.
frequency: Número de observaciones por año (4 en series trimestrales, 12 en series mensuales).

Un ejemplo de elaboración de un objeto “ts” es el siguiente:

ts(1:10, frequency = 4, start = c(1959, 2)) # 2º trimestre de 1959

##      Qtr1 Qtr2 Qtr3 Qtr4
## 1959         1    2    3
## 1960    4    5    6    7
## 1961    8    9   10

8.2 Métodos de suavizado

8.2.1 Médias móviles

En el análisis de series temporales, el método de medias móviles tiene diversas aplicaciones: así, este método puede sernos útil si queremos calcular la tendencia de una serie temporal sin tener que ajustarnos a una función previa, ofreciendo así una visión suavizada o alisada de una serie, ya que promediando varios valores se elimina parte de los movimientos irregulares de la serie; también puede servirnos para realizar predicciones cuando la tendencia de la serie tiene una media constante.

Veamos qué es una media móvil: se trata, sencillamente de una media aritmética que se caracteriza porque toma un valor para cada momento del tiempo y porque en su cálculo no entran todas las observaciones de la muestra disponible.

Entre los distintos tipos de medias móviles que se pueden construir nos vamos a referir a dos tipos: medias móviles centradas y medias móviles asimétricas. El primer tipo se utiliza para la representación de la tendencia, mientras que el segundo lo aplicaremos para la predicción en modelos con media constante.

Las medias móviles centradas se caracterizan porque el número de observaciones que entran en su cálculo es impar, asignándose cada media móvil a la observación central. Así, una media móvil centrada en $t$ de longitud $2n + 1$ viene dada por la siguiente expresión:

\[MM(2n+1)_t=\frac{Y_{t-n}+Y_{t-n+1}+...+Y_t+...+Y_{t+n-1}+Y_{t+n}}{2n+1}\]

Como puede observarse, el subíndice asignado a la media móvil, $t$, es el mismo que el de la observación central, $Y_t$. Obsérvese también que, por construcción, no se pueden calcular las medias móviles correspondientes a las $n$ primeras y a las $n$ últimas observaciones.

Por su parte, en el caso de las medias móviles asimétricas (no centradas) se asigna cada media móvil al período correspondiente a la observación más adelantada de todas las que intervienen en su cálculo. Así, la media móvil asimétrica de $n$ puntos asociada a la observación $t$ tendrá la siguiente expresión:

\[MMA(n)_t=\frac{Y_{t-n+1}+Y_{t-n+2}+...+Y_{t-1}+Y_{t}}{n}\]

La utilización de medias móviles implica la elección arbitraria de su longitud u orden, es decir, del número de observaciones que intervienen en el cálculo de cada media móvil. Cuanto mayor sea la longitud, mejor se eliminarán las irregularidades de la serie, ya que al intervenir más observaciones en su cálculo se compensarán las fluctuaciones de este tipo, pero por el contrario, el coste informativo será mayor. Por el contrario, cuando la longitud es pequeña, la media móvil refleja con mayor rapidez los cambios que puedan producirse en la evolución de la serie. Es conveniente, pues, sopesar estos factores al decidir la longitud de la media móvil.

Con datos trimestrales de la tasa de desempleo de Canada, representamos una tasa movil de cuatro periodos centrada y no centrada. La función R que genera medias móviles es “rollMean”, en “align = c(”center“,”left“,”right“)”, se elige como alinear la media, en su defecto calcula medias móviles centradas.

library(vars)

## Loading required package: strucchange

## Loading required package: urca

data("Canada")
str(Canada)

##  Time-Series [1:84, 1:4] from 1980 to 2001: 930 930 930 931 933 ...
##  - attr(*, "dimnames")=List of 2
##   ..$ : NULL
##   ..$ : chr [1:4] "e" "prod" "rw" "U"

plot(Canada[, "U"], main='Desempleo', xlab='Mes/Año', ylab='Tasa')
lines(rollmean(Canada[, "U"], 4), col="red", lwd=2)
lines(rollmean(Canada[, "U"], 4,align="right"), col="blue", lwd=2)
legend("bottomleft", c("Original", "Media móvil centrada",
   "Media móvil no centrada"),
   lwd=c(1,2,2), col=c("black", "red", "blue"))
grid()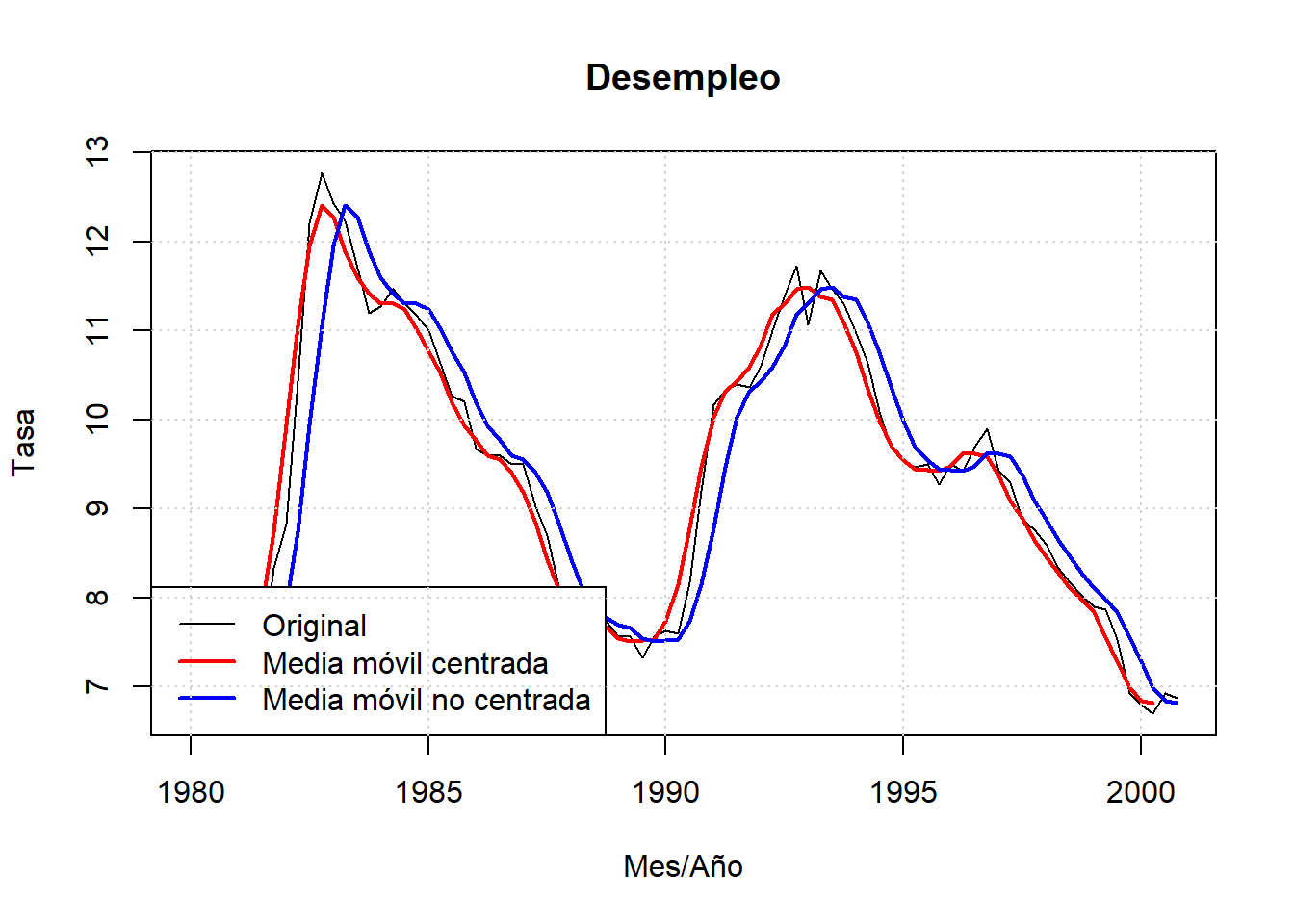

La función R filter() tambien permite calcular medias móviles.

#Medias Móviles
#Alisado MA centrados
alisado1 = filter(Canada[, "U"], rep(1,4)/4, side=2)
#Alisado MA no centrados
alisado2 = filter(Canada[, "U"], rep(1,4)/4, side=1)
#Hacemos la gráfica para comparar
plot.ts(Canada[, "U"],main="Desempleo",xlab="Tiempo",ylab="Tasa")
lines(alisado1, col="red")
lines(alisado2, col="blue")
legend("bottomleft", c("Original", "Media móvil centrada",
   "Media móvil no centrada"),
   lwd=c(1,2,2), col=c("black", "red", "blue"))
grid()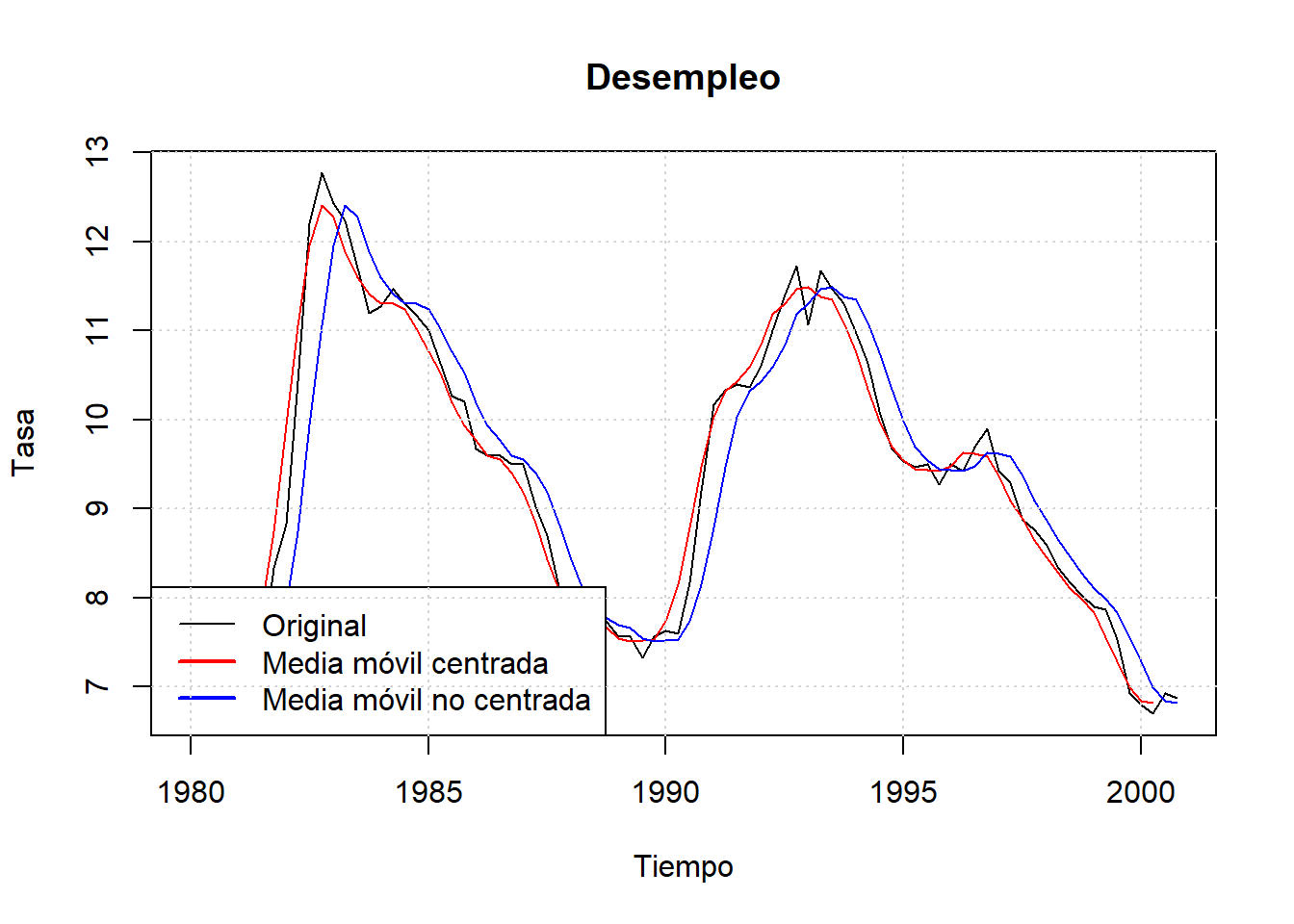

8.2.2 Alisado Exponencial Simple

El método del alisado exponencial simple consiste, al igual que en el caso de las medias móviles, en una transformación de la variable original. Si una variable $Y_t$ es sometida a un proceso de alisado exponencial simple se obtiene como resultado la variable alisada $S_t$. Teóricamente, la variable alisada $S_t$ se obtendría según la expresión:

\[S_t = (1 – w) Y_t + (1 – w) wY_{t-1}+ (1-w) w^2 Y_{t-2} + (1 – w) w^3 Y_{t-3} +...\ \ \ \ \ \ (1)\]

donde $w$ es un parámetro que toma valores comprendidos entre 0 y 1, y los puntos suspensivos indican que el número de términos de la variable alisada puede ser infinito. La expresión anterior en realidad no es más que una media aritmética ponderada de infinitos valores de $Y$.

Se denomina alisada ya que suaviza o alisa las oscilaciones que tiene la serie, al obtenerse como una media ponderada de distintos valores. Por otra parte, el calificativo de exponencial se debe a que la ponderación o peso de las observaciones decrece exponencialmente a medida que nos alejamos del momento actual $t$. Esto quiere decir que las observaciones que están alejadas tienen muy poca incidencia en el valor que toma $S_t$. Finalmente, el calificativo de simple se aplica para distinguirla de otros casos en que, como veremos más adelante, una variable se somete a una doble operación de alisado.

Una vez que se han visto estos aspectos conceptuales, vamos a proceder a la obtención operativa de la variable alisada, ya que la expresión no es directamente aplicable por contener infinitos términos. Retardando un período en la expresión anterior se tiene que:

\[S_{t-1} = (1 – w) Y_{t-1} + (1 – w) wY_{t-2} + (1-w) w^2 Y_{t-3} +...\]

Multiplicando ambos miembros por $w$ se obtiene:

\[wS_{t-1} = (1 – w) wY_{t-1} + (1 – w) w^2 Y_{t-2} + (1 – w) w^3 Y_{t-3} + ...\ \ \ \ \ \ (2)\]

Restando (1) de (2) miembro a miembro y ordenando los términos se tiene que:

\[S_t = (1 - w) Y_t + wS_{t-1}\]

O también:

\[S_t = \alpha Y_t + (1 - \alpha) S_{t-1} \ \ \ \ \ \ \ \ \ \ \ \ \ \ )\]

donde $\alpha = 1 – w$.

Ahora ya sólo nos falta calcular los valores de $\alpha$ y $S_0$, parámetros a partir de los cuales resulta sencillo hallar los valores de la variable alisada de manera recursiva, tal que:

\[S_1 = \alpha Y_1 + (1 - \alpha) S_0\] \[S_2 = \alpha Y_2 + (1 - \alpha) S_1\] \[S_3 = \alpha Y_3 + (1 - \alpha) S_2\] \[...\]

Al asignar un valor a $\alpha$ hay que tener en cuenta que un valor pequeño de $\alpha$ significa que estamos dando mucho peso a las observaciones pasadas a través del término $S_{t-1}$. Por el contrario, cuando $\alpha$ es grande se da más importancia a la observación actual de la variable $Y$. En general, parece que un valor de $\alpha$ igual a $0.2$ es apropiado en la mayor parte de los casos. Alternativamente, se puede seleccionar aquel valor de $\alpha$ para el que se obtenga una Raíz del Error Cuadrático Medio menor en la predicción del período muestral.

Respecto a la asignación de valor a $S_0$, se suelen hacer estos supuestos: cuando la serie tiene muchas oscilaciones se toma $S_0 = Y_1$; por el contrario, cuando la serie tiene una cierta estabilidad, se hace $S_0 = \bar Y$.

8.2.3 Método de Holt-Winters

El método de Holt-Winters es una técnica de suavizado que utiliza un conjunto de estimaciones recursivas a partir de la serie histórica. Estas estimaciones utilizan una constante de nivel, $\alpha$, una constante de tendencia, $\beta$, y una constante estacional multiplicativa, $\gamma$.

Las estimaciones recursivas se basan en las siguientes ecuaciones:

\[\hat Y_t=\alpha(\hat Y_{t-1}-T_{t-1})+(1-\alpha)\frac{Y_t}{F_{t-s}}\ \ \ 0< \alpha <1\]

\[T_t=\beta T_{t-1}+(1-\beta)(\hat Y_{t}-\hat Y_{t-1})\ \ \ 0< \beta <1\]

\[F_t=\gamma F_{t-s}+(1-\gamma)\frac{Y_t}{\hat Y_{t}}\ \ \ 0< \gamma <1\]

donde $s=4$ en el caso de datos trimestrales y $s=12$ en el caso de datos mensuales. $\hat Y_t$ sería el nivel suavizado de la serie, $T_t$ la tendencia suavizada de la serie y $F_t$ el ajuste estacional suavizado de la serie.

Utilizando el programa R se va a desarrollar un alisado exponencial doble, para lo cual hay que invocar la función “HoltWinters”, que tiene la siguiente estructura:

HoltWinters(x, alpha = NULL, beta = NULL, gamma = NULL, seasonal = c(“additive”,multiplicative“), start.periods = 2, l.start = NULL, b.start = NULL, s.start = NULL, optim.start = c(alpha = 0.3, beta = 0.1, gamma = 0.1), optim.control = list())

Hay que tener presente que “x” es el conjunto de datos, alpha, beta y gamma, son las constantes $\alpha$, $\beta$ y $\gamma$ del sistema de ecuaciones descrito.

Si se desea, la función elige los coeficientes $\alpha$, $\beta$ y $\gamma$ óptimos, en la opción “optim.start”, hay que indicar los valores de partida y la function intenta encontrar el valor óptimo minimizando el RECM en la opción por defecto. Si no se le indican los valores de partida, los encuetra a través de una simple descomposición temporal de la serie utilizando medias móviles.

Utilizando la base de datos CO2 que se obtiene en R, relativa a concentraciones atomosféricas de CO2 en partes por millón (ppm), realizamos un suavizado por el metodo de Holt-Winters en R:

data("co2")
HoltWinters(co2)

## Holt-Winters exponential smoothing with trend and additive seasonal component.
## 
## Call:
## HoltWinters(x = co2)
## 
## Smoothing parameters:
##  alpha: 0.51265
##  beta : 0.0094977
##  gamma: 0.47289
## 
## Coefficients:
##          [,1]
## a   364.76162
## b     0.12474
## s1    0.22153
## s2    0.95528
## s3    1.59847
## s4    2.87580
## s5    3.28201
## s6    2.44070
## s7    0.89694
## s8   -1.37964
## s9   -3.41124
## s10  -3.25702
## s11  -1.91349
## s12  -0.58442

plot(HoltWinters(co2))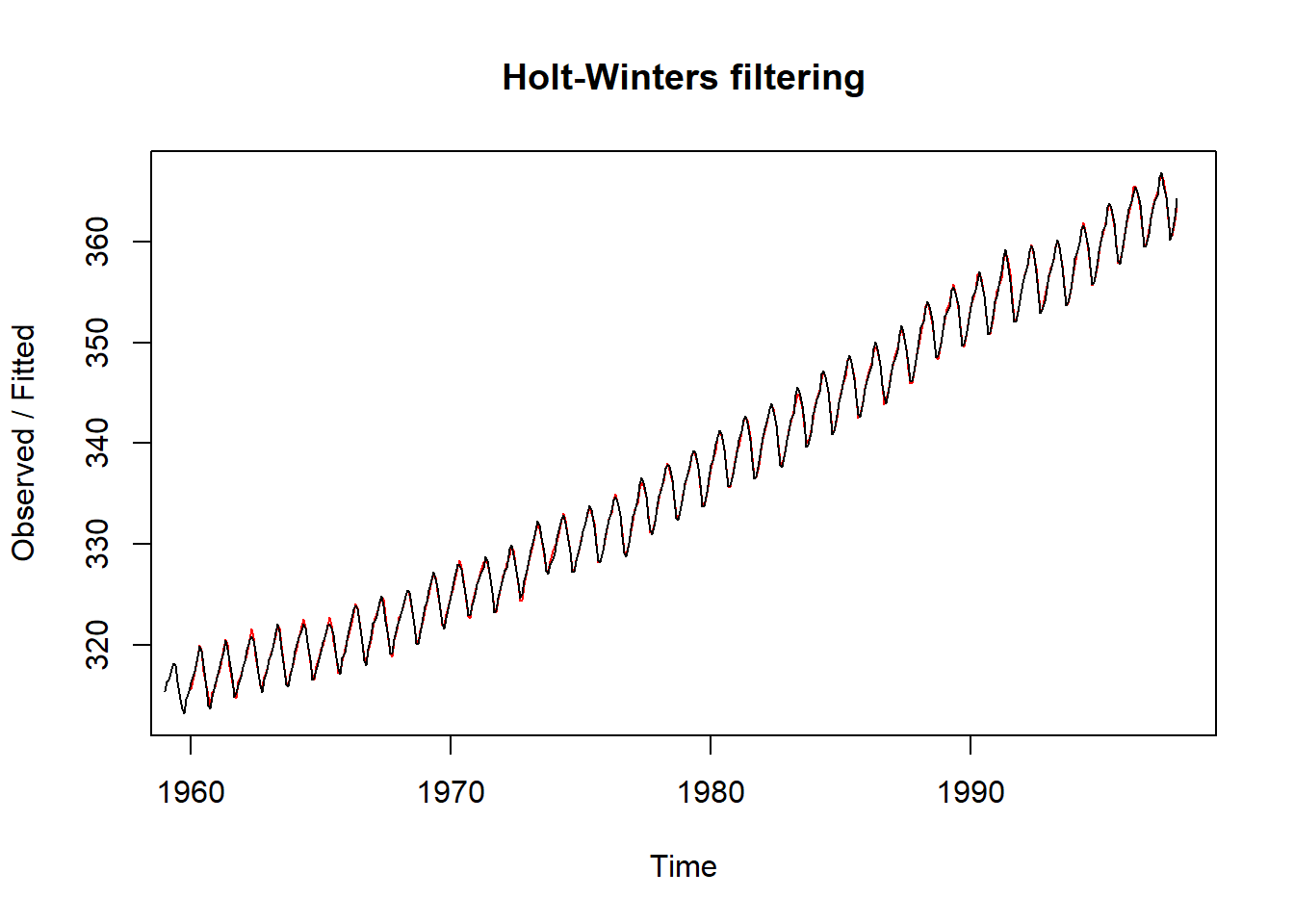

La función HoltWinters, puede ser utilizada para realizar suavizados exponenciales simples, declarando al parámetro beta=FALSE y gamma=FALSE.

HoltWinters(co2,beta=FALSE,gamma=FALSE)

## Holt-Winters exponential smoothing without trend and without seasonal component.
## 
## Call:
## HoltWinters(x = co2, beta = FALSE, gamma = FALSE)
## 
## Smoothing parameters:
##  alpha: 0.99993
##  beta : FALSE
##  gamma: FALSE
## 
## Coefficients:
##     [,1]
## a 364.34

plot(HoltWinters(co2,beta=FALSE,gamma=FALSE))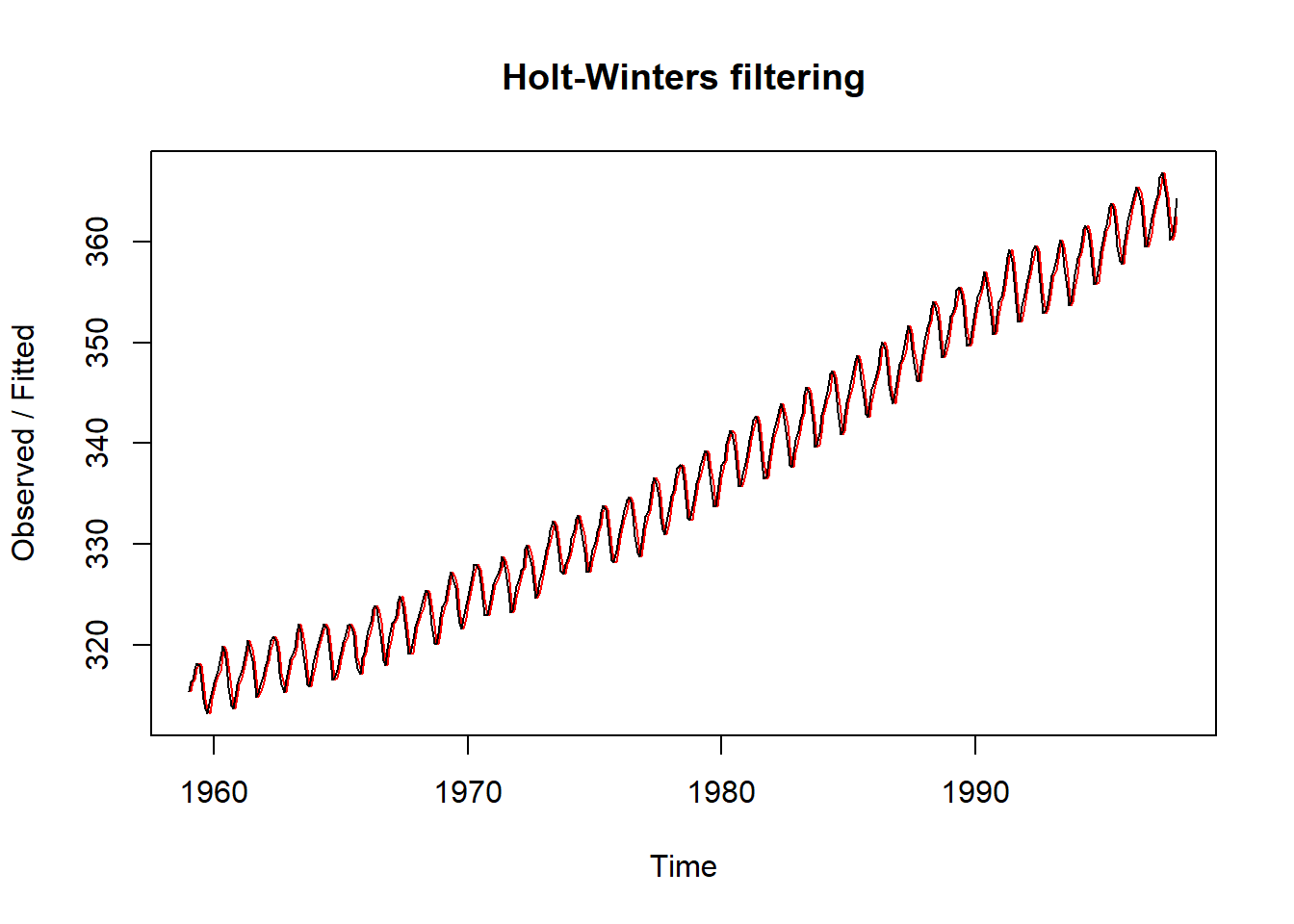

8.3 Descomposición temporal

Tradicionalmente, en los métodos de descomposición de series temporales, se parte de la idea de que la serie temporal se puede descomponer en todos o algunos de los siguientes componentes:

Tendencia (T), que representa la evolución de la serie en el largo plazo
Fluctuación cíclica (C), que refleja las fluctuaciones de carácter periódico, pero no necesariamente regular, a medio plazo en torno a la tendencia. Este componente es frecuente hallarlo en las series económicas, y se debe a los cambios en la actividad económica.

Para la obtención de la tendencia es necesario disponer de una serie larga y de un número de ciclos completo, para que ésta no se vea influida por la fase del ciclo en que finaliza la serie, por lo que, a veces, resulta difícil separar ambos componentes. En estos casos resulta útil englobar ambos componentes en uno solo, denominado ciclo-tendencia o tendencia generalizada.

Variación Estacional (S): recoge aquellos comportamientos de tipo regular y repetitivo que se dan a lo largo de un período de tiempo, generalmente igual o inferior a un año, y que son producidos por factores tales como las variaciones climatológicas, las vacaciones, las fiestas, etc.
Movimientos Irregulares (I), que pueden ser aleatorios, la cual recoge los pequeños efectos accidentales, o erráticos, como resultado de hechos no previsibles, pero identificables a posteriori (huelgas, catástrofes, etc.)

En este punto, cabe señalar que en una serie concreta no tienen por qué darse los cuatro componentes. Así, por ejemplo, una serie con periodicidad anual carece de estacionalidad.

La asociación de estos cuatro componentes en una serie temporal, $Y$, puede responder a distintos esquemas; así, puede ser de tipo aditivo:

\[Y_t=T_t+C_t+S_t+e_t\]

También puede tener una forma multiplicativa:

\[Y_t=T_tC_tS_te_t\]

O bien ser una combinación de ambos, por ejemplo:

\[Y_t=T_tC_tS_t+e_t\]

En este capítulo se introducen algunas de las herramientas de R para la implementación de la descomposición $Y_t=T_t+S_t+e_t$, y para la estimación de la tendencia $T_t$. Hay que hacer énfasis en que estos métodos no asumen un modelo global para la tendencia, sino local, es decir, no son modelos con parámetros fijos, de la forma, por ejemplo, $T_t=\beta_0+\beta_1t$, sino que $\beta_0$ y $\beta_1$ cambian en el tiempo para permitir mayor flexibilidad.

Las funciones decompose() y stl() realizan una descomposición de la serie $Y_t$ en las tres componentes.
La librería “timsac” incluye la función decomp(), que realiza una descomposición temporal incluyendo una componente autoregresiva $TA_t$ y otra para fechas de intervenciones,$R_t$, $Y_t=T_t+S_t+R_t+TA_t+e_t$.
La librería “descomponer” incluye la función descomponer(), que realiza una descomposición temporal de $Y_t$ transformando las series de tiempo en series de frecuencia.
Hay librerías con varios tipos de filtros para suavizar y extraer los componentes de tendencia y estacionales como “mFilter”, que tiene implementado el filtro Hodrick-Prescott, o la libreria “stats”, que incluye la función filter(), con la que se pueden implementar varios tipos de medias móviles y filtros lineales, por ejemplo, fitros tipo Henderson y filtros recursivos.

La función R “decompose”, obtiene las componentes de tendencia, estacionalidad e irregular de una serie temporal a través de medias móviles, y además permite obtener los componentes en base a un esquema aditivo ó multiplicativo. Es una función generica de R, lo que significa que no requiere de la instalación de ninguna librería. Su uso es el siguiente:

decompose(x, type = c(“additive”, “multiplicative”), filter = NULL)

El modelo aditivo que usa la función es:

\[Y_t = T_t + S_t + e_t\]

Y el multiplicativo:

\[Y_t = T_t S_t e_t\]

La función calcula el componente de tendencia utilizando medias móviles, (si filter = NULL, se utilizan medias móviles simétricas), los índices de estacionalidad son promedios de los indices de estacionalidad que se obtienen al desestacionalizar la serie por el modelo elegido, por último, el componente irregular se obtiene eliminando la tendencia y estacionalidad de la serie temporal.

La función requiere que los datos tengan forma de serie temporal.

A continuación se realiza un sencillo ejercicio de utilización de la función “descomponse”:

plot(decompose(co2))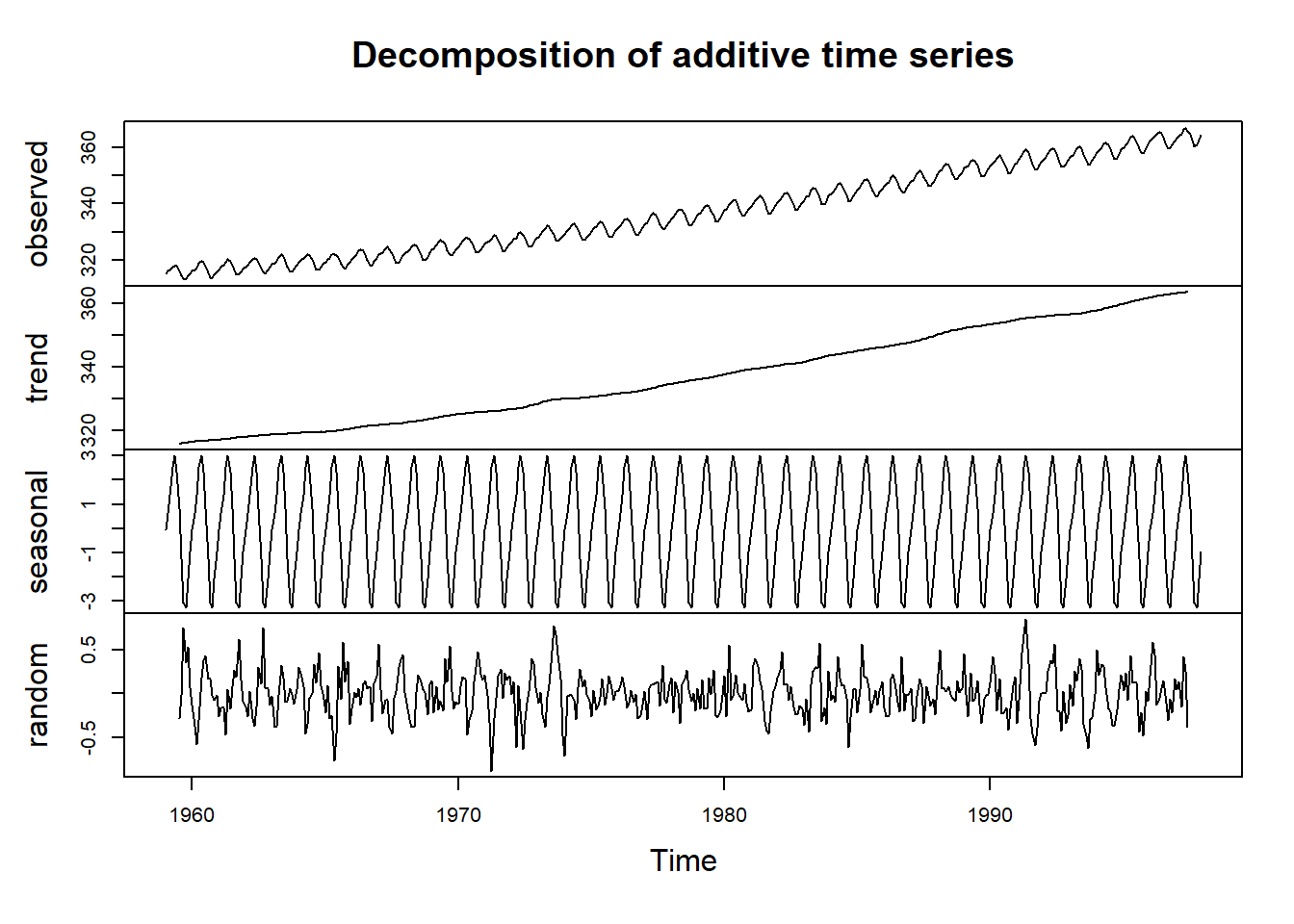

STL es un método para estimar las componentes $T_t$ y $S_t$ con base en Regresión Loess, desarrollado por Cleveland et al. [1990]. STL consiste de una secuencia de dos aplicaciones iteradas de Regresión Loess. Para aplicar este método se debe especificar una frecuencia de muestreo relacionada con el periódo de la componente estacional. La forma de especificar esta frecuencia es declarando la variable en donde se encuentran los datos como un objeto “ts”con frecuencia (52, 12, 4, 1), es decir, semanal, mensual, trimestral o anual, respectivamente.

El ejercicio anterior realizado con la función “stl”.

plot(stl(co2,"per"))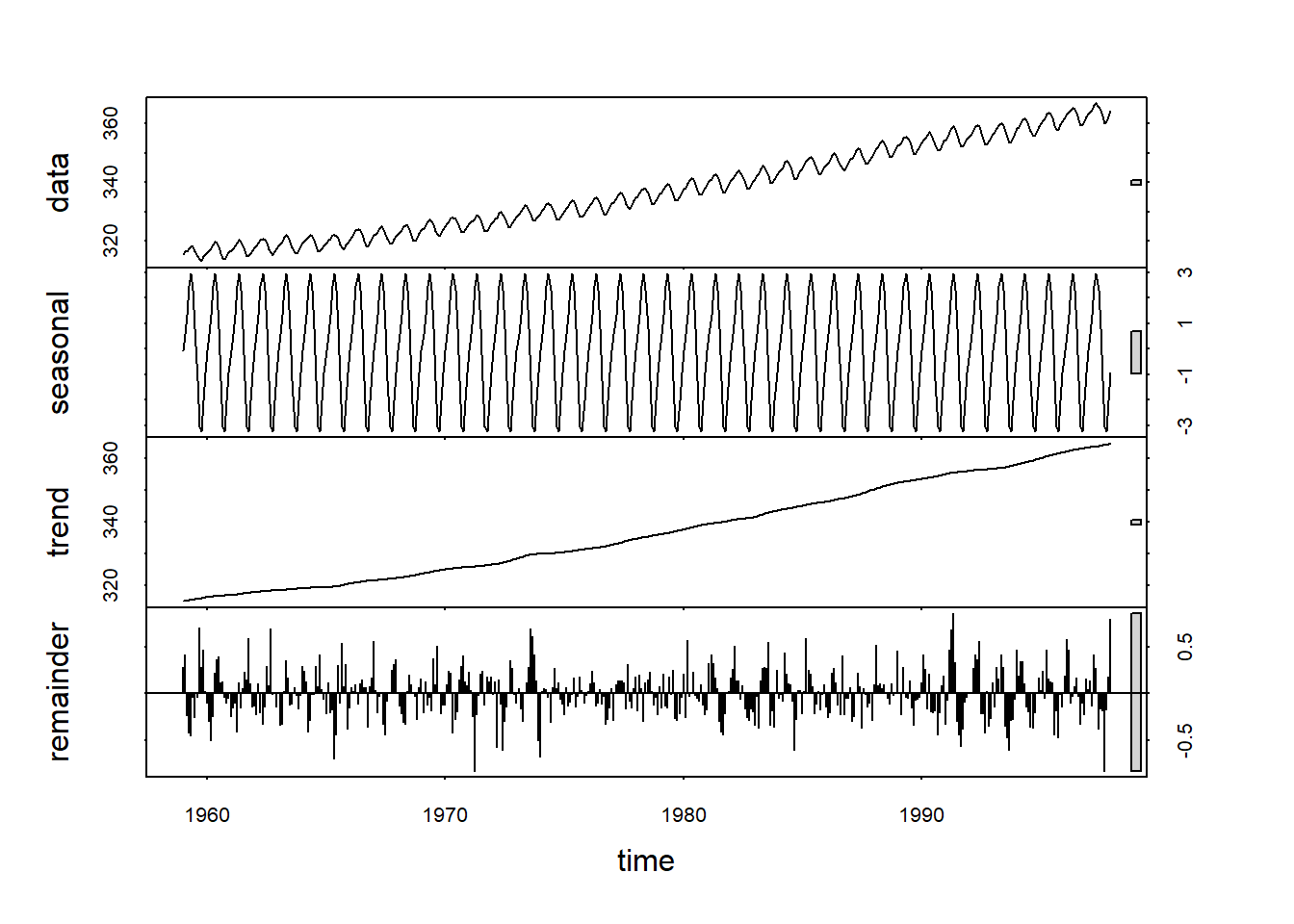

La función decomp() de la libreria timsac, al utilizar tecnica ARIMA (ver apartado siguiente) precisa qeu se le indique al estructura del modelo, su síntaxis es:

decomp(y, trend.order=2, ar.order=2, frequency=12,seasonal.order=1, log=FALSE, trade=FALSE, diff=1,year=1980, month=1, miss=0, omax=99999.9, plot=TRUE)

La opción trade, realiza el ajuste de los efectos calendario.

library(timsac)
decomp(co2, trade=TRUE)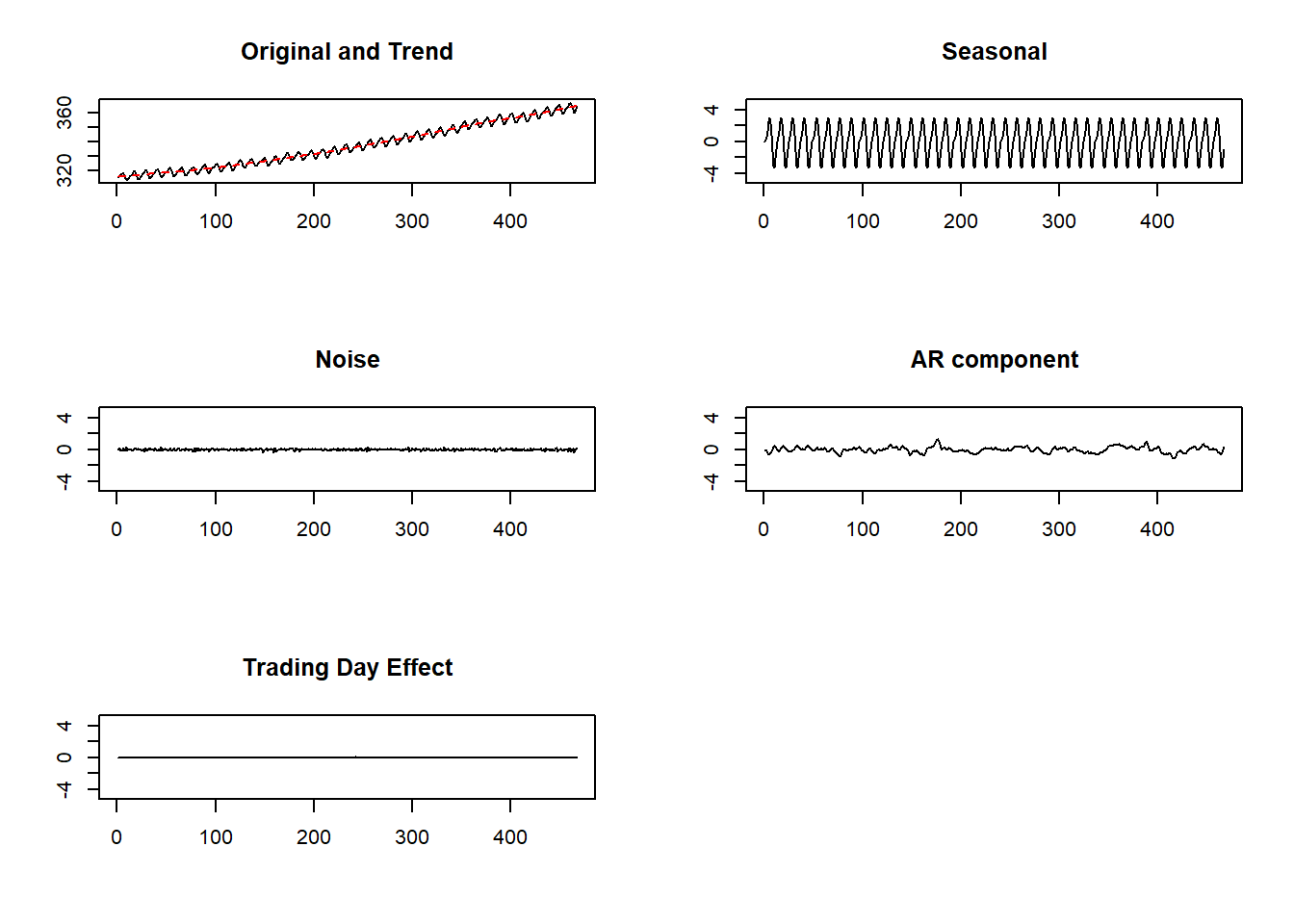

## $trend
##   [1] 315.55 315.61 315.67 315.74 315.80 315.87 315.93 316.00 316.06 316.13
##  [11] 316.19 316.25 316.32 316.38 316.44 316.51 316.57 316.63 316.70 316.76
##  [21] 316.82 316.88 316.94 317.01 317.07 317.13 317.19 317.25 317.31 317.37
##  [31] 317.43 317.49 317.55 317.61 317.67 317.73 317.79 317.85 317.91 317.97
##  [41] 318.02 318.08 318.14 318.20 318.25 318.31 318.37 318.42 318.48 318.54
##  [51] 318.60 318.65 318.71 318.77 318.82 318.88 318.94 318.99 319.05 319.11
##  [61] 319.17 319.23 319.29 319.34 319.40 319.46 319.52 319.58 319.65 319.71
##  [71] 319.77 319.83 319.90 319.96 320.02 320.09 320.16 320.22 320.29 320.36
##  [81] 320.43 320.50 320.57 320.64 320.71 320.79 320.86 320.93 321.01 321.08
##  [91] 321.16 321.24 321.31 321.39 321.47 321.55 321.62 321.70 321.78 321.86
## [101] 321.95 322.03 322.11 322.19 322.28 322.36 322.44 322.53 322.62 322.70
## [111] 322.79 322.88 322.96 323.05 323.14 323.23 323.32 323.41 323.50 323.59
## [121] 323.68 323.77 323.86 323.96 324.05 324.14 324.23 324.32 324.42 324.51
## [131] 324.60 324.69 324.79 324.88 324.97 325.07 325.16 325.25 325.34 325.44
## [141] 325.53 325.63 325.72 325.81 325.91 326.00 326.10 326.19 326.29 326.38
## [151] 326.48 326.57 326.67 326.77 326.87 326.96 327.06 327.16 327.26 327.36
## [161] 327.46 327.56 327.66 327.76 327.86 327.96 328.06 328.16 328.26 328.36
## [171] 328.46 328.56 328.66 328.76 328.86 328.96 329.06 329.16 329.25 329.35
## [181] 329.45 329.55 329.64 329.74 329.84 329.94 330.03 330.13 330.23 330.33
## [191] 330.43 330.52 330.62 330.72 330.82 330.92 331.02 331.12 331.22 331.32
## [201] 331.43 331.53 331.63 331.74 331.84 331.95 332.05 332.16 332.27 332.37
## [211] 332.48 332.59 332.70 332.82 332.93 333.04 333.15 333.27 333.38 333.50
## [221] 333.62 333.73 333.85 333.97 334.09 334.21 334.33 334.45 334.57 334.69
## [231] 334.81 334.93 335.05 335.17 335.30 335.42 335.54 335.66 335.79 335.91
## [241] 336.03 336.16 336.28 336.40 336.53 336.65 336.78 336.90 337.02 337.15
## [251] 337.27 337.40 337.52 337.64 337.77 337.89 338.01 338.14 338.26 338.38
## [261] 338.51 338.63 338.75 338.87 339.00 339.12 339.24 339.36 339.48 339.61
## [271] 339.73 339.85 339.97 340.09 340.21 340.34 340.46 340.58 340.70 340.82
## [281] 340.95 341.07 341.19 341.32 341.44 341.56 341.69 341.81 341.94 342.06
## [291] 342.19 342.31 342.44 342.57 342.70 342.82 342.95 343.08 343.21 343.33
## [301] 343.46 343.59 343.72 343.85 343.98 344.11 344.24 344.37 344.50 344.63
## [311] 344.76 344.90 345.03 345.16 345.29 345.43 345.56 345.69 345.83 345.96
## [321] 346.10 346.23 346.37 346.50 346.64 346.78 346.92 347.05 347.19 347.33
## [331] 347.47 347.61 347.75 347.89 348.03 348.18 348.32 348.46 348.60 348.75
## [341] 348.89 349.03 349.17 349.32 349.46 349.60 349.75 349.89 350.03 350.17
## [351] 350.31 350.45 350.59 350.73 350.87 351.01 351.14 351.28 351.41 351.55
## [361] 351.68 351.81 351.94 352.07 352.20 352.32 352.45 352.58 352.70 352.82
## [371] 352.94 353.07 353.19 353.31 353.42 353.54 353.66 353.77 353.89 354.00
## [381] 354.11 354.23 354.34 354.45 354.56 354.67 354.78 354.88 354.99 355.10
## [391] 355.20 355.31 355.42 355.52 355.63 355.73 355.84 355.94 356.05 356.15
## [401] 356.26 356.36 356.47 356.57 356.68 356.78 356.89 357.00 357.11 357.22
## [411] 357.33 357.44 357.55 357.67 357.78 357.90 358.01 358.13 358.25 358.37
## [421] 358.49 358.61 358.73 358.86 358.98 359.11 359.24 359.36 359.49 359.62
## [431] 359.75 359.88 360.01 360.14 360.28 360.41 360.54 360.68 360.81 360.94
## [441] 361.08 361.21 361.35 361.48 361.62 361.76 361.89 362.03 362.16 362.30
## [451] 362.44 362.57 362.71 362.85 362.98 363.12 363.26 363.39 363.53 363.67
## [461] 363.81 363.94 364.08 364.22 364.36 364.50 364.64 364.77
## 
## $seasonal
##   [1] -0.045091  0.628530  1.370162  2.505990  2.985461  2.330269  0.811891
##   [8] -1.252543 -3.069440 -3.251475 -2.062433 -0.951314 -0.045074  0.628474
##  [15]  1.370194  2.505988  2.985493  2.330209  0.811921 -1.252495 -3.069525
##  [22] -3.251417 -2.062486 -0.951274 -0.045060  0.628404  1.370253  2.505986
##  [29]  2.985514  2.330149  0.811936 -1.252423 -3.069627 -3.251346 -2.062536
##  [36] -0.951256 -0.045017  0.628330  1.370271  2.506060  2.985460  2.330131
##  [43]  0.811943 -1.252366 -3.069689 -3.251332 -2.062566 -0.951226 -0.044992
##  [50]  0.628293  1.370244  2.506142  2.985427  2.330120  0.811911 -1.252243
##  [57] -3.069839 -3.251258 -2.062616 -0.951175 -0.045001  0.628266  1.370242
##  [64]  2.506220  2.985370  2.330102  0.811904 -1.252118 -3.069999 -3.251202
##  [71] -2.062637 -0.951123 -0.045021  0.628242  1.370212  2.506338  2.985310
##  [78]  2.330071  0.811913 -1.252023 -3.070114 -3.251193 -2.062636 -0.951080
##  [85] -0.045007  0.628172  1.370217  2.506403  2.985302  2.330064  0.811832
##  [92] -1.251829 -3.070316 -3.251118 -2.062703 -0.950985 -0.044994  0.628079
##  [99]  1.370242  2.506434  2.985335  2.330041  0.811745 -1.251624 -3.070559
## [106] -3.250977 -2.062811 -0.950853 -0.045035  0.628000  1.370302  2.506449
## [113]  2.985349  2.330020  0.811699 -1.251460 -3.070775 -3.250852 -2.062908
## [120] -0.950750 -0.045053  0.627922  1.370351  2.506469  2.985375  2.329998
## [127]  0.811631 -1.251284 -3.070991 -3.250742 -2.062970 -0.950655 -0.045114
## [134]  0.627905  1.370354  2.506512  2.985378  2.330027  0.811500 -1.251046
## [141] -3.071266 -3.250618 -2.063008 -0.950586 -0.045155  0.627883  1.370364
## [148]  2.506507  2.985431  2.330048  0.811370 -1.250811 -3.071542 -3.250511
## [155] -2.063031 -0.950498 -0.045219  0.627860  1.370345  2.506571  2.985450
## [162]  2.330074  0.811236 -1.250605 -3.071767 -3.250430 -2.063048 -0.950426
## [169] -0.045246  0.627764  1.370433  2.506566  2.985450  2.330155  0.811079
## [176] -1.250397 -3.071980 -3.250365 -2.063073 -0.950344 -0.045255  0.627638
## [183]  1.370524  2.506585  2.985431  2.330233  0.810955 -1.250229 -3.072179
## [190] -3.250299 -2.063130 -0.950247 -0.045205  0.627456  1.370621  2.506615
## [197]  2.985381  2.330365  0.810808 -1.250080 -3.072356 -3.250242 -2.063187
## [204] -0.950150 -0.045135  0.627239  1.370741  2.506642  2.985337  2.330471
## [211]  0.810681 -1.249917 -3.072565 -3.250176 -2.063235 -0.950056 -0.045067
## [218]  0.627035  1.370842  2.506661  2.985316  2.330578  0.810532 -1.249725
## [225] -3.072807 -3.250091 -2.063273 -0.949968 -0.045034  0.626882  1.370922
## [232]  2.506672  2.985305  2.330685  0.810357 -1.249472 -3.073121 -3.249973
## [239] -2.063300 -0.949884 -0.045036  0.626794  1.370952  2.506676  2.985343
## [246]  2.330760  0.810192 -1.249229 -3.073439 -3.249832 -2.063357 -0.949763
## [253] -0.045088  0.626768  1.370917  2.506714  2.985393  2.330804  0.810065
## [260] -1.249039 -3.073725 -3.249685 -2.063420 -0.949623 -0.045209  0.626855
## [267]  1.370771  2.506804  2.985458  2.330809  0.809962 -1.248860 -3.073985
## [274] -3.249579 -2.063465 -0.949492 -0.045294  0.626910  1.370629  2.506895
## [281]  2.985528  2.330805  0.809861 -1.248676 -3.074239 -3.249471 -2.063528
## [288] -0.949345 -0.045386  0.626988  1.370439  2.507021  2.985581  2.330825
## [295]  0.809731 -1.248476 -3.074495 -3.249359 -2.063589 -0.949224 -0.045435
## [302]  0.627014  1.370301  2.507126  2.985625  2.330848  0.809635 -1.248357
## [309] -3.074681 -3.249282 -2.063593 -0.949174 -0.045453  0.627025  1.370214
## [316]  2.507170  2.985695  2.330873  0.809542 -1.248285 -3.074801 -3.249221
## [323] -2.063613 -0.949145 -0.045436  0.627061  1.370059  2.507261  2.985745
## [330]  2.330895  0.809463 -1.248204 -3.074955 -3.249122 -2.063644 -0.949131
## [337] -0.045417  0.627101  1.369933  2.507321  2.985798  2.330907  0.809391
## [344] -1.248071 -3.075201 -3.248965 -2.063684 -0.949113 -0.045429  0.627169
## [351]  1.369812  2.507380  2.985838  2.330890  0.809386 -1.247975 -3.075452
## [358] -3.248797 -2.063740 -0.949071 -0.045425  0.627173  1.369741  2.507421
## [365]  2.985892  2.330862  0.809381 -1.247884 -3.075683 -3.248653 -2.063792
## [372] -0.948992 -0.045482  0.627197  1.369713  2.507405  2.985968  2.330852
## [379]  0.809341 -1.247780 -3.075896 -3.248523 -2.063846 -0.948906 -0.045525
## [386]  0.627196  1.369670  2.507450  2.985987  2.330866  0.809312 -1.247716
## [393] -3.076066 -3.248398 -2.063905 -0.948869 -0.045510  0.627195  1.369612
## [400]  2.507505  2.985976  2.330876  0.809316 -1.247673 -3.076214 -3.248281
## [407] -2.063968 -0.948841 -0.045493  0.627208  1.369550  2.507550  2.985993
## [414]  2.330826  0.809369 -1.247650 -3.076322 -3.248224 -2.064001 -0.948788
## [421] -0.045532  0.627282  1.369439  2.507635  2.985995  2.330740  0.809460
## [428] -1.247639 -3.076407 -3.248201 -2.064011 -0.948720 -0.045621  0.627393
## [435]  1.369326  2.507700  2.986006  2.330666  0.809536 -1.247622 -3.076488
## [442] -3.248172 -2.064028 -0.948672 -0.045670  0.627449  1.369289  2.507695
## [449]  2.986053  2.330590  0.809578 -1.247555 -3.076616 -3.248090 -2.064099
## [456] -0.948591 -0.045706  0.627479  1.369217  2.507749  2.986078  2.330528
## [463]  0.809595 -1.247490 -3.076712 -3.248038 -2.064138 -0.948538
## 
## $ar
##   [1] -0.07441946 -0.14007085 -0.41139244 -0.57637588 -0.54562069
##   [6] -0.34883351 -0.23889124  0.01926391  0.37720474  0.40795226
##  [11]  0.37958996  0.19471084 -0.01124151 -0.18320200 -0.25085057
##  [16] -0.07119531  0.20930967  0.39564439  0.42597181  0.31245506
##  [21]  0.20644029  0.07335244 -0.02000976 -0.10459804 -0.21746504
##  [26] -0.22341305 -0.21493616 -0.23447392 -0.04880364  0.01420631
##  [31]  0.15876265  0.31833968  0.43454580  0.52925889  0.35939641
##  [36]  0.16346113  0.06246196  0.02272492  0.06885698 -0.01607910
##  [41] -0.04926038  0.10762688  0.34221637  0.46760359  0.58028900
##  [46]  0.36974945  0.21587117  0.09017883  0.01149568 -0.12368205
##  [51] -0.13158020  0.05321101  0.20893614  0.16404117  0.03791930
##  [56]  0.03554550  0.08965213  0.07720471  0.01844528  0.08682609
##  [61]  0.17873300  0.14377875 -0.02560398 -0.25172631 -0.25237491
##  [66] -0.12430519 -0.00246175  0.09206661  0.07350381  0.06128337
##  [71] -0.13245872 -0.32129065 -0.43892779 -0.44953508 -0.58789559
##  [76] -0.72709497 -0.88004466 -0.69613044 -0.34179910 -0.19782017
##  [81]  0.04159829  0.01835923 -0.01741521 -0.19316463 -0.17498922
##  [86] -0.06142073 -0.00556285  0.03808461  0.02712231  0.14310942
##  [91]  0.22731701  0.21840076  0.14462359  0.03099698  0.16473599
##  [96]  0.27590148  0.32081392  0.09406506 -0.12417155 -0.16177845
## [101] -0.21830585 -0.35176015 -0.39108570 -0.21864021 -0.07411281
## [106]  0.08779839  0.14449152  0.08389302 -0.13071428 -0.30369817
## [111] -0.41380922 -0.47453870 -0.40783973 -0.22002729 -0.05832235
## [116] -0.04180021 -0.06836331 -0.10591035 -0.11421266  0.01833136
## [121]  0.09664858  0.03693927  0.10331086  0.10048376  0.14230922
## [126]  0.23222105  0.46381631  0.54469093  0.61317539  0.43212939
## [131]  0.24425134  0.20082953  0.20062108  0.28431407  0.32610499
## [136]  0.23403758 -0.01330233 -0.03989641  0.09622510  0.28712270
## [141]  0.41343430  0.40227869  0.25308025  0.13438267  0.05179181
## [146] -0.17340630 -0.49023370 -0.72486150 -0.56450174 -0.32958023
## [151] -0.15401527 -0.13007978 -0.22503166 -0.18433688 -0.17884048
## [156] -0.23727537 -0.36936911 -0.47178026 -0.64874686 -0.53899801
## [161] -0.59706602 -0.72381216 -0.58898437 -0.35033162 -0.06787339
## [166]  0.18836058  0.27711299  0.24470191  0.24596533  0.31168897
## [171]  0.31398129  0.37797544  0.59263263  0.82105261  1.05587802
## [176]  1.29123152  1.26809916  1.05490534  0.67995442  0.22204763
## [181]  0.03104586  0.19887185  0.25659407  0.19708349  0.09694783
## [186]  0.00155865  0.12676856  0.21027778  0.15084979  0.07138587
## [191] -0.04840590 -0.16381679 -0.22485544 -0.21712277 -0.27239394
## [196] -0.25167864 -0.18683805 -0.13774931 -0.17093483 -0.13537441
## [201] -0.06262730 -0.12040393 -0.19347369 -0.20884318 -0.19065941
## [206] -0.16545899 -0.16202376 -0.28399710 -0.44451307 -0.48787163
## [211] -0.48682348 -0.54006372 -0.57192549 -0.67010245 -0.66345307
## [216] -0.55084717 -0.47311705 -0.46695596 -0.29263690 -0.13497414
## [221] -0.04643496  0.02567380  0.06185399  0.06301390  0.17328322
## [226]  0.08977461  0.06377122  0.12281278  0.14502359  0.09092661
## [231]  0.16889729  0.10090701  0.02255269  0.14093136  0.22287677
## [236]  0.23573026  0.13913968  0.01897177 -0.01918991 -0.06506372
## [241] -0.03496507 -0.08168191 -0.02883885 -0.11238153 -0.08873796
## [246]  0.02108843  0.05374928  0.06650005 -0.08960691 -0.14109831
## [251] -0.05119004  0.09486267  0.22890618  0.22282645  0.41738796
## [256]  0.34056805  0.33543484  0.39503827  0.33966324  0.31528559
## [261]  0.31903350  0.35653816  0.25307309  0.18498044  0.22900306
## [266]  0.42647551  0.49794061  0.43343577  0.28031242  0.08567564
## [271] -0.13227195 -0.28053026 -0.28905584 -0.17179677 -0.02407987
## [276]  0.06338017  0.16725631  0.25449509  0.29740991  0.13604429
## [281] -0.00397455 -0.14003864 -0.23194344 -0.39495693 -0.51018193
## [286] -0.56171055 -0.55595026 -0.54737012 -0.57103306 -0.47221265
## [291] -0.38933432 -0.12564759  0.10785635  0.23855480  0.31461270
## [296]  0.31919097  0.05264229 -0.02781439  0.01272739  0.20197833
## [301]  0.16807362  0.12965814  0.15571007  0.31504334  0.27984702
## [306]  0.20365233  0.09951167 -0.06695546 -0.27277904 -0.17454908
## [311] -0.02059259  0.00069553 -0.04024475  0.11484912  0.33501625
## [316]  0.27706127  0.18386958  0.01642051 -0.14330835 -0.19281415
## [321] -0.19736400 -0.27091764 -0.25614402 -0.28769110 -0.41971323
## [326] -0.52813240 -0.48521179 -0.29581328 -0.24005582 -0.32214325
## [331] -0.44970567 -0.44983893 -0.32058680 -0.44875051 -0.49074498
## [336] -0.49846539 -0.54558683 -0.66444652 -0.62843996 -0.46663684
## [341] -0.33452476 -0.34971963 -0.42444309 -0.26891771 -0.16246037
## [346] -0.12863441 -0.07672664  0.01934937  0.26133705  0.48465721
## [351]  0.44622493  0.45068825  0.46570753  0.51941275  0.53667613
## [356]  0.52998723  0.53472470  0.59306629  0.60013289  0.63472386
## [361]  0.69756048  0.53963119  0.43216142  0.48185048  0.40789228
## [366]  0.35984685  0.34005064  0.20896730  0.13536436  0.18923099
## [371]  0.24891133  0.30667833  0.39971878  0.46938396  0.35902911
## [376]  0.18632627  0.16987283  0.05052108 -0.01777092 -0.03203064
## [381] -0.06397184  0.10456791  0.31133259  0.37397270  0.28619004
## [386]  0.46087151  0.78429913  1.00433815  0.99002736  0.63422888
## [391]  0.17569632 -0.09013899 -0.19702457 -0.11301183  0.01050184
## [396]  0.08144230  0.09073847  0.13248586  0.25599964  0.35656087
## [401]  0.34932884  0.22675674 -0.13567545 -0.38106987 -0.50979893
## [406] -0.50419361 -0.62408268 -0.64383173 -0.55970823 -0.57162999
## [411] -0.46478071 -0.44798180 -0.42722356 -0.58337495 -0.92486444
## [416] -1.11617878 -1.13192153 -0.97318619 -0.81049903 -0.55321565
## [421] -0.30347315 -0.25597048 -0.19506351 -0.18864918 -0.30876678
## [426] -0.43271231 -0.49719854 -0.54564329 -0.50312539 -0.34438270
## [431] -0.12878562  0.01914738  0.07565764  0.17799925  0.19697803
## [436]  0.35324821  0.32336845  0.28456324  0.18849191  0.01855912
## [441]  0.00786251  0.01869340  0.18918366  0.30005517  0.51416389
## [446]  0.71486583  0.65459953  0.40645257  0.35147703  0.35760159
## [451]  0.34507254  0.18296563  0.01155722 -0.01243199 -0.00527791
## [456]  0.07694061  0.05960777 -0.00478601 -0.07619040  0.02625662
## [461] -0.09532179 -0.36349383 -0.44468369 -0.53909716 -0.68201676
## [466] -0.40683615 -0.05007161  0.30120914
## 
## $trad
##   [1]  0.02137555  0.00425428 -0.02562983  0.00025715  0.01643660
##   [6] -0.01669375  0.02137555  0.03142312 -0.00822817 -0.01894067
##  [11]  0.02716884 -0.05254152  0.01643660  0.00000000  0.02787675
##  [16] -0.02319495  0.03142312 -0.00822817 -0.01894067 -0.02562983
##  [21]  0.00025715  0.01643660 -0.01669375  0.02137555  0.03142312
##  [26]  0.00000000 -0.05254152  0.02537268 -0.02562983  0.00025715
##  [31]  0.01643660  0.02787675 -0.02319495  0.03142312 -0.00822817
##  [36] -0.01894067 -0.02562983  0.00000000  0.02137555 -0.00468180
##  [41]  0.02787675 -0.02319495  0.03142312 -0.05254152  0.02537268
##  [46] -0.02562983  0.00025715  0.01643660  0.02787675 -0.04431336
##  [51]  0.01643660 -0.01669375  0.02137555 -0.00468180  0.02787675
##  [56] -0.01894067  0.02716884 -0.05254152  0.02537268 -0.02562983
##  [61]  0.02137555  0.00000000  0.03142312 -0.00822817 -0.01894067
##  [66]  0.02716884 -0.05254152  0.01643660 -0.01669375  0.02137555
##  [71] -0.00468180  0.02787675 -0.01894067  0.00000000 -0.02562983
##  [76]  0.00025715  0.01643660 -0.01669375  0.02137555  0.03142312
##  [81] -0.00822817 -0.01894067  0.02716884 -0.05254152  0.01643660
##  [86]  0.00000000  0.02787675 -0.02319495  0.03142312 -0.00822817
##  [91] -0.01894067 -0.02562983  0.00025715  0.01643660 -0.01669375
##  [96]  0.02137555  0.03142312 -0.05279867  0.02137555 -0.00468180
## [101]  0.02787675 -0.02319495  0.03142312 -0.05254152  0.02537268
## [106] -0.02562983  0.00025715  0.01643660  0.02787675  0.00000000
## [111] -0.01894067  0.02716884 -0.05254152  0.02537268 -0.02562983
## [116]  0.02137555 -0.00468180  0.02787675 -0.02319495  0.03142312
## [121] -0.05254152  0.00000000  0.01643660 -0.01669375  0.02137555
## [126] -0.00468180  0.02787675 -0.01894067  0.02716884 -0.05254152
## [131]  0.02537268 -0.02562983  0.02137555  0.00000000  0.03142312
## [136] -0.00822817 -0.01894067  0.02716884 -0.05254152  0.01643660
## [141] -0.01669375  0.02137555 -0.00468180  0.02787675 -0.01894067
## [146] -0.00893608  0.02787675 -0.02319495  0.03142312 -0.00822817
## [151] -0.01894067 -0.02562983  0.00025715  0.01643660 -0.01669375
## [156]  0.02137555  0.03142312  0.00000000 -0.05254152  0.02537268
## [161] -0.02562983  0.00025715  0.01643660  0.02787675 -0.02319495
## [166]  0.03142312 -0.00822817 -0.01894067 -0.02562983  0.00000000
## [171]  0.02137555 -0.00468180  0.02787675 -0.02319495  0.03142312
## [176] -0.05254152  0.02537268 -0.02562983  0.00025715  0.01643660
## [181]  0.02787675  0.00000000 -0.01894067  0.02716884 -0.05254152
## [186]  0.02537268 -0.02562983  0.02137555 -0.00468180  0.02787675
## [191] -0.02319495  0.03142312 -0.05254152  0.02111840  0.03142312
## [196] -0.00822817 -0.01894067  0.02716884 -0.05254152  0.01643660
## [201] -0.01669375  0.02137555 -0.00468180  0.02787675 -0.01894067
## [206]  0.00000000 -0.02562983  0.00025715  0.01643660 -0.01669375
## [211]  0.02137555  0.03142312 -0.00822817 -0.01894067  0.02716884
## [216] -0.05254152  0.01643660  0.00000000  0.02787675 -0.02319495
## [221]  0.03142312 -0.00822817 -0.01894067 -0.02562983  0.00025715
## [226]  0.01643660 -0.01669375  0.02137555  0.03142312  0.00000000
## [231] -0.05254152  0.02537268 -0.02562983  0.00025715  0.01643660
## [236]  0.02787675 -0.02319495  0.03142312 -0.00822817 -0.01894067
## [241] -0.02562983  0.04457050 -0.01894067  0.02716884 -0.05254152
## [246]  0.02537268 -0.02562983  0.02137555 -0.00468180  0.02787675
## [251] -0.02319495  0.03142312 -0.05254152  0.00000000  0.01643660
## [256] -0.01669375  0.02137555 -0.00468180  0.02787675 -0.01894067
## [261]  0.02716884 -0.05254152  0.02537268 -0.02562983  0.02137555
## [266]  0.00000000  0.03142312 -0.00822817 -0.01894067  0.02716884
## [271] -0.05254152  0.01643660 -0.01669375  0.02137555 -0.00468180
## [276]  0.02787675 -0.01894067  0.00000000 -0.02562983  0.00025715
## [281]  0.01643660 -0.01669375  0.02137555  0.03142312 -0.00822817
## [286] -0.01894067  0.02716884 -0.05254152  0.01643660  0.03610492
## [291] -0.05254152  0.02537268 -0.02562983  0.00025715  0.01643660
## [296]  0.02787675 -0.02319495  0.03142312 -0.00822817 -0.01894067
## [301] -0.02562983  0.00000000  0.02137555 -0.00468180  0.02787675
## [306] -0.02319495  0.03142312 -0.05254152  0.02537268 -0.02562983
## [311]  0.00025715  0.01643660  0.02787675  0.00000000 -0.01894067
## [316]  0.02716884 -0.05254152  0.02537268 -0.02562983  0.02137555
## [321] -0.00468180  0.02787675 -0.02319495  0.03142312 -0.05254152
## [326]  0.00000000  0.01643660 -0.01669375  0.02137555 -0.00468180
## [331]  0.02787675 -0.01894067  0.02716884 -0.05254152  0.02537268
## [336] -0.02562983  0.02137555  0.00425428 -0.02562983  0.00025715
## [341]  0.01643660 -0.01669375  0.02137555  0.03142312 -0.00822817
## [346] -0.01894067  0.02716884 -0.05254152  0.01643660  0.00000000
## [351]  0.02787675 -0.02319495  0.03142312 -0.00822817 -0.01894067
## [356] -0.02562983  0.00025715  0.01643660 -0.01669375  0.02137555
## [361]  0.03142312  0.00000000 -0.05254152  0.02537268 -0.02562983
## [366]  0.00025715  0.01643660  0.02787675 -0.02319495  0.03142312
## [371] -0.00822817 -0.01894067 -0.02562983  0.00000000  0.02137555
## [376] -0.00468180  0.02787675 -0.02319495  0.03142312 -0.05254152
## [381]  0.02537268 -0.02562983  0.00025715  0.01643660  0.02787675
## [386] -0.04431336  0.01643660 -0.01669375  0.02137555 -0.00468180
## [391]  0.02787675 -0.01894067  0.02716884 -0.05254152  0.02537268
## [396] -0.02562983  0.02137555  0.00000000  0.03142312 -0.00822817
## [401] -0.01894067  0.02716884 -0.05254152  0.01643660 -0.01669375
## [406]  0.02137555 -0.00468180  0.02787675 -0.01894067  0.00000000
## [411] -0.02562983  0.00025715  0.01643660 -0.01669375  0.02137555
## [416]  0.03142312 -0.00822817 -0.01894067  0.02716884 -0.05254152
## [421]  0.01643660  0.00000000  0.02787675 -0.02319495  0.03142312
## [426] -0.00822817 -0.01894067 -0.02562983  0.00025715  0.01643660
## [431] -0.01669375  0.02137555  0.03142312 -0.05279867  0.02137555
## [436] -0.00468180  0.02787675 -0.02319495  0.03142312 -0.05254152
## [441]  0.02537268 -0.02562983  0.00025715  0.01643660  0.02787675
## [446]  0.00000000 -0.01894067  0.02716884 -0.05254152  0.02537268
## [451] -0.02562983  0.02137555 -0.00468180  0.02787675 -0.02319495
## [456]  0.03142312 -0.05254152  0.00000000  0.01643660 -0.01669375
## [461]  0.02137555 -0.00468180  0.02787675 -0.01894067  0.02716884
## [466] -0.05254152  0.02537268 -0.02562983
## 
## $noise
##   [1] -0.0279123124  0.2069586077 -0.1077216295 -0.1087577807 -0.1295490487
##   [6]  0.1675347151 -0.1365404261 -0.1447423525  0.3195003498 -0.0826717929
##  [11]  0.1265417974 -0.0137895547 -0.0066974448 -0.0153620668 -0.1707196743
##  [16] -0.0484250264  0.0737569228  0.0793811402  0.0953336718 -0.0524979942
##  [21]  0.0424375433 -0.0407610616 -0.0050036863  0.0586820098 -0.1061582821
##  [26]  0.0064442720  0.0875083980 -0.2375899284  0.1973595250 -0.1068185616
##  [31]  0.0002114219  0.0433386560 -0.0645370896  0.2381903598 -0.0204357094
##  [36] -0.0741273191 -0.0015171496 -0.0993951623  0.1627030912 -0.0303343918
##  [41] -0.1371898711 -0.0456195938  0.1255777869 -0.1091080156  0.3202451419
##  [46] -0.1336963149  0.0085474467 -0.0501575921  0.1040325592 -0.0786665507
##  [51] -0.1502835533  0.0252794515  0.1552886508  0.0546246987 -0.1205840968
##  [56] -0.0343507499  0.0657705559  0.0619381591 -0.1234497093 -0.0201013134
##  [61]  0.0867340295  0.0714770465  0.0788646166 -0.1902768625 -0.0574448910
##  [66]  0.0338081518 -0.0104115847  0.0993635824 -0.0922590209  0.1713959971
##  [71] -0.0395751125 -0.0376072882 -0.1226952441  0.1415729819 -0.0512294112
##  [76]  0.1003935744 -0.2781450807 -0.1308755372  0.2668933138 -0.2318855721
##  [81]  0.2670364906 -0.1079590338  0.1824680219 -0.1949453045 -0.0501861305
##  [86]  0.0768155567 -0.0222794687  0.0850271621 -0.1420529756  0.0417139683
##  [91]  0.0607542073  0.0237889841  0.0934034101 -0.2456503066  0.0774324105
##  [96] -0.0219448565  0.2381730961 -0.0333345232 -0.1713828468  0.0455413266
## [101]  0.0894822829 -0.0524064849 -0.1817315821  0.0901904037 -0.0568565141
## [106]  0.0685609170  0.0332193552  0.1205994116 -0.0676150365 -0.0358832873
## [111]  0.0042213428 -0.0745044036 -0.0881536606  0.0131552513  0.1120112230
## [116] -0.0075282890  0.0048370882  0.0099492772 -0.1389473311  0.0510411302
## [121]  0.1500037617 -0.1770428845  0.1162093438 -0.0456745444  0.0135956402
## [126] -0.1569903142  0.1849556813 -0.0985231042  0.2341938233 -0.0177032917
## [131] -0.1179754530  0.0315678573 -0.0734291110  0.0284756724  0.0699831694
## [136]  0.1726576930 -0.2011151394 -0.0684040257 -0.0195808070  0.0396542482
## [141]  0.0731509847  0.1019567687 -0.0541335100 -0.0643158639  0.1155628003
## [146]  0.0634136918  0.0063788882 -0.3289833464  0.0217587050  0.0261334968
## [151]  0.0838839428  0.1024414227 -0.1744431552  0.0506209108  0.0234215945
## [156]  0.0535875219 -0.0776296911  0.1547981183 -0.3468426499  0.2102084551
## [161]  0.0810352517 -0.2423991787 -0.0145794946 -0.0231131181 -0.0138133489
## [166]  0.1134144094  0.0763327388 -0.0437357491 -0.0640222711  0.1011489064
## [171] -0.0255297213 -0.1098058837  0.0440493103  0.0121813552 -0.0577154037
## [176]  0.2031734594  0.0711806808  0.0853553844  0.1190604487 -0.1597535410
## [181] -0.2829752620  0.1765390391  0.0673356879  0.0072267831  0.0508155561
## [186] -0.2139401846  0.0636105396  0.1166855917 -0.0335553731  0.0336489227
## [191] -0.0006668737 -0.0310190698 -0.0696295671  0.0973859534 -0.0801174265
## [196] -0.0269137116 -0.0000034678  0.0891488000 -0.0795457804 -0.0548759113
## [201]  0.1255534911 -0.0096243542 -0.0509133584 -0.0151316677 -0.0061582652
## [206] -0.0179867198  0.0947149868  0.0282263628 -0.1135339669 -0.0303651865
## [211]  0.0613284520 -0.0646474065  0.0889390893 -0.0959358709 -0.0878453848
## [216]  0.0330469780  0.0975424254 -0.1888328208  0.0398659424  0.0514827037
## [221] -0.0169221812  0.0181807648  0.0550378005 -0.1674075876  0.2307858395
## [226] -0.0837516456 -0.0710237184  0.0385548854  0.1009888798 -0.1861184830
## [231]  0.1733530100  0.0263416725 -0.1945565732  0.0738735851  0.0239176971
## [236]  0.0770935185  0.0158717009 -0.0844437277  0.0537787514 -0.0961476943
## [241]  0.1223174544 -0.1564163620  0.1865180849 -0.1154505983 -0.0718572646
## [246]  0.0910734151 -0.0539793489  0.1816875149 -0.1059342511 -0.0846422292
## [251] -0.0140200352 -0.0123409958  0.1889063402 -0.3032981322  0.3377521510
## [256] -0.1217109677 -0.0667976113  0.1409263483 -0.0486447627 -0.0013027309
## [261] -0.0592645333  0.1562762931 -0.0368707422 -0.0438584899 -0.1414657214
## [266]  0.1283189386  0.0696263792  0.0360244534  0.0096110823  0.0312740248
## [271] -0.0317063113 -0.0751268534 -0.0699599108 -0.0114186251  0.0689834501
## [276] -0.0369168348  0.0098198009 -0.0206667477  0.1861264497 -0.0769567369
## [281]  0.0157854510 -0.0629694910  0.0888802022 -0.0528244161 -0.0359300552
## [286] -0.0423758632 -0.0045018285  0.0577348323 -0.1366464654  0.0969615860
## [291] -0.1866387179  0.0488650038  0.0711671678  0.0024324401 -0.0258666279
## [296]  0.2889371506 -0.2150051660 -0.0121788015 -0.1670079280  0.2516291769
## [301] -0.0402371940 -0.0188177345 -0.1587088016  0.2117468950 -0.0237632856
## [306] -0.0016025678  0.0389956466  0.1070091992 -0.2794778611 -0.0032169490
## [311]  0.1197854248  0.0761216646 -0.1801999902 -0.0823646226  0.2704150066
## [316] -0.0677638297  0.0632314759  0.0038746253 -0.0881541046 -0.0323449447
## [321]  0.0998248708 -0.1201443184  0.0346923710  0.0808430525 -0.0136482467
## [326] -0.0975304713 -0.1376752622  0.1205502942  0.0694928637  0.0333184993
## [331] -0.0998499314 -0.1652963487  0.2955858142 -0.1532332552 -0.0258813457
## [336]  0.0167132733  0.0911767086 -0.1375921230 -0.0890786647  0.0130620924
## [341]  0.1033567174  0.0735630125 -0.2513076447  0.0875181294  0.0548724398
## [346] -0.0272715876  0.0068652066 -0.1263383644 -0.0128924933  0.2562039488
## [351] -0.1066980011  0.0221493590 -0.0354564225  0.0466582028  0.0236300989
## [356]  0.0072320261 -0.0521750864  0.0813015179 -0.0220737191 -0.0728010182
## [361]  0.2382864510 -0.0562684361 -0.1591012859  0.1763508951 -0.0453603791
## [366] -0.0453364626  0.1336274723 -0.0445540251 -0.0961715444  0.0351954165
## [371]  0.0181762797 -0.0348161988 -0.0148320726  0.1480301014  0.0563372366
## [376] -0.1897949322  0.1592195489 -0.0606688902 -0.0400821134  0.0914587384
## [381] -0.1794247150 -0.0166412868  0.1044648168  0.1799098211 -0.2371711762
## [386] -0.0817684735  0.0828596405  0.1001598577  0.2305685675  0.0609299423
## [391] -0.1576139927 -0.0336280461 -0.1199122059  0.0029111328  0.0419601753
## [396]  0.0521021344 -0.0223431385 -0.0701756501  0.0176840462  0.0640338007
## [401]  0.0085612795  0.2250153587 -0.1466254642 -0.0389631407 -0.1348093191
## [406]  0.1767447487 -0.1090779181 -0.1051927524  0.1451940735 -0.1742755903
## [411]  0.1115475729 -0.0906178008  0.1016116092  0.1527515299 -0.1566509602
## [416] -0.0837334318 -0.1261751936  0.0600420889 -0.1017499103 -0.0344042533
## [421]  0.1827142484 -0.0930322833  0.0131934259  0.0958916225 -0.0216333619
## [426] -0.0583586417  0.0216273824 -0.0535245104 -0.0714250737 -0.0436598638
## [431]  0.0498031648  0.0779431796 -0.0929019888  0.1341853934 -0.2031966424
## [436]  0.2154164111 -0.0587712984  0.0328477368  0.1014732518 -0.1617707998
## [441]  0.0752113100 -0.1579200633  0.1362634344 -0.1116643883 -0.0259407045
## [446]  0.1922567673  0.1637146837 -0.2086152343  0.0016268094 -0.0031428967
## [451]  0.1351164661  0.0109961901 -0.1289452918  0.0373352629 -0.0895094149
## [456]  0.1012238142  0.0125966486  0.0440958559 -0.2299854208  0.2146758825
## [461]  0.1222523652 -0.2257128575  0.0458835187  0.1560235879 -0.3863293067
## [466]  0.0408587204 -0.0565706892  0.2385951943
## 
## $aic
## [1] 208.83
## 
## $lkhd
## [1] -77.417
## 
## $sigma2
## [1] 0.026877
## 
## $tau1
## [1] 0.00043757
## 
## $tau2
## [1] 1.0001
## 
## $tau3
## [1] 0.0001
## 
## $arcoef
## [1]  1.16782 -0.29758
## 
## $tdf
## [1]  0.0361049 -0.0527987  0.0445705 -0.0443134  0.0211184  0.0042543
## [7] -0.0089361

La función descomponer() de la libreria descomponer, descompone la tendencia siguiendo un modelo multiplicativo $Y_t=T_tS_t+e_t$, tiene la siguiente sintesis:

descomponer(y,frequency,type)

En type se elige un modelo lineal (1) ó cuadrático (2) para la tendencia.

La representación gráfica se realiza con gdescomponer(y,freq,type,year,q).

library(descomponer)
par(mar = c(2, 2, 2.5, 2.5), font = 2)
gdescomponer(co2,12,1,1959,1)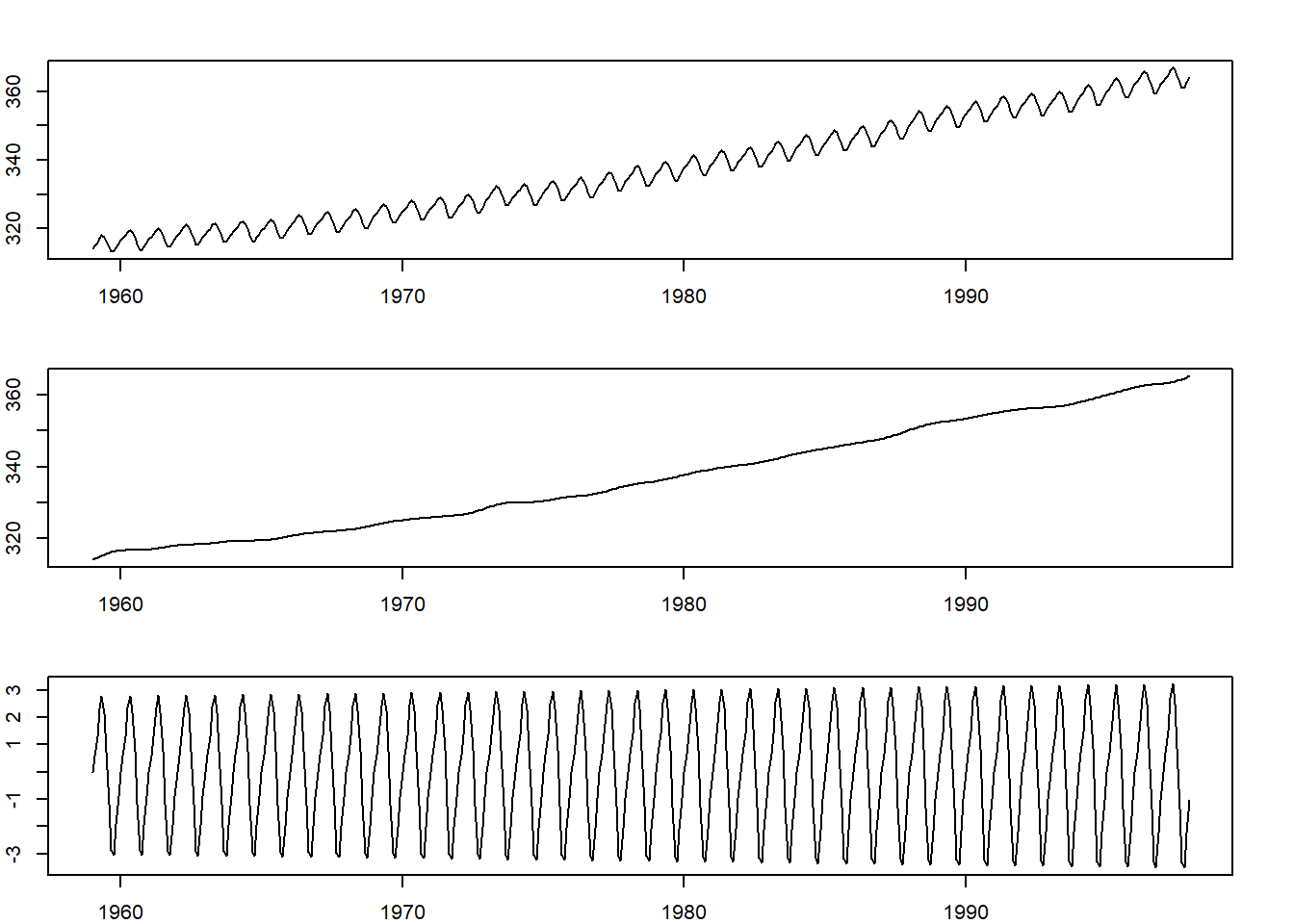

# dev.off()

Las series de tendencia y estacionalidad son por lo general muy similares en todos los métodos.

# Representación gráfica de la tendencia
plot(co2, main="Tendencia")
lines (decompose(co2)$trend,col=2)
lines(stl(co2,"per")$time.series[,2],col=3)
lines(ts(descomponer(co2,12,1)$datos$TD, frequency = 12, start = c(1959, 1)), col=4)
legend("bottomright", c("Original", "decompose", "stl", "descomponer"), lwd=c(1,2,2,2), col=c("black",2,3,4))
grid()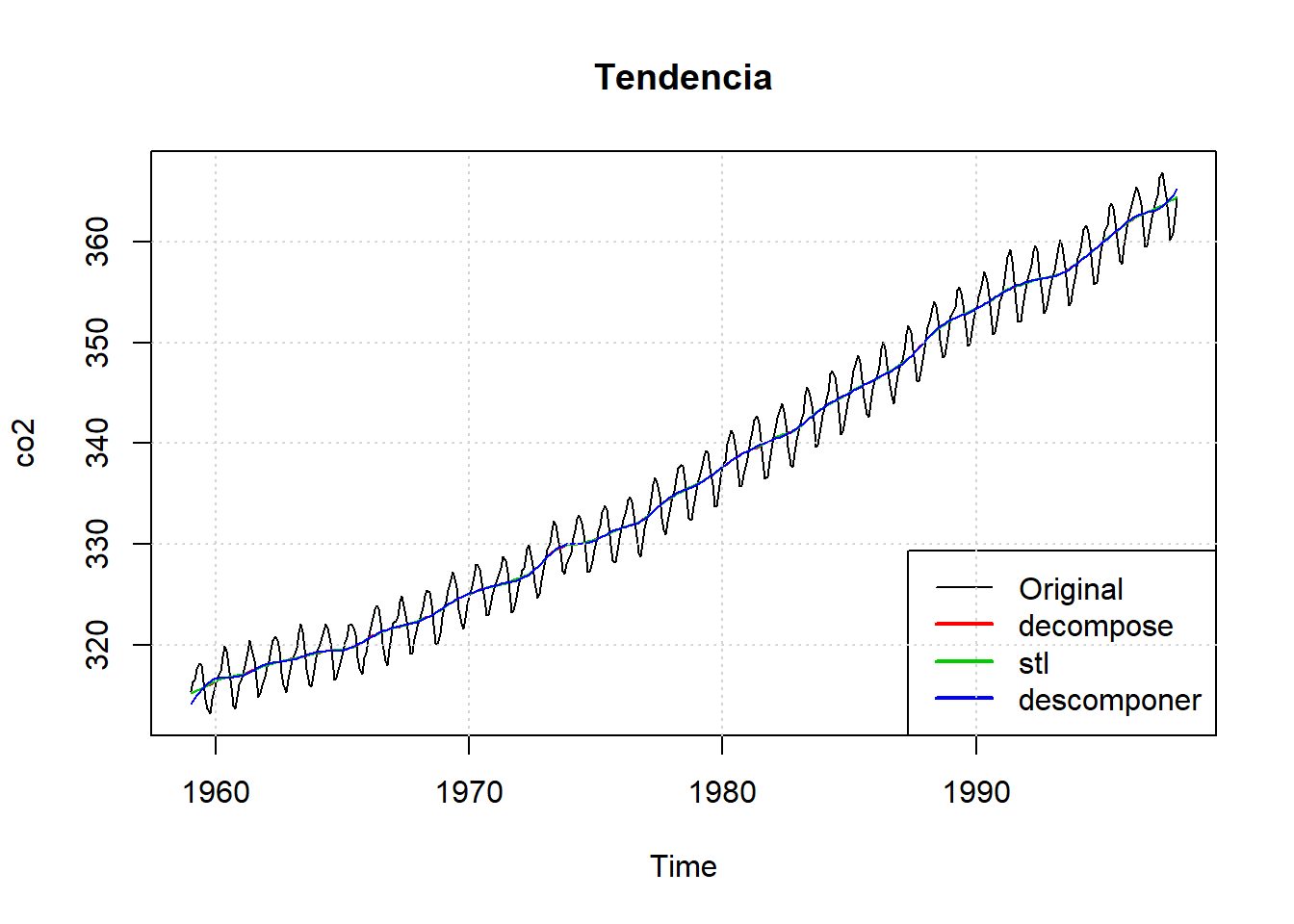

# Representación gráfica de la estacionalidad

plot (decompose(co2)$seasonal, col=2, main="Estacionalidad")
lines(stl(co2,"per")$time.series[,1],col=3)
lines(ts(descomponer(co2,12,1)$datos$ST, frequency = 12, start = c(1959, 1)), col=4)
legend("bottomright", c("decompose", "stl","descomponer"), lwd=c(2,2,2), col=c(2,3,4))
grid()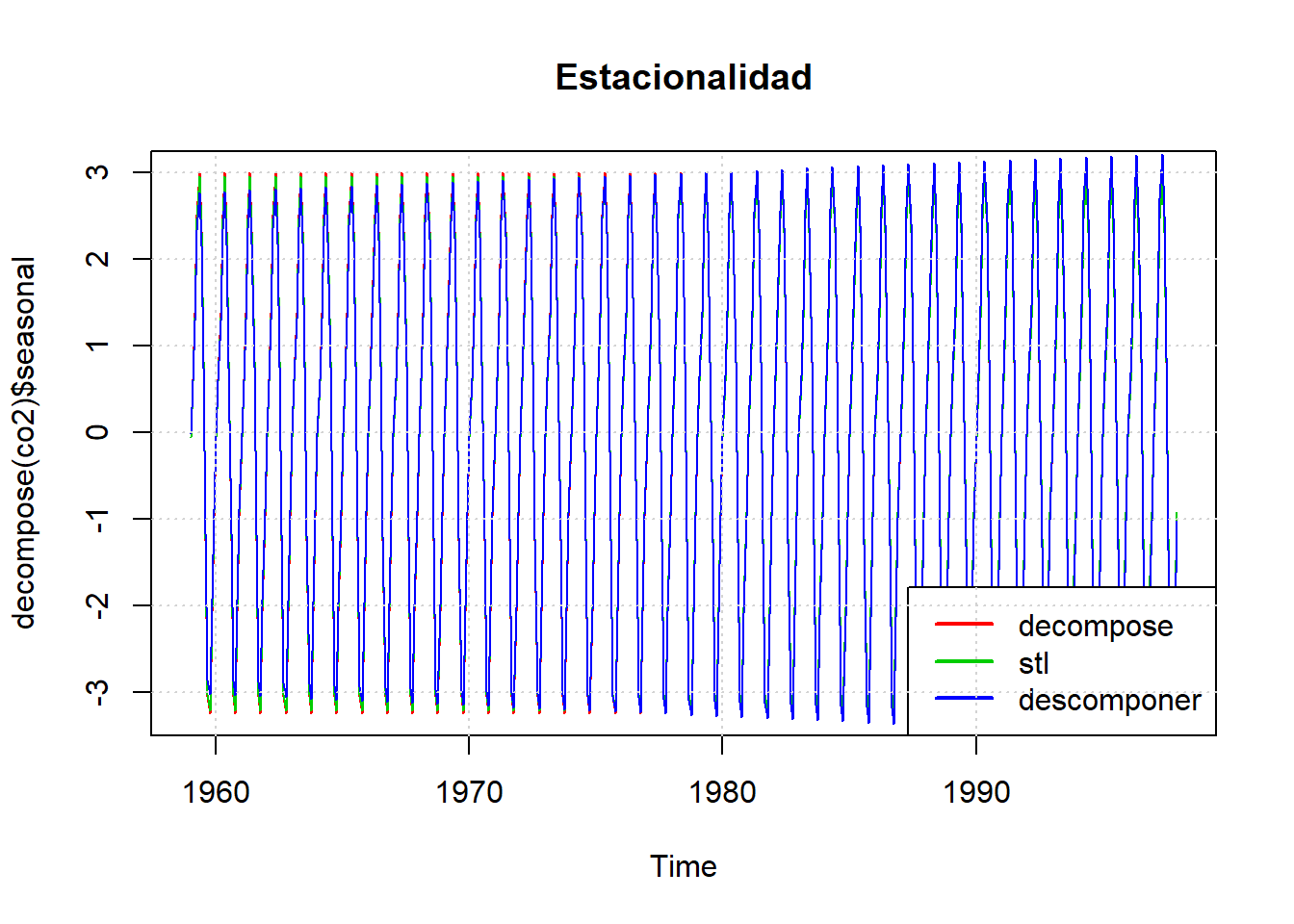

8.4 Métodos de Predicción

8.4.1 Métodos paramétricos: modelos ARIMA

8.4.1.1 Introducción

La publicación de la obra Time Series Analysis: Forecasting and Control por G. E. P. Box y G. M. Jenkins en 1976 estableció un punto de inflexión en las técnicas cuantitativas de predicción en Economía. La metodología propuesta por estos autores, también conocida como metodología ARIMA, trata de realizar previsiones acerca de los valores futuros de una variable utilizando únicamente como información la contenida en los valores pasados de la propia serie temporal. Este enfoque supone una alternativa a la construcción de modelos uniecuacionales o de ecuaciones simultáneas, pues supone admitir que las series temporales poseen un carácter estocástico, lo que implica que deben analizarse sus propiedades probabilísticas para que éstas “hablen por sí mismas”.

El análisis univariante de series temporales presenta como ventaja frente a otros métodos de predicción el no depender de los problemas de información asociados a las variables endógenas o exógenas. Como hemos visto en capítulos anteriores, los modelos económicos que hemos estimado hasta el momento requerían un conjunto de variables exógenas que se utilizaban para explicar el comportamiento de una variable endógena. Sin embargo, en muchas ocasiones no se dispone de observaciones para alguna de las variables exógenas, ya sea porque no es posible medir la variable (por ejemplo, las expectativas de los agentes) o porque la muestra de datos de que disponemos para representar dicha variable presenta errores de medida. Este problema desaparece cuando se trata de modelizar una variable endógena mediante un modelo de tipo univariante como el propuesto por Box y Jenkins, ya que se hace depender a dicha variable tan sólo de su propio pasado y un conjunto de perturbaciones aleatorias, pero no de otras variables, caracterizando así las series económicas en su dimensión temporal.

En el presente apartado vamos a definir y caracterizar una amplia familia de estructuras estocásticas lineales, así como la metodología a seguir para seleccionar aquel modelo univariante que resulte más adecuado para representar la estructura estocástica de la variable económica que estemos analizando.

8.4.1.2 Procesos estocásticos

Podemos definir un proceso estocástico como un conjunto de variables aleatorias asociadas a distintos instantes del tiempo. Así, en cada período o momento temporal se dispone de una variable que tendrá su correspondiente distribución de probabilidad; por ejemplo, si consideramos el proceso $Y_t$, para $t = 1$, tendremos una variable aleatoria, $Y_1$, que tomará diferentes valores con diferentes probabilidades.

La relación existente, por tanto, entre una serie temporal y el proceso estocástico que la genera es análoga a la que existe entre una muestra y la población de la que procede, de tal forma que podemos considerar una serie temporal como una muestra o realización de un proceso estocástico, formada por una sola observación de cada una de las variables que componen el proceso. La tarea del investigador será, por tanto, inferir la forma del proceso estocástico a partir de las series temporales que genera.

Un proceso estocástico, $Y_t$, se suele describir mediante las siguientes características: esperanza matemática, varianza, autocovarianzas y coeficientes de autocorrelación.

La esperanza matemática de $Y_t$ se traduce en la sucesión de las esperanzas matemáticas de las variables que componen el proceso a lo largo del tiempo, tal que:

\[E(Y_t)=\mu_t,\ \ t=1,2,3...\]

Por su parte, la varianza de un proceso aleatorio es una sucesión de varianzas, una por cada variable del proceso:

\[Var(Y_t)=E(Y_t–\mu_t)^2,\ \ t=1,2,3...\]

Las autocovarianzas, por su parte, son las covarianzas entre cada par de variables del proceso, tales que:

\[\gamma_k=Cov(Y_t,Y_{t+k})=E[(Y_t–\mu_t)(Y_{t+k}–\mu_{t+k})]=\gamma_{t,t+k},\ \ t=1,2,3...\]

Finalmente, los coeficientes de autocorrelación son los coeficientes de correlación lineal entre cada par de variables que componen el proceso:

\[\rho_{t,t+k}=\frac{\gamma_{t,t+k}}{Var(Y_t)Var(Y_{t+k})},\ \ t=1,2,3...,\ \ -1 \leq \rho_{t,t+k} \leq 1\]

Por último, a partir de los coeficientes de autocorrelación, vamos a definir dos funciones que nos serán muy útiles a lo largo del presente tema:

Por un lado, la función de autocorrelación simple (fas) o correlograma, la cual es la representación gráfica de los coeficientes de autocorrelación en función de los distintos retardos o desfases entre las variables.
La función de autocorrelación parcial (fap), que mide la correlación existente entre dos variables del proceso en distintos períodos de tiempo, pero una vez eliminados los efectos sobre las mismas de los períodos intermedios. Por ejemplo, puede que exista cierta correlación entre $Y_t$ e $Y_{t-2}$, debido a que ambas variables estén correlacionadas con $Y_{t-1}$.

Dado que en la práctica se dispone de una muestra de un proceso estocástico, $Y_1, ...Y_T$, se pueden obtener los coeficientes de autocorrelación simple y parcial muestral y utilizarlos como estimadores de los parámetros de la función de autocorrelación simple y parcial teórica.

Así, la función de autocorrelación simple (fas) puede estimarse a partir de las autocovarianzas del proceso tal que:

\[\hat \rho_{k}=\frac{\hat \gamma_k}{\hat \gamma_0}\]

Siendo:

\[\hat \gamma_0=\frac{\sum_{t=1}^{T}(Y_t-\bar Y)^2}{T}\]

\[\hat \gamma_k=\frac{\sum_{t=k+1}^{T}(Y_t-\bar Y)(Y_{t+k}-\bar Y)}{T-k}\]

La estimación de los parámetros de la función de autocorrelación parcial (fap) resulta algo más compleja, por lo que se verá en epígrafes posteriores.

8.4.1.3 Procesos estacionarios

Se dice que un proceso estocástico es estacionario en sentido estricto si todas las variables aleatorias que componen el proceso están idénticamente distribuidas, independientemente del momento del tiempo en que se estudie el proceso.

Es decir, la función de distribución de probabilidad de cualquier conjunto de k variables (siendo k un número finito) del proceso debe mantenerse estable (inalterable) al desplazar las variables s períodos de tiempo tal que, si $P(Y_{t+1}, Y_{t+2}, …, Y_{t+k} )$ es la función de distribución acumulada de probabilidad, entonces:

\[P(Y_{t+1},Y_{t+2},…,Y_{t+k}) = P(Y_{t+1+s}, Y_{t+2+s},…,Y_{t+k+s}),\ \ \forall t, k, s\]

Sin embargo, la versión estricta de la estacionariedad de un proceso suele ser excesivamente restrictiva para las necesidades prácticas de un economista. Es por ello que generalmente nos conformaremos con un concepto menos exigente, el de estacionariedad en sentido débil o de segundo orden, la cual se da cuando la media del proceso es constante e independiente del tiempo, la varianza es finita y constante, y el valor de la covarianza entre dos periodos depende únicamente de la distancia o desfase entre ellos, sin importar el momento del tiempo en el cual se calculan. Dicho de otro modo, todos los momentos de primer y segundo orden de un proceso estocástico que sea estacionario en sentido débil deben ser invariantes en el tiempo.

La contrastación empírica de algunas de estas condiciones puede realizarse fácilmente mirando el gráfico de la serie temporal. Así, una serie temporal que exhiba una marcada tendencia creciente tendrá una media también creciente en el tiempo, por lo que lo más probable es que el proceso estocástico que ha generado dicha serie temporal no sea estacionario en media; del mismo modo, una serie temporal que muestre fluctuaciones de amplitud desigual en el tiempo seguramente no procederá de un proceso estocástico estacionario en varianza. La diferencia entre ambos tipos de series queda patente en los gráficos siguientes.

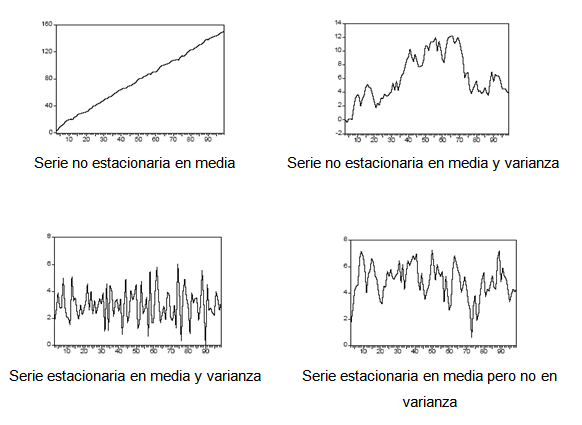
Pero, ¿por qué resulta importante para el investigador que el proceso analizado sea estacionario? La razón fundamental es que los modelos de predicción de series temporales que veremos a continuación están diseñados para ser utilizados con procesos de este tipo. Si las características del proceso cambian a lo largo del tiempo, resultará difícil representar la serie para intervalos de tiempo pasados y futuros mediante un modelo lineal sencillo, no pudiéndose por tanto realizar previsiones fiables para la variable en estudio.

Sin embargo, por regla general, las series económicas no son series que procedan de procesos estacionarios, sino que suelen tener una tendencia, ya sea creciente o decreciente, y variabilidad no constante. Dicha limitación en la práctica no es tan importante porque las series no estacionarias se pueden transformar en otras aproximadamente estacionarias después de aplicar diferencias a la serie en una ó más etapas. Por ello, cuando estemos analizando una serie económica que no sea estacionaria en media, deberemos trabajar con la serie en diferencias, especificando y estimando un modelo para la misma. Si además, observamos que la serie presenta no estacionariedad en varianza, deberemos transformarla tomando logaritmos antes de aplicar diferencias en la serie.

Posteriormente, la predicción que realicemos con las series transformadas habrá que traducirla a una predicción para la serie original, en cuyo análisis estaba interesado inicialmente el investigador, deshaciendo las diferencias y aplicando antilogaritmos según convenga.

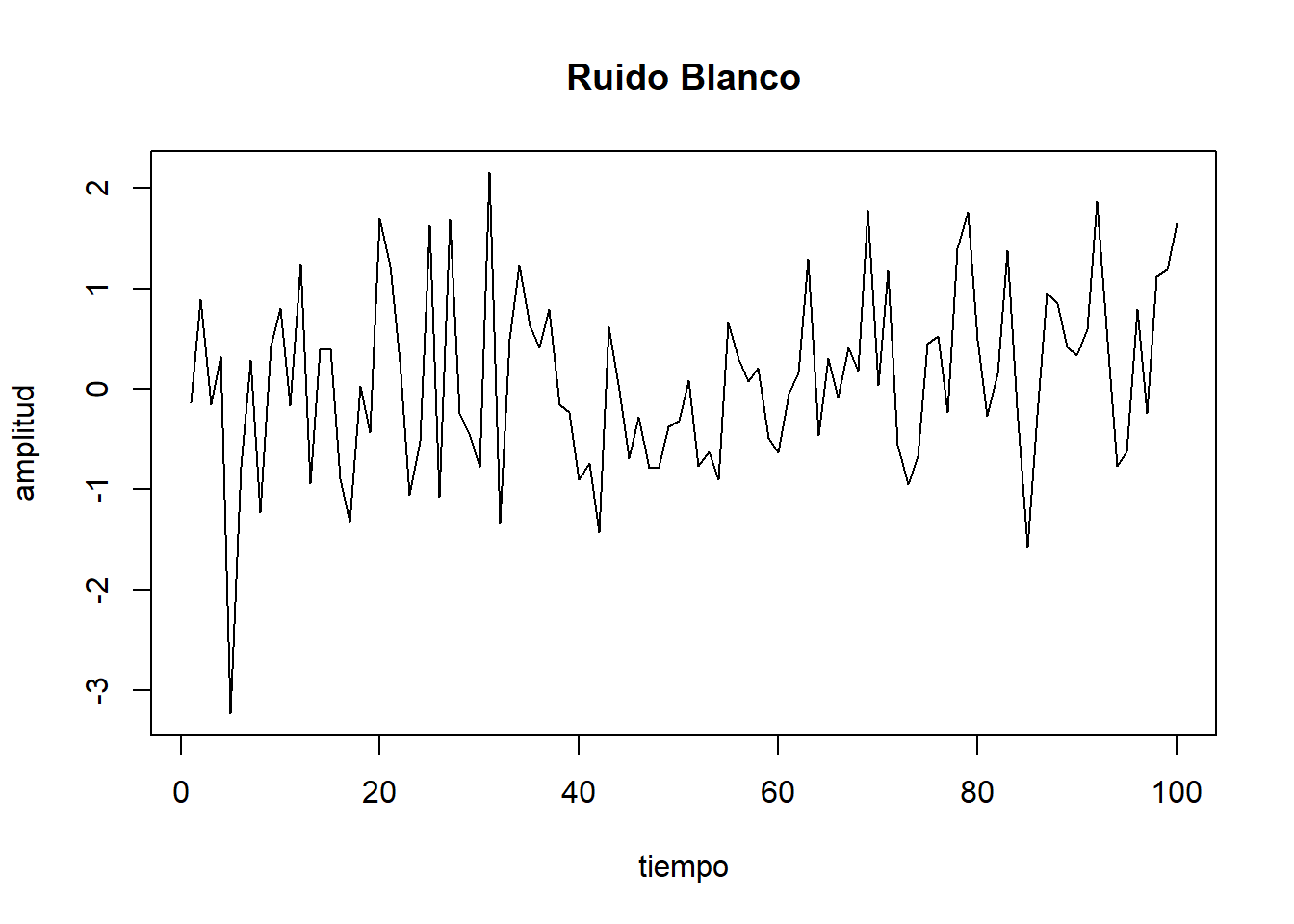
Por último, antes de continuar avanzando, debemos hacer mención a un tipo de proceso estacionario particular: es el denominado ruido blanco, un proceso estocástico en el que las variables aleatorias que lo forman no están correlacionadas entre sí, siendo su esperanza matemática igual a cero y su varianza constante e igual a $\sigma^2$.

En particular, supondremos que los errores de los procesos que veremos a continuación son ruidos blancos gaussianos, formados por una sucesión de variables aleatorias con distribución Normal, esperanza cero, varianza constante e incorrelacionadas serialmente entre sí. Es decir, si $e_t$ es ruido blanco gaussiano, entonces $e_t \sim N(0,\sigma^2)$ y $cov(e_t,e_{t+k})=0$.

En la figura siguiente se muestra la representación de un ruido blanco, en la que se puede apreciar claramente la estacionariedad de este proceso:

8.4.1.4 Operador de Retardos y Operador Diferencia

Antes de seguir avanzando, debemos mencionar dos operadores que utilizaremos frecuentemente a lo largo del capítulo. Por un lado, se define el operador de retardos, que denotaremos por B, como aquel operador que al ser aplicado a la serie la transforma de tal forma que: $BY_t = Y_{t-1}$

Es decir, el resultado de aplicar el operador $B$ corresponde a retardar las observaciones un período.

Aplicada dos veces sobre la variable $Y_t$ tendremos que: $B(BY_t) = B^2Y_t = Y_{t-2}$

y, en general, podemos decir que el operador $B^k$ aplicado sobre una variable en el periodo t, la retarda k períodos tal que: $B^kY_t = Y_{t-k}$

Por su parte, el operador diferencia, el cual denotaremos por $\Delta$, aplicado a una serie la transformará de tal forma que: $\Delta Y_t = Y_t – Y_{t-1} = (1 – B) Y_t$

Si aplicamos el operador diferencia dos veces a la serie tendremos que:

\[\Delta^2 Y_t =\Delta (\Delta Y_t) = \Delta (Y_t – Y_{t-1}) = \Delta Y_t – \Delta Y_{t-1} = Y_t – 2Y_{t-1} +Y{t-2} = (1–B)^2Y_t\]

Y en general, podemos escribir: $\Delta^kY_t = (1 – B)^kY_t$

Por lo que resulta evidente que la relación existente entre el operador diferencia y el operador retardo es: $\Delta^k = (1 – B)^k$

8.4.1.5 Modelización univariante de series temporales

La representación formal de los procesos aleatorios que generan series reales se puede realizar mediante modelos lineales de series temporales. Considerando que una determinada serie temporal ha sido generada por un proceso estocástico, en este epígrafe pasamos a describir los posibles modelos teóricos que permiten explicar el comportamiento de la misma y, por tanto, el de su proceso generador.

Las estructuras estocásticas estacionarias lineales que se tratarán de asociar a una serie de datos económicos se clasifican en tres tipos: modelos autorregresivos, modelos de medias móviles y modelos mixtos, los cuales pasamos a ver a continuación.

8.4.1.5.1 Modelos autorregresivos AR(p)

Los procesos autorregresivos son aquellos que representan los valores de una variable durante un instante del tiempo en función de sus valores precedentes. Así, un proceso autorregresivo de orden p, AR(p), tendrá la siguiente forma:

\[Y_t=\delta +\phi_1 Y_{t-1}+\phi_2 Y_{t-2}+...+\phi_p Y_{t-p}+e_t\]

donde $\delta$, es un término constante y $e_t$ es un ruido blanco, que representa los errores del ajuste y otorga el carácter aleatorio al proceso.

Haciendo uso del operador de retardos que veíamos anteriormente, el proceso también puede expresarse como:

\[Y_t=\delta + \phi_1 BY_{t}+\phi_2 B^2Y_{t}+...+\phi_p B^pY_{t}+e_t\]

operando:

\[(1-\phi_1B- \phi_2B^2-...-\phi_pB^p)Y_t=\phi_p(L)Y_t=\delta+e_t\]

Veamos a continuación las características particulares de dos procesos autorregresivos elementales, el de orden 1 ó AR(1) y el de orden 2, ó AR(2). Posteriormente, los resultados obtenidos se generalizarán al caso de un proceso autorregresivo de orden p, AR(p).

Modelos autorregresivos de primer orden AR(1)

Un proceso AR(1) se genera a partir de:

\[Y_t=\delta +\phi_1 Y_{t-1}+e_t\]

Si el proceso es estacionario en media y varianza entonces se verificará que $E(Y_t) = E(Y_{t-1})$ y $Var (Y_t) = Var(Y_{t-1})$, $\forall$ $t$ de tal forma que:

\[E(Y_t) = E(Y_{t-1})=\mu=\delta +\phi_1\mu \rightarrow \mu=\frac{\delta}{1-\phi_1}\]

\[Var(Y_t) = Var(Y_{t-1})=\gamma_0=\phi_1^2\gamma_0 +\sigma_e^2 \rightarrow \gamma_0=\frac{\sigma_e^2}{1-\phi_1^2}\]

La condición a cumplir para que $\mu$ y $\gamma_0$ sean positivas y finitas es que $|\phi_1|<1$. En ese caso, el proceso será estacionario en media y varianza. Del mismo modo, si el proceso es estacionario, también se verificará para las covarianzas que:

\[cov(Y_t,Y_{t-1})=cov(Y_{t-1},Y_t)=E[(Y_t-\mu)(Y_{t-1}-\mu)]=E(y_t y_{t-1})=\gamma_1\]

Dado que:

\[Y_t-\mu=\phi_1(Y_{t-1}-\mu)+e_t=y_t=\phi_1y_{t-1}+e_t\]

Entonces:

\[\gamma_1=E(y_{t-1} y_t)=E[y_{t-1} (\phi_1y_{t-1}+e_t)]=\phi_1 E(Y_{t-1}^2)+E(Y_{t-1}e_t)=\phi_1\gamma_0\]

El resultado anterior puede generalizarse si tomamos esperanzas entre $y_t$ e $y_{t-k}$ obteniéndose que, en general: $\gamma_k=\phi_1^k \gamma_0$

Resultados que dejan determinados los coeficientes de las funciones de autocorrelación simple (fas) y parcial (fap):

# Simulamos AR(1) con \phi_1=0.9
AR.1<-arima.sim(model=list(ar=c(.9)), n=100)
ts.plot(AR.1)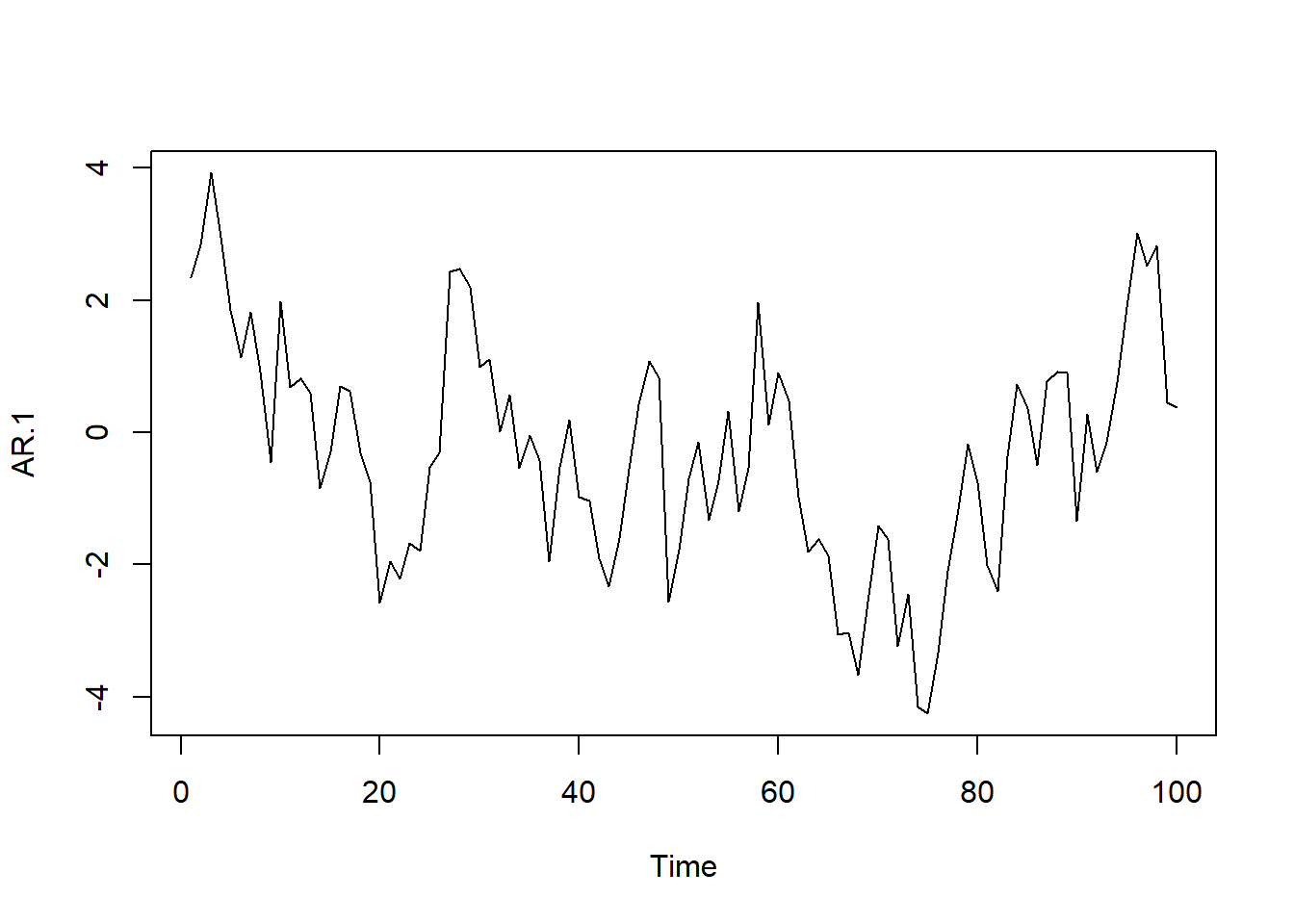

plot(acf(AR.1, type="correlation", plot=T))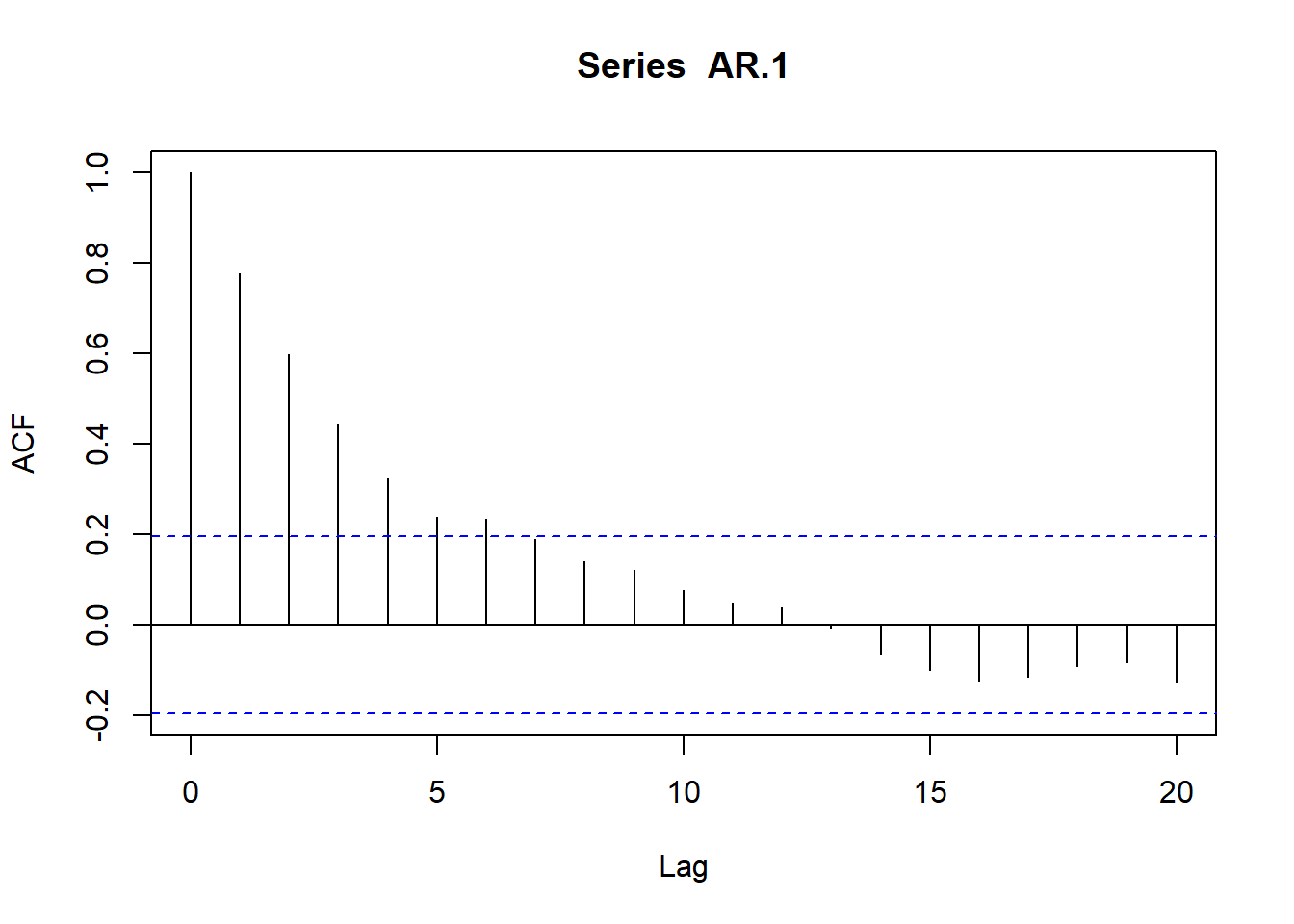

plot(acf(AR.1, type="partial", plot=T))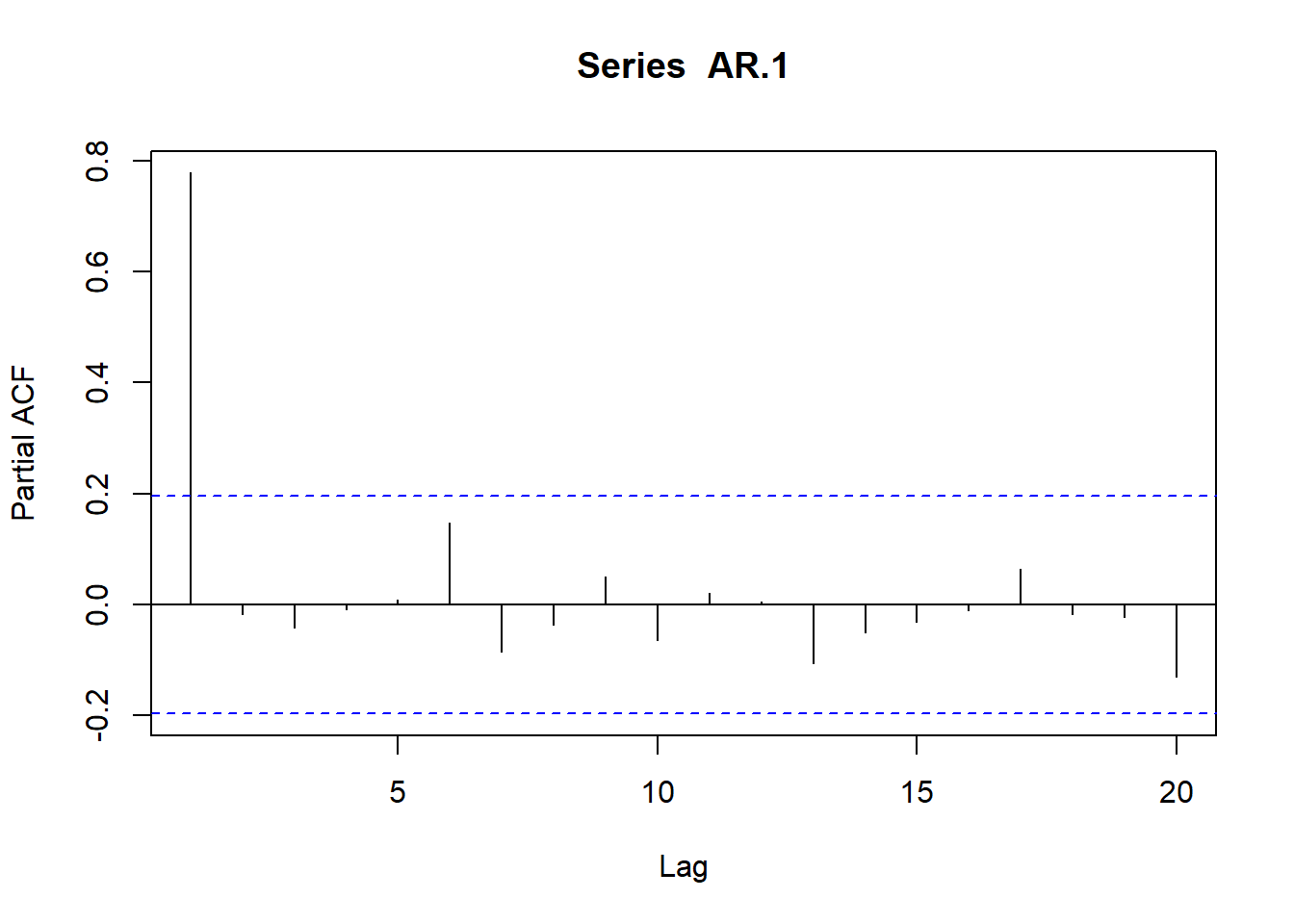

# Simulamos AR(1) con \phi_1=-0.9
AR.1<-arima.sim(model=list(ar=c(-.9)), n=100)
ts.plot(AR.1)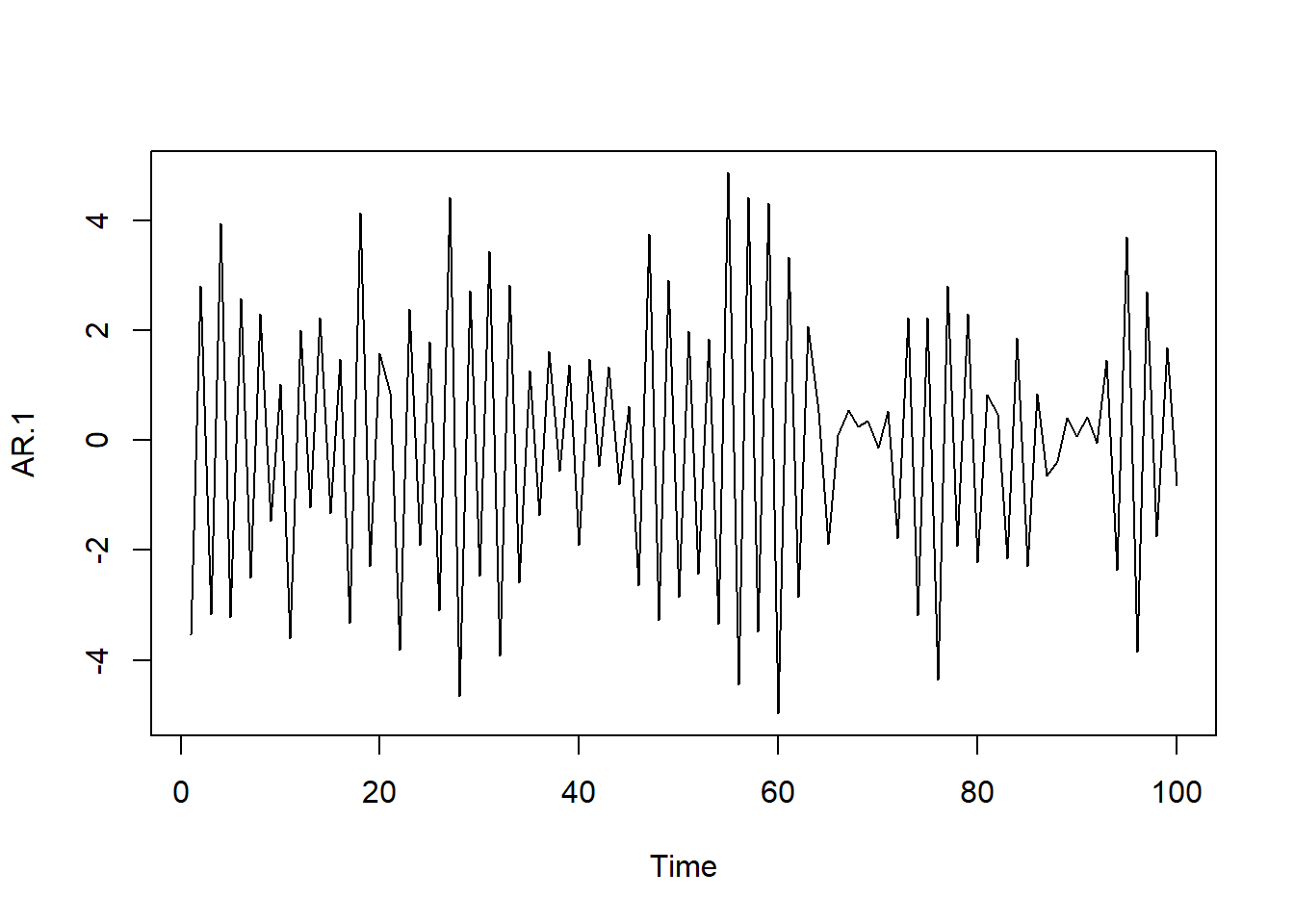

plot(acf(AR.1, type="correlation", plot=T))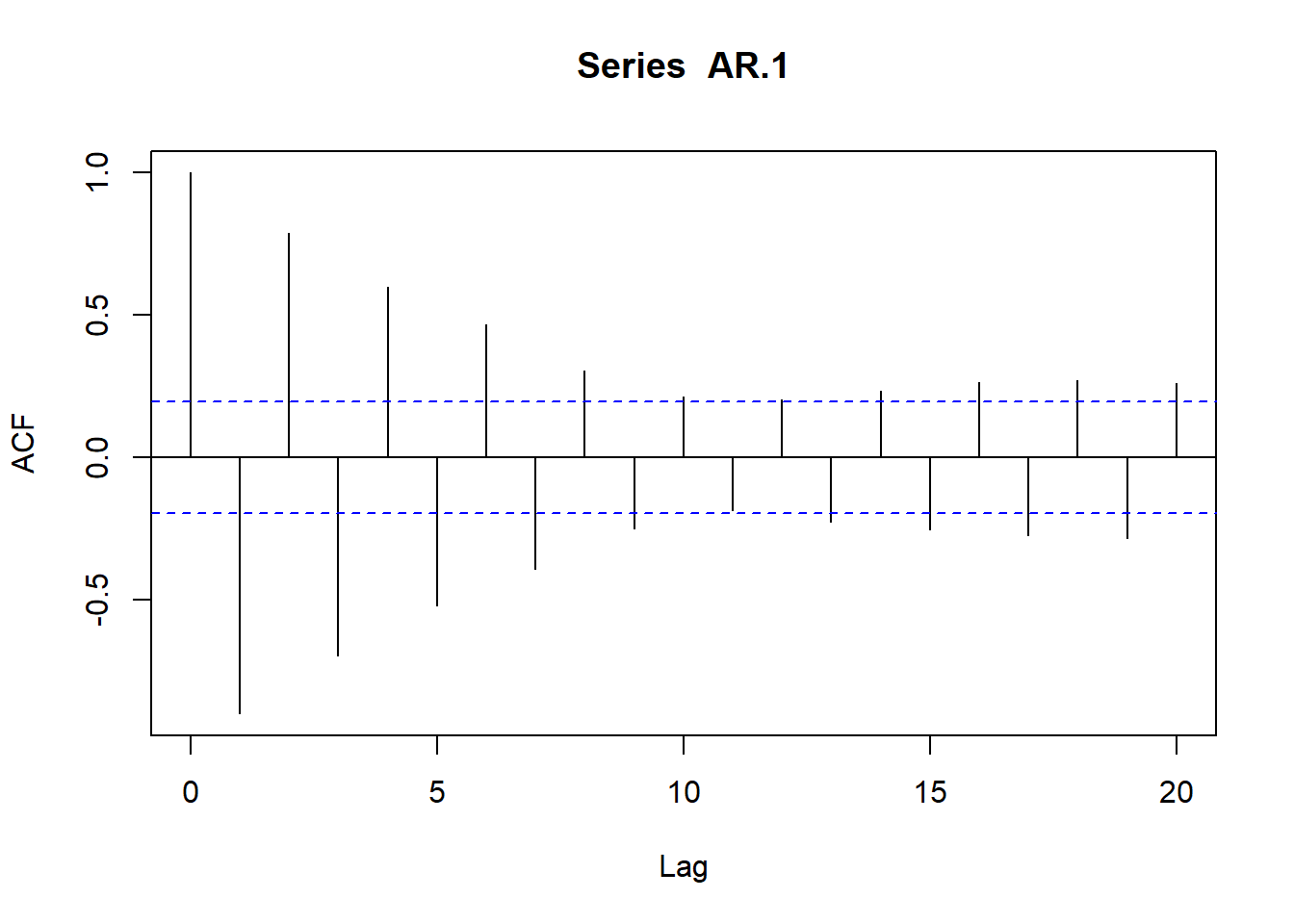

plot(acf(AR.1, type="partial",plot=T))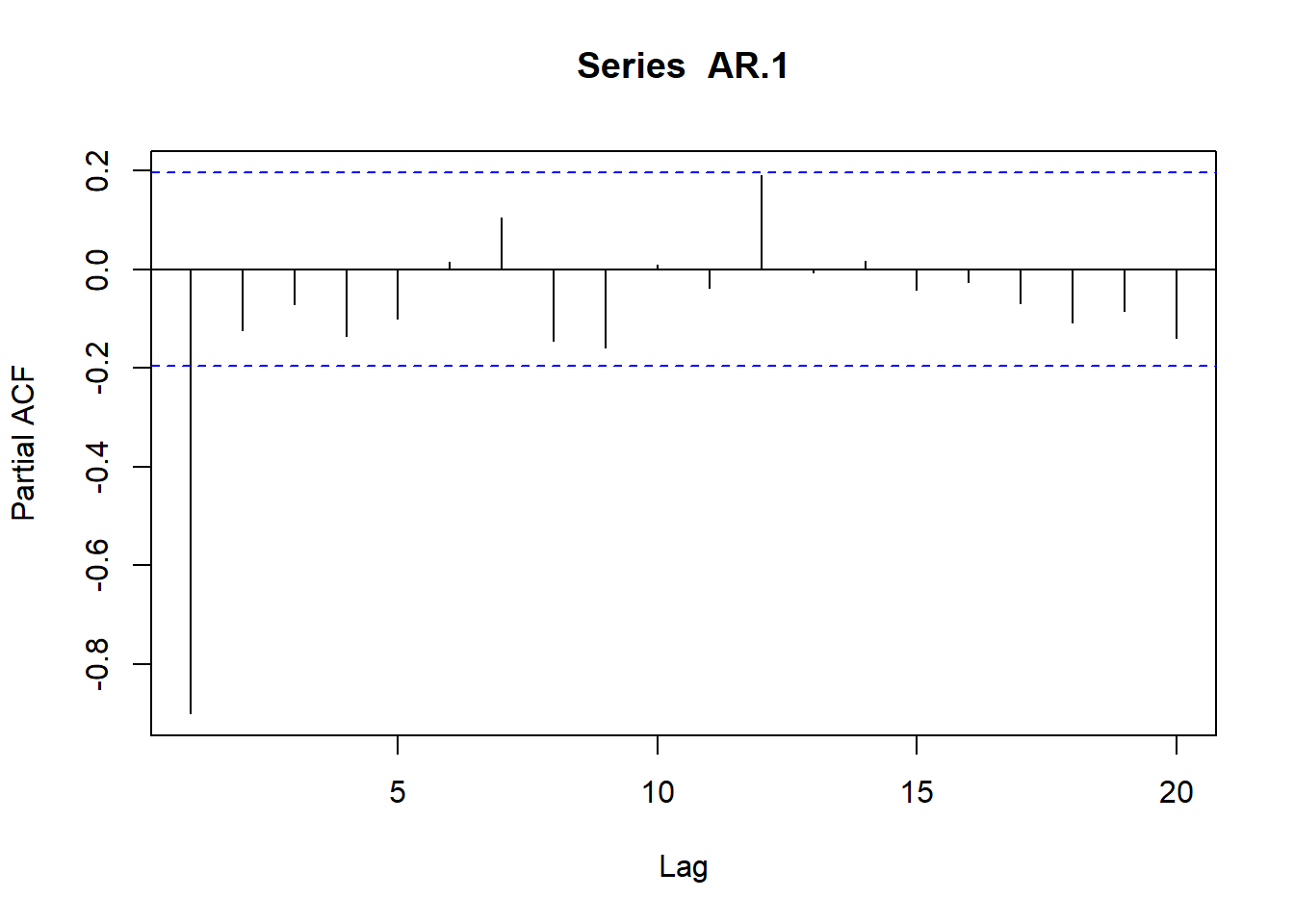

Modelos autorregresivos de segundo orden AR(2)

Un proceso AR(2) se genera a partir de:

\[Y_t=\delta +\phi_1 Y_{t-1} + \phi_2 Y_{t-2}+e_t\]

Si el proceso es estacionario en media y varianza entonces se verificará que $E(Y_t) = E(Y_{t-1})$ y $Var (Y_t) = Var(Y_{t-1})$, $\forall$ $t$ de tal forma que:

\[E(Y_t) = E(Y_{t-1})=\mu=\delta +\phi_1\mu+\phi_2\mu \rightarrow \mu=\frac{\delta}{1-\phi_1-\phi_2}\]

Debiéndose verificar, para que la media sea finita,que $\phi_1+\phi_2 \neq 1$.

\[Var(Y_t) = Var(Y_{t-1})=\gamma_0=\phi_1^2\gamma_0 + \phi_2^2\gamma_0+\sigma_e^2 \rightarrow \gamma_0=\frac{\sigma_e^2}{1-\phi_1^2-\phi_2^2}\]

También se verificará para las covarianzas que:

\[cov(Y_t,Y_{t-1})=cov(Y_{t-1},Y_t)=E[(Y_t-\mu)(Y_{t-1}-\mu)]=E(y_t y_{t-1})=\gamma_1\]

\[\gamma_1=E(y_{t-1} y_t)=E[y_{t-1} (\phi_1y_{t-1}+\phi_2y_{t-2}+e_t)]=\phi_1\gamma_0+\phi_2\gamma_1\]

\[\gamma_2=E(y_{t-2} y_t)=E[y_{t-2} (\phi_1y_{t-1}+\phi_2y_{t-2}+e_t)]=\phi_1\gamma_1+\phi_2\gamma_0\]

…

\[\gamma_k=E(y_{t-k} y_t)=E[y_{t-k} (\phi_1y_{t-1}+\phi_2y_{t-2}+e_t)]=\phi_1\gamma_{k-1}+\phi_2\gamma_{k-2}\]

De donde podemos derivar las expresiones para los coeficientes de la fas y la fap.

# Simulamos AR(2) con \phi_1=0.5 y \phi_2=0.2
AR.2<-arima.sim(model=list(ar=c(0.5,.2)),n=100)
ts.plot(AR.2)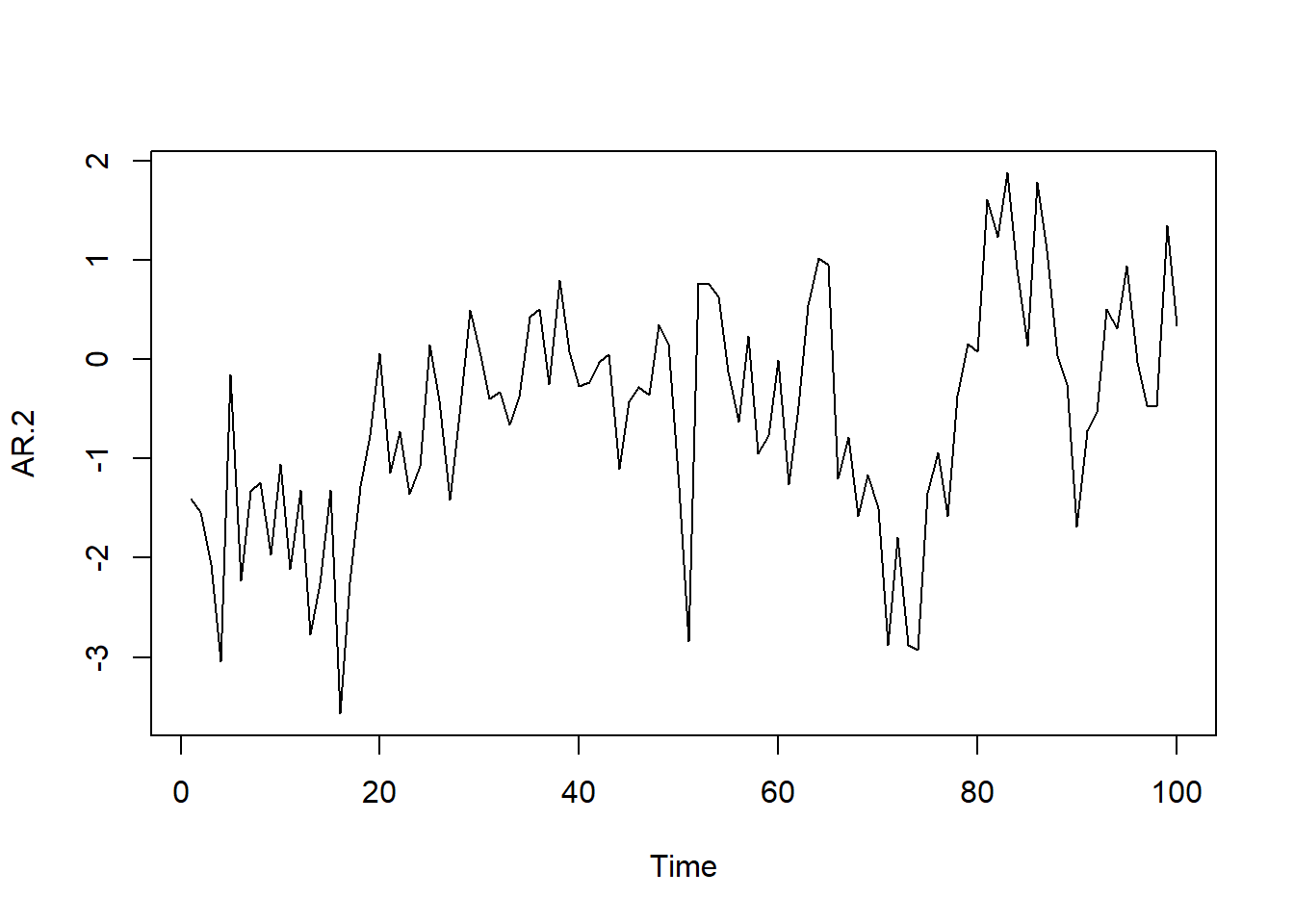

plot(acf(AR.2,type="correlation",plot=T))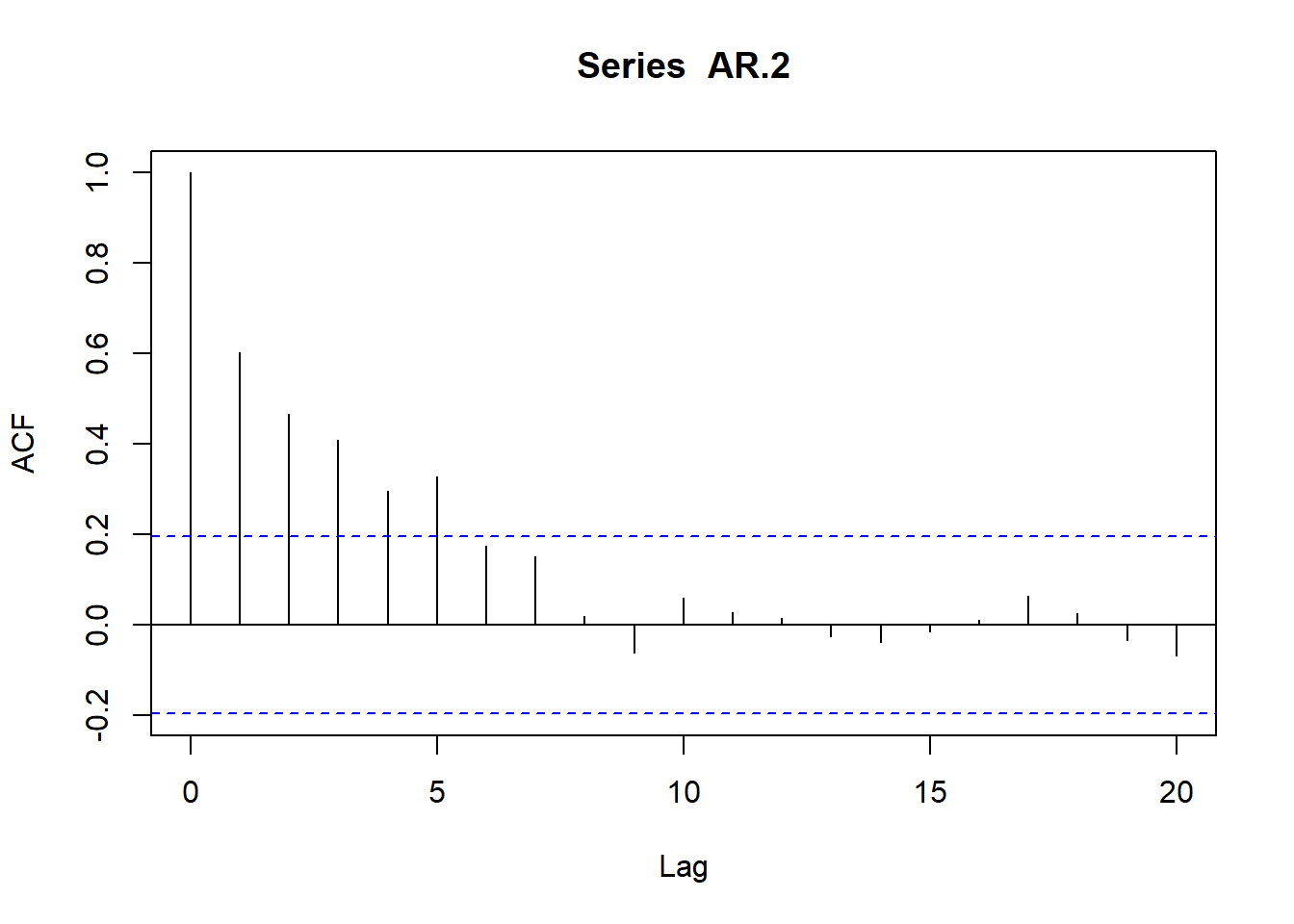

plot(acf(AR.2,type="partial",plot=T))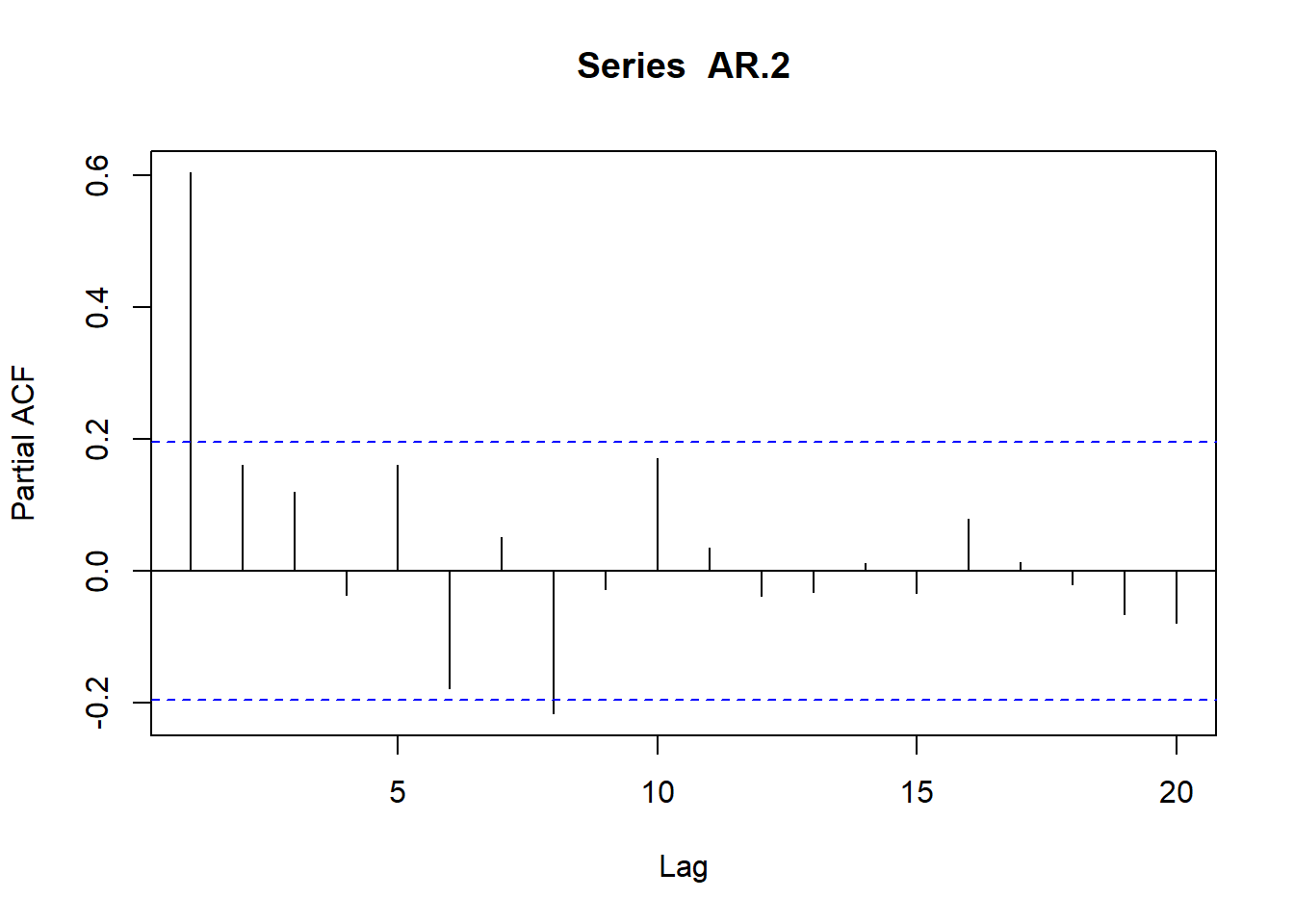

# Simulamos AR(2) con \phi_1=0.5 y \phi_2=-0.2
AR.2<-arima.sim(model=list(ar=c(.5,-.2)),n=100)
ts.plot(AR.2)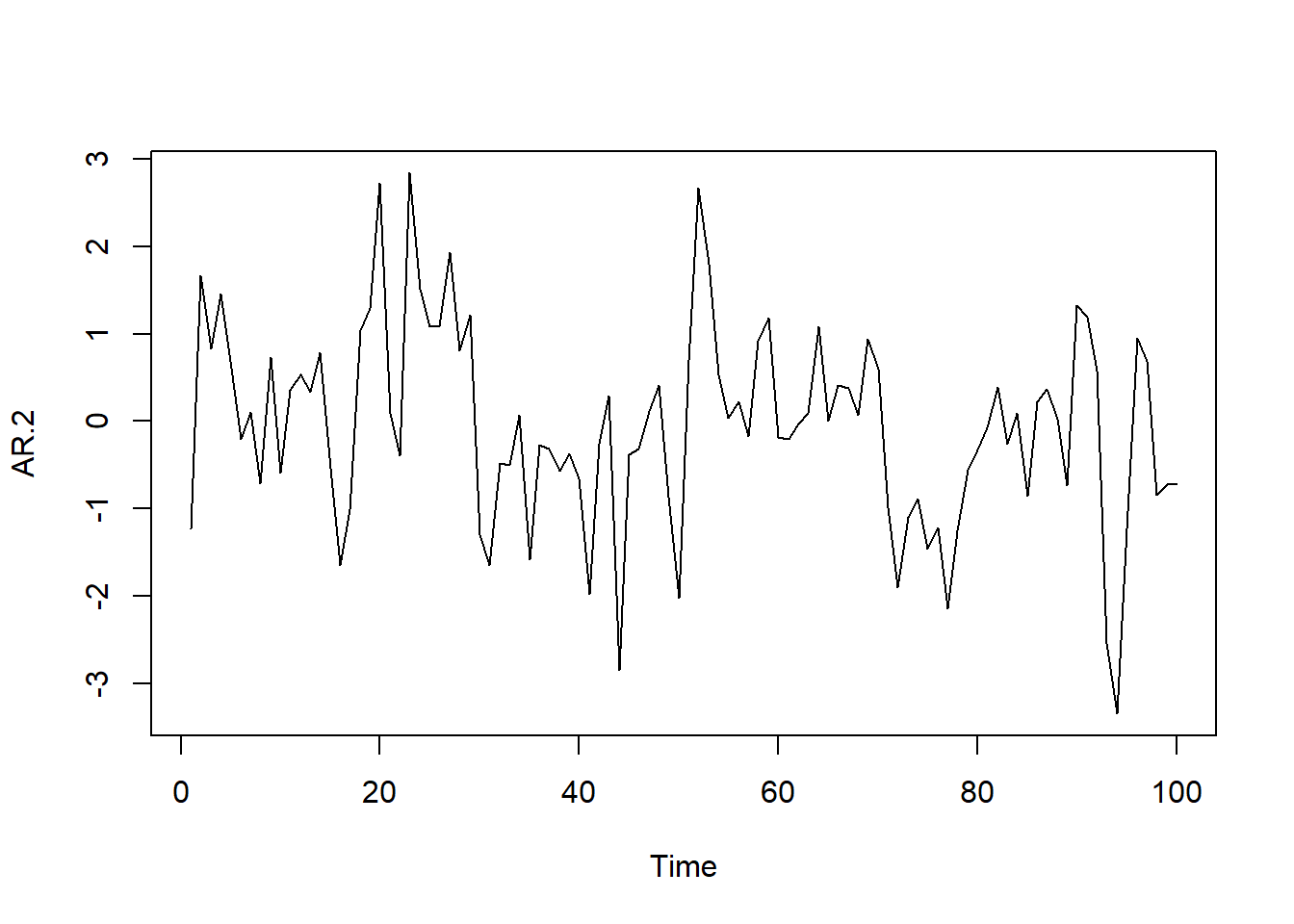

plot(acf(AR.2,type="correlation",plot=T))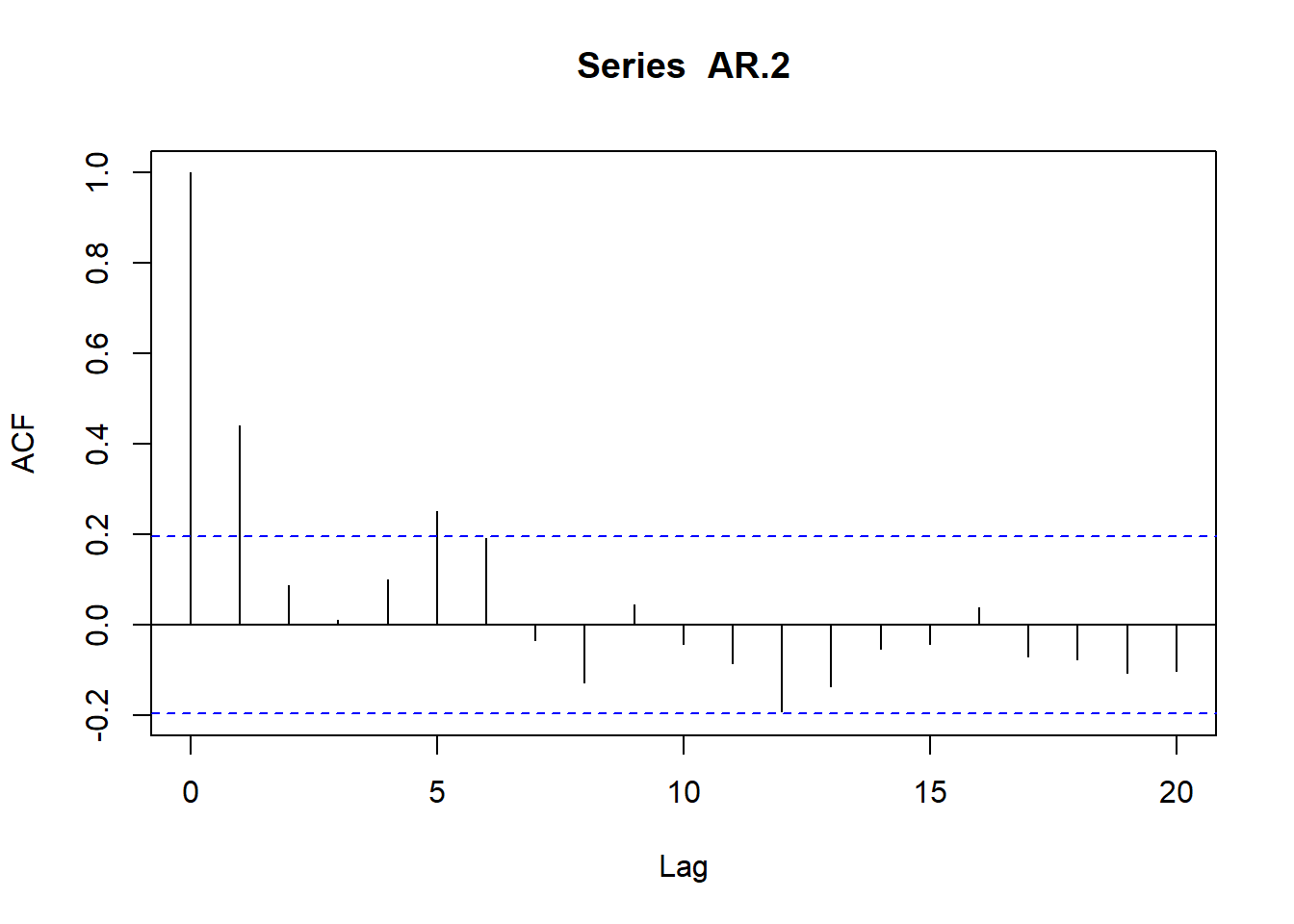

plot(acf(AR.2,type="partial",plot=T))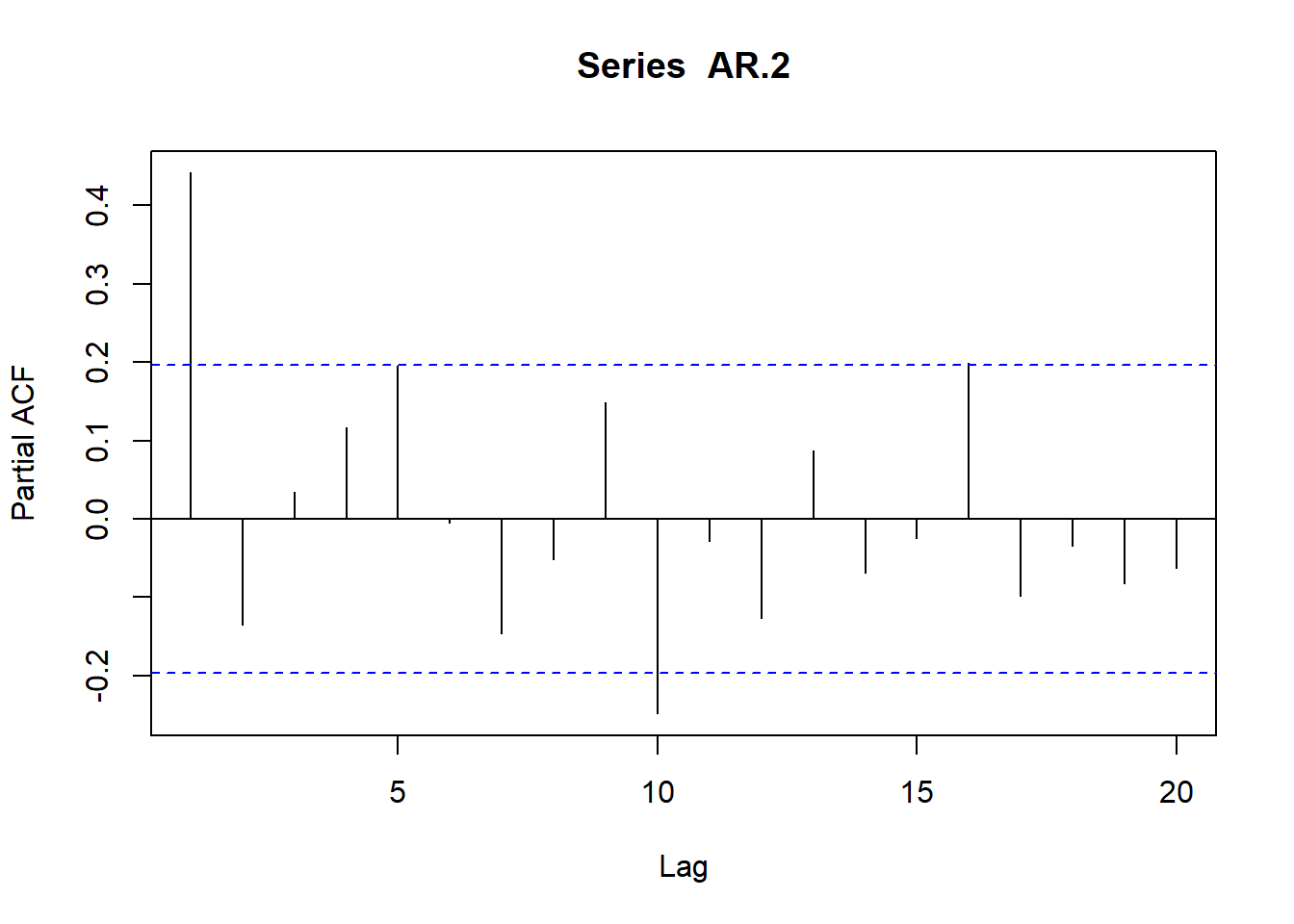

La condición de estacionariedad utilizando la notación en retardos es que las raíces del polinomio de retardos, al igual que en el caso del proceso AR(1), estén fuera del círculo unidad de tal forma que verifiquen: $(1-\phi_1B-\phi_2B^2)=0$

Modelos autorregresivos de primer orden AR(p)

A partir de los resultados obtenidos para los procesos AR(1) y AR(2), podemos generalizar las expresiones obtenidas para un proceso de orden p.

Sea el proceso autorregresivo de orden p:

\[Y_t=\delta +\phi_1 Y_{t-1} +\phi_2 Y_{t-2} +...+ \phi_p Y_{t-p}+ e_t\]

Si el proceso es estacionario en media y varianza entonces se verificará que $E(Y_t) = E(Y_{t-1})$ y $Var (Y_t) = Var(Y_{t-1})$, $\forall$ $t$ de tal forma que:

\[E(Y_t) = E(Y_{t-1}) \rightarrow \mu=\frac{\delta}{1-\phi_1-\phi_2-...-\phi_p}\]

Debiéndose verificar, para que la media sea finita,que $\phi_1+...+\phi_p \neq 1$.

\[Var(Y_t) = Var(Y_{t-1}) \rightarrow \gamma_0=\frac{\sigma_e^2}{1-\phi_1^2-\phi_2^2...-\phi_p^2}\]

También se verificará para las covarianzas que:

\[\gamma_1=\phi_1\gamma_0+\phi_2\gamma_1+...+\phi_p\gamma_{p-1}\]

\[\gamma_2=\phi_1\gamma_1+\phi_2\gamma_0+...+\phi_p\gamma_{p-2}\]

…

\[\gamma_k=\phi_1\gamma_{k-1}+\phi_2\gamma_{k-2}+...+\phi_p\gamma_{p-k}\]

Dichas ecuaciones también se pueden expresar en términos de los coeficientes de autocorrelación dividiendo por $\gamma_0$ ambos miembros (ecuaciones de Yule-Walker), tal que:

\[\rho_1=\phi_1\rho_0+\phi_2\rho_1+...+\phi_p\rho_{p-1}\]

\[\rho_2=\phi_1\rho_1+\phi_2\rho_0+...+\phi_p\rho_{p-2}\]

…

\[\rho_k=\phi_1\rho_{k-1}+\phi_2\rho_{k-2}+...+\phi_p\rho_{p-k}\]

Si se resuelve sucesivamente el sistema de ecuaciones de Yule-Walker bajo la hipótesis de que la serie es un AR(1), AR(2), AR), etc., y se toma el último coeficiente de cada uno de los procesos, se obtiene lo que se conoce como función de autocorrelación parcial (fap); dicha función mide el coeficiente de correlación entre observaciones separadas k períodos, eliminando el efecto de los valores intermedios.

Dado que p es el orden del proceso autorregresivo, resulta evidente que los coeficientes de autocorrelación parcial serán distintos de cero para retardos iguales o inferiores a p.

Finalmente, y de forma análoga a los resultados obtenidos en los procesos AR(1) y AR(2), para que un proceso autorregresivo de orden p sea estacionario, las raíces del polinomio de retardos del proceso,$(1-\phi_1B-\phi_2B^2-...-\phi_pB^p)=0$, deberán ser menores a la unidad en valor absoluto.

8.4.1.5.2 Modelos de media móvil MA(p)

En los procesos de media móvil de orden q, cada observación $Y_t$ es generada por una media ponderada de perturbaciones aleatorias con un retardo de q períodos, tal que:

\[Y_t=\delta +e_t - \theta_1 e_{t-1} -\theta_2 e_{t-2} -...- \theta_q e_{t-q}\]

donde $e_t$ es un ruido blanco.

Pasamos a ver a continuación las características particulares de dos procesos de medias móviles básicos, el de orden 1 ó MA(1), y el de orden 2 ó MA(2). Posteriormente, los resultados obtenidos se generalizarán, como ya hicimos en el caso de los procesos autorregresivos, al caso de un proceso de medias móviles de orden q, MA(q).

Modelos de medias móviles de primer orden MA(1)

Veamos el caso particular de un proceso de media móvil de orden 1 ó MA(1). Formalmente su expresión sería:

\[Y_t=\delta +e_t - \theta_1 e_{t-1}\]

siendo su media $E(Y_t) =\delta$ y su varianza $Var (Yt) = Var(e_t) + \theta_1^2 Var(e_{t-1})=\sigma^2_e(1+\theta_1^2)=\gamma_0$

En el caso de las covarianzas tenemos que:

\[\gamma_1=E[(Y_t-\delta)(Y_{t-1}-\delta)]=E[(e_t-\theta_1 e_{t-1})((e_{t-1}-\theta_1 e_{t-2})]=-\theta_1\sigma^2_e\]

\[\gamma_2=E[(Y_t-\delta)(Y_{t-2}-\delta)]=E[(e_t-\theta_1 e_{t-1})((e_{t-2}-\theta_1 e_{t-3})]=0\]

…

\[\gamma_k=0\]

El resultado obtenido pone de manifiesto que los procesos de media móvil poseen memoria de sólo un período, ya que cualquier valor de $Y_t$ está correlacionado con $Y_{t-1}$ e $Y_{t+1}$ pero con ningún otro valor de la serie.

A partir de las expresiones anteriores, y de modo análogo a como procedíamos en el caso de los modelos AR, podemos obtener los coeficientes de la fas y la fap.

# Simulamos MA(1) con \theta_1=-0.7
MA.1<-arima.sim(model=list(ma=c(-.7)),n=100)
ts.plot(MA.1)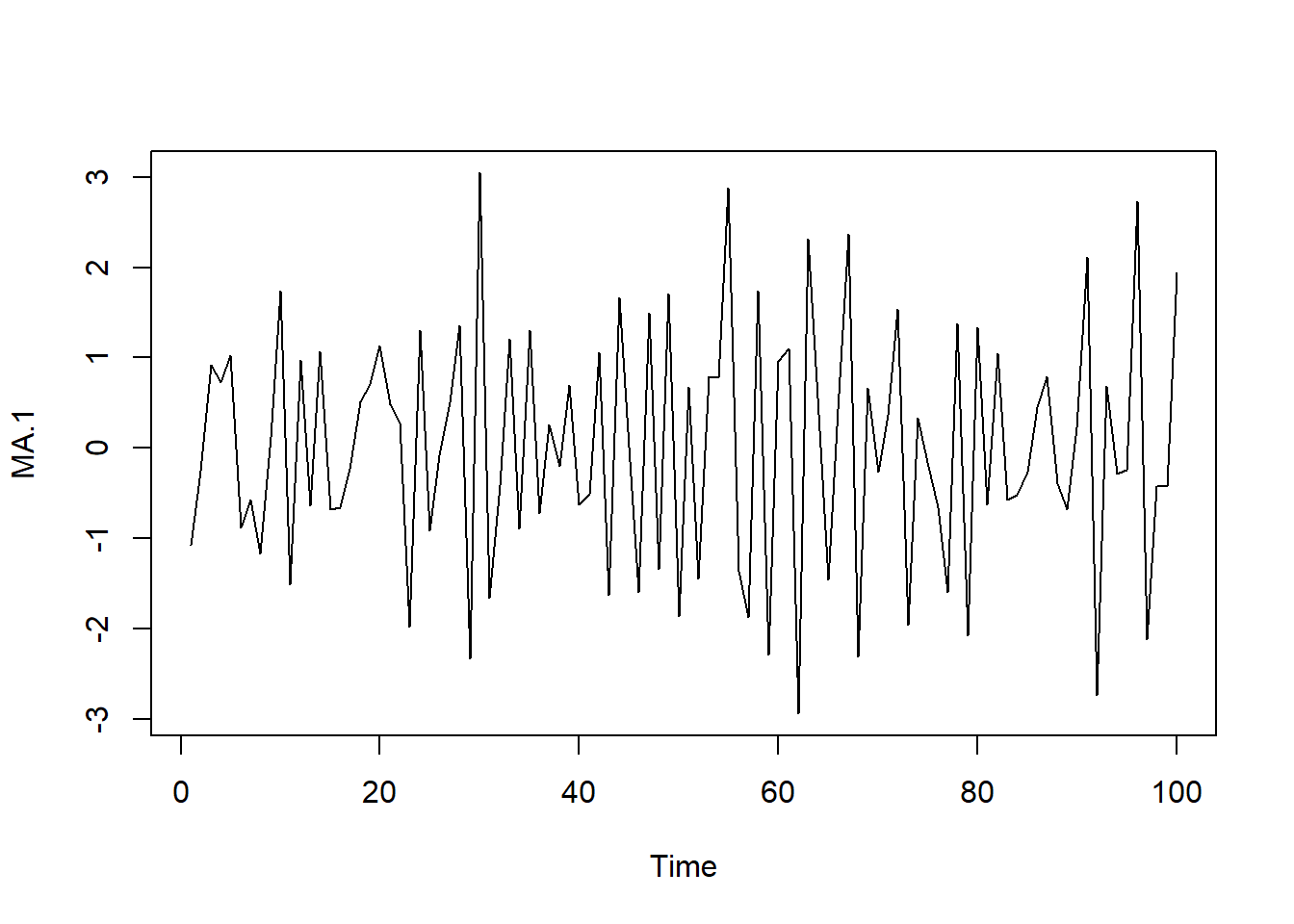

plot(acf(MA.1,type="correlation",plot=T))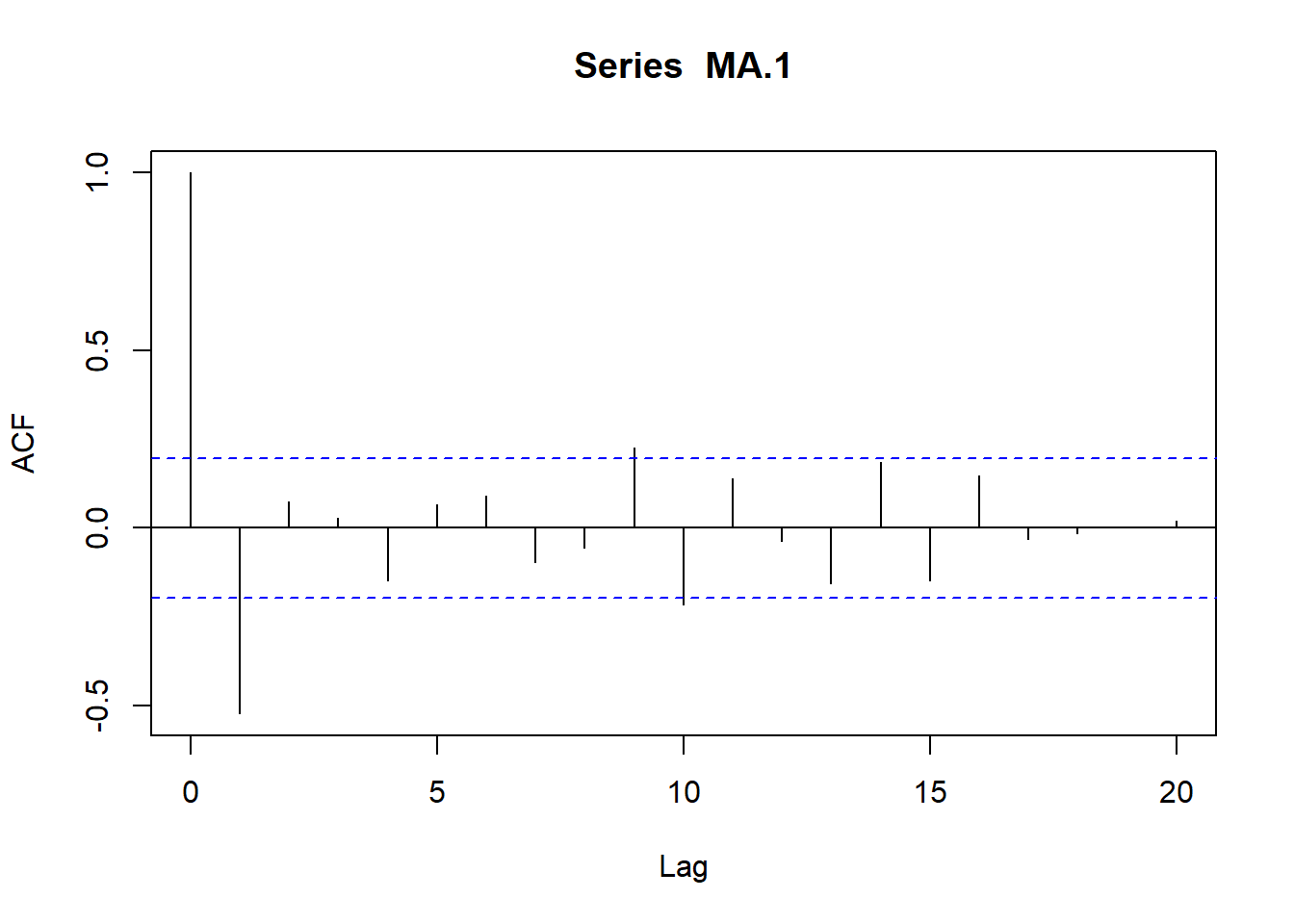

plot(acf(MA.1,type="partial",plot=T))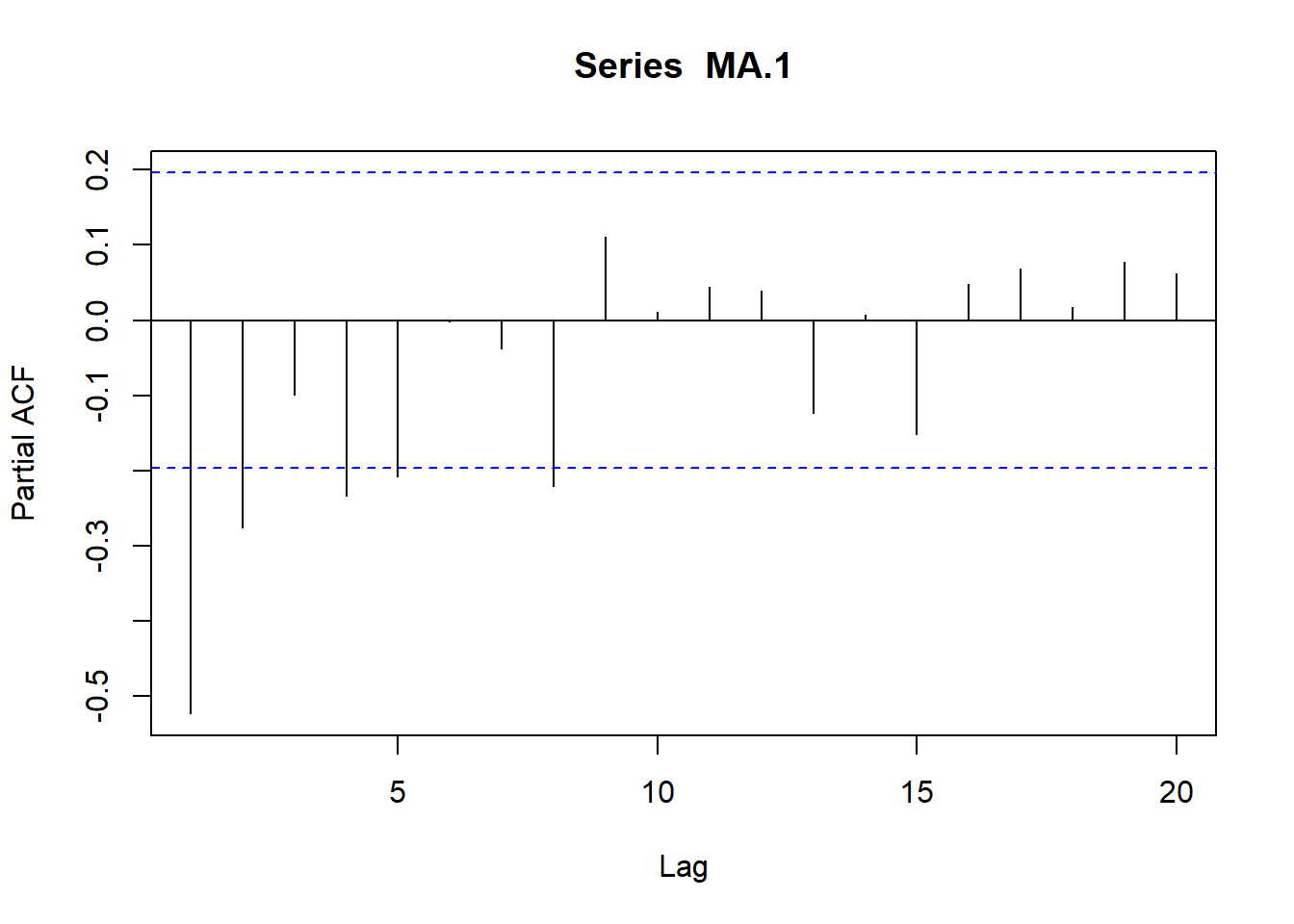

# Simulamos MA(1) con \theta_1=+0.7
MA.1<-arima.sim(model=list(ma=c(.7)),n=100)
ts.plot(MA.1)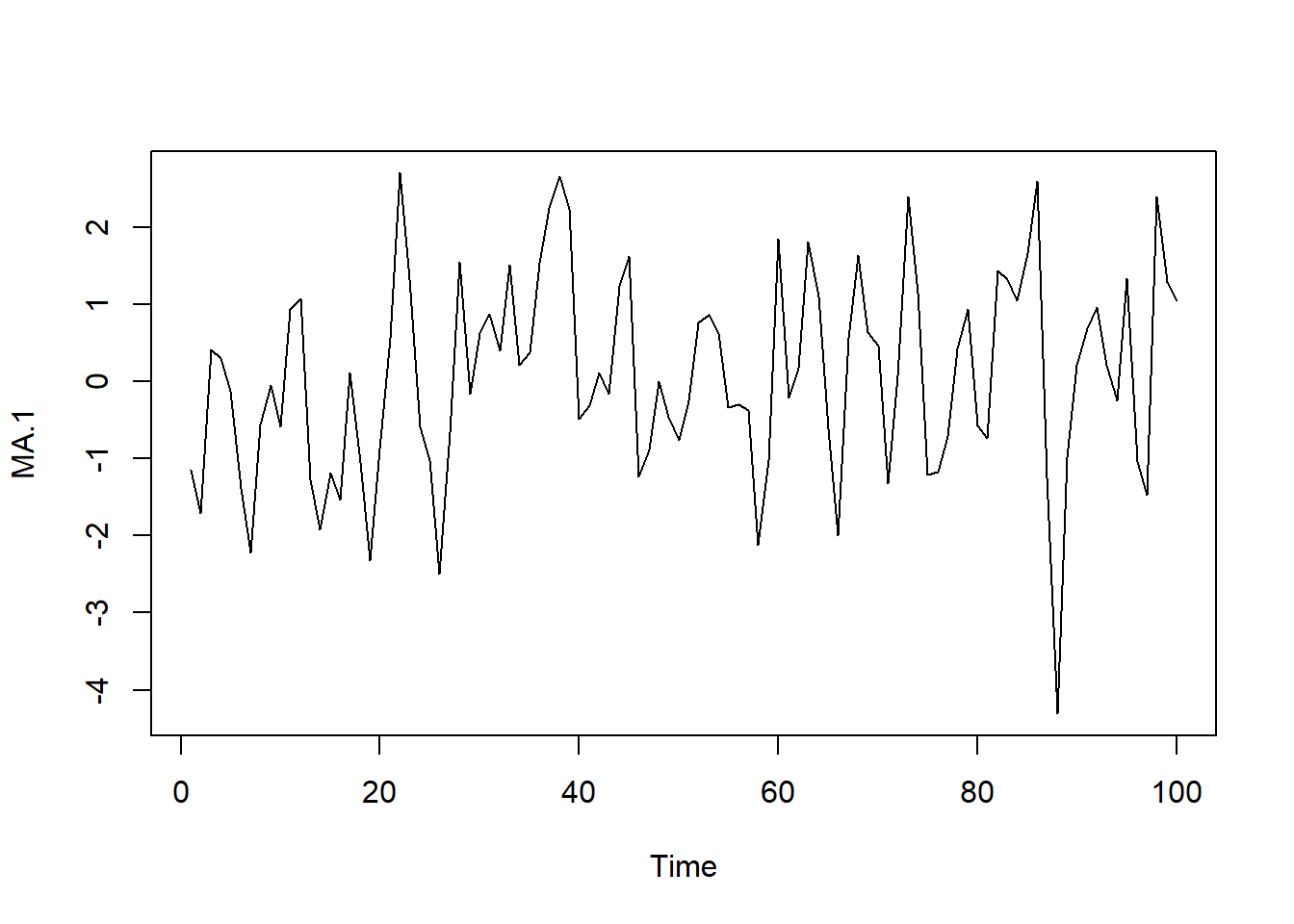

plot(acf(MA.1,type="correlation",plot=T))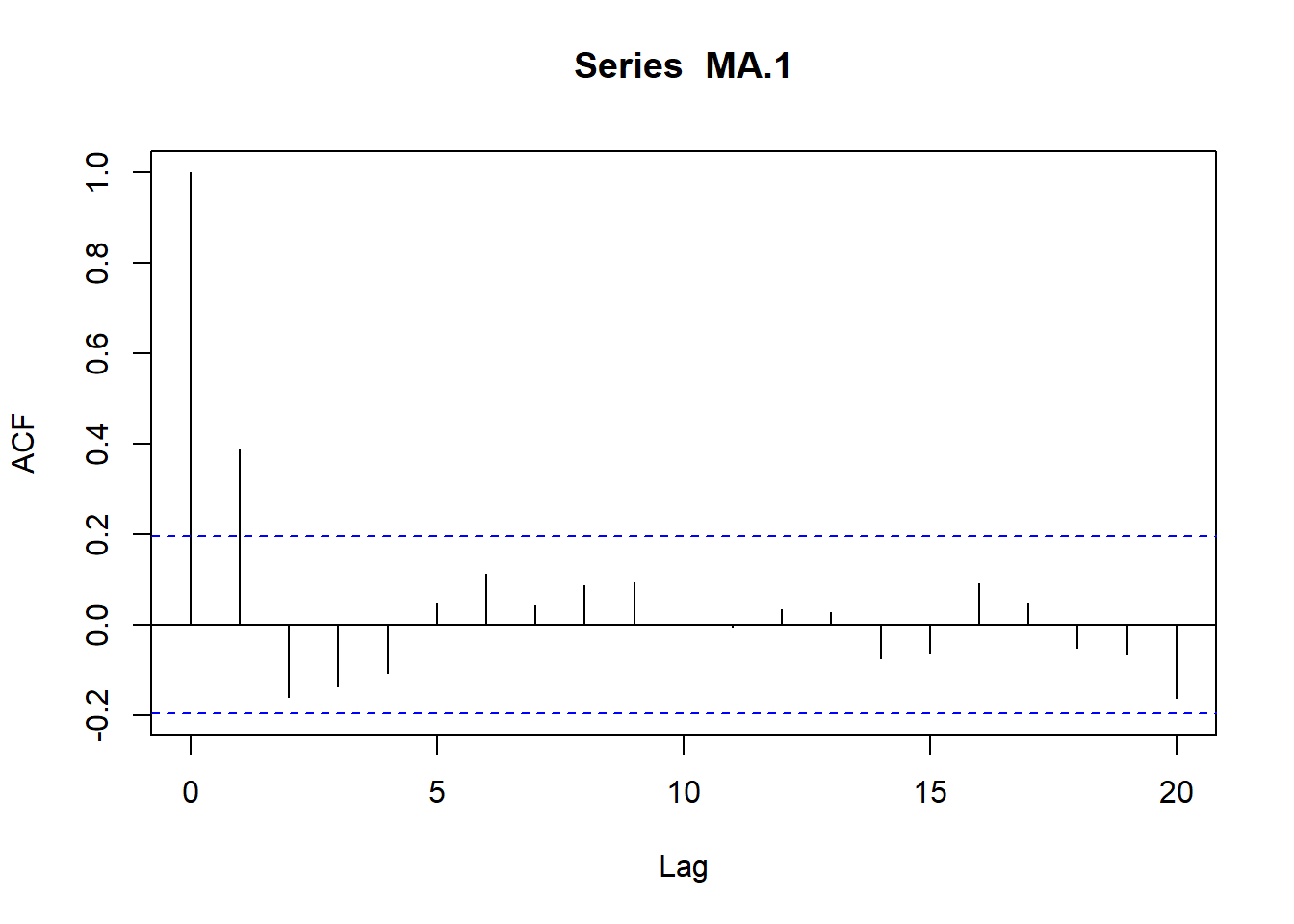

plot(acf(MA.1,type="partial",plot=T))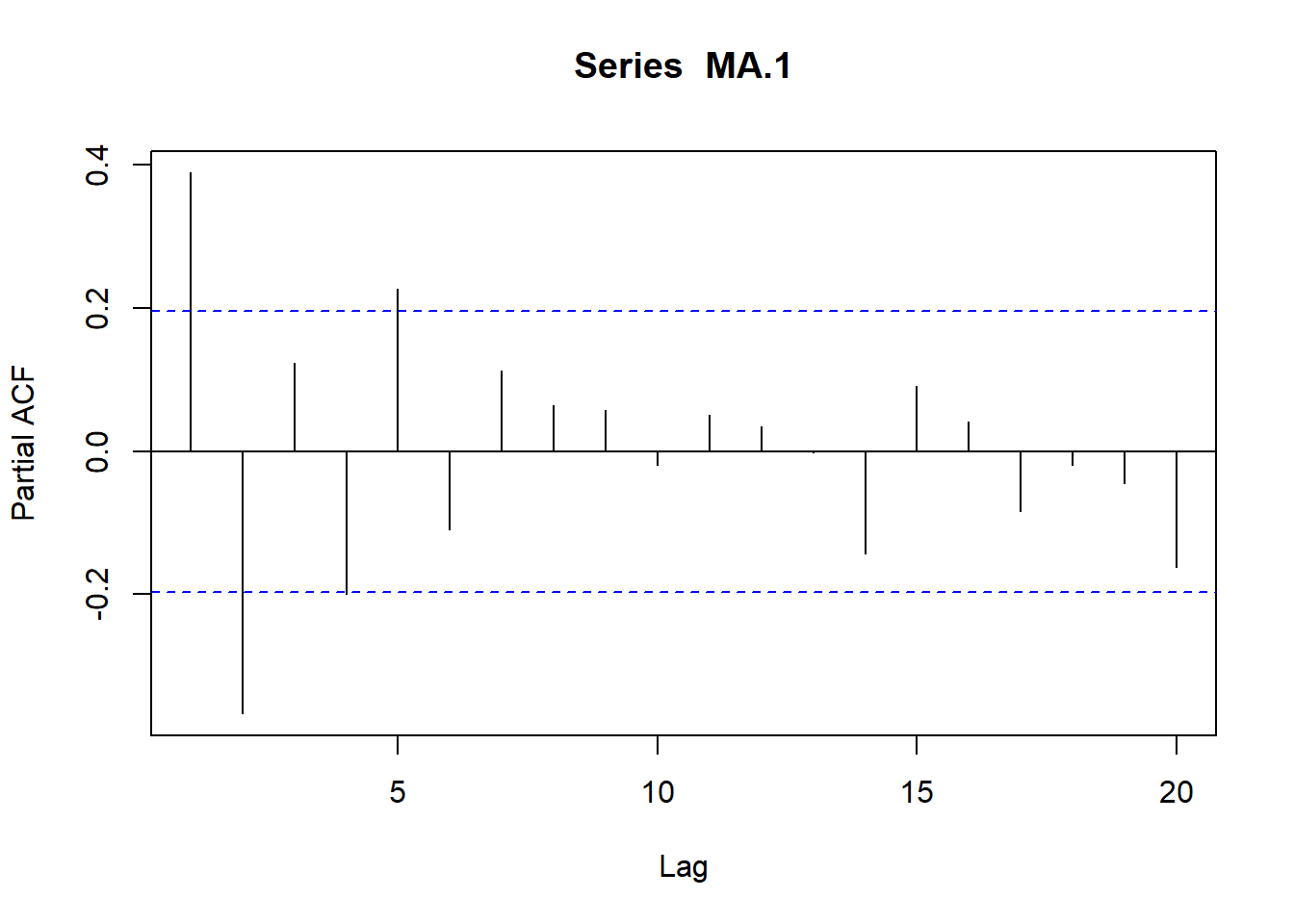

De todos estos resultados se desprende que un proceso MA(1) siempre es estacionario con independencia del valor de $\theta_1$.

La representación gráfica de la función de autocorrelación simple viene determinada por el signo de $\theta_1$.

Modelos de medias móviles de segundo orden MA(2)

Analizamos ahora el caso particular de un proceso de media móvil de orden 2 ó MA(2). Formalmente su expresión sería:

\[Y_t=\delta +e_t - \theta_1 e_{t-1} - \theta_2 e_{t-2}\]

siendo su media $E(Y_t) =\delta$ y su varianza $Var (Y_t) = Var(e_t) + \theta_1^2 Var(e_{t-1}) + \theta_2^2 Var(e_{t-2})=\sigma^2_e(1+\theta_1^2+\theta_2^2)=\gamma_0$.

Las covarianzas del proceso son:

\[\gamma_1=E[(Y_t-\delta)(Y_{t-1}-\delta)]=E[(e_t-\theta_1 e_{t-1}-\theta_2 e_{t-2})((e_{t-1}-\theta_1 e_{t-2})-\theta_2 e_{t-3})]=(-\theta_1+\theta_1 \theta_2) \sigma^2_e\]

\[\gamma_2=E[(Y_t-\delta)(Y_{t-2}-\delta)]=E[(e_t-\theta_1 e_{t-1}-\theta_2 e_{t-2})((e_{t-2}-\theta_1 e_{t-3}-\theta_2 e_{t-4})]=-\theta_2 \sigma^2_e\]

…

\[\gamma_k=0\]

Y a partir de las expresiones anteriores, y de modo análogo a como procedíamos en el caso de los modelos AR, podemos obtener los coeficientes de la fas y la fap.

# Simulamos MA(2) con \theta_1=-0.7 y \theta_2=0.1
MA.2<-arima.sim(model=list(ma=c(-.7,.1)),n=100)
ts.plot(MA.2)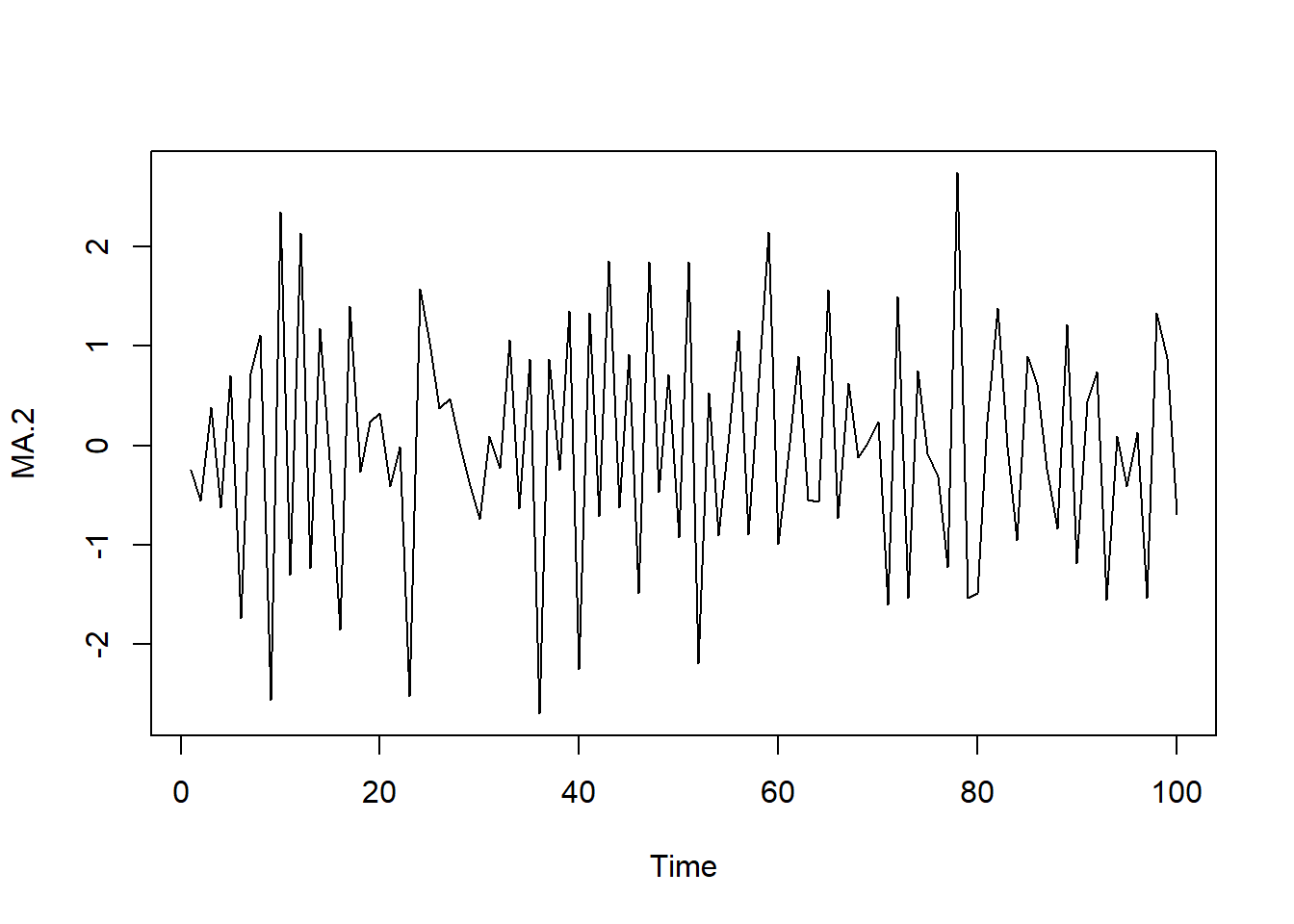

plot(acf(MA.2,type="correlation",plot=T))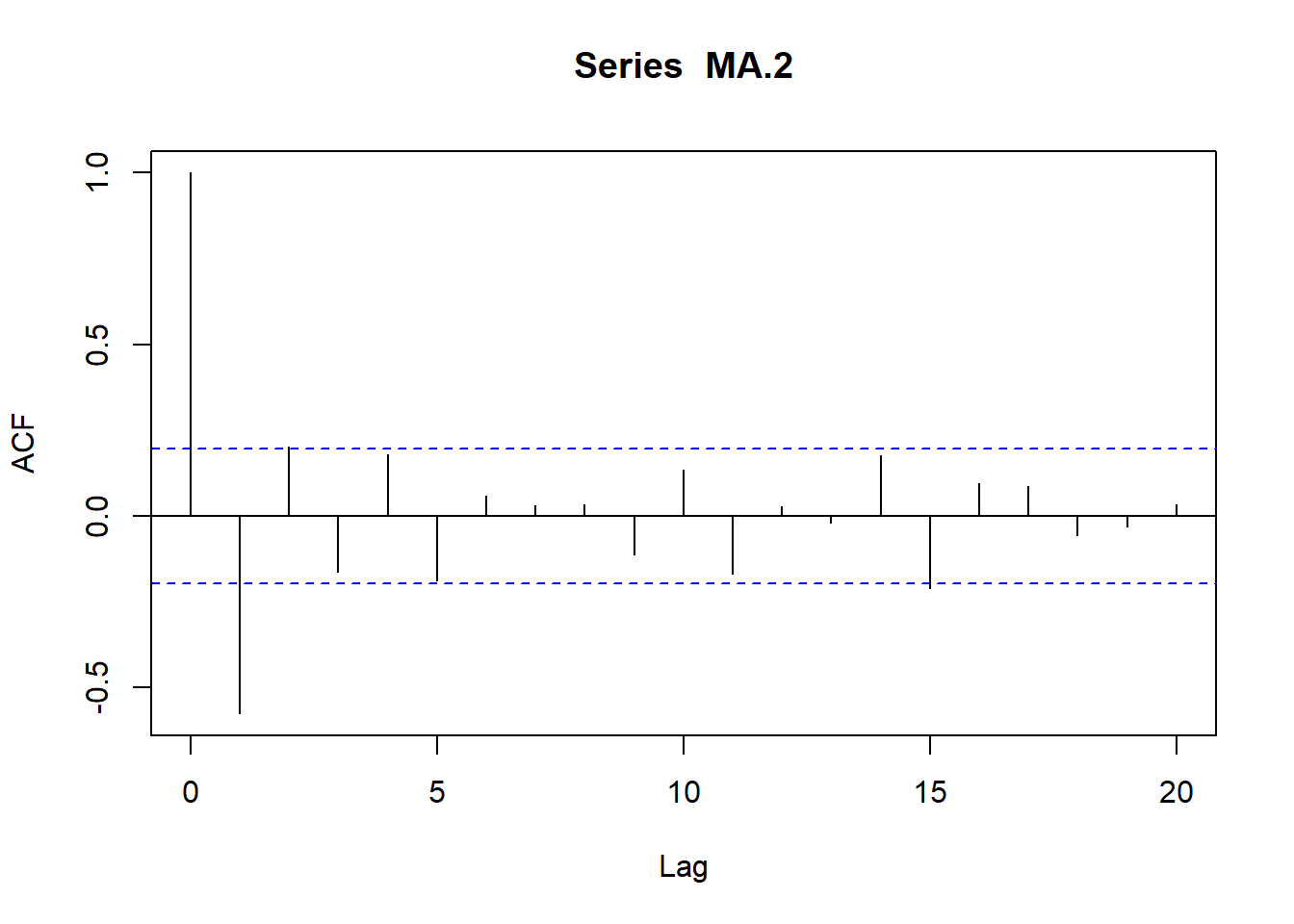

plot(acf(MA.2,type="partial",plot=T))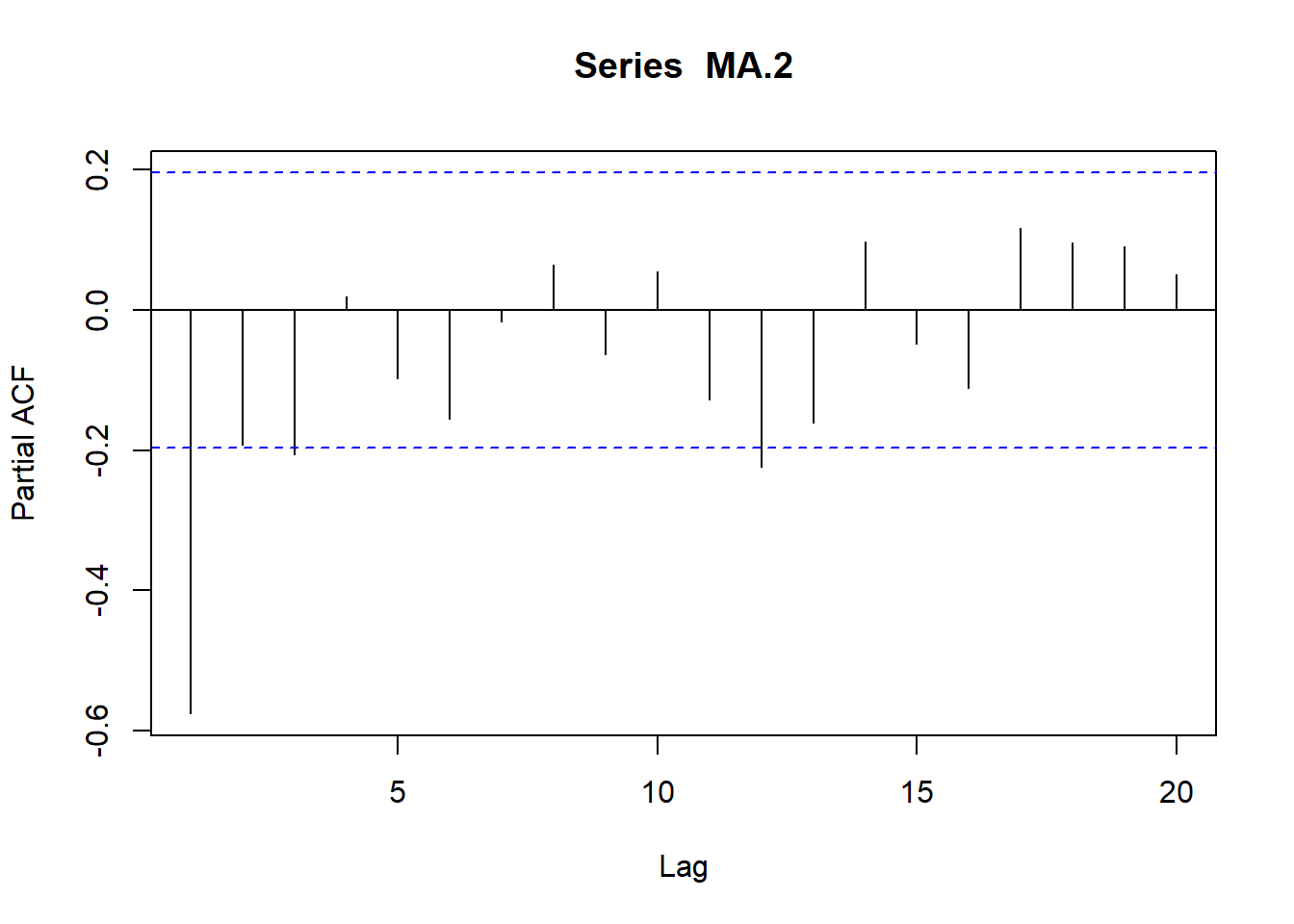

# Simulamos MA(2) con \theta_1=+0.7 y \theta_2=0.1
MA.2<-arima.sim(model=list(ma=c(.7,.1)),n=100)
ts.plot(MA.2)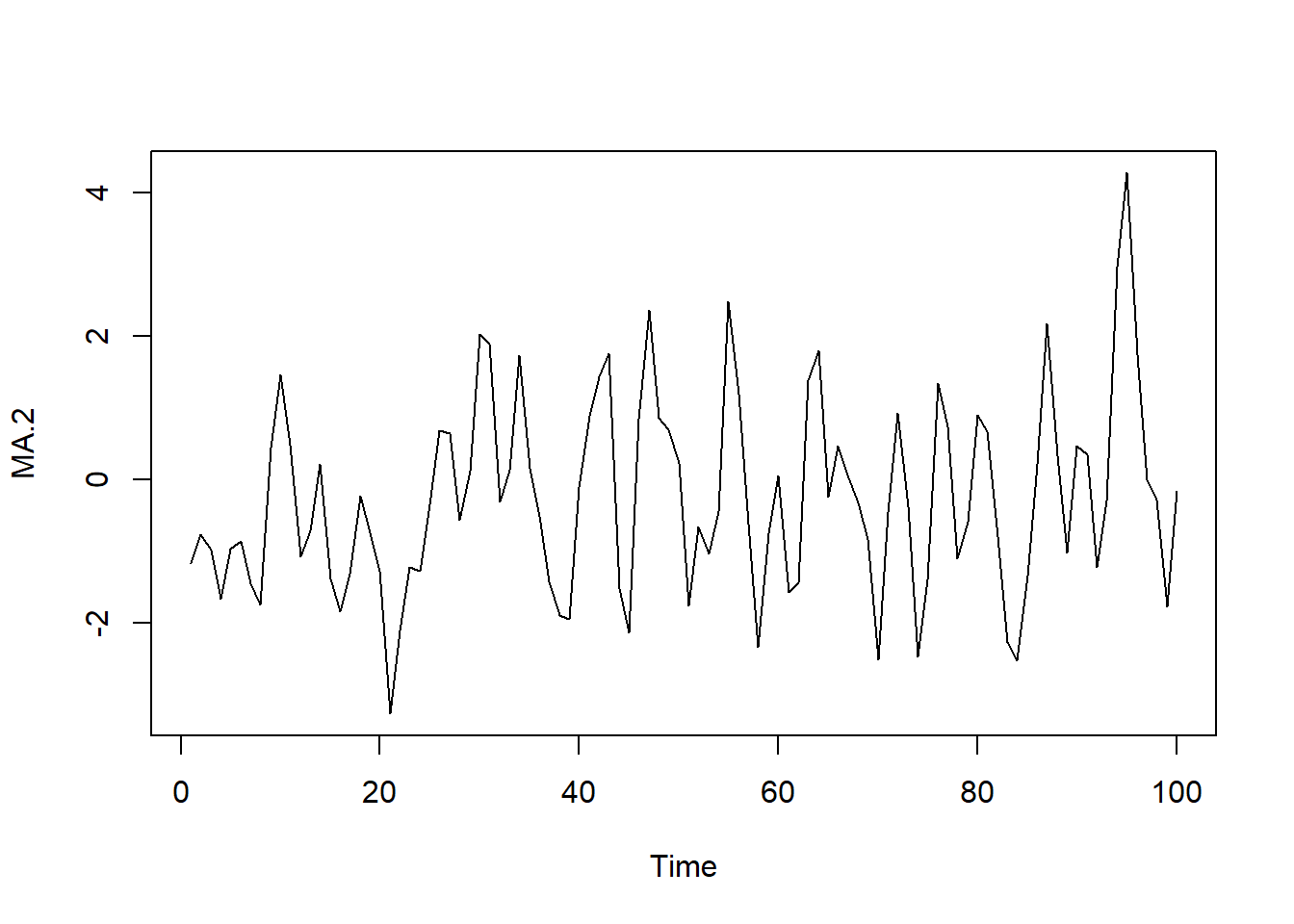

plot(acf(MA.2,type="correlation",plot=T))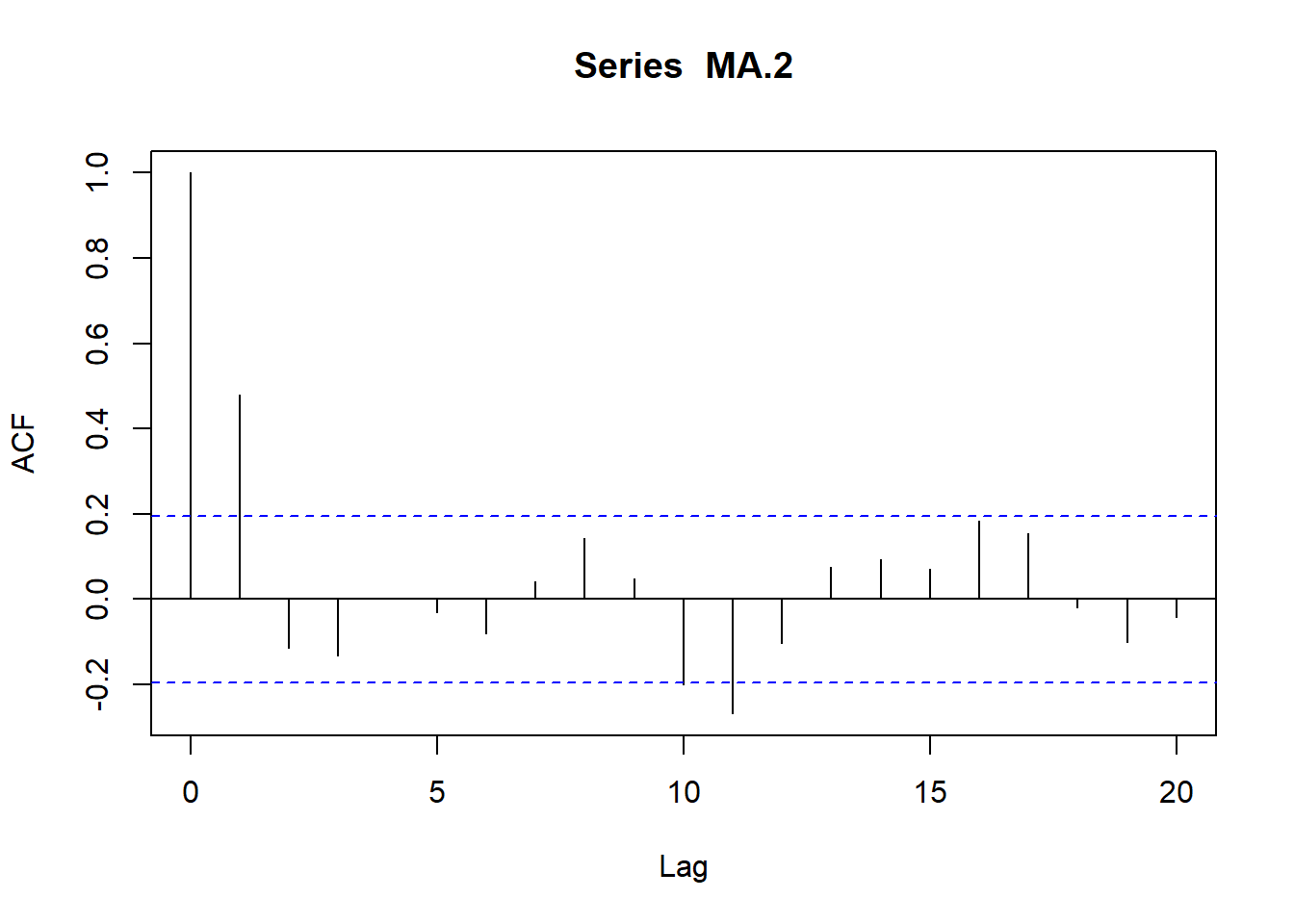

plot(acf(MA.2,type="partial",plot=T))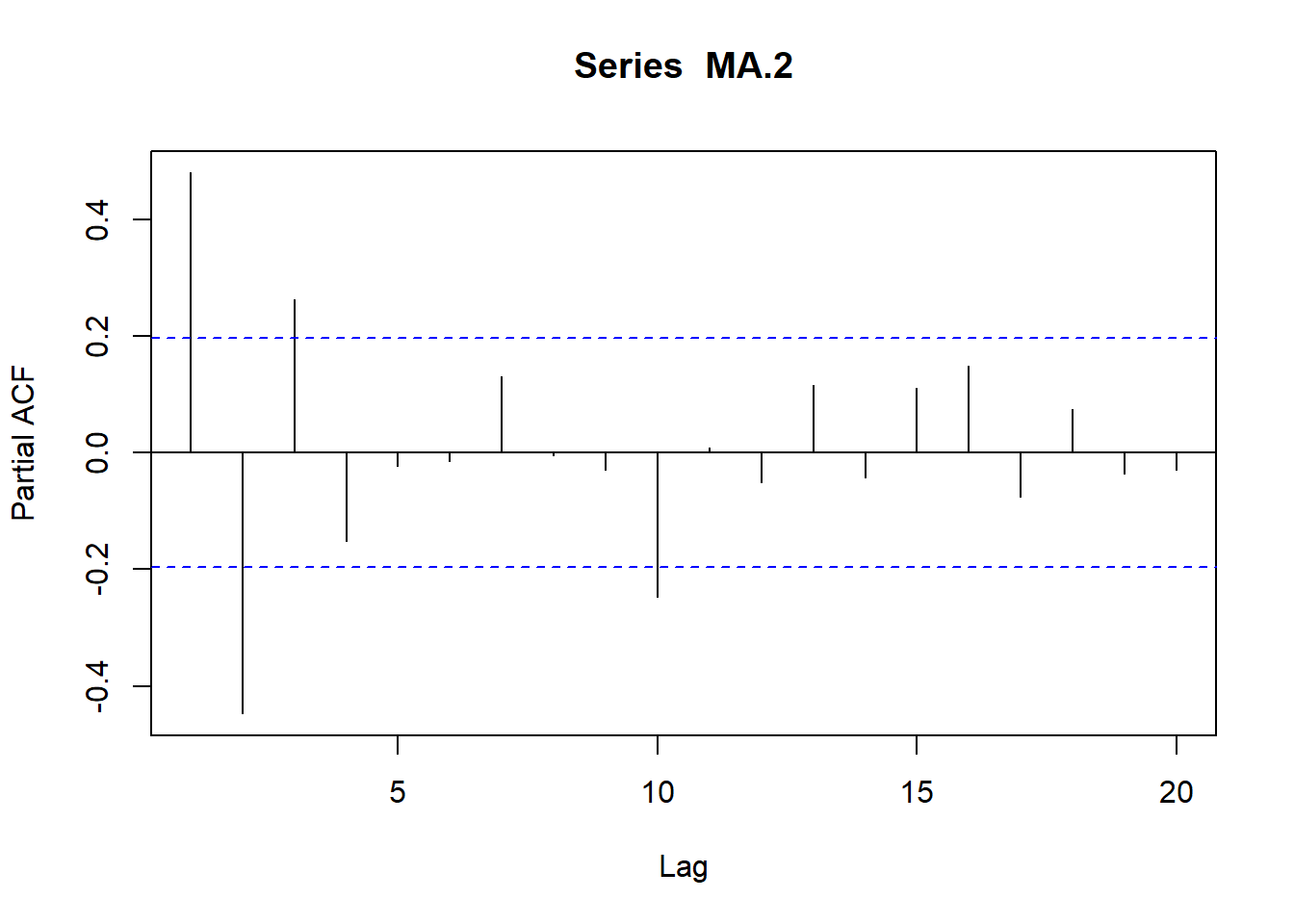

De los resultados obtenidos para el modelo MA(2) también se desprende que siempre es estacionario con independencia del valor de sus parámetros, siendo su memoria en este caso de dos períodos.

Modelos de medias móviles de orden q, MA(q)

Una vez analizados los resultados obtenidos para los procesos de media móvil de orden 1 y 2, ya podemos obtener una generalización de las expresiones anteriores para un proceso de media móvil de orden q cualquiera.

Sea el proceso MA(q):

\[Y_t=\delta +e_t - \theta_1 e_{t-1} - \theta_2 e_{t-2} -...- \theta_q e_{t-q}\]

Con media $E(Y_t) =\delta$ y varianza $Var (Yt) = Var(e_t) + \theta_1^2 Var(e_{t-1}) + \theta_2^2 Var(e_{t-2}) + ...+\theta_q^2 Var(e_{t-q})=\sigma^2_e(1+\theta_1^2+\theta_2^2+...+\theta_q^2)=\gamma_0$.

Las covarianzas del proceso son:

\[\gamma_1=E[(Y_t-\delta)(Y_{t-1}-\delta)]=(-\theta_1+\theta_1 \theta_2+\theta_2 \theta_3+...+\theta_{q-1} \theta_q) \sigma^2_e\]

\[\gamma_2=E[(Y_t-\delta)(Y_{t-2}-\delta)]=(-\theta_2+\theta_1 \theta_3+\theta_2 \theta_4+...+\theta_{q-2} \theta_q) \sigma^2_e\]

…

\[\gamma_q=E[(Y_t-\delta)(Y_{t-q}-\delta)]=-\theta_q \sigma^2_e\]

…

\[\gamma_k=0\]

Los coeficientes de la función de autocorrelación simple pueden ser obtenidos a partir de las expresiones anteriores de autocovarianzas, no siguiendo los mismos una expresión regular. En cualquier caso, cualquier proceso MA de orden finito es estacionario.

8.4.1.5.3 Relación entre procesos AR y MA

Cualquier proceso MA(q) puede expresarse como un AR de orden infinito. Así, por ejemplo, si consideramos un modelo MA(1) cuya expresión es, como sabemos:

\[Y_t=\delta +e_t- \theta_1 e_{t-1}\]

Y dado que:

\[Y_{t-1}=\delta +e_{t-1} - \theta_1 e_{t-2}\]

\[Y_{t-2}=\delta +e_{t-2} - \theta_1 e_{t-3}\]

Despejando el valor de $e_t$ y operando:

\[e_t=Y_t - \delta +\theta_1 e_{t-1}=Y_t - \delta +\theta_1(Y_{t-1} - \delta +\theta_1 e_{t-2})=\] \[=Y_t - \delta + \theta_1 Y_{t-1} - \delta \theta_1 + \theta_1^2 e_{t-2}=Y_t - \delta + \theta_1 Y_{t-1} - \delta \theta_1 + \theta_1^2 (Y_{t-2} - \delta +\theta_1 e_{t-3})=\] \[=Y_t - \delta + \theta_1 Y_{t-1} - \delta \theta_1 + \theta_1^2 Y_{t-2}- \delta \theta_1^2+\theta_1^3 e_{t-3}\] \[\rightarrow Y_t = \delta (1+ \theta_1 + \theta_1^2) - \theta_1 Y_{t-1} - \theta_1^2 Y_{t-1}- \theta_1^3 e_{t-3} + e_t\]

Si continuamos sustituyendo $e_{t-3}$ y siguientes, el procedimiento continuará hasta el infinito, lo que permite expresar a $Y_t$ como función de todos sus valores pasados más una constante y un término de error.

El resultado anterior tendrá sentido sólo si $\mid \theta_1 \mid < 1$ (o su equivalente en términos de raíces de polinomio de retardos, $1-\theta_1B=0 \rightarrow \mid B \mid > 1$ ya que, de otro modo, el efecto del pasado sería más importante para explicar el comportamiento actual.

Del mismo modo, puede comprobarse que en el caso de un modelo MA(2), la condición que debe verificarse es $\mid \theta_1 + \theta_2 \mid < 1$, en términos de raíces del polinomio de retardos, $1-\theta_1 B - \theta_2 B^2=0 \rightarrow \mid B \mid > 1$, y en general, para cualquier modelo MA(q), la condición es $1-\theta_1 B - \theta_2 B^2 - \theta_q B^q=0 \rightarrow \mid B \mid > 1$.

Si se verifica esta condición, denominada condición de invertibilidad, entonces es posible expresar un proceso MA(q) como un proceso AR de orden infinito, lo que implica que un proceso de media móvil consta de infinitos coeficientes de autocorrelación parcial distintos de cero, si bien a partir de q comenzarán a decaer rápidamente. Así, la función de autocorrelación parcial de un proceso de media móvil se comportará de manera análoga a como lo hace la función de autocorrelación simple de un proceso autorregresivo.

8.4.1.5.4 Procesos ARMA(p,q)

Los procesos ARMA (p, q) son, como su nombre indica, un modelo mixto que posee una parte autorregresiva y otra de media móvil, donde p es el orden de la parte autorregresiva y q el de la media móvil. La expresión genérica de este tipo de procesos es:

\[Y_t=\delta + \phi_1 Y_{t-1} + \phi_2 Y_{t-2} +....+\phi_p Y_{t-p} +e_t - \theta_1 e_{t-1} - \theta_2 e_{t-2} -...- \theta_q e_{t-q}\]

En este tipo de modelos se deben verificar las dos condiciones que hemos visto hasta el momento: por un lado, la condición de estacionariedad, debiéndose cumplir que las raíces del polinomio de retardos de la parte autorregresiva estén fuera del círculo unidad, $\phi(B)=0$; y por otro, la condición de invertibilidad, debiéndose verificar que las raíces del polinomio de retardos de la parte MA, $\theta(B)=0$, estén fuera del círculo unidad.

Modelos ARMA (1,1)

Veamos las características particulares de un modelo ARMA (1,1). La ecuación que define este tipo de proceso es:

\[Y_t=\delta + \phi_1 Y_{t-1} + e_t - \theta_1 e_{t-1}\]

El cual presenta las siguientes características:

Media: $\mu=\frac{\delta}{1-\phi_1} < \infty$, $\forall \mid \phi_1 \mid \neq 1$
Varianza: $\gamma_0=\frac{\sigma_e^2(1 + \theta_1^2 - 2 \phi_1\sigma_e^2) )}{(1-\phi_1)^2}$, con $\mid \theta_1 \mid < 1$

A su vez, las autocovarianzas del proceso serán:

\[\gamma_1=\phi_1 \gamma_0 + \theta_1 \sigma_e^2\]

\[\gamma_2=\phi_1 \gamma_1\]

….

\[\gamma_k=\phi_1 \gamma_{k-1}\]

Simulamos un proceso ARMA (1,1) y obtenemos las fas y fap del proceso:

# Simulamos MA(1) con \phi_1=0.7 y \theta_1=-0.1
ARMA.1<-arima.sim(model=list(ma=c(.7),ar=c(.1)),n=100)
ts.plot(ARMA.1)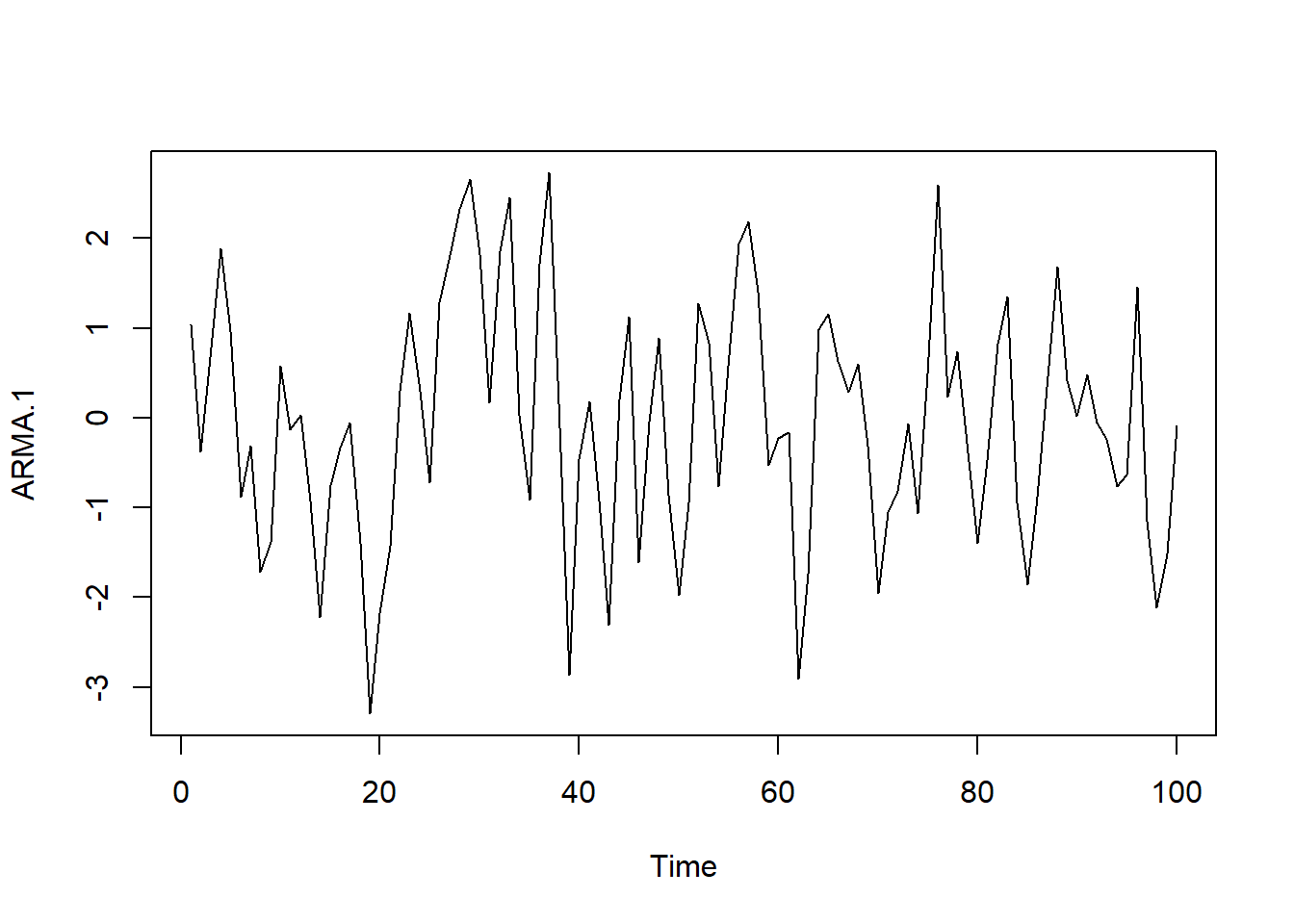

plot(acf(ARMA.1,type="correlation",plot=T))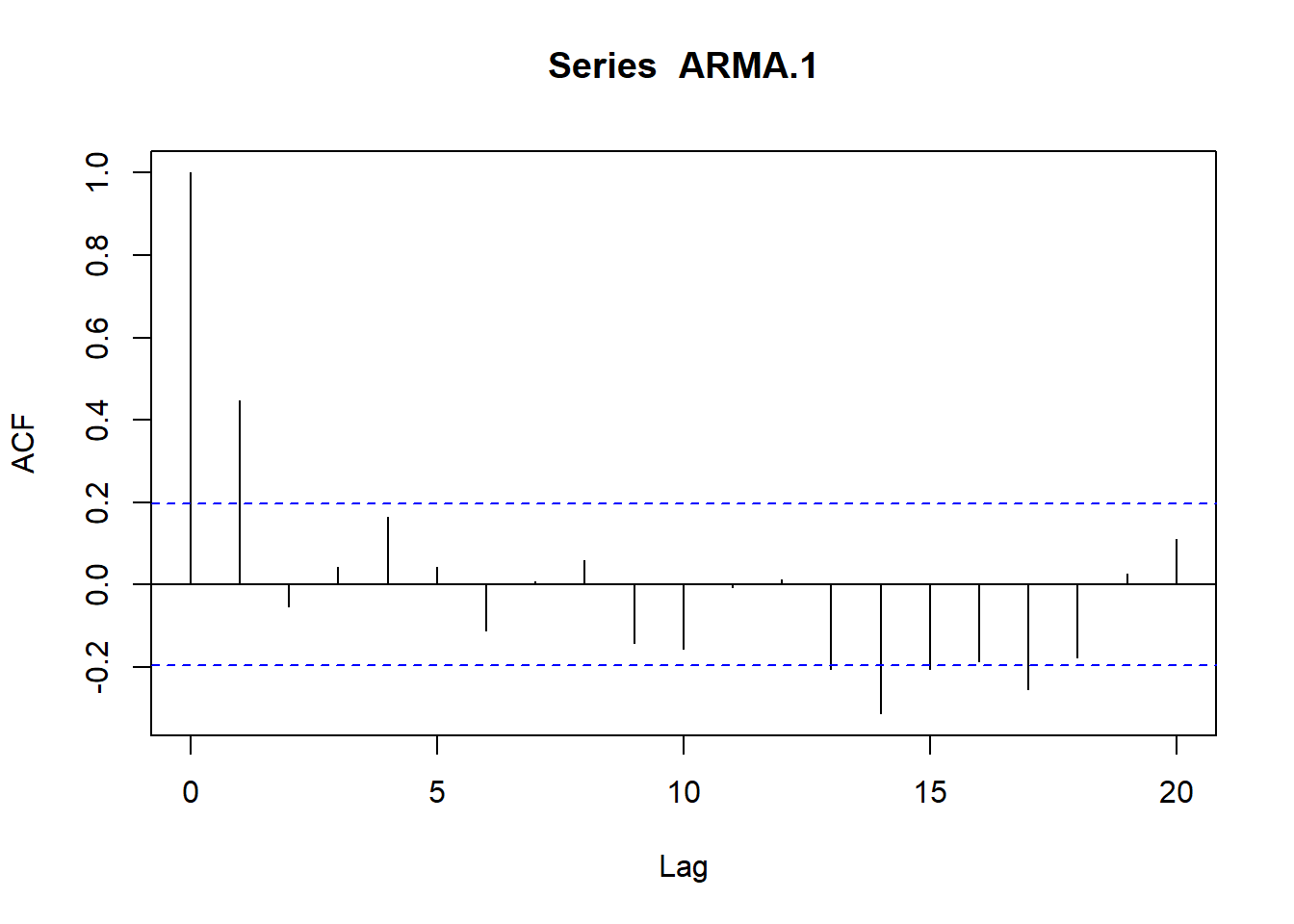

plot(acf(ARMA.1,type="partial",plot=T))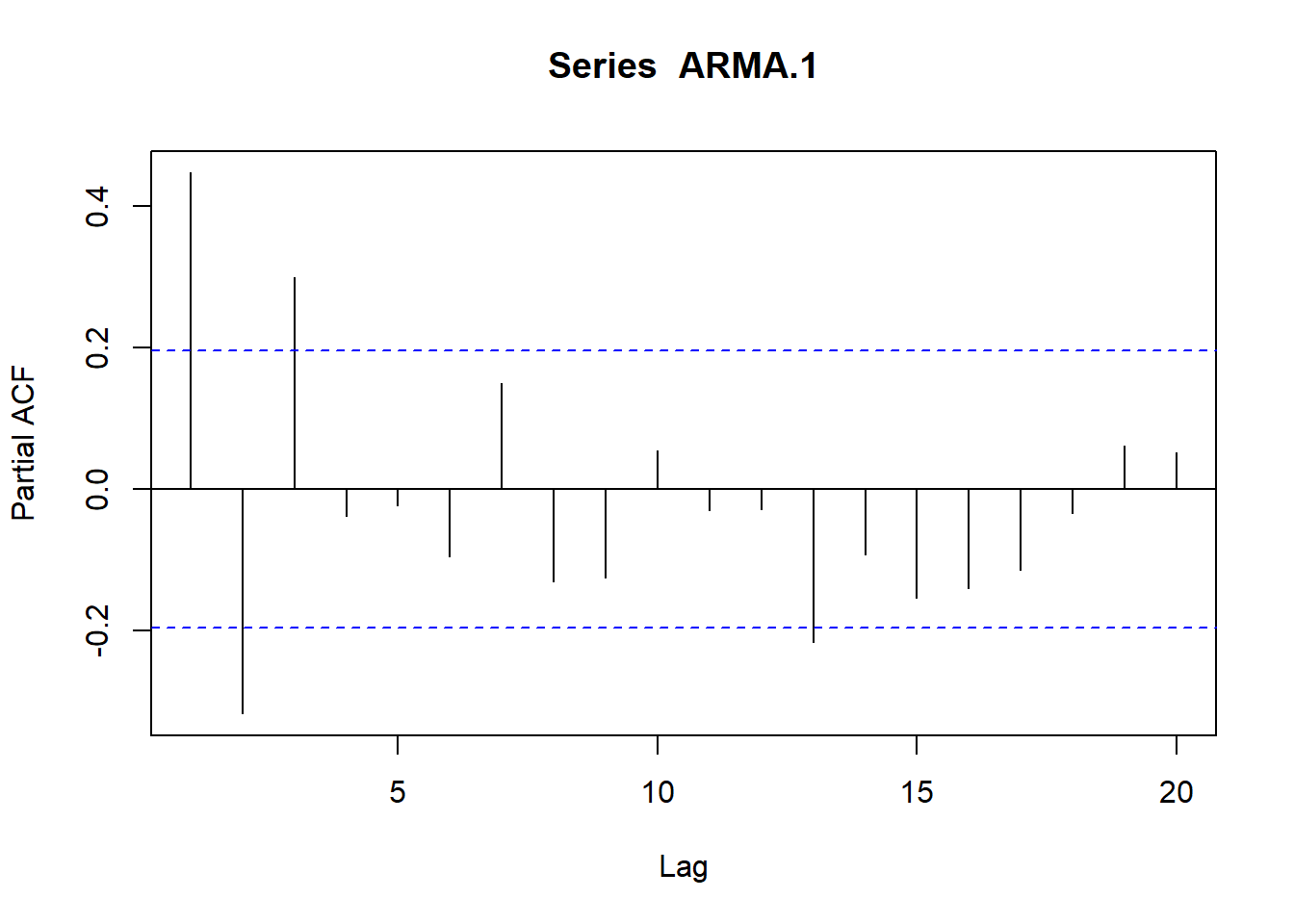

No resulta nada sencillo en la práctica identificar un proceso ARMA (1, 1) a través de sus fas y fap, ya que es fácil confundir dichas funciones con las de otros procesos univariantes. A este respecto, se aconseja especifiquar y estimar inicialmente un modelo más sencillo, como por ejemplo un AR(2); posteriormente el análisis de los residuos obtenidos en dicha estimación pondrá de manifiesto la presencia de otras estructuras. Si, por ejemplo, el investigador detecta en las funciones de autocorrelación simple y parcial de los residuos obtenidos una estructura de MA(1) será necesario incorporar dicha estructura especificando un modelo ARMA (2,1), el cual sin duda tendrá una mayor capacidad explicativa.

Modelos ARIMA

Si la serie $Y_t$ no fuera estacionaria y tomando $d$ diferencias logramos que lo sea tal que $\omega_t=\Delta^d Y_t$ sí es estacionaria, entonces diremos que $Y_t$ sigue un proceso autorregresivo integrado de media móvil de orden (p, d, q) y se denominará ARIMA (p,d,q) o, lo que es lo mismo, que $\omega_t$ sigue un proceso estacionario de tipo ARMA (p, q) tal que:

\[\omega_t=\delta + \phi_1 \omega_{t-1} + \phi_2 \omega_{t-2} +....+\phi_p \omega_{t-p} +e_t - \theta_1 e_{t-1} - \theta_2 e_{t-2} -...- \theta_q e_{t-q}\]

O también, expresando el proceso en notación de polinomios de retardos:

\[(1-\phi_1 B -\phi_2 B^2 -...-\phi_p B^p) \omega_t=\delta +e_t (1 - \theta_1 B - \theta_2 B^2 -...- \theta_q B^q)\]

\[\phi(B)\omega_t=\delta + \theta(B)e_t\]

El modelo ARIMA(p, d, q) puede ser considerado como el modelo estocástico lineal general, del cual derivan el resto de procesos que hemos visto. Así, si $p=d=0$, estaremos ante un modelo ARIMA(0, 0, q) equivalente a un modelo MA(q); si $q=0$ tendríamos un modelo ARIMA (p, d, 0) ó ARI(p,d) (es decir, un modelo autorregresivo en el que se han tomado d diferencias para hacer estacionaria a la serie analizada).

8.4.1.5.5 Procesos Estacionales

Cuando trabajamos con series temporales cuya frecuencia de medida es inferior al año (mensuales, trimestrales, cuatrimestrales), es frecuente encontrarse con patrones estacionales, es decir, ciclos u oscilaciones estrictamente periódicos, siendo dicho período igual o inferior al año. Por ejemplo, si una serie trimestral presenta estacionalidad diremos que su periodo estacional será igual a cuatro cuando en dicha serie se aprecian similitudes en su comportamiento cada cuatro trimestres.

La presencia de este componente se explica por la existencia de las estaciones y su impacto sobre la actividad económica (por ejemplo, en la producción agropecuaria o en el turismo), las costumbres (fin de año, Semana Santa) o los procesos físicos (temperatura, pluviosidad, etc.).

Otra manera para detectar un comportamiento estacional consiste en analizar las funciones de autocorrelación simple y parcial de la serie de la que se sospecha que presenta un comportamiento de tipo estacional. Si al representar dichas funciones se aprecian valores muy altos, significativamente distintos de cero, para los retardos estacionales podremos concluir que la serie presenta un componente estacional el cual debe presentar un carácter estacionario, es decir, debemos exigir que el componente estacional se mantenga constante a lo largo del tiempo.

Nuevamente, el análisis de las funciones de autocorrelación simple y parcial en los retardos estacionales nos dirá si el componente estacional de la serie es estacionario o no. Así, si observamos que la función de autocorrelación simple presenta un lento decaimiento en los valores correspondientes a los retardos estacionales y el valor del primer retardo estacional es próximo a uno tanto en la función de autocorrelación simple como parcial, es muy probable que el comportamiento estacional de la serie no presente un carácter estacionario, por lo que será necesario tomar diferencias de tipo estacional.

En caso de que la serie $Y_t$ presente un comportamiento estacional no estacionario, habrá que tomar diferencias entre aquellas observaciones separadas por el periodo que presenta el comportamiento estacional, aplicando para ello el operador diferencia estacional, $\Delta_s$, que se define como:

\[\Delta_s Y_t=Y_t-Y_{t-s}=(1-B^s)Y_t\]

donde $s$ es el periodo estacional de la serie.

La detección del comportamiento estacional de la serie y su carácter estacionario es importante ya que, tal y como Box y Jenkins plantearon, es posible incorporar a un modelo ARIMA (p,d,q) las correlaciones existentes entre pares de observaciones separadas por periodos estacionales suponiendo que el término de error de un modelo ARIMA para la parte estacional está correlacionado serialmente.

Así, podemos especificar el siguiente modelo para la parte estacional detectada en la serie:

\[(1-\Phi_1 B^s -\Phi_2 B^{2s} -...-\Phi_P B^{Ps}) (1-B^s)^D Y_t=(1 - \Theta_1 B^s - \Theta_2 B^{2s} -...- \Theta_Q B^{Qs})u_t\]

Que se denomina $ARIMA(P,D,Q)_s$ para la parte estacional de la serie.

A su vez, podemos suponer que el término de error de este modelo, $u_t$, viene generado por un proceso $ARIMA(p,d,q)$ en lugar de ser ruido blanco, tal que:

\[(1-\phi_1 B -\phi_2 B^{2} -...-\phi_p B^{p}) (1-B)^d u_t=(1 - \theta_1 B - \theta_2 B^{2} -...- \Theta_q B^{q})e_t\]

Sustituyendo, obtendremos la expresión del proceso estacional multiplicativo general, el cual denotaremos por $ARIMA(p,d,q)XARIMA(P,D,Q)_s$, y que podemos escribir como:

\[(1-\Phi_1 B^s -\Phi_2 B^{2s} -...-\Phi_P B^{Ps})(1-\phi_1 B -\phi_2 B^{2} -...-\phi_p B^{p}) (1-B)^d (1-B^s)^D Y_t=\]

\[=(1 - \Theta_1 B^s - \Theta_2 B^{2s} -...- \Theta_Q B^{Qs})(1 - \theta_1 B - \theta_2 B^{2} -...- \Theta_q B^{q})e_t\]

O, de forma más abreviada, expresando el modelo en notación de retardos y generalizándolo incluyendo un término constante:

\[\Phi(B^s)\phi(B)[(1-B)^d (1-B^s)^D Y_t-\delta]=\Theta( B^s)\theta(B)e_t\]

donde:

-$\phi(B)$ es el polinomio de retardos autorregresivo de la parte regular de la serie.

$\theta(B)$ es el polinomio de retardos de medias móviles de la parte regular de la serie.

-$d$ es el número de diferencias aplicadas a la parte regular de la serie para hacerla estacionaria.

$\Phi(B^s)$ es el polinomio de retardos autorregresivo de la parte estacional de la serie.
$\Theta(B^s)$ es el polinomio de retardos de medias móviles de la parte estacional de la serie.

-$D$ es el número de diferencias aplicadas a la parte estacional de la serie para hacerla estacionaria.

Así, por ejemplo, si deseamos especificar un modelo para una serie con estacionalidad mensual podemos especificar un $ARIMA(1,1,1)XARIMA(1,1,1)_{12}$, el cual puede escribirse como:

\[(1-\Phi_1 B^{12})(1-\phi_1 B) (1-B) (1-B^{12}) Y_t=(1 - \Theta_1 B^{12})(1 - \theta_1 B)e_t\]

La estructura de las funciones de autocorrelación simple y parcial de este tipo de modelos suele ser generalmente muy compleja, por lo que no vamos a entrar en detalle en sus expresiones.

8.4.1.6 Fases para la elaboración de modelos univariantes

Aunque las fases que vamos a explicar a continuación son válidas para cualquier tipo de proceso univariante, vamos a centrarnos fundamentalmente en los procesos de tipo ARIMA. Básicamente, se trata de buscar un proceso ARIMA que de forma verosímil haya podido generar la serie temporal, es decir, que se adapte mejor a las características de la misma. Para ello seguiremos las siguientes fases:

Fase de identificación.
Fase de estimación
Fase de validación
Fase de predicción

8.4.1.6.1 Fase de identificación

Dado que los procesos ARIMA están diseñados para modelizar datos de carácter estacionario, lo primero que debemos hacer es efectuar un análisis de la estacionariedad de los datos. Con tal fin se utilizan los siguientes instrumentos:

• Representación gráfica de los datos. Si el gráfico de la serie temporal presenta fluctuaciones cuya amplitud cambia para distintos intervalos del período muestral, seguramente el proceso que genera la serie es no estacionario. Lo mismo sucede cuando la tendencia es creciente o decreciente con el tiempo.

• A través del gráfico desviación típica-media. Si en el gráfico realizado observamos que, conforme crece la media, la desviación típica aumenta, la varianza del proceso será creciente, por lo que diremos que la serie es no estacionaria en varianza.

• Análisis del correlograma. El hecho de que la función de autocorrelación simple o correlograma de la serie decrezca muy lentamente al aumentar el retardo, ha demostrado ser una señal de tendencia no estacionaria. Puesto que en la práctica se dispone de una realización de un proceso estocástico, podemos obtener los coeficientes de autocorrelación muestral y, a partir de ellos, el correlograma muestral. Una vez representado el correlograma muestral, podrá analizarse si la serie es o no estacionaria. Asimismo, en este punto también es conveniente examinar la apariencia de la función de autocorrelación parcial de la serie, para ver si existen similitudes con alguno de los patrones estudiados.

Si la serie temporal que estamos analizando no es estacionaria se deberán aplicar las transformaciones adecuadas con objeto de convertirla en estacionaria. Si la serie no es estacionaria en varianza, deberemos tomar logaritmos sobre la serie; si además la serie presenta no estacionariedad en media, se aplicará el proceso de diferenciación que ya hemos comentado al comienzo del capítulo.

En este punto cabe señalar que es preferible trabajar con series económicas en niveles en lugar de tasas de variación ya que, en caso de detectarse no estacionariedad en la varianza, no podremos aplicar logaritmos si existe alguna tasa negativa. Asimismo, debemos tener en cuenta que, normalmente, las series originales transformadas aplicando logaritmos y tomando posteriormente una diferencia constituyen una aproximación a una tasa de variación, tal que $\Delta ln(Y_t)=\frac {(Yt – Y{t-1})}{Y{t-1}}$

Una vez transformada la serie en estacionaria, se determinará el orden de la parte autorregresiva (p) y el de la parte de media móvil (q) del proceso ARMA que se considere que haya podido generar la serie estacionaria. Para tal fin utilizaremos la representación gráfica de las funciones de autocorrelación simple y parcial de la serie transformada, con objeto de obtener pistas acerca del proceso univariante del que puede proceder la serie transformada. Las siguientes reglas pueden resultar útiles a la de inspeccionar los gráficos de la fas y la fap de la serie:

• En los modelos AR(p), la función de autocorrelación parcial presenta los p primeros coeficientes distintos de cero y el resto nulos. Asimismo, generalmente la función de autocorrelación simple presenta un decrecimiento rápido de tipo exponencial, sinusoidal o ambos.

• En los modelos MA(q), se da el patrón opuesto: la función de autocorrelación simple se anula para retardos superiores a q y la función de autocorrelación parcial decrece exponencial o sinusoidalmente.

• Sin embargo, como ya hemos visto, la especificación de los modelos ARMA no se ajusta a unas normas tan bien definidas. Por ejemplo, en un modelo AR(1), la función de autocorrelación parcial es cero para k>1, pero esto no ocurre en un ARMA(1,1), pues a la componente AR(1) hay que superponer la MA(1) cuya función de autocorrelación parcial converge exponencialmente a cero.

Lo habitual en estos casos es que el investigador especifique inicialmente un modelo más simple y, posteriormente, mediante el análisis de los residuos de la estimación de dicho modelo se detecte un proceso que no ha sido especificado inicialmente y que debe ser incorporado al modelo.

• En cualquier caso, para que una serie sea fácilmente identificable hay que considerar un tamaño muestral elevado, superior a 50 observaciones.

En general, la etapa de identificación suele plantear ciertas dificultades y su objetivo es determinar la especificación tentativa de unos pocos modelos con estructuras sencillas. Las posteriores etapas de estimación y validación de los resultados confirmarán los indicios o, por el contrario, servirán de base para reformular el modelo propuesto.

8.4.1.6.2 Fase de estimación

Una vez identificado el modelo apropiado, se procede a la estimación definitiva de sus parámetros. En este punto, no debemos olvidar que si hemos tomado d diferencias en la serie se perderán d observaciones, quedando $T–d$ datos disponibles para la estimación.

Asimismo, debemos tener presente que el proceso estimado debe verificar las siguientes hipótesis:

El término $e_t$ posee estructura de ruido blanco y sigue una distribución Normal con media cero y varianza constante.
La parte AR del proceso es estacionaria.
La parte MA del proceso es invertible.

Veamos a continuación brevemente cómo se realiza la estimación de los distintos modelos univariantes que hemos visto en los epígrafes anteriores:

• Estimación de procesos AR. Un proceso autorregresivo no cumple la hipótesis del modelo clásico de regresión basada en regresores fijos que veíamos en el capítulo 2, ya que los retardos de $Y_t$ son variables aleatorias al serlo la propia $Y_t$. Sin embargo, en presencia de errores que no presentan autocorrelación, los estimadores mínimo-cuadráticos son consistentes por lo que en la práctica la estimación de un proceso autorregresivo se realiza por MCO, siendo los retardos de la variable endógena las variables explicativas del modelo. Sólo si el término de error presentase algún tipo de correlación y no fuera ruido blanco, los estimadores obtenidos dejarían de ser consistentes.

• Estimación de procesos MA y ARMA. La estimación de modelos de medias móviles y ARMA resulta algo más compleja y se lleva a cabo maximizando el logaritmo de la función de verosimilitud.

8.4.1.6.3 Fase de validación

En esta etapa se comprobará la capacidad de ajuste del modelo propuesto y estimado a los datos. En caso de que el modelo no supere satisfactoriamente este paso, será necesario reformularlo. En este sentido, cabe señalar que los resultados de la comprobación de la validez del modelo, suelen dar pistas para la especificación de un modelo alternativo.

Para la aceptación del modelo, éste debe cumplir los siguientes requisitos:

• Análisis de los residuos. Como sabemos, una de las hipótesis de los modelos univariantes es que el término de error del modelo es ruido blanco. Por ello, los residuos obtenidos tras la estimación del modelo deben seguir un proceso puramente aleatorio con distribución Normal, ya que de lo contrario, contendrían información relevante para la predicción que se estaría despreciando.

• Análisis de los coeficientes estimados.

Significatividad de los coeficientes: Lo primero es verificar si los coeficientes son significativos mediante el estadístico t. Dicho estadístico está construido bajo la hipótesis nula de que el coeficiente es cero y sigue una distribución t-Student con T–m grados de libertad, siendo m el número de parámetros incluidos. Si concluimos que alguno no es significativo (estadístico t mayor, en valor absoluto, que su valor en tablas) se puede eliminar del modelo.
Condiciones de estacionariedad e invertibilidad: El modelo debe verificar las condiciones ya vistas a lo largo del capítulo; de lo contrario, si alguna de las raíces del polinomio de retardos del componente autorregresivo o del componente media móvil fuese inferior a la unidad (o, alternativamente, alguno de los parámetros estimados fuera mayor de uno), se rechazaría automáticamente el modelo.

En el límite, si alguna de las raíces del polinomio de retardos (o alguno de los parámetros) del componente autorregresivo estuviera muy próxima a uno, es posible que la serie original esté subdiferenciada por lo que puede que sea necesaria tomar alguna diferencia adicional.

Del mismo modo, si las raíces del polinomio de retardos (o alguno de sus parámetros) del componente media móvil del modelo estuviera cercana a uno, posiblemente el modelo esté sobrediferenciado.

• Análisis de la bondad de ajuste. Generalmente en este aspecto se suele utilizar el coeficiente de determinación, $R^2$, si bien los coeficientes de determinación de diferentes modelos univariantes sólo son comparables en aquellos modelos en los que se hayan tomado idéntico número de diferencias, debido a que para que éste sea un elemento de comparación directa, la varianza de la variable debe ser la misma. Para paliar este inconveniente, se han propuesto medidas alternativas como el estadístico AIC (Akaike Information Criterion) o el SIC (Schwarz Information Criterion).Siguiendo estos criterios, se seleccionará aquel modelo para el que se obtenga un AIC o SIC más bajo.

• Análisis de la estabilidad. Finalmente, de cara a la predicción, conviene saber si el modelo estimado para el período muestral sigue siendo válido para períodos futuros. Para ello, podemos aplicar el test de estabilidad estructural de Chow.

8.4.1.6.4 Fase de predicción

Una vez que el modelo ha superado la fase de diagnosis, se convierte en un instrumento útil para la predicción. La realización de predicciones y el error cometido al realizar dicha predicción dependerá del tipo de modelo univariante que estemos considerando.

8.4.1.7 Ejemplos don R

8.4.1.7.1 Ejemplo 1: Pasajeros en Líneas Aéreas

El siguiente ejemplo utiliza los totales mensuales de pasajeros de líneas aéreas internacionales para el periodo comprendido entre Enero de 1949 y Diciembre de 1962 incluidos en libro de Box y Jenkins. Esta base de datos está disponible en R:

data(AirPassengers)
x<-AirPassengers

En la figura siguiente se muestra la representación gráfica de la serie en la que puede apreciarse claramente una fuerte estacionalidad en los datos y una varianza creciente en el tiempo.

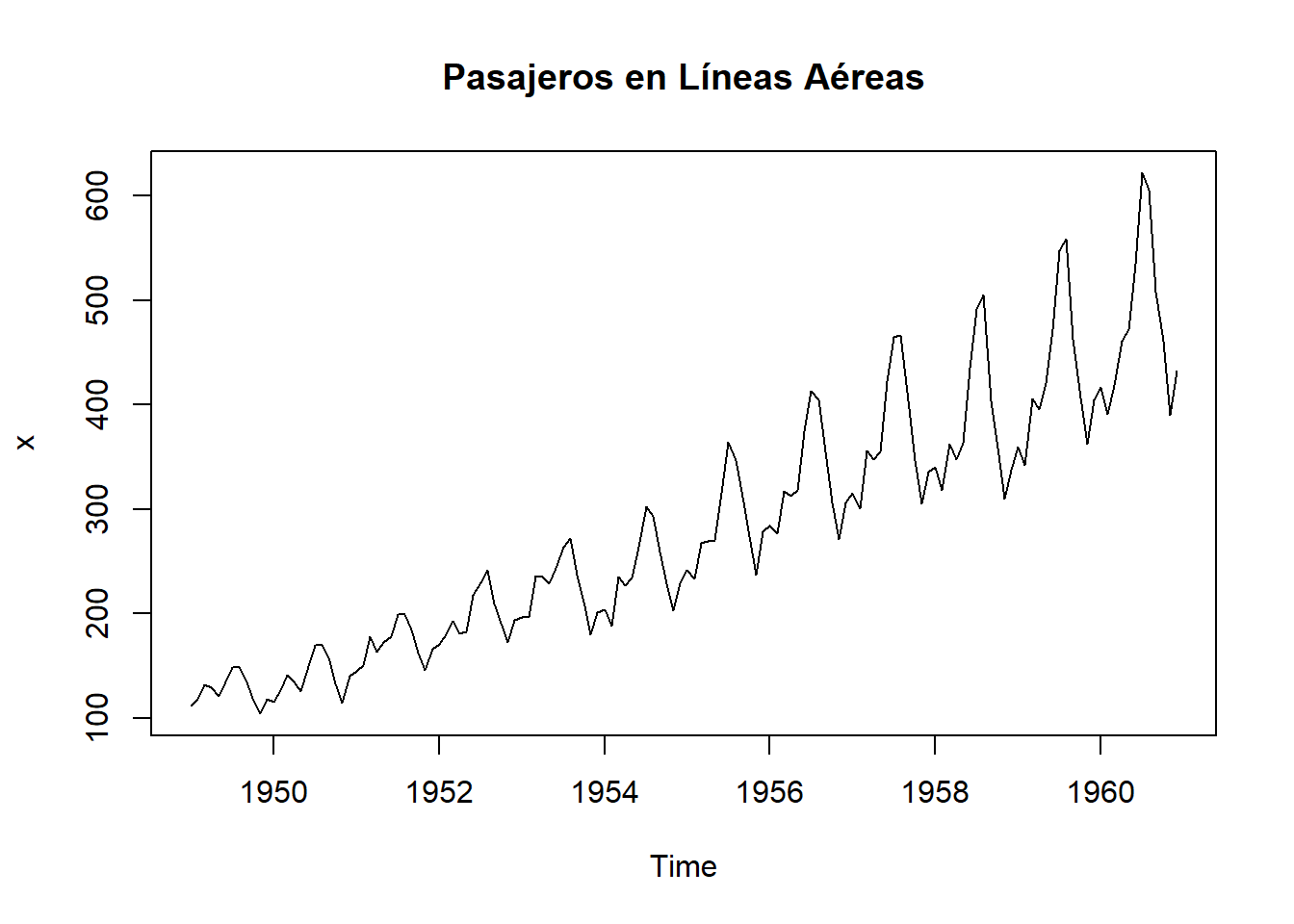
El hecho de que la varianza de la serie no sea constante en el tiempo sugiere que lo primero que debemos hacer es transformar la serie tomando logaritmos para hacer que sea estacionaria en varianza.

x =log(x)

Tras tomar logaritmos, la serie presenta ahora el siguiente aspecto:

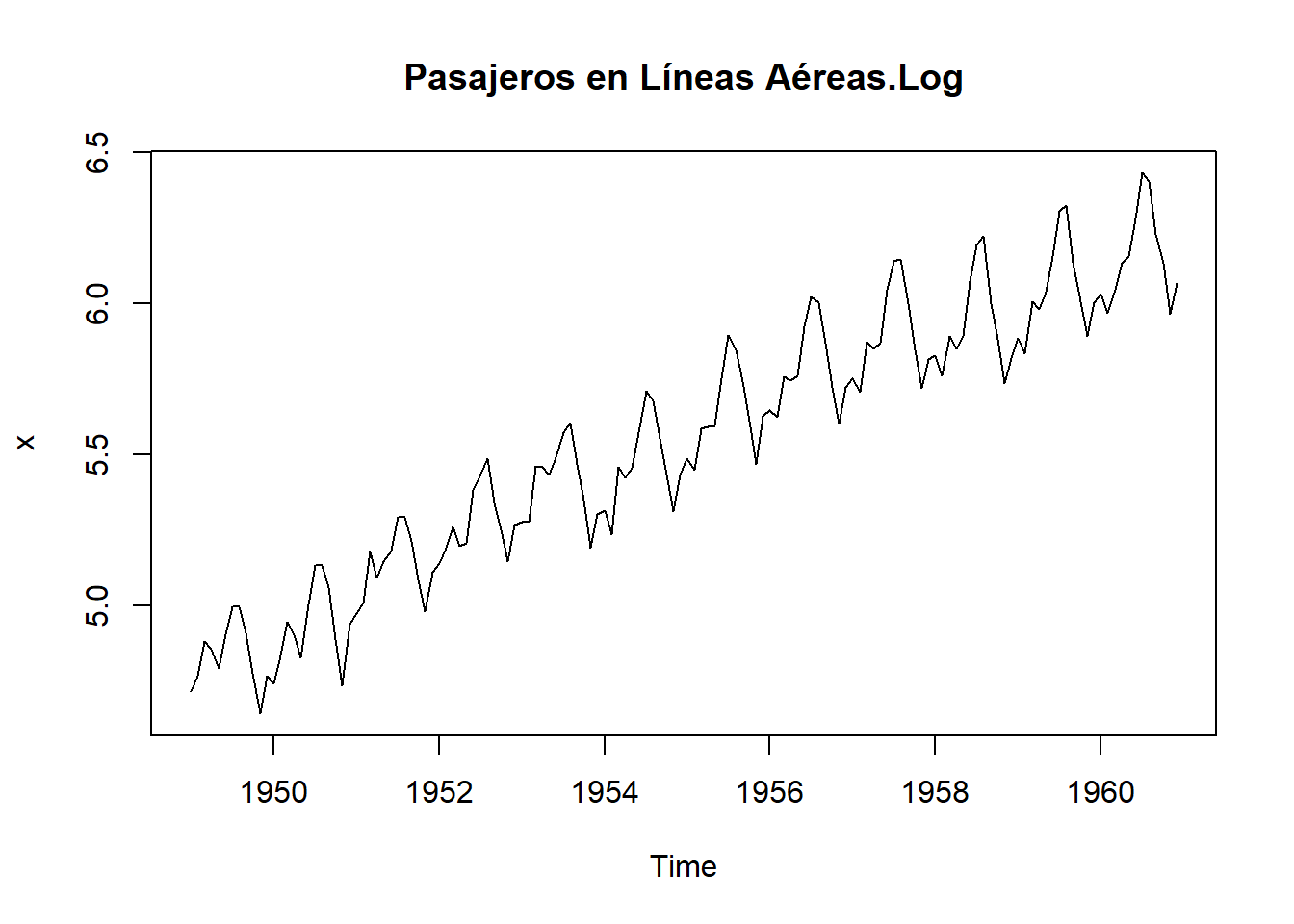El análisis de la serie en logaritmos y de sus funciones de autocorrelación simple y parcial confirman que la serie no es estacionaria en media por lo que debemos tomar una diferencia.

par(mfcol = c(1, 2))
acf(x) 
pacf(x)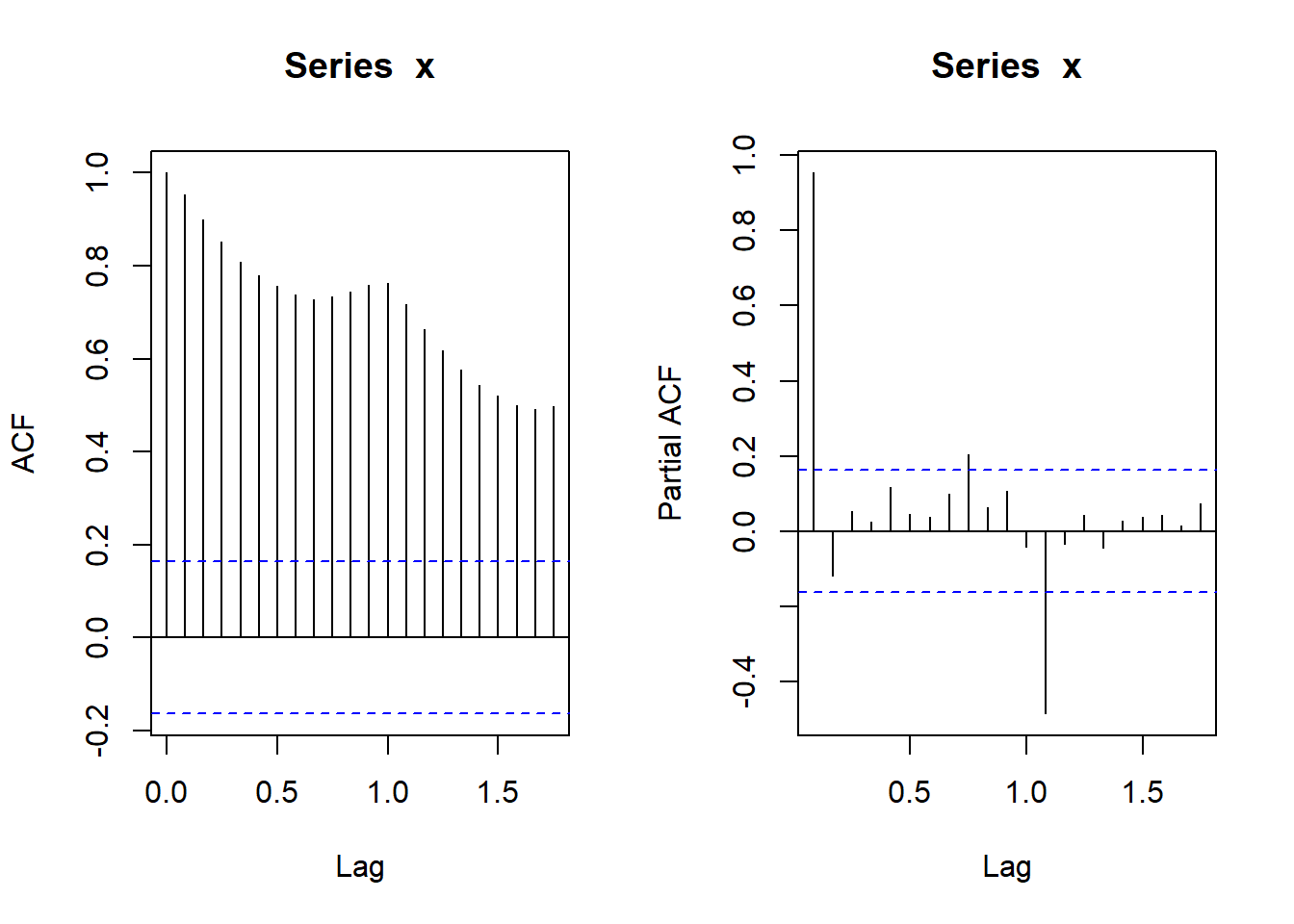

Tras tomar una diferencia, el aspecto de la serie es el siguiente:

par(mfcol = c(1, 1))
x1 <- diff(x)
plot(x1, main="Pasajeros en Líneas Aéreas. Diferencias Log.")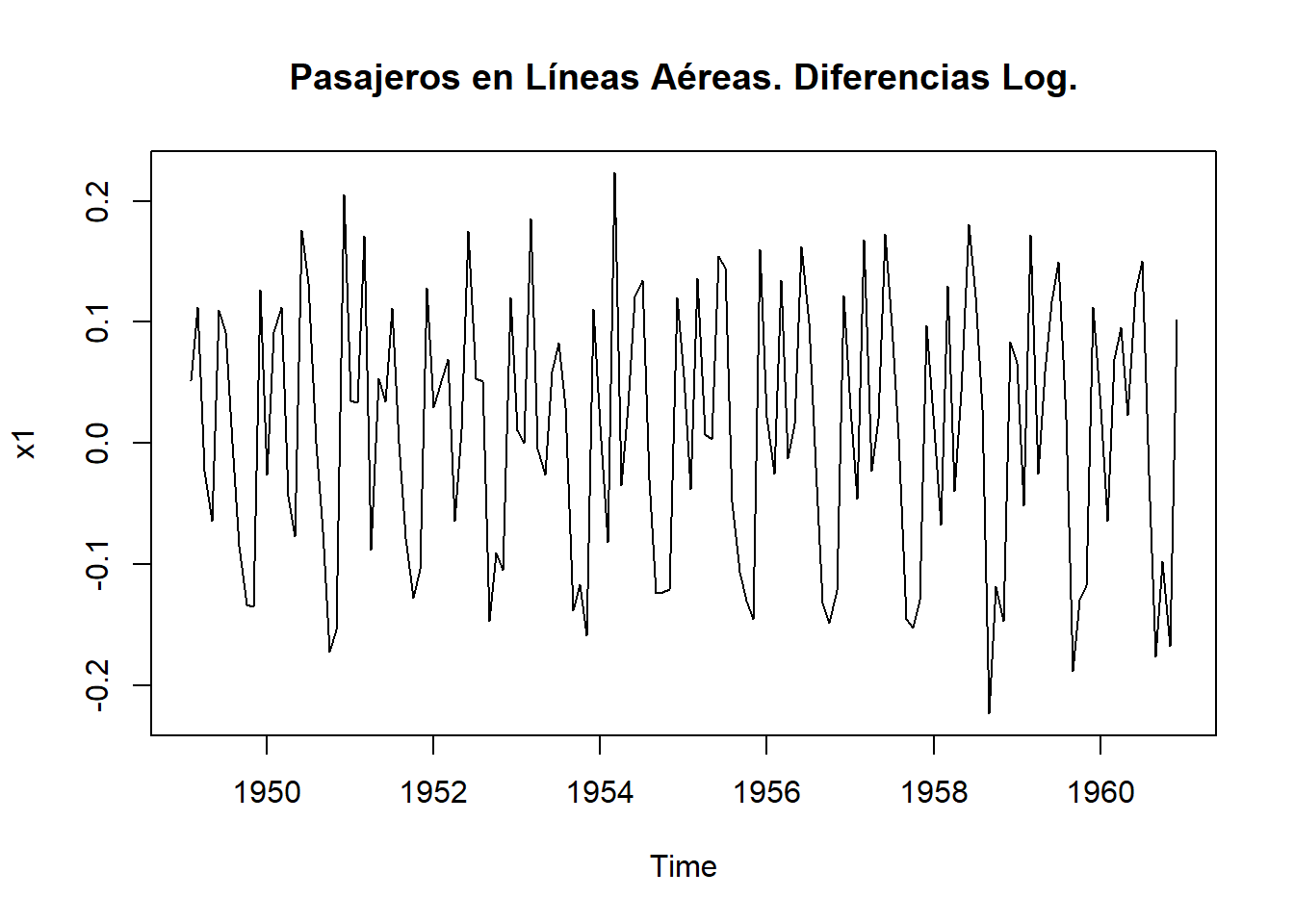

Las funciones de autocorrelación simple y parcial de la serie logarítmica en diferencias se muestran en la figura siguiente, en las que puede apreciarse el marcado componente estacional en los meses de Diciembre, lo que nos obliga a tomar una diferencia estacional de 12 meses para hacer estacionaria la parte estacional de la serie.

par(mfcol = c(1, 2))
acf(x1) 
pacf(x1)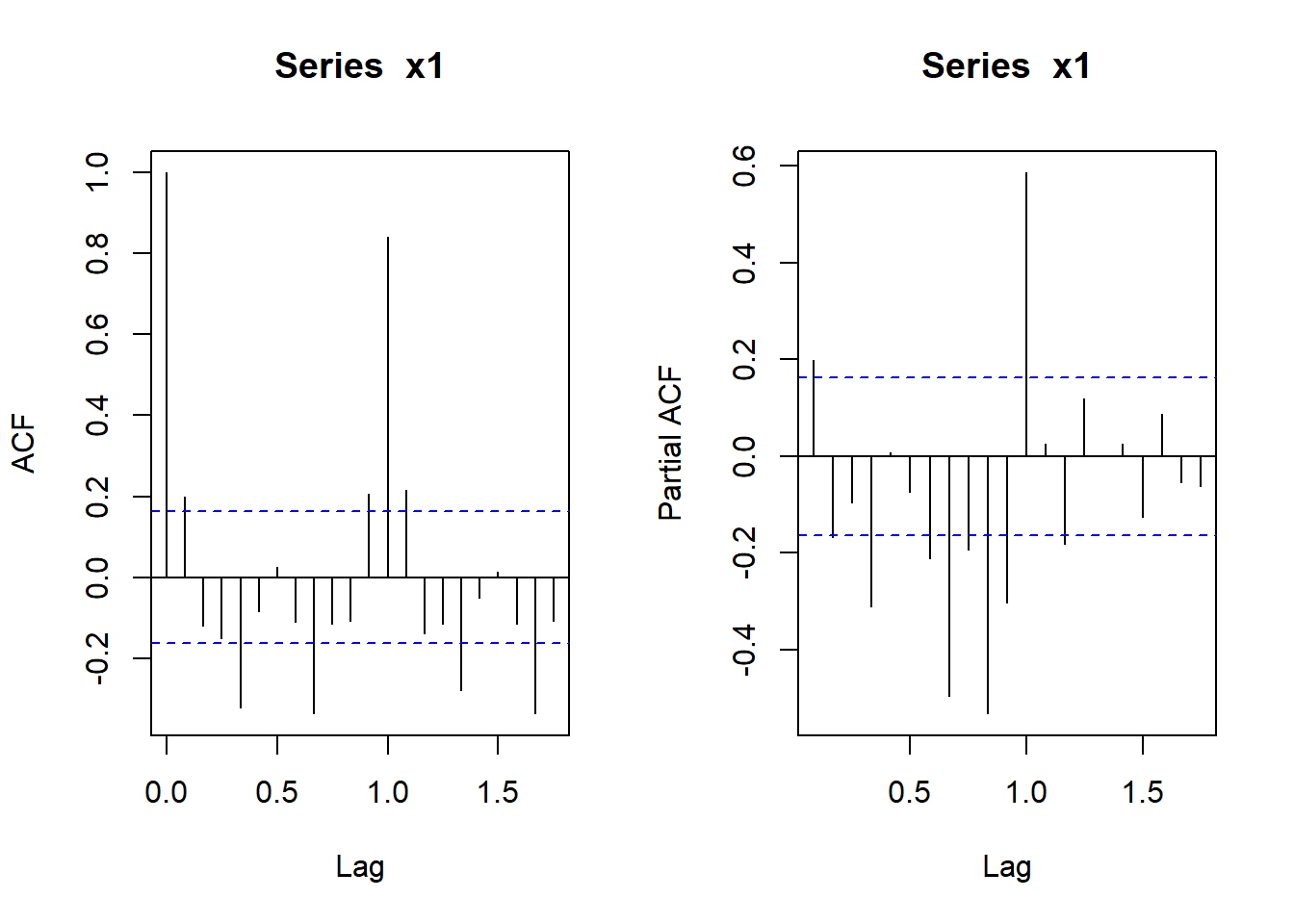

El gráfico siguiente muestra la serie logarítmica con una diferencia regular y una diferencia estacional de periodo 12; en ella podemos apreciar la pérdida de las 13 primeras observaciones al haber aplicado las diferencias indicadas. Tras haber aplicado las transformaciones que hemos comentado, la serie presenta ahora un claro comportamiento estacionario, el cual viene confirmado por las funciones de autocorrelación simple y parcial de la serie:

par(mfcol = c(1, 1))
x1_12 <- diff(x1, 12)
plot(x1_12, main="Pasajeros en Líneas Aéreas. Diferencias Log. Estacionales")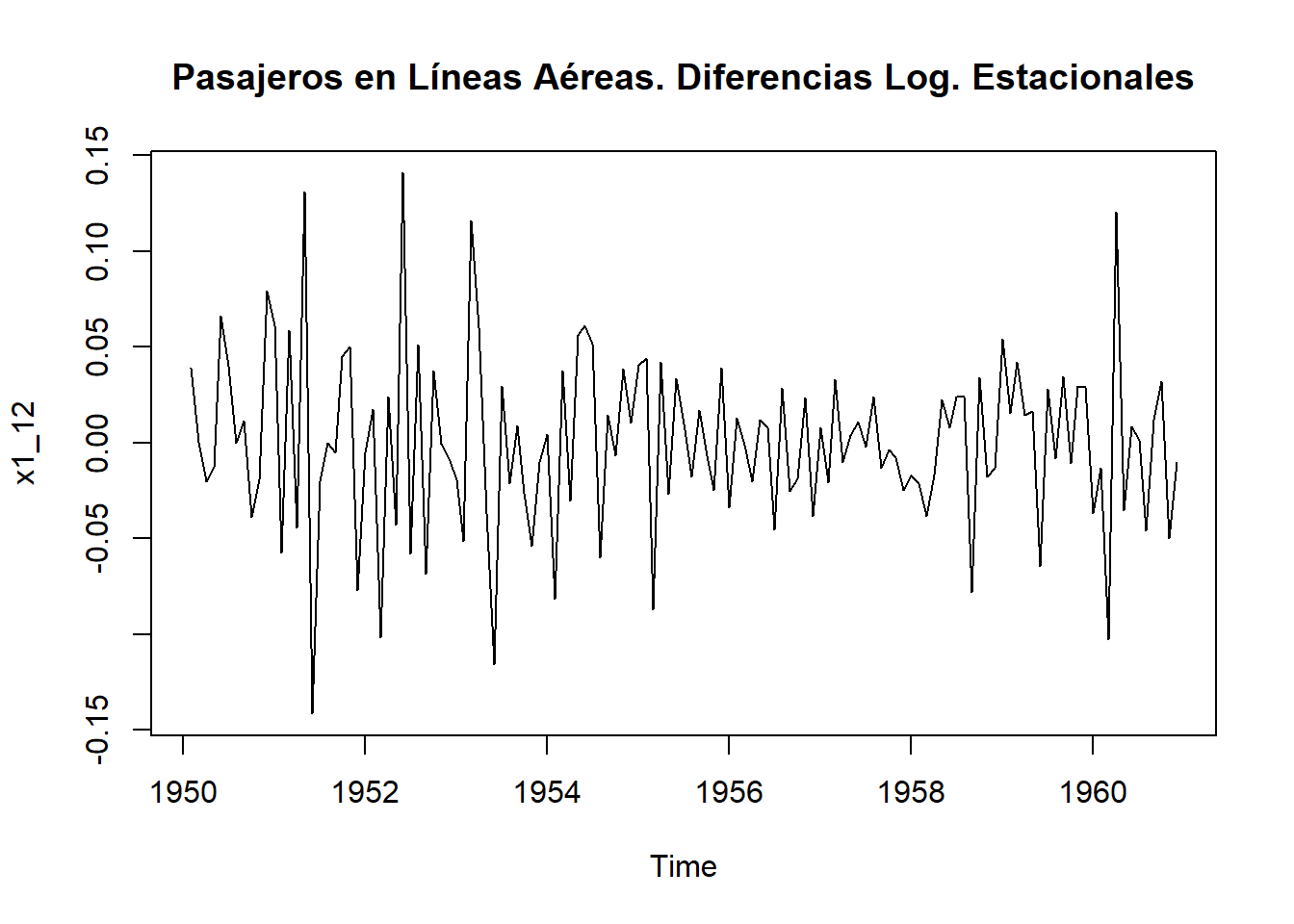

par(mfcol = c(1, 2))
acf(x1_12) 
pacf(x1_12)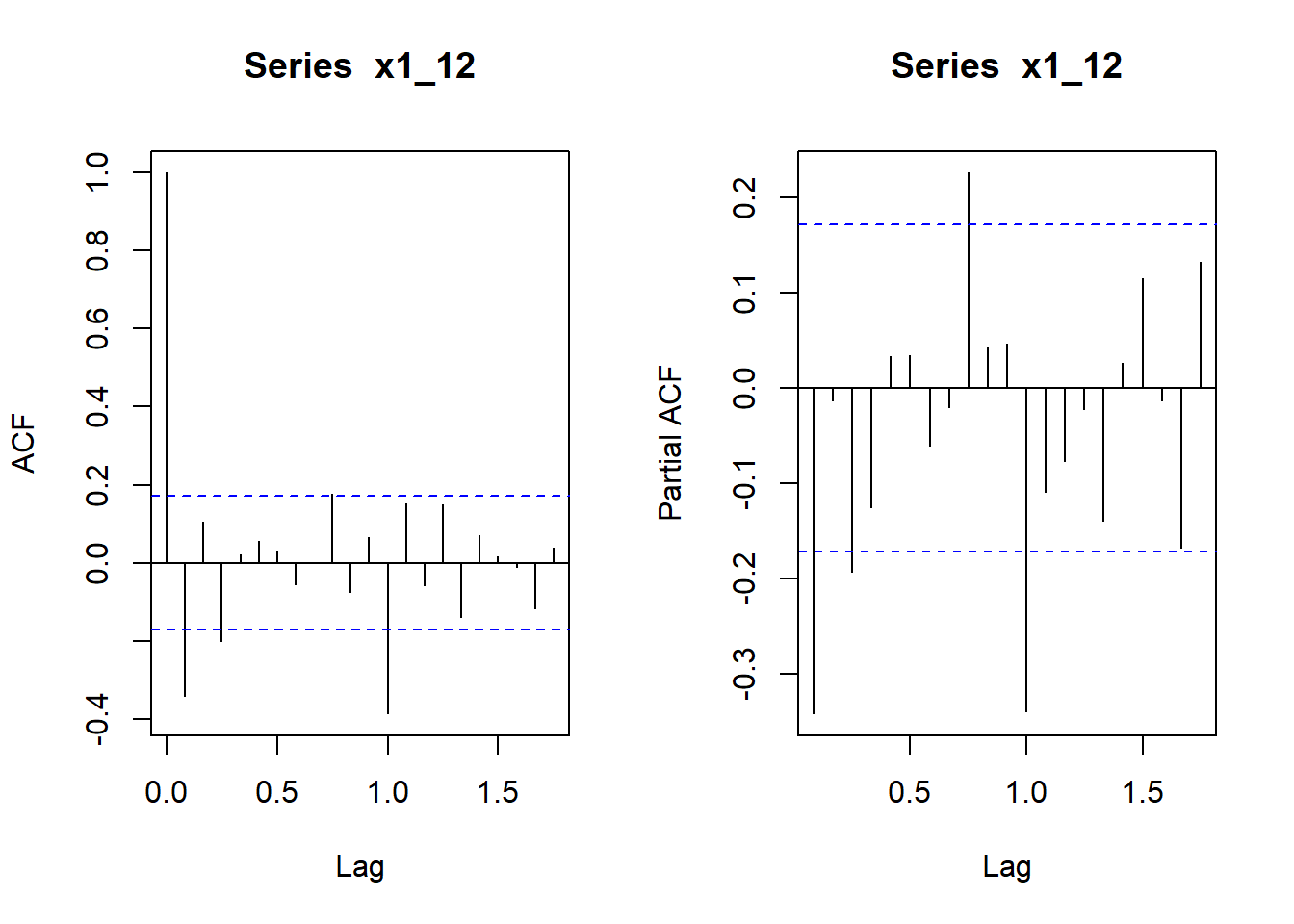

De las funciones de autocorrelación simple y parcial podemos extraer algunas conclusiones: por un lado, en la parte regular podemos comprobar que las funciones de correlación simple y parcial son muy parecidas, siendo el primer retardo significativo para ambos casos. Esto indica que quizás el modelo sea un ARIMA(1,1,0), un ARIMA(0,1,1) o un ARIMA(1,1,1), en cualquier caso un modelo de primer orden.

Por otro lado, en la parte estacional vemos que el retardo 12 es significativo y que en sus cercanías hay muy poca correlación, lo que sugiere un proceso con muy poca memoria, posiblemente un $ARIMA(0,1,1)_{12}$ en la parte estacional.

Las conclusiones anteriores nos llevan a estimar tres modelos: un $ARIMA(1,1,0)×(0,1,1)_{12}$, un $ARIMA(0,1,1)×(0,1,1)_{12}$ y un $ARIMA(1,1,1)×(0,1,1)_{12}$. Presentamos a continuación, de forma resumida, los resultados obtenidos para los tres modelos.

Para estimar un modelo ARIMA en R hay que utilizar la función “arima”, cuya sintaxis es la siguiente:

arima(x, order = c(0L, 0L, 0L), seasonal = list(order = c(0L, 0L, 0L), period = NA), xreg = NULL, include.mean = TRUE, transform.pars = TRUE, fixed = NULL, init = NULL, method = c(“CSS-ML”, “ML”, “CSS”), n.cond, SSinit = c(“Gardner1980”, “Rossignol2011”), optim.method = “BFGS”, optim.control = list(), kappa = 1e6)

destacar, la opción order, en donde se especifican los elementos (p,d,q) de la parte no estacional del modelo arima, y seasonal, en donde se especifican los elementos de la parte estacional.

Resultados de la estimación

$ARIMA(1,1,0)×(0,1,1)_{12}$

mod1 <- arima(x,c(1,1,0),c(0,1,1))
mod1

## 
## Call:
## arima(x = x, order = c(1, 1, 0), seasonal = c(0, 1, 1))
## 
## Coefficients:
##          ar1    sma1
##       -0.340  -0.562
## s.e.   0.082   0.075
## 
## sigma^2 estimated as 0.00137:  log likelihood = 243.74,  aic = -481.49

$ARIMA(0,1,1)×(0,1,1)_{12}$

mod2 <- arima(x,c(0,1,1),c(0,1,1))
mod2

## 
## Call:
## arima(x = x, order = c(0, 1, 1), seasonal = c(0, 1, 1))
## 
## Coefficients:
##          ma1    sma1
##       -0.402  -0.557
## s.e.   0.090   0.073
## 
## sigma^2 estimated as 0.00135:  log likelihood = 244.7,  aic = -483.4

$ARIMA(1,1,1)×(0,1,1)_{12}$

mod3 <- arima(x,c(1,1,1),c(0,1,1))
mod3

## 
## Call:
## arima(x = x, order = c(1, 1, 1), seasonal = c(0, 1, 1))
## 
## Coefficients:
##         ar1     ma1    sma1
##       0.196  -0.578  -0.564
## s.e.  0.247   0.213   0.075
## 
## sigma^2 estimated as 0.00134:  log likelihood = 244.95,  aic = -481.9

Como puede observarse, la estimación de este último modelo contiene un parámetro no significativo, AR(1), por lo que podemos excluirlo de nuestro análisis.

Ajuste del modelo

$ARIMA(1,1,0)×(0,1,1)_{12}$

par(mfcol = c(1, 2))
plot(x)
lines(x-mod1$residuals,col="red")
plot(mod1$residuals)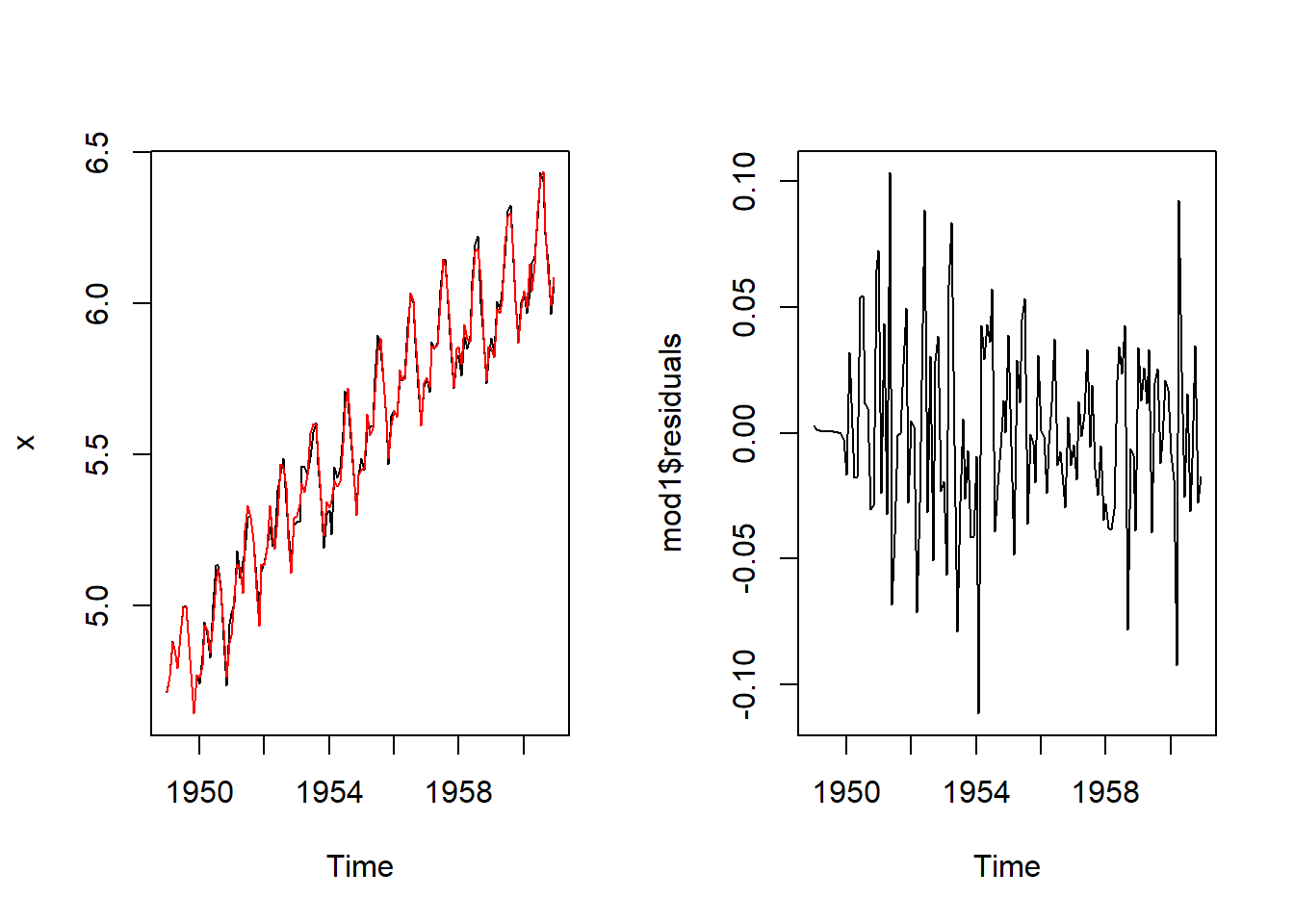

$ARIMA(0,1,1)×(0,1,1)_{12}$

par(mfcol = c(1, 2))
plot(x)
lines(x-mod2$residuals,col="red")
plot(mod1$residuals)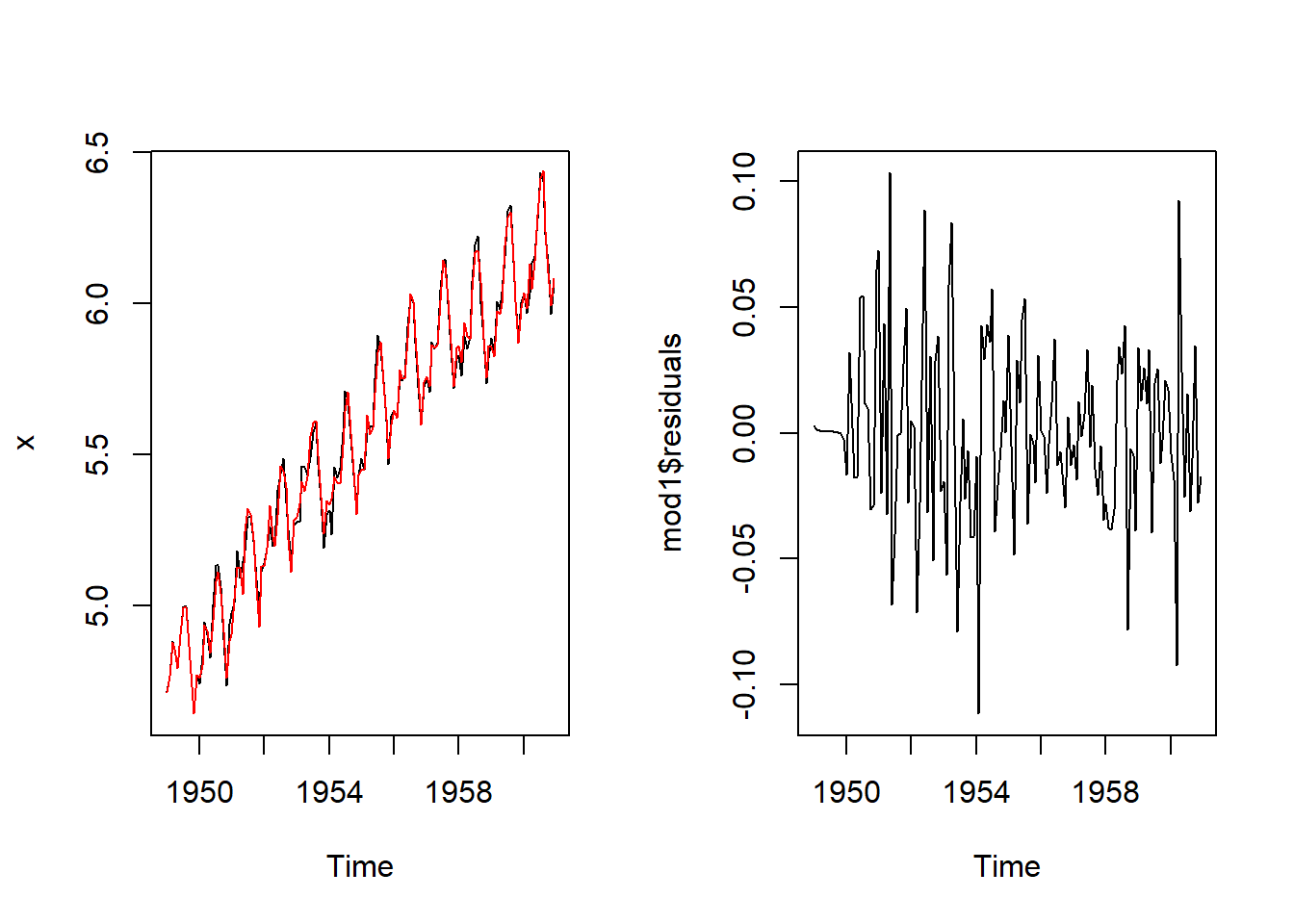

$ARIMA(1,1,1)×(0,1,1)_{12}$

par(mfcol = c(1, 2))
plot(x)
lines(x-mod3$residuals,col="red")
plot(mod1$residuals)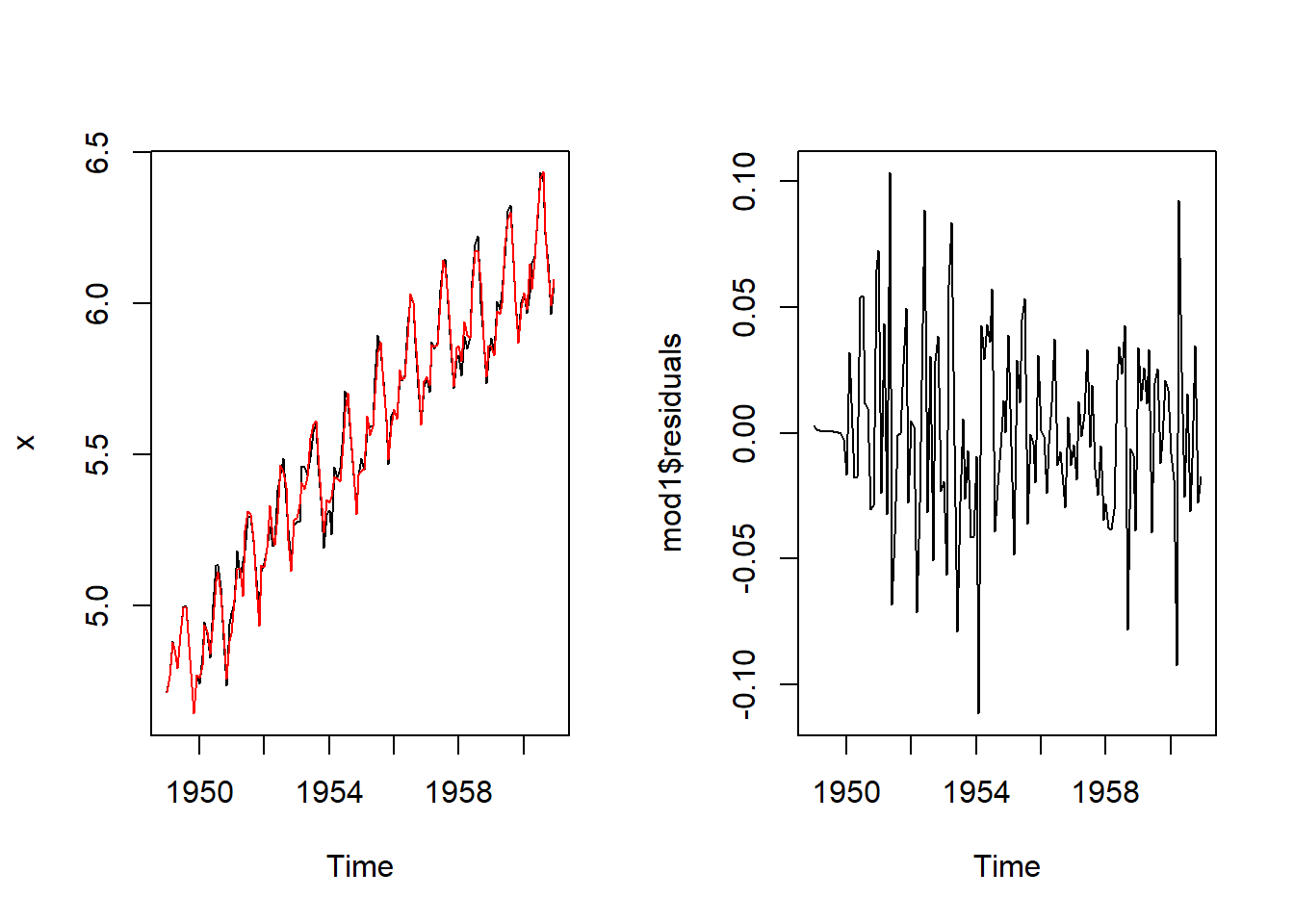

Funciones de autocorrelación simple y parcial.

$ARIMA(1,1,0)×(0,1,1)_{12}$

par(mfcol = c(1, 2))
acf(mod1$residuals)
pacf(mod1$residuals)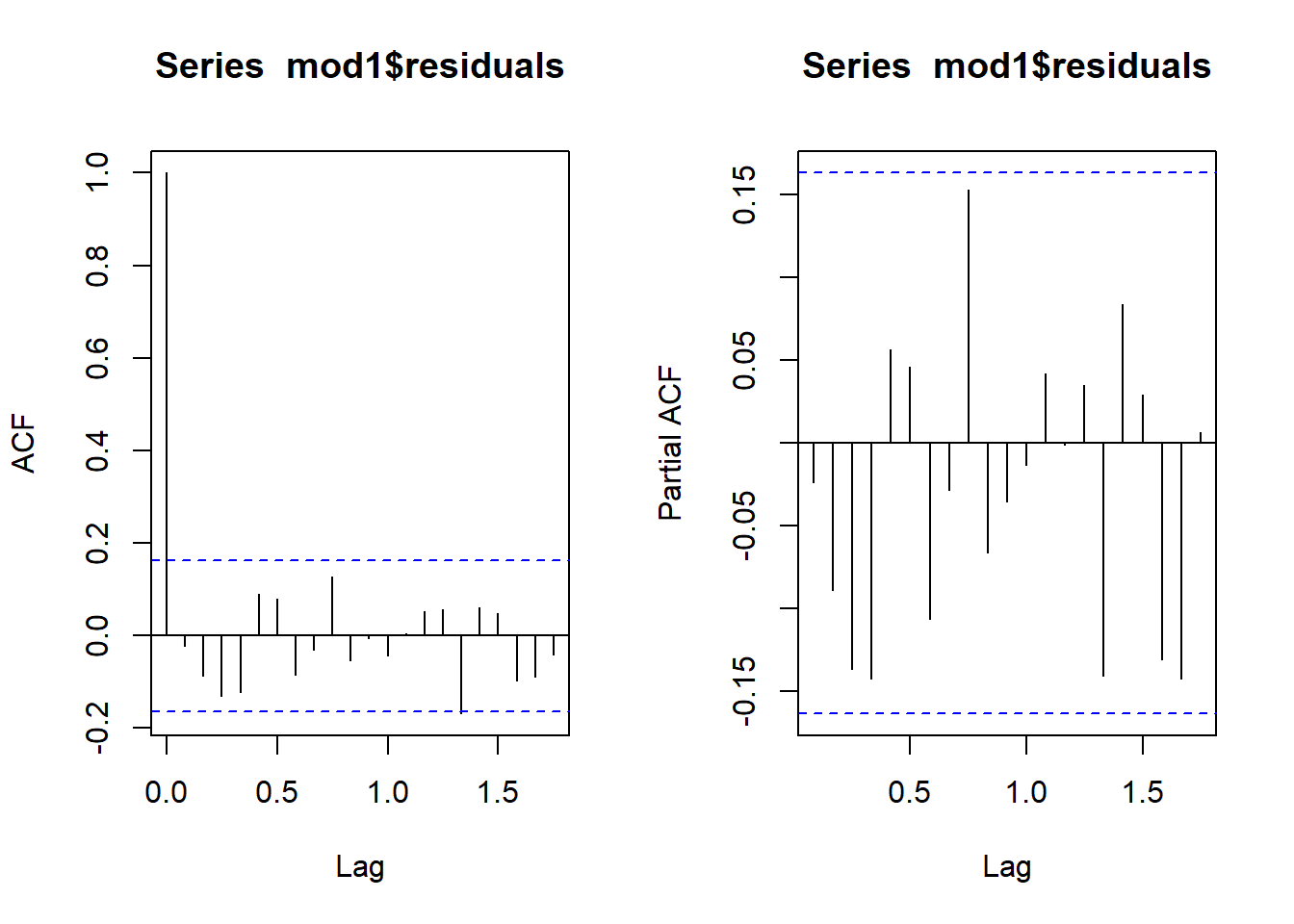

$ARIMA(0,1,1)×(0,1,1)_{12}$

par(mfcol = c(1, 2))
acf(mod2$residuals)
pacf(mod2$residuals)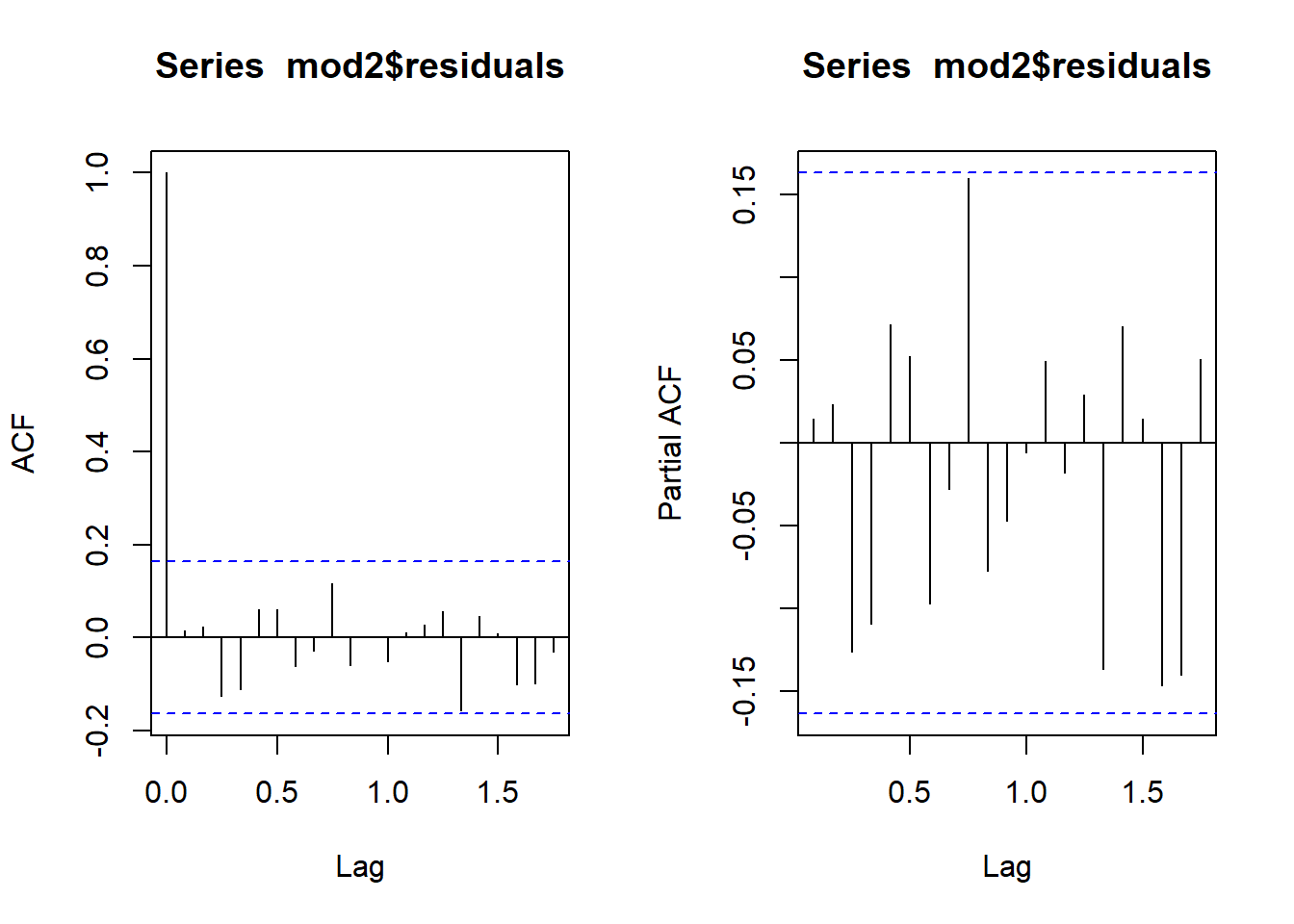

$ARIMA(1,1,1)×(0,1,1)_{12}$

par(mfcol = c(1, 2))
acf(mod3$residuals)
pacf(mod3$residuals)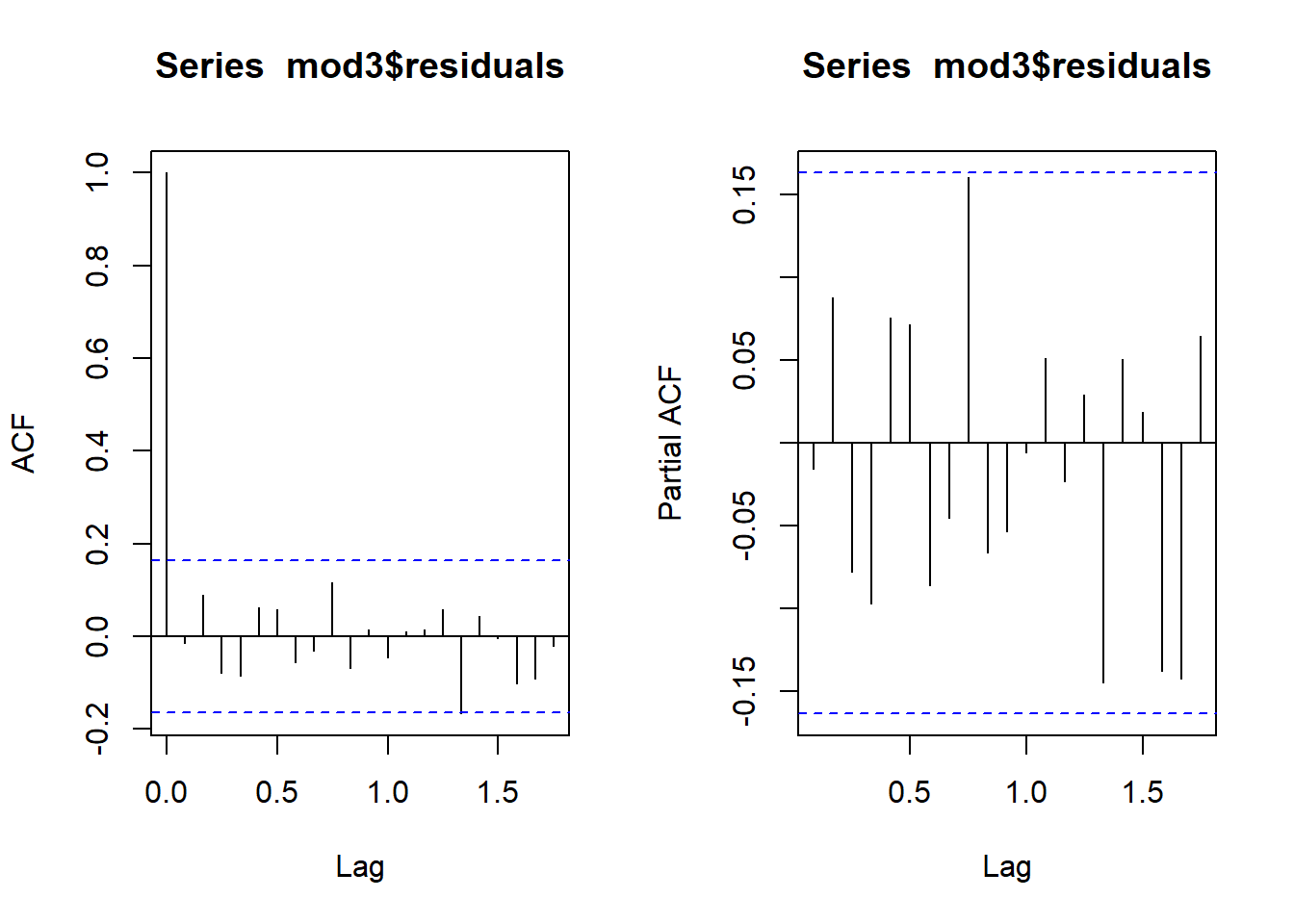

Test de Normalidad en los residuos

$ARIMA(1,1,0)×(0,1,1)_{12}$

summary(mod1$residuals)

##      Min.   1st Qu.    Median      Mean   3rd Qu.      Max. 
## -0.111464 -0.023269 -0.000446  0.000450  0.023806  0.103239

par(mfcol = c(1, 1))
hist(mod1$residuals)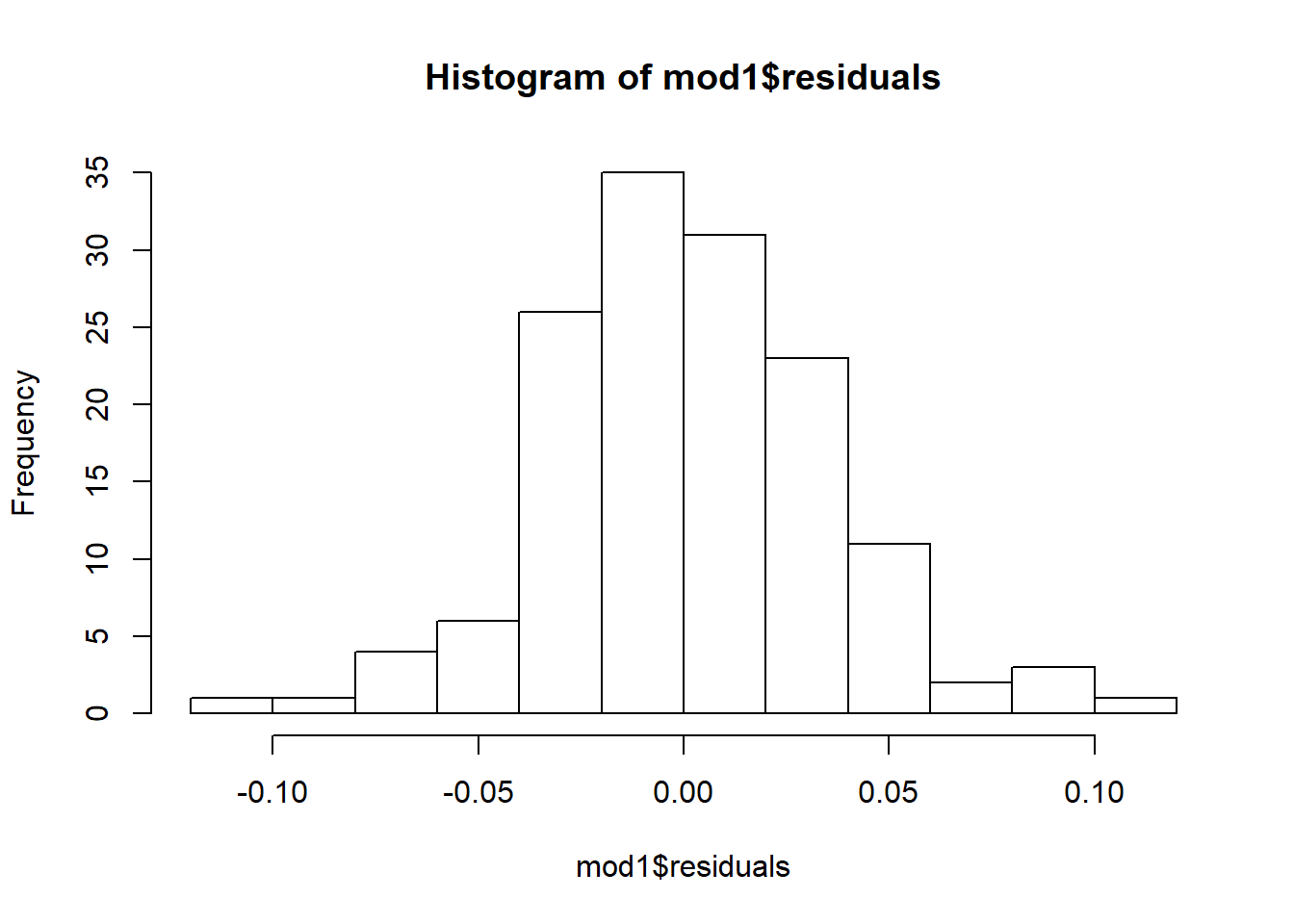

library(tseries)
jarque.bera.test(mod1$residuals)

## 
##  Jarque Bera Test
## 
## data:  mod1$residuals
## X-squared = 3.61, df = 2, p-value = 0.16

$ARIMA(0,1,1)×(0,1,1)_{12}$

summary(mod2$residuals)

##      Min.   1st Qu.    Median      Mean   3rd Qu.      Max. 
## -0.118590 -0.019163 -0.000051  0.000573  0.022327  0.108513

par(mfcol = c(1, 1))
hist(mod2$residuals)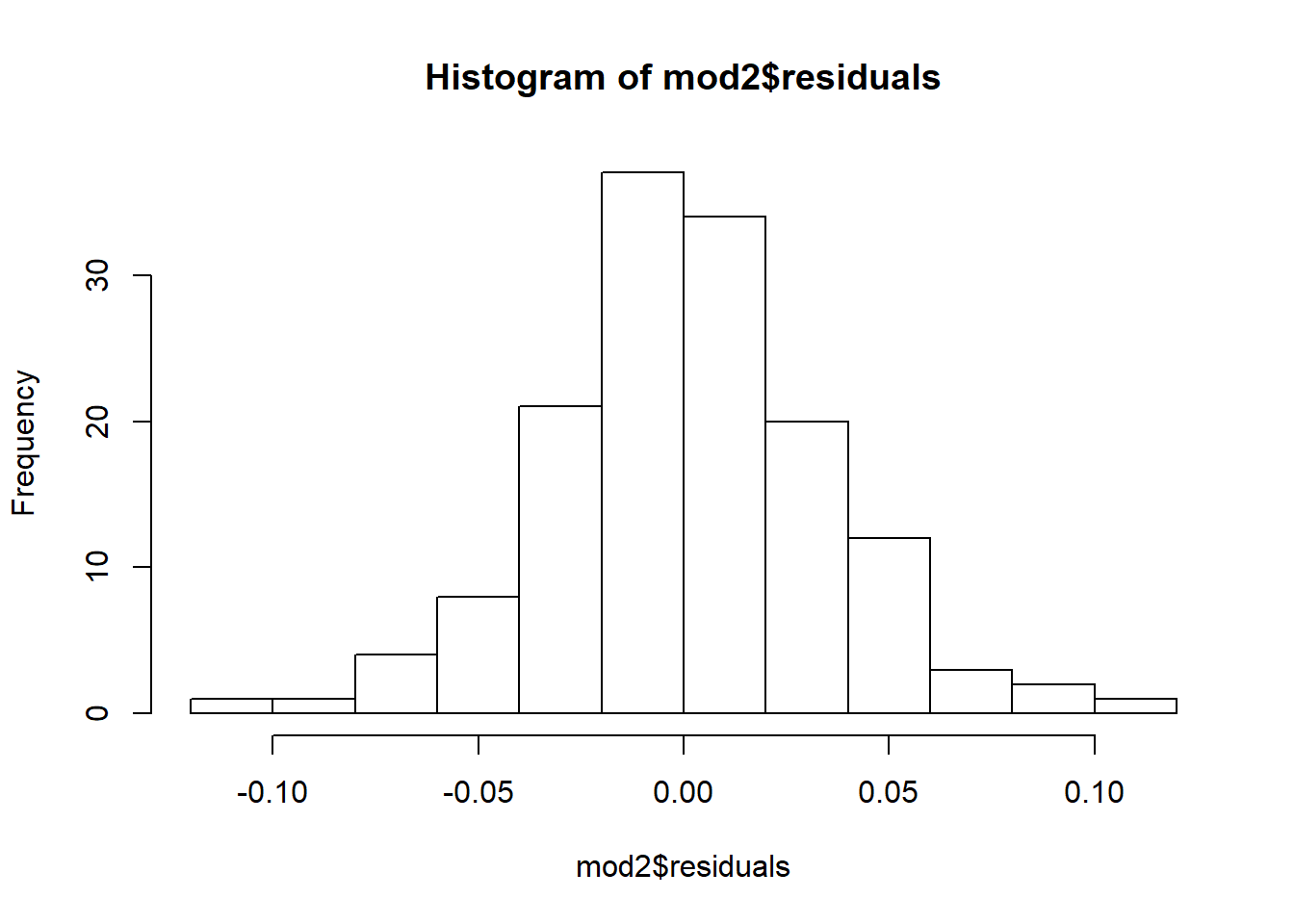

library(tseries)
jarque.bera.test(mod2$residuals)

## 
##  Jarque Bera Test
## 
## data:  mod2$residuals
## X-squared = 5.23, df = 2, p-value = 0.073

$ARIMA(1,1,1)×(0,1,1)_{12}$

summary(mod3$residuals)

##      Min.   1st Qu.    Median      Mean   3rd Qu.      Max. 
## -0.124459 -0.020053  0.000085  0.000621  0.023496  0.113759

par(mfcol = c(1, 1))
hist(mod3$residuals)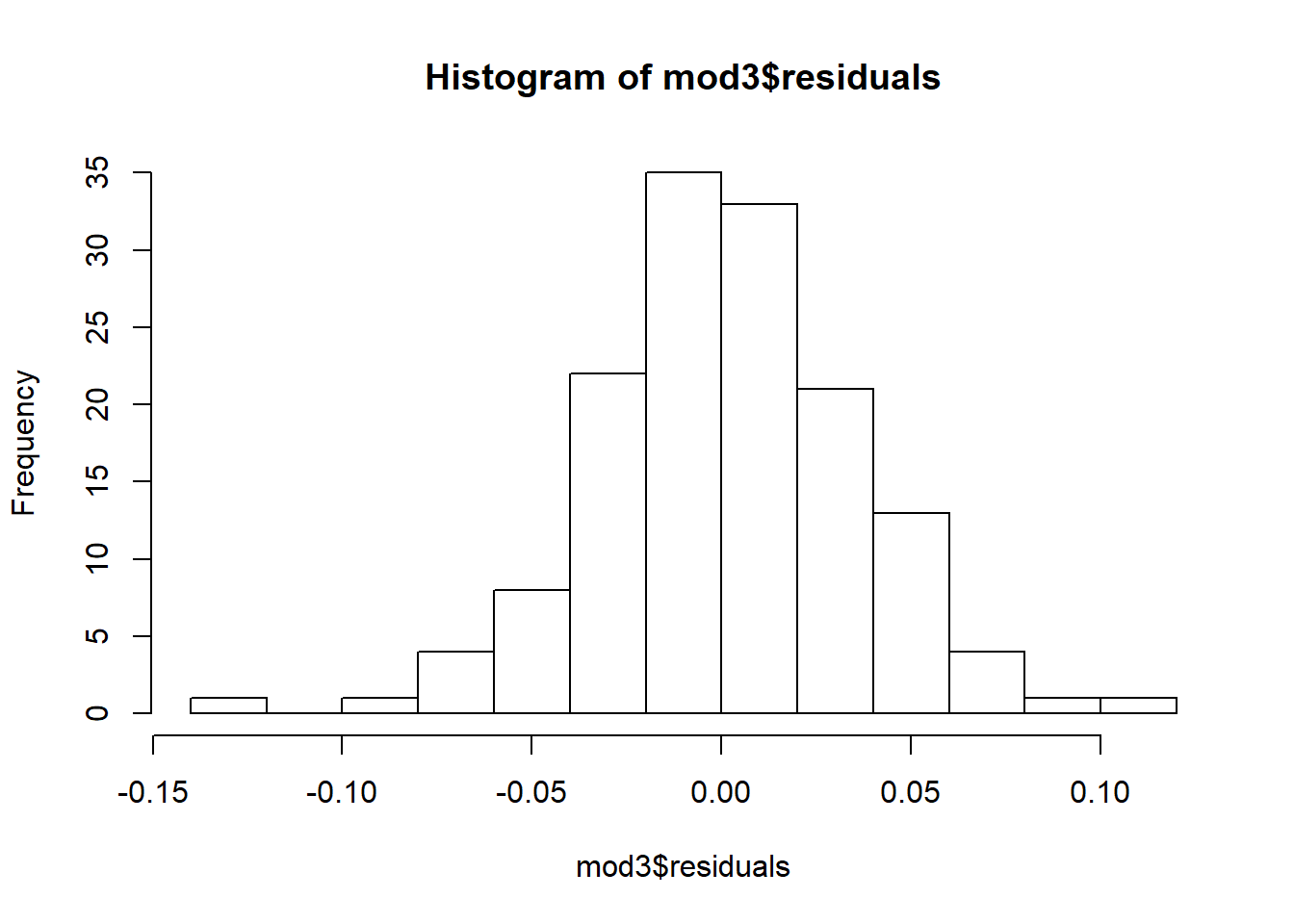

library(tseries)
jarque.bera.test(mod3$residuals)

## 
##  Jarque Bera Test
## 
## data:  mod3$residuals
## X-squared = 8.15, df = 2, p-value = 0.017

En definitiva los dos primeros modelos que hemos estimado superan las pruebas de diagnosis perfectamente y realizan un ajuste muy parecido de los datos. La elección del modelo ahora sí resulta sencilla a la luz de los valores de los estadísticos AIC, pues el segundo modelo presenta valores para estos estadísticos menores, en términos absolutos, que el primero. Así pues, el modelo seleccionado para modelizar el número de pasajeros que viaja mensualmente en líneas aéreas internacionales es un $ARIMA(0,1,1)×(0,1,1)_{12}$.

8.4.1.7.2 Ejemplo 2: Indice de Producción Industrial de Cantabria

El siguiente ejemplo utiliza los totales mensuales del índice de producción industrial (IPI) de Cantabria Base 2010 para el periodo comprendido entre Enero de 2000 y Abril de 2014, incluidos en libro de Box y Jenkins. Esta base de datos está disponible en la librería “descomponer” de R:

library(descomponer)
data(ipi)
y<-ts(ipi,c(2000,1),frequency=12)

En la representación gráfica de la serie puede apreciarse claramente una fuerte estacionalidad en los datos y una varianza creciente en el tiempo.

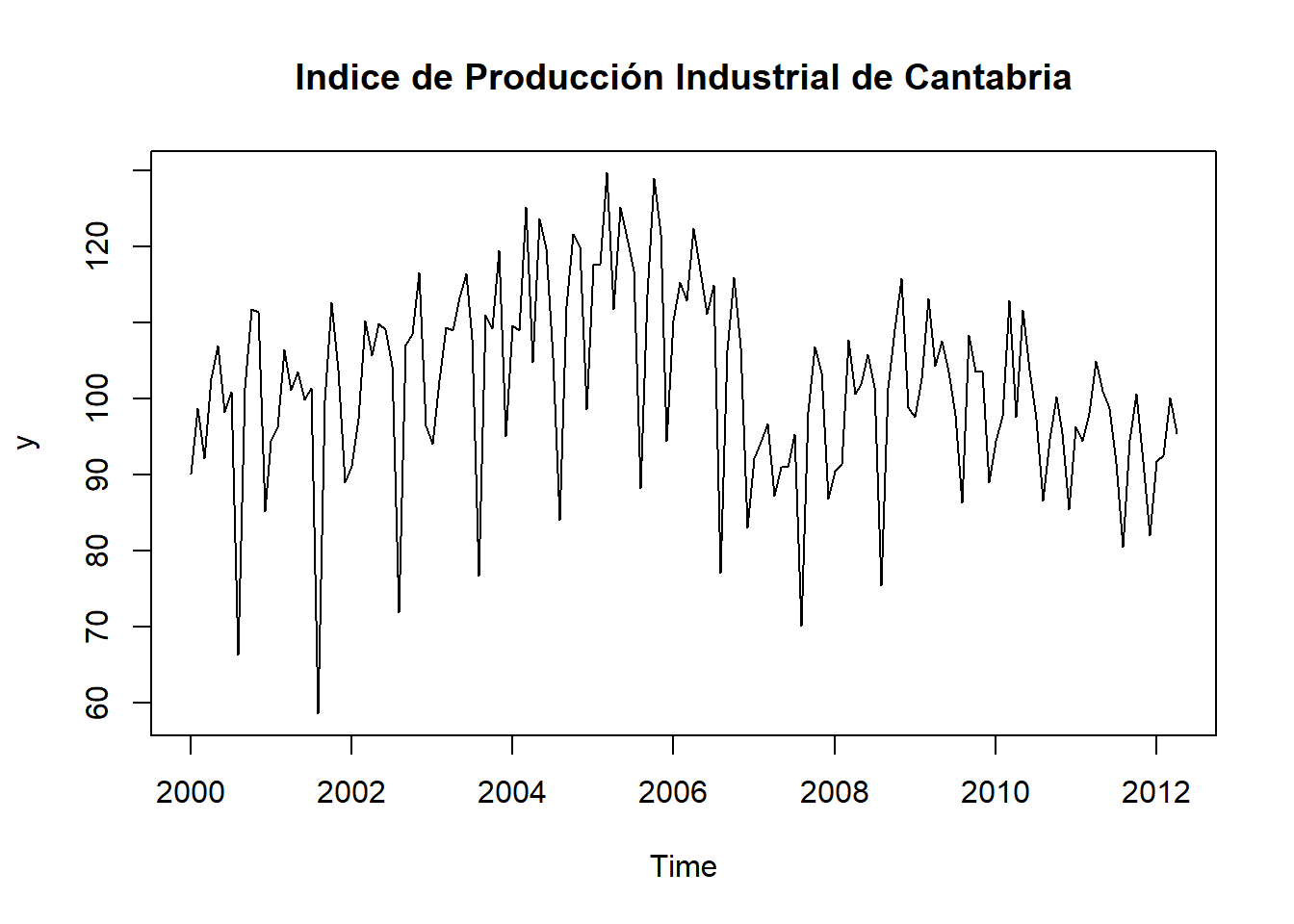
El hecho de que la varianza de la serie no sea constante en el tiempo sugiere que lo primero que debemos hacer es transformar la serie tomando logaritmos para hacer que sea estacionaria en varianza.

y =log(y)

Tras tomar logaritmos, la serie presenta ahora el siguiente aspecto:

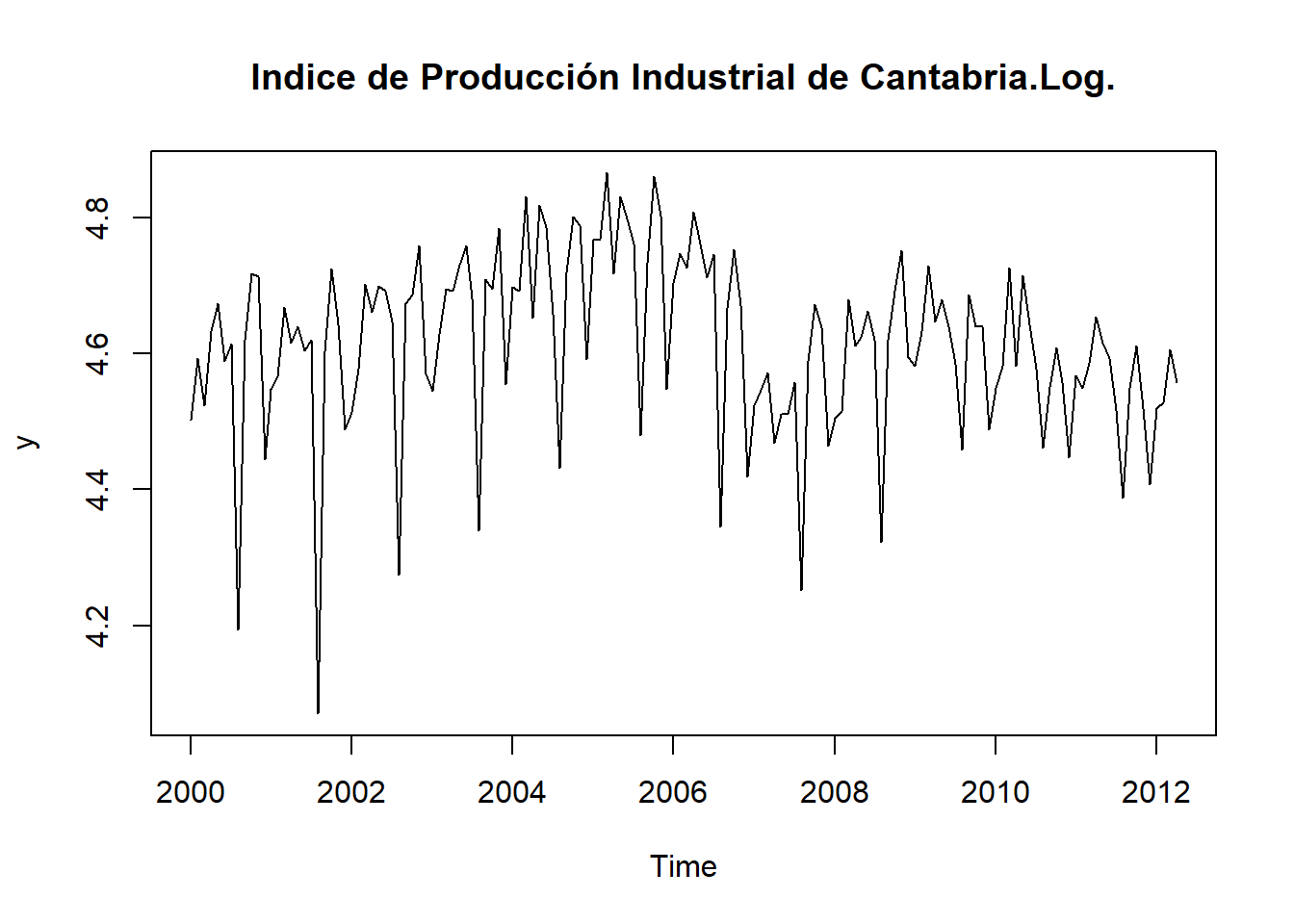
En la librería “forecast” hay una función “auto.arima” que selecciona el mejor modelo ARIMA atendiendo al AIC. Su estructura es la siguiente:

auto.arima(y, d = NA, D = NA, max.p = 5, max.q = 5, max.P = 2, max.Q = 2, max.order = 5, max.d = 2, max.D = 1, start.p = 2, start.q = 2, start.P = 1, start.Q = 1, stationary = FALSE, seasonal = TRUE, ic = c(“aicc”, “aic”, “bic”), stepwise = TRUE, trace = FALSE, approximation = (length(x) > 150 | frequency(x) > 12), truncate = NULL, xreg = NULL, test = c(“kpss”, “adf”, “pp”), seasonal.test = c(“seas”, “ocsb”, “hegy”, “ch”), allowdrift = TRUE, allowmean = TRUE, lambda = NULL, biasadj = FALSE, parallel = FALSE, num.cores = 2, x = y, …)

La función permite establecer el orden de diferenciación regular o estacional. Si no se indica ningún orden, utiliza el test KPSS para establecer el orden regular, y el test OCSB para el estacional. En la opción test, se puede cambiar este criterio de diferenciación por el “test Dikey-Fuller Aumentado” (“adf”) ó el test de Phillips-Perron (“pp”) y en “sasonal.test” permite elegir el test “ch”.

En la función se puede indicar el orden de los coeficientes AR(p) y MA(q) regulares, y AR(P) y MA(Q) estacionales con que iniciar la selección del mejor modelo (“start”) y con que acabar la selección del mejor modelo (“max”), si no se le indica nada los valores por defecto son los que figuran en la estructura de la función.

Señalar, por último, que en “ic” se puede optar por el criterio de selección: AICC, AIC y BIC ).

A continuación, buscamos con los parámetros de los coeficientes establecidos por defecto en la funcion auto.arima, el mejor modelo ARIMA en la serie del IPI de Cantabria:

library(forecast)

## 
## Attaching package: 'forecast'

## The following object is masked from 'package:rcompanion':
## 
##     accuracy

## The following object is masked from 'package:nlme':
## 
##     getResponse

mod1 <- auto.arima(y)
mod1

## Series: y 
## ARIMA(0,1,1)(0,1,2)[12] 
## 
## Coefficients:
##          ma1    sma1    sma2
##       -0.637  -0.419  -0.222
## s.e.   0.060   0.094   0.097
## 
## sigma^2 estimated as 0.00354:  log likelihood=187.93
## AIC=-367.85   AICc=-367.54   BIC=-356.23

8.4.2 Métodos no paramétricos: splines, aproximación por series de Fourier, función núcleo

8.4.2.1 Introducción

Se dice que se ajusta el modelo paramétrico cuando se estiman sus parámetros a partir de un conjunto de observaciones que siguen dicho modelo, de manera que pueden hacerse predicciones de nuevos valores de $Y$ conocido el valor de $X$, y tener información precisa acerca de la incertidumbre asociada a la estimación y a la predicción.

Sin embargo, si el modelo paramétrico no es el adecuado al análisis de datos que estamos realizando, puede llevar a conclusiones que queden muy alejadas de la realidad, dado que el modelo paramétrico conlleva un grado de exactitud en las afirmaciones que de él se derivan y que son adecuadas siempre y cuando se cumplan los supuestos básicos sobre los que se apoya su construcción teórica. De hecho, los modelos paramétricos presentan una estructura teórica tan rígida que no pueden adaptarse a muchos conjuntos de datos de los que hoy día se disponen para el análisis económico.

La econometría no paramétrica aparece como consecuencia de intentos por solucionar problemas que existen en la econometría paramétrica como, por ejemplo, la consistencia entre los datos y los principios de maximización, homocedasticidad, o la necesidad de asumir una determinada relación, por lo general de forma lineal, entre las variables de interés. Esta preocupación llevó a una serie de investigadores a utilizar formas funcionales flexibles para aproximarse a relaciones desconocidas entre las variables. El plantear formas funcionales flexibles requiere el conocimiento del valor esperado de la variable $Y$, condicional en las otras, $X$. Esto conlleva la necesidad de estimar la función de densidad de $Y$ condicional en $X$.

La econometría no paramétrica no parte de supuestos sobre la distribución de probabilidad de las variables bajo estudio, sino que trata de estimar dicha distribución para encontrar la media condicional y los momentos de orden superior (por ejemplo, la varianza) de la variable de interés. Una de las desventajas de este método es, sin embargo, la necesidad de contar con muestras muy grandes si es que se desea estimar la función de relación entre ambas variables de manera precisa. Además el tamaño de la muestra debe aumentar considerablemente conforme aumenta el número de variables involucradas en la relación.

Los modelos de regresión paramétricos suponen que los datos observados provienen de variables aleatorias cuya distribución es conocida, salvo por la presencia de algunos parámetros cuyo valor se desconoce.

\[y_i= \beta_0 + \beta_1 x_i + e_i,\ \ i=1,2,…,n\]

con $e_i\approx N(0;\sigma^2)$

Este es un modelo estadístico con tres parámetros desconocidos: $\beta_0$; $\beta_1$ y $\sigma^2$.

Una formulación general de un modelo de regresión paramétrico es la siguiente:

\[y_i=m(x_i;\theta)+e_i,\ \ i=1,2,…, n,\ \ \theta \in \Theta \in \Re\]

Donde $m(x_i;\theta)$ es una función conocida de $X$ y de $\theta$, que es desconocido, $e_i$ es una variable aleatoria idénticamente distribuida con $E(e_i)=0$ y $Var(e_i)=\sigma^2$. El modelo de regresión lineal simple sería un caso particular con $\theta=(\beta_0, \beta_1)$ y $m(x_i;\theta)=\beta_0 + \beta_1 x_i$.

Donde los valores de la variable explicativa son conocidos, por lo que se dice que el modelo tiene diseño fijo, y dado que la varianza de los errores es constante el modelo es Homocedástico.

Considerando una variable aleatoria bivariante con densidad conjunta $(Y,X)$, cabe definir la función de regresión $f(y,x)$ como $m(x,\theta)=E(Y/X=x)$, es decir, el valor esperado de $Y$ cuando $X$ toma el valor conocido $x$. Entonces $E(Y/X)=m(X,\theta))$, y definiendo $e=Y-m(X,\theta)$, se tiene que: $Y=m(X,\theta)+e$, $E(e/X)=0$ y $Var(e/X)=\sigma^2$.

Se supone que se observan ahora $n$ pares de datos $(y_i,x_i),\ \ i=1…n$. Estos datos siguen el modelo de regresión no paramétrico: $y_i=m(x_i;\theta)+e_i$.

Una vez establecido el modelo, el paso siguiente consiste en estimarlo (o ajustarlo) a partir de las n observaciones disponibles. Es decir, hay que construir un estimador de la función de regresión y un estimador de la varianza del error. Los procedimientos de estimación se conocen como métodos de suavizado.

El abanico de técnicas disponibles para estimar no paramétricamente la función de regresión es amplísimo e incluye, entre otras, las siguientes:

• Ajuste local de modelos paramétricos. Se basa en hacer varios (o incluso infinitos, desde un punto de vista teórico) ajustes paramétricos teniendo en cuenta únicamente los datos cercanos al punto donde se desea estimar la función.

• Suavizado mediante splines. Se plantea el problema de buscar la función $\hat m(x)$ que minimiza la suma de los cuadrados de los errores ($e_i=y_i-\hat m(x)$) más un término que penaliza la falta de suavidad de las funciones ($\hat m(x)$) candidatas (en términos de la integral del cuadrado de su derivada segunda).

• Métodos basados en series ortogonales de funciones. Se elige una base ortonormal del espacio vectorial de funciones y se estiman los coeficientes del desarrollo en esa base de la función de regresión. Los ajustes por series de Fourier y mediante wavelets son los dos enfoques más utilizados.

• Técnicas de aprendizaje supervisado. Las redes neuronales, los k vecinos más cercanos y los árboles de regresión se usan habitualmente para estimar $m(x)$.

8.4.2.2 Ajuste local (estimadores núcleo)

Los histogramas son siempre, por naturaleza, funciones discontinuas; sin embargo, en muchos casos es razonable suponer que la función de densidad de la variable que se está estimando es continua. En este sentido, los histogramas son estimadores insatisfactorios. Los histogramas tampoco son adecuados para estimar las modas, a lo sumo, pueden proporcionar “intervalos modales”, y al ser funciones constantes a trozos, su primera derivada es cero en casi todo punto, lo que les hace completamente inadecuados para estimar la derivada de la función de densidad.

Los estimadores de tipo núcleo (o kernel) fueron diseñados para superar estas dificultades. La idea original es bastante antigua y se remonta a los trabajos de Rosenblatt y Parzen en los años 50 y primeros 60. Los estimadores kernel son, sin duda, los más utilizados y mejor estudiados en la teoría no paramétrica.

Dada un m.a.s ($X_1,X_2,...X_n$) con densidad $f$, estimamos dicha densidad en un punto $t$ por medio del estimador:

\[\hat f(t)=\frac{1}{nh}\sum_{i=1}^n K(\frac{t-X_i}{h})\]

donde $h$ es una sucesión de parámetros de suavizado, llamados ventanas, amplitudes o ancho de banda (windows, bandwidths) que deben tender a cero ”lentamente" ($h \Rightarrow 0$, $nh\Rightarrow \infty$) para poder asegurar que $\hat f$ tiende a la verdadera densidad $f$ de las variables $X_i$ y $K$ es una función que cumple $\int K=1$. Por ejemplo:

• Nucleo Gaussiano $\frac{1}{\sqrt{2 \pi}}e^{- \frac {u^2} 2}$

• Núcleo Epanechnikov $\frac 3 4 (1-u^2)I_{\mid u \mid < 1}$

donde $I_{\mid u \mid < 1}$ es la función que vale 1 si ${\mid u \mid < 1}$ y cero si ${\mid u \mid \geq 1}$

• Núcleo Triangular $(1-\mid u \mid)I_{\mid u \mid < 1}$

• Núcleo Uniforme $\frac 1 2 I_{\mid u \mid < 1}$

• Núcleo Biweight $\frac {15} {16} (1-u^2)I_{\mid u \mid < 1}$

• Núcleo Triweight $\frac {35} {32} (1-u^2)I_{\mid u \mid < 1}$

Los programas informáticos eligen el ancho de ventana, $h$, siguiendo criterios de optimización (error cuadrático medio).

En R la estimación de una función de densidad kernel se realiza con la función “density”. Con los datos del vector $x$, hay que realizar el siguiente programa:

x <- c(2.1,2.6,1.9,4.5,0.7,4.6,5.4,2.9,5.4,0.2)
density(x, kernel="epanechnikov")

## 
## Call:
##  density.default(x = x, kernel = "epanechnikov")
## 
## Data: x (10 obs.);   Bandwidth 'bw' = 1.065
## 
##        x                 y         
##  Min.   :-2.9942   Min.   :0.0000  
##  1st Qu.:-0.0971   1st Qu.:0.0237  
##  Median : 2.8000   Median :0.0943  
##  Mean   : 2.8000   Mean   :0.0862  
##  3rd Qu.: 5.6971   3rd Qu.:0.1524  
##  Max.   : 8.5942   Max.   :0.1695

plot(density(x, kernel="epanechnikov"))

Los estimadores núcleo establecen que el peso de ($X_i$,$Y_i$) en la estimación de $m(x)$ es:

\[W_i(t,X_i)=\frac {\frac 1 h K(\frac{t-X_i}{h})}{\hat f(t)}\]

donde $K(t)$ es una función de densidad simétrica (por ejemplo, la normal estándar) y $\hat f(t)$ es un estimador kernel de la densidad como el definido en el apartado anterior.

$W_i(t,X_i)$ es, para cada i, una función de ponderación que da “mayor importancia” a los valores $X_i$ de la variable auxiliar que están cercanos a t.

Una expresión alternativa para $W_i(t,X_i)$

\[W_i(t,X_i)=\frac {K(\frac{t-X_i}{h})}{\sum_{j=1}^nK(\frac{t-X_i}{h})}\]

A partir de los pesos puede resolverse el problema de mínimos cuadrados ponderados siguiente:

\[min_{a,b}\sum_{i=1}^n W_i(Y_i-(\beta_0+\beta_1(t-X_i)))^2\]

los parámetros así obtenidos dependen de $t$, porque los pesos $W_i$ también dependen de $t$. La recta de regresión localmente ajustada alrededor de $t$ sería:

\[l_t(X)=\hat \beta_0(t)+\hat \beta_1(t)(t-X_i)\]

Y la estimación de la función en el punto en donde $X=t$

\[\hat m(t) =l_t(t)=\hat \beta_0(t)\]

Las funciones núcleo usadas en la estimación no paramétrica de la regresión son las mismas que en la densidad.

Si se generaliza al ajuste local de regresiones polinómicas de mayor grado, es decir si pretendemos estimar una forma lineal del tipo:

\[\beta_0+\beta_1 X_i+\beta_3 X_i^2+...+\beta_q X_i^q\]

con la salvedad de que en vez del valor $X_i$ en la regresión lineal múltiple se utiliza el valor $t-X_i$. El estimador de polinomios locales de grado $q$, asignando los pesos obtenidos mediante la función núcleo. se resuelve mediante el siguiente problema de regresión polinómica ponderada:

\[min_{a,b}\sum_{i=1}^n W_i(Y_i-(\beta_0+\beta_1(t-X_i)+\beta_2(t-X_i)^2+...+\beta_q(t-X_i)^q))^2\]

Los parámetros $\hat \beta_j= \hat \beta_j(t)$ dependen del punto t en donde se realiza la estimación, y el polinomio ajustado localmente alrededor de t sería:

\[P_{q,t}=\sum_{j=0}^q \hat \beta_j(t-X_i)^j\]

Siendo $m(t)$ el valor de dicho polinomio estimado en el punto en donde $X=t$:

\[\hat m(t) =P_{q,o}= \hat \beta_0(t)\]

En el caso particular del ajuste de un polinomio de grado cero, se obtiene el estimador de Nadaraya−Watson, o estimador núcleo de la regresión:

\[\hat m_k(t)=\frac {\sum_{i=0}^n K(\frac{t-X_i}{h})Y_i}{\sum_{i=0}^n K(\frac{t-X_i}{h})}\]

El estimador del parámetro de suavizado $h$ tiene una importancia crucial en el aspecto y propiedades del estimador de la función de regresión. Valores pequeños de $h$ dan mayor flexibilidad al estimador y le permiten acercarse a todos los datos observados, pero originan altos errores de predicción (sobre-estimación). Valores mas altos de $h$ ofrecerán un menor grado de ajuste a los datos pero predicen mejor, aunque si $h$ es demasiado elevado tendremos una falta de ajuste a los datos (sub-estimación).

Utilizando la base de datos “cars” de R, que contiene las variables “dist” (distancia de parada) y “speed” (velocidad), vamos a realizar la representación gráfica de la regresión kernel realizada con el estimador de Nadaraya–Watson con diferentes parámetros de suavizado.

data(cars)
plot(cars$speed, cars$dist, ylab="Distancia", xlab="Velocidad", main="Regresión kernel con diferentes parámetros de suavizado")
lines(ksmooth(cars$speed, cars$dist, "normal", bandwidth = 2), col = 2)
lines(ksmooth(cars$speed, cars$dist, "normal", bandwidth = 5), col = 3)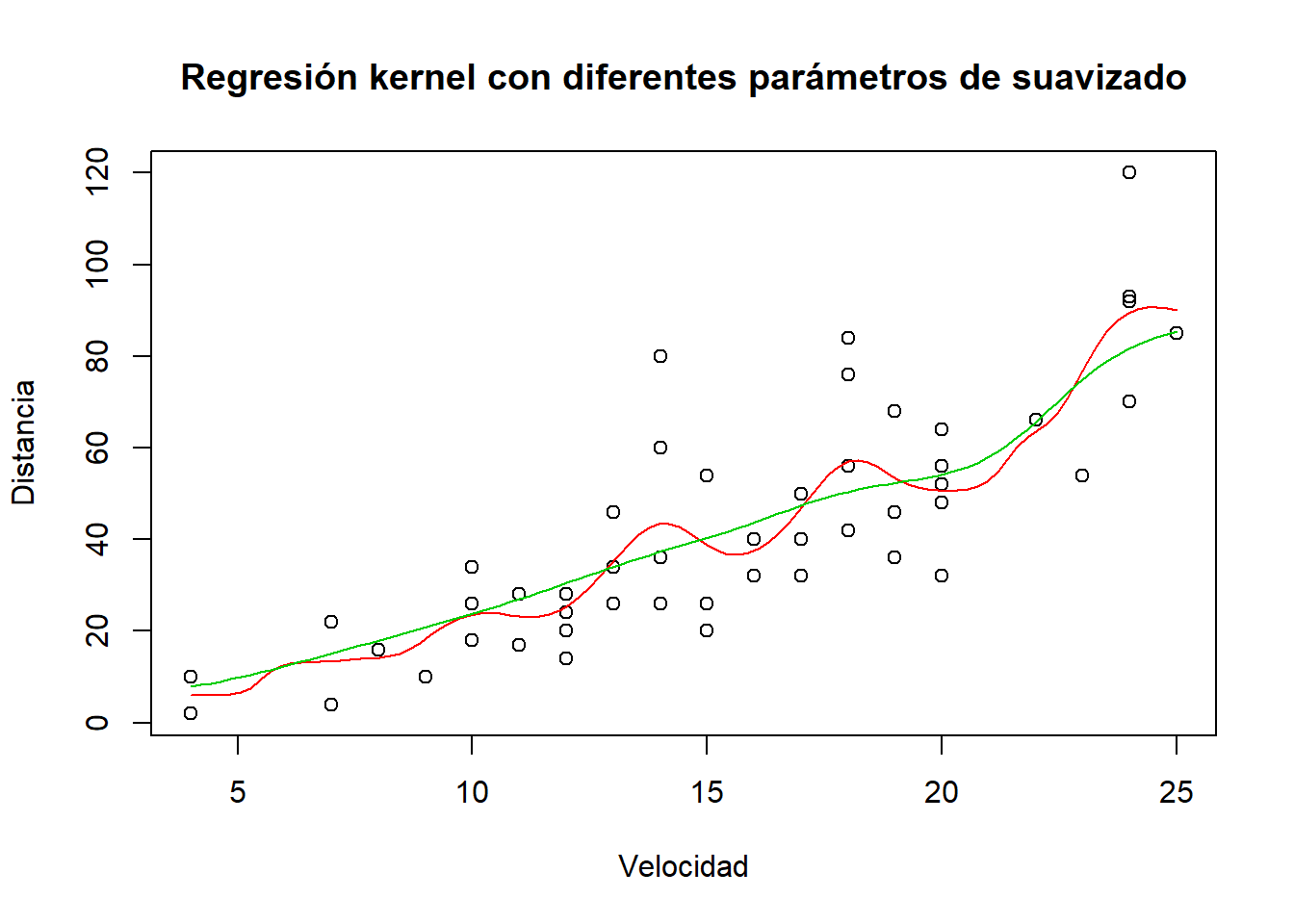

8.4.2.3 Regresión LOESS

La Regresión LOESS (inicialmente Lowess: Locally Weighted Scatterplot Smoothing) es un modelo de regresión no-paramétrica que también se conoce como regresión local.

LOESS combina la sencillez de la regresión lineal por mínimos cuadrados con la flexibilidad de la regresión no lineal. Mediante el ajuste de modelos sencillos sobre subconjuntos locales de datos, crea una función que describe la parte determinista de la variación en los datos punto a punto. Uno de los principales atractivos de este método es que no resulta necesario especificar una función global para ajustar un modelo a los datos.

La regression LOESS, fue propuesta originalmente por Cleveland (1979) y desarrollada por Cleveland y Devlin (1988).

Dado un conjunto de pares de datos, $(x_t,y_t)$, correspondientes a observaciones de las variables $(X,Y)$. El objetivo de un suavizado en un diagrama de dispersión es estimar la componente determinística,$\mu(\cdot)$ cuando se utiliza el siguiente modelo de la relación entre las variables:

\[y_t=\mu(x_t)+e_t\]

Un modelo de regresió lineal simple, supone estimar:

\[\mu(X_t)=\beta_0+\beta_1x_t\]

con todas las observaciones participando en la estimación.

La regresión local es un enfoque de ajuste de curvas (o superficies) a datos mediante suavizados en los que el ajuste en $x$ se realiza utilizando únicamente observaciones en un entorno de $x$. Al realizar una regresión local puede utilizarse una familia paramétrica al igual que en un ajuste de regresión global pero solamente se realiza el ajuste localmente.

En la práctica se realizan ciertas suposiciones:

sobre la función de regresión $\mu(\cdot)$ tales como continuidad y derivabilidad de manera que pueda estar bien aproximada localmente por polinomios de un cierto grado.
sobre la variabilidad de $Y$ alrededor de la curva $\mu(\cdot)$.

Los métodos de estimación que resultan de este tipo de modelos, requieren que para cada punto $x$, se defina un entorno. Dentro de ese entorno suponemos que la función regresora es aproximada por una función paramétrica polinómica.Por ejemplo, un polinomio cuadrático: $g(u) = a_0 + a_1 (u - x) +a_2 (u -x)^2$.

Se estiman los parámetros con las observaciones en ese entorno, denominándose ajuste local a la función ajustada evaluada en $x$.

Generalmente, se incorpora una función de peso, $w(u)$, para dar mayor peso a los valores $x_t$ que se encuentran cerca de $x$. Los criterios de estimación dependen de los supuestos que se realicen sobre la distribución de $Y$ dado $x$. Si, por ejemplo, suponemos que tiene distribución Gaussiana con varianza constante, es adecuado utilizar el Método de Mínimos Cuadrados.

Los subconjuntos de los datos utilizados para el ajuste por mínimos cuadrados ponderados acaban estando determinados por un parámetro de suavización que define el ancho de banda, $\alpha$. Este parámetro es un número entre $\frac {(\lambda + 1)}{n}$ y 1, donde $\lambda$ denota el grado del polinomio local. El valor de $\alpha$ es la proporción de los datos utilizados en cada ajuste. A $\alpha$ se le llama parámetro de suavización porque controla la flexibilidad de la función de regresión. Valores grandes de $\alpha$ producen curvas suaves; valores pequeños hacen que la curva se ajuste tal vez demasiado a los datos. En ocasiones se recomienda utilizar valores en el rango que va de $0.25$ a $0.5$.

Este es el codigo en R para el suavizado con Loess.

co2.l=loess(co2~time(co2))
summary(co2.l)

## Call:
## loess(formula = co2 ~ time(co2))
## 
## Number of Observations: 468 
## Equivalent Number of Parameters: 4.34 
## Residual Standard Error: 2.11 
## Trace of smoother matrix: 4.72  (exact)
## 
## Control settings:
##   span     :  0.75 
##   degree   :  2 
##   family   :  gaussian
##   surface  :  interpolate      cell = 0.2
##   normalize:  TRUE
##  parametric:  FALSE
## drop.square:  FALSE

plot (co2, main="Regresión LOESS")
lines (ts(co2.l$fitted, frequency = 12, start = c(1959, 1)), col=2)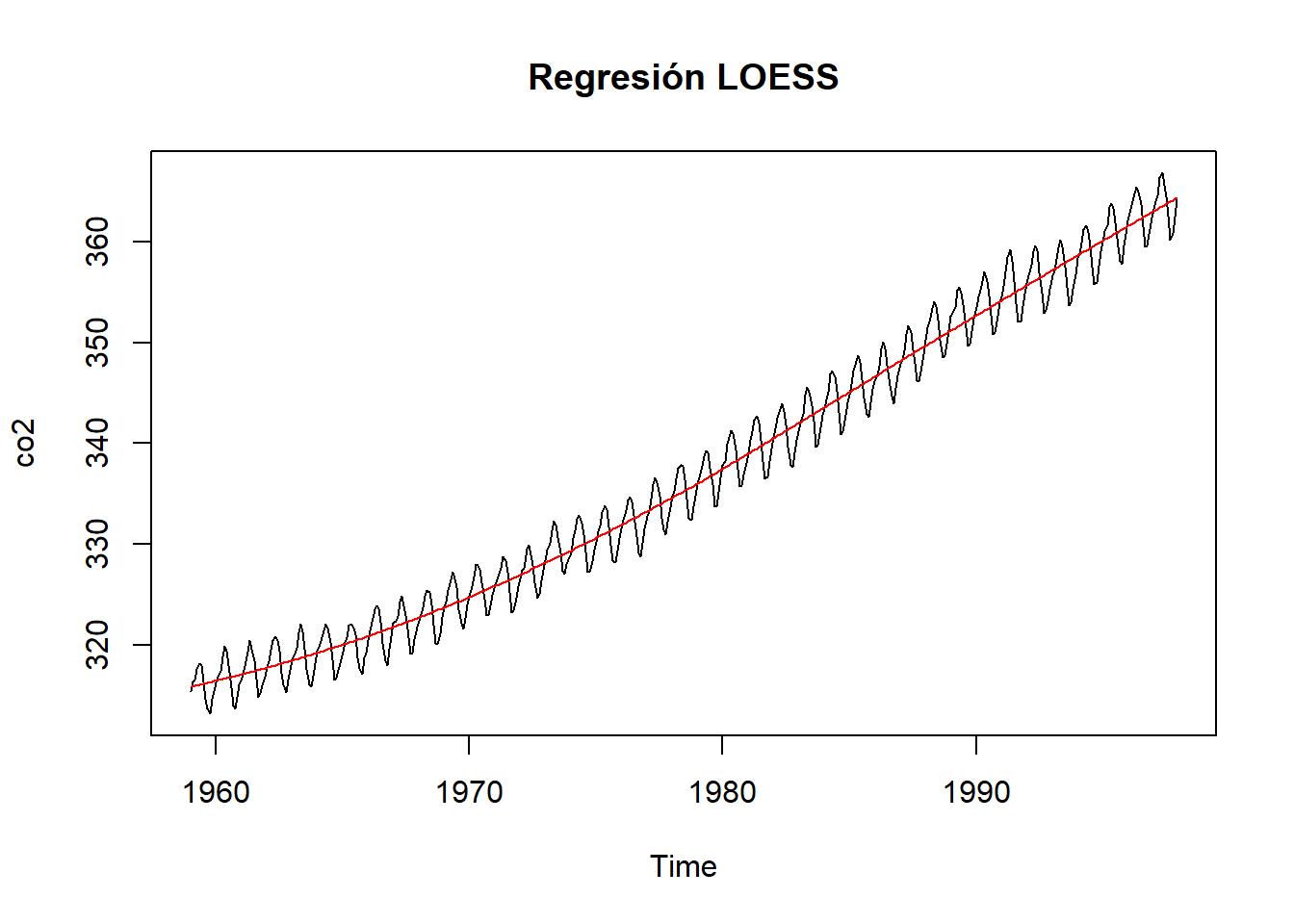

8.4.2.4 Splines

Para poder estimar la función $f$ de la forma más sencilla posible, deberíamos poder representarla de forma que $Y_i=f(x_i)+e_i$, $i=1,2,...,n$ se convierta en un modelo lineal.

Y esto se puede hacer eligiendo una base de funciones de dimensión $q$ que genere un subespacio de funciones que incluya a $f$ como elemento y que pueda expresarse como:

\[f(x)=\sum_{j=1}^q \beta_j s_j(x)\]

siendo $\beta_j$ un parámetro desconocido, asociado al elemento $j$, $s_j(x)$ de dicha base de funciones, de manera que:

\[Y_i=\sum_{j=1}^q \beta_j s_j(x) + e_i\] (1)

se convierte en un modelo lineal de dimensión $q$.

La regresión con funciones base polinómicas es la propuesta más sencilla para este tipo de estimaciones.

Supongamos que $f$ es un polinomio de grado 4 de forma que el espacio de polinomios de grado 4 contiene a $f$. Una base de este subespacio es:

\[\begin{equation} \left\lbrace\begin{array}{ll} s_1(x)=1\\ s_2(x)=x\\ s_3(x)=x^2\\ s_4(x)=x^3\\ s_5(x)=x^4 \end{array}\right.\end{equation}\]

De manera que el modelo (1) se convierte en:

\[Y_i=\beta_1 + \beta_2 x_i + \beta_3 x_i^2 + \beta_4 x_i^3 + \beta_5 x_i^4 + e_i\]

Un spline es una curva diferenciable definida en porciones mediante polinomios, que se utiliza como base de funciones para aproximar curvas con formas complicadas.

Las bases de spilines más populares:

• Bases de polinomios truncados.

• Bases de splines cúbicos.

• Bases de B-splines.

• Bases de thin plate splines.

Una función spline está formada por varios polinomios, cada uno definido sobre un subintervalo, que se unen entre sí obedeciendo a ciertas condiciones de continuidad.

Supongamos que se ha fijado un entero $q \neq 0$, de manera que disponemos de $q+1$ puntos, a los que denominaremos nodos, tales que $t_0<t_1<t_2<...<t_q$, en los que troceamos nuestro conjunto de datos. Decimos entonces que una función spline de grado $q$ con nodos en $t_0,t_1,t_2,...,t_q$ es una función $S$ que satisface las condiciones:

en cada intervalo $[t_{j-1}, t_j)$, $S$ es un polinomio de grado menor o igual a $q$.
$S$ tiene una derivada de orden $(q-1)$ continua en $[t_0,t_q]$.

Los splines de grado $0$ son funciones constantes por zonas. La expresión matemática de un spline de grado $0$ es la siguiente:

\[\begin{equation} \left\lbrace\begin{array}{ll} s_0(x)=c_0 & x \in [t_0,t_1) \\ s_j(x)=c_j & x \in [t_{j-1},t_j) \\ ...\\ s_{q-1}(x)=c_{q-1} & x \in [t_{q-1},t_q) \end{array}\right.\end{equation}\]

En la figura siguiente se muestran las gráficas correspondientes a los splines de grado cero:

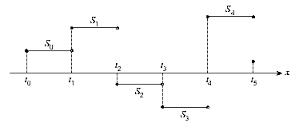
Los splines de grado $0$, se definen en un solo tramo de nodo, y ni siquiera es continua en los nodos. Equivale a realizar una regresión por tramos.

\[Y_i=\beta_0 c_0 x_i + \beta_1 c_1 x_i + ... + \beta_{q-1} c_{q-1} x_i+ e_i\]

donde $c_j$ toma valor $1$ en $[t_{j-1},t_j)$ y cero en el resto.

Un spline de grado 1 o lineal se expresa como:

\[\begin{equation} \left\lbrace\begin{array}{ll} s_0(x)=a_0x + b_0 & x \in [t_0,t_1) \\ s_j(x)=a_jx + b_j & x \in [t_{j-1},t_j) \\ ...\\ s_{q-1}(x)=a_{q-1}x + b_{q-1} & x \in [t_{q-1},t_q) \end{array}\right.\end{equation}\]

La representación gráfica de un spline lineal aparece en la figura siguiente:

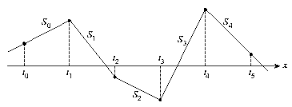
Las funciones de spilines más comúnmente utilizadas son las de grado tres ó cúbicas. Son polinomios de grado tres a trozos, que son continuos en los nodos al igual que su primera y segunda derivada, proporcionando un excelente ajuste a los puntos tabulados y a través de un cálculo que no es excesivamente complejo.

Sobre cada intervalo $[t_{j-1},t_j)$, $S$ está definido por un polinomio cúbico diferente.

\[\begin{equation} \left\lbrace\begin{array}{ll} s_0(x)=a_0x^3 + b_0x^2 + c_0x + d_0 & x \in [t_0,t_1) \\ s_j(x)=a_jx^3 + b_jx^2 + c_jx + d_0 & x \in [t_{j-1},t_j) \\ ...\\ s_{q-1}(x)=a_{q-1}x^3 + b_{q-1}x^2 + c_{q-1}x + d_{q-1} & x \in [t_{q-1},t_q) \end{array}\right.\end{equation}\]

Los polinomios $S_{j-1}$ y $S_j$ interpolan el mismo valor en el punto $t_j$, para que se cumpla: $S_{j-1}(x_i)=y_i=S_j(x_i)$, por lo que se garantiza que $S$ es continuo en todo el intervalo. Además, se supone que $S'$ y $S''$ son continuas, condición que se emplea en la deducción de una expresión para la función del spline cúbico.

Aplicando las condiciones de continuidad del spline $S$ y de las derivadas primera $S'$ y segunda $S''$, es posible encontrar la expresión analítica del spline.

Una de las bases de splines cúbicos más utilizadas, basada en $(q-2)$ nodos interiores, $x^*_j$, $j=1,2,...,q-2$ es:

\[\begin{equation} \left\lbrace\begin{array}{ll} s_0(x)=1 \\ s_1(x)=x \\ s_{j+2}(x)=R[x_j,x^*_j] \end{array}\right.\end{equation}\]

Siendo $R[x,z]=\frac 1 4[(z-\frac 1 2)^2-\frac 1 {12}][(x-\frac 1 2)^2-\frac 1 {12}]-\frac 1 {24}[(\mid z- x \mid - \frac 1 2)^4- [(\mid z- x \mid - \frac 1 2)^2+\frac 7 {240}]$

Con esta base de splines definimos $f$ a través de un modelo lineal con matriz de regresores $X$ con $n$ filas y $q$ columnas, cuya i_esima fila es:

\[X_i=[1,x_i,R[x_i,x^*_1],R[x_i,x^*_2],...,R[x_i,x^*_{q-2}]]\]

Los elementos de una base de splines cúbicos son polinomios de grado 3. Un Spline cúbico se representa en la figura siguiente:

Hay dos grandes enfoques en el tema de modelos de suavizado con splines:

splines de suavizado (smoothing splines) y
splines de regresión (regression splines).

Los splines de suavizado utilizan tantos parámetros como observaciones, lo que hace que su implementación no sea eficiente cuando el número de datos es muy elevado.

Los splines de regresión pueden ser ajustados mediante mínimos cuadrados una vez que se ha seleccionado el número de nodos, pero la selección de los nodos requiere de algoritmos bastante complicados.

Los splines con penalizaciones (B-splines) combinan lo mejor de ambos enfoques: utilizan menos parámetros que los splines de suavizado y la selección de los nodos no es tan determinante como en los splines de regresión. Pero sí lo es, la elección del grado de suavización del spline.

Si se mantiene fija la base de splines y se controla el grado de suavización añadiendo una penalización a la función objetivo de mínimos cuadrados:

\[\lambda \beta' S \beta\]

donde $S$ es una matriz de orden $q*q$ con coeficientes conocidos que dependen de la base elegida y un parámetro de suavizado $\lambda$, la solución del modelo de regresión lineal penalizado, en donde la matriz de regresores está ahora definida por la base de splines y la penalización, sería:

\[\hat \beta = (X'X - \lambda S)^{-1}X'y\]

El modelo de regresión lineal con spilines penalizados es equivalente al modelo de regresión lineal:

\[Y'=\beta X' + e\]

donde $Y'=(y,0,0...0)$ es un vector de dimensión $(n+q)$, es decir el vector $y$ seguido de tantos ceros como nodos se han utilizado en la base de los splines.

La matriz de regresores

\[X' = \begin{bmatrix}X\\ B \sqrt \lambda\\ \end{bmatrix}\]

tiene ahora orden $(n+q)*q$, siendo $B$ una matriz que cumple $B=S'S$ y que se obtiene a través de la descomposición de Cholesky, $\lambda$ el parámetro de suavizado y $e$ un vector de $(n+q)$ errores aleatorios.

El parámetro de suavización,$\lambda$,es a priori desconocido y hay que determinarlo, si es muy alto suaviza los datos en exceso. Un criterio utilizado para elegir el parámetro es del valor que minimiza el estadístico general de validación cruzada.

La regresión por splines puede realizarse con múltiples variables explicativas, si tenemos ahora dos explicativas, $x_i$ y $z_i$,y queremos estimar el siguiente modelo aditivo:

\[y_i=f_1(x_i)+f_2(z_i)+e_i\]

Representaríamos cada una de estas dos funciones a través de una base de splines penalizados, que tomando la base cúbica quedaría:

\[f_1(x)=\delta_1+\delta_2X_i+\sum_{j=1}^{q-2} \delta_jR[x_i,x_j^*]\]

\[f_2(z)=\gamma_1+\gamma_2X_i+\sum_{j=1}^{q-2} \gamma_jR[z_i,z_j^*]\]

Partiendo de la base de datos “cars”, la función R “smooth.spline” realiza la regresión por splines utilizando una base de splinee cúbicos penalizados:

attach(cars)
plot(speed, dist, main = "data(cars) & smoothing splines")
cars.spl1 <- smooth.spline(speed, dist)
cars.spl1

## Call:
## smooth.spline(x = speed, y = dist)
## 
## Smoothing Parameter  spar= 0.78013  lambda= 0.11122 (11 iterations)
## Equivalent Degrees of Freedom (Df): 2.6353
## Penalized Criterion (RSS): 4187.8
## GCV: 244.1

cars.spl2 <- smooth.spline(speed, dist, spar=0.10)
lines(cars.spl1, col = "blue")
lines(cars.spl2, col = "red")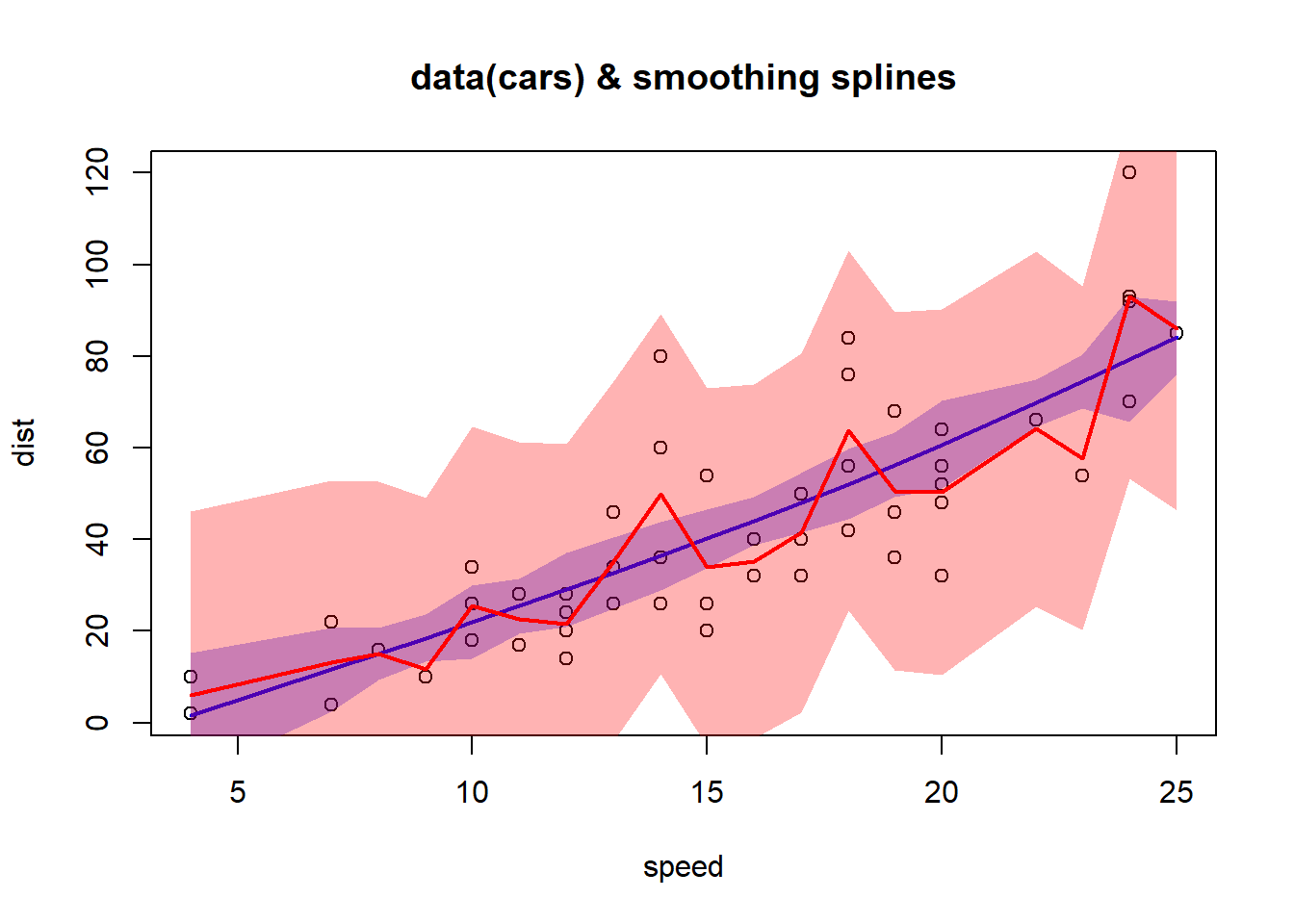

En la función “smooth.spline” el parámetro de suavizado es un valor generalmente entre 0 y 1, en tanto que el coeficiente $\lambda$ se obtiene en el criterio de aceptación (logaritmo de verosimilitud penalizado). En el ejercicio el programa elige un $\lambda=0.7801305$. Si se desea una función menos suavizada, habrá que elegir un parámetro de suavizado más bajo. En línea roja se representa en el gráfico la regresión por splines que se obtendría con un parámetro de suavizado de valor $0.10$.

8.4.2.5 Aproximación por series de Fourier

La forma de Fourier permite aproximar arbitrariamente cerca, tanto a la función como a sus derivadas, sobre todo el dominio de definición de las mismas. La idea que subyace en este tipo de aproximaciones (que podrían denominarse semi-no-paramétricas) es ampliar el orden de la base de expansión, cuando el tamaño de la muestra aumenta, hasta conseguir la convergencia asintótica de la función aproximante a la verdadera función generadora de los datos y a sus derivadas (Gallant, A.R.; 1981, 1984).

Un polinomio de Fourier viene dado por la expresión:

\[\frac \eta 2 + \sum_{j=1}^k[a_j\cos(jw_0t)+b_j\sin(jw_0t)]\]

donde $k$ es es el número de ciclos teóricos o armónicos que consideramos, siendo el máximo $N/2$, $w_0=\frac {2\pi} N$ es la frecuencia fundamental (también denominada frecuencia angular fundamental) y $t$ toma los valores enteros comprendidos entre $1$ y $N$ (es decir, $t = 1, 2, 3, ...N$).

Los coeficientes de los armónicos vienen dados por las expresiones:

\[\frac \eta 2 = \frac 2 N \sum_{i=1}^N y_i\]

\[a_j=\frac 2 N \sum_{i=1}^N y_i \cos(jw_0t)\]

\[b_j=\frac 2 N \sum_{i=1}^N y_i \sin(jw_0t)\]

La aproximación a una función no periódica $m(x_i;\theta)$ por una serie de expansión de Fourier se escribe como:

\[m(x_i;\theta)= \eta + \sum_{j=1}^J[a_j\cos(jx_i)+b_j\sin(jx_i)]\]

El vector de parámetros es $\theta=(\eta, a_1, b_1,...,a_J,b_J)$ de longitud $K=1+2J$.

Suponiendo que los datos siguieran el modelo $y_i=m(x_i;\theta)+e_i$, para $i=1,2,…,N$, estimariamos $\theta$ por mínimos cuadrados minimizando:

\[S_n(\theta)=\frac 1 N \sum_{i=1}^N[y_i-m_K(x_i;\theta)]^2\]

Dado que la variable exógena $x_i$ no esta expresada en forma periódica, debe de transformase o normalizarse en un intervalo de longitud menor que $2\pi$, $[0,2\pi]$.

Como ejemplo, vamos a utilizar la base de datos de la Agencia Española de Meteorológica (Aemet) desde el R-package fda.usc. La base de datos contiene mediciones diarias de temperatura, velocidad del viento y precipitaciones de 73 diferentes estaciones meteorológicas de España para los años 1980 a 2009. En este ejemplo, vamos a analizar las temperaturas medias diarias de Santander, que representamos gráficamente en R con la siguiente programación:

library(fda)

## Loading required package: splines

## Loading required package: Matrix

## 
## Attaching package: 'fda'

## The following object is masked from 'package:forecast':
## 
##     fourier

## The following object is masked from 'package:graphics':
## 
##     matplot

library(fda.usc)

## Loading required package: mgcv

## This is mgcv 1.8-26. For overview type 'help("mgcv-package")'.

data(aemet, package = "fda.usc")
tt = aemet$temp$argvals
temp = as.data.frame(aemet$temp$data, row.names=F)
range.tt = aemet$temp$rangeval
inv.temp = data.frame(t(aemet$temp$data)) # 365 x 73 matrix
names(inv.temp) = aemet$df$name 
plot(ts(inv.temp[,21]),main="Temperaturas medias diarias Santander 1980-2009")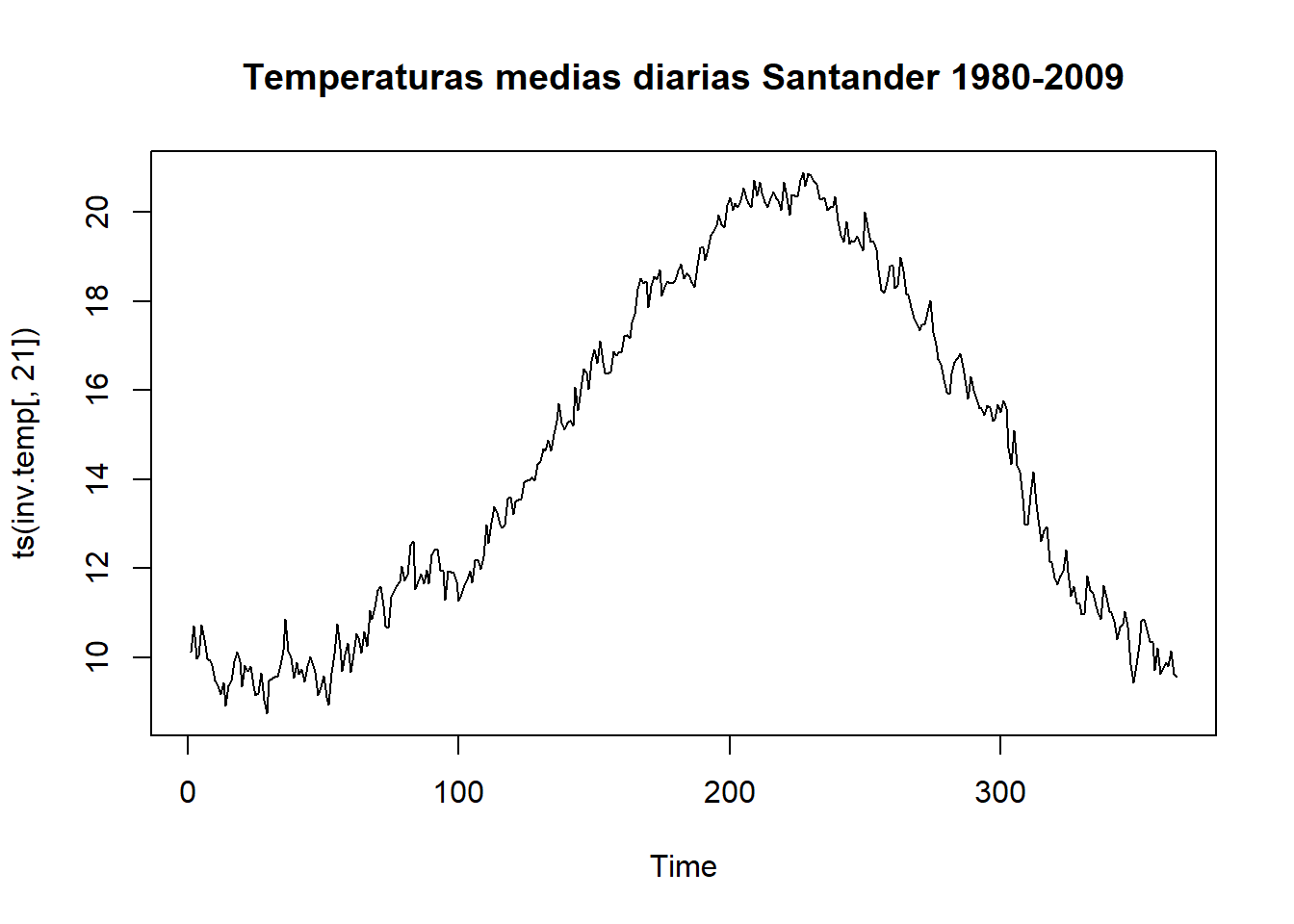

A continuación se van a suavizar estas temperaturas diarias utilizando funciones periódicas de Fourier, en concreto vamos a utilizar las funciones de base igual a 5. Es decir, los armónicos que se obtendrían con:

\[\sum_{j=1}^5[a_j\cos(jw_0t)+b_j\sin(jw_0t)]\]

Santander5 = create.fourier.basis(rangeval = range(tt), nbasis = 5)
plot(Santander5)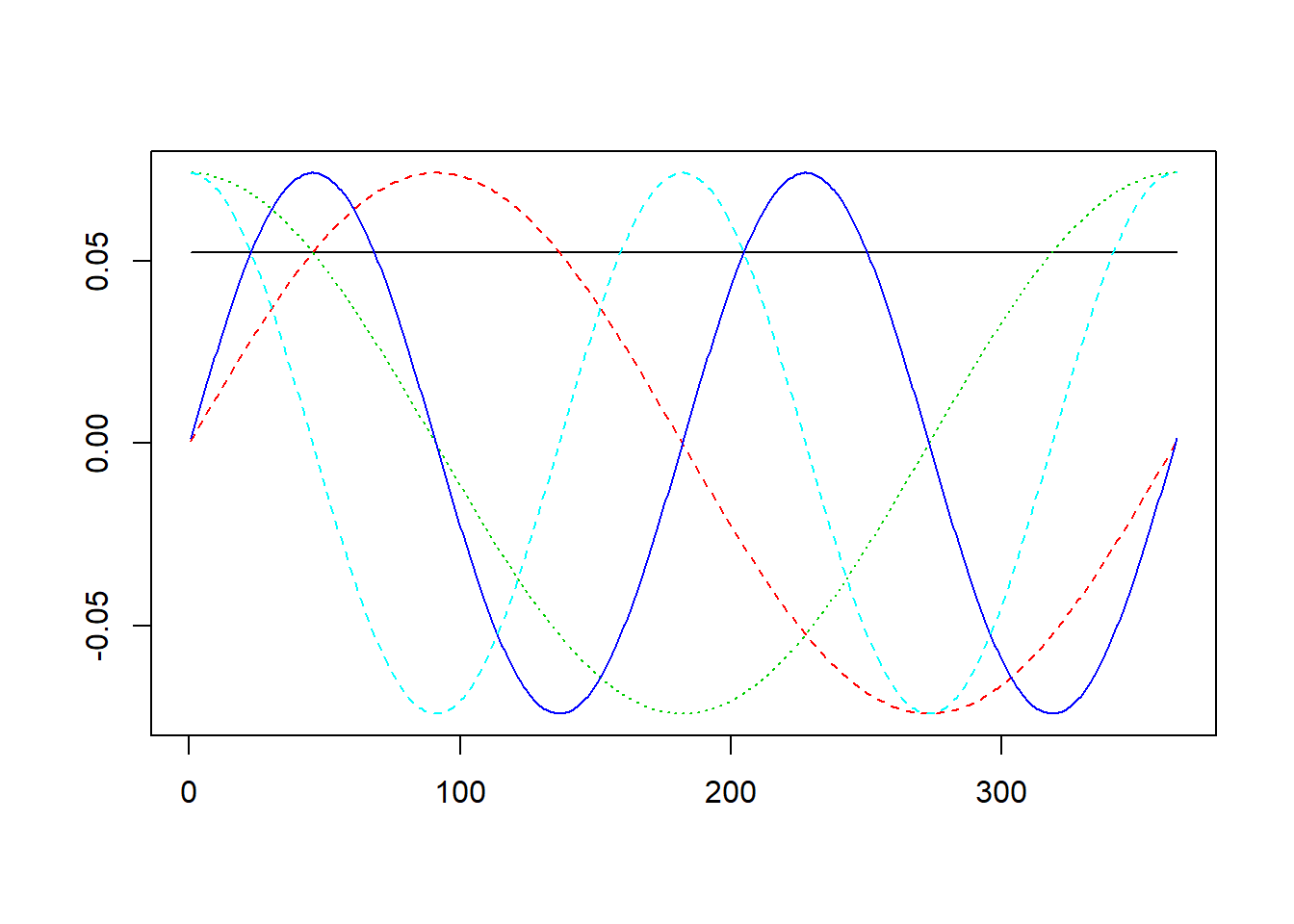

Con la función smooth.basis(argvals=1:n, y, fdParobj) del R-package fda obtenemos la serie suavizada. Respecto a los parámetros, argvals es el dominio, y es el conjunto de valores a suavizar y fdParobj la función base utilizada como regresores:

Santanderfourier5.fd = smooth.basis(argvals = tt, y = inv.temp[,21], fdParobj = Santander5)
plot(ts(inv.temp[,21]), main="Temperaturas medias diarias Santander 1980-2009")
lines(Santanderfourier5.fd,col="red")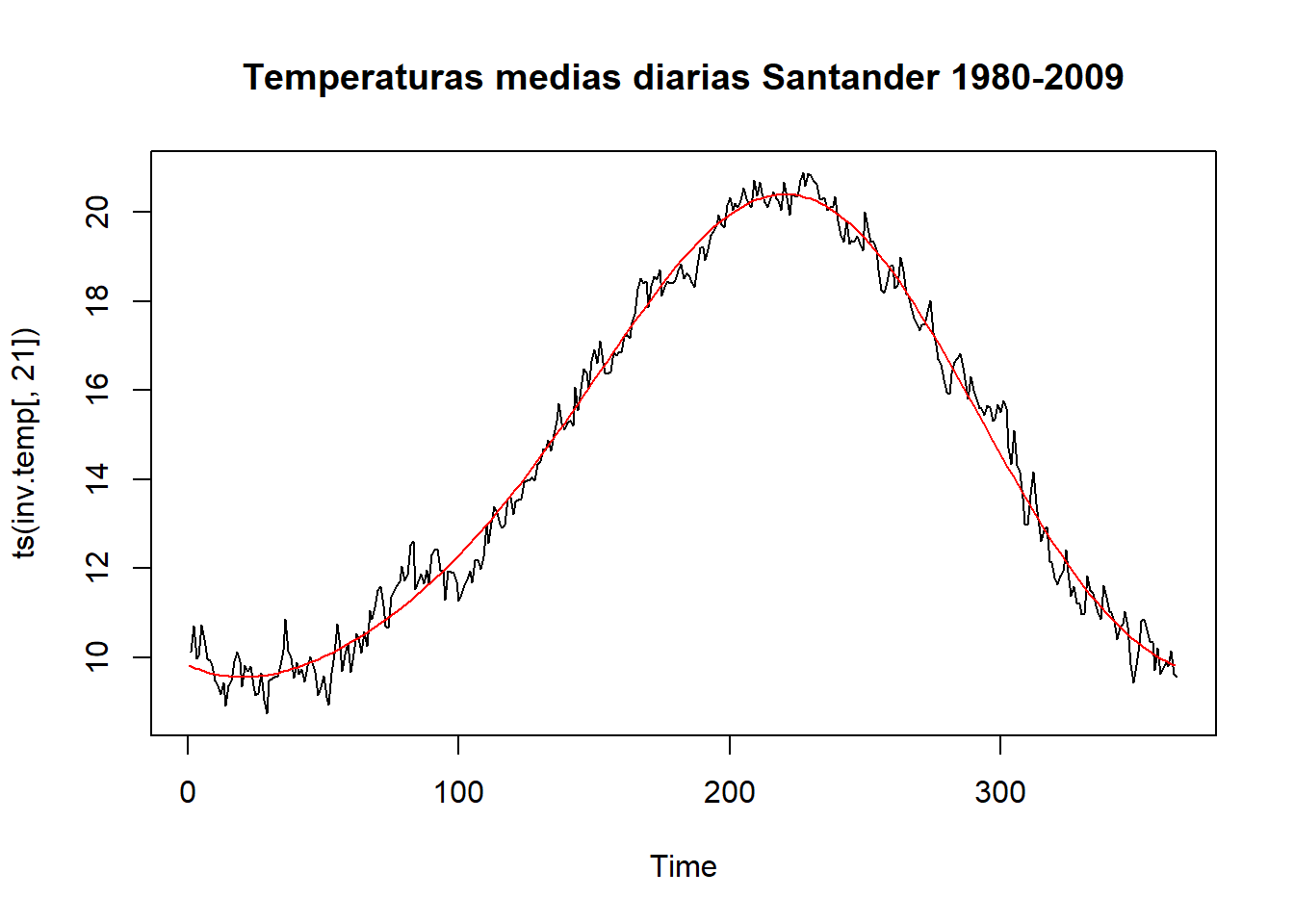

8.4.2.6 Regresión band spectrum

Nerlove (1964) y Granger (1969) fueron los primeros investigadores en aplicar el analisis espectral a las series de tiempo en economía. El uso del analisis espectral requiere un cambio en el modo de ver las series económicas, al pasar de la perspectiva del tiempo al dominio de la frecuencia. El analisis espectral parte de la supsición de que cuanquier serie $X_t$, puede ser transformada en ciclos formados con senos u cosenos:

\[X_t=\eta+\sum_{j=1}^N\left[a_j\cos \left(2\pi\frac{ft}n\right) +b_j\sin\left(2\pi\frac{ft}n\right)\right] \ \ \ \ \ \ (1)\]

donde $\eta$ es la media de la serie, $a_j$ y $b_j$ son su amplitud, $f$ son las frecuencias del conjunto de las $n$ observaciones, $t$ es un indice de tiempo que va de 1 a N, siendo N el numero de periodos para los cuales tenemos observaciones en el conjunto de datos.

El cociente $(\frac{ft}n)$ convierte cada valor de $t$ en escala de tiempo en proporciones de $2n$ y rango $j$, desde $1$ hasta $n$, siendo $n=\frac{N}2$ (es decir, 0,5 ciclos por intervalo de tiempo).

La dinámica de las altas frecuencias (los valores más altos de f) corresponden a los ciclos cortos en tanto que la dinámica de la bajas frecuencias (pequeños valores de f) van a corresponder con los ciclos largos. Si nosotros hacemos que $\frac{ft}n=w$, la ecuación (1) quedaría así:

\[X_t=\eta+\sum_{j=1}^N[a_j\cos(\omega_j)+b_j\sin(\omega_j)] \ \ \ \ \ \ (2)\]

El análisis espectral puede utilizarse para identificar y cuantificar, en procesos aparentemente aperiodicos, sucesiones de ciclos de corto y largo plazo. Una serie dada ${X_t}$ puede contener diversos ciclos de diferentes frecuencias y amplitudes, y esa combinación de frecuencias y amplitudes de carácter cíclico la hacen aparecer como una serie no periódica e irregular. De hecho, la ecuación (2) muestra que cada observación $t$ de una serie de tiempo, es el resultado de sumar los valores en $t$ que resultan de $N$ ciclos de diferente longitud y amplitud, a los que habría que añadir, si cabe, un término de error.

Una manera practica de pasar desde el dominio del tiempo al dominio de la frecuencia es premultiplicando los datos originales por una matriz ortogonal, $W$, sugerida por Harvey (1978), con el elemento (j,t)th:

\[\begin{equation} w_{jt} = \left\lbrace\begin{array}{ll}\left(\frac{1}T\right) ^\frac{1}2 & \forall j=1\\ \left(\frac{2}T\right) ^\frac{1}2 \cos\left[\frac{\pi j(t-1)}T\right] & \forall j=2,4,6,..\frac{(T-2)}{(T-1)}\\ \left(\frac{2}T\right) ^\frac{1}2 \sin\left[\frac{\pi (j-1)(t-1)}T\right] & \forall j=3,5,7,..\frac{(T-2)}T\\ \left(\frac{1}T\right) ^\frac{1}2 (-1)^{t+1} & \forall j=T\end{array}\right.\end{equation}\]

La matriz $W$ tiene la ventaja de ser ortogonal por lo que $WW^T=I$.

Sea $a$ un vector n x 1, el modelo transformado en el dominio de la frecuencia esta dado por: $\hat a= Wa$.

Engle (1974), demostró que una regresión realizada con las series transformadas en el dominio de la frecuencia, Regresión Band Spectrum (RBS), no alteraba los supuestos básicos de la regresión clásica, cuyos estimadores eran Estimadores Lineales, Insesgados y Optimos (ELIO).

\[y=X\beta+u \ \ \ \ \ \ (3)\]

donde $X$ es una matriz $n x k$ de observaciones de $k$ variables independientes, $\beta$ es un vector $k x I$ de parámetros, $y$ es un vector $n x 1$ de observaciones de la variable dependiente, y $u$ en un vector $n x I$ de pertubacciones de media cero y varianza constante, $\sigma^2$.

El modelo se expresaría en el dominio de la frecuencia aplicando una transformación lineal a las variables dependiente e independientes, por ejemplo, premultiplicando todas las variables por la matriz ortogonal $W$. La técnica de la RBS consiste en realizar el analisis de regresión en el dominio de la frecuencia, pero omitinedo determinadas oscilaciones periodicas. Con este procedimiento pueden tratarse problemas derivados de la estacionalidad de las series o de la autocorrelación en los residuos. Engle (1974) muestra que si los residuos están correlacionados serialmente y son generados por un procieso estacionario estocástico, la regresión en el dominio de la frecuencia es el estimador asintóticamente más eficiente de $\beta$.

La transformación de la ecuación (3) del dominio del tiempo al dominio de la frecuencia en Engle (1974), se basa en la matriz $W$, cuyo elemento $(t, s)$ esta dado por:

\[w_{ts}=\frac{1}{\sqrt n} e^{i\lambda_t s} \ \ \ \ \ \ s= 0,1,...,n-1\]

donde $\lambda_t = 2\pi \frac{t}n$, $t=0,1,...,n-1$, y $i=\sqrt{-1}$.

Premultiplicando las observaciones de (3) por $W$, obtenemos:

\[\dot y=\dot X\beta+\dot u \ \ \ \ \ \ (4)\]

donde $\dot y = Wy$, $\dot X = WX$,ç y $\dot u = Wu$.

Si el vector de las perturbaciones en (3) cumple las hipótesis clásicas del modelo de regresión: $E[u] = 0$ y $E[uu']=\sigma^2 I_n$, entonces el vector de perturbaciones transformado al dominio de la frecuencia, $\dot u$, tendrá las mimas propiedades.

Por otro lado, dado que la matriz W es ortogonal, $WW^{T}= I$, entonces $W^T$ sería la transpuesta de la completa conjugada de $W$, de forma que las observaciones del modelo (4) acaban conteniendo el mismo tipo de información que las observaciones del modelo inicialmente planteado.

\[var(\dot u)=E(\dot u \dot u^T)=E(Wuu'W^T)=WE(uu')W^T=\sigma^2W \Omega W^T\]

si $\Omega=I$ entonces $var(\dot u)=\sigma^2I$.

Asuminendo que $x$ es independiente de $u$, el toerema de Gauss-Markov implicaría que:

\[\hat \beta = (\dot x' \dot x)^{-1}\dot x'\dot y\]

es el mejor estimador lineal insesgando (ELIO) de $\dot \beta$. El estimador obtenido sería de hecho idéntico al estimador MCO de (3).

Estimar (4) manteniendo únicamente determinadas frecuencias, puede llevarse a cabo omitiendo las observaciones correspondientes a las restantes frecuencias, si bien, dado que las variables en (4) son complejas, Engle (1974) sugiere la transformada inversa de Fourier para recomponer el modelo estimado en términos de tiempo.

Definiendo una matriz $A$ de tamaño n x n de ceros excepto en las posiciones de la diagonal principal, correspondientes a las frecuencias que queremos incluir en la regresión, y premultiplicando $\dot y$ y $\dot X$ por $A$ eleminamos determindas observaciones y las reemplazamos por ceros para realizar la regresión band spectrum. Devolver al dominio del tiempo a estas observaciones requiere:

\[y^* = W^{T}A\dot y = W^{T}AWy\] \[x^* = W^{T}A\dot x = W^{T}AWx \ \ \ \ \ \ (5)\]

Al regresar $y^*$ sobre $x^*$ obtenemos un $\beta$ idéntico al estimador que obtendríamos al estimar por MCO $\dot y$ frente a $\dot x$.

Cuando se realiza la regresión band spectrum de esta manera, ocurre un problema asociado a los grados de libertad de la regresión de $y^*$ sobre $x^*$ que asumen los programas estadisticos convencionales, $n - k$. Los grados de libertad reales serían únicamente $n'- k$, donde $n'$ es el numero de frecuencias incluidas en la regresión band spectrum.

Tan H.B and Ashley R (1999), señalan que el procedimiento de elaboración de una RBS consta de tres etapas:

1.- Transformar los datos originales del dominio del tiempo al dominio de la frecuencia utilizando series finitas de senos y cosenos. Implicaría premultiplicar los datos originales por la matriz ortogonal $W$ sugerida por Harvey (1978).

2.- Permitir la variación a través de m bandas de frecuencia usando variables Dummy $D_j^1,..D_j^m$. Estas variables se elaboran a partir de submuestras de las $n$ observaciones del dominio de frecuencias. De esta forma, $D_j^s=\dot x_{j,k}$ si la observación $j$ está en la banda de frecuencias $s$ y $D_j^s=0$, en el resto de los casos.

3.- Re-estimar el resultado del modelo de regresión en el dominio del tiempo con las estimaciones y los coeficientes de las $m$ variables Dummy. Implicaría premultiplicar la ecuación de regresión ampliada por las variables Dummy por la transpuesta de $W$.

Realizamos una RBS con datos trimestrales del PIB y empleo en Canada, correspondientes al primer trimestre de 1980 finalizando el cuarto trimestre de 2000. En la libreria “descomponer”, las funciones “gdf” y “gdt” transforman las series del tiempo a la frecuencia y de la frecuencia al tiempo, siguiendo la transformación sugerida por Harvey (1978).

library(descomponer)
library(vars)
data("Canada")
summary(Canada)

##        e            prod           rw            U        
##  Min.   :929   Min.   :401   Min.   :386   Min.   : 6.70  
##  1st Qu.:935   1st Qu.:405   1st Qu.:424   1st Qu.: 7.78  
##  Median :946   Median :406   Median :444   Median : 9.45  
##  Mean   :944   Mean   :408   Mean   :441   Mean   : 9.32  
##  3rd Qu.:950   3rd Qu.:411   3rd Qu.:461   3rd Qu.:10.61  
##  Max.   :962   Max.   :418   Max.   :470   Max.   :12.77

P <- as.numeric(Canada[, "prod"])
E <- as.numeric(Canada[, "e"])
PIB <- P-E
summary(lm(E~PIB))

## 
## Call:
## lm(formula = E ~ PIB)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -7.495 -2.363  0.543  2.050  7.123 
## 
## Coefficients:
##             Estimate Std. Error t value             Pr(>|t|)    
## (Intercept) 158.7771    32.6261    4.87            0.0000054 ***
## PIB          -1.4643     0.0608  -24.08 < 0.0000000000000002 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.24 on 82 degrees of freedom
## Multiple R-squared:  0.876,  Adjusted R-squared:  0.875 
## F-statistic:  580 on 1 and 82 DF,  p-value: <0.0000000000000002

K <- c(rep(1,84))
PIB.1 = gdf(PIB)
E.1=gdf(E)
K.1=gdf(K)
summary(lm(E.1~0+K.1+PIB.1))

## 
## Call:
## lm(formula = E.1 ~ 0 + K.1 + PIB.1)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -13.563  -0.784  -0.133   0.420  18.278 
## 
## Coefficients:
##       Estimate Std. Error t value             Pr(>|t|)    
## K.1   158.7771    32.6261    4.87            0.0000054 ***
## PIB.1  -1.4643     0.0608  -24.08 < 0.0000000000000002 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.24 on 82 degrees of freedom
## Multiple R-squared:     1,   Adjusted R-squared:     1 
## F-statistic: 3.56e+06 on 2 and 82 DF,  p-value: <0.0000000000000002

Teniendo presente el periodograma de la productividad y el empleo:

gperiodograma(PIB)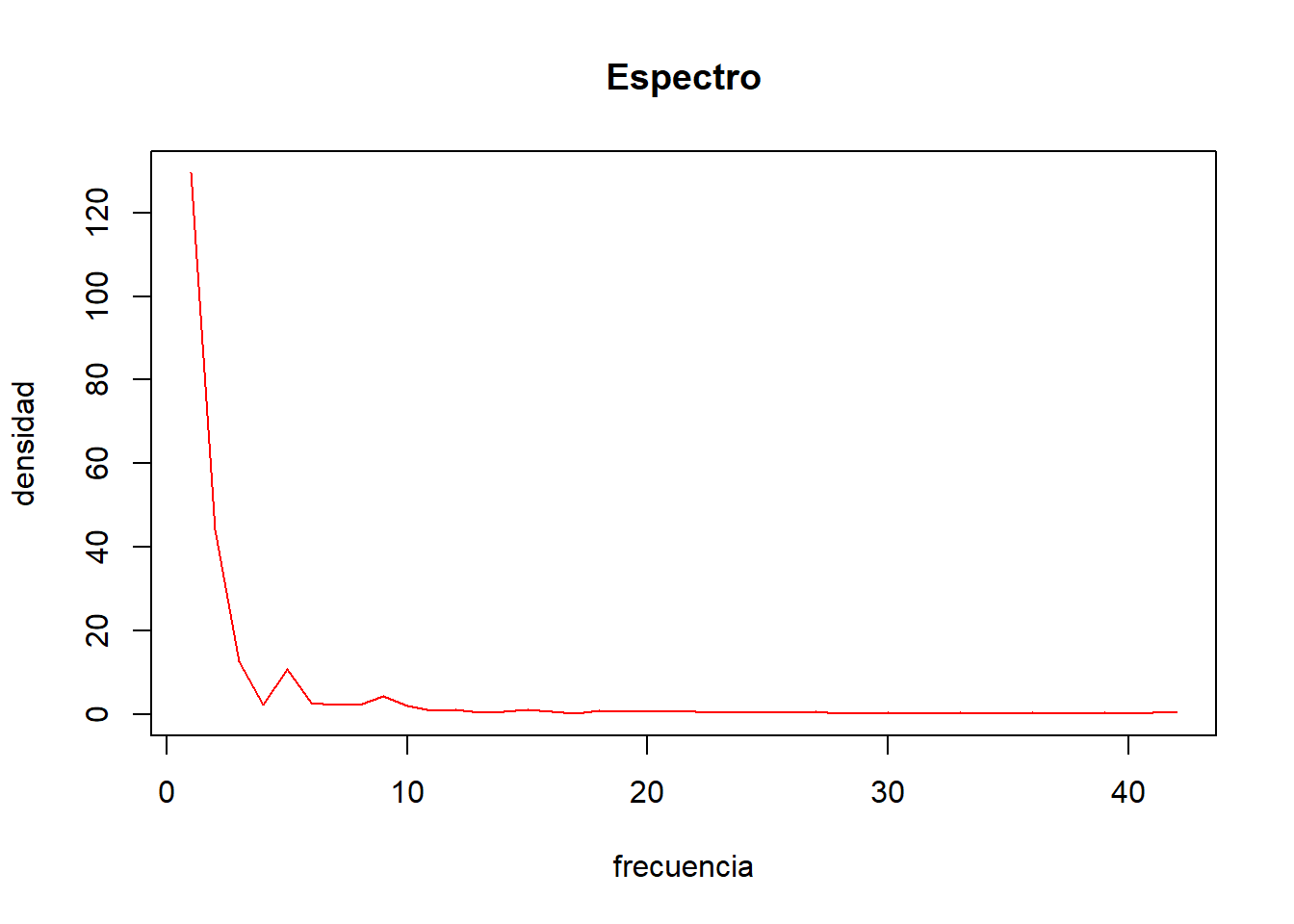

gperiodograma(E)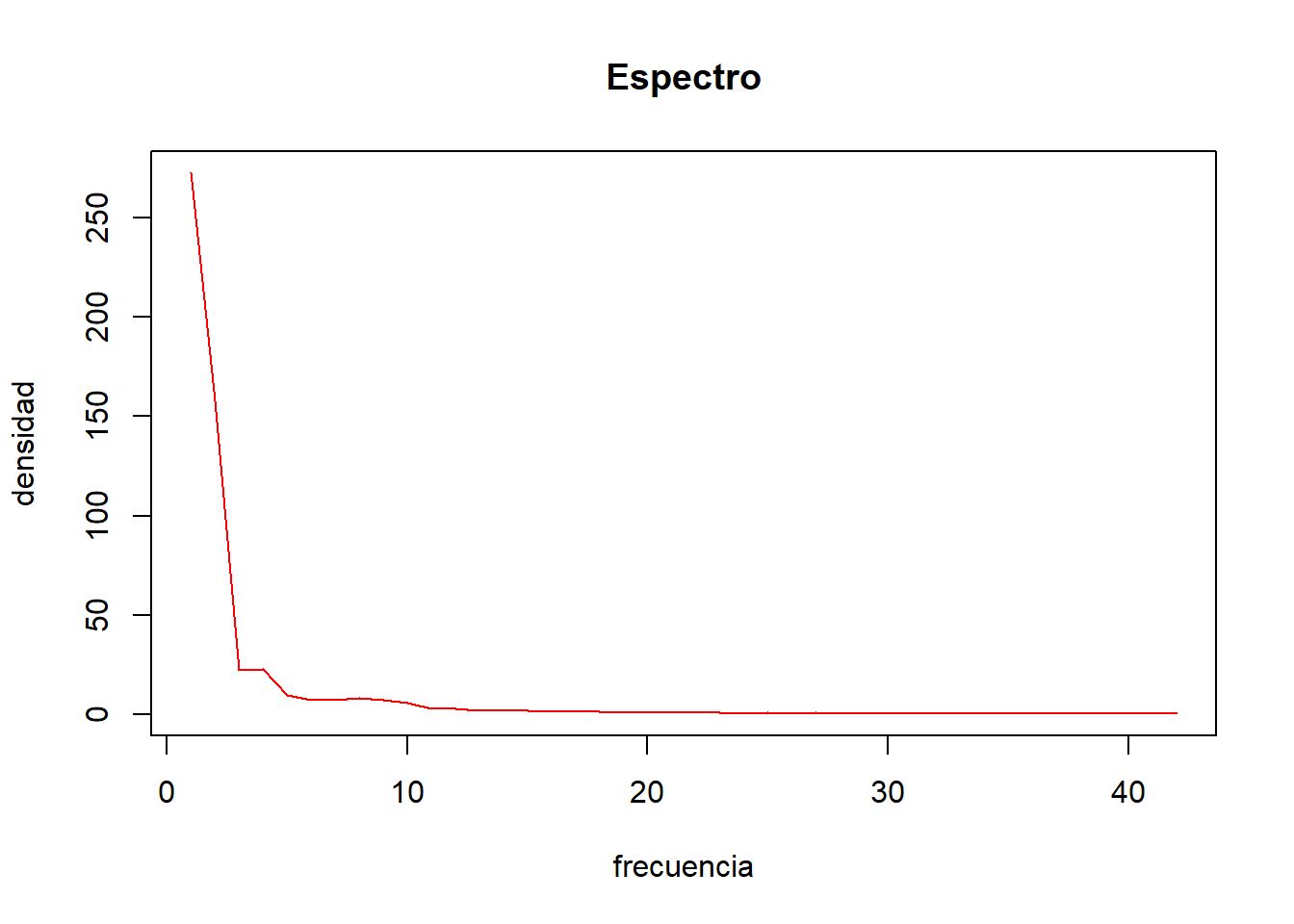

Utilizamos variables Dummys para separar los ciclos de menor frecuencia del resto, y realizamos una RBS para los ciclos de menor frecuencia.

D1 <- c(rep(1,10),rep(0,74)) 
PIB.1.1=D1*PIB.1
rbs.fit=lm(E.1~0+K.1+PIB.1.1)
plot(ts(E,frequency = 4, start = c(1980, 1)),type="l",main="Empleo.Canada",ylab="")
lines(ts(lm(E~PIB)$fitted,frequency = 4, start = c(1980, 1)),type="l",col=2)
lines(ts(gdt(rbs.fit$fitted),frequency = 4, start = c(1980, 1)),type="l",col=3)
legend("top", ncol=3,c("E","Estimado LM","Estimado RBS"),cex=0.6,bty="n",fill=c(1,2,3))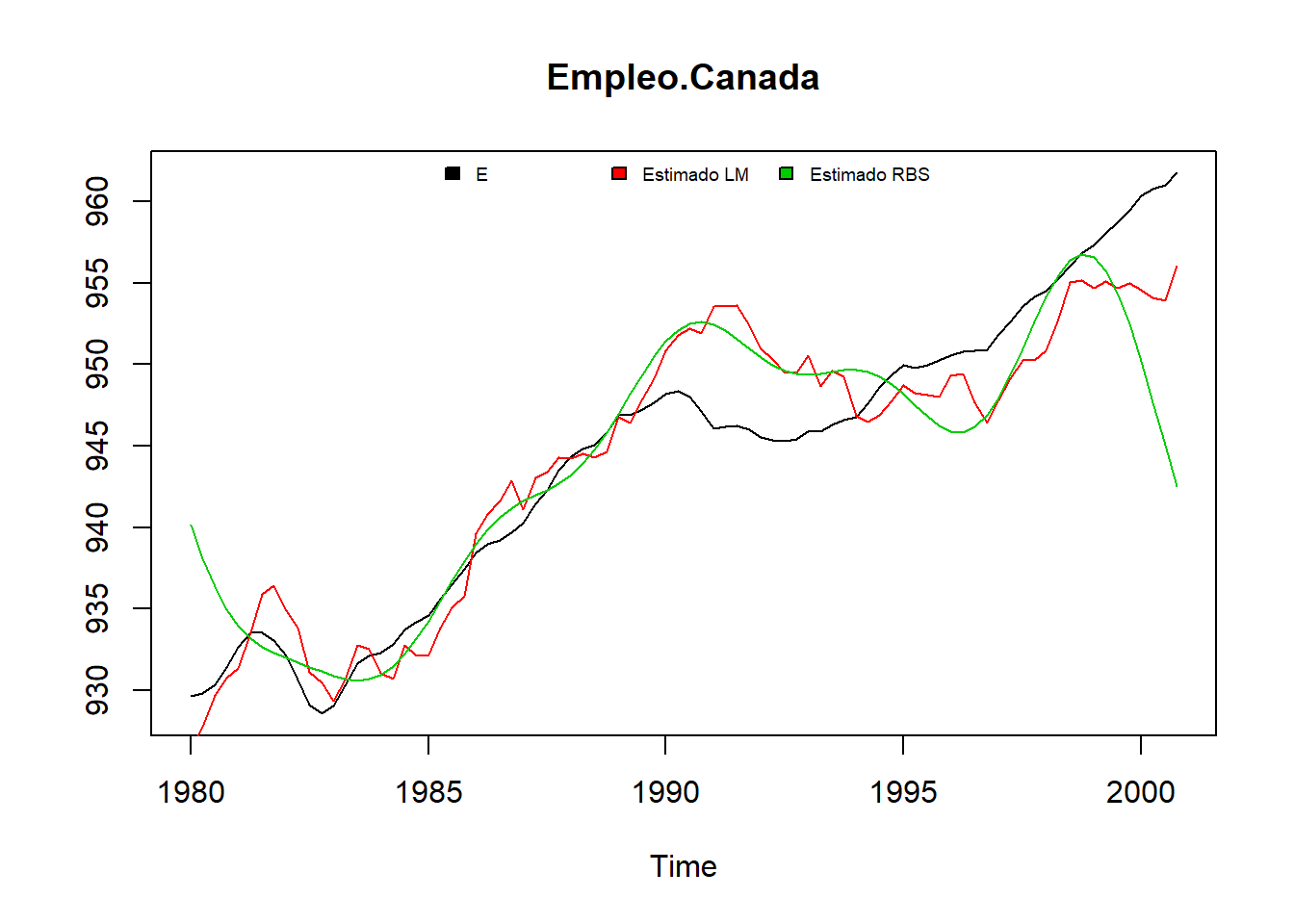

La regresión RBS cuando se utiliza diferenciando o filtrando frecuencias mediante variables Dummys, opera como un filtro frecuencial. Hay que tener presente que las series originales se transforman del dominio del tiempo a la frecuencia por la matriz ortogonal que hemos denominado $W$, y dicha matriz tiene una dimensión (n x n). Esto determina que la matriz de regresores para la predicción, ahora de tamaño (n+1 x k), de ser transformados al dominio de la frecuencia por una matriz W de tamaño (n+1 x n+1), se encontrarían en una frecuencia distinta a la que recogen las variables Dummys.

Para solucionar estos problemas de falta de sintonía entre las series de frecuencia, la predicción ha de realizarse sobre la matriz W de dimensión (n x n), y las observaciones (2 a n+1) de la matriz de regresores.

Vamos a realizar la predicción correspondiente a un incremento trimestral del empleo del 0,25%. Como la preducción se realiza en el dominio de la frecuencia, hay transformar los datos al dominio del tiempo.

PIB_2.1980_1.2001=c(PIB[2:84],PIB[84]*1.0025)
D1 <- c(rep(1,10),rep(0,74)) 
PIB.2 = gdf(PIB_2.1980_1.2001)
PIB.2.1=D1*PIB.2
E.2.fitted=rbs.fit$coefficients[1]*K.1+rbs.fit$coefficients[2]*PIB.2.1
E_2.1980_1.2001.fitted=gdt(E.2.fitted)
E_2.1980_1.2001.fitted[84]

## [1] 943.78

plot(ts(E,frequency = 4, start = c(1980, 1)),type="l",main="Empleo.Canada",ylab="")
lines(ts(lm(E~PIB)$fitted,frequency = 4, start = c(1980, 1)),type="l",col=2)
lines(ts(E_2.1980_1.2001.fitted,frequency = 4, start = c(1980, 2)),type="l",col=3)
legend("top", ncol=3,c("E","Estimado LM","Estimado RBS"),cex=0.6,bty="n",fill=c(1,2,3))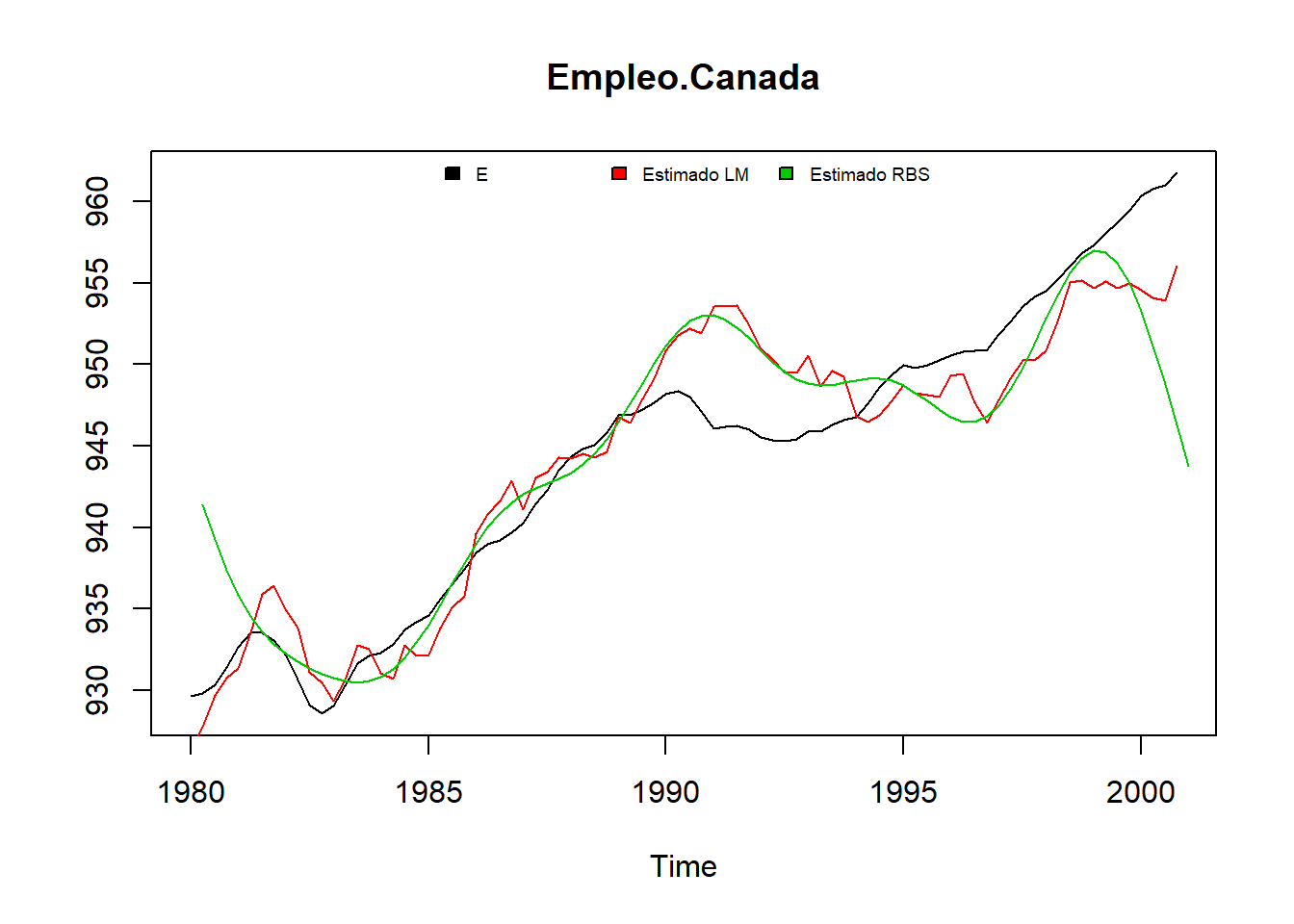

8.4.2.7 Regresión en el dominio de la frecuencia con un modelo no lineal.

Asumiendo que las series, $y_t$, $x_t$, $\beta_t$ y $u_t$ pueden ser transformadas en el dominio de la frecuencia:

\[y_t=\eta^y+\sum_{j=1}^N[a^y_j\cos(\omega_j)+b^y_j\sin(\omega_j)\]

\[x_t=\eta^x+\sum_{j=1}^N[a^y_j\cos(\omega_j)+b^y_j\sin(\omega_j)]\]

\[\beta_t=\eta^\beta+\sum_{j=1}^N[a^\beta_j\cos(\omega_j)+b^\beta_j\sin(\omega_j)]\]

\[(6)\]

Premultiplicando (6) por $W$ obtenemos:

\[\dot y=\dot x\dot\beta+\dot u \ \ \ \ \ \ (7)\]

donde $\dot y = Wy$,$\dot x = Wx$, $\dot \beta = W\beta$ y $\dot u = Wu$

El sistema (7) puede reescribirse como:

\[\begin{equation} \dot y=Wx_tI_nW^T\dot \beta + WI_nW^T\dot u \end{equation}\]

Si denominamos $\dot e=WI_nW^T\dot u$, podrían buscarse los $\dot \beta$ que minimizaran la suma cuadrática de los errores $e_t=W^T\dot e$.

Una vez encontrada la solución a dicha optimización, se transformarían las series al dominio del tiempo para obtener el sistema (6).

Para obtener una solución a la minimización de los errores que ofrezca el mismo resultado que la regresión lineal por mínimos cuadrados ordinarios, requiere utilizar una matriz de regresores cuya primera columna sería el vector de tamaño $N$, $(1,0,0,...)$, la segunda columna sería la primera fila de la matriz $WI_NX_tW^T$, y las columnas siguientes, corresponderían las a las frecuencias de senos o cósenos que queremos regresar.

Denominando a esta nueva matriz, de tamaño (Nxp), $\dot X$, donde $p=2+j$, siendo $j$ las frecuencias de seno y coseno elegidas como explicativas, los coeficientes de la solución MCO serían:

\[\dot \beta = (\dot X' \dot X)^{-1}\dot X' \dot y\]

donde $\beta_{0,1}$ sería el parámetro asociado a la constante, $\beta_{1,1}$ el asociado a la pendiente, y $\beta_{1,j}$ los asociados a las frecuencias de senos y cósenos elegidas.

En la libreria descomponer, hay una función “rdf” para realizar dicha regresión.

El algoritmo de calculo “rdf” se realiza en las siguentes fases:

Calcula el co-espectro de la serie “x” e “y”

Sea $x$ un vector n x 1 el modelo transformado en el dominio de la frecuencia esta dado por: $\hat x= Wx$.

Sea $y$ un vector n x 1 el modelo transformado en el dominio de la frecuencia esta dado por: $\hat y= Wy$

Denominando $p_j$ el ordinal del cross-periodograma de $\hat x$ y $\hat y$ en la frecuencia $\lambda_j=2\pi j/n$, y $\hat x_j$ el j-th elemento de $\hat x$ y $\hat y_j$ el j-th elemento de $\hat y$, entonces

\[ \left\lbrace \begin{array}{ll} p_j=\hat x_{2j}\hat y_{2j}+\hat x_{2j+1}\hat y_{2j+1} & \forall j = 1,...\frac{n-1}{2}\\ p_j=\hat x_{2j}\hat y_{2j}& \forall j = \frac{n}{2}-1 \end{array} \right. \]

\[p_0=\hat x_{1}\hat y_{1}\]

Ordena el co-espectro en base al valor absoluto de $|p_j|$ y genera un índice en base a ese orden para cada coeficiente de fourier.
Calcula la matriz $Wx_tI_nW^T$ y la ordena en base al indice anterior.
Obtiene $\dot e=WI_nW^T\dot u$, incluyendo el vector correspondiente al parámetro constante, $(1,0,...0)^n$, y calucula el modelo utilizando los dos primeros regresores de la matriz $Wx_tI_nW^T$ reordenada y ampliada, calcula el modelo para los 4 primeros, para los 6 primeros, hasta completar los $n$ regresores de la matriz.
Realiza el Test de Durbin (1967) a los modelos estimados, y selecciona aquellos en donde los $e_t=W^T\dot e$ están dentro de las bandas elegidas.

Denominando $p_j$ al ordinal del periodograma de $\hat a$ en la frecuencia $\lambda_j=2\pi j/n$, y $\hat a_j$ el j-th elemento de $\hat a$, entonces

\[\left\lbrace \begin{array}{ll} p_j=\hat a_{2j}^{2}+\hat a_{2j+1}^{2} & \forall j = 1,...\frac{n-1}{2}\\ p_j=\hat a_{2j}^{2}& \forall j = \frac{n}{2}-1 \end{array} \right.\]

\[p_0=\hat a_{1}^{2}\]

Entonces, el cuadrado de $\hat a$ puede ser utilizado como un estimador consistente del periodograma de $a$.

El test de Durbin está basado en el siguiente estadistico:

\[s_j=\frac{\sum_{r=1} ^j p_r}{\sum_{r=1}^m p_r}\]

donde $m=\frac{1}{2}n$ para $n$ par y $\frac{1}{2}(n-1)$ para $n$ impar.

El estadístico $s_j$ ha de encontrarse entre unos límites inferior y superior de valores críticos que han sido tabulados por Durbin (1969). Si bien, hay que tener presente que el valor $p_0$ no se considera en el cálculo del estadístico, esto es, $p_0=\hat v_1=0$.

De todos ellos, elige aquél que tiene menos regresores. Si no encuentra modelo, devuelve la solución MCO.

rdf.mod=rdf(E,PIB)
str(rdf.mod)

## List of 6
##  $ datos      :'data.frame': 84 obs. of  4 variables:
##   ..$ Y  : num [1:84] 930 930 930 931 933 ...
##   ..$ X  : num [1:84] -524 -525 -527 -527 -528 ...
##   ..$ F  : num [1:84] 930 931 932 932 931 ...
##   ..$ res: num [1:84] -0.251 -0.71 -1.344 -0.308 1.368 ...
##  $ Fregresores: num [1:84, 1:18] 1 0 0 0 0 0 0 0 0 0 ...
##   ..- attr(*, "dimnames")=List of 2
##   .. ..$ : chr [1:84] "X1" "X2" "X3" "X4" ...
##   .. ..$ : chr [1:18] "C" "1" "2" "3" ...
##  $ Tregresores: num [1:84, 1:18] 0.109 0.109 0.109 0.109 0.109 ...
##   ..- attr(*, "dimnames")=List of 2
##   .. ..$ : NULL
##   .. ..$ : chr [1:18] "C" "1" "2" "3" ...
##  $ Nregresores: num 18
##  $ sse        : num 36.5
##  $ gcv        : num 0.705

plot(ts(E,frequency = 4, start = c(1980, 1)),type="l", main="Empleo. Canada", ylab="")
lines(ts(lm(E~PIB)$fitted, frequency = 4, start = c(1980, 1)), type="l", col=2)
lines(ts(rdf.mod$datos$F, frequency = 4, start = c(1980, 2)), type="l", col=3)
legend("top", ncol=3, c("E","Estimado LM","Estimado RBS"), cex=0.6, bty="n", fill=c(1,2,3))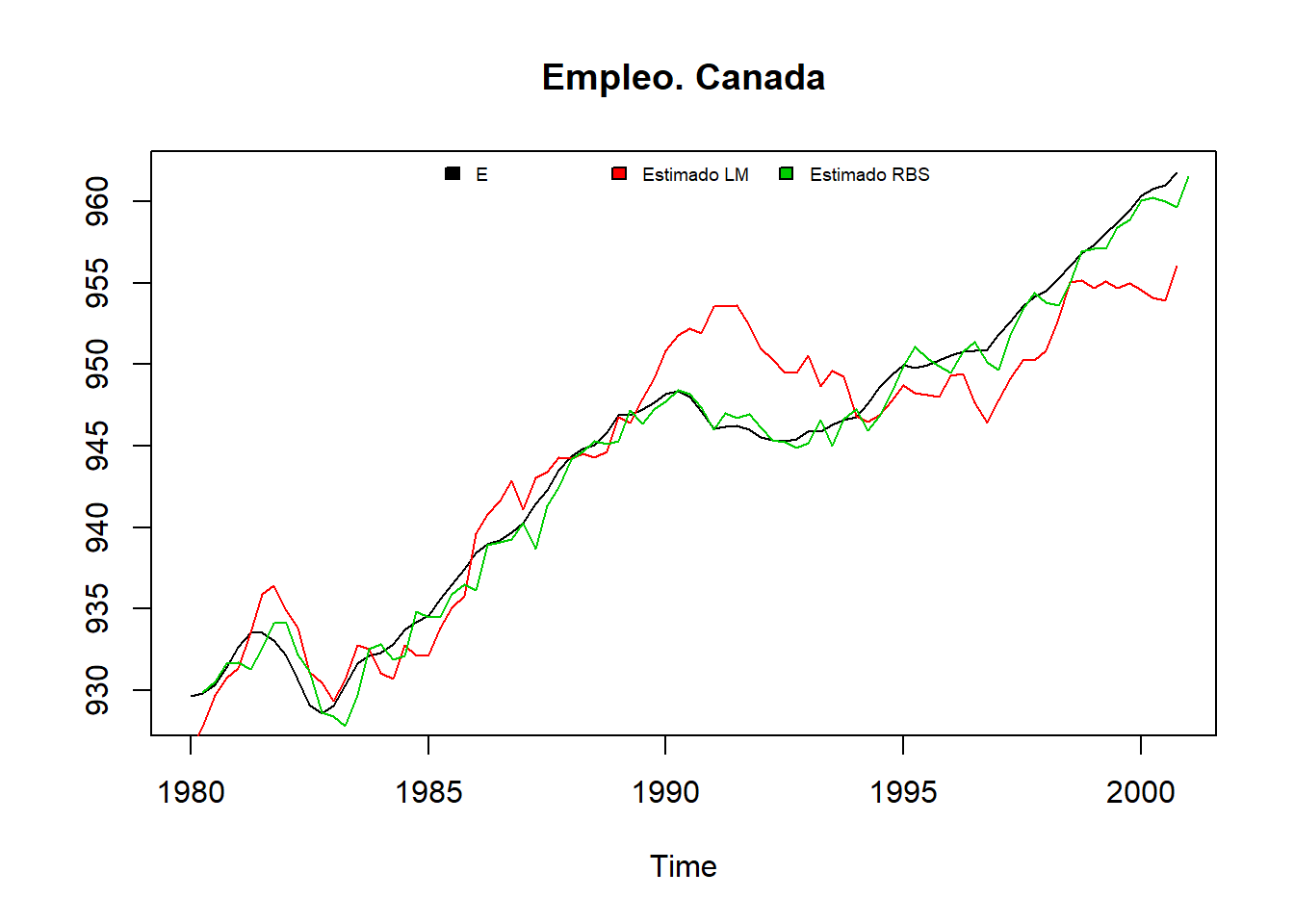

8.4.2.8 Redes Neuronales Artificiales

La RNA es una técnica de inferencia basada en Machine Learnig (aprendizaje máquina). Existen distintos modelos de redes neuronales, los más utilizados son el “Perceptron” y el “backpropagation”.

Hay que tener presente que una red neuronal se considera una “caja negra”, donde lo importante es la predicción, y no cómo se hace.

El proceso incluye, como ocurre con este tipo de técnicas, una fase de entrenamiento (training) para la optimización de las predicciones, y otra de test o prueba.

Los elementos de la red son:

Las neuronas o nodos
Las capas
- De entrada
- De salida
- Oculta (puede tener a su vez varias capas)
Los pesos
La función de combinación
La función de activación
El objetivo (target)

Los nodos (neuronas) de la capa de entrada, se combinan con los nodos de la capa oculta mediante la función de combinación, que suele ser una combinación lineal de los nodos de entrada mediante los pesos. A las neuronas de las capas ocultas, se les aplica una función de activación, que suele ser la tangente hiperbólica de la anterior combinación más un parámetro por nodo oculto, con la que estimamos las neuronas de la capa de salida, y sus errores.

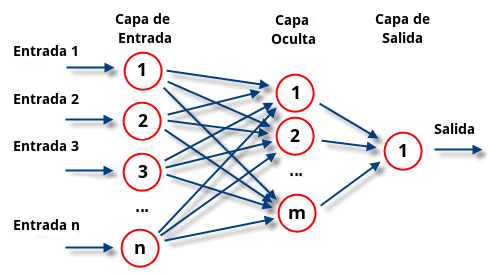
http://www.esacademic.com/dic.nsf/eswiki/994505

El siguiente script utiliza el package neuralnet para hacer una regresión y predecir el valor de viviendas (expresado en $1000), usando el data set Boston, incluido en el package MASS. Para un mejor ajuste del modelo (es decir, para que la red aprenda mejor), se hace un preprocesamiento de los datos, donde se normaliza el data set Boston. En consecuencia, una vez se obtiene la predicción con la red neural, al presentarse en valores normalizados, hay que transformar los datos para obtener la valoración en términos de precios de la vivienda.

Como es habitual en los ejercicios de minería de datos, el conjunto de datos se divide en una muestra de entrenamiento (el 70%) y otra de test.

La programación procede de http://apuntes-r.blogspot.com.es/2015/12/regresion-con-red-neuronal.html, en donde se destacan las siguientes notas:

El parametro threshol = 0.05 indica que las iteraciones se detendrán cuando el “Cambio” del error sea menor a 5% entre una iteracion de optimizacion y otra. Este “Cambio” es calculado como la derivada parcial de la funcion de error respecto a los pesos.
El parámetro algorithm = “rprop+” refiere al algoritmo “Resilient Backpropagation”, que actualiza los pesos considerando únicamente el signo del cambio, es decir, si el cambio del error es en aumento (+) o disminución (-) entre una iteración y otra. Para detalles ver: https://en.wikipedia.org/wiki/Rprop
El parámetro hidden = c(7,5) especifica una primera capa oculta con 7 neuronas y una segunda capa oculta con 5 neuronas.

#LIBRERIAS Y DATOS
library(MASS); library(neuralnet); library(ggplot2)
set.seed(65)
datos    <- Boston
n        <- nrow(datos)
muestra  <- sample(n, n*.70)
train    <- datos[muestra, ]
test     <- datos[-muestra, ]
 
# NORMALIZACION DE VARIABLES
maxs      <- apply(train, 2, max)
mins      <- apply(train, 2, min)
datos_nrm <- as.data.frame(scale(datos, center = mins, scale = maxs - mins))
train_nrm <- datos_nrm[muestra, ]
test_nrm  <- datos_nrm[-muestra, ]
 
# FORMULA
nms  <- names(train_nrm)
frml <- as.formula(paste("medv ~", paste(nms[!nms %in% "medv"], collapse = " + ")))
 
# MODELO
modelo.nn <- neuralnet(frml,
                       data          = train_nrm,
                       hidden        = c(7,5), # ver Notas para detalle 
                       threshold     = 0.05,   # ver Notas para detalle
                       algorithm     = "rprop+" 
                       )
 
# PREDICCION
pr.nn   <- compute(modelo.nn,within(test_nrm,rm(medv)))
 
# se transforma el valor escalar al valor nominal original
medv.predict <- pr.nn$net.result*(max(datos$medv)-min(datos$medv))+min(datos$medv)
medv.real    <- (test_nrm$medv)*(max(datos$medv)-min(datos$medv))+min(datos$medv)
 
# SUMA DE ERROR CUADRATICO
(se.nn <- sum((medv.real - medv.predict)^2)/nrow(test_nrm))

## [1] 8.730475173

#GRAFICOS

# Errores
qplot(x=medv.real, y=medv.predict, geom=c("point","smooth"), method="lm", 
      main=paste("Real Vs Prediccion. Summa de Error Cuadratico=", round(se.nn,2)))

## Warning: Ignoring unknown parameters: method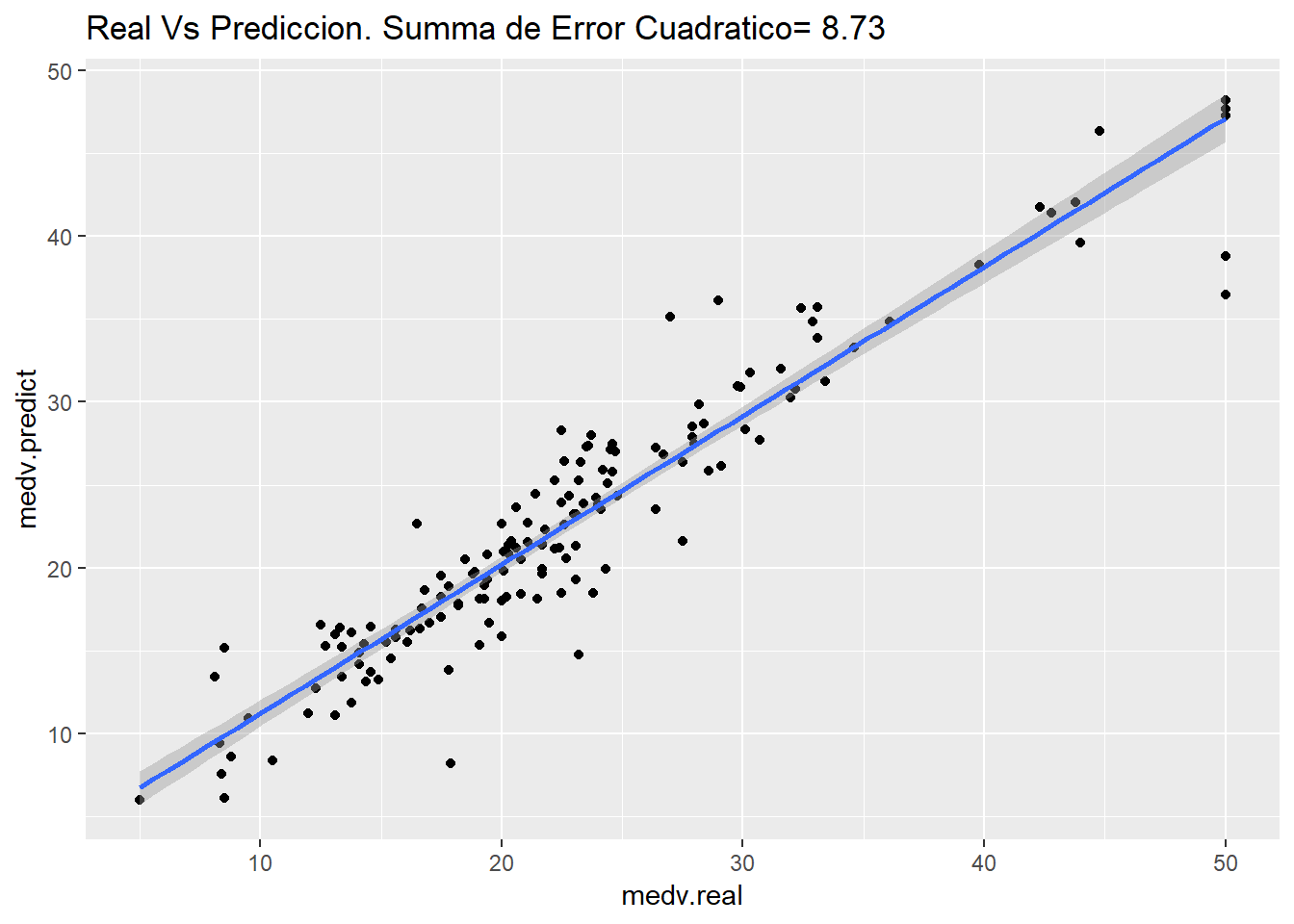

# Red
plot(modelo.nn)

Red Neuronal Artificial Precio Vivienda

8.4.2.9 Árbol de regresión

El árbol de decisión puede ser utilizado para clasificar unidades y tambien para realizar una regresión no paramétrica (Árbol de regresión). Si utilizamos la función “rpart” hay que seleccionar en “method” la elección “ANOVA”.

En la opción “control” encontramos parámetros opcionales para controlar el crecimiento de los árboles. Por ejemplo, en control = rpart.control (minsplit = 30, cp = 0.001) se le indica que el número mínimo de observaciones en un nodo sea 30 antes de intentar una división y que una división debe pararse cuando el Coste factor de complejidad sea inferior a un 0.001. Con el método anova, esto significa que el R-cuadrado total debe aumentar en 0.001 en cada división.

Utilizando una base de datos “cu.summary” de precios de automoviles, paises en donde han sido fabricados, confiabilidad, consumo de gasolina y gama del vehiculo, realizamos una estimación con un árbol de regresión.

# Ejemplo de árbol de regresión
library(rpart)

# Construyendo el árbol
fit <- rpart(Mileage~Price + Country + Reliability + Type,method="anova", data=cu.summary)

printcp(fit) # mostramos los resultados

## 
## Regression tree:
## rpart(formula = Mileage ~ Price + Country + Reliability + Type, 
##     data = cu.summary, method = "anova")
## 
## Variables actually used in tree construction:
## [1] Price Type 
## 
## Root node error: 1354.5833/60 = 22.576389
## 
## n=60 (57 observations deleted due to missingness)
## 
##            CP nsplit  rel error     xerror        xstd
## 1 0.622885266      0 1.00000000 1.03031850 0.175417788
## 2 0.132060610      1 0.37711473 0.52551930 0.100727441
## 3 0.025440940      2 0.24505412 0.36722405 0.080138910
## 4 0.011603894      3 0.21961318 0.38568677 0.090458117
## 5 0.010000000      4 0.20800929 0.40256940 0.089130973

plotcp(fit) # visualizamos el resultado de la validación cruzada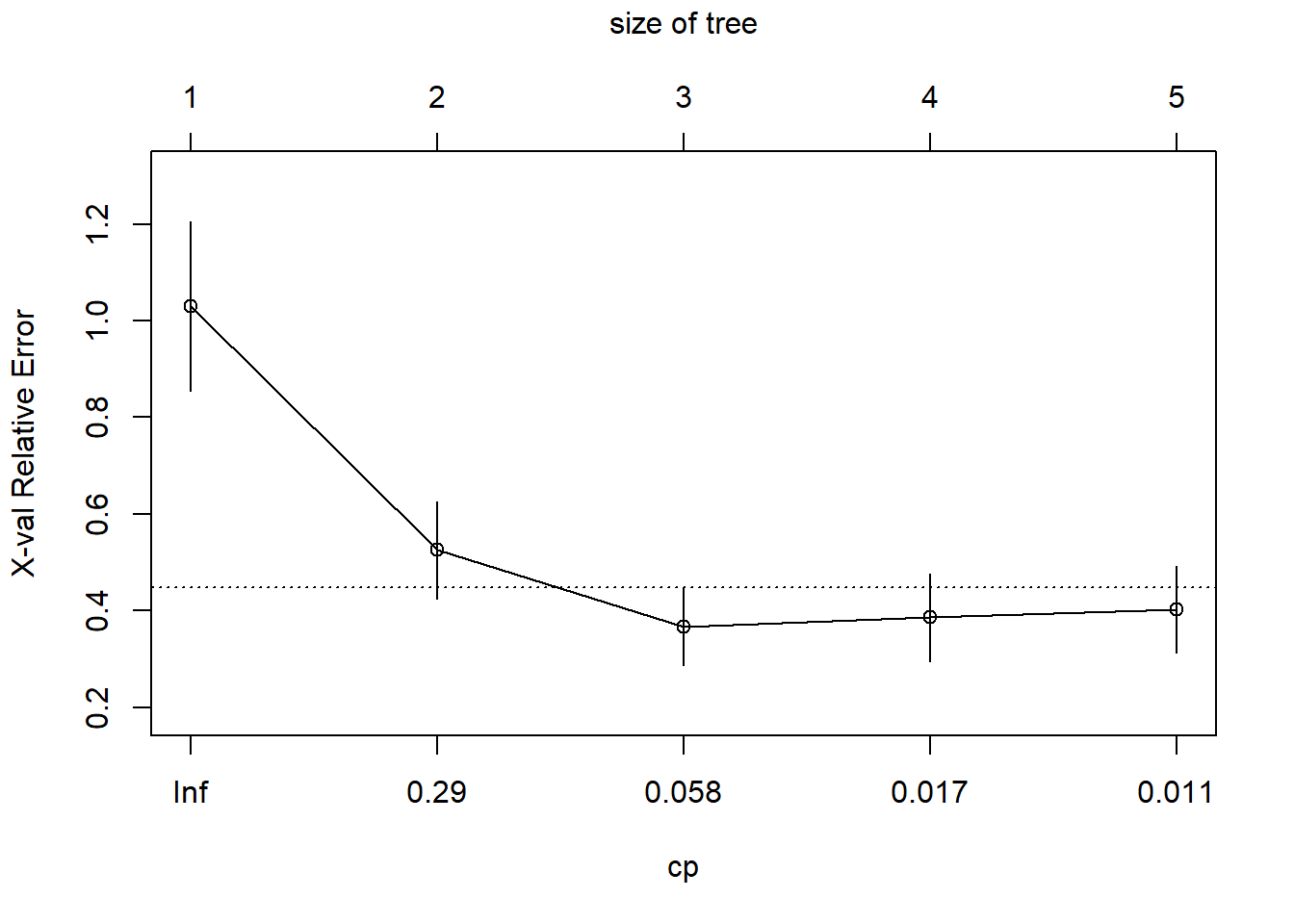

summary(fit) #sumario

## Call:
## rpart(formula = Mileage ~ Price + Country + Reliability + Type, 
##     data = cu.summary, method = "anova")
##   n=60 (57 observations deleted due to missingness)
## 
##              CP nsplit    rel error       xerror          xstd
## 1 0.62288526607      0 1.0000000000 1.0303184965 0.17541778783
## 2 0.13206061011      1 0.3771147339 0.5255192987 0.10072744084
## 3 0.02544093971      2 0.2450541238 0.3672240504 0.08013890951
## 4 0.01160389411      3 0.2196131841 0.3856867743 0.09045811723
## 5 0.01000000000      4 0.2080092900 0.4025694027 0.08913097265
## 
## Variable importance
##   Price    Type Country 
##      48      42      10 
## 
## Node number 1: 60 observations,    complexity param=0.6228852661
##   mean=24.58333333, MSE=22.57638889 
##   left son=2 (48 obs) right son=3 (12 obs)
##   Primary splits:
##       Price       < 9446.5  to the right, improve=0.6228852661, (0 missing)
##       Type        splits as  LLLRLL,      improve=0.5044405322, (0 missing)
##       Reliability splits as  LLLRR,       improve=0.1263005365, (11 missing)
##       Country     splits as  --LRLRRRLL,  improve=0.1243525220, (0 missing)
##   Surrogate splits:
##       Type    splits as  LLLRLL,     agree=0.950, adj=0.750, (0 split)
##       Country splits as  --LLLLRRLL, agree=0.833, adj=0.167, (0 split)
## 
## Node number 2: 48 observations,    complexity param=0.1320606101
##   mean=22.70833333, MSE=8.498263889 
##   left son=4 (23 obs) right son=5 (25 obs)
##   Primary splits:
##       Type        splits as  RLLRRL,      improve=0.43853834880, (0 missing)
##       Price       < 12154.5 to the right, improve=0.25748498350, (0 missing)
##       Country     splits as  --RRLRL-LL,  improve=0.13345695140, (0 missing)
##       Reliability splits as  LLLRR,       improve=0.01637085564, (10 missing)
##   Surrogate splits:
##       Price   < 12215.5 to the right, agree=0.812, adj=0.609, (0 split)
##       Country splits as  --RRLRL-RL,  agree=0.646, adj=0.261, (0 split)
## 
## Node number 3: 12 observations
##   mean=32.08333333, MSE=8.576388889 
## 
## Node number 4: 23 observations,    complexity param=0.02544093971
##   mean=20.69565217, MSE=2.907372401 
##   left son=8 (10 obs) right son=9 (13 obs)
##   Primary splits:
##       Type    splits as  -LR--L,      improve=0.515359607900, (0 missing)
##       Price   < 14962   to the left,  improve=0.131259377800, (0 missing)
##       Country splits as  ----L-R--R,  improve=0.007022106632, (0 missing)
##   Surrogate splits:
##       Price < 13572   to the right, agree=0.609, adj=0.1, (0 split)
## 
## Node number 5: 25 observations,    complexity param=0.01160389411
##   mean=24.56, MSE=6.4864 
##   left son=10 (14 obs) right son=11 (11 obs)
##   Primary splits:
##       Price       < 11484.5 to the right, improve=0.09693168203, (0 missing)
##       Reliability splits as  LLRRR,       improve=0.07767167054, (4 missing)
##       Type        splits as  L--RR-,      improve=0.04209833909, (0 missing)
##       Country     splits as  --LRRR--LL,  improve=0.02201687475, (0 missing)
##   Surrogate splits:
##       Country splits as  --LLLL--LR, agree=0.80, adj=0.545, (0 split)
##       Type    splits as  L--RL-,     agree=0.64, adj=0.182, (0 split)
## 
## Node number 8: 10 observations
##   mean=19.3, MSE=2.21 
## 
## Node number 9: 13 observations
##   mean=21.76923077, MSE=0.7928994083 
## 
## Node number 10: 14 observations
##   mean=23.85714286, MSE=7.693877551 
## 
## Node number 11: 11 observations
##   mean=25.45454545, MSE=3.520661157

# Creamos una gráfica adicional
par(mfrow=c(1,2)) # Dos gráficos en una página
rsq.rpart(fit) # visualizamos el resultado de la validación cruzada

## 
## Regression tree:
## rpart(formula = Mileage ~ Price + Country + Reliability + Type, 
##     data = cu.summary, method = "anova")
## 
## Variables actually used in tree construction:
## [1] Price Type 
## 
## Root node error: 1354.5833/60 = 22.576389
## 
## n=60 (57 observations deleted due to missingness)
## 
##            CP nsplit  rel error     xerror        xstd
## 1 0.622885266      0 1.00000000 1.03031850 0.175417788
## 2 0.132060610      1 0.37711473 0.52551930 0.100727441
## 3 0.025440940      2 0.24505412 0.36722405 0.080138910
## 4 0.011603894      3 0.21961318 0.38568677 0.090458117
## 5 0.010000000      4 0.20800929 0.40256940 0.089130973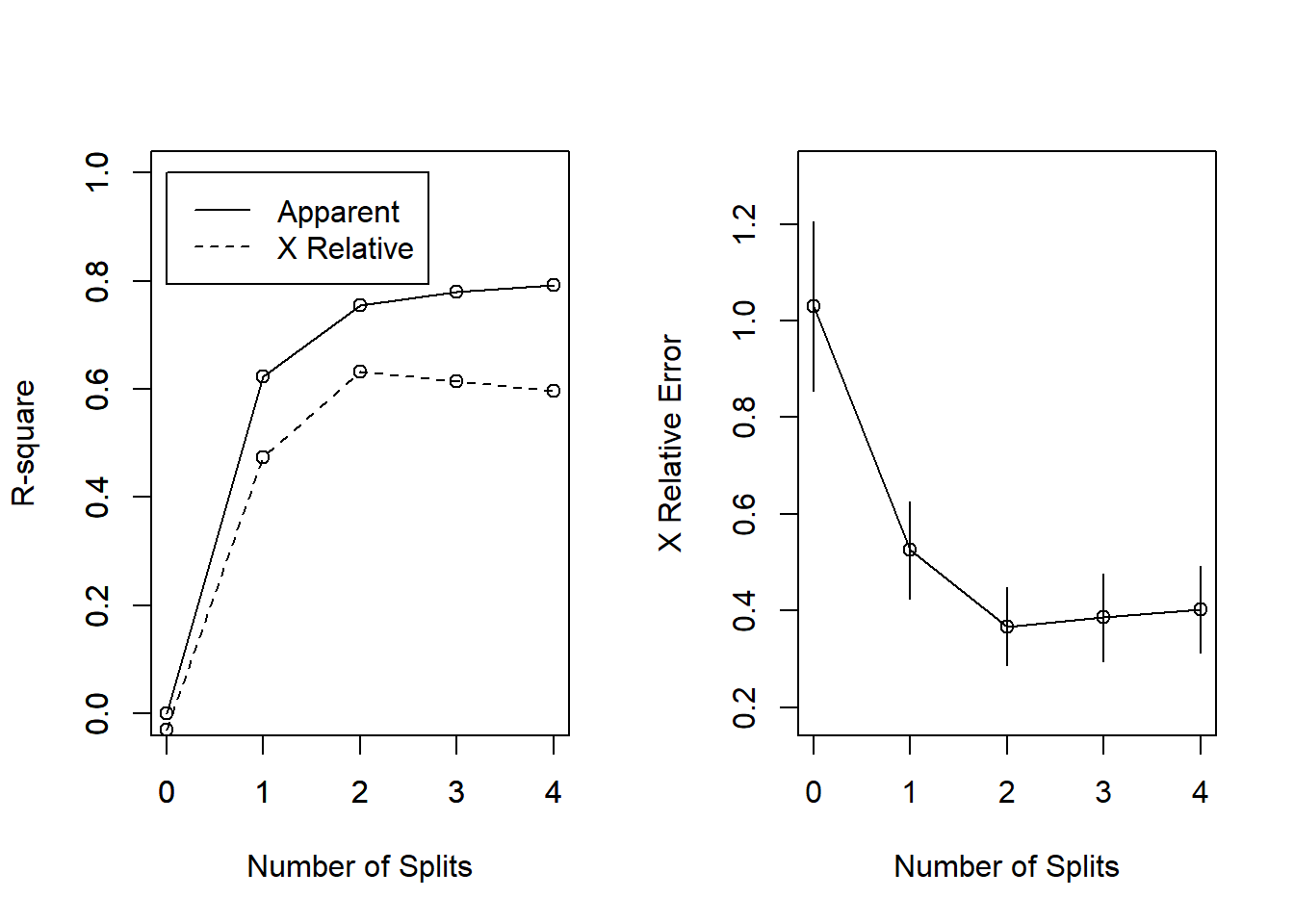

dev.off()

## pdf 
##   3

# Gráfico de árbol
plot(fit, uniform=TRUE,
   main="Árbol de regresión para el Kilometraje ")
text(fit, use.n=TRUE, all=TRUE, cex=.8)