5 Modelos con Variables Cualitativas
5.1 Introducción
En un modelo econométrico, las variables representan a los conceptos u operaciones económicas que queremos analizar. Normalmente utilizamos variables cuantitativas, es decir, aquellas cuyos valores vienen expresados de forma numérica; sin embargo, también existe la posibilidad de incluir en el modelo econométrico información cualitativa, siempre que esta pueda expresarse de esa forma.
Las variables cualitativas expresan cualidades o atributos de los agentes o individuos (sexo, religión, nacionalidad, nivel de estudios, etc.) y también recogen acontecimientos extraordinarios como guerras, terremotos, climatologías adversas, huelgas, cambios políticos, etc.
No cabe duda de que una forma de recoger factores de este tipo sería la utilización de variables proxy o aproximadas a las variables utilizadas. Por ejemplo, si quiero utilizar una variable que mida el nivel cultural de un país (variable cualitativa) puedo utilizar como variable proxy el número de bibliotecas existentes en un país, o representar una climatología adversa a partir de las temperaturas medias o precipitaciones. Sin embargo, no siempre es posible encontrar este tipo de variables y, en cualquier caso, debemos de ser conscientes de la posible existencia de errores en la definición de la variable.
Puesto que las variables cualitativas normalmente recogen aspectos de la presencia o no de determinado atributo (ser hombre o mujer, tener estudios universitarios o no tenerlos, etc.…) se utilizan variables construidas artificialmente, llamadas también ficticias o dummy, que generalmente toman dos valores, 1 ó 0, según se dé o no cierta cualidad o atributo. Habitualmente a la variable ficticia se le asigna el valor 1 en presencia de la cualidad y 0 en caso contrario. Las variables que toman valores 1 y 0, también reciben el nombre de variables dicotómicas o binarias.
Las variables dicotómicas pueden combinarse para caracterizar variables definidas por su pertenencia o no a un grupo. Si incluyo una variable cualitativa que me define la pertenencia o no de un país a un grupo, por ejemplo renta alta, media y baja, introduciré tres variables cualitativas en el modelo asociadas a la pertenencia o no a cada grupo; la primera caracterizaría a los individuos con renta alta, la segunda a los individuos con renta media, y la tercera a los individuos con renta baja.
Los modelos que utilizan variables cualitativas como regresores se diferencian en dos grupos, los modelos de Análisis de la Varianza o modelos ANOVA, que únicamente incluyen variables cualitativas como regresores; y los modelos de Análisis de la Covarianza o modelos ANCOVA que incluyen tanto variables cualitativas como cuantitativas. Los modelos ANOVA son muy utilizados en Sociología, Psicología, Educación, etc.; en Economía son más comunes los modelos ANCOVA.
5.2 Modelos ANOVA: efectos fijos
Un problema estadístico clásico es la comparación de medias de dos distribuciones normales. Supongamos que las observaciones de la variable \(Y_i\) provienen de dos distribuciones normales con medias \(\mu_1\) y \(\mu_2\) y varianza común \(\sigma^2\). El tamaño de la primera distribución se circunscribe a las \(n_1\) primeras observaciones, y el de la segunda a las \(n-n_1\) restantes. Queremos constrastar la hipótesis \(H_0:\mu_1=\mu_2\) frente a la alternativa \(H_1:\mu_1 \neq \mu_2\) al nivel de significación de \(\alpha\).
Este contraste de igualdad de medias cabe formularlo en el marco del modelo lineal general. Así, bajo \(H_0\) tenemos el siguiente modelo de regresión múltiple utilizando variables Dummy:
\[ Y_i=\mu_1 D_{1i} + \mu_2 D_{2i} + u_i \ \ \ \ (1)\]
donde \(D_{1i}\) toma valor uno en las \(n_1\) primeras observaciones y cero en las restantes, y \(D_{2i}\) toma cero en las \(n_1\) primeras observaciones y uno en las restantes, o lo que es lo mismo \(D_{2i} = 1-D_{1i}\).
Este modelo ANOVA puede formularse tambien a partir de las siguientes expresiones:
\[ Y_i=\beta_0 + \mu_1 D_{1i} + u_i \ \ \ \ (2)\]
\[ Y_i=\beta_0 + \mu_2 D_{2i} + u_i \ \ \ \ (3)\]
El contraste de igualdad de medias, se realiza a través del contraste de significación global, para el que construimos el estadístico experimental \(F_{exp}=\frac {\frac {R^2}{k-1}}{\frac {1-R^2}{n-k}}\), siendo el estadístico teórico \(F_{tco}\). La hipótesis se rechazaría con la regla de decisión \(F_{exp}>F_{tco}\).
Si se utiliza la especificación del modelo (2), el coeficiente asociado a la categoria \(D_1\) vendrá dado por la suma (\(\beta_0+\mu_1\)), y para \(D_2\) por \(\beta_1\). Si queremos contrastar la hipótesis de igualdad de medias en ambos grupos, equivaldría a contrastar la hipótesis nula \(H_0:\mu_1=0\).
Si se utiliza la especificación del modelo (3), el coeficiente asociado a la categoria \(D_2\) vendrá dado por la suma (\(\beta_0+\mu_2\)), y para \(D_1\) por \(\beta_0\). Si queremos analizar la hipótesis de igualdad de medias en ambos grupos, equivaldría a contrastar la hipótesis nula \(H_0:\mu_2=0\)
El análisis de la varianza (ANOVA) se debe al estadístico-genético Sir Ronald Aylmer Fisher (1890-1962), autor del libro “Statistics Methods for Research Workers” publicado en 1925 y pionero de la aplicación de métodos estadísticos en el diseño de experimentos, introduciendo el concepto de aleatorización. Fue creado para resolver diversos problemas agrícolas y tiene por objetivo descomponer la variabilidad de los datos asociados a un experimento en componentes independientes, las cuales, son asignables a distintas causas.
Por tanto, este análisis surge en el ámbito del diseño de experimentos, cuya metodología estudia como realizar comparaciones lo más homogéneas posibles, para aumentar, en consecuencia, la probabilidad de detectar cambios o identificar variables influyentes.
Respecto a la aleatorización, se establece el siguiente principio: todos los factores no controlados por el experimentador y que pueden influir en los resultados se asignan al azar a las observaciones. La aleatorización es fundamental, ya que:
Previene la existencia de sesgos.
Evita la dependencia entre observaciones.
Confirma la validez de los procedimientos estadísticos más comunes.
El problema que vamos a estudiar es, si disponemos de n elementos que se diferencian en un factor, por ejemplo, estudiantes de distintas aulas, vehículos de distinta marca, efectos de distintos medicamentos, productos sometidos a diferentes canales de distribución, fondos de inversión en distintos momentos temporales, etc. En cada elemento estudiado (fondos, productos, personas, vehículos,…) observamos cierta característica, variable respuesta, que varía aleatoriamente de un elemento a otro, como el consumo de combustible, la altura de cada persona, las ventas de un producto, etc. Se desea conocer si hay o no relación entre el valor medio esperado de la característica objeto de estudio y el factor.
Por tanto podemos decir que el análisis de la varianza es un método estadístico para determinar si una variable determinada, llamada dependiente y medida en escala no métrica, toma valores medios iguales o distintos en los grupos que forma otra variable, llamada independiente y en escala métrica. Como ejemplo, partiendo de la base de datos “mtcars”, vamos a analizar si la autonomía de los vehículos, medida en millas por galón de combustible, es la misma según su número de cilindros (4, 6 ó 8).
5.2.1 Análisis de la varianza de un factor
El diseño que hemos planteado se conoce como análisis de la varianza de un factor, puesto que se considera la influencia de una sola variable (número de cilindros). En el siguiente apartado se verá el análisis de la varianza con dos o más factores, donde como ejemplo se considerará la influencia conjunta de dos variables independientes, el número de cilindros (4, 6 ó 8) y el tipo de transmisión (automática [0] o manual [1]).
Planetamiento
El objetivo del análisis de la varianza es contrastar la homogeneidad simultánea de k poblaciones (\(k \geq 2\)) que siguen la ley de probabilidad \(N(\mu_i, \sigma^2)\) para i=1,…,L, con varianza común desconocida. Es necesario suponer que las distribuciones tienen varianza común para plantear el modelo.
La homogeneidad de las poblaciones se contrastará mediante la igualdad simultánea de sus medias \(\mu_i\), es decir, trataremos de contrastar la hipótesis nula:
\[H_0: \mu_1 = \mu_2 = ... = \mu_L = \mu \ \ \ (homogeneidad\ de\ las\ k\ poblaciones)\]
frente a la alternativa
\[H_1: \exists\ \mu_i\neq \mu_j \ \ \ (al\ menos\ existen\ dos\ medias\ que\ son\ diferentes)\]
El objetivo del análisis es comprobar la hipótesis (nula) de que la media es igual en las distintas poblaciones. Si la hipótesis es cierta, entonces las diferencias entre los valores obtenidos y los valores medios son debidas al azar (variabilidad aleatoria) y no a un efecto sistemático.
Se denomina factor a la variable que supuestamente ejerce una influencia sobre la variable dependiente. En nuestro ejemplo, la variable dependiente sería la autonomía de los vehículos, medida en millas por galón, mientras que el factor el número de cilindros.
Los niveles del factor serán cada uno de los valores posibles del factor (4, 6, 8).
El error muestral es el error debido a la aleatoriedad en la selección de los elementos muestrales. Se representa por: \(u_{ij}=y_{ij}-\mu_i\ \forall i,j\)
Un modelo es replicado si el experimento se repite varias veces para cada nivel de factor.
Un modelo de análisis de la varianza se llama equilibrado (balanced) cuando todos los grupos que forma la variable independiente son de igual tamaño, es decir cuando el número de observaciones para cada nivel del factor es siempre el mismo (el experimento se repite para cada nivel del factor el mismo número de veces). En caso de no ser igual, se llama no equilibrado (unbalanced).
Modelo
El planteamiento anteriormente expuesto da lugar a la formulación de un modelo matemático. Dicho modelo es el siguiente:
\[y_{ij} = \mu + \alpha_i + u_{ij}\]
donde \(\mu_i = \mu + \alpha_i\) serán las medias estimadas por el modelo, siendo, por tanto, \(\mu\) la media general, \(\alpha_i\) el efecto del factor en cada nivel y \(\sum\alpha_i=0\).
La estimación de estos parámetros teóricos se realiza del siguiente modo:
\[\hat \mu = \bar y_{..} \ \ \ \ \ \ \ \ \ \ \ \hat \alpha_i = \bar y_{i.} - \bar y_{..} \ \ \ \ \ \ \ \ \ \ \ \hat \mu_i = \hat \mu + \hat \alpha_i = \bar y_{i.} \ \ \ \ \ \ \ \ \ \ \ \hat u_{ij}= e_{ij} = y_{ij} - \bar y_{i.}\]
Siendo \(\bar y_{i.} = \frac {\sum_{j=1}^{n_i}y_{ij}} {n_i}\) la media muestral para cada grupo (en nuestro caso las autonomías medias de los vehículos según tengan 4, 6 ó 8 cilindros), con \(n_i\) el número de observaciones o muestras, y \(\bar y_{..} = \frac {\sum_{i=1}^{L} \sum_{j=1}^{n_i}y_{ij}} {n}\) la media global, o autonomía media del conjunto de vehículos analizados.
El modelo estimado queda por tanto:
\[y_{ij} = \bar y_{..} + (\bar y_{i.} - \bar y_{..}) + (y_{ij} - \bar y_{i.})\]
Tabla ANOVA
Partiendo de la expresión anterior, la variabilidad total (\(VT\)) de la variable respuesta será igual a:
\[VT = \sum_{i=1}^L \sum_{j=1}^{n_i}(y_{ij}-\bar y_{..})^2 = \sum_{i=1}^L \sum_{j=1}^{n_i}[(\bar y_{i.} - \bar y_{..}) + (y_{ij} - \bar y_{i.})]^2\]
Es fácilmente demostrable que:
\[2\sum_{i=1}^L \sum_{j=1}^{n_i}(\bar y_{i.} - \bar y_{..}) (y_{ij} - \bar y_{i.}) = 2\sum_{i=1}^L (\bar y_{i.} - \bar y_{..})\sum_{j=1}^{n_i} (y_{ij} - \bar y_{i.}) = 0\]
y por tanto:
\[VT = \sum_{i=1}^L \sum_{j=1}^{n_i}(\bar y_{i.} - \bar y_{..})^2 + \sum_{i=1}^L \sum_{j=1}^{n_i}(y_{ij} - \bar y_{i.})^2 = VE + VNE\]
El primer sumatorio de cuadrados constituye la variabilidad explicada (VE) por el modelo y el segundo la variabilidad no explicada (VNE), es decir:
\[VE=\sum_{i=1}^L \sum_{j=1}^{n_i}(\bar y_{i.} - \bar y_{..})^2 = \sum_{i=1}^L n_i(\bar{y}_{i.}-\bar{y}_{..})^2 = \sum_{i=1}^L n_i\hat \alpha_{i}^2\]
\[VNE=\sum_{i=1}^L \sum_{j=1}^{n_i} ({y}_{ij}-\bar{y}_{i.})^2 = \sum_{i=1}^L \sum_{j=1}^{n_i}e_{ij}^2\]
La tabla ANOVA queda, por tanto, como sigue:
Tabla nº 2. Tabla ANOVA. Modelo con un factor
| Fuente de variación | Suma de cuadrados | Grados de libertad | Cuadrado medio | Estadistico \(F\) |
|---|---|---|---|---|
| Entre grupos | \(VE\) | \(L-1\) | \(\frac {VE}{L-1}=\hat S_R^2\) | \(\frac {\hat S_R^2}{\hat S_e^2}\) |
| Dentro de los grupos | \(VNE\) | \(n-L\) | \(\frac {VNE}{n-L}=\hat S_e^2\) | |
| Total | \(VT\) | \(n-1\) | \(\frac {VT}{n-1}=\hat S_y^2\) |
Si las medias de la autonomía de los vehículos fueran muy distintas entre sí y, además, la varianza dentro de cada grupo fuera pequeña (los grupos muy distintos entre sí y, dentro de cada grupo un comportamiento muy homogéneo), la variabilidad total sería debida a la diferencia entre grupos. Sin embargo, si las medias en los grupos fueran muy parecidas entre sí, dado que se supone que la varianza dentro de cada grupo es la misma, la variabilidad total sería debida a la variabilidad dentro de los grupos.
Para contrastar la hipótesis nula de igualdad de medias se construye el estadístico F, que compara la variabilidad debida a las diferencias entre los grupos y la variabilidad debida a la diferencia dentro de los grupos. El estadístico F nos ha de decir si tenemos pruebas suficientes” para rechazar o aceptar la hipótesis nula, y se distribuye según una F de Snedecor con L-1 grados de libertad en el numerador y N-L en el denominador. Si el p-valor asociado a este estadístico es menor que el grado de significación fijado, rechazaremos la hipótesis de igualdad de medias.
En términos del modelo planteado, la hipótesis nula es: \(H_0:\alpha_i=0 \ \ \forall i\).
En el siguiente “Chunk” construimos la tabla anova con la función “aov” (Analysis Of Variance) y estimamos un modelo ANOVA con la función “model.tables”. Finalmente, representamos las tres distribuciones a través de un diagrama de cajas múltiple.
summary(aov(mpg~as.factor(cyl),data=mtcars))## Df Sum Sq Mean Sq F value Pr(>F)
## as.factor(cyl) 2 824.8 412.4 39.7 4.98e-09 ***
## Residuals 29 301.3 10.4
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1model.tables(aov(mpg~as.factor(cyl),data=mtcars),type="means")## Tables of means
## Grand mean
##
## 20.09062
##
## as.factor(cyl)
## 4 6 8
## 26.66 19.74 15.1
## rep 11.00 7.00 14.0library(ggplot2)
ggplot(mtcars, aes(as.factor(cyl), mpg)) + geom_boxplot()
La hipótesis más relevante que deben cumplir los datos para poder aplicar un análisis de la varianza, es la hipótesis de homoscedasticidad, es decir, que la varianza de la variable dependiente (millas por galón) es constante en los grupos definidos por el factor (número de cilindros). Esta prueba puede realizarse a través de la función leveneTest de la librería car, y como vemos, existe heterocedasticidad, dado que el grupo de 4 cilindros presenta una variabilidad mayor al resto, tal como se puede intuir en el diagrama de cajas. También puede verse como a mayor número de cilindros la variabilidad disminuye.
library(car)## Loading required package: carDataleveneTest(mtcars$mpg,as.factor(mtcars$cyl),center=mean)## Levene's Test for Homogeneity of Variance (center = mean)
## Df F value Pr(>F)
## group 2 6.4843 0.004703 **
## 29
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Algunos autores (Uriel, 1995; Stevens, 1986) afirman, sin embargo, que el estadístico F no se ve muy afectado por el hecho de que no exista homoscedasticidad siempre que las muestras de los diferentes grupos sean del mismo o similar tamaño. Se afirma que el estadístico se verá afectado cuando la razón entre el tamaño muestral del grupo de mayor tamaño y el más pequeño sea superior a 2.
Por otro lado, en el caso particular de que la hipótesis de homogeneidad de varianzas sea rechazada debido a que la varianza cambia con la media, existe una familia de transformaciones que proporciona, en general, homogeneidad en varianzas. Esta familia es de la forma:
\[T(X)=\begin{bmatrix} X^p \ \ si\ p\ne0\\ ln(X) \ \ si\ p=0 \end{bmatrix}\]
Aplicando el logaritmo neperiano, es decir, con p=0, obtenemos ya un p-valor no significativo en el test de Levene, y por tanto homogeneidad de varianzas, obteniendo como resultado del ANOVA lo siguiente:
library(car)
lnmpg <- log(mtcars$mpg)
cylf <- as.factor(mtcars$cyl)
leveneTest(lnmpg,cylf,center=mean)## Levene's Test for Homogeneity of Variance (center = mean)
## Df F value Pr(>F)
## group 2 1.6622 0.2073
## 29modelo.aov <- aov(lnmpg~cylf)
summary(modelo.aov)## Df Sum Sq Mean Sq F value Pr(>F)
## cylf 2 2.0081 1.0040 39.31 5.52e-09 ***
## Residuals 29 0.7407 0.0255
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1model.tables(modelo.aov)## Tables of effects
##
## cylf
## 4 6 8
## 0.3129 0.02292 -0.2573
## rep 11.0000 7.00000 14.0000Existen en R diferentes pruebas de cara a verificar la hipótesis de normalidad. Usando la variable transformada, y dado que la muestra es pequeña, optamos por el test de Shapiro-Wilk, donde como vemos, al no ser significativo (p-valor mayor que 0,05), podemos asumir que las distribuciones son normales:
logmpg <- split(log(mtcars$mpg), as.factor(mtcars$cyl))
for (i in 1:length(logmpg)){
logmpg.i <- as.vector(logmpg[i])
print(shapiro.test(logmpg.i[[1]]))
}##
## Shapiro-Wilk normality test
##
## data: logmpg.i[[1]]
## W = 0.91722, p-value = 0.2961
##
##
## Shapiro-Wilk normality test
##
## data: logmpg.i[[1]]
## W = 0.89736, p-value = 0.3153
##
##
## Shapiro-Wilk normality test
##
## data: logmpg.i[[1]]
## W = 0.89341, p-value = 0.09052Para muestras grandes, es preferible la prueba de Lilliefors (Kolmogorov-Smirnov), disponible en el paquete nortest. A pesar de que continuamente se alude al test Kolmogorov-Smirnov como un test válido para contrastar la normalidad, esto no es del todo cierto. Este test asume que se conoce la media y varianza poblacional, lo que en la mayoría de los casos no es posible. Esto hace que el test sea muy conservador y poco potente. Para solventar este problema, se desarrolló una modificación del Kolmogorov-Smirnov conocida como test Lilliefors. El test Lilliefors asume que la media y varianza son desconocidas, estando especialmente desarrollado para contrastar la normalidad. Es la alternativa al test de Shapiro-Wilk cuando el número de observaciones es mayor de 50.
Los resultados para nuestro ejemplo serían los siguientes:
library(nortest)
for (i in 1:length(logmpg)){
logmpg.i <- as.vector(logmpg[i])
print(lillie.test(logmpg.i[[1]]))
}##
## Lilliefors (Kolmogorov-Smirnov) normality test
##
## data: logmpg.i[[1]]
## D = 0.16847, p-value = 0.5164
##
##
## Lilliefors (Kolmogorov-Smirnov) normality test
##
## data: logmpg.i[[1]]
## D = 0.2343, p-value = 0.2907
##
##
## Lilliefors (Kolmogorov-Smirnov) normality test
##
## data: logmpg.i[[1]]
## D = 0.19852, p-value = 0.1412El test de Jarque-Bera no requiere estimaciones de los parámetros que caracterizan la normal. El estadístico de Jarque-Bera cuantifica que tanto se desvían los coeficientes de asimetría y curtosis de los esperados en una distribución normal. Su formulación es la siguiente:
\[JB = \frac {n-k+1} {6} (S^2 + \frac {1} {4} (C-3)^2)\]
donde \(n\) es el número de observaciones (o grados de libertad en general); \(S\) es la asimetría de la muestra, \(C\) la curtosis y \(k\) el número de regresores.
El estadístico de Jarque-Bera se distribuye asintóticamente como una distribución chi cuadrado con dos grados de libertad y puede usarse para probar la hipótesis nula de que los datos pertenecen a una distribución normal. Como hipótesis nula se considera que la asimetría y el exceso de curtosis, conjuntamente, son nulos, es decir:
\[H_0: C=0;\ \ S=3\]
Puede calcularse mediante la función jarque.bera.test() del paquete tseries. Los resultados con este test serían:
library(tseries)
for (i in 1:length(logmpg)){
logmpg.i <- as.vector(logmpg[i])
print(jarque.bera.test(logmpg.i[[1]]))
}##
## Jarque Bera Test
##
## data: logmpg.i[[1]]
## X-squared = 0.99886, df = 2, p-value = 0.6069
##
##
## Jarque Bera Test
##
## data: logmpg.i[[1]]
## X-squared = 0.71437, df = 2, p-value = 0.6996
##
##
## Jarque Bera Test
##
## data: logmpg.i[[1]]
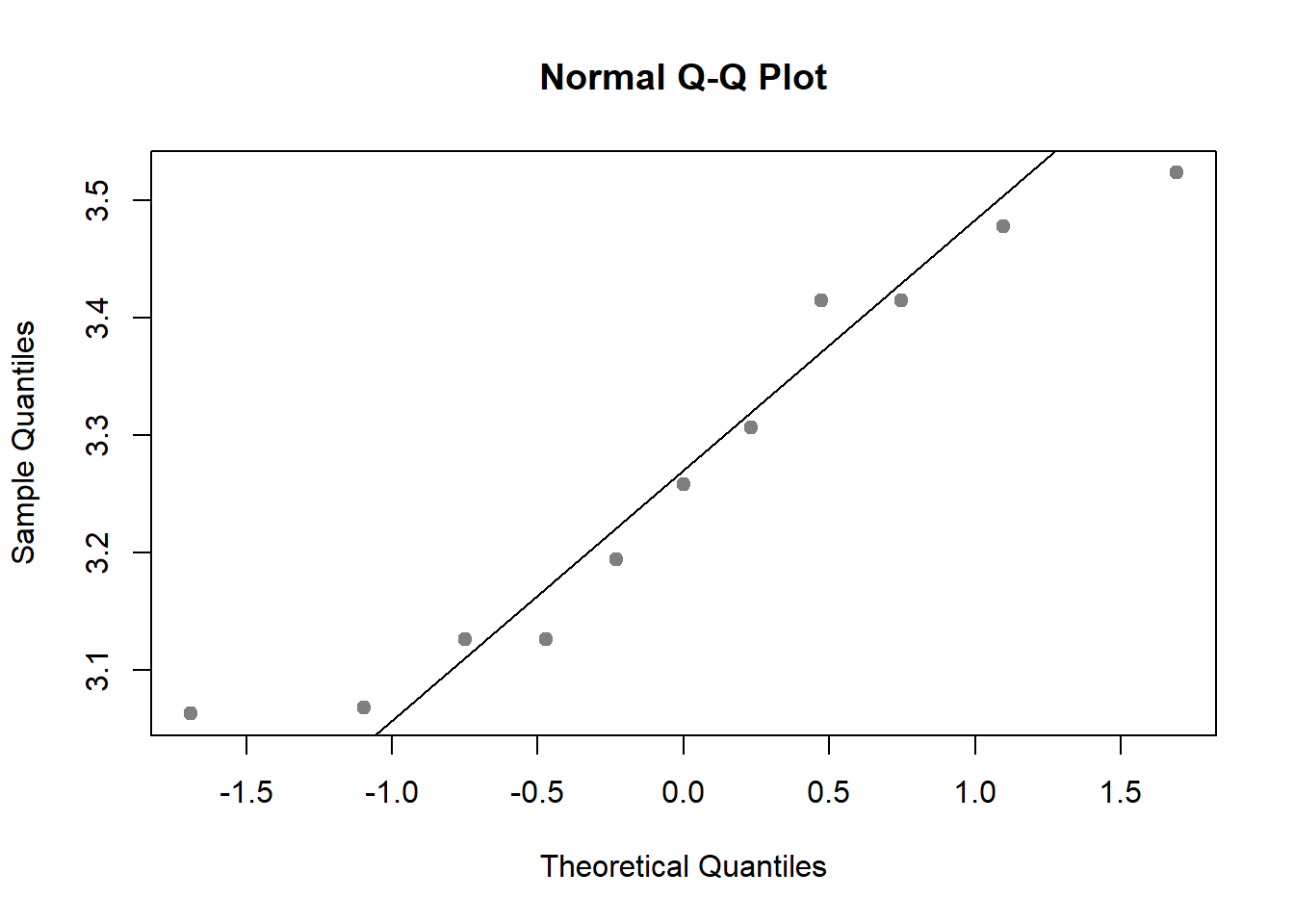
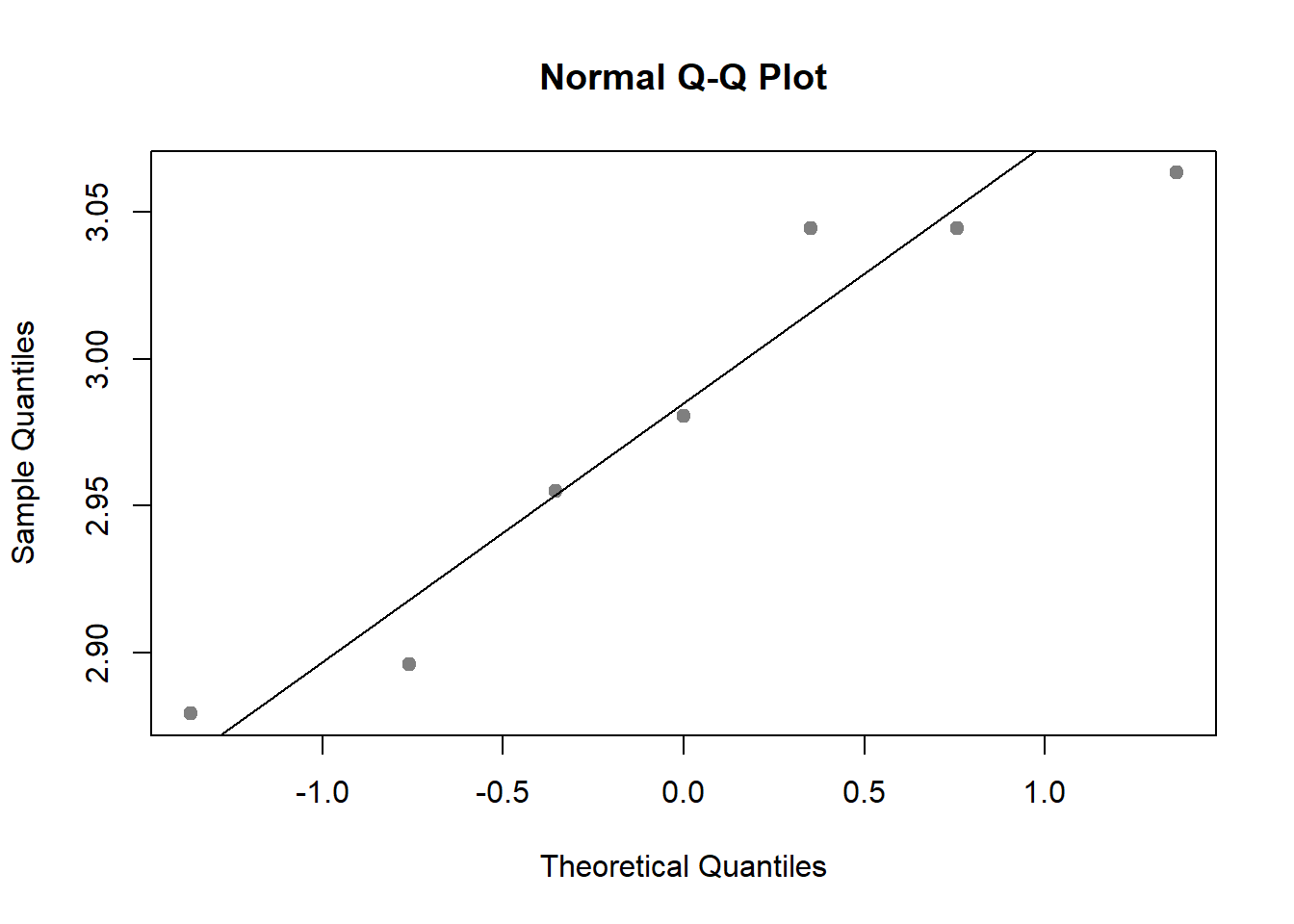
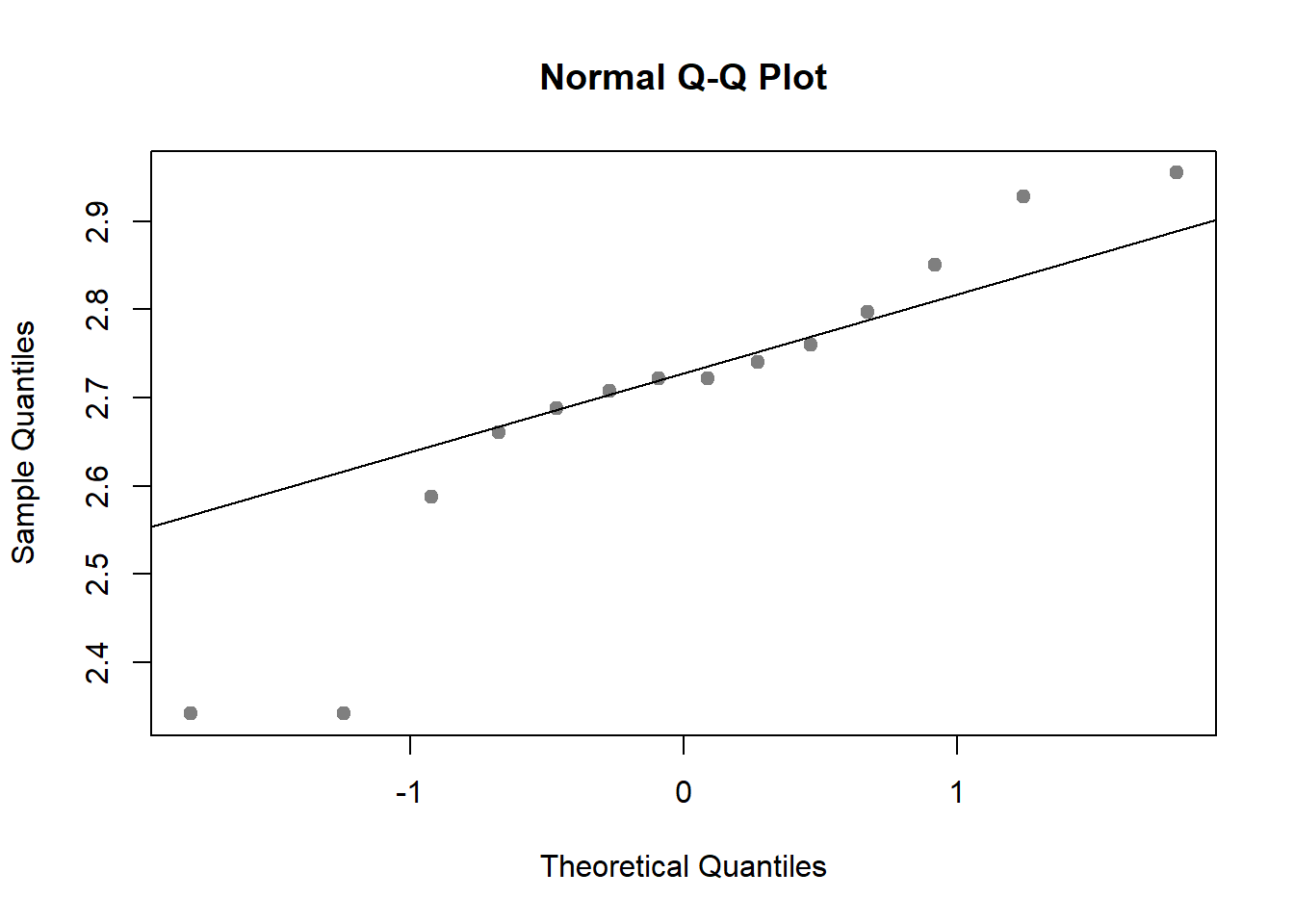
## X-squared = 1.549, df = 2, p-value = 0.4609También podemos utilizar métodos gráficos, representando el histograma junto a la curva normal teórica o el denominado gráfico de cuantiles teóricos (gráfico Q-Q). Este último, se realiza a partir de la función qqnorm.
for (i in 1:length(logmpg)){
logmpg.i <- as.vector(logmpg[i])
qqnorm(logmpg.i[[1]], pch = 19, col = "gray50")
qqline(logmpg.i[[1]])
}
Con estos resultados, lo que sabemos es que alguna de las medias es diferente. Para averiguar que medias diieren de las otras, se pueden efectuar comparaciones de medias dos a dos y evaluar en cada caso las diferencias con el resto de los grupos.
Los dos procedimientos más utilizados para la comparación de medias por pares son los tests de Tukey y de Scheffe. El primero será preferible en modelos balanceados, en el caso de no balanceados, como el ejemplo que estamos realizando, optaremos por Scheffe.
El test de Scheffe está disponible en el paquete agricolae, disponiendo de dos opciones de presentación de resultados. Si queremos agrupar los niveles del factor con medias similares, especificamos la opción group=TRUE.
library(agricolae)
scheffe.test(modelo.aov,"cylf", group=TRUE,console=TRUE,
main="Autonomía según cilindrada")##
## Study: Autonomía según cilindrada
##
## Scheffe Test for lnmpg
##
## Mean Square Error : 0.02553996
##
## cylf, means
##
## lnmpg std r Min Max
## 4 3.270454 0.16762136 11 3.063391 3.523415
## 6 2.980439 0.07431982 7 2.879198 3.063391
## 8 2.700171 0.18113932 14 2.341806 2.954910
##
## Alpha: 0.05 ; DF Error: 29
## Critical Value of F: 3.327654
##
## Groups according to probability of means differences and alpha level( 0.05 )
##
## Means with the same letter are not significantly different.
##
## lnmpg groups
## 4 3.270454 a
## 6 2.980439 b
## 8 2.700171 cSi lo que buscamos es realizar todas las comparaciones de pares posibles, debemos especificar la opción group=FALSE.
library(agricolae)
scheffe.test(modelo.aov,"cylf", group=FALSE,console=TRUE,
main="Autonomía según cilindrada")##
## Study: Autonomía según cilindrada
##
## Scheffe Test for lnmpg
##
## Mean Square Error : 0.02553996
##
## cylf, means
##
## lnmpg std r Min Max
## 4 3.270454 0.16762136 11 3.063391 3.523415
## 6 2.980439 0.07431982 7 2.879198 3.063391
## 8 2.700171 0.18113932 14 2.341806 2.954910
##
## Alpha: 0.05 ; DF Error: 29
## Critical Value of F: 3.327654
##
## Comparison between treatments means
##
## Difference pvalue sig LCL UCL
## 4 - 6 0.2900143 0.0032 ** 0.1145018 0.4655268
## 4 - 8 0.5702825 0.0000 *** 0.4240221 0.7165429
## 6 - 8 0.2802682 0.0029 ** 0.1122278 0.4483086Como puede observarse, a mayor número de cilindros se obtiene una menor autonomía, es decir, un mayor consumo de combustible, siendo todas las comparaciones estadísticamente significativas.
Para realizar el test de Tukey, se ha de utilizar la función glht del paquete multcomp. Los resultados para nuestro ejemplo serían los siguientes:
require(multcomp)## Loading required package: multcomp## Loading required package: mvtnorm## Loading required package: survival## Loading required package: TH.data##
## Attaching package: 'TH.data'## The following object is masked from 'package:MASS':
##
## geysersummary(glht(modelo.aov, linfct = mcp(cylf = "Tukey")))##
## Simultaneous Tests for General Linear Hypotheses
##
## Multiple Comparisons of Means: Tukey Contrasts
##
##
## Fit: aov(formula = lnmpg ~ cylf)
##
## Linear Hypotheses:
## Estimate Std. Error t value Pr(>|t|)
## 6 - 4 == 0 -0.29001 0.07727 -3.753 0.00222 **
## 8 - 4 == 0 -0.57028 0.06439 -8.857 < 0.001 ***
## 8 - 6 == 0 -0.28027 0.07398 -3.788 0.00189 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## (Adjusted p values reported -- single-step method)5.2.2 Análisis de la varianza con dos factores
En el ejemplo anterior estudiábamos el posible efecto del número de cilindros del motor en el consumo de combustible de los vehículos. Imaginemos ahora que se desea estudiar además el posible efecto del tipo de transmisión (automática [0] o manual [1]).
Podríamos pensar que es necesario llevar a cabo un análisis de la varianza de un factor para cada uno de ellos, sin embargo es posible trabajar con las dos variables independientes de manera simultánea en un único estudio.
El diseño experimental que se sigue en estos casos, es conocido como diseño factorial, donde dos o más variables independientes son manipuladas en un único estudio de tal forma que en el análisis se representan todas las posibles combinaciones de los diversos niveles de las variables independientes. Teóricamente, aunque un diseño factorial puede incluir cualquier número de variables independientes, en la práctica resulta poco adecuado utilizar más de tres o cuatro.
En síntesis, en nuestro caso queremos constatar si:
La autonomía de los vehículos varía dependiendo del número de cilindros del motor.
La autonomía de los vehículos varía dependiendo del tipo de transmisión.
La autonomía de los vehículos varía de forma conjunta según el número de cilindros del motor y el tipo de transmisión.
Modelo
El modelo matemático subyacente es el siguiente:
\[y_{ijk} = \mu + \alpha_i + \beta_j + (\alpha\beta)_{ij} + u_{ijk}\]
siendo \(\alpha_i\) el efecto del primer factor, \(\beta_j\) el del segundo y \((\alpha\beta)_{ij}\) la interacción entre ambos.
La estimación de estos parámetros teóricos se realiza, análogamente al caso anterior, del siguiente modo:
\[\hat \mu = \bar y_{...} \ \ \ \ \ \ \ \ \ \ \ \hat \alpha_i = \bar y_{i..} - \bar y_{...} \ \ \ \ \ \ \ \ \ \ \ \hat \beta_j = \bar y_{.j.} - \bar y_{...} \ \ \ \ \ \ \ \ \ \ \ \hat {(\alpha\beta)}_{ij} = \bar y_{ij.} - \bar y_{i..} -\bar y_{.j.} + \bar y_{...}\] \[\hat \mu_{ij} = \hat \mu + \hat \alpha_i + \hat \beta_i + \hat {(\alpha\beta)}_{ij}\ \ \ \ \ \ \ \ \ \ \ \hat u_{ijk}= e_{ijk} = y_{ijk} - \bar y_{ij.}\]
Siendo \(\bar y_{i..}\), \(\bar y_{.j.}\) y \(\bar y_{ij.}\) las medias muestrales para el primer factor, para el segundo y para el cruce de ambos respectivamente..
El modelo estimado queda por tanto:
\[y_{ijk} = \bar y_{...} + (\bar y_{i..} - \bar y_{...}) + (\bar y_{.j.} - \bar y_{...}) + (\bar y_{ij.} - \bar y_{i..} - \bar y_{.j.} + \bar y_{...}) + (y_{ijk} - \bar y_{ij.})\]
Tabla ANOVA
De una manera similar al caso de un factor, la varianza total puede descomponerse del siguiente modo (donde I es el número total de grupos del primer factor, en nuestro caso, los tres niveles del número de cilindros; J es el número total de grupos del segundo factor, en nuestro caso 2, transmisión automática y manual):
\[VT = \sum_{i=1}^I \sum_{j=1}^J \sum_{k=1}^{n_{ij}} ({y}_{ijk} - \bar{y}_{...})^2 = \sum_{i=1}^I \sum_{j=1}^J n_{ij} (\bar {y}_{ij.} - \bar{y}_{...})^2 + \sum_{i=1}^I \sum_{j=1}^J \sum_{k=1}^{n_{ij}} ({y}_{ijk} - \bar{y}_{ij.})^2 = VE + VNE\]
El primer término de la expresión anterior refleja la suma de los cuadrados con respecto a la media muestral global. El triple sumatorio se refiere: el primero a los niveles del primer factor (número de cilindros), el segundo a los del segundo factor (tipo de transmisión) y el tercero a los datos individuales del cruce de los dos anteriores.
El segundo término de la expresión se descompone en dos sumandos. El primero refleja las diferencias al cuadrado entre la media de cada celda y la media global, y constituye la variabilidad explicada por el modelo \(VE\), mientras que el segundo sumando es la suma de cuadrados residual o variación no explicada \(VNE\).
Lo interesante está en analizar qué ocasiona las diferencias del primer sumando, es decir, las diferencias al cuadrado entre la media de cada celda. Puede demostrarse que:
\[VE = \sum_{i=1}^I \sum_{j=1}^J n_{ij} (\bar{y}_{ij.} - \bar{y}_{...})^2 = \sum_{i=1}^I \sum_{j=1}^J n_{ij} (\bar{y}_{i..} - \bar{y}_{...})^2 + \sum_{i=1}^I \sum_{j=1}^J n_{ij} (\bar{y}_{.j.} - \bar{y}_{...})^2 +\] \[+\sum_{i=1}^I \sum_{j=1}^J \sum_{k=1}^{n_{ij}} (\bar{y}_{ij.} - \bar{y}_{i..} - \bar{y}_{.j.} + \bar{y}_{...})^2 = VE_A + VE_B + VE_{AxB}\]
Se ve claramente en esta expresión que los dos primeros sumandos corresponden a sumas; las denominaremos \(VE_A\) y \(VE_B\) y reflejan la variabilidad explicada por cada uno de los dos factores. El último término refleja la interacción de los factores A y B, es decir, el efecto de los dos factores que no es debido individualmente a ninguno de ellos. El efecto interacción, será denominado \(VE_{AxB}\).
La interacción será significativa si el comportamiento de la variable respuesta en un factor es diferente en función de los niveles del otro factor. Así, partiendo de nuestro ejemplo, hemos visto que en media el consumo de combustible aumenta a medida que aumenta el número de los cilindros del motor. Si consideramos el tipo de transmisión, y resultara que esto ocurre en los coches automáticos, pero en los manuales disminuyera el consumo con el aumento del número de cilindros, existirá efecto de interacción.
En síntesis, la suma total de cuadrados puede descomponerse, en el caso de dos factores del siguiente modo:
\[VT = VE_A+VE_B+VE_{AxB}+VNE\]
Al igual que en el caso de un factor, cada suma de cuadrados tiene sus propios grados de libertad, igual al número de niveles del factor menos 1. Los grados de libertad asociados a la interacción será la multiplicación de los asociados a ambos factores, es decir, \((I-1)*(J-1)\). Se muestra a continuación la tabla ANOVA donde se construye cada uno de los estadísticos F que, ahora, han de permitirnos determinar si el efecto de cada factor por separado y la interacción de ambos, son o no significativos.
Tabla nº 3. Tabla ANOVA. Modelo con dos factores e interacción
| Fuente de variación | Suma de cuadrados | Grados de libertad | Cuadrado medio (MC) | E(MC) | Estadistico \(F\) |
|---|---|---|---|---|---|
| Factor A | \(VE_A=JK\sum_i\hat\alpha_i^2\) | \(I-1\) | \(MCF_A=\frac{VE_A}{I-1}\) | \(\sigma^2+JK\frac{\sum\alpha_i^2}{I-1}\) | \(F=\frac{MCF_A}{MCR}\) |
| Factor B | \(VE_B=IK\sum_j\hat\beta_j^2\) | \(J-1\) | \(MCF_B=\frac{VE_B}{J-1}\) | \(\sigma^2+IK\frac{\sum\beta_j^2}{J-1}\) | \(F=\frac{MCF_B}{MCR}\) |
| Interacción | \(VE_{AxB}=K\sum_{ij}\hat {(\alpha\beta)}_{ij}^2\) | \((I-1)(J-1)\) | \(MCF_{AxB}=\frac{VE_{AxB}}{(I-1)(J-1)}\) | \(\sigma^2+K\frac{\sum(\alpha\beta)_j^2}{(I-1)(J-1)}\) | \(F=\frac{MCF_{AxB}}{MCR}\) |
| Error o residual | \(VNE=\sum_{ijk}e_{ijk}\) | \(IJ(K-1)=n-IJ\) | \(MCR=\frac{VNE}{n-IJ}\) | \(\sigma^2\) | |
| Total | \(VT=VE_A+VE_B+VNE\) | \(n-1\) | \(MCT=\frac {VT}{n-1}\) |
La columna E(MC) hace referencia al valor esperado o esperanza matemática de las varianzas o medias cuadráticas de las distintas fuentes de variación. Esta esperanza, como puede observarse, es igual a la suma de la varianza residual y J*K veces la media cuadrática del propio factor. Al construir los estadísticos F como el cociente entre la media cuadrática estimada para cada factor y la del error, en términos de esperanza, obtenemos (tomando como ejemplo el factor A):
\[\frac{E(MCF_A)}{E(MCR)} = \frac{\sigma^2+JK\frac{\sum\alpha_j^2}{I-1}}{\sigma^2}\]
Por tanto, si consideramos válida la hipótesis nula correspondiente a \(\alpha_i=0\) \(\forall i\), la esperanza matemática del estadítico F será igual a 1, aumentando su valor a medida que aumenta la media cuadrática del factor.
Se muestra a continuación el ANOVA planteado en R, donde como vemos, tanto el tipo de transmisión como la interacción de éste con el número de cilindros resultan ser no significativos.
lnmpg <- log(mtcars$mpg)
cylf <- as.factor(mtcars$cyl)
amf <- as.factor(mtcars$am)
# Test de Levene para factor Número de cilindros
leveneTest(lnmpg,cylf,center=mean)## Levene's Test for Homogeneity of Variance (center = mean)
## Df F value Pr(>F)
## group 2 1.6622 0.2073
## 29# Test de Levene para factor Tipo de transmisión
leveneTest(lnmpg,amf,center=mean)## Levene's Test for Homogeneity of Variance (center = mean)
## Df F value Pr(>F)
## group 1 0.4653 0.5004
## 30# Test de Shapiro-Wilk para factor Número de cilindros
logmpg <- split(log(mtcars$mpg), as.factor(mtcars$cyl))
for (i in 1:length(logmpg)){
logmpg.i <- as.vector(logmpg[i])
print(shapiro.test(logmpg.i[[1]]))
}##
## Shapiro-Wilk normality test
##
## data: logmpg.i[[1]]
## W = 0.91722, p-value = 0.2961
##
##
## Shapiro-Wilk normality test
##
## data: logmpg.i[[1]]
## W = 0.89736, p-value = 0.3153
##
##
## Shapiro-Wilk normality test
##
## data: logmpg.i[[1]]
## W = 0.89341, p-value = 0.09052# Test de Shapiro-Wilk para factor Tipo de transmisión
logmpg <- split(log(mtcars$mpg), as.factor(mtcars$am))
for (i in 1:length(logmpg)){
logmpg.i <- as.vector(logmpg[i])
print(shapiro.test(logmpg.i[[1]]))
}##
## Shapiro-Wilk normality test
##
## data: logmpg.i[[1]]
## W = 0.9557, p-value = 0.4909
##
##
## Shapiro-Wilk normality test
##
## data: logmpg.i[[1]]
## W = 0.94212, p-value = 0.485# Modelo ANOVA
modelo.aov <- aov(lnmpg~cylf+amf+cylf:amf)
summary(modelo.aov)## Df Sum Sq Mean Sq F value Pr(>F)
## cylf 2 2.0081 1.0040 40.362 1.06e-08 ***
## amf 1 0.0681 0.0681 2.737 0.110
## cylf:amf 2 0.0258 0.0129 0.519 0.601
## Residuals 26 0.6468 0.0249
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1model.tables(modelo.aov)## Tables of effects
##
## cylf
## 4 6 8
## 0.3129 0.02292 -0.2573
## rep 11.0000 7.00000 14.0000
##
## amf
## 0 1
## -0.03253 0.04754
## rep 19.00000 13.00000
##
## cylf:amf
## amf
## cylf 0 1
## 4 -0.061 0.023
## rep 3.000 8.000
## 6 0.015 -0.020
## rep 4.000 3.000
## 8 0.010 -0.061
## rep 12.000 2.000Por último, el gráfico de interacción se construye del siguiente modo:
interaction.plot(cylf,amf,lnmpg)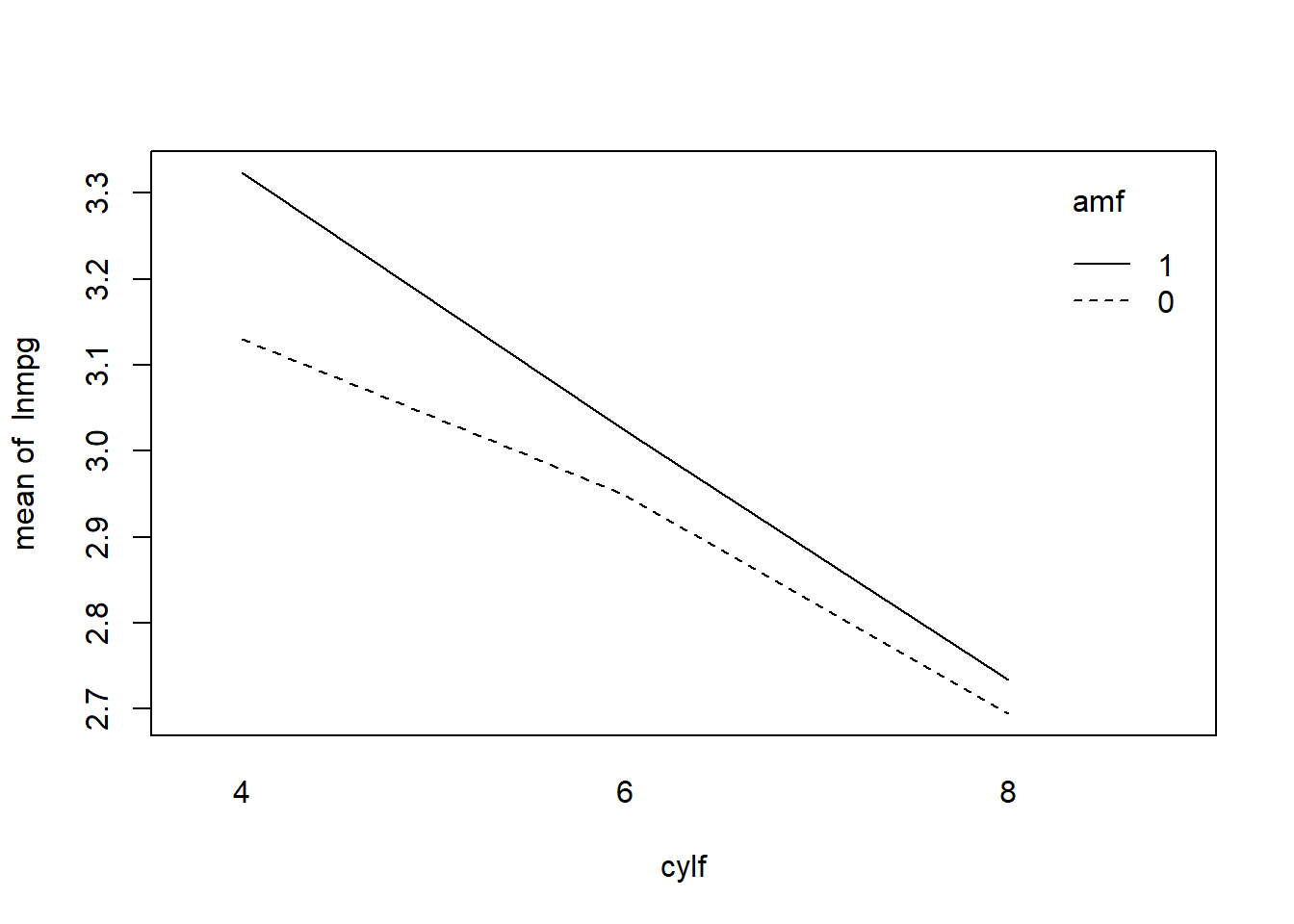
donde si bien puede apreciarse un ligero mayor consumo de los vehículos automáticos (menor autonomía), dicha diferencia, eliminando el efecto del número de cilindros, no llega a ser estadísticamente significativa, tal y como hemos visto.
5.2.3 Modelos con más de dos factores
La generalización del modelo de dos factores con interacción a uno con tres o más factores es inmediata.
Por ejemplo, es fácil comprobar que en el diseño factorial completo de tres factores con réplicas, incluyendo la interacción de tercer orden, quedaría:
\[y_{ijkl} = \mu + \alpha_i + \beta_j + \gamma_k + (\alpha\beta)_{ij} + (\alpha\gamma)_{ik} + (\beta\gamma)_{jk} + (\alpha\beta\gamma)_{ijk} + u_{ijkl}\]
la variabilidad total (\(VT\)) se desglosa en:
\[VT = VE_A +VE_B + VE_C + VE_{AxB} + VE_{AxC} + VE_{BxC} + VE_{AxBxC} + VNE\]
y la tabla ANOVA:
Tabla nº 4. Tabla ANOVA. Modelo con tres factores e interacción
| Fuente de variación | Suma de cuadrados | Grados de libertad | Cuadrado medio | Estadistico \(F\) |
|---|---|---|---|---|
| Factor A | \(VE_A\) | \(I-1\) | \(MCF_A=\frac{VE_A}{I-1}\) | \(F=\frac{MCF_A}{MCR}\) |
| Factor B | \(VE_B\) | \(J-1\) | \(MCF_B=\frac{VE_B}{J-1}\) | \(F=\frac{MCF_B}{MCR}\) |
| Factor C | \(VE_C\) | \(K-1\) | \(MCF_C=\frac{VE_C}{K-1}\) | \(F=\frac{MCF_C}{MCR}\) |
| Interacción AxB | \(VE_{AxB}\) | \((I-1)(J-1)\) | \(MCF_{AxB}=\frac{VE_{AxB}}{(I-1)(J-1)}\) | \(F=\frac{MCF_{AxB}}{MCR}\) |
| Interacción AxC | \(VE_{AxC}\) | \((I-1)(K-1)\) | \(MCF_{AxC}=\frac{VE_{AxC}}{(I-1)(K-1)}\) | \(F=\frac{MCF_{AxC}}{MCR}\) |
| Interacción BxC | \(VE_{BxC}\) | \((J-1)(K-1)\) | \(MCF_{BxC}=\frac{VE_{BxC}}{(J-1)(K-1)}\) | \(F=\frac{MCF_{BxC}}{MCR}\) |
| Interacción AxBxC | \(VE_{AxBxC}\) | \((I-1)(J-1)(K-1)\) | \(MCF_{AxBxC}=\frac{VE_{AxBxC}}{(I-1)(J-1)(K-1)}\) | \(F=\frac{MCF_{AxBxC}}{MCR}\) |
| Error o residual | \(VNE\) | \(n-IJK\) | \(MCR=\frac{VNE}{n-IJK}\) | |
| Total | \(VT\) | \(n-1\) | \(MCT=\frac {VT}{n-1}\) |
Al igual que en el modelo de regresión, es conveniente la aplicación de técnicas se selección de factores (fordward, backward, stepwise). Al eliminar los efectos no significativos del modelo, además de facilitar su interpretación, ganamos grados de libertad en el término error y reducimos su variabilidad.
5.3 Modelos de componentes de la varianza: efectos aleatorios
Como hemos visto hasta ahora, el factor es una variable independiente o experimental controlada por el investigador. Puede tomar pocos o muchos valores o niveles, a cada uno de los cuales se asignan los grupos o muestras.
Si se toman L niveles y las inferencias se refieren exclusivamente a los L niveles y no a otros que podrían haber sido incluidos, el ANOVA se llama de efectos fijos, sistemático o paramétrico. El interés del diseño se centra en saber si esos niveles concretos difieren entre sí.
Cuando los niveles son muchos y se seleccionan al azar L niveles, pero las inferencias se desean hacer respecto al total de niveles, el análisis de varianza se denomina de efectos aleatorios. La idea básica es que el investigador no tiene interés en niveles particulares del factor.
Los modelos basados en factores aleatorios se denominan Componentes de la varianza, y lo que se persigue es evaluar la cantidad de variación de la variable dependiente que se asocia con una o más variables de efectos aleatorios.
5.3.1 Modelo de un factor aleatorio
En estos modelos se mide que parte de la variabilidad de la respuesta es debida al factor. Dado que el factor es una variable aleatoria, la variabilidad observada en el experimento será:
\[\sigma^2_y = \sigma^2_{\alpha} + \sigma^2\]
Por tanto, lo que se pretende averiguar es si \(\sigma^2_{\alpha}\) es igual a 0 (hipótesis nula) o, por el contrario, el factor incorpora al experimento una variabilidad significativa.
El modelo queda por tanto:
\[y_{ik} = \mu + \alpha_i + u_{ik}\]
con \(\alpha_i \rightarrow N(0,\sigma^2_{\alpha})\) y \(u_{ik} \rightarrow N(0,\sigma^2)\), siendo la hipótesis nula del modelo:
\[H_0: \sigma^2_{\alpha} = 0\]
De forma análoga al modelo con efectos fijos, los estimadores de los parámetros del modelo serían:
\[\hat \mu = \bar y_{..}\] \[\hat \alpha_i = \bar y_{i.} - \bar y_{..}\]
\[e_{ik} = y_{ik} - \bar y_{i.}\]
donde la descomposición de la variabilidad quedaría:
\[VE(\alpha) = K \sum_{i=1}^I(\bar y_{i.} - \bar y_{..})^2\] \[VNE = \sum_{i=1}^I \sum_{k=1}^K (y_{ik} - \bar y_{i.})^2 = \sum_{i=1}^I \sum_{k=1}^K e^2_{ik}\] \[VT = VE(\alpha) + VNE\]
quedando la tabla ANOVA de la siguiente manera:
| Fuente de variación | Suma de cuadrados | Grados de libertad | Cuadrado medio (MC) | E(MC) | Estadistico \(F\) |
|---|---|---|---|---|---|
| Entre grupos (VE) | \(VE(\alpha)\) | \(I-1\) | \(\hat S^2_{\alpha}=\frac{VE(\alpha)}{I-1}\) | \(\sigma^2+K\sigma^2_{\alpha}\) | \(F=\frac{\hat S^2_{\alpha}}{\hat S^2_R}\) |
| Interna (VNE) | \(VNE\) | \(I(K-1)\) | \(\hat S^2_R=\frac{VNE}{n-I}\) | \(\sigma^2\) | |
| Total | \(VT=VE+VNE\) | \((I-1)+I(K-1)=n-1\) | \(\hat S^2_y=\frac {VT}{n-1}\) |
Si \(\alpha\) fuera un efecto fijo, recordar que la esperanza de la media cuadrática sería:
\[E(MC(\alpha)) = \sigma^2 + K \frac {\sum_{i=1}^I\alpha_i^2} {I-1}\] es decir, cambian las esperanzas de las medias cuadráticas.
Teniendo en cuenta las esperanzas de las medias cuadráticas, las variabilidades del error (interna) y entre grupos se estimarían del siguiente modo:
\[\hat \sigma^2 = \hat S^2_R\] \[\hat S^2_{\alpha} = \hat \sigma^2 + K \hat \sigma^2_{\alpha} => \] \[\hat \sigma^2_{\alpha} = \frac {\hat S^2_{\alpha}-\hat S^2_R} {K}\]
5.3.2 Modelo de dos factores aleatorios con interacción
En este modelo la variabilidad observada en el experimento será:
\[\sigma^2_y = \sigma^2_{\alpha} + \sigma^2_{\beta} + \sigma^2_{\alpha\beta} + \sigma^2\]
El modelo a estimar sería el siguiente:
\[y_{ijk} = \mu + \alpha_i + \beta_j + \alpha\beta_{ij} + u_{ijk}\]
con \(\alpha_i \rightarrow N(0,\sigma^2_{\alpha})\), \(\beta_j \rightarrow N(0,\sigma^2_{\beta})\) y \(u_{ijk} \rightarrow N(0,\sigma^2)\), siendo las hipótesis nulas del modelo:
\[H_{01}: \sigma^2_{\alpha} = 0\] \[H_{02}: \sigma^2_{\beta} = 0\] \[H_{03}: \sigma^2_{\alpha\beta} = 0\]
Los estimadores de los parámetros del modelo se calculan del siguiente modo:
\[\hat \mu = \bar y_{...}\] \[\hat \alpha_i = \bar y_{i..} - \bar y_{...}\] \[\hat \beta_j = \bar y_{.j.} - \bar y_{...}\] \[\hat {\alpha\beta_j} = \bar y_{ij.} - \bar y_{i..} - \bar y_{.j.} + \bar y_{...}\] \[e_{ijk} = y_{ijk} - \bar y_{ij.}\]
y la descomposición de la variabilidad quedaría:
\[VE(\alpha) = JK \sum_{i=1}^I\hat \alpha_i^2 \ \ \ \ \ \ \ VE(\beta) = IK \sum_{j=1}^I\hat \beta_j^2 \ \ \ \ \ \ \ VE(\alpha\beta) = K \sum_{i=1}^I \sum_{j=1}^J\hat {\alpha\beta_j}^2\] \[VNE = \sum_{i=1}^I \sum_{j=1}^J \sum_{k=1}^K (y_{ijk} - \bar y_{ij.})^2 = \sum_{i=1}^I \sum_{j=1}^J \sum_{k=1}^K e^2_{ijk}\] \[VT = VE(\alpha) + VE(\beta) + VE(\alpha\beta) + VNE\]
quedando la tabla ANOVA de la siguiente manera:
| Fuente de variación | Suma de cuadrados | Grados de libertad | Cuadrado medio (MC) | E(MC) | Estadistico \(F\) |
|---|---|---|---|---|---|
| Tratamiento A | \(VE(\alpha)\) | \(I-1\) | \(\hat S^2_{\alpha}=\frac{VE(\alpha)}{I-1}\) | \(\sigma^2+JK\sigma^2_{\alpha}+K\sigma^2_{\alpha\beta}\) | \(F_\alpha=\frac{\hat S^2_{\alpha}}{\hat S^2_{\alpha\beta}}\) |
| Tratamiento B | \(VE(\beta)\) | \(J-1\) | \(\hat S^2_{\beta}=\frac{VE(\beta)}{J-1}\) | \(\sigma^2+IK\sigma^2_{\beta}+K\sigma^2_{\alpha\beta}\) | \(F_\beta=\frac{\hat S^2_{\beta}}{\hat S^2_{\alpha\beta}}\) |
| Interacción | \(VE(\alpha\beta)\) | \((I-1)(J-1)\) | \(\hat S^2_{\alpha\beta}=\frac{VE(\alpha\beta)}{(I-1)(J-1)}\) | \(\sigma^2+K\sigma^2_{\alpha\beta}\) | \(F_{\alpha\beta}=\frac{\hat S^2_{\alpha\beta}}{\hat S^2_R}\) |
| Error (VNE) | \(VNE\) | \(IJ(K-1)\) | \(\hat S^2_R=\frac{VNE}{IJ(K-1)}\) | \(\sigma^2\) | |
| Total | \(VT=VE+VNE\) | \(n-1\) | \(\hat S^2_y=\frac {VT}{n-1}\) |
Como vemos, el denominador del test en los efectos principales es ahora la Media Cuadrática de la interacción.
5.3.3 Modelos con más de dos factores y modelos mixtos
Al igual que en el caso de los modelos ANOVA con efectos fijos, analizamos a continuación el modelo con tres efectos aleatorios y las correspondientes interacciones. Como veremos a continuación, la generalización a más de dos factores es también directa, si bien se complica la construcción de las pruebas F para los tres efectos principales.
Los grados de libertad y las esperanzas de las medias cuadráticas quedarían en este caso:
| Fuente de variación | Grados de libertad | E(MC) |
|---|---|---|
| Tratamiento A | \(I-1\) | \(\sigma^2+JKL\sigma^2_{\alpha}+KL\sigma^2_{\alpha\beta}+JL\sigma^2_{\alpha\gamma}+L\sigma^2_{\alpha\beta\gamma}\) |
| Tratamiento B | \(J-1\) | \(\sigma^2+IKL\sigma^2_{\beta}+KL\sigma^2_{\alpha\beta}+IL\sigma^2_{\beta\gamma}+L\sigma^2_{\alpha\beta\gamma}\) |
| Tratamiento C | \(K-1\) | \(\sigma^2+IJL\sigma^2_{\gamma}+JL\sigma^2_{\alpha\gamma}+IL\sigma^2_{\beta\gamma}+L\sigma^2_{\alpha\beta\gamma}\) |
| Interacción AB | \((I-1)(J-1)\) | \(\sigma^2+KL\sigma^2_{\alpha\beta}+L\sigma^2_{\alpha\beta\gamma}\) |
| Interacción AC | \((I-1)(K-1)\) | \(\sigma^2+JL\sigma^2_{\alpha\gamma}+L\sigma^2_{\alpha\beta\gamma}\) |
| Interacción BC | \((J-1)(K-1)\) | \(\sigma^2+IL\sigma^2_{\beta\gamma}+L\sigma^2_{\alpha\beta\gamma}\) |
| Interacción ABC | \((I-1)(J-1)(K-1)\) | \(\sigma^2+L\sigma^2_{\alpha\beta\gamma}\) |
| Error (VNE) | \(IJK(L-1)\) | \(\sigma^2\) |
Como puede observarse, en el cálculo de la esperanza de la media cuadrática o varianza de cada fuente de variación o efecto, interviene la varianza del error, la de la propio efecto y la de todas aquellas interacciones donde aparezca dicho efecto.
Teniendo en cuenta estas esperanzas, es inmediato el cálculo de los estadísticos F para contrastar los efectos de las interacciones:
\[F_{\alpha\beta\gamma} = \frac {\hat S^2_{\alpha\beta\gamma}} {\hat S^2_R}\] \[F_{\alpha\beta} = \frac {\hat S^2_{\alpha\beta}} {\hat S^2_{\alpha\beta\gamma}}\] \[F_{\alpha\gamma} = \frac {\hat S^2_{\alpha\gamma}} {\hat S^2_{\alpha\beta\gamma}}\] \[F_{\beta\gamma} = \frac {\hat S^2_{\beta\gamma}} {\hat S^2_{\alpha\beta\gamma}}\]
Para los efectos principales (A, B, C) necesitamos estimar una media cuadrática para el denominador de la prueba. Suponiendo que estamos evaluando el efecto A, se pueden considerar.
\[F_{\alpha} = \frac {\hat S^2_{\alpha}} {\hat S^2_{\alpha\beta}+\hat S^2_{\alpha\gamma}-\hat S^2_{\alpha\beta\gamma}}\] \[F'_{\alpha} = \frac {\hat S^2_{\alpha}+\hat S^2_{\alpha\beta\gamma}} {\hat S^2_{\alpha\beta}+\hat S^2_{\alpha\gamma}}\]
Los grados de libertad de las sumas de las medias cradráticas (denominador de \(F_{\alpha}\) y numerador y denominador de \(F'_{\alpha}\)) se calculan en base al procedimiento de Satterthwaite.
Este procedimiento establece que dada una función lineal M definida como:
\[M = \alpha_1 · (MC)_1 + \alpha_2 · (MC)_2 + \cdots + \alpha_k · (MC)_k\]
siendo \((MC)_1, (MC)_2, \cdots , (MC)_k\) cuadrados medios con grados de libertad \(v_1, v_2, \cdots , v_k\).
Los grados de libertad para M son aproximadamente:
\[v = \frac {M^2} {\sum_{i=1}^k \frac {(\alpha_i · (MC)_i)^2} {v_i}}\]
Cuando se utilizan dos o más factores, cada uno con varios niveles, unos de efectos fijos y otros de efectos aleatorios, el análisis de varianza es mixto.
La función de R que permite estimar modelos ANOVA con efectos aleatorios se encuentra en la libreria “nlme”.
Con la base de datos Orthodontic de R, que contiene datos de medidas ortodónticas se plantea un modelo ANOVA de efectos aleatorios sobre un solo factor, y un modelo mixto, en donde la constante es el factor aleatorio y utiliza dos factores fijos: la edad y el sexo.
library(nlme)
data("Orthodont")
# Modelo efectos aleatorios
fm1 <- lme(distance ~ age, data = Orthodont) # random is ~ age
summary(fm1)## Linear mixed-effects model fit by REML
## Data: Orthodont
## AIC BIC logLik
## 454.6367 470.6173 -221.3183
##
## Random effects:
## Formula: ~age | Subject
## Structure: General positive-definite
## StdDev Corr
## (Intercept) 2.3270339 (Intr)
## age 0.2264276 -0.609
## Residual 1.3100399
##
## Fixed effects: distance ~ age
## Value Std.Error DF t-value p-value
## (Intercept) 16.761111 0.7752461 80 21.620375 0
## age 0.660185 0.0712533 80 9.265334 0
## Correlation:
## (Intr)
## age -0.848
##
## Standardized Within-Group Residuals:
## Min Q1 Med Q3 Max
## -3.223106016 -0.493760867 0.007316632 0.472151090 3.916032742
##
## Number of Observations: 108
## Number of Groups: 27# Modelo Mixto
fm2 <- lme(distance ~ age + Sex, data = Orthodont, random = ~ 1)
summary(fm2)## Linear mixed-effects model fit by REML
## Data: Orthodont
## AIC BIC logLik
## 447.5125 460.7823 -218.7563
##
## Random effects:
## Formula: ~1 | Subject
## (Intercept) Residual
## StdDev: 1.807425 1.431592
##
## Fixed effects: distance ~ age + Sex
## Value Std.Error DF t-value p-value
## (Intercept) 17.706713 0.8339225 80 21.233044 0.0000
## age 0.660185 0.0616059 80 10.716263 0.0000
## SexFemale -2.321023 0.7614168 25 -3.048294 0.0054
## Correlation:
## (Intr) age
## age -0.813
## SexFemale -0.372 0.000
##
## Standardized Within-Group Residuals:
## Min Q1 Med Q3 Max
## -3.74889609 -0.55034466 -0.02516628 0.45341781 3.65746539
##
## Number of Observations: 108
## Number of Groups: 275.4 Modelos ANCOVA
Los modelos ANCOVA son modelos ANOVA que incluyen ademas de las variables cualitativas o categóricas, variables cuantitativas entre las variables dependientes.
En determinadas ocasiones, en lugar de disponer de un factor bloque se tiene en su lugar una variable cuantitativa. Esta variable, si no está controlada por el investigador, se ha de incluir en el modelo con el fin de eliminar el efecto que pudiera tener sobre la estimación de los niveles del factor principal. Las variables explicativas cuantitativas se denominan covariables.
Partiendo de la especificación de un modelo ANOVA de un factor con dos niveles, al introducir la variable explicativa cuantitativa, \(X_i\), tendríamos:
\[ Y_i=\mu_1 D_{1i} + \mu_2 D_{2i} +\beta_1 X_i+ u_i\]
o sus equivalentes:
\[ Y_i=\beta_0 + \mu_1 D_{1i} +\beta_1 X_i+ u_i\]
\[ Y_i=\beta_0 + \mu_2 D_{2i} +\beta_1 X_i+ u_i\]
Para el análisis del comportamiento de cada grupo respecto a la pendiente, habría que especificar los siguientes modelos ANCOVA:
\[ Y_i=\delta_1 D_{1i}X_i + \delta_2 D_{2i}X_i + u_i\]
\[ Y_i=\beta_0 +\beta_1 X_i+ \delta_1 D_{1i} X_i+ u_i\]
\[ Y_i=\beta_0 +\beta_1 X_i+ \delta_2 D_{2i} X_i+ u_i\]
En los modelos ANOVA y ANCOVA se pueden incluir distintas variables categóricas. Consideremos una categórica \(E\) con tres categorías (1,2,3):
\(E_{1i}\) que toma valor uno en los individuos pertenecientes a la categoría 1, y cero en los restantes
\(E_{2i}\) que toma valor uno en los individuos pertenecientes a la categoría 2, y cero en los restantes
\(E_{3i}\) que toma valor uno en los individuos pertenecientes a la categoría 3, y cero en los restantes.
Si bien a la hora de especificar el modelo hay que evitar los problemas de multicolinealidad entre todas las variables dummy incluidas y el término constante.
Una forma de evitar los problemas es no incluir alguna de las categorías en forma de variable dummy, y dejar que la constante recoja el efecto de la categoría no incluida.
Una especificación posible de este modelo ANCOVA sería entonces:
\[ Y_i=\beta_0 +\beta_1 X_i+ \mu_2 D_{2i} + \alpha_1 E_{1i} + \alpha_2 E_{2i} + \alpha_3 E_{3i} + u_i\]
Modelo
Desarrolamos a continuación el modelo más simple de ANCOVA, es decir, un factor y una covariable, que se supone relacionada linealmente con la variable dependiente:
\[y_{ij} = \mu + \alpha_i + \beta(x_{ij} - \bar x_{..})+u_{ij}\ \ \ i=1,.. L; j=1,...,n_i\] siendo \(\beta\) el coeficiente de la regresión lineal entre \(X\) e \(Y\). Las medias estimadas para los tratamientos bajo este modelo serían entonces:
\[\mu_i = \mu + \alpha_i + \beta( \bar x_{i.} - \bar x_{..})\]
Construyendo dos rectas de regresión con la misma pendiente, \(\beta\), pero con distinta ordenada en el origen \(\mu + \alpha_i\).
La diferencia con la media glogal \(\mu\) se descompone en dos elementos, el efecto del factor \(\alpha_i\) y el de la covariable \(\beta( \bar x_{i.} - \bar x_{..})\)
La hipóteis nula de este modelo será por tanto:
\[H_0: \beta = 0; \ \ \ \ \alpha _i = 0 \ \ \ \forall i \]
Los parámetros se estiman:
\[\hat \alpha_i = \bar y_{i.} - \bar y_{..} \ \ \ \ \ \hat \beta = \frac {S_{xy}} {S_x^2}\]
Y la descomsisición de la varibilidad \(VT\) será:
\[VT = \sum_{i=1}^L \sum_{j=1}^{n_i} (y_{ij} - \bar y_{..})^2 = \sum_{i=1}^L n_i(\bar y_{i.} - \bar y_{..})^2 + \sum_{i=1}^L \sum_{j=1}^{n_i} [\hat\beta(x_{ij} - \bar x_{..})]^2+VNE\]
Luego la variabilidad explicada por el factor será:
\[VE_A = \sum_{i=1}^L n_i(\bar y_{i.} - \bar y_{..})^2 = \sum_{i=1}^L n_i\hat \alpha_i^2\]
La variabilidad explicada por la covariable será entonces:
\[VE_{XxY} = \hat\beta^2 \sum_{i=1}^L \sum_{j=1}^{n_i} (x_{ij} - \bar x_{..})^2 = \frac {[\sum_{i=1}^L\sum_{j=1}^{n_i} (x_{ij} - \bar x_{..}) (y_{ij} - \bar y_{..})]^2} {\sum_{i=1}^L \sum_{j=1}^{n_i} (x_{ij} - \bar x_{..})^2}\]
y la variabilidad no expicada:
\[VNE = \sum_{i=1}^L \sum_{j=1}^{n_i} (y_{ij}-\bar y_{i.} + \hat\beta(x_{ij} - \bar x_{..}))^2 \]
donde como vemos, puede descomponerse en aquella proveniente del factor y la asociada a la covariable.
Tabla ANOVA
La tabla ANOVA quedaría como sigue:
Tabla nº 4. Tabla ANOVA. Modelo con un factor y una covabiable
| Fuente de variación | Suma de cuadrados | Grados de libertad | Cuadrado medio | Estadistico \(F\) |
|---|---|---|---|---|
| Factor A | \(VE_A\) | \(L-1\) | \(MCF_A=\frac{VE_A}{L-1}\) | \(F=\frac{MCF_A}{MCR}\) |
| Covariable | \(VE_{XxY}\) | \(1\) | \(MCF_{XxY}=\frac{VE_{XxY}^2}{VE_X}\) | \(F=\frac{MCF_{XxY}}{MCR}\) |
| Error o residual | \(VNE\) | \(n-L-1\) | \(MCR=\frac{VNE}{n-L-1}\) | |
| Total | \(VT\) | \(n-1\) | \(MCT=\frac {VT}{n-1}\) |
Podemos tener más de un factor y/o covariable,e incluso plantear efecto interacción entre un factor y una covariable, obteniendo en este caso dos rectas con distinta ordenada en el origen y distinta pendiente. Hay que tener en cuenta también las hipótesis del modelo sobre los residuos, la selección de variables, etc.
Tomando como covariable la variable peso (wt), en miles de libras, obtenemos de nuevo como resultado un contraste no significativo para el efecto del factor tipo de transmisión. Esta corrección es efectiva gracias a la relación existente entre el peso de los vehículos y el consumo de combustible, pues lógicamente a mayor peso, menos millas recorridas por galón de combustible.
lnmpg <- log(mtcars$mpg)
amf <- as.factor(mtcars$am)
modelo.lm <- lm(lnmpg~amf+mtcars$wt)
summary(modelo.lm)##
## Call:
## lm(formula = lnmpg ~ amf + mtcars$wt)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.21351 -0.08281 0.00304 0.04962 0.32349
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.89834 0.13567 28.734 < 2e-16 ***
## amf1 -0.04307 0.06865 -0.627 0.535
## mtcars$wt -0.28699 0.03501 -8.198 4.87e-09 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.1376 on 29 degrees of freedom
## Multiple R-squared: 0.8003, Adjusted R-squared: 0.7865
## F-statistic: 58.1 on 2 and 29 DF, p-value: 7.186e-11Otros modelos ANCOVA podrían ser:
##
## Call:
## lm(formula = mpg ~ 0 + as.factor(am) + wt, data = mtcars)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.5295 -2.3619 -0.1317 1.4025 6.8782
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## as.factor(am)0 37.3216 3.0546 12.218 5.84e-13 ***
## as.factor(am)1 37.2979 2.0857 17.883 < 2e-16 ***
## wt -5.3528 0.7882 -6.791 1.87e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3.098 on 29 degrees of freedom
## Multiple R-squared: 0.9802, Adjusted R-squared: 0.9781
## F-statistic: 478.1 on 3 and 29 DF, p-value: < 2.2e-16##
## Call:
## lm(formula = mpg ~ am + wt, data = mtcars)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.5295 -2.3619 -0.1317 1.4025 6.8782
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 37.32155 3.05464 12.218 5.84e-13 ***
## am -0.02362 1.54565 -0.015 0.988
## wt -5.35281 0.78824 -6.791 1.87e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3.098 on 29 degrees of freedom
## Multiple R-squared: 0.7528, Adjusted R-squared: 0.7358
## F-statistic: 44.17 on 2 and 29 DF, p-value: 1.579e-09##
## Call:
## lm(formula = mpg ~ am + wt + wt * am, data = mtcars)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.6004 -1.5446 -0.5325 0.9012 6.0909
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 31.4161 3.0201 10.402 4.00e-11 ***
## am 14.8784 4.2640 3.489 0.00162 **
## wt -3.7859 0.7856 -4.819 4.55e-05 ***
## am:wt -5.2984 1.4447 -3.667 0.00102 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.591 on 28 degrees of freedom
## Multiple R-squared: 0.833, Adjusted R-squared: 0.8151
## F-statistic: 46.57 on 3 and 28 DF, p-value: 5.209e-11##
## Call:
## lm(formula = mpg ~ 0 + as.factor(am) + as.factor(gear) + wt,
## data = mtcars)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.5798 -2.4056 -0.3692 1.8198 5.7713
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## as.factor(am)0 35.0955 3.1862 11.015 1.72e-11 ***
## as.factor(am)1 35.2838 3.0091 11.726 4.20e-12 ***
## as.factor(gear)4 2.0769 1.7343 1.198 0.242
## as.factor(gear)5 -1.0615 2.3845 -0.445 0.660
## wt -4.8782 0.7945 -6.140 1.46e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.968 on 27 degrees of freedom
## Multiple R-squared: 0.9831, Adjusted R-squared: 0.9799
## F-statistic: 313.4 on 5 and 27 DF, p-value: < 2.2e-16La función R “lm”, presenta siempre una especificación que evita la multicolinealidad perfecta.
Realizar ejercicio libre con base de datos “npk”.
## 'data.frame': 24 obs. of 5 variables:
## $ block: Factor w/ 6 levels "1","2","3","4",..: 1 1 1 1 2 2 2 2 3 3 ...
## $ N : Factor w/ 2 levels "0","1": 1 2 1 2 2 2 1 1 1 2 ...
## $ P : Factor w/ 2 levels "0","1": 2 2 1 1 1 2 1 2 2 2 ...
## $ K : Factor w/ 2 levels "0","1": 2 1 1 2 1 2 2 1 1 2 ...
## $ yield: num 49.5 62.8 46.8 57 59.8 58.5 55.5 56 62.8 55.8 ...5.5 Modelo Lineal Generalizado
5.5.1 Formulación general
Los modelos lineales (regresión, ANOVA, ANCOVA), se basan en los siguientes supuestos:
Los errores se distribuyen normalmente.
La varianza es constante.
La variable dependiente se relaciona linealmente con las variables independientes.
De manera analítica tendríamos: \[Y_i=\beta_0 + \beta_1X_{1i}+\beta_2X_{2i}+...+\beta_kX_{ki}+u_i,\ \ \ \ i=1,2,…, n\]
donde \(e_i\) esta distribuida de cómo una normal de media cero, varianza constante (homocedástica),y donde la covarianza entre \(e_i\) y \(e_j\) es nula para \(e_i\neq e_j\) (ausencia de autocorrelación). Es decir, estos supuestos llevan implícito que la distribución de la variable dependiente \(Y_i\) sea también una normal \(Y_i\sim(\mu,\sigma^2)\), donde \(\mu=\beta_0+\beta_1 \bar X_1+\beta_2 \bar X_2+...+\beta_k \bar X_k\).
En muchas ocasiones, sin embargo, nos encontramos con que uno o varios de estos supuestos no se cumplen por la naturaleza de la información. En algunos casos, estos problemas se pueden llegar a solucionar mediante la transformación de la variable respuesta (por ejemplo tomando logaritmos). Sin embargo estas transformaciones no siempre consiguen corregir la falta de normalidad, la heterocedasticidad (varianza no constante) o la no linealidad de nuestros datos.
Una alternativa a la transformación de la variable dependiente/respuesta y a la falta de normalidad es el uso de los modelos lineales generalizados (MLG).
Los MLG fueron formulados por John Nelder y Robert Wedderburn (1989) como una manera de unificar varios modelos estadísticos, incluyendo la regresión lineal, regresión logística y regresión de Poisson, bajo un solo marco teórico.
Los MLG son, por tanto, una extensión de los modelos lineales que permiten utilizar distribuciones no normales de los errores (binomiales, Poisson, gamma, etc) y varianzas no constantes.
Los MLG permiten especificar distintos tipos de distribución de errores. Cayuela (2010) expone los siguientes ejemplos:
Poisson, muy útiles para conteos de acontecimientos, por ejemplo: número de heridos por accidentes de tráfico; número de hogares asegurados que dan parte de siniestro al día.
Binomiales, de gran utilidad para proporciones y datos de presencia/ausencia, por ejemplo: tasas de mortalidad; tasas de infección; porcentaje de siniestros mortales.
Gamma, muy útiles con datos que muestran un coeficiente de variación constante, esto es, en donde la varianza aumenta según aumenta la media de la muestra de manera constante, por ejemplo: número de heridos en función del número de siniestros.
Exponencial, muy útiles para los análisis de supervivencia.
Otra razón por la que un modelo lineal puede no ser adecuado para describir un fenómeno determinado es que la relación entre la variable respuesta y las variables independientes no es siempre lineal.
La función de vínculo se encarga de linealizar la relación entre la variable dependiente y las variables independientes mediante la transformación de la variable respuesta:
Tabla nº 5. Funciones de ligadura-vínculo más usadas
| Función Vínculo | Formula | Uso |
|---|---|---|
| Identidad | \(\mu\) | Datos continuos con errores normales (regresión y ANOVA) |
| Logaritmica | \(log(\mu)\) | Conteos con errores de tipo de Poisson |
| Logit | \(log(\frac{\mu}{n-\mu})\) | Proporciones (datos entre O y 1) con errores binomiales |
| Recíproca | \(\frac{1}{\mu}\) | Datos continuos con errores Gamma |
| Cuadrada | \(\sqrt{\mu}\) | Conteos |
| Exponencial | \(\mu^n\) | Funciones de potencia |
Fuente: (Cayuela, 2016)
Tabla nº 6. Modelos MLG más comunes
| Tipo de análisis | Variable respuesta | Variable explicativa | Función vínculo | Distribución de errores |
|---|---|---|---|---|
| Regresión | Continua | Continua | Identidad | Normal |
| ANOVA | Continua | Factor | Identidad | Normal |
| Regresión | Continua | Continua | Identidad | Gamma |
| Regresión | Conteo | Continua | Recíproca | Poisson |
| Tabla de contingencia | Conteo | Factor | Logarítmica | Poisson |
| Proporciones | Proporción | Continua | Logarítmica | Binomial |
| Regresión logística | Binaria | Continua | Logit | Binomial |
| Análisis de superviviencia | Tiempo | Recíproca | Identidad | Exponencial |
Fuente: (Cayuela, 2016)
La estimación de los parámetros \(\beta\) se realiza por máximo verosimilitud, y los ajustes de \(\hat \mu_i\) se calculan como \(g^{-1}(x'_i\beta)\), una vez estimados los parámetros del vector \(\beta\).
La especificación de un MLG se realiza en tres partes:
La componente aleatoria correspondiente a la variable \(Y_i\) que sigue una distribución de la familia exponencial (normal, log-normal, poisson, gamma,…)
La componente sistemática, o predictor, que se denota \(\eta\) y corresponde al vector de \(n\) componentes \(\eta_i=\beta_0 + \beta_1X_{1i} + \beta_2X_{2i}+...+\beta_kX_{ki}\)
La función de ligadura (o función link \(g(•)\)) que relaciona la esperanza matemática de la variable con el predictor lineal \(\eta_i=g(\mu_i)\), que debe de ser monótona y diferenciable.
5.5.2 Modelos con variables cualitativas endógenas
5.5.2.1 Modelo probabilístico lineal
El modelo de probabilidad lineal se caracteriza por tener la variable endógena Y dicotómica o binaria, es decir toma el valor \(Y_i=1\) si un determinado suceso ocurre y el valor \(Y_i=0\) en caso contrario. Estos modelos están muy extendidos en el análisis estadístico pero encuentran una difícil aplicación en Economía debido a las dificultades de interpretación económica de los resultados que ofrecen este tipo de investigaciones. A este respecto, hay que considerar que estos modelos lo que realmente investigan es la probabilidad de que se dé una opción (valores \(Y_i=1\)) o no se dé (\(Y_i=0\)).
A pesar del carácter dicotómico de la variable endógena, el modelo de probabilidad lineal se especifica de la forma habitual, teniendo presente que las variables exógenas no son dicotómicas sino continuas:
\[ Y_i=\beta_0 + \beta_1 X_i + e_i\]
De acuerdo con esta expresión, y dado el hecho de que la variable endógena tome valores discretos (1 ó 0), el término de perturbación \(e_i\), puede tomar también dos valores únicamente:
Si \(Y_i=0 \Rightarrow e_i=-\beta_0 - \beta_1X_i\) con probabilidad \(p\).
Si \(Y_i=1 \Rightarrow e_i=1- \beta_0 - \beta_1X_i\) con probabilidad \((1-p)\).
Dado que la esperanza del término de error ha de ser nula \(E(e_i)=0\), entonces se demuestra que \(p=1-\beta_0 - \beta_1X_i\) y \((1-p) = \beta_0 + \beta_1X_i\), lo que permite evaluar la probabilidad de que la variable endógena tome el valor correspondiente:
\(Prob (Y_i=0) = Prob (e_i=-\beta_0 - \beta_1X_i=p=1-\beta_0 - \beta_1X_i\).
\(Prob (Y_i=1) = Prob (e_i=1-\beta_0 - \beta_1X_i=(1-p)=\beta_0 + \beta_1X_i\).
A su vez, la varianza del término de perturbación se calcularía a partir de:
\[Var(e_i)=p(1-p)=(1-\beta_0 - \beta_1X_i)(\beta_0 + \beta_1X_i)\]
Una problemática inherente a los estimadores MCO de estos modelos es la siguiente:
La perturbación aleatoria \(e_i\) no sigue una distribución Normal. Es sencillo observar este hecho ya que el carácter binario (1 ó 0) de la variable endógena afecta a la distribución de la perturbación, teniendo ésta una distribución Binomial. Este problema se atenúa cuando se utilizan tamaños de muestra (\(N\)) grandes en donde la distribución Binomial es susceptible de aproximarse a una Normal.
La perturbación aleatoria no tiene una varianza constante (es heteroscedástica), lo cual supone una falta de eficiencia. Para solucionarlo habría que realizar transformaciones que nos diesen una perturbación homocedástica; esta transformación consiste en multiplicar todas las variables por una cierta cantidad que elimine el problema de la heteroscedasticidad. Dicha cantidad es:
\[\frac{1}{\sqrt{(1-\hat\beta_0 - \hat\beta_1X_i)(\hat\beta_0 + \hat\beta_1X_i)}}\]
siendo \(\hat\beta_0\) y \(\hat\beta_1\) los estimaciones MCO del modelo.
- No obstante, el mayor problema que plantean estos modelos es que las predicciones realizadas sobre la variable endógena no siempre se encuentran en el intervalo [0,1], ya que pueden ser menores que cero y mayores que uno. Este problema tiene dos soluciones, una es tomar como valor cero todas las estimaciones de la variable endógena con valores negativos, y uno cuando estas resulten mayores que uno; la segunda solución es utilizar funciones de distribución que estén acotadas entre cero y uno como son la Logística y la Normal; de éstas se derivan los modelos Logit y Probit que pasamos a ver a continuación.
5.5.2.2 Modelo Logit
Planteamiento del modelo
El problema que presentan los modelos probabilísticos lineales en cuanto a la existencia de predicciones establecidas fuera de rango (negativas o mayores que uno), es debido a que utilizan una función de probabilidad que depende linealmente de las variables explicativas (\(X_i\)), que se resolverían acotando dicha distribución de probabilidad. El modelo Logit en concreto utiliza, para ello, la función de distribución logística:
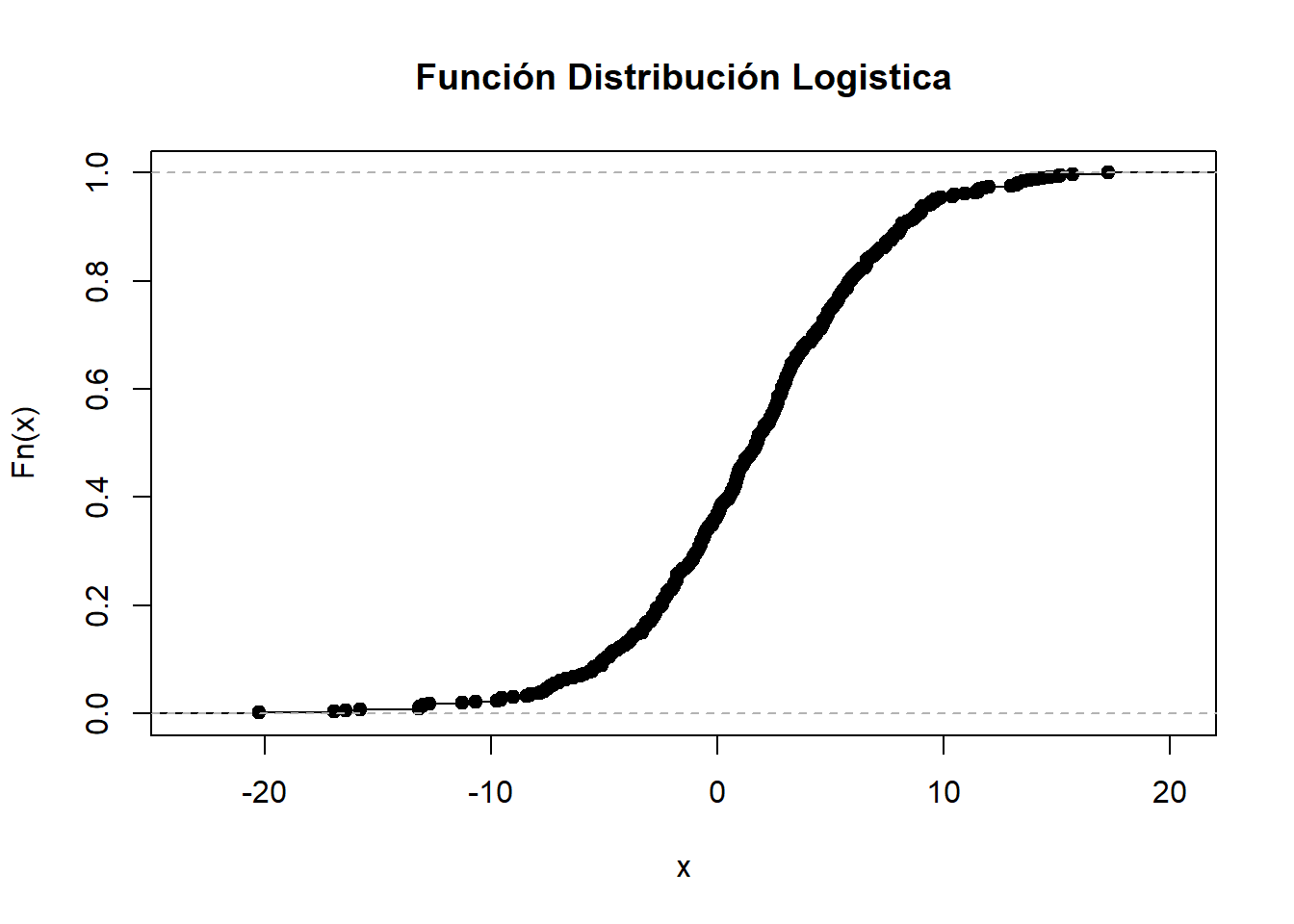
Debido a que la función de distribución logística no tiene forma lineal, el modelo Logit se estima de forma diferente, así en vez de minimizar las sumas de las diferencias al cuadrado entre los valores observados y los estimados por el modelo, el carácter no lineal de los modelos Logit requiere la utilización del método de Máxima Verosimilitud para ser estimado, maximizando la verosimilitud de que un suceso tenga lugar, aunque se podría estimar por MCO mediante una transformación logarítmica de los datos (Gujarati, 1997).
La probabilidad de que \(Y_i=0\) (\(p_i\)) se define ahora mediante la siguiente expresión:
\[p_i=\frac{1}{1+e^{-z_i}}\]
donde \(z_i=\beta_0 + \sum_j\beta_jX_{ji}\).
La probabilidad de que \(Y_i=1\) (\(1-p_i\)) sería:
\[1-p_i=\frac{1}{1+e^{z_i}}\]
En consecuencia, la razón entre ambas será igual a:
\[\frac{p_i}{1-p_i}=\frac{1+e^{z_i}}{1+e^{-z_i}}=e^{z_i}\]
Tomando el logaritmo de la expresión anterior se obtiene:
\[L_i=log(\frac{p_i}{1-p_i})=log(e^{z_i})=\beta_0 + \sum_{j=1}^k\beta_jX_{ji}+u_i\]
donde \(L_i\) es denominado Logit.
Los coeficientes \(\beta\) indican el cambio en el Logit causado por el cambio en una unidad en el valor de \(X_i\), mientras que los \(e^{\beta}\) definen el cambio en la razón de probabilidades \(\frac{p}{1-p}\) causado por el cambio en una unidad en el valor de \(X_i\). Si \(\beta\) es positivo,\(e^{\beta}\) será mayor que 1, es decir, \(\frac{p}{1-p}\) se incrementará; si \(\beta\) es negativo, \(e^{\beta}\) será menor que 1, y \(\frac{p}{1-p}\) disminuirá. Adicionalmente, puede demostrarse que el cambio en la probabilidad (\(p\)) causado por el cambio en una unidad en el valor de \(X_i\) es \(\beta(\frac{p}{1-p})\), es decir, depende no sólo del coeficiente, sino también del nivel de probabilidad a partir del cual se mide el cambio.
A la hora de estimar un modelo Logit, hay que tener presente que además de los valores \(X_i\), se necesitan los valores del Logit (\(L_i\)). Por otro lado, la estimación de los coeficientes del modelo ha de realizarse utilizando el método de Máxima Verosimilitud, a través del algoritmo de Newton-Raphson, es decir, eligiendo como estimadores de los coeficientes a aquellos que maximizan la función de verosimilitud, construida sobre la base de \(p=\frac{1}{1+e^{-z}}\). Pero si tenemos la posibilidad de agrupar los datos individuales, entonces podría estimarse el modelo por MCO.
Contrastes sobre los parámetros
Para evaluar si cada variable individualmente contribuye significativamente al modelo se utiliza el estadístico de Wald, definido como el cociente entre el valor del parámetro estimado al cuadrado dividido entre su varianza:
\[W(\beta_j) = \frac{\hat\beta_j^2}{Var(\hat\beta_j)}\]
Este estadístico, bajo la hipótesis nula \(H_0:\beta_j=0\), se distribuye como una Chi-Cuadrado con un grado de libertad. Una estimación adecuada de \(Var(\hat\beta_j)\) se puede obtener a través del inverso de la información de Fisher del parámetro.
Leemos base de datos de prestamos fallidos al consumo:
library(ISLR)
str(Default) ## 'data.frame': 10000 obs. of 4 variables:
## $ default: Factor w/ 2 levels "No","Yes": 1 1 1 1 1 1 1 1 1 1 ...
## $ student: Factor w/ 2 levels "No","Yes": 1 2 1 1 1 2 1 2 1 1 ...
## $ balance: num 730 817 1074 529 786 ...
## $ income : num 44362 12106 31767 35704 38463 ...La variable dependiente será default, \(Y=YES\) e \(Y=No\).
# Frecuencias variable respuesta
table(Default$default)##
## No Yes
## 9667 333# Frecuencias relativas variable respuesta
prop.table(table(Default$default))##
## No Yes
## 0.9667 0.0333Tenemos entonces tres variables predictivas: student, que caracteriza al consumidor como estudiante; balance, que es el saldo promedio de la tarjeta de crédito, e income que la renta del cliente.
Estimamos un modelo logit para explicar la admisión de alumnos, y evaluamos la tasa de acierto:
# Regresion logistica
mylogit=glm(default~student+balance+income,family="binomial",data=Default)
summary(mylogit) ##
## Call:
## glm(formula = default ~ student + balance + income, family = "binomial",
## data = Default)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.4691 -0.1418 -0.0557 -0.0203 3.7383
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -1.087e+01 4.923e-01 -22.080 < 2e-16 ***
## studentYes -6.468e-01 2.363e-01 -2.738 0.00619 **
## balance 5.737e-03 2.319e-04 24.738 < 2e-16 ***
## income 3.033e-06 8.203e-06 0.370 0.71152
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 2920.6 on 9999 degrees of freedom
## Residual deviance: 1571.5 on 9996 degrees of freedom
## AIC: 1579.5
##
## Number of Fisher Scoring iterations: 8summary(mylogit$fitted.values)## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.0000103 0.0002798 0.0019662 0.0333000 0.0132244 0.9776263# Tabla de clasificación Predichos * Observados
fit.pred=ifelse(mylogit$fitted.values>0.5,1,0)
table(fit.pred,Default$default)##
## fit.pred No Yes
## 0 9627 228
## 1 40 1055.5.2.3 Modelo Probit
Mientras que el modelo Logit utiliza la función de distribución logística para acotar la distribución de probabilidad en el modelo de probabilidad lineal, el modelo Probit utiliza la función de distribución Normal.
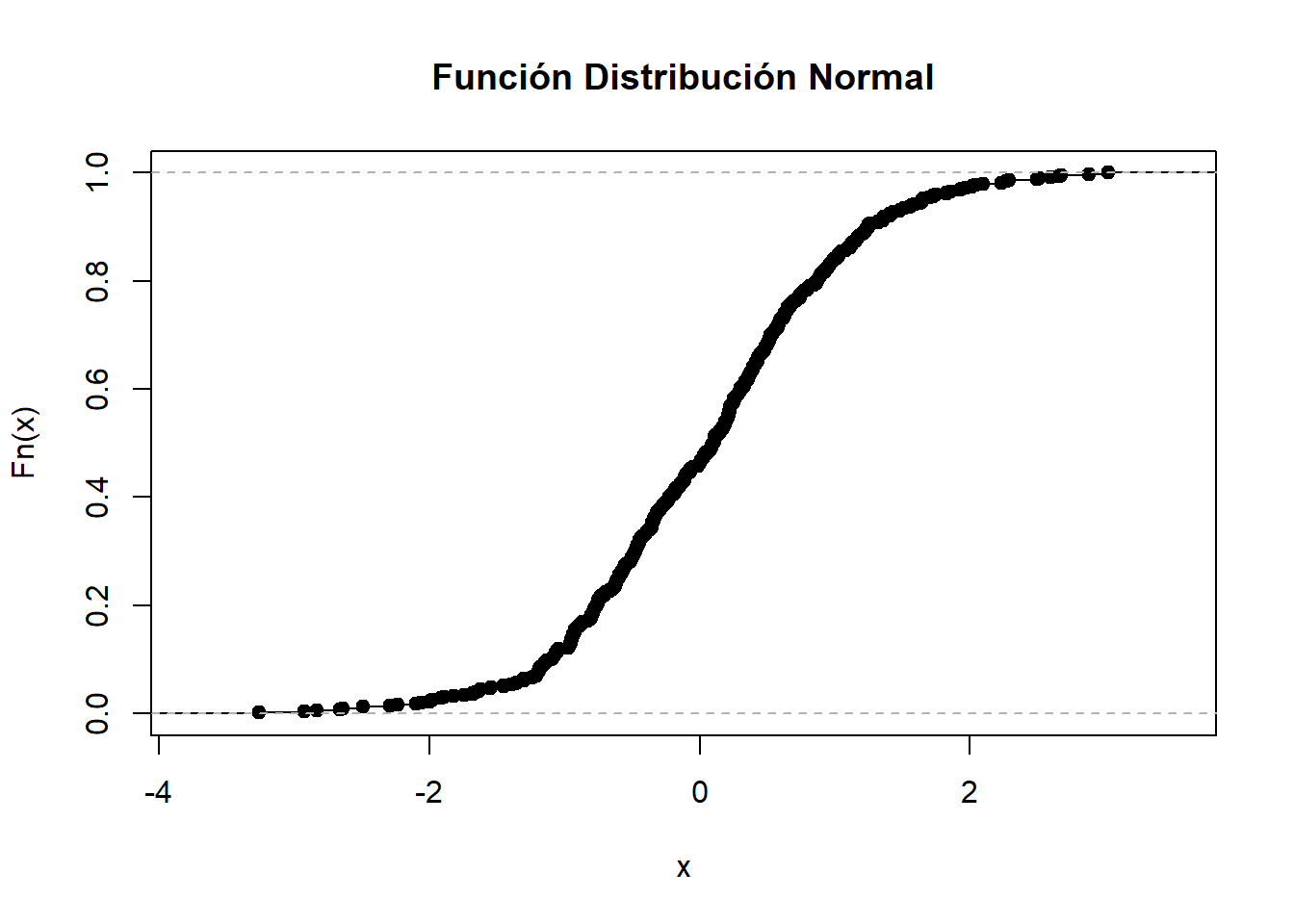
Las funciones de distribución normal y logística son muy semejantes; la diferencia principal es que la función de distribución normal se acerca más rápidamente a los ejes que la logística.
Para entender la filosofía del modelo Probit, vamos a suponer que existe una variable desconocida \(s\) que cumple lo siguiente:
Si \(I_i=\beta_0+\sum_j\beta_jX_{ji} \geq s\) entonces \(Y_i=1\)
Si \(I_i=\beta_0+\sum_j\beta_jX_{ji}<s\) entonces \(Y_i=0\)
Dado el supuesto de normalidad en un suceso, la probabilidad de que este sea menor o igual al valor (\(s\)), se calcula a partir de la función de distribución acumulada de una distribución Normal estandarizada, esto es, con esperanza cero y desviación típica uno.
\[pr(Y_i=1)=pr(I^*_i\geq I_i)=pr(\beta_0+\sum_{j=1}^k\beta_jX_{ji} \geq s)=F(\beta_0+\sum_{j=1}^k\beta_jX_{ji})\]
\(F\) es la FDA normal estandar:
\[F(I_i)=\frac{1}{\sqrt{2\pi}}\int_{- \infty}^{\beta_0+\sum_j\beta_jX_{ji}}{e^{-\frac{z^2}{2}d(z)}}\]
donde \(Z\) es la variable normal estandarizada \(Z \sim N(0,\sigma^2)\)
Lo anterior equivale a que la relación entre la endógena y las explicativas venga dada por la siguiente expresión:
\[y_i=F(I_i=\beta_0+\sum_{j=1}^k\beta_jX_{ji})+u_i => y_i=\frac{1}{\sqrt{2\pi}}\int_{- \infty}^{\beta_0+\sum_j\beta_jX_{ji}}{e^{-\frac{z^2}{2}d(z)}}+u_i\]
Ahora para obtener información sobre \(I_i\), se toma la inversa de \(F(I_i)\):
\[I_i=F^{-1}(I_i)=F^{-1}(P)=\beta_0+\sum_{j=1}^k\beta_jX_{ji}\]
Donde \(I_i\) es negativa siempre que \(p_i<0.5\); en la práctica se agrega el número 5 a \(I_i\) y a su resultado se le denomina Probit. Es decir, \(Probit=5+I_i\).
El término de la perturbación es no obstante heteroscedástico. Gujarati (1999) sugiere que se realice la transformación comentada en el apartado 1.3.2.1 (análisis de la varianza de un factor), para que el modelo transformado sea homocedástico.
Al igual que ocurre en el logit, si tenemos la posibilidad de agrupar los datos individuales, entonces podría estimarse el modelo por MCO.
La estimación en R del modelo probit estimado en el ejemplo anterior se programa:
# Regresion logistica
mylogit=glm(default~student+balance+income,family="binomial"(link=probit),data=Default)
summary(mylogit) ##
## Call:
## glm(formula = default ~ student + balance + income, family = binomial(link = probit),
## data = Default)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.2226 -0.1354 -0.0321 -0.0044 4.1254
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -5.475e+00 2.385e-01 -22.960 <2e-16 ***
## studentYes -2.960e-01 1.188e-01 -2.491 0.0127 *
## balance 2.821e-03 1.139e-04 24.774 <2e-16 ***
## income 2.101e-06 4.121e-06 0.510 0.6101
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 2920.6 on 9999 degrees of freedom
## Residual deviance: 1583.2 on 9996 degrees of freedom
## AIC: 1591.2
##
## Number of Fisher Scoring iterations: 8summary(mylogit$fitted.values)## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.0000000 0.0000183 0.0007723 0.0334850 0.0130713 0.9609657# Tabla de clasificación Predichos * Observados
fit.pred=ifelse(mylogit$fitted.values>0.5,1,0)
table(fit.pred,Default$default)##
## fit.pred No Yes
## 0 9639 238
## 1 28 955.5.2.4 Modelo Logit vs Modelo Probit
Desde un punto de vista teórico, si se plantean las covariables como directamente relacionadas con la probabilidad de éxito, entonces normalmente se elegiría la Regresión Logística, porque es el enlace canónico.
Si el resultado binario depende de una variable Gaussiana oculta parece razonable optar a priori, por razones teóricas. por el modelo Probit. Consideremos el siguiente ejemplo: se plantea la realización de un modelo de presión arterial alta como una función de algunas covariables. Parece razonable la asunción de que la presión arterial en sí misma se distribuya normalmente en la población, pero sin embargo, los médicos la dicotomizaron durante el estudio (es decir, sólo se registró como “alta” o “normal”).
Otra consideración es que tanto logit como probit son simétricos. Si se piensa que la probabilidad de éxito sube lentamente de cero, pero luego disminuye más rápidamente cuando se acerca a uno, sería preferible optar por una función vínculo tipo CLogLog, la cual se define como:
\[y=CLogLog(x)=ln(-ln(1-x)) => x=CLogLog^{-1}(y)=1-e^{-e^y}\]
Por último, cabe señalar que es improbable que el ajuste empírico del modelo a los datos sea de ayuda en la selección de una función vínculo, a menos que las formas de las funciones de enlace en cuestión difieran sustancialmente (cosa que no sucede en Logit y Probit). Por ejemplo, considere la siguiente simulación:
library(ggplot2)
set.seed(5000)
probMenor = vector(length=100)
devprobit = vector(length=100)
devlogit = vector(length=100)
# Genera un modelo probit en cada paso (100 modelos) con 1.000 datos
for(i in 1:100){
x = rnorm(1000)
y = rbinom(n=1000, size=1, prob=pnorm(x))
logitModel = glm(y~x, family=binomial(link="logit"))
probitModel = glm(y~x, family=binomial(link="probit"))
probMenor[i] = deviance(probitModel)<deviance(logitModel)
devprobit[i] = deviance(probitModel)
devlogit[i] = deviance(logitModel)
}
# Porcentaje de casos en que deviance Probit es menor a Deviance Logit (Probit mejor modelo)
sum(probMenor)/100## [1] 0.65# Gráfico de ambas devianzas
comparaPL <- cbind(devprobit, devlogit, probMenor)
comparaPLdf <- as.data.frame(comparaPL)
ggplot(comparaPLdf, aes(devprobit, devlogit)) + geom_point()+ geom_smooth()## `geom_smooth()` using method = 'loess' and formula 'y ~ x'
Incluso cuando sabemos que los datos han sido generados por un modelo probit, y tenemos 1000 puntos de datos, el modelo probit sólo da un mejor ajuste el 65% del tiempo, e incluso entonces, a menudo por sólo una cantidad trivial. Consideremos, por ejemplo, las 5 primeras iteraciones:
comparaPL[1:5,]## devprobit devlogit probMenor
## [1,] 1013.6699 1014.5126 1
## [2,] 1061.7100 1062.4248 1
## [3,] 965.5274 967.6012 1
## [4,] 1007.5088 1007.2238 0
## [5,] 917.3673 916.2442 0La razón de esto es simplemente que las funciones de enlace logit y probit producen salidas muy similares, al ser ambas prácticamente idénticas.
5.5.3 Modelo Tobit
Este modelo está diseñado para el caso en que los valores de la variable respuesta \(Y\) están acotados inferior y/o superiormente. Luego la expresión matemática de este modelo sería la siguiente:
\[y_i^*=X_i'\beta+u_i\] \[y_i=\begin{bmatrix} a \ \ si\ y_i^*\le a\\ y_i^* \ \ si\ a<y_i^*<b\\ b \ \ si\ y_i^*\geq b \end{bmatrix}\]
Un modelo de regresión lineal ignorando que hay observaciones censuradas ofrece una estimación sesgada.
Como ejemplo, pongamos el modelo propuesto por Tobin (1958), conocido como modelo estándar Tobit:
\[y_i=\begin{bmatrix} 0 \ \ si\ y_i^*< 0\\ y_i^* \ \ si\ y_i^*\ge 0 \end{bmatrix}\]
Como puede deducirse de su formulación, este modelo es un mixto entre un modelo Logit y uno de regresión lineal. Con la aplicación del esquema Logit, se deberá determinar las unidades iguales a 0 y las distintas de cero. En estas últimas es donde se aplicará la regresión lineal.
Implementamos a continuación un ejemplo en R. El fichero de datos de partida está en formato SPSS. La información que contiene son las puntuaciones de una prueba de lectura, otra de matemáticas, las relativas a la prueba de aptitud global y el tipo de programa de estudios cursado.
Queremos establecer la relación entre la infidelidad matrimonial y una serie de covariables :edad, años de matrimonio, religión, ocupación, y valoración de matrimonio (rating), utilizando la base de datos Affairs de la libreria AER, donde el numero de relaciones extramatrimoniales por años se censura en 4 .
library(AER)## Loading required package: sandwichlibrary(censReg)## Loading required package: maxLik## Loading required package: miscTools##
## Please cite the 'maxLik' package as:
## Henningsen, Arne and Toomet, Ott (2011). maxLik: A package for maximum likelihood estimation in R. Computational Statistics 26(3), 443-458. DOI 10.1007/s00180-010-0217-1.
##
## If you have questions, suggestions, or comments regarding the 'maxLik' package, please use a forum or 'tracker' at maxLik's R-Forge site:
## https://r-forge.r-project.org/projects/maxlik/##
## Please cite the 'censReg' package as:
## Henningsen, Arne (2017). censReg: Censored Regression (Tobit) Models. R package version 0.5. http://CRAN.R-Project.org/package=censReg.
##
## If you have questions, suggestions, or comments regarding the 'censReg' package, please use a forum or 'tracker' at the R-Forge site of the 'sampleSelection' project:
## https://r-forge.r-project.org/projects/sampleselection/library(foreign)
data( "Affairs", package = "AER" )
# Modelo de Regresión Censurada
estResult <- censReg( affairs ~ age + yearsmarried + religiousness +
occupation + rating, data = Affairs, right = 4 )## Warning in censReg(affairs ~ age + yearsmarried + religiousness +
## occupation + : at least one value of the endogenous variable is larger than
## the right limitsummary(estResult)##
## Call:
## censReg(formula = affairs ~ age + yearsmarried + religiousness +
## occupation + rating, right = 4, data = Affairs)
##
## Observations:
## Total Left-censored Uncensored Right-censored
## 601 451 70 80
##
## Coefficients:
## Estimate Std. error t value Pr(> t)
## (Intercept) 7.90098 2.80385 2.818 0.004834 **
## age -0.17760 0.07991 -2.223 0.026244 *
## yearsmarried 0.53230 0.14117 3.771 0.000163 ***
## religiousness -1.61634 0.42440 -3.809 0.000140 ***
## occupation 0.32419 0.25388 1.277 0.201624
## rating -2.20701 0.44983 -4.906 9.28e-07 ***
## logSigma 2.07232 0.11040 18.772 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Newton-Raphson maximisation, 7 iterations
## Return code 1: gradient close to zero
## Log-likelihood: -500.0428 on 7 DfComo ejercicio se propone contrastar los resultados de este modelo con los del modelo de regresión lineal.
5.6 Evaluación de modelos
Para medir la bondad del ajuste de un modelo MLG se disponen de varias opciones:
Cuando los datos están en forma binaria, una manera de detectar la falta de ajuste es realizando contrastes condicionales de razón de verosimilitudes entre modelos anidados.
Cuando los datos se pueden agrupar, se pueden comparar las frecuencias esperadas y observadas en cada combinación de variables explicativas mediante el contraste usual con el estadístico \(\chi^2\) de Pearson o con el \(G^2\) basado en la devianza. Estos estadísticos se distribuyen asintóticamente según una chi-cuadrado con grados de libertad igual al número de perfiles distintos menos el número de parámetros en el modelo, si el número de combinaciones o perfiles posibles de las variables explicativas no es elevado y se tienen suficiente número de frecuencias observadas y esperadas en cada combinación.
Otra opción es utilizar el estadístico de Hosmer-Lemeshow, que realiza una partición de los datos en base a las probabilidades predichas, y analiza posteriormente la tabla de contingencia resultante a través de su estadístico \(\chi^2\) asociado.
Otras aproximaciones calculan medidas tipo \(R^2\), o analizan el poder predictivo del modelo mediante la tasa de clasificaciones correctas o el análisis de curvas ROC.
Se describen a continuación los contrastes y métodos más utilizados y su aplicación en R. Vamos a comparar la bondad del ajuste de los modelos Logit y Probit sobre la pobreza desarrollados en los apartados 2.2.2 y 2.2.3.
5.6.1 Devianza. Estadístico G2 de Wilks de razón de verosimilitudes
La función de verosimilitud en un proceso binomial (modelos Logit y Probit) con \(y_i\) el número de éxitos en \(m_i\) i = 1 . . . n, (datos agrupados) y un conjunto de predictores \(X_i\)
\[y_i/X\leadsto Bin(m_i,\theta(X)_i) \]
es de la forma:
\[L=\prod_{i=1}^nP(Y_i=y_i/X)=\prod_{i=1}^n\binom{m_i}{y_i}{\theta(X)_i}^{y_i}(1-\theta(X)_i)^{m_i-y_i}\]
Donde \(\theta_X\) para el modelo logístico será:
\[\theta(X)_i=\frac{1}{1+e^{-(\beta_0 + \sum_j\beta_jX_{ji})}}\]
mientras que para el modelo Probit:
\[\theta(X)_i=\frac{1}{\sqrt{2\pi}}\int_{- \infty}^{\beta_0+\sum_j\beta_jX_{ji}}{e^{-\frac{z^2}{2}d(z)}}\]
estimando \(y_i\) a través de la expresión: \[\hat y_i=m_i·\hat \theta(X)_i\]
La log-verosimilitud, operando, será por tanto:
\[LogL = \sum_{i=1}^n [y_i·log(\frac {\theta(X)_i}{1-\theta(X)_i}) + m_i·log(1-\theta(X)_i) + log\binom{m_i}{y_i}]\]
Los modelos de regresión logística binaria, como se ha visto, son aquellos en los que la variable dependiente será una variable dicotómica que se codificará como 0 ó 1 (“ausencia” y “presencia”, respectivamente).
En este tipo de modelos más sencillos La log-verosimilitud se reduce a:
\[LogL = \sum_{i=1}^n [y_i·log(\frac {\theta(X)_i}{1-\theta(X)_i}) +(1-y_i)log(1-\theta(X)_i)]\]
La devianza es una medida del ajuste del modelo en relación al número de parámetros del mismo. Si un modelo explica lo mismo que otro, pero es más sencillo (menor número de párametros) es, por regla general, mejor modelo. Y esto es lo que va a indicar la devianza.
La devianza asociada a un modelo (\(M\)) se basa en comparar la log-verosimilitud bajo dicho modelo con la log-verosimilitud bajo el modelo saturado (\(S\)). El modelo saturado es aquel modelo que se ajusta perfectamente a los datos, es decir, las frecuencias de respuesta \(Y = 1\) estimadas por el modelo coinciden con las observadas, y tiene tantos parámetros libres/desconocidos como observaciones diferentes de las variables explicativas. En el modelo saturado, \(\theta_X\) se estima a través de la proporción observada de éxitos, es decir, \(\frac{y_i}{m_i}\).
La devianza se define entonces como dos veces la diferencia entre estas dos log-verosimilitudes. Operando se obtiene:
\[G^2(M)=2[log(L_S)-log(L_M)]=2\sum_{i=1}^n[y_i·log(\frac{y_i}{\hat y_i})+(m_i-y_i)·log(\frac{m_i-y_i}{m_i-\hat y_i})]\]
Bajo la hipótesis nula de que el modelo (\(M\)) es adecuado y los \(m_i\) son suficientemente grandes, \(G^2(M)\) se distribuye aproximadamente como una \(\chi^2_{n-k-1}\), dónde n es el número de datos o muestras binomiales (o número de combinaciones de valores de las k variables explicativas) y \(k+1\), por tanto, será el número de parámetros estimados (número de variabbles más término independiente). La diferencia entre la devianza de dos modelos anidados también sigue una distribución \(\chi^2\) y es la base de los procedimientos de selección de modelos.
En el caso de datos no agrupados (\(m_i=1\ \forall i\)), la devianza no es una medida de la bondad del ajuste del modelo \(M\), y tampoco sigue una distribución \(\chi^2\). No obstante, la diferencia entre las devianzas de dos modelos ajustados si se distribuye como una \(\chi^2\) y se puede utilizar para seleccionar el modelo con mejor ajuste.
Los residuos de la devianza, definidos como:
\[e^D_i=signo(y_i-\hat y_i)([2y_i·log(\frac{y_i}{\hat y_i})+(m_i-y_i)·log(\frac{m_i-y_i}{m_i-\hat y_i})])^{1/2}\]
bajo la hipótesis nula de que son igual a 0, tienen distribución asintótica de media 0 y varianza menor que 1.
El R también ofrece la posibilidad de calcular estos residuos estandarizados y studentizados, a través de las funciones rstandard y rstudent.
Partiendo de los modelos Logit y Probit anteriores (se ha incluido también el código de ejecución del modelo), la Devianza la podemos obtener a partir de la función deviance o del campo del modelo $deviance. Para obtener el p-valor de \(G^2(M)\) se ha de utilizar la función pchisq, obteniendo los grados de libertad a partir del campo $df.residual de cada modelo.
A partir de la función residuals, podemos obtener los residuos de la devianza, del siguiente modo:
resid.dev <- residuals(modelo, type = “deviance”)
donde modelo sería est3 o est4 en nuestro caso.
est1 <-glm(default~student+balance+income,family="binomial",data=Default)
est2 <- glm(default~student+balance+income,family="binomial"(link=probit),data=Default)
# Devianza
paste("G2 Logit: ", est1$deviance)## [1] "G2 Logit: 1571.54482757896"paste("G2 Probit: ", deviance(est2))## [1] "G2 Probit: 1583.21711271221"# Cálculo de p-valor para la Devianza (no existe función específica)
pD.logit <- 1 - pchisq(deviance(est1), est1$df.residual)
pD.probit <- 1 - pchisq(deviance(est2), est2$df.residual)
paste("p-valor Logit: ", pD.logit)## [1] "p-valor Logit: 1"paste("p-valor Probit: ", pD.probit)## [1] "p-valor Probit: 1"5.6.2 Estadístico \(\chi^2\) de Pearson
La formulación del estadístico es la siguiente:
\[\chi^2(M)=\sum_{i=1}^n \frac{(y_i-m_i\hat \theta(X)_i)^2}{m_i\hat \theta(X)_i(1-\hat \theta(X)_i)} \]
dónde \(\hat \theta(X)_i\) son las probabilidades estimadas en cada combinación de las variables predictoras y \(m_i\) el número de casos totales en cada combinación.
Este estadístico tiene, bajo la hipótesis nula de que el modelo es adecuado, la misma distribución asintótica que el estadístico de Wilks.
El estadístico X2 de Pearson se puede calcular fácilmente partiendo de los residuos de pearson (que también pueden ser estandarizados y studentizados), tal como veremos en el ejemplo siguiente.
# Estadístico chi-cuadrado
chi2.logit <- sum(residuals(est1, type = "pearson")^2)
chi2.probit <- sum(residuals(est2, type = "pearson")^2)
# p-valores
pchi.logit <- 1 - pchisq(chi2.logit, est1$df.residual)
pchi.probit <- 1 - pchisq(chi2.probit, est2$df.residual)
paste("Logit. Chi-cuadrado, p-valor: ", chi2.logit, " ", pchi.logit)## [1] "Logit. Chi-cuadrado, p-valor: 7004.05765469377 1"paste("Probit. Chi-cuadrado, p-valor: ", chi2.probit, " ", pchi.probit)## [1] "Probit. Chi-cuadrado, p-valor: 14592.0466854781 0"5.6.3 Criterio de información de Akaike (AIC) y Criterio de Información Bayesiano (BIC)
El estadístico AIC (Akaike Information Criterion), formulado por Akaike (1974):
\[AIC= p(k+1) - 2 log(L_M) \ \ \ \ \ \ con\ p=2 \ =>\] \[AIC=2(k+1)-2log(L_M)\]
donde \(log(L_M)\) es el valor en el óptimo del logaritmo de la función de verosimilitud del modelo \(M\) con \(k+1\) parámetros estimados. Siguiendo estos criterios, se seleccionará aquel modelo para el que se obtenga un AIC más bajo.
AIC no proporciona una prueba de un modelo en el sentido de probar una hipótesis nula, es decir AIC no puede decir nada acerca de la calidad del modelo en un sentido absoluto. Si todos los modelos candidatos encajan mal, AIC no dará ningún aviso de ello.
Este criterio penaliza los modelos con muchos parámetros frente a los modelos más parsimoniosos. Con p = log(n) se obtiene un AIC modificado al que se le denomina BIC (Criterio de Información Bayesiano).
\[BIC=log(n)·(k+1)-2log(L_M)\]
Estos estadísticos se usan en los procedimientos de selección de variables. La función R que implementa estos procedimientos se denomina stepAIC. Esta función permite variar el criterio de penalización eligiendo el valor de \(p\).
Se muestra a continuación cómo calcular en R estos estadísticos y cómo ejecutar el procedimiento de selección de variables.
# Modelo Logit
paste ("AIC: ",AIC(est1))## [1] "AIC: 1579.54482757896"paste ("BIC: ",BIC(est1))## [1] "BIC: 1608.38618906686"# Modelo Probit
paste ("AIC: ",AIC(est2))## [1] "AIC: 1591.21711271221"paste ("BIC: ",BIC(est2))## [1] "BIC: 1620.05847420011"Aplicamos ahora el procedimiento de selección de variables al modelo Logit utilizando la función stepAIC.
En el argumento scope indicamos el modelo más complejo (en nuestro caso \(est3\)) y el más simple (donde se ha especificado el modelo nulo). Para especificar las interacciones en las fórmulas se utiliza el símbolo “:”. Así, la expresión relativa a un modelo saturado con 3 factores y sus interacciones, sería la siguiente:
\[glm(y \sim x_1 + x_2 + x_3 + x_1:x_2 + x_1:x_3 + x_2:x_3 + x_1:x_2:x_3,\ data=dataframe,\ family=binomial)\]
Otra opción equivalente, pero más cómoda, sería utilizar el operador “*“, el cual incorpora todos los efectos involucrados junto con sus interacciones. Así, \(x_1*x_2 \equiv x_1+x_2+x_1:x_2\) o la expresión anterior, relativa a un modelo saturado con 3 factores, sería equivalente a:
\[glm(y \sim x_1*x_2*x_3,\ data=dataframe,\ family=binomial)\]
Con el argumento direction=”both” indicamos que el procedimiento sea stepwise. La función stepAIC comprueba en cada paso como varía el AIC con la inclusión o supresión de variables. El procedimiento termina cuando la inclusión / supresión de variables no aumenta / disminuye el valor del AIC. También de dispone de los parámetros “fordward” y “backward”. Por éltimo, por defecto se dispone del parámetro “k” con un valor por defecto de 2 (parámetro de penalización \(p\) en nuestra notación), es decir, estadístico AIC.
Dado que todas las variables con las que definimos el modelo eran significativas, el procedimiento incluye a todas ellas, obteniendo como resultado el propio modelo inicial.
modelo.stp <- stepAIC(est1, scope = list(upper = est1$formula, lower = ~1), direction = "both")## Start: AIC=1579.54
## default ~ student + balance + income
##
## Df Deviance AIC
## - income 1 1571.7 1577.7
## <none> 1571.5 1579.5
## - student 1 1579.0 1585.0
## - balance 1 2907.5 2913.5
##
## Step: AIC=1577.68
## default ~ student + balance
##
## Df Deviance AIC
## <none> 1571.7 1577.7
## + income 1 1571.5 1579.5
## - student 1 1596.5 1600.5
## - balance 1 2908.7 2912.7modelo.stp##
## Call: glm(formula = default ~ student + balance, family = "binomial",
## data = Default)
##
## Coefficients:
## (Intercept) studentYes balance
## -10.749496 -0.714878 0.005738
##
## Degrees of Freedom: 9999 Total (i.e. Null); 9997 Residual
## Null Deviance: 2921
## Residual Deviance: 1572 AIC: 15785.6.4 Prueba de Hosmer-Lemeshaw
El uso de los contrastes basados en los estadísticos \(\chi^2\) o \(G^2\) no resulta adecuado en el caso de datos no agrupados.
Un contraste alternativo es el propuesto por Hosmer y Lemeshow. Los importantes trabajos de Hosmer y Lemeshow (1980) concluyeron con la aportación de una serie de tests estadísticos para medir la bondad del ajuste basándose en la agrupación de las probabilidades estimadas por el modelo. Fueron fundamentalmente dos propuestas de estadísticos que llamaron \(C_g\) y \(H_g\).
La construcción del estadístico se basa en la agrupación de probabilidades estimadas bajo el modelo de regresión formando, en principio, diez grupos que se denominan deciles de riesgo y se calculan, para estos grupos, las frecuencias esperadas. Finalmente, se comparan las frecuencias de éxito observadas con las estimadas, mediante el estadístico usual \(\chi^2\) de Pearson.
Para la creación de los grupos hay que elegir los puntos de corte de las probabilidades estimadas. Existen dos formas:
Dividir las probabilidades estimadas en intervalos de igual amplitud.
Dividir los datos en base a los cuantiles de la distribución, obteniendo grupos más homogéneos.
En R se realiza a través de la función hoslem.test implementada en la librearía ResourceSelection. Los tests para nuestros modelos Logit Y Probit sugieren la revisión de los mismos, obteniendo no obstante un resultado ligeramente mejor en el modelo Logit.
library(ResourceSelection)## ResourceSelection 0.3-4 2019-01-08# Hosmer-Lemeshaw con g=10 grupos
# Modelo Logit
hl.est1 <- hoslem.test(est1$y, fitted(est1), g=10)
hl.est1##
## Hosmer and Lemeshow goodness of fit (GOF) test
##
## data: est1$y, fitted(est1)
## X-squared = 3.6823, df = 8, p-value = 0.8846# Modelo Probit
hl.est2 <- hoslem.test(est2$y, fitted(est2), g=10)
hl.est2##
## Hosmer and Lemeshow goodness of fit (GOF) test
##
## data: est2$y, fitted(est2)
## X-squared = 9.9481, df = 8, p-value = 0.26875.6.5 Medidas tipo \(R^2\)
En la regresión lineal por mínimos cuadrados tenemos una medida \(R^2\), que nos ofrece una medida de la bondad del ajuste comparando sumas de cuadrados la variabilidad explicada por el modelo y la total de la variable respuesta.
\[R^2 = 1 - \frac {\sum_i (y_i - \hat y_i)^2} {\sum_i (y_i - \bar y_i)^2}\]
Podríamos considerar esta medida en el caso de la regresión logística o el modelo Probit sustituyendo \(\hat y_i\) por \(m_i \hat p_i\), pero esta medida presenta varios inconvenientes:
Los estimadores máximo verosímiles no son los estimadores que maximizan esta medida.
No tiene en cuenta la dependencia de la varianza de Y respecto de p.
Para solventar estos problemas se han propuesto medidas alternativas, denominadas pseudo \(R^2\). Las principales son los \(pseudo\ R^2\) de McFadden, Cox-Snell y Nagelkerke.
Estas medidas están implementadas en la función nagelkerke de la librería rcompanion.
5.6.6 Pseudo R2 de McFadden
Esta medida (McFadden, 1974) compara la log-verosimilud del modelo ajustado con la log-verosimilud del modelo que sólo tiene el término constante
\[R^2_{MF}=1- \frac {log(L_M)} {log(L_{Null})}\]
Asemejándose a la expresión del \(R^2\) en la estimación por mínimos cuadrados, dónde \(log(L_{Null})\) sería la suma de cuadrados total y \(log(L_M)\) haría el papel de la suma de cuadrados de los errores. Este \(R^2\) informa de en cuánto se reduce la devianza de los datos al ajustar el modelo.
Su rango teórico es el intervalo [0, 1], si bien muy raramente su valor se aproxima a 1. Suele considerarse una buena calidad del ajuste valores comprendidos en [0,2, 0,4] y excelente para valores superiores.
A partir del modelo, podemos calcularlo del siguiente modo.
estnull <- glm(default~1,family="binomial",data=Default)
R2MFLogit <- 1 - logLik(est1)/logLik(estnull)
R2MFProbit <- 1 - logLik(est2)/logLik(estnull)
R2MFLogit## 'log Lik.' 0.4619194 (df=4)R2MFProbit## 'log Lik.' 0.457923 (df=4)5.6.7 Pseudo R2 de Cox-Snell
Este coeficiente (Cox & Snell, 1989) se define como:
\[R^2_{CS}=1- \frac {(\sqrt[n]{L_{Null}})^2} {(\sqrt[n]{L_M})^2} = 1 - exp(\frac {log(L_M)-log(L_{Null})}{n})\]
siendo \(L_{Null}=exp(-log(L_{Null})/2)\) y \(L_M=exp(-log(L_M)/2))\).
El rango de valores de este coeficiente es \([0, (\sqrt[n]{L_M})^2]\) lo que le hace poco interpretable al depender de \(L_M\).
5.6.8 Pseudo R2 de Nagelkerke
El pseudo \(R^2\) de Nagelkerke (Nagelkerke, 1991) corrige el problema del límite superior del coeficiente estandarizando el anterior, es decir:
\[R^2_{N}= \frac {R^2_{CS}} {1-(\sqrt[n]{L_M})^2}\]
tomando valores comprendidos en el intervalo [0, 1], por lo que puede interpretarse de igual modo que el coeficiente de determinación de la regresión lineal clásica, aunque es más difícil que alcance valores próximos a 1.
Se muestra a continuación el cálculo de los tres coeficientes en el programa R a través de la función nagelkerke.
library(rcompanion)
nagelkerke(est1, restrictNobs = TRUE)## $Models
##
## Model: "glm, default ~ student + balance + income, binomial, Default"
## Null: "glm, default ~ 1, binomial, fit$model"
##
## $Pseudo.R.squared.for.model.vs.null
## Pseudo.R.squared
## McFadden 0.461919
## Cox and Snell (ML) 0.126206
## Nagelkerke (Cragg and Uhler) 0.498286
##
## $Likelihood.ratio.test
## Df.diff LogLik.diff Chisq p.value
## -3 -674.55 1349.1 3.2575e-292
##
## $Number.of.observations
##
## Model: 10000
## Null: 10000
##
## $Messages
## [1] "Note: For models fit with REML, these statistics are based on refitting with ML"
##
## $Warnings
## [1] "None"nagelkerke(est2, restrictNobs = TRUE)## $Models
##
## Model: "glm, default ~ student + balance + income, binomial(link = probit), Default"
## Null: "glm, default ~ 1, binomial(link = probit), fit$model"
##
## $Pseudo.R.squared.for.model.vs.null
## Pseudo.R.squared
## McFadden 0.457923
## Cox and Snell (ML) 0.125185
## Nagelkerke (Cragg and Uhler) 0.494257
##
## $Likelihood.ratio.test
## Df.diff LogLik.diff Chisq p.value
## -3 -668.72 1337.4 1.1107e-289
##
## $Number.of.observations
##
## Model: 10000
## Null: 10000
##
## $Messages
## [1] "Note: For models fit with REML, these statistics are based on refitting with ML"
##
## $Warnings
## [1] "None"5.7 Regresión bayesiana
5.7.1 Introducción
La aplicación del modelo bayesiano en modelos de regresión, ya sea estándar, logística, Poisson, etc., sigue el esquema general de la estadística bayesiana:
Definir la distribución a priori correspondiente para los parámetros.
Determinar la verosimilitud de los datos.
Aplicar el teorema de Bayes para actualizar la distribución a priori en forma de distribución a posteriori.
Desde el punto de vista computacional, se tienen bastantes opciones de aplicación. El programa más generalista que se puede aplicar es WinBugs, como programa original, o sus sucesores: OpenBugs, Jags o Stan. Se disponen de librerías específicas para trabajar en entorno R (BRugs, R2WinBUGS, R2OpenBUGS, MCMCpack)
5.7.2 El teorema de Bayes
Empezamos primeramente definiendo un par de conceptos clave:
Experimento aleatorio: aquel cuyo resultado no es predecible con exactitud, aún repitiéndolo en igualdad de condiciones.
Espacio muestral: el conjunto de todos los posibles resultados de un experimento aleatorio. Se simboliza por \(U\).
Evento: uno cualquiera de los posibles resultados de un experimento aleatorio. Se simbolizan con letras mayúsculas: \(A, B, C,...\).
Teniendo en cuenta lo anterior, los tres axiomas de Kolmogorov establecen que:
Axioma 1. Para todo evento \(A \in U\), \(P(A) \geq 0\).
Axioma 2. \(P(U) = 1\).
Axioma 3. Si \(A, B \in U\) son dos eventos mutuamente excluyentes o disjuntos, entonces \(P(A \cup B) = P(A) + P(B)\).
A partir de estos axiomas, tenemos las siguientes reglas de operación con probabilidades:
\(P(\emptyset) = 0\). El evento vacío es el evento resultante de la intersección de dos eventos excluyentes o disjuntos.
\(P(\bar A) = 1 - P(A)\), siendo \(\bar A\) el complemento del evento \(A\).
\(P(A \cup B) = P(A) + P(B) - P(A \cap B)\).
Si ambos eventos fueran independientes, entonces: \(P(A \cup B) = P(A) + P(B)\).
Para dos eventos, \(A\) y \(B\), la probabilidad marginal de \(A\) viene dada por: \(P(A) = P(A \cap B)+P(A \cap \bar B)\), es decir, su probabilidad es la suma de las probabilidades de los dos eventos disjuntos posibles.
La probabilidad de \(B\) condicionada a \(A\) se expresa como: \[P(B/A) = \frac {P(A \cap B)} {P(A)}\]es decir, la probabilidad condicionada de \(B\), una vez sabido que se ha dado el evento \(A\), es proporcional a la probabilidad conjunta de ambos eventos, ponderada por la probabilidad del evento condicionante. El evento \(B\) no es observable, \(A\) es el evento observable y pasa a ser el espacio muestral reducido de este experimento.
Cambiando el rol de los eventos, tenemos:
\[P(A/B) = \frac {P(A \cap B)} {P(B)} \Rightarrow P(A \cap B) = P(B)*P(A/B)\] o, de igual modo:
\[P(A \cap \bar B) = P(B)*P(A/\bar B)\] lo cual se conoce como regla de la multiplicación.
- Esta última regla se conoce como regla de la probabilidad total. Dados los eventos \(B_1, B_2,...,B_n\) que particionan el espacio muestral \(U\), y dado el evento \(A\), entonces:
\[P(A) = \sum_{i=1}^n P(B_i \cap A)\]
Utilizando la Regla de la multiplicación, obtenemos:
\[P(A) = \sum_{i=1}^n P(B_i) * P(A/B_i)\] Si partimos de la expresión:
\[P(B_i/A) = \frac {P(A \cap B_i)} {P(A)}\] y utilizamos la regla de la multiplicación para evaluar el numerador y la regla de la probabilidad total para evaluar el denominador, llegamos a:
\[P(B_i/A) = \frac {P(B_i) * P(A/B_i)} {\sum_{i=1}^n P(B_i) * P(A/B_i)}\] que representa la formulación del Teorema de Bayes, publicada en 1763. En esta formulación, los \(B_i\) son eventos no observables, siendo \(A\) el evento observable. Las probabilidades \(P(B_i)\) son establecidas a priori. La presencia de estas probabilidades a priori ha sido la principal crítica a la aplicación del teorema.
5.7.3 Proceso de inferencia
Aunque esta teoría fue seguida inicialmemnte con gran entusiasmo por Laplace y otros notables matemáticos, cayó en desuso debido al problema del establecimiento de las probabilidades a priori.
En la segunda mitad del siglo XX, con el enfoque frecuentista en pleno auge, surge el nuevo movimiento bayesiano, con nombres como Jimmy Savage o Dennis Lindley, si bien la realización práctica de estos modelos tendría que esperar hasta las últimas décadas de dicho siglo, gracias a las modernas capacidades de cálculo que han ido incorporando los ordenadores actuales.
El enfoque bayesiano ha sido recientemente adoptado con gran éxito por los estadísticos y científicos de datos, y se configura como una opción muy interesante de cara al futuro de la modelización.
Bajo la inferencia bayesiana, las hipótesis científicas se expresan a partir de distribuciones de probabilidad formuladas a partir de la observación de los datos. Estas distribuciones dependen de magnitudes desconocidas denominadas parámetros, \(\theta\), asignando a priori una distribución, \(p(\theta)\).
La información que contienen los datos en relación a los parámetros es expresada en la función de verosimilitud, que es proporcional a la distribución de los datos observados, dados los parámetros, y que se representa como \(p(y/\theta)\). Esta información es utilizada para actualizar la distribución a priori \(p(\theta)\).
El teorema de Bayes establece como actualizar la distribución a posteriori de \(p(\theta)\). En este sentido, la distribución a posteriori es proporcional a la distribución a priori multiplicada por la función de verosimilitud, es decir:
\[P(\theta/y) = \frac {P(\theta) * P(y/\theta)} {\int P(\theta) * P(y/\theta)d\theta}\] o, alternativamente:
\[posterior \propto prior \times verosimilitud\]
Esta distribución a posteriori es evaluable, si bien puede ser muy complicada de obtener.
Los procedimientos de cálculo utilizados para la estimación de los modelos se engloban bajo las siglas MCMC (Markov Chain Monte Carlo), y son métodos de integración que utilizan Cadenas de Markov. La integración Monte Carlo genera muestras de gran tamaño de la distribución de probabilidad de interés, a partir de las cuales evalúa los momentos de la distribución de probabilidad a posteriori.
Para construir estas cadenas se utiliza el procedimiento desarrollado por Metropolis et al. (1953) y Hastings (1970). Las propuestas desarrolladas posteriormente son casos especiales de éste.
Así, partiendo de la distribución a posteriori, podemos analizar cualquier característica (media, momentos, cuantiles, percentiles, zonas de mayor probabilidad,…), simplemente considerando su esperanza:
\[E(f(\theta/y)) = \frac {\int f(\theta )P(\theta) * P(y/\theta)d(\theta)} {\int P(\theta) * P(y/\theta)d\theta}\] Generalizando, dado un vector \(X\) con distribución de probabilidad \(\pi(·)\), se trata de evaluar el valor esperado para una función \(f(·)\) de interés, es decir:
\[E(f(X)) = \frac {\int f(x)\pi (x)dx} {\int \pi (x) dx}\]
Con la integración de Monte Carlo, este valor se estima a través del promedio de las muestras realizadas, {\(X_t; t=1, 2, ...,n\)}, obtenidas de \(\pi(·)\), es decir:
\[E(f(X)) = \frac 1 n \sum_{t=1}^n f(x_t)\] Si las muestras \(X_t\) son independientes, la ley de los grandes números asegura la precisión que se desee, simplemente aumentando el tamaño de la muestra, \(n\). Estas muestras no han de ser necesariamente independientes, lo que sí se requiere es que provengan de la distribución \(\pi(·)\), y la forma de hacerlo es a partir de Cadenas de Markov que tengan a \(\pi(·)\) como distribución estacionaria de base, lo que se logra mediante los procedimientos de MCMC.
5.7.4 Cadenas de Markov
Una Cadena de Markov es una secuencia de variables aleatorias, \(X_0, X_1, X_2,...\) tal que en cada momento \(t\ge 0\), el siguiente estado \(X_{t+1}\) es muestreado a partir de la distribución \(P(X_{t+1}/X_t)\), es decir, sólo se tiene en cuenta el estado actual de la cadena, obviando su historia \(X_0, X_1, X_2,...,X_{t-1}\). La distribución \(P(·/·)\) se supone independiente de \(t\), y se conoce como el kernel de transición de la cadena.
Bajo estas condiciones, \(X_t\) depende directamente de \(X_0\), ahora bien, ¿cómo afecta \(X_0\) a \(X_t\)? Tendremos que analizar la distribución \(P^t(X_t/X_0)\). En condiciones generales de regularidad, la cadena irá olvidando su estado inicial, y \(P^t(·/X_0)\) terminará convergiendo a una distribución estacionaria o invariante, independiente de \(t\) o de \(X_0\). Sea \(\phi(·)\) dicha distribución.
Por tanto, al aumentar \(t\), los valores de la muestra \(X_t\) irán asemejándose cada vez más a los valores muestrales de \(\phi(·)\). Así, tras un largo periodo de adaptación (pongamos m repeticiones), conocido como burn-in, los valores \(X_{m+1}, X_{m+2},..., X_n\), se aproximarán a los de la distribución \(\phi(·)\). Podemos estimar, pues, la \(E(f(X))\) como:
\[E(f(X)) = \bar f= \frac 1 {n-m} \sum_{t=m+1}^n f(x_t)\]
Esta expresión se conoce como media ergódica o promedio ergódico, y muestra como una Cadena de Markov puede ser utilizada para estimar \(E(f(X))\), tomando como base la distribución estacionaria \(\phi(·)\). La cuestión será, pues, construir una Cadena de Markov cuya distribución estacionaria \(\phi(·)\) se corresponda con la distribución de interés \(\pi(·)\). Para lograrlo, se utiliza el procedimiento debido a Hastings (1970), que es una generalización de Metropolis et al. (1953). Como ya se ha comentado, un caso especial de este procedimiento Metropolis-Hastings es el denominado Gibbs Sampler.
En estadística bayesiana, los resultados muestran resúmenes de la distribución a posteriori \(\pi(·)\) (medias, desviaciones estándar, cuantiles, correlaciones, regiones de mayor probabilidad, etc.).
5.7.5 Regresión lineal bayesiana
En un modelo de regresión simple, es decir, \(y_i = \alpha + \beta x_i + \epsilon_i\), se necesita definir la distribución conjunta a priori sobre \(\alpha\), \(\beta\) y \(\sigma\), es decir, intercept, pendiente de la recta y error.
Se especifican como distribuciones a priori independientes (cuando se multiplican producen una distribución conjunta a priori). Si suponemos:
\[\alpha \sim N(-\infty, \infty) \ \ \ \ \ \ \ \ \beta \sim N(-\infty, \infty) \ \ \ \ \ \ \ \ log(\sigma) \sim N(-\infty, \infty)\] se pueden aproximar los resultados de la regresión clásica. Se necesita considerar el logaritmo de la desviación estándar, dado que la varianza debe ser positiva. La distribución a priori es equivalente a una densidad que es proporcional a \(\frac 1 {\sigma^2}\).
Verosimilitud
Dado que los residuos se distribuyen como una normal, \(\epsilon_i \sim N(0,\sigma)\), la esperanza de la regresión será:
\[E(y) = \alpha + \beta x\] y, por tanto, se puede deducir que: \(y \sim N(\alpha+\beta x, \sigma)\).
La función de verosimilitud será:
\[f(y_i)= \frac 1 {\sqrt{2\pi}\sigma} exp[\frac 1 {\sigma^2}(y_i - (\alpha + \beta x_i))^2]\] y la conjunta, \(\prod_{i=1}^nf(y_i)\), será por tanto una distribución normal multivariante de dimensión \(n\).
Las distribuciones a posteriori de \(\alpha\) y de \(\beta\) son t-Student con n-2 grados de libertad, y \(\sigma^2\) se distribuye como una chi cuadrado inversa.
5.7.5.1 Inferencia con R. Markov Chain Monte Carlo (MCMC) Package
Por su facilidad en el uso, hemos optado por trabajar con el paquete MCMCpack.
La función utilizada para realizar la regresión lineal es MCMCregress. Esta función genera una muestra de la distribución a posteriori de un modelo de regresión lineal con errores gaussianos usando el muestreo de Gibbs (suponiendo una distribución a priori normal multivariante en el vector beta, y una Gamma inversa en la varianza del error condicional). Es decir, partiendo del modelo:
\[y_i=x_i'\beta + \epsilon_i\ \ \ \ \ \ con \ \ \ \ \ \epsilon_i \sim N(0, \sigma^2)\]
y asumiendo:
\[\beta \sim N(b_0,B_0^{-1})\ \ \ \ \ \ y \ \ \ \ \ \sigma^{-2} \sim Gamma(c_0/2,d_0/2)\] donde \(\beta\) y \(\sigma^{-2}\) se suponen a proiri independientes.
La sintaxis de la función y sus valores predeterminados es la siguiente:
| MCMCregress(formula, data = NULL, burnin = 1000, mcmc = 10000, thin = 1, verbose = 0, seed = NA, beta.start = NA, b0 = 0, B0 = 0, c0 = 0.001, d0 = 0.001, sigma.mu = NA, sigma.var = NA, marginal.likelihood = c(“none”, “Laplace”, “Chib95”), …) |
Como vemos, el burnin por defecto tiene un valor de 1.000, y se generan después una muestra de la distribución a posteriori de 10.000, devolviéndose como un objeto MCMC, que puede analizarse posteriormente con las funciones proporcionadas en el paquete coda.
Veamos un ejemplo con la base de datos mtcars, donde predecimos el consumo (millas por galón) en función del peso de los vehículos. Como puede observarse, los resultados son muy similares a la regresión clásica.
library ( MCMCpack )## Loading required package: coda## ##
## ## Markov Chain Monte Carlo Package (MCMCpack)## ## Copyright (C) 2003-2019 Andrew D. Martin, Kevin M. Quinn, and Jong Hee Park## ##
## ## Support provided by the U.S. National Science Foundation## ## (Grants SES-0350646 and SES-0350613)
## ##DatosRB = list ( X = mtcars$wt , Y = mtcars$mpg )
# Modelo clásico. Regresión por Mínimos cuadrados ordinarios
modeloRMCO = lm ( Y∼X , data = DatosRB )
summary(modeloRMCO)##
## Call:
## lm(formula = Y ~ X, data = DatosRB)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.5432 -2.3647 -0.1252 1.4096 6.8727
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 37.2851 1.8776 19.858 < 2e-16 ***
## X -5.3445 0.5591 -9.559 1.29e-10 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3.046 on 30 degrees of freedom
## Multiple R-squared: 0.7528, Adjusted R-squared: 0.7446
## F-statistic: 91.38 on 1 and 30 DF, p-value: 1.294e-10# Modelo bayesiano
modeloRB = MCMCregress ( Y∼X , data = DatosRB )
summary(modeloRB)##
## Iterations = 1001:11000
## Thinning interval = 1
## Number of chains = 1
## Sample size per chain = 10000
##
## 1. Empirical mean and standard deviation for each variable,
## plus standard error of the mean:
##
## Mean SD Naive SE Time-series SE
## (Intercept) 37.308 1.9495 0.019495 0.019093
## X -5.351 0.5816 0.005816 0.005816
## sigma2 9.967 2.7838 0.027838 0.030019
##
## 2. Quantiles for each variable:
##
## 2.5% 25% 50% 75% 97.5%
## (Intercept) 33.514 36.045 37.325 38.566 41.159
## X -6.519 -5.725 -5.352 -4.978 -4.209
## sigma2 5.928 7.996 9.503 11.413 16.543plot(modeloRB)
5.7.6 Modelos lineales generalizados
Se pueden generalizar los modelos de regresión habituales para modelizar relaciones entre variables discretas y también para modelos de clasificaciónn. Se trataría simplemente de definir una función link que relacione la media de los datos y el modelo lineal.
Es decir, partiendo de \(E(y) = \mu\), se define una función link tal que aplicada al parámetro \(\mu\):
\[g(\mu) = \theta = X\beta\]
lo cual implica:
\[\mu = g^{-1}(X\beta) = E(Y)\]
Se muestran a continuación, los principales ejemplos de modelos y funciones link:

El paquete MCMCpack dispone de diversas funciones para ejecutar estos modelos, como por ejemplo MCMClogit, MCMCprobit, MCMCtobit, MCMCpoisson, etc.
Veamos ahora los resultados de la aplicación de un modelo Logit bayesiano, con diferentes opciones de configuración iniciales.
La función utilizada tiene la siguiente sintaxis:
| MCMClogit(formula, data = NULL, burnin = 1000, mcmc = 10000, thin = 1, tune = 1.1, verbose = 0, seed = NA, beta.start = NA, b0 = 0, B0 = 0, user.prior.density = NULL, logfun = TRUE, marginal.likelihood = c(“none”, “Laplace”), …) |
El ejemplo está basado en el dataset birthwt, que contiene 189 observaciones y 10 variables. Los datos fueron tomados en el Baystate Medical Center, Springfield, Massachusetts durante 1986.
Las variables contienen la siguiente información:
| Nombre | Valor |
|---|---|
| low | Indicador de peso al nacer menor a 2,5 kg. |
| age | Edad de la madre en años |
| lwt | Peso de la madre en libras en el último período menstrual |
| race | Raza de la madre (1 = blanca, 2 = negra, 3 = otra) |
| smoke | Fumaba durante el embarazo |
| ptl | Número de partos prematuros previos |
| ht | Historia de hipertensión |
| ui | Presencia de irritabilidad uterina |
| ftv | Número de visitas al médico durante el primer trimestre |
| bwt | Peso al nacer en gramos |
Nos planteamos analizar la influencia de la edad de la madre, la raza y el hábito de fumar sobre el indicador de peso al nacer menor a 2,5 kg.
# Con distribución a priori impropia
data(birthwt)
posterior <- MCMClogit(low~age+as.factor(race)+smoke, data=birthwt)
plot(posterior)
summary(posterior)##
## Iterations = 1001:11000
## Thinning interval = 1
## Number of chains = 1
## Sample size per chain = 10000
##
## 1. Empirical mean and standard deviation for each variable,
## plus standard error of the mean:
##
## Mean SD Naive SE Time-series SE
## (Intercept) -0.98190 0.9109 0.009109 0.038909
## age -0.03812 0.0341 0.000341 0.001403
## as.factor(race)2 1.03851 0.5002 0.005002 0.020253
## as.factor(race)3 1.08242 0.4185 0.004185 0.017995
## smoke 1.12993 0.3922 0.003922 0.016334
##
## 2. Quantiles for each variable:
##
## 2.5% 25% 50% 75% 97.5%
## (Intercept) -2.72363 -1.60072 -1.00723 -0.31925 0.87166
## age -0.11025 -0.06131 -0.03675 -0.01468 0.02623
## as.factor(race)2 0.06971 0.69756 1.03927 1.38325 2.01703
## as.factor(race)3 0.30514 0.79286 1.06132 1.36351 1.94954
## smoke 0.38584 0.85418 1.14129 1.39460 1.88826# Con una distribución a priori normal multivariante
data(birthwt)
posterior <- MCMClogit(low~age+as.factor(race)+smoke, b0=0, B0=.001, data=birthwt)
plot(posterior)
summary(posterior)##
## Iterations = 1001:11000
## Thinning interval = 1
## Number of chains = 1
## Sample size per chain = 10000
##
## 1. Empirical mean and standard deviation for each variable,
## plus standard error of the mean:
##
## Mean SD Naive SE Time-series SE
## (Intercept) -1.04275 0.91241 0.0091241 0.038374
## age -0.03591 0.03414 0.0003414 0.001384
## as.factor(race)2 1.03163 0.49963 0.0049963 0.020275
## as.factor(race)3 1.08843 0.41973 0.0041973 0.017280
## smoke 1.13528 0.38761 0.0038761 0.015654
##
## 2. Quantiles for each variable:
##
## 2.5% 25% 50% 75% 97.5%
## (Intercept) -2.7988 -1.69138 -1.06366 -0.40923 0.79022
## age -0.1074 -0.05856 -0.03523 -0.01299 0.03033
## as.factor(race)2 0.0360 0.69870 1.02284 1.37216 2.01679
## as.factor(race)3 0.2908 0.80183 1.08516 1.36941 1.92019
## smoke 0.3795 0.87363 1.13227 1.40031 1.92418# Con una distribución de Cauchy independiente definida por el usuario
logpriorfun <- function(beta){
sum(dcauchy(beta, log=TRUE))
}
posterior <- MCMClogit(low~age+as.factor(race)+smoke, data=birthwt, user.prior.density=logpriorfun, logfun=TRUE)##
##
## @@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@
## The Metropolis acceptance rate was 0.24009
## @@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@plot(posterior)
summary(posterior)##
## Iterations = 1001:11000
## Thinning interval = 1
## Number of chains = 1
## Sample size per chain = 10000
##
## 1. Empirical mean and standard deviation for each variable,
## plus standard error of the mean:
##
## Mean SD Naive SE Time-series SE
## (Intercept) -0.40814 0.6527 0.006527 0.0232254
## age -0.04996 0.0263 0.000263 0.0009499
## as.factor(race)2 0.68141 0.4311 0.004311 0.0177350
## as.factor(race)3 0.77314 0.3677 0.003677 0.0151453
## smoke 0.88192 0.3540 0.003540 0.0149930
##
## 2. Quantiles for each variable:
##
## 2.5% 25% 50% 75% 97.5%
## (Intercept) -1.77381 -0.8203 -0.38388 0.04041 0.79752
## age -0.09825 -0.0683 -0.05058 -0.03306 0.00463
## as.factor(race)2 -0.16551 0.3842 0.68357 0.96837 1.55685
## as.factor(race)3 0.07497 0.5236 0.76898 1.01143 1.52065
## smoke 0.20889 0.6377 0.86394 1.12221 1.59196# Con una distribución de Cauchy independiente definida por el usuario con argumentos adicionales
logpriorfun <- function(beta, location, scale){
sum(dcauchy(beta, location, scale, log=TRUE))
}
posterior <- MCMClogit(low~age+as.factor(race)+smoke, data=birthwt, user.prior.density=logpriorfun, logfun=TRUE, location=0, scale=10)##
##
## @@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@
## The Metropolis acceptance rate was 0.27836
## @@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@plot(posterior)
summary(posterior)##
## Iterations = 1001:11000
## Thinning interval = 1
## Number of chains = 1
## Sample size per chain = 10000
##
## 1. Empirical mean and standard deviation for each variable,
## plus standard error of the mean:
##
## Mean SD Naive SE Time-series SE
## (Intercept) -0.98411 0.9119 0.009119 0.036997
## age -0.03732 0.0344 0.000344 0.001358
## as.factor(race)2 1.01322 0.5005 0.005005 0.020335
## as.factor(race)3 1.06728 0.4063 0.004063 0.016361
## smoke 1.13741 0.3834 0.003834 0.015338
##
## 2. Quantiles for each variable:
##
## 2.5% 25% 50% 75% 97.5%
## (Intercept) -2.78270 -1.58588 -0.99597 -0.35814 0.74844
## age -0.10305 -0.06047 -0.03663 -0.01391 0.02713
## as.factor(race)2 0.01562 0.68500 1.02547 1.34953 1.95738
## as.factor(race)3 0.26263 0.79343 1.05667 1.34001 1.87670
## smoke 0.39856 0.87754 1.13049 1.39627 1.89643