4 Extensiones al modelo de regresión lineal
4.1 Introducción
Como veíamos en el capitulo anterior, el modelo de regresión lineal requiere que se cumplan las siguientes hipótesis sobre los términos de error:
Media cero: \(E(e_i) = 0\) \(i=1,…,n\)
Varianza constante: \(Var(e_i)=\sigma^2 I\) \(i=1,…,n\)
Residuos incorrelacionados: \(Cov(e_i,e_j) = 0\)
El incumplimiento de alguna de dichas hipótesis, implica la no aleatoriedad de los residuos y, por tanto, la existencia de alguna estructura o relación de dependencia en los residuos que puede ser estimada, debiendo ser considerada en la especificación inicial del modelo. Los principales problemas asociados al incumplimiento de las hipótesis de normalidad de los residuos son, por un lado, la heteroscedasticidad, cuando la varianza de los mismos no es constante, y la autocorrelación o existencia de relación de dependencia o correlación entre los diferentes residuos, lo que violaría el supuesto de términos de error incorrelacionados.
Si se construye una gráfica de los resultados de una estimación mínimo cuadrática (en ordenadas) frente al valor absoluto de los residuos (en abscisas), cuando éstos últimos presentan una distribución aleatoria, es decir una distribución Normal de media cero y varianza constante, , el resultado obtenido muestra que el tamaño del error es independiente del tamaño de la variable estimada, ya que errores con valor elevado se corresponden con valores bajos y altos de la variable dependiente estimada; sin embargo, una distribución de residuos con problemas de heteroscedasticidad da lugar a una representación como la que puede observarse en la figura siguiente, en donde se manifiesta una clara relación de dependencia entre la variable estimada y el tamaño del error. En este caso los errores de mayor tamaño se corresponden con los valores más altos de la variable estimada.

Figure 4.1: Residuos homocedásticos

Figure 4.2: Residuos heterocedásticos
La representación gráfica de los errores en forma de serie temporal, es decir, poniendo en el eje de ordenadas los errores y en abscisas el periodo temporal en que están datados, permite apreciar la ausencia o presencia de correlación ya que a los residuos no correlacionados les corresponde una representación gráfica en la que no se aprecia pauta temporal alguna, sucediéndose de forma impredecible o aleatoria, mientras que en los residuos con problemas de autocorrelación la pauta temporal es evidente, evidenciándose que cada residuo podría ser previsto en función de la sucesión de los errores correspondientes a periodos temporales pasados:

Figure 4.3: Residuos con Autocorrelación
Estos problemas asociados a los errores pueden detectarse con tests estadísticos diseñados para ello.
4.2 Heterocedasticidad
Si existe heterocedasticidad en los residuos de nuestro modelo, esto implicará que la precisión de la explicación del modelo no es constante. En el campo de la economía, la heterocedasticidad puede provenir de cambios estructurales, eventos especiales, etc.
La consecuencia que lleva asociada es que la estimación de la varianza de los parámetros no es correcta, es decir, \(\sigma^2(X'X)^{-1}\) no es una estimación consistente de \(Var(\hat\beta)\), pudiendo llevar a conclusiones erróneas sobre los \(\beta_k\). Sin embargo, la expresión \(\hat\beta=(X'X)^{-1}X'Y\) sigue siendo una estimación consistente de \(\beta\).
Para tratar este problema podemos optar por:
Mejorar la especificación del modelo (añadir, quitar o transformar variables).
Utilizar estimadores consistentes para \(Var(\beta)\), como por ejemplo los propuestos por White (1980) o por Newey y West (1987).
La detección de la heteroscedasticidad se realiza a través de diversos contrastes paramétricos, entre los que cabe destacar el contraste de Bartlett (Mood, 1950), el constraste de Goldfeld-Quandt (1965) y los contrastes de Breusch-Pagan (1979) y White (1980).
El contraste de White se basa en que, bajo la hipótesis nula de homocedasticidad, la matriz de varianzas y covarianzas de los estimadores MCO de \(\hat \beta\) es: \(\sigma^2(X'X)^{-1}\)
Por el contrario, si existe heteroscedasticidad, la matriz de varianzas y covarianzas viene dada por:
\[(X'X)^{-1}X'\Omega X(X'X)^{-1},\Omega=(\sigma_1^2,\sigma_2^2,...\sigma_n^2)\]
Por tanto, si tomamos la diferencia entre ambas queda:
\[(X'X) ^{-1}X'\Omega X(X'X)^{-1}-\sigma^2(X'X) ^{-1}\]
Por ello, basta con contrastar la hipótesis nula de que todas estas diferencias son iguales a cero, lo que equivale a contrastar que no hay heteroscedasticidad.
Los pasos a seguir para realizar el contraste de White son los siguientes:
Estimar el modelo original y obtener la serie de residuos estimados.
Realizar una regresión del cuadrado de la serie de residuos obtenidos en el paso anterior sobre una constante, las variables exógenas del modelo original, sus cuadrados y los productos cruzados de segundo orden (los productos resultantes de multiplicar cada variable exógena por cada una de las restantes). Es decir, se trata de estimar por MCO la relación:
\[e_i^2= \alpha + \varphi_1 X_{1i}+...+\varphi_k X_{ki}+ \eta_1 X_{1i}^2+...+\eta_k X_{ki}^2+ \varpi_1 X_{1i}X_{2i}+...+ \varpi_k X_{1i}X _{ki}+ ....+\rho X_{k-1i }X_{ki} + u_i\]
- Al aumentar el tamaño muestral, el producto \(nR^2\) (donde n es el número de observaciones y \(R^2\) es el coeficiente de determinación de la última regresión) sigue una distribución Chi-cuadrado con \(p – 1\) grados de libertad, donde \(p\) es el número de variables exógenas utilizadas en la segunda regresión. Se aceptará la hipótesis de existencia de heteroscedasticidad cuando el valor del estadístico supere el valor crítico de la distribución Chi-cuadrado (\(c\)) al nivel de significación estadística fijado (\(nR^2>c\)).
El constraste de Breusch-Pagan es similar al de White pero utilizando como la ecuación auxiliar en el punto 2 la siguiente: \[e_i^2= \alpha + \varphi_1 X_{1i}+...+\varphi_k X_{ki} + u_i\].
El constraste de heterocedasticidad de White en R se realiza a partir del de Breusch-Pagan, función bptest de la librería “lmtest”, extendiendo la forma de la ecuación auxiliar:
library(lmtest)## Loading required package: zoo##
## Attaching package: 'zoo'## The following objects are masked from 'package:base':
##
## as.Date, as.Date.numericm <- lm(mpg ~ hp+wt, data = mtcars)
bptest(m, ~ hp*wt + I(hp^2) + I(wt^2), data = mtcars)##
## studentized Breusch-Pagan test
##
## data: m
## BP = 6.5431, df = 5, p-value = 0.25694.3 Autocorrelación
Decimos que existe autocorrelación cuando el término de error de un modelo econométrico está correlacionado consigo mismo a través del tiempo, tal que \(Cov(e_i,e_j) \neq 0\). Ello no significa que la correlación entre los errores se dé en todos los periodos, sino que puede darse tan sólo entre algunos de ellos.
La razón más frecuente es que uno o varios de los parámetros \(\beta_j\) no son constantes durante la muestra. En el campo de la economía, puede provenir de cambios estructurales, eventos especiales, etc.
Al igual que en el caso anterior, en presencia de autocorrelación, los estimadores MCO siguen siendo insesgados pero no poseen mínima varianza, debiéndose utilizar en su lugar el método de estimación de los Mínimos Cuadrados Generalizados (MCG). Lógicamente, si la falta de constancia en el valor de los parámetros es grave, nuestra estimación no servirá para nada.
Para tratar este problema podemos optar por:
Mejorar la especificación del modelo (añadir, quitar o transformar variables) o añadir términos de tipo MA para neutralizar la autocorrelación.
Utilizar estimadores consistentes para \(Var(\beta)\), como por ejemplo el de Newey y West (1987).
La existencia de autocorrelación en los residuos es fácilmente identificable obteniendo las funciones de autocorrelación (acf) y autocorrelación parcial (acp) de los errores mínimo-cuadráticos obtenidos en la estimación. Si dichas funciones corresponden a un ruido blanco, se constatará la ausencia de correlación entre los residuos. Sin embargo, el mero examen visual de las funciones anteriores puede resultar confuso y poco objetivo, por lo que en la práctica econométrica se utilizan diversos contrastes para la autocorrelación, siendo el más utilizado el de Durbin-Watson (1950), que pasamos a ver seguidamente.
4.3.1 Contraste de Durbin-Watson
Si se sospecha que el término de error del modelo econométrico tiene una estructura como la siguiente:
\[\hat e_t=\rho\hat e_{t-1}+u_t\]
entonces el contraste de Durbin-Watson permite contrastar la hipótesis nula de ausencia de autocorrelación.
Dicho contraste se basa en el cálculo del estadístico \(d\), utilizando para ello los errores mínimo-cuadráticos resultantes de la estimación:
\[d=\frac {\sum_{t=2}^n (\hat e_t - \hat e_{t-1})^2}{\sum_{t=1}^n \hat e_t^2}\]
El valor del estadístico d oscila entre 0 y 4, siendo los valores cercanos a 2 los indicativos de ausencia de autocorrelación de primer orden. La interpretación exacta del test resulta compleja, ya que los valores críticos apropiados para contrastar la hipótesis nula de no autocorrelación requieren del conocimiento de la distribución de probabilidad bajo el supuesto de cumplimiento de dicha hipótesis nula, y dicha distribución depende a su vez de los valores de las variables explicativas, por lo que habría que calcularla en cada aplicación. Se ha demostrado que el valor esperado de d, cuando \(\rho=0\), está dado por la siguiente relación (Maddala,1996).
\[E(d) \approx 2 + \frac {2k}{n-k-1}\]
Para facilitar la interpretación del test, Durbin y Watson derivaron dos distribuciones: \(d_L\) y \(d_U\), que no dependen de las variables explicativas y entre las cuales se encuentra la verdadera distribución de \(d\), de forma que a partir de un determinado nivel de significación, se adoptan la siguientes reglas de decisión:
Si \(d \leq d_L\) rechazamos la hipótesis nula de no autocorrelación frente a la hipótesis alternativa de autocorrelación positiva.
Si \(d \geq (4-d_L)\) rechazamos la hipótesis nula de no autocorrelación frente a la hipótesis alternativa de autocorrelación negativa.
Si \(d_U \leq d \leq (4-d_U)\) aceptamos la hipótesis nula de no autocorrelación.
Si \(d_L \leq d \leq d_U\) ó \((4-d_U) \leq d \leq (4-d_L)\) la prueba no es concluyente.
La figura siguiente muestra esta interpretación de forma gráfica.

El estadístico de Durbin-Watson es aproximadamente igual a \(2(1-r)\) en donde \(r\) es el coeficiente de autocorrelación simple muestral del retardo 1.
En R, el test de Durbin-Watson se encuentra en el Package-R “lmtest”, y su sintaxis es:
library(lmtest)
dwtest(dist~speed, data = cars)##
## Durbin-Watson test
##
## data: dist ~ speed
## DW = 1.6762, p-value = 0.09522
## alternative hypothesis: true autocorrelation is greater than 04.3.2 Contraste de Breush-Godfrey
El test de correlación serial de Breusch–Godfrey es un test de autocorrelación en los errores y residuos estadísticos en un modelo de regresión. Hace uso de los errores generados en el modelo de regresión y un test de hipótesis derivado de éste. La hipótesis nula es que no exista correlación serial de cualquier orden de \(\rho\) .
El test es más general que el de Durbin–Watson, que solo es válido para regresores no-estocásticos y para testear la posibilidad de un modelo autorregresivo de primer orden para los errrores de regresión. El test Breusch–Godfrey no tiene estas restricciones, y es estadísticamente más poderoso que el estadístico \(d\).
Los pasos para realizar el contraste son los siguientes:
Estimar el modelo original y obtener la serie de residuos estimados.
Estimar la ecuación de regresión auxiliar: \[\hat e_t = \alpha + \omega_1X_1 + \omega_2X_2 +...+ \omega_kX_k + \delta_1\hat e_{t-1} +...+ \delta_p\hat e_{t-p} + \epsilon_t\]
Al aumentar el tamaño muestral, el producto \((n-p)R^2\) (donde \(n\) es el número de observaciones, \(p\) el número de retardos del error utilizados en la regresión auxiliar y \(R^2\) es el coeficiente de determinación de dicha regresión) sigue una distribución Chi-cuadrado con \(p\) grados de libertad. Se aceptará la hipótesis de existencia de autocorrelación cuando el valor del estadístico supere el valor crítico de la distribución Chi-cuadrado (\(c\)) al nivel de significación estadística fijado \((n-p)R^2>c\).
El test de Breusch–Godfrey tambien se realiza con la librería-R “lmtest”, y se programa para \(p=3\) del siguiente modo:
library(lmtest)
bgtest(dist~speed, order = 3, data = cars)##
## Breusch-Godfrey test for serial correlation of order up to 3
##
## data: dist ~ speed
## LM test = 3.0936, df = 3, p-value = 0.37744.4 Deficiencias muestrales
El fenómeno de la multicolinealidad aparece cuando las variables exógenas de un modelo econométrico están correlacionadas entre sí, lo que tiene consecuencias negativas para la estimación por MCO, ya que la existencia de una relación lineal entre las variables exógenas, implica que la matriz (\(X'X\)) va a tener determinante cero, es decir será una matriz singular y por tanto no será invertible. Dado que \(\hat \beta = (X'X) ^{-1} X'y\), no será posible calcular la estimación mínimo cuadrática de los parámetros del modelo ni, lógicamente, la varianza de los mismos. Esto es lo que se conoce por el nombre de multicolinealidad exacta.
4.5 Errores de especificación
Los errores de especificación hacen referencia a un conjunto de errores asociados a la especificación de un modelo econométrico. En concreto cabe referirse a:
Omisión de variables relevantes
Inclusión de variables innecesarias
Adopción de formas funcionales equivocadas
En Economía la teoría no suele concretar la forma funcional de las relaciones que estudia. Así, por ejemplo, cuando se analiza la demanda se señala que la cantidad demandada es inversamente proporcional al precio; cuando se estudia el consumo agregado se apunta que la propensión marginal a consumir (relación entre renta y/o consumo) es mayor que cero y menor que uno. Por otro lado es frecuente utilizar la condición “ceteris paribus” para aislar la información de otras variables relevantes que influyen y/o modifican la relación estudiada. Por esta razón, la existencia de errores de especificación en la relación estimada es un factor a considerar y a resolver en el proceso de la estimación econométrica.
Con independencia de la naturaleza de los errores de especificación, dado que el proceso de estimación MCO deben de cumplirse determinadas hipótesis básicas, que los estimadores MCO deben de ser insesgados, eficientes y consistentes, y que el estimador de la varianza del término de error ha de ser insesgado, debemos preguntarnos: ¿qué ocurriría con estas propiedades ante errores de especificación?.
La omisión de variables relevantes provoca que el estimador MCO sea sesgado en media (se obtiene un valor distinto que el que se obtendría al incorporar la variable relevante omitida) y en varianza. La incorporación de variables innecesarias determina que la varianza de los estimadores MCO sea mas elevada (sesgo en la varianza), dificultando la interpretación del contraste de significación individual sobre los parámetros.
Si especificamos la forma funcional de una relación (ya sea lineal, cuadrática, cúbica, exponencial, logarítmica, etc.) y la verdadera relación presenta una forma diferente a la especificada tiene, en algunos casos, las mismas consecuencias que la omisión de variables relevantes, es decir, proporciona estimadores sesgados e inconsistentes. En general, una especificación funcional incorrecta lleva a obtener perturbaciones heteroscedásticas y/o autocorrelacionadas, o alejadas de los parámetros de la distribución del término de error del modelo correctamente especificado.
4.6 Métodos de selección de variables en el modelo lineal general
Una de las cuestiones más importantes a la hora de encontrar el modelo de ajuste más adecuado cuando se dispone de un amplio conjunto de variables explicativas, es la correcta especificación del modelo teórico, ya que como se ha visto la inclusión de una variable innecesaria o la omisión de una variable relevante, condiciona los estadísticos que resultan en la estimación MCO del modelo, por otro lado, en un elevado número de explicativas no cabe descartar la existencia de correlaciones que originen un problema de multicolinealidad aproximada, y en estos casos hay que determinar cual de ellas cabe incluir en la especificación del modelo.
En otras palabras, ante un conjunto elevado de explicativas debemos seleccionar de entre todas, un subconjunto de ellas que garanticen que el modelo esté lo mejor especificado posible. Este análisis cabe hacerlo estudiando las características y propiedades de cada una de las variables independientes, a partir, por ejemplo, de los coeficientes de correlación de cada una de ellas y la dependiente, y de cada explicativa con las restantes, seleccionando modelos alternativos y observando los resultados estadísticos de la estimación MCO de cada uno de ellos. Sin embargo, en la práctica, la selección del subconjunto de variables explicativas de los modelos de regresión se deja en manos de procedimientos más o menos automáticos.
Los procedimientos más usuales son los siguientes:
• Método backward: se comienza por considerar incluidas en el modelo teórico a todas las variables disponibles y se van eliminando del modelo de una en una según su capacidad explicativa. En concreto, la primera variable que se elimina es aquella que presenta un menor coeficiente de correlación parcial con la variable dependiente-o lo que es equivalente, un menor valor del estadístico t– y así sucesivamente hasta llegar a una situación en la que la eliminación de una variable más suponga un descenso demasiado acusado en el coeficiente de determinación.
• Método forward: se comienza por un modelo que no contiene ninguna variable explicativa y se añade como primera de ellas a la que presente un mayor coeficiente de correlación -en valor absoluto- con la variable dependiente. En los pasos sucesivos se va incorporando al modelo aquella variable que presenta un mayor coeficiente de correlación parcial con la variable dependiente dadas las independientes ya incluidas en el modelo. El procedimiento se detiene cuando el incremento en el coeficiente de determinación debido a la inclusión de una nueva variable explicativa en el modelo ya no es importante.
• Método stepwise: es uno de los más empleados y consiste en una combinación de los dos anteriores. En el primer paso se procede como en el método forward pero a diferencia de éste, en el que cuando una variable entra en el modelo ya no vuelve a salir, en el procedimiento stepwise es posible que la inclusión de una nueva variable haga que otra que ya estaba en el modelo resulte redundante.
El modelo de ajuste al que se llega partiendo del mismo conjunto de variables explicativas es distinto según cuál sea el método de selección de variables elegido, por lo que la utilización de un procedimiento automático de selección de variables no significa que con él se llegue a obtener el mejor de los modelos a que da lugar el conjunto de datos con el que se trabaja.
Para realizar la selección de un modelo por cualquira de los métodos descritos, necesitamos instalar la librería-R: “leaps”, una vez instalada ejecutamos el siguiente Chunk, para seleccionar según el método “forward” :
library(leaps)
regfit.fwd=regsubsets(mpg~.,data=mtcars,method="forward")
plot(regfit.fwd,scale="r2")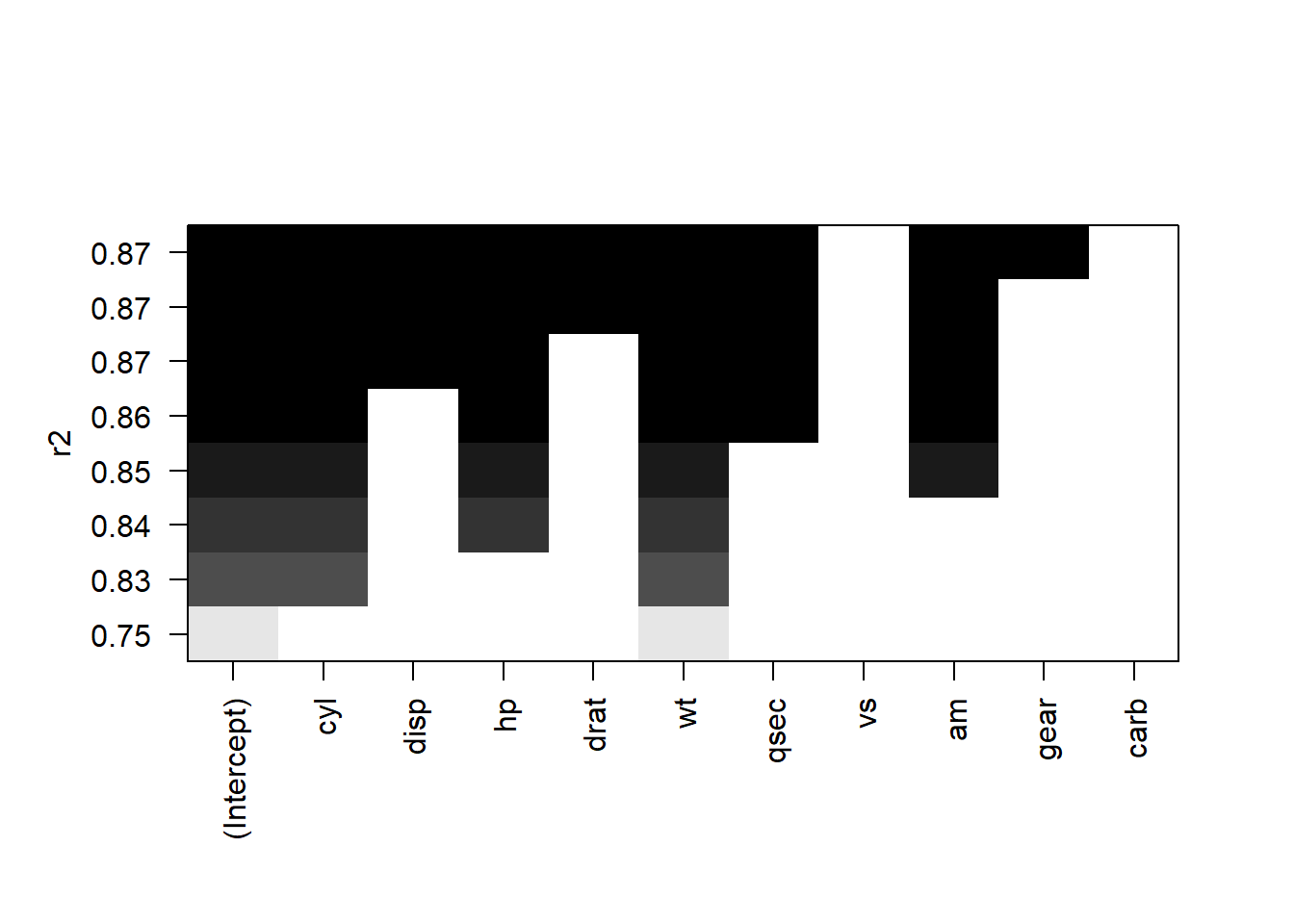
summary(regfit.fwd) ## Subset selection object
## Call: regsubsets.formula(mpg ~ ., data = mtcars, method = "forward")
## 10 Variables (and intercept)
## Forced in Forced out
## cyl FALSE FALSE
## disp FALSE FALSE
## hp FALSE FALSE
## drat FALSE FALSE
## wt FALSE FALSE
## qsec FALSE FALSE
## vs FALSE FALSE
## am FALSE FALSE
## gear FALSE FALSE
## carb FALSE FALSE
## 1 subsets of each size up to 8
## Selection Algorithm: forward
## cyl disp hp drat wt qsec vs am gear carb
## 1 ( 1 ) " " " " " " " " "*" " " " " " " " " " "
## 2 ( 1 ) "*" " " " " " " "*" " " " " " " " " " "
## 3 ( 1 ) "*" " " "*" " " "*" " " " " " " " " " "
## 4 ( 1 ) "*" " " "*" " " "*" " " " " "*" " " " "
## 5 ( 1 ) "*" " " "*" " " "*" "*" " " "*" " " " "
## 6 ( 1 ) "*" "*" "*" " " "*" "*" " " "*" " " " "
## 7 ( 1 ) "*" "*" "*" "*" "*" "*" " " "*" " " " "
## 8 ( 1 ) "*" "*" "*" "*" "*" "*" " " "*" "*" " "Si queremos ver las estimaciones MCO de los parámetros del modelo 8:
coef(regfit.fwd,8)## (Intercept) cyl disp hp drat wt
## 12.56350226 -0.23126963 0.01611609 -0.02339020 0.70893592 -4.08155351
## qsec am gear
## 0.91812006 2.47759723 0.504039574.7 Regresión Ridge
Uno de los supuestos básicos del métodos de mínimos cuadrados es que el rango de \(X\), es decir el número de columnas (o filas) linealmente independientes tiene que ser \(k\), ya que \(\rho(X)=k\), entonces \(\rho(X′X) =k\) y el sistema de ecuaciones normales tiene solución única. Si el supuesto se incumple, \(\rho(X) < k\), entonces las columnas de la matriz \(X\) son linealmente dependientes, \(\rho(X′X) < k\) y el sistema de ecuaciones normales tiene soluciones múltiples. El término multicolinealidad hace referencia a la existencia de una o más relaciones lineales exactas o perfectas entre las variables explicativas.
Este es el caso de la multicolienealidad exacta, si entre los regresores hay variables correlacionadas, estamos ante un problema de multicolinualidad imperfecta, que conduce a sesgos en la estimación de los parámetros asociados a las variables correlacionadas.
La regresión contraída o regresión ridge trata de dar solución a estos problemas de presencia de multicolinealidad, estimando unos parametros “\(\beta\) contraidos”:
\(\hat \beta^k = (X’X + \lambda I)^{-1}X’y\)
Si lambda es 0 estamos ante mínimos cuadrados ordinarios, en otro caso estamos ante un estimador sesgado de \(\beta\). Este estimador sesgado es la solución a un problema de mínimos cuadrados penalizados que contrae los \(\beta\) en torno a 0.
En definitiva, se trata de de encontrar el coeficiente \(\lambda\) que contrae las estimaciones de \(\beta\), y para encontrarlo se utiliza un criterio generalizado de validación cruzada, generalized cross-validation (GCV). El proceso fija un rango de posibles \(\lambda\) entre \([0, c]\) y calcula la validación cruzada \(CV\), siendo el \(\lambda\) óptimo aquel que minimiza el CV.
A continuación se presenta un ejemplo de un modelo \(Y_{t} = \beta_0 + \beta_1 X_{1,t} + \beta_2 X_{2,t} + + \beta_3 X_{3,t} e_t\). Donde las variables son generadas de forma aleatoria, en \(X_{3c}\) se introduce una dependencia lineal entre las variables \(X_1\) y \(X_3\).
La estimación de la regresión ridge se realiza con la función “lm.ridge” de la liberia “MASS”, fijando un rango de posibles \(\lambda\) entre \([0, 10]\). Se elige finalmente un \(\lambda=4\).
# Three variables are measured: x1,x2,x3.
# x1 and x1 are U(0,1); x3=10 * X1 + unif(0,1).
# This causes corr(X1,X3)=sqrt(100/101)=0.995.
# We will fit OLS and ridge regressions to these data,
# use the data to select the "best" constant to add,
# and then evaluate the two regressions on a new test set.
# Ridge regression function, ridge.lm(), is on MASS package
library(MASS)
# Generating the data
set.seed(558562316)
N <- 20 # Sample size
x1 <- runif(n=N)
x2 <- runif(n=N)
x3 <- runif(n=N)
x3c <- 10*x1 + x3 # New variable
ep <- rnorm(n=N)
y <- x1 + x2 + ep
# OLS fit of 3-variable model using independent x3
ols <- lm(y~ x1 + x2 + x3)
summary(ols)##
## Call:
## lm(formula = y ~ x1 + x2 + x3)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.19698 -0.28592 0.04026 0.24016 1.20322
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.4293 0.4916 -0.873 0.3954
## x1 1.7851 0.4812 3.710 0.0019 **
## x2 0.7119 0.4622 1.540 0.1430
## x3 0.2839 0.5122 0.554 0.5870
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.6306 on 16 degrees of freedom
## Multiple R-squared: 0.4831, Adjusted R-squared: 0.3862
## F-statistic: 4.984 on 3 and 16 DF, p-value: 0.0125# OLS fit of 3-variable model using correlated x3.
olsc <- lm(y~ x1 + x2 + x3c)
summary(olsc)##
## Call:
## lm(formula = y ~ x1 + x2 + x3c)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.19698 -0.28592 0.04026 0.24016 1.20322
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.4293 0.4916 -0.873 0.395
## x1 -1.0540 5.1966 -0.203 0.842
## x2 0.7119 0.4622 1.540 0.143
## x3c 0.2839 0.5122 0.554 0.587
##
## Residual standard error: 0.6306 on 16 degrees of freedom
## Multiple R-squared: 0.4831, Adjusted R-squared: 0.3862
## F-statistic: 4.984 on 3 and 16 DF, p-value: 0.0125# Ridge regression using independent variables
ridge <- lm.ridge (y ~ x1+x2+x3, lambda = seq(0, .1, .001))
summary(ridge)## Length Class Mode
## coef 303 -none- numeric
## scales 3 -none- numeric
## Inter 1 -none- numeric
## lambda 101 -none- numeric
## ym 1 -none- numeric
## xm 3 -none- numeric
## GCV 101 -none- numeric
## kHKB 1 -none- numeric
## kLW 1 -none- numericplot(ridge)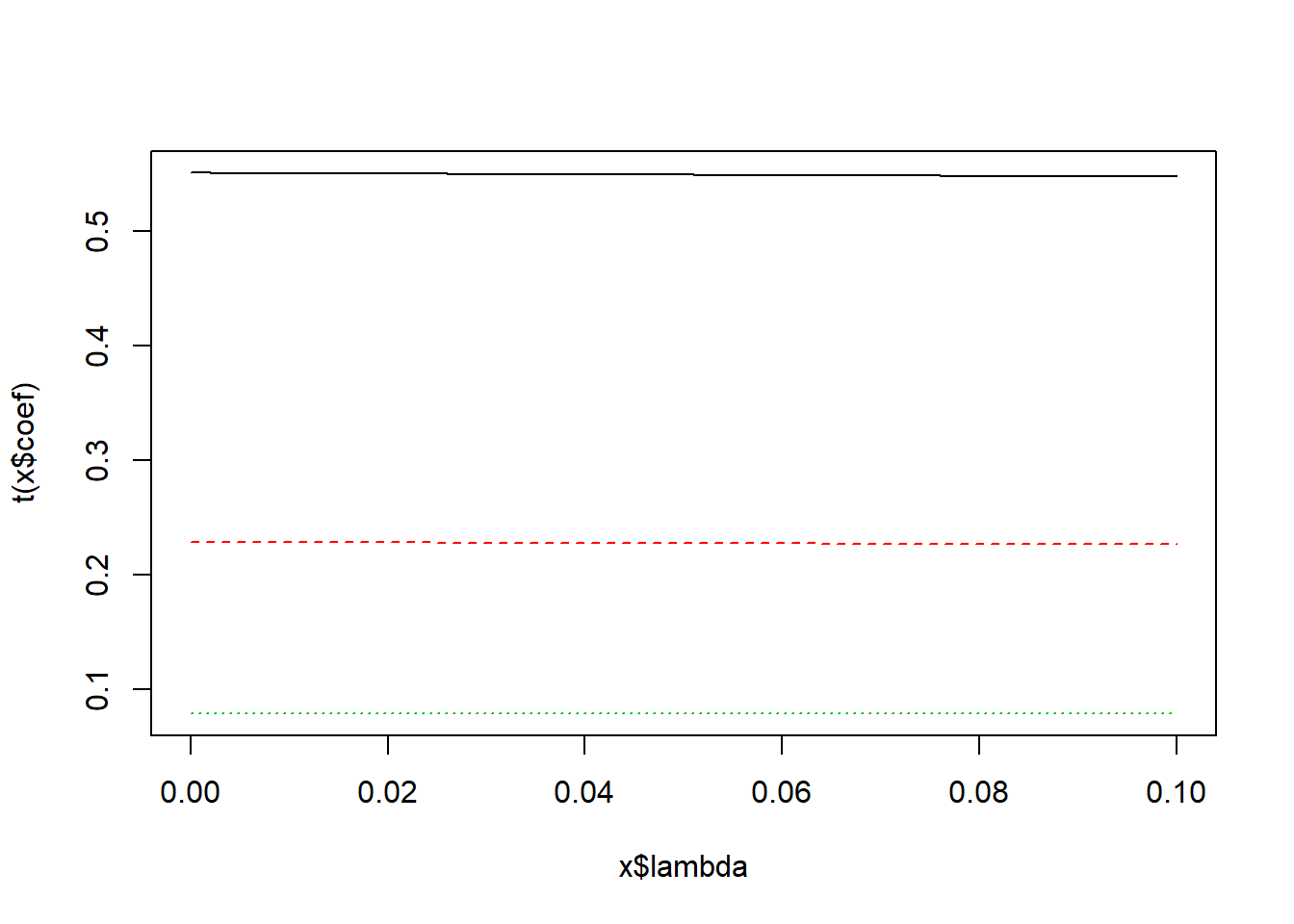
# Ridge regression using correlated variables
ridgec <- lm.ridge (y ~ x1+x2+x3c, lambda = seq(0, .1, .001))
plot(ridgec)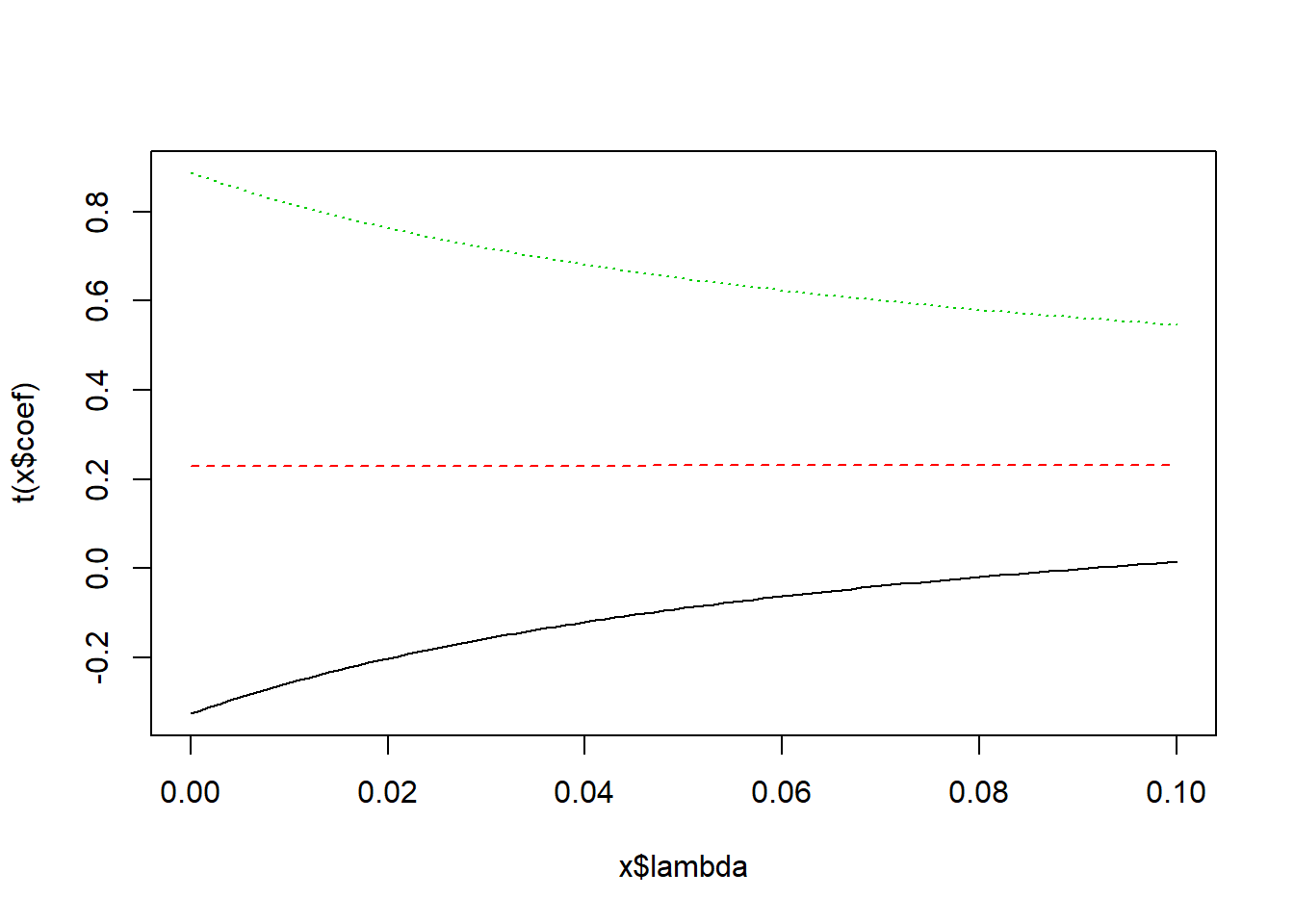
select(ridgec)## modified HKB estimator is 0.4209458
## modified L-W estimator is 1.337588
## smallest value of GCV at 0.1# Selection of constant is at endpoint. Extend endpoint and try again
ridgec <- lm.ridge (y ~ x1+x2+x3c, lambda = seq(0, 1, .1))
plot(ridgec)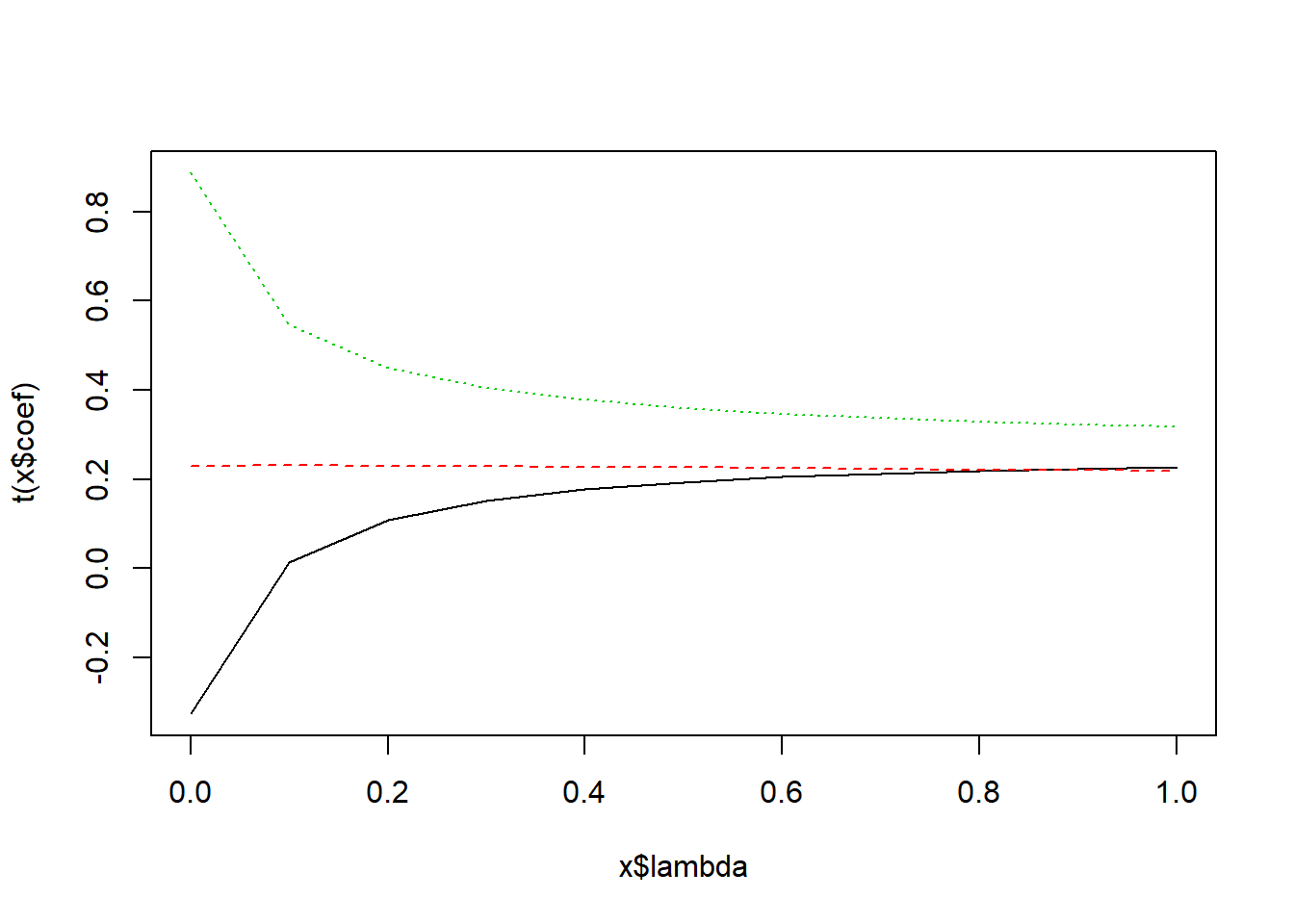
select(ridgec)## modified HKB estimator is 0.4209458
## modified L-W estimator is 1.337588
## smallest value of GCV at 1# Selection of constant is at endpoint. Extend endpoint and try again
ridgec <- lm.ridge (y ~ x1+x2+x3c, lambda = seq(0, 10, .01))
plot(ridgec)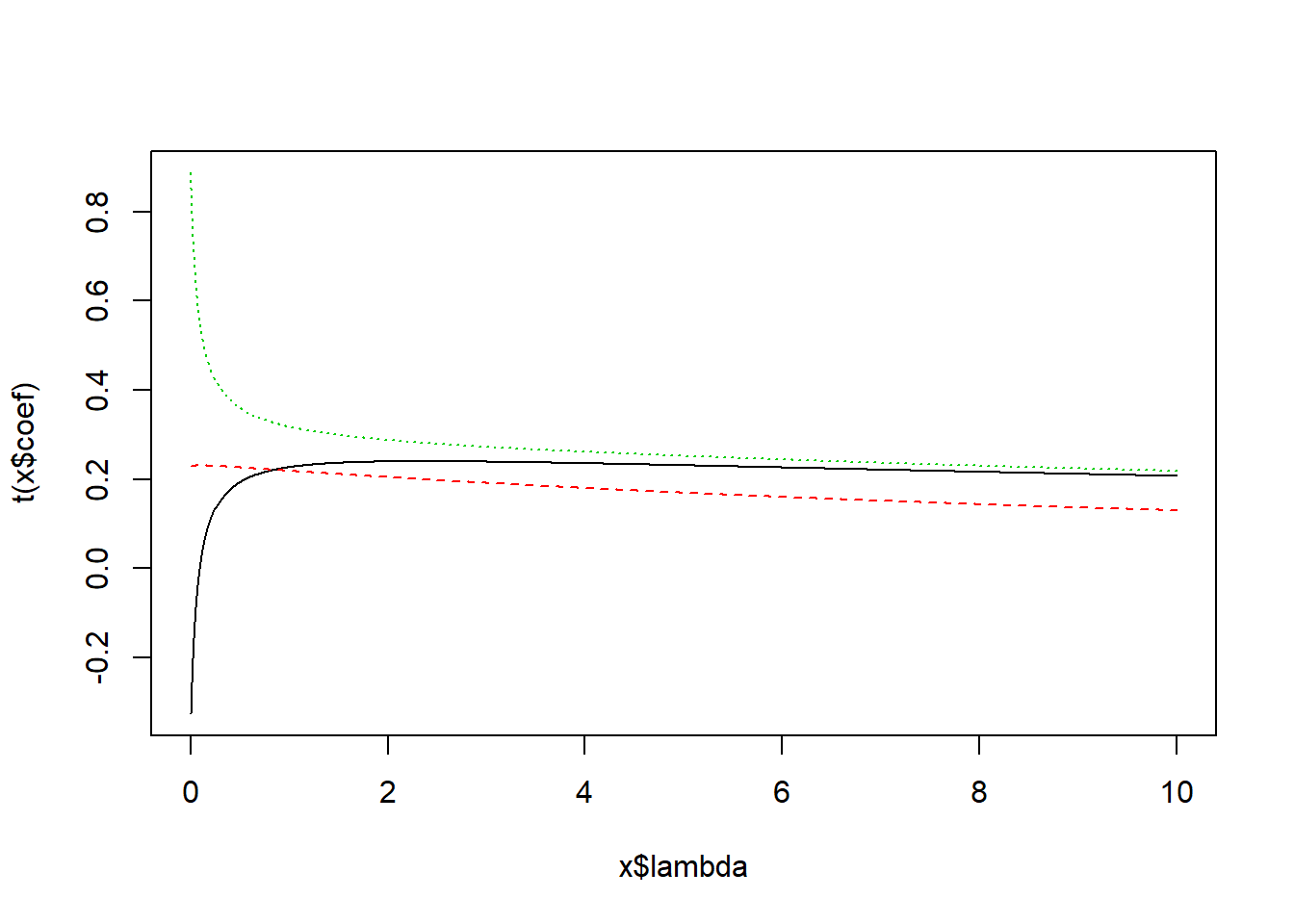
select(ridgec)## modified HKB estimator is 0.4209458
## modified L-W estimator is 1.337588
## smallest value of GCV at 4.01# Final model uses lambda=4.
ridge.final <- lm.ridge (y ~ x1+x2+x3c, lambda = 4)
ridge.final## x1 x2 x3c
## -0.13809086 0.76302466 0.56030303 0.08372054summary(ridge.final)## Length Class Mode
## coef 3 -none- numeric
## scales 3 -none- numeric
## Inter 1 -none- numeric
## lambda 1 -none- numeric
## ym 1 -none- numeric
## xm 3 -none- numeric
## GCV 1 -none- numeric
## kHKB 1 -none- numeric
## kLW 1 -none- numeric# Create test data and compute predicted values for OLS and ridge.
# There's no predict() method for "ridgelm" objects
test <- expand.grid(x1 = seq(.05,.95,.1), x2 = seq(.05,.95,.1), x3=seq(.05,.95,.1))
mu <- test$x1 + test$x2
test$x3c <- 10*test$x1 + test$x3
pred.ols <- predict(ols,newdata=test) # y ~ X1 + X2 + X3
pred.olsc <- predict(olsc,newdata=test) # y ~ X1 + X2 + X3c
pred.ridge <- coef(ridge.final)[1] + coef(ridge.final)[2]*test[,1] +
coef(ridge.final)[3]*test[,2] + coef(ridge.final)[4]*test[,4]
MSPE.ols <- sum((pred.ols - mu)^2)/length(mu)
MSPE.olsc <- sum((pred.olsc - mu)^2)/length(mu)
MSPE.ridge <- sum((pred.ridge - mu)^2)/length(mu)
MSPE.ols## [1] 0.06585964MSPE.olsc## [1] 0.06585964MSPE.ridge## [1] 0.046505894.8 Regresión robusta
En la regresión lineal, un valor atípico u outlier es una observación con un gran residuo. En otras palabras, es una observación cuyo valor de variable dependiente es inusual dado su valor en las variables de predicción. Un valor atípico puede indicar una peculiaridad de la muestra, un error de entrada de datos u otro problema.
Una observación con un valor extremo en una variable de predicción es un punto con alto apalancamiento o leverage. El leverage es una medida de hasta qué punto una variable independiente se desvía de su media. Los puntos de leverage altos pueden tener un gran efecto en la estimación de los coeficientes de regresión.
Se dice que una observación es influyente si la eliminación de la observación cambia sustancialmente la estimación de los coeficientes de regresión. La influencia puede ser considerada como el producto del apalancamiento y la atonía.
La Distancia de Cook (o D de Cook) es una medida que combina la información del apalancamiento y el valor residual de la observación. Es recomendable detectar aquellos valores que tengan un valor alto de distancia de Cook, en concreto, las observaciones en las que D sea mayor que F(0.5, p, n-p), la mediana de una distribución F, donde p es el número de términos del modelo (incluyendo la constante) y n es el número de observaciones. En general, un caso con una distancia de Cook superior a 1 debe ser revisado.
La fórmula asociada a su cálculo sería la siguiente:
\[D_i= \frac {\sum_{j=1}^n(\hat Y_j-\hat Y_{j(i)})^2}{p·MSE} = \frac {e_i^2}{p·MSE}[\frac {h_{ii}}{(1-h_{ii})^2}]\]
donde:
\(\hat Y_j\) es la predicción del modelo para la observación j.
\(\hat Y_{j(i)}\) es la predicción para la observación j de un modelo de regresión reformado en el que la observación i se omite.
\(h_{ii}\) es el elemento i-ésimo de la diagonal de la matriz de proyección \(X(X'X)^{-1}X'\)
\(e_i\) es el residuo bruto (es decir, la diferencia entre el valor observado y el valor ajustado por el modelo propuesto).
\(MSE\) es el error cuadrado medio del modelo de regresión.
\(p\) es el número de parámetros ajustados en el modelo.
En R, estas distancias se calculan a través de la función cooks.distance().
La regresión robusta se puede usar en cualquier situación en la que use la regresión por mínimos cuadrados. Al ajustar una regresión por mínimos cuadrados, es posible que encontremos algunos valores atípicos o puntos de datos de alto leverage. Si tras su análisis, vemos que estos puntos de datos no son errores de entrada de datos, ni son de una población diferente a la mayoría de nuestros datos, entonces no tenemos una razón convincente para excluirlos del análisis.
La regresión robusta puede ser una buena estrategia, ya que es una solución de compromiso entre excluir estos puntos del análisis e incluir todos los puntos de datos y tratarlos a todos por igual en la regresión MCO. La idea de la regresión robusta es ponderar las observaciones de forma diferente en función del comportamiento de estas observaciones. En términos generales, es una forma de regresión de mínimos cuadrados ponderada y reponderada.
En este apartado veremos como estimar un modelo de regresión lineal de forma robusta utilizando un estimador \(M\) robusto. Al utilizar este tipo de estimación, se reduce la influencia de los puntos atípicos u outlier en la estimación del modelo. Si no tenemos puntos atípicos, se recurrirá a la estimación mínimo cuadrática.
El estimador M es una clase amplia de estimadores, que son obtenidos como la minimización de la suma de funciones de residuos. Técnicas como la conocida mínimos cuadrados, son ejemplos de estimadores M.
En 1964 Huber et al propusieron una generalización para la estimación de parámetros de un modelo de máxima verosimilitud con la reducción de una función de la forma:
\[\sum_{k=1}^Nf_{\phi}(e_k,\theta)\] siendo \(f_{\phi}\) una funciónn simétrica de \(\phi\) argumentos, La función \(f_{\phi}\), o su derivada, \(f'_{\phi}\), pueden ser elegidas de tal manera que el estimador proporcione propiedades deseables (en términos de sesgo y eficiencia) cuando los datos son distribuidos bajo el supuesto deseado. Las soluciones de la forma:
\[\hat\theta=\min_\theta(\sum_{k=1}^Nf_{\phi}(e_k,\theta))\]
son llamadas M-estimadores, donde “M” hace referencia a “máxima veosimilitud”.
Otros tipos de estimadores robustos serían los L-estimadores, R-estimadores y S-estimadores, siendo también estimadores de máxima verosimilitud.
Los estimadores de la forma \(\sum_{k=1}^Nf_{\phi}(e_k,\theta)\), incluyendo la técnica de mínimos cuadrados, cumplen con las características de un estimador \(M\) debido a que buscan minimizar la norma euclidiana o norma dos (L2), la norma uno (L1), combinación de ambas (L1 − L2), la norma p (\(L_p\)) de Cauchy, German-McClure, Welsch, Tukey, Huber, entre otros.
La norma dos ha sido utilizada en innumerables ocasiones para la estimación de parámetros donde los datos no se encuentran contaminados con valores atípicos. Sin embargo, el uso de la norma dos con la adición de outliers hace que la estimación se realice de manera ineficiente debido a que la reducción de la norma tiende a diverger en la etapa de optimización.
En el estimador M de Huber se mezcla el comportamiento de la norma uno (con un límite o penalización en función del factor \(\phi\)) y la norma dos dentro de una función compuesta por ambas.
Los M-estimadores se utilizan con el fin de lidiar con el efecto de los outliers, ya sea para incluir el efecto de los valores atípicos dentro de la estimación, minimizar el efecto de los mismos, o filtrarlos de la población.
Definimos ahora un vector de parámetros a estimar \(\hat w = [w_1,..., w_n]'\). El estimador M robusto (EMR) de \(\hat w\) basado en la función \(f_{\phi}(e_k,\theta)\) será la solución de las siguientes n ecuaciones:
\[\sum_{k=1}^Nf'_{\phi}(e_k,\theta) \frac {\partial e_k}{\partial w_i}=0\ \ \ \ i=1,..., n\]
donde la derivada parcial \[f'_{\phi}(e_k,\theta)=\frac {\partial f_{\phi}(e_k,\theta)}{\partial e_k}\]
es llamada función de influencia. Si definimos la función peso como:
\[g_\phi(e_k,\theta) = \frac {f'_{\phi}(e_k,\theta)}{e_k}\]
el sistema de ecuaciones a resolver quedará como:
\[\sum_{k=1}^Ng_{\phi}(e_k,\theta)·e_k·\frac {\partial e_k}{\partial w_i}=0\ \ \ \ i=1,..., n\]
Las funciones objetivo \(f_{\phi}(x))\) más utilizadas, junto con sus funciones de influencia y de peso son las que se muestran en la siguiente figura.

La función de influencia f’ mide la infuencia de un dato en función del parámetro estimado. Por ejemplo, para mínimos cuadrados ordinarios, con función objetivo:
\[f_{\phi}(e_k,\theta)=\frac {e_k^2} {2}\] la función de influencia será igual a:
\[f'_{\phi}(e_k,\theta)=e_k\] y la función de peso:
\[g_{\phi}(e_k,\theta)=1\] pudiéndose ver cómo el error crece linealmente con respecto al tamaño del residuo, sin estar acotado, es decir, si \(e_k \rightarrow \infty \Rightarrow f_{\phi}(e_k,\theta)\rightarrow \infty\). Por tanto, no existe ninguna robustez en la estimación con mínimos cuadrados.
Existen diversas características que un EMR debe cumplir:
El estimador debe tener una función de influencia limitada. Es decir, que a partir de cierto valor la función comienza a converger.
La función objetivo (\(f_{\phi}(e_k,\theta)\)) del vector de parámetros \(\hat w\) debe de tener un mínimo único. Esto requiere que la función \(f_{\phi}(e_k,\theta)\) sea convexa con la variable \(\hat w\). La restricción de convexidad es equivalente a imponer que \(\frac {\partial^2 f_\phi(e_k,\theta)}{\partial \hat w^2}\) sea definido positivo.
Siempre que \(\frac {\partial^2 f_\phi(e_k,\theta)}{\partial \hat w^2}\) sea singular, la función objetivo debe tener gradiente, es decir, \(\frac {\partial f_\phi(e_k,\theta)}{\partial \hat w} \neq 0\).
Nótese que no todas las funciones cumplen satisfactoriamente con los requerimientos anteriores. Los estimadores de mínimos cuadrados (\(L2\)) no son robustos debido a que su función de influencia no está delimitada. Los estimadores de mínimos absolutos (\(L1\)) no son estables, porque la función \(f\) no es estrictamente convexa. En realidad, la segunda derivada cuando x = 0 no existe, otorgando un valor indefinido. Los estimadores absolutos reducen la influencia de errores numéricamente grandes, pero aún así estos errores tienen influencia en el comportamiento de la función \(f\) porque esta última carece de un punto de corte.
Respecto a los estimadores de mínimos “p” o mínima potencia, señalar que se ha investigado la selección de un valor óptimo para \(v\), determinándose que debe encontrarse alrededor de 1.2 para esperar una estimación efectiva.
La función de Cauchy, también llamada función Lorenziana, no garantiza una solución única. Para cubrir el 95% de los datos con una distribución normal y con ruido Gaussiano se debe definir \(c = 2,3849\), en el caso de la función de Welsch \(c = 2,9846\) y con la función de Tukey \(c = 4,6851\).
Por último, señalar que en el estimador M de Huber la función \(f\) cumple con las siguientes características:
Es derivable, es decir, existe \(f'\).
Es simétrica, es decir, \(f_\phi(x)=f_\phi(-x)\).
Es convexa.
\(f_\phi(0)=0\).
Para estimar en R un modelo de regresión con estimadores robustos se usa la función \(rlm\) del paquete \(MASS\).
El comando rlm implementa varias versiones de regresión robusta. En este caso, mostraremos la M-estimation con Huber y la ponderación bisquare, siendo quizás los dos procedimientos más utilizados. La estimación M define una función de ponderación de tal manera que la ecuación de estimación se convierte en:
\[\sum_{i=1}^n w_i(y_i-x'b)x_i' = 0\]
Pero los pesos dependen de los residuos y los residuos de los pesos. La ecuación se resuelve utilizando Iteratively Reweighted Least Squares (IRLS). Por ejemplo, la matriz de coeficientes en la iteración j es:
\[B_j = [X'W_{j-1}X]^{-1}X'W_{j-1}Y\]
donde los subíndices indican la matriz en una iteración particular. El proceso continúa hasta que converge. En la ponderación de Huber, las observaciones con pequeños residuos obtienen un peso de 1 y cuanto mayor es el residual, menor es el peso. Esto está definido por la función de peso:
\[w(e)=\begin{bmatrix} 1 \ \ si\ |e|\le k\\ \frac k {|e|} \ \ si\ |e|\gt k \end{bmatrix}\]
Con la ponderación bisquare, todas los casos con un residuo distinto de cero se ponderan por lo menos un poco.
A través del dataframe \(stackloss\), con 21 observaciones sobre 4 variables.
[, 1] Air Flow. Flujo de aire de refrigeración
[, 2] Water Temp. Temperatura de entrada de agua de refrigeración
[, 3] Acid Conc. Concentración de ácido [por 1000, menos 500]
[, 4] stack.loss. Pérdida de pila
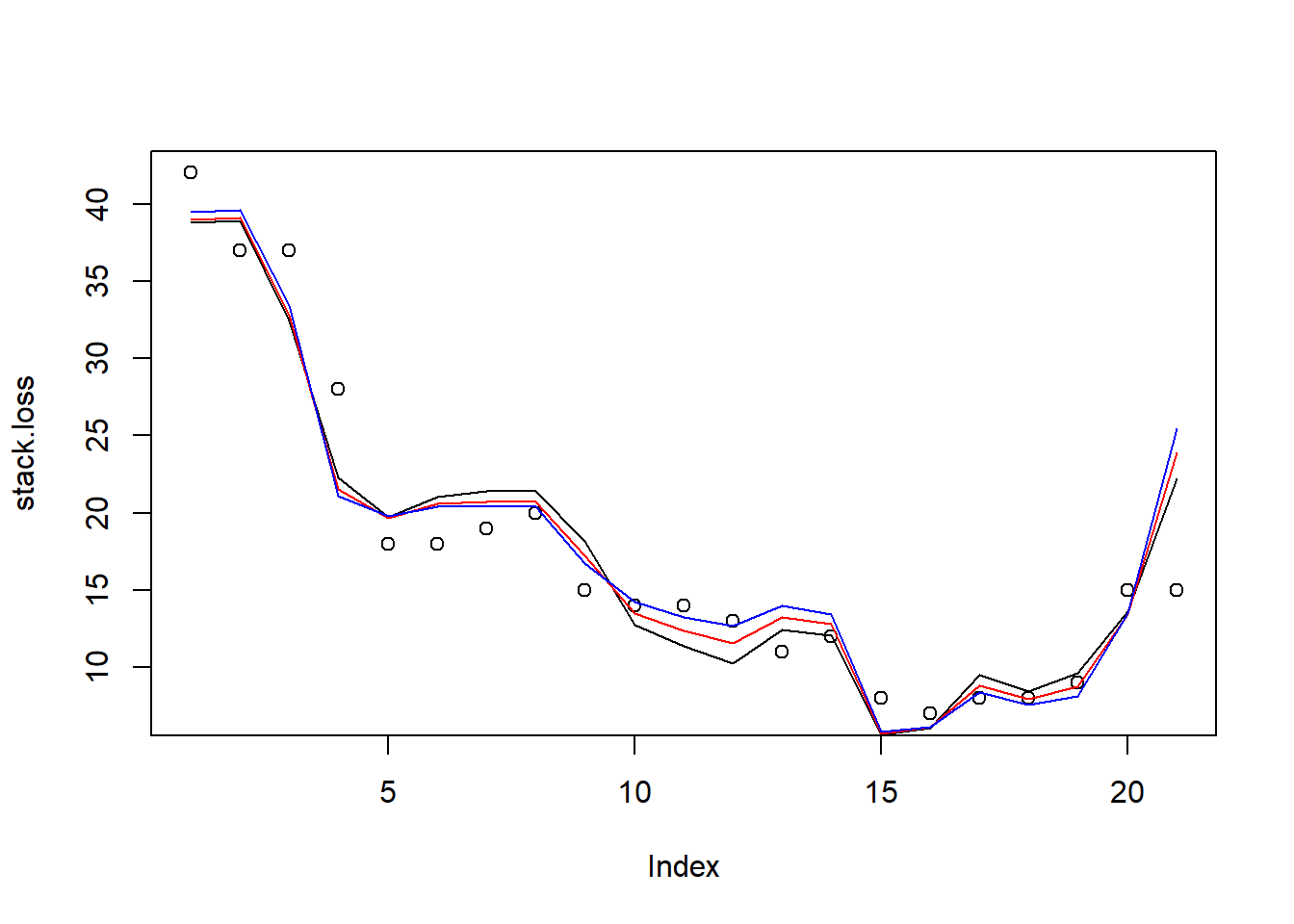
Estimaremos la regresión clásica y robusta de la pérdida de pila frente a las demás. Como vemos, los resultados mejoran significativamente, pasando de un error estándar residual de 3,243 a 2,282 en la regresión robusta, es decir, un 30% inferior.
library(MASS)
# Modelo lineal MCO y distancias de Cook
summary(lm(stack.loss ~ ., stackloss))##
## Call:
## lm(formula = stack.loss ~ ., data = stackloss)
##
## Residuals:
## Min 1Q Median 3Q Max
## -7.2377 -1.7117 -0.4551 2.3614 5.6978
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -39.9197 11.8960 -3.356 0.00375 **
## Air.Flow 0.7156 0.1349 5.307 5.8e-05 ***
## Water.Temp 1.2953 0.3680 3.520 0.00263 **
## Acid.Conc. -0.1521 0.1563 -0.973 0.34405
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3.243 on 17 degrees of freedom
## Multiple R-squared: 0.9136, Adjusted R-squared: 0.8983
## F-statistic: 59.9 on 3 and 17 DF, p-value: 3.016e-09cooks.distance(lm(stack.loss ~ ., stackloss))## 1 2 3 4 5
## 1.537104e-01 5.968309e-02 1.264141e-01 1.305420e-01 4.047671e-03
## 6 7 8 9 10
## 1.956520e-02 4.880159e-02 1.650192e-02 4.455581e-02 1.192969e-02
## 11 12 13 14 15
## 3.586597e-02 6.506585e-02 1.076480e-02 1.977781e-05 3.851572e-02
## 16 17 18 19 20
## 3.379436e-03 6.547308e-02 1.121836e-03 2.178786e-03 4.491653e-03
## 21
## 6.919999e-01# Estimador Huber
summary(rlm(stack.loss ~ ., stackloss))##
## Call: rlm(formula = stack.loss ~ ., data = stackloss)
## Residuals:
## Min 1Q Median 3Q Max
## -8.91753 -1.73127 0.06187 1.54306 6.50163
##
## Coefficients:
## Value Std. Error t value
## (Intercept) -41.0265 9.8073 -4.1832
## Air.Flow 0.8294 0.1112 7.4597
## Water.Temp 0.9261 0.3034 3.0524
## Acid.Conc. -0.1278 0.1289 -0.9922
##
## Residual standard error: 2.441 on 17 degrees of freedom# Estimador bisquare
summary(rlm(stack.loss ~ ., stackloss, psi = psi.bisquare))##
## Call: rlm(formula = stack.loss ~ ., data = stackloss, psi = psi.bisquare)
## Residuals:
## Min 1Q Median 3Q Max
## -10.4356 -1.7065 -0.2392 0.8797 6.9326
##
## Coefficients:
## Value Std. Error t value
## (Intercept) -42.2853 9.5316 -4.4363
## Air.Flow 0.9275 0.1081 8.5841
## Water.Temp 0.6507 0.2949 2.2068
## Acid.Conc. -0.1123 0.1252 -0.8970
##
## Residual standard error: 2.282 on 17 degrees of freedom# Gráfico de valores observados frente a predichos en ambas regresiones
plot(stack.loss, type="p")
lines(lm(stack.loss ~ ., stackloss)$fitted.values, col="black")
lines(rlm(stack.loss ~ ., stackloss)$fitted.values, col="red")
lines(rlm(stack.loss ~ ., stackloss, psi = psi.bisquare)$fitted.values, col="blue")