3 Modelo Lineal General

3.1 Introducción

La regresión lineal es la técnica básica del análisis econométrico. Mediante dicha técnica tratamos de determinar relaciones de dependencia de tipo lineal entre una variable dependiente o endógena, respecto de una o varias variables explicativas o exógenas. Gujarati (1975), define el análisis de regresión como el estudio de la dependencia de la variable dependiente, sobre una o más variables explicativas, con el objeto de estimar o predecir el valor promedio poblacional de la primera en términos de los valores conocidos o fijos (en medias muestrales repetidas) de las últimas.

En este capitulo abordaremos el estudio del caso de una única ecuación de tipo lineal con una variable dependiente y una independiente, y la generalización del modelo al caso de múltiples variables exógenas. Las extensiones del modelo lineal general se analizarán en capítulos siguientes.

3.2 Modelo de Regresión Lineal Simple

Partimos de la existencia de una relación lineal entre una variable endógena (\(Y_i\)) y una variable exógenas (\(X_i\)):

\[\begin{equation} Y_i= \beta_1 + \beta_2 X_i + e_i, i=1,2,…, n \end{equation}\]

Nuestro objetivo consiste en estimar los dos parámetros de la ecuación anterior a partir de los datos muestrales de los que disponemos. Para ello utilizaremos el método de los Mínimos Cuadrados Ordinarios (MCO), pero antes de ver en que consiste este método debemos plantear ciertas hipótesis sobre el comportamiento de las variables que integran el modelo.

La variable \(e_i\) la denominamos término de perturbación o error, y en ella recogemos todos aquellos factores que pueden influir a la hora de explicar el comportamiento de la variable \(Y_i\) y que, sin embargo, no están reflejados en las variables explicativas, \(X_i\). Estos factores deberían ser poco importantes, ya que no debería existir ninguna variable explicativa relevante omitida en el modelo de regresión. En caso contrario estaríamos incurriendo en lo que se conoce como un error de especificación del modelo. El término de perturbación también recogería los posibles errores de medida de la variable dependiente, \(Y_i\).

De lo anterior se desprende que, a la hora de estimar los parámetros del modelo, resultará de vital importancia que dicho término de error no ejerza ninguna influencia determinante en la explicación del comportamiento de la variable dependiente. Por ello, si el modelo está bien especificado, cuando se aplica el método de Mínimos Cuadrados Ordinarios, cabe realizar las siguientes hipótesis de comportamiento sobre el término de error:

La esperanza matemática de et es cero, tal que \(E(e_i) = 0\). Es decir, el comportamiento del término de error no presenta un sesgo sistemático en ninguna dirección determinada. Por ejemplo, si estamos realizando un experimento en el cual tenemos que medir la longitud de un determinado objeto, a veces al medir dicha longitud cometeremos un error de medida por exceso y otras por defecto, pero en media los errores estarán compensados.
La covarianza entre \(e_i\) y \(e_j\) es nula para tal que \(E (e_i•e_j) = 0\). Ello quiere decir que el error cometido en un momento determinado, i, no debe estar correlacionado con el error cometido en otro momento del tiempo, j, o dicho de otro modo, los errores no ejercen influencia unos sobre otros. En caso de existir este tipo de influencia o correlación, nos encontraríamos ante el problema de la autocorrelación en los residuos, el cual impide realizar una estimación por Mínimos Cuadrados válida.
La matriz de varianzas y covarianzas del término de error debe ser escalar tal que \(Var(e_i)=\sigma^2I\), \(i=1,…,n\), donde I es la matriz unidad. Dado que siempre que medimos una variable, se produce un cierto error, resulta deseable que los errores que cometamos en momentos diferentes del tiempo sean similares en cuantía. Esta condición es lo que se conoce como supuesto de homocedasticidad que, en caso de no verificarse, impediría un uso correcto de la estimación lineal por Mínimos Cuadrados.

Estas hipótesis implican que los errores siguen una distribución Normal de media cero y varianza constante por lo que, dado su carácter aleatorio, hace que los errores sean por naturaleza impredecibles.

Asimismo, las variables incluidas en el modelo deben verificar que:

La variable dependiente \(Y_i\) se ajusta al modelo lineal durante todo el periodo muestral, es decir, no se produce un cambio importante en la estructura de comportamiento de \(Y_i\) a lo largo de la muestra considerada, es decir, se distribuira como una normal con \(\mathrm{E}((Y_i)=\beta_1 + \beta_2 X_i\) y \(\mathrm{Var}(Y_i)=\mathrm{Var}(e_i)\).
La variable explicativa, \(X_i\), es no estocásticas, es decir, es considerada fija en muestreos repetidos.

Si suponemos que se verifican los supuestos anteriores, la estimación mínimo cuadrática de los parámetros \(\beta_1\) y \(\beta_2\), dará como resultado gráfico una recta que se ajuste lo máximo posible a la nube de puntos definida por todos los pares de valores muestrales \((X_i,Y_i)\), tal y como se puede apreciar en el figura siguiente.

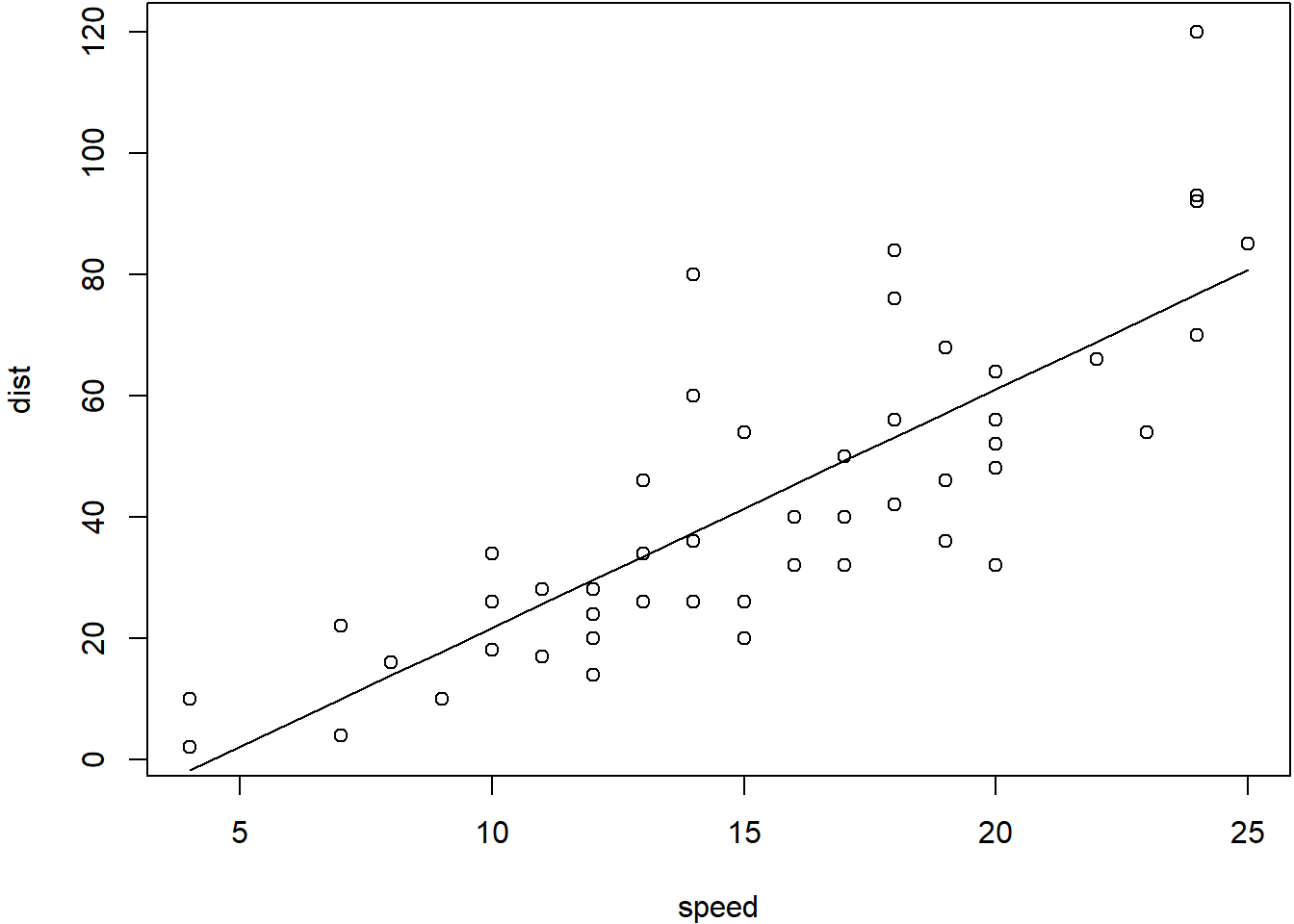
Figure 3.1: Relación entre la Velocidad y la Distancia de Frenado

El término de error, \(e_i\), puede ser entendido, a la vista del gráfico anterior, como la distancia que existe entre el valor observado, \(Y_i\), y el correspondiente valor estimado, que sería la imagen de \(X_i\) en el eje de ordenadas. El objetivo de la estimación por Mínimos Cuadrados Ordinarios es, precisamente, minimizar el sumatorio de todas esas distancias al cuadrado; es decir :

\[\begin{equation} Min \sum (e_i)^2= \sum (Y_i - \hat Y_i)^2= \sum (Y_i - \hat\beta_1 + \hat\beta_2 X_i)^2 \end{equation}\]

Derivando esta expresión respecto a los coeficientes \(\hat\beta_1\) y \(\hat\beta_2\) e igualando a cero obtenemos el sistema de ecuaciones normales:

\[\begin{equation} \sum Y_i= n\hat\beta_1 + \sum \hat\beta_2 X_i \\ \sum (Y_i•X_i)= \sum \hat\beta_1 X_i + \sum \hat\beta_2 (X_i)^2 \end{equation}\]

donde n representa el tamaño muestral.

Resolviendo dicho sistema de ecuaciones obtenemos la solución para los parámetros \(\hat\beta_1\) y \(\hat\beta_2\): \[\begin{equation} \hat\beta_1 =\bar Y - \hat\beta_2 \bar X \\ \hat\beta_2=\frac{\sum ((Y_i-\bar Y)•(X_i-\bar X)} {\sum (X_i-\bar X)^2} \end{equation}\]

3.3 Modelo de Regresión Lineal Múltiple

Pasamos a continuación a generalizar el modelo anterior al caso de un modelo con varias variables exógenas, de tal forma que se trata de determinar la relación que existe entre la variable endógena Y y variables exógenas: \(X_2, X_3,…, X_k\). Dicho modelo se puede formular matricialmente de la siguiente manera:

\[\begin{equation} y=\beta X+e=Y_i= \beta_1 + \beta_2 X_{2i} +\beta_3 X_{3i} +...+\beta_k X_{ki} e_i, i=1,2,…, n \end{equation}\]

donde: \[y = \begin{bmatrix} Y_{1}\\ Y_{2}\\ .\\ Y_{n} \end{bmatrix}\] es el vector de observaciones de la variable endógena

\[X = \begin{bmatrix}1 & X_{21} & X_{31} & ... & X_{k1}\\ 1 & X_{22} & X_{32} & ... & X_{k2}\\ .& . & . & ... & .\\ 1 & X_{2n} & X_{3n} & ... & X_{kn} \end{bmatrix}\] es el vector de observaciones de las variables exogenas. \[\beta = \begin{bmatrix} \beta_{1}\\ \beta_{2}\\ .\\ \beta_{k} \end{bmatrix}\] es el vector de los coeficientes que pretendemos estimar.

\[e = \begin{bmatrix} e_{1}\\ e_{2}\\ .\\ e_{n} \end{bmatrix}\] es el vector de términos de error.

Suponiendo que se verifican las hipótesis que veíamos antes, el problema a resolver nuevamente es la minimización de la suma de los cuadrados de los términos de error tal que:

\[\begin{equation} Min \sum (e_i)^2= \sum (Y_i - \hat Y_i)^2 =\sum (Y_i - \hat\beta X)^2 \end{equation}\]

Desarrollando dicho cuadrado y derivando respecto a cada \(\hat\beta_i\) obtenemos el siguiente sistema de ecuaciones normales expresado en notación matricial:

\[ X'X\hat \beta = X'y\]

en donde basta con despejar \(\hat\beta\) premultiplicando ambos miembros por la inversa de la matriz para obtener la estimación de los parámetros del modelo tal que:

\[ \hat \beta =X'X ^{-1} X'y\]

donde:

\[X'X = \begin{bmatrix}n & \sum X_{2i} & \sum X_{3i} & ... & \sum X_{ki}\\ \sum X_{2i} & \sum X_{2i}^2 & \sum (X_{2i}X_{3i}) & ... & \sum (X_{2i}X_{ki})\\ .& . & . & ... & .\\ \sum X_{ki} & \sum (X_{ki}X_{2i}) & \sum (X_{ki}X_{3i}) & ... & \sum X_{ki}^2 \end{bmatrix}\]

\[X'y = \begin{bmatrix} \sum Y_{i}\\ \sum (Y_{i}X_{2i})\\ \\ \sum (Y_{i}X_{ki}) \end{bmatrix}\]

\[\hat \beta = \begin{bmatrix} \hat \beta_{1}\\ \hat \beta_{2}\\ .\\ \hat \beta_{k} \end{bmatrix}\]

Cada uno de los coeficientes estimados,\(\hat \beta_i\), son una estimación insesgada del verdadero parámetro del modelo y representa la variación que experimenta la variable dependiente \(Y_i\) cuando una variable independiente \(X_i\) varía en una unidad y todas las demás permanecen constantes (supuesto ceteris paribus). Dichos coeficientes poseen propiedades estadísticas muy interesantes ya que, si se verifican los supuestos antes comentados, son insesgados, eficientes y óptimos.

La valores estimados de la variable dependiente en expresión matricial vienen dados por:

\[\hat y = X \hat \beta \]

Y la distribución estadística de la variable dependiente, se expresa en forma matricial:

\[\mathrm{E}(y)= X \beta\]

\[\mathrm{Var}(y)=\sigma^{2}I\]

3.4 Propiedades estadísticas del estimador MCO

Si se cumplen las hipótesis de comportamiento sobre el término error, la distribución de probabilidad del estimador MCO \(\hat \beta\) será una distribución Normal multivariante con vector de medias \(\beta\) y matriz de varianzas y covarianzas \(\sigma^2(X'X) ^{-1}\). La esperanza matemática del estimador MCO se demuestra a partir de:

\[ \mathrm{E}(\hat \beta) = \mathrm{E}(X'X ^{-1}X'u) \\ =X'X ^{-1}X'\mathrm{E}(y) \\ =X'X^{-1}X'X\beta= \beta \]

De la definición de matriz de varianzas y covarianzas, y se tiene que:

\[\begin{equation} \begin{split} \mathrm{Var}(\hat{\beta}) & =\mathrm{Var}((X'X)^{-1}X'y)\\ & =(X'X)^{-1}X'\mathrm{Var}(y)((X'X)^{-1}X')'\\ & =(X'X)^{-1}X'\mathrm{Var}(y)X(X'X)^{-1}\\ & =(X'X)^{-1}X'\sigma^{2}IX(X'X)^{-1}\\ & =(X'X)^{-1}\sigma^{2} \end{split} \end{equation}\]

El estimador \(\hat \beta\) del parámetro \(\beta\) es insesgado porque su esperanza matemática coincide con el verdadero valor del parámetro \(\mathrm{Var}(\hat \beta)=\beta\) . Se dice que un estimador insesgado es mas eficiente que otro estimador insesgado, si la varianza muestral de dicho estimado res menor que la varianza muestral de ese otro estimador. El teorema de Gauss-Markov demuestra que el estimador MCO es el más eficiente de la clase de estimadores lineales e insesgados de \(\beta\).

3.5 Coeficiente de determinación

Una vez estimada la ecuación de regresión lineal tiene interés determinar la exactitud del ajuste realizado. Para ello hay que analizar la variación que experimenta esta variable dependiente y, dentro de esta variación, se estudia qué parte está siendo explicada por el modelo de regresión y qué parte es debida a los errores o residuos.

La forma de realizar dicho análisis es a partir de la siguiente expresión:

\[SCT=SCE+SCR\]

donde:

\(SCT\): es la Suma de Cuadrados Totales y representa una medida de la variación de la variable dependiente.
\(SCE\) es la Suma de Cuadrados Explicados por el modelo de regresión.
\(SCR\) es la Suma de Cuadrados de los Errores

Cuando el modelo tiene término independiente, cada una de estas sumas viene dada por:

\[SCT=y'y-n\bar Y^2=\sum Y_i^2 -n\bar Y^2\]

\[SCE=\hat \beta' X'X \hat \beta-n\bar Y^2=\sum \hat Y_i^2 -n\bar Y^2\]

\[SCR=y'y - \hat \beta' X'X \hat \beta =\sum \hat e_i^2\]

A partir de las expresiones anteriores es posible obtener una medida estadística acerca de la bondad de ajuste del modelo mediante lo que se conoce como coeficiente de determinación (\(R^2\)), que se define como:

\[R^2=\frac{SCE}{SCT}=1-\frac{SCR}{SCT}, 0 \leq R^2 \leq 1\]

Mediante este coeficiente es posible seleccionar el mejor modelo de entre varios que tengan el mismo número de variables exógenas, ya que la capacidad explicativa de un modelo es mayor cuanto más elevado sea el valor que tome este coeficiente. Sin embargo, hay que tener cierto cuidado a la hora de trabajar con modelos que presenten un R2 muy cercano a 1 pues, aunque podría parecer que estamos ante el modelo “perfecto”, en realidad podría encubrir ciertos problemas de índole estadística como la multicolinealidad que veremos en el capítulo 3.

Por otra parte, el valor del coeficiente de determinación aumenta con el número de variables exógenas del modelo por lo que, si los modelos que se comparan tienen distinto número de variables exógenas, no puede establecerse comparación entre sus \(R^2\). En este caso debe emplearse el coeficiente de determinación corregido (\(\bar R^2\)) , el cual depura el incremento que experimenta el coeficiente de determinación cuando el número de variables exógenas es mayor.

La expresión analítica de la versión corregida es:

\[R^2=1-\frac{\frac{SCR}{n-k}}{\frac{SCT}{n-1}}\]

3.6 Inferencia acerca de los estimadores

Hasta el momento hemos visto como la estimación por MCO permite obtener estimaciones puntuales de los parámetros del modelo. La inferencia acerca de los mismos permite completar dicha estimación puntual, mediante la estimación por intervalos y los contrastes de hipótesis. Los primeros posibilitan la obtención de un intervalo dentro del cual, con un determinado nivel de confianza, oscilará el verdadero valor de un parámetro, mientras que los segundos nos permitirán extraer consecuencias del modelo, averiguando si existe o no, evidencia acerca de una serie de conjeturas que pueden plantearse sobre sus parámetros.

La inferencia estadística consiste en la estimación de los parámetros poblacionales a partir de la información extraída de una muestra de dicha población. El número de estimaciones que podemos realizar de una población, a través de la extracción de diferentes muestras de un mismo tamaño, es generalmente muy grande porque cada una de las muestras posibles que se pueden sacar de la población arrojaría una estimación.

Por esta razón, a la estimación que obtenemos en una investigación por muestreo la acompañamos con un intervalo de valores posibles. La amplitud de dicho intervalo dependerá del grado de confianza que establezcamos.

El grado o nivel de confianza nos expresa el número de veces que la media verdadera de la población está incluida en cien intervalos de cien muestras extraídas de una población dada. El nivel de confianza más utilizado es el 95%, lo que quiere decir que 95 de cada 100 intervalos construidos contendrán el verdadero valor de la media.

El intervalo de confianza para la media de una población normalmente distribuida se construye en base a la probabilidad de que dicha media esté comprendida entre dos valores \(\bar X_a\) y \(\bar X_b\) equidistantes a ella:

\[\mathrm{P}(\bar X_a \leq \mu_{\bar X} \leq \bar X_b)=1-\alpha\]

siendo \(1-\alpha\) el nivel o grado de confianza asociado a dicho intervalo.

En términos generales, los intervalos de confianza para los estadísticos muestrales se expresan como:

Estimador ± (Factor de Fiabilidad)(Error Típico del Estimador)

3.6.1 Intervalos de Confianza

Para construir los intervalos de confianza de los parámetros \(\beta_i\), se parte de que la estimación MCO proporciona el valor medio de los posibles valores que pudiera tener dicho parámetro, y de que la distribución de dichos valores sigue una distribución derivada de la Normal que se conoce como t de Student.

Dicha distribución es simétrica presentando mayor dispersión que la curva Normal estándar para un tamaño muestral \(n\) pequeño. A medida que \(n\) aumenta (\(n > 100\)) es prácticamente igual que la distribución Normal.

El cálculo del intervalo de confianza para se realiza mediante la siguiente expresión:

\[\hat \beta_i \pm S_{\hat \beta_i}t_{n-k}\]

donde \(S_{\hat \beta_i}\) es la desviación típica estimada para el coeficiente, que se obtiene de la matriz de varianzas y covarianzas de los estimadores MCO \(\hat {Var} (\hat \beta) =(X'X)^{-1} \hat \sigma^{2}\), calculado \(\hat \sigma^{2}\) a partir de:

\[\hat \sigma^{2}=\frac{\sum \hat e_i^2}{n-k}=\frac{e'e}{n-k}\]

3.6.2 Contraste de hipótesis

Una buena parte de las investigaciones estadísticas están orientadas al desarrollo de procesos encaminados a la contrastación de hipótesis que previamente se han establecido.

Una hipótesis es una afirmación que está sujeta a verificación o comprobación. Hay que tener presente que una hipótesis no es un hecho establecido o firme, las hipótesis están basadas en la experiencia, en la observación, en la experimentación o en la intuición del sujeto que las formula.

Cuando las hipótesis se plantean de tal modo que se pueden comprobar por medio de métodos estadísticos reciben el nombre de hipótesis estadísticas. Estas hipótesis son afirmaciones que se efectúan sobre uno o más parámetros de una o más poblaciones. Las hipótesis estadísticas son de dos tipos: hipótesis nula e hipótesis alternativa. La hipótesis nula, o que no se verifique dicha afirmación, simbolizada por \(H_0\), es la hipótesis que se debe comprobar.

Para contrastar una hipótesis nula examinamos los datos de la muestra tomados de la población y determinamos si son o no compatibles con dicha hipótesis. Si son compatibles entonces \(H_0\) se acepta, en caso contrario se rechaza. Si se acepta la hipótesis nula afirmamos que los datos de esa muestra en concreto no dan suficiente evidencia para que concluyamos que la hipótesis nula sea falsa; si se rechaza decimos que los datos particulares de la muestra ponen de manifiesto que la hipótesis nula es falsa, entonces la hipótesis alternativa,\(H_1\), es considerada verdadera.

El criterio que permite decidir si rechazamos o no la hipótesis nula es siempre el mismo. Definimos un estadístico de prueba, y unos límites que dividen el espacio muestral en una región en donde se rechaza la hipótesis establecida, y otra región en la que no se rechaza, llamada región de aceptación. A la región donde se rechaza la hipótesis nula se le llama región crítica. Esta región es un subconjunto del espacio muestral, y si el valor del estadístico de prueba pertenece a él se rechaza la hipótesis nula.

El límite entre la región crítica y la región de aceptación viene determinado por la información previa relativa a la distribución del estadístico de prueba.

Señalar que un estadístico de prueba es una fórmula que nos dice como confrontar la hipótesis nula con la información de la muestra y es, por tanto, una variable aleatoria cuyo valor cambia de muestra a muestra.

Otra de las consideraciones a realizar en el contraste de hipótesis es fijar la probabilidad del error de rechazar la prueba siendo cierta, a este error se le denomina nivel de significación. Por ejemplo, si se utiliza un nivel de significación de \(\alpha =0,05\), equivale a decir que si para realizar un contraste tomáramos infinitas muestras de la población, rechazaríamos la hipótesis nula de forma incorrecta un 5 % de las veces.

En la formalización del procedimiento de contrastación podemos distinguir siete pasos principales:

Formular las hipótesis \(H_0\) y \(H_1\) a contrastar;
Proponer un estadístico de contraste;
Elegir un nivel de significación aceptable;
Determinar la región crítica y/o calcular el p-valor;
Tomar la decisión de aceptar o rechazar la hipótesis nula.

Para contrastar la hipótesis de que el parámetro poblacional \(\beta_i\) tome el valor \(\beta_i^0\), necesitamos:

Formular las hipótesis:

\(H_0: \beta_i=\beta_i^0\)

\(H_1:\beta_i \neq \beta_i^0\)

Calcular el estadístico de contraste:

\(t_i=\frac{\hat \beta_i - \beta_i}{S_{\hat \beta_i}}\)

Elegir el nivel de significación:

\(\alpha=0.05\) ó \(\alpha=0.1\)

Obtener en las tablas de la distribución t-student el valor crítico para un contraste bilateral (2 colas):

\(t_{n-k,0.025}\) ó \(t_{n-k,0.05}\)

Tambien se puede calcular p-valor asociado al valor de la t de student correspondiente al estadistico de contraste. El p-valor se define como la probabilidad de obtener un estadístico de contraste al menos tan extremo como el que evaluo.

Establecer la regla de decisión para aceptar la hipotesis nula \(H_0\):

Si \(\mid t_i \mid < t_{n-k,\frac{\alpha}{2}}\) acepto \(H_0\).

En el caso de que obtenga el p-valor del estadístico de contraste, este debe ser inferior al nivel de significación \(\alpha\) elegido.

3.6.3 Constraste de significación individual

Se denomina constraste de significación individual al contraste de hipótesis de que el parámetro \(\beta_i=0\). Es decir a:

Formular las hipótesis:

\(H_0: \beta_i=0\)

\(H_1:\beta_i \neq 0\)

Calcular el estadístico de contraste:

\(t_i=\frac{\hat \beta_i}{S_{\hat \beta_i}}\)

Elegir el nivel de significación:

\(\alpha=0.05\) ó \(\alpha=0.1\)

Obtener en las tablas de la distribución t-student el valor crítico o p-valor para un contraste bilateral (2 colas):

\(t_{n-k,0.025}\) ó \(t_{n-k,0.05}\)

Establecer la regla de decisión para aceptar la hipotesis nula \(H_0\):

Si \(\mid t_i \mid < t_{n-k,\frac{\alpha}{2}}\) acepto \(H_0\).

Aceptar \(H_0\) en este caso equivale a decir que el parámetro \(\beta_i\) es no significativo, ya que el valor cero entra dentro de los posibles valores que puede tomar el coeficiente en la población. En cambio rechazar \(H_0\), que ocurre cuando \(\mid t_i \mid > t_{n-k,\frac{\alpha}{2}}\) equivale a decir que el coeficiente \(\beta_i\) es significativo, y por tanto a adminitir algún tipo de influencia entre la variable \(X_i\) y la dependiente \(Y_i\).

3.6.4 Contraste de significación global(Tabla ANOVA)

La hipótesis de no significación global \(H_0:\beta_2=\beta_3=...=\beta_k=0\) se rechaza al nivel de significación \(α\) construyendo el estadístico experimental: \[F_{exp}=\frac {\frac {SCE}{k-1}}{\frac {SCR}{n-k}}\]

y la regla de decisión que rechaza la hipótesis \(H_0\) ocurre cuando \(F_{exp}>F_{k-1,n-k,\alpha}\) .

El contraste de significación global se resume en el cuadro siguiente, en donde la variación total de la variable dependiente (\(SCT\)) se descompone en la explicada por la regresión (\(SCE\)) y en la no explicada (\(SCR\)). Los grados de libertad de estas tres sumas de cuadrados son \(n-1\),\(k-1\) y \(n-k\), respectivamente.

A partir de esta información muestral, podemos calcular el numerador y denominador del estadístico \(F_{exp}\).

Fuente de variación	Suma de cuadrados	Grados de libertad	Cuadrado medio	Estadistico \(F\)
Regresión	\(SCE\)	\(k-1\)	\(\frac {SCE}{k-1}\)	\(\frac {\frac {SCE}{k-1}}{\frac {SCR}{n-k}}\)
Residual	\(SCR\)	\(n-k\)	\(\frac {SCR}{n-k}\)
Total	\(SCT\)	\(n-1\)

3.7 Predicción

Una vez estimado y validado el modelo, una de sus aplicaciones más importantes consiste en poder realizar predicciones acerca del valor que tomaría la variable endógena en el futuro o para una unidad extramuestral. Esta predicción se puede realizar tanto para un valor individual como para un valor medio, o esperado, de la variable endógena, siendo posible efectuar una predicción puntual o por intervalos. Su cálculo se realiza mediante las expresiones que figuran a continuación:

Predicción individual: se trata de hallar el valor estimado para la variable Y un periodo hacia delante. En este caso basta con sustituir el valor de las variables exógenas en el modelo en el siguiente periodo y calcular el nuevo valor de Y:

\[\hat y_{t+1}= \hat \beta_1 x_{1,t+1} + ...+\hat \beta_k x_{k,t+1}=X_{t+1}\hat \beta\]

Intervalo de predicción. Para hallar un intervalo de predicción debe utilizarse la siguiente expresión:

\[\hat y_{t+1} \pm t_{n-k,\frac{\alpha}{2}}\hat \sigma \sqrt{1+X'_{t+1}(X'X)^{-1}X_{t+1}} \]

Intervalos de predicción para un valor medio o esperado,\(y_i\):

\[\hat y_{i} \pm t_{n-k,\frac{\alpha}{2}}\hat \sigma \sqrt{X'_{i}(X'X)^{-1}X_{i}} \]

3.8 Estimacion del modelo de regresión con R

R es un entorno especialmente diseñado para el tratamiento de datos, cálculo y desarrollo gráfico. Permite trabajar con facilidad con vectores y matrices y ofrece diversas herramientas para el análisis de datos.

R es una implementación open-source del lenguaje S (Bell Labs -principios de los 90), que también es la base del sistema S-Plus (entorno comercial). R y S-Plus aún comparten una gran mayoría de código e instrucciones, si bien R es software libre, gratuito en donde los usuarios disponen de libertad para ejecutar, copiar, distribuir, estudiar, cambiar y mejorar el software. De hecho R dispone de una comunidad de desarrolladores/usuarios detrás que se dedican constantemente a la mejora y a la ampliación de las funcionalidades y capacidades del programa. En la web http://www.r-project.org/ se encuentra disponible toda la información acerca de R. La instalación de R se realiza a través de la CRAN (ComprehensiveR Archive Network): http://cran.r-project.org

Actualmente R se distribuye para los siguientes Sistemas Operativos:

•Windows: entorno gráfico.

•Linux (Debian/Mandrake/SuSe/RedHat/VineLinux)

•MacOSX

•Código fuente: ampliación a sistemas Unix

Las funciones de R se agrupan en paquetes (packages, libraries), los que contienen las funciones más habituales se incluyen por defecto en la distribución de R, y el resto se encuentran disponibles en la Comprehensive R Archive Network (CRAN).

Las entidades que R crea y manipula se llaman objetos. Dichos objetos pueden ser:

•Escalares: números, caracteres, lógicos (booleanos), factores

•Vectores/matrices/listas de escalares

•Funciones

•Objetos ad-hoc

Dichos objetos se guardan en un workspace. Durante una sesión de R todos los objetos estarán en memoria, y se pueden guardar en disco para próximas sesiones.

R trabaja sobre estructuras de datos. La estructura más simple es un vector numérico, que consiste en un conjunto ordenado de números.

Un vector de reales se crea mediante la función c y se guarda con el nombre “Cantidad”.

Cantidad <-c(2.456,2.325,2.250,2.200,2.100,2.082,2.045,2.024)

Se crea ahora el vector de nombre “Precio”. mediana, se utilizan las siguientes funciones R:

Precio<-c(82,92,94,99,106,108,112,115)

Para obtener los estadísticos básicos del vector (Cantidad): media, desviación estandar, varianza y

mean(Cantidad)

## [1] 2.18525

sd(Cantidad)

## [1] 0.1515847

var(Cantidad)

## [1] 0.02297793

median(Cantidad)

## [1] 2.15

Si se quiere tener un resumen sumario de estadístico de una variable:

summary(Cantidad)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   2.024   2.073   2.150   2.185   2.269   2.456

En R los valores “desconocidos” o “no disponibles” (missings) se simbolizan con el valor especial NA (NotAvailable). Cualquier operación que incluya un NA en general devolverá NA como resultado.La función is.na nos permite saber si un elemento es missing o no.

Otros tipos de objectosen R.

•Arrays y matrices (matrix): generación multidimensional de los vectores. Todos los elementos de la matriz han de ser del mismo tipo.

•Factores (factor): útiles para el uso de datos categóricos.

•Listas (list): generalización de los vectores donde los elementos pueden ser de diferentes tipos (incluso vectores o nuevas listas).

•Data frames: matrices donde las diferentes columnas pueden tener valores de diferentes tipos.

•Funciones (function): conjunto de código de R ejecutable y parametrizable.

Una tabla debe estar en un objecto tipo matriz.

Ejemplo:

Tabla<-matrix(c(652,1537,598,242,36,46,38,21,218,327,106,67),nrow=3,byrow=T)

La función de R que nos permite estimar un modelo de regresión lineal es la función lm. La forma de invocar a la función para estimar un modelo de regresión lineal simple es lm(y~x). Se puede consultar la ayuda de la función para ver todas las posibilidades que ofrece.

En nuestro ejemplo, obtenemos:

lm(Cantidad~Precio)

## 
## Call:
## lm(formula = Cantidad ~ Precio)
## 
## Coefficients:
## (Intercept)       Precio  
##     3.53427     -0.01336

En lugar de invocar simplemente la función podemos guardar su resultado en una variable y veremos así que obtenemos más información.

reg = lm(Cantidad~Precio)

Si queremos obtener una gráfica con los resultados de la regresión realizada:

plot(Cantidad~Precio)
lines(reg$fitted~Precio)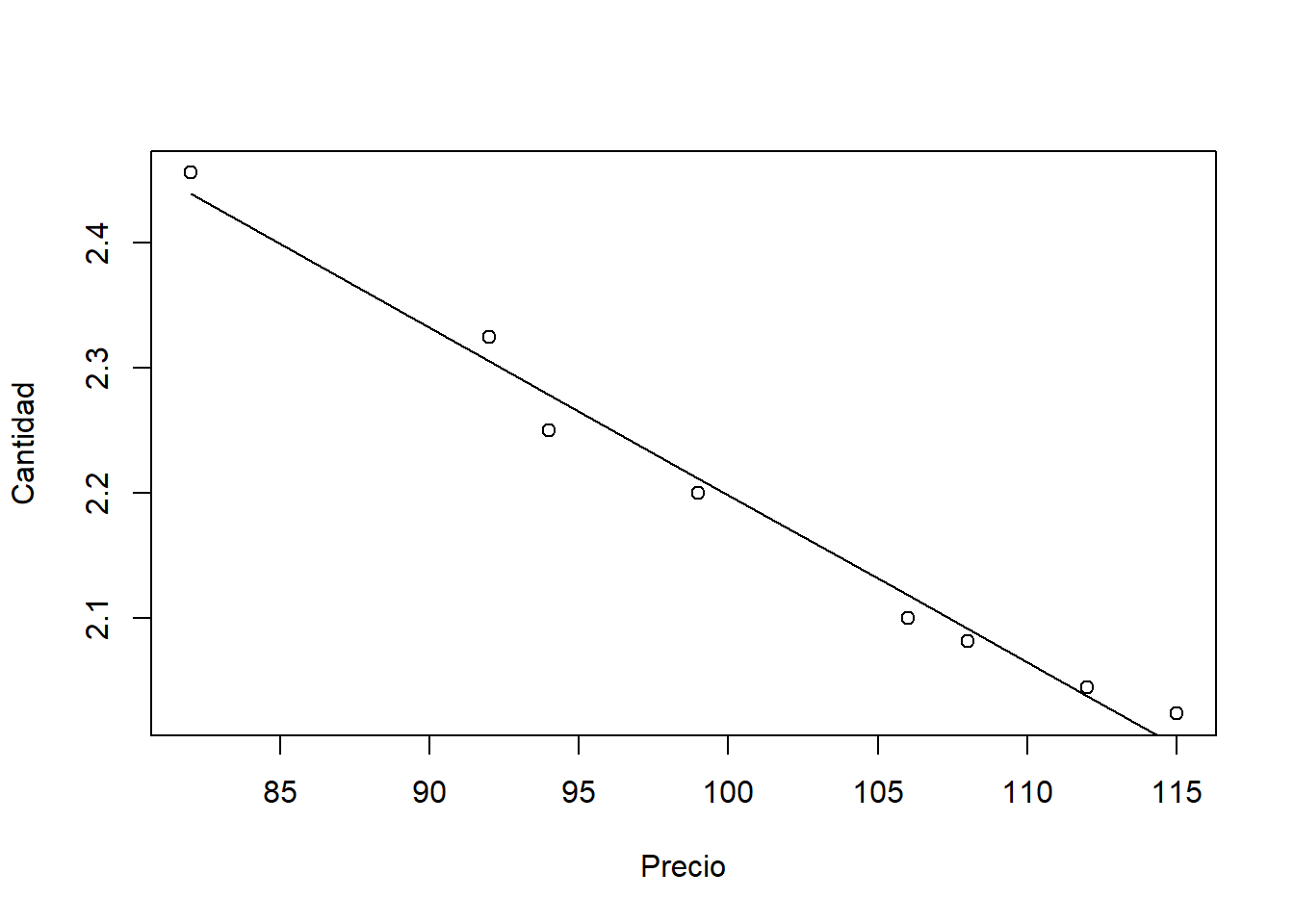

Para realizar el análisis del modelo estimado utilizaremos la función summary. Así:

summary(reg)

## 
## Call:
## lm(formula = Cantidad ~ Precio)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.02875 -0.01359 -0.00154  0.01762  0.02574 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  3.5342726  0.0734707   48.10 5.41e-09 ***
## Precio      -0.0133567  0.0007235  -18.46 1.63e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.02154 on 6 degrees of freedom
## Multiple R-squared:  0.9827, Adjusted R-squared:  0.9798 
## F-statistic: 340.8 on 1 and 6 DF,  p-value: 1.629e-06

Utilizando la base de datos “mtcars”, con datos sobre automoviles y sus características que incluye el programa R, cuya estructura se lista con la función “str”:

data(mtcars)
str(mtcars)

## 'data.frame':    32 obs. of  11 variables:
##  $ mpg : num  21 21 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 ...
##  $ cyl : num  6 6 4 6 8 6 8 4 4 6 ...
##  $ disp: num  160 160 108 258 360 ...
##  $ hp  : num  110 110 93 110 175 105 245 62 95 123 ...
##  $ drat: num  3.9 3.9 3.85 3.08 3.15 2.76 3.21 3.69 3.92 3.92 ...
##  $ wt  : num  2.62 2.88 2.32 3.21 3.44 ...
##  $ qsec: num  16.5 17 18.6 19.4 17 ...
##  $ vs  : num  0 0 1 1 0 1 0 1 1 1 ...
##  $ am  : num  1 1 1 0 0 0 0 0 0 0 ...
##  $ gear: num  4 4 4 3 3 3 3 4 4 4 ...
##  $ carb: num  4 4 1 1 2 1 4 2 2 4 ...

Realizamos una regresión lineal multiple entre el consumo de gasolina de cada coche y todas las caracteristicas que la base de datos incorpora para cada coche,

summary(lm(mpg~.,data=mtcars))

## 
## Call:
## lm(formula = mpg ~ ., data = mtcars)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -3.4506 -1.6044 -0.1196  1.2193  4.6271 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)  
## (Intercept) 12.30337   18.71788   0.657   0.5181  
## cyl         -0.11144    1.04502  -0.107   0.9161  
## disp         0.01334    0.01786   0.747   0.4635  
## hp          -0.02148    0.02177  -0.987   0.3350  
## drat         0.78711    1.63537   0.481   0.6353  
## wt          -3.71530    1.89441  -1.961   0.0633 .
## qsec         0.82104    0.73084   1.123   0.2739  
## vs           0.31776    2.10451   0.151   0.8814  
## am           2.52023    2.05665   1.225   0.2340  
## gear         0.65541    1.49326   0.439   0.6652  
## carb        -0.19942    0.82875  -0.241   0.8122  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.65 on 21 degrees of freedom
## Multiple R-squared:  0.869,  Adjusted R-squared:  0.8066 
## F-statistic: 13.93 on 10 and 21 DF,  p-value: 3.793e-07

El sumario de estadística sobre la regresión nos ofrece los resultados de los contrastes de significación individual sobre los parámetros y el de significación global.

Para realizar una preducción del consumo de gasolina (mpg) en el modelo lineal que utiliza como explicativas el peso del vehículo (wt) y los caballos de vapor (hp), en un coche que pese, 3(1000lbs) y tenga 120 hp hay que utilizar la función R: “predict”

summary(lm(mpg~wt+hp,data=mtcars))

## 
## Call:
## lm(formula = mpg ~ wt + hp, data = mtcars)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -3.941 -1.600 -0.182  1.050  5.854 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 37.22727    1.59879  23.285  < 2e-16 ***
## wt          -3.87783    0.63273  -6.129 1.12e-06 ***
## hp          -0.03177    0.00903  -3.519  0.00145 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.593 on 29 degrees of freedom
## Multiple R-squared:  0.8268, Adjusted R-squared:  0.8148 
## F-statistic: 69.21 on 2 and 29 DF,  p-value: 9.109e-12

newdatos=data.frame(wt=3,drat=120)
predict(lm(mpg~wt+drat,data=mtcars),newdatos,interval="prediction",type="response")

##        fit       lwr      upr
## 1 189.0406 -158.0087 536.0898