6 Métodos de clasificación

6.1 Introducción

La clasificación supervisada es una de las tares que más frecuentemente son llevadas a cabo por los denominados Sistemas Inteligentes. Por lo tanto, un gran número de paradigmas desarrollados bien por la Estadística (Regresión Logística, Análisis Discriminante) o bien por la Inteligencia Artificial (Redes Neuronales, Inducción de Reglas, Árboles de Decisión, Redes Bayesianas) son capaces de realizar las tareas propias de la clasificación.

En el apartado anterior se han estudidado los métodos desarrollados por la estadística basados en el análisis de regresión: Regresión Logística y Probit, aquí estudiaremos otros métodos estadísticos como lo son, el Análisis Discriminantes y los K vecinos próximos, y los Arboles de Decisión, las Máquinas Soporte Vector, Redes Neuronales y el Clasificador Bayesiano desarrollados por la Inteligencia Artificial.

Paso previo a aplicar un método de clasificación, es la partición del conjunto de datos en dos conjuntos de datos más pequeños que serán utilizadas con los siguientes fines: entrenamiento y test . El subconjunto de datos de entrenamiento es utilizado para estimar los parámetros del modelo y el subconjunto de datos de test se emplea para comprobar el comportamiento del modelo estimado. Cada registro de la base de datos debe de aparecer en uno de los dos subconjuntos, y para dividir el conjunto de datos en ambos subconjuntos, se utiliza un procedimiento de muestreo: muestreo aleatorio simple o muestreo estratificado. Lo ideal es entrenar el modelo con un conjunto de datos independiente de los datos con los que realizamos el test.

Como resultado de aplicar un método de clasificación, se cometerán dos errores, en el caso de una variable binaria que toma valores 0 y 1, habrá ceros que se clasifiquen incorrectamente como unos y unos que se clasifiquen incorrectamente como ceros. A partir de este recuento se puede construir el siguiente cuadro de clasificación:

Valor real $Y_i$ Valor estimado $\hat Y_i$	$Y_i=0$	$Y_i=1$
$\hat Y_i=0$	$P_{11}$	$P_{12}$
$\hat Y_i=1$	$P_{21}$	$P_{22}$

Donde $P_{11}$ y $P_{22}$ corresponderán a predicciones correctas (valores 0 bien predichos en el primer caso y valores 1 bien predichos en el segundo caso), mientras que $P_{12}$ y $P_{21}$ corresponderán a predicciones erróneas (valores 1 mal predichos en el primer caso y valores 0 mal predichos en el segundo caso). A partir de estos valores se pueden definir los índices que aparecen en el siguiente cuadro:

Indice	Definición	Expresión
Tasa de aciertos	Cociente entre las predicciones correctas y el total de predicciones	$\frac {P_{11}+P_{22}}{P_{11}+P_{12}+P_{21}+P_{22}}$
Tasa de errores	Cociente entre las predicciones incorrectas y el total de predicciones	$\frac {P_{12}+P_{21}}{P_{11}+P_{12}+P_{21}+P_{22}}$
Especificidad	Proporción entre la frecuencia valores cero correctos y el total de valores cero observados	$\frac {P_{11}}{P_{11}+P_{21}}$
Sensibilidad	Proporción entre la frecuencia de valores uno correctos y el total de valores uno observados	$\frac {P_{22}}{P_{12}+P_{22}}$
Tasa de falsos ceros	Proporción entre la frecuencia de valores cero incorrectos y el total de valores cero observados	$\frac {P_{21}}{P_{11}+P_{21}}$
Tasa de falsos unos	Proporción entre la frecuencia de valores uno incorrectos y el total de valores uno observados	$\frac {P_{12}}{P_{12}+P_{22}}$

Un método para evaluar clasificadores alternativo a la métrica expuesta es la curva ROC (Receiver Operating Characteristic). La curva ROC es una representación gráfica del rendimiento del clasificador que muestra la distribución de las fracciones de verdaderos positivos y de falsos positivos. La fracción de verdaderos positivos se conoce como sensibilidad, sería la probabilidad de clasificar correctamente a un individuo cuyo estado real sea definido como positivo. La especificidad es la probabilidad de clasificar correctamente a un individuo cuyo estado real sea clasificado como negativo. Esto es igual a restar uno de la fracción de falsos positivos.

La curva ROC también es conocida como la representación de sensibilidad frente a (1-especificidad). Cada resultado de predicción representa un punto en el espacio ROC. El mejor método posible de predicción se situaría en un punto en la esquina superior izquierda, o coordenada (0,1) del espacio ROC, representando un 100% de sensibilidad (ningún falso negativo) y un 100% también de especificidad (ningún falso positivo). Una clasificación totalmente aleatoria daría un punto a lo largo de la línea diagonal, que se llama también línea de no-discriminación. En definitiva, se considera un modelo inútil, cuando la curva ROC recorre la diagonal positiva del gráfico. En tanto que en un test perfecto, la curva ROC recorre los bordes izquierdo y superior del gráfico. La curva ROC permite comparar modelos a través del área bajo su curva.

Figure 6.1: Curva ROC

En R existe varias librería que ayuda a la representación de la curva ROC, el R-package ROCR y pROC.

library (pROC)

## Type 'citation("pROC")' for a citation.

## 
## Attaching package: 'pROC'

## The following objects are masked from 'package:stats':
## 
##     cov, smooth, var

data(aSAH)
plot.roc(aSAH$outcome, aSAH$s100b)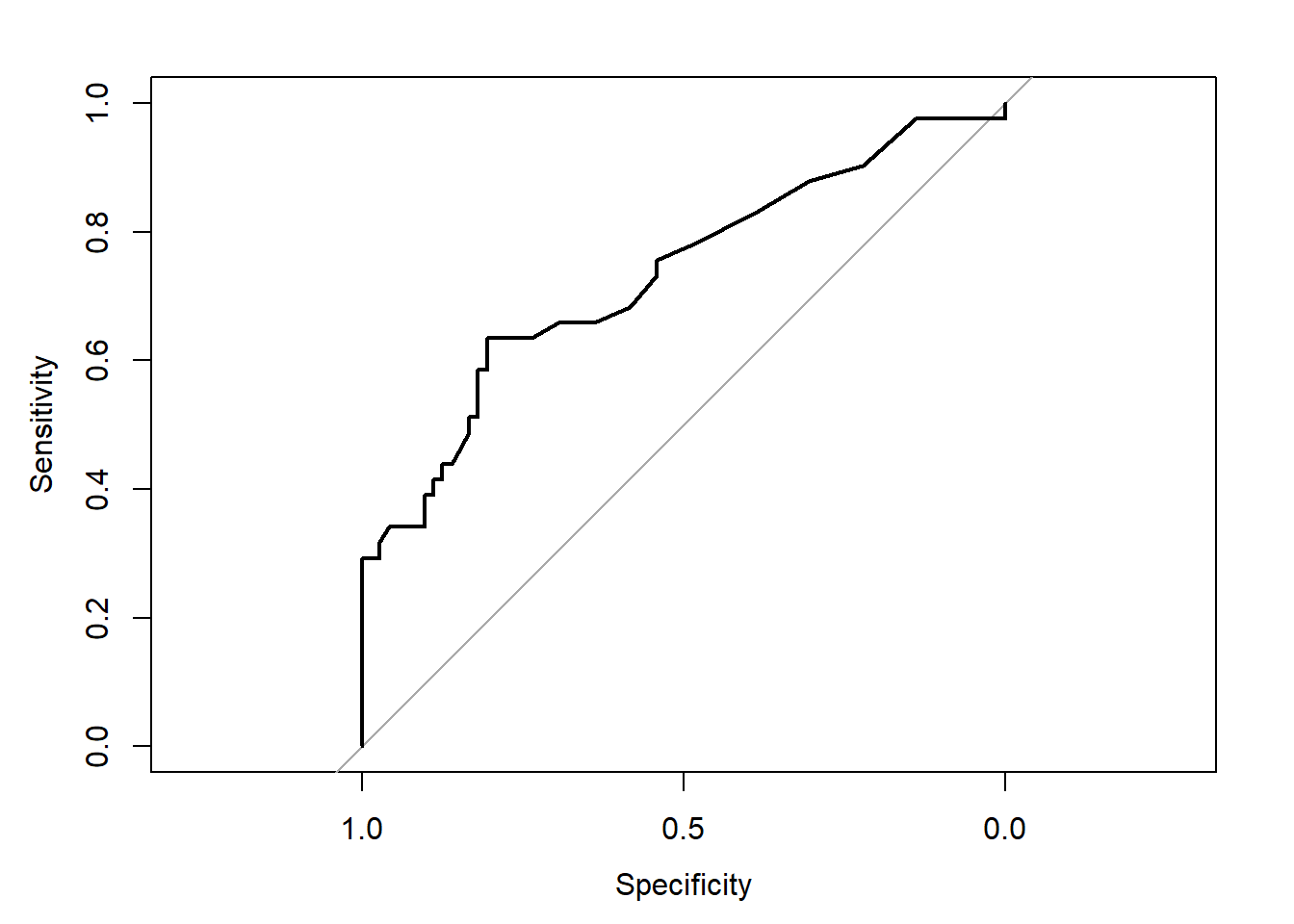

tiff("plot1.tiff", height = 12, width = 17, units = 'cm',
     compression = "lzw", res = 300)
dev.off()

## png 
##   2

6.2 Validación cruzada

La validación cruzada o cross-validation es una técnica utilizada para evaluar los resultados de un análisis estadístico cuando el conjunto de datos se ha segmentado en una muestra de entrenamiento y otra de prueba, la validación cruzada comprueba si los resultados del análisis son independientes de la partición. Aunque la validación cruzada es una técnica diseñada para modelos de regresión y predicción, su uso se ha extendido a muchos otros ejercicios de machine learning.

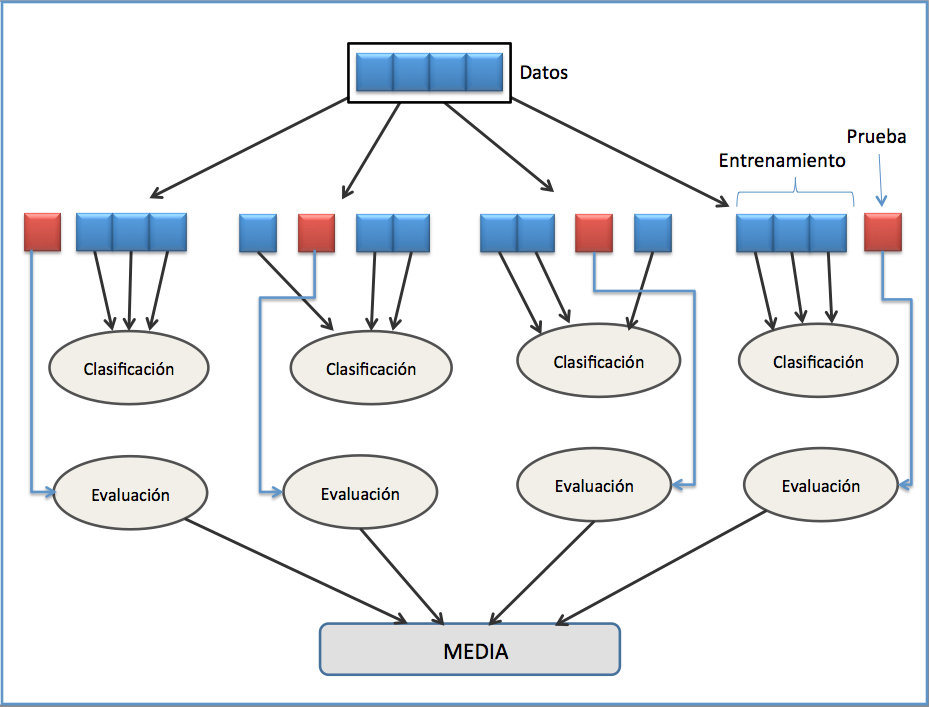
Figure 6.2: Validación cruzada(De Joan.domenech91 - Trabajo propio, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=17617674)

La manera más sencilla de realizar la validación cruzada es una vez segmentado el conjunto de datos en la muestra de entrenamiento y test, consiste en resolver el modelo con los datos de entrenamiento, y probar el modelo estimado en la muestra de test, la simple comparación del resultado obtenido en dicha muestra con las observaciones reales nos permite validar el modelo en termino de error (proceso hold-out). Una aplicación alternativa consiste en repetir el proceso anterior, seleccionando aleatoriamente distintos conjuntos de datos de entrenamiento, y calcular los estadísticos de validación a partir de la media de los valores en cada una de las repeticiones. A este método se le denomina Validación cruzada aleatoria. Los inconvenientes es que hay algunas muestras que quedan sin evaluar y otras que se evalúan más de una vez, es decir, los subconjuntos de prueba y entrenamiento se pueden solapar.

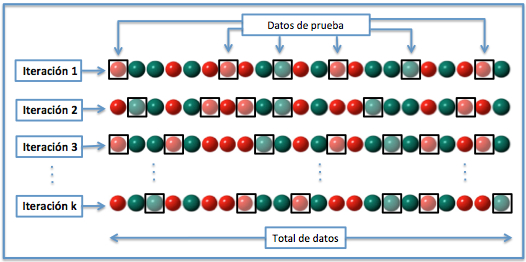
Figure 6.3: Validación cruzada aleatoria (De Joan.domenech91 - Trabajo propio, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=17616794)

Basado en el método anterior y con mayor utiliad cuando el conjunto de datos es pequeño es la Validación cruzada de K iteraciones o K-fold cross-validation. En este metodo, el total de los datos se dividen en k subconjuntos, de manera que aplicamos el método hold-out k veces, utilizando cada vez un subconjunto distinto para validar el modelo entrenado con los otros k-1 subconjuntos. El error medio obtenido de los k análisis realizados nos proporciona el error cometido por el método. En la práctica, la elección del número de iteraciones depende de la medida del conjunto de datos. Lo más común es utilizar la validación cruzada de 10 iteraciones (10-fold cross-validation).

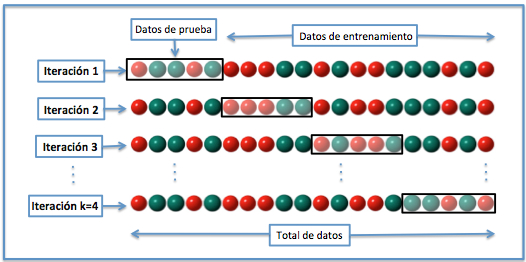
Validación cruzada dejando k interaciones (De Joan.domenech91 - Trabajo propio, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=17616792)

Figure 6.4: Validación cruzada dejando k interaciones (De Joan.domenech91 - Trabajo propio, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=17616792)

Por ultimo en la Validación cruzada dejando uno fuera o Leave-one-out cross-validation (LOOCV). Se separan los datos de forma que en cada iteración tengamos una solo dato para el test, constituyendo el resto la muestra de entrenamiento, el error obtenido sería el promedio de los errores cometidos en cada iteración. En este método la estimación del error es más estable, pero en cambio, a nivel computacional es muy costoso, puesto que se tienen que realizar un elevado número de iteraciones, tantas como sea el tamaño de nuestro conjunto de datos ya que cada dato se evalua en la fase de test.

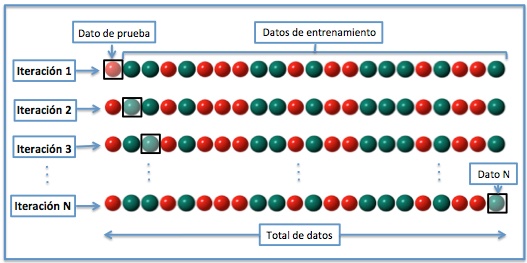
Figure 6.5: Validación cruzada aleatoria (De Joan.domenech91 - Trabajo propio, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=17616792)

6.3 Análisis discriminante

El Análisis Discriminante (AD), introducido por Fisher (1936), es una técnica que se utiliza para predecir la pertenencia a un grupo (variable dependiente) a partir de un conjunto de predictores (variables independientes). El objetivo del AD es entender las diferencias de los grupos y predecir la verosimilitud de que una persona o un objeto pertenezca a una clase o grupo basándose en los valores que toma en los predictores. Ejemplos de análisis discriminante son distinguir entre innovadores y no innovadores de acuerdo a sus perfiles demográficos y sociales o el riesgo de impago de un préstamo a través de predictores económicos y sociodemográficos.

Existen dos enfoques en la clasificación discriminante:

El basado en la obtención de funciones discriminantes de cálculo similar a las ecuaciones de regresión lineal múltiple.
Empleando técnicas de correlación canónica y de componentes principales, denominado análisis discriminante canónico.

El primer enfoque es el más común y es el que abordamos en este apartado. Su fundamento matemático está en conseguir, a partir de las variables explicativas, unas funciones lineales de éstas con capacidad para clasificar a otros individuos, donde la función de mayor valor define el grupo a que pertenece de forma más probable.

El AD solo admite variables cuantitativas como regresores, por lo que si alguna de las variables independientes es categórica, hay que utilizar otros métodos alternativos de clasificación.

El propósito del AD consiste en aprovechar la información contenida en las variables independientes para crear una función Z combinación lineal de las p variables explicativas, capaz de diferenciar lo más posible a los 2 grupos. La combinación lineal para el análisis discriminante, función discriminante de Fisher, se formula:

\[ z_{i}= \beta_0 + \beta_1 x_{1i} + \beta_2x_{2i}+...+ \beta_px_{pi}\]

donde,

$z_{i}$ es la puntuación $Z$ discriminante para el objeto $i$.

$\beta_0$ es el término constante.

$\beta_j$ es la ponderación discriminante para la variable independiente $j$.

$x_{ji}$ es la variable independiente $j$ para el objeto $i$.

Una vez hallada la función discriminante, el resultado es una única puntuación $z_i$ discriminante compuesta para cada individuo en el análisis. Promediando las puntuaciones discriminantes para todos los individuos dentro de un grupo particular, obtenemos la media del grupo. Esta media es conocida como centroide.

Sustituyendo en la función discriminante el valor de las medias del grupo 1 en las variables $X_1$ y $X_2$, obtenemos el centroide del grupo 1:

\[\bar z_{I}= \beta_0 + \beta_1 \bar x_{1,I} + \beta_2 \bar x_{2,I} + \cdots + \beta_p \bar x_{p,I}\]

De igual modo, sustituyendo las medias del grupo 2, obtenemos el centroide del grupo 2:

\[\bar z_{II}= \beta_0 + \beta_1 \bar x_{1,II} + \beta_2 \bar x_{2,II} + \cdots + \beta_p \bar x_{p,II}\]

La función $Z$ debe ser tal que la distancia entre los dos centroides sea máxima, consiguiendo de esta forma que los grupos estén lo más distantes posible. Podemos expresar esta distancia de la siguiente manera:

\[h= \bar z_{I}-\bar z_{II}\]

Es importante señalar que los grupos deben diferenciarse de antemano en las variables independientes. El análisis busca diferenciar los dos grupos al máximo combinando las variables independientes pero si los grupos no difieren en las variables independientes, no podrá encontrar una dimensión en la que los grupos difieran:

FAnálisis Discriminante

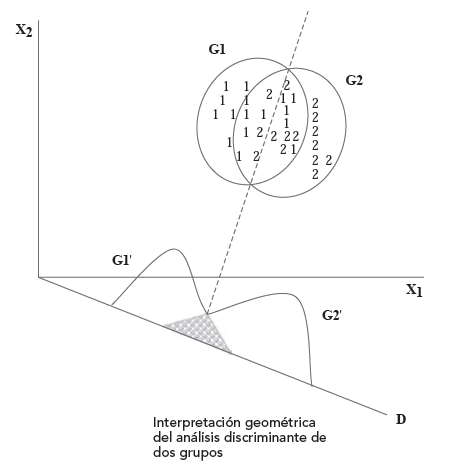
Dicho de otro modo, si el solapamiento entre los casos de ambos grupos es excesivo, los centroides se encontrarán en la misma o parecida ubicación en el espacio p-dimensional y en esas condiciones, no será posible encontrar una función discriminante útil para la clasificación. Si los centroides están muy próximos, las medias de los grupos en la función discriminante serán tan parecidas que no será posible distinguir a los sujetos de uno y otro grupo.

La mayor utilidad de una función discriminante radica en su capacidad para clasificar nuevos casos. Ahora bien, la clasificación de casos es algo muy distinto de la estimación de la función discriminante. De hecho, una función perfectamente estimada puede tener una pobre capacidad clasificatoria.

Una vez obtenida la función discriminate podemos utilizarla, en primer lugar, para efectuar una clasificación de los mismos casos utilizados para obtener la función: esto permitirá comprobar el grado de eficacia de la función desde el punto de vista de la clasificación. Si los resultados son satisfactorios, la función discriminante podrá utilizarse, en segundo lugar, para clasificar futuros casos de los que, conociendo su puntuación en las variables independientes, se desconozca el grupo al que pertenecen.

Una manera de clasificar los casos consiste en calcular la distancia existente entre los centroides de ambos grupos y situar un punto de corte $z_0=\frac{\bar z_{1}+\bar z_{2}}{2}$ equidistante de ambos centroides. A partir de ese momento, los casos cuyas puntuaciones discriminantes sean mayores que el punto de corte discriminante $z_0$, serán asignados al grupo superior, y los casos cuyas puntuaciones discriminantes sean menores que el punto de corte $z_0$, serán asignados al grupo inferior.

La regla de clasificación descrita sólo permite distinguir entre dos grupos, con lo que es difícilmente aplicable al caso de más de dos grupos e incluso a dos grupos con distinto tamaño. Con tamaños desiguales es preferible utilizar una regla de clasificación que desplace el punto de corte hacia el centroide del grupo de menor tamaño buscando igualar los errores de clasificación. Para calcular este punto de corte se utiliza una distancia ponderada:

\[z_0=\frac{n_I\bar z_{I}+n_{II}\bar z_{II}}{n_{I}+n_{II}}\]

La función discriminante de Fisher $Z$ se obtiene como función lineal de las p variables explicativas X, es decir:

\[z_i = \beta_1x_{1i}+\cdots+\beta_px_{pi}\ con\ i=1,\cdots,n\]

donde $z_i$ será la puntuación discriminante. En notación matricial, el modelo queda expresado como:

\[Z=X\beta\]

Donde las variables explicativas se expresarán en desviaciones respecto a la media y, de esta manera, las puntuaciones $z_i$ también lo estarán.

La variabilidad de la función discriminante (suma de cuadrados de las variables discriminantes en desviaciones respecto a su media) se expresa entonces como:

\[Z'Z = \beta'X'X\beta\]

La matriz $X'X$ es una matriz simétrica, y puede considerarse como la Suma de Cuadrados Total $(SCT)$ de las variables (explicativas) de la matriz X. Según la teoría del Análisis Multivariante de la Varianza, $X'X$ $(VT)$ se puede descomponer en la suma de la matriz entre-grupos $F$ y la matriz intra-grupos $W$ (o residual). Por tanto, la variabilidad quedaría expresada como:

\[Z'Z = \beta'X'X\beta = \beta'F\beta + \beta'W\beta\]

donde $F$ y $W$ son las matrices correspondientes a las sumas de cuadrados entre-grupos e intra-grupos respectivamente, que se calculan con los datos muestrales, mientras que los coeficientes $\beta_1,\cdots,\beta_p$ están por determinar.

Fisher (1936) obtuvo los $\beta_j$ maximizando la razón de la variabilidad entre-grupos respecto de la variación intra-grupos. Con este criterio se trata de determinar el eje discriminante de forma que las distribuciones proyectadas sobre el mismo estén lo más separadas posible entre sí (mayor variabilidad entre-grupos) y, al mismo tiempo, que cada una de las distribuciones esté lo menos dispersa (menor variabilidad intra-grupos).

Analíticamente, esto se expresa:

\[Max\lambda = \frac {\beta'F\beta}{\beta'W\beta}\]

La solución a este problema se obtiene derivando $\lambda$ respecto de $\beta$ e igualando a cero, es decir:

\[\frac {\partial \lambda}{\partial \beta} = \frac {2F \beta (\beta'W\beta) - 2W \beta (\beta' F \beta)} {(\beta' W \beta)^2} = 0 \Rightarrow F \beta (\beta' W \beta ) - W \beta (\beta' F \beta) = 0\]

Lo cual implica que:

\[\frac {F\beta} {W\beta} = \frac {\beta'F\beta}{\beta'W\beta} = \lambda \Rightarrow F\beta = W\beta \lambda \Rightarrow W^{-1} F \beta = \lambda \beta\]

En consecuencia, la ecuación para obtener el primer eje discriminante se traduce en la obtención de un vector propio $\beta$ asociado a la matriz no simétrica $W^{-1} F$.

Dado que $\lambda$ es la ratio a maximizar, cuando se calcule medirá el poder discriminante del primer eje discriminante. Como se está realizando un análisis discriminante con dos grupos, no se necesitan más ejes discriminantes.

Los coeficientes $(\hat \beta_1, \cdots,\hat \beta_p)$ normalizados correspondientes a las coordenadas del vector propio unitario asociado al mayor valor propio de la matriz $W^{-1} F$ obtenidos en el proceso de maximización, pueden contemplarse como un conjunto de cosenos directores que definen la situación del eje discriminante.

En general, al aplicar el análisis discriminante se le resta el valor de $z_0$ a la función discriminante, es decir, que vendrá dada por:

\[d_i = z_i - z_0 = \hat \beta_1x_{1i} + \hat \beta_2x_{2i} + \cdots + \beta_px_{pi} - z_0\]

Luego si $d_i<0$ el individuo i se clasificará en el primer grupo y si $d_i>0$ en el segundo.

En el caso general de un análisis discriminante con G grupos (G>2), el número máximo de ejes discriminantes que se pueden obtener viene dado por $Min(G-1,p)$. Por tanto, pueden obtenerse hasta G-1 ejes discriminantes si el número de variables explicativas p es mayor que G-1, lo cual suele ser cierto en la gran mayoría de las aplicaciones prácticas.

El resto de los ejes discriminantes vendrán dados por los vectores propios asociados a los valores propios de la matriz $W^{-1} F$ ordenados de mayor a menor. Así, el segundo eje discriminante tendrá menos poder discriminante que el primero, pero más que cualquiera de los restantes.

Como la matriz $W^{-1} F$ no es simétrica, los ejes discriminantes no serán en general ortogonales.

La generalización del procedimiento se realiza considerando la construcción de funciones discriminantes para cada grupo de la siguiente manera:

\[\begin{bmatrix}f_{1,i} = \alpha_{1,1}x_{1i} + \alpha_{1,2}x_{2i} + \cdots + \alpha_{1,p}x_{pi} - \bar z_1 \\ f_{2,i} = \alpha_{2,1}x_{1i} + \alpha_{2,2}x_{2i} + \cdots + \alpha_{2,p}x_{pi} - \bar z_2 \\ \vdots \\ f_{G,i} = \alpha_{G,1}x_{1i} + \alpha_{G,2}x_{2i} + \cdots + \alpha_{G,p}x_{pi} - \bar z_G \\ \end{bmatrix}\]

Y se clasifica a los individuos en el grupo para el que la función $F_g$ sea mayor.

Si consideramos el caso de dos grupos y restamos las funciones:

\[f_{2,i} - f_{1,i} = (\alpha_{2,1} - \alpha_{1,1})x_{1i} + (\alpha_{2,2} - \alpha_{1,2})x_{2i} + \cdots + (\alpha_{2,p} - \alpha_{1,p})x_{pi} - (\bar z_2 - \bar z_1)\]

es fácil ver que sería equivalente a la situación anterior, ya que:

\[\beta_1 = \alpha_{2,1} - \alpha_{1,1} \\ \beta_2 = \alpha_{2,2} - \alpha_{1,2} \\ \vdots \\ \beta_p = \alpha_{2,p} - \alpha_{1,p}\]

\[z_0 = \bar z_2 - \bar z_1\]

Y por tanto:

\[f_{2,i} - f_{1,i} = z_i - z_0 = d_i\]

La función R que realiza el Análisis Discriminante Lineal es “lda”. Para los 5 primeros datos, se dan los resultados de la clasificación (class), las probabilidades posteriores de pertenecer a la clase cero (posterior.0) o de pertenecer a la clase 1 (posterior.1), la probabilidad posterior es la probabilidad condicional que es asignada después de que la evidencia es tomada en cuenta.

Con la base de datos de R, Aid2, que contiene datos acerca de pacientes con sida,realizaremos un ejercicio de clasifición con AD, y evaluaremos los resultados con una métrica de porcentaje de aciertos y la curva ROC.

library(MASS)
data("Aids2")
str(Aids2)

## 'data.frame':    2843 obs. of  7 variables:
##  $ state  : Factor w/ 4 levels "NSW","Other",..: 1 1 1 1 1 1 1 1 1 1 ...
##  $ sex    : Factor w/ 2 levels "F","M": 2 2 2 2 2 2 2 2 2 2 ...
##  $ diag   : int  10905 11029 9551 9577 10015 9971 10746 10042 10464 10439 ...
##  $ death  : int  11081 11096 9983 9654 10290 10344 11135 11069 10956 10873 ...
##  $ status : Factor w/ 2 levels "A","D": 2 2 2 2 2 2 2 2 2 2 ...
##  $ T.categ: Factor w/ 8 levels "hs","hsid","id",..: 1 1 1 5 1 1 8 1 1 2 ...
##  $ age    : int  35 53 42 44 39 36 36 31 26 27 ...

# Lineal Discriminat Analisys
ad=lda(status~diag+age,data=Aids2)
#predicción
probs=predict(ad,newdata=Aids2,type="prob")
data.frame(probs)[1:5,]

##   class posterior.A posterior.D        LD1
## 1     A  0.54097063   0.4590294 -0.6423339
## 2     A  0.53868200   0.4613180 -0.6355380
## 3     D  0.03063147   0.9693685  2.0271192
## 4     D  0.03154984   0.9684502  2.0046295
## 5     D  0.09943774   0.9005623  1.1042254

table(probs$class,Aids2$status)

##    
##        A    D
##   A  794  332
##   D  288 1429

mean(probs$class==Aids2$status) #porcentaje de bien clasificados

## [1] 0.7819205

# Curva ROC
# Curva ROC
library(pROC)
plot.roc(Aids2$status,probs$posterior[,2])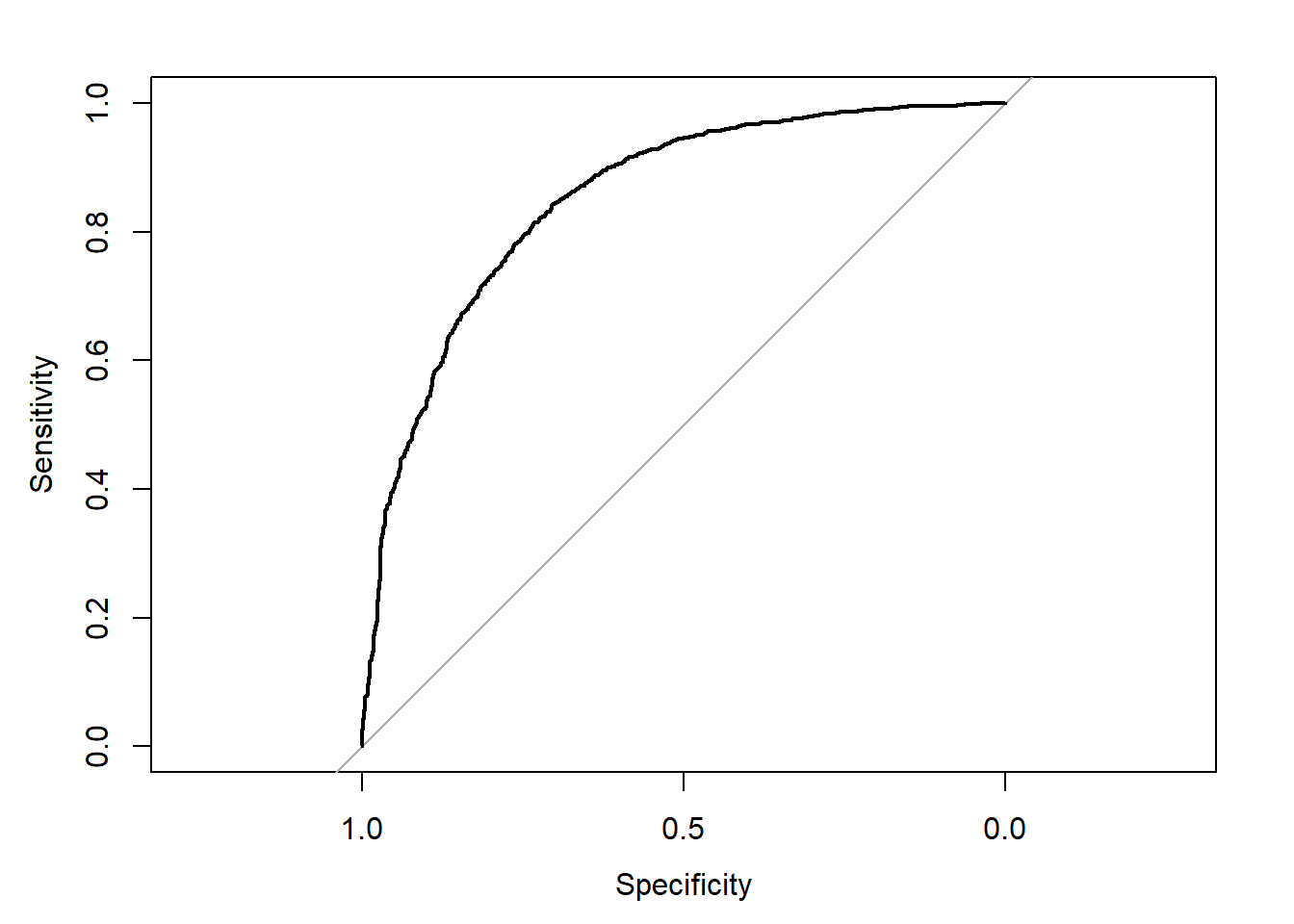

tiff("plot2.tiff", height = 12, width = 17, units = 'cm',
     compression = "lzw", res = 300)
dev.off()

## png 
##   2

Para realizar este ejercicio vamos a realizar una mineria de datos, dividiendo la base de datos en una muestra de entrenamiento y otra de test, la muestra de entrenamiento incluirá el 70% de las observaciones de la base de datos.

library(MASS)
data(iris)
attach(iris)
# división de la muestra en entrenamiento y validación
train=sample(seq(length(iris$Species)),length(iris$Species)*0.70,replace=FALSE)
# Lineal Discriminat Analisys
lda.tr=lda(Species[train]~.,data=iris[train,])
#predicción
probs=predict(lda.tr,newdata=iris[-train,],type="prob")
data.frame(probs)[1:5,]

##        class posterior.setosa posterior.versicolor posterior.virginica
## 1  virginica        0.3241278            0.3135759           0.3622963
## 4  virginica        0.2958421            0.2791339           0.4250240
## 7  virginica        0.3180254            0.2926340           0.3893406
## 8  virginica        0.3050308            0.2920003           0.4029689
## 10 virginica        0.2920032            0.2867852           0.4212116
##          x.LD1      x.LD2
## 1   0.09847649 -1.0257026
## 4  -0.54498513 -0.9637051
## 7  -0.18281033 -0.7901482
## 8  -0.32281753 -1.0161475
## 10 -0.50798780 -1.1730442

table(probs$class,iris$Species[-train])

##             
##              setosa versicolor virginica
##   setosa          5         13        10
##   versicolor      1          0         0
##   virginica      10          4         2

mean(probs$class==iris$Species[-train]) #porcentaje de bien clasificados

## [1] 0.1555556

6.4 Algorítmo K-vecinos más cercanos

El método K-nn (K nearest neighbors Fix y Hodges, 1951) es un método de clasificación supervisada (Aprendizaje, estimación basada en un conjunto de entrenamiento y prototipos) que sirve para estimar la función de densidad $F(x / C_j)$ de las predictora $x$ por cada clase $C_j$.

Este es un método de clasificación no paramétrico, que estima el valor de la función de densidad de probabilidad o directamente la probabilidad a posteriori de que un elemento $x$ pertenezca a la clase $C_j$ a partir de la información proporcionada por el conjunto de prototipos o ejemplos. En el proceso de aprendizaje no se hace ninguna suposición acerca de la distribución de las variables predictoras.

Figure 6.6: K-vecinos

En la figura nº 5.2 se ilustra el funcionamiento de este método de clasificación. En la figura se encuentran representadas 12 muestras pertenecientes a dos clases distintas: la Clase 1 está formada por 6 cuadrados de color azul y la Clase 2 formada por 6 círculos de color rojo. En este ejemplo, se han seleccionado tres vecinos, es decir, (k=3).

De los 3 vecinos más cercanos a la muestra $x$, representada en la figura por un aspa, uno de ellos pertenece a la Clase 1 y los otros dos a la Clase 2. Por tanto, la regla 3-nn asignará la muestra a la Clase 2. Es importante señalar que si se hubiese utilizado como regla de clasificación k=1, la 1-nn, la muestra sería asignada a la Clase 1, pues el vecino más cercano de la muestra pertenece a la Clase 1.

Un ejemplo de entrenamiento, $x_i$, es un vector en un espacio característico multidimensional, que está descrito en términos de atributos, y pertenecerá a una de las clases de la clasificación. Los valores de los atributos del i-esimo ejemplo se representan por el vector -dimensional:

\[x_i=(x_{1i},x_{2i},...,x_{pi}) \epsilon X\]

El espacio es particionado en regiones por localizaciones y etiquetas de clases de los ejemplos de entrenamiento. Un punto en el espacio es asignado a la clase si esta es la clase más frecuente entre los k ejemplos de entrenamiento más cercano. Generalmente se usa la distancia euclidiana.

\[ d(x_i,x_j)=\sqrt{\sum_{r=1}^p(x_{ri}-x_{rj})^2} \]

La fase de entrenamiento del algoritmo consiste en almacenar los vectores característicos y las etiquetas de las clases de los ejemplos de entrenamiento. En la fase de test, la evaluación del ejemplo (del que no se conoce su clase) es representada por un vector en el espacio característico. Se calcula la distancia entre los vectores almacenados y el nuevo vector, y se seleccionan los k ejemplos más cercanos. El nuevo ejemplo es clasificado con la clase que más se repite en los vectores seleccionados.

El método k-nn supone que los vecinos más cercanos nos dan la mejor clasificación y esto se hace utilizando todos los atributos; el problema de dicha suposición es que es posible que se tengan muchos atributos irrelevantes que dominen sobre la clasificación, de manera que los atributos relevantes perderían peso entre otros veinte irrelevantes.

La mejor elección de k depende fundamentalmente de los datos; generalmente, valores grandes de k reducen el efecto de ruido en la clasificación, pero crean límites entre clases parecidas. Un buen k puede ser seleccionado mediante un procedimiento de optimización. El caso especial en que la clase es predicha para ser la clase más cercana al ejemplo de entrenamiento (cuando k=1) es llamada Nearest Neighbor Algorithm, Algoritmo del vecino más cercano.

Con la base de datos de R, Aid2, vamos a realizar una minería de datos, dividiendo la encuesta en dos muestras una de entrenamiento con el 70% de los datos y una muestra test con el 30% restante, se va a realizar el proceso con el primer vecino próximo k=1 (Nearest Neighbor Algorithm), para ello hay que instalar el package-R class, e invocar la función knn, dentro de esta librería la función knn permite elegir el numero de vecinos a aproximar, en está función todas las covariables han de ser numéricas, por este motivo seleccionamos en un “data.frame”" las variables numéricas de la base de datos. Evaluaremos los resultados con una métrica de porcentaje de aciertos.

library(class)
# Selección de variables
x=data.frame(Aids2[,3],Aids2[,7])
str(x)

## 'data.frame':    2843 obs. of  2 variables:
##  $ Aids2...3.: int  10905 11029 9551 9577 10015 9971 10746 10042 10464 10439 ...
##  $ Aids2...7.: int  35 53 42 44 39 36 36 31 26 27 ...

# Selección muestra entrenamiento
train=sample(seq(length(Aids2$status)),length(Aids2$status)*0.70,replace=FALSE)
# K-Nearest Neighbors
knn.prd=knn(x[train,],x[-train,],Aids2$status[train],k=3,prob=TRUE)
table(knn.prd,Aids2$status[-train])

##        
## knn.prd   A   D
##       A 212  94
##       D 111 436

mean(knn.prd==Aids2$status[-train]) #porcentaje de bien clasificados

## [1] 0.7596717

# Validación cruzada con la muestra de entrenamiento
knn.cross=knn.cv(x[train,],Aids2$status[train],k=3,prob=TRUE)
table(knn.cross,Aids2$status[train])

##          
## knn.cross   A   D
##         A 477 235
##         D 282 996

6.5 Arboles de clasificación

6.5.1 Introducción.

Los árboles de decisión o clasificación tampoco es un modelos estadístico basado en la estimación de los parámetros de la ecuación propuesta, por tanto, no tenemos que estimar un modelo estadístico formal, son algoritmos para clasificar utilizando particiones sucesivas. Son apropiados cuando hay un número elevado de datos, siendo una de sus ventajas su carácter descriptivo que permite entender e interpretar fácilmente las decisiones tomadas por el modelo, revelando formas complejas en la estructura de datos que no se pueden detectar con los métodos convencionales de regresión.

Los árboles de decisión o de clasificación son un modelo surgido en el ámbito del aprendizaje automático (Machine Learning) y de la Inteligencia Artificial que partiendo de una base de datos, crea diagramas de construcciones lógicas que nos ayudan a resolver problemas. A esta técnica también se la denomina segmentación jerárquica. Es una técnica explicativa y descomposicional que utiliza un proceso de división secuencial, iterativo y descendente que partiendo de una variable dependiente, forma grupos homogéneos definidos específicamente mediante combinaciones de variables independientes en las que se incluyen la totalidad de los casos recogidos en la muestra.

Suponemos que se dispone de una muestra de entrenamiento que incluye la información del grupo al que pertenece cada caso y que sirve para construir el criterio de clasificación. Se comienza con un nodo inicial, dividiendo la variable dependiente a partir de una partición de una variable independendiente que se escoge de modo tal que de lugar a dos conjuntos homogeneos de datos (que maximizan la reducción en la impureza). Se elige, por ejemplo, la variable $x_1$ y se determina un punto de corte, por ejemplo $c$, de modo que se puedan separar los datos en dos conjuntos: aquellos con $x_1 \leq c$ y los que tienen $x_1 > c$. De este nodo inicial saldrán ahora dos: uno al que llegan las observaciones con $x_1 \leq c$ y otro al que llegan las observaciones con $x_1 > c$. En cada uno de estos nodos se vuelve a repetir el proceso de seleccionar una variable y un punto de corte para dividir la muestra. El proceso termina cuando se hayan clasificado todas las observaciones correctamente en su grupo.

En los árboles de decisión se encuentran los siguientes componentes: nodos, ramas y hojas. Los nodos son las variables de entrada, las ramas representan los posibles valores de las variables de entrada y las hojas son los posibles valores de la variable de salida. Como primer elemento de un árbol de decisión tenemos el nodo raíz que va a representar la variable de mayor relevancia en el proceso de clasificación. Todos los algoritmos de aprendizaje de los árboles de decisión obtienen modelos más o menos complejos y consistentes respecto a la evidencia, pero si los datos contienen incoherencias, el modelo se ajustará a estas incoherencias y perjudicará su comportamiento global en la predicción, es lo que se conoce como sobreajuste. Para solucionar este problema hay que limitar el crecimiento del árbol modificando los algoritmos de aprendizaje para conseguir modelos más generales. Es lo que se conoce como poda en los árboles de decisión.

Figure 6.7: Arboles de decisión

Las reglas de parada tratan de preguntar si merece la pena seguir o detener el proceso de crecimiento del árbol por la rama actual, se denominan reglas de prepoda ya que reducen el crecimiento y complejidad del árbol mientras se está construyendo:

Pureza de nodo. Si el nodo solo contiene ejemplos o registros de una única clase se decide que la construcción del árbol ya ha finalizado.
Cota de profundidad. Previamente a la construcción se fija una cota que nos marque la profundidad del árbol, cuando se alcanza se detiene el proceso.
Umbral de soporte. Se especifica un número de ejemplos mínimo para los nodos, y cuando se encuentre un nodo con ejemplos por debajo del mínimo se para el proceso, ya que no consideramos fiable una clasificación abalada con menos de ese número mínimo de ejemplos.

Existen dos formas de poda muy comunes utilizadas en los diferentes algoritmos: la poda por coste-complejidad y la poda pesimista. En la poda por coste-complejidad se trata de equilibrar la precisión y el tamaño del árbol. La complejidad está determinada por el número de hojas que posee el árbol (nodos terminales). La poda pesimista utiliza los casos clasificados incorrectamente y obtiene un error de sustitución, eliminando los subárboles que no mejoran significativamente la precisión del clasificador.

6.5.2 Características de los algoritmos de clasificación.

Los algoritmos que se encuentran, o bien solos o bien integrados en diferentes paquetes informáticos, son los que determinan o generan el procedimiento de cálculo que establece el orden de importancia de las variables en cada interacción. También se pueden imponer ciertas limitaciones en el número de ramas en que se divide cada nodo.

Los elementos y las herramientas de los algoritmos que determinan la construcción de un árbol son varios:

• El criterio para determinar la partición de cada nodo.

• La regla que declara un nodo terminal.

• La asignación de una clase a cada nodo terminal, lo que determina la regla de clasificación.

•Fusión: En relación a la variable dependiente, las categorías de las variables predictoras no significativas se agrupan juntas para formar categorías combinadas que sean significativas.

• Partición. Selección del punto de división. La variable utilizada para dividir el conjunto de todos los datos se elige por comparación con todas las demás.

• Poda. Se eliminan las ramas que añaden poco valor de predicción al árbol.

• La evaluación de la bondad del clasificador obtenido. La estimación de la validación del árbol y el cálculo del riesgo. Los métodos utilizados son los mismos, independientemente del método que se utilice para la generación del árbol.

6.5.3 Árbol CHAID (CHi-square Automatic Interaction Detection) y CHAID exhaustivo.

El algoritmo en el que se basa el CHAID, el AID (Automatic Interaction Detection) o Detección Automática de Interaciones, fue uno de los más utilizados en la década de los años setenta y principios de los ochenta hasta que surgió el CHAID. Se le llama así porque la idea inicial no perseguía el objetivo de la clasificación, sino que estaban centrados en las interacciones entre las variables.

Las primeras ideas de la segmentación AID fueron recogidas por Morgan y Sonquist (1963) que propusieron la utilización recursiva del Análisis de la Varianza con todos los pares posibles de las variables candidatas.

Este algoritmo presenta dos limitaciones muy importantes, derivadas, por una parte, del elevado número de elementos muestrales que requieren para efectuar los análisis y, por otra, de la carencia de un modelo explícito que explique o determine la relación existente entre la variable dependiente y las variables explicativas.

En el algoritmo AID las variables explicativas han de estar medidas en escalas nominales u ordinales y la variable a explicar, variable criterio o dependiente, puede medirse en una escala métrica (medida con una escala proporcional o de intervalo) o ficticia (dicotómica con valores 0 y 1).

El análisis AID constituye un Análisis de la Varian entre las categorías de la variable independiente, que maximiza la varianza za secuencial que se realiza mediante divisiones dicotómicas de la variable dependiente que busca en cada etapa la partición intergrupos y minimiza la varianza intragrupos.

La agrupación de categorías se efectúa probando todas las combinaciones binarias posibles de las variables. Es la prueba estadística F la que se utiliza para seleccionar las mayores diferencias posibles.

En este algoritmo, el proceso de subdivisión de la muestra en grupos dicotómicos continúa hasta que se verifica alguna de estas circunstancias:

• El tamaño de los grupos llega a un mínimo que se ha establecido de antemano.

• Las diferencias entre los valores medios de los grupos no son significativas, bien porque ninguna de las variables predictoras reduce significativamente la varianza residual, o bien porque los grupos son muy homogéneos y, por tanto, existe poca varianza intragrupos.

Las limitaciones de este algoritmo son importantes:

• Si se utilizan variables predictoras que difieren mucho en el número de categorías, el algoritmo tiende a seleccionar como más significativas y, por tanto, como más explicativas, aquellas variables que posean un número más elevado de categorías.

• Las particiones resultantes dependen de la variable que es elegida en primer lugar, lo que condiciona las sucesivas particiones.

• El carácter exclusivamente dicotómico de las particiones. Particiones con tres o más ramas reducen más la varianza residual y, además, pueden permitir una mejor selección de otras variables.

Muchas de las limitaciones del AID son corregidas por CHAID, que es un acrónimo de Chisquared Automatic Interaction Detection (detector automático de interacciones mediante Ji cuadrado). En lugar del Análisis de la Varianza, el arbol se desarrollas sobre las tablas de contingencia y el estadístico $\chi^2$. Aunque en un prinicipio fue diseñado para trabajar sólo con variables categóricas, posteriormente se incluyó la posibilidad de trabajar con variables categóricas nominales, categóricas ordinales y variables continuas, permitiendo generar tanto árboles de decisión para resolver problemas de clasificación como árboles de regresión.

En este algoritmo los nodos se pueden dividir en más de dos ramas. La construcción del árbol se basa en el cálculo de la significación de un contrate estadístico como criterio para definir la jerarquía de las variables predictoras o de salida, al igual que para establecer las agrupaciones de valores similares respecto a las variables de salida, a la vez que conserva inalterables todos los valores distintos. Todos los valores estadísticamente homogéneos son clasificados en una misma categoría y asignados a una única rama. Como medida estadística, si la prueba es continua, se utiliza la prueba F, mientras que si la variable predicha es categórica se utiliza la prueba Chi-cuadrado.

Para detectar si una relación es significativa, se utilizan varios métodos diferentes dependiendo del tipo de variables implicadas: variable dependiente nominal, ordinal, o de intervalo. Para el caso de que la variable dependiente sea nominal disponemos de dos test estadísticos: el criterio de la $\chi^2$ y la razon de verosimilitud ($G^2$).

La razón de verosimilitud en una tabla de contingencia se calcula:

\[G^2= \sum_{j=1}^J \sum_{i=1}^I n_{ij}\frac {n_{ij}}{n_{ij}^*}\]

Donde $ n_{ij}$ es el valor de la casilla (i,j) de la tabla de contingencia, y $n_{ij}^*$ son las frecuencias esperadas que se calculan:

\[n_{ij}^* \frac {\sum_{i=1}^I n_{ij} \sum_{j=1}^J} {n}\]

6.5.4 Árbol CART (Classification and Regression Trees)

El algoritmo CART es el acrónimo de Classification And Regression Trees (Árboles de Clasificación y de Regresión) fue diseñado por Breiman et al. (1984). Con este algoritmo, se generan árboles de decisión binarios, lo que quiere decir que cada nodo se divide en exactamente dos ramas.

Este modelo admite variables de entrada y de salida nominales, ordinales y continuas, por lo que se pueden resolver tanto problemas de clasificación como de regresión.

El algoritmo utiliza el índice de Gini para calcular la medida de impureza:

\[G(A_i)=\sum_{j=i}^{M_i}p(A_{ij})G(C/A_{ij})\]

Siendo, $G(C/A_{ij})$ igual a:

\[G(A_{ij})=-\sum_{j=i}^{M_i}p(C_k/A_{ij})(1-p(C_k/A_{ij}))\]

$A_{ij}$ es el atributo empleado para ramificar el árbol,
J es el número de clases,
$M_i$ es el de valores distintos que tiene el atributo $A_i$
$p(A_{ij})$ constituye la probabilidad de que $A_i$ tome su j-ésimo valor y
$p(C_k/A_{ij})$ representa la probabilidad de que un ejemplo sea de la clase $C_k$ cuando su atributo $A_i$ toma su j-ésimo valor.

El índice de diversidad de Gini toma el valor cero cuando un grupo es completamente homogéneo y el mayor valor lo alcanza cuando todas las $p(A_{ij})$ son contantes, entonces el valor del índice es $\frac {(J-1)}{J}$.

6.5.5 Árbol QUEST (Quick, Unbiased, Efficient Statistical Tree)

Este procedimiento denominado QUEST es el acrónimo de Quick, Unbiased, Efficient Statistical Tree (Árbol Estadístico Eficiente, Insesgado y Rápido). Este método fue propuesto por Loh y Shih (1997).

Este algoritmo trata de corregir y de restringir la exhaustiva búsqueda de particiones significativas que se generan tanto en los algoritmos AID y CHAID como en el CART.

Este método selecciona de forma previa la variable que segmenta mejor los datos, y después realiza la división óptima de ella.

Sintetizando el procedimiento, primero se elige la mejor variable predictora cuyo objetivo es que el número de categorías que poseen las variables no afecte a la elección de la mejor variable, para realizar después la mejor segmentación de la variable que ha seleccionado.

Este método QUEST sólo puede ser utilizado si la variable de salida es categórica nominal.

Además de empezar el proceso de segmentación con la selección de variables, en vez de con la fusión de categorías, se procede después a la mejor división de los valores de la variable elegida. Otros cambios propuestos en este algoritmo es la eliminación de la poda, la transformación de las variables cualitativas en cuantitativas a través del procedimiento CRIMCOORD y un cambio en los valores perdidos de los clasificadores en los distintos nodos. Además, el algoritmo contiene la posibilidad de construir particiones no binarias como CHAID y, a semejanza del método CART, el rechazo a la validación cruzada propuesta por Breiman et al. (1984). Respecto a estos algoritmos, la diferencia está en la forma de particionar los nodos.

Los autores propusieron una clasificación arbórea basada en el análisis discriminante, a la que llamaron FACT (Fast Algorithm for Classification Trees). Así, una vez que se ha seleccionado la variable, se procede a ver cuál es la mejor partición binaria del nodo, donde nos podemos encontrar en alguno de los casos siguientes:

• Si la variable dependiente tiene J categorías y necesitamos reducirla a 2, se realiza a través de un procedimiento de conglomerados K-means. Como centros de los conglomerados se escogen las medias muestrales de los pronosticadores más extremos y para cada media adicional se calcula la distancia cuadrática a los centros anteriormente elegidos y se agrupan al más cercano. Se vuelven a recalcular los centros y se vuelve a asignar un grupo dependiendo de la proximidad a los nuevos centros recalculados.

• Si la variable elegida es nominal hay que convertirla en un vector de variables ficticias empleando el análisis discriminante, que convierte cada valor discreto en otro continuo con valores entre -1 y +1. El valor asignado es la puntuación discriminante, calculada como se explica a continuación.

6.6 Árbol C5.0

El algoritmo C5 y, sobre todo, su versión no comercial, C4.5, es uno de los algoritmos más utilizados en el ámbito de los árboles de clasificación.

La forma de inferir árboles de decisión a través de este algoritmo es el resultado de la evolución del algoritmo C4.5 (Quinlan, 1993) diseñado por el mismo autor y que a su vez es el núcleo del programa perteneciente a la versión ID3 (Quinlan, 1986b).

Este algoritmo crea modelos de árbol de clasificación, permitiendo sólo variables de salida categórica. Las variables de entrada pueden ser de naturaleza continua o categórica.

El algoritmo básico ID3 construye el árbol de decisión de manera descendente y empieza preguntándose, ¿qué atributo es el que debería ser colocado en la raíz del árbol. Para resolver esta cuestión cada atributo es evaluado a través de un test estadístico que determina cómo clasifica él solo los ejemplos de entrenamiento. Cuando se selecciona el mejor atributo éste es colocado en la raíz del árbol. Entonces una rama y su nodo se crea para cada valor posible del atributo en cuestión. Los ejemplos de entrenamiento son repartidos en los nodos descendentes de acuerdo al valor que tengan para el atributo de la raíz.

El proceso se repite con los ejemplos, para seleccionar un atributo que será ahora colocado en cada uno de los nodos generados. Generalmente el algoritmo se detiene cuando los ejemplos de entrenamiento comparten el mismo valor para el atributo que está siendo probado. Sin embargo, es posible utilizar otros criterios para finalizar la búsqueda:

• Cobertura mínima de tal forma que el número de ejemplos por cada nodo está por debajo de cierto umbral.

• Pruebas estadísticas para probar si las distribuciones de las clases en los subárboles difieren significativamente.

Una de las maneras de cuantificar la bondad de un atributo consiste en considerar la cantidad e información que proveerá ese atributo tal y como está definido en la teoría de la información. Por tanto, este algoritmo está basado en el concepto de “ganancia de información”.

Si el conjunto de los registros de la base de datos T se agrupan en función de las categorías de la variable de salida S, obteniéndose una proporción pk para cada grupo asociado a un posible resultado o categoría, la función de entropía, en el caso de dos atributos de salida, con probabilidades p, y su complementaria, 1-p, que toma la siguiente expresión:

\[INFO(T)=p log_2 (p) (1-p) log_2 (1-p)\]

La ganancia de información teniendo en cuenta una variable de entrada, toma la siguiente expresión:

\[GANANCIA(X,T)=INFO(T)-INFO(X,T)\] Donde

\[INFO(X,T)=\sum_{i=1}^k \frac {T_i}{T} INFO(T_i)\]

$INFO(X,T)$ es la información aportada por la variable de salida $S$ cuando se tiene en cuenta una variable de entrada $X$.

$INFO(X,T_i)$ es la entropía de la variable de salida $S$ en cada subconjunto $T_i$ determinado por las k categorías de la variable de entrada $X$. Y $T_i$ es el número de registros asociados a una categoría i de la variable $X$.

El concepto de ganancia representa la diferencia necesitada para identificar la categoría destino asociada a un elemento $T$ y la información necesitada para identificar dicha categoría cuando se conoce el valor de una variable de entrada para ese mismo elemento. Lo que esto significa es que esa variable mostrará menor incertidumbre a la hora de la clasificación que el resto de variables de entrada.

6.6.1 Ejemplo con R

Con la base de datos de R, iris, vamos a realizar una minería de datos, dividiendo la encuesta en dos muestras una de entrenamiento con el 70% de los datos y una muestra test con el 30% restante, se va ha realizar la clasificación utilizando arboles de decisión CART, para ello hay que instalar el package-R: “tree”, e invocar la función tree. Se realiza una poda por el procedimiento de coste-complejidad, y mediante un procedimiento de validación cruzada elegirá el mejor resultado. Para ello hay que invocar la función cv.tree con la opción FUN=prune.misclas. Evaluaremos los resultados con una métrica de porcentaje de aciertos. La salida ofrece la tasa de errores (Misclassification error rate).

library(tree)
# Selección muestra entrenamiento
train=sample(seq(length(iris$Species)),length(iris$Species)*0.70,replace=FALSE)
iris.tree = tree(iris$Species~.,iris,subset=train)
summary(iris.tree)

## 
## Classification tree:
## tree(formula = iris$Species ~ ., data = iris, subset = train)
## Variables actually used in tree construction:
## [1] "Petal.Length" "Petal.Width"  "Sepal.Length"
## Number of terminal nodes:  5 
## Residual mean deviance:  0.1173 = 11.73 / 100 
## Misclassification error rate: 0.02857 = 3 / 105

plot(iris.tree);text(iris.tree,pretty=0)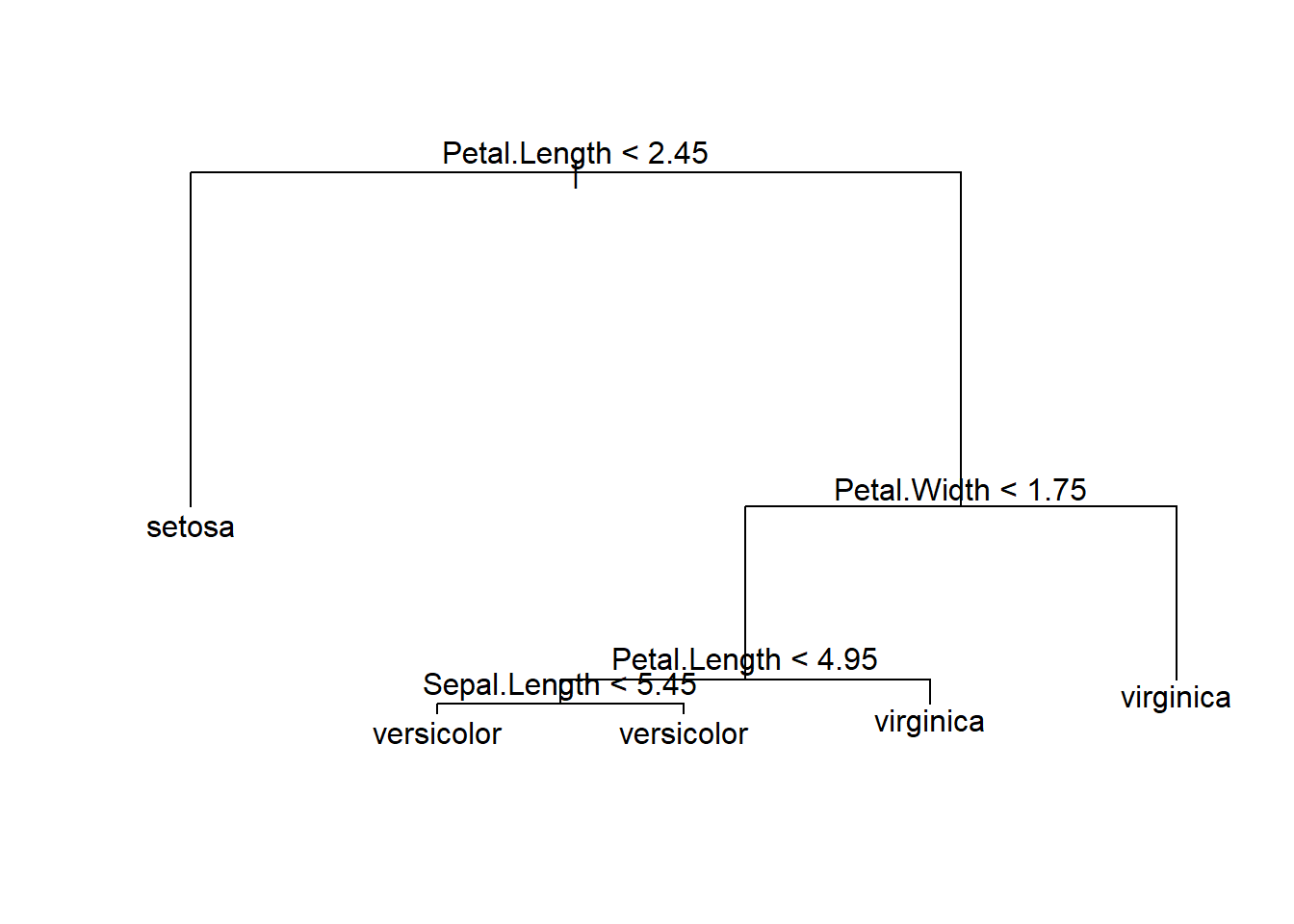

iris.tree

## node), split, n, deviance, yval, (yprob)
##       * denotes terminal node
## 
##  1) root 105 230.700 setosa ( 0.3429 0.3238 0.3333 )  
##    2) Petal.Length < 2.45 36   0.000 setosa ( 1.0000 0.0000 0.0000 ) *
##    3) Petal.Length > 2.45 69  95.640 virginica ( 0.0000 0.4928 0.5072 )  
##      6) Petal.Width < 1.75 38  25.570 versicolor ( 0.0000 0.8947 0.1053 )  
##       12) Petal.Length < 4.95 33   8.962 versicolor ( 0.0000 0.9697 0.0303 )  
##         24) Sepal.Length < 5.45 5   5.004 versicolor ( 0.0000 0.8000 0.2000 ) *
##         25) Sepal.Length > 5.45 28   0.000 versicolor ( 0.0000 1.0000 0.0000 ) *
##       13) Petal.Length > 4.95 5   6.730 virginica ( 0.0000 0.4000 0.6000 ) *
##      7) Petal.Width > 1.75 31   0.000 virginica ( 0.0000 0.0000 1.0000 ) *

tree.pred=predict(iris.tree,iris[-train],type="class")
summary(tree.pred)

##     setosa versicolor  virginica 
##         50         48         52

with(iris[-train],table(tree.pred,Species))

##             Species
## tree.pred    setosa versicolor virginica
##   setosa         50          0         0
##   versicolor      0         47         1
##   virginica       0          3        49

# Mediante validación cruzada se busca el mejor arbol de decision
cv.iris=cv.tree(iris.tree,FUN=prune.misclass)
cv.iris

## $size
## [1] 5 4 3 2 1
## 
## $dev
## [1]  6  6  6 60 80
## 
## $k
## [1] -Inf    0    1   30   35
## 
## $method
## [1] "misclass"
## 
## attr(,"class")
## [1] "prune"         "tree.sequence"

plot(cv.iris)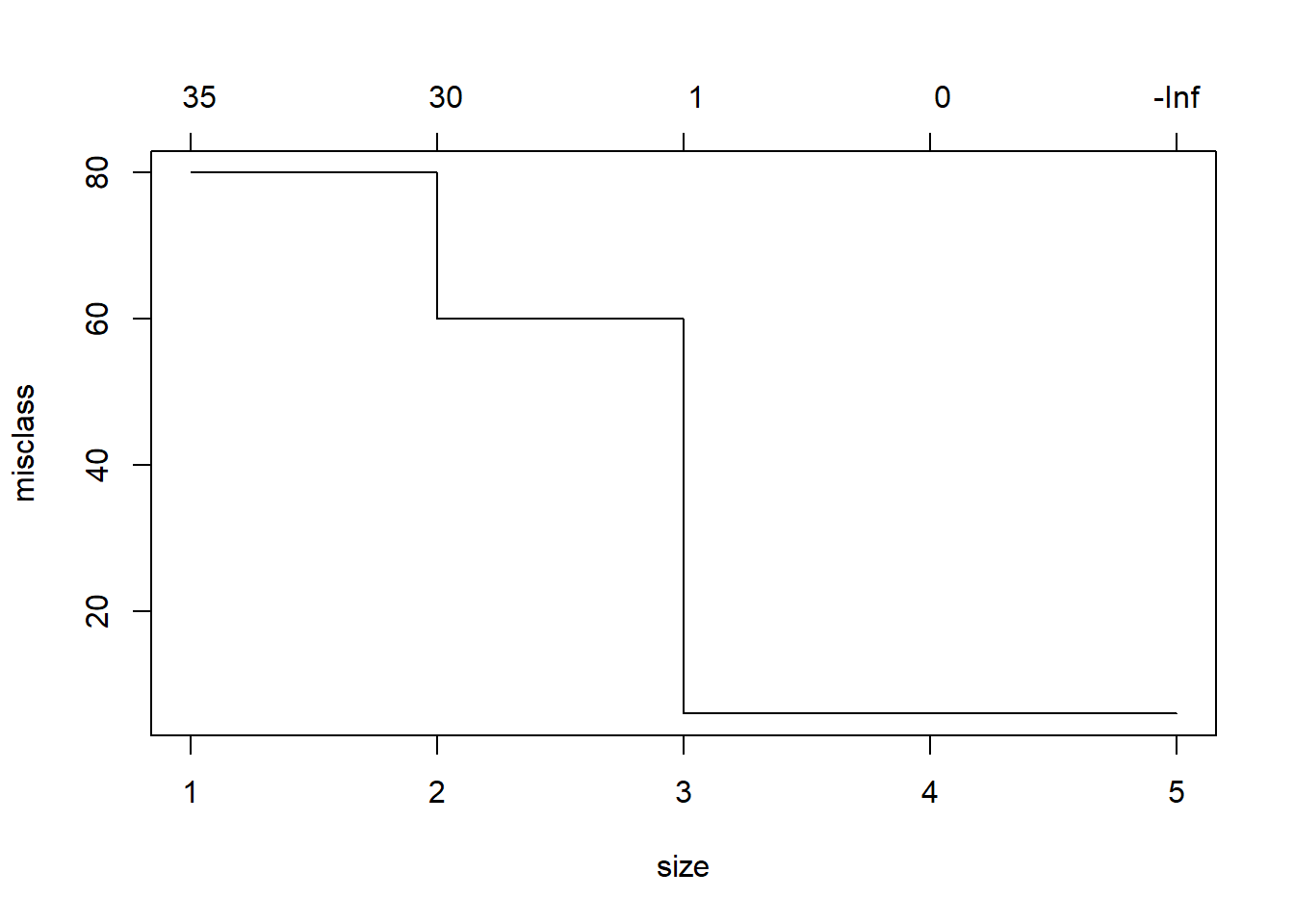

El mismo ejercicio realizado con la función C5.0 del package C50.

library(C50)
data(iris)
 

# Selección de una submuestra de 105 (el 70% de los datos)
set.seed(101)
iris.indices <- sample(1:nrow(iris),size=105)
iris.entrenamiento <- iris[iris.indices,]
iris.test <- iris[-iris.indices,]
 
modelo <- C5.0(Species~., data = iris.entrenamiento,rules=TRUE)
modelo

## 
## Call:
## C5.0.formula(formula = Species ~ ., data = iris.entrenamiento, rules
##  = TRUE)
## 
## Rule-Based Model
## Number of samples: 105 
## Number of predictors: 4 
## 
## Number of Rules: 4 
## 
## Non-standard options: attempt to group attributes

# predicción
prediccion <- predict(modelo,newdata=iris.test)
# Matriz de confusión
tabla <- table(prediccion, iris.test$Species)
tabla

##             
## prediccion   setosa versicolor virginica
##   setosa         15          0         0
##   versicolor      0         11         0
##   virginica       0          1        18

# % correctamente clasificados
100 * sum(diag(tabla)) / sum(tabla)

## [1] 97.77778

La función, rpart, del package “rpart” (Recursive Partitioning and Regression Trees), tambien permite realizar arboles de decisión. Por defecto utiliza en metodo “Class”, que es el apropiado para estimar arboles de decisión. En la opción “control” encontramos parámetros opcionales para controlar el crecimiento del árbol. Por ejemplo, en control = rpart.control (minsplit = 30, cp = 0.001) se le indica que el número mínimo de observaciones en un nodo sea 30 antes de intentar una división y que una división debe pararse cuando el Coste factor de complejidad sea inferior a un 0.001.

En este caso utilizamos un ejemplo de niños que tienen problemas de espalda (Kyphosis). El conjunto de datos se encuetra en la librería “rpart”, las variables sobre las que vamos a clasificar son: Age, la edad; Number, el número de vertebras;Start, el número de la primera vertebra (más alta) operada.

library(rpart)

## 
## Attaching package: 'rpart'

## The following object is masked from 'package:survival':
## 
##     solder

fit <- rpart(Kyphosis ~ Age + Number + Start, data = kyphosis)
plot(fit)
text(fit, use.n = TRUE)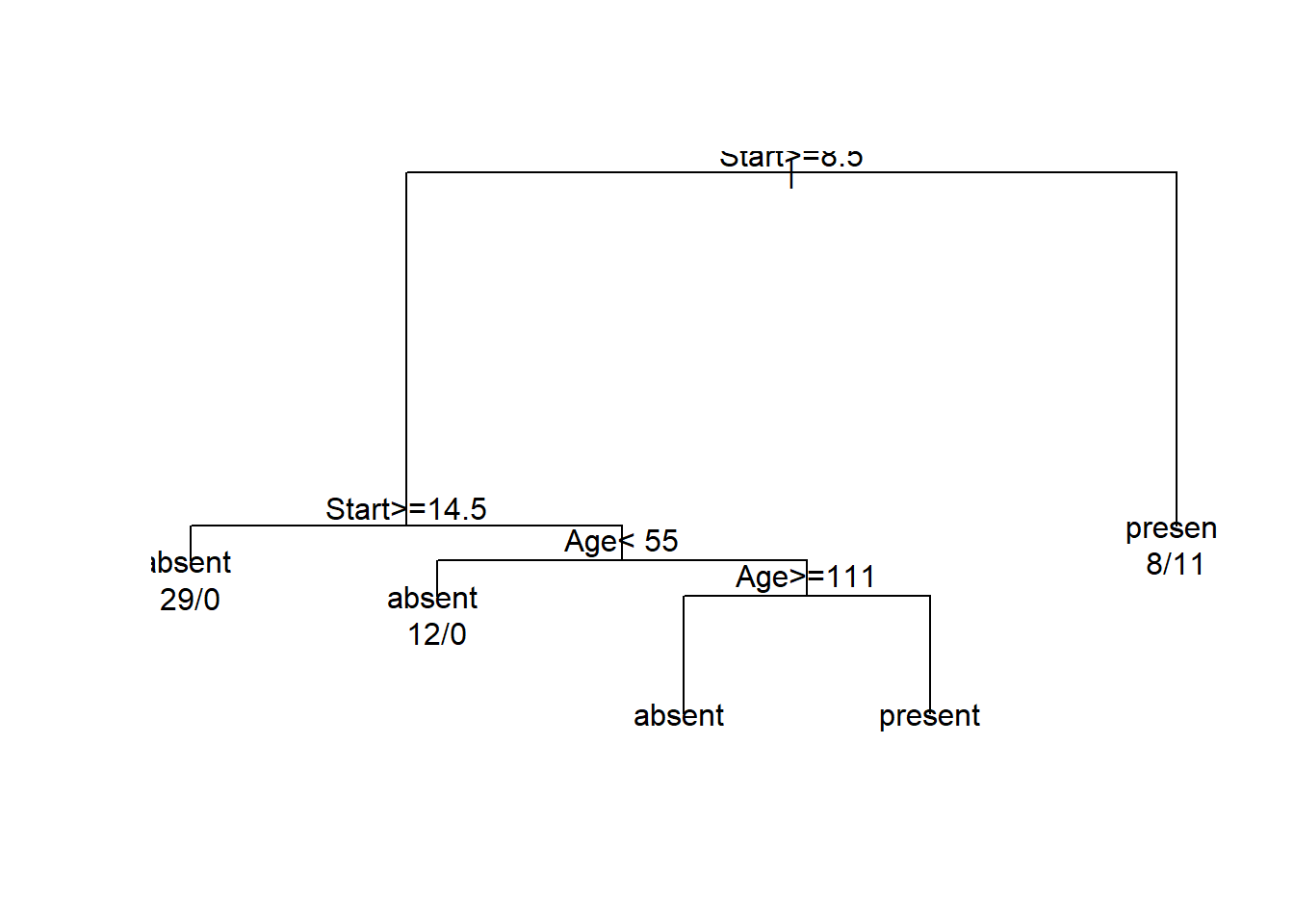

El algoritmo CHAID algorithm esta implementado en un package de R-Forge: https://R-Forge.R-project.org/R/?group_id=343

Realizar el ejercicio con la base de datos Aids2

6.7 Máquina Soporte Vector

Las Máquinas de Soporte Vectorial (Support Vector Machines SVMs) son un conjunto de algoritmos de aprendizaje supervisados que desarrollan métodos relacionados con los problemas de clasificación y regresión.

Como en la mayoría de los métodos de clasificación supervisada, los datos de entrada (los puntos) son vistos como un vector p-dimensional (una lista de p números). Dado un conjunto de puntos como un subconjunto de un conjunto mayor (espacio), en el que cada uno de ellos pertenece a una de dos posibles categorías, de manera que un algoritmo basado en SVM construye un modelo capaz de predecir si un punto nuevo (cuya categoría desconocemos) pertenece a una categoría o a la otra.

La SVM, intuitivamente, es un modelo que partiendo de un conjunto de ejemplos de entrenamiento, podemos etiquetarlos en diferentes clases y representar dichas muestras en puntos en el espacio para tratar de separar las diferentes clases mediante un espacio lo más amplio posible, para que cuando las nuevas muestras de los casos de test se pongan en correspondencia con dicho modelo puedan ser clasificadas correctamente en función de su proximidad.

En ese concepto de “separación óptima” es donde reside la característica fundamental de las SVM: este tipo de algoritmos buscan el hiperplano que tenga la máxima distancia (margen) con los puntos que estén más cerca de él mismo. Por eso también a veces se les conoce a las SVM como clasificadores de margen máximo. De esta forma, los puntos del vector que son etiquetados con una categoría estarán a un lado del hiperplano y los casos que se encuentren en la otra categoría estarán al otro lado.

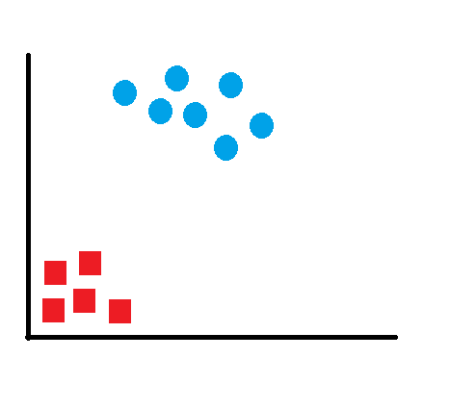
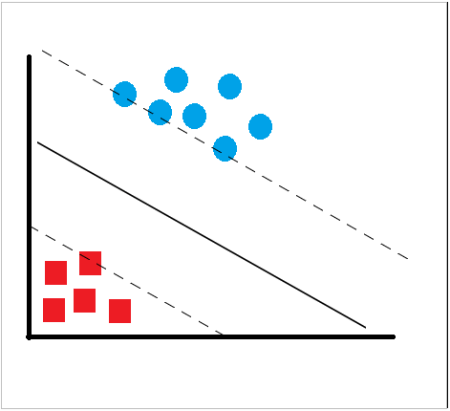
Figure 6.8: Máquinas Soporte Vector

La manera más simple de realizar la separación es mediante una línea recta, un plano recto o un hiperplano N-dimensional, pero los universos a clasificar no se suelen presentar en el ideal de las dos dimensiones como ocurre en el ejemplo gráfico, sino que un algoritmo SVM debe tratar con más de dos variables predictoras, curvas no lineales de separación, casos donde los conjuntos de datos no pueden ser completamente separados, clasificaciones en más de dos categorías. La representación por medio de funciones núcleo ó Kernel ofrece una solución a este problema, proyectando la información a un espacio de características de mayor dimensión el cual aumenta la capacidad computacional de la máquinas de aprendizaje lineal.

En la figura siguiente se presenta una programación R en donde SVM traza un hiperplano para clasificar la categoría de sertosa de la base de datos iris. Para ello hay que instalar el package-R: “e1017”, e invocar la función svm. Se estima un modelo con un lineal y un Kernel de base lineal (la función permite además funciones base polinomiales y sigmoides).

library("e1071")

## 
## Attaching package: 'e1071'

## The following objects are masked from 'package:agricolae':
## 
##     kurtosis, skewness

library("rgl")
train <- iris
train$y <-ifelse(train[,5]=="setosa", 1, -1)
sv <- svm(y~Petal.Length+Petal.Width+Sepal.Length,data=train,kernel="linear",scale=FALSE,type="C-classification")
W <- rowSums(sapply(1:length(sv$coefs), function(i)sv$coefs[i]*sv$SV[i,]))
plot3d(train$Petal.Length, train$Petal.Width,train$Sepal.Length, col=ifelse(train$y==-1,"red","blue"),size = 2, type='s', alpha = .6)
rgl.planes(a = W[1], b=W[2], c=W[3],d=-sv$rho,color="gray", alpha=.4)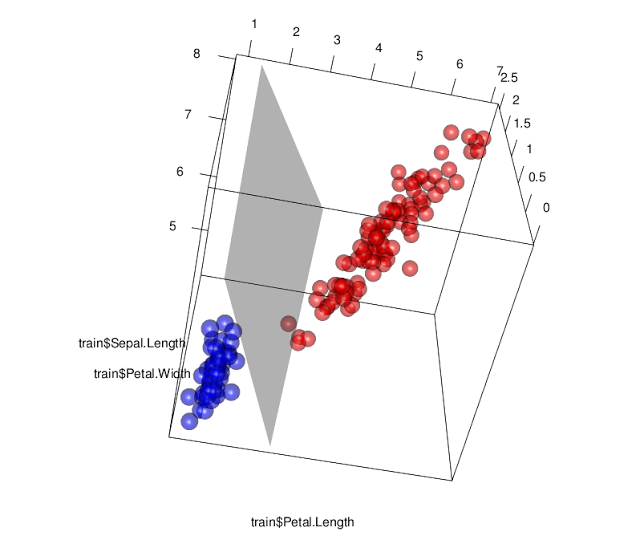

Figure 6.9: Clasificación de la clase Sertosa por SMV

Utilizamos la base de datos Aids, y realizamos un ejercicio de clasificación por svm, utilizando una muestra de entrenamiento y otra de test:

library(e1071)
# Selección de variables
datos=data.frame(Aids2[,-4])
str(datos)

## 'data.frame':    2843 obs. of  6 variables:
##  $ state  : Factor w/ 4 levels "NSW","Other",..: 1 1 1 1 1 1 1 1 1 1 ...
##  $ sex    : Factor w/ 2 levels "F","M": 2 2 2 2 2 2 2 2 2 2 ...
##  $ diag   : int  10905 11029 9551 9577 10015 9971 10746 10042 10464 10439 ...
##  $ status : Factor w/ 2 levels "A","D": 2 2 2 2 2 2 2 2 2 2 ...
##  $ T.categ: Factor w/ 8 levels "hs","hsid","id",..: 1 1 1 5 1 1 8 1 1 2 ...
##  $ age    : int  35 53 42 44 39 36 36 31 26 27 ...

# Selección muestra entrenamiento
train=sample(seq(length(Aids2$status)),length(Aids2$status)*0.70,replace=FALSE)
# se estima un modelo svm lineal para la muestra de entrenamiento
svmfit=svm(datos$status~.,data=datos,kernel="linear",scale=FALSE,subset=train)
print(svmfit)

## 
## Call:
## svm(formula = datos$status ~ ., data = datos, kernel = "linear", 
##     subset = train, scale = FALSE)
## 
## 
## Parameters:
##    SVM-Type:  C-classification 
##  SVM-Kernel:  linear 
##        cost:  1 
##       gamma:  0.07142857 
## 
## Number of Support Vectors:  645

table(datos$status[train],svmfit$fitted)

##    
##       A   D
##   A 542 188
##   D 261 999

# Predicción para la muestra test
svm.pred=predict(svmfit,datos[-train,])
summary(svm.pred)

##   A   D 
## 375 478

with(datos[-train,],table(svm.pred,status))

##         status
## svm.pred   A   D
##        A 268 107
##        D  84 394

# se estima un modelo svm lineal para la muestra de entrenamiento y se predice la muestra de test
svmfit2=svm(datos$status~.,data=datos,kernel="radial",scale=FALSE,subset=train,probability=TRUE)
print(svmfit2)

## 
## Call:
## svm(formula = datos$status ~ ., data = datos, kernel = "radial", 
##     probability = TRUE, subset = train, scale = FALSE)
## 
## 
## Parameters:
##    SVM-Type:  C-classification 
##  SVM-Kernel:  radial 
##        cost:  1 
##       gamma:  0.07142857 
## 
## Number of Support Vectors:  1913

svm.pred=predict(svmfit2,datos[-train,],probability=TRUE)
summary(svm.pred)

##   A   D 
## 191 662

with(datos[-train,],table(svm.pred,status))

##         status
## svm.pred   A   D
##        A 145  46
##        D 207 455

6.8 Red Neuronal Artificial

6.8.1 Introducción

Una Red Neuronal Artificial (RNA) es un modelo matemático inspirado en el comportamiento biológico de las neuronas y en cómo se organizan formando la estructura del cerebro. Las redes neuronales intentan aprender mediante ensayos repetidos como organizarse mejor a si mismas para conseguir maximizar la predicción.

El primer modelo matemático de una neurona artificial, creado con el fin de llevar a cabo tareas simples, fue presentado en el año 1943 en un trabajo conjunto entre el psiquiatra y neuroanatomista Warren McCulloch y el matemático Walter Pitts. Un modelo de red neuronal se compone de nodos, que actúan como input, output o procesadores intermedios. Cada nodo se conecta con el siguiente conjunto de nodos mediante una serie de trayectorias ponderadas. Basado en un paradigma de aprendizaje, el modelo toma el primer caso, y toma inicial basada en las ponderaciones. Se evalúa el error de predicción y modifica las ponderaciones para mejorar la predicción, a continuación se evalúa el siguiente caso con las nuevas ponderaciones y se modifican para mejorar la predicción de los casos ya evaluados, el ciclo se repite para cada caso en lo que se denomina la fase de preparación o evaluación. Cuandos se ha calibrado el modelo, con la muesta test se evalúan los resultados globales.

Las redes neuronales se hicieron operativas por primera vez a finales de los 50. Rosenblat F. (1958) creó el perceptrón , un algoritmo de reconocimiento de patrones basado en una red de aprendizaje de computadora de dos capas usando una simple suma y la resta. A finales de los 60 el proceso de investigación sufrío un estancamiento, y ha sido a partir de los años 80 del siglo pasado, cuando se produjo el mayor desarrollo teórico. Son muchos los modelos de redes neuronales, el más utilizado es el algoritmo backpropagation fue creado por Werbos P. (1990).

6.8.2 Tipos de modelos de redes neuronales

Existen actualmente más de 40 paradigmas de redes neuronales artificiales. Se estima que tan sólo cuatro arquitecturas:

el modelo perceptrón multicapa (MLP),
los mapas autoorganizados de Kohonen, (SOFM),
el vector de cuantificación (LVQ) y
las redes de base radial (RBF)

cubren, aproximadamente, el 90% de las aplicaciones prácticas de redes neuronales.

El modelo más utilizado es el perceptrón multicapa, que abarca el 70% de las aplicaciones, dado que se ha demostrado que este modelo es un aproximador universal de funciones (Funahashi 1989).

6.8.3 Ejemplo de red neuronal: El perceptón.

El elemento básico de una red neuronal es un nodo. Es la unidad de procesamiento que actúa en paralelo con otros nodos de la red. Es similar a las neuronas del cerebro humano: acepta input y genera output. Los nodos aceptan input de otros nodos. La primera tarea del nodo es procesar los datos de entrada creando un valor resumen que es la suma de todas las entradas multiplicadas por sus ponderaciones. Este valor resumen se procesa a continuación mediante una función de activación para generar una salida que se envía al siguiente nodo del sistema.

Se considera una red neuronal la ordenación secuencial de tres tipos básicos de nodos o capas: nodos de entrada, nodos de salida y nodos intermedios (capa oculta o escondida).

Los nodos de entrada se encargan de recibir los valores iniciales de los datos de cada caso para transmitirlos a la red. Los nodos de salida reciben entradas y calculan el valor de salida (no van a otro nodo). En casi todas las redes existe una tercera capa denominada oculta.

Este conjunto de nodos utilizados por la red neuronal, junto con la función de activación, posibilita a las redes neuronales representar fácilmente las relaciones no lineales, que son muy problemáticas para las técnicas multivariantes.

Un ejemplo de modelo neuronal con $n$ entradas, consta de:

Un conjunto de entradas $x_1,…x_n$.
Los pesos sinápticos $w_1,…w_n$, correspondientes a cada entrada.
Una función de agregación,$\sum$.
Una función de activación,$f$.
Una salida,$Y$.

Las entradas son el estímulo que la neurona artificial recibe del entorno que la rodea, y la salida es la respuesta a tal estímulo. La neurona puede adaptarse al medio circundante y aprender de él modificando el valor de sus pesos sinápticos, y por ello son conocidos como los parámetros libres del modelo, ya que pueden ser modificados y adaptados para realizar una tarea determinada.

En este modelo, la salida neuronal $Y$ está dada por:

$Y=f(\sum_{i=1}^{n}w_ix_i)$

La función de activación se elige de acuerdo a la tarea realizada por la neurona. Entre las más comunes dentro del campo de las RNAs podemos destacar:

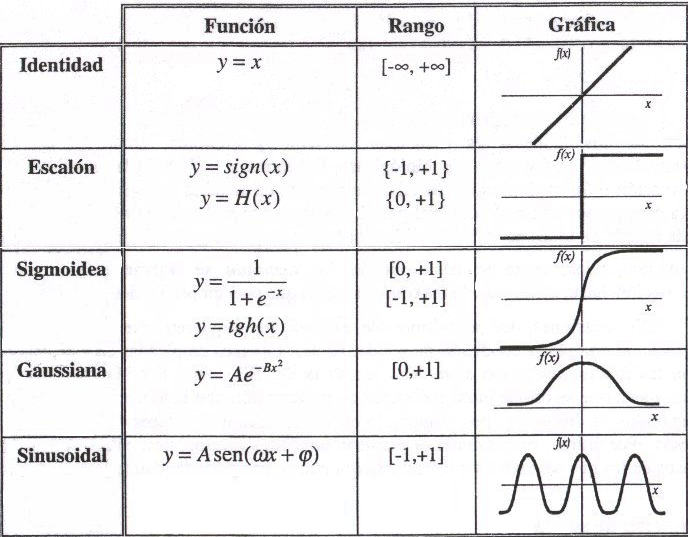
Figure 6.10: Funciones de Activación

En un modelo de red neuronal para realizar tareas de clasificación en el plano (por lo que solo haremos uso de dos entradas, $x_1$ y $x_2$), vamos a considerar que existe una entrada de peso 1, llamada $b$ y consideraremos como función de activación a la función signo definida por:

$\Gamma(s) = \left\{ \begin{array}{cl} 1 & \mbox{si } s \geq 0 \\ -1 & \mbox{si } s < 0 \end{array} \right.$

Por lo tanto, la salida neuronal $Y$ estará dada en este caso por:

$Y =\left\{ \begin{array}{cl} 1 & \mbox{si } w_1 x_1 + w_2 x_2 + b \geq 0 \\ -1 & \mbox{si } w_1 x_1 + w_2 x_2 + b < 0 \end{array} \right.$

Supongamos que tenemos dos clases en el plano: la clase $C_1$, formada por los círculos rojos, y la clase $C_2$, formada por los círculos azules, donde cada elemento de estas clases está representado por un punto (x,y) en el plano. Supondremos además que tales clases son separables linealmente, es decir, es posible trazar una recta que separe estrictamente ambas clases.

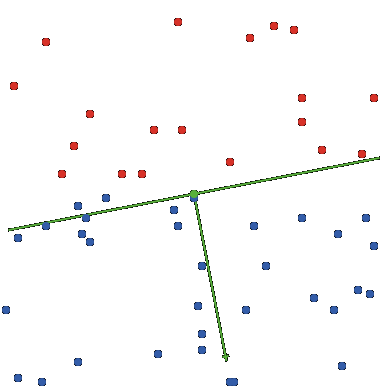
Figure 6.11: Red Neuronal

Diremos que la neurona artificial clasifica correctamente las clases $C_1$ y $C_2$ si dados los pesos sinápticos $w_1$ y $w_2$ y el término aditivo $b$, la recta con ecuación:

$y = −\frac{w_1}{w_2} x − \frac{b}{w_2}$

es una recta que separa las dos clases. La ecuación implícita de la recta es $w_1x + w_2y + b = 0$.Obsérvese que si el punto $(x_0,y_0) \in C_1$ entonces $w_1x_0+ w_2y_0+ b < 0$ y si $(x_0,y_0) \in C_2$ entonces $w_1x_0+ w_2y_0+ b > 0$ Por lo tanto, dado el par $(x_0,y_0) \in C_1\cup C_2$, la neurona clasifica de la siguiente manera:

$(x_0,y_0) \in C_1 \Leftrightarrow Y = −1$

$(x_0,y_0) \in C_2 \Leftrightarrow Y = 1$

Si ahora tomamos dos clases $C^∗_1$ y $C^∗_2$ (separables linealmente) distintas a las anteriores, entonces la neurona puede no clasificar correctamente a estas clases, pues la recta anterior puede no ser una recta válida para separarlas. Sin embargo, es posible modificar los parámetros anteriores y obtener nuevos parámetros $w^∗_1$,$w^∗_2$ y $b^∗$ tal que la recta $y = −\frac{w^*_1}{w^*_2} x − \frac{b^*}{w^*_2}$, sirva ahora de separación entre ellos.

El proceso por el cual la neurona pasa de los parámetros $w_1$,$w_2$,$b$ a los parámetros $w^∗_1$,$w^∗_2$, $b^∗$ se conoce como método de aprendizaje. Este proceso es el que permite modificar los parámetros libres con el fin de que la neurona se adapte y sea capaz de realizar diversas tareas.

El método de aprendizaje que detallaremos a continuación y que utilizaremos para adaptar los parámetros libres con el fin de clasificar correctamente las clases $C^∗_1$ y $C^∗_2$ se conoce como método de error-corrección. Para aplicarlo es necesario:

Un conjunto de entrenamiento, $D = C_1\cup C_2$.
Un instructor.
Valores iniciales, $w'_1$,$w'_2$, $b'$, arbitrarios de los parámetros libres.

El entrenamiento consiste en lo siguiente:

El instructor toma un elemento $(x_0,y_0)\in D$ al azar y presenta éste a la neurona.
Si la neurona clasifica mal este punto, es decir, si la salida de la neurona es $Y=−1$ cuando $(x_0,y_0) \in C_2$ o $Y=1$ cuando $(x_0,y_0) \in C_1$, entonces se aplica la siguiente corrección a los parámetros libres iniciales

$w_1= w'_1+ d x_0$

$w_2= w'_2+ d y_0$

$b = b'+ d$

donde el valor de $d$ se obtiene de la siguiente manera:

$d = =\left\{ \begin{array}{cl} 1 & \mbox{si } Y=-1 \mbox{ y } (x_0,y_0)\in C_2 \\ -1 & \mbox{si } Y=1 \mbox{ y } (X_0,y_0)\in C_1 \end{array} \right.$

Si la neurona clasifica bien el punto $(x_0,y_0)$, entonces no se realiza ninguna corrección.
El procedimiento se repite pasando a la neurona otro punto del conjunto $D$ y usando los últimos parámetros$w_1$,$w_2$, $b$ corregidos (no los iniciales). Nuevamente, si la neurona clasifica mal el punto, entonces se aplica una corrección similar a la anterior.
Esta tarea se repite con todos los puntos del conjunto $D$.
Si en el proceso hubo correcciones, entonces el procedimiento es repetido nuevamente con todos los puntos de $D$.
El entrenamiento termina cuando la neurona clasifica correctamente todos los elementos del conjunto de entrenamiento.

Un modelo neuronal utilizado para clasificación, cuya salida está dada de la forma anterior y que utiliza el método de error-corrección para modificar sus parámetros libres se conoce como Perceptron (el nombre deriva de la palabra en inglés “perception”). Estas neuronas pueden agruparse formando una RNA conocida como Perceptron múltiple.

Mas detalles en: http://www.cs.us.es/~fsancho/?e=72

6.8.4 Propiedades de los sistemas neuronales

Se puede decir que una red neuronal tiene tres ventajas que le hacen muy atractiva en el tratamiento de los datos: aprendizaje, robustez y paralelismo masivo:

Aprendizaje adaptativo a través de ejemplos

Una de las características más sobresalientes de las redes neuronales y que la aleja del resto de las técnicas multivariantes es su capacidad de aprender o de corregirse a sí misma basándose en los errores. Se puede considerar que el conocimiento se encuentra representado en los pesos de las conexiones entre las neuronas y en sus umbrales. El proceso de aprendizaje implica cierto número de cambios en estos valores de tal forma que se puede decir que “se aprende modificando los valores de los pesos y umbrales de las neuronas de la red”.

Un criterio para clasificar las redes neuronales es respecto a las reglas de aprendizaje. Si el aprendizaje se basa en la existencia de un agente externo decimos que la red neuronal es supervisada, mientras que cuando no interviene el analista estamos frente a una red neuronal no supervisada. Un ejemplo de una red supervisada es el perceptrón multicapa que se describe a continuación, mientras que una red neuronal no supervisada es la red de Kohonen, que también se describe en este módulo.

Tolerancia a fallos

Algunas de las capacidades de la red, se pueden retener aún si ésta sufre daños. Las redes neuronales artificiales son muy robustas en el tratamiento de la información redundante e imprecisa.

Paralelismo masivo

Lo que significa que las operaciones se realizan en tiempo real. Los cómputos de la red pueden realizarse en paralelo para lo cual se pueden fabricar máquinas con hardware especial.

6.8.5 Ejercicios con R

Vamos a realizar una ejercicio de clasificación binaria con un conjunto de datos sobre fertilidad despues de abortos inducidos o expontaneos, que se encuentran el la librería “datasets”, la red neuronal que se utiliza por defecto es “rprot+”, relativa al algoritmo “Resilient Backpropagation”, que actualiza los pesos considerando únicamente el signo del cambio, es decir, si el cambio del error es en aumento (+) o disminución (-) entre una iteración y otra. Para detalles ver: https://en.wikipedia.org/wiki/Rprop

Los algoritmos de red que permite esta función R son:‘backprop’, ‘rprop+’, ‘rprop-’, ‘sag’, or ‘slr’.

La función para el calculo de error es la de entropía cruzada, que utiliza la distancia Kullback-Leibler.

library(neuralnet)
# Leemos los datos y hacemos dos conjuntos uno de entrenamiento y otro de test
data(infert, package="datasets")
str(infert)

## 'data.frame':    248 obs. of  8 variables:
##  $ education     : Factor w/ 3 levels "0-5yrs","6-11yrs",..: 1 1 1 1 2 2 2 2 2 2 ...
##  $ age           : num  26 42 39 34 35 36 23 32 21 28 ...
##  $ parity        : num  6 1 6 4 3 4 1 2 1 2 ...
##  $ induced       : num  1 1 2 2 1 2 0 0 0 0 ...
##  $ case          : num  1 1 1 1 1 1 1 1 1 1 ...
##  $ spontaneous   : num  2 0 0 0 1 1 0 0 1 0 ...
##  $ stratum       : int  1 2 3 4 5 6 7 8 9 10 ...
##  $ pooled.stratum: num  3 1 4 2 32 36 6 22 5 19 ...

n        <- nrow(infert)
muestra  <- sample(n,n*.70)
train    <- infert[muestra, ]
test     <- infert[-muestra, ]
# Entrenamos la red neuronal
net.infert <- neuralnet(case~parity+induced+spontaneous, train,err.fct="ce", linear.output=FALSE,likelihood=TRUE)
plot(net.infert)
# Computamos la red neuronal
resultados <- compute(net.infert,data.frame(test[,3:4],spontaneus=test[,6]))$net.result
# recodificamos los resultados y evaluamos
test.result=ifelse(resultados>0.5,1,0)
table(test.result,test$case)

##            
## test.result  0  1
##           0 38 14
##           1  5 18

6.9 Clasificador Bayesiano

Naïve Bayes es uno de los clasificadores más utilizados por su simplicidad y rapidez. Se trata de una técnica de clasificación y predicción supervisada que construye modelos que predicen la probabilidad de posibles resultados, en base al Teorema de Bayes, tambiéń conocido como teorema de la probalibidad condicionada:

\[P(A/B)=\frac{P(B/A)P(A)}{P(B)}\]

Un ejemplo nos servirá para entender la operativa de este clasificador. Supongamos un típico problema de clasificación en Minería de Datos, donde tenemos unos cuantos ejemplos que queremos clasificar. Cada ejemplo (también llamados instancias), se caracteriza por una serie de atributos. Además como estamos en clasificación supervisada, dichos ejemplos deben estar etiquetados, es decir, se debe conocer de qué clase son. Por tanto, tenemos un conjunto de 4 ejemplos con 3 atributos cada uno y 2 posibles clases.

Ejemplos	Atr. 1	Atr. 2	Atr. 3	Clase
$x_1$	1	2	1	positiva
$x_2$	2	2	2	positiva
$x_3$	1	1	2	negativa
$x_4$	2	1	2	negativa

Fuente:

Caben destacar dos partes en el algoritmo. La primera es la construcción del modelo, y la segunda clasificar un nuevo ejemplo con dicho modelo:

PARTE 1: Crear el modelo.

Para ello se necesitan cuatro pasos:

Calcular las probabilidades a priori de cada clase.
Para cada clase, realizar un recuento de los valores de atributos que toma cada ejemplo. Se debe distribuir cada clase por separado para mayor comodidad y eficiencia del algoritmo.
Aplicar la Corrección de Laplace, para que los valores “cero” no den problemas.
Normalizar para obtener un rango de valores [0,1].

A continuación se detalla cada paso:

Paso 1: Hay varias formas de establecer la probabilidad a priori a cada clase. La más intuitiva es que todas ellas tengan la misma probabilidad, es decir, 1 divido entre el número de clases. Si contamos con la opinión de un experto, puede que éste nos proporciones dichas probabilidades.

En este caso, vamos a considerar cada clase equiprobable. Por tanto:

$P(positivo) = 1/2 = 0,5$

$P(negativo) = 1/2 = 0,5$

Paso 2: Se crea una tabla (un otro contenedor) para cada clase y se hace un recuento de valores:

positivo	valor 1	valor 2
atr.1	1	1
atr.2	0	2
atr.3	1	1

negativo	valor 1	valor 2
atr.1	1	1
atr.2	2	0
atr.3	0	2

Paso 3: Se suma una unidad a cada valor de la tabla anterior.

positivo	valor 1	valor 2
atr.1	2	2
atr.2	1	3
atr.3	2	2

negativo	valor 1	valor 2
atr.1	2	2
atr.2	3	1
atr.3	1	3

Paso 4: Se normalizan todos los valores de la tabla del siguiente modo. Cada celda se divide por la suma de los valores de la fila. Por ejemplo, el valor: “valor 1” del atributo: “atr. 2” se actualiza con: 1 / (1+3) = 0,25.

positivo	valor 1	valor 2
atr.1	0.5	0.5
atr.2	0.25	0.75
atr.3	0.5	0.5

negativo	valor 1	valor 2
atr.1	0.5	0.5
atr.2	0.75	0.25
atr.3	0.25	0.75

PARTE 2: Clasificar un nuevo ejemplo. Por ejemplo, $x_5 = (1,1,1)$.

Para ello se necesitan dos pasos:

Para cada clase disponible, se determinan los valores de probabilidad de cada valor de los atributos del nuevo ejemplo.
Aplicar la fórmula de Naïve Bayes.

Si generalizamos el teorema de Bayes a $n$ atributos, obtenemos la siguiente expresión:

$P(A | b_1,b_2,...,b_n)=P(A) P(b_1| A) P(b_2| A),...,P(b_n | A) = P(A)P(b_j| A)$

que resolvemos:

$Solucion=argmax_{i=1}^n P(A) P(b_i| A)$

A continuación se detalla cada paso:

Paso 1: En este caso, se para cada tabla escogemos los valores: 1 de cada atributo, es decir, la primera columna de cada tabla, ya que todos los valores del ejemplo $x_5$ son: $1$.

positivo	valor 1	valor 2
atr.1	0.5	0.5
atr.2	0.25	0.75
atr.3	0.5	0.5

negativo	valor 1	valor 2
atr.1	0.5	0.5
atr.2	0.75	0.25
atr.3	0.25	0.75

Paso 2: Se aplica la fórmula:

$P(positivo | x_5 ) = 0,5 • ( 0,5 • 0,25 • 0,5 ) = 0,03125$ $P( negativo | x_5 ) = 0,5 • ( 0,5 • 0,75 • 0,25 ) = 0,046875$ Como la clase más probable es “negativa”, clasificamos el nuevo ejemplo ($x_5$) como negativo.

Esta forma de clasificar, se denomina Tecnica de maximo a posteriori.

A continuación se presenta un ejemplo de clasificar clientes con el método Naive Bayes. El objetivo es clasificar a los clientes según su probabilidad de compra (Si o No) y en base a determinados atributos personales (Estado Civil, Profesión, etc.).

La programación en R sería la siguiente:

library(e1071)
data(iris)
m <- naiveBayes(Species ~ ., data = iris)
## alternativamente:
m <- naiveBayes(iris[,-5], iris[,5])
m

## 
## Naive Bayes Classifier for Discrete Predictors
## 
## Call:
## naiveBayes.default(x = iris[, -5], y = iris[, 5])
## 
## A-priori probabilities:
## iris[, 5]
##       setosa   versicolor    virginica 
## 0.3333333333 0.3333333333 0.3333333333 
## 
## Conditional probabilities:
##             Sepal.Length
## iris[, 5]     [,1]         [,2]
##   setosa     5.006 0.3524896872
##   versicolor 5.936 0.5161711471
##   virginica  6.588 0.6358795933
## 
##             Sepal.Width
## iris[, 5]     [,1]         [,2]
##   setosa     3.428 0.3790643691
##   versicolor 2.770 0.3137983234
##   virginica  2.974 0.3224966382
## 
##             Petal.Length
## iris[, 5]     [,1]         [,2]
##   setosa     1.462 0.1736639965
##   versicolor 4.260 0.4699109772
##   virginica  5.552 0.5518946957
## 
##             Petal.Width
## iris[, 5]     [,1]         [,2]
##   setosa     0.246 0.1053855894
##   versicolor 1.326 0.1977526800
##   virginica  2.026 0.2746500556

table(predict(m, iris), iris[,5])

##             
##              setosa versicolor virginica
##   setosa         50          0         0
##   versicolor      0         47         3
##   virginica       0          3        47

6.10 Combinado clasificadores

Recientemente en el área de la Inteligencia Artificial el concepto de combinación de clasificadores ha sido propuesto como una nueva dirección para mejorar el rendimiento de los clasificadores individuales. Estos clasificadores pueden estar basados en una variedad de metodologías de clasificación, y pueden alcanzar diferentes ratios de individuos bien clasificados. El objetivo de la combinación de clasificadores individuales es el ser más certeros, precisos y exactos. Los métodos multiclasificadores más conocidos son el Bagging (Breiman, 1966) y Boosting (Freund y Schapire, 1996).

El método propuesto por Breinan (1996) intenta aunar las características del Boostrapping y la agregación incorporando los beneficios de ambos (Boostrap AGGregatiNG). La operativa del método es la siguiente:

• Se generan muestras aleatorias que serán los conjuntos de entrenamiento. Las muestras se generan a través de un muestreo aleatorio con reemplazamiento.

• Cada subconjunto de entrenamiento aprende un modelo.

• Para clasificar un ejemplo se predice la clase de ese ejemplo para cada clasificador y se clasifica en la clase con mayor voto.

El método propuesto por Freund y Schapire (1996), está basado en la asignación de un peso a cada conjunto de entrenamiento. Cada vez que se itera se aprende un modelo que minimiza la suma de los pesos de aquellos ejemplos clasificados erróneamente. Los errores de cada iteración sirven para actualizar los pesos del conjunto de entrenamiento, incrementando el peso de los mal clasificados y reduciendo el peso de aquellos que han sido correctamente clasficados. La decisión final para un nuevo patrón de clasificación viene dada por la votación mayoritaria ponderada entre los diferentes conjuntos de entrenamiento.

El package R: “ipred” opera multiclasificadores por los métodos bagging y boosting.

Bagging (o Bootstrap Aggregating), consiste en crear diferentes modelos usando muestras aleatorias con reemplazo y luego combinar o ensamblar los resultados.

La técnica de Bagging sigue estos pasos:

Divide el set de Entrenamiento en distintos sub set de datos, obteniendo como resultado diferentes muestras aleatorias con las siguientes características:

Muestra uniforme (misma cantidad de individuos en cada set)
Muestras con reemplazo (los individuos pueden repetirse en el mismo set de datos).
El tamaño de la muestra es igual al tamaño del set de entrenamiento, pero no contiene a todos los individuos ya que algunos se repiten.
Si se usan muestras sin reemplazo, suele elegirse el 50% de los datos como tamaño de muestra

Luego se crea un modelo predictivo con cada set, obteniendo modelos diferentes
Luego se construye o ensambla un único modelo predictivo, que es el promedio de todos los modelos.

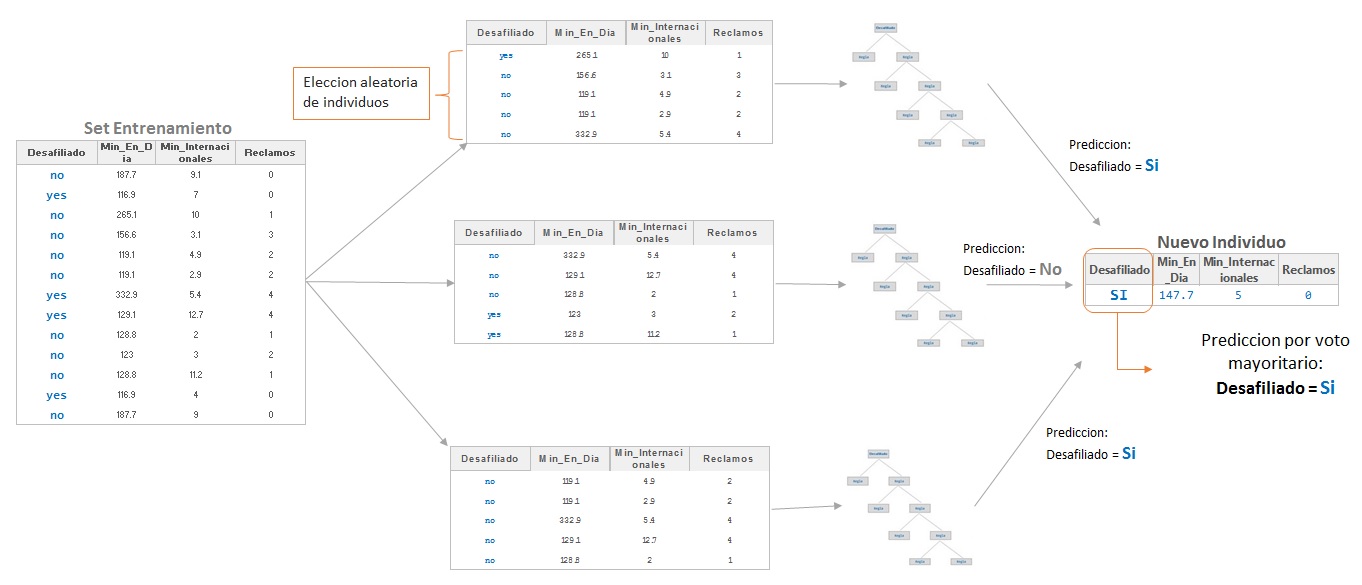
Figure 6.12: Red Neuronal Artificial Precio Vivienda

Sobre el Bagging hay que tener presente (http://apuntes-r.blogspot.com.es/search/label/Bagging):

• Disminuye la varianza de un data set al realizar remuestreo con reemplazo..

• Si no existe varianza en el data set, la tecnica de Baggin no mejora significativamente el modelo.

• Es recomendable en modelos de alta inestabilidad (data set con mucha varianza). Ejemplo de inestabilidad: el % de error de la predicción de fraudes de enero , es muy diferente al de febrero.

• Mientras más inestable es un modelo, mejor será la predicción al usar Bagging.

• Se reduce el overfetting o sobre entrenamiento de modelos. Esto porque los modelos no pueden sobreaprender o memorizar ya que ninguno tiene todos los datos de entrenamiento.

• Mejora la predicción, ya que lo que no detecta un modelo lo detectan los otros.

• Reduce el ruido de los outliers, ya los outliers no pueden estar presenten en todos los modelos.

• No mejora significativamente las funciones lineales, ya que el ensamble de una función lineal da como resultado otra función linear.

• Una técnica mejorada del Bagging es el Random Forest que ademas de elegir un grupo aleatorio de individuos, también elige un grupo aleatorio de variables.

• Los diferentes modelos creados con la técnica Bagging pueden considerarse como algoritmos que buscan respuestas (o hipótesis) en un data set (o espacio h). Como cada algoritmo tiene un set de datos diferentes, cada uno creará una hipótesis diferentes sobre la realidad.

Realizamos un bagging para un clasificador binario, utilizando un scrip obtendido en: http://apuntes-r.blogspot.com.es/2015/01/bagging-para-clasificador-binario.html#more

# Bagging para un clasificador binario
 
 
# -----------------------------------------------------------
# PASO 1. Carga de package y datos
suppressMessages(library(C50));data(churn);   # para datos
suppressMessages(library(foreach))            # para la logica de bagging
library(rpart)                                # para algoritmo Arbol Decision
 
Train        <- churnTrain[,1:20]
Test         <- churnTest [,1:20]
Clase        <- unique(churnTrain$churn)
Iteraciones  <- 5  # Debe ser impar, para evitar el empate en el "Voto mayoritario"
 
#-----------------------------------------------------------
# PASO 2. Crea modelos y crea predicciones en columnas
Prediccion   <- foreach(i=1:Iteraciones,.combine=cbind) %do% {
muestra    <- sample(nrow(Train), size=floor((nrow(Train)*.7)))
modelo     <- rpart(churn ~., data=Train[muestra,])
as.character(predict(modelo, Test, type="class"))
}  
 
# -----------------------------------------------------------
# PASO 3. Evaluación del Voto Mayoritario
Prediccion                 <- as.data.frame(Prediccion)
Prediccion$Cantidad_yes    <- rowSums(Prediccion [, 1:Iteraciones] == "yes")
Prediccion$Cantidad_no     <- rowSums(Prediccion [, 1:Iteraciones] == "no")
Prediccion$Prediccion      <- with(Prediccion,ifelse(Cantidad_yes>Cantidad_no,"yes","no"))
MC                         <- table(Test[, "churn"],Prediccion[,"Prediccion"])
Efectividad                <- MC["yes","yes"]/(MC["yes","yes"]+MC["yes","no"])
print(MC)

##      
##         no  yes
##   yes   82  142
##   no  1430   13

print(Efectividad)

## [1] 0.6339285714

Valor real \(Y_i\) Valor estimado \(\hat Y_i\)	\(Y_i=0\)	\(Y_i=1\)
\(\hat Y_i=0\)	\(P_{11}\)	\(P_{12}\)
\(\hat Y_i=1\)	\(P_{21}\)	\(P_{22}\)

Indice	Definición	Expresión
Tasa de aciertos	Cociente entre las predicciones correctas y el total de predicciones	\(\frac {P_{11}+P_{22}}{P_{11}+P_{12}+P_{21}+P_{22}}\)
Tasa de errores	Cociente entre las predicciones incorrectas y el total de predicciones	\(\frac {P_{12}+P_{21}}{P_{11}+P_{12}+P_{21}+P_{22}}\)
Especificidad	Proporción entre la frecuencia valores cero correctos y el total de valores cero observados	\(\frac {P_{11}}{P_{11}+P_{21}}\)
Sensibilidad	Proporción entre la frecuencia de valores uno correctos y el total de valores uno observados	\(\frac {P_{22}}{P_{12}+P_{22}}\)
Tasa de falsos ceros	Proporción entre la frecuencia de valores cero incorrectos y el total de valores cero observados	\(\frac {P_{21}}{P_{11}+P_{21}}\)
Tasa de falsos unos	Proporción entre la frecuencia de valores uno incorrectos y el total de valores uno observados	\(\frac {P_{12}}{P_{12}+P_{22}}\)

Ejemplos	Atr. 1	Atr. 2	Atr. 3	Clase
\(x_1\)	1	2	1	positiva
\(x_2\)	2	2	2	positiva
\(x_3\)	1	1	2	negativa
\(x_4\)	2	1	2	negativa