Bölüm11 Numerik Verilerin Analizi
Bu bölümde veri tabanında bulunan ve nümerik olarak (sayı hali ile) kaydedilmiş değişkenlerin incelenmesi üzerinde duracağız. Daha önceki örneklerde kullandığımız dt veri tabanına bir defa daha göz atalım
str(dt)## 'data.frame': 1000 obs. of 23 variables:
## $ idnum : int 517 297 811 461 607 186 879 887 622 423 ...
## $ cinsiyet : Factor w/ 2 levels "Erkek","Kadin": 1 2 2 1 2 1 1 1 2 2 ...
## $ bolge : Factor w/ 4 levels "Bati","Dogu",..: 3 3 4 4 2 4 2 3 2 2 ...
## $ gelir : int 22559 12072 40815 44135 48246 15263 4122 6345 35840 46321 ...
## $ egitim : int 1 5 1 1 1 2 1 2 2 1 ...
## $ muhafazakar : int 2 2 2 3 2 2 1 3 1 3 ...
## $ liberal : int 4 3 5 5 3 5 5 4 5 5 ...
## $ milliyetci : int 2 1 1 3 1 3 1 1 1 1 ...
## $ p1 : int 1 1 0 0 0 0 0 0 1 0 ...
## $ p2 : int 1 1 1 1 1 1 1 0 1 1 ...
## $ p3 : int 0 0 0 1 0 0 0 1 0 0 ...
## $ siyasete_guven : int 88 10 44 58 22 45 11 21 93 17 ...
## $ yas : int 34 30 58 31 54 27 61 76 43 30 ...
## $ gocmenler : int 22 55 99 98 90 87 10 26 56 72 ...
## $ oy : Factor w/ 4 levels "PartiA","PartiB",..: 2 2 2 3 2 2 2 3 2 2 ...
## $ kurtaj : Factor w/ 3 levels "DurumaGore","Serbest",..: 1 3 2 2 2 1 3 3 2 2 ...
## $ sendikalasma : int 24 22 14 10 10 13 8 25 1 4 ...
## $ gelenek : int 1 1 1 1 1 1 1 1 1 0 ...
## $ bagis : int 11 28 50 0 0 0 0 13 0 36 ...
## $ askere_guven : num -1.152 1.421 0.107 -0.641 0.382 ...
## $ adalete_guven : num 2.98 2.93 2.81 2.67 2.51 ...
## $ burokrasiye_guven: num 2.649 2.035 0.299 3.134 1.451 ...
## $ meclise_guven : num 2.98 2.93 2.81 2.67 2.51 ...Yukarıdaki çıktıdan dt veri tabanında 22 değişken ve 1000 gözlem olduğunu anlıyoruz. Çıktı ayrıca bu 22 değişkenin tiplerini de raporluyor. Örneğin “bölge” değişkeninin faktör değişken olduğunu, “askere_guven” değişkeninin ise nümerik bir değişken olduğunu bu çıktıdan anlıyoruz. Bir grup değişkenin ise int yani integer/tam sayı değişkeni olduğunu da görebiliyoruz. Hem int hem de num şeklide kodlanmış değişkenler nümerik değişkenlerdir. Aralarındaki tek fark int değişkenleri tam sayı num ise ondalıklı sayı halinde kodlanmış olmalarıdır.
Şimdi gelin bu veriyi daha yakından incelemek için bazı grafikler çizelim. Nokta grafikleri oluşturmak nümerik verinin anlaşılması için sıklıkla başvurulan bir yöntemdir. Nokta grafiklerinde her bir değer ilgili kategoriye işlenir ve üst üste noktalar halinde ifade edilir.
ggplot(dt, aes(gelir))+
geom_dotplot(dotsize = 0.3)# dotsize argümanı noktaların büyüklüğünü ayarlar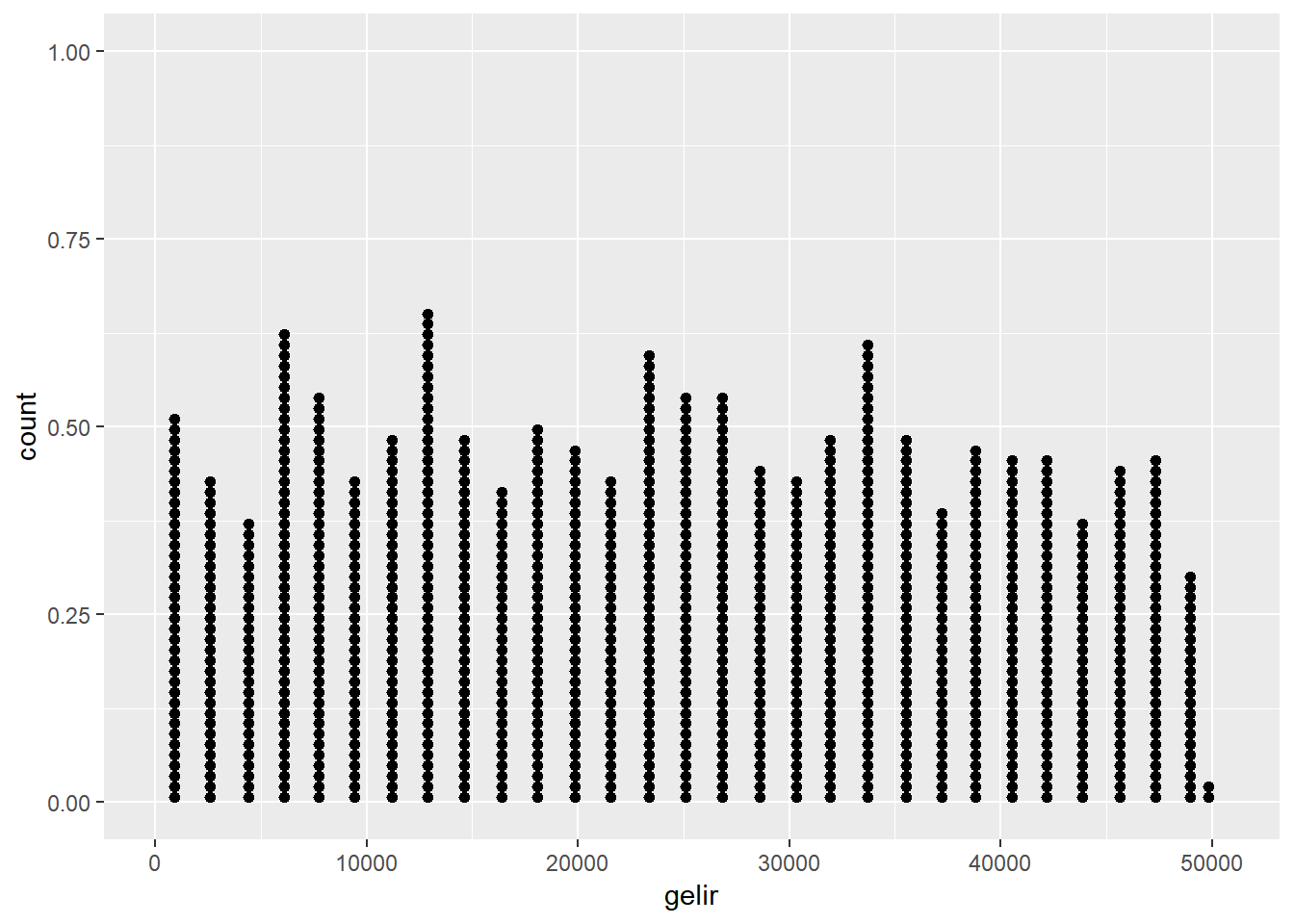
Yukarıdaki nokta grafik cevaplayıcıların raporladıkları gelir seviyelerini tek tek “x” ekseninde ilgili yere noktaları üstüste koyarak işledi. Sizin de farkedeceğiniz gibi gözlem sayısının arttığı durumlarda bu grafiğin okunması hayli zorlaşacaktır. Bu sorunun üstesinden gelmek için diğer bir grafik tipi olan histogramlar kullanılır. Histogramlar nokta grafiklerde kullanılan noktaları x ekseni üstünde tanımlanan “sepetler”de birleştirerek veriyi görselleştirir. Histogramlardaki sepetlerin tepe noktaları o sepete ait frekansı ifade eder.
ggplot(dt, aes(gelir))+
geom_histogram(bins=50) # bins argümanı ile sepet sayısını belirliyoruz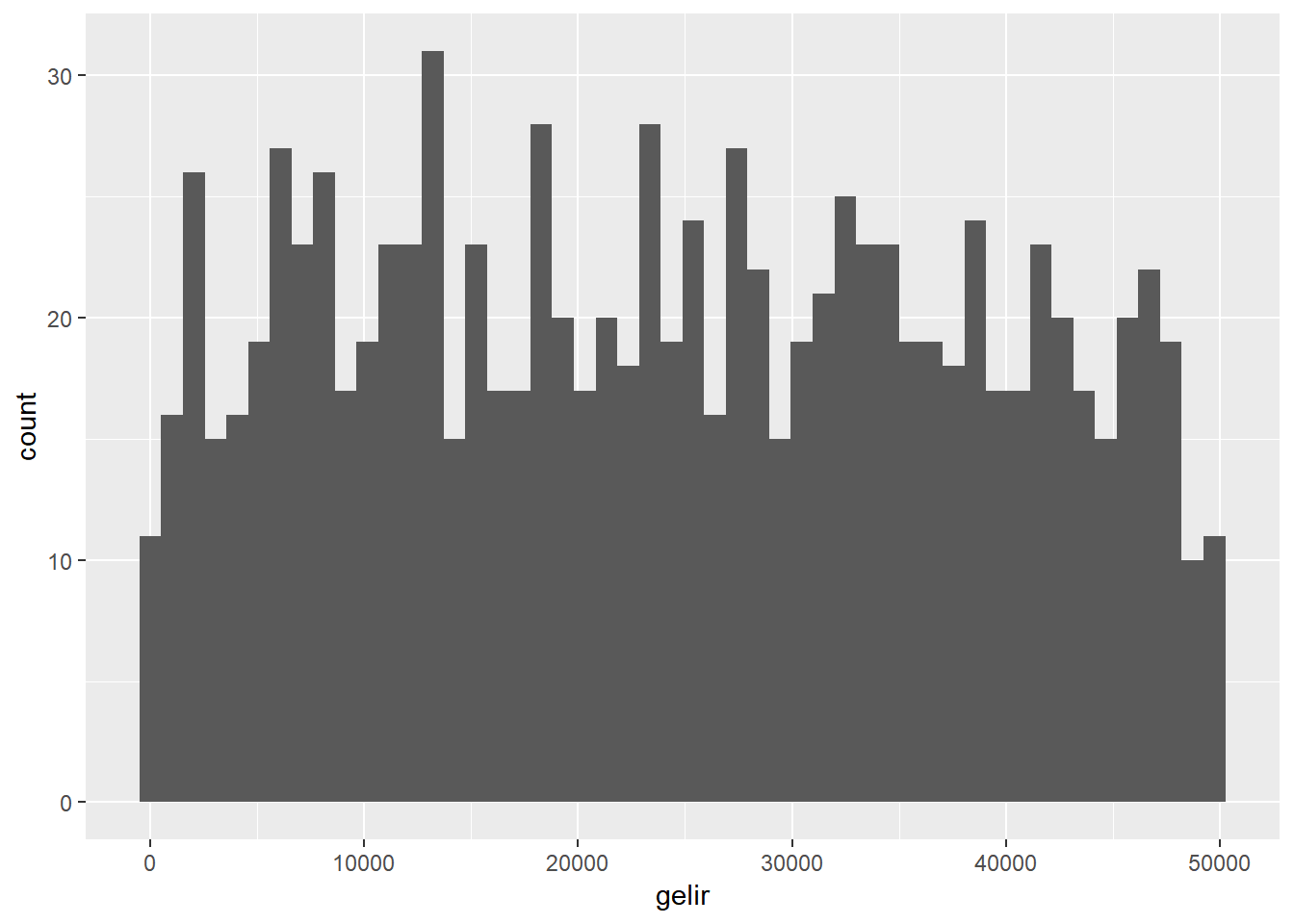
Bu grafik görsel açıdan çok çekici olmasa da, veri hakkında önemli ipuçları sağlar. Aynı veriyi görsel olarak daha basitleştirmek için yoğunluk (density) grafikleri kullanılabilir.`Yoğunluk grafikleri histogram verisini çizgi halinde görselleştirir.
ggplot(dt, aes(gelir))+
geom_density()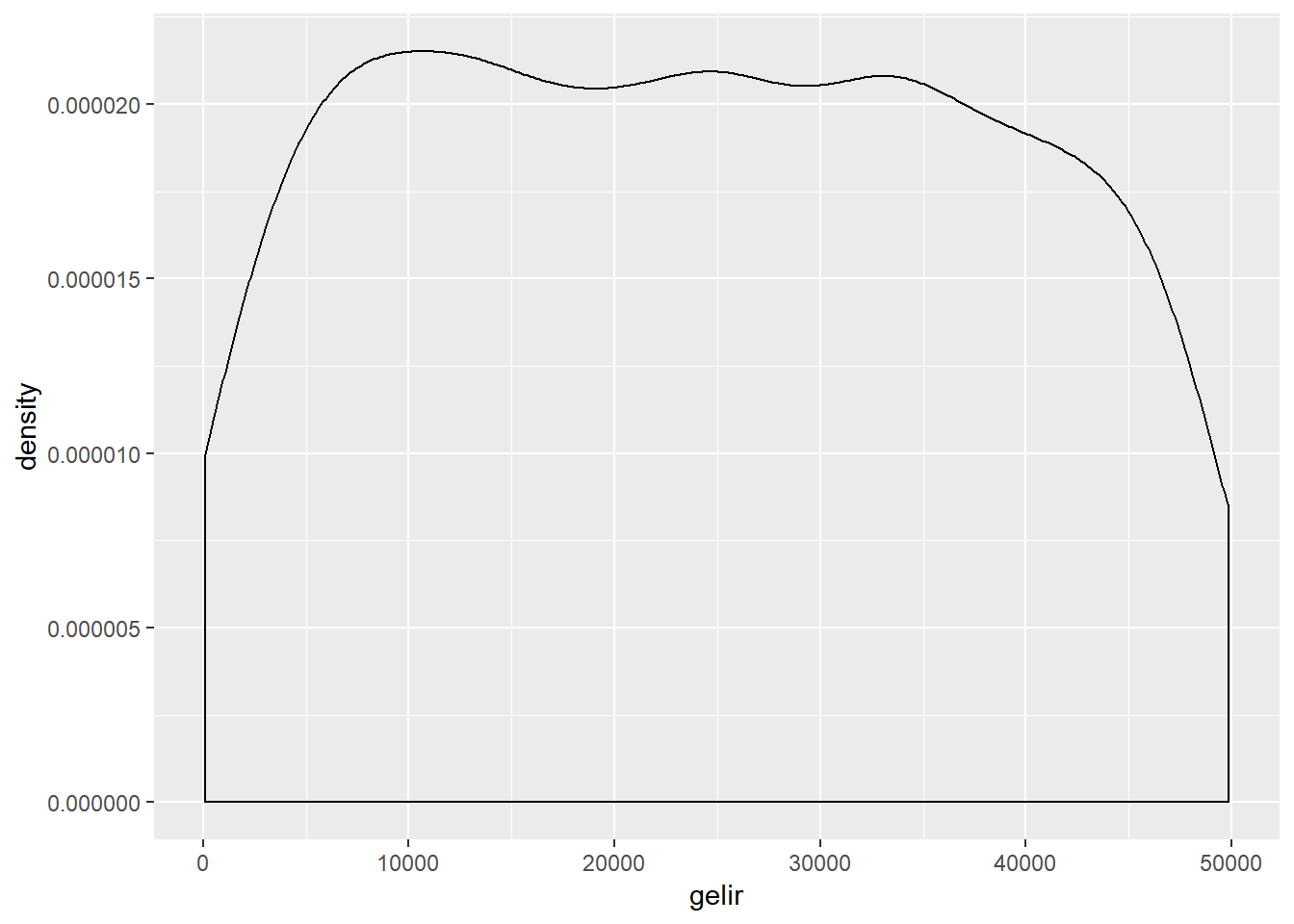
Sütun grafiklerde kullandığımız facet_wrap() argümanını bu grafikler için de kullanıp, tek değişkenli analizimizi çeşitlendirebiliriz.
ggplot(dt, aes(gelir))+
geom_density() +
facet_wrap(~ bolge)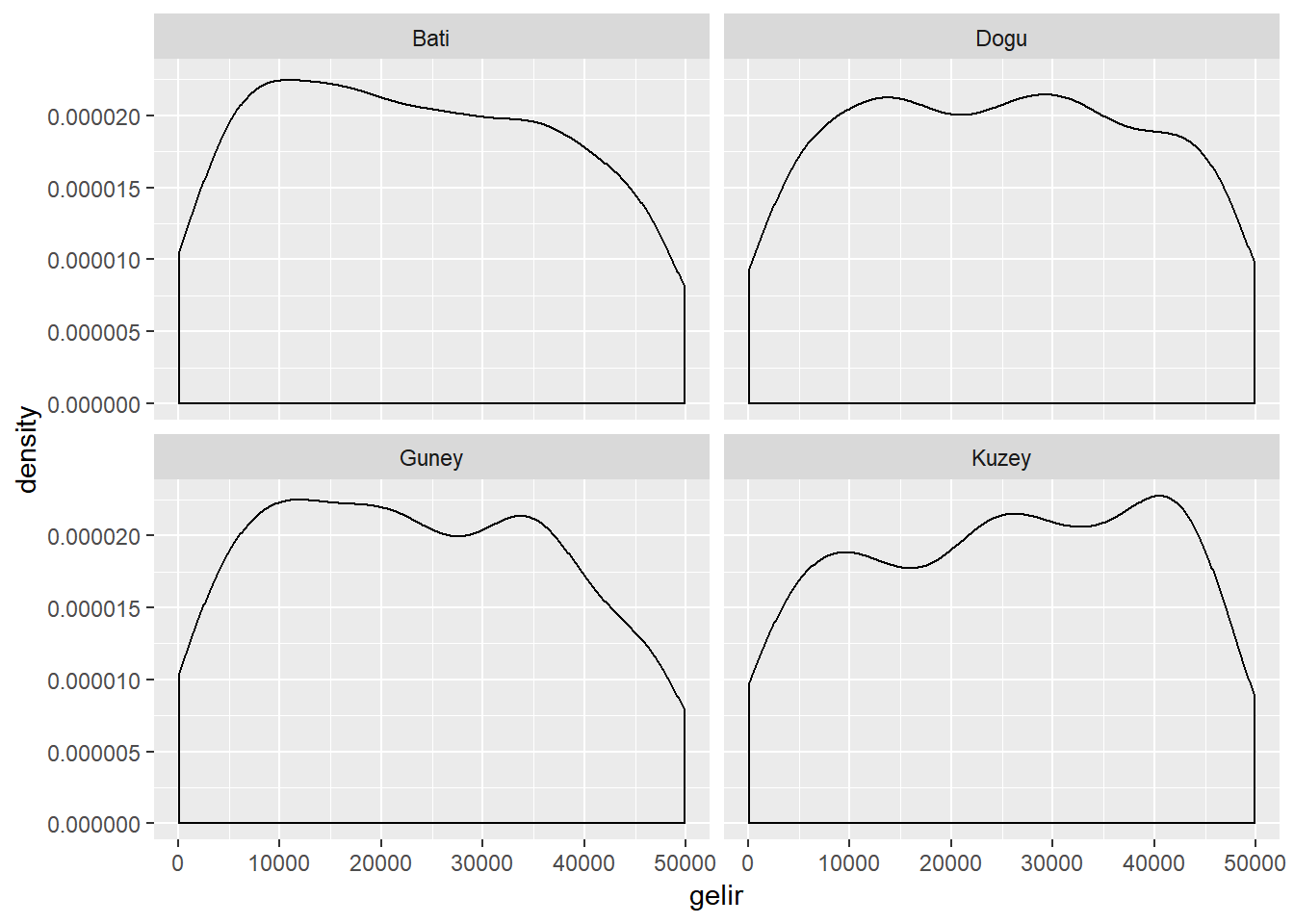
Yukarıdaki grafikten Kuzey bölgesinde gelirin diğer bölgelere nazaran daha yüksek olduğunu görebiliyoruz. Aynı grafiği üst üste binmiş yoğunluk grafiği olarak çizmek istersek aşağıdaki kodu kullanmamız gerekir.
ggplot(dt, aes(x = gelir, fill = bolge)) +
geom_density(alpha = .4) # alpha argümanı renk saydamlığını ayarlar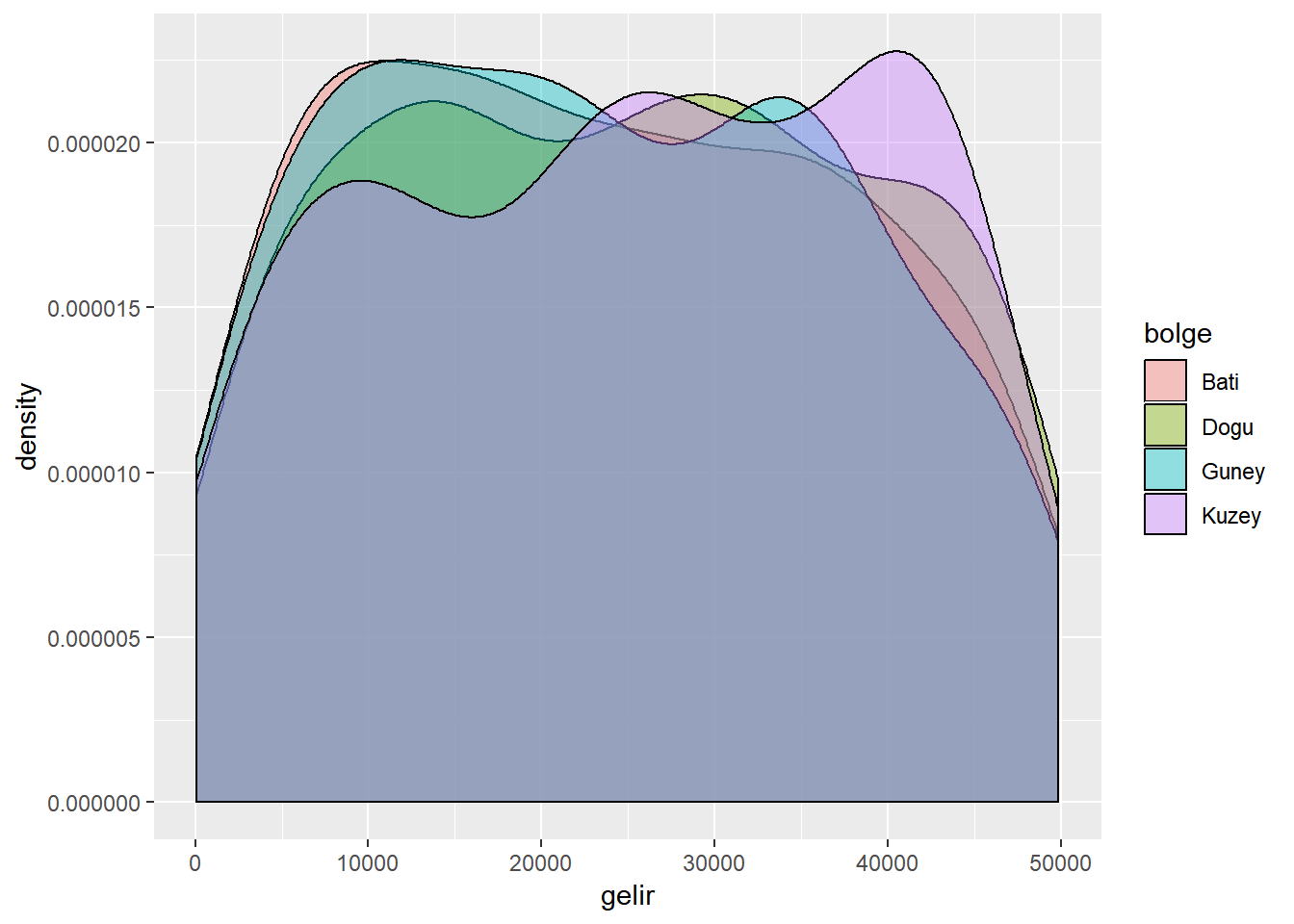
Eğer tek bir nümerik değişkenin dağılımı konusunda bilgi almak istiyorsak yukarıdaki anlatılan marjinal ve durumsal analiz yöntemleri dışında bir yol daha kullanılabilir. Eğer istenirse nümerik verinin daha spesifik bir kısmı piple line operatörü %>% kullanılarak ayrıştırılır ve yukarıdaki işlemler bu ayrıştırılan veri üzerinde uygulanır. Bu yöntemde veri nümerik olarak kodlandığından facet() argümanını kullanamayız. Aşağıdaki örnekte yukarıda bölgelere göre yaptığımız analizi eğitim değişkeninin belli bir kısmını (bu örnekte 4 değerinden fazla olanlar, yani yüksek eğitimliler) ayrıştırarak yapan kodu bulabilirsiniz.
dt %>%
filter(egitim > 4) %>%
ggplot(aes(x=gelir)) +
geom_histogram(binwidth =3000) # sepetleri 3000 lik olrak ayarla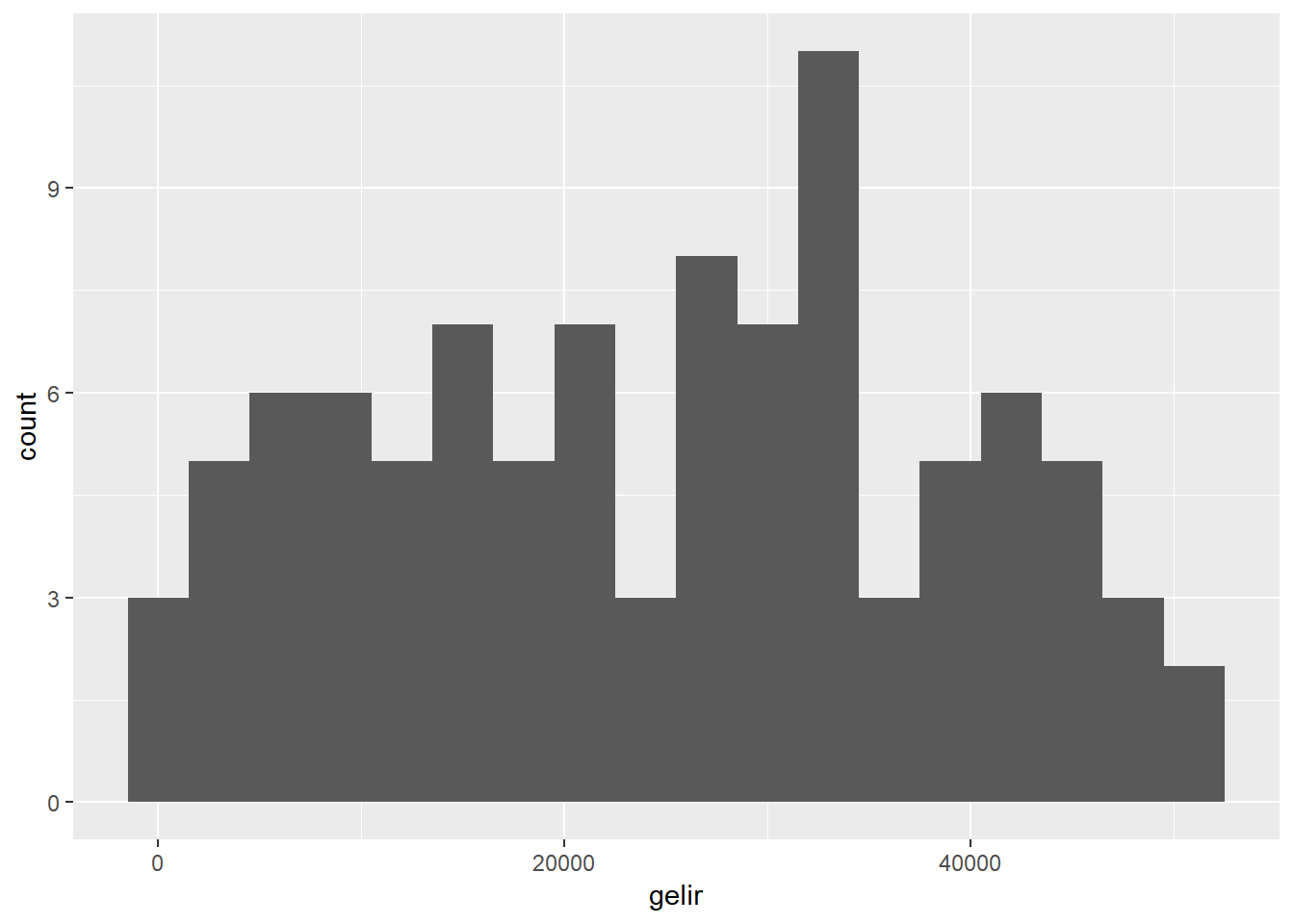
Hatırlayacağınız üzere%>% operatörü kendinden önce yapılan işlemi bir sonraki satıra taşımaya yarar. Yukarıdaki kod “dt veri tabanını al, sonra eğitim seviyesi 4’ün üzerindekileri filtrele, sonra histogram grafiğini x eksenine gelir gelecek şekilde çiz” şeklinde okunabilir. Aynı grafiği yoğunluk grafiği tipinde de çizelim
dt %>%
filter(egitim > 4) %>%
ggplot(aes(x=gelir)) +
geom_density(bw =1000) # sepetleri 1000 lik olrak ayarla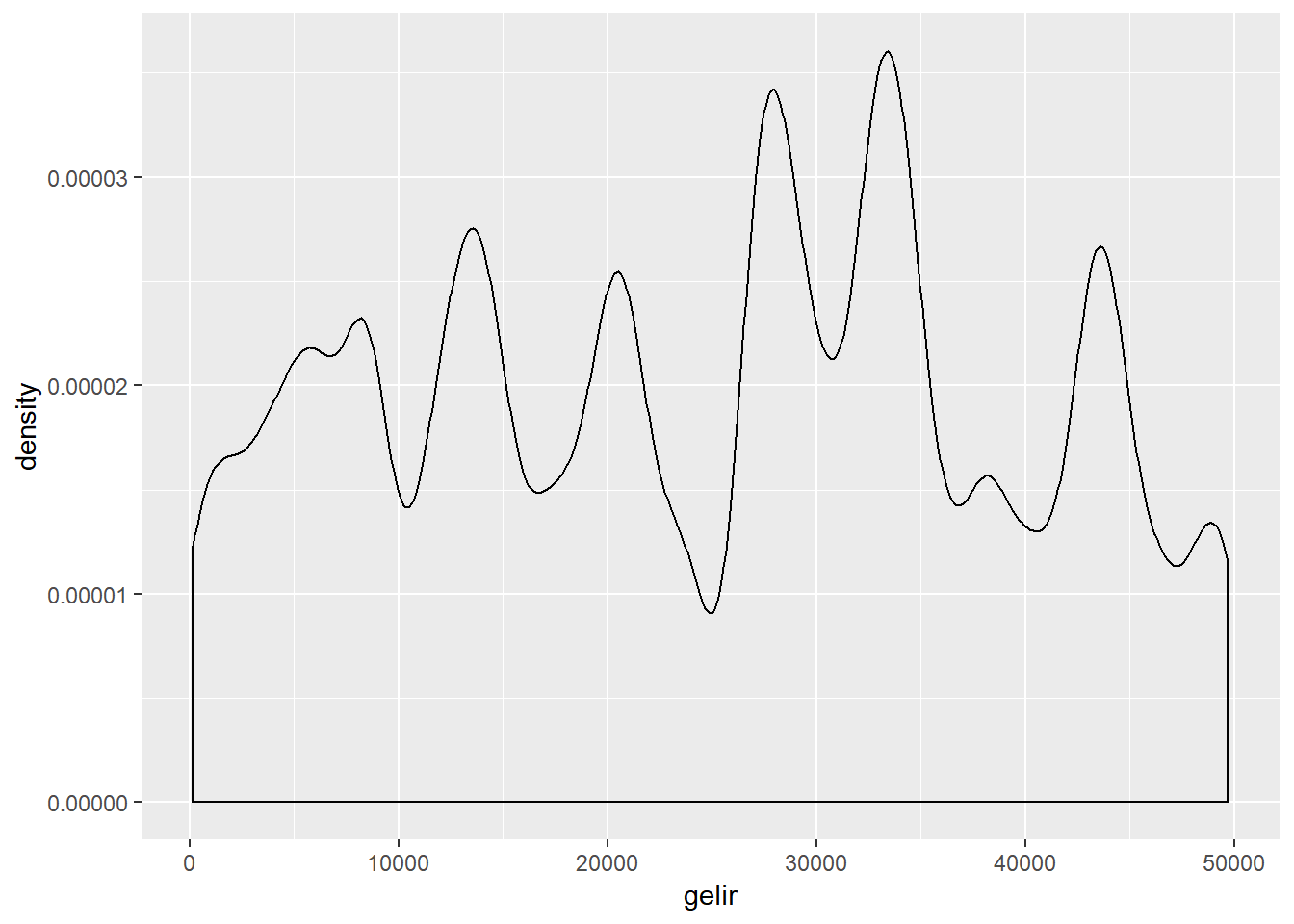
11.1 Kutu Grafikleri
Kutu grafikleri ile bir serideki merkezi eğilim ölçümleri ve dağılımı saptayabileceğimizi biliyoruz. Ancak kutu grafikler ile bu bilgilerin yanı sıra uç değerleri de görebiliriz. Aşağıdaki ilk kutu grafiğinde meclise güven değişkenine ait değerler incelenmektedir. İkincisinde ise -13’den yüksek uç değerler atılarak aynı grafik tekrar çizilmiştir.
dt %>%
ggplot(aes(x = 1, y = meclise_guven)) +
geom_boxplot()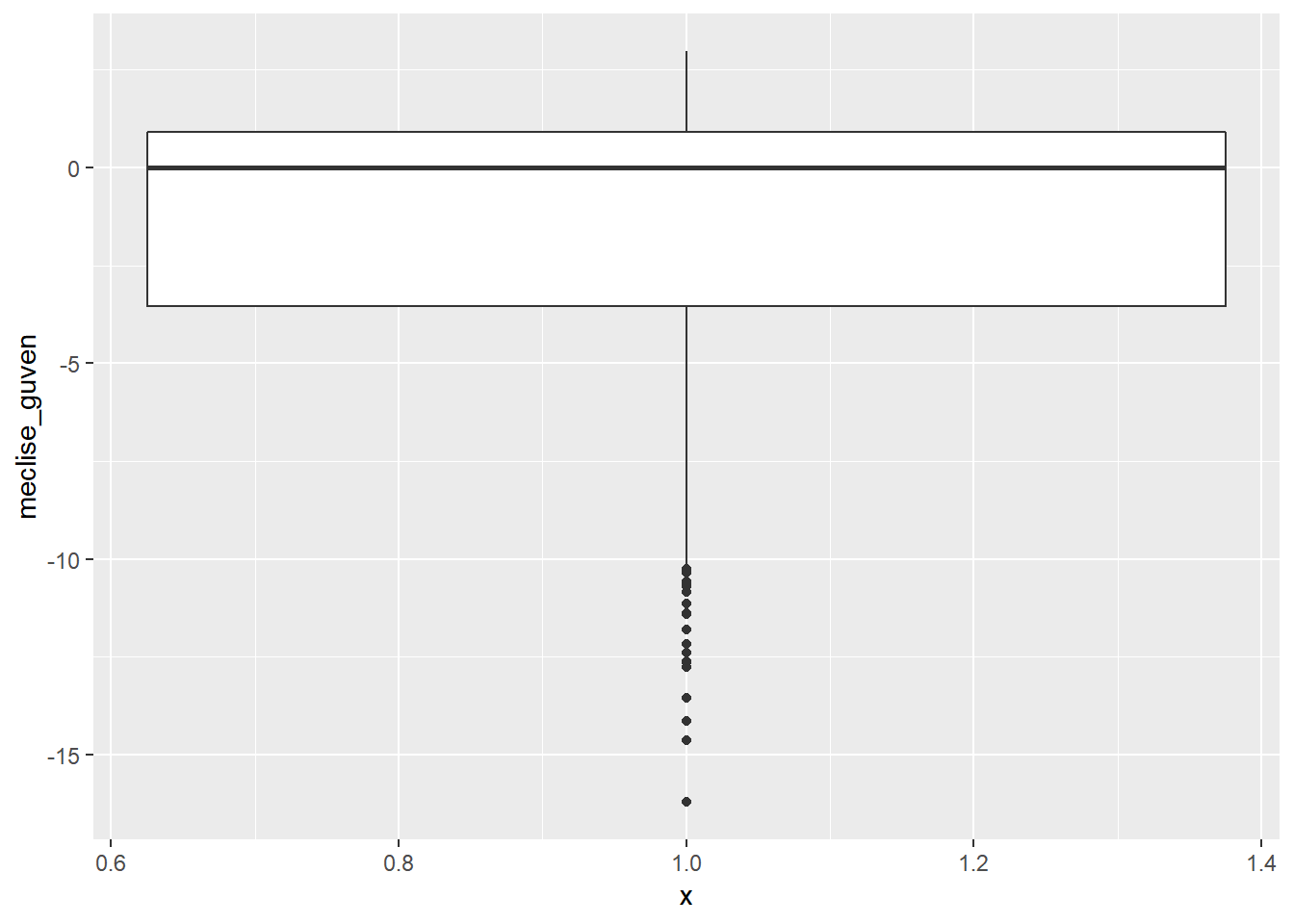
dt %>%
filter(meclise_guven > -13) %>% # -13 den küçük değerleri filtrele
ggplot(aes(x = 1, y = meclise_guven)) +
geom_boxplot()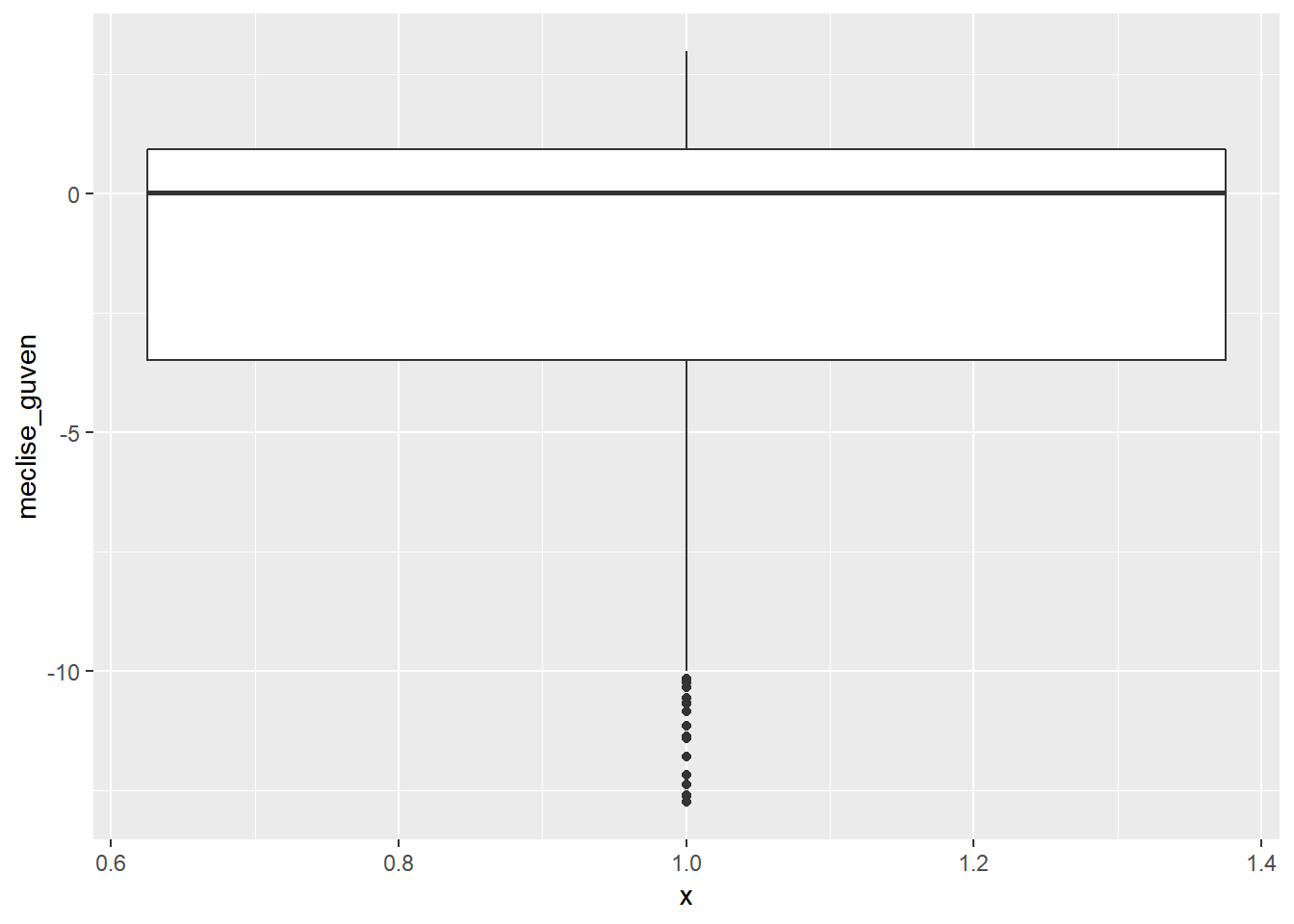
11.2 İkiden fazla değişken analizi
Şu ana kadar yaptığımız incelemeler iki değişkenin birbiri ile olan bağlantısını ortaya koymaya yönelik idi. Ancak değişkenler arasındaki bağlantıları iki değişkenden fazla örneğin üç değişken kullanarak da görebiliriz. Bu işlem için ggplot2 paketindeki facet_grid() fonksiyonunu kullanacağız. Bu fonksiyon sayesinde nümerik bir değişkenin iki kategorik değişken üzerindeki dağılımını görebiliriz. Aşağıdaki kod meclise güven değişkenini hem parti hem de bölge değişkenlerine göre analiz ediyor.
dt%>%
ggplot(aes(x = meclise_guven)) +
geom_density() +
facet_grid(bolge ~ oy) +
ggtitle("Bölge ve Partil Göre Meclise Güven")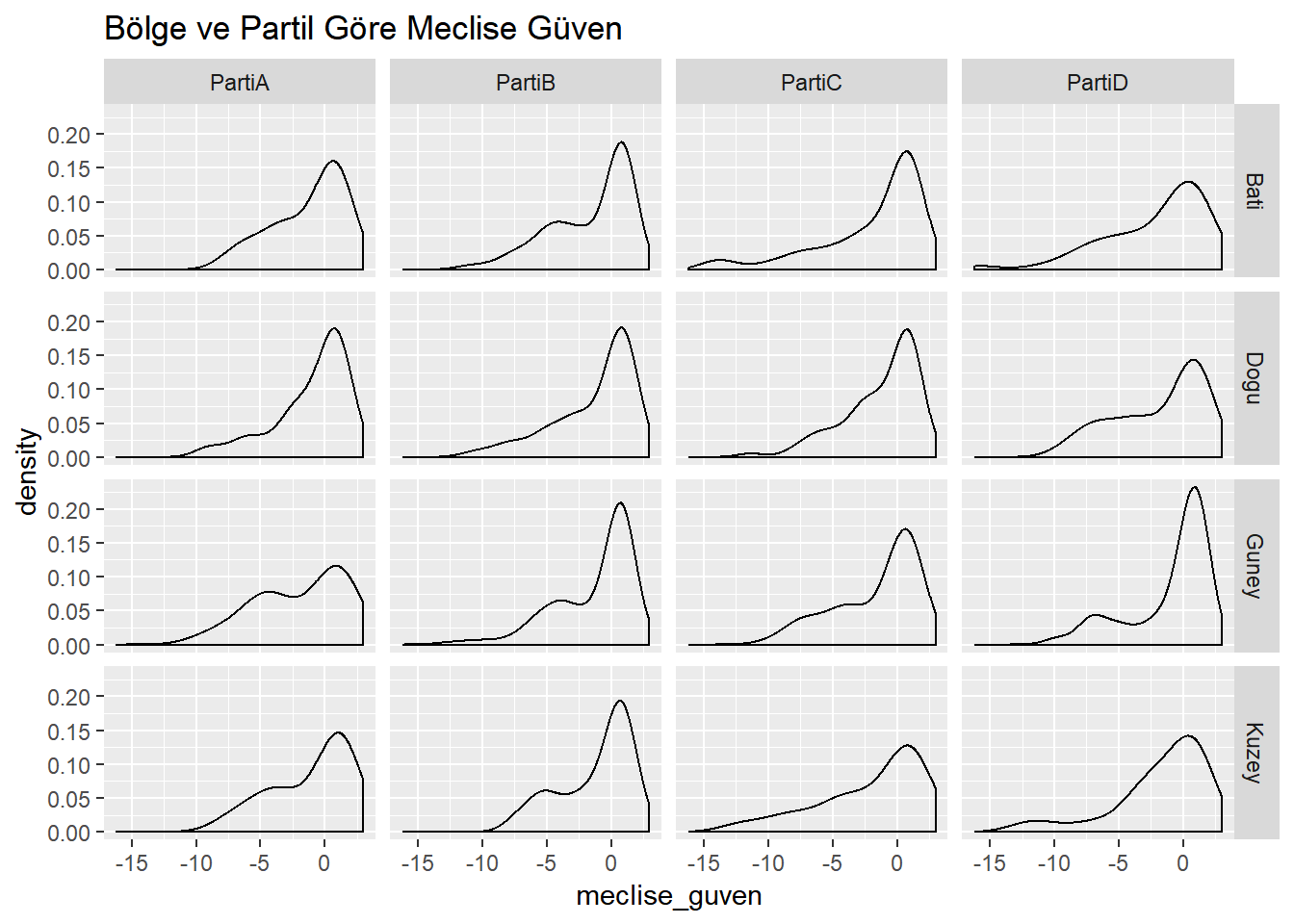
Grafikten de anlaşılacağı üzere meclise olan güvenin en düşük olduğu seçmen grubu PartiD’ye ait. PartiD içinde de en düşük güven seviyesi Batı bölgesinde görünüyor. Benzer bir durum PartiC’nin Kuzey bölgesi seçmeni için de geçerli. Lütfen diğer kutulara bakarak oluşan grafiği yorumlamaya çalışınız.
11.3 Nümerik Özetler
Bir serideki en tipik değer nedir? Bir başka deyişle yaptığımız gözlemleri en kısa ve en iyi şekilde hangi değer temsil eder? Bu sorulara cevapları “merkezi eğilim ölçümleri” denilen bir dizi ölçüm ile verebiliriz. Bu ölçümlerin en fazla kullanılanları “mod/tepe değer”, “median/ortanca” ve “mean/aritmetik ortalama” hesaplamalarıdır. Mod bir dağılımda en fazla tekrar eden değerdir. Median ise veri setini tam ortadan ikiye ayıran değere verilen isimdir. Aritmetik ortalama ise bir dizideki tüm gözlemlerin toplanıp o dizideki gözlem sayısına bölünmesi ile hesaplanır. Tüm bu üç hesaplama da keşifsel veri analizi sırasında sıkça kullanılır. Bu bölümde gapminder paketinde bulunan aynı isimli “gapminder” veri setini kullanacağız. Öncelikle paketi ve veriyi yükleyelim ardından veriye göz atalım
library(gapminder)
data(gapminder)
str(gapminder)## Classes 'tbl_df', 'tbl' and 'data.frame': 1704 obs. of 6 variables:
## $ country : Factor w/ 142 levels "Afghanistan",..: 1 1 1 1 1 1 1 1 1 1 ...
## $ continent: Factor w/ 5 levels "Africa","Americas",..: 3 3 3 3 3 3 3 3 3 3 ...
## $ year : int 1952 1957 1962 1967 1972 1977 1982 1987 1992 1997 ...
## $ lifeExp : num 28.8 30.3 32 34 36.1 ...
## $ pop : int 8425333 9240934 10267083 11537966 13079460 14880372 12881816 13867957 16317921 22227415 ...
## $ gdpPercap: num 779 821 853 836 740 ...Görüldüğü üzere gapminder veritabanı 6 değişkenden ve 1704 gözlemden oluşmaktadır. Bu veri tabanındaki 6 değişkenin ülkeler (country), kıtalar (continent), yıllar(year), yaşam beklentisi(lifeExp), nüfus(pop) ve kişi başına gelir(gdpPercap) değişkenlerinin kaydedilmiş olduğunu da bu çıktıdan anlıyoruz.
İlk başta yaşam beklentisinin kıtalar arasında farklılık gösterip göstermediğini anlamaya çalışalım. Bu analiz için analizimizi kıta seviyesinde yapmamız gerekiyor. Bu iş için dplyr paketindeki group_by() ve summarize() fonksiyonlarından yararlanacağız. Öncelikle “v2007” ismi ile sadece 2007 yılına ait gözlemleri içeren bir veri seti oluşturalım. Daha sonra bu veri setini kullanarak her kıta için yaşam beklentisi değişkeninin ortalama ve medyan değerlerini hesaplayalım ve kutu grafiği ile görselleştirelim.
v2007 <- filter(gapminder, year == 2007) # 2007 yılı için filtreleme
# Ortalama ve medyan değerleri hesabı
v2007 %>%
group_by(continent) %>% # hangi değişken ile veriyi gruplayacağımız
summarize(mean(lifeExp),
median(lifeExp))## # A tibble: 5 x 3
## continent `mean(lifeExp)` `median(lifeExp)`
## <fct> <dbl> <dbl>
## 1 Africa 54.8 52.9
## 2 Americas 73.6 72.9
## 3 Asia 70.7 72.4
## 4 Europe 77.6 78.6
## 5 Oceania 80.7 80.7# Kıtalar için kutu grafikler
v2007 %>%
ggplot(aes(x = continent, y = lifeExp)) +
geom_boxplot()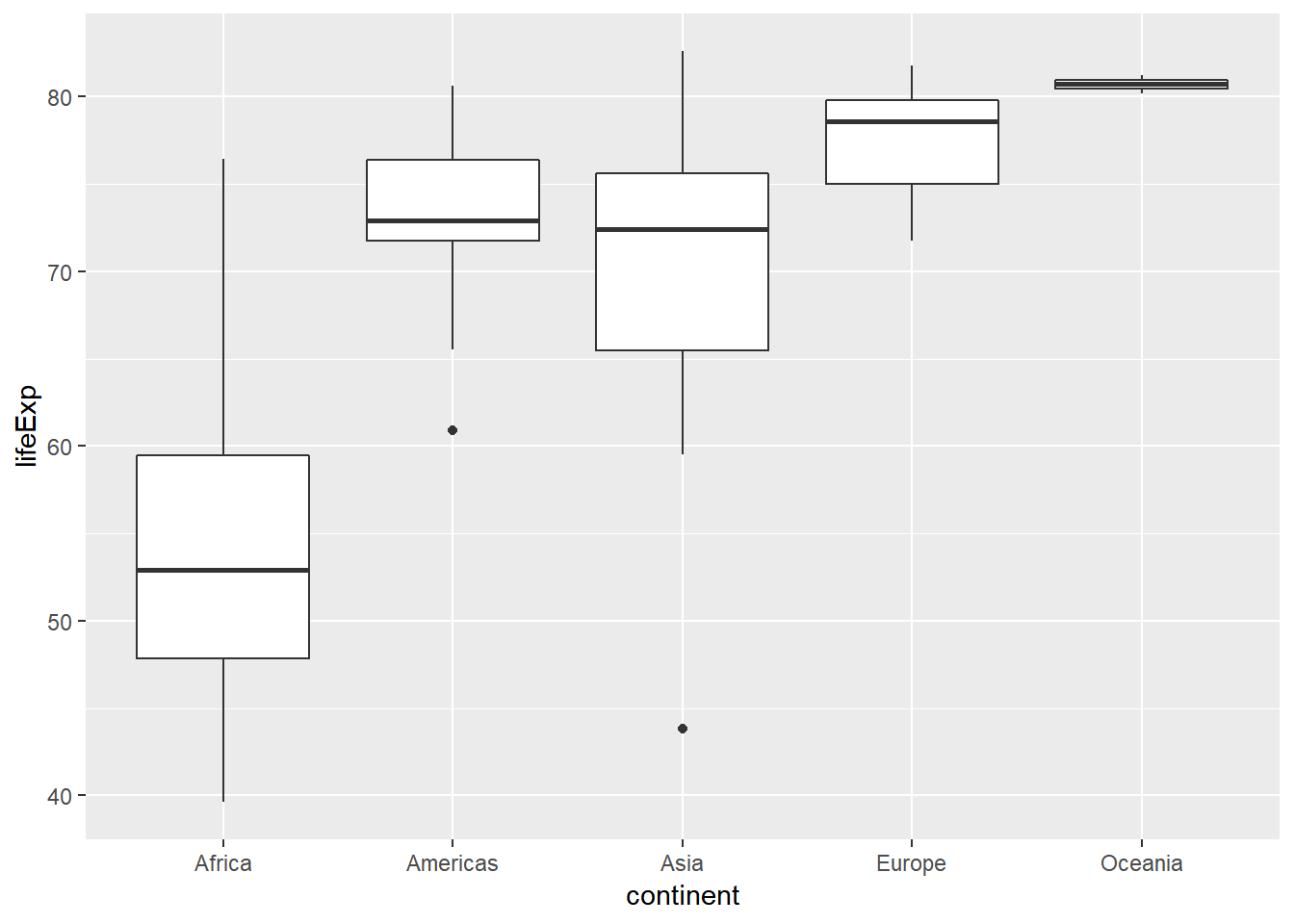
Nümerik veriyi anlamanın ikinci aşaması verinin değişkenliği/dağılımı üzerine yapılacak analizleri gerektirir. Bu bölümde dağılım ölçülerinden varyans, standart sapma, çeyrekler arası açıklık ve açıklık üzerinde duracağız. Bilinmesi gerekir ki varyans, standart sapma ve açıklık gözlemlerdeki uç değerlerden etkilenirken, çeyreklerarası açıklık uç değerlerden etkilenmez.
group_by() ve summarize() fonksiyonlarını dağılım ölçüleri için de kullanabiliriz. Eğer verinizin uç değer içerip içermediğinden emin değilseniz, bir başka deyişle dağılımın simetrik olmadığından şüpheleniyorsanız, standart sapma gibi hesapları çeyrekler arası açıklığı hesapladıktan sonra yapmak daha uygun olur.
Daha önceden oluşturduğumuz “v2007” veri tabanını kullanarak yaşam beklentisine ait standart sapmayı sd(), çeyrekler arası açıklığı ise IQR() ve her kıtada bulunan ülke sayısını da n() fonksiyonları ile hesaplayalım. Daha sonra bu dağılımları kıtalar bazında yoğunluk grafikleri halinde grafikleyelim.
# Dağılım ölçümlerini hesaplayalım
v2007 %>%
group_by(continent) %>% # kıta bazında grupla
summarize(sd(lifeExp), # lifeExp değişkeninin standart sapmasını hesapla
IQR(lifeExp), # lifeExp değişkeninin çeyrekler arası açıklığını hesapla
n())## # A tibble: 5 x 4
## continent `sd(lifeExp)` `IQR(lifeExp)` `n()`
## <fct> <dbl> <dbl> <int>
## 1 Africa 9.63 11.6 52
## 2 Americas 4.44 4.63 25
## 3 Asia 7.96 10.2 33
## 4 Europe 2.98 4.78 30
## 5 Oceania 0.729 0.516 2# Yoğunluk grafikleri
v2007 %>%
ggplot(aes(x = lifeExp, fill = continent)) +
geom_density(alpha = 0.3)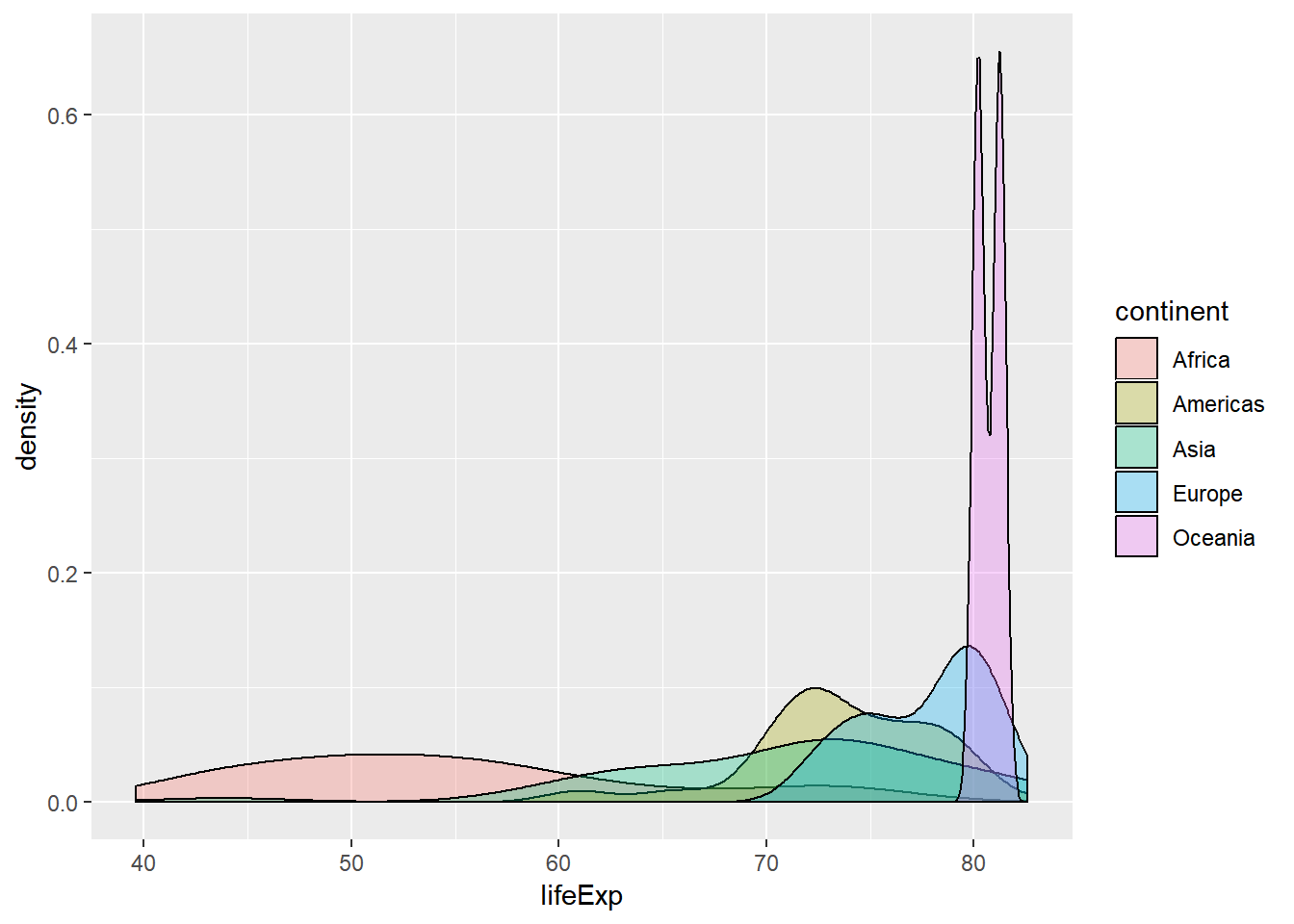
Dağılımların sınıflandırılmasında kullanılan diğer bir kıstas ise dağılımın şeklilleri ile ilgilidir. Bu sınıflandırma tipinde dağılımların “tepe noktaları” ve “simetrileri” incelenir Tepe noktaları açısından değerlendirildiğinde eğer bir dağılımda tek bir tepe noktası bulunuyorsa yani dağılım içindeki mod tek bir sayı ile belirlenmişse “tek modlu”, iki tepe noktası bulunuyorsa “çift modlu”, ikiden fazla tepe noktası bulunuyorsa “çok modlu” dağılım olarak nitelendirilir. Simetri açısından ise dağılımın simetrik, sağa veya sola yaslı olma durumu değerlendirilir. Eğer bir dağılımda değerlerin çoğu dağılımın solunda bulunuyorsa bu dağılım sağa yaslı, değerlerin çoğu sağda bulunuyorsa sola yaslı olarak nitelendirilir. Değerlerin çoğu dağılımın ortasında yoğunlaşmışsa dağılım simetrik olarak nitelendirilir. Aşağıdaki şekilde A tek modlu sola yaslı, B tek modlu simetrik, C tek modlu sağa yaslı ve D iki modlu simetrik dağılımları göstermektedir.
[]dagilimlar.PNG
Dağılımların sağa ve sola yaslı olmaları durumunda grafik yolu ile veriyi anlamak kolay olmaz. Bu durumlarda veriyi çeşitli matematiksel işlemler ile, örneğin logaritmasını veya karekökünü alarak, transforme etmek bir çözüm yolu olabilir. Aşağıdaki örnek sağa yaslı olan population (nüfus) değişkeninin logaritmasını alarak bu işlemi uyguluyor.
# nüfus değişkeninin transforme edilmeden önceki hali
v2007 %>%
ggplot(aes(x = pop)) +
geom_density()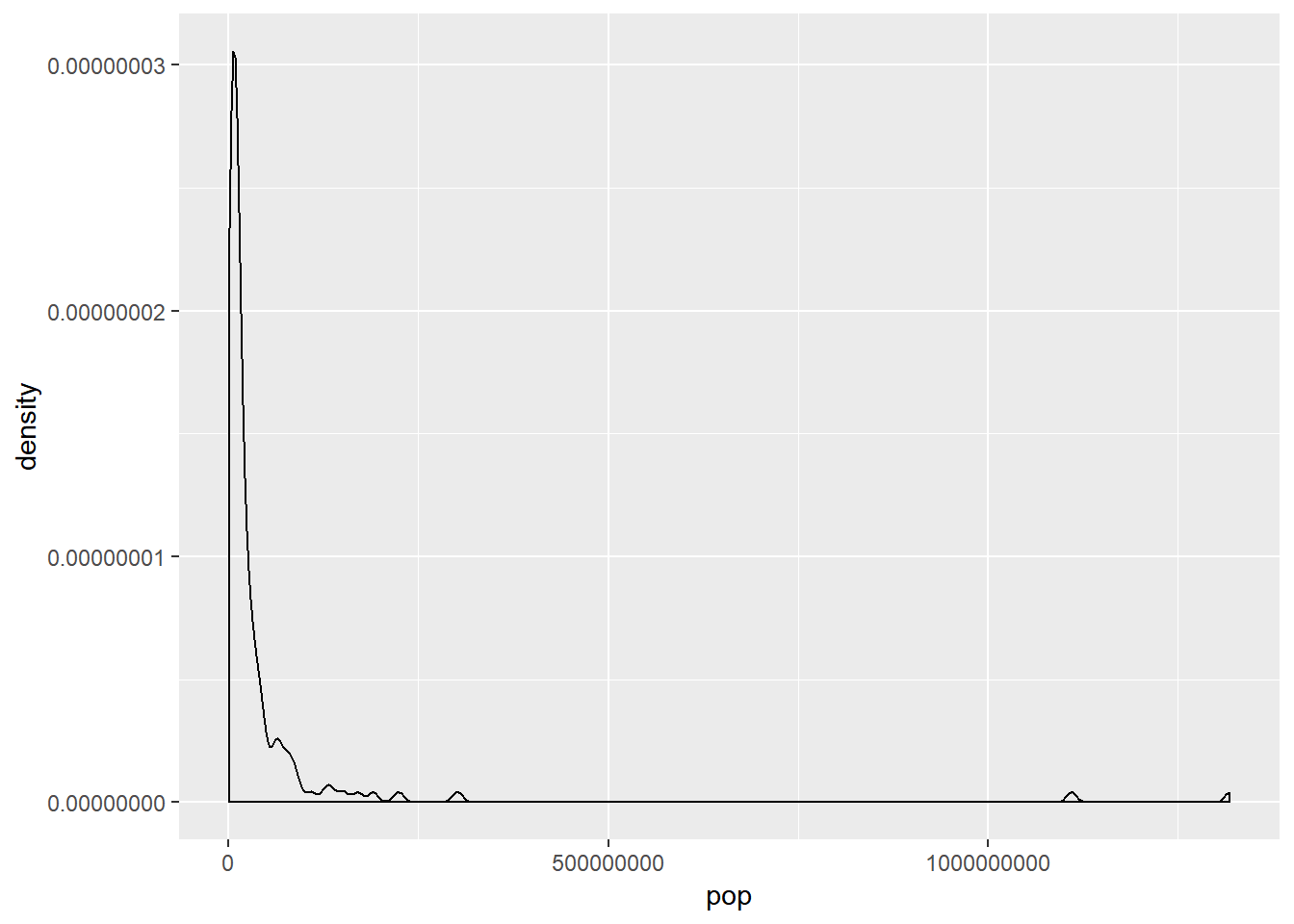
# log_pop adı ile değişkenin logaritması alınarak yeniden yaratılan değişken
v2007 <- v2007 %>%
mutate(log_pop = log(pop))
# Yeni değişkenin grafiği
v2007 %>%
ggplot(aes(x = log_pop)) +
geom_density()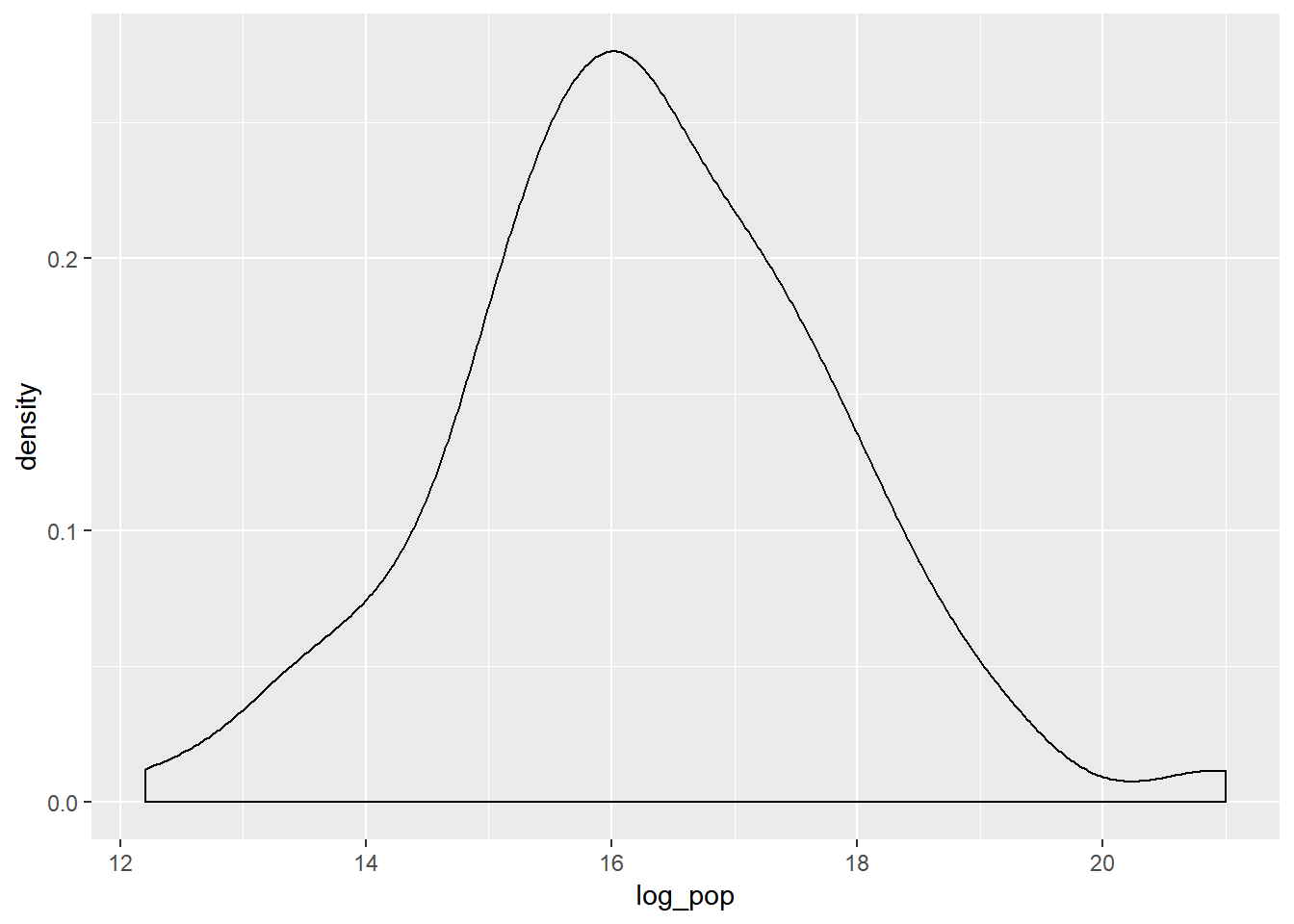
Dağılımlar ile ilgili son olarak incelenmesi gereken özellik, uç değerler içerip içermediklerinin kontrolüdür. Uç değerler kendi başlarına analizler için ilginç vakalar oluştursalar da merkezi eğilim ölçüleri üzerinde etkili olduklarından kimi zaman analiz dışında tutulmaları gerekebilir. Aşağıdaki örnekte Asya kıtasındaki ülkeler için yaşam beklentisi kutu grafik ile betimlenmiş durumdadır.
# ga isminde sadece asya ülkelerinden oluşan veri tabanı
ga <- v2007 %>%
filter(continent == "Asia")
# ga veri tabanına ait kutu grafik
ggplot(ga, aes(x=1, y= lifeExp)) +
geom_boxplot()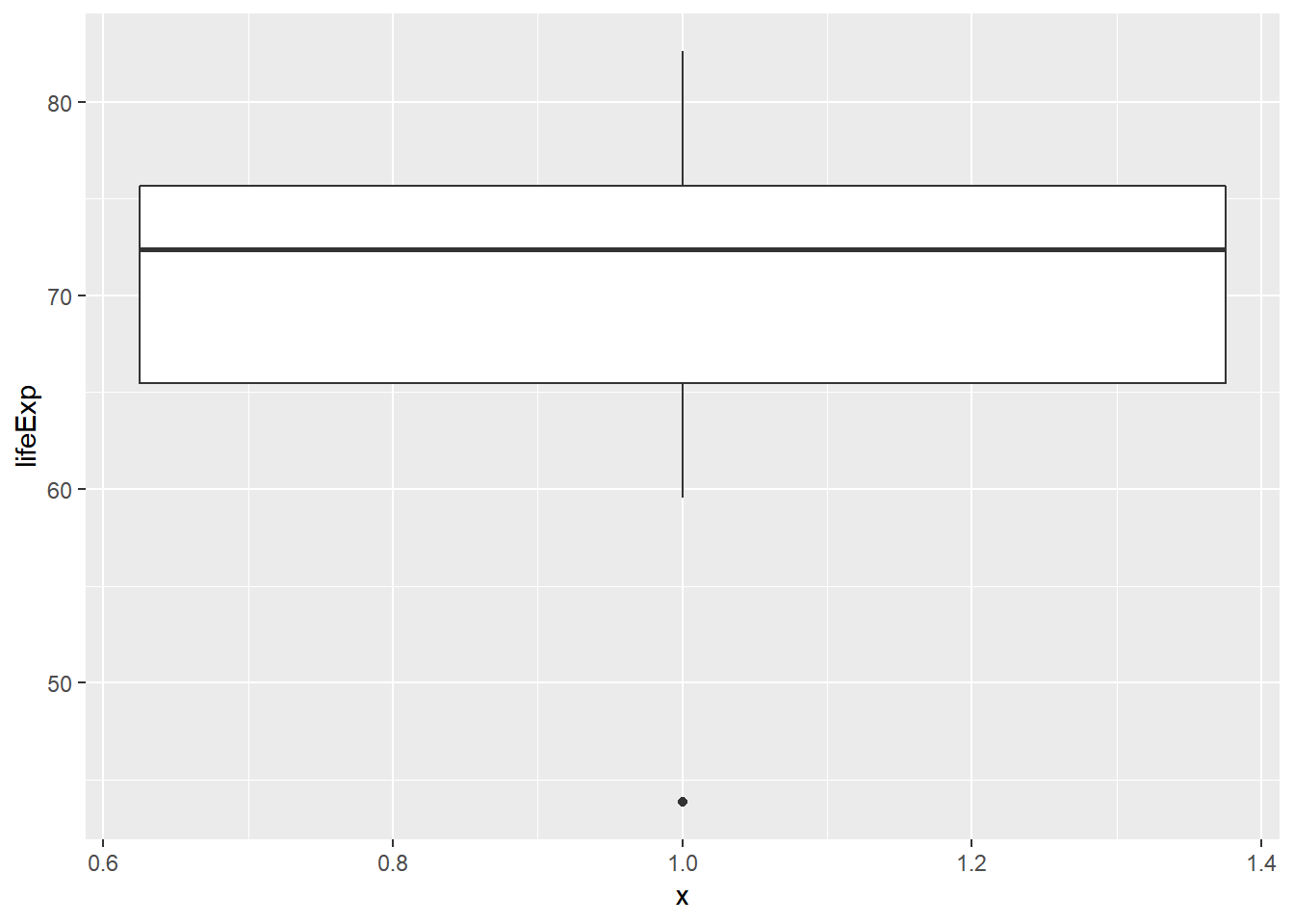
Görüldüğü üzere tek bir ülkende yaşam beklentisi 50 yaşın altında kaydedilmiş. Şimdi bu ülkeyi analizden çıkartarak grafiği tekrar çizelim.
# 50 düşük yaşbeklentisi olan ülkeleri eleyelim
gap_asya <- v2007 %>%
filter(continent == "Asia") %>%
mutate(uc_deger = lifeExp < 50)
# oluşan yeni veri tabanı ile grafiği tekrarlayalım
gap_asya %>%
filter(!uc_deger) %>% #buradaki "!" ünlem işareti uc değer olmayanları kullan anlamındadır.
ggplot(aes(x = 1, y = lifeExp)) +
geom_boxplot()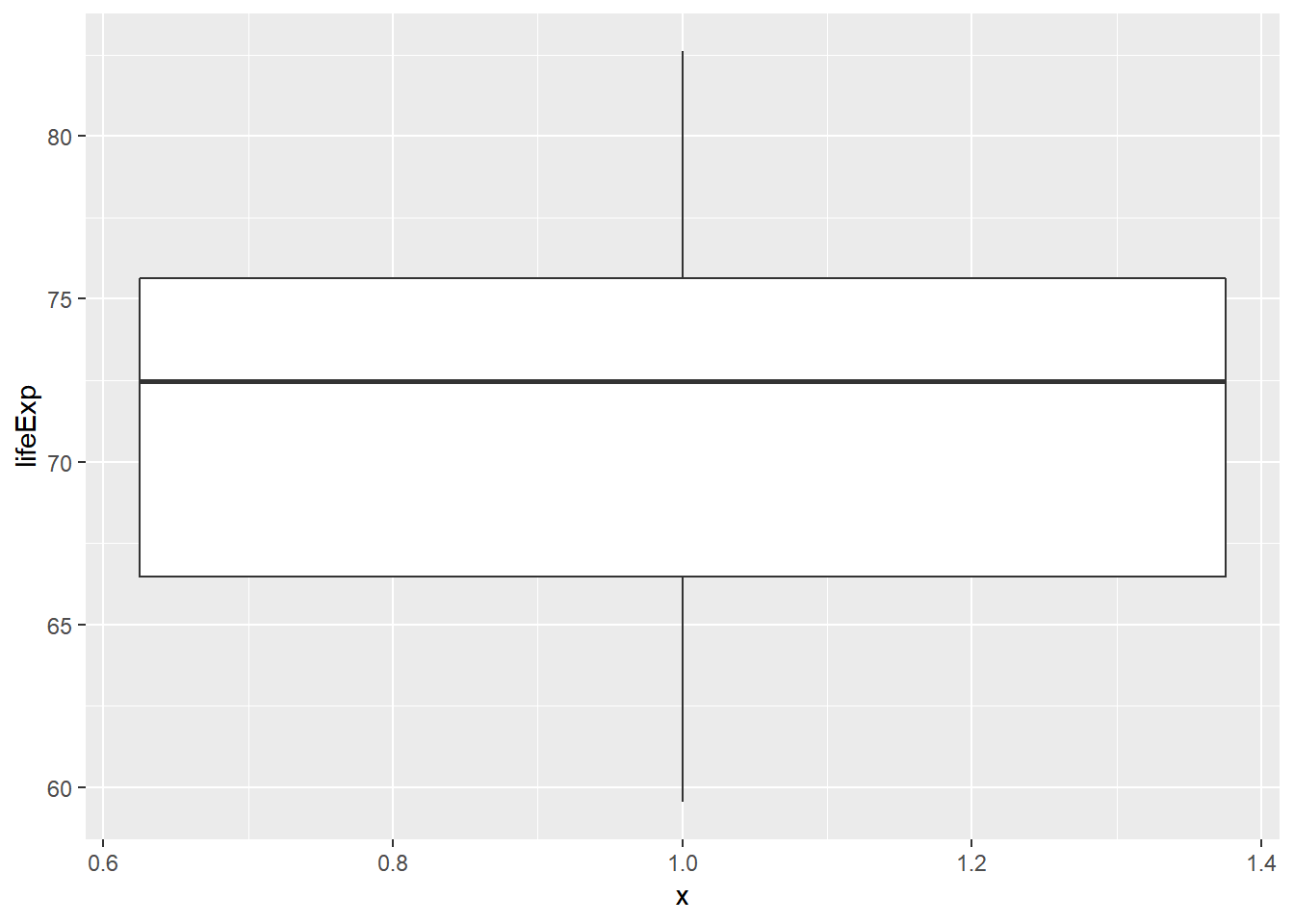
11.4 Uygulama Örneği: İstenmeyen e-posta (spam) incelemesi
Bu bölümde bir e-posta hasabına gelen iletilerin kaydını tutan “emails” isimli veri tabanını kullanacağız. Veri tabanına https://tinyurl.com/yabhoe56 adresinden ulaşabilirsiniz.
Acaba bir e-postanın uzunluğu ile istenmeyen bir e-posta (spam) olması arasında bir ilişki kurulabilir mi? İstenmeyen e-postaların genellikle bir veya bir kaç link içeren kısa metinlerden oluştuğu düşünülürse bu yaklaşım analize başlangıç için mantıklı olabilir. emails isimli veritabanı üzerinde dplyr ve ggplot paketlerini kullanarak bu ilişkinin testini yapabiliriz. Ancak işlemlere başlamadan önce ?email komutu ile veritabanı hakkında bilgi sahibi olalım. Aşağıdaki kod bahsettiğimiz ilişkiyi inceliyor
Şimdi e-postaların içindeki karakter sayılarını bildiren num_char değişkeni üzerinde uygun merkezi eğilim ölçüleri ve dağılım denetlemelerini yapalım
email %>%
group_by(spam) %>% #gruplama değişkenimiz
summarize(median(num_char), # inceleme değişkenimizin medyanı
IQR(num_char)) #inceleme değişkenimizin çeyrekler arası açıklığı## # A tibble: 2 x 3
## spam `median(num_char)` `IQR(num_char)`
## <fct> <dbl> <dbl>
## 1 no-spam 6.83 13.6
## 2 spam 1.05 2.82Yukarıdaki tablodan spam olmayan normal bir e-postanın, spam olan e-postalara kıyasla kabaca 6 kat daha fazla karakter içerdiğini anlıyoruz. Aynı değerlendirmeyi çeyreklerarası açıklık değeri de onaylıyor. Bu değerleri kutu grafik kullanarak grafikleyelim. Grafik için değişkenin logaritmasını almak daha anlaşılır bir çıktı elde etmemizi sağlıyor.
email %>%
mutate(log_num_char = log(num_char)) %>% # değişkenin logaritması
ggplot(aes(x = spam, y = log_num_char)) + #spam değişkenini
# factor değişken olarak tanımlama
geom_boxplot()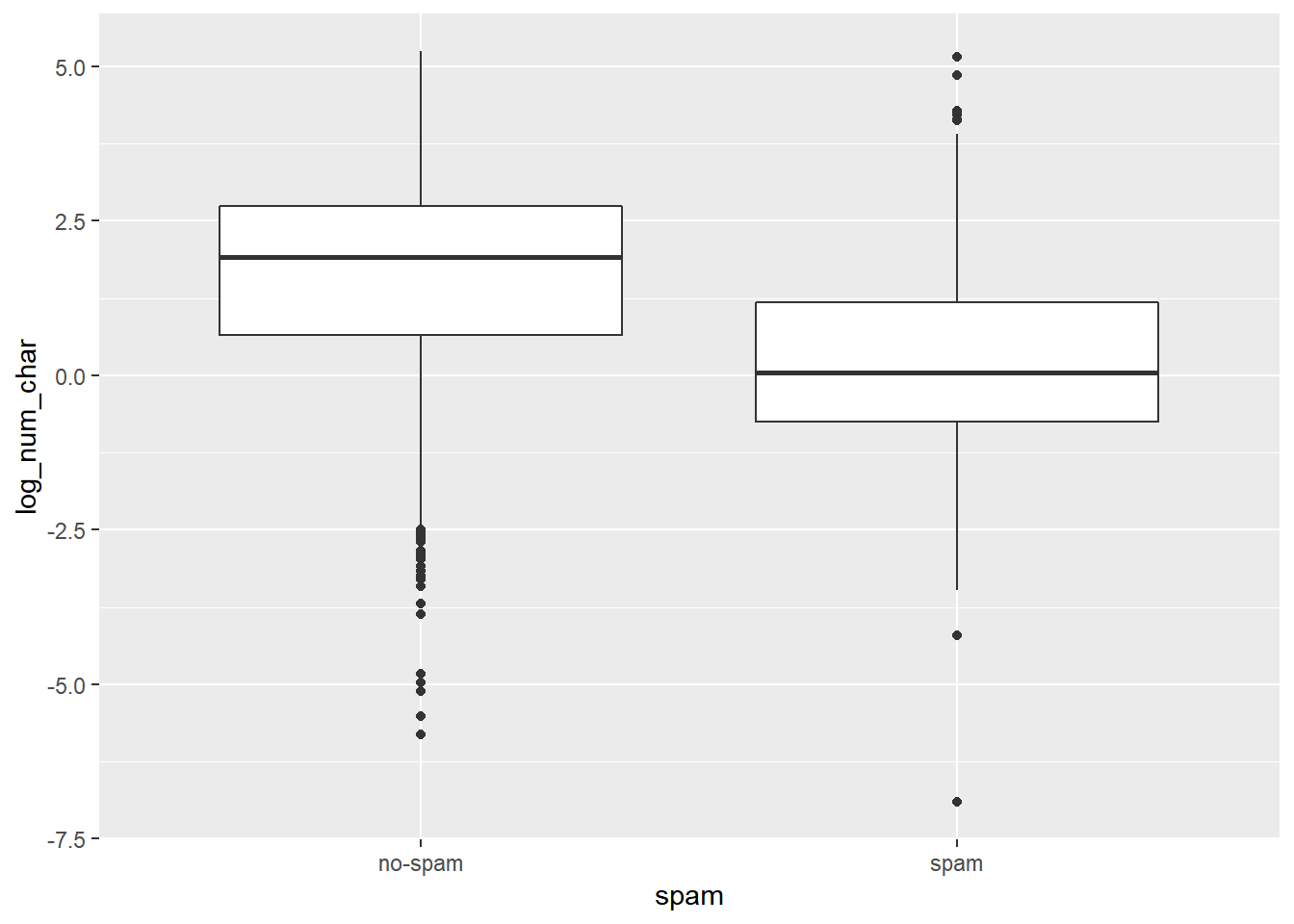
İstenmeyen e-postaların bir diğer özelliği çok fazla sayıda ünlem işareti içermeleridir. Veri tabanındaki exclaim_mess değişkeni bir mesaj içerisindeki ünlem işaretlerinin sayısını ölçmektedir. Özet istatistikleri ve görselleştirme kullanarak bu ilişkiyi inceleyelim. Lütfen aşağıdaki kodları ve oluşturdukları grafikleri yorumlayınız. Bahsettiğimiz türden bir ilişkiyi görebiliyor muyuz?
email %>%
group_by(spam) %>% #gruplama değişkeni
summarize(median(exclaim_mess), #inceleme değişkeni medyanı
IQR(exclaim_mess))## # A tibble: 2 x 3
## spam `median(exclaim_mess)` `IQR(exclaim_mess)`
## <fct> <dbl> <dbl>
## 1 no-spam 1 5
## 2 spam 0 1# Spam and exclaim_mess değişkenleri histogramı
email %>%
mutate(log_exclaim_mess = log(exclaim_mess + .01)) %>%
ggplot(aes(x = log_exclaim_mess)) +
geom_histogram() + #histogram
facet_wrap(~ spam) #spam kategorilerine göre ayrıştırma## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.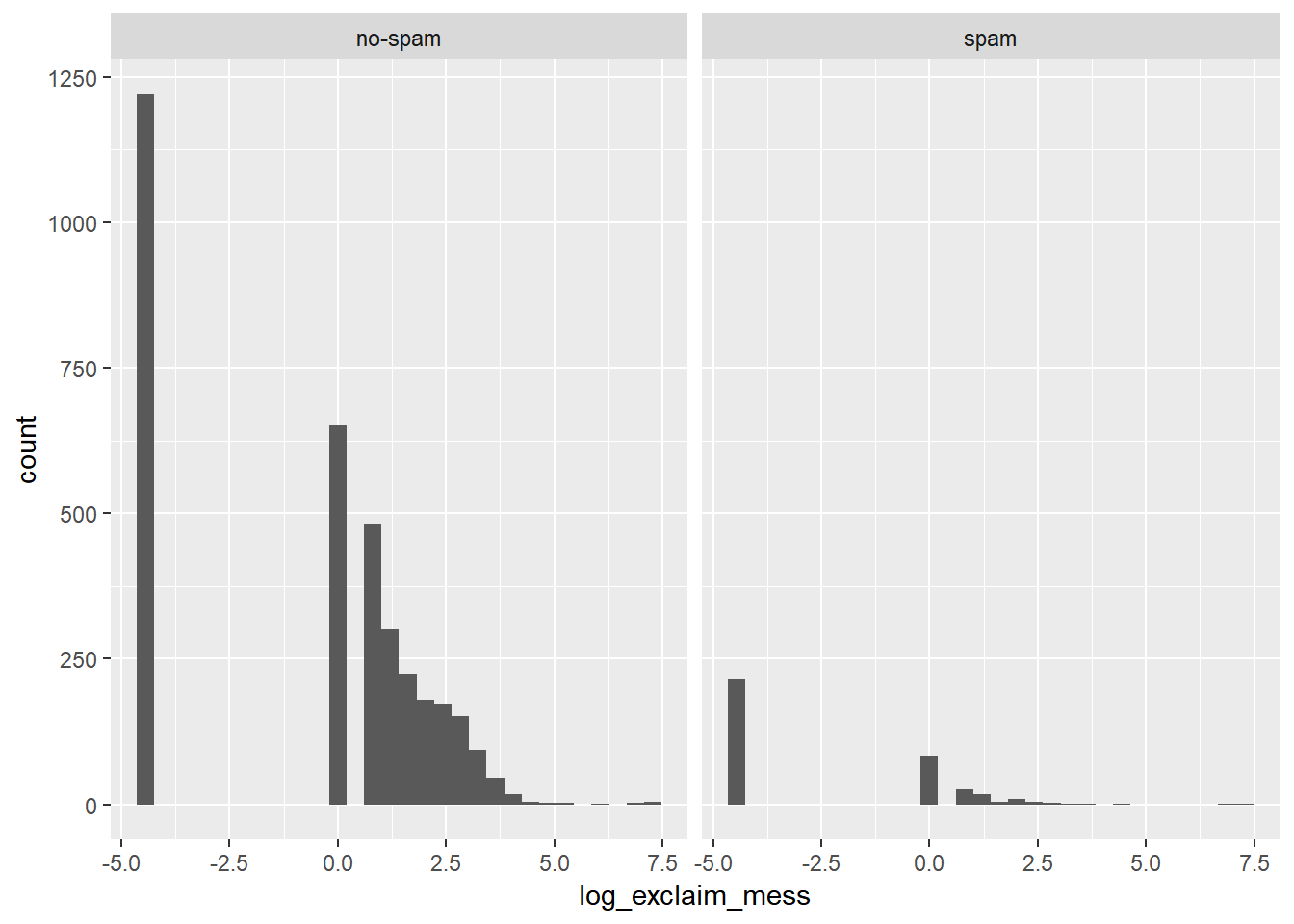
# Alternatif grafik: Kutu Grafik
email %>%
mutate(log_exclaim_mess = log(exclaim_mess + .01)) %>%
ggplot(aes(x = 1, y = log_exclaim_mess)) +
geom_boxplot() +
facet_wrap(~ spam)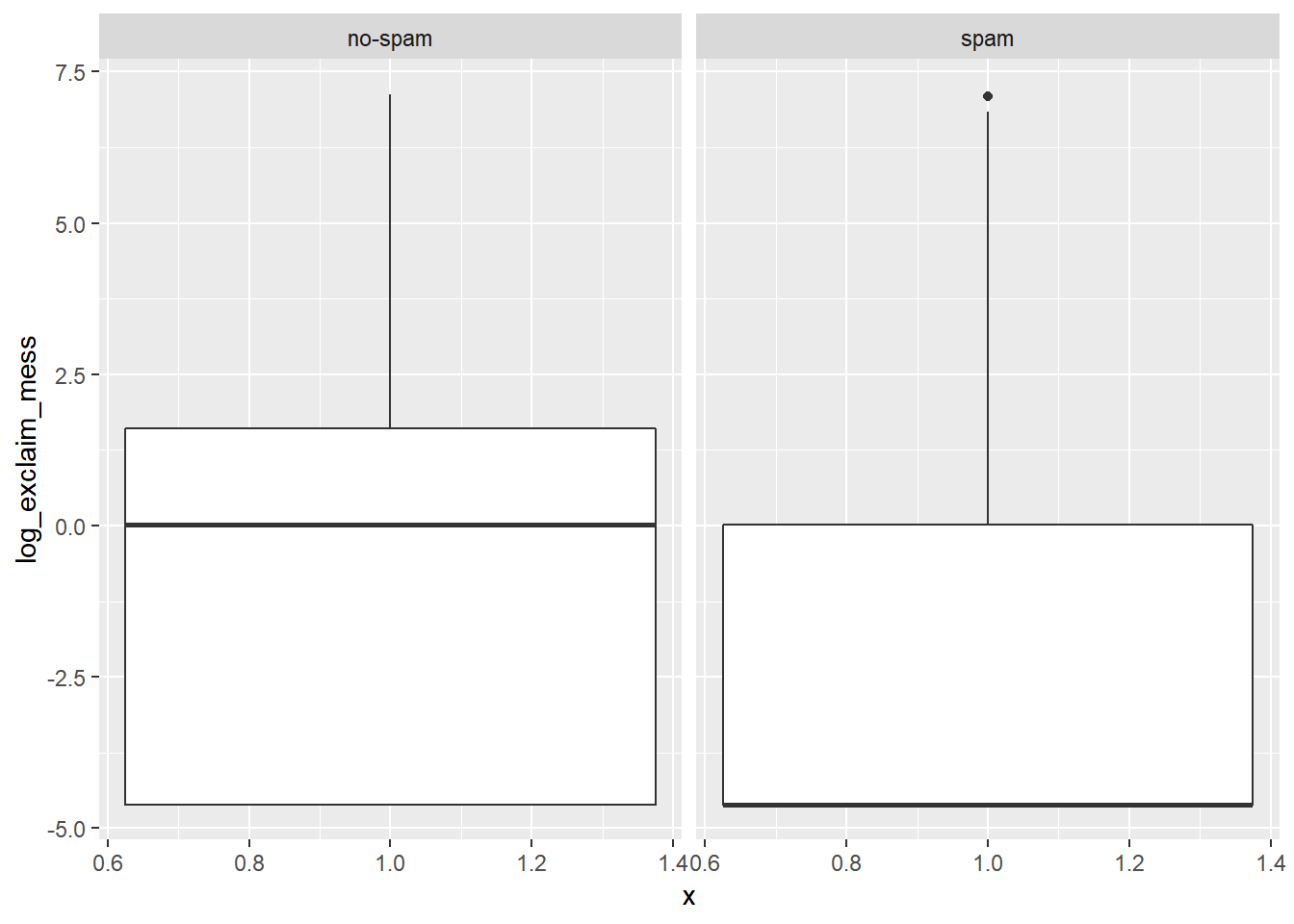
# Alternative plot: Overlaid density plots
email %>%
mutate(log_exclaim_mess = log(exclaim_mess + .01)) %>%
ggplot(aes(x = log_exclaim_mess, fill = spam)) +
geom_density(alpha = 0.3)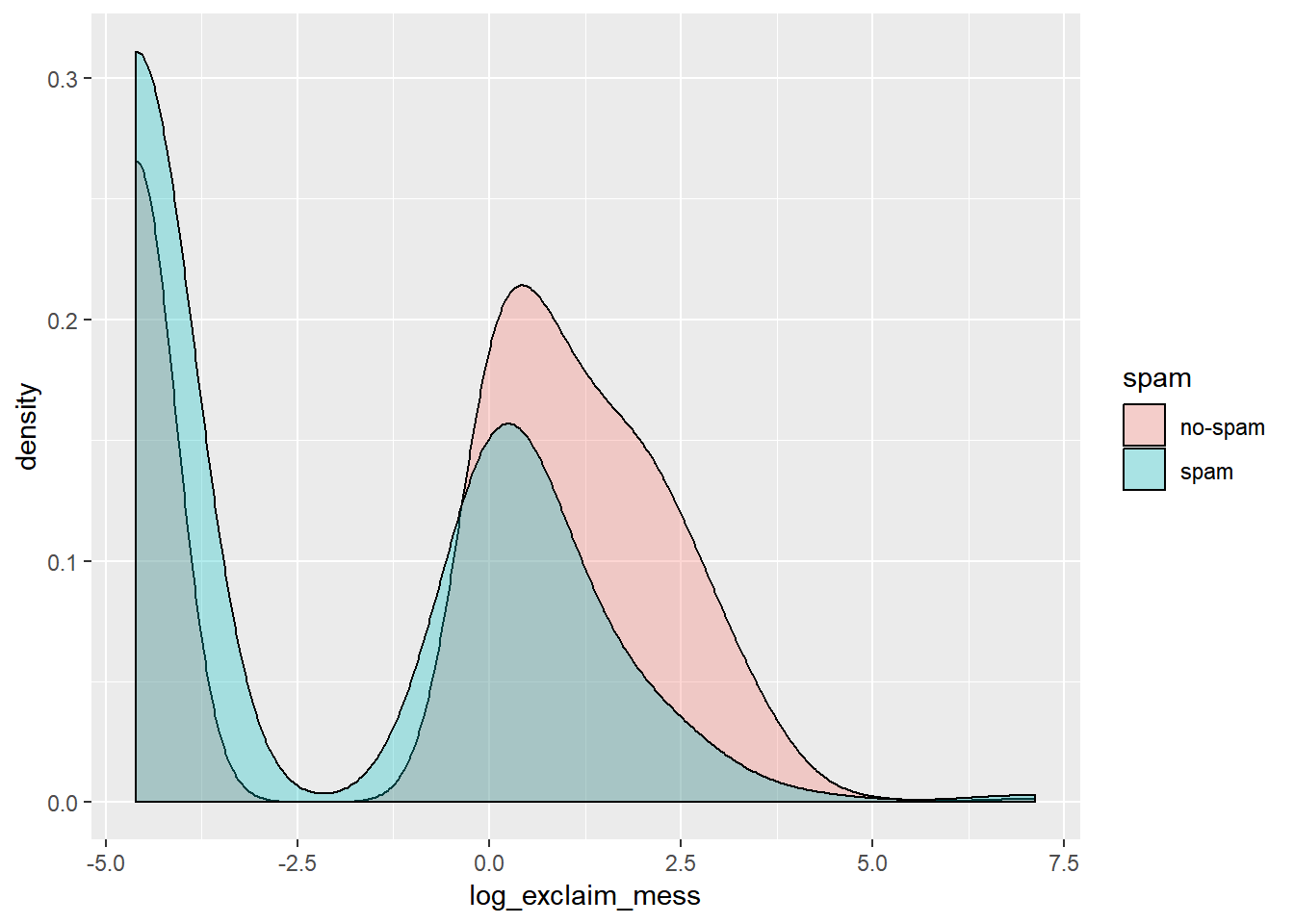
Bir veri seti incelenmeden önce kodlanmış olan verinin düzgünlüğünün testi gerekir. Örneğin num_char değişkeninin bir mesajdaki karakter sayısını içerdiğini biliyoruz. Dolayısıyla bu değişkende herhangi bir negatif değer bulunmaması gerekir. Bu durumun testi için email$num_char < 0 kodunu kullanabiliriz. Bu kodu çalıştırdığınız konsolunuzda bahsettiğimiz koşulun doğru TRUE veya yanlış FALSE olduğunu kontrol eden uzun bir liste oluşur. Bu uzun listeden hoşlanmadıysanız alternatif olarak sum(email$num_char < 0) kodunu kullanabilirsiniz. R TRUE değerlerini 1 FALSE değerlerini 0 olarak algıladığından eğer 0’dan büyük bir değer elde edersek değişkende negatif bir değer olduğunu anlamış oluruz
sum(email$num_char < 0)## [1] 0Veritabanı ile ilgili bazı spesifik sorularınıza dplyr zincirleri ile kolayca yanıt bulmak olasıdır. Örneğin “Dollar” kelimesi, spam olmayan e-postalara kıyasla, spam olan e-postaların içeriğinde daha fazla bulunur" iddiasına aşağıdaki zincir kod ile yanıt bulabiliriz.
email %>%
filter(dollar > 0) %>%
group_by(spam) %>%
summarize(median(dollar))## # A tibble: 2 x 2
## spam `median(dollar)`
## <fct> <dbl>
## 1 no-spam 4
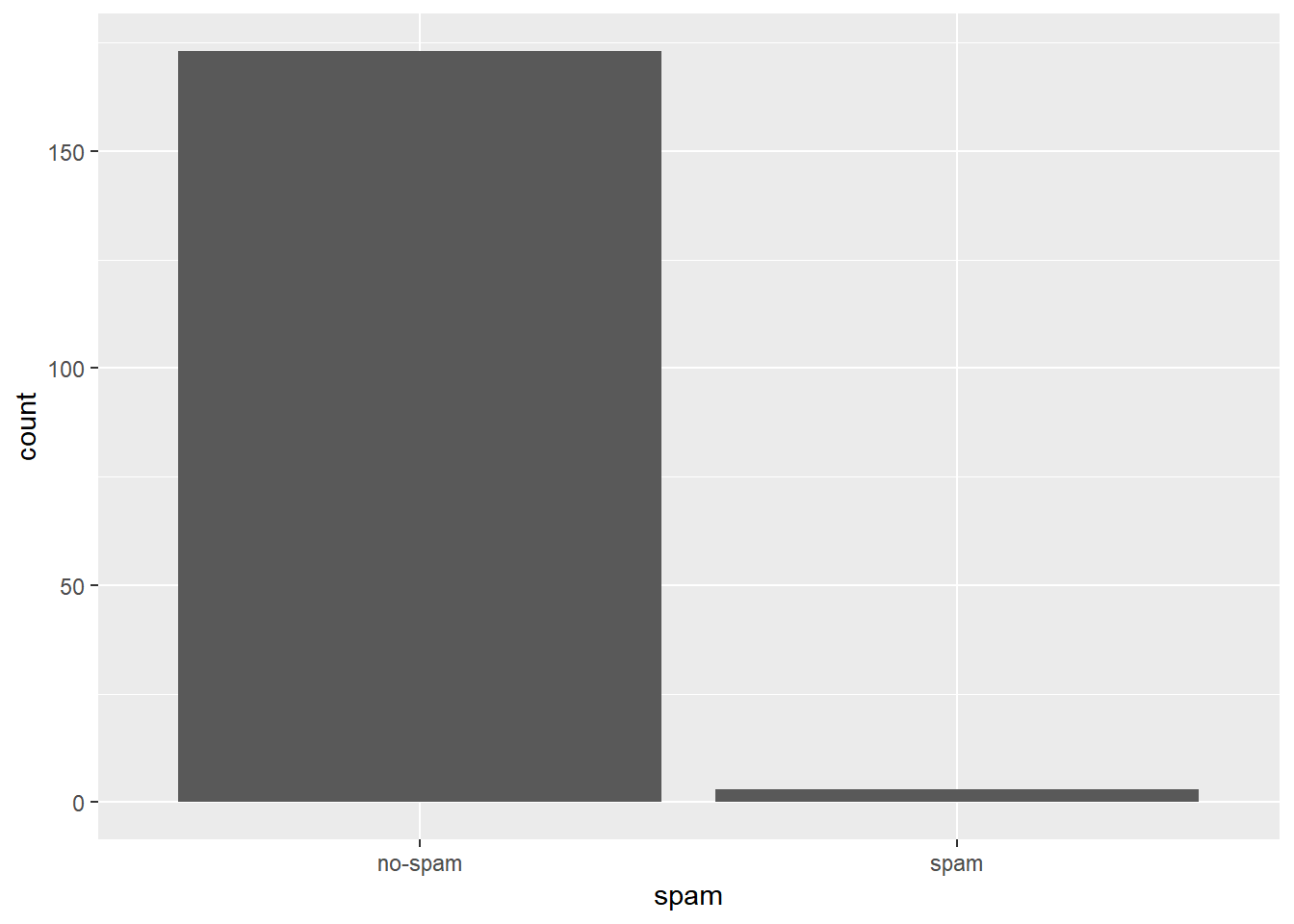
## 2 spam 2Aynı soruyu bir de şöyle soralım: “Bir mesajda 10 kereden fazla”dollar" kelimesi geçiyorsa, o e-posta istenmeyen e-postadır“. Aşağıdaki kod soruya bir sütun grafik ile cevap vermeye çalışıyor.
email %>%
filter(dollar > 10) %>%
ggplot(aes(x = spam)) +
geom_bar()