Bölüm8 Korelasyon ve Regresyon

8.1 İki Değişkenli Analizler

Bu bölümde sayısal olarak kodlanmış iki veya daha fazla değişken arasındaki ilişkileri anlamaya çalışacağız. İstatistiki modellerde çoğunlukla çıktı değerini ifade eden bir bağımlı değişken ve bu çıktı değerini etkileyen bir veya daha fazla girdi değişkeni (bağımsız değişkenler/açıklayıcı değişkenler) bulunur. Bağımlı değişken “y” harfi ile gösterilirken bağımsız değişkenler ise “x” harfi ile gösterilir. İlk aşamada sadece bir bağımlı ve bir bağımsız değişken ile örneklerimizi oluşturacağız.

İki nümerik değişken arasındaki ilişkiyi en hızlı ve etkili şekilde anlamak için çoğunlukla “saçınım grafikleri/scatter plots” kullanılır. Saçınım grafikleri x ve y boyutlarının eksenlere işlendiği ve her bir noktanın ilgili değişken değerine denk geldiği grafik tipidir. İlke olarak saçınım grafiklerinde bağımlı değişken y ekseninde, bağımsız değişken ise x ekseninde gösterilir.

Bu bölümde 2018 Haziran ve 2015 Kasım seçim sonuçlarını il bazında barındıran “dat” isimli veri tabanı kullanacağız. Öncelikle bu veri tabanını yükleyelim.

dat <- read.csv("C:/Users/emretoros/OneDrive/Makale/R/book/dat.csv", encoding="UTF8")

Görüldüğü üzere bu veri tabanında partilerin 2015 Kasım ve 2018 Haziran seçimlerinde aldıkları oylar ile cumhurbaşkanı adaylarının aldıkları oylar da bulunmaktadır.

İlk saçınım grafiğimiz için parti ve parti adayının aldığı oy arasındaki ilişkiyi gözden geçirelim: Acaba cumhurbaşkanı adayının aldığı oy ile bu adayın partisinin aldığı oy arasında nasıl bir ilişki var? Bu soruyu CHP ve Muharrem İnce için cevaplayan grafik kodunu aşağıda bulabilirsiniz.

library(ggplot2)

akp_rte_p <- ggplot(data = dat, aes(x = akp2018, y = rte)) + 
  geom_point()

akp_rte_p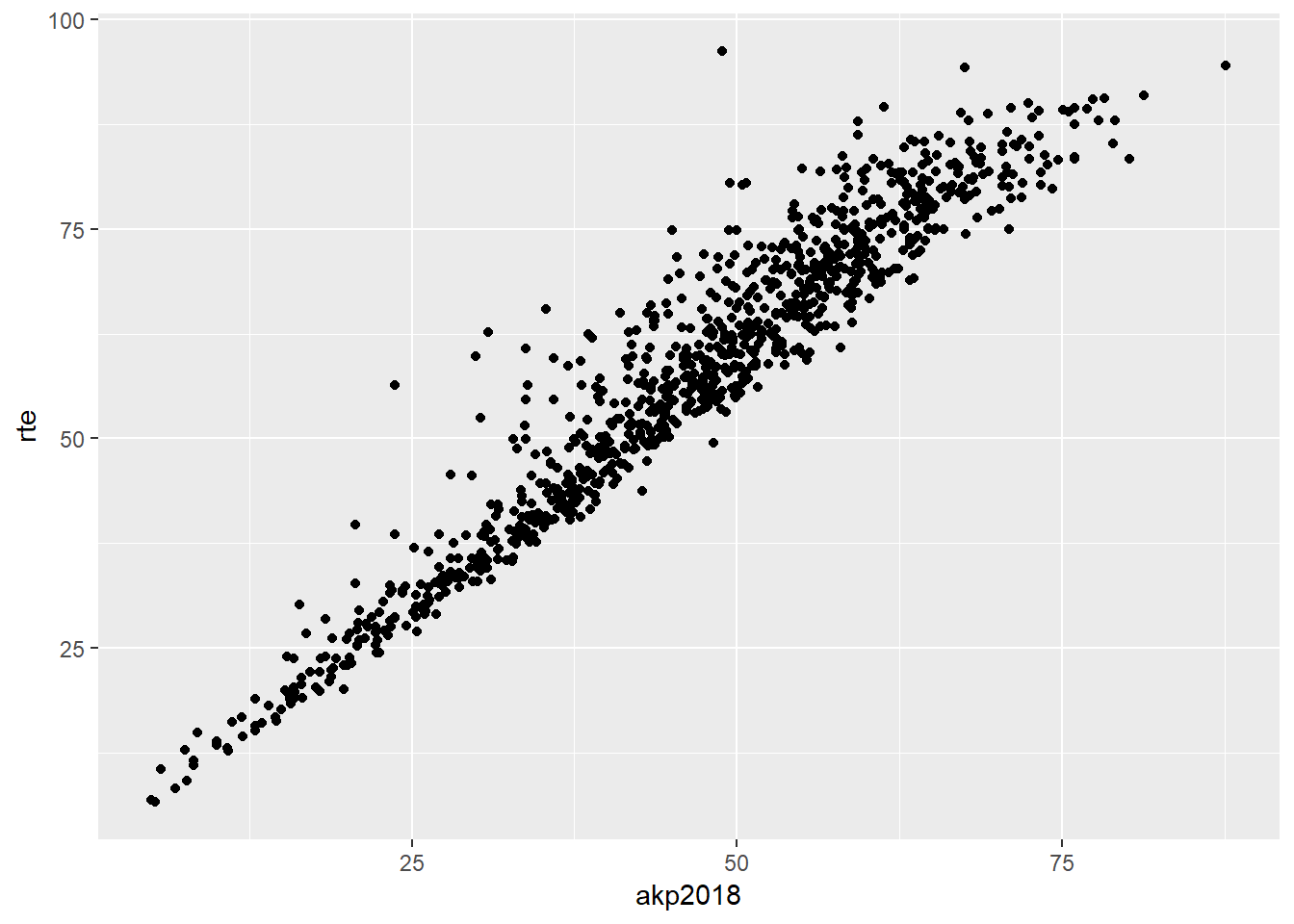

Grafikten anlaşılan bu iki değişken arasında aynı yönde ve gayet kuvvetli bir lineer ilişki olduğudur. Grafiği daha detaylandırmak adına gelin oy yüzdelerini gruplayalım ve grafiği tekrar çizelim. Bu iş için cut() fonksiyonunu kullanacağız. Bu fonksiyon iki argüman içerir: birincisi parçalara ayırmak istediğiniz değişken ve ikincisi ise kaç parçaya ayırmak istediğiniz (breaks). Aşağıdaki grafikte parti oyu beş ayrı parçaya ayrıştırılıyor ve nokta yerine kutu grafiği olarak çiziliyor.

akp_rte <- ggplot(data = dat, 
       aes(x = cut(akp2018, breaks = 5), y = rte)) + 
  geom_boxplot()

akp_rte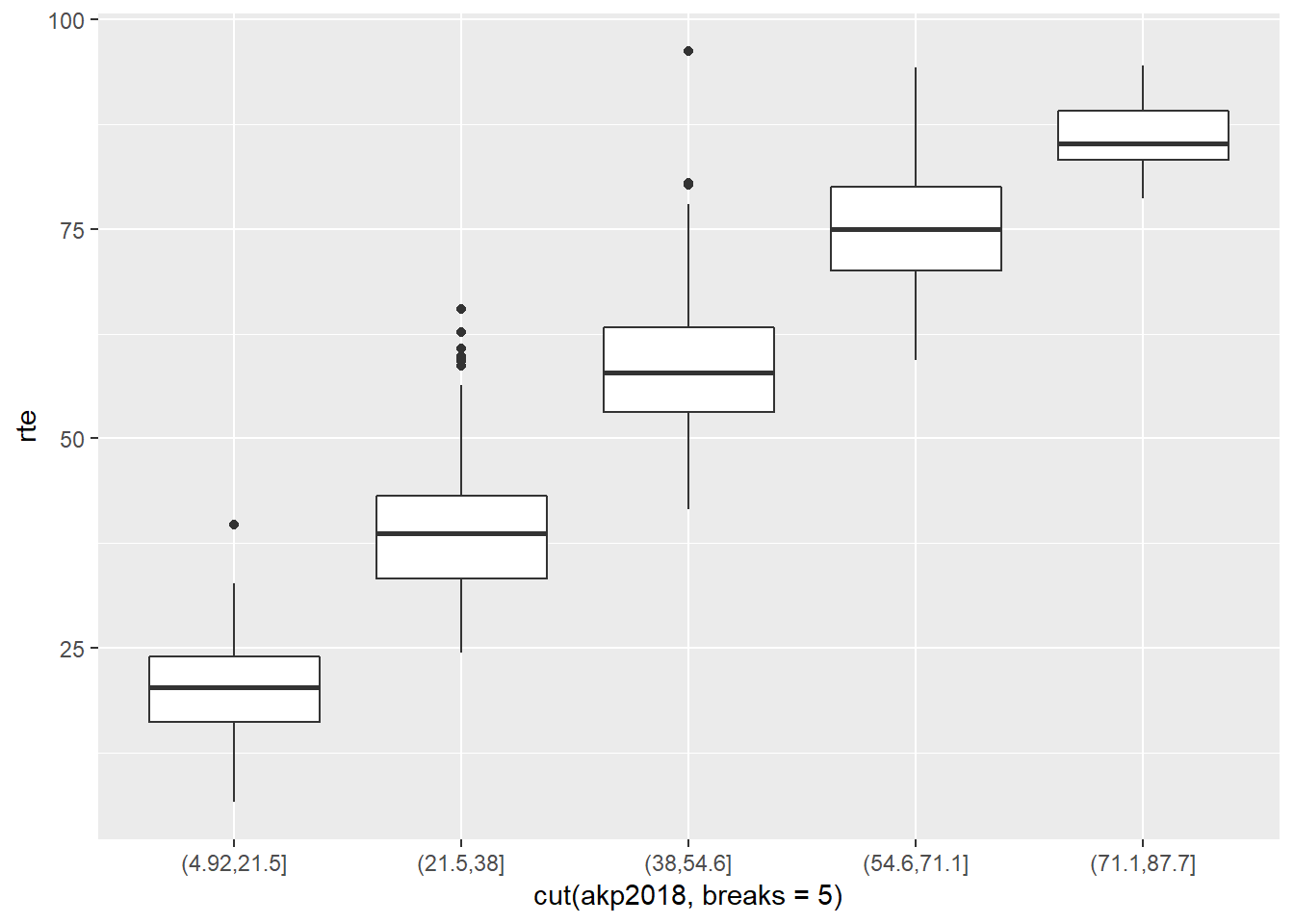

Çizdiğimiz ikinci grafikte de bu lineer yapıyı gözlemleyebiliyoruz. Şimdi gelin aynı grafiği AKP yerine MHP oylarını kullanarak çizelim ve iki grafiği yorumlayalım.

mhp_rte_p <- ggplot(data = dat, aes(x = mhp2018, y = rte)) + 
  geom_point()

mhp_rte_p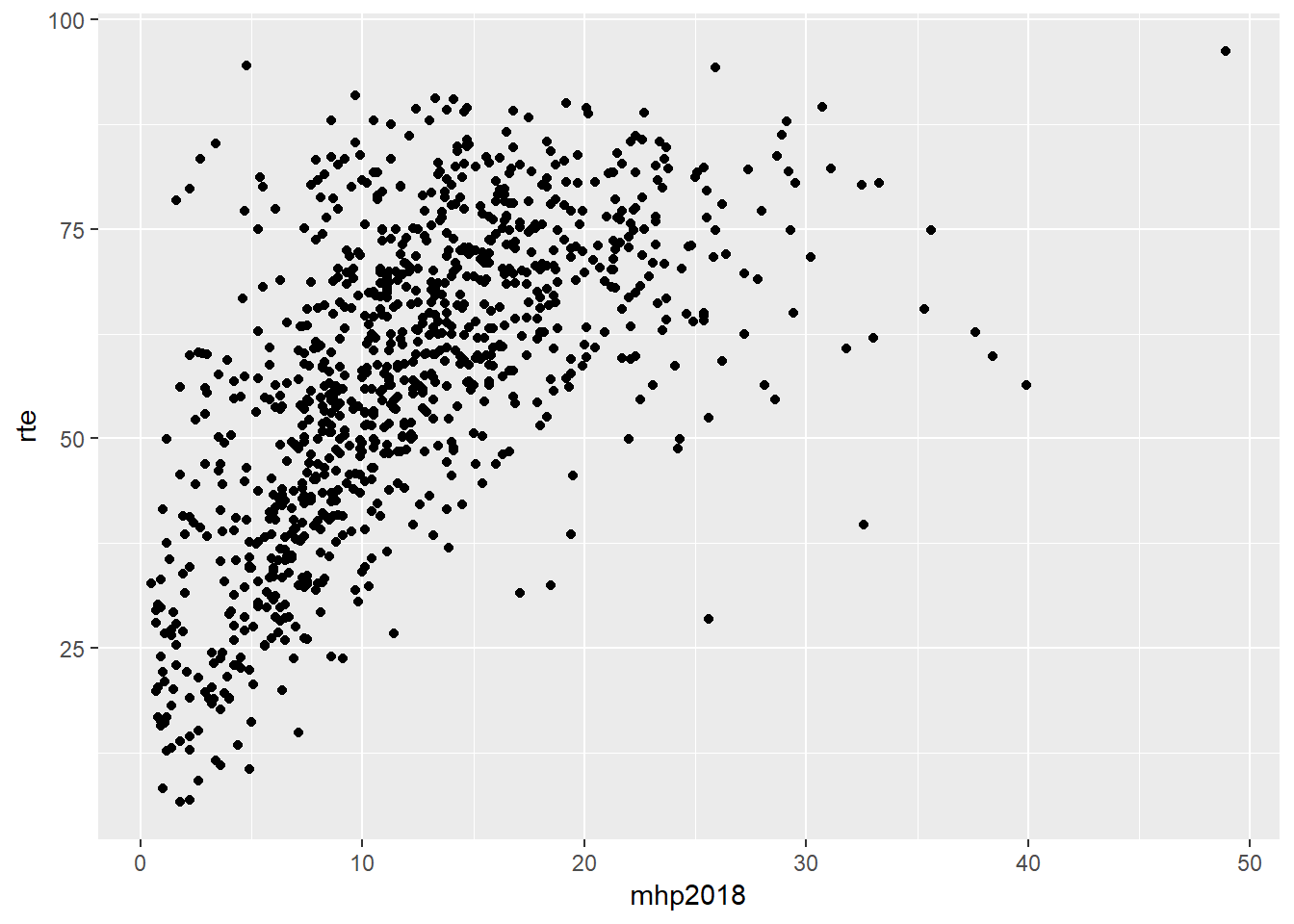

mhp_rte <- ggplot(data = dat, 
       aes(x = cut(mhp2018, breaks = 5), y = rte)) + 
  geom_boxplot()

mhp_rte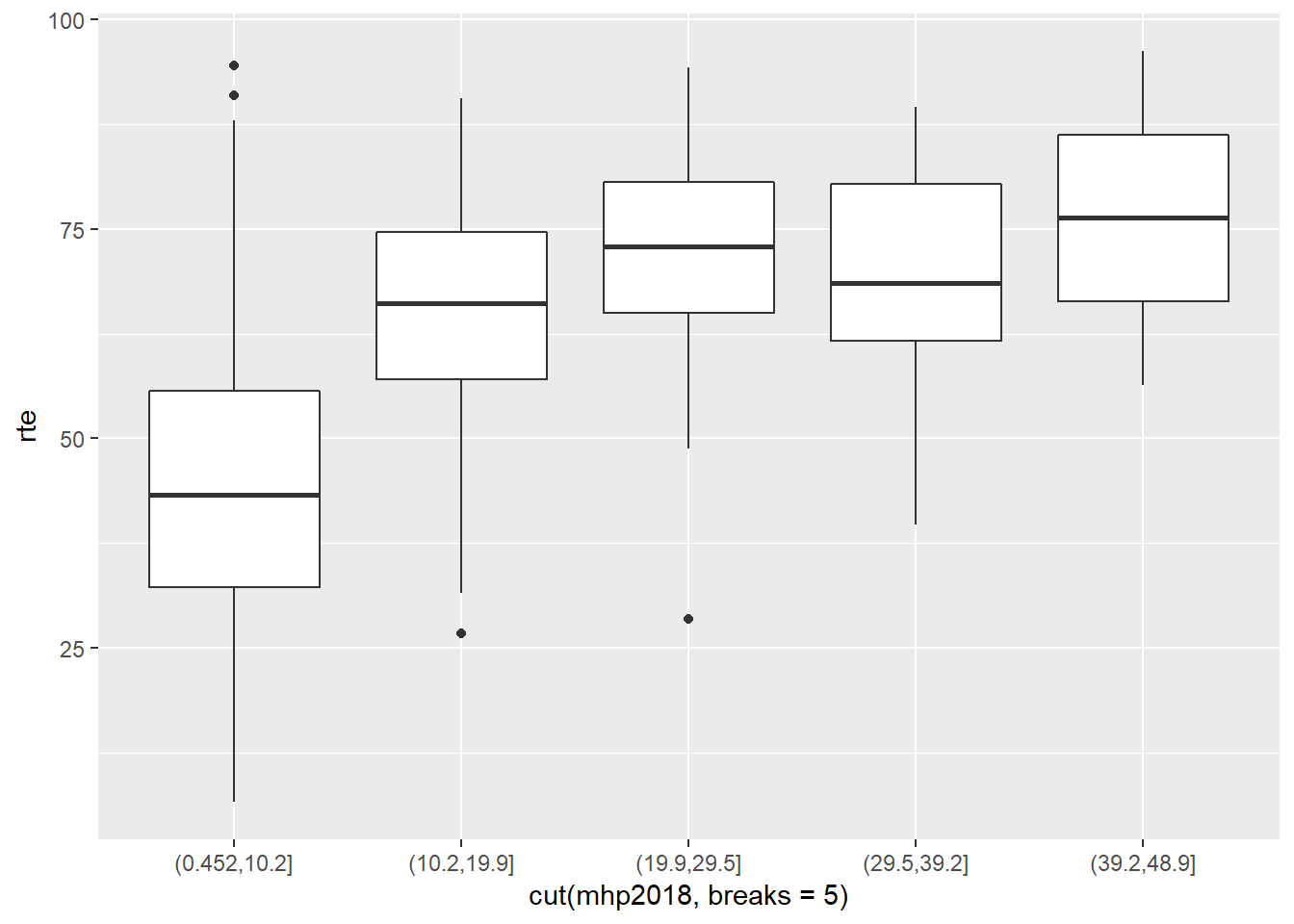

MHP için çizdiğimiz grafiklerde lineer görüntünün AKP grafiğinde olduğu kadar net olmadığını söyleyebiliriz.

8.2 İki değişkenli dağılımın yapısı

Saçınım grafikleri ile değişkenler arasındaki ilişkiyi dört açıdan görme şansı olur.

Form (lineer, karesel, lineer olmayan vb)
Yön (aynı yönde -her iki değişken de aynı anda artıyor veya azalıyor- veya ters yönde -bir değişken artarken diğeri azalıyor-)
Kuvvet (Görünen yapı ne kadar bütünsel ne kadar sapma/gürültü var?)
Uç değerler (Görünen yapıdan belirgin bir şekilde ayrılan gözlemler var mı?)

Çizdiğimiz ilk grafikteki görüntüyü bu dört açıdan değerlendirdiğimizde lineer, aynı yönde, kuvvetli ve uç değerleri olmayan bir ilişki olarak değerlendirebiliriz.

Aşağıda ise lineer olmayan bir ilişkinin grafiğini görebilirsiniz. Bu dağılımda aynı zamanda sol ve sağ başlarda bulunan uç değerler de dikkat çekiyor

Lineer olmayan ilişki

Son olarak vantilatör tipi (fan type) denen dağılıma göz atalım.

Vantilatör ilişki

Burada ilişki her ne kadar lineer de olsa değerler arttıkça dağılımdan sapma da artmaktadır. Bu tip değişkenler için daha sonra göreceğimiz regresyon uygulamalarında değişkenlerin logaritmalarının alınması modelin daha güçlü sonuçlar üretmesine yol açar

Bu bölümde son olarak uç değerlerin saptanmasını ele alacağız. Uç değerlerin saptanması için her ne kadar konulmuş belli bir kural olmasa da saçınım grafikleri ile bu gözlemleri saptayabiliriz. Aşağıdaki grafik 2015 ve 2018 MHP oylarını karşılaştırıyor.

mhp_kar <- ggplot(data = dat, aes(x = mhp2018, y = mhp2015)) +
  geom_point()

mhp_kar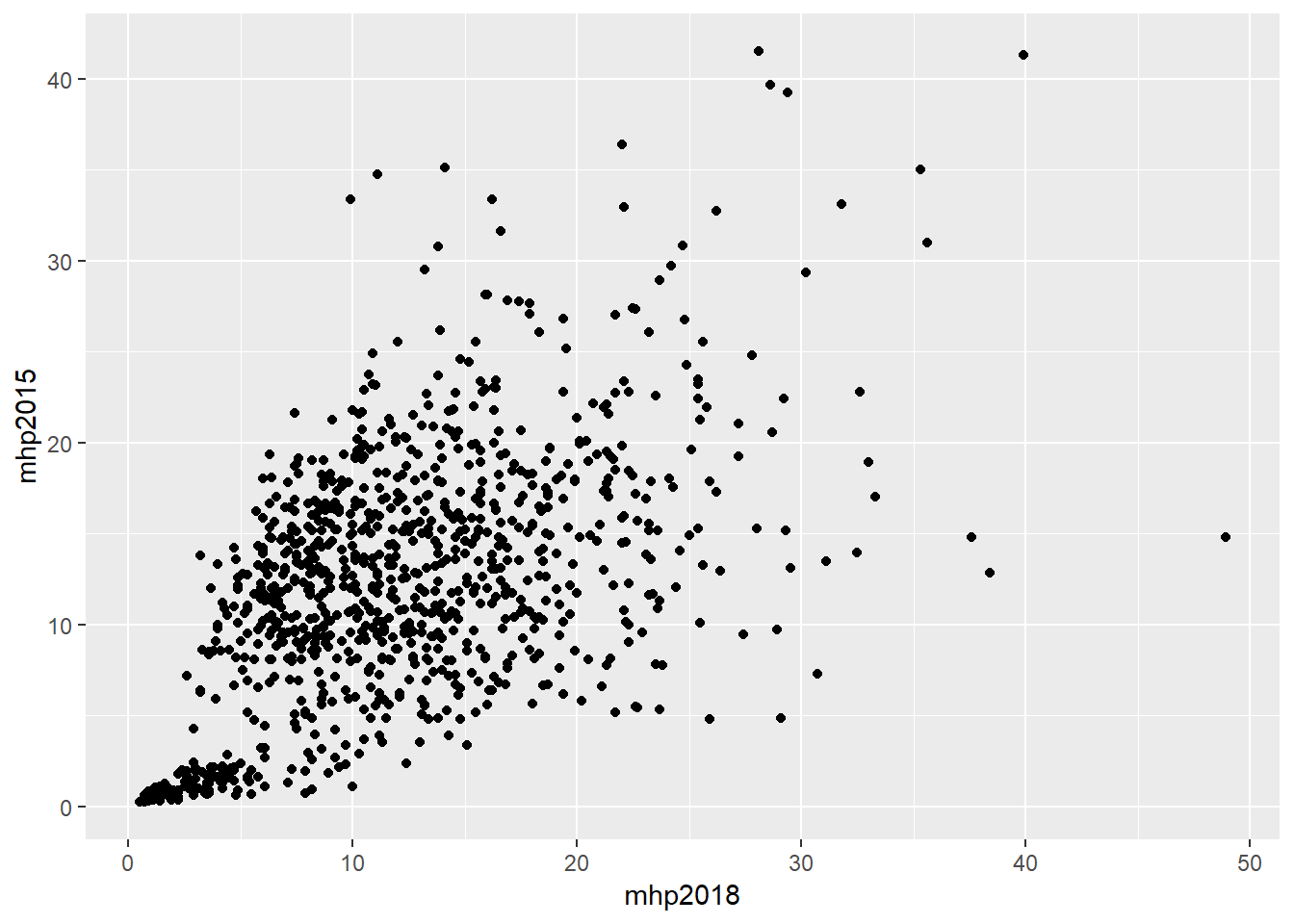

Bu grafik aslında vantilatör tipi ilişkiye bir örnek oluşturuyor. Bu grafikte x ekseninde en sağda bulunan 50 değerine yakın tek nokta dikkat çekiyor. Bu gözlemin hangi ilçeye ait olduğunu bulmak için aşağıdaki kodu kullanabiliriz

library(dplyr)
dat %>% 
  filter (mhp2018 > 45) %>% 
  dplyr::select (NAME_TR)

##   NAME_TR
## 1  HARRAN

8.3 Korelasyon

Yukarıdaki örneklerde ilişkilerin yapısını gözlemledik ama kuvvetlerini sayısal hale dönüştürmedik. İlişkilerin kuvvetini belirten sayısal değeri ortaya koyan istatistiğe korelasyon denir. Korelasyon değeri/katsayısı -1 ve +1 değerleri arasında yer alır. Buradaki - ve + değerleri ilişkinin yönünü pozitif/aynı yönde ve negatif/ters yönde olmak üzere tanımlar. Korelasyon katsayısının büyüklüğü ise ilişkinin kuvvetini betimler. Bu değer “+1”e yaklaştıkça kuvvetli aynı yönde ilişki ve “-1”e yaklaştıkça ise ters yönde kuvvetli ilişki saptanmış olur. “±0.5” e yakın değerler orta seviye ilişkiyi, “±0.2”’ye yakın değerler zayıf ilişkileri ifade eder. Lineer bir ilişkinin olmadığı durumlarda korelasyon katsayısı “0” değerine yakın olur. Korelasyon katsayısı hakkında unutulmaması gereken bir nokta bu katsayının lineer ilişkiler için kuvveti hesaplıyor olmasıdır. Dolayısıyla korelasyon katsayısının bir anlam ifade etmesi için ilişkinin lineerliği kontrol edilmelidir. Aşağıdaki grafikte gösterilen karesel ilişkinin korelasyon katsayısı hesaplandığında “0” değerine yakın çıkacaktır ama bu değişkenler arasında ilişki olmadığı anlamına gelmez.

Karesel ilişki

İstatistik bilimi içerisinde korelasyon değeri çeşitli yöntemler ile tanımlansa da en sık kullanılanı kısaca “r” değeri olarak bilenen “Pearson product-moment correlation” adıyla bilenen hesaplama yöntemidir. Teknik notasyonunu aşağıda görebilirsiniz.

Korelasyon Formülü

cor(x,y) fonksiyonu x ve y değişkenleri arasındaki korelasyon katsayısını hesaplar. Aşağıdaki kod CHP parti adayı ve parti oyu arasındaki korelasyonu hesaplıyor. Son kısımda bulunan use=pairwise.complete.obs argümanı veride bulunabilecek NA değerlerini (yani kayıp veriyi) hesaba katmadan bu işlemi gerçekleştirmek için kullanılır.

kor_chp <- dat %>% 
  summarize(N = n(), r = cor(chp2018, mi, use = "pairwise.complete.obs"))

kor_chp

##     N         r
## 1 970 0.9705862

Görüldüğü üzere Muharrem İnce ve CHP oyları arasında aynı yönde ve kuvvetli bir ilişki bulunuyor.

Korelasyon analizlerinde asla unutulmaması gereken bir konuya dikkat çekmek gerekir. Korelasyon değişkenler arasındaki bağlantıya işaret eder ama değişkenler arasında nedensellik kurmaz. Yani bir korelasyon testinde yüksek çıkan r katsayısı, x değişkenindeki değişime y değişkenindeki değişkenliğin neden olduğu anlamına gelmez. Bu kullanım hatasına, sıkça, gazetelerde yayınlanan bilimsel araştırma haberlerinde rastlayabilirsiniz. Özetle

KORELASYON NEDENSELLİK GÖSTERMEZ!

8.4 Basit Lineer Regresyon

Regresyon bir bağımlı değişken ile bir veya birden fazla bağımsız değişken arasındaki ilişkinin incelenmesi için kullanılan istatistiki yönteme verilen isimdir. Regresyon testleri iki amaç için kullanılır: tahmin ve nedenselliğin incelenmesi

1.Tahmin: Buradaki amaç bağımlı değişkeni tahmin etmek için bağımsız değişkenlerin gözlemlenmiş değerlerini kullanarak bir formül üretmektir. Örn: Salıverilmiş bir suçlunun tekrar tutuklanması ihtimalinin kestirimi için, işlediği suç, yaşı, daha önce işlediği suç miktarı gibi değişkenlerin kullanımı

Nedensellik: Bu analizde bağımsız değişkenler bağımlı değişkenin “nedenleri” olarak varsayılır. Amaç varsayılan bağımsız değişkenlerin gerçekten bağımlı değişken ile bağlantısı olup olmadığını ve varsa bu bağlantının boyutunu anlamaktır.

Lineer regresyona bu isimin verilmesinin nedeni doğrusal olması yani doğrusal bir denklem kullanmasından kaynaklanır. Doğrusal denklem ise adını grafik olarak çizildiğinde bir doğru üretmesi nedeniyle alır. Doğrusal denklem bağımlı değişken üzerinde tek bir bağımsız değişken incelendiğinde net olarak görünür.

Bu denklemde “y” bağımlı değişken, “a” kesen, “b” eğim(katsayı) ve “x” ise bağımsız değişkeni ifade eder.

Regresyon analizinde çoğunlukla birden fazla bağımsız değişken kullanılır. Böylece bir bağımsız değişkenin etkisine bakılırken diğer bağımsız değişken kontrol edilmiş olur.

Bir önceki örneğe “yaş” değişkenini de katalım. GELİR = 6000 + (800 x Eğitim Yılı) +(400 x Yaş) 14 yıl eğitim almış 40 yaşında birisinin gelirini hesapladığımızda GELİR = 6000 + (800 x 14) +(400 x 40) = 33200

Bu hesaplamanın yazımı ise aşağıdaki gibidir.

Regresyon analizlerinde nümerik değerler veya kategorik değişkenlerin nümerik halleri kullanılır. Rastlantısal çekilmiş örneklemin ürettiği gözlemler ve vaka sayısının artması analizin kuvvetini arttırır. Eğer değişkenin sadece iki kategorisi varsa (örn: evet - hayır) değişkenlere sayı değerleri verilerek regresyon analizi için kullanılır hale getirilebilir. Bu değişkenlere “göstermelik değişken” veya “kukla değişken” denir.

Regresyon formülünde bulunan katsayıların (a ve b1, b2, … ler) hesaplanması için başvurulan yöntemlerin en popüleri OLS(Ordinary Least Squares/En Küçük Kareler) yöntemidir. Regresyon katsayıları bilindiğinde doğrusal denklemi kullanarak bağımlı değişkeni tahmin edebiliriz. Kesen değeri 0 (x), eğitim katsayısı (b1) 1000 ve yaş katsayısı (b2) 500 olarak tanımlanmış lineer denklemi sınayan aşağıdaki örneğe bir göz atalım

Şekilden de görüldüğü üzere bu katsayıları kullanarak yapılan 3 hesaplamada 1. ve 3. hesaplamalarda belli bir hata payı oluştu. (2. hesaplama tamamen şans eseri bir hata üretmedi!). Hiç hatasız bir tahmin yapmak sosyal bilimlerde mümkün olmadığından amaçlanan şey en az hatadır ve en küçük kareler kriteri de bu kullanılan katsayıları en az hata ile saptamak için kullanılır: tahminde gerçekleşen hataların kareleri alınıp toplandığında en ufak değerin oluşması hedeflenir.

Örnekte oluşan hatalar:

- 9000’ın karesi 81000
0’ın karesi 0
- 9000’ın karesi 81000
…..
…..

Toplam : 12,296,499,985 Acaba bu değer olası en küçük değer midir? Bu hesabı bilgisayara yaptırttığımızda oluşan regresyon katsayıları ve formülü

GELİR = - 25965 + (2057 x Eğitim Yılı) + (600 x Yaş)
Kareler toplamı: 9,364,695,694 (bizim tahminimizden %24 daha küçük)

Bu denklemden şunu anlıyoruz: gelir geçirilen her bir yıl fazla eğitim için 2057 lira ve fazladan her yaş için 600 lira artmaktadır.

Regresyon ile tahmin geliştirebiliriz ama bu tahminin ne kadar güçlü olduğunu anlamak için belirleme katsayısı R2 (Coefficient of determination) isimli başka bir teste daha ihtiyaç duyulur. Bu denklem için R2 değeri 0.28 olarak hesaplandı. Buradan şu anlaşılmaktadır: Eğitimde geçirilen yıl ve yaş gelirdeki değişikliğin yüzde 28’ini açıklar.

Son olarak katsayıların kuvvetinin yorumlanması konusuna değinelim. Regresyon analizi sonucunda oluşan katsayıların kuvvetini anlamak için hipotez testi kullanılır. Bir bağımsız değişkenin bağımlı değişken üzerinde etkisi yoksa katsayısı sıfır olacaktır. Hipotez testi ile sıfır değerinden farklı bir katsayı üretildiğinde bu katsayının hata sonucu oluşup oluşmadığını anlamak mümkün olur.

Hipotez testi ile sorumuza (Katsayı sıfırdan farklı ama bu durum gerçekten böyle mi?) basit “evet hatalı” veya “hayır hatasız” cevabı vermez. Hipotez testi ile bu duruma ait (hatalı olma veya olmama) bir olasılık hesabı yapılır. Bu hesaptan çıkan değer “p” değeri olarak adlandırılır. p değeri katsayıların standart hatalarına bölünmesi ile bulunan “t” değeri ile saptanır. p değerinin düşük çıkması katsayının sıfırdan farklı olduğunun kanıtı olarak değerlendirilir. Örneğimizde yaş için katsayı olan 600 standart hata olan 210 a bölündüğünde, t değeri olarak 2.86 elde edilir. t değeri olan 2.86’nın p değeri .005 civarındadır. Bu sonuçtan şu yorum yapılır: Eğer yaş için gerçek katsayı sıfır olsaydı (yani bu bağımsız değişkenin bağımlı değişken üzerinde hiçbir etkisi bulunmasaydı), bu OLS ile hesapladığımız regresyon katsayısını bulma olasılığımız, .005, binde 5, iki yüzde bir olacaktı. Yani katsayının sıfırdan farklı olma olasılığı gayet yüksektir. İlkesel olarak düşük p değerleri katsayıların sıfırdan farklılığının ve dolayısıyla katsayıların gücünün ispatı olarak yorumlanır. Sosyal bilimler analizlerinde regresyon katsayılarına ait p değerlerinin .05 veya düşük olması genel bir beklentidir.

8.5 Lineer Regresyonun Görselleştirilmesi

Lineer regresyon modelleri saçınım grafiği üzerinde düz bir çizgi ile görselleştirilir. Bu düz çizgi tüm noktalara uzaklığı en aza indirgeyerek saçınım grafiğinde bulunan noktaların arasından geçer.

ggplot2 paketinde bulunan geom_smooth() fonksiyonu saçınım grafikleri üzerine regresyon modelini çizmek için kullanılır. Bu fonksiyon eğer lineer regresyon modelini çizmek için kullanılıyorsa “lm” argümanı le beraber kullanılmalıdır.

Şimdi 2018 seçim verimizi kullanarak İyi Parti oyları ile Meral Akşener oylarını saçınım grafiğine yerleştirelim.

library(ggplot2)
ggplot(data = dat, aes(x = iyi2018, y = ma)) + 
  geom_point()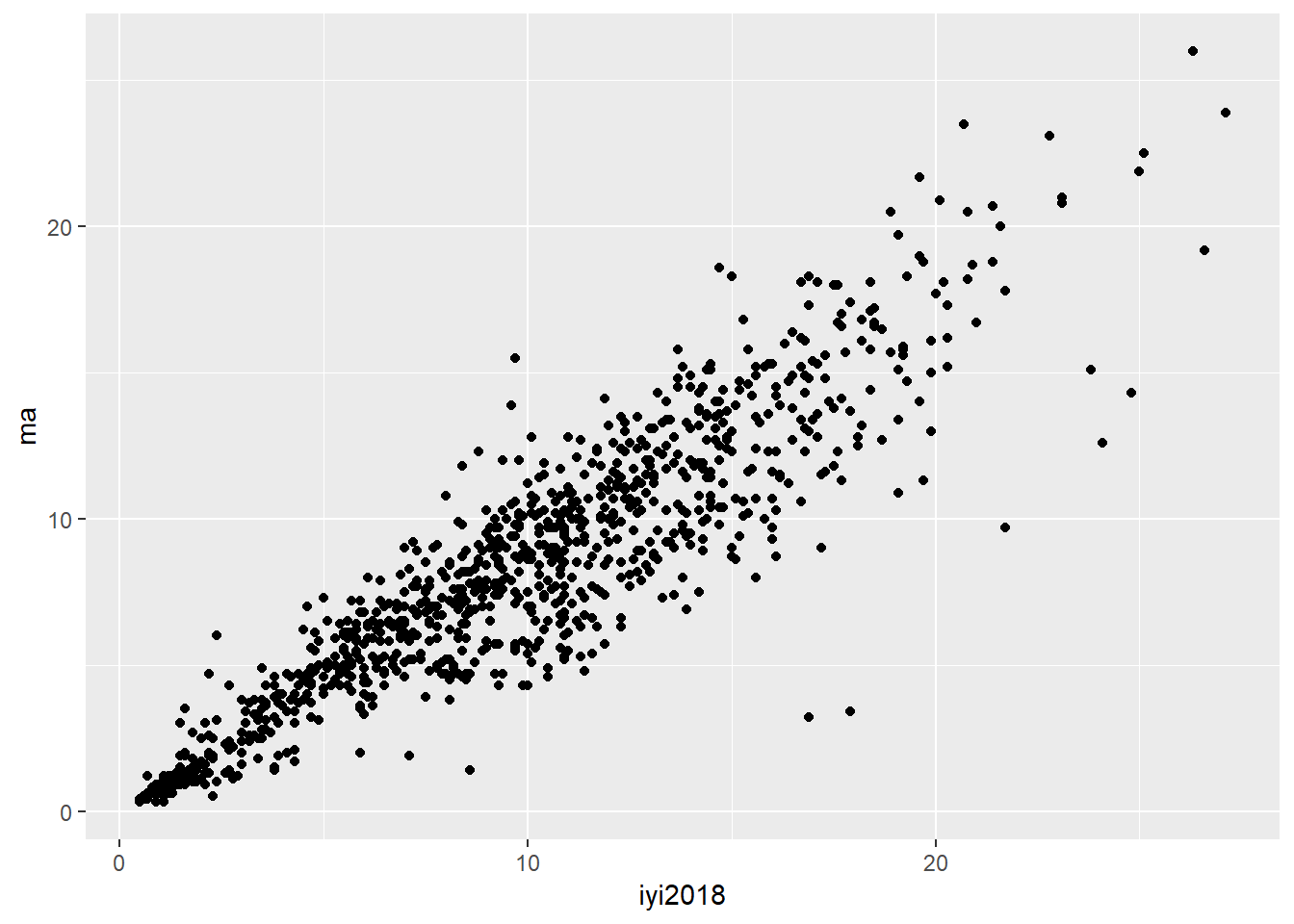

Şimdi aynı grafiğe regresyon modeline ait çizgiyi ekleyelim.

ggplot(data = dat, aes(x = iyi2018, y = ma)) + 
  geom_point() +
  geom_smooth(method = "lm", se = FALSE)

Bu modelin (çizginin) ne anlama geldiğini anlamak regresyon analizi için son derece önemlidir. İstatistiki modeller bağımlı değişkeni bağımsız değişkenin bir fonksiyonu olarak tanımamakla beraber işin içine açıklan(a)mayan ve rastlantısal olduğu varsayılan bir bileşke ekler. Modellerde bu bileşke noise/gürültü olarak adlandırılır ve hem sabit bir standart sapmaya sahip olduğu hem de rastlantısal olarak dağıldığı varsayılır. Anlatılanı notasyona dökersek

Y bağımlı değişken, beta 0 kesen, beta bir eğim/katsayı, epsilon ise gürültüyü temsil etmektedir. Eğer denklemden epsilonu çıkarırsak bu fonksiyon gözlemler üzerinden hesaplanmış değerleri ortaya koyan bir fonksiyon haline gelir. Bu tip fonksiyonlar ise “şapka”lı olarak yazılır:

Y ve şapkalı Y arasındaki fark ise Y’nin gerçekte gözlemlenen değeri, şapkalı Y’nin ise modelin hesapladığı bağımsız değişken değerini ifade etmesinden kaynaklanır. Y ve şapkalı Y arasındaki fark ise residual/artık değer olarak adlandırılır.

Dolayısıyla şapkalı Y’yi elimizdeki bağımsız değişken x’i kullanarak yapabildiğimiz en iyi tahmin olarak düşünebiliriz.

8.6 Regresyon Modellerinin Yorumlanması

Şimdi openintro paketinde bulunan bdims verisi ile bazı modeller oluşturalım. Bu veri tabanında bulunan wgt değişkeni deneklerin kilosunu, hgt değişkeni ise boylarını ifade ediyor.

library(openintro)
data(bdims)
head(bdims)

##   bia.di bii.di bit.di che.de che.di elb.di wri.di kne.di ank.di sho.gi
## 1   42.9   26.0   31.5   17.7   28.0   13.1   10.4   18.8   14.1  106.2
## 2   43.7   28.5   33.5   16.9   30.8   14.0   11.8   20.6   15.1  110.5
## 3   40.1   28.2   33.3   20.9   31.7   13.9   10.9   19.7   14.1  115.1
## 4   44.3   29.9   34.0   18.4   28.2   13.9   11.2   20.9   15.0  104.5
## 5   42.5   29.9   34.0   21.5   29.4   15.2   11.6   20.7   14.9  107.5
## 6   43.3   27.0   31.5   19.6   31.3   14.0   11.5   18.8   13.9  119.8
##   che.gi wai.gi nav.gi hip.gi thi.gi bic.gi for.gi kne.gi cal.gi ank.gi
## 1   89.5   71.5   74.5   93.5   51.5   32.5   26.0   34.5   36.5   23.5
## 2   97.0   79.0   86.5   94.8   51.5   34.4   28.0   36.5   37.5   24.5
## 3   97.5   83.2   82.9   95.0   57.3   33.4   28.8   37.0   37.3   21.9
## 4   97.0   77.8   78.8   94.0   53.0   31.0   26.2   37.0   34.8   23.0
## 5   97.5   80.0   82.5   98.5   55.4   32.0   28.4   37.7   38.6   24.4
## 6   99.9   82.5   80.1   95.3   57.5   33.0   28.0   36.6   36.1   23.5
##   wri.gi age  wgt   hgt sex
## 1   16.5  21 65.6 174.0   1
## 2   17.0  23 71.8 175.3   1
## 3   16.9  28 80.7 193.5   1
## 4   16.6  23 72.6 186.5   1
## 5   18.0  22 78.8 187.2   1
## 6   16.9  21 74.8 181.5   1

Deneklerin kilolarını boylarının bir fonksiyonu olarak tanımlayan model için kod aşağıdaki gibi yazılır

lm(wgt ~ hgt, data = bdims)

## 
## Call:
## lm(formula = wgt ~ hgt, data = bdims)
## 
## Coefficients:
## (Intercept)          hgt  
##    -105.011        1.018

Yukarıdaki hesaplamayı notasyon olarak aşağıdaki gibi yazılır

Bu notasyona göre lineer modelimiz deneklerin boylarında (hgt) gerçekleşen bir birimlik artışın (ki buradaki birim cm olarak kaydedilmiş), deneklerin kilolarında (wgt) 1.018 birimlik (ki burada kilo cinsinden kaydedilmiş) bir artışa denk geldiği tahmin etmektedir. Tahmin etmektedir diyoruz zira wgt şapka altında ifade edilmiş. Daha düz bir Türkçe ile fazladan her bir cm kabaca bir kiloya denk gelmektedir.

Regresyon modellerini R nesnesi olarak sakladığımızda modelin içinde bulunan birçok bilgiye de erişme şansımız olur. Yukarıdaki modeli “mod” adı ile kaydedelim ve model ile ilgili bilgilere summary() fonksiyonu ile erişelim.

mod <- lm(wgt ~ hgt, data = bdims)

summary(mod)

## 
## Call:
## lm(formula = wgt ~ hgt, data = bdims)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -18.743  -6.402  -1.231   5.059  41.103 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -105.01125    7.53941  -13.93   <2e-16 ***
## hgt            1.01762    0.04399   23.14   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 9.308 on 505 degrees of freedom
## Multiple R-squared:  0.5145, Adjusted R-squared:  0.5136 
## F-statistic: 535.2 on 1 and 505 DF,  p-value: < 2.2e-16

Yukarıdan da anlaşılacağı üzere summary() fonksiyonu, her bağımsız değişken için p değerini ve modelin R2 değerini de içeren bir rapor çıktısı hazırladı.

Bir regresyon modeli oluşturduğunuzda modelinizde kullandığınız bağımsız değişkenlere ait, tahmin değerleri (fitted values) artık değerler (residuals), standart sapmalar gibi değişik bilgileri bir veri tabanı olarak görmek için broom paketindeki augment() fonksiyonunu kullanacağız. Aşağıdaki kod bu işlemi gerçekleştiriyor.

library(broom)

#modele ait veri tabanının oluşturulması
mod_veriler <- augment(mod)

#Glimpse the resulting data frame
glimpse(mod_veriler)

## Observations: 507
## Variables: 9
## $ wgt        <dbl> 65.6, 71.8, 80.7, 72.6, 78.8, 74.8, 86.4, 78.4, 62....
## $ hgt        <dbl> 174.0, 175.3, 193.5, 186.5, 187.2, 181.5, 184.0, 18...
## $ .fitted    <dbl> 72.05406, 73.37697, 91.89759, 84.77427, 85.48661, 7...
## $ .se.fit    <dbl> 0.4320546, 0.4520060, 1.0667332, 0.7919264, 0.81834...
## $ .resid     <dbl> -6.4540648, -1.5769666, -11.1975919, -12.1742745, -...
## $ .hat       <dbl> 0.002154570, 0.002358152, 0.013133942, 0.007238576,...
## $ .sigma     <dbl> 9.312824, 9.317005, 9.303732, 9.301360, 9.312471, 9...
## $ .cooksd    <dbl> 5.201807e-04, 3.400330e-05, 9.758463e-03, 6.282074e...
## $ .std.resid <dbl> -0.69413418, -0.16961994, -1.21098084, -1.31269063,...

Regresyon modellerinin en önemli özelliklerinden biri modelde tahmin edilen değerleri (fitted values) modelin kullandığı değerlerden başka değerler üzerinde kullanarak tahmin üretmesidir. Buna “örneklem dışı tahmin/out-of-sample prediction” adı verilir.

Yukarıdaki regresyon işlemi kişilerin kilolarını boylarının bir fonksiyonu olarak modellemişti. Ağırlığı 74.8 kg ve boyu 182.8 olan bir deneğe ait olan tek gözlemli bir veri tabanı yaratalım ve modelimizi bu veri tabanı üzerinde predict() fonksiyonu ve newdata argümanı kullanarak çalıştıralım. Bu işlem için yeni veri tabanının kullandığı bağımlı ve bağımsız değişken isimlerinin aynı olması gerekir.

#yeni veri tabanı
wgt <- 74.8
hgt <- 182.8
yeni_vt <- data.frame(wgt, hgt)

predict(mod, newdata = yeni_vt)

##        1 
## 81.00909

8.7 Kategorik Değişkenler ile Çoklu Regresyon

Yukarıdaki örneklerde kullandığımız lm() fonksiyonu hep tek bağımsız değişken üzerinden modelleri oluşturdu. Sosyal bilimlerde çoğu zaman açıklamak istediğimiz bağımlı değişkeni birden fazla bağımsız değişken kullanarak modelleriz.

Aşağıdaki örneklerde openintro paketinde bulunan ‘MarioKart’ isimli bir veritabanı kullanacağız. Bu veritabanında MarioKart oyunlarının ebay üzerinden satışı sırasında kaydedilmiş, oyunun kullanılmış olup olmadığı, oyun paketinde paketle beraber kaç tane direksiyon verildiği, oyunun fiyatı, oyuna ait resim bulunup bulunmadığı gibi veriler kaydedilmiş.

library(openintro)
data(marioKart)
glimpse(marioKart)

## Observations: 143
## Variables: 12
## $ ID         <dbl> 150377422259, 260483376854, 320432342985, 280405224...
## $ duration   <int> 3, 7, 3, 3, 1, 3, 1, 1, 3, 7, 1, 1, 1, 1, 7, 7, 3, ...
## $ nBids      <int> 20, 13, 16, 18, 20, 19, 13, 15, 29, 8, 15, 15, 13, ...
## $ cond       <fct> new, used, new, new, new, new, used, new, used, use...
## $ startPr    <dbl> 0.99, 0.99, 0.99, 0.99, 0.01, 0.99, 0.01, 1.00, 0.9...
## $ shipPr     <dbl> 4.00, 3.99, 3.50, 0.00, 0.00, 4.00, 0.00, 2.99, 4.0...
## $ totalPr    <dbl> 51.55, 37.04, 45.50, 44.00, 71.00, 45.00, 37.02, 53...
## $ shipSp     <fct> standard, firstClass, firstClass, standard, media, ...
## $ sellerRate <int> 1580, 365, 998, 7, 820, 270144, 7284, 4858, 27, 201...
## $ stockPhoto <fct> yes, yes, no, yes, yes, yes, yes, yes, yes, no, yes...
## $ wheels     <int> 1, 1, 1, 1, 2, 0, 0, 2, 1, 1, 2, 2, 2, 2, 1, 0, 1, ...
## $ title      <fct> ~~ Wii MARIO KART &amp; WHEEL ~ NINTENDO Wii ~ BRAN...

Buradaki modelde amacımız tek bir değişken ile değil, birden fazla değişken kullanarak oyunun fiyatını(totalPr) modellemek olacak. Bunun için oyunun kullanılmış veya sıfır olduğunu içeren cond değişkenini, oyun paketi ile beraber verilen direksiyon adedini gösteren wheels değişkeni ile beraber kullanacağız. Bu tipteki yani bir nümerik (direksiyon sayısı) bir de kategorik değişken (kullanılmış/used veya sıfır durumda/new) içeren modellere “paralel eğimler modeli/parallel slopes model” adı verilir. Aşağıdaki kod bu işlemi gerçekleştiriyor.

mario_model <- lm(totalPr ~ wheels + cond, data = marioKart)
summary(mario_model)

## 
## Call:
## lm(formula = totalPr ~ wheels + cond, data = marioKart)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -11.0078  -3.0754  -0.8254   2.9822  14.1646 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  42.3698     1.0651  39.780  < 2e-16 ***
## wheels        7.2328     0.5419  13.347  < 2e-16 ***
## condused     -5.5848     0.9245  -6.041 1.35e-08 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 4.887 on 138 degrees of freedom
## Multiple R-squared:  0.7165, Adjusted R-squared:  0.7124 
## F-statistic: 174.4 on 2 and 138 DF,  p-value: < 2.2e-16

Yukarıdaki formül basit lineer regresyondan farklı olarak lm() fonksiyonuna ikinci değişkeni de katarak modeli oluşturdu. Bu modellere paralel eğimler modeli denmesinin sebebi, modelleri görselleştirdiğimizde bir değil iki adet birbirine paralel çizgi oluşturmasıdır. Bunun görselleştirme için önce kategorileri ayrı renkler halinde gösteren bir saçınım grafiği ve her bir kategori için bir çizgi çizeceğiz. Bu iş için gene broom paketini ve augment() fonksiyonunu kullanacağız.

#Model özelliklerini içeren veri tabanını oluşturalım
mario_model_veriler<- augment(mario_model)
glimpse(mario_model_veriler)

## Observations: 141
## Variables: 10
## $ totalPr    <dbl> 51.55, 37.04, 45.50, 44.00, 71.00, 45.00, 37.02, 53...
## $ wheels     <int> 1, 1, 1, 1, 2, 0, 0, 2, 1, 1, 2, 2, 2, 2, 1, 0, 1, ...
## $ cond       <fct> new, used, new, new, new, new, used, new, used, use...
## $ .fitted    <dbl> 49.60260, 44.01777, 49.60260, 49.60260, 56.83544, 4...
## $ .se.fit    <dbl> 0.7087865, 0.5465195, 0.7087865, 0.7087865, 0.67645...
## $ .resid     <dbl> 1.9473995, -6.9777674, -4.1026005, -5.6026005, 14.1...
## $ .hat       <dbl> 0.02103158, 0.01250410, 0.02103158, 0.02103158, 0.0...
## $ .sigma     <dbl> 4.902339, 4.868399, 4.892414, 4.881308, 4.750591, 4...
## $ .cooksd    <dbl> 1.161354e-03, 8.712334e-03, 5.154337e-03, 9.612441e...
## $ .std.resid <dbl> 0.40270893, -1.43671086, -0.84838977, -1.15857953, ...

#Grupları (kullanılmış veya sıfır durumda) renk ile ayrıştıran saçınım grafiği
mario_grafik <- ggplot(mario_model_veriler, aes(x = wheels, y = totalPr, color = cond)) + 
  geom_point()
  
#geom_line() ile çizgilerin eklenmesi
mario_grafik + 
  geom_line(aes(y = .fitted))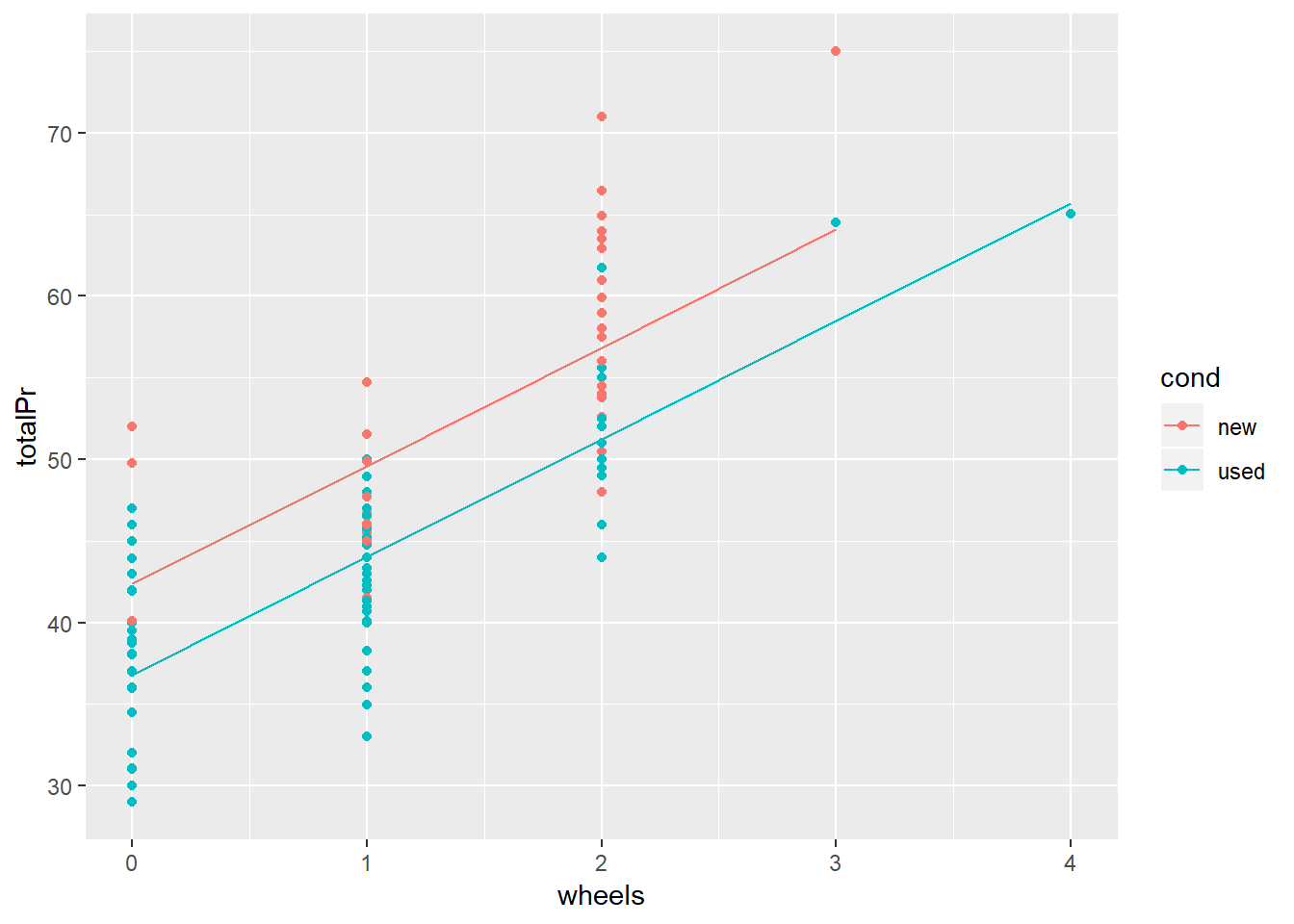

Şimdi modelimiz ile ilgili bilgileri içeren çıktıya geri dönelim ve değişkenlere ait katsayıları yorumlayalım. Direksiyon sayısını içeren “wheels” değişkeninin katsayısı 7.233, ürünün kullanılmış veya sıfır olduğunu gösteren “cond” değişkeninin ise -5.585 olarak raporlanmış. Çoklu regresyon modellerinde değişkenlerin katsayıları yorumlanırken, yorumun dışında bırakılan değişken “kontrol edildiğinde” ifadesi kullanılır. Yani modelimizdeki direksiyon sayısı değişkeninin fiyat üzerindeki etkisini yorumlamak istediğimizde:

“Ürünün kullanılmış veya sıfır olma durumu kontrol edildiğinde, oyunla beraber gelen her bir direksiyon, ürünün fiyatını 7 dolar 233 sent arttırmaktadır.”

şeklinde ifade ederiz.

Ürünün durumu (kullanılmış veya sıfır) gibi kategorik değişkenleri yorumlamak istediğimizde ise raporda kullanılmış referans kategorisini dikkate alarak yorumlamamız gerekir. Burada R ‘used’ yani kullanılmış kategorisini referans kategorisi olarak almış. Bu durumda bu değişken yorumlanmak istendiğinde:

“Ürünle beraber gelen direksiyon sayısı kontrol edildiğinde, ürününün kullanılmış olması sıfır olmasına göre fiyatını 5 dolar 585 sent azaltmaktadır”

şeklinde ifade edilir. Her ne kadar resmi olarak bu şekilde (ve garip bir dil ile) ifade edilse de, düz bir Türkçe ile söylersek oyunun kullanılmış olması ürünün fiyatını düşürürken, oyunla beraber gelen direksiyon sayısının artması ürün fiyatını yükseltiyor diyebiliriz.

8.8 Model Değerlendirmeleri

Bir sosyal olgunun açıklanması için şüphesiz ki birden fazla model oluşturulabilir. Bu bölümde farklı modellerin değişik kriterlere göre değerlendirilmesini yapıp hangi modelin daha kuvvetli olduğuna karar vereceğiz.

Bir regresyon modelinin kuvveti genellikle R2 ve uyarlanmış R2 değerlerinin kontrolü ile saptanır. Aşağıdaki kod elimizdeki mario_kart oyun konsolu verisini kullanarak modele noise(gürültü) adı ile üçüncü bir uydurulmuş bir değişkeni ekliyor ve mario_model2 adı ile saklıyor

#İlk modelimizin R2 ve uyarlanmış R2 değerlerini hatırlayalım
summary(mario_model)

## 
## Call:
## lm(formula = totalPr ~ wheels + cond, data = marioKart)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -11.0078  -3.0754  -0.8254   2.9822  14.1646 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  42.3698     1.0651  39.780  < 2e-16 ***
## wheels        7.2328     0.5419  13.347  < 2e-16 ***
## condused     -5.5848     0.9245  -6.041 1.35e-08 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 4.887 on 138 degrees of freedom
## Multiple R-squared:  0.7165, Adjusted R-squared:  0.7124 
## F-statistic: 174.4 on 2 and 138 DF,  p-value: < 2.2e-16

#gürültü değişkeni ekliyeceğimiz yeni bir tabanı oluşturalım
mario_kart_noisy <- marioKart %>%
  mutate(noise = rnorm(nrow(marioKart)))
  
#yeni model oluşturalım
mario_model2 <- lm(totalPr ~ wheels + cond + noise, data = mario_kart_noisy)

#yeni R^2 veadjusted R^2
summary(mario_model2)

## 
## Call:
## lm(formula = totalPr ~ wheels + cond + noise, data = mario_kart_noisy)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -10.8140  -3.1279  -0.7929   2.9218  14.3822 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  42.3154     1.0831  39.067  < 2e-16 ***
## wheels        7.2499     0.5465  13.266  < 2e-16 ***
## condused     -5.5450     0.9366  -5.920 2.45e-08 ***
## noise         0.1177     0.3830   0.307    0.759    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 4.904 on 137 degrees of freedom
## Multiple R-squared:  0.7167, Adjusted R-squared:  0.7105 
## F-statistic: 115.5 on 3 and 137 DF,  p-value: < 2.2e-16

Çıktılardaki uyarlanmış R2 değerlerinden de anlaşılacağı üzere eklediğimiz yeni noise değişkeni modelin gücüne herhangi bir katkı sağlamadı.

Bir modeli oluşturduğumuzda modelin bağımsız değişkenler için saptadığı katsayıları, aynı özelliklerde olan başka veriler için de kullanarak kestirimler(tahmin/prediction) yapabiliriz. Bu iş için broom paketindeki augment() fonksiyonunu kullanacağız. Bu fonksiyon sayesinde regresyon modelimizin özellikleri (katsayılar, standard sapmalar, artık değerler vb.) bir veri tabanı olarak karşımıza çıkacak. Aşağıdaki kod ilk modelimize augment() fonksiyonunu uyguluyor

augment(mario_model)

## # A tibble: 141 x 10
##    totalPr wheels cond  .fitted .se.fit  .resid   .hat .sigma .cooksd
##  *   <dbl>  <int> <fct>   <dbl>   <dbl>   <dbl>  <dbl>  <dbl>   <dbl>
##  1    51.6      1 new      49.6   0.709   1.95  0.0210   4.90 1.16e-3
##  2    37.0      1 used     44.0   0.547  -6.98  0.0125   4.87 8.71e-3
##  3    45.5      1 new      49.6   0.709  -4.10  0.0210   4.89 5.15e-3
##  4    44        1 new      49.6   0.709  -5.60  0.0210   4.88 9.61e-3
##  5    71        2 new      56.8   0.676  14.2   0.0192   4.75 5.57e-2
##  6    45        0 new      42.4   1.07    2.63  0.0475   4.90 5.05e-3
##  7    37.0      0 used     36.8   0.707   0.235 0.0209   4.91 1.68e-5
##  8    54.0      2 new      56.8   0.676  -2.85  0.0192   4.90 2.25e-3
##  9    47        1 used     44.0   0.547   2.98  0.0125   4.90 1.59e-3
## 10    50        1 used     44.0   0.547   5.98  0.0125   4.88 6.40e-3
## # ... with 131 more rows, and 1 more variable: .std.resid <dbl>

8.9 Etkileşim terimleri

Regresyon modellerinde kullandığımız bağımsız değişkenler bağımlı değişkenler üzerinde kimi zaman beraberce etki üretebilirler. Oyun konsolu örneğini düşünelim: bir oyun konsolunun fiyatını ebay’de açık arttırmada durduğu süre ve kullanılmış olup olmadığına göre modelleyebiliriz, zira bu her iki özellik de bağımsız olarak oyun konsolunun fiyatını belirler. Ancak eğer bir konsol hem kullanılmış hem de uzun süre açık arttırmada duruyorsa, yani uzun süredir satılmadıysa, fiyatının daha düşük olması gerektiğini de düşünebiliriz. Bu gibi durumlarda düşündüğümüz değişkenleri modelimize etkileşim değişkeni (interaction term) olarak ekleyebiliriz. Bu iş için aşağıdaki kod şablonu kullanılır.

lm(y ~ x + z + x:z, data = veritabanı)

Yukarıdaki örnekte x ve z değişkenlerinin etkileşimi modele “:” işareti kullanılarak üçüncü bir değişken olarak eklenmiş. Şimdi oyun konsolu ile ilgili yukarıdaki örneği modelleyelim. Modelde kullanılan “totalPr” konsolun fiyatını, “duration” konsolun açık arttırmada kaldığı süreyi ve “cond” ise konsolun kullanılmış olup olmadığını ifade eden değişkenlerdir.

lm(totalPr ~ duration + cond + cond:duration, data = marioKart)

## 
## Call:
## lm(formula = totalPr ~ duration + cond + cond:duration, data = marioKart)
## 
## Coefficients:
##       (Intercept)           duration           condused  
##            58.268             -1.966            -17.122  
## duration:condused  
##             2.325

Etkileşim modellerdeki eğimlerin birbirine paralel olmaktan çıkartır. Yukarıdaki model için bu cümleyi uygularsak; konsolun fiyatı ile açık arttırmada durduğu süre arasındaki ilişki, konsolun kullanılmış olup olmadığı tarafından şekillendirilmektedir (moderated).

Yukarıdaki modeli ggplot ile grafiklediğimizde, “cond” değişkeni için birbirine paralel olmayan iki ayrı regresyon çizgisi oluştuğunu görürüz.

#etkileşim grafiği
ggplot(marioKart, aes(y = totalPr, x = duration, color = cond)) + 
  geom_point() + 
  geom_smooth(method = "lm", se = FALSE)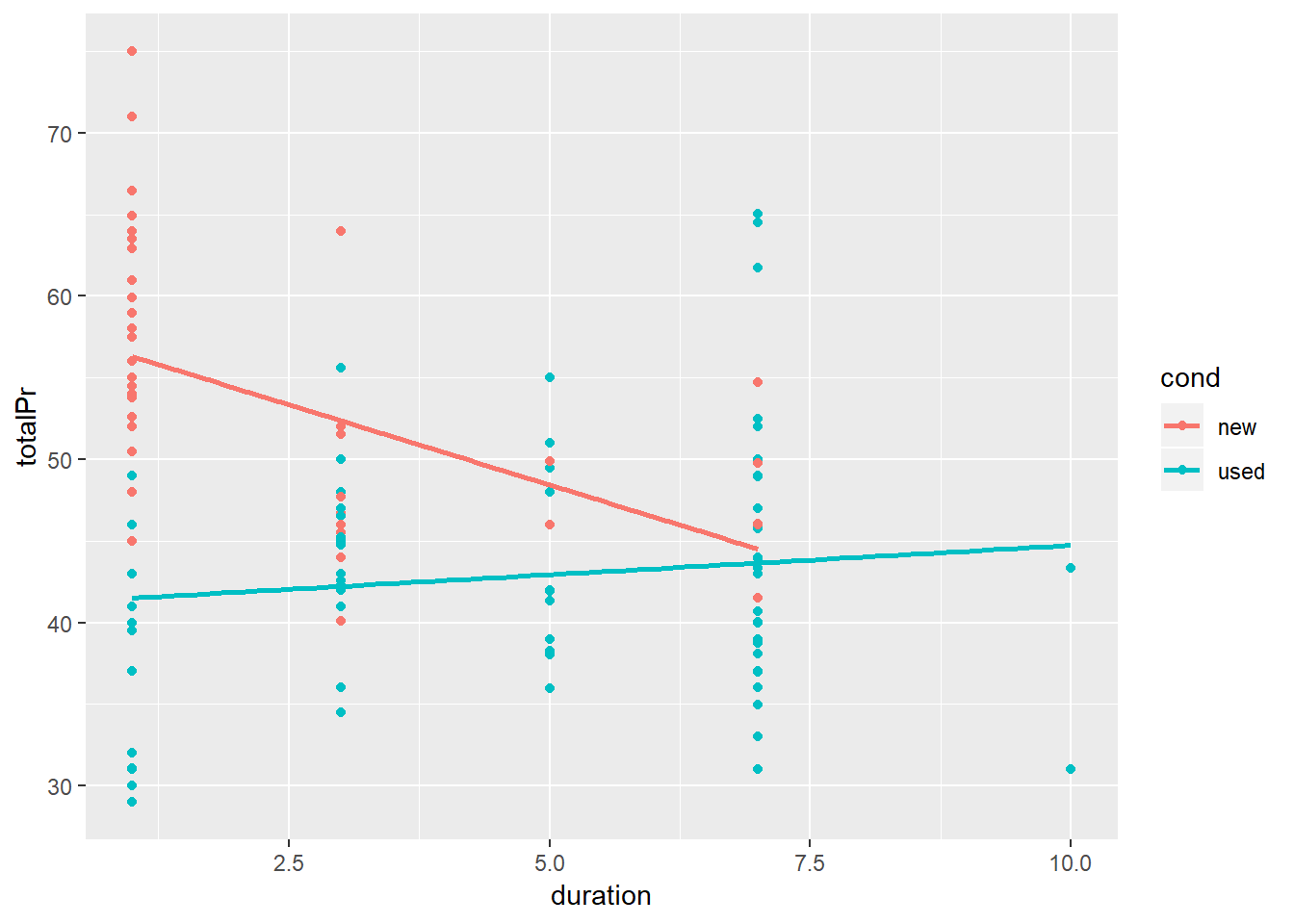

Yukarıdaki grafikten de anlaşılacağı üzere bir konsolun fiyatı açık arttırmada geçirdiği süre dikkate alınarak değerlendirildiğinde o konsolun kullanılmış olup olmaması fiyat üzerinde farklı bir etki yaratmaktadır. Bu duruma yani iki değişken arasındaki ilişkinin, bağımsız değişkenin alt gruplara/kategorilere bölündüğünde yön değiştirmesine Simpson Tezatı adı verilir.

Bir oyun konsolunun açık arttırmada geçirdiği süre arttıkça fiyatının düşmesini bekleyebiliriz. Satıcıların ürünleri satılmadıkça fiyatları düşürme eğilimine girmesi gayet doğaldır. Aşağıdaki grafik bu ilişkiyi regresyon modeli ile anlatmaktadır.

slr <- ggplot(marioKart, aes(y = totalPr, x = duration)) + 
  geom_point() + 
  geom_smooth(method = "lm", se = 0)

slr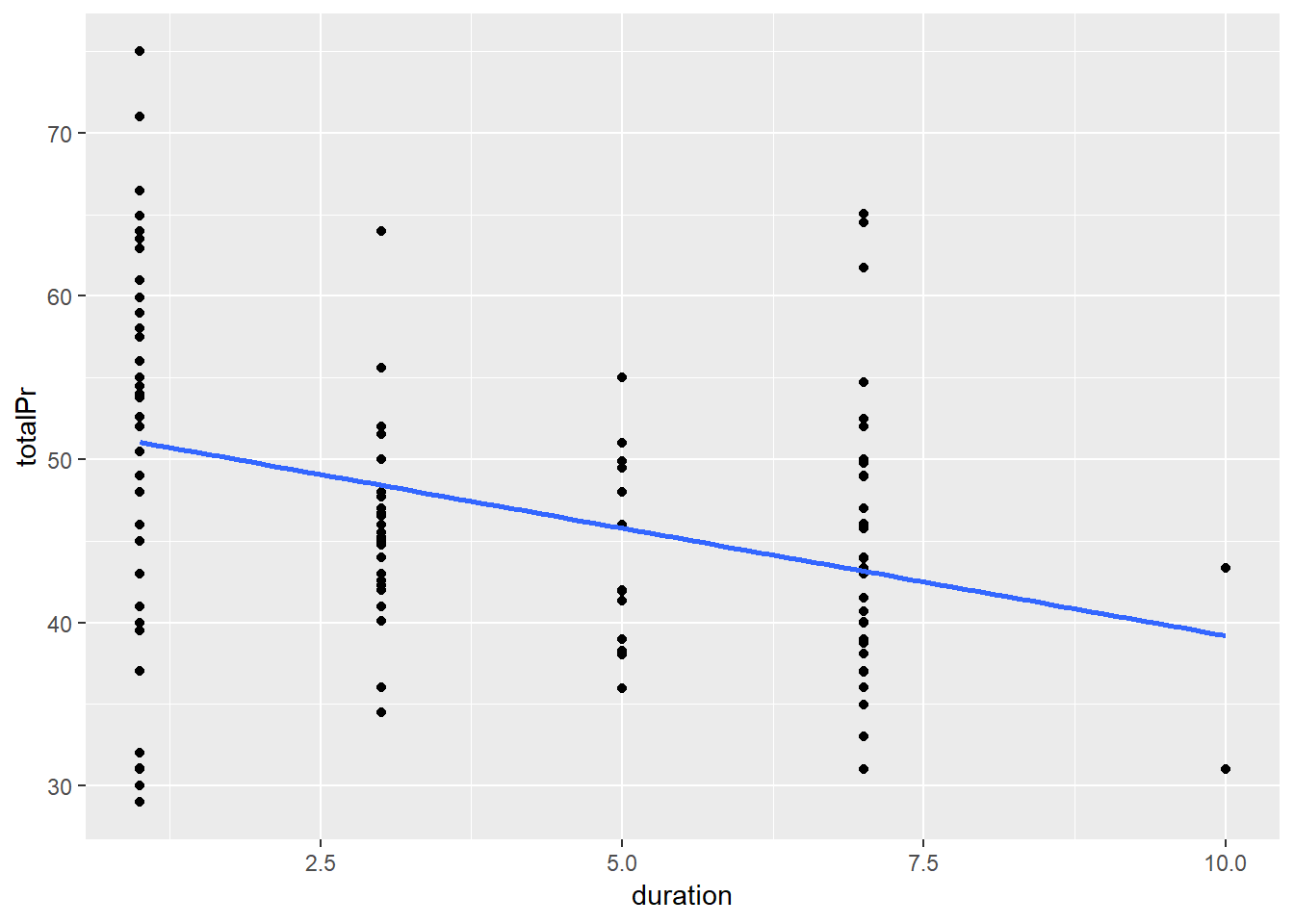

Halbuki süreyi (duration) alt gruplara böldüğümüzde (kullanılmış ve kullanılmamış) ilk grafiği görürürüz.

8.10 Nümerik Değişkenler ile Çoklu Regresyon

Nümerik değişkenler içeren bir regresyon modeli için lm() fonksiyonun içinde bağımsız değişkenleri yerleştirmemiz gerekir. Aşağıdaki kod oyun konsolunun fiyatını konsolun başlangıç fiyatı ve açık arttırmada kalma süresinin bir fonksiyonu olarak tanımlamaktadır.

lm(totalPr ~ duration + startPr, data = marioKart)

## 
## Call:
## lm(formula = totalPr ~ duration + startPr, data = marioKart)
## 
## Coefficients:
## (Intercept)     duration      startPr  
##      51.030       -1.508        0.233

Bu tip modellerde oluşan katsayılar, modelde bulunan diğer katsayılar sabit tutarak yorumlanır. Örneğin yukarıdaki modelde bulunan açık attırmada bulunma süresi değişkenini (duration) yorumlarken: “Başlangıç fiyatı (startPr) sabit tutulduğunda, açık arttırmada geçirilen her bir fazladan gün, oyun konsolunun fiyatını ortalama olarak 1.5$ düşürmektedir” denir.

8.11 Lojistik Regresyon

Regresyon modellerinde eğer bağımlı değişken sadece iki değer alabilen bir değişken ise, örneğin son seçimde oy kullandı (1) kullanmadı (0) şu ana kadar lineer modellerin hesaplanması için kullandığımız lm() fonksiyonunu kullanmak bazı hatalı sonuçlar üretecektir. Bu hataların en temeli oluşan katsayıların bağımlı değişkenin sınır değerleri olan 0 ve 1 limitlerinin altında veya üstünde oluşabilmesidir. Aşağıdaki örnekte üniversiteye kabul edilme ile (Acceptance değişkeni kabul 1, red 0) lise başarı ortalaması (GPA) arasındaki ilişki incelenmektedir

library(ggplot2)
library(Stat2Data)
data(MedGPA)
ac_model1 <- ggplot(data = MedGPA, aes(y = Acceptance, x = GPA)) + 
  geom_jitter(width = 0, height = 0.05, alpha = 0.5)

#linear regression line
ac_model1 + 
  geom_smooth(method = "lm", se = FALSE)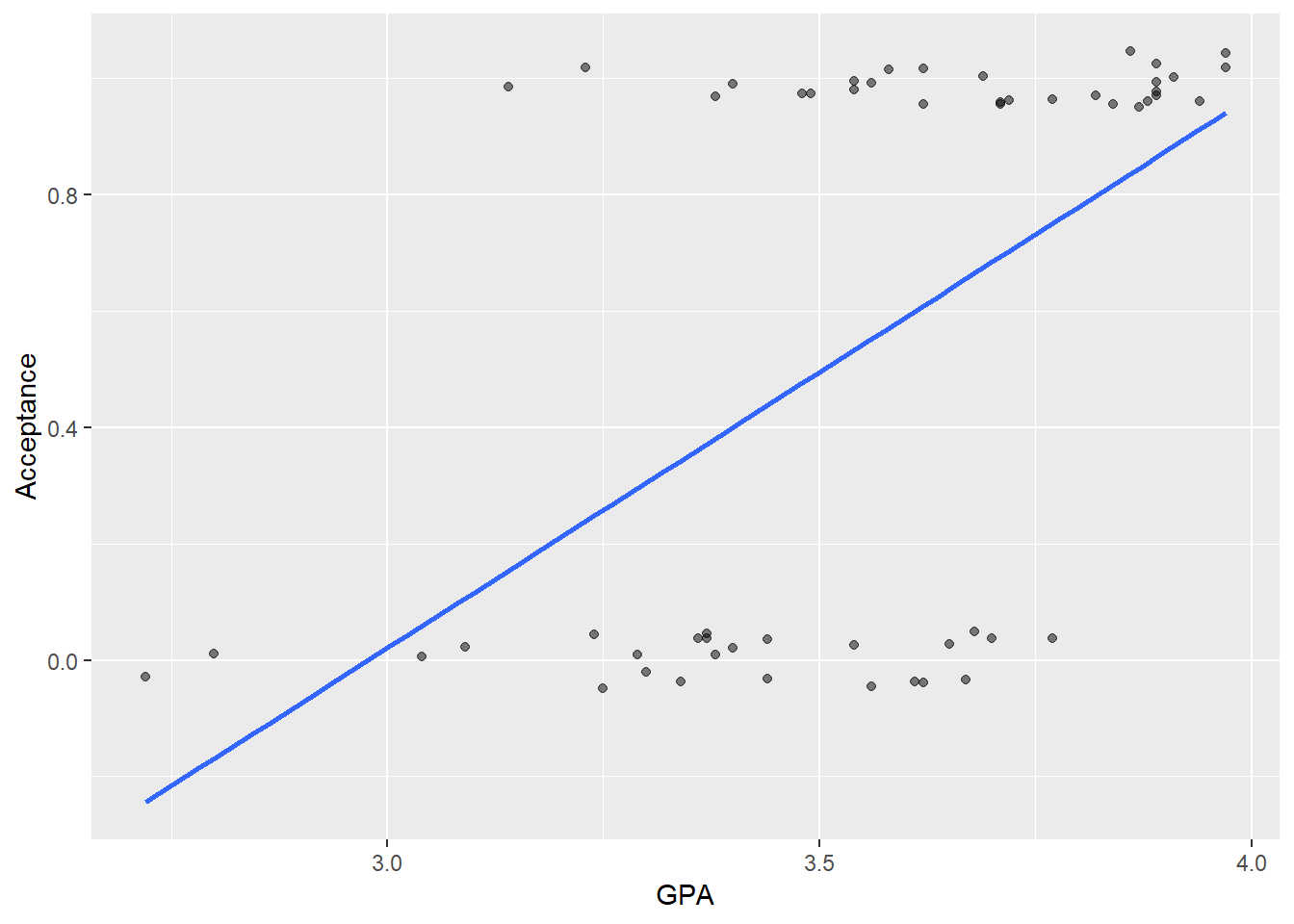

Görüldüğü üzere regresyon lm() fonksiyonu ile çizilen regresyon çizgisi 0 değerinin altına doğru inmektedir ki bu pratik olarak hiç bir anlam ifade etmez.

Bağımlı değişkenin sadece iki değer alabildiği bu gibi durumlarda Generalized Linear Models adı verilen alternatif bir model ailesi kullanılır. R içerisinde bu tip modeller için lm() yerine glm() fonksiyonu kullanılır. GLM kendi içerisinde birden fazla tip barındırdığından ayrıca fonksiyona kullanılmak istenen tip de eklenir ve lojistik regresyon için GLM ailesinde binominal tipi kullanılır. Yukarıdaki örneği glm() fonksiyonu ile tekrarlayalım.

#fit model
ac_model3 <- glm(Acceptance ~ GPA, data = MedGPA, family = binomial)

summary(ac_model3)

## 
## Call:
## glm(formula = Acceptance ~ GPA, family = binomial, data = MedGPA)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -1.7805  -0.8522   0.4407   0.7819   2.0967  
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  -19.207      5.629  -3.412 0.000644 ***
## GPA            5.454      1.579   3.454 0.000553 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 75.791  on 54  degrees of freedom
## Residual deviance: 56.839  on 53  degrees of freedom
## AIC: 60.839
## 
## Number of Fisher Scoring iterations: 4

Oluşan modeli grafikleyelim

ac_model2 <- ggplot(data = MedGPA, aes(y = Acceptance, x = GPA)) + 
  geom_jitter(width = 0, height = 0.05, alpha = 0.5)

ac_model2+
  geom_smooth(method = "glm", se = FALSE, method.args = list(family = "binomial"))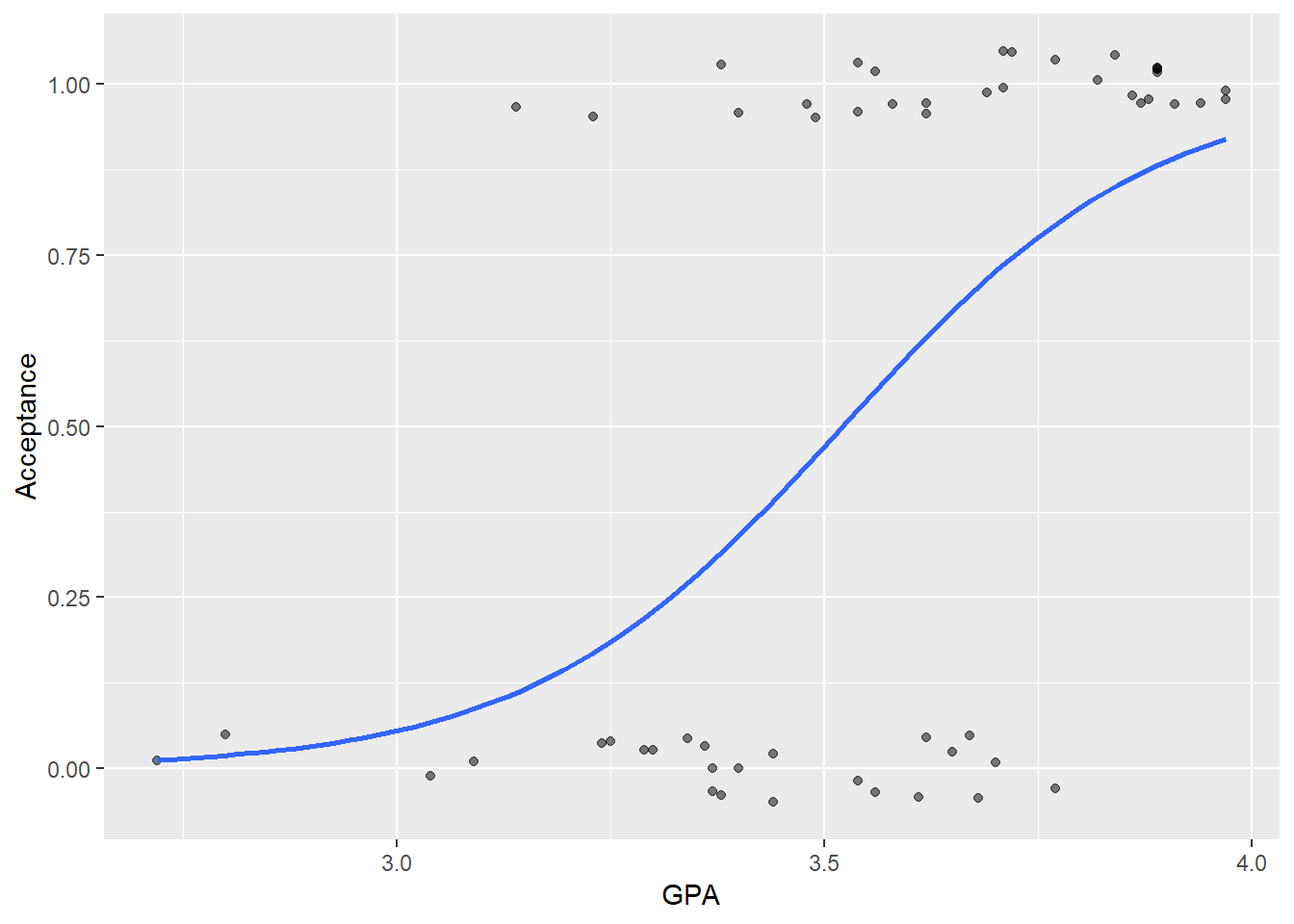

Grafikten de görüldüğü gibi model sonunda oluşan regresyon çizgisi 0 ve 1 değerlerinin içerisinde kaldı.

Aslında yukarıdaki regresyon hesabı temelde bir adayın üniversiteye kabul edilme ihtimalini adayın lise başarısının bir fonksiyonu olarak tanımlar. Daha da basit söylemek gerekirse yukarıdaki hesaplama adayın lise başarı ortalamasındaki değişikliğin programa kabul edilme ihtimali üzerindeki etkisini ortaya koymaya çalışır ve bu hesabı burada tüm detayları ile kapsama ihtimalimiz olmayan matematiksel bir işlem sonucunda yapar. Bu matematiksel işlem sonunda oluşan ve lojistik regresyon katsayıları olarak ifade edilen katsayılar bağımsız değişkende gerçekleşen bir birimlik değişimin bağımlı değişkenin 0 veya 1 değeri alma ihtimalini ifade eder. Ancak bu katsayılar “odds” adı verilen ve bildiğimiz ve sıkça kullanılan olasılık ifadesinden farklı bir şekilde hesaplanır. Odds aslında bir ihtimal belirtme yöntemidir. Bir zar atıldığında herhangi bir sayının gelme olasılığı 1/6 iken odds hesabında olayın gerçekleşme olasılığı gerçekleşmeme olasılığı ile oranlanır. Yani zar atıldığında bir sayının gelme ihtimali odds cinsinden 1/5 olarak ifade edilir. Bu iki ihtimal hesaplama aracının birbiri cinsinde ifadesi de mümkündür: Eğer bir olayın gerçekleşme ihtimali olasılık cinsinden y ise odds cinsinden y/(1-y) olarak hesaplanır. Ancak odds şeklinde ifade edilen katsayıların yorumlanması çok zor olduğundan bu katsayıların logaritması alınarak “odds ratio” cinsinden yorumlanır.

Yukarıdaki modelimizde lise başarı ortalamasının katsayısı olan 5.454 sayısının yorumlanması için öncelikle logaritması alınması gerekir. Aşağıdaki kod, coef() fonksiyonu ile modelin katsayılarını çeker ve exp() fonksiyonu ile katsayının logaritmasını alarak bu işlemi gerçekleştirmektedir.

exp(coef(ac_model3))

##  (Intercept)          GPA 
## 4.557449e-09 2.337298e+02

Bu işlem sonunda oluşan 233 sayısı (2.337298e+02 sayısının düz hali) bir birimlik GPA değişkeni için bağımlı değişkende gerçekleşen değişimi odds cinsinden hesaplanmış ihtimalin logaritması olarak ifade eder. Ancak bu ifade sizin de tahmin edebileceğiniz gibi günlük dilde anlaşılır olmaktan çok uzaktır.

Bu yüzden lojistik regresyon modelleri farklı bir grup işlemden geçirilir ve gözlemler hakkında daha net yorumlar elde edilir. Bu işlem için broom paketindeki augment() fonksiyonunu kullanacağız. Aşağıdaki kod veri tabanımızda bulunan her bir gözlem için üniversiteye kabul edilme ihtimalini bilindik olasılık hesabı üzerinden gerçekleştirmektedir.

library(broom)
augment(ac_model3, type.predict = "response")

## # A tibble: 55 x 9
##    Acceptance   GPA .fitted .se.fit .resid   .hat .sigma .cooksd .std.resid
##  *      <int> <dbl>   <dbl>   <dbl>  <dbl>  <dbl>  <dbl>   <dbl>      <dbl>
##  1          0  3.62   0.631  0.0790 -1.41  0.0268   1.03 0.0242      -1.43 
##  2          1  3.84   0.850  0.0701  0.569 0.0386   1.04 0.00368      0.581
##  3          1  3.23   0.169  0.0861  1.88  0.0527   1.01 0.144        1.94 
##  4          1  3.69   0.715  0.0787  0.819 0.0304   1.04 0.00644      0.832
##  5          1  3.38   0.316  0.0930  1.52  0.0400   1.02 0.0470       1.55 
##  6          1  3.72   0.747  0.0781  0.764 0.0323   1.04 0.00584      0.776
##  7          1  3.89   0.882  0.0642  0.501 0.0396   1.04 0.00287      0.512
##  8          0  3.34   0.271  0.0936 -0.795 0.0444   1.04 0.00904     -0.813
##  9          1  3.71   0.737  0.0783  0.782 0.0316   1.04 0.00603      0.795
## 10          1  3.89   0.882  0.0642  0.501 0.0396   1.04 0.00287      0.512
## # ... with 45 more rows

Ouluşan tablodaki “.fitted” sütunu modele göre her bir öğrencinin üniversiteye kabul edilme ihtimalini olasılık olarak ifade ediyor. Örneğin modelimiz 7. satırda bulunan ve 3.89 ortalamaya sahip öğrencinin üniversiteye kabul edilme olasılığını yüzde 88 olarak hesaplıyor.

Yukarıdaki tabloda aslında bu öğrencinin gerçekten üniversiteye kabul edilip edilmediğini de “Acceptance” sütunundan görebiliyoruz. Bu açıdan bakıldığında olasılık cinsinden tahmin yerine ikili tahmin, kabul veya red, yapma şansımız ortaya çıkar. Böylece modelimizin ne kadar başarılı olduğunu anlayabiliriz. Aşağıdaki kod bu işlemi gerçekleştiriyor.

#Modelimizin olasılık tahminini içeren sütuna "model.tahmin" ve gerçekten kabul edilme durumunu belirtilen sütununa "gerçek durum "adını verelim ve veri tabanını yaratalım

ac_model3_t <- augment(ac_model3, type.predict = "response")
ac_model3_t <- ac_model3_t %>% 
  mutate(model.tahmin = round(.fitted)) %>% 
  mutate(gercek.durum = Acceptance)

  
#confusion matrix
ac_model3_t%>% 
  select(gercek.durum, model.tahmin) %>%
  table()

##             model.tahmin
## gercek.durum  0  1
##            0 16  9
##            1  6 24

“Confusion matrix” adı verilen bu tablodan şunu anlıyoruz: modelimiz 22 öğrencinin red, 33 öğrencinin kabul alacağını tahmin ederken (yukarıdan aşağıya okuma), gerçekte 25 öğrenci red 30 öğrenci kabul almış (sağdan sola okuma). Hem modelin hem de gerçek durumun kesiştiği diyagonaldeki 16 ve 24 sayılarını toplayıp toplam gözleme böldüğümüzde modelin başarısını hesaplamış oluruz: 40/55 = 0.72