Bölüm10 Keşifsel Veri Analizi
10.1 Giriş
Bu bölümde ilk olarak bir veritabanını R içerisine aktarılması ve veritabanının incelenmesi konularını işleyeceğiz. Bölüm boyunca kullanacağımız veritabanları openintro paketinde bulunduğundan öncelikle bu paketin bilgisayarınızda bulunduğundan ve R oturumuna eklendiğinden emin olunuz. İhtiyacımız olan diğer paket ise dplyr paketi olacak. Her iki paketi de öncelikle yükleyerek işe başlayalım
library(openintro)
library(dplyr)Şimdi openintro paketinde bulunan email50 isimli veritabanını çalışma ortamımıza getirelim ve yapısına glimpse() fonksiyonu ile bakalım
data(email50)
glimpse(email50)## Observations: 50
## Variables: 21
## $ spam <dbl> 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0...
## $ to_multiple <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0...
## $ from <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1...
## $ cc <int> 0, 0, 4, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0...
## $ sent_email <dbl> 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1...
## $ time <dttm> 2012-01-04 15:19:16, 2012-02-16 22:10:06, 2012-0...
## $ image <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0...
## $ attach <dbl> 0, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 0, 0, 0...
## $ dollar <dbl> 0, 0, 0, 0, 9, 0, 0, 0, 0, 23, 4, 0, 3, 2, 0, 0, ...
## $ winner <fct> no, no, no, no, no, no, no, no, no, no, no, no, y...
## $ inherit <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0...
## $ viagra <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0...
## $ password <dbl> 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 2, 0, 0, 0, 0, 0...
## $ num_char <dbl> 21.705, 7.011, 0.631, 2.454, 41.623, 0.057, 0.809...
## $ line_breaks <int> 551, 183, 28, 61, 1088, 5, 17, 88, 242, 578, 1167...
## $ format <dbl> 1, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1...
## $ re_subj <dbl> 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1...
## $ exclaim_subj <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0...
## $ urgent_subj <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0...
## $ exclaim_mess <dbl> 8, 1, 2, 1, 43, 0, 0, 2, 22, 3, 13, 1, 2, 2, 21, ...
## $ number <fct> small, big, none, small, small, small, small, sma...10.2 Değişken Tipleri
İkinci aşamada veritabanındaki değişkenlerin tiplerini, ölçüm seviyelerini dikkate alarak saptamamız gerekir. Veri kullanarak yapılan tüm niceliksel sosyal bilimler analizlerinde ilk yapılması gereken işlemlerden biri olan bu saptama, ölçümler için daha sonra kullanacağımız istatistiki araçların belirlenmesi için hayati önem taşır. Temel olarak iki ölçüm seviyesi bulunur: Nümerik/niceliksel ve Kategorik/Niteliksel. Nümerik/Niceliksel ölçüm seviyesi iki alt tipe ayrılır: Sürekli değişkenler ve kesikli değişkenler. Sürekli değişkenler bir aralık içinde sınırsız değer alabilirken, kesikli değişkenler ise ancak sayılabilir durumda olan belli değerler alabilirler. Sürekli değişkenlere uzunluk, kilo gibi ölçümler örnek verilebilir. Kesikli değişkenlere ise bir evdeki televizyon sayısı, geçtiğimiz hafta tüketilen ekmek sayısı gibi örnekler verilebilir. Kategorik/Niteliksel değişkenler de ikiye ayrılır: Bir aralıkta tanımlanmış belli değer alabilen ve sıralanabilen değişkenler ve sıralanamayan belli bir aralıkta değer alabilen değişkenler. Birinci tipe örnek olarak anket tipi soru kağıtlarında sıklıkla kullanılan Likert ölçeği verilebilir. Bu ölçeklerde cevaplayıcıya çoğunlukla bir fikre veya ifadeye ne derece katıldığı sorulur ve cevap kategorileri kendi içinde, -genellikle “kesinlikle katılmıyorum”dan “kesinlikle katılıyorum”a doğru giden bir dizge içerisinde- sıralıdır. İkinci tip Kategorik/Niteliksel değişkenlerde ise bir sıralama yapmak mümkün olmaz, cevap kategorileri sadece birbirinden ayrılabilir durumdadır. Cinsiyet, oy verilen parti gibi örnekler bu tipe girer. Şimdi dplyr paketindeki glimpse() fonksiyonunu kullanarak yukarıda özetlediğimiz veri tabanına bir de bu gözle bakarak değişkenlerin tiplerini anlamaya çalışınız.
10.3 Filtreleme
Kategorik/Niteliksel değişkenler R içerisinde çoğunlukla factor olarak bulunurlar. Bu değişkenlerin istatistiki ölçümlerde kullanımı özel bir dizi işlem gerektirdiğinden bu değişkenlere ait isim, ölçüm kategorileri gibi niteliklerinin bilinmesi yapılacak işlemler için çok önemlidir. Kategorik/Niteliksel değişkenler ayrıca alt-grup analizleri için oldukça kullanışlıdır. Bu değişkenlerin bir kategorisi kullanılarak, (örneğin cinsiyet değişkeninin sadece erkek kategorisi gibi) alt-grup analizleri gerçekleştirilebilir.
Şimdi email50 veritabanında bulunan number değişkeni üzerinde birkaç uygulama yapalım. Bu değişkenin bir e-pota içerisinde bulunan sayıları none (hiç yok), small (küçük) ve big (büyük) kategorileri halinde kodlanmış olduğunu biliyoruz. dplyr paketinde bulunan filter() fonksiyonunu kullanarak bu değişkenden istediğimiz bir kesiti almak için aşağıdaki kodu kullanabiliriz.
email50_buyuk <- email50 %>%
filter(number == "big")
glimpse(email50_buyuk)## Observations: 7
## Variables: 21
## $ spam <dbl> 0, 0, 1, 0, 0, 0, 0
## $ to_multiple <dbl> 0, 0, 0, 0, 0, 0, 0
## $ from <dbl> 1, 1, 1, 1, 1, 1, 1
## $ cc <int> 0, 0, 0, 0, 0, 0, 0
## $ sent_email <dbl> 0, 0, 0, 0, 0, 1, 0
## $ time <dttm> 2012-02-16 22:10:06, 2012-02-05 01:26:09, 2012-0...
## $ image <dbl> 0, 0, 0, 0, 0, 0, 0
## $ attach <dbl> 0, 0, 0, 0, 0, 0, 0
## $ dollar <dbl> 0, 0, 3, 2, 0, 0, 0
## $ winner <fct> no, no, yes, no, no, no, no
## $ inherit <dbl> 0, 0, 0, 0, 0, 0, 0
## $ viagra <dbl> 0, 0, 0, 0, 0, 0, 0
## $ password <dbl> 0, 2, 0, 0, 0, 0, 8
## $ num_char <dbl> 7.01, 10.37, 42.79, 26.52, 6.56, 11.22, 10.61
## $ line_breaks <int> 183, 198, 712, 692, 140, 512, 225
## $ format <dbl> 1, 1, 1, 1, 1, 1, 1
## $ re_subj <dbl> 0, 0, 0, 0, 0, 0, 0
## $ exclaim_subj <dbl> 0, 0, 0, 1, 0, 0, 0
## $ urgent_subj <dbl> 0, 0, 0, 0, 0, 0, 0
## $ exclaim_mess <dbl> 1, 1, 2, 7, 2, 9, 9
## $ number <fct> big, big, big, big, big, big, bigYukarıdaki örnek email50 veritabanında bulunan number değişkeninin sadece big kategorisini filtreledi ve bunu email50_buyuk isimli başka bir veritabanı olarak sakladı. Şimdi bu yeni veritabanındaki number değişkenine ait bir tablo oluşturalım ve big kategorisinde kaç tane e-posta olduğuna bakalım.
table(email50_buyuk$number)##
## none small big
## 0 0 7Görüldüğü üzere her ne kadar filtrelemeyi yapmış olsak da, değişkene ait kullanılmayan kategoriler de (none ve small kategorileri) oluşturduğumuz tabloda yer aldı. Bu kullanılmayan kategorileri değişkenden çıkarmak için droplevels() fonksiyonunu kullanmamız gerekir.
email50_buyuk$number <- droplevels(email50_buyuk$number)
table(email50_buyuk$number)##
## big
## 710.4 Ayrıştırma
Analizlerde çoğu zaman nümerik değerleri ayrıştırarak ek değerlendirmeler yapmak gerekir. Örneğin tekil bir gözlemin tüm seri ortalamasının üstünde veya altında olup olmadığının değerlendirilmesi (bir öğrencinin notunun sınır ortalamasının altında veya üstğnde olması gibi) sıklıkla yapılan bir işlemdir. Aşağıdaki örnekte email50 veritabanındaki bir e-posta içindeki karakter sayısını ölçen num_char değişkenini böyle bir analize tabi tutacağız. İşlem sırasında ortalama_ustu ve ortalama_alti olarak iki kategorisi olan num_char_cat ismi ile yeni bir değişken oluşturcağız. İşlem ayrıca orjinal num_char değişkenini ortalama değeri üzerinden kontrol edip sonucu numchar_cat değişkenine ortalama_ustu ve ortalama_alti olarak işleyecek.
# numchar değişkeninin ortalamasını hesaplayalım
ortalama_numchar <- mean(email50$num_char)
# num_char_cat değişkenini oluşturalım
email50 <- email50 %>%
mutate(num_char_cat = ifelse(num_char < ortalama_numchar, "ortalama_alti", "ortalama_ustu" ))
# yeni değişkenin tablosuna bakalım
table(email50$num_char_cat)##
## ortalama_alti ortalama_ustu
## 35 15Yukarıdaki çıktıdan 50 e-postanın 35 tanesinin ortalama değerin üzerinde, 15 tanesinin de altında olduğunu anlıyoruz. Oluşan yeni değişkeni kontrol etmek isterseniz Global Environment penceresindeki email50 veritabanının sonuna da bakabilirsiniz.
Analizlerde sıkça gereken bir başka işlem ise Kategorik/Niteliksel değişkene ait değerlerin birleştirilmesi işidir. email50 veritabanında bulunan number değişkenini ele alalım. Bu değişken none, small ve big olarak tanımlanmış üç seviyede bir e-postanın içeriğindeki sayıları belirtiyor. Bizim ise bir e-postada sadece sayı olup olmadığını merak ettiğimizi varsayalım. Bu durumda none (hiç) seviyesini ayrı tutup small (küçük) ve big (büyük) seviyelerinin birleştirilmesi gerekir. Aşağıdaki kod hem bu işlemi gerçekleştiriyor, hem de sonucu grafikliyor.
library(ggplot2)
email50 <- email50 %>%
mutate (sayi_var_yok = ifelse(number == "none", "yok", "var"))
table(email50$sayi_var_yok)##
## var yok
## 44 6ggplot(email50, aes(sayi_var_yok)) +
geom_bar()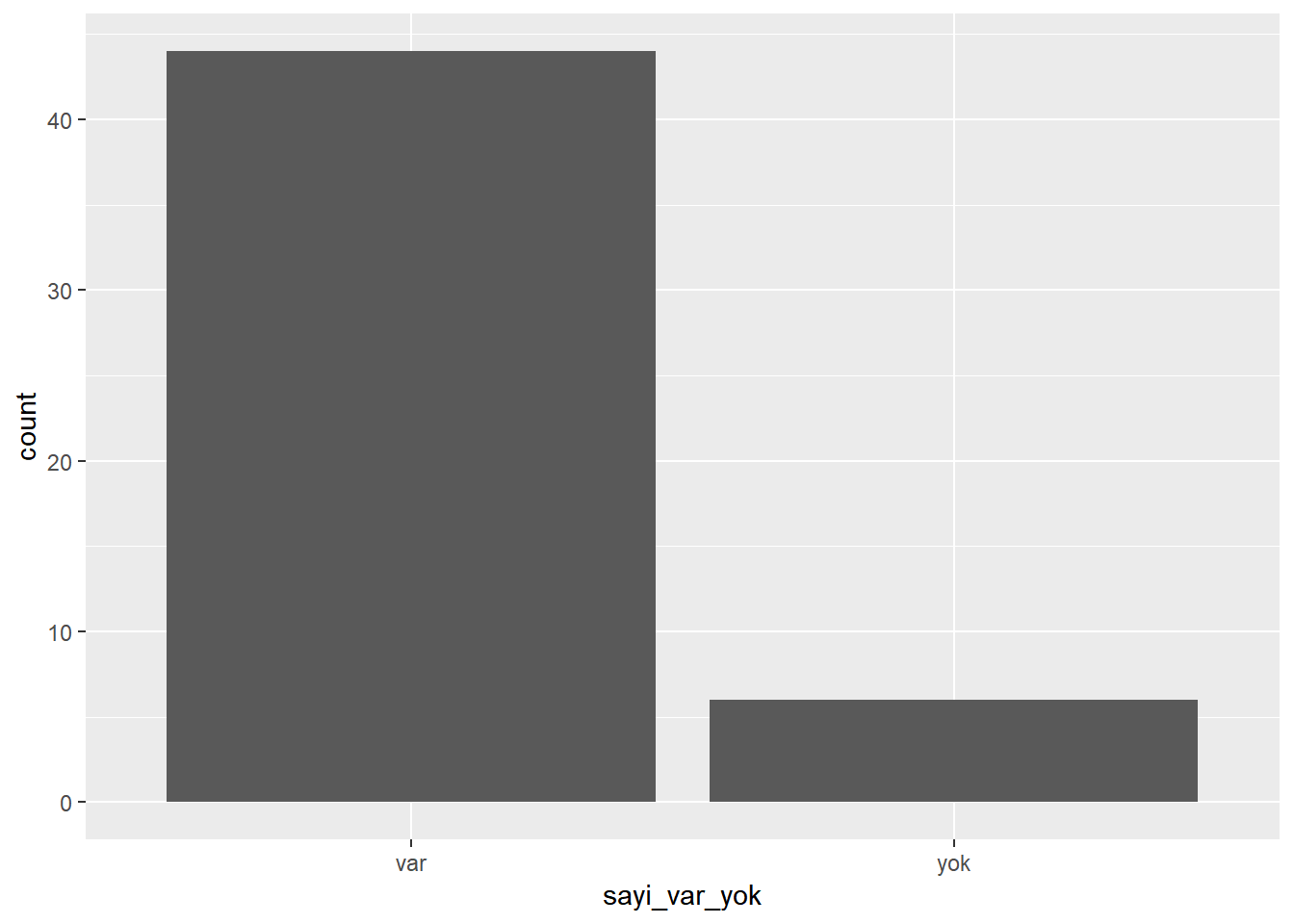
10.5 Görselleştirme
Bu bölümde değişkenler arasındaki ilişkiler anlamak üzere kullanılan temel grafikleme yöntemlerine değineceğiz ve tüm grafikleme işlemleri için ggplot2 paketini kullanacağız.. (Daha detaylı grafikleme uygulamaları için lütfen ilgili bölümlere göz atınız)
İlk olarak email50 veritabanında bulunan iki nümerik değişkeni (num_char ve exclaim_mess), e-postanın istenmeyen bir e-posta olup olmadığını gözeterek karşılaştıralım.
# spam değişkenini factor olarak tanımlandığına dikkat ediniz!
ggplot(email50, aes(exclaim_mess, num_char, color= factor(spam)))+
geom_point()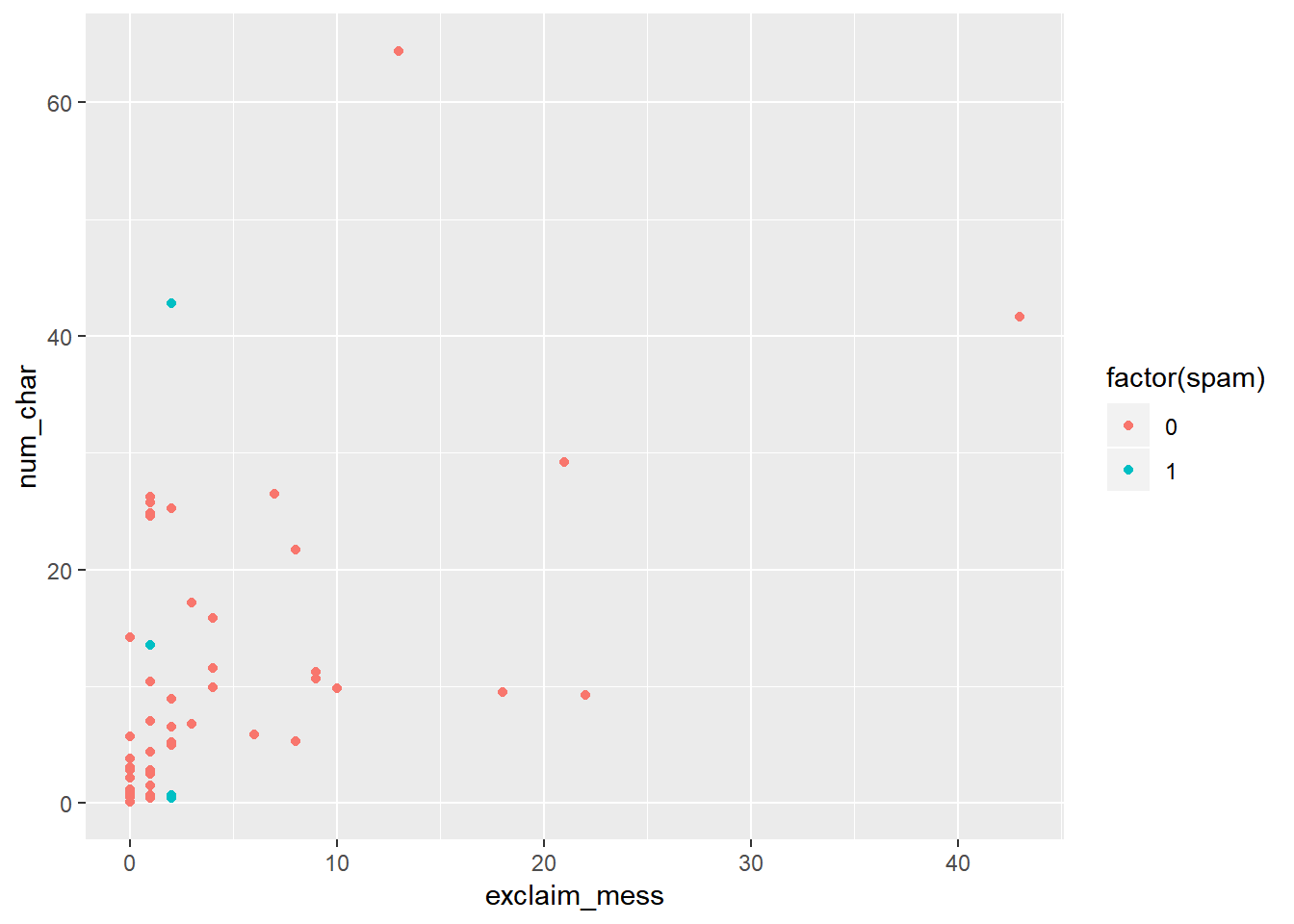
10.6 Gözleme Dayalı Araştırmalar ve Deneyler
Sosyal bilimler araştırmalarında sıkça başvurulan iki tip araştırma yöntemi bulunur: gözleme dayalı araştırmalar ve deneyler. Bu bölümde bu iki yöntemi ayrıştırmayı ve her biri için uygun hesaplama kestirim olanaklarını inceleyeceğiz.
Gözleme dayalı araştırmalarda araştırmacı verinin oluşma sürecine dahil olmadan ve bu sürece müdahale etmeden veriyi toplamaya çalışır. Gözleme dayalı çalışmalar ile toplanmış veriler ile nedensellik iddiası olmadan sadece değişkenler arası ilişkiler ortaya konabilir. Öte yandan deneylerde araştırmacı gözlemlerini deney ve kontrol gruplarına rastlantısal olarak yerleştirir ve bu durum bağımlı ve bağımsız değişkenler arasındaki ilişkiyi nedensellik temelinde açıklamayı olanaklı kılar.
Negatif siyasi kampanya reklamlarına maruz kalma ve siyasete güven arasındaki ilişkiyi merak ettiğimizi varsayalım. Bu çalışmayı hem gözleme dayalı hem de deneysel araç kullanarak tasarlayabiliriz. Gözleme dayalı yapmak istersek önce nüfustan negatif siyasi reklam seyretmiş ve seyretmemiş iki ayrı örneklem çekeriz ve devamında bu grupların siyasete güven derecelerini ölçer ve karşılaştırırız. Eğer deney yapmak istersek, nüfustan örneklemimizi çekip bu örneklemdeki denekleri rastlantısal olarak deney ve kontrol gruplarına yerleştirdikten sonra, deney grubuna negatif kampanya reklamlarını seyrettiririz. Deneyin gözleme dayalı tasarımdan farkı, deneylerde siyasi kampanyaya maruz kalma durumunun araştırmacı tarafından manipüle ediliyor olmasıdır. Deney tasarımında da her iki grubun siyasete güven dereceleri ölçülür ve karşılaştırılır.
Gözleme dayalı tasarımlarda bahsedilen gruplar arasında fark saptansa bile, bu fark tamamen kullanılan bağımsız değişkene (negatif siyasi reklama maruz kalma) bağlı değildir: İnsanların siyasete olan güveni sadece maruz kaldıkları siyasi reklam tipi tarafından belirlenmez, konunun anlaşılması için ideolojik konum, yaş, gelir gibi kontrol edilmesi gereken başka değişkenler bulunur. Ancak deneylerde yukarıda anlatılan ve sonucu etkileyen değişkenler, rastlantısal olarak seçilmiş deney ve kontrol grupları arasında eşit olarak dağılır. Dolayısıyla gruplar arasındaki farkları bağımsız değişkenin etkisi olarak değerlendirebiliriz.
10.7 Rastlantısal Örneklem ve Rastlantısal Atama
Rastlantısal örneklem deneklerin örnekleme seçilmesi sırasında kullanılan ve örneklem ölçümlerinin nüfusa genellenmesi için gereken öncelikli bir prosedürdür. Rastlantısal örneklemde birimlerin örnekleme çıkma şansının eşit ve hesaplanabilir olması gerekir. Rastlantısal atama ise deneyler sırasında deneklerin gruplara rastlantısal olarak yerleştirilmesine verilen isimdir. Böylece denekler farklı manüpülasyonlara tabi tutulabilir ve bağımsız değişkenin etkisi bağımlı değişken üzerindeki etkisi ölçülebilir. Aşağıdaki şekil farklı tasarımların çıkarım sınırlarını belirtmektedir.
Şüphesiz beyaz zeminli seçeneklerden sol üst köşede bulunan nedensellik ve genellenebilirlik niteliklerini içeren tasarım en kuvvetli sonuçları üretir. Hem deneklerin rastlantısal olarak nüfustan seçildiği, hem de rastlatısal olarak deney gruplarına atandığı bu tasarım hayli masraflı ve uygulaması zor olan bir seçimdir. Bu nedenle deneyler çoğunlukla sol alt köşede bulunan nedensellik içeren ama genellenemeyen tasarımlarda gönüllüler üzerinden gerçekleştirilir.
10.8 Kategorik Verilerin Analizi
10.9 Çapraz tablolar
Bu bölümde 1000 gözlemden oluşan ve cevaplayıcıların siyasi ve sosyal değerlerini içeren ve tamamen kurgusal olan dt isimli veri tabanını kullanacağız. Bu kurgusal veri tabanı cevaplayıcıların parti tercihleri, kürtaj hakkındaki düşünceleri, yaşları gibi bilgileri içermektedir ve https://tinyurl.com/yabhoe56 adresinden indirilebilir.
Öncelikle veri tabanımızı çalışma ortamımıza getirelim, character olarak kodlanmış tüm sütunları factor değişken haline getirelim ve üzerinde daha kolay çalışmak için veri tabanımızı tibble formatına çevirelim.
library(readr)
library(tibble)
dt <- read.csv("C:/Users/emretoros/OneDrive/Makale/R/toros/dt.csv")
dt <- as.data.frame(unclass(dt))
as.tibble(dt)## # A tibble: 1,000 x 23
## idnum cinsiyet bolge gelir egitim muhafazakar liberal milliyetci p1
## <int> <fct> <fct> <int> <int> <int> <int> <int> <int>
## 1 517 Erkek Guney 22559 1 2 4 2 1
## 2 297 Kadin Guney 12072 5 2 3 1 1
## 3 811 Kadin Kuzey 40815 1 2 5 1 0
## 4 461 Erkek Kuzey 44135 1 3 5 3 0
## 5 607 Kadin Dogu 48246 1 2 3 1 0
## 6 186 Erkek Kuzey 15263 2 2 5 3 0
## 7 879 Erkek Dogu 4122 1 1 5 1 0
## 8 887 Erkek Guney 6345 2 3 4 1 0
## 9 622 Kadin Dogu 35840 2 1 5 1 1
## 10 423 Kadin Dogu 46321 1 3 5 1 0
## # ... with 990 more rows, and 14 more variables: p2 <int>, p3 <int>,
## # siyasete_guven <int>, yas <int>, gocmenler <int>, oy <fct>,
## # kurtaj <fct>, sendikalasma <int>, gelenek <int>, bagis <int>,
## # askere_guven <dbl>, adalete_guven <dbl>, burokrasiye_guven <dbl>,
## # meclise_guven <dbl>Özetten de anlaşılacağı üzere veri tabanımızda 1000 gözlem ve 22 değişken bulunuyor
Aşağıdaki kodlar verimiz ile ilgili bazı temel işlemleri gerçekleştiriyor.
# Cinsiyet değişkeninin aldığı değerlere bakalım
levels(dt$cinsiyet)## [1] "Erkek" "Kadin"# Bölge değişkeninin aldığı değerlere bakalım
levels(dt$bolge)## [1] "Bati" "Dogu" "Guney" "Kuzey"# Bu değişkenler ile bir çapraz tablo oluşturalım
table(dt$cinsiyet, dt$bolge)##
## Bati Dogu Guney Kuzey
## Erkek 136 115 138 120
## Kadin 130 141 120 10010.10 Değişken seviyelerinin ayıklanması
Yukarıdaki tablo bölgelere göre dağılmış erkek ve kadın cevaplayıcıların sayılarını raporladı. Çalışmamızı sadece kadınlar üzerinden yapmak istediğimizi varsayalım. Bu durumda erkek cevaplayıcıları veri tabanından ayıklamamız gerekiyor. R içinde bu işlem için iki adım gerekir. Önce ayıklamak istediğimiz değişkenin seviyesini dplyr paketinde bulunan filter() fonksiyonu ile tanımlarız (bu durumda “Erkek” seviyesi), daha sonra ise bu seviyeyi ilgili değişkenden droplevels() fonksiyonu ile ayıklarız. Aşağıdaki kod bu işlemi gerçekleştirmektedir.
library(dplyr)
dt_k <- dt %>%
filter (cinsiyet != "Erkek") %>%
droplevels()Yukarıdaki kod sadece bu ayıklamayı yapmak ile kalmadı aynı zamanda yaptığı işlemi dt_k ismi ile yeni bir veri tabanına kaydetti. ÇApraz tabloyu bu yeni veri tabanında oluşturalım
table(dt_k$cinsiyet, dt_k$bolge)##
## Bati Dogu Guney Kuzey
## Kadin 130 141 120 100Her ne kadar çapraz tablolar değişkenlere ait frekansları sayı olarak raporlasa da, bu frekansları görsel olarak sunmak çoğu zaman daha anlamlıdır.
Aynı verinin birden fazla şekilde görselleştirilebileceğini anlatmak adına aşağıdaki kod yanyana iki sütun grafik oluşturuyor. Kod içindeki geom_bar() fonksiyonundaki dodge argümanının kullanımı grafikleri üstüste değil yan yana getirir.
# Grafik için ggplot2 paketini yükleyelim
library(ggplot2)
# Yanyana olacak şekilde cinsiyet bazında bölgelerin grafiğini çizelim
ggplot(dt, aes(x = cinsiyet, fill = bolge)) +
geom_bar(position = "dodge")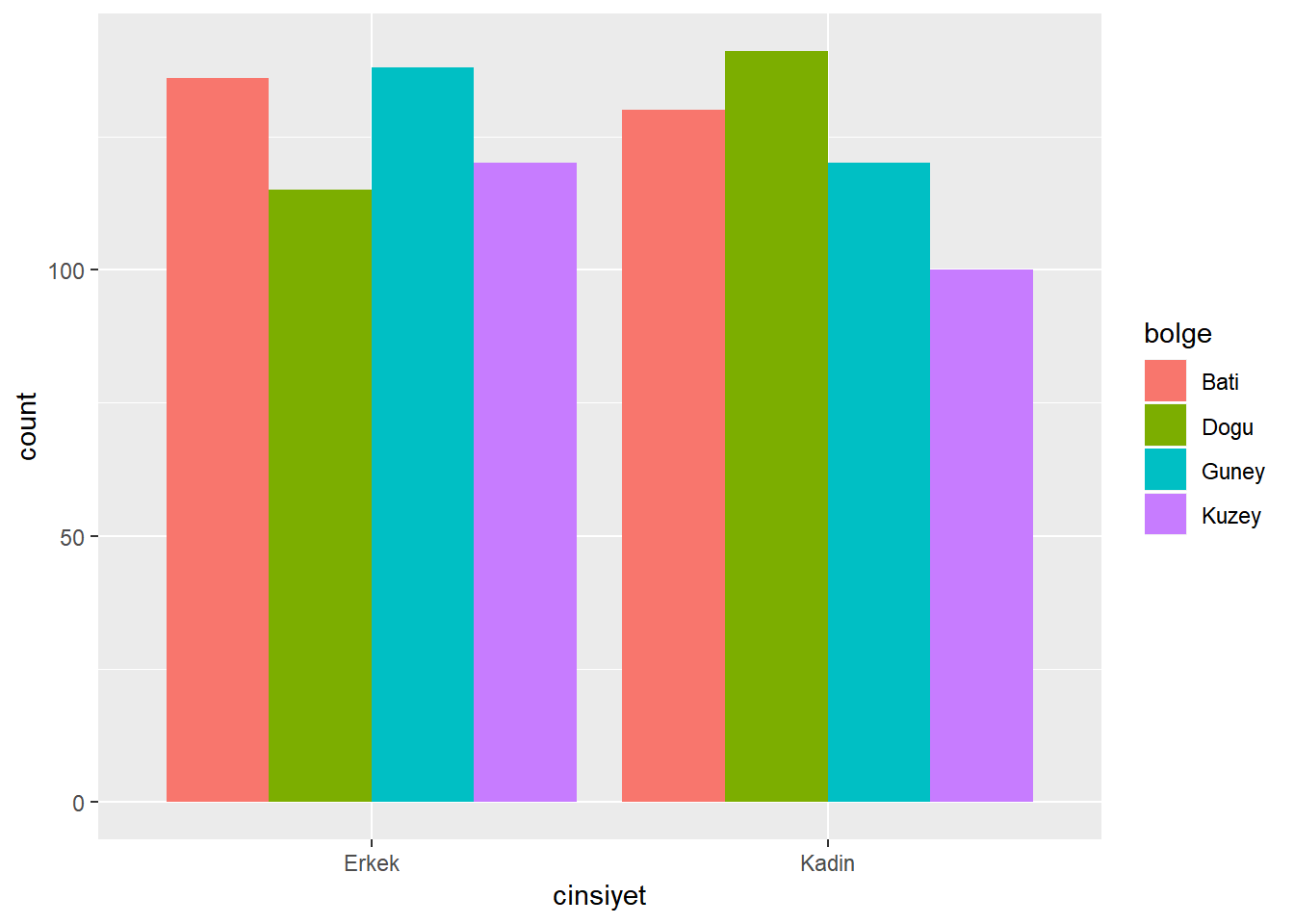
# Yanyana olacak şekilde bölgeler bazında göre cinsiyetin grafiğini çizelim
ggplot(dt, aes(x = bolge, fill = cinsiyet)) +
geom_bar(position = "dodge") +
theme(axis.text.x = element_text(angle = 90))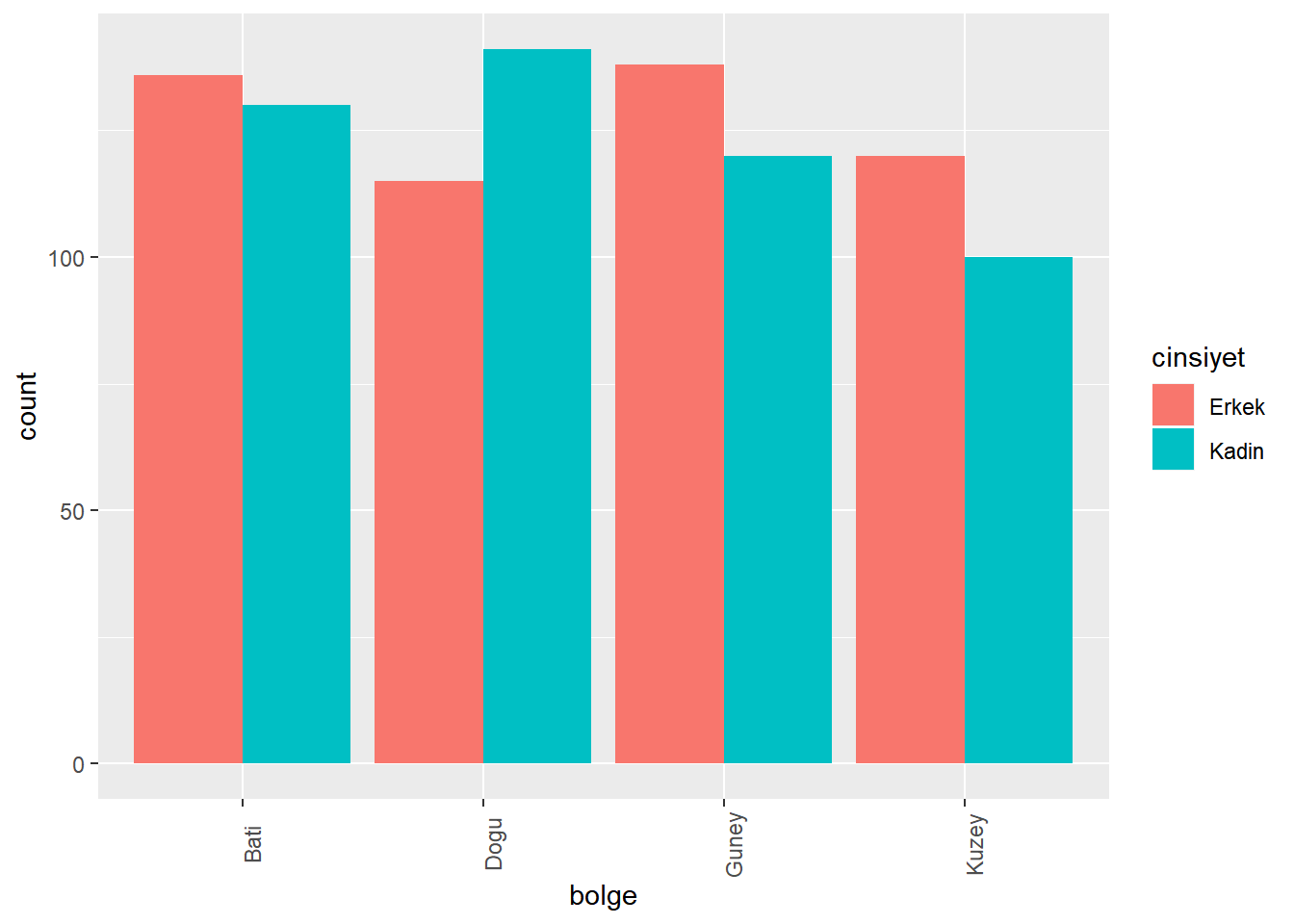
Lütfen oluşan grafikleri yorumlamaya çalışın. Hangi bölgede kadın gözlem sayısı erkek gözlem sayısından fazladır? En fazla erkek gözlemi hangi bölgede gerçekleşmiş? Güneyde erkekler mi kadınlar mı daha fazladır?
10.11 Frekanslar, Oranlar ve Durumsal Oranlar
Çoğu zaman gözlemlere ait frekanslar önemli bilgiler içerse de, bu frekansların başka gözlemler ile birleştirilmiş oransal ifadeleri içerik açısından daha zengindir. Elimizdeki dt veri tabanı ile bölgelere göre parti dağılımını gösteren basit bir tablo ile işe başlayalım
options(scipen = 999, digits = 3) # Tablo çıktısını basitleştirmek için
tab_frekans <- table(dt$oy, dt$bolge)
tab_frekans##
## Bati Dogu Guney Kuzey
## PartiA 15 24 15 13
## PartiB 133 119 130 110
## PartiC 78 74 73 69
## PartiD 40 39 40 28ikinci kod satırında table() fonksiyonu kullanarak yarattığımız ve tab_frekans ismi ile kaydettiğimiz yukarıdaki tablo partilerin bölgelere göre aldığı oy miktarını gösteriyor. Şimdi aynı tabloyu parti oylarının oranlarını gösterecek şekilde prop.table() fonksiyonunu kullanarak tekrar oluşturalım.
prop.table(tab_frekans)##
## Bati Dogu Guney Kuzey
## PartiA 0.015 0.024 0.015 0.013
## PartiB 0.133 0.119 0.130 0.110
## PartiC 0.078 0.074 0.073 0.069
## PartiD 0.040 0.039 0.040 0.028Yukarıdaki tabloda PartiB ile Batı değişkenlerinin kesiştiği hücrenin en yüksek orana sahip olduğunu görüyoruz. Buradan tüm seçim bölgelerindeki en yüksek yüzdeyi PartiB’nin Batı bölgesinde gerçekleştirdiğini anlıyoruz. Yukarıdaki tablodaki değerler oran temsil ettiğinden tüm hücre değerleri toplandığında “1” değeri bulunur.
Oy verme ile bölgeler arasındaki bağlantıyı daha net ortaya çıkartmak için durumsal oranlara bakılması gerekir. Hesaplamak istediğimiz oranlarını “durum”u (condition) kodda yapacağımız bir değişiklikle tanımlanır. Eğer oranları satır bazında istersek koda “1” değeri, sütun bazında istersek koda “2” değeri eklenir. Aşağıdaki kodları inceleyiniz.
prop.table(tab_frekans, 1) # (satır bazlı durum tanımı, partiye göre durum)##
## Bati Dogu Guney Kuzey
## PartiA 0.224 0.358 0.224 0.194
## PartiB 0.270 0.242 0.264 0.224
## PartiC 0.265 0.252 0.248 0.235
## PartiD 0.272 0.265 0.272 0.190prop.table(tab_frekans, 2) # (sütun bazlı durum tanımı, bölgeye göre durum)##
## Bati Dogu Guney Kuzey
## PartiA 0.0564 0.0938 0.0581 0.0591
## PartiB 0.5000 0.4648 0.5039 0.5000
## PartiC 0.2932 0.2891 0.2829 0.3136
## PartiD 0.1504 0.1523 0.1550 0.1273Yukarıdaki tabloları yorumlamaya çalışalım. Üstteki tablodan PartiC’nin aldığı toplam oyun yüzde 23’ünü Kuzey bölgesinden aldığını görüyoruz. PartiA’ya baktığımızda ise PartiA oylarının üçte birinden fazlasının (%35) Doğu bölgesinden geldiğini görüyoruz. İkinci tablo ise oranları sütunlara göre hesapladı. Buna göre PartiB Doğu bölgesi hariç diğer bölgelerde oyların yarısını almış görünüyor.
Yukarıdaki tablolar her ne kadar önemli bilgiler içeriyor olsa da verinin daha kolay anlaşılması için grafikler yoluyla ifade edilmesi uygun olur. Bu tip karşılaştırmalar için yukarıda kullandığımız sütun grakileri bazı ek modifikasyonlar ile tekrar kullanabiliriz. Şİmdi aşağıdaki kodu inceleyiniz
ggplot(dt, aes(x=oy, fill=bolge)) +
geom_bar(position="fill")+
ylab("oran")
ggplot(dt, aes(x=bolge, fill=oy)) +
geom_bar(position="fill")+
ylab("oran")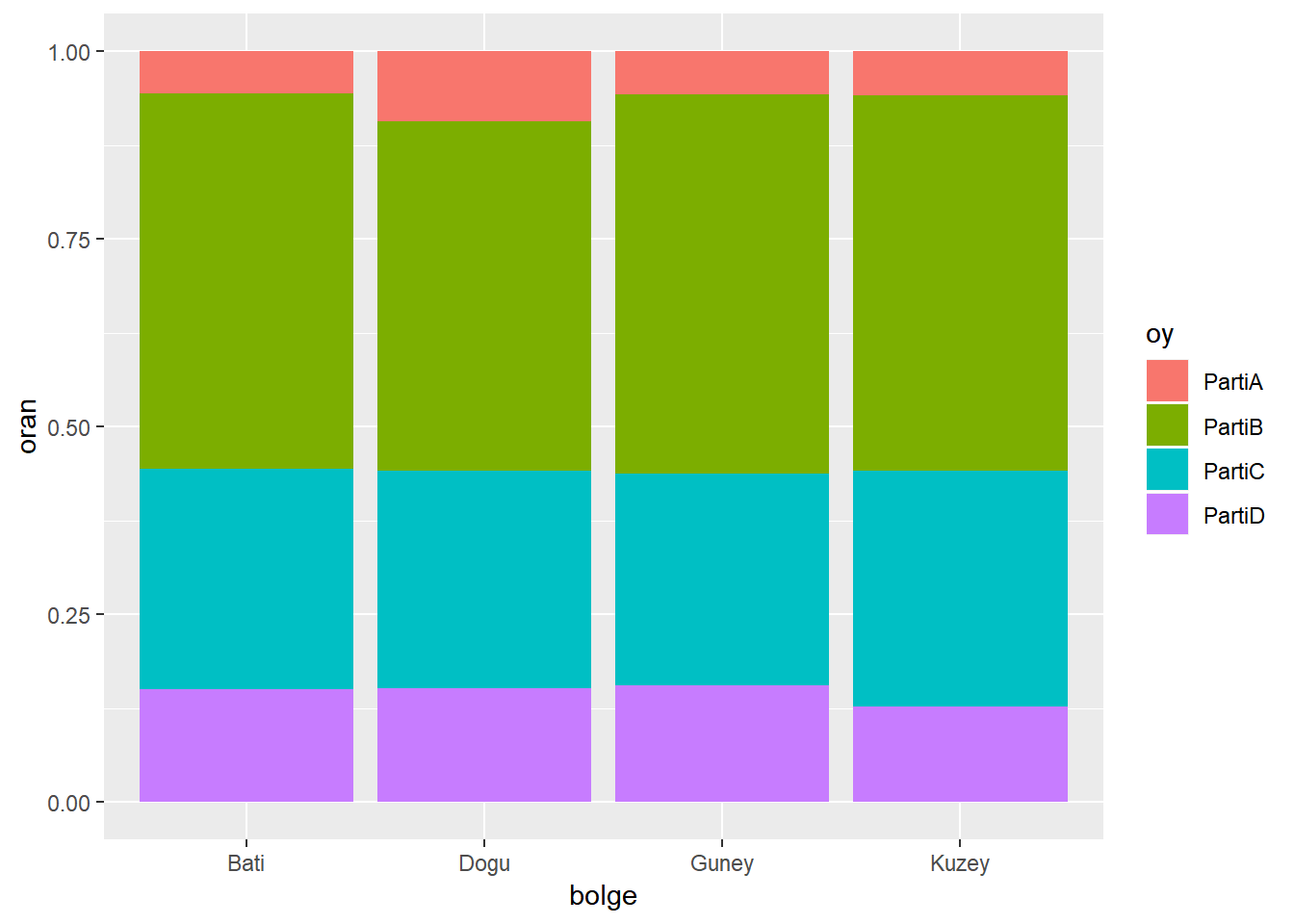
Yukarıdaki grafiklerden ilki birinci tabloya, ikincisi ise ikinci tabloya ait. Kodda yaptığımız değişiklik ise geom_bar() fonksiyonuna position="fill" argümanını eklemek oldu. Bu argüman ile frekanslar yerine oranları istediğimizi ifade etmiş olduk. İkinci grafikte PartiB’nin diğer partilere karşı olan üstünlüğü açıkça farkediliyor. İlk grafikte ise PartiA’nın diğer bölgelere kıyasla Doğu bölgesinde başarılı olduğunu görebiliyoruz.
10.12 Tek Değişkene Ait Dağılımlar
Farkedeceğiniz üzere yukarıdaki örneklerde iki ayrı değişkenin birbiri ile olan ilişkisini ortaya koyan analizler yaptık. Kimi zaman tek değişkenlere ait dağılımlar da araştırma sorumuza yanıt vermek için gerekli olabilir. Bu bölümde tek değişkene ait dağılımların nasıl oluşturulacağına bakacağız.
Aşağıdaki kodu tüm partilere ait frekansları sütun grafik halinde göstermek için kullanabiliriz
ggplot(dt, aes(oy))+
geom_bar()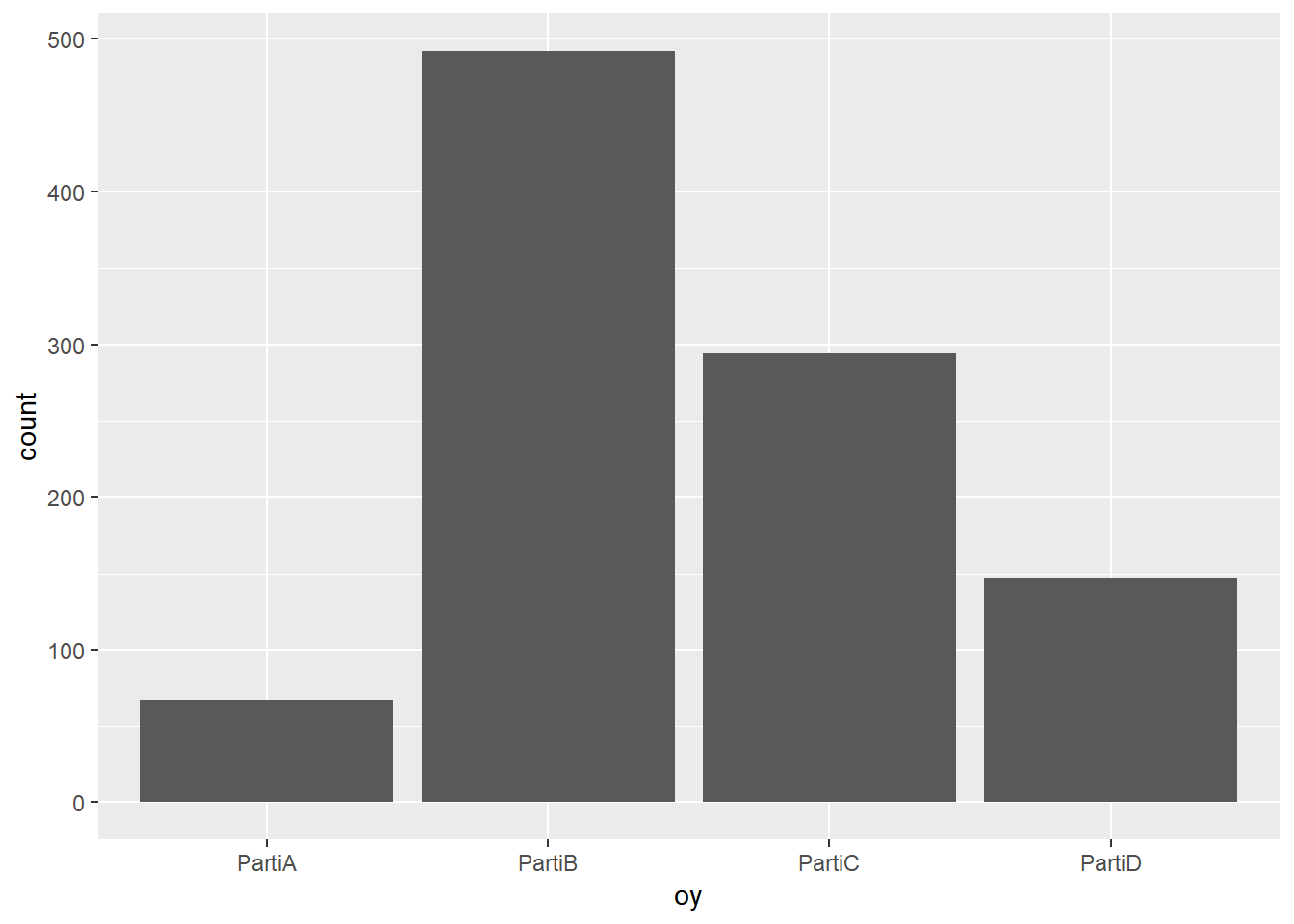
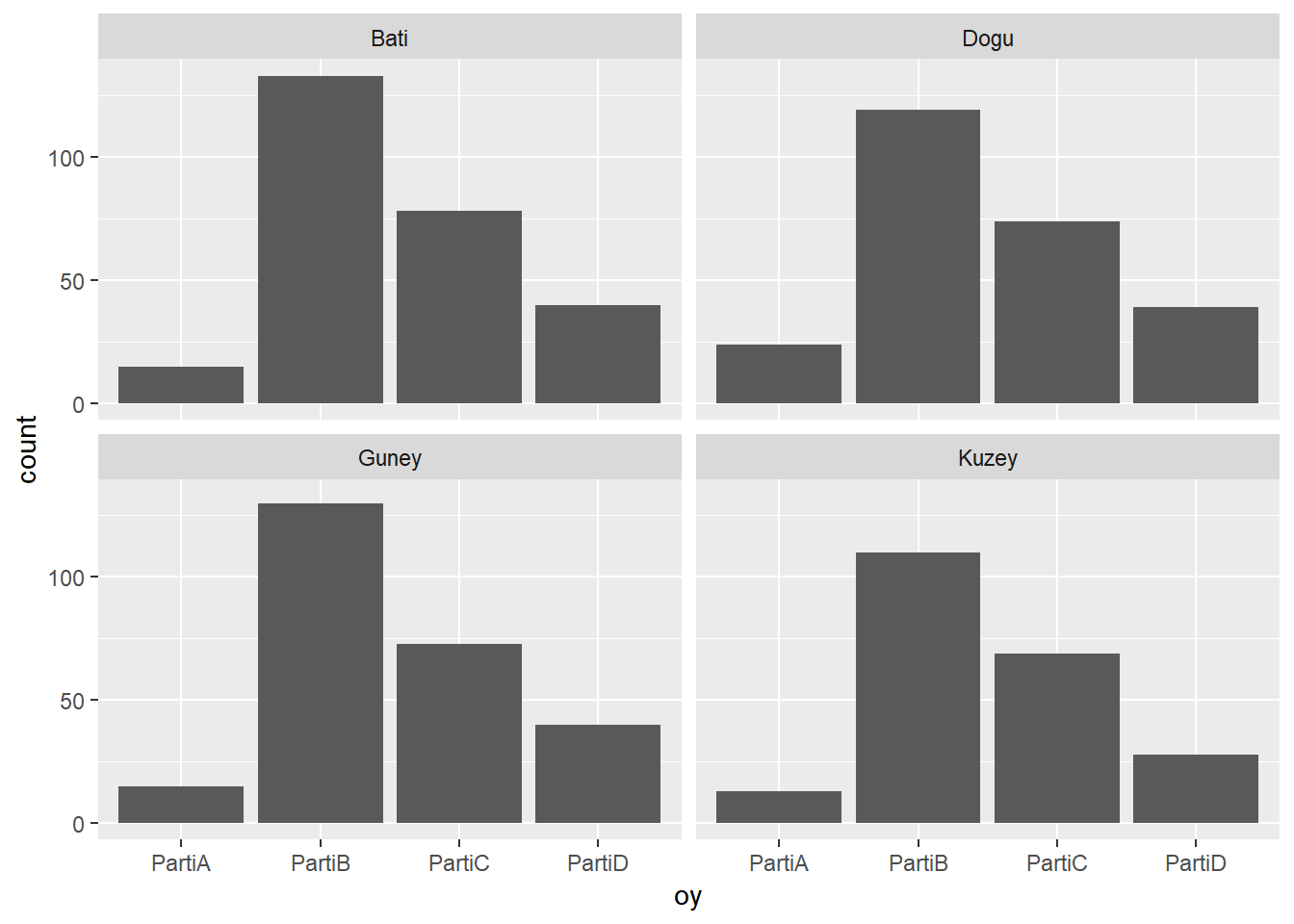
Yukarıdaki basit grafiğe bölge değişkenini ekleyerek ayrı grafikler haline getirmek istediğimizde facet_wrap() fonksiyonunu kullanılır. Bu fonksiyon ~ işareti ile kullanılır ve grafiği ayrıştırmak istediğimiz değişken ~ işaretinden sonra tanımlanır.
ggplot(dt, aes(oy))+
geom_bar()+
facet_wrap(~ bolge)