Capítulo 8 Entendendo e Avaliando sua Hipóteses
Olá, neste capítulo iremos aprender sobre o Teste de Hipóteses. Ele é mais uma das ferramentas estatísticas que auxilia a nossa tomada de decisão com base em informações de uma amostra! Lembre-se que: ao selecionarmos uma amostra precisamos atender alguns pressupostos que foram discutidos nos capítulos 6 e 7. Se as condições da seleção forem adequadas estatisticamente, então dizemos que esta amostra representa bem a população, não é mesmo? Com isso, qualquer estatística que calcularmos sobre a amostra poderá ser generalizada para a nossa população. Esse processo de generalização é o conhecido Teste de Hipóteses. Mas a discussão não para por aqui. Ainda temos muita coisa interessante para aprender! Então, vamos começar?
8.1 O que é “Teste de Hipóteses”?
Vamos utilizar um exemplo sobre pesquisas eleitorais. Observe as manchetes na 8.1 e tente compreendê-las.
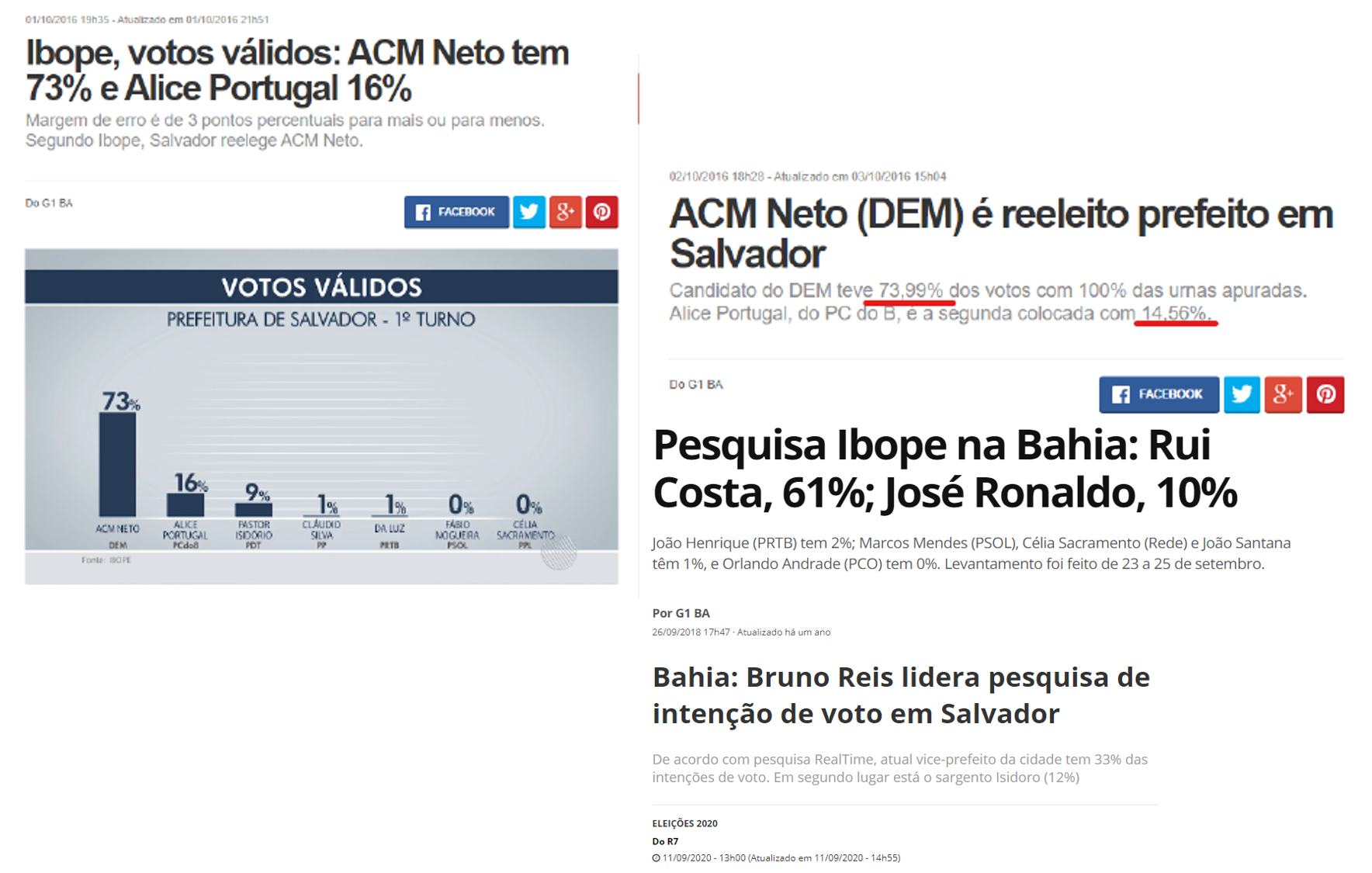
Figura 8.1: Pesquisas de intenção de voto
Vemos que essas pesquisas utilizam a estatística para apontar os possíveis “vencedores” para os cargos de prefeito de Salvador e governador do Estado da Bahia. Mas, devemos nos lembrar que essas pesquisas não foram realizadas com TODOS os eleitores, ou seja, não foi realizada com toda a população de eleitores dessas localidades. Isso porquê, como visto no 7, uma entrevista com toda a população de interesse demandaria muito tempo e recursos financeiros para deslocamento, contratações, entre outros fatores.
Por isso, utiliza-se amostras, uma parcela de indivíduos capaz de representar bem a população. Por conta disso, precisamos fazer algumas suposições ou hipóteses para verificar se é possível que a população tenha um determinado valor para o parâmetro que investigamos a partir da amostra selecionada. Veja que legal, o teste de hipóteses garante que, mesmo tendo utilizado dados de amostra, os nossos resultados são confiáveis para serem extrapolados para a população. Esse processo de generalização é denominado Inferência Estatística. Observe a Figura 8.2, que ilustra esse conceito.
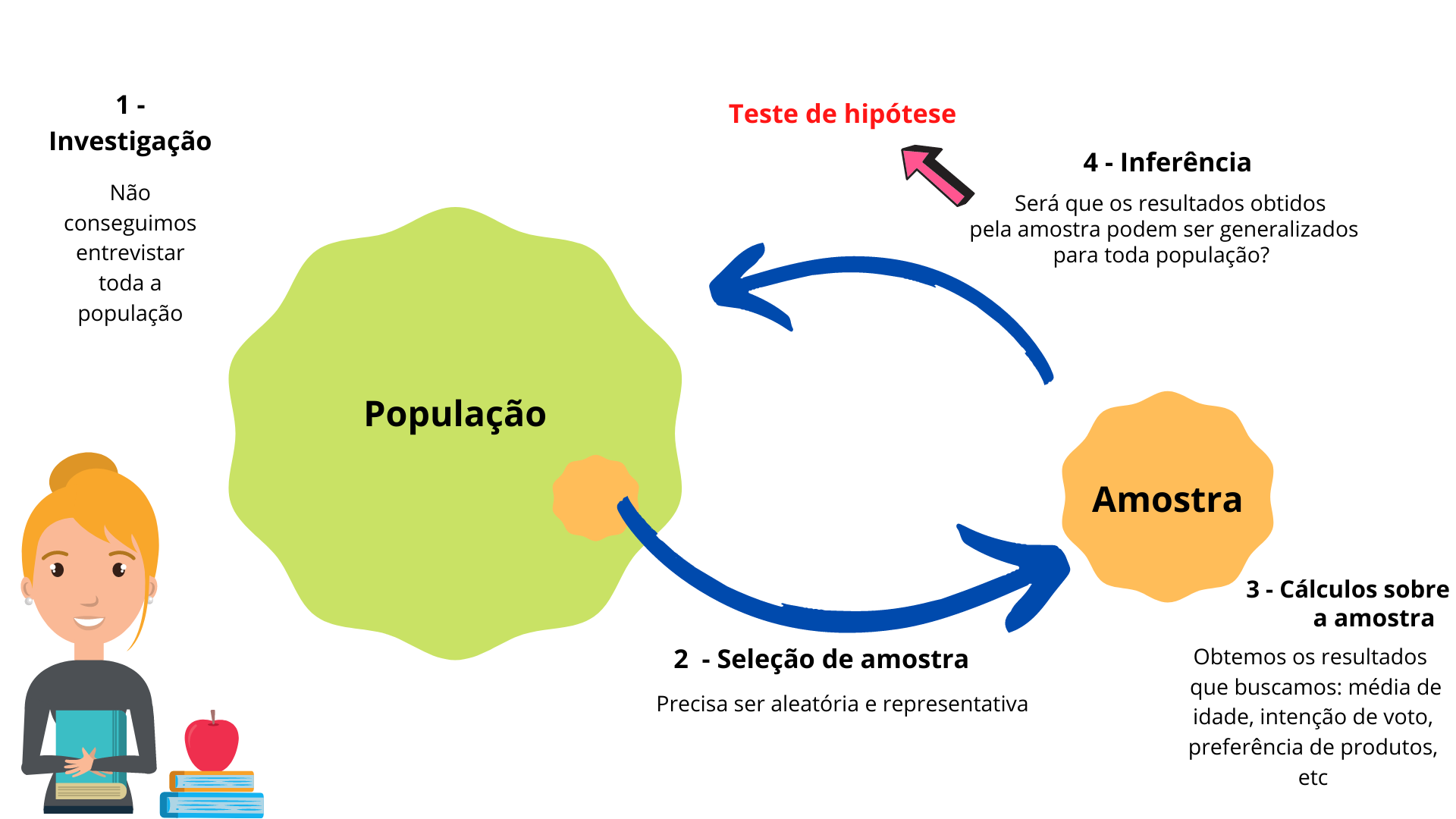
Figura 8.2: Porquê fazer teste de hipótese?
Inferência: a partir de dados amostrais é feita uma generalização para características populacionais.
Mas atenção, o processo de Inferência está sujeito a erro!
Sim, simplesmente pelo fato de selecionarmos uma amostra que será base para a generalização dos resultados para uma população. Esse erro nunca será zero, a menos que não trabalhemos com amostra, e sim diretamente com a população, como é feito com as pesquisas do CENSO.
8.2 Hipóteses estatísticas
As Hipóteses Estatísticas são suposições feitas sobre o valor de um parâmetro populacional, ou a natureza da distribuição da população.
1 - A temperatura corporal média de adultos é \(37°C\)? 2 - A taxa de natalidade de Salvador mudou nos últimos 5 anos? 3 - A proporção de mulheres com depressão é \(5\%\). 4 - A carga horária média de trabalho de funcionários de uma empresa é 40 horas semanais.
Observe que as suposições dos exemplos ocorrem sobre uma população de interesse. Para ficar mais claro, observe para cada pergunta:
1 - “… de adultos”: todos os adultos, não há nenhum critério que defina uma característica específica dos adultos. 2 - “… de Salvador”: engloba toda a população de Salvador, não trouxe informações sobre um bairro específico. 3 - “…mulheres”: mesma situação da pergunta 1 4 - “… de funcionários de uma empresa”: todos os funcionários da empresa, não houve especificação do setor, por exemplo.
Para verificar essas suposições precisamos fazer cálculos, baseados em valores obtidos por uma amostra. Portanto, de acordo com os resultados desses cálculos, a nossa hipótese estatística poderá ser rejeitada ou falhar em ser rejeitada.
Podemos então pensar uma hipótese para o caso da Figura 8.1, com a intenção de votos do candidato Rui Costa. Imagine que a pesquisa ainda não tenha sido feita, portanto ainda não temos o resultado final! Vamos criar uma situação fictícia, onde inicialmente, o candidato estava afirmando que teria \(63\%\) dos votos. Nossa primeira suposição a ser investigada seria:
1 - A proporção de votos para o candidato Rui Costa é \(63\%\).
O teste de hipóteses é composto por duas afirmativas. A primeira, que já elaboramos, é conhecida por hipótese nula. E a segunda afirmativa, complementar, é conhecida como hipótese alternativa. A hipótese nula é uma afirmativa de que um parâmetro populacional é igual a um determinado valor. Já a hipótese alternativa é uma afirmativa de que o parâmetro populacional avaliado apresenta um valor que difere da hipótese nula.
Mas, o que é o parâmetro populacional? Basicamente, ele é uma medida que caracteriza a população. No caso deste exemplo, nosso parâmetro populacional é a proporção de votos para o candidato Rui Costa.
Convencionalmente, utilizamos símbolos para identificar cada hipótese:

Figura 8.3: Porquê fazer teste de hipótese?
Assim, vamos continuar o nosso exemplo com a definição da hipótese alternativa. Nesse caso, podemos nos basear na informação da Figura 8.1 para estabelecer nossa afirmação:
2 - A proporção de votos para o candidato Rui Costa é menor do que \(63\%\).
Em termos matemáticos, podemos escrever as nossas duas hipóteses da seguinte forma:
H0: A proporção de votos para o candidato Rui Costa é igual a \(63\%\).
H1: A proporção de votos para o candidato Rui Costa é menor que \(63\%\).
Observe que as hipóteses são complementares, isso implica que o que está sendo afirmado em uma hipótese não deve ser afirmado na outra. Em um teste de hipóteses temos duas opções:
1 - Rejeitar H0: confirmamos que a proporção de votos não equivale a \(63\%\). 2- Não rejeitamos H0: não temos evidências suficientes para afirmar que a proporção de votos seja diferente de \(63\%\).
Nesse caso, atribuímos o \(<\) (menor que) para a nossa hipótese alternativa, uma vez que nos baseamos em uma manchete que aformou que a proporção de votos equivale a \(61\%\), um valor menor que \(63\%\). Entretanto, é importante compreender que a hipótese alternaiva é feita com base na suposição do investigador sobre os dados. Ou seja, quando avaliarmos outro estudo de caso obviamente faremos suposições diferentes acerca dos dados. Por isso, a hipótese alternativa possibilita usar os símbolos $ < $ (menor que) , $ > $ (maior que) ou diferente.

Figura 8.4: Símbolos para o teste de hipóteses
8.3 \(p\)-valor
O \(P\)-valor também é conhecido como nível descritivo, representa uma probabilidade em se obter estimativas iguais ou mais extremas do que a que foi observada na amostra, supondo que a hipótese nula seja verdadeira.

Eu sei que parece complicado! Mas vamos destrinchar cada parte desta afirmação e você verá que é possível entendê-la. Para isto, vamos voltar ao exemplo da intenção de votos, cujas hipótestes eram:
H0: A proporção de votos para o candidato Rui Costa é = a 63%
H1:A proporção de votos para o candidato Rui Costa é menor que 63%
Bom, como já discutimos, é inviável entrevistar cada eleitor, por isso selecionamos uma amostra representativa. Então, acreditamos que a proporção populacional seja \(63\%\), mas como estamos fazendo uma amostragem esperamos que nosso resultado final tenha alguma variação em relação aos \(63\%\) (lembra quando citamos o erro estatístico?).
Também já vimos pela Figura 8.1, divulgado na mídia, que após as entrevistas, a proporção de votos para o candidato Rui Costa foi igual a \(61\%\). O valor de \(61\%\) claramente é menor/ diferente dos \(63\%\) que estamos supondo no teste, concorda?
A primeira coisa que passa pela mente é rejeitar logo a nossa hipótese nula, não é mesmo? Aqui é o grande ponto: será que essa diferença é de fato estatisticamente significativa ou será um mero acaso? Podemos fazer esta pergunta de forma um pouco mais estatística: se pegássemos outras amostras para realizar essa mesma análise, qual a probabilidade do valor 63% de proporção de votos ocorrer?
Esta pergunta é importante porque se esta probabilidade for alta, significa que nossa hipótese nula H0 não deve ser rejeitada. Mas, se esta probabilidade for mínima, quer dizer que o valor de \(63\%\) ocorreu devido ao acaso e, nossa hipótese nula H0 deve ser rejeitada. Essa probabilidade é conhecida como p-valor, ou nível descritivo.
Quando utilizamos expressões como estatisticamente significativa ou significância estatística, estamos na realidade querendo saber a que condições a nossa hipótese nula deve ser rejeitada ou falhar em ser rejeitada.
Se você chegou até aqui, parabéns! Já entendeu metade da afirmação inicial:
“P-valor também é conhecido como nível descritivo, e representa uma probabilidade em se obter estimativas iguais ou mais extremas”
Vamos continuar a discussão…

A segunda parte da afirmação diz:
“supondo que a hipótese nula seja verdadeira.”
Isto significa que sempre vamos partir da crença de que nossa H0 é realmente verdadeira. Caso contrário, não faria sentido testá-la, automaticamente já aceitaríamos a hipótese alternativa.
Suponha agora, que os dados das entrevistas de intenção de votos já tenham sido coletados e, foram enviados para as análises estatísticas. Temos um interesse específico sobre quantos entrevistados afirmaram votar em Rui Costa, lembra?!
Atenção, até este momento ainda não confirmamos nada sobre a nossa hipótese. Toda esta discussão está nos direcionando ao próximo passo do nosso teste que é justamente a avaliação do p-valor. Vamos observar graficamente o comportamento da nossa amostra.
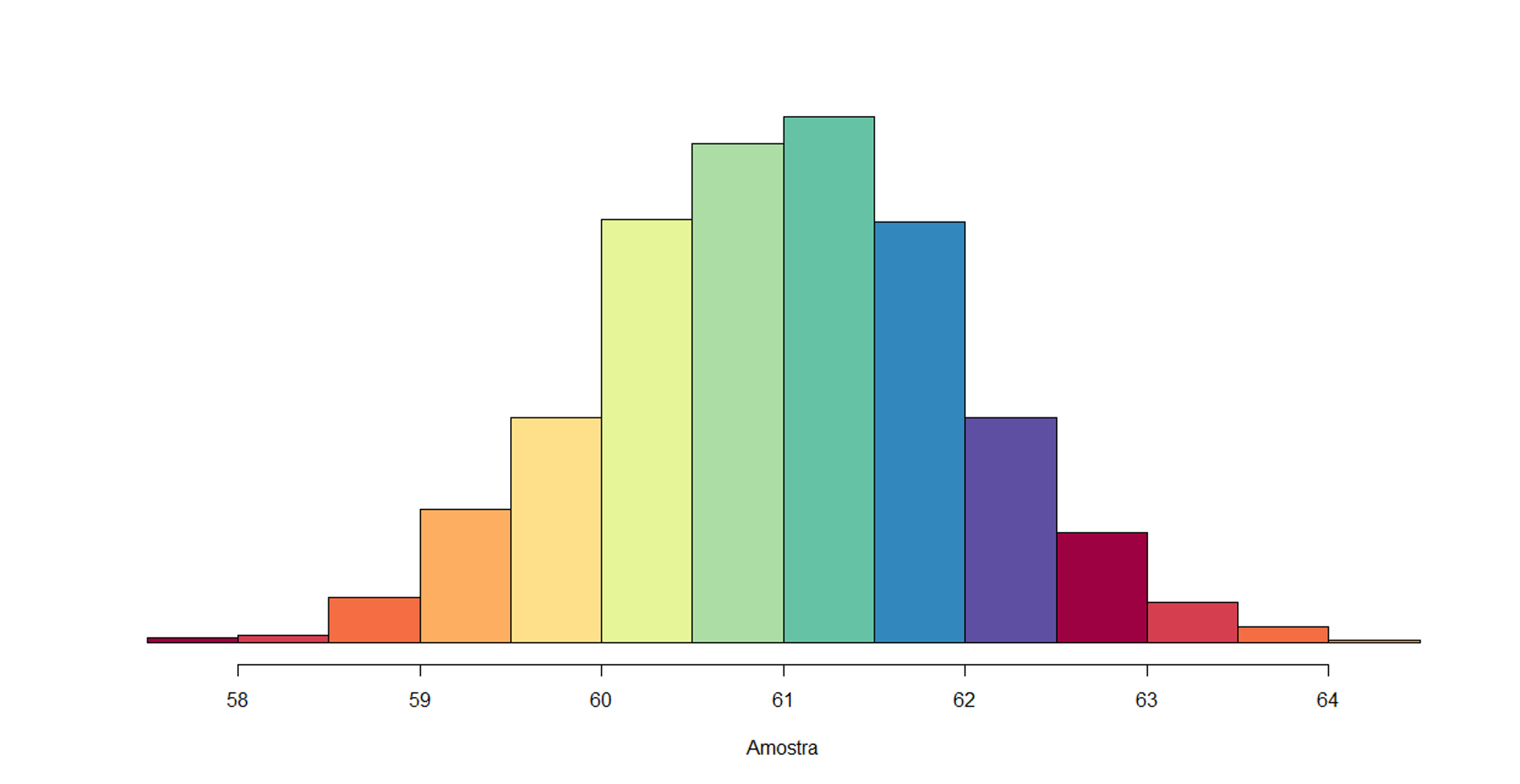
Figura 8.5: Histograma
Este gráfico não é uma novidade para você! No Capítulo 3 diversos tipos de gráficos foram apresentados, inclusive este, o Histograma. Além disso, no capítulo anterior 7 você viu a importância do histograma para identificar e avaliar o formato de distribuições estatísticas. O Histograma é uma excelente ferramenta visual para identificarmos se a distribuição dos dados é uma Distribuição Normal.
E por que isto é importante? Porque, como visto no capítulo anterior, as hipóteses e considerações estatísticas se baseiam em um distribuição normal. A Figura 8.5 indica no eixo x, a proporção de pessoas que afirmaram votar no candidato Rui Costa com base na amostra analisada. Observe que a proporção varia de 57 a 65, sendo indicado no eixo, 58 a 64. Sabemos que o eixo y indica a frequência destas observações. O nosso valor com maior frequência de ocorrência ou o mais provável é \(61\%\). Isto significa, que se selecionássemos várias amostras de entrevistados, a maioria delas iria indicar a porcentagem de votos para Rui Costa está nesse intervalo. Percebemos uma tendência central de ocorrência deste valor.
Perceba também, que é muito pouco provável a ocorrência de \(63\%\) de votos para o candidato, uma vez que este valor apresenta uma frequência muito baixa. Mas, vamos prosseguir nossas confirmações. Lembrando, nossas hipóteses são:
H0: A proporção de votos para o candidato Rui Costa é \(=\ 63%\).
H1:A proporção de votos para o candidato Rui Costa é \(<\ 63%\).
Assim, a Figura abaixo mostra a probabilidade, o p-valor da ocorrência da nossa hipótese nula.
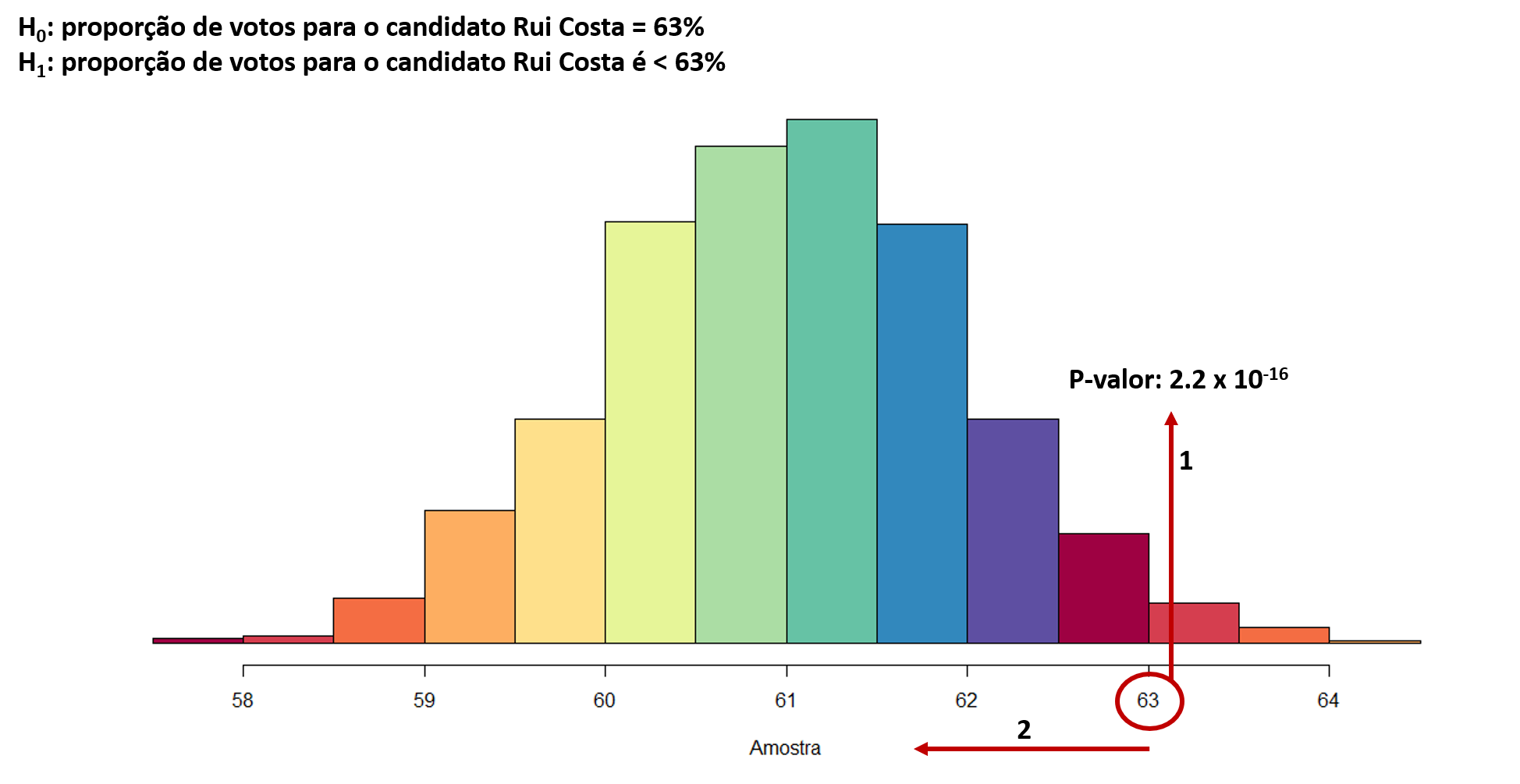
Figura 8.6: p-valor da hipótese nula
Então, testar a nossa H0, é como dizer: “quão provável é que as intenções de voto para Rui Costa sejam 63%?” O teste de hipótese acontece por meio do cálculo de um parâmetro estatístico de teste, vinculado ao p-valor desse teste. O p-valor obtido foi \(2,2\times10^{-16}\) (\(0,0000000000000022\)). Esse valor, indicado pela seta 1, pode ser considerado 0.
Por este motivo, podemos rejeitar a nossa hipótese nula. Ou seja, o nosso p-valor com valor 0 indica que praticamente não há chances da proporção de votos ser \(63\%\). Nesse caso, passamos a ter mais argumentos a favor da nossa hipótese alternativa, de que a proporção de votos \(<\) \(63\%\). Portanto: REJEITAMOS a hipótese nula! Observe a seta 2 que indica para o centro do histograma. Ela ilustra o que percebemos ao olhar para o gráfico, o intervalo de valores em torno de \(61\%\) é o de maior chance de ocorrência!
Mas, existe um fator muito importante que determina a nossa rejeição ou não rejeição de uma hipótese. Nós precisamos definir o nível de significância do nosso teste antes de fazer a análise. Isto porque é a partir dele que vamos saber o que podemos considerar “provável” ou não. O nível de significância é representado pela letra grega \(\alpha\) (alpha).
Então, quando decidimos a qual nível de significância estamos trabalhando, teremos uma noção de quão pequeno o p-valor deve ser, para termos resultados estatisticamente significativos. Na prática, o alfa é um ponto de corte para a rejeição da hipótese nula. Podemos traduzir toda essa explicação em:
Se o p-valor menor ou igual a \(\alpha\): rejeitamos a hipótese nula em favor da alternativa.
Se o p-valor maior que \(\alpha\): não rejeitamos a hipótese nula.
No caso do exemplo, vamos supor que $ = 5%$, o que implica em um Intervalo de Confiança de \(95\%\). Mas poderiam ser utilizados outros valores, como \(90\%\), \(98\%\), \(99\%\), ou outros.
Assim, finalizamos o nosso teste de hipóteses para a intenção de votos no candidato Rui Costa. Poderíamos fazer o seguinte enunciado: O candidato Rui Costa afirmou que teria \(63\%\) de intenção de votos na disputa eleitoral. Queremos verificar se esta informação é verídica, utilizando dados da pesquisa de intenção de votos realizada posteriormente. Portanto, queremos testar se a intenção de votos para o candidato Rui Costa é \(63\%\) à um nível de significância (\(\alpha = 5\%\)).
H0: A proporção de votos para o candidato Rui Costa é \(=\ 63%\).
H1:A proporção de votos para o candidato Rui Costa é \(<\ 63%\).
Assim, nossa resposta a este teste poderia ser: A um nível de significância α = 5%, nosso resultado é estatisticamente significativo (p-valor \(= 2,2\times10^{-16}\)). Concluímos que a intenção de votos para o candidato Rui Costa não será igual a \(63\%\). Segundo o p-valor obtido no teste, rejeitamos a hipótese nula.
E por que não dizer que aceitamos a hipótese alternativa? Bom, basicamente, a nossa motivação e análise do teste foi feita para H0, lembra? Por isso, nossa conclusão também deve ser relacionada a essa hipótese.
E com isso, vimos que a afirmação do candidato estava equivocada e, como foi comprovado e divulgado depois, a intenção de votos para ele é \(61\%\), um valor menor do que o testado!
8.4 Verificando a normalidade
Você já sabe a importância da normalidade, mas já parou pra pensar que precisamos garantir que estamos trabalhando sobre a hipótese da normalidade? Para isto, podemos utilizar ferramentas como a interpretação gráfica ou podemos testar estatisticamente os dados para verificar se a distribuição é de fato Normal.
8.4.1 Gráficos de normalidade: Histograma e Q-Q Plot
No exemplo da pesquisa eleitoral você viu o Histograma. Pois bem, ele é a primeira ferramenta que pode ser aplicada para verificar a normalidade da distribuição de variáveis. Nesse sentido, observamos que a curva apresentada tende a se assemelhar com o formato de um sino, um valor que ocorre mais vezes, assim como vimos na Figura 8.5 cujo valor central é 0.61.
Uma outra forma gráfica bastante utilizada é o Q-Q Plot. Observe a Figura 8.7, o qq-plot dos dados do nosso exemplo. No eixo y indicam-se os valores obserbados na amostra e no eixo x indica-se os quantis teóricos padronizados. Isso significa que ao fazer um qqplot de um conjunto de dados, estamos comparando os valores reais com os valores teóricos ou seja, valores que ocorreriam caso a distribuição dos dados fosse normal. Quanto mais próximos os os pontos estiverem da reta vermelha maior a probabilidade de estejam seguindo a distribuição é normal.
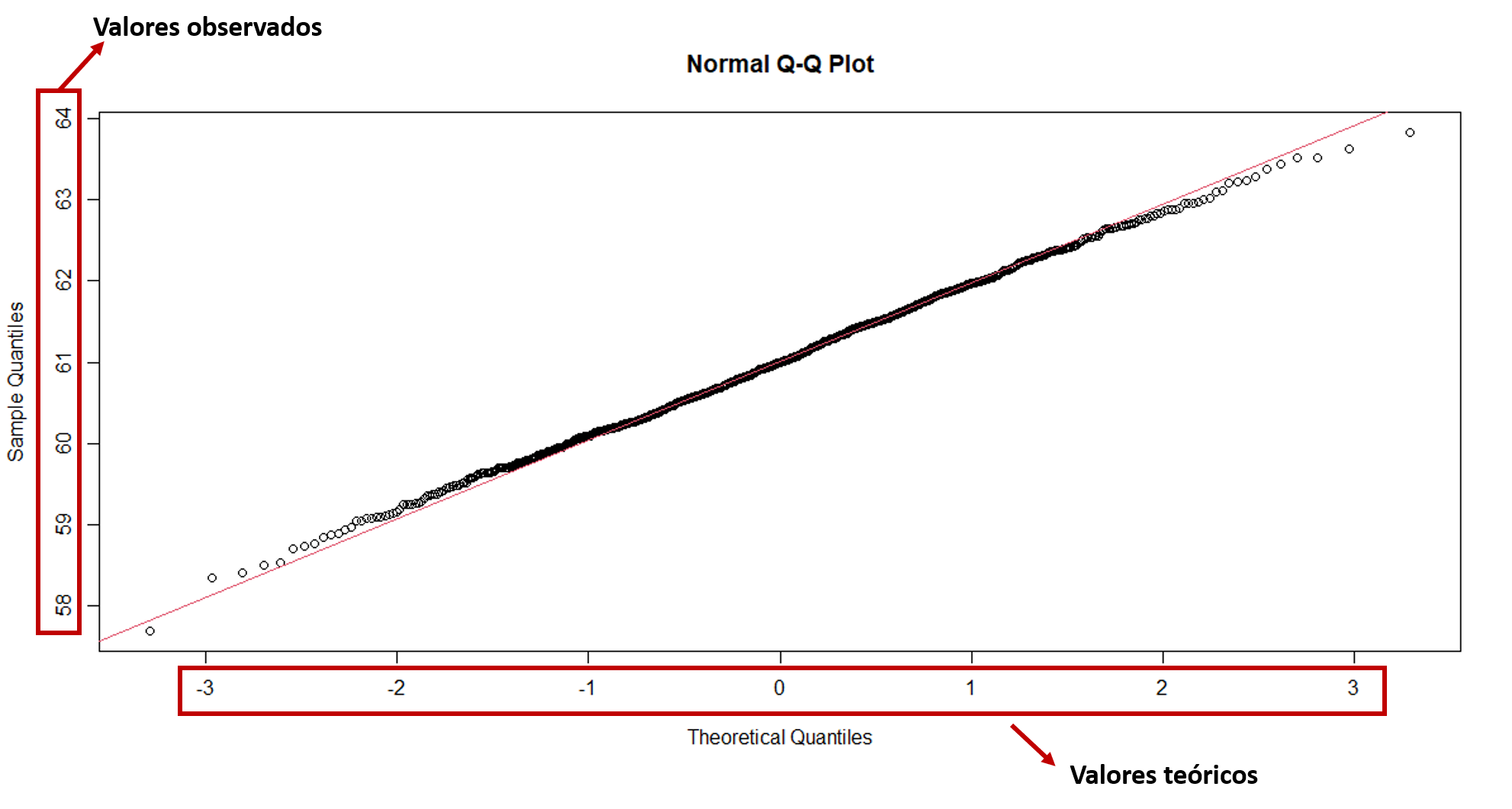
Figura 8.7: q-q plot de distribuição normal
Mas, e quando observamos outras distribuições? Naturalmente, o perfil visual verificado graficamente será diferente do observado acima. A figura abaixo mostra um exemplo de formato de uma distribuição que não apresenta o perfil de normalidade.
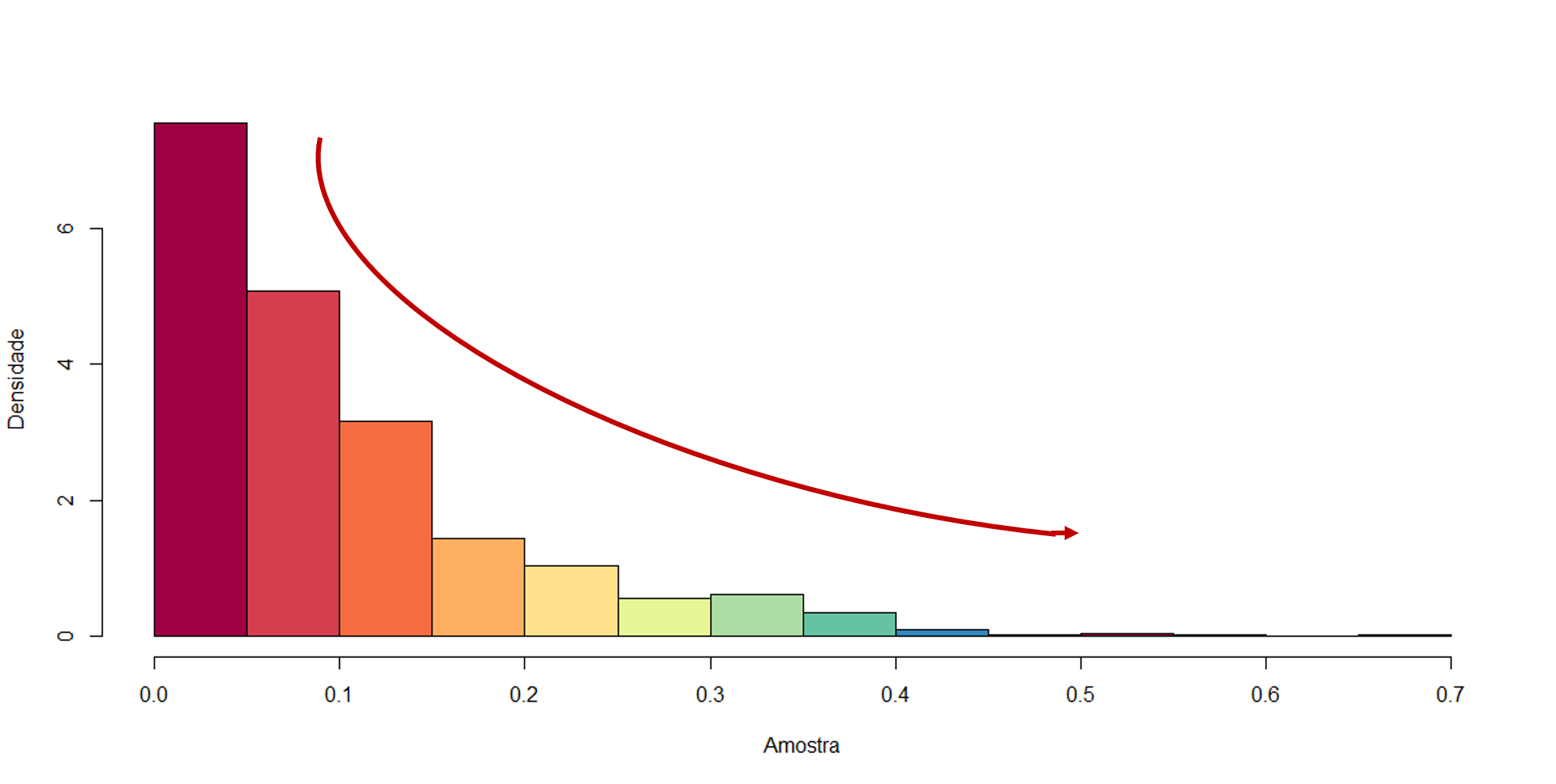
Figura 8.8: Formato da distribuição Exponencial
O qq-Plot desses dados segue o seguinte formato:
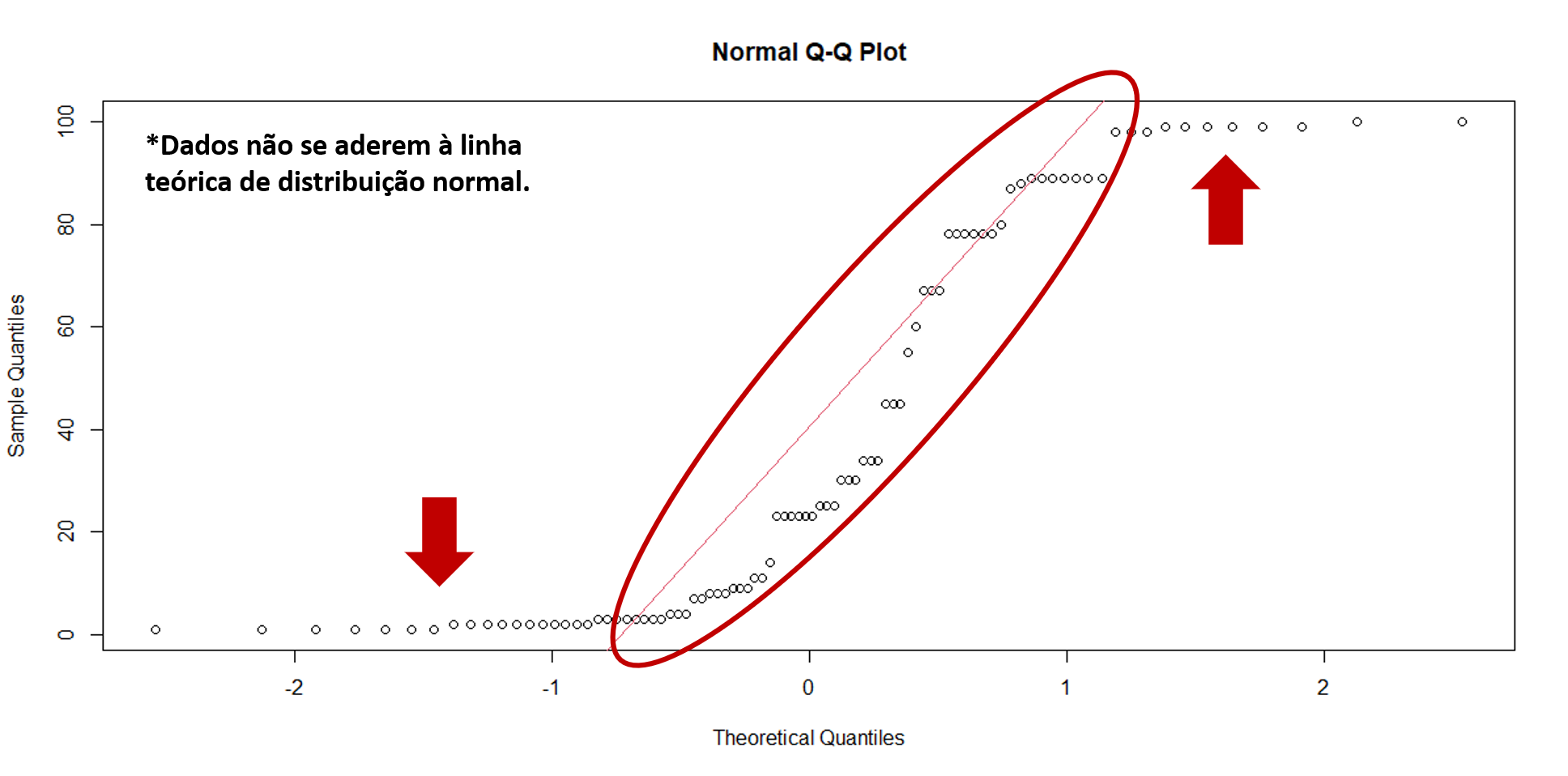
Figura 8.9: q-q plot disrtibuição não normal
Compare a Figura 8.9, com a Figura 8.7 e perceba as diferenças em como os pontos se ajustam à linha vermelha. Essa linha indica teoricamente onde os pontos deveriam estar se os dados seguissem uma distribuição normal. Por isso, na Figura 8.7 vemos uma aderência à linha, que não é vista na Figura 8.9.
Apesar de ser visualmente possível detectar uma distribuição normal, essa forma de análise não é a mais segura. Isso porque há muitas variações no perfil geral dos gráficos, que nos faz acreditar que uma distribuição é normal, quando na realidade pode não ser. E sabe como comprovar de forma confiável? Através do teste de normalidade. O teste de normalidade é complementar à análise gráfica.
8.5 Testes de normalidade
Os testes de normalidade são importantes porque verificam a normalidade de dados através de cálculos estatísticos. Esta opção é mais segura por não ser subjetiva como a análise gráfica.
Existem vários testes de normalidade que dependem do tipo de dados considerados e tamanho da amostra. Shapiro Wilk, Kolmorogov-Smirnov, Anderson-Darling, são alguns dos testes de normalidade mais aplicados. Em geral, quanto maior a amostra, mais esperamos que a distribuição siga um perfil normal, de acordo com o Teorema do Limite Central.
Os testes de normalidade são definidos a partir de hipóteses! Na realidade, testes de normalidade são testes de hipóteses sobre a normalidade da população de onde a amostra foi retirada. Assim, vamos fazer duas aplicações do teste de normalidade de Shapiro Wilk para \(\alpha = 5\%\), cujas hipóteses são:
H0: a amostra provém de uma população normal
H1: a amostra não provém de uma população normal
Vamos iniciar fazendo o teste para para o conjunto de dados da Figura (fig:figura88). Esse teste nos fornece como resultado a estatística do teste, indicado por \(W = 0,81389\), e o p-valor do teste é \(2.727\times10^{-9}\). Lembre-se das nossas condições para o p-valor: se ele for menor que o nível de significância, temos evidências para rejeitar a hipótese nula! Portanto, o nosso p-valor que é praticamente 0 é menor do que \(0,05\), o que nos leva a rejeitar a hipótese nula H0 do nosso teste, trazendo evidências à favor do argumento de que nossa amostra não provém de uma população normal.
E para o caso da pesquisa de intenção de votos? Bom, neste caso, vamos testar a normalidade para \(\alpha = 5\%\), as hipóteses são as mesmas:
H0: a amostra provém de uma população normal
H1: a amostra não provém de uma população normal
O resultado obtido do parâmetro do teste foi de: \(W = 0,99895\), com p-valor \(= 0,8448\). Como vemos, o nosso p-valor é maior que o nível de significância \(0,05\), portanto não rejeitamos a hipótese nula! Ou seja, nossa amostra realmente provém de uma população normal.
8.6 Uma breve contextualização!
Após uma longa explicação, é possível que você ainda se pergunte de que forma todos os conceitos vistos aqui serão utilizados. Por isso, este tópico traz uma breve discussão sobre como os artifícios estatísticos são aplicados em conjunto para direcionar a tomada de decisão! Ainda sobre uma pesquisa eleitoral, ao verificar a Figura 8.10, vemos que abaixo dos títulos há outras informações relevantes: Margem de erro e Nível de Confiança.
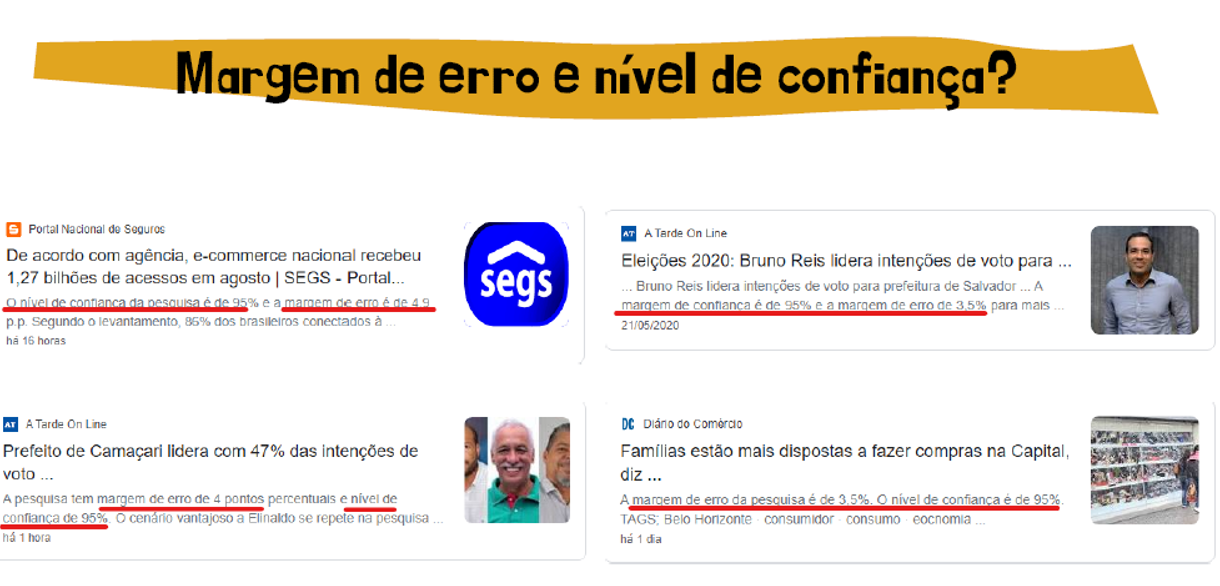
Figura 8.10: Dados fictícios
Vamos entender primeiro o que é a margem de erro. Como o próprio nome diz, esse valor mede quão exato é o resultado de uma pesquisa. No capítulo 6, você aprendeu o processo de coleta de dados para pesquisas e viu que ele está sujeito a erros, lembra? Pois bem, você também deve se lembrar que trabalhamos com uma amostra porque não conseguimos abranger toda a população de interesse. Por isso, a margem de erro indica a estimativa máxima de erro da pesquisa. Se ela aumenta, a nossa confiança na pesquisa acaba sendo reduzida. Para reduzir a margem de erro, uma alternativa é aumentar o tamanho da amostra, de forma que os resultados fiquem mais confiáveis.
Veja na Figura 8.10 o exemplo do prefeito de Camaçari, que liderava as pesquisas com \(47\%\) das intenções de voto, com margem de erro de 4 pontos para mais ou para menos e, nível de confiança \(95\%\). Como interpretar essa informação?
Bom, se ele tem \(47\%\) das intenções de voto, mas a uma margem de erro de \(4\%\) para mais ou para menos, significa que a intenção de votos para ele pode variar de \(43\%\) até \(51\%\)!
O Intervalo de Confiança (IC) indica quão provável é a pesquisa obter os mesmos resultados se for repetida diversas vezes com uma nova amostra da população. Ou seja, se entrevistássemos outros grupos de pessoas da mesma população (eleitores de Camaçari), teríamos os \(47\%\) de intenção de votos, com \(4\%\) de margem de erro? O valor \(95\%\) indica justamente isso, que em \(95\%\) das vezes o candidato estaria dentro da margem de erro.
Como você já deve ter notado, o IC é um indicativo extremamente importante para análises estatísticas. Tanto que ao longo do capítulo, percebemos a importância de indicar qual o nível de confiança estamos trabalhando. Portanto, não apenas em pesquisas eleitorais, mas em qualquer investigação que você pretenda tomar uma decisão baseada em dados é preciso utilizá-lo.
8.7 Concluindo…
E aí, gostou deste capítulo? Apesar de serem muitos conceitos, lembre-se que eles são essenciais para você desenvolver uma pesquisa, ou ter mais criticidade ao ler notícias que divulgam resultados de pesquisas. Para te auxiliar a fixar os conteúdos discutidos, a Figura abaixo traz uma síntese dos principais aspectos tratados neste capítulo! E assim, finalizamos mais uma etapa de aprendizado, até a próxima!!!

Figura 8.11: Síntese de conceitos
8.8 Indo além
Foi realizada uma pesquisa para verificar a idade média dos estudantes da modalidade EJA (Educação para Jovens e Adultos) em uma escola de Salvador. Um estudo antigo apontou que a idade média da turma era de 38 anos e, atualmente, os professores têm suspeitado da presença predominante de estudantes mais jovens. Foi utilizada uma amostra aleatória de 30 elementos para a investigação.
Como você definiria as hipóteses do seu teste?
Qual o elemento essencial para definir o que será considerado estatisticamente significativo?
Foi realizado um teste de normalidade nos dados de idades coletadas e os resultados foram: \(W = 0,97135\) e p-valor \(= 0,557\), à \(95\%\) de confiança. O que você pode concluir?
A média amostral das idades é 43 anos. Sabe-se que o teste de hipóteses teve p-valor de \(0,9841\), a nível de significância \(95\%\). Qual a sua conclusão?