Capítulo 4 Correlação e Causalidade

Seja em situações da nossa vida cotidiana, seja no desenvolvimento de pesquisas científicas, os questionamentos são o ponto inicial para qualquer tipo de investigação. Nossa mente naturalmente busca padrões, ainda que eles não existam. Por conta disso, antes de tomarmos uma opinião como verdade, aplicar conceitos estatísticos em nossas investigações permite avaliar respostas obtidas com segurança a fim de embasar nossas conclusões. Para isso, uma forma muito comum de avaliação é a análise de correlação entre variáveis, que vamos aprender nos próximos tópicos!

4.1 O que é correlação?

Dizemos que há correlação, quando verifica-se uma relação de associação entre duas variáveis! Nesse caso, é possível verificar para as duas variáveis, ao mesmo tempo, uma tendência de comportamento. Para entender melhor, imagine que estamos avaliando se pessoas com maior massa corporal (kg) consomem mais água durante o dia. Caso essa hipótese seja confirmada, significa que a depender da massa corporal do indivíduo, a quantidade de água ingerida irá variar. Assim, o estudo de correlação busca descobrir se variações em uma característica (variável) se associam a variações em outra característica. Para auxiliar no entendimento, vamos iniciar nossa discussão com um estudo de caso de desempenho de atletas de vôlei! Poderemos analisar quais variáveis estão associadas à pontuação das partidas de vôlei. A base de dados utilizada foi adaptada de https://www.kaggle.com/code/beyzanurarslan/best-women-volleyball-players-eda-visualization/notebook, que traz dados das top 30 jogadoras de vôlei para o ano de 2019. A variável “Ranking Geral” trata a pontuação de todos os anos. Na Tabela 4.2 é possível observar todas as variáveis da nossa base de dados, para as cinco primeiras observações. Perceba que existem variáveis numéricas e também categóricas.

Figura 4.1: Tabela de dados do desempenho das 30 melhores jogadoras de vôlei de 2019

Para seguir a convenção estatística, denominamos “Ranking Geral” como variável resposta ou dependente ou ainda, variável Y. O comportamento dela pode estar associado às alterações das outras variáveis da tabela. As demais variáveis são denominadas de variáveis independentes, ou ainda, variáveis X, pois a variação delas poderá causar uma resposta na variável Y.

Ao verificar a parte dos dados exibida na Tabela 4.1, sem qualquer informação prévia, qual destas variáveis você acredita que mais influencia o Ranking Geral?

Um levantamento bibliográfico indicou que alguns estudos de correlação foram realizados em relação a aspectos que podem afetar o desempenho de jogadores de vôlei. Diferentes variáveis diferentes foram avaliadas, deixando claro o potencial da análise de correlação como ferramenta para gerar melhorias e estratégias de treino.

Um estudo de Crivelin et al., 2015 indicou alta correlação entre a composição corporal de jogadores (variável X) e a altura do salto em cm (variável Y).

Outro estudo (de Marques Júnior, 2015) verificou alta correlação entre o ataque, bloqueio e saque para a realização de pontuação ao longo de uma partida de vôlei.

A Correlação (ou associação) linear pode ser definida pelo seu sentido e ser visualizada em um Diagrama de dispersão. Assim, ocorrem três formas distintas de correlação:

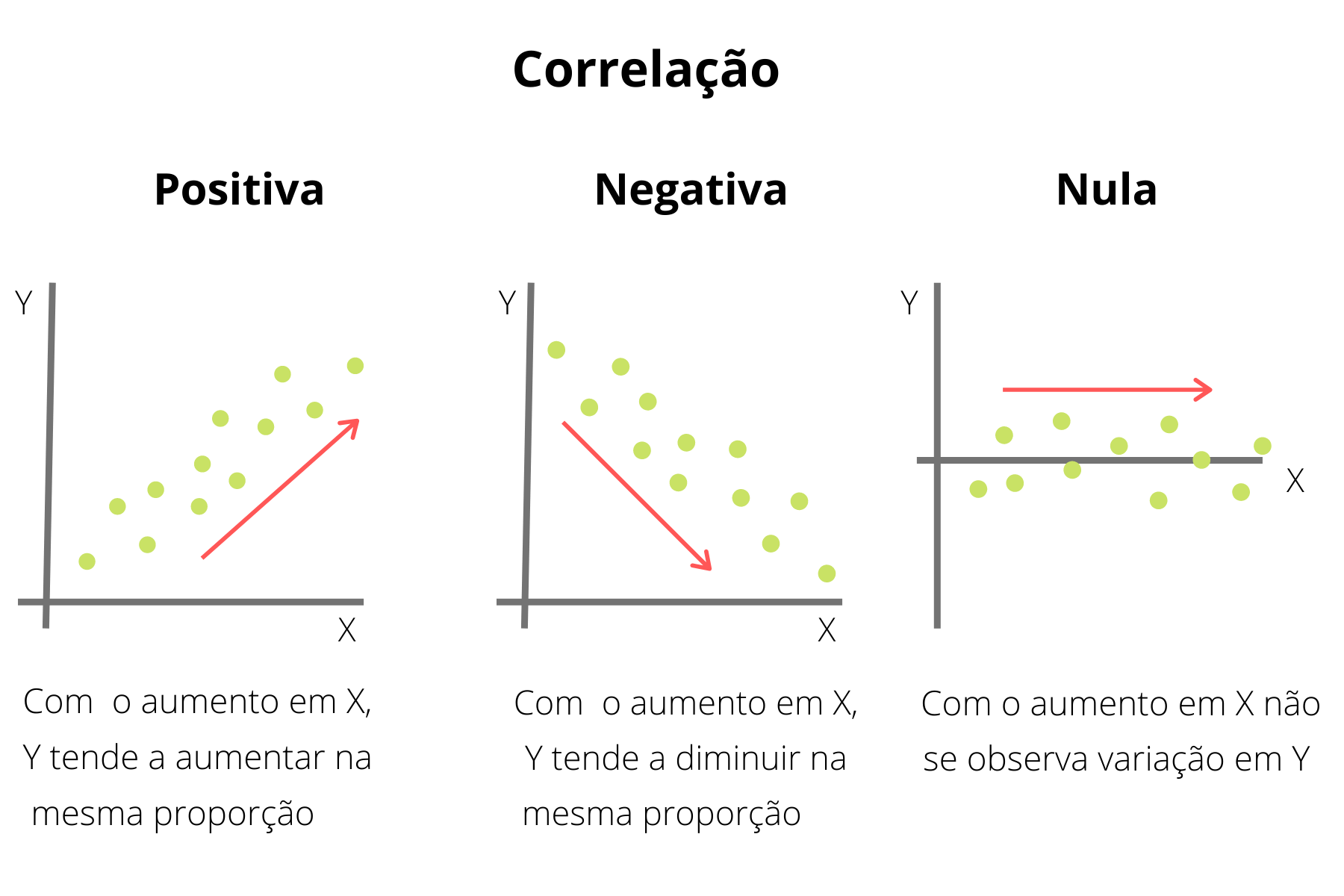
Figura 4.2: Tipos de correlação

4.2 Quão forte é a correlação?

Além do sentido, uma forma de melhor entender a correlação é através da análise do grau ou intensidade que ocorre. Essa intensidade é avaliada a partir do coeficiente de correlação, um valor numérico que indica o grau e a direção da associação entre as variáveis. Vamos comentar dois métodos de obtenção do Coeficiente de Correlação. Todavia, é importante você saber que existem outras formas de se verificar o coeficiente de correlação e a escolha irá depender das características verificadas na sua amostra.

4.2.1 Coeficiente de Pearson

Esse coeficiente é representado pela letra r e também pode ser chamado de correlação linear ou r de Pearson, e expressa o grau de correlação linear entre variáveis numéricas . Seus valores se situam entre -1 e +1, e a interpretação ocorre da forma indicada na Figura 4.3. Se a correlação é 0, significa que não há associação linear entre as variáveis. Quando o valor do r de Pearson é 1, independente do sentido, dizemos que esta correlação é perfeita, por ser a mais forte possível. Quanto mais próximo de zero, menor é a correlação. Vale lembrar que esse coeficiente expressa o grau de associação entre duas variáveis quantitativas.

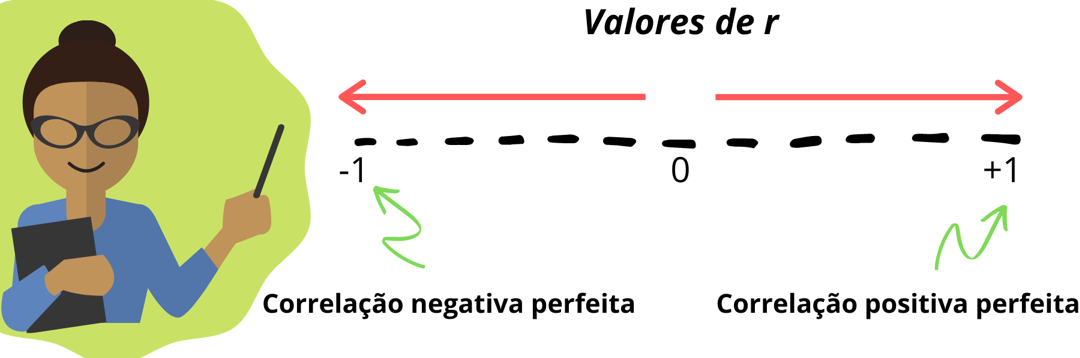
Figura 4.3: Coeficiente de Pearson

Já sabemos que o valor 0 indica que não há correlação linear, e que o valor de 1 indica o maior grau dessa estatística. Mas, como classificar os outros valores encontrados? Observe a Figura 4.4 abaixo, que é uma das formas de classificação da correlação de Pearson:

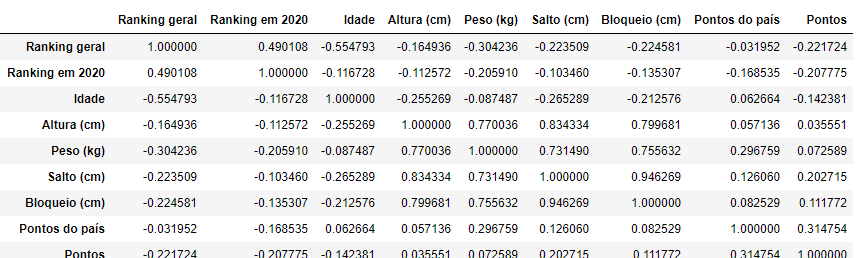
Figura 4.4: Gráfico de dispersão

Para entender melhor, vejamos então qual o valor do coeficiente de Pearson (r) para a nossa variável dependente “Ranking Geral” e a variável independente “Altura”.

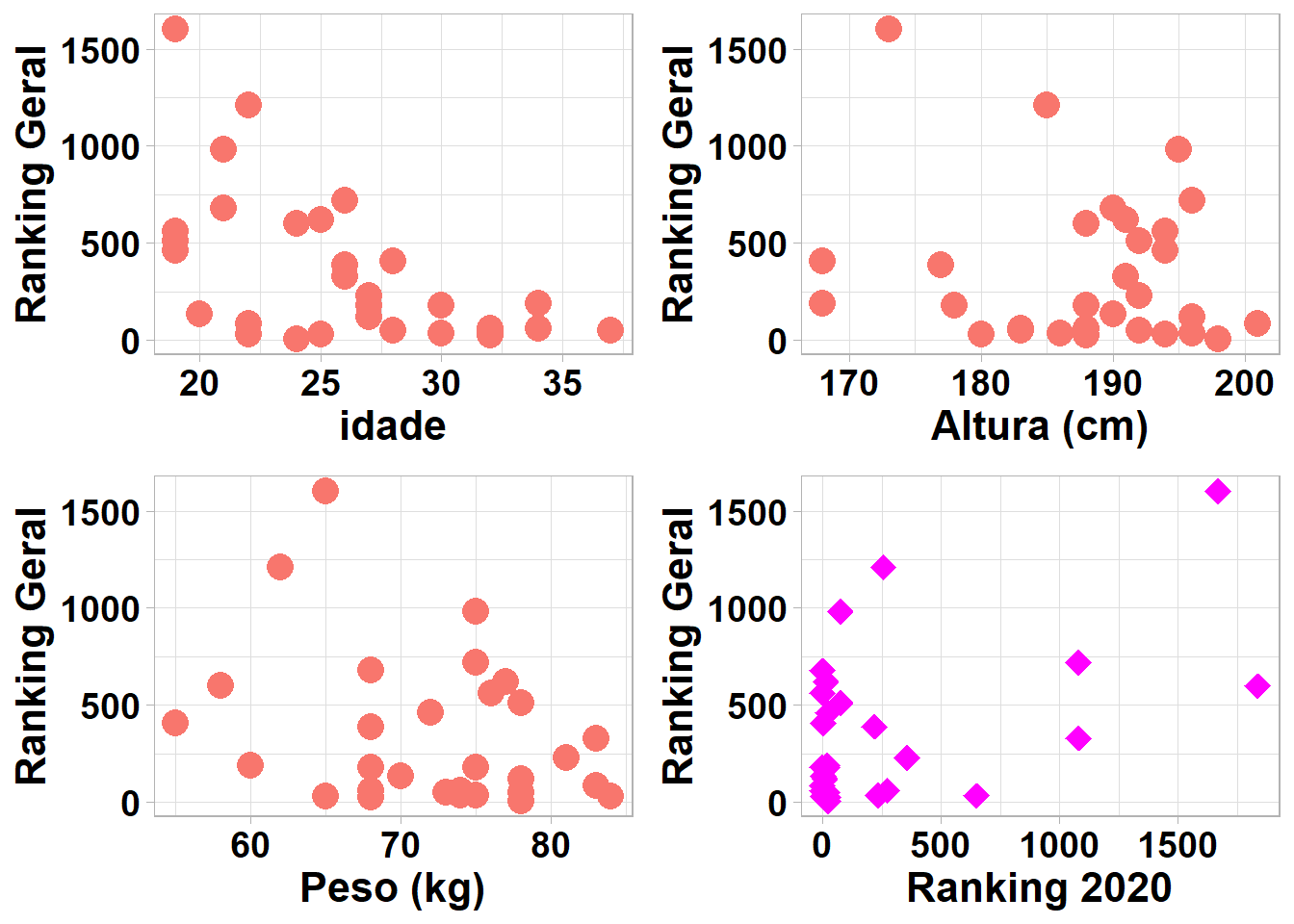
Figura 4.5: Hierarquia de valores - Correlação de Pearson

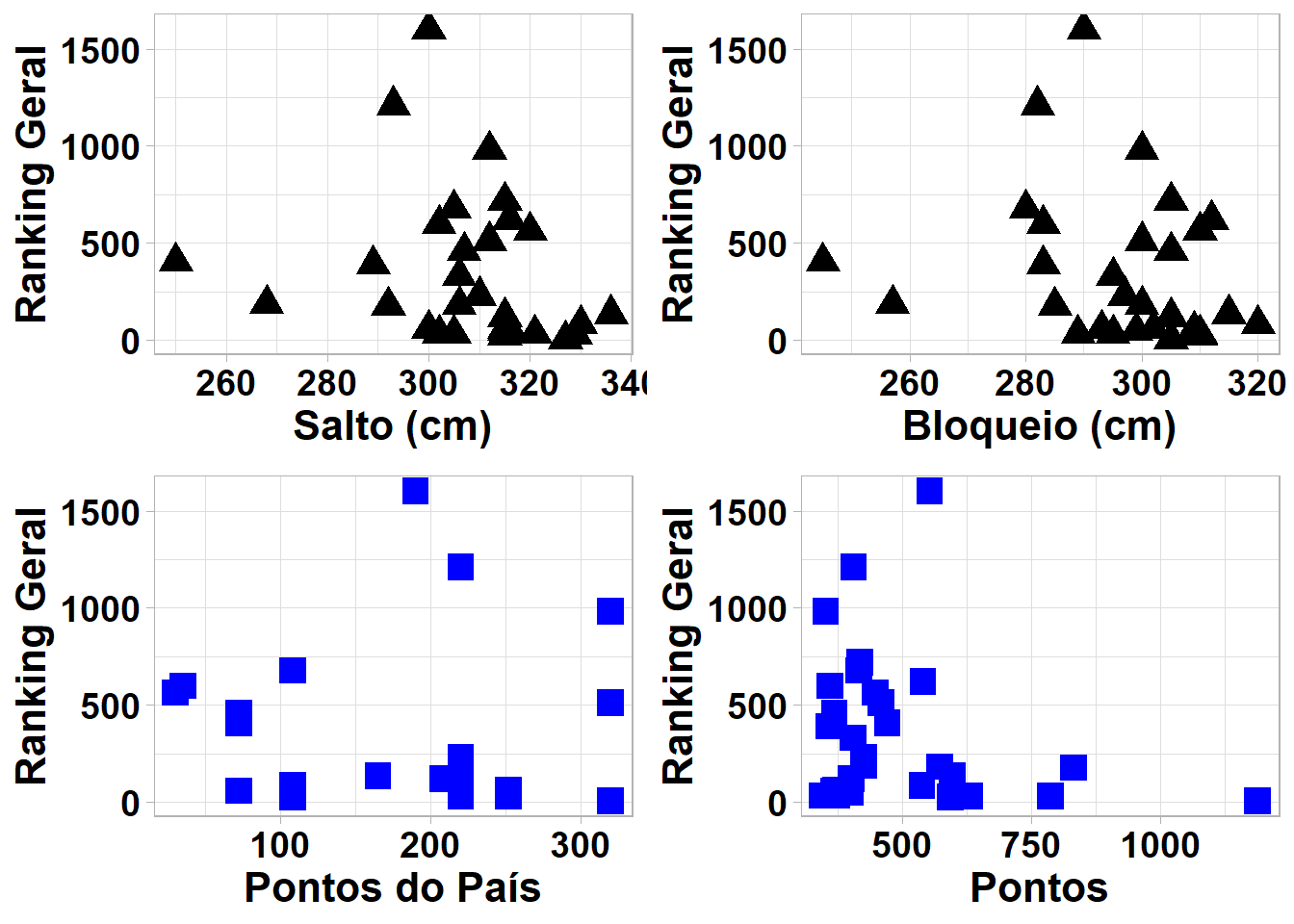
Figura 4.6: Hierarquia de valores - Correlação de Pearson

Observe que o gráfico (Ranking Geral vs Altura) mostra pontos bastante dispersos, onde não é possível verificar uma tendência linear. Assim, visualmente identificamos um comportamento que indica uma correlação muito fraca entre essas variáveis. Isso se confirma ao verificarmos que o valor da correlação é \(-0,16\). Ou seja, o fato de a altura das jogadoras variarem tem muito pouca ou quase nenhuma relação com o Ranking Geral das jogadoras. Podemos fazer essa análise para as demais variáveis independentes, o que gera vários gráficos de “Ranking Geral” versus variáveis independentes, como indicado na Figura 4.4.

E aí, o que você percebeu para as outras variáveis independentes? Bom, é possível notar que os valores das alturas de bloqueios ou saltos são altos e a maior parte dos pontos observados se encontram abaixo do Ranking Geral de 800. Apesar disso, não verificamos evidências de associação entre essas variáveis.

Essa mesma situação ocorre para as outras variáveis independentes, que pela análise gráfica nos dá indícios de que a correlação entre as variáveis independentes e a dependente é baixa.

Quando tratamos de um problema que considera mais de uma variável independente, como ocorre no nosso caso, é comum optarmos por verificar o grau de associação por meio de uma Matriz de correlação. Nesse caso, a matriz de correlação irá indicar o grau de associação entre todas as variáveis da base de dados.

Como comentado anteriormente, a variável independente “Idade” apresenta uma associação negativa e muito fraca com a variável dependente “Ranking Geral”. Observe como a associação entre essas variáveis é representada na Figura 4.7, onde a matriz de correlação é exibida.

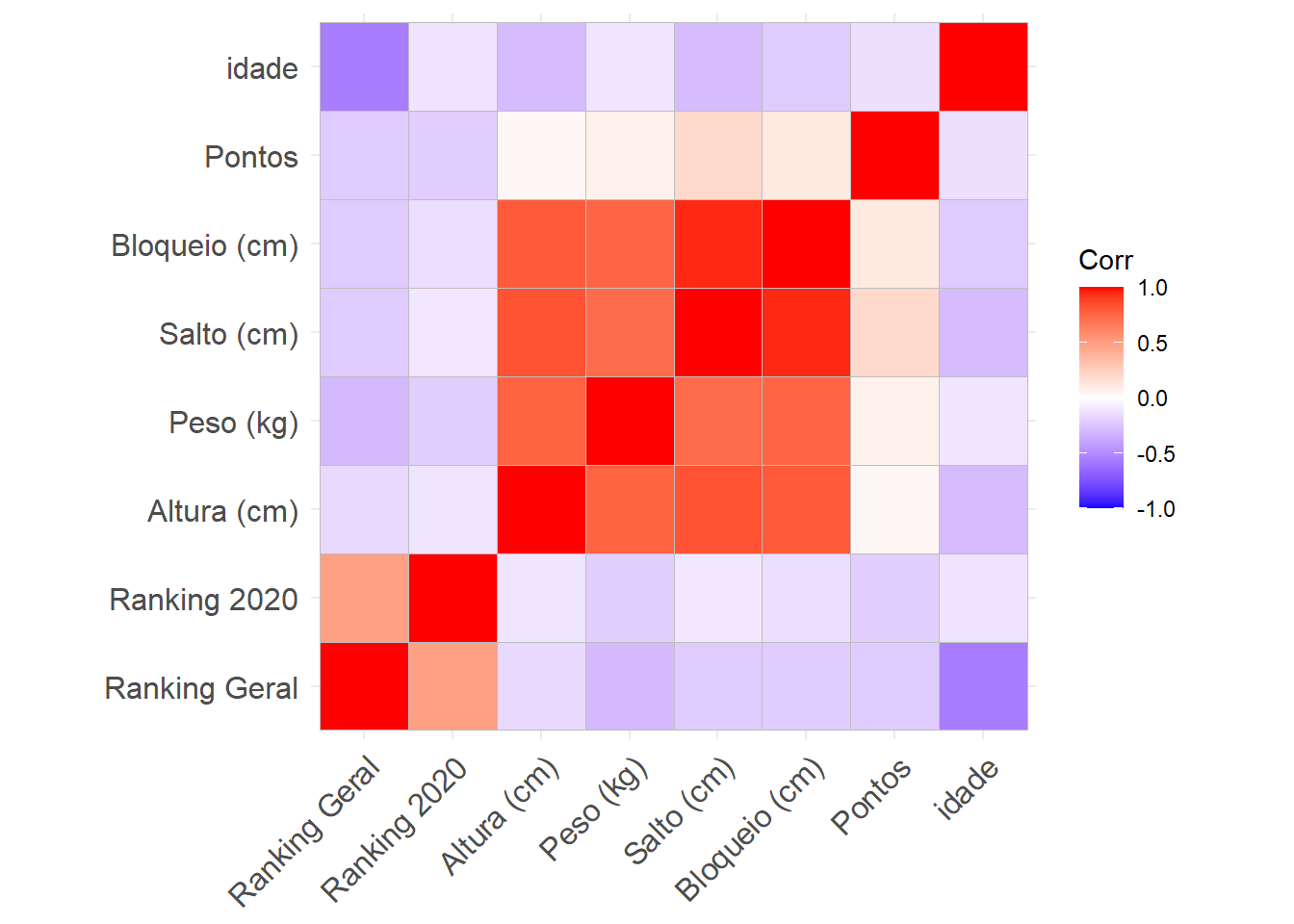
Figura 4.7: Hieraquia de valores - Correlação

Analisando a matriz de correlação, observamos que o quadrado que indica a associação entre Ranking Geral e Idade apresenta um tom de verde claro. Ao verificar na legenda, compreendemos que os tons de azul sólido são usados para indicar correlações positivas e os tons de azul claro a verde claro indicam correlações negativas.

Verificamos também, que o valor da correlação de Pearson entre Ranking Geral e Ranking 2020 é \(0,49\), representado por um tom de azul escuro. Isso indica que há uma relação linear moderada positiva, em que quanto maior a posição de uma jogadora no ranking de 2020, pode-se acreditar que sua posição no ranking geral também será maior. Da mesma forma, para as jogadoras que se mantêm nas top posições de Ranking em 2020 há uma chance que também estejam entre as top posições do Ranking geral.

A vantagem de se utilizar essa forma gráfica é que ela torna possível identificar se mesmo as variáveis independentes possuem um grau de associação entre si, como é o caso de Altura x Peso, Salto x Peso e Bloqueio e Salto. Observe o centro da imagem da matriz de correlação, em tons de azul escuro. Individualmente Altura, Peso e Salto apresentam uma associação fraca para a determinação do Ranking Geral, mas entre si apresentam um alto grau de associação. Por exemplo, de acordo com a matriz é possível ponderar que quanto mais alta espera-se que a jogadora tenha maior peso. Observe que essa é uma relação em que as variáveis se alteram juntas, ambas para o sentido positivo de aumento de valores.

Além dessa situação, a matriz de correlação também pode indicar a autocorrelação, quando a variável se associa com ela mesma. Por exemplo, a variável Ranking Geral será completamente associada a ela mesma, assim como a variável Idade também apresenta uma correlação perfeita com ela mesma. Por isso, quando observa-se na matriz de correlação a relação entre cada variável com ela mesma, será indicado o tom vermelho mais forte da paleta de cores, pois é uma correlação com r igual a 1.

Observe também que a correlação com as outras variáveis têm sentido negativo e são bastante fracas, se aproximando de zero. Desta forma, podemos dizer que estas variáveis praticamente não são relacionadas linearmente à Ranking geral. Ou seja, não percebemos uma tendência que indique associação linear entre estas variáveis, por isso o r de Pearson é um valor próximo ao zero. Mas atenção, isso não significa que essas variáveis não sejam associadas, uma vez que o r de Pearson avalia somente a associação linear. É possível que essas variáveis estejam associadas de modo não linear, o que pode ser observado pelo aplicação de outros critérios de análise, que estão além da discussão deste capítulo.

4.2.2 Relações de causa e efeito: conhecendo a causalidade

De acordo com o dicionário, a palavra “causalidade” se refere à condição ou qualidade do que é causal, do que produz efeito. É uma relação direta entre causa-efeito.Veja estas frases e reflita sobre a mensagem que você compreende.

Pare o aquecimento global: se torne um pirata
Habilidades em linguagens reduzem ataques de raiva na pré escola
Qual a causa de câncer?
chocolate faz bem?

Observe que essas frases passam uma relação imediata de causa e efeito entre as variáveis. Em “a”, dá a entender que é possível parar o aquecimento global ao se tornar um pirata. Mas, será que estas alegações fazem sentido?

Uma relação de causa-efeito pode ser descrita por meio de palavras como impacta, afeta ou efeito. Desse modo, este tipo de relação sugere que uma variável dependente têm alto grau de associação com uma ou mais variáveis independentes. Assim, o fato de uma ou mais variáveis independente ocorrer causa o efeito na variável dependente.

Observe este outro exemplo: Em países do hemisfério norte as pessoas gastam mais em compras no frio. À primeira vista, tendemos a achar que o frio provoca um aumento nas vendas. Porém, se pensarmos um pouco vamos perceber que datas festivas como Natal e Ano Novo nestes países, ocorrem no inverno. Portanto, esta pode ser a causa do aumento das compras.

Ou seja, não podemos simplesmente atribuir uma relação de causa e efeito a um evento, pois podem haver muitos fatores que influenciam este contexto.

4.2.3 Coincidência ou Causalidade?

A única forma de provar uma causalidade é a partir de uma análise detalhada dos dados. Estas análises são realizadas por meio de estudos observacionais ou estudos experimentais aleatórios, em um grupo de indivíduos divididos em: grupo controle e grupo de tratamento. Este último sofre intervenção por algum fator que se deseja analisar. Estes grupos são monitorados nas mesmas condições, e a diferença nas respostas finais são computadas.

Uma questão central para respondermos é se de fato o tratamento aplicado produz efeito na resposta obtida. Caso isto ocorra, a associação é causal. Observe que quando investigamos a causalidade, não queremos saber apenas se há uma associação entre variáveis. Mas sim, se esta relação implica diretamente causa-efeito.

Desta forma, afirmar a ocorrência de causalidade exige a verificação de alguns aspectos:

1 - Observar a correlação entre variáveis (uma vez que quanto maior o grau de associação entre elas, maior a chance de haver uma relação causal)

2 - Análise cuidadosa de causalidade

3 - Temporalidade (a causa sempre ocorre antes do efeito) Algumas situações não permitem a realização de experimentos aleatórios, ainda que seja para verificar a causalidade. Por exemplo, para avaliar os efeitos do consumo de álcool durante a gravidez, é necessário convidar algumas grávidas para o experimento. Mas, isto seria sensato? Em situações desse tipo, deve ser realizado um estudo observacional. Se o grupo de tratamento e o grupo de controle apresentarem diferenças além do tratamento aplicado, tomar conclusões sobre a causalidade se torna algo difícil. Esta diferença é provocada por um fator de confusão, que é uma variável que influencia tanto o efeito quanto a causa!

Vamos entender melhor a partir de um exemplo. Nos anos 60, alguns estudos apontaram que pessoas que ingeriam café tinham altas taxas de câncer de pulmão se comparadas às que não ingeriam. Devido a isto, algumas pessoas começaram a atribuir o café como causa de câncer de pulmão. Porém, hoje sabemos que café não é a causa desta doença! Na verdade, essa análise tinha um fator de confusão: o hábito de fumar. Naquela época, pessoas que ingeriam café provavelmente também tinham o hábito de fumar. E esta prática sim, causa câncer de pulmão. Então, podemos concluir que: o consumo de café estava associado ao câncer de pulmão, porém não é o causador da doença!

A ocorrência de fatores de confusão é bastante comum. Por conta disso, estudos confiáveis buscam reduzir a confusão e saber o quanto ela afeta a análise.

4.2.4 Correlações espúrias

Bom, já aprendemos o conceito de correlação e também sabemos que a correção não implica causalidade. Veja a Figura 4.13 e avalie a tendência entre afogamentos e aparições do ator Nicholas Cage em filmes.

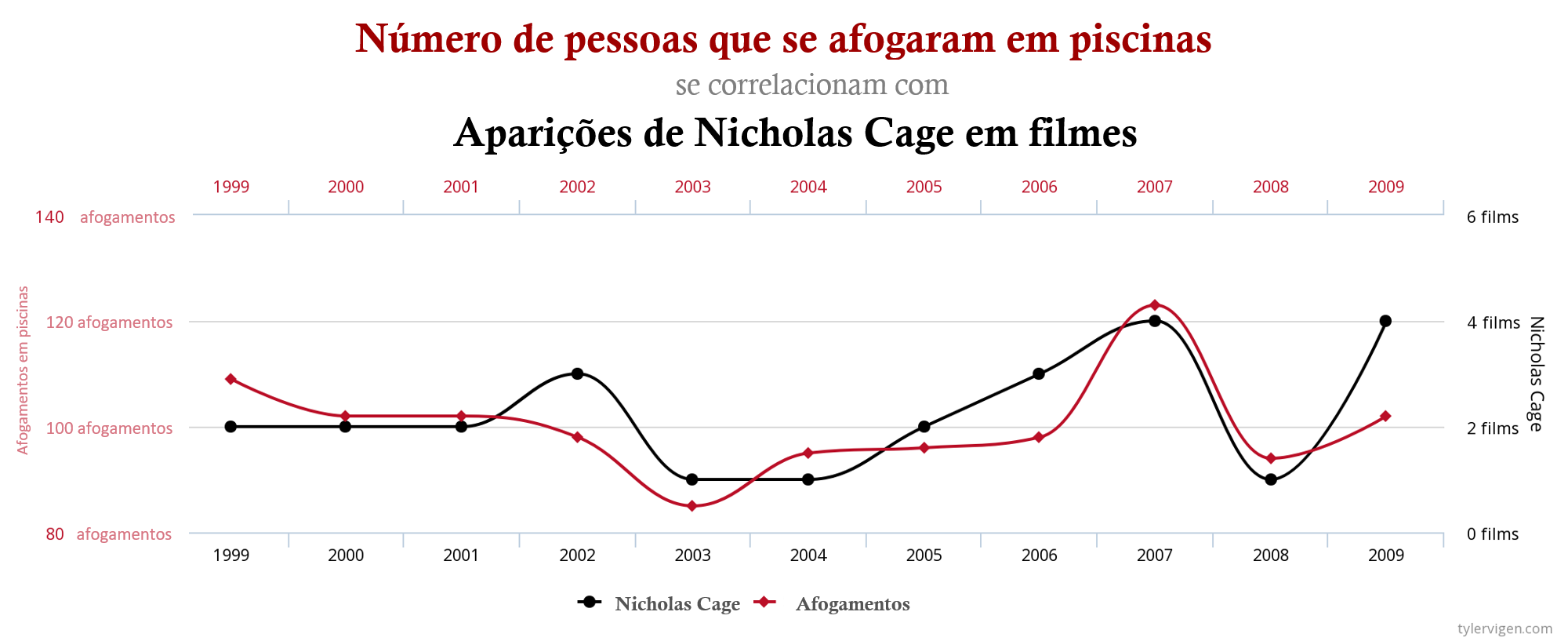
Figura 4.8: Afogamentos e aparições do Nicholas Cage

A associação entre estas variáveis é nítida, não é mesmo? Portanto, claro que elas são correlacionadas (\(r = 0,666\))! E mais, a causa dos afogamentos é a aparição do Nicholas Cage em filmes!

O que acha dessa declaração?

Assim como muitas outras afirmativas questionáveis que ouvimos no dia a dia, essa declaração reflete uma certa negligência à compreensão de Correlação e Causalidade. Ainda que a associação seja visível graficamente, o senso crítico prevalecerá, caso contrário seguiremos acreditando em informações dúbias e tomando decisões incorretas.

Para não sermos reféns deste tipo de conclusão, é necessário conhecer dois fatores que acarretam na conclusão errônea:

1 - Fator de confusão: pode haver uma terceira variável que afeta o resultado, mas que não está sendo considerada.

2 - Acaso: sim, coincidências acontecem e precisamos ter criticidade para avaliar se a informação é lógica.

Uma crítica semelhante pode ser feita ao caso seguinte. Em alguns meses do ano, foi observado que o número de afogamentos aumenta. Ao mesmo tempo, as vendas de sorvete também aumentam! Antes de você refletir, vamos a mais informações. Os meses recorde de afogamentos e vendas de sorvete são Dezembro e Janeiro. Segundo os dados estas variáveis estão correlacionadas positivamente, com um \(r = 0,98\). E mais do que isso, será que poderíamos concluir que as vendas de sorvete causam afogamentos? Errado. Temos uma terceira variável em comum a estas duas, a Temperatura. Em dias mais quentes as pessoas vão à praia, ou tomam sorvete, e com isso, mais pessoas ficam expostas à chances de afogamento. Portanto, neste problema deve ser levado em conta a Temperatura, que está associada aos afogamentos e às vendas de sorvete.

4.2.5 Considerações Finais

Neste capítulo, aprendemos a avaliar afirmações, com embasamento estatístico. A Figura 4.9 exibe um mapa conceitual do que foi discutido.

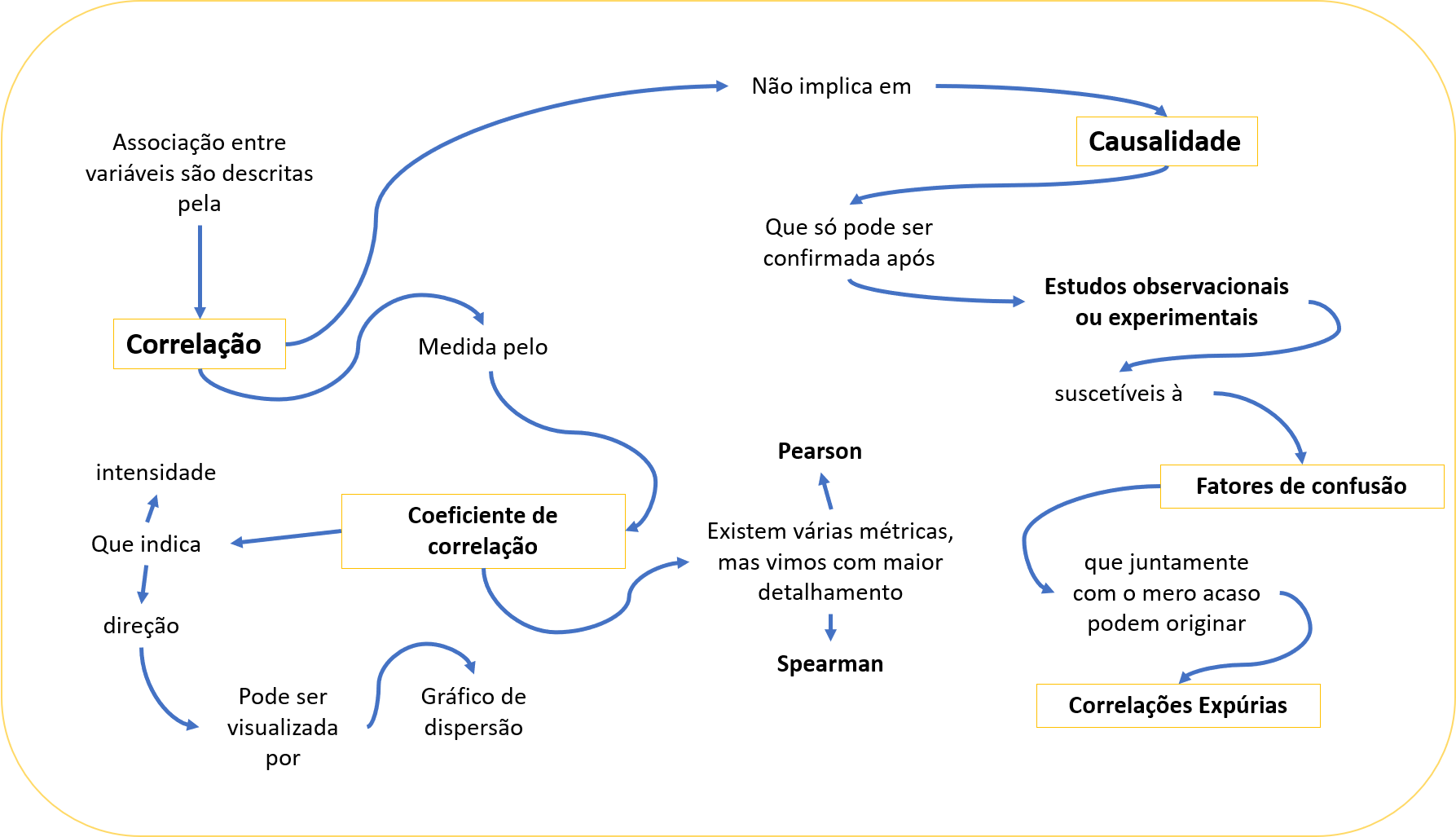
Figura 4.9: Mapa conceitual do capítulo 4

O que achou do tema deste capítulo? Com certeza, a partir de hoje você será muito mais crítico ao ler ou ouvir uma informação. É exatamente isto que buscamos, ter um senso crítico e conhecer formas de análise que garantam a veracidade em relação às informações que chegam a nós! Bons estudos!

4.2.6 Dados das seleções brasileiras

https://en.volleyballworld.com/en/vnl/2018/women/teams/bra-brazil/facts_and_figures

Referências Bibliográficas

1: Correlações espúrias

2: Inferential Thinking. Causality and Experiments. UC Berkeley.

3 : IDS Curriculum v5_0

[4]CRIVELIN, Vitor Xavier et al. Correlação entre altura do salto e composição corporal em atletas profissionais de voleibol. Arquivos de Ciências do Esporte, v. 6, n. 1, 2018.

[5] MARQUES JUNIOR, Nelson Kautzner. Fundamentos que fazem ponto durante o jogo de voleibol: um estudo de correlação. Revista Observatorio del Deporte, p. 134-145, 2015.