Capítulo 5 Indicadores Básicos na Ciência de Dados

Apesar da ciência de dados ser bem conhecida atualmente através das aplicações mais práticas e incríveis da Inteligência Artificial como demonstrado no vídeo abaixo:

Ela está presente de outras formas no dia a dia do brasileiro de forma sutil. Na Figura 5.1 destacamos alguns termos desta área. Consegue identificá-los?

Figura 5.1: Manchetes de jornais com termos da ciência de dados

Os termos grifados são muito recorrentes neste imenso universo que é a ciência de dados e seus conceitos são bem simples de entender, além de práticos!

Porém, você pode estar se questionando “Porque devo aprender mais sobre eles?” ou “Vou usar isso em algum momento da minha vida?”. Questões como essas podem ser comuns durante a aprendizagem e precisam ser endereçadas. A área que é apresentada na Figura 5.1 e que será discutida neste capítulo é chamada de estatística descritiva. Ao estudar os dados, é comum o cientista buscar padrões desconhecidos e resumir grandes quantidades de números em um só valor e é neste aspecto que esta ferramenta simples e eficaz é aplicada.

O nome pode parecer complicado, porém se trata de um ramo da matemática com uma série de técnicas para descrever e resumir dados ou informações em indicadores de fácil compreensão. Essa área pode ser dividida em três grupos de medidas: tendência central, dispersão e forma. Neste capítulo focaremos nas duas primeiras. Além disso, iremos explorar formas de visualização como o diagrama de caixas ou gráfico de distribuições.

5.1 Objeto de estudo

Para compreender a importância dessas medidas estatísticas e como usá-las, vamos estudar os dados de segurança pública da cidade de Salvador disponibilizados pela Secretaria de Segurança Pública (SSP) no portal¹ para compreender um pouco da realidade que Salvador convive em relação à violência. Porém, antes de apresentar nosso tema central de estudo precisamos entender como funciona essa base de dados.

Disponibilizados através de boletins mensais, as ocorrências dos principais delitos na capital baiana são separadas por áreas e regiões. Os principais tipos de delitos considerados são:

• Homicídio Doloso
• Lesão Corporal Seguida de Morte
• Roubo com Resultado Morte (Latrocínio)
• Tentativa de Homicídio
• Estupro
• Roubo a Ônibus (Urbano e em Rodovia)
• Roubo de Veículo
• Furto de Veículo
• Uso/Porte de Substância Entorpecentes (Usuários)

Você viu que eu citei “áreas” e “regiões” certo? Em Salvador, elas são definidas pela SSP respectivamente como Área Integrada de Segurança Pública (AISP) e Região Integrada de Segurança Pública (RISP). Para entender melhor essas divisões, vamos explicar através da Figura 5.2 estes conceitos usando uma abordagem de conjuntos.

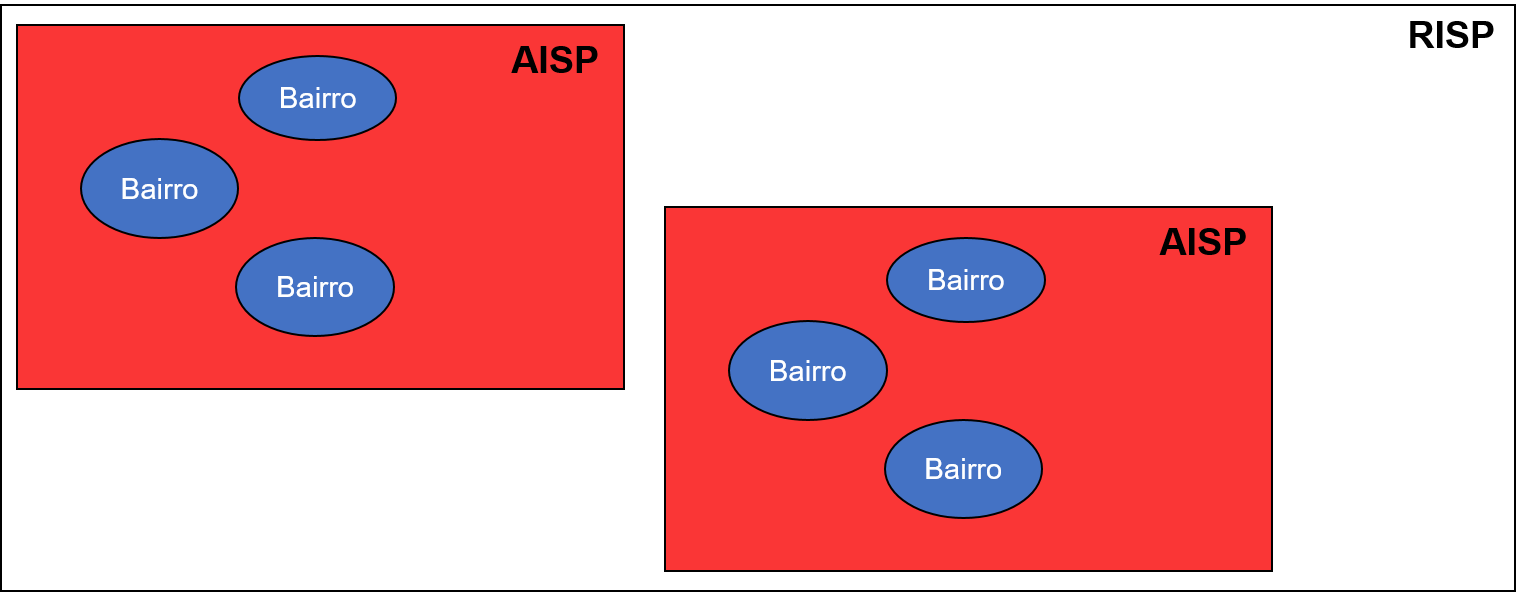
Figura 5.2: Conceito por trás das divisões AISP e RISP

AISP são conjuntos de bairros, ou seja, cada AISP representa uma quantidade de bairros da cidade. Já RISP se trata de um conjunto de AISP e finalmente, o conjunto total de RISP representa toda a extensão da cidade de Salvador. Essa divisão é realizada para facilitar o trabalho dos profissionais de segurança em compreender como cada região se comporta de acordo a um determinado tipo de delito, além de agrupar melhor os bairros, que somam um valor superior a 160 em Salvador. Imagina como seria mais complexo apresentar um plano para cada bairro em específico para um gestor municipal ou estadual?

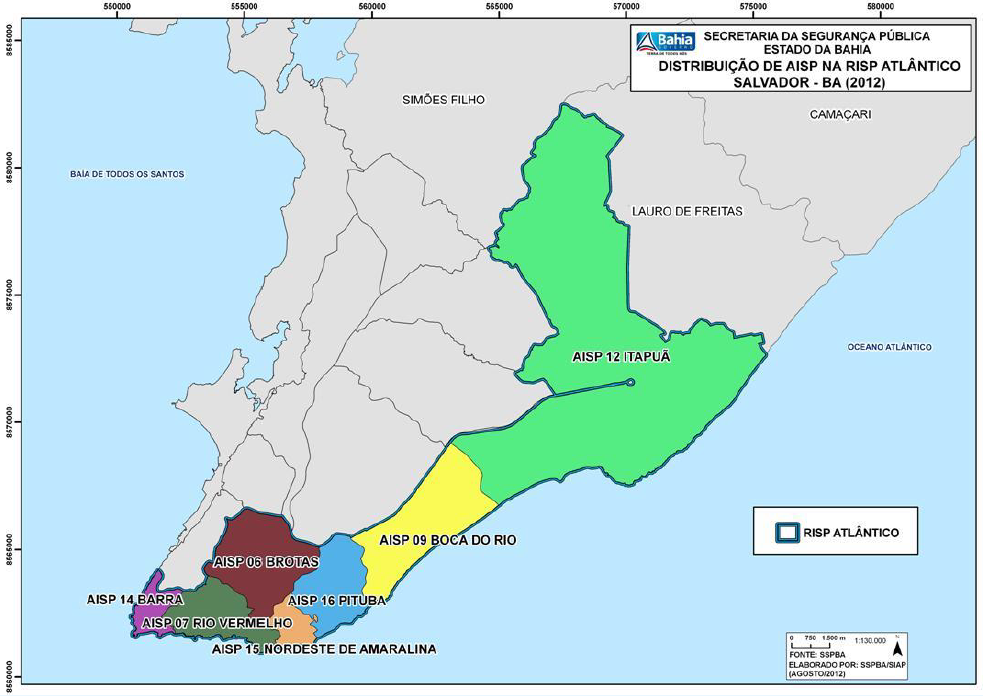
Figura 5.3: RISP Atlântico de Salvador realizado pela SSP

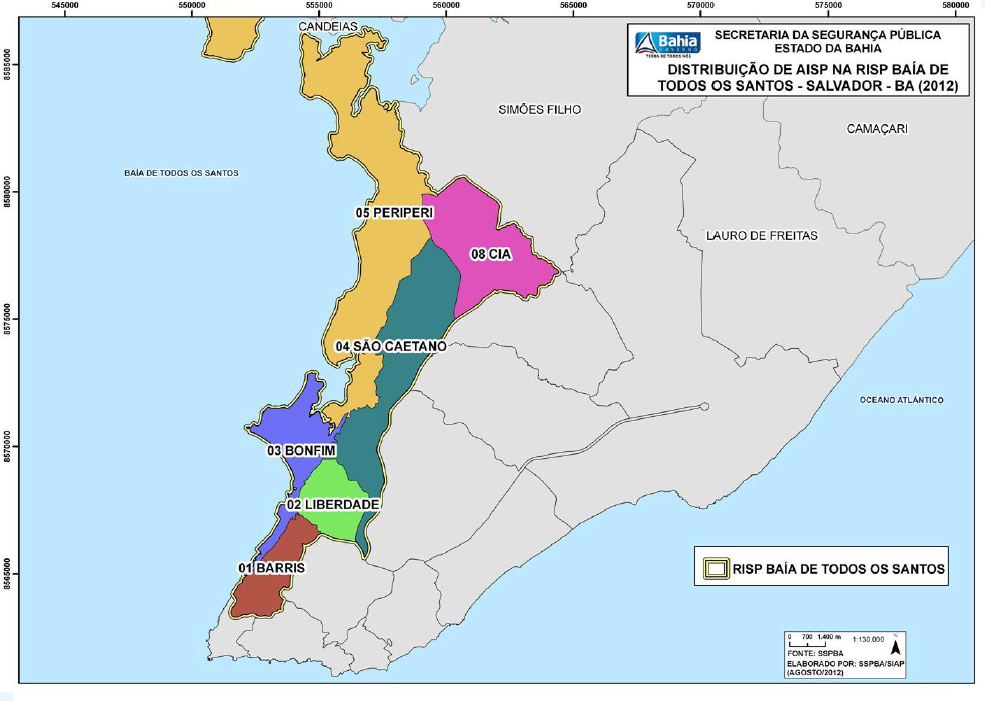
Figura 5.4: RISP Baía de Todos os Santos (BTS) de Salvador realizado pela SSP

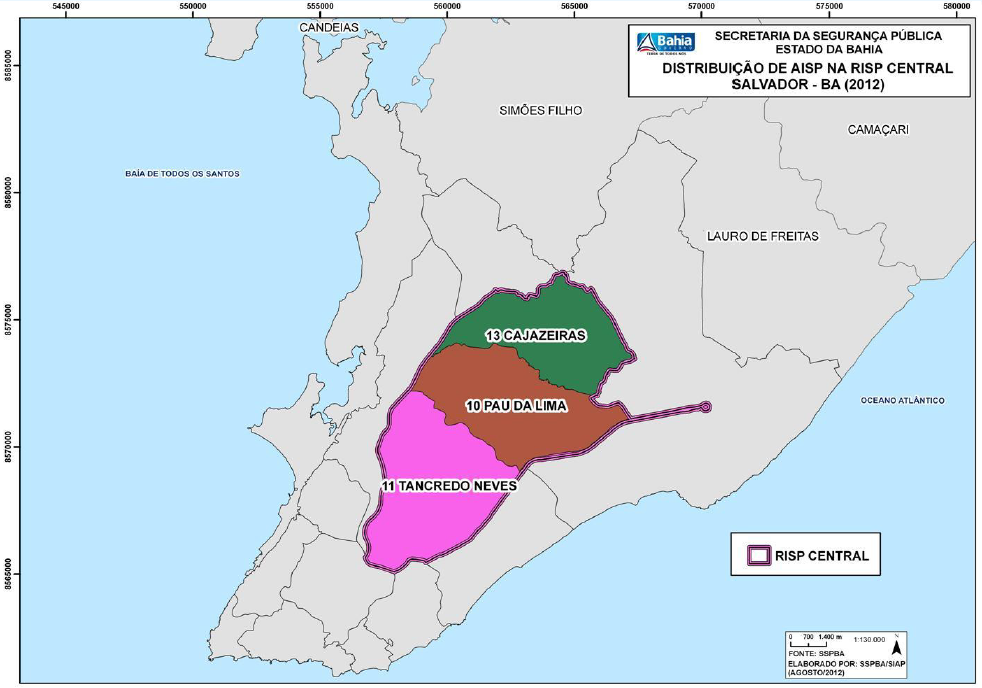
Figura 5.5: RISP Central de Salvador realizado pela SSP

As Figuras 5.3, 5.4 e 5.5 mostram as divisões referentes às AISP e RISP em Salvador. Para contextualizar, a maioria das escolas que participaram do projeto “Meninas na Ciência de Dados” estão localizadas no bairro da Federação e esse bairro está contido na AISP - Rio Vermelho que, por sua vez, está contida na RISP - Atlântico.

Dessa forma, analisaremos especificamente um tipo de delito principal nos meses de janeiro, fevereiro e março de 2019 em Salvador: Roubo a Ônibus urbano e em rodovia. Essas escolhas não foram aleatórias. Os três meses citados foram escolhidos por ser um período de grande movimentação na capital: estação de verão, um dos principais períodos para turismo em Salvador, onde a grande maioria dos trabalhadores entram de férias. Além disso, o delito de roubo a ônibus é uma realidade presente para quem depende do serviço público para se locomover na capital baiana, seja a trabalho, estudos ou a lazer.

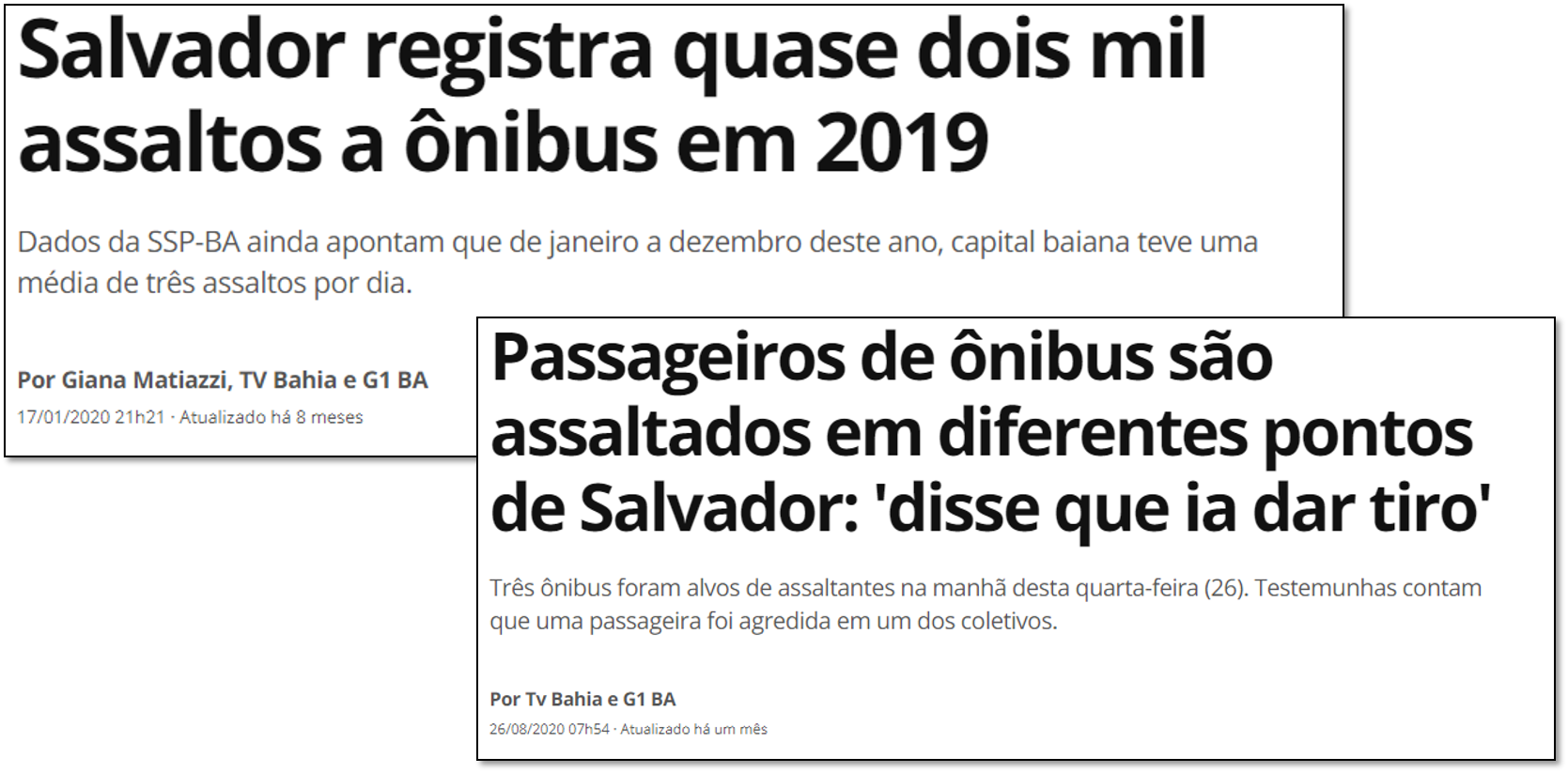
Figura 5.6: Manchetes sobre roubos a ônibus na cidade de Salvador

Na Figura 5.6 podemos verificar uma realidade referente a este crime: em média ocorreram 3 assaltos em Salvador por dia avaliados durante 2019. Neste capítulo, frases como essa serão compreendidas de forma mais simples e intuitiva!

A base de dados referente aos assaltos a coletivos na cidade de Salvador na estação do verão em 2019 é apresentada abaixo:

Tabela 5.1: Ocorrência de assaltos no 1° trimestre de 2019

RISP	AISP	Janeiro	Fevereiro	Março
Atlântico	Brotas	17	6	16
Atlântico	Rio Vermelho	7	10	5
Atlântico	Boca do Rio	5	1	7
Atlântico	Itapuã	17	11	8
Atlântico	Barra	2	2	1
Atlântico	Nordeste	4	1	6
Atlântico	Pituba	13	8	4
BTS	Barris	17	5	10
BTS	Liberdade	8	8	11
BTS	Bonfim	8	12	12
BTS	São Caetano	22	15	16
BTS	Periperi	13	11	20
BTS	CIA	1	1	2
Central	Pau da Lima	5	4	9
Central	Tancredo Neves	40	25	33
Central	Cajazeiras	11	9	6

Na Tabela 5.1 observamos as ocorrências para cada região, sendo que alguns valores são bem alarmantes como a AISP Tancredo Neves com um total de 40 ocorrências de assalto a coletivos em janeiro e 33 em março! Em contrapartida, outras AISP como Barra e CIA apresentam valores muito baixos em comparação, com 1 ou 2 ocorrências.

E se quisermos resumir esses valores para gerar indicadores para uma determinada região (RISP) ou para a cidade no período de Janeiro a Março? Como esses indicadores poderiam ajudar os gestores a entender como está a situação de uma determinada região ou área em relação ao aumento da violência, considerando este delito? E principalmente: Como podemos visualizar e passar estas respostas de forma fácil e intuitiva para gerar ações públicas de combate a esse tipo de delito?

Para responder esses e outros questionamentos, vamos estudar alguns conceitos importantes da ciência de dados como medidas de tendência central, medidas de dispersão, diagrama de caixas e distribuição no decorrer deste capítulo.

5.2 Medidas de tendência central

As medidas de tendência central são aquelas que buscam refletir o ponto de equilíbrio dos dados, ou seja, o seu ponto central. Diversas medidas existem com esse intuito e as de uso mais comum são: média, mediana e moda. Porém, você pode se perguntar “Porque existe mais de uma medida se elas têm a mesma finalidade?” Bom, cada uma dessas medidas possui suas vantagens e desvantagens,e entendê-las é fundamental para compreender aquele conjunto de dados da forma mais coerente com a realidade².

Porém, antes de cair de cabeça nestas medidas vamos avaliar a Tabela apresentada na seção anterior (número de ocorrências de roubo à ônibus) através de um mapa de calor.

Na Figura 5.7 apresentamos um mapa de calor para todas as áreas de Salvador considerando o número de ocorrências, onde quanto mais avermelhada for aquela região, maior é a incidência de delitos e quanto menor for o número de ocorrências mais branca se torna a célula.

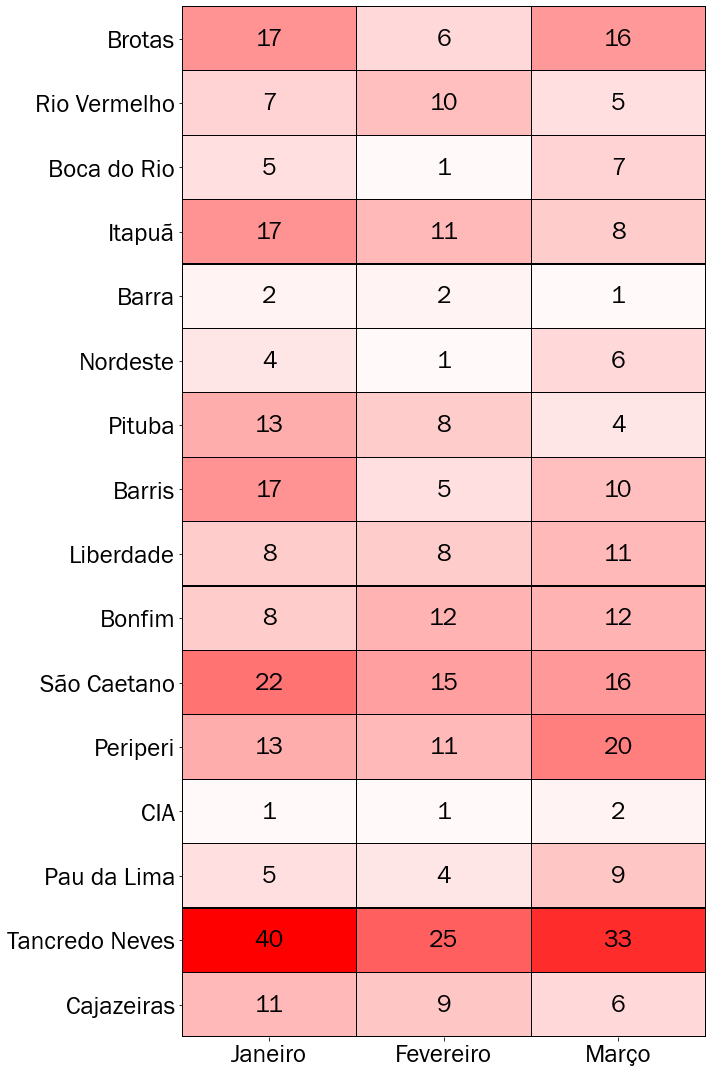
Figura 5.7: Mapa de calor da incidência de roubos à ônibus nas áreas de Salvador

Apesar do mapa de calor parecer bastante com uma tabela na Figura 5.7, existe uma diferença: Cada célula (campo do gráfico) apresenta uma coloração de acordo com a grandeza representada. Além disso, podemos verificar que o setor Tancredo Neves, localizado na RISP Central, apresenta os maiores valores, enquanto o restante em sua grande maioria aparece com um tom mais rosa. Em contrapartida, as áreas Barra e CIA apresentam os menores números de ocorrências, não passando de duas ocorrências por mês. Visualmente falando, já conseguimos extrair algumas informações deste gráfico, não é?

Em geral percebemos que:

O setor com maior incidência é, de forma disparada, Tancredo Neves em todos os meses do verão. - Barra e CIA são os setores com os menores números de ocorrência. - Somando o número total de ocorrências por área para cada mês encontramos para janeiro, fevereiro e março respectivamente 190, 129 e 166 ocorrências. Logo, o mês de Janeiro se destaca inicialmente por apresentar maior quantidade de ocorrências.

Além dessas informações, você consegue extrair mais conhecimento deste gráfico? Apesar da Figura 5.7 apresentar um panorama completo das ocorrências, podemos notar um detalhe curioso: O fato da área Tancredo Neves apresentar altas incidências, torna outros setores, visualmente, menos perigosos. E se fizermos uma análise por região, será que conseguiremos identificar novas zonas com alta incidência de assaltos? Na Figura 5.8 apresentamos novamente o mapa de calor, agora separado por regiões.

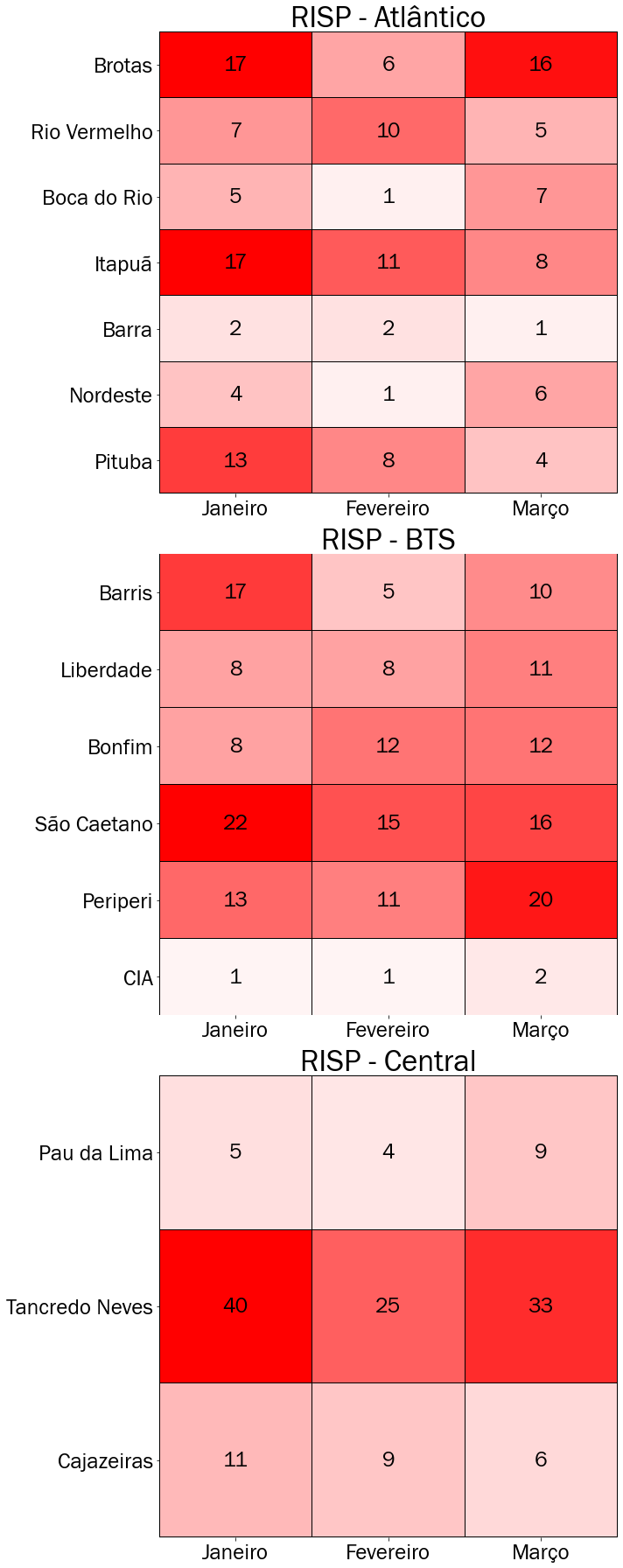
Figura 5.8: Mapa de calor particionado por regiões de Salvador

Cada uma das três regiões apresentaram características interessantes no verão:

• Na região Atlântico podemos verificar que as áreas Brotas e Itapuã são as mais perigosas de modo geral, onde em Janeiro ocorreu em ambas o maior número de ocorrências com 17 casos. Além disso, Pituba e Rio Vermelho possuem um tom de rosa mais forte, mostrando que elas não são tão seguras.

• Na região BTS nota-se que diversas áreas apresentam tons avermelhados, mostrando um grande perigo com destaque para São Caetano e Periperi que apresentam os maiores valores.

• Na região Central é possível perceber que a área Tancredo Neves é a mais perigosa, mantendo o mesmo padrão apresentado na Figura 5.8.

Com esta nova análise conseguimos perceber que às vezes até uma imagem podem acabar nos enganando no que se refere a perspectiva: Na Figura 5.7 apenas a área de Tancredo Neves se destacava em comparação às outras, porém ao fazer uma análise mais aprofundada, considerando uma comparação apenas dentro das regiões definidas pela SSP, verificamos que outras áreas também apresentam uma grande quantidade de ocorrências. Este padrão será observado nesta seção quando avaliarmos as medidas de tendência central, onde vamos entender o impacto de um valor aberrante.

Acesse o link Ocorrências de crimes - Salvador para ver esses dados representados de forma dinâmica e veja quais informações a mais é possível obter!

A primeira medida de tendência central a ser analisada será a Média. Trata-se da medida mais conhecida e usada em nosso dia a dia, como vimos no início deste capítulo. Ela é calculada através do somatório de todos os valores dividido pela sua quantidade. Com este conhecimento em mãos vamos montar uma tabela da média de ocorrência para os meses do verão de acordo com a região:

Tabela 5.2: Médias encontradas para as ocorrências de assalto à ônibus separada por região

RISP	Janeiro	Fevereiro	Março
Atlântico	9,29	5,57	6,71
BTS	11,50	8,67	11,83
Central	18,67	12,67	16,00

Porém, antes de analisar a Tabela 5.2, por que calculamos a média? Bom, o intuito é apresentar um indicador para o número de ocorrências das regiões de Salvador, encontrando uma medida capaz de resumir todos os valores de cada área. Assim, ao invés de avaliar área por área, temos um valor único que resume aquela imensa quantidade de dados em um só representativo.

Através das médias calculadas na Tabela 5.2, podemos perceber que:

• O mês de fevereiro como um todo possui os menores índices de ocorrências em comparação a janeiro e fevereiro.

• A RISP Central possui as maiores médias de ocorrências nos meses de verão, mesmo sendo uma região com apenas 3 áreas catalogadas. Note que a área com maior incidência, Tancredo Neves, pertence a esta região.

• A RISP Atlântico possui os melhores indicadores em todos os meses, ou seja, possui a menor média de ocorrências e, portanto, poderia ser considerada a região mais segura.

Através da média conseguimos extrair indicadores capazes de fazer comparações diretas entre as regiões! Para deixar ainda mais claro o cálculo desta medida, a Figura 5.9 apresenta as etapas para calculá-la através do estudo de caso.

Figura 5.9: Etapas para calcular a média

Note que ao final a média apresentou um resultado aproximado, diferente da Tabela 5.2 que apresentou alguns valores decimais, mas qual seria o motivo? Estamos tratando de números de ocorrências, certo? Você nunca ouviu algo como “Ontem aconteceu \(2,5\) assaltos naquele ponto de ônibus” ou “Aconteceu em Salvador \(30,5\) furtos de veículos na região do litoral”. Mesmo assim, o valor da média é decimal na Tabela 5.2. Isso ocorre, pois estamos tratando de uma variável que por natureza é inteira, ou seja, aumenta em unidades, porém a forma como a média é calculada não garante que o resultado seja também um inteiro (algumas vezes pode acontecer). Logo, é comum realizar uma aproximação simples seguindo as regras:

• Caso a parte decimal seja maior ou igual \(0,5\), você aproxima para o maior valor inteiro próximo do seu número
• Caso a parte decimal seja menor que \(0,5\), você aproxima para o menor valor inteiro próximo do seu número
• Esta regra vale para qualquer valor decimal que você queira representar e não somente a média. Aplicando esta regra na Tabela 5.2, assim como foi aplicada na Figura 5.9, temos:

Tabela 5.3: Médias encontradas após aproximação para as ocorrências de assalto à ônibus separada por região

RISP	Janeiro	Fevereiro	Março
Atlântico	9	6	7
BTS	12	9	12
Central	19	13	16

A Tabela 5.3 mostra a média com a mesma natureza da grandeza estudada, ou seja, em valores inteiros, mantendo o seu conceito: representar um ponto de equilíbrio para o número de ocorrências de assaltos a ônibus por região em Salvador.

Com os valores das médias calculados por região, podemos assinalar outra situação, protagonizada pela novamente pela área Tancredo Neves na região Central… Você conseguiu perceber?

Olhe para as médias da região Central: 19 ocorrências em Janeiro, 13 ocorrências em Fevereiro e 16 ocorrências em Março. Agora olhe novamente para esta mesma região na Figura 5.8 e responda: estes valores de média representam bem os valores de ocorrência observadas?

Infelizmente não. A situação que ocorre aqui mostra uma das fraquezas desta medida: valores aberrantes. Tratam-se de observações demasiadamente grandes ou pequenas que apresentam um grande afastamento das demais.

Neste caso, o responsável por esses valores é o setor Tancredo Neves, que tem números de ocorrências muito maiores em comparação aos demais. Os valores aberrantes influenciam bastante na média e isso será discutido mais à frente … Agora que aprendemos como calcular e utilizar a média, podemos compreender a frase dita no início desta seção:

“Em média ocorreram 3 assaltos em Salvador por dia avaliados durante o ano”

Basicamente, o que o jornal apresentou foi um tratamento similar ao que fizemos anteriormente: Adquiriu todos os os boletins mensais disponibilizados pela SSP, somou todos os números de ocorrências de Janeiro até Dezembro e então dividiu pelo total de dias que existem no ano, 365 dias. É provável que o valor encontrado tenha sido decimal também, e então foi aproximado para este valor que verificamos: três ocorrências em média!

Podemos aplicar esta mesma análise para o nosso banco de dados. Considerando os dias vigentes de cada mês no ano de 2019, podemos dizer que:

• Em Janeiro ocorreram em média 6 assaltos a ônibus por dia em Salvador.
• Em fevereiro ocorreram em média 5 assaltos a ônibus por dia em Salvador.
• Em março ocorreram em média 5 assaltos a ônibus por dia em Salvador.

Note que esses valores foram encontrados considerando a aproximação discutida anteriormente. Além disso, com a tabela calculada podemos dizer frases como:

• “Durante o período de Janeiro, em média ocorreram doze assaltos à ônibus na Região BTS”
• “Em Fevereiro, na Região BTS, aconteceram nove assaltos à ônibus em média”

Depois de compreender um pouco sobre a medida mais usada e saber uma de suas falhas (é influenciada por valores aberrantes), será que existe alguma outra medida que seja blindada a esta questão?

Para nossa sorte, ela existe sim e se chama Mediana.

A mediana é definida como o valor que divide os dados na metade, 50% estão acima da mediana e 50% estão abaixo. A obtenção da mediana é feita ordenando-se os dados e escolhendo-se o valor do meio. Por exemplo, se temos 11 valores, a mediana estará na 6º posição (5 valores abaixo e 5 valores acima). No caso de uma quantidade amostral par, computamos a média dos dois valores “centrais”.

Tabela 5.4: Medianas encontradas para as ocorrências de assalto à ônibus separada por região

RISP	Janeiro	Fevereiro	Março
Atlântico	7,0	6,0	6,0
BTS	10,5	9,5	11,5
Central	11,0	9,0	9,0

A Tabela 5.4 apresenta os valores das medianas para cada região de Salvador. Note que algumas regiões apresentam valores decimais, assim como aconteceu com a média e o motivo é o mesmo: ao calcular a média dos valores “centrais” não garantimos um resultado inteiro.

Para compreender melhor este resultado, na Figura 5.10 apresentamos o passo a passo para calcular a mediana.

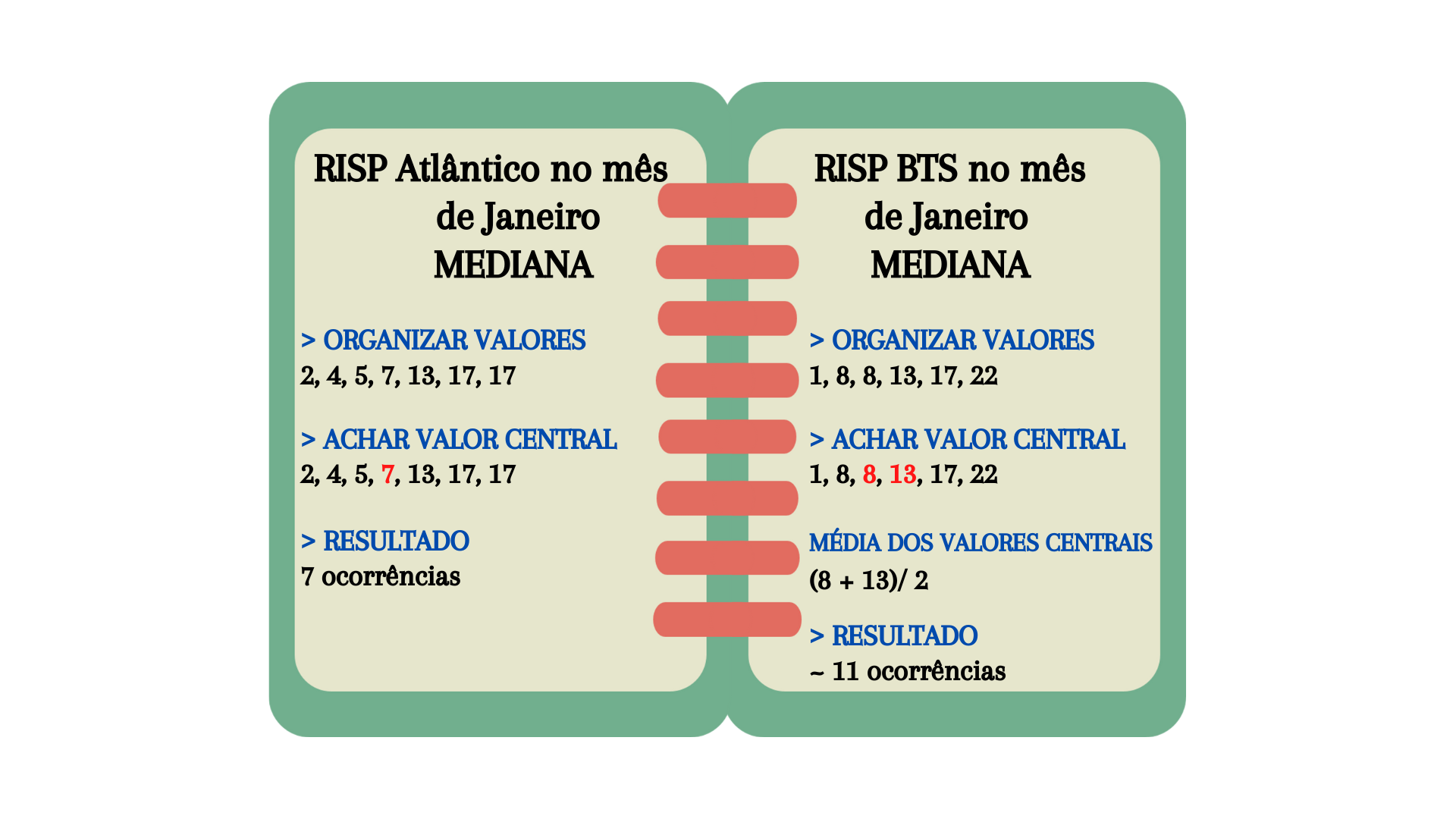
Figura 5.10: Etapas para calcular a mediana

Na Figura 5.11 mostramos em duas regiões diferentes de Salvador como calcular a mediana. Note que ela pode ser encontrada de duas maneiras distintas a depender da quantidade de valores como apresentamos anteriormente.

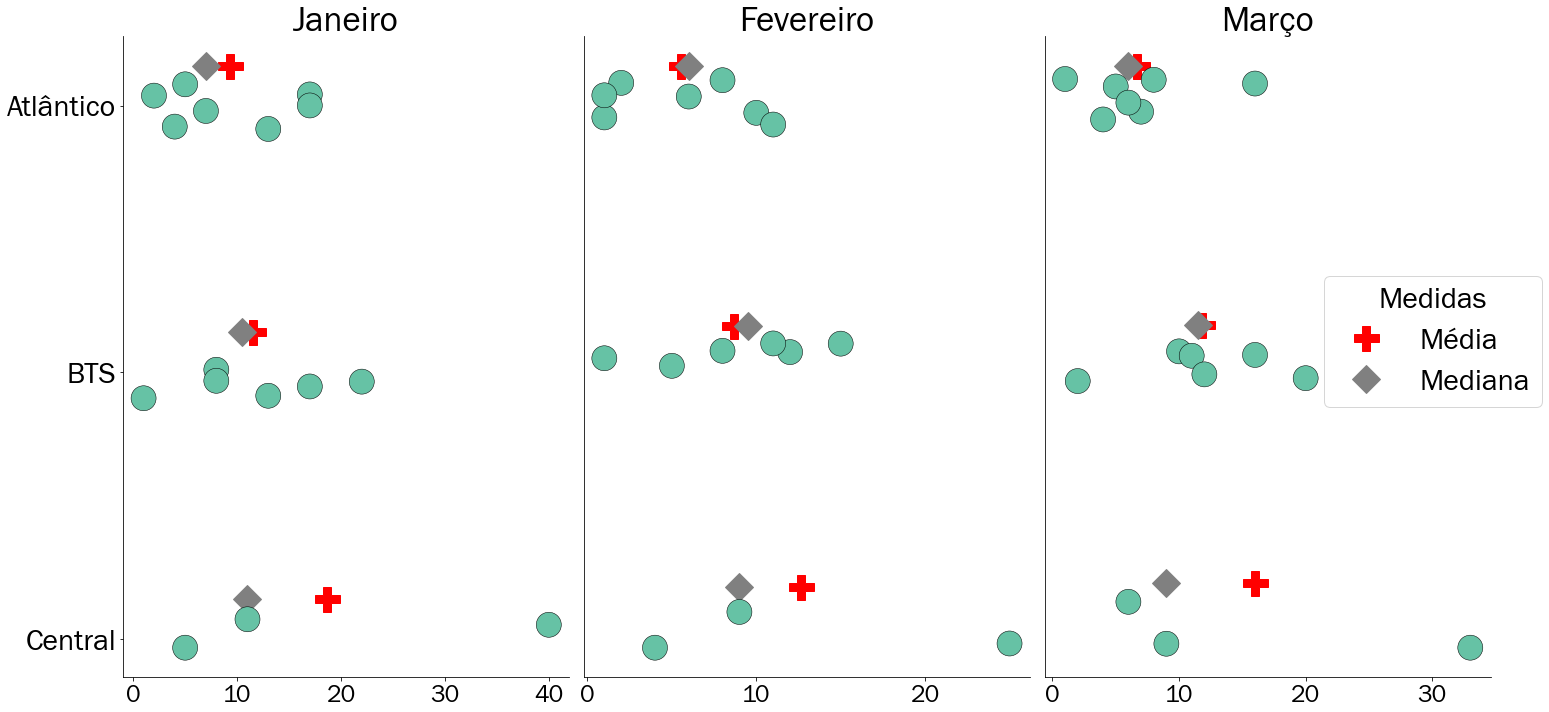
Figura 5.11: Gráfico de pontos para as ocorrências em Salvador

Podemos perceber na Figura 5.11 que para as regiões Atlântico e BTS os valores de média e mediana são próximos, diferente da região Central. Essa disparidade é explicada pelo que vimos anteriormente: O valor aberrante distorce o valor da média, puxando-a em sua direção.

A comparação de média e mediana pode ser um bom indicativo para verificar a presença de um valor aberrante: quanto mais próximas essas medidas forem, mais provável a ausência de valores aberrantes.

Nesta análise em específico, verificamos que a mediana seria a melhor medida para representar a região Central como um todo, já para as outras duas regiões a escolha entre ambas as medidas é arbitrária, pois elas estão bem próximas.São visualizações como essas que ajudam o cientista de dados a tomar melhores decisões na escolha de indicadores ou medidas de resumo.

Finalmente, a última medida de tendência central a ser mencionada neste capítulo é a moda. Trata-se da medida de maior frequência em um conjunto de dados, em outras palavras, o valor que mais se repete em uma amostra será a moda deste dado! Este conceito é muito usado para variáveis categóricas. Como neste capítulo trabalhamos com valores numéricos, não cabe a análise dessa medida, nesse momento.

5.3 Medidas de dispersão

Como já foi visto, as medidas de posição ou se preferir, tendência central, podem ser utilizadas para descrever as informações através de um único valor. Porém, se dois conjuntos possuírem o mesmo valor de média ou mediana, podemos dizer que eles são equivalentes?

A resposta é Não! Apesar destas medidas resumirem bem os conjuntos de dados, ao aplicá-las individualmente, perdemos outras características importantes. Para alcançar uma visão geral e expandir nossas análises, usamos também as medidas de dispersão².

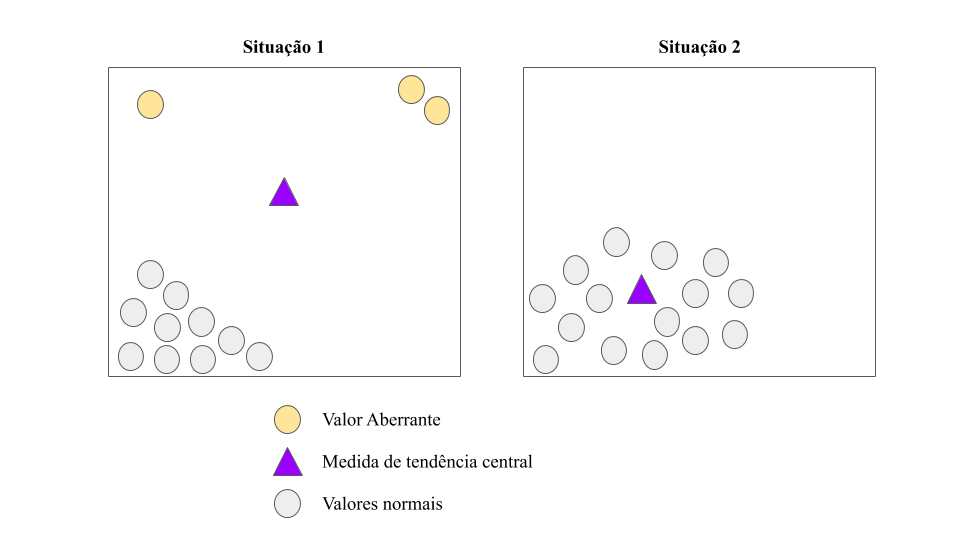
Figura 5.12: Explicação das medidas de dispersão

Para entender melhor este conceito e o motivo de entender as medidas de dispersão avalie a Figura 5.12 em que apresentamos duas situações: Na “Situação 1” podemos perceber que os dados apresentam um espalhamento (ou dispersão) em relação a medida de posição, lembre que o triângulo busca resumir todos os círculos. Portanto, existe variação entre os valores observados (valores normais) em comparação a uma medida qualquer de posição. Isso torna este conjunto de dados heterogêneo, ou seja, bem diversificado. Já na “Situação 2”, observamos que a massa de dados está bem localizada ao redor da medida de posição, mostrando assim um conjunto de dados homogêneo.

Quanto mais homogêneo for um conjunto em relação a uma medida de posição, maior será o poder de explicação desta medida sobre o conjunto.

Portanto, medidas de dispersão são medidas capazes de relacionar o afastamento dos dados em comparação à uma medida de posição. Existem várias formas de se medir a dispersão, porém trataremos aqui da Amplitude, Desvio padrão e Distância Interquartil. Essas medidas se tratam de um complemento à medida de tendência central, pois agora conseguimos entender como os dados estão espalhados em relação a medida central calculada.

A primeira medida a ser trabalhada é a amplitude definida como:

\[Amplitude=Valor\ Máximo\ -\ Valor\ Minímo\]

Seu conceito é bastante simples de entender.

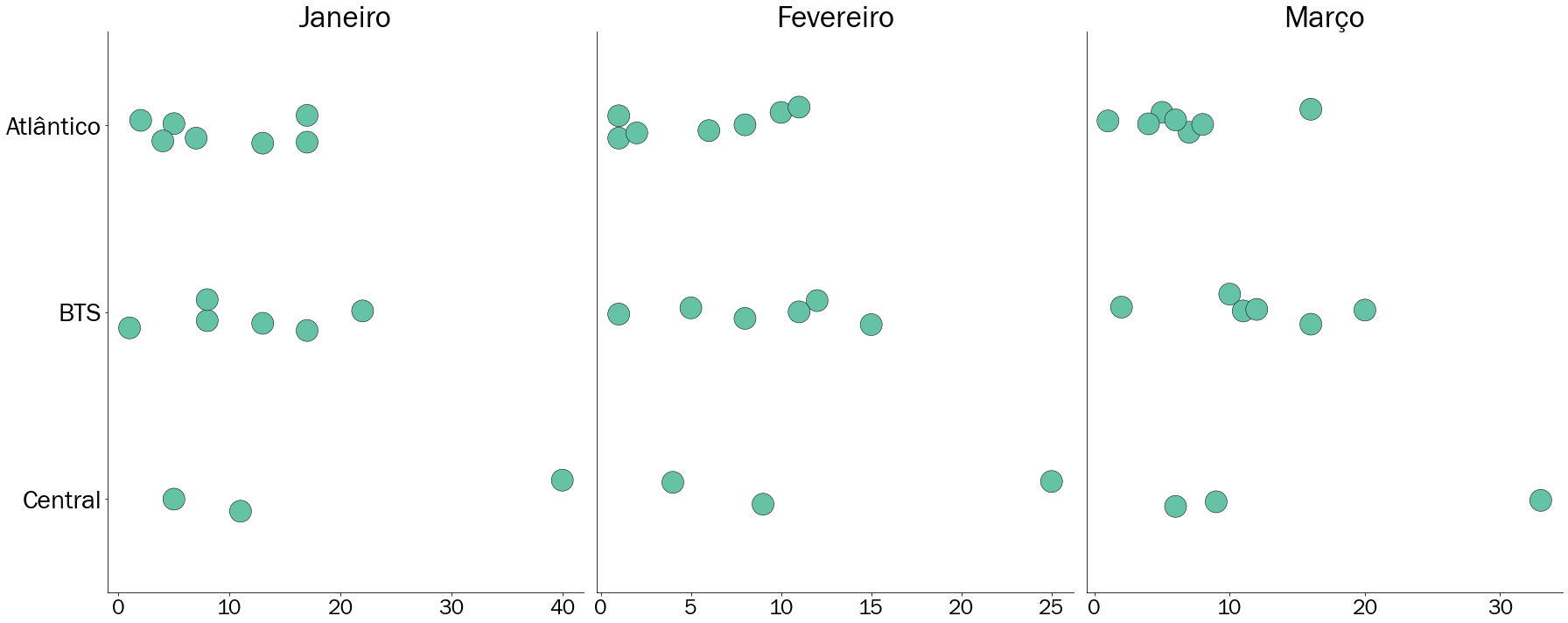
Figura 5.13: Gráfico de pontos para as ocorrências em Salvador

Na Figura 5.13 apresentamos novamente o gráfico de pontos da seção anterior para o número de ocorrências. Podemos perceber de forma visual, que a amplitude da região Central será maior do que a das outras regiões para todos os meses, uma vez que a área Tancredo Neves apresenta grandes índices de assaltos. Assim, verificamos no gráfico que para a região Central, sempre haverá um ponto mais afastado indicando um valor mais alto.

Em geral, a amplitude apenas permite comparar dois ou mais conjuntos de dados no sentido de avaliar quem apresenta a maior ou menor variação, porém não indica a distribuição dos dados. Ou seja, não informa como eles estão espalhados em torno de uma medida de posição. Além disso, assim como a média, a amplitude sofre bastante com a presença de valores aberrantes. Vamos agora partir para a compreensão de dois conceitos um pouco mais complexos: Desvio padrão e Distância Interquartil.

O Desvio Padrão relaciona a diferença entre cada elemento do conjunto com a média aritmética através de uma fórmula matemática. Ou seja, cada elemento terá um determinado valor de variação em relação à média do grupo e desta forma, é possível saber quando os conjuntos analisados são heterogêneos ou homogêneos. Isso confirma que esta medida consegue representar a dispersão dos dados, já que utiliza todos os valores do conjunto no seu cálculo. Na ciência, o desvio padrão juntamente com a média é essencial para construir análises e resultados, pois esta dupla se complementa.

A Distância Interquartil, diferente da amplitude, lida bem com valores aberrantes. Mas, para entender a distância interquartil precisamos inicialmente definir os quartis. Quartis são valores que dividem os dados em quatro partes e eles são:

• \(Q1\) (primeiro quartil) define o valor para o qual \(25\%\) dos valores estão abaixo dele;
• \(Q2\) (segundo quartil) é o valor que tem \(50\%\) dos valores abaixo e 50% acima;
• \(Q3\) (terceiro quartil) define o valor que possui \(75\%\) dos dados abaixo dele.

A fórmula para a distância interquartil será a diferença entre o primeiro e terceiro quartil:

\[Distância\ Interquartil\ =Q3-Q1\]

Note que o \(Q2\) é um conhecido nosso: a mediana! Logo, dá para perceber que para calcular a distância interquartil precisamos fazer o mesmo método que utilizamos para calcular a mediana: ordenar os dados e extrair os quartis. Para facilitar o cálculo desta medida, podemos utilizar o seguinte procedimento:

1. Ordenar os dados de forma crescente
2. Seja N a quantidade de valores do seu conjunto, podemos calcular as posições dos quartis \(Q3\) e \(Q1\) da seguinte forma: \[Posição\ de\ Q1=N*0,25\]

\[Posição\ de\ Q3=N*0,75\] 3) Verificar se as posições encontradas são valores inteiros ou decimais. Se for decimal, aproximar para o valor inteiro mais próximo seguindo a regra ensinada na seção anterior. 4) Encontrar os quartis \(Q1\) e \(Q3\) da seguinte forma: calculando a média entre o valor na posição encontrada com o valor seguinte na sequência. 5) Finalmente, com os quartis em mãos, calcule a distância entre o terceiro e o primeiro quartis para encontrar a Distância Interquartil.

Na Figura 5.14 apresentamos os passos explicados anteriormente de forma prática em nosso estudo de caso.

Figura 5.14: Etapas para calcular Distância Interquartil

A Figura 5.14 detalha os passos apresentados para o cálculo da distância interquartil na RISP Atlântico no mês de Janeiro, mostrando que apesar de parecer complexo as etapas são bem simples de resolver! Porém, o mais comum no dia a dia de um cientista de dados é utilizar o computador através de programas e códigos para encontrar esses resultados.

Para entender melhor as medidas de dispersão, vamos calculá-las para o nosso caso de estudo: número de ocorrências de assalto a ônibus em Salvador. A Figura 5.15 resume os resultados encontrados dessas medidas para cada região de Salvador separado por mês.

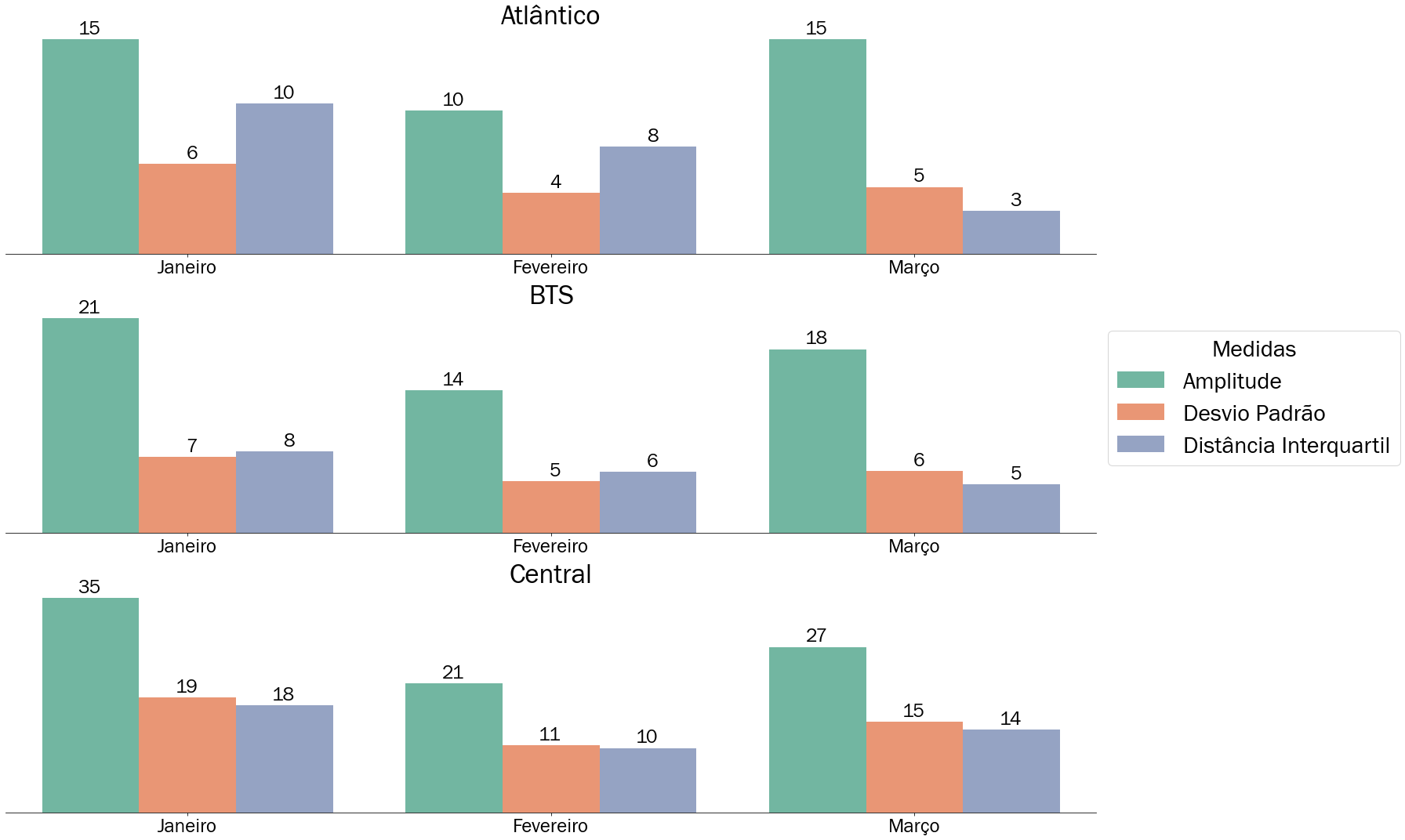
Figura 5.15: Medidas de dispersão aproximadas em gráfico de barras das ocorrências de Salvador

Conseguimos extrair as seguintes informações:

• Considerando a amplitude, vemos que a região central é a que mais varia em todos os meses em comparação com BTS e Atlântico. Isso indica uma grande disparidade entre o máximo de ocorrências, Tancredo Neves, com as demais. Esta região impacta inclusive no resultado do Desvio Padrão que é o dobro em comparação às demais regiões.

• O menor Desvio Padrão avaliado foi no mês de fevereiro para a RISP Atlântico. O valor 4 pode ser lido da seguinte forma “No mês de fevereiro a diferença entre o número de ocorrências por área com a média da região é de quatro ocorrências”

• No geral, o conjunto com maior espalhamento é representado pela RISP Central, que demonstrou os maiores valores em todas medidas. Essa tendência é observada também na Figura 5.13 onde as outras regiões mostram número de ocorrências similares.

Um fato a ser ressaltado sobre a Distância Interquartil: Apesar de ser uma medida robusta a valores aberrantes, assim como a mediana, ao avaliá-la com um conjunto muito pequeno, como é o caso da RISP Central, essa robustez acaba se tornando fraca.

Outro ponto a ser ressaltado é que amplitude e desvio padrão possuem uma relação: quanto mais próximos os dados estiverem do valor médio, significa que há uma amplitude menor e consequentemente um desvio padrão dos dados também será pequeno, por outro lado quando os dados se afastam do valor da média, é indicado que a amplitude será maior e consequentemente, o desvio padrão também será maior.

No geral, utilizar mais de uma medida descritiva é essencial para se atingir uma boa conclusão a respeito dos dados que estão sendo avaliados. Além disso, o diagnóstico encontrado ao se utilizar uma medida é confirmado pelas outras. Por isso a importância de conhecer as medidas de Tendência Central e Dispersão para interpretar nossos dados e garantir conclusões confiáveis!

Na próxima seção iremos expandir ainda mais o que aprendemos aqui, trazendo conclusões mais factíveis ao nosso caso de estudo através do Diagrama de caixas.

5.4 Diagramas de Caixa

Nesta seção vamos tratar sobre o Diagrama de Caixa (chamado comumente de boxplot), uma das formas de visualização de dados numéricos mais completas, muito aplicada pelos cientistas de dados. O Diagrama de Caixa resume as duas ideias apresentadas anteriormente: tendência central e dispersão.

Antes de mergulhar em sua utilização através do nosso caso de estudo, vamos explicar o que é cada parte dessa “caixinha”.

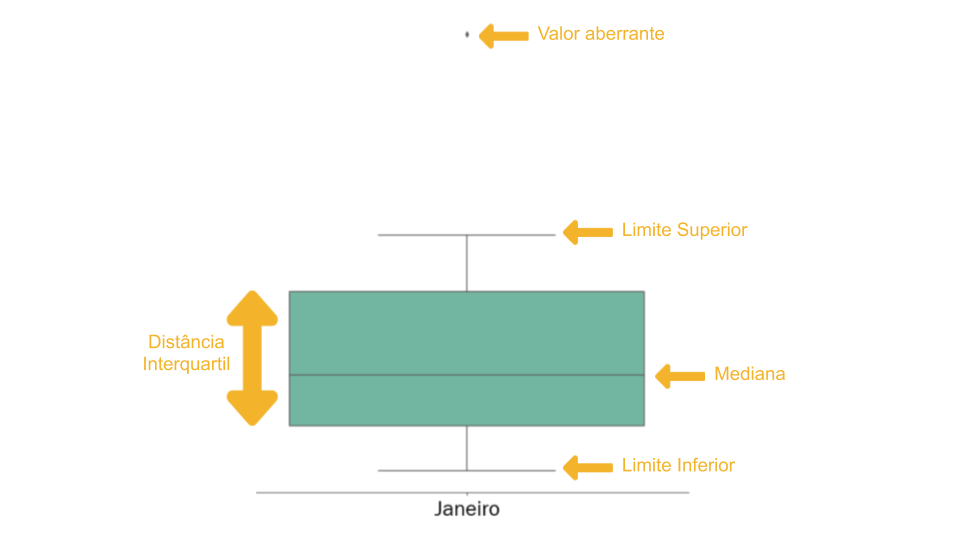
Figura 5.16: Diagrama de caixa explicado para o mês de Janeiro

Na Figura 5.16 apresentamos de forma elegante nosso diagrama de blocos referente ao mês de janeiro. No geral, quando olhamos este tipo de visualização focamos em 4 elementos principais:

• Mediana: Trata-se da medida de blindada a valores aberrantes e que separa o conjunto de dados em 50% para cada lado como aprendemos anteriormente.
• Distância Interquartil: Nossa medida de dispersão definida anteriormente. Assim como a mediana, trata-se de uma medida blindada a valores aberrantes.
• Limites: São valores calculados a partir da distância interquartil e de seus elementos. Responsáveis por definir “a última fronteira” entre valores comuns e aberrantes. São separados em dois como vimos na Figura 5.16: Limite Superior e Limite Inferior.

O Limite Superior é calculado por:

\[Limite\ Superior=Q3+1,5*Distância\ Interquartil\]

Já o Limite Inferior é calculado por:

\[Limite\ Inferior=Q1-1,5*Distância\ Interquartil\] - Valor Aberrante: Todo valor que ultrapassa a barreira definida pelos limites. Na maioria das vezes são definidos como pontos ou asteriscos.

Considerando os elementos discutidos, percebemos que: a linha superior da nossa caixa retrata o \(Q3\), já a linha inferior o \(Q1\), pois \[Q3-Q1=Distância\ Interquartil\] como vemos na Figura 5.16. Finalmente, a linha do meio, que divide a caixa em duas, é a nossa Mediana.

• Não é garantido a existência de valores aberrantes como na Figura 5.16. Eles só ocorrem se algum valor ultrapassar o limite superior ou inferior.

• Apesar de usarmos mediana e distância interquartil, poderíamos ter utilizado a média junto com o desvio padrão, porém o mais comum é utilizar os dois primeiros.

Neste momento você pode se perguntar: “Mas o que este gráfico pode me oferecer? Qual o sentido de eu aprender seus elementos?” E a resposta é simples:

Ele condensa muitas informações de forma robusta e de fácil percepção!

O diagrama de caixas nos fornece: dispersão dos dados (distância interquartil) em torno de uma medida de posição (mediana), presença de valores aberrantes e assimetria dos dados.

Vamos discuti-las através do nosso caso de estudo através da construção de diagramas de caixa para cada mês do verão em 2019.

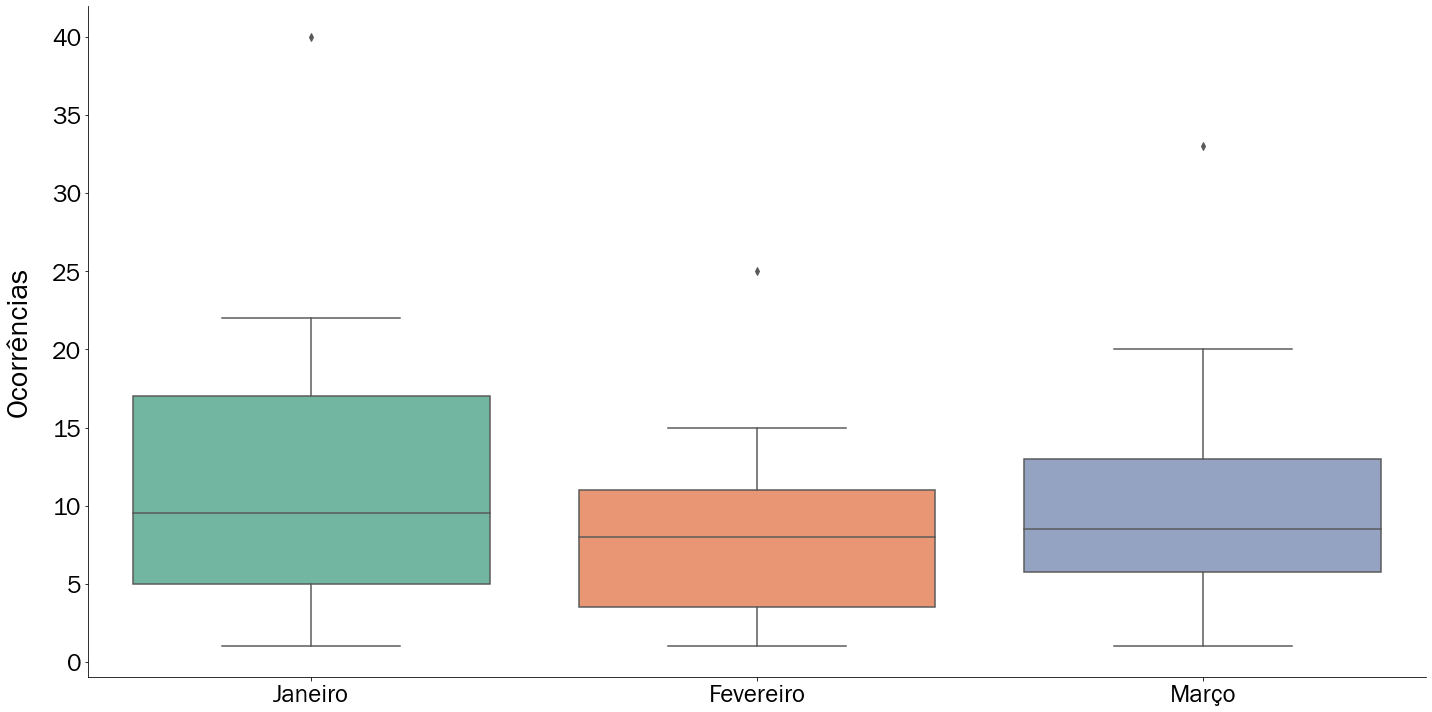
Figura 5.17: Diagrama de caixa das ocorrências mensais

Através da Figura 5.17 avaliamos as ocorrências de assaltos à ônibus em Salvador para os meses do verão. Note que não estamos trabalhando mais com AISP ou RISP e sim com a cidade de Salvador como um todo, ou seja, reduzimos toda aquela tabela inicial em apenas três caixinhas!

Primeiramente, antes de entrar em uma análise mais aprofundada dessa Figura, vamos responder em tópicos a seguinte pergunta:

Qual seria o melhor diagrama de caixas para o número de ocorrências de assalto a ônibus em Salvador para um determinado mês?

Com o que aprendemos até então nesse capítulo, poderíamos dizer:

• Um baixo valor de mediana, pois assim teríamos uma baixa incidência de assaltos.

• Sem valores aberrantes. Caso exista incidência de valores aberrantes acima da caixa, estaremos enfrentando casos extremos, certo? Afinal eles estariam muito acima das outras áreas. Já valores aberrantes abaixo da caixa podem demonstrar que apenas poucas regiões são seguras na cidade em comparação aos demais.

Esses dois tópicos resumem bem o que um policial ou delegado gostaria de ver em relação a sua cidade: um baixo número de ocorrências. Vamos agora avaliar de forma aprofundada o que conseguimos verificar nesses três meses de 2019:

• Se considerarmos a mediana, podemos verificar que Janeiro apresentou o maior valor, logo um cenário ruim em comparação aos demais. Em outras palavras, podemos dizer que foi o mês com maior incidência central.

• Considerando a distância interquartil, ou se preferir a altura da caixa, verificamos que o mês de janeiro apresentou a maior variação em torno da mediana, valor que separa o conjunto em duas partes de \(50\%\). Mas … o que significa dizer isso? Significa dizer que tivemos áreas com muitos assaltos e outras com poucos assaltos.

Considerando o mês de janeiro, por exemplo, vemos que o limite inferior é equivalente a 5 ocorrências de assalto, enquanto o limite superior está entre 15 e 20 ocorrências, mais de três vezes o valor inferior! Isso demonstra um desbalanceamento entre áreas neste mês e uma assimetria na ocorrência de casos.

• Conseguem ver aqueles pontinhos em cima de cada caixa? Eles são nossos valores aberrantes e representam uma área bastante citada neste capítulo: AISP Tancredo Neves. Os valores de ocorrência foram tão altos nessa região, durante todos os meses, que o diagrama de caixa os coloca como valores aberrantes.

De forma geral, conseguimos verificar que janeiro foi o mês com maiores ocorrências por região apresentando os maiores: Limite superior, \(Q3\) e Mediana, ou seja, podemos dizer que foi o pior mês do verão de 2019 para se andar de ônibus. Já fevereiro pode ser considerado o melhor: sua caixa se concentra em uma região de 3 à 10 ocorrências com um limite superior máximo de 15 ocorrências. Além disso, apresentou a menor ocorrência do setor Tancredo Neves, com 25 ocorrências. Finalmente, em Março ocorreu uma piora em comparação a fevereiro através do deslocamento da caixa para uma região de 5 à 12 assaltos, porém não superou janeiro.

Perceba que através dessa simples visualização, conseguimos extrair muitas respostas acerca do nosso caso de estudo, especialmente por meio de comparação!

Para desvendar mais respostas sobre esse tema tão importante, acesse o site (re)Conhecendo Salvador e veja mais dados que foram levantados sobre diferentes crimes na cidade de Salvador!

5.5 Concluindo …

Através deste capítulo conseguimos entender que através de alguns indicadores conseguimos analisar e discutir grandes tabelas. Além disso, avaliamos uma nova forma de visualizar nossas informações: o diagrama de caixa. Por meio do infográfico da Figura 5.18 resumimos o verão de 2019 de Salvador em relação aos assaltos à ônibus na cidade.

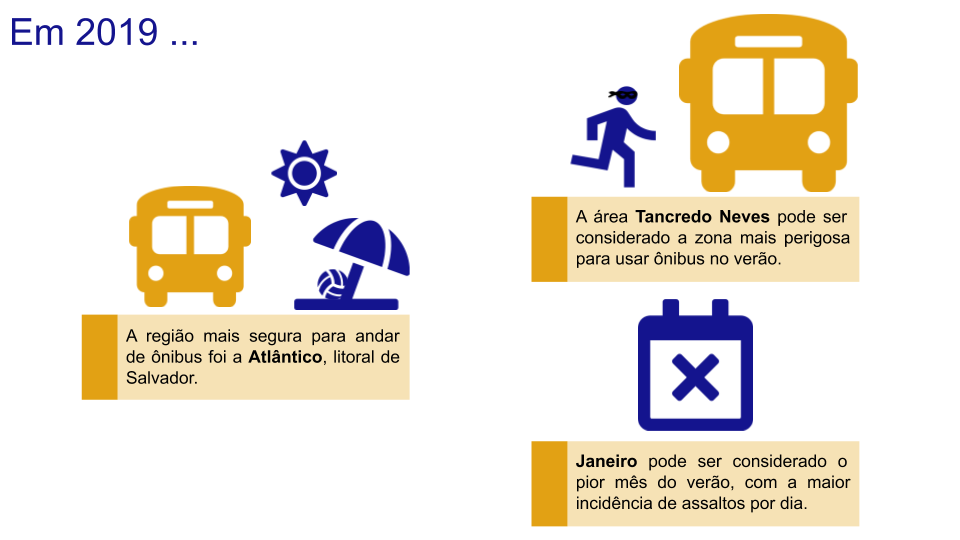
Figura 5.18: Conclusões sobre o tema do nosso capítulo

Podemos perceber que através de uma análise descritiva simples, conseguimos chegar em diversas conclusões a respeito do tema estudado. Estas conclusões podem embasar políticas públicas para melhorar esses indicadores.

Além disso, aprendemos que:

• Apesar de existirem diferentes tipos de medidas para apresentar um mesmo conceito, elas apresentam diferentes aplicações e interpretações.

• O diagrama de caixa é uma ótima ferramenta para ter uma visão geral a respeito do nosso conjunto de dados.

• Dominar essas ferramentas é uma peça fundamental para o cientista de dados exercer seu trabalho e responder questões.

5.6 Indo Além

Agora que já aprendemos um pouco sobre Estatística Descritiva, que tal aplicá-la na prática? Você agora é cientista de dados contratado (a) pelo governo de Salvador para compreender e descrever melhor as ocorrências de roubo de veículos na capital baiana durante o mês de Dezembro. A Figura 5.19 mostra o boletim da SSP que lhe foi enviado (no formato .csv), contendo as ocorrências de todos os delitos na capital baiana no mês de Dezembro¹.

Figura 5.19: Boletim de dezembro de 2019 produzido pela SSP

O gestor pediu que apresentasse, em relação ao delito de roubo de veículos:

• Qual a RISP que precisa ser mais monitorada pelos profissionais?
• Em média, quantos roubos estão acontecendo por região?
• Qual a região com menor incidência de casos? Consegue descrever uma motivação para isso?
• Descrição completa deste delito através de uma visualização gráfica.

Então, com o conhecimento que desenvolvemos até aqui, resolva essas questões!

Citações no capítulo

[1] Secretaria de Segurança Pública. Boletins mensais de delitos. Disponível em: link de acesso

[2] Sergio Miranda Freire. Bioestatística Básica, Capítulo 3 – Medidas de Tendência Central e Dispersão Disponível em: link de acesso