Capítulo 3 Visualização e Ciência de Dados

O capítulo 2 apresenta a tabela como uma forma poderosa para estruturar e consultar informações. No entanto, quando trabalhamos com tabelas com número muito grande de linhas e colunas, torna-se difícil interpretar suas informações, não importa o quão organizadas elas estejam. Às vezes, é muito mais fácil interpretar essas informações através dos gráficos, conteúdo que será explorado no decorrer deste capítulo.

A construção e visualização gráfica é de extrema importância na área de ciência de dados, pois a partir de um bom gráfico é possível extrair ideias, hipóteses e o melhor entendimento a respeito de um tema ou uma pergunta. Logo, como diz o ditado popular “Uma imagem vale mais que mil palavras”.

3.1 Objeto de estudo

Para compreender a importância da análise gráfica e como utilizá-la corretamente, investigaremos os perfis dos estudantes de Salvador que realizaram a prova do Exame Nacional do Ensino Médio (ENEM) no período de 2015 até 2019. Incialmente, é necessário compreender a definição de Perfil: esse termo é muito usado na ciência de dados para descrever um determinado processo ou objeto de estudo através de padrões e características que o representam.

A nossa avaliação utilizará o conjunto de dados dos estudantes da cidade de Salvador, particularmente os microdados do ENEM, publicados pelo Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira (INEP), disponíveis ao público através deste link de acesso¹.

Microdados são um conjunto de dados ou banco de dados no qual os registros das variáveis estão disponíveis na sua mais elementar e específica atribuições de valores, status e demais características de um indivíduo ou ação. Estes conjuntos podem ser resultado dos registros individualizados de variáveis segundo a perspectiva da gestão de uma determinada atividade, serviço, pesquisa, produto ou transações de um determinado negócio ou prestação de um serviço público.

Como o termo perfil pode ser bem vasto e diversas características podem ser extraídas do nosso objeto de estudo, é necessário concentrar essa análise em perguntas mais específicas para nortear o caminho. No decorrer deste capítulo, serão exploradas graficamente as seguintes questões:

• a quantidade de estudantes que realizaram o ENEM aumentou de 2015 para 2019 na capital baiana?
• Como é a distribuição de estudantes em Salvador por cor/raça? Conseguimos identificar algum padrão para esses valores?
• Na dita era da informação, onde tudo está conectado, como está o acesso dos estudantes a internet em suas residências? E a computadores pessoais?
• O tipo de escola (pública ou privada) pode influenciar nas notas dos estudantes neste exame?

A compreensão desses dados é de suma importância para entender melhor o perfil dos estudantes de Salvador que possuem o ENEM como uma oportunidade de acesso, às vezes única, ao ensino superior no Brasil. A comunidade escolar, formado por professores, estudantes, pais, funcionários da escolas etc., podem formar uma visão crítica à respeito das consequências das condições sobre as quais estudamos na educação público e a privado e potencial impacto sobre o resultado no desempenho dos estudantes. A partir de debates, reflexões e trocas entre os paticipantes da comunidade escolar; políticos, gestores de políticas públicas de educação, professores, diretores e coordenadores podem organizar os caminhos para as mudanças.

Na seção seguinte, algumas transformações matemáticas e suas representações gráficas que facilitam a interpretação dos dados associados aos tópicos associados ao cenário do ENEM.

3.2 Gráfico de barra

O Gráfico de barras é uma forma bastante comum e versátil de visualização na área de ciência de dados. Ele pode ser utilizado tanto com variáveis categóricas quanto numéricas para expressar grandezas.

Na Figura 3.1 é apresentada a quantidade de inscritos (uma grandeza numérica) que realizaram o ENEM de 2015 até 2019 na capital baiana. É possível notar uma queda na participação dentre os períodos de 2016 até 2019. Apesar de simples e direto, a análise desse mesmo resultado através de uma tabela pode se mostrar confusa.

## 
## Attaching package: 'dplyr'

## The following objects are masked from 'package:stats':
## 
##     filter, lag

## The following objects are masked from 'package:base':
## 
##     intersect, setdiff, setequal, union

## Warning: The `size` argument of `element_rect()` is deprecated as of
## ggplot2 3.4.0.
## ℹ Please use the `linewidth` argument instead.

## Warning: The `size` argument of `element_line()` is deprecated as of
## ggplot2 3.4.0.
## ℹ Please use the `linewidth` argument instead.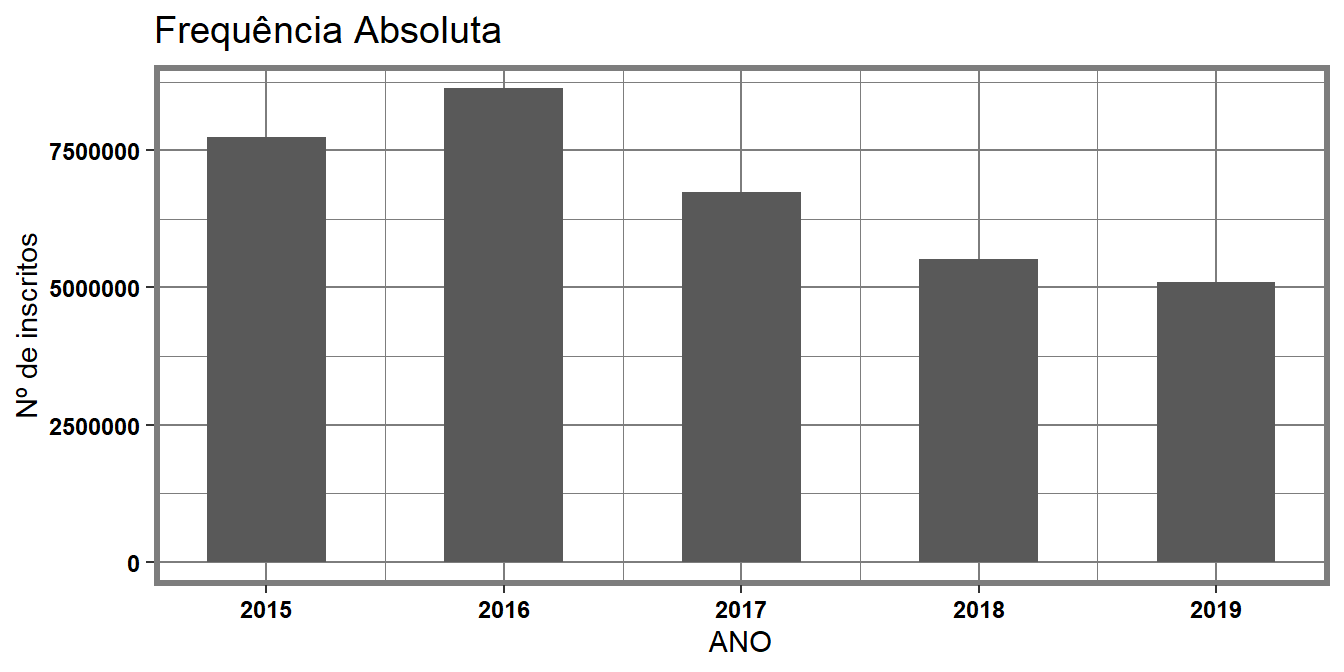

Figura 3.1: Número de inscritos no ENEM na capital baiana

A Tabela 3.1 mostra os mesmos dados apresentados na Figura 3.1. Note que nenhuma informação visual é passada para destacar os anos com mais ou menos participantes. Além disso, torna-se mais perceptível através da visualização gráfica que ocorre a queda de inscrições no ENEM entre os anos de \(2016\) e \(2019\). O gráfico de barras apresenta uma característica muito importante relacionado ao tamanho das barras, elas crescem proporcionalmente de acordo com as grandezas que referem, ou seja, quanto maior o valor maior será sua barra. Comumente, essas barras apresentam a mesma largura neste tipo de gráfico.

Tabela 3.1: Número de inscritos no ENEM em Salvador

Ano	Nº Inscritos
2015	159835
2016	175873
2017	121063
2018	93852
2019	88557

É através da Figura 3.1 que podemos responder à primeira pergunta: “A quantidade de estudantes que realizaram o ENEM aumentou de 2015 para 2019 na capital baiana?”

Com um grau de segurança é possível afirmar que não aumentou a quantidade de estudantes que realizaram o ENEM neste período.

Apesar do número de estudantes crescer de 2015 para 2016, observa-se uma queda do número de inscritos no ENEM de Salvador, chegando a diminuir pela metade este número de 2016 para 2019.

Essa resposta pode levar a novos questionamentos, por exemplo, “O que realmente motivou essa queda?”. Infelizmente, encontrar a resposta para este questionamento não é tão simples, requer pesquisas mais específicas sobre o tema, o que foge do objetivo deste capítulo. Todavia, é interessante refletir como a partir de um simples gráfico, podemos alcançar perguntas ainda mais complexas.

Agora que respondemos a primeira questão, podemos perceber que a pergunta “Como é a distribuição de estudantes em Salvador por cor/raça?Conseguimos identificar algum padrão para esses valores?” está relacionada àquele resultado. Inicialmente, para entender essa relação, precisamos conhecer como as quantidades de estudantes se distribuem em função da identidade de raça no questionário no ENEM. Portanto, trata-se de uma avaliação à respeito da autoidentificação racial do estudante no momento da inscrição do ENEM. As opções do formulário do ENEM são limitadas a 6 opções de respostas:

• Não declarado;
• Pardo;
• Preta;
• Branco;
• Amarelo;
• Indígena.

No Capítulo 2, definimos como uma variável categórica aquela que apresenta uma quantidade finita de opções, como aquelas opções para auto identificação de raça no formulário do ENEM.

Guiados inicialmente por uma lógica do senso comum, é possível esperar que a redução do número de estudantes resulte na redução proporcional do número de estudantes nas diferentes categorias da identificação racial.

Contudo, esta avaliação pode ser precipitada. É preciso investigar os efeitos da redução do número de inscritos no ENEM sobre as diferentes categorias.

Como tivemos uma diferença expressiva do número de inscritos entre os anos de 2016 e 2019 (ver Figura 3.1), é possível explorar os principais efeitos sobre as diferentes categorias de identidade racial.

Por meio da Figura 3.2, são apresentados os valores absolutos da quantidade de estudantes que realizaram o ENEM em cada ano, identificados pela sua raça. Note que a grande queda encontrada na Figura 3.1 se reflete neste gráfico também.

A comparação entre os anos de 2016 e 2019 revela que há redução do número de inscritos em todas as categorias de identidade racial. Por exemplo, a quantidade de pessoas pardas que realizaram o ENEM caiu quase pela metade, assim como as pessoas autodeclaradas pretas. Além disso, podemos observar uma baixíssima quantidade de pessoas indígenas e amarelas que realizaram este exame. Também podemos notar que, em sua grande maioria, os estudantes da capital baiana se declaram como pardos e pretos.

## Scale for fill is already present.
## Adding another scale for fill, which will replace the existing
## scale.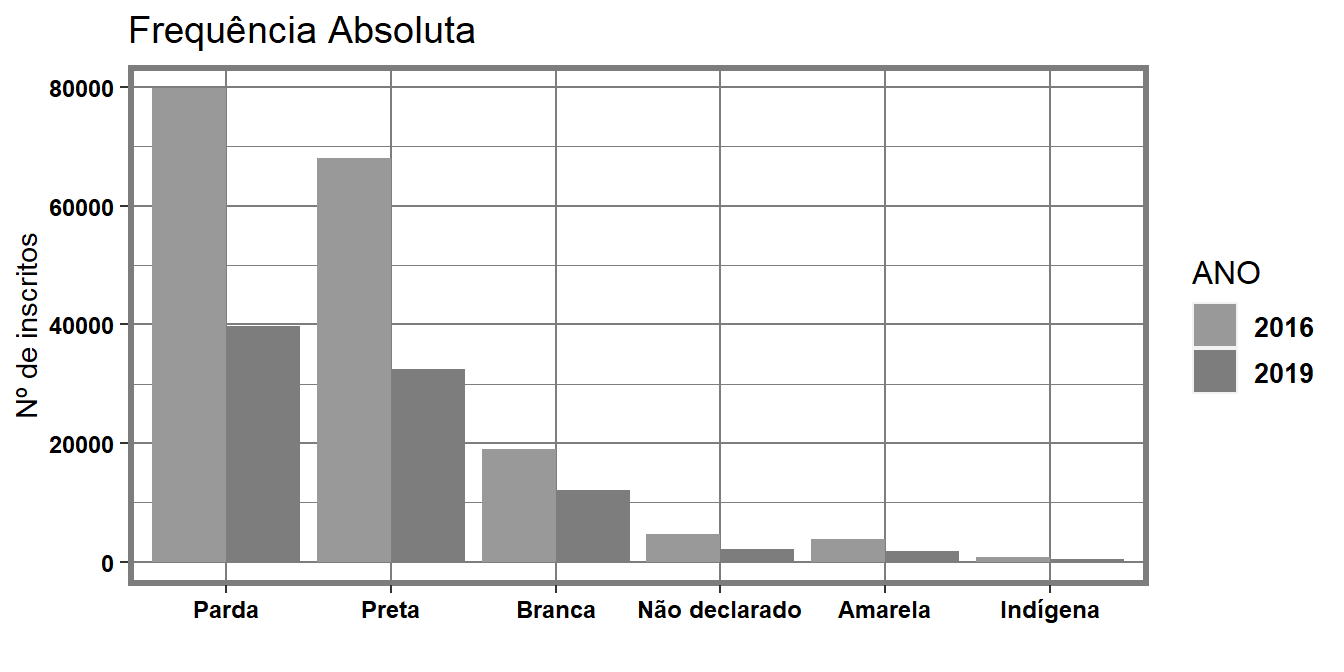

Figura 3.2: Distinção de estudantes inscritos por cor/raça da cidade de Salvador para os anos de 2016 e 2019

Segundo o Instituto Brasileiro de Estatística e Geografia (IBGE), em uma pesquisa realizada no segundo semestre de 2017, Salvador é considerada a capital mais preta do Brasil, onde 8 em cada 10 moradores se autodeclararam de cor preta ou parda.

Na Figura 3.2 exploramos uma das principais funções do gráfico de barras, dimensionar variáveis categóricas de acordo com a frequência de ocorrência de suas categorias.

Frequência para uma variável categórica pode ser definida como a quantidade de vezes que ela é representada, podendo ser apresentada como absoluta ou relativa.

A frequência absoluta se trata da representação da quantidade de vezes que cada categoria ocorre. Este tipo de frequência é trabalhada na Figura 3.2, onde apresentamos a quantidade de estudantes por cor/raça que realizaram o ENEM nos anos de 2016 e 2019. Ainda na Figura 3.2, conseguimos notar que todas as categorias apresentaram uma queda na quantidade de estudantes que realizaram em 2016 para 2019, mas se quisermos comparar este valores ainda utilizando um gráfico de barras, seria possível?

Uma possibilidade é o uso da frequência relativa, que consiste na razão entre a frequência absoluta de uma determinada categoria pela soma da frequência de todas as categorias, sendo representada pela equação a seguir:

\[Frequência\ Relativa\ (\%) = 100*\frac{\text{frequência absoluta de uma categoria}}{\text{soma da frequência absoluta de todas as categorias}}\]

Note que não foi mencionado o valor 100 presente na fórmula. Ele é apresentado para tornar o resultado da frequência relativa em porcentagem. Para compreender melhor este conceito apresentado, vamos continuar respondendo a segunda questão utilizando agora este novo aprendizado.

Mas fique atento, cada deve ser avaliado separadamente. Vamos avaliar primeiro para o ano de 2016 apenas na Figura 3.3.

## Scale for fill is already present.
## Adding another scale for fill, which will replace the existing
## scale.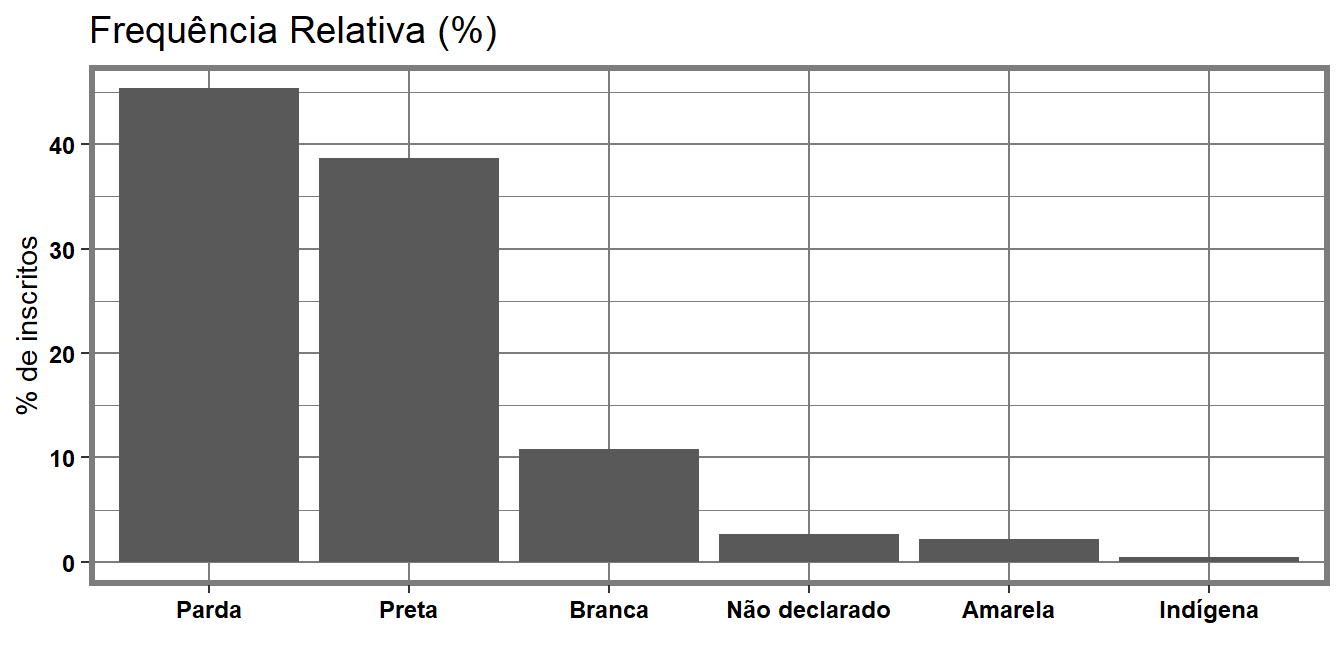

Figura 3.3: Frequência relativa percentual desagregados por auto identificação racial (2016)

A Figura 3.4 pode ser vista como uma extensão da Figura 3.2, utilizando a frequência relativa que ajuda a evidenciar características que apenas com a frequência absoluta não é possível, como a variação da proporção de estudantes em uma das categorias de auto identificação de raça/cor. Ao analisar a Figura Figura 3.4 nota-se que o percentual dos autoidentificados como raça cor/branca cresceu quando se compara 2016 e 2019. Sendo esta categoria a única que teve crescimento, enquanto a maior redução ocorreu para os grupos que se autoidenticam com a raça/cor preta.

Transcrevendo a fórmula da frequência relativa apresentada anteriormente, temos:

## Scale for fill is already present.
## Adding another scale for fill, which will replace the existing
## scale.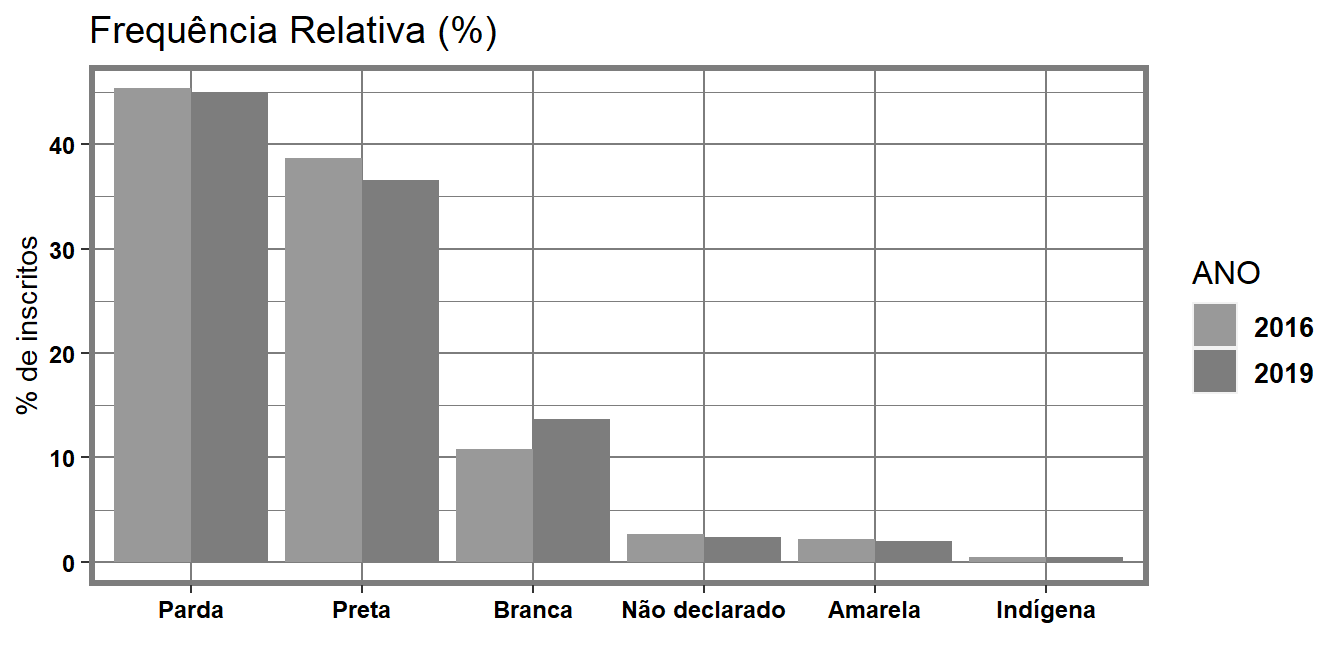

Figura 3.4: Comparação entre os estudantes inscritos de Salvador por cor/raça para 2016 e 2019

Podemos identificar, por exemplo, que com exceção dos estudantes autodeclarados de cor branca, todas as outras raças apresentaram uma proporção de aproximadamente 50%, ou seja, o número de estudantes pardos, pretos, amarelos, indígenas e não declarados caíram pela metade em comparação ao ano de 2016. Esta informação confirma ainda mais o resultado apresentado na Figura 3.1, mostrando que ocorreu uma grande queda na quantidade de inscrições no geral, porém isso é verificado com maior intensidade entre estudantes não declarados brancos.

Vimos até aqui que a escolha do gráfico está relacionado com as perguntas e dados disponibilizados e que por vezes é necessário realizar alguma transformação de variáveis para que o uso dos gráficos seja mais eficiente.

Nesta seção utilizamos gráficos de barras para avaliar uma série temporal, para comparar a quantidade de indivíduos em diferentes categorias. E por fim, comparamos e diagnosticamos que além da redução do número de inscritos no ENEM, por meio da frequência relativa foi possível identificar no gráfico que uma da categorias teve a maior redução proporcional e outro teve um aumento proporcional. Assim é possível visualizar que alguns grupos sociais são mais prejudicados em períodos de redução das inscrições gerais.

Nas próximas seções analisaremos como esses resultados ocorreram ao longo dos anos entre 2016 e 2019, para isto usaremos outros tipos de gráficos.

3.3 Gráfico de tendências

Na seção anterior, utilizando gráficos de barras conhecemos os dados de inscritos no ENEM ao longo dos anos. Também com aquele tipo de gráfico comparamos as mudanças entre a proporção de inscritos entre os anos de 2016 e 2019. Nesta seção exploraremos os detalhes ao longo dos anos para cada uma das categorias de raça/cor. Os dados desagregados pelos anos 2015 à 2019 e pelas categorias de raça/cor formam um conjunto maior que aquele apresentado na seção anterior. Além disso, para investigar mais detalhadamente as questões:

• A quantidade de estudantes que realizaram o ENEM aumentou de 2015 para 2019 na capital baiana?
• Como é a distribuição de estudantes em Salvador por cor/raça?Conseguimos identificar algum padrão para esses valores?

é preciso um tipo de gráfico que auxilie na construção da ideia de um comportamento geral ao longo do tempo. Para isto utilizaremos o gráfico de tendências. Este tipo de gráfico trata a visualização de uma coleção de observações realizadas ao longo do tempo para acompanhar um evento ou processo. Por se tratar de uma coleta sequencial, ou seja, feita uma após a outra, o fator de ordem é fundamental. Logo, devemos estabelecer uma relação gráfica entre o tempo e o valor da variável observada.

Este conceito será importante para expandir as análises realizadas apenas com os anos de 2016 e 2019 para a participação dos estudantes de Salvador por cor e raça apresentadas através dos gráficos de barras na seção 3.2. Será que através deste tipo de gráfico podemos avaliar como a quantidade de inscrições por raça/cor se comportou (aumentou ou diminuiu) de 2015 à 2019?

Note que realizamos este mesmo conceito no início da seção 3.2 demonstrando o número absoluto de inscrições no ENEM na capital baiana de 2015 até 2019, porém, ao avaliar-se vários anos e possibilidades de raça/cor, a utilização do gráficos de barras não demonstra ser a melhor opção, pois a visualização se torna mais difícil de ser interpretada.

Antes de mergulhar na análise desses dois questionamentos utilizando o gráfico de tendências, é importante explorar mais um conceito novo por meio da comprrensão alguns conceitos, começaremos pelo plano cartesiano.

A Figura 3.5 apresenta um plano cartesiano simplificado. São definidos dois eixos principais sendo eles o eixo horizontal e o eixo vertical. Cada eixo pode demonstrar o comportamento de uma variável desejada: para o eixo horizontal, à medida que caminhamos para a direita (\(\rightarrow\)) o valor aumenta e quando caminhamos para a esquerda (\(\leftarrow\)) o valor diminui. No eixo vertical, quando caminhamos para cima (\(\uparrow\)) o valor aumenta e quando caminhamos para baixo (\(\downarrow\)) o valor diminui. Ter esse conceito em mente será importante para as análises futuras.

Figura 3.5: Plano cartesiano simplificado

O gráfico apresentado na Figura 3.6 fortalece ainda mais a resposta trazida para o primeiro questionamento, o número de estudantes que realizaram este exame não vem aumentando nos últimos cinco anos. É observada uma queda acentuada de 2016 para 2019. Porém, através da análise dessa tendência, é possível verificar que a maior redução ocorreu entre os anos de 2016 e 2017, com uma diminuição de mais de 50 mil inscrições. Esse gráfico mostra que a tendência de queda no ENEM não ocorreu de forma abrupta de 2016 para 2019, mas de forma gradual, já que a partir de 2016 os valores apenas diminuíram, sendo 2019 o menor deles.

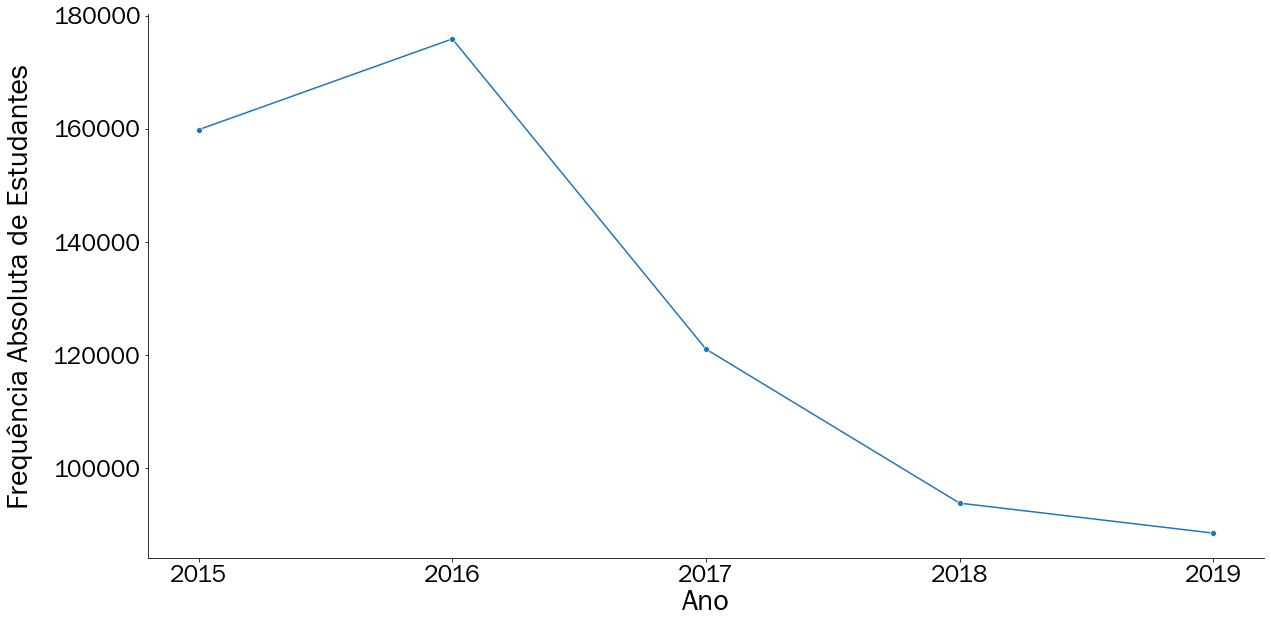
Figura 3.6: Quantidade de estudantes inscritos no ENEM na capital baiana

Ainda neste gráfico, podemos extrair um conceito bem interessante referente a este tipo de visualização: o pico. O pico pode ser definido como o maior valor identificado em um determinado período. No nosso caso, o pico de inscrições no ENEM em Salvador ocorreu em 2016, pois é o maior valor verificado dentro deste intervalo de cinco anos.

A Figura 3.7 é endereçada ao segundo questionamento. Podemos notar que a tendência das duas primeiras curvas, referente às cores parda e preta dos estudantes de Salvador, seguem um padrão similar ao que foi apresentado na Figura 3.6. Ocorre um pico em 2016 e a partir desse ano os valores decaem gradualmente. Porém este padrão fica bem claro para essas duas primeiras curvas, enquanto as outras se mostram aparentemente retilíneas, ou seja, não demonstram grandes mudanças. Esse tipo de oconslusão deve ser observado com detalhes, pois podemos acreditar que, para as outras opções, não ocorreu nenhuma mudança ao longo do tempo. A dificuldade em concluir sobre as outras categorias está relacionada à grandeza de suas respectivas curvas. A ordem de grandeza dos valores das categorias preta e pardo produzem um efeito visual que permite observar apenas grandes variações, contudo, categorias de pessoas indigenas e amarelas tem um número de inscritos de ordem grandeza bem menor, portanto, as variações ficam quase imperceptíveis. Talvez você já enfrentado esta dificuldade ao tentar encontrar sua cidade no mapa do Brasil sem dar “zoom” no seu celular. Cidades tem ordens de grandeza bem menor que um país como o Brasil.

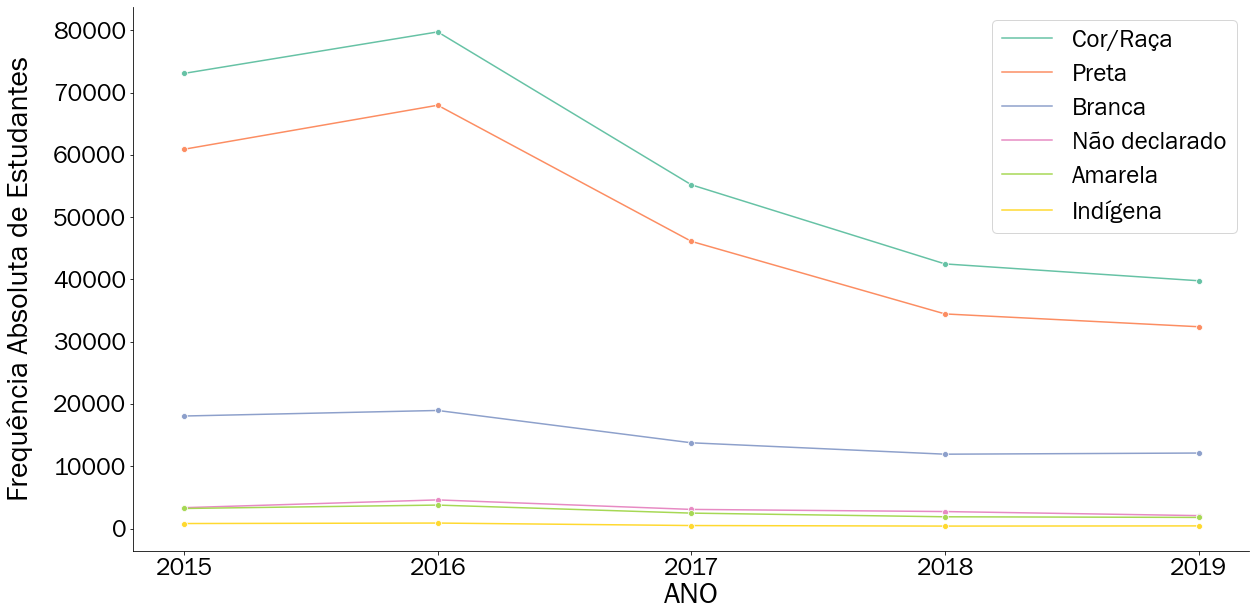
Figura 3.7: Tendência da quantidade de estudantes inscritos no ENEM por cor de 2015 até 2019

Para melhor visualização e discussão à respeito da questão

• Como é a distribuição de estudantes em Salvador por cor/raça?Conseguimos identificar algum padrão para esses valores?, cada curva foi separada de acordo com a raça que ela representa.

Na Figura 3.8 conseguimos notar a diferença de grandezas que foi mencionado anteriormente ao visualizar o eixo vertical (frequência absoluta de estudantes). Para a cor parda, por exemplo, é possível enxergar valores próximos de setenta e cinco mil estudantes enquanto que para a cor amarela os valores ficam próximos de três mil estudantes, mostrando assim uma grande disparidade. Ao separar os gráficos, cada um consegue ter sua própria escala, diferente da Figura 3.7 onde todos compartilhavam o mesmo eixo.

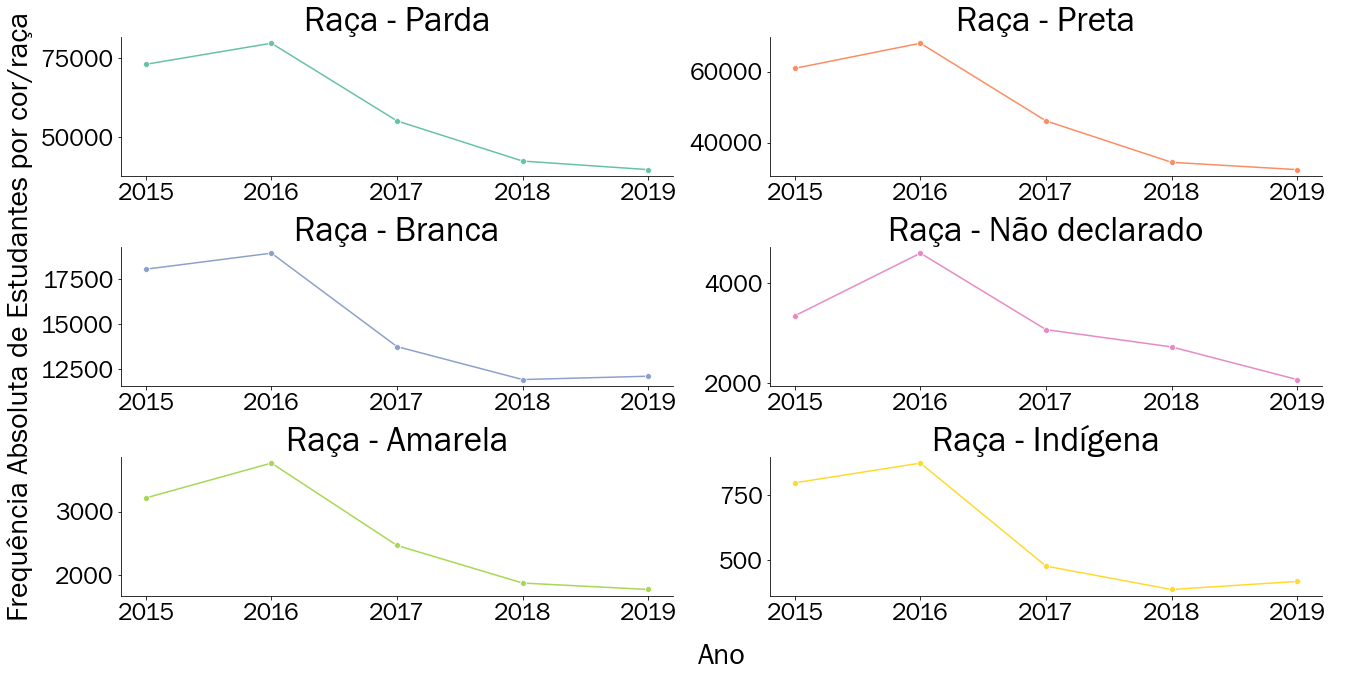
Figura 3.8: Tendência da quantidade de estudantes inscritos no ENEM particionado por cor de 2015 até 2019

Verifica-se que as categorias parda, preta, amarela e as pessoas não declaradas seguem o padrão verificado dos estudantes inscritos em Salvador exposto na Figura 3.6. Ocorre um pico em 2016, e a partir desse período os números de inscrições apenas caem. Todavia, para as pessoas de cor branca e indígena o padrão se mantém, porém, difere em 2019, onde ocorre um leve aumento em comparação ao ano anterior. Esse aumento no entanto é bem diferente ao considerar a ordem de grandeza entre as raças. Enquanto que para cor branca esse valor aumenta em torno de doze mil estudantes, para os indígenas eles aumentam em torno de 400 estudantes, ou seja, por mais que ambas as inscrições tenham aumentado, o número de inscritos de cor branca é aproximadamente 30 vezes maior que o número de inscritos indígenas.

Através dessa análise gráfica conseguimos compreender e acompanhar como o número de inscritos no ENEM em Salvador veio se alterando nos últimos anos. Essa análise poderia ser utilizada para justificar tomadas de decisão na área da educação, buscando formas de aumentar a participação de estudantes no ENEM, através de programas sociais de fomento à educação. Além disso, é interessante ressaltar a importância deste exame para o ingresso nas instituições de ensino superior do país, onde em Salvador, infelizmente é mostrado uma tendência de saída dos estudantes nesse exame, principalmente aqueles de cor/raça preta e parda. Essa situação apresenta ainda mais a importância de integrar esses indivíduos para compreender a causa/motivo dessa evasão.

3.4 Gráfico de setores

Nas seções anteriores, conseguimos entender melhor o panorama dos estudantes de Salvador inscritos no ENEM nos últimos anos e como seus valores foram sendo alterados de acordo a quantidade e raça. Agora iremos avaliar o terceiro questionamento proposto no estudo de perfil: “Na dita era da informação, onde tudo está conectado, como está o acesso dos estudantes a internet em suas residências? E a computadores pessoais?”. Essa pergunta é importante, pois acredita-se que hoje tudo está conectado e que o acesso a essas ferramentas, facilitadoras do aprendizado, é algo comum a todos, mas … será? É possível que todos os estudantes do ENEM possuam fácil acesso as essas ferramentas no dias atuais? Iremos buscar responder este questionamento no decorrer deste capítulo.

Para isso será apresentado uma nova modalidade gráfica: o gráfico de setores. Este gráfico, usado comumente com variáveis categóricas, apresenta sua forma mais comum equivalente ao desenho de uma “pizza”, onde cada fatia é referente a uma determinada categoria e seu tamanho é proporcional a sua representatividade. Para responder o primeiro questionamento, relacionado ao acesso da internet, vamos verificar um cenário mais atual e um cenário mais antigo, sendo respectivamente 2019 e 2015. Será que ocorreu melhorias no acesso à internet pelos estudantes do ENEM em Salvador?

Na Figura 3.9 é apresentada a frequência relativa dos estudantes com e sem acesso a internet de acordo ao total de estudantes soteropolitanos inscritos naquele ano. O uso da frequência relativa neste caso permite uma melhor comparação entre os anos e os resultados foram positivos: Em 2015 tinhamos \(72,6\%\) estudantes com acesso a internet e esse valor aumentou para \(84,7\%\) em 2019, mostrando uma melhora de \(12,1\%\)! Essa melhora é mostrada visualmente atráves do tamanho da fatia referente a resposta “Sim” de 2015 para 2019. Este resultado pode estar associado a diversos fatores como mais acessibilidade a esta ferramenta como a redução de custos, aperfeiçoamento dos projetos sociais de inclusão digital e etc. Deixamos a cargo do leitor buscar compreender os motivos que levaram a melhora nestes resultados.

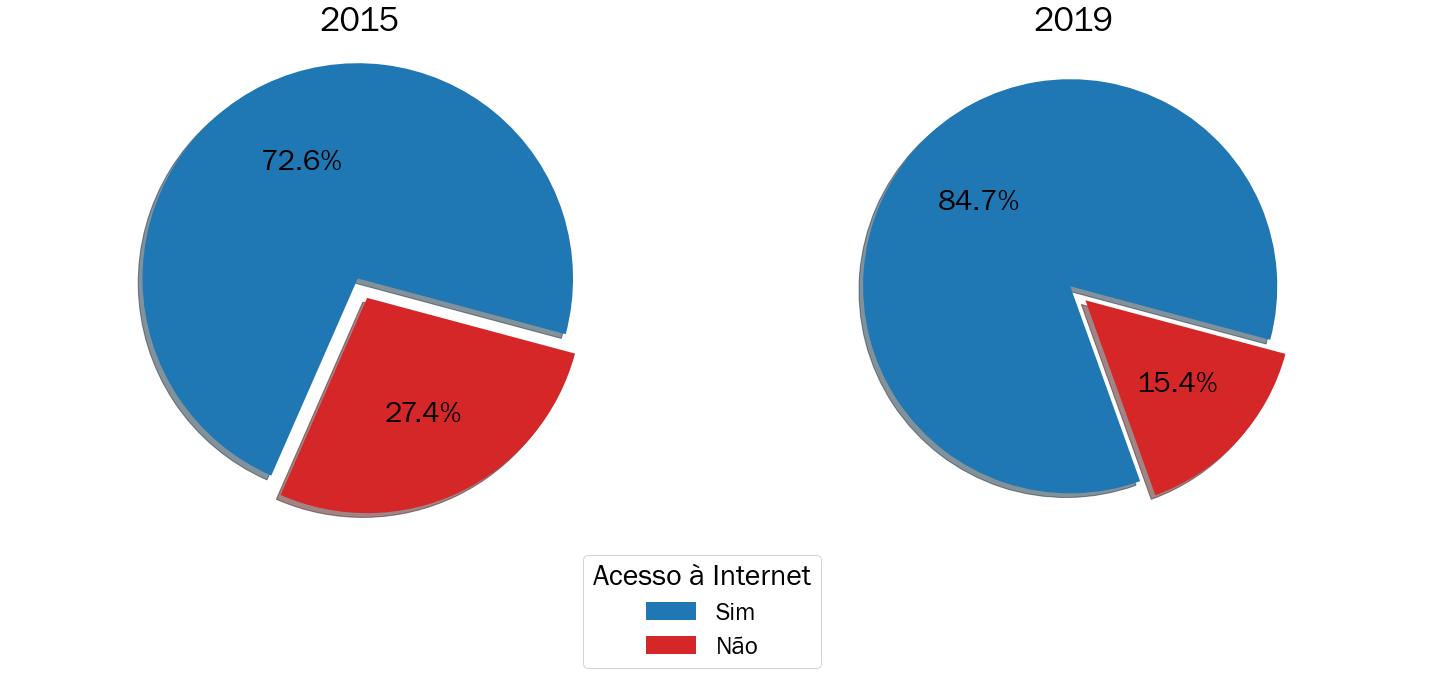
Figura 3.9: Porcentagem de estudantes inscritos no ENEM em Salvador com acesso a internet em 2015 e 2019

Note que neste tipo de gráfico, ao utilizar frequência relativa, é necessário que a soma dos valores em todos os setores seja igual a 100%, isso não ocorre para o ano de 2015 devido a aproximação decimal utilizada de uma casa decimal.

Conseguimos encontrar parte da resposta do terceiro questionamento: “Na dita era da informação, onde tudo está conectado, como está o acesso dos estudantes a internet em suas residências?” E a resposta é que o acesso dos estudantes inscritos no ENEM à internet melhorou de 2015 para 2019, mas e o acesso a computadores pessoais em suas residências? Vamos utilizar novamente os anos de 2015 e 2019 para continuar esta pergunta:

Na Figura 3.10 podemos verificar que o questionário do ENEM em relação a esta pergunta possui 5 respostas representativas. Todavia, diferente do acesso a internet conseguimos avaliar que a fatia referente aos estudantes que possuem pelo menos um computador pessoal diminuiu de \(61,5\%\) em 2015 para \(46,1\%\) em 2019 enquanto o número de estudantes que não possuiam nenhum computador pessoal em sua residência aumentou de \(28,1\%\) em 2015 para \(43,6\%\) em 2019. A diferença entre essas duas proporções são semelhantes: enquanto uma fatia caiu \(15,4\%\) a outra aumentou \(15,5\%\) respectivamente. Esse resultado, associado ao encontrado na Figura 3.9 pode indicar que o acesso a internet realizado pelos estudantes podem surgir de outra fonte: o telefone celular, visto a queda considerável no acesso a computadores pessoais durante o mesmo período.

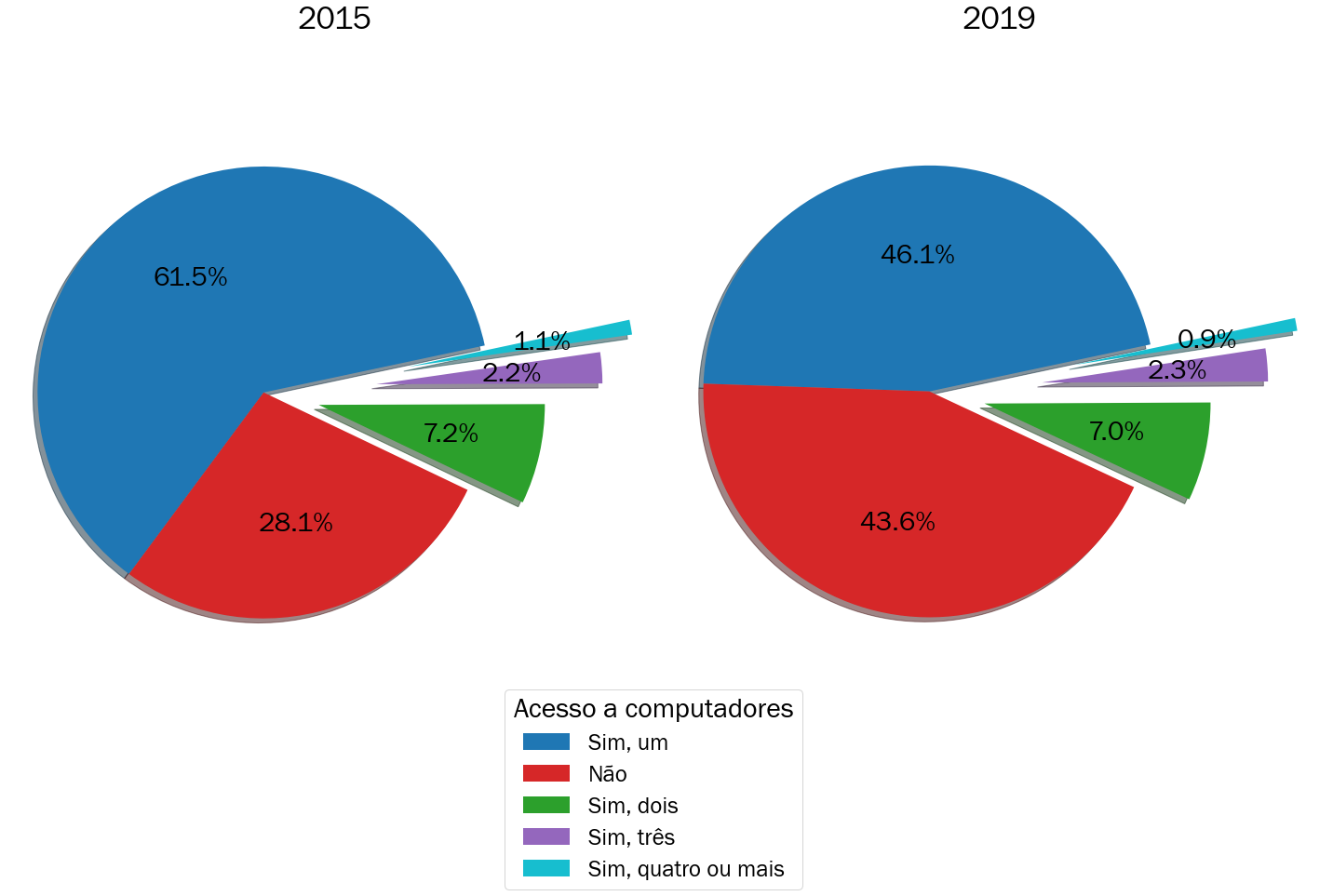
Figura 3.10: Porcentagem de estudantes inscritos no ENEM em Salvador com acesso a computadores pessoais em 2015 e 2019

Ainda na Figura 3.10, podemos avaliar que algumas fatias, referentes a estudantes com mais de um computador pessoal, são menos representativas dado o seu tamanho. Essa situação indica um dos problemas ao utilizar este tipo de visualização: quando uma variável possui muitas categorias ou categorias com pouca representatividade pode dificultar a visualização das informações para o leitor. Em casos como esse uma das recomendações é a utilização dos gráficos de barras. Porém existem outras formas de melhorar essa visualização: Como vimos que as categorias mais dominantes se referem aos estudantes sem ou com pelo menos um computador em casa, vamos juntar as categorias: “Sim, dois”, “Sim, três” e “Sim, quatro ou mais” em uma só categoria: “Sim, mais de um”. Será que isso pode melhorar a visualização do gráfico anterior?

Na Figura 3.11 é apresentado o resultado desta alteração. A confecção dessa nova categoria permitiu encontrar uma informação implícita no gráfico anterior: a proporção de estudantes com mais de um computador pessoal em casa se manteve praticamente constante de 2015 para 2019. Isso fortalece ainda mais a narrativa de uma queda na proporção de pessoas com pelo menos um computador pessoal em casa para a proporção de pessoas sem computador pessoal. Esse tipo de informação pode ser utilizada em programas sociais ou intervenções para reverter este quadro e entender quem são as pessoas que sofrem deste tipo de necessidade digital.

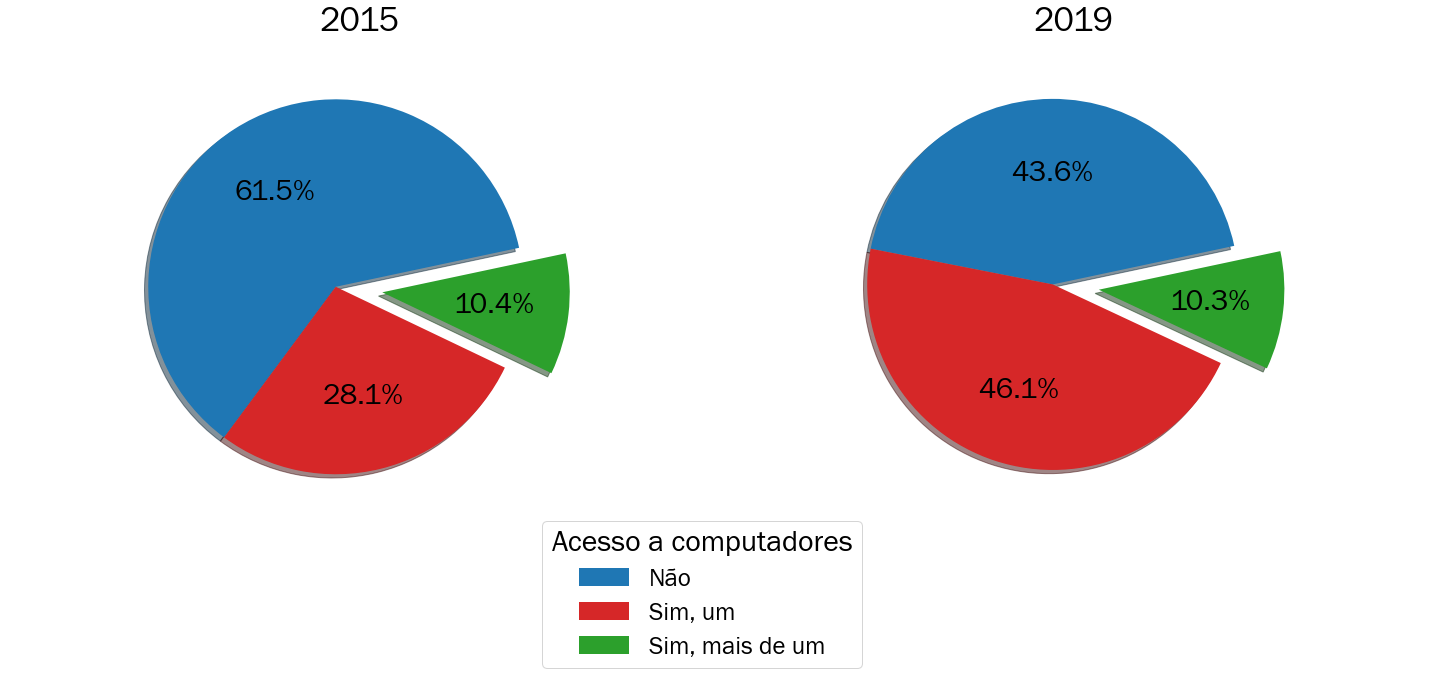
Figura 3.11: Porcentagem de estudantes inscritos no ENEM em Salvador com acesso a computadores pessoais em 2015 e 2019

Neste momento o leitor pode estar se questionando: Seria possível unir os dois resultados avaliados para este questionamento, acesso à internet e computador pessoal, em um só gráfico? Abaixo é mostrado que sim, podemos.

Na Figura 3.12 são mostradas as proporções de estudantes de Salvador que não possuem acesso à internet em 2015 e 2019 em relação ao acesso de computador pessoal. Podemos extrair deste gráfico algumas informações:

• Pode existir alguma incongruência na construção dessa base de dados, pois existem estudantes com mais de um computador pessoal, porém sem acesso à internet o que pode gerar questionamentos. Essa situação pode apresentar diversos motivos e uma das hipóteses mais plausíveis seria algum erro do estudante ao responder este questionário.
• É possível verificar que a maioria dos estudantes sem acesso à internet também não possui computadores pessoais em casa. Esta proporção cresce de \(78,8\%\) em 2015 para \(88,8\%\) em 2019 seguido pela queda da proporção de estudantes que possui pelo menos um computador pessoal em casa.

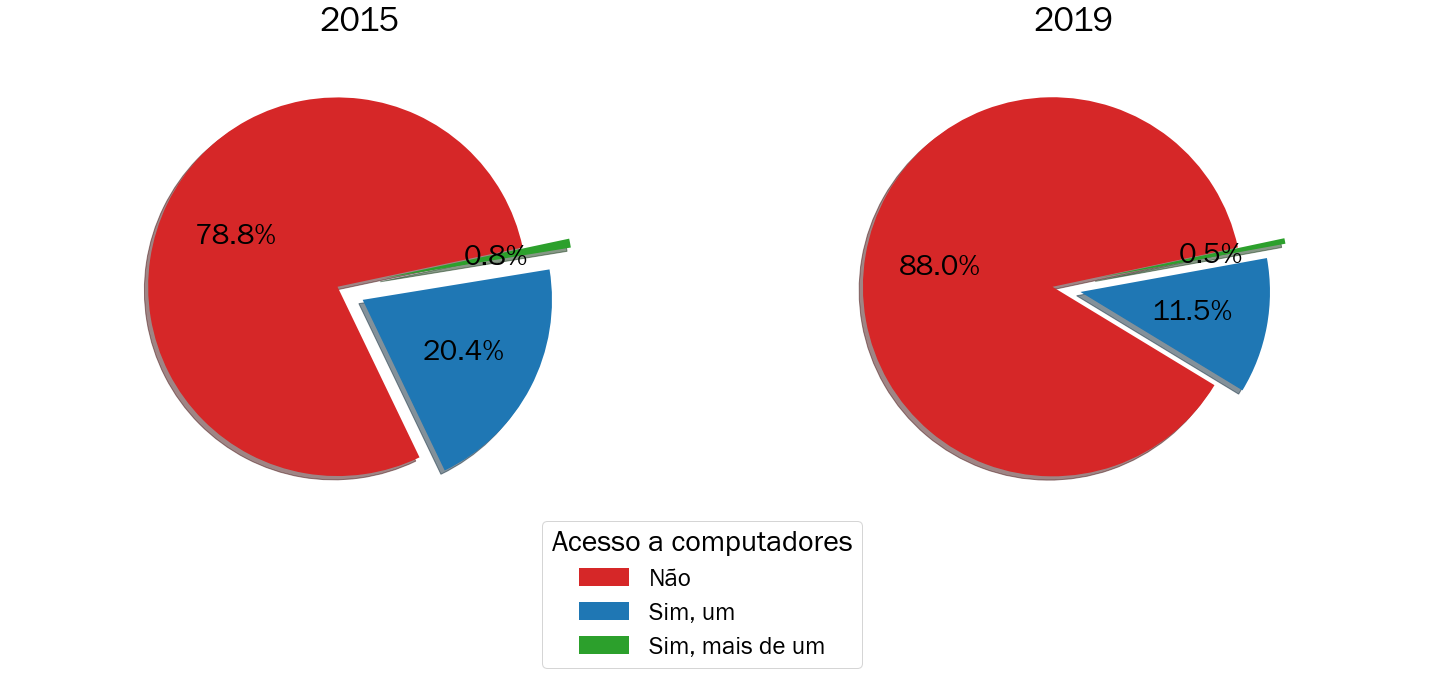
Figura 3.12: Porcentagem de estudantes inscritos no ENEM em Salvador sem acesso à internet em relação ao acesso a computadores pessoais em 2015 e 2019

Essas informações podem indicar uma possível correlação, conceito que será estudado em capítulos futuros e de grande importância na área de ciência de dados. Assim é possível concluir o terceiro questionamento, que nessa era digital as situações melhoraram em partes: ocorreu um aumento, em termos proporcionais, de estudantes com acesso à internet, porém em contrapartida ocorreu um aumento de estudantes sem acesso a pelo menos um computador pessoal em suas residências o que pode dificultar sua navegação e uso desta ferramenta para o seu aprendizado.

3.5 Gráfico de dispersão

Até o momento conseguimos observar os dados e refletir sobre três dos quatro questionamentos referente ao perfil dos estudantes de Salvador que realizaram o ENEM. Para responder o quarto questionamento: “O tipo de escola (pública ou privada) pode influenciar nas notas dos estudantes neste exame?” vamos utilizar uma nova ferramenta visual: o gráfico de dispersão. Para entender os motivos da escolha desta ferramenta precisamos antes apresentar seu conceito.

Gráficos de dispersão se tratam de representações usando duas ou mais variáveis através das coordenadas cartesianas para exibir valores de um conjunto de dados. Para ficar mais claro este conceito, vamos focar em responder o quarto questionamento utilizando as notas dos estudantes de Salvador no ano de 2019, considerando apenas aqueles que:

• Apresentaram uma pontuação maior que zero em todas as provas, com exceção no exame de Redação;
• Definiram o tipo de colégio no ensino médio: público ou privado.

Essas condições foram colocadas para evitar valores atípicos nas análises, pois apenas pessoas ausentes no exame possuem suas notas zeradas (com exceção da nota em Redação) e para focar nossa nossa análise em estudantes de escolas públicas e privadas, desconsiderando aqueles que optaram por não informar o tipo de colégio. Além disso é importante mencionar que no ano de 2019, cerca de \(75\%\) dos estudantes de Salvador não responderam a questão referente ao tipo de colégio, logo as análises apresentadas aqui representam cerca de \(25\%\) dos estudantes inscritos no ENEM 2019 na capital baiana, ou seja, 15996 estudantes no total sendo 10760 de escola pública e 5236 de escola privada.

Inicialmente, será mostrado um gráfico de dispersão para as provas da área de exatas: matemática e ciências naturais, mas não se assuste! O gráfico será explicado passo a passo.

Na Figura 3.13 são apresentadas as notas dos estudantes de Salvador em matemática no eixo vertical e no eixo horizontal as notas em ciências naturais, destacando em cores o tipo de colégio: azul escola pública e em amarelo escola privada totalizando assim três variáveis representadas em uma só imagem. Neste gráfico de dispersão são contemplados todos os estudantes que atenderam todos os requisitos expressos anteriormente, onde cada estudante é representado por um ponto de coordenada \((x,\ y)\) ou se preferir \((nota \ em \ ciências \ naturais, \ nota \ em \ matemática)\). Como o ENEM funciona por pontuação, o aluno que apresentar as maiores pontuações em todas as provas possui maior vantagem na escolha de um curso superior, ou seja, os estudantes com melhor rendimento são aqueles que se aproximam do canto superior direito. Apesar desta modalidade gráfica ser bem simples, ela pode trazer resultados interessantes e intuitivos. Através da Figura 3.13 podemos verificar que a maioria dos estudantes de escolas públicas se localizam no canto inferior esquerdo, ou seja, estudantes com notas menores em ambas as provas e a medida que crescemos em ambos os eixos, mais dominante se tornam os estudantes de escolas privadas, mostrando um maior rendimento.

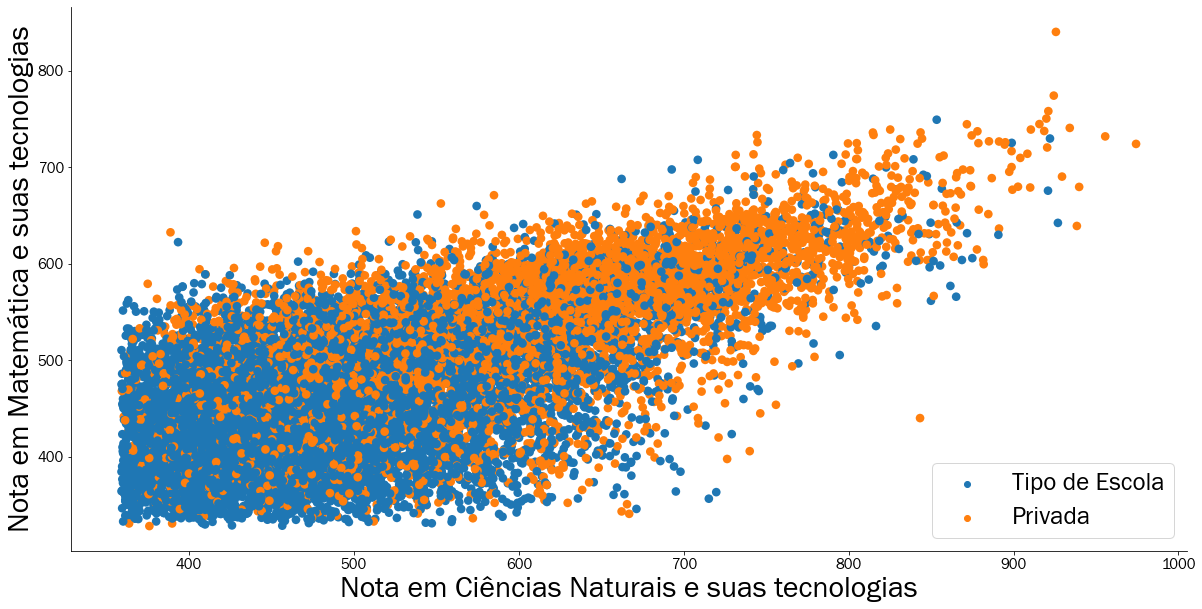
Figura 3.13: Relação entre nota de Ciências Naturais e Matemática particionado pelo tipo de escola em 2019

Além desta análise, no geral é possível verificar uma tendência crescente, onde ao aumentarmos a nota de matemática vemos que a maioria dos estudantes também aumentam a nota em ciências naturais. Compreender tendências deste tipo faz parte do dia a dia do cientista de dados, pois essas tendências são as mais comuns e intuitivas na natureza. Na Figura 3.14 é apresentado dois padrões: em vermelho está uma tendência linear crescente e em azul uma tendência linear decrescente representadas em um plano cartesiano.

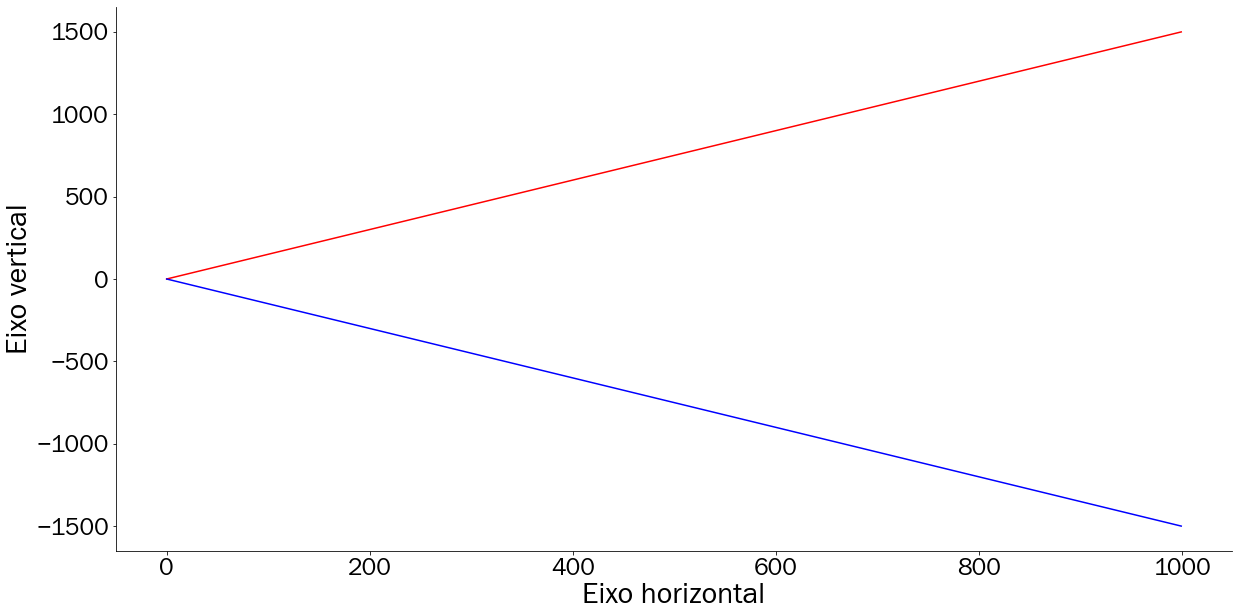
Figura 3.14: Tendências lineares em um plano cartesiano

É dito linear, pois seu comportamento lembra o formato de uma uma linha: mostra um padrão que está aumentando ou diminuindo a uma taxa constante (fixa).

Os termos crescente e descrescente se referem a como os valores de um eixo se comportam em relação ao outro: na tendência linear crescente, ao aumentarmos o valor em um eixo é esperado aumentarmos também o valor no outro eixo, já na tendência linear decrescente ocorre o inverso: ao aumentarmos o valor em um dos eixos, é esperado que o valor no outro eixo decaia na mesma proporção.

Na Figura 3.13 conseguimos visualizar o padrão exposto pela reta linear vermelha, ou seja, ao crescermos as notas em matemática, esperamos que cresça as notas em ciências naturais.

Através da Figura 3.13 verificamos que, de certa forma, o tipo de escola que o estudante frequentou possui um fato impacto nas notas dos estudantes de Salvador, porém este padrão se repete caso seja avaliado outra prova?

A Figura 3.15 apresenta o gráfico de dispersão entre a nota em matemática (eixo vertical) e a nota em Linguagens (eixo horizontal) semelhante a Figura 3.13 e o padrão se repete: no geral, os estudantes de escolas públicas apresentam um rendimento inferior aos estudantes de escolas privadas. Este conhecimento é importante para ressaltar a necessidade do aperfeiçoamento das escolas públicas no município e buscar formas de reverter ou equiparar este quadro que impacta de forma negativa padrões e classes sociais, dificultando o ingresso de estudantes de escolas públicas em cursos mais concorridos como Engenharia, Direito e Medicina.

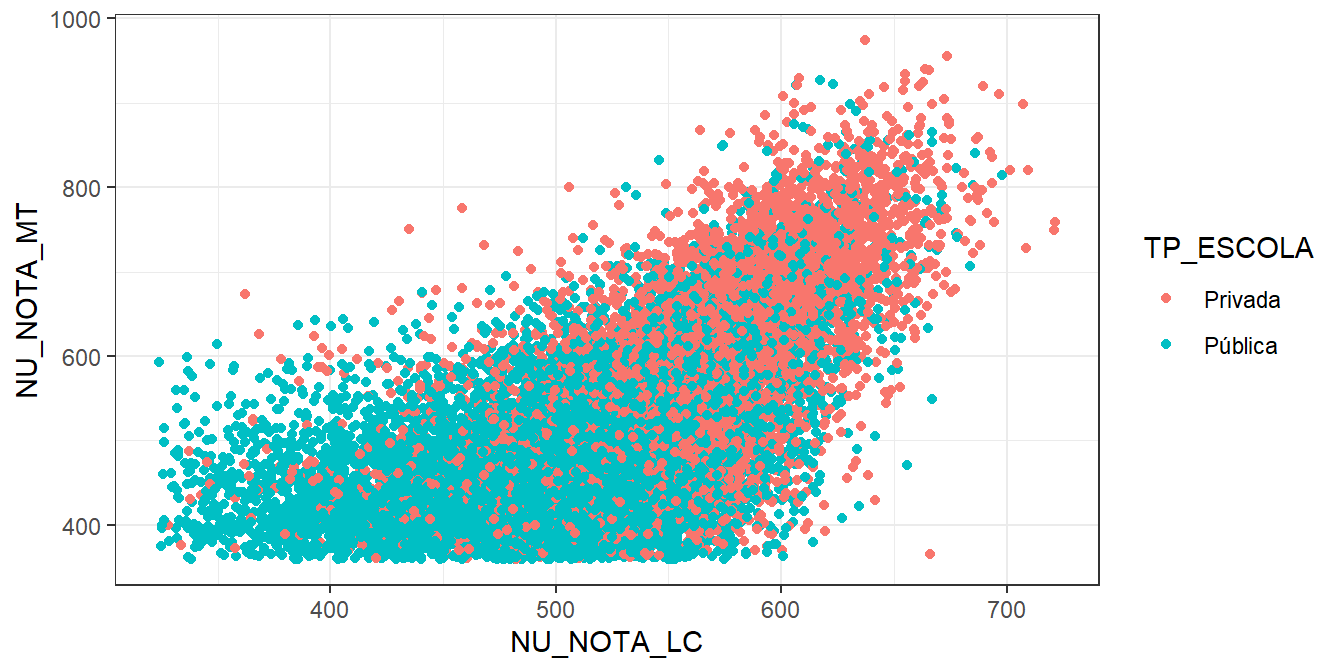
Figura 3.15: Relação entre nota de Linguagens e Matemática particionado pelo tipo de escola em 2019

3.6 Histograma

Para expandir ainda mais as discussões referentes ao quarto questionamento, vamos utilizar mais uma ferramenta gráfica de visualização: o histograma. Um histograma de um conjunto de dados numéricos se parece muito com um gráfico de barras apresentado anteriormente, embora tenha algumas diferenças importantes que examinaremos nesta seção.

A Figura 3.16 apresenta o histograma das notas dos estudantes de escolas públicas e privadas de Salvador em matemática no ano de 2019. No eixo horizontal está representado os valores numéricos das notas dos participantes agrupados em intervalos discretos. Fazendo um paralelo com o capítulo 2, o intervalo contínuo numérico estudado foi transformado para K valores categóricos/discretos. Este valor K pode ser definido pelo usuário de duas formas: um valor inteiro, onde o algoritmo irá particionar os números em K categorias de mesmo tamanho (largura), ou através de intervalos definidos pelo próprio usuário como foi feito na Figura 3.16 onde foi são definidos limites de 50 em 50 pontos começando em 300 pontos até 1000 pontos. Você pode perceber isso ao contar a quantidade de “caixinhas” que existem no histograma. Já o eixo vertical representa a quantidade de valores que estão em cada categoria, ou seja, quanto mais valores são representados por aquela classe maior será a altura de sua barra. Caso você esteja atento, provavelmente notou uma semelhança com a frequência absoluta apresentada durante a seção do gráfico de barras.

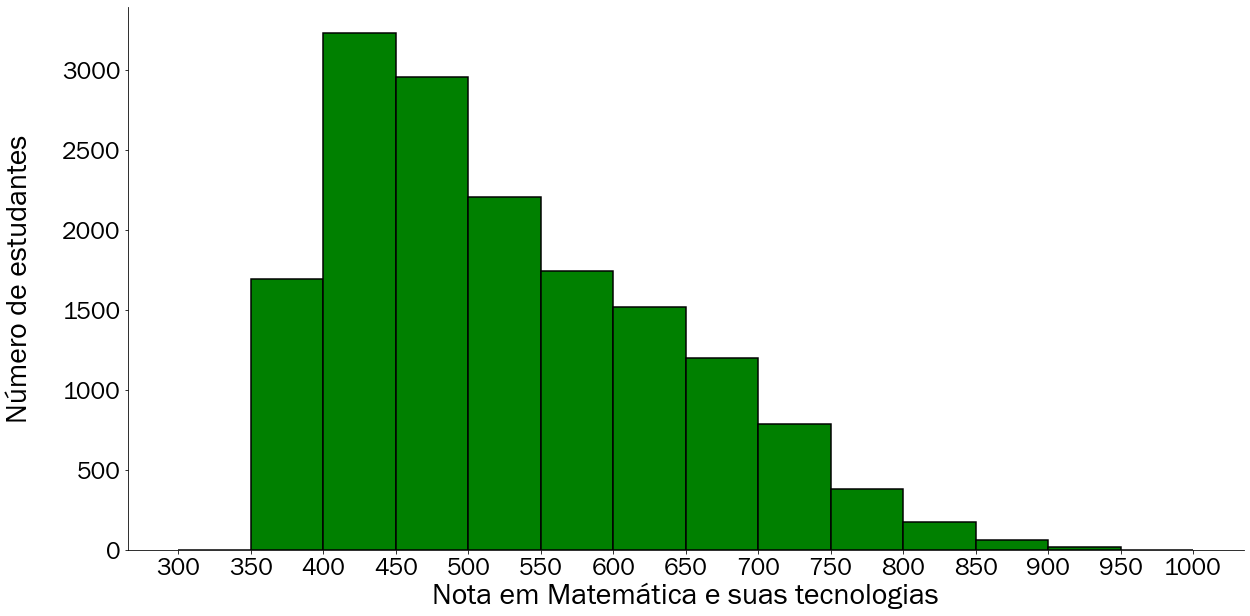
Figura 3.16: Histograma com as notas de matemática dos estudantes de escolas públicas e privadas de Salvador em 2019 de 300 à 1000 pontos com resolução de 50 pontos

Antes de discutirmos o quarto questionamento, é importante entender que ao avaliar um histograma é preciso compreender que cada barra representa uma categoria que define um intervalo numérico limitado. Esse intervalo é na maioria das vezes apresentado da seguinte forma:

\[[limite\ inferior,\ limite\ superior)\]

Onde o limite inferior representa o menor valor contido naquela categoria e limite superior o maior valor daquela categoria. Porém, na matemática os sinais \([\) e \()\) apresentam um significado específico, importantes para compreender a definição de uma categoria do histograma: o primeiro representa um intervalo fechado já o segundo um intervalo aberto.

Juntando todo este conhecimento é possível dizer que cada K categoria em um histograma contém seu limite inferior, mas não contém seu limite superior. Em outras palavras, uma determinada barra (categoria) não representa seu limite superior, logo uma categoria começa no limite inferior e termina no superior, sem incluí-lo.

Na 3.16 é possível observar que a medida que aumentamos a nota em matemática menos representativa se torna aquelas categorias, dificultando a visibilidade das barras. Além disso, o intervalo mais dominante se encontra na faixa entre 400 e 450 pontos. Caso seja desejado melhorar a resolução desses intervalos, será necessário realizar o aumento de categorias.

Ao utilizar um espaçamento de 25 pontos como apresentado na Figura 3.17 é possível identificar como mais precisão os intervalos de notas dos estudantes da cidade de Salvador. Podemos destacar agora, através da Figura 3.17 que o intervalo mais representado é aquele que começa em 425 pontos até 450 pontos. Isso foi possível graças ao aumento da quantidade de categorias por meio da diminuição do espaçamento de 50 pontos para 25 pontos. Porém este gráfico apresenta, sem distinção, estudantes de escolas privadas e públicas, mas separando encontramos valores diferentes?

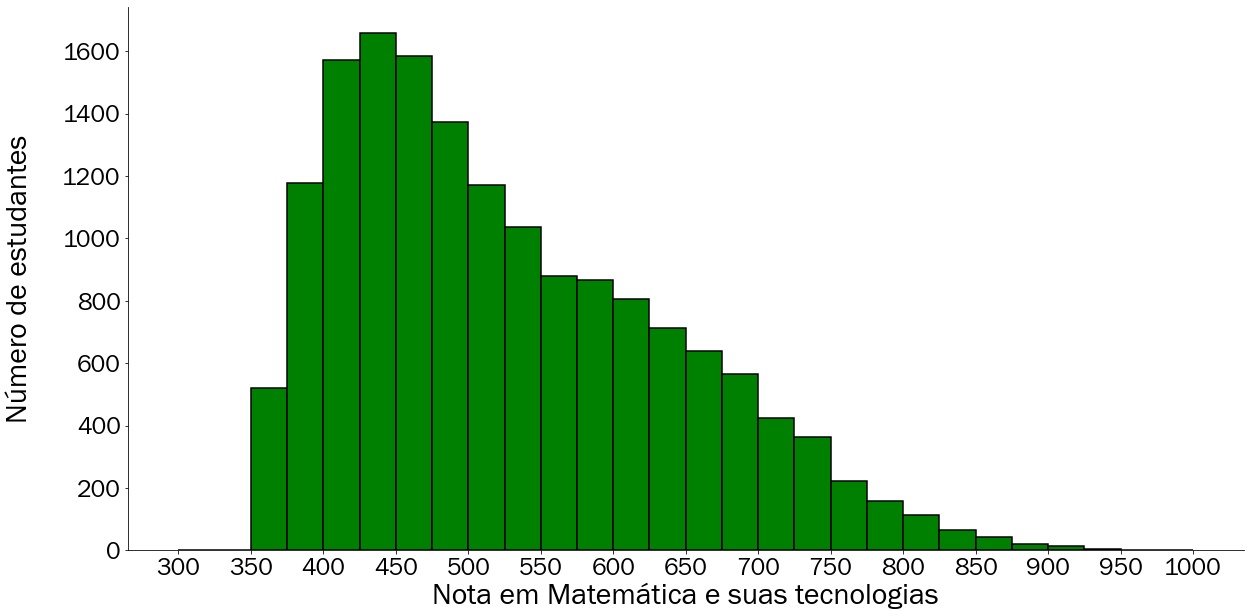
Figura 3.17: Histograma com as notas de matemática dos estudantes de escolas públicas e privadas de Salvador em 2019 de 300 à 1000 pontos com resolução de 25 pontos

A Figura 3.18 mostra o mesmo histograma agora com distinção entre os tipos de escola. Inicialmente verificamos que existe uma diferença na quantidade de estudantes de colégio público e privado na edição de 2019, como apontado na seção anterior. Além disso, é possível verificar que o perfil dos estudantes de colégio público é semelhante ao apresentado na Figura 3.16: O intervalo mais representativo está próximo de 450 pontos, porém e para os estudantes de escola privada os intervalos mais representativos estão em entre 600 e 700 pontos. Para uma melhor visualização e contornar o problema de diferença de escala entre os tipos de escolas, visto anteriormente na seção 3.3, vamos separar os histogramas em diferentes gráficos com seus eixos representativos próprios:

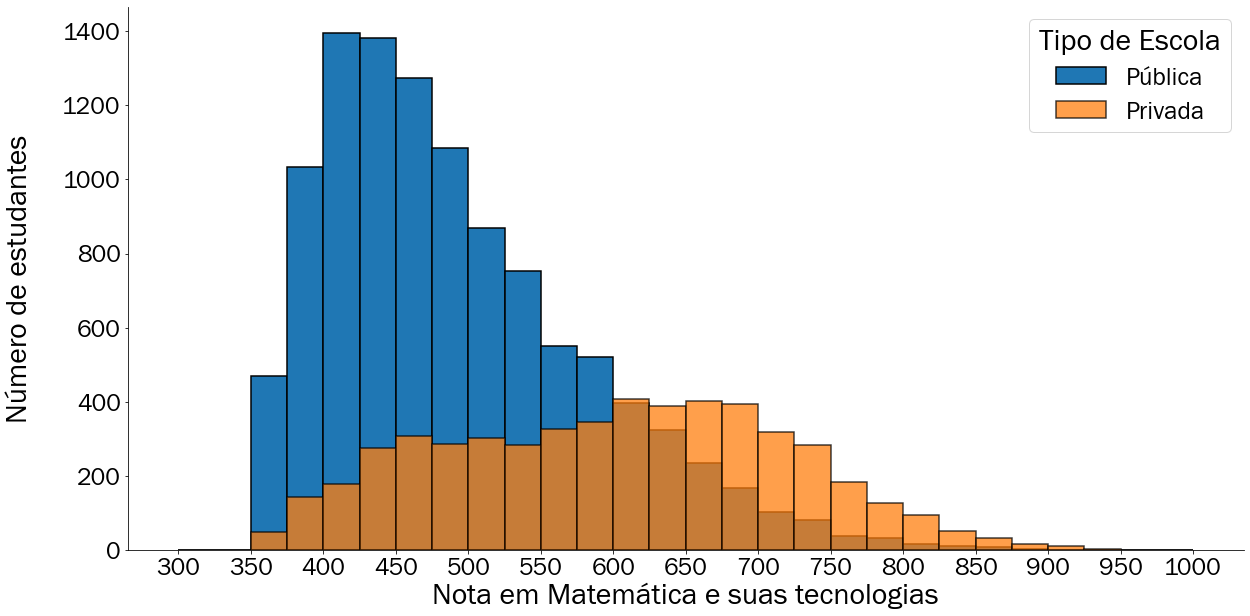
Figura 3.18: Histograma com 25 categorias de notas de matemática dos estudantes de Salvador em 2019 particionado pelo tipo de escola

A Figura 3.19 apresenta ambos os histogramas lado a lado com escalas de grandezas próprias. Você pode notar isso pelos valores máximos alcançados onde na escola pública foi alcançado aproximadamente 1400 em uma categoria enquanto na escola privada foi alcançado 400 em uma categoria.

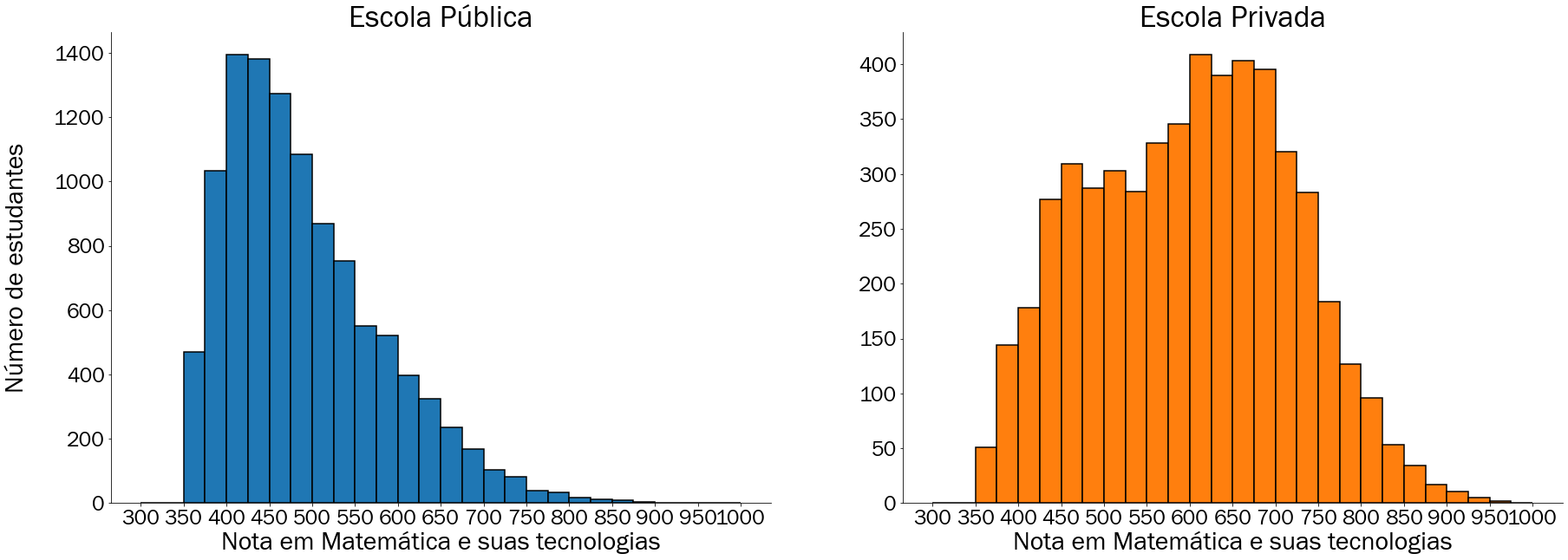
Figura 3.19: Histograma com 25 categorias de notas de matemática dos estudantes de Salvador em 2019 particionado pelo tipo de escola

Ainda na Figura 3.19 é possível notar que os valores máximos de cada histogramas são bem diferentes: para escola pública, as categorias mais representativas começam em 400 pontos e vão até 475 pontos, já para as escolas privadas gira em torno de 600 a 700 pontos, apresentando assim uma diferença em torno de 200 pontos de diferença. Além disso, um fator alarmante no histograma que representa os estudantes das escolas públicas é a queda nas notas de matemática a medida que a pontuação (eixo horizontal) aumenta a partir dos 475 pontos. Este padrão também ocorre para as escolas privadas, porém para um valor superior a 700 pontos.

Assim, em relação a nota de matemática, podemos dizer que a resposta para o quarto questionamento: “O tipo de escola (pública ou privada) pode influenciar nas notas dos estudantes neste exame?” apresenta uma resposta positiva, ou seja, é possível verificar uma diferença visual entre os tipos de escolas através dos histogramas discussões até o momento. Fica a cargo do leitor avaliar se o comportamento das notas de matemática no ENEM 2019 se repetem para as outras avaliações do exame.

Nota: É importante ressaltar que alguns materiais trazem o conceito da densidade para o eixo vertical do histograma, porém dado o direcionamento do livro será mantido uma análise sem abordar este conceito visto sua complexidade. A ideia de densidade é importante quando é analisado histogramas com intervalos de tamanhos diferentes, mas para intervalos iguais tanto o conceito de frequência absoluta (contagem) quanto densidade funcionam para o mesmo propósito.

Após concluir a leitura desta seção você pode notar a semelhança entre histograma e gráfico de barras, porém não confunda, eles são diferentes! Suas principais diferenças são:

• Os gráficos de barras exibem uma quantidade por categoria. Eles são frequentemente usados para exibir as distribuições de variáveis categóricas. Os histogramas exibem as distribuições contagens de eventos que ocorrem em intervalos de valores possíveis de variáveis numéricas, sejam contínuas ou discreta.
• Todas as barras em um gráfico de barras têm a mesma largura e há uma quantidade igual de espaço entre as barras consecutivas. As barras de um histograma podem ter larguras diferentes e são contíguas.

Nos capítulos 7 e 8 revisitaremos esta forma gráfica da representação do histograma e conheceremos suas aplicações e sua importância para a ciência de dados.

3.7 Concluindo …

Através deste capítulo conseguimos entender como a visualição gráfica pode trazer diferentes ideias e esclarecimentos a respeito dos nossos questionamentos, apresentando informações de forma simples e de fácil entendimento. Vimos também que cada gráfico pode trazer uma visão distinta e cabe ao leitor saber escolher qual a melhor abordagem a partir da sua pergunta e conjuntos de dados. Nosso questionamento sobre o perfil dos estudantes de Salvador que realizaram o ENEM conseguiu apresentar diversos insights, porém desanimadores. Na Figura 3.20 é apresentado o infográfico resumindo as informações extraídas a partir da análise gráfica.

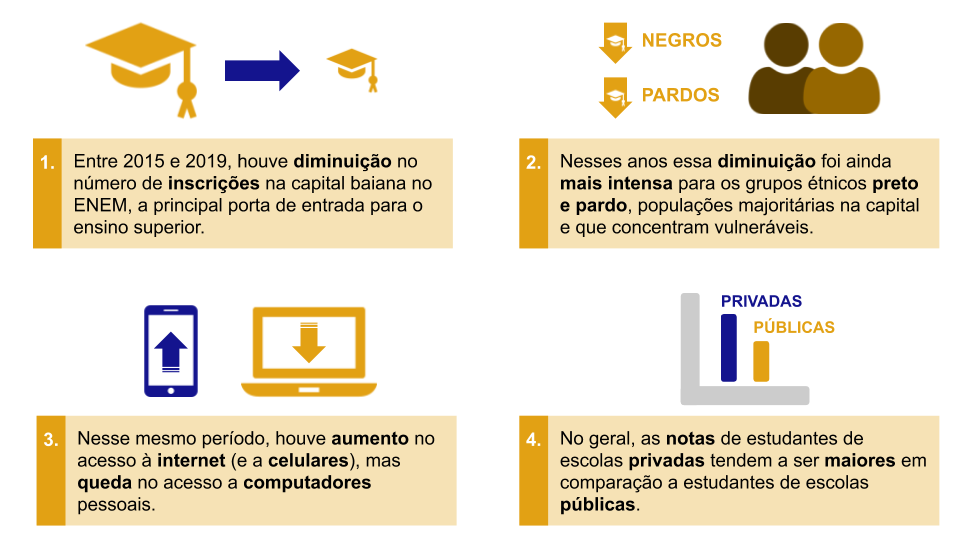
Figura 3.20: Infográfico dos resultados encontrados para o nosso questionamento

Esses resultados são desanimadores, pois no geral mostra uma grande evasão no número de inscritos de estudantes de vulnerabilidade social e um baixo rendimento dos estudantes de escolas públicas em comparação aos de escola privada. Todavia, para confirmar esses resultados apenas a visualização gráfica é insuficiente: Na ciência de dados precisamos de indicadores e medidas matemáticas para expressar se de nossas hipóteses são verídicas. Esse ferramental será explorado nos próximos capítulos deste livro, então mantenha o estudo!

3.8 Indo Além

Fizemos diversas análises e respondemos alguns questionamentos a respeito do perfil dos estudantes de Salvador que realizaram o ENEM não foi? Porém com a riqueza que esta base de dados possui o leitor pode explorar ainda mais! Utilizando Python, explicada em nosso capítulo de programação, você conseguiria ir além e responder os seguintes questionamentos?

• Através do infográfico na Figura 3.20 avaliamos que ocorreu um aumento no número de estudantes sem acesso a computadores pessoais no ENEM de 2015 para 2019, o que pode dificultar os estudos desta parcela de estudantes. Você consegue avaliar a distribuição de cor/raça para esses estudantes em 2019 utilizando o gráfico de barras?
• Na seção 3.6 verificamos que, infelizmente, na edição de 2019 do ENEM as notas dos estudantes de escolas públicas são menores em comparação aos estudantes de escolas privadas para a prova de Matemática.
• Utilizando o histograma, você consegue avaliar se este padrão se repete para as notas de Linguagens nesta mesma edição?

3.9 Citações no capítulo

[1] Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira. Microdados Exame Nacional do Ensino Médio. Disponível em: link de acesso

[2] Acorda Cidade. IBGE-BA: Salvador é a capital mais negra do Brasil e com a maior desigualdade salarial entre brancos e pretos. Publicado em 19 de novembro de 2018. Disponível em: link de acesso