Capítulo 10 Regressão

Olá, jovens cientistas! Que bom chegarmos juntos ao último capítulo do nosso ebook! Percorremos uma série de conteúdos super importantes que permitem analisar dados e tomar melhores decisões. Nesse último capítulo, vamos aprender a representar um processo ou sistema através de um modelo matemático que seja fiel ao fenômeno avaliado. Entre diversas possibilidades de modelos, você serão apresentados à Regressão Linear e irão aprender: a identificar um comportamento linear, verificar a associação linear entre variáveis e, a construir um modelo de Regressão linear e interpretá-lo!

Nesse capítulo, vamos trabalhar com dados de coleta de de Resíduos Sólidos Urbanos relativos ao Município de Salvador-BA entre os anos 2008 a 2020. Os dados estão disponíveis na plataforma SNIS \url(http://www.snis.gov.br/menu-coleta-dados).

Sabemos que o Saneamento básico é essencial para a saúde e bem estar da população, já que através dele é possível minimizar a proliferação de parasitas e insetos causadores de doenças! Uma etapa muito importante do Saneamento Básico é o gerenciamento de Resíduos Sólidos, que engloba os processos de coleta, seleção de componentes (triagem), tratamento e a disposição final desses resíduos. A etapa de coleta é extremamente importante porque ela garante que os resíduos que nós geramos e eliminamos nas lixeiras do nosso bairro sejam coletados e levados para um galpão onde esse resíduo será separado de acordo com os componentes encontrados e a partir daí ele é enviado para o tratamento adequado.

Animados? Então vamos começar!

10.1 Qual é a tendência?

Ao longo do ebook, aprendemos que pro meio de gráficos que é possível verificar a tendência das variáveis. A tendência observada nada mais é do que um padrão de comportamento que as variáveis apresentam. Observe o gráfico de linhas indicado na Figura ref(f101):

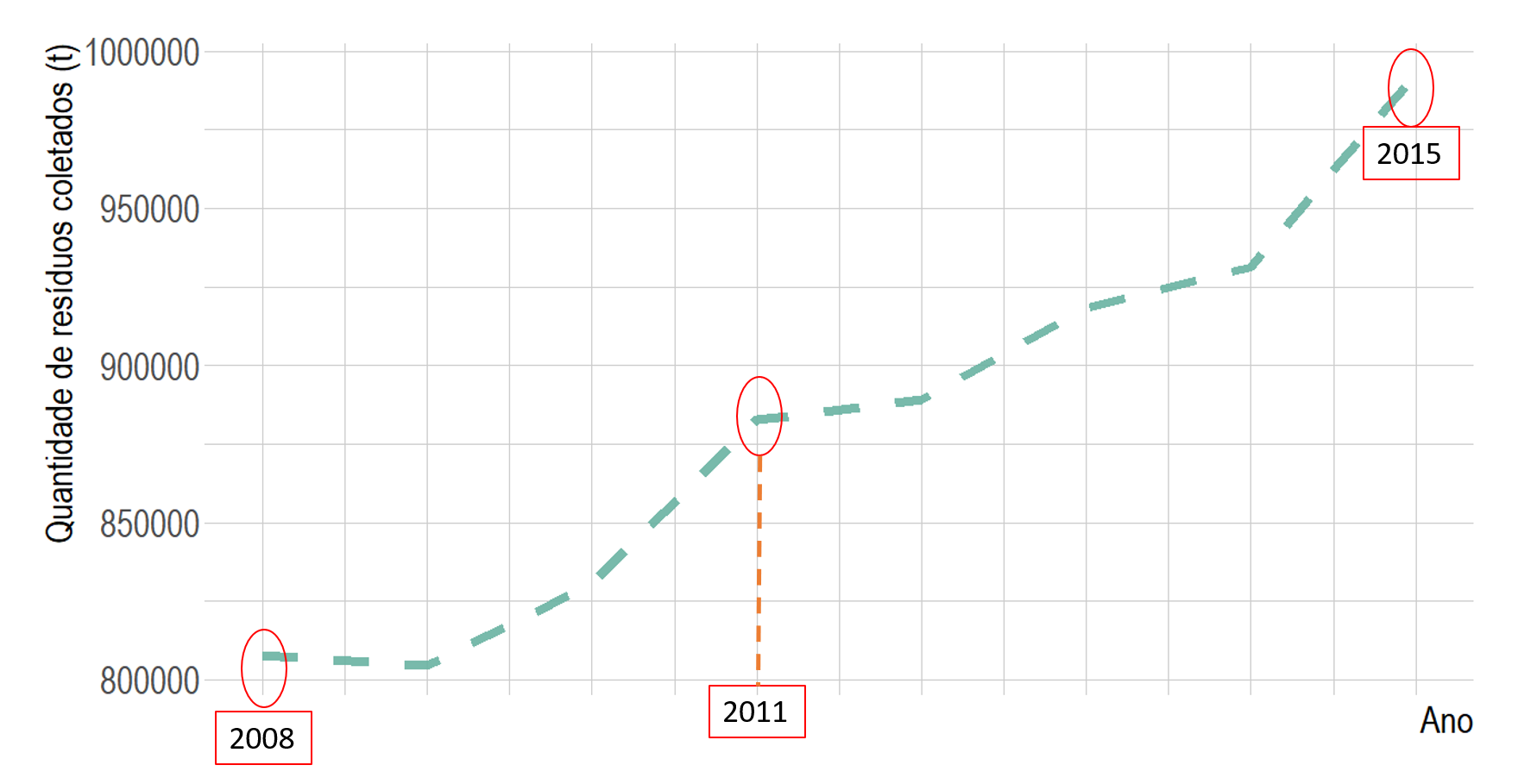
Figura 10.1: Quantidade de resíduos coletados

Vemos aqui a tendência anual para a quantidade de resíduos urbanos (em toneladas) coletados para a cidade de Salvador. A figura mostra que entre os anos 2008 a 2015 houve uma tendência de crescimento, sendo que o início do eixo x corresponde ao ano 2008 e o final corresponde ao ano de 2015. Dessa forma, com base no gráfico, se alguém te questionasse sobre qual a quantidade aproximada de resíduos coletados (toneladas) no ano de 2013, o que você responderia?

Observando a tendência de crescimento mostrada no gráfico, é possível afirmar que a quantidade de resíduos coletados em 2013 será maior do que a dos anos anteriores. Além disso, sabemos que o eixo x é dividido em partes iguais para representar as observações e, vemos a localização do ano 2011. Esses indícios apontam que o valor coletado em 2013 é pouco maior do que 900 000 t de resíduos, indicado por “?”. Observe na Figura 02 como encontrar esse valor.

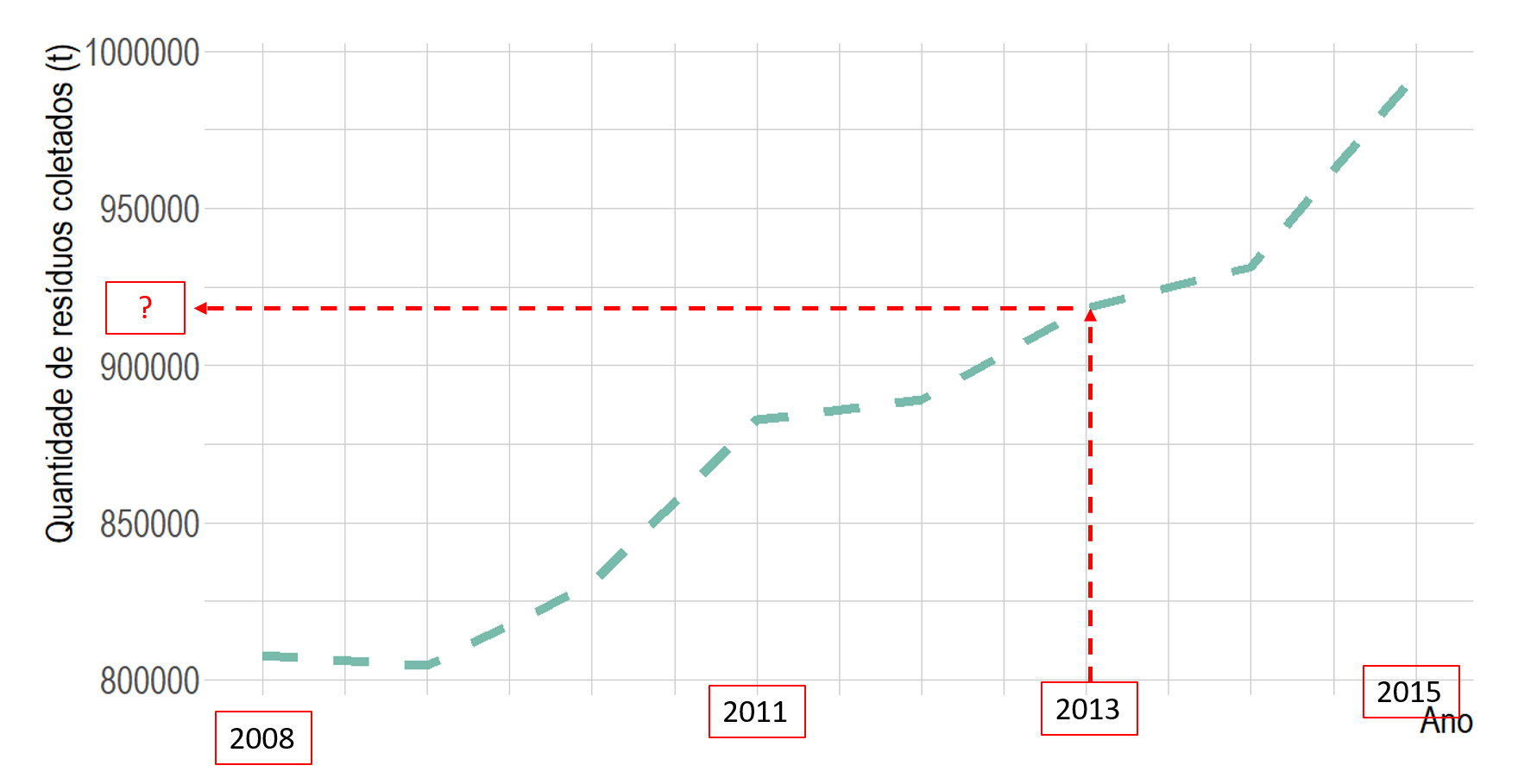
Figura 10.2: Como ler a quantidade de resíduos coletados para um ano qualquer

Perceba que verificando a tendência de crescimento, foi possível localizar o ano de interesse e depois, traçar o ponto correspondente no eixo Y (quantidade de resíduos coletados). Além disso, ao avaliar a tendência exibida é possível concluir que o crescimento observado apresenta uma tendência positiva, em que à medida que os anos passam há um aumento na quantidade de resíduos coletados. Ou seja, há uma associação positiva entre as variáveis consideradas e, observa-se uma tendência linear.

Esses tópicos foram trabalhados no Capítulo 4, onde verificamos que uma forma de quantificar a tendência linear é através do estudo da correlação entre variáveis, por meio do Coeficiente de Correlação de Pearson r, lembra?

Bom, esse exemplo inicial foi demonstrado para que você entenda a importância de se reconhecer a relação de associação por meio de gráficos, já que essa associação permite supor novas respostas frente à um mesmo padrão observado. Foi exatamente isso que fizemos ao verificar a quantidade de resíduos coletados em 2013. Além disso, o exemplo reforça que o Conteúdo do Capítulo 04 é essencial para iniciarmos a discussão do capítulo 10. Isso porquê antes de propor um modelo linear, é preciso verificar se há uma associação linear entre as variáveis.

Vamos então continuar a investigação sobre a coleta de resíduos. O gráfico de dispersão indicado na Figura 3 mostra as variáveis “quantidade de resíduos coletados(t)” no eixo x e “massa de resíduos sólidos urbanos (RSU) coletada per capita” no eixo y. A unidade de medida do eixo y é Kg/(hab.x dia) que indica a taxa em kilogramas de resíduo coletada por dia para cada habitante. Assim, queremos saber se a massa per capita de resíduo coletada pode ser representada por um modelo que considere a quantidade total de resíduos coletados.

Para verificar isso, o primeiro passo é avaliar se essas duas variáveis apresentam uma associação linear e qual é a força dessa associação. Pela Figura 3 verificamos que há uma tendência linear positiva e, o coeficiente de correlação de Pearson equivale a 0.84. Isso indica que essas duas variáveis são fortemente associadas, de forma que o aumento da quantidade de resíduos coletados se associa ao aumento da quantidade de resíduos per capita coletados.

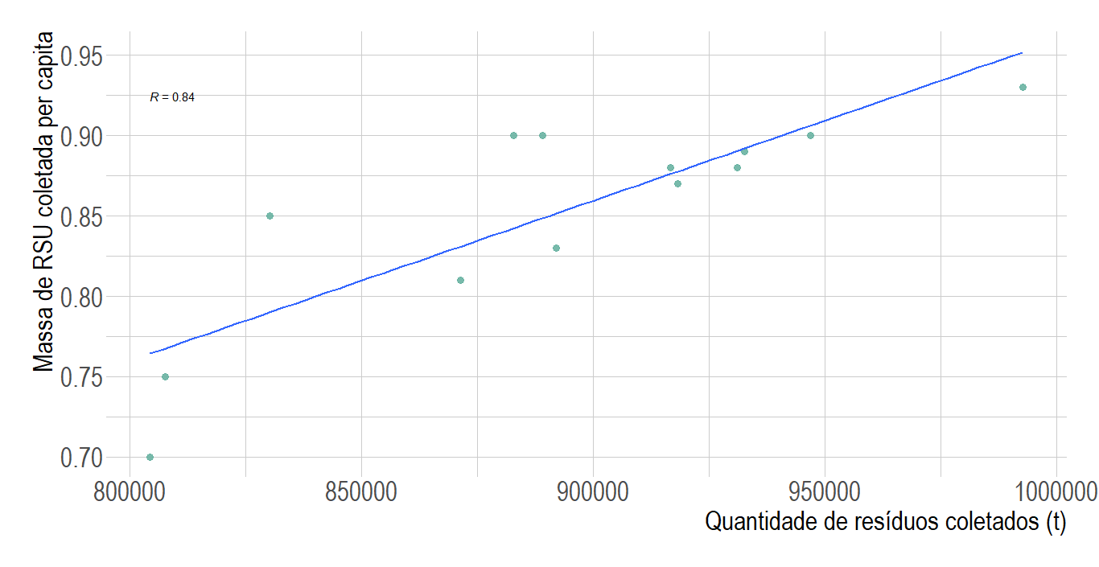
Figura 10.3: Massa de resíduo sólido coletada per capita

10.2 Predição a partir de duas variáveis

Já vimos que construindo um gráfico de dispersão é possível verificar a tendência entre variáveis. E esse é o primeiro passo para avaliar se há uma associação linear e o sentido da associação. Uma vez que a associação linear foi verificada na Figura 3, temos o aval para prosseguir com a nossa análise. Nossa intenção aqui é conseguir estimar a massa de resíduos per capita coletada com base na quantidade total de resíduos coletada (t)!

Com base nos valores observados para o eixo x = quantidade de resíduos coletados (t) e eixo y = massa de RSU coletada per capita (kg/hab x dia), imagine que novas coletas de resíduos foram feitas e portanto, você tenha novos valores da variável “quantidade de resíduos coletados (t)”! Já que essa variável possui uma relação linear com a variável “massa de RSU coletada per capita’’, podemos utilizar a quantidade de resíduos coletados para verificar a massa de RSU coletada, concorda? Mas, como fazer essa estimativa se você não sabe qual é a relação matemática entre as duas variáveis? Bom, é justamente isso que vamos aprender aqui nesse tópico!

Esse processo de entrada de novos dados e novas estimativas de valores da variável Y é conhecido como predição! Significa que, vamos considerar novos valores para uma variável x e cada novo valor será substituído em uma fórmula matemática que gera resultados para a variável y. As variáveis x ou y são escolhidas pelo investigador. Mas basicamente, no nosso caso, temos o interesse de estimar a massa de resíduos per capita coletada com base na quantidade total de resíduos coletada (t)! Portanto, a massa de resíduos per capita coletada é dependente da quantidade total de resíduos coletada! Por conta disso, a variável “massa de RSU percapita coletada” é conhecida como variável dependente, ou variável predita. Ao mesmo tempo, a “quantidade total de resíduos coletada” é a variável independente ou variável preditora.

Figura 10.4: Diagrama esquemático de variáveis

Ja avançamos bastante nos conceitos, mas, ainda não sabemos nada sobre qual é a fórmula que representa a relação entre essas duas variáveis… Pois bem, a primeira dica é: vimos que elas são linearmente associadas, então, essa fórmula deverá indicar um comportamento linear!

Dessa forma, podemos pensar o seguinte: Como criar uma regra que sempre irá retornar a melhor suposição de valor de massa de RSU per capita independente do valor de quantidade de resíduos coletados? Em outras palavras, queremos uma regra matemática que para qualquer valor da variável x, retorne a melhor predição da nossa variável y!

10.3 Predizendo valores

Como comentado na seção anterior, a fórmula que quantifica a relação entre nossas variáveis precisa ser encontrada, para que assim, possamos substituir os valores de x e encontrar os valores de y.

Uma vez que estamos trabalhando com um comportamento linear, logicamente nossa equação será linear. Dessa forma, a equação linear será:

\[\begin{equation} Y = B_0 + B_1X \end{equation}\]

Observe que temos o \(X\) e o \(Y\) claramente indicados. Temos também outros dois termos: \(B_0\) e \(B_1\), que devem ter seus valores calculados e substituídos na fórmula. Esses dois termos são chamados de parâmetros do modelo. O processo de cálculo deles depende de conceitos mais avançados, que não é o nosso foco nesse momento. Mas, o que você precisa saber é que, para calculá-los dependemos dos valores de média de \(X\) e \(Y\). Vamos ver na prática?

Pois bem, a Tabela 1 exibe os valores que verificamos no Gráfico 3, agora relativos aos anos de 2008 - 2020 para Salvador:

Tabela 10.1: Quantidade de resíduo sólido urbano
Quantidade de resíduos coletados (t)	Massa de RSU coletada per capita (kg/(hab x dia)
807595.0	0.75
804387.0	0.70
830230.8	0.85
882819.5	0.90
889079.6	0.90
918272.1	0.87
931184.0	0.88
992822.0	0.93
892034.0	0.83
871395.0	0.81
916648.8	0.88
932585.3	0.89
946960.9	0.90

Para calcular \(B_0\) e \(B_1\), devemos calcular antes os valores de média e desvio padrão para cada variável. A fórmula para o cálculo desses parâmetros não será exibida aqui, mas depende essencialmente para cada coluna da média, desvio padrão e termos como o somatório dos valores elevado ao quadrado e o somatório de cada valor elevado ao quadrado. Conhecendo todos esses valores, chegamos à resposta de que \(B_0 = -3.678\times10^{-02}\) e \(B_1 = 9.959\times10^{-07}\). Assim, substituímos na equação:

\[\begin{equation} y = -3.678\times 10^{-2} + (9.959\times10^{-07})x \end{equation}\] Essa é a fórmula que quantifica a relação entre nossas variáveis x e y. Essa fórmula é conhecida como a linha de melhor ajuste, porque a partir dela, vamos substituir em x os valores novos da nossa variável preditora e, obteremos a resposta em y. Isso considerando que, como falado na sessão anterior, buscamos uma linha que seja sempre a melhor aproximação entre a associação das variáveis. Ou seja, ela é a regra que sempre irá retornar a melhor suposição de valor de massa de RSU per capita independente do valor de quantidade de resíduos coletados!

Assim, por meio da nossa Equação de Regressão linear, que gera a linha de regressão, podemos predizer a massa de RSU per capita coletada através de outra variável, a quantidade de resíduos coletada.

Vamos recapitular a Figura 3, quando ainda não entendíamos o que a linha em azul significava. Agora sabemos que ela é a linha de regressão linear. Com base nos valores observados das variáveis no eixo x e y, calculamos os parâmetros B0 e B1 e a linha de regressão foi construída chegando à equação \(y = -3.678\times 10^{-2} + (9.959\times10^{-07})x\) , que nos retornou valores preditos de y para novos valores de x.

Figura 10.5: Regressão linear da Massa de RSU coletada versus Quantidade de resíduo coletada

Um exemplo simples para entender como isso se dá é: Com base na associação linear vista e na linha de regressão estimada, qual seria a massa de RSU per capita coletada quando observamos uma quantidade de resíduos coletada (t) equivalente a 950 000 toneladas?

Já sabemos que a quantidade de resíduos coletados é a variável preditora, portanto, ela é indicada pelo x, e acompanha o parâmetro \(B_1\),

\[\begin{equation} y = -3.678\times 10^{-2} + (9.959\times10^{-07})x \end{equation}\]

assim podemos substituir o valor de \(x = 950000\) na equação acima

\[\begin{equation} y = -3.678\times 10^{-2} + (9.959\times10^{-07})(950000), \end{equation}\]

e obter o valor \(y = 0.909325\) kg (hab x dia) de RSU per capita coletados.

Perceba como o modelo de Regressão Linear é importante! Imagine que os gestores da prefeitura de Salvador tenham acesso a esses dados e, com base na tendência observada, queiram fazer predições futuras para diversas outras quantidade de resíduos coletados. As respostas obtidas pela Regressão linear permitem que esses gestores saibam com considerável grau de confiança as quantidades futuras de massa per capita coletada. Assim, os gestores teriam evidências suficientes para projetar melhores instalações de triagem e tratamento além de ser um ótimo indicativo para campanhas em prol da redução da produção de resíduos!

Agora que sabemos como encontrar a linha de regressão e como utilizá-la para fazer predições, precisamos saber como avaliar os resultados obtidos. É nisso que a nossa próxima sessão irá focar.

10.4 Avaliando os resultados

Tão importante quanto conhecer uma nova ferramenta para tomar decisões, é saber avaliar o quanto essa ferramenta é eficiente. Por isso esse tópico irá abordar uma forma de verificar o quanto o modelo de Regressão Linear proposto é válido.

Antes de iniciarmos com o exemplo, precisamos recapitular que o modelo de regressão construído será usado para fazer predições de y com base nos valores de entrada de x. Assim, como vimos no exemplo acima, para cada valor de “quantidade total de resíduos coletados” (variável x) considerado, teremos uma resposta de valor de “massa per capita de resíduos coletada” (variável y) associada. Ao final, quando utilizarmos todas as observações de x, teremos uma lista de valores preditos em y, concorda?

No caso do nosso exemplo, para cada valor da quantidade total de resíduos coletados substituído na Equação de Regressão Linear, obtivemos as seguintes respostas de massa de resíduos per capta coletados, indicado na Tabela 2:

Tabela 10.2: Valores preditos de Y
Y
0.7674862
0.7642914
0.7900288
0.8424010
0.8486353
0.8777077
0.8905664
0.9519507
0.8515776
0.8310236
0.8760910
0.8919619
0.9062784

De posse desses valores, podemos avaliar o quanto esse valor das predições de “massa de resíduos per capita coletados” se desviam (são diferentes) dos valores reais observados para essa variável! Ou seja, a equação de regressão que construímos irá gerar resultados com um certo grau de diferença dos valores observados incialmente. Essa diferença é conhecida como desvio! Conhecendo esse valor residual é possível avalair se o nosso modelo gera desvios baixos ou altos, verificando assim a capacidade de predição do nosso modelo.

O desvio é a diferença entre o valor predito e a saída verdadeira! O desvio pode também ser chamado de resíduo!

A Figura 5 ilustra os resíduos! Observe que eles correspondem a distância entre os valores observados e os preditos pela regressão linear. Para alguns pontos, perceba que a linha de regressão passa muito próximo de observações reais (pontos em verde). Isso signfica que nosso modelo gerou um resultado muito próximo ao valor observado, ou seja, teve um erro muito baixo. Situação diferente observamos para outros pontos, onde vemos uma distância bem maior entre o ponto observado e a linha de regressão construída.

Ao verificar o gráfico é possível notar que os desvios (ou resíduos) não tem um padrão específico, podem ocorrer em diferentes sentidos (para baixo ou para cima)!

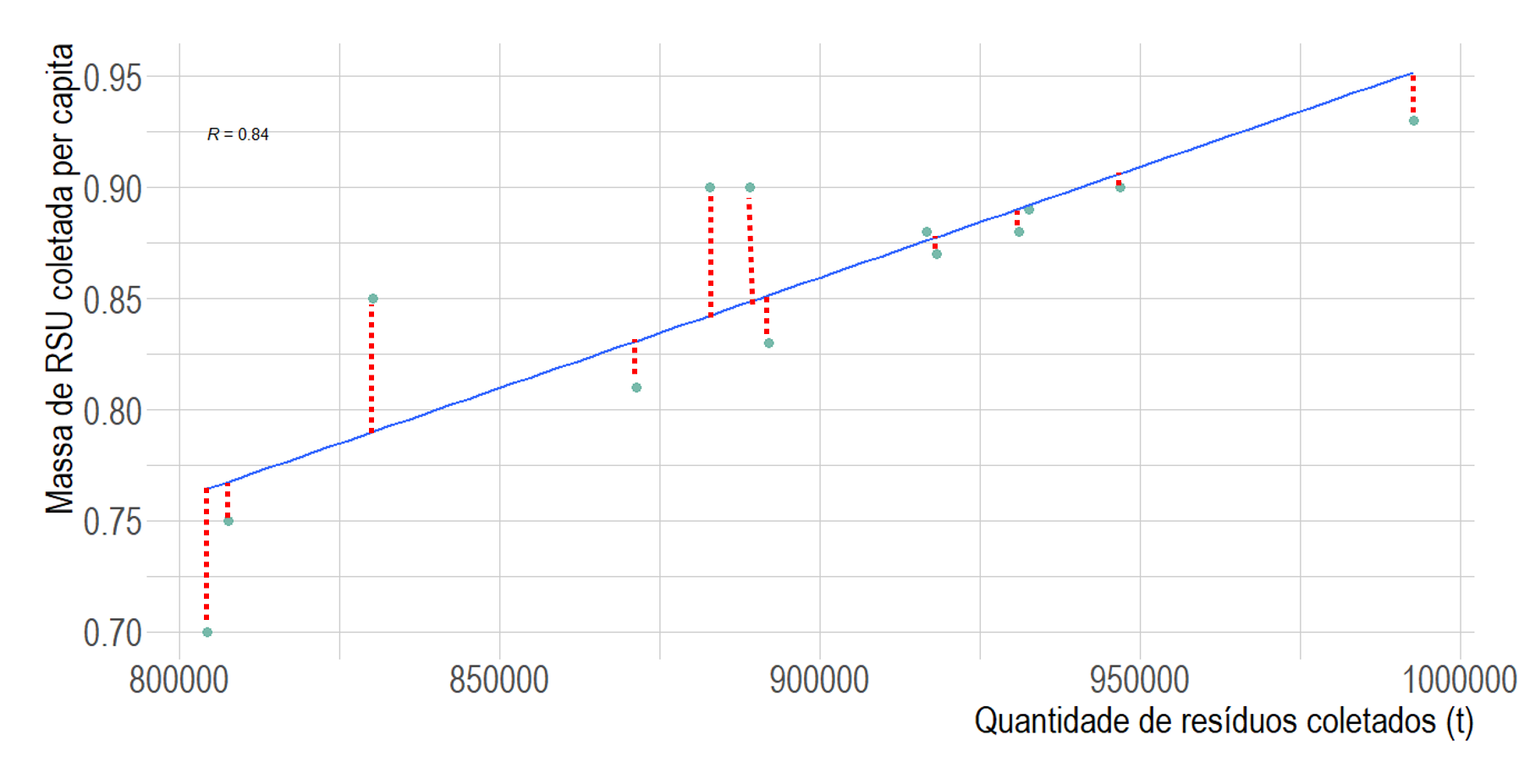
Figura 10.6: Resíduos da regressão linear da Massa de RSU coletada versus Quantidade de resíduo coletada

Um dos métodos muito aplicados por cientistas de dados para avaliar os residuos de um modelo é o Erro médio Absoluto (sigla em inglês: MAE / Mean absolute error). O MAE é expresso pelo somatório do módulo da diferença entre os valores observados e valores preditos divido pelo tamanho amostral. Aplicando o MAE, consideramos os desvios para cada predição e chegamos a um único valor final, que resume todos os devios verificados. A fórmula a seguir vai deixar mais claro:

\[\begin{equation} \sum \frac{|y_{obs} -y_{pred}|}{n} \end{equation}\]

\(y_{obs}\) representa os valores da variável \(y\) observados na Tabela 1 (Massa de RSU coletada per capita observada);
y_{pred} representa os valores preditos de \(y\) na Tabela 2 (Massa de RSU coletada per capita predita) e
\(n\) é o tamanho amostral (quantidade de osbervações).

Assim, ao realizar o cálculo do MAE, chegado ao resultado: \(MAE = 0,027\). Isso significa que a diferença média entre todos os valores observados e os preditos é \(0.027\)! Esse valor é satisfatório, já que quanto menor o valor do MAE, melhor.

10.5 Avaliação de problemas com mais de uma variável preditora variáveis

No nosso exemplo estamos trabalhando com uma variável preditora (x) e uma variável predita (y). Entretanto, os sistema e fenômenos avaliados são influenciados por diversas variáveis que atuam simultaneamente. Por isso, a Regressão Linear traz uma etapa mais avançada que é a construção de um modelo de Regressão Linear Múltipla, ou seja, com múltiplas variáveis.

Assim, é possível construir um modelo que seja mais fiel a realidade observada. Da mesma forma que o modelo de Regressao Linear Simples para um preditor, as etapas de investigação na Regressão Linear Múltipla serão as mesmas.

A diferença é que agora considera-se mais de uma variável preditora, ou seja, ao invés de termos apenas uma variável x, no nosso exemplo a quantidade total de resíduos coletados (t), teremos novas variáveis x, como Ano, Total população, População Urbana, Quantidade de empregados totais. A saber:

Total pulação: expressa a quantidade total da população (urbana + rural) População urbana: relata apenas a quantidade de habitante da área urbana Quantidade de empregados totais: se refere à quantidade de funcionários oficialmente contratados para exercer os serviços de menejo dos Resíduos Sólidos Urbanos.

Dessa forma, considera-se no nosso exemplo:

preditoras: Ano, Total população, População urbana, Quantidade de empregados totais e a quantidade de resíduos coletados (t); predita: massa de resíduos coletada per capita.

Iniciamos pela verificação de associação linear entre as variáveis preditoras e a predita. Entretanto, não precisamos plotar vários gráficos de dispersão. Podemos plotar diretamente a correlação de Pearson! O correlograma abaixo ilustra:

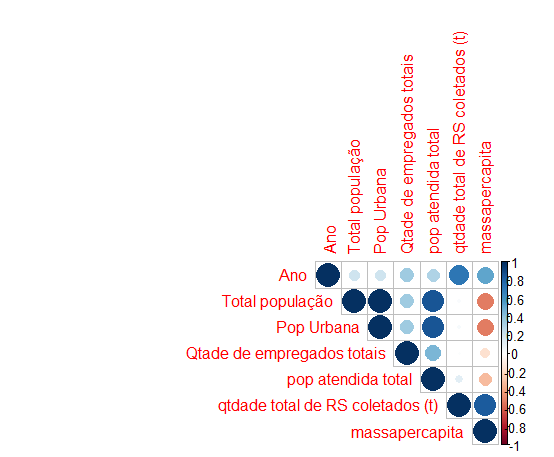
Figura 10.7: Resíduos da regressão linear da Massa de RSU coletada versus Quantidade de resíduo coletada

Através dele podemos perceber que o tom azul indica correlações positivas e o tom vermelho indica correlações negativas. O tamanho do círculo é baseado no valor encontrado para o r. Portanto, quanto mais próximo de 1 maior será o círculo e, quanto mais próximo de zero, menor será. Além disso, quanto mais próximo de -1 ou 1 for o r, mais forte é essa correlação. Esse grau de correlação é ilustrado pela intensidade da cor aplicada. Por exemplo, verificamos que a variável dependente “massapercapita” que indica a massa de RSU per capita coletada tem uma forte associação com a “quantidade total de resíduos sólidos coletados”. Ou seja, compreendemos que o aumento na quantidade de resíduos sólidos totais coletados se associa ao aumento da massa de resíduos per capita coletados. E faz sentido, pois siginifica que cada pessoas estará produzindo uma quantidade maior de resíduos. Uma situação diferente pode ser observada entre a variável “quantidade de empregados totais” e a variável predita “massapercapita” , elas possuem uma correlação muito fraca que indica que outros fatores podem estar mais foretemente associados à condição de contratação de novos funcionários para o setor.

Observa-se também que as variáveis “população total” e “população urbana” estão fortemente correlacionadas. Isso ocorre porque essas duas variáveis apresentam o mesmo significado dentro do nosso problema, uma vez que “população total” é o somatório entre a população urbana e rural. Por isso, ao se construir um modelo de regressão linear múltipla é necessário avaliar se existe correlação entre as variáveis preditoras. No caso em que se avança para a construção do modelo, uma dessas variáveis deveria ser retirada para não prejudicar a nossa predição.

Quando verificamos variáveis preditoras correlacionadas, perdemos a capacidade explicativa sobre o nosso modelo. Imagine, como poderíamos dizer qual variável (população total ou população urbana) tem maior influência sobre a massa de resíduos per capita coletada? É uma questão que infelizmente não é possível fazer uma afirmaçãoa ssertiva, pois essas variáveis apresentam forte influência entre si.

Por isso o Correlograma é tão importante! Ele nos dá um indício inicial das variáveis que podem ser incluidas ou excluídas do modelo de Regressão Linear Múltipla. Não faz sentido considerar variáveis que não estão correlacionadas com a variável predita, concorda?

A partir desse ponto, a análise de regressão pode ser prosseguida e a equação de regressão estimada. Devido ao fato de considerarmos mais de uma variável preditora, os cálculos para chegarmos à equação final raramente serão feitos à mão, uma vez que exigirão capacidade de solucionar um sistema matricial! Por isso, comumente utilizamos softwares como Excel, Minitab, SAS ou linguagens de programação como R e Pyhton para performar as análises.

10.6 Concluindo…

Nossa discussão vai se encerrar por aqui, uma vez que atingimos um ponto onde é necessário um conhecimento mais aprofundado de estatística para avançar. Reforço que o que foi explicado até agora também não é um conteúdo trivial! Entretanto, diversas adaptações foram feitas de forma a tornar todo esse conteúdo compreensível para você, jovem cientista!

Por isso, espero que você tenha gostado dessa discussão e se interessado para aplicar o método de Regressão Linear em outras situações do seu cotidiano! Com isso, encerramos o último capítulo do ebook e tenha certeza, que os conteúdos que foram apresentados ao longo dos capítulos irão te auxiliar em diversos momentos, reforçando o pensamento crítico, analítico e conexão com problemas sociais. Então, parabéns por ter acompanhando até aqui e desejo que você tenha um excelente caminho em tudo que desejar aprender!

10.7 Bibliografia

Diagnóstico SNIS - Manejo de Resíduos Sólidos Urbanos. Dados

Introduction to Data Science curriculum v 5. Lesson 6: Statistical Predictions Applying the Rule.

Introduction to Data Science curriculum v 5. Lesson 7: Statistical Predictions Using Two Variables.

Introduction to Data Science curriculum v 5.Lesson 8: What’s the Trend?

Introduction to Data Science curriculum v 5. Lesson 9: Spaghetti Line.

Introduction to Data Science curriculum v 5. Lesson 10: Predicting Values.