Capítulo 7 Distribuições, Probabilidade e Possibilidade

Nos capítulos anteriores falamos de muitos temas importantes para a nossa vida como cidadãos, passando por sistemas de recomendações, dados abertos, informações sobre esportes, dados sobre o ENEM, sobre a segurança pública e ainda há muitos outros para conhecermos.

Percebemos até aqui que é possível pensar como os sistemas funcionam, como as informações são escolhidas para serem armazenadas, analisadas e finalmente tomar decisões sobre elas.

Entretando, há no mundo que vivemos uma complexa relação entre conhecer os dados e dar passos orientados baseado neles. É possível que algumas vezes ao longo da sua vida você tenha ouvido sobre os benefícios de comer algo aparentemente simples como ovos e algum tempo depois ser retratado como algo maléfico a saúde. A ciência passa por uma constante mudança e em alguns momentos da história essas mudanças são mais abruptas. Neste livro temos o foco nas informações mais precisas do momento que vivemos, das experiências mais próximas do nosso cotidiano.

Entre os campos da vida que deveríamos nos guiar menos pela sorte está a saúde, nossas decisões podem ser orientadas por dados e informações para alcançarmos um maior bem estar. De alguma maneira somos apresentados a várias boas práticas que deixariam uma parte da população com uma boa saúde, por exemplo:

Praticar exercícios físicos com regularidade;
Manter-se hidratado;
Comer alimentados não industrializados etc.

Porém, devemos ser cautelosos ao afirmar que imersos em diversos hábitos comuns de uma localidade, resultantes de aspectos
culturais e econômicos, podemos nos guiar de maneira plena pelos dados e informações científicas. Ser parcimonioso pode ser a priori o caminho de transformação. Cientistas de dados ao apresentar soluções devem se preocupar com esta variedade, com as diferenças dos públicos para os quais ele propõem suas informações. Nas próximas seções conheceremos um poucos dos conceitos mais fundamentais da estatística que fortalecem a nossa capacidade de organizar, analisar e criticar os problemas sobre os quais devemos tomar decisões.

7.1 Experimento, Espaço amostral e Evento

Gostaria de convidá-las a pensar sobre uma forma que tipicamente é definido o estado de saúde de uma pessoa, sob a perspectiva do trabalho. É muito comum que as pessoas digam que alguém está doente se não pode trabalhar e são se está com plena condição de trabalho.

Para facilitar nosso raciocínio vamos identificar estes dois estados da seguinte forma:

Doente pela letra D e
São pela letra S,

então temos apenas duas possibilidades de condição de saúde de um trabalhador. Continuemos com nosso raciocínio, o fato de existir apenas duas possibilidades nessa situação problema não quer dizer que seja igual ao experimento no qual fazemos o lançamento de uma moeda e as possibilidades são Cara e Coroa. Por favor, não pensem em lançar para cima um familiar, pois o resultado será um pé machucado sempre ou você mesmo poderia se machucar. Nosso caso é similar a uma situação na qual selecionamos uma bola numa caixa, na qual contém bolas rosas ou amarelas.

Imaginemos o caso de uma escola que tenha 4 turmas; sendo que cada uma é acompanhada por um professor no turno da manhã. Se as aulas começam às 8:00, desde às 7:00 da manhã é preciso que o coordenador tenha conhecimento da situação de saúde do professor. Lembremos que só existem duas possibilidades do estado de saúde de uma pessoa, doente (D) ou sã (S). Ou seja, na perspectiva estatística da coordenadora, o estado de saúde de seus professores às 7:00 da manhã é um experimento. Porém, neste novo experimento estamos interessados em ajudar sobre as decisões da coordenadora. Na perspectiva da escola não basta olhar apenas para um professor, é necessário avaliar quantos professores de fato estão doentes (D). Então, podemos imaginar e descrever pelas letras D e S todas as combinações possíveis entre os 4 professores do turno matutino: #(sem se importar qual professor está doente):

Figura 7.1: Possíveis resultados para a condição de saúde do professor

A este conjunto de possibilidades de resultados associado ao experimento nomeamos de espaço amostral.

Cada linha desse quadro representa uma possibilidade de resultado. Na linha 1, por exemplo, temos um possível resultado no qual todos os professores estão doentes \(\{D,D,D,D\}\), enquanto que na linha 16 notamos que todos estão sãos \(\{S,S,S,S\}\). Na maioria dos possíveis resultados sempre há pelo menos um professor no estado de saúde doente (D). É necessário ficarmos atentos que embora estes resultados sejam possíveis, não necessariamente serão observados com a frequência equivalente aos disponíveis na quadro 7.1.

Um ano escolar é formado por 200 dias letivos. Para cada um dos dias haverá a condição de saúde dos 4 professores, podendo ocorrer de acordo com os 16 possíveis resultados do espaço amostral apresentado no quadro acima 7.1.

Agora, observando o quadro 7.1 de possíveis resultados, que chamamos de espaços amostral, podemos ter foco em situações específicas. Particularmente, a coordenadora pensou em avaliar o caso em que exatamente 3 professores tivessem doentes (D), no quadro 7.1 verificamos que os resultados das linhas \(2,3,5,9\) apresentam estas condições.

Figura 7.2: Possíveis resultados com 3 professores doentes

A escolha de um subconjunto de resultados possíveis é definida como evento.

No nosso problema, o conjunto dos resultados observados nas linhas \(2,3,5,9\) na Tabela 7.2, ou seja, os resultados \(\{SDDD,DSDD,DDSD,DDDS\}\) constituem o nosso evento. Como identificamos 4 resultados possíveis, podemos ser induzidos a afirmar que 4 a cada 16 realizações do experimento podem gerar um resultado definido como nosso evento, entretanto, isto só seria uma avaliação correta se os resultados apresentados no espaço amostral fossem igualmente possíveis. Não parece razoável que uma escola com apenas 4 professores tenha por exemplo, o evento todos sãos \(\{S,S,S,S\}\) apenas em 1 a cada 16 realizações do experimento. Portanto, para tornar esta avaliação mais verdadeira é preciso que se associe um número relativo a possibilidade deste evento se repetir. Dedicaremos as próximas seções a esta área da estatística que relaciona tais valores aos eventos de um determinado espaço amostral associado a um experimento.

7.2 Probabilidade

Sabe-se que alguns tipos de doenças acometem com maior frequência pessoas que nascem com sexo masculino e enquanto outras àquelas que nascem com sexo feminino. Um caso emblemático trata-se do câncer de mama. Todos os anos são realizadas campanhas para alertar a população desta terrível
doença e da necessidade de realizar exames para alcançar diagnóstico precoce. A principal campanha de conscientização do câncer de mama é o Outubro Rosa. Em 2020, a Superintência de Estudos de Impacto Econômico e Sociais da Bahia (SEI) divulgou um cartaz sobre câncer de mama no qual apresenta em números o cenário da Bahia e Salvador quanto ao câncer de mama. Mas antes de analisar este rico documento com estatísticas a respeito desta doença, vamos definir o nosso experimento aleatório:

Experimento: Exame de detecção precoce do câncer de mama.

Se simplificarmos este problema podemos associar apenas dois possíveis resultados, ou diagnóstico positivo (P), no qual o paciente foi diagnosticado com câncer de mama, ou diagnóstico negativo (N), em casos em que o câncer de mama não foi detectado. Se inicialmente não temos nenhuma outra informação, somos induzidos a pensar que ao realizar este exame temos chances iguais para ser diagnósticado positivo ou negativo para a presença de câncer de mama. Ou seja, seria equivalente ao famoso problema do lançamento de uma moeda (cara ou coroa?!). Para comprovar essa afirmação você pode fazer um teste simples:

Procedimento para criar o ambiente de lançamento de moeda

Entre no ambiente do Mathigon;
Na aba ao lado esquerdo deste ambiente clique em “Probabilidade e dados”;
Em seguida, selecione “Moedas, dados e spinners”;
Clique na figura da moeda e arraste para a direita e solte sobre a área branca;
Clique com o botão direito sobre a moeda e verá que pode optar por Giro, esse procedimento é equivalente ao lançamento de uma moeda.

Avaliação estatística dos lançamentos

Repita o procedimento de giro por 30 vezes e a cada novo lançamento anote o resultado;
Ao final, faça uma avaliação do resultado e compare com um dos colegas.
Descreva suas conclusões.

Depois desta experiência, imaginamos que você esteja convencido de que quando desconhecemos completamente as informações não somos capazes de definir qual evento tem mais chances de ocorrer. Na próxima seção vamos refletir sobre uma doença muita importante para saúde da mulher e como é possível avaliá-la sob a perspectiva dos dados disponíveis.

7.3 Câncer de mama e dados

Nosso corpo está sujeito a diversos tipos de câncer e todos eles promovem consequências que não se limitam ao campo biológico. Particularmente, devido à posição socialmente enfrentada pela mulher as consequências são bem mais amplas.

Nesta seção, vamos pensar sobre o problema do câncer de mama sob a perspectiva da probabilidade. Possivelmente você já ouviu falar do câncer de mama e em particular conheceu a palavra mamografia. A momografia é um exame de imagem que utiliza raio X sendo muito importante no diagnóstico precoce de câncer de mama.

Em geral, acreditamos que o número de pessoas acometidas por esta doença é bem menor que a população que realiza os exames para tal diagnóstico. O exame mais indicado para a primeira avaliação do tecido da mama é a mamografia, para entender um pouco sobre a evolução da forma como a medicina aborda este tipo de câncer vamos ouvir o Dr. Dráuzio Varela:

Nestes quase 4 minutos de vídeo o Dr. Dráuzio Varela apresenta dados e informações a respeito do Câncer de Mama, precisamos pensar um pouco mais sobre este problema.

No diagrama a seguir na Figura~7.3, demonstramos que podemos ter dois possíveis resultados, como não temos quaisquer resultados dos experimentos, as chances de ocorrências dos dois diagnósticos assumiremos como iguais:

Figura 7.3: Diagrama de diagnóstico positivo ou negativo

Agora, pensemos a respeito do espaço amostral associado a este experimento, a avaliação de 1 paciente pode resultar em muitos resultados positivos possíveis como indica o Instituto Nacional de Câncer:

P1 “Qualquer nódulo mamário em mulheres com mais de 50 anos.”
P2 “Nódulo mamário em mulheres com mais de 30 anos, que persistem por mais de um ciclo menstrual.”
P3 “Nódulo mamário de consistência endurecida e fixo ou que vem aumentando de tamanho, em mulheres adultas de qualquer idade.”
P4 “Descarga papilar sanguinolenta unilateral.”
P5 “Lesão eczematosa da pele que não responde a tratamentos tópicos.”
P6 “Homens com mais de 50 anos com tumoração palpável unilateral.”
P7 “Presença de linfadenopatia axilar.”
P8 “Aumento progressivo do tamanho da mama com a presença de sinais de edema, como pele com aspecto de casca de laranja.”
P9 “Retração na pele da mama.”
P10 “Mudança no formato do mamilo.”
N1 e naturalmente sabemos que é possível ocorrer o resultado negativo, que “o paciente não tenha câncer de mama”.

De acordo com as possibildiades de diagnóstico de câncer indicados pelo INCA, podemos construir um diagrama que tem os casos diagnósticados como positivos, para o qual existem 10 possíveis especificidades e que até então são igualmente prováveis e uma possibilidade de diagnóstico negativo:

Figura 7.4: Diagrama de diagnóstico positivo ou negativo INCA

O diagrama da Figura~7.4 é muito detalhado, porém muitas associações definem de maneira diferente e com quantidades diferentes de diagnósticos, o que dificulta a comparação de resultados e adoção de procedimentos de forma padronizadas. Contudo, como veremos numa definição de diagnósticos mais padronizados, Breast Imaging-Reporting and Data System representada pelo acrônimo BI-RADS, a chance de ocorrências dos diferentes diagnósticos não é exatamente igual.

Para isto nos debruçaremos sobre os dados oficiais sobre câncer disponibilizados pelo sistema de dados do Sistema Único de Saúde (SUS) DATASUS. Estas novas informações serão avaliadas adicionalmente em relação às nossas discussões sobre espaço amostral, experimento, eventos e probabilidade.

Primeiramente, descreveremos as categorias adotadas pelo BI-RADS a partir da sua forma simplificada na Nota Técnica 8 SISCAN - MAMOGRAFIA e disponibilizada no quadro na 7.1 a seguir:

Tabela 7.1: BI-RADS - classificação de resultados das mamografias segundo os achados:
Descrição	Categoria
Indefinido	0
Negativo	1
Benigno	2
Provavelmente Benigno	3
Suspeito	4
Altamente Suspeito	5
Já com diagnóstico de câncer	6

Figura 7.5: Diagrama de diagnóstico indefinido, positivo ou negativo (BIRADS)

Segundo o nosso diagrama da Figura~7.5, sem dados analisados a priori e observando somente o espaço amostral associado, ou seja, Indefinido, Negativo e Positivo {\(\{I,N,P\}\)} temos três possibilidades com a mesma chance de ocorrência. Assim, teríamos 1 chance em 3 de serem Indefinidos, ou serem Negativos ou diagnósticos Positivos. Logo, com as informações disponíveis, são estimadas as probabilidades de ser indefinido, positivo e negativo, que inicialmente são calculadas pela atribuição de suas simples equivalências com o espaço amostral,

\(P(Indefinido) = \frac{1}{3}\),
\(P(Negativo) = \frac{1}{3}\) e
\(P(Positivo) = \frac{1}{3}\).

Se fizermos um gráfico dos valores atribuídos de probabilidade para os itens a), b) e c) teremos a seguinte distribuição de probabilidades:

Figura 7.6: Distribuição de valores de probabilidade

Portanto, por esta abordagem, eles são entendidos como equiprováveis, pois tem a mesma chance de ocorrência. Dentro do ramo Negativo do diagrama, podemos ainda ter o diagnóstico C1, que é a única categoria dentro dos diagnósticos negativos, assim, dentre os casos de diagnósticos negativo será \(\frac{1}{1}=1\), que equivale a 100% das chances de ocorrências do diagnósticos Negativos são da categoria C1, este mesmo raciocínio se aplica a categoria de indefinidos quanto a categoria C0. Quando analisamos os casos de diagnósticos Positivos percebemos que agora são 5 possíveis categorias \({C2,C3,C4,C5,C6}\) para este caminho, assim, a probabilidade de ocorrer para o evento Categoria 2 (C2) será a chance de ocorrer em 5, logo a possibilidade de ocorrer C2 dado que saiba que o diagnóstico é positivo é \(P(C2|Positivo) = \frac{1}{5}\), afinal são 5 possíveis caminhos por essa rota que ainda desconhecemos
a frequência medida de ocorrências. Como todos os caminhos do diagnóstico positivo são considerados equiprováveis temos \[P(C3|Positivo) = P(C4|Positivo) = P(C5|Positivo) = P(C6|Positivo) = P(C2|Positivo)\].

Vamos pensar este problema de maneira mais prática, imaginemos a seguinte situação:

Um médico recomendou que 45 pacientes fizessem o exame de mamografia, o que ele pode esperar dos resultados se a única informação que ele conhece a priori é o diagrama 7.5? Qual seria a probabilidade de ser positivo e ser diagnóstico C6?

Segundo o diagrama 7.5, se 45 pacientes realizarem o procedimento, há a probabilidade de que 1/3 deles tenham diagnóstico negativo (\(P(Negativo) = \frac{1}{3}\)), como são 45 pacientes, a terça parte será formada por 15 pacientes. Como haviámos definido que a probabilidade de ocorrências das outras categorias, “Positivo” e “Negativo” eram iguais, ou seja, os eventos são equiprovavéis, essas categorias terão o mesmo número de pacientes em suas respectivas categorias, portanto 15 para cada, como apresentado no na figura 7.7. Mas se tivermos interessados especialmente naquele grupo que é formado por diagnóstico C6, pacientes já com diagnóstico de cancêr 7.1, devemos lembrar que a probabilidade que associamos a esta categoria é de apenas \(\frac{1}{5}\) dos diagnósticos positivos, ou seja, daqueles 15 pacientes que tiveram diagnóstico positivo, apenas 3 provavelmente pertecem a esta categoria.
Agora, podemos fazer uma “mágica”, se a nossa pergunta referia-se a probabilidade do diagnóstico C6, pacientes já com diagnóstico de cancêr então basta dividir número de pacientes com este diagnóstico pelo número total de pacientes \[P(C6) = \frac{Nº~de~C6}{Nº~de~pacientes} = \frac{3}{45} = \frac{1}{15}\]. Se pensarmos na probabilidade como a chance de seguir um dos caminhos, por exemplo, de um dos pacientes ser positivo e além disso ser da categoria C6 veremos que \[P(Positivo~e~C6) = P(C6|Positivo)*P(Positivo)\] assim

\[P(Positivo~e~C6) = \frac{1}{5}*\frac{1}{3} = \frac{1}{15}\].

Este procedimento é conhecido na matemática pela definição de teorema da multiplicação.

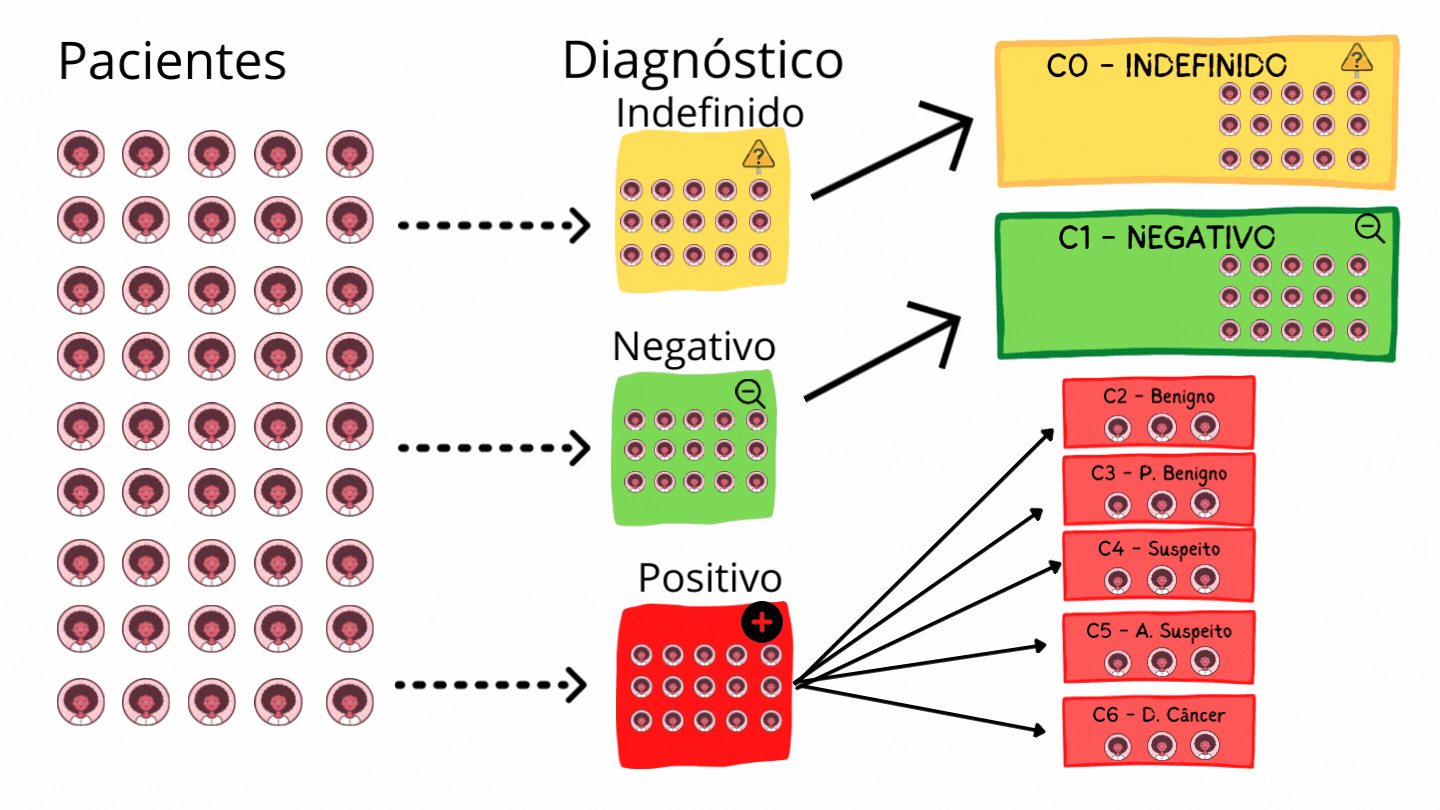
Figura 7.7: Exemplo de pacientes BIRADS

Feita esta análise inicial, podemos nos debruçar sobre os dados, aqueles registros das ocorrências do Sistema Único de Saúde (SUS), e avaliar quais são de fato as ocorrências de diagnósticos dentro das categorias propostas pelo BI-RADS .

Para analisarmos estes números é necessário que acessemos o banco de dados por consulta ao departamento de informática do Sitema Único de Saúdo do Brasil (DATASUS) via uma aplicação web chamada de Tabnet. Os bancos de dados do SUS armazenam diariamente informações de: - consulta ambulatórias; - internação em hospitais; - número de equipamentos de imagem; - endereços de unidades de saúde; - dados sobre hemoterapia, - quimioterapia etc.

Acho que já deu pra imaginar como ele é gigante!

Mas nos concentraremos especialmente no Sistema de Informação do Câncer (SISCAN), que organiza separadamente um grupo de variáveis de interesse relacionadas ao câncer de mama. Isso nos ajudará a entender quais os diagnósticos mais frequentes de cada uma das categorias apresentadas no diagrama do BI-RADS.

Tabela 7.2: Dados de mamografias das categorias do BI-RADS obtios do SISCAN
Ano	C0	C1	C2	C3	C4	C5	C6
2013	3	11	2	0	0	1	0
2014	1844	6749	4570	240	76	8	0
2015	2197	6058	4969	406	81	7	1
2016	2368	5752	5902	508	141	12	1
2017	4768	9856	13806	1213	510	42	3
2018	4615	8764	15129	1413	572	56	6
2019	7679	14355	23443	1957	900	77	6
2020	5365	13375	15348	1220	527	48	23
2021	9133	17946	23135	1357	857	87	65

O primeiro passo é conhecer um pouco sobre os registros de dados do sistema SISCAN para o caso da Bahia. Cada linha da Tabela 7.2 corresponde aos dados de exames de mamografia realizados pelo sistema SISCAN para a cidade de Salvador para um ano específica. E cada coluna refere-se a uma das categorias do BI-RADS. Para conhecer um pouco das informações utilizaremos um gráfico de linhas:

Figura 7.8: Evolução do número de exames de mamografia segundo protocolo BI-RADS

A partir da Figura 7.8 podemos observar que houve um aumento expressivo do número de exames realizados por ano para momografias paras os diferentes de cada categoria de diagnóstico segundo o BI-RADS. Algumas perguntas chave surgem a partir destes dados:

Por que o número de diagnósticos estão aumentando segundo o protocolo BI-RADS?
Por que apenas no ano de 2020 houve redução do número de registros em todas as categorias do BI-RADS, exceto da C6?
A pandemia do coranavírus interferiu no número de exames realizados ou aprovados?

Observemos os dados da Figura 7.8 respeitando as definições de Indefinido, Negativo e Positivo do diagrama da Figura 7.5, obtemos a seguinte tabela:

Tabela 7.3: Dados de mamografias das categorias do BI-RADS obtios do SISCAN resumidos em Indefinido (C0), Negativo (C1) e Positivo (C2,C3,C4,C5 e C6)
Ano	Indefinido	Negativo	Positivo
2013	3	11	3
2014	1844	6749	4894
2015	2197	6058	5464
2016	2368	5752	6564
2017	4768	9856	15574
2018	4615	8764	17176
2019	7679	14355	26383
2020	5365	13375	17166
2021	9133	17946	25501

Por conta das questões acima, resolvemos analisar um caso mais simples, os dados do ano de 2018 da Tabela 7.2. Na Figura 7.3 a seguir, dividindo em três categorias, indefinida, positiva e negativa:

Figura 7.9: Dados de mamografia de Salvador ano 2018

Diferentemente da situação idealizada na Figura 7.7, na qual há equiprobabilidade, ou seja, a chance de ocorrências dos três diagnósticos são iguais, a Figura 7.9 que tem o gráfico de setores com dados dos diagnósticos Idefinido, Positivo e Negativo para o ano de 2018 para a cidade de Salvador tem proporções diferentes entre si. Como notamos a maior chance de ocorrências está concentrada em casos Positivo, depois Negativo e por fim Indefinido. Analisamos apenas pela visualização do gráfico da Figura 7.9 percebemos que mais da metade dos eventos é de diagnósticos positivos, logo, podemos dizer que mais de 50% dos casos são Positivo. Portanto, aqui vale uma ressalva, para aqueles casos que foram acompanhados por médico e foi recomendado a mamografia no ano de 2018, há uma distribuição não uniforme entre as categorias de diagnósticos. Vamos enxergar estes dados por meio de um gráficos de barras do número de ocorrências de cada uma das categorias.

Agora, analisaremos a distribuição de casos pelas categorias do BI-RADS:

Neste gráfico de frequência de ocorrências por categorias do BI-RADS observamos que as categorias C0, C1 e C2 acumulam a maioria dos diagnósticos. Na nossa abordagem adotamos o caso C2 (Benigno) como Positivo, se lembrarmos da nossa avaliação baseada somente no espaço amostral, tinhamos atribuído para a probabilidade de ocorrer a categoria C2 dado que saibamos que é positivo de \(P(C2|Positivo)=\frac{1}{5}=0.2\), contudo se calcularmos a esta probabilidade de C2 com o total de positivos para 2018 e o número de caso de C2 do mesmo ano teremos:

\[P(C2|Positivo)=\frac{15129}{17176}\approx 0.881.\] A probabilidade calculada a partir dos registros dos dados do sistema SISCAN são pelos menos 4 vezes maior que aquela primeira abordagem avaliada por meio do espaço amostral e a hipótese de equiprobabilidade entre os casos positivos. Aprofundando neste casos positivos podemos ainda observar que todos os outros casos positivos C3, C4, C5 e C6 são o complementar dessa probabilidade de C2 dado que saibamos que é positivo. A soma das probabilidades sempre serão igual a 1 para um dado espaço amostral ou subespaço amostral assim:

\[P(C3|Positivo)+P(C4|Positivo)+P(C5|Positivo)+P(C6|Positivo) = 1-P(C2|Positivo),\] assim a probabilidade das outras categorias é \(0.119\) que equivale a aproximadamente \(12\%\). Contudo, na perspectiva médica esse valor é muito importante, ainda que seja bem menor que os \(4/5\) que avaliamos na primeira abordagem. Devemos lembrar que a detecção precoce só ocorre se os exames são realizados com a frequência recomendada pelos protocolos da medicina.

7.4 Desafio

Agora, com a ajuda de um professor, pesquise o conceito de prevalência e avalie a probabilidade de uma pessoa com mais 50 anos ter diagnóstico positivo para câncer de mama. Disponibilizamos os dados de casos de câncer de mama para Bahia. Entre outras estratégias para alcançar este resultado é necessário conhecer a pirâmide etária.

Uma característica muito interessante da distribuição de idades de pessoas diagnósticadas com câncer de mama é seu formato que se assemelha a um sino. Para estastíticos experientes é muito comum trabalhar com distribuições com esta forma, afinal, frequentemente a natureza se manifesta dessa maneira. Além disso, a maioria dos métodos estatísticos desenvolvidos nestes dois últimos séculos de alguma maneira utilizam distribuições com esta forma. Ela foi batizada como distribuição Gaussiana, portanto, sempre que algum histograma apresentar esta curva,

lembrem-se de Gauss!

7.5 Comentários finais

Estas análises não são simples, porém a estatística dispõem de muitas abordagens para atribuir valores das chances de ocorrências de um determinado evento. Particularmente em dados de saúde, que a precisão na atribuição de probabilidade depende de muitos fatores e do controle de muitas condições para que o experimento tenha um valor científico rigoroso é importante ter diferentes formas de atribuição de valores de probabilidade. Cada uma tão mais precisa quanto melhor se controla as condições dos exames. Vimos que na falta de informação, a priori o que há de melhor para ser atribuido é probabilidade igual para todas as possibilidades de resultados. Na perspectiva da ciência de dados, a atribuição de valores de probabilidade ou sua atualização deve ser realizada à medida que são coletados novos dados. Isto pode ser realizado por exemplo por algorítimos que classificam determinadas imagens de diagnósticos de pacientes com alguma problema de saúde como por exemplo a avaliação automática do diagnóstico do câncer de mama. Assim, a atribuição de que os eventos tem chances iguais ou pela atribuição dos valores resultantes da observação dos bancos de dados permitem que avaliemos e tomemos decisões sobre estes sistemas. Fique atenta, a ideia de que um fenômeno pode ser aleatório e que é possível atribuir valores para a chances de ocorrências em diferentes categorias é um pilar para a maioria dos seus métodos utilizados pelos cientistas de dados.