Chapter 7 시간의존성 공변량을 갖는 생존자료분석
이제 pbcseq 데이터를 보자. 이 데이터는 pbc 데이터의 연장으로 각 환자들의 추적 검사소견을 담고 있다. pbc에 등록된 환자가 418명이고 pbcseq에는 모두 312명의 추적검사 데이터(1945건)로 환자 1명당 1번 에서 16번의 추적검사 결과가 포함되어 있다. 다음 그래프는 환자당 추적검사 횟수를 나타낸 것이다.
library(survival)
library(ggplot2)
library(mgcv)
x=table(pbcseq$id)
df=as.data.frame(table(x))
ggplot(df,aes(x=x,y=Freq))+
geom_col(fill="grey80",color="black")+
labs(x="Follow-up", y="N")+
theme_bw()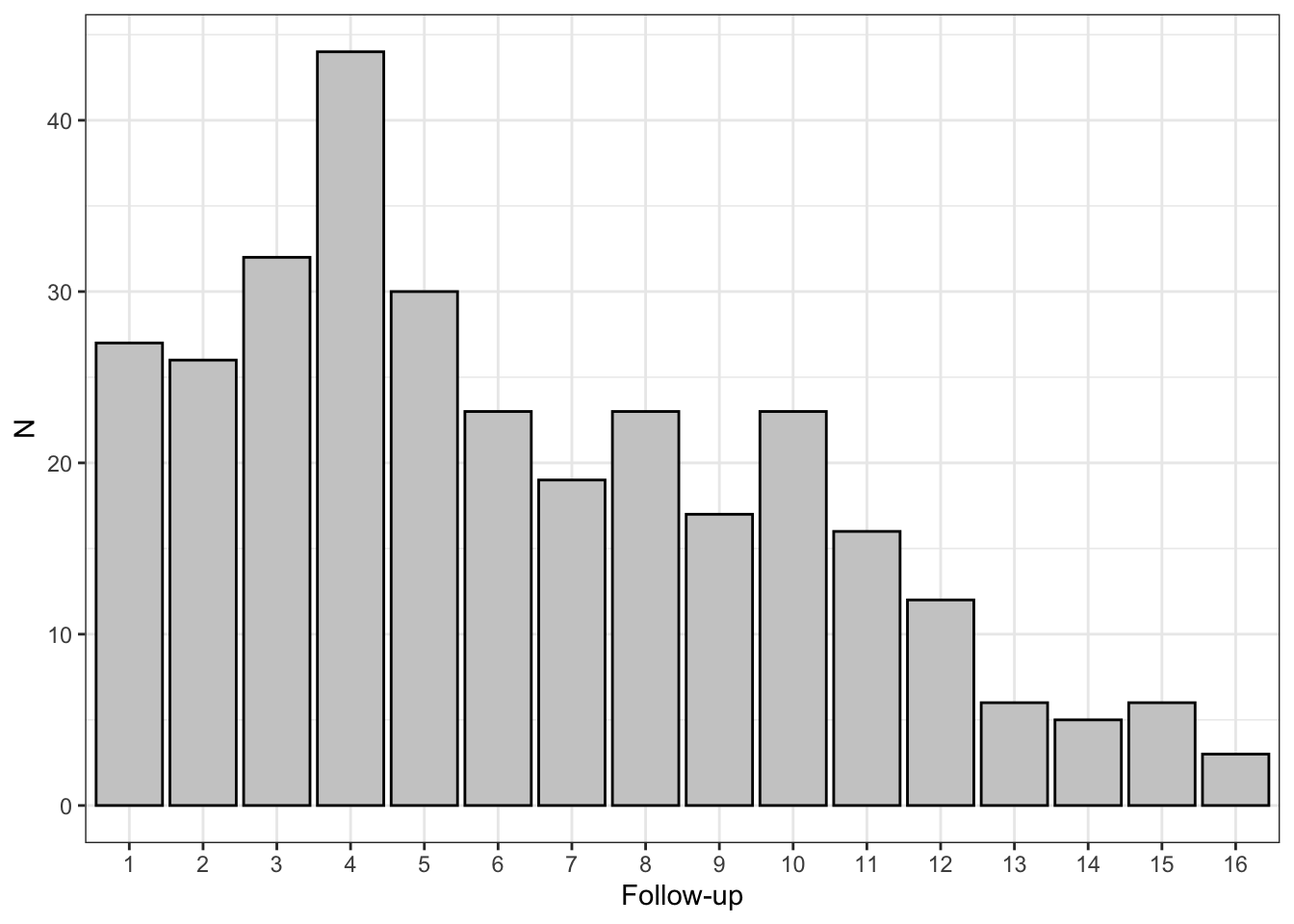
cox.ph는 공변량이 고정되어 있는 경우에 분석을 할 수 있도록 고안된 것이지만 이를 이용하면 벌점평활모형(penalized smooth model)으로도 사용할 수 있다. 이제 모형에 적합시키기 앞서 관찰되지 않은 기간의 공변량을 어떻게 어림잡을 것인가 하는 결정을 내려야 하는데 이는 Cox 비례위험 모형의 시간의존적모형에 필요하기 때문이다. 모든 환자에 대해 각 시간별로 측정한 자료를 갖고 있지 않기 때문에 각 시간 별로 측정한 것은 이전에 측정하지 못한 수치와 같다고 가정한다. 이러한 단계적인 보간(stepwise interpolation)은 기술적으로 쉽지만 명백히 실제수치를 반영하는 것은 아닐 것이다. 선형보간이나 스플라인 보간이 더 선호될 수도 있다. 가장 먼저 할 일은 pbcseq데이터를 시간에 따라 변화하는 공변량을 채워넣은 인공적인 포아송데이터로 변환하는 것이다. 이를 위해 다음과 같은 tdpois함수를 사용한다. 이 함수는 ggGam()패키지에 포함되어 있다.
app <- function(x,t,to) {
## wrapper to approx for calling from apply...
y <- if (sum(!is.na(x))<1) rep(NA,length(to)) else
approx(t,x,to,method="constant",rule=2)$y
if (is.factor(x)) factor(levels(x)[y],levels=levels(x)) else y
} ## app
tdpois <- function(dat,event="z",et="futime",t="day",status="status1",
id="id") {
## dat is data frame. id is patient id; et is event time; t is
## observation time; status is 1 for death 0 otherwise;
## event is name for Poisson response.
if (event %in% names(dat)) warning("event name in use")
require(utils) ## for progress bar
te <- sort(unique(dat[[et]][dat[[status]]==1])) ## event times
sid <- unique(dat[[id]])
inter <- interactive()
if (inter) prg <- txtProgressBar(min = 0, max = length(sid), initial = 0,
char = "=",width = NA, title="Progress", style = 3)
## create dataframe for poisson model data
dat[[event]] <- 0; start <- 1
dap <- dat[rep(1:length(sid),length(te)),]
for (i in 1:length(sid)) { ## work through patients
di <- dat[dat[[id]]==sid[i],] ## ith patient's data
tr <- te[te <= di[[et]][1]] ## times required for this patient
## Now do the interpolation of covariates to event times...
um <- data.frame(lapply(X=di,FUN=app,t=di[[t]],to=tr))
## Mark the actual event...
if (um[[et]][1]==max(tr)&&um[[status]][1]==1) um[[event]][nrow(um)] <- 1
um[[et]] <- tr ## reset time to relevant event times
dap[start:(start-1+nrow(um)),] <- um ## copy to dap
start <- start + nrow(um)
if (inter) setTxtProgressBar(prg, i)
}
if (inter) close(prg)
dap[1:(start-1),]
} ## tdpois이 함수를 사용하여 다음과 같이 데이터를 변환한다.
pbcseq$status1 <- as.numeric(pbcseq$status==2) ## deaths
pb <- tdpois(pbcseq) ## conversion
pb$tf <- factor(pb$futime) ## add factor for event time변환한 후 만들어지는 pb데이터는 모두 28,380 건에 해당한다. 이 자료를 REML(restricted maximal likelihood)방법으로 일반화가법모형을 이용해 동등포아송모형에 적합시키면 cox.ph로 분석한 것과 같은 결과가 나오지만 데이터의 크기가 크고 tf 의 범주수가 많아 시간이 많이 걸리므로 discrete=TRUE 옵션을 사용하여 bam을 이용해 적합시킨다.(이 방법은 수백만건의 자료에도 사용할 수 있다.)
7.1 초기 모형 적합
초기모형으로 다음의 R 코드를 사용해 모형적합시켰다. 처음 선형항으로 tf-1을 사용한 것은 절편이 없는 모형을 선택한 것이고 ntreads=2는 가능하면 CPU를 두개 사용하라는 뜻이다.
b0 <- bam(z ~ tf - 1 + trt + sex +stage+s(sqrt(protime))+s(platelet)+
s(age)+s(bili)+s(albumin)+s(sqrt(ast))+s(alk.phos),
family=poisson, data=pb, discrete=TRUE,nthreads=2)
anova(b0)
Family: poisson
Link function: log
Formula:
z ~ tf - 1 + trt + sex + stage + s(sqrt(protime)) + s(platelet) +
s(age) + s(bili) + s(albumin) + s(sqrt(ast)) + s(alk.phos)
Parametric Terms:
df Chi.sq p-value
tf 137 105.439 0.979
trt 1 0.143 0.705
sex 1 0.675 0.411
stage 1 1.014 0.314
Approximate significance of smooth terms:
edf Ref.df Chi.sq p-value
s(sqrt(protime)) 1.784 2.266 16.134 0.000485
s(platelet) 1.291 1.531 3.627 0.062963
s(age) 1.000 1.000 19.089 1.25e-05
s(bili) 2.434 3.063 159.018 < 2e-16
s(albumin) 2.706 3.435 85.699 < 2e-16
s(sqrt(ast)) 1.000 1.000 3.894 0.048469
s(alk.phos) 1.000 1.000 0.285 0.593605anova 결과에서 p 이 높은 alk.phos, sex 와 stage를 후향적선택으로 탈락시킨다. trt는 p값은 높지만 이 임상시험의 관심의 대상이므로 탈락시키지 않았다.
7.2 최종 모형
최종적으로 다음의 모형을 선택하였다.
b <- bam(z ~ tf - 1 + trt + s(sqrt(protime))+s(platelet)+
s(age)+s(bili)+s(albumin)+s(sqrt(ast)),
family=poisson, data=pb, discrete=TRUE,nthreads=2)
anova(b)
Family: poisson
Link function: log
Formula:
z ~ tf - 1 + trt + s(sqrt(protime)) + s(platelet) + s(age) +
s(bili) + s(albumin) + s(sqrt(ast))
Parametric Terms:
df Chi.sq p-value
tf 137 390.053 <2e-16
trt 1 0.155 0.694
Approximate significance of smooth terms:
edf Ref.df Chi.sq p-value
s(sqrt(protime)) 1.607 2.020 16.999 0.000212
s(platelet) 1.396 1.701 4.928 0.036139
s(age) 1.000 1.000 24.415 7.77e-07
s(bili) 2.584 3.252 163.983 < 2e-16
s(albumin) 2.655 3.369 95.893 < 2e-16
s(sqrt(ast)) 1.000 1.000 4.316 0.037766모형의 요약결과를 보면 trt에 대한 p값은 약 0.7 정도로 역시 치료가 효과적이라는 근거는 없다. 잔차는 시간의존적모형에서 쉽게 계산할 수 있다. 각 개인의 누적 위험은 공변량의 변동성을 고려해야 하지만 잔차의 계산은 쉽다.
7.3 모형의 시각화
다음으로 이 모형을 시각화해본다.
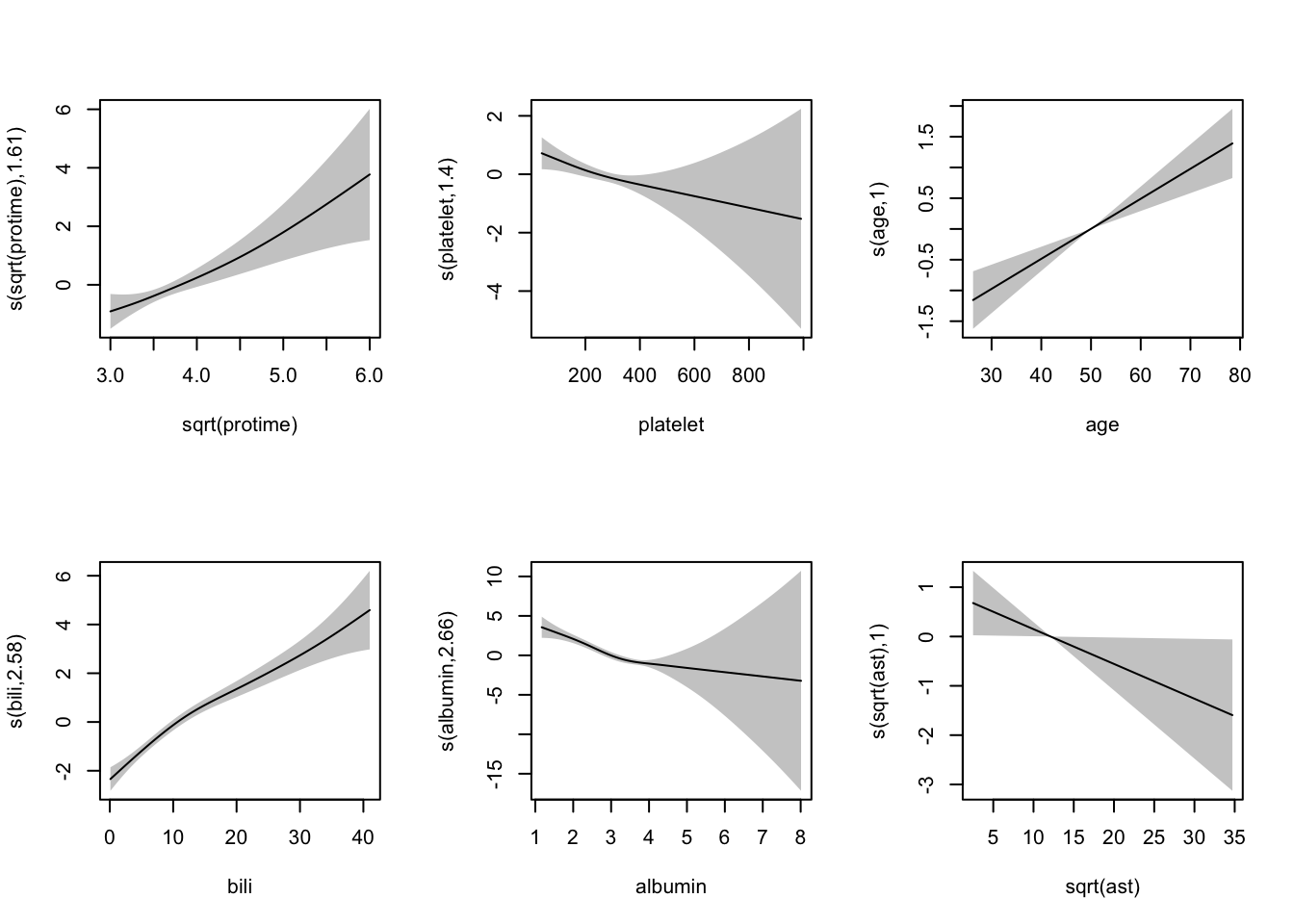이 결과를 기저상태의 결과와 비교해보면 프로트롬빈시간(sqrt(protime))과 혈소판(platelet), 알부민(albumin)의 경우 추정효과가 보다 비선형이라는 근거를 보이고 있으며 나이의 경우 선형효과를 보이고 있다. 효과의 방향과 넓은 신뢰구간은 변화가 없다.
7.4 생존곡선 추정
생존곡선을 그리는 과정은 다음과 같다. 25번째 환자의 생존곡선을 그려본다.
te <- sort(unique(pb$futime)) ## event times
di <- pbcseq[pbcseq$id==25,] ## data for subject 25
## interpolate to te using app from ?cox.pht...
pd <- data.frame(lapply(X=di,FUN=app,t=di$day,to=te))
pd$tf <- factor(te)
X <- predict(b,newdata=pd,type="lpmatrix")
eta <- drop(X%*%coef(b)); H <- cumsum(exp(eta))
J <- apply(exp(eta)*X,2,cumsum)
se <- diag(J%*%vcov(b)%*%t(J))^.5
plot(stepfun(te,c(1,exp(-H))),do.points=FALSE,ylim=c(0.7,1),
ylab="S(t)",xlab="t (days)",main="",lwd=2)
lines(stepfun(te,c(1,exp(-H+se))),do.points=FALSE)
lines(stepfun(te,c(1,exp(-H-se))),do.points=FALSE)
rug(pbcseq$day[pbcseq$id==25]) ## measurement times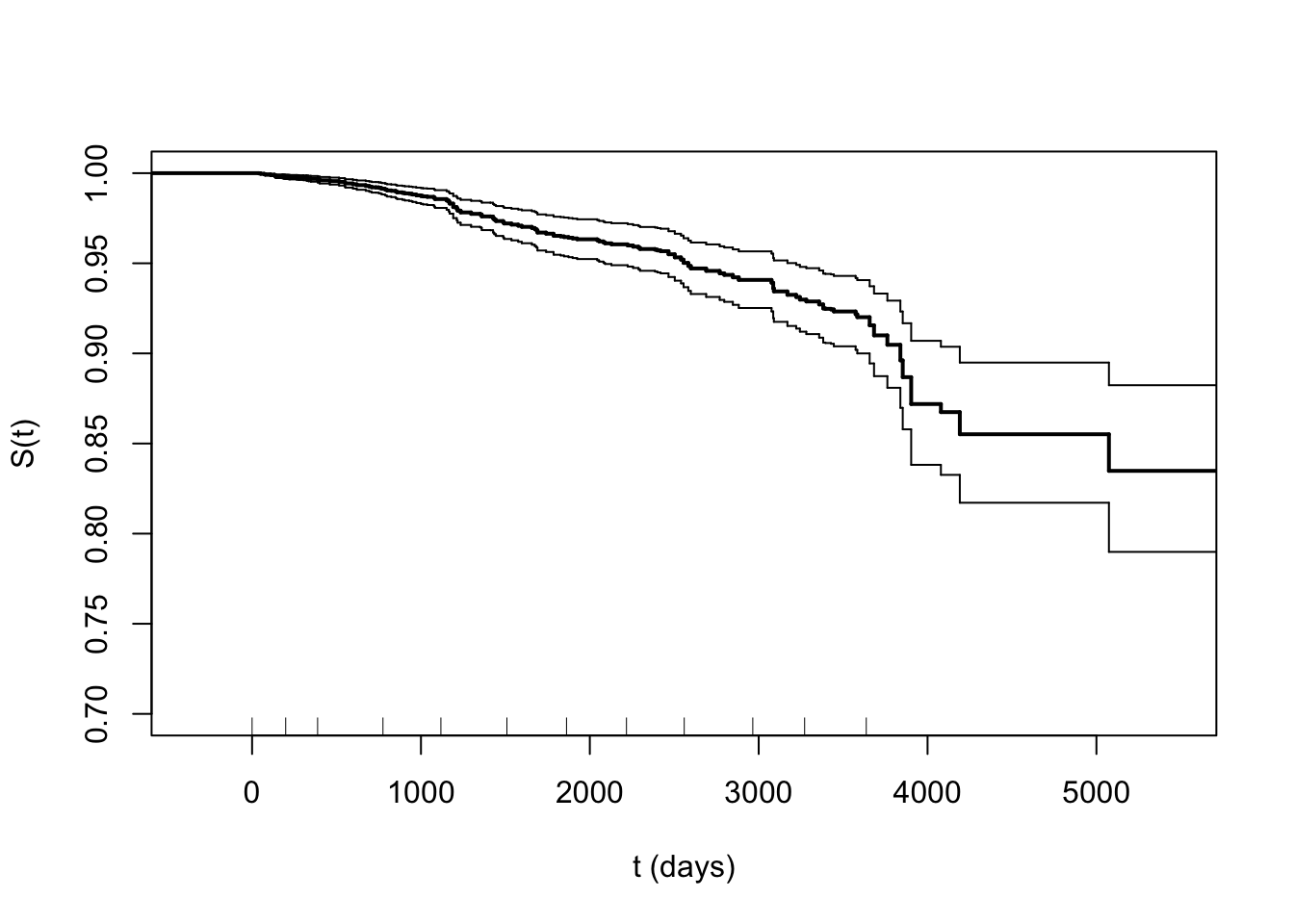
ggGam패키지의 drawFUSurv()함수를 이용하면 ggplot를 이용한 그래프를 그릴 수 있다.
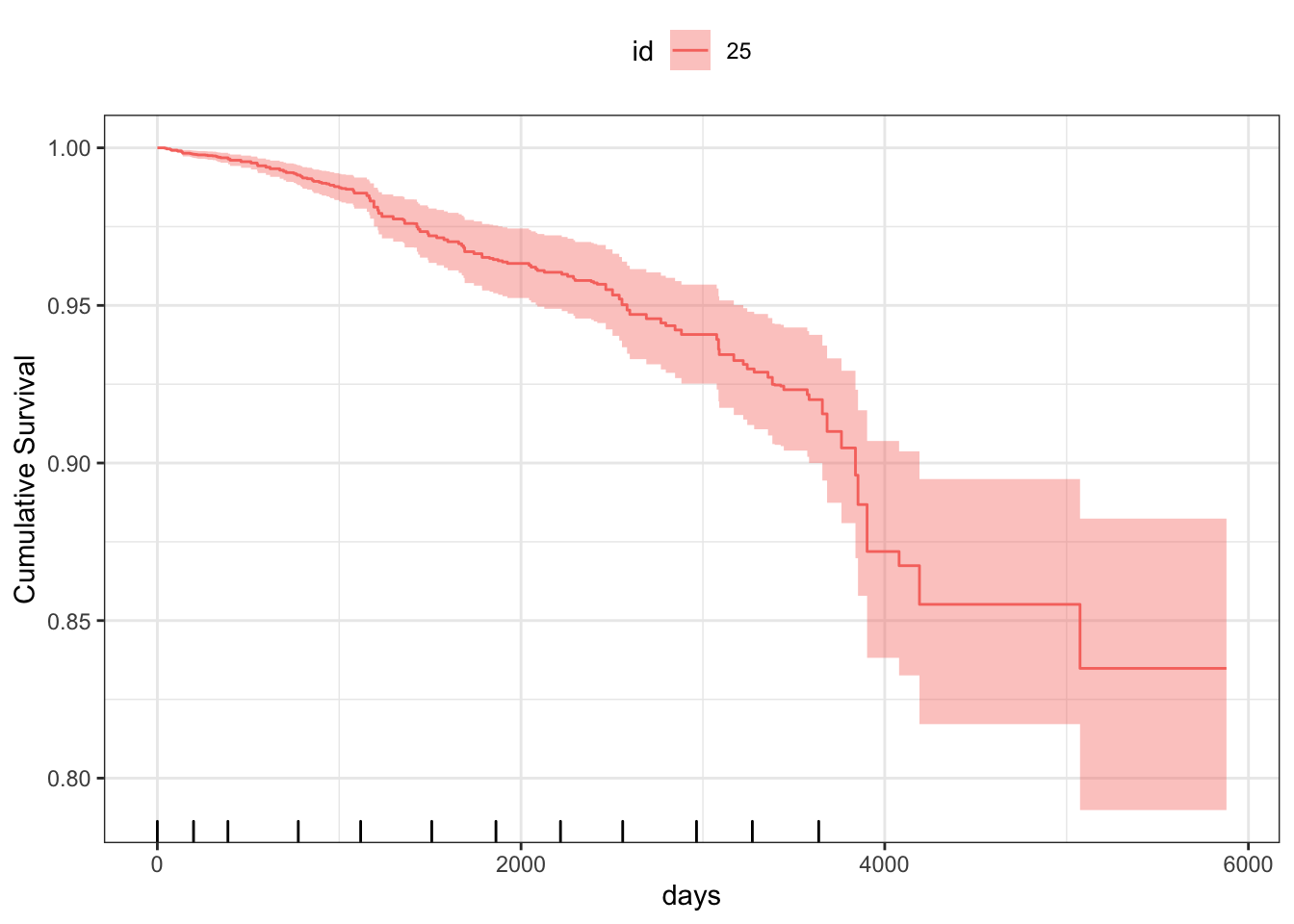
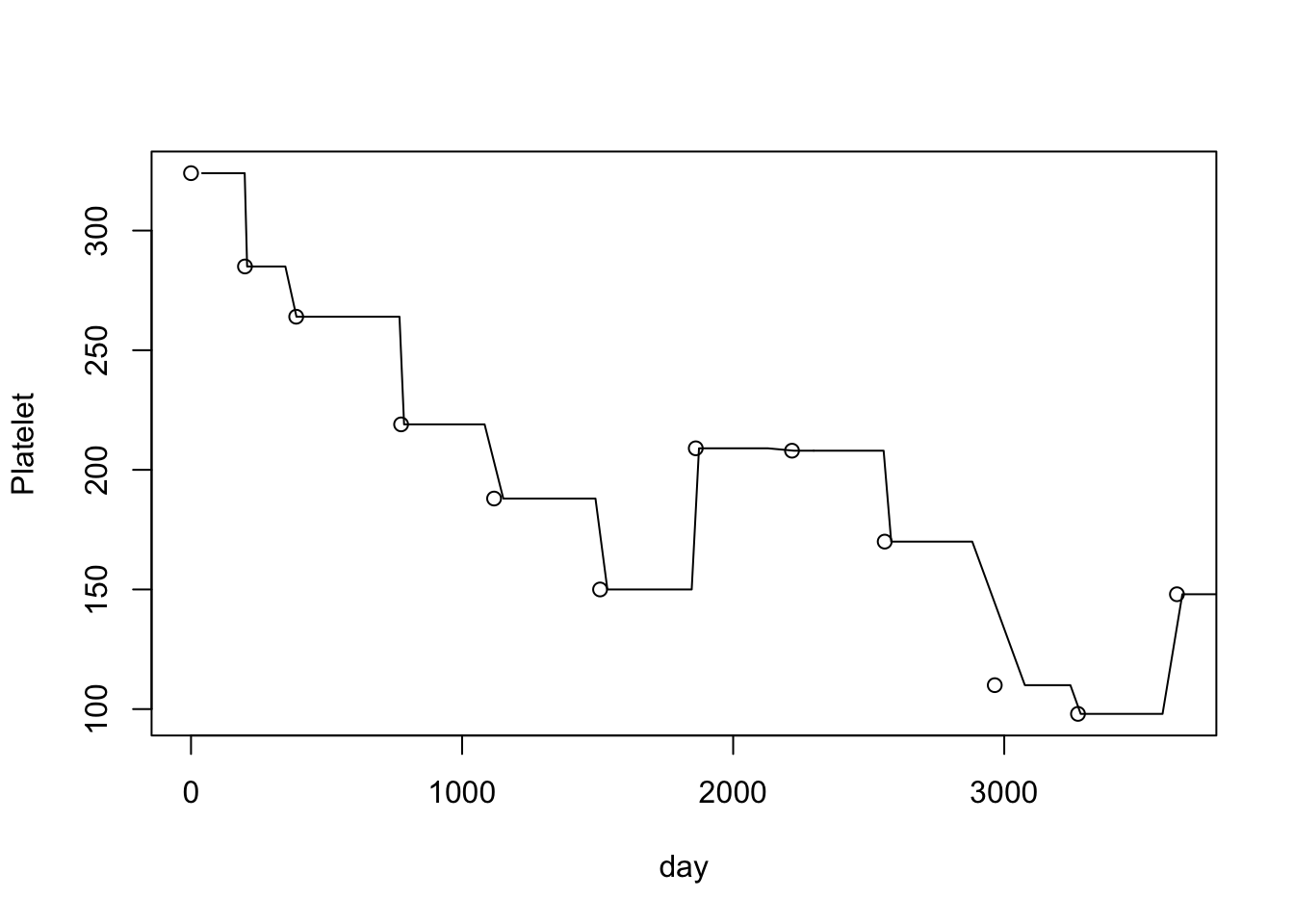
또한 생존과 관련된 다른 공변량의 변화 또한 관심이 있다. 다음 코드로 시간에 따른 공변량의 변화를 시각화할 수 있다. 다음은 25번째 환자의 시간에 따른 protime과 platelet의 변화이다.
er <- pbcseq[pbcseq$id==25,]
plot(er$day,er$protime,xlab="day",ylab="Prothrombin Time")
lines(te,pd$protime)
plot(er$day,er$platelet,xlab="day",ylab="Platelet")
lines(te,pd$platelet)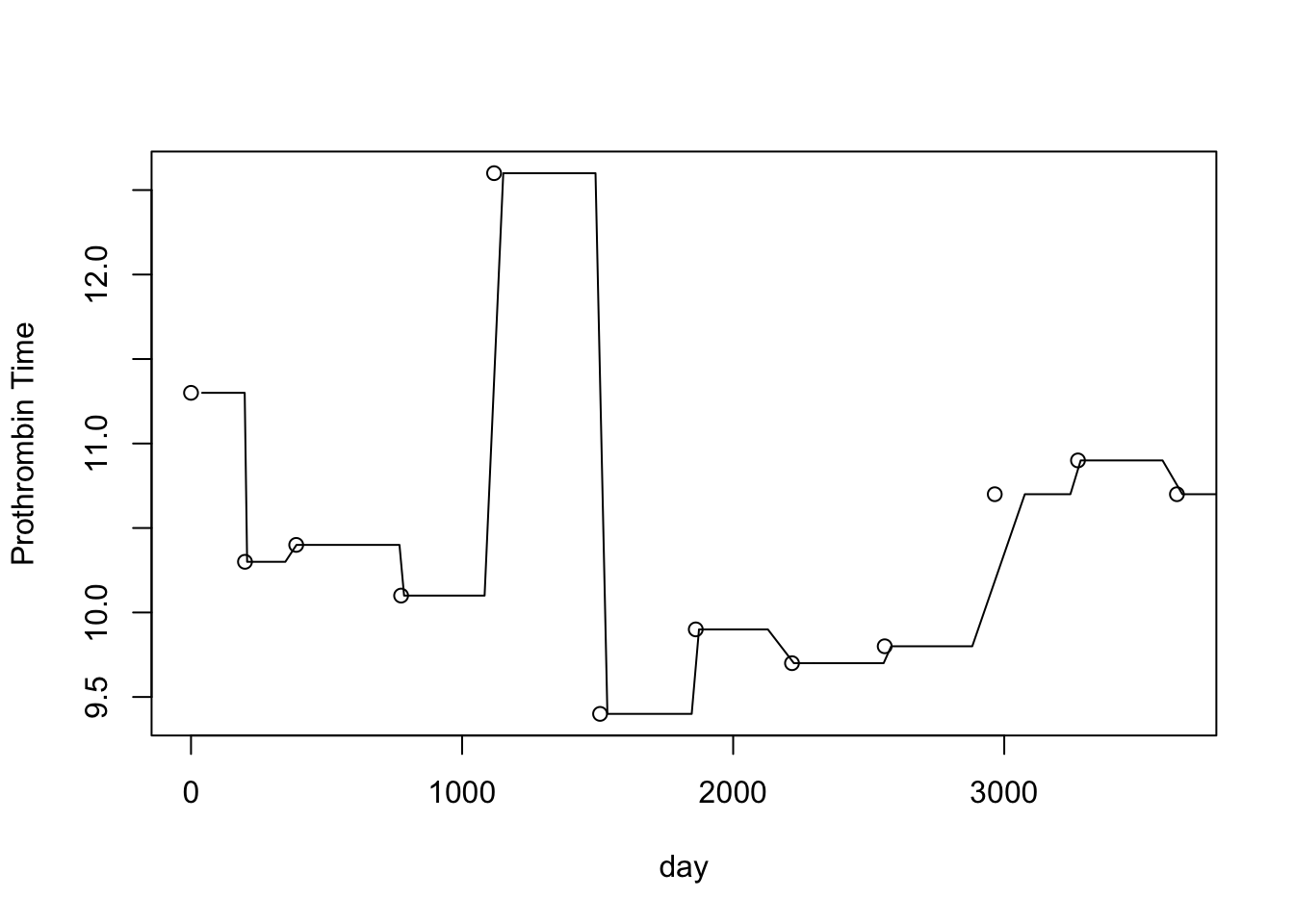
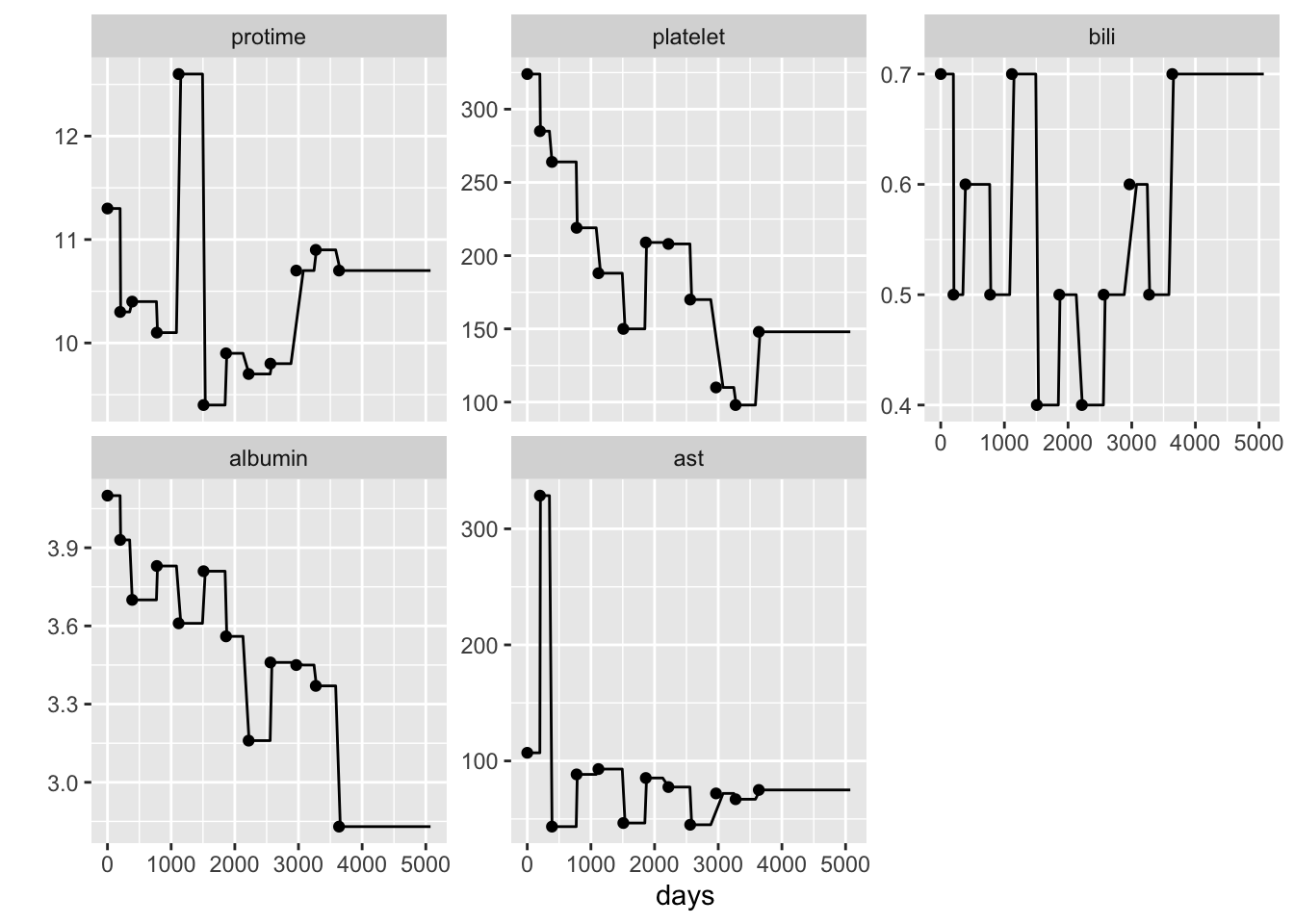
ggGam 패키지의 drawFUData()함수로 다음 그림을 그릴 수 있다.
이 환자에서 기저상태의 생존곡선과 추적검사소견으로 본 생존곡선을 비교해 보면 다음과 같다.
pbc$status1 <- as.numeric(pbc$status==2)
bb = gam(time ~ trt +sex + s(sqrt(protime))+s(platelet)+ s(age)+s(bili)+s(albumin),
weights=status1, family=cox.ph, data=pbc, method="REML")
drawSurv(bb,data=pbc[c(25),],id=list(id=c(25)))+
theme(legend.position="None")+
ggtitle("Prediction with baseline data")+
ylim(c(0.7,1))
drawFUSurv(b,data)+theme(legend.position="None")+
ggtitle("Prediction with follow-up data")+
ylim(c(0.7,1))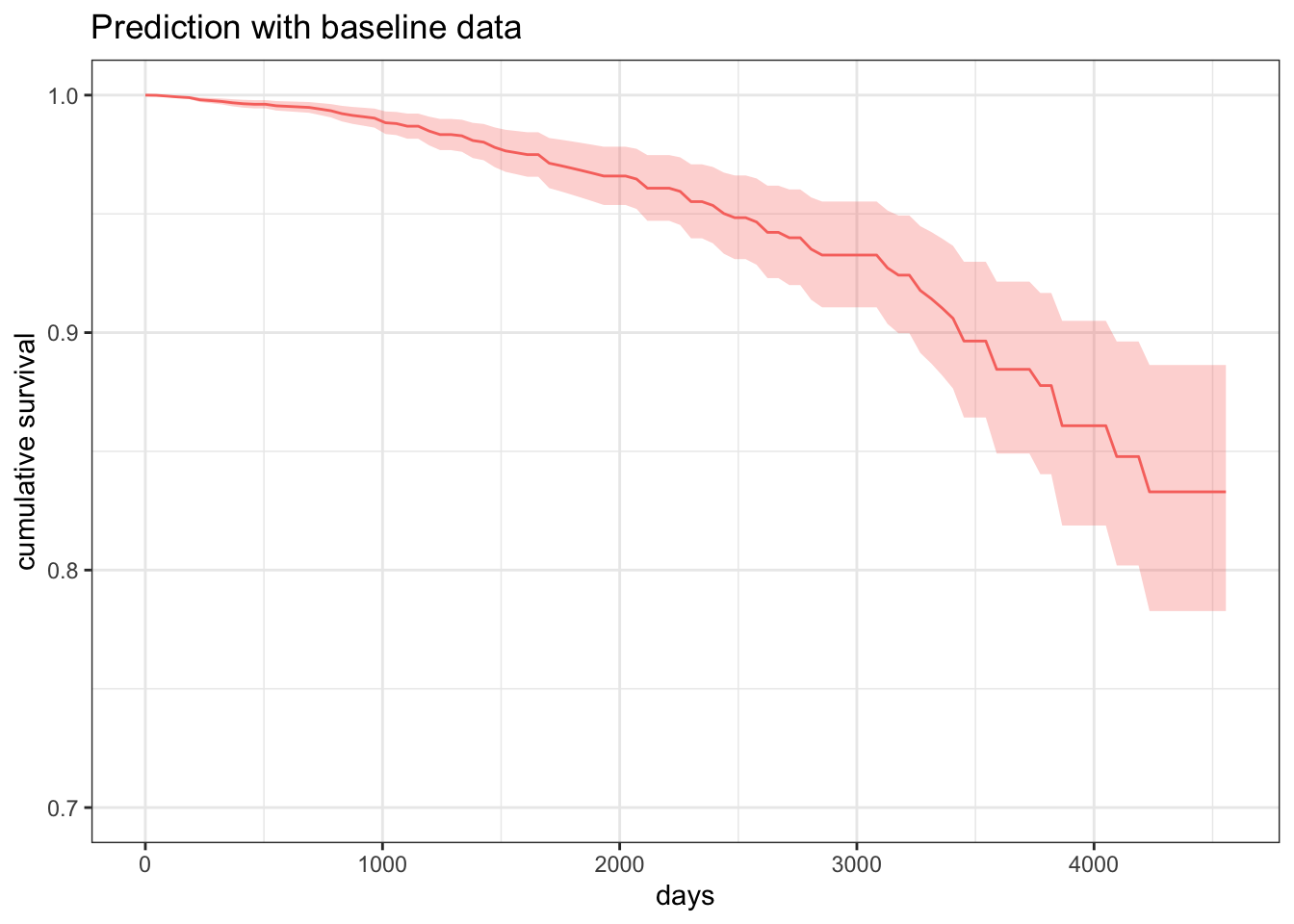
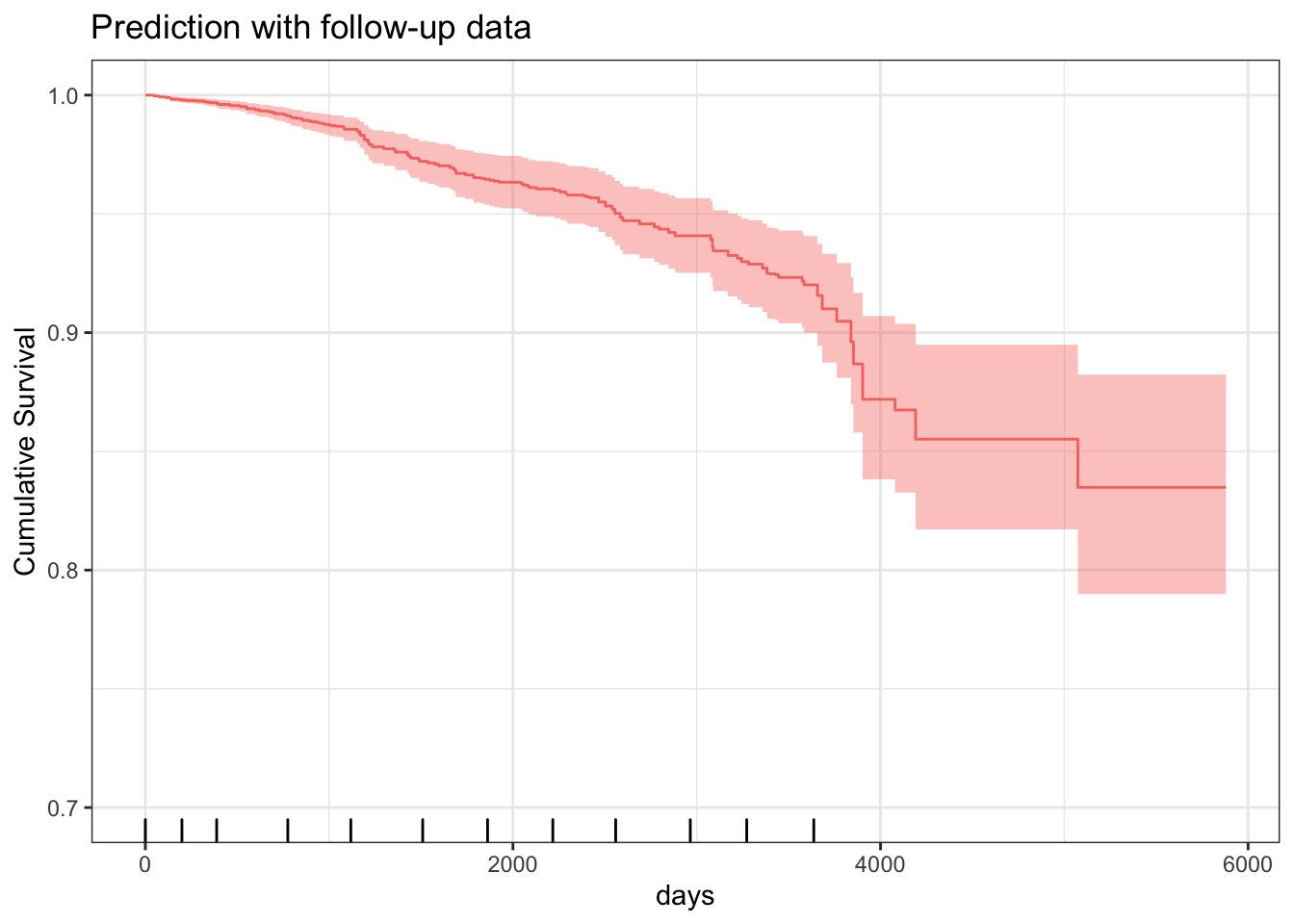
이 환자에서 기저상태의 공변량이 일정하다고 본 생존곡선에 비해 추적검사가 반영된 생존의 추정이 감소된 것은 추적 기간 중 혈중 알부민과 혈소판의 감소에 의한 것으로 추정할 수 있다.