Chapter 4 공간자료를 다루는 Spatial GAMs 과 상호작용

지금까지 하나 또는 몇 개의 평활항으로 이루어진 모형을 다루었지만 이제 여러 개의 변수들과 변수들의 상호작용으로 이루어진 모형을 다루고자 한다. 공간자료는 하나의 평활항이 아닌 복잡한 표면을 가진 자료로 GAMs을 이용해 공간자료를 다룰 수 있다.

4.1 회귀모형에서의 상호작용

선형회귀모형에서의 상호작용의 개념을 복습해보자. 상호작용이란 변수 자체들의 영향과는 별개로 변수들의 상호작용이 독립적으로 결과에 영향을 미치는 것으로 선형모형에서는 두 변수들의 곱(\(x1x2\))으로 상호작용항을 나타낸다. 상호작용이 있는 경우 두 변수의 영향에 의한 결과보다 더 크거나 더 작은 결과를 보일수 있다.

\(y = \beta_0+\beta_1x_1+\beta_2x_2+\beta_3x_1x_2\)

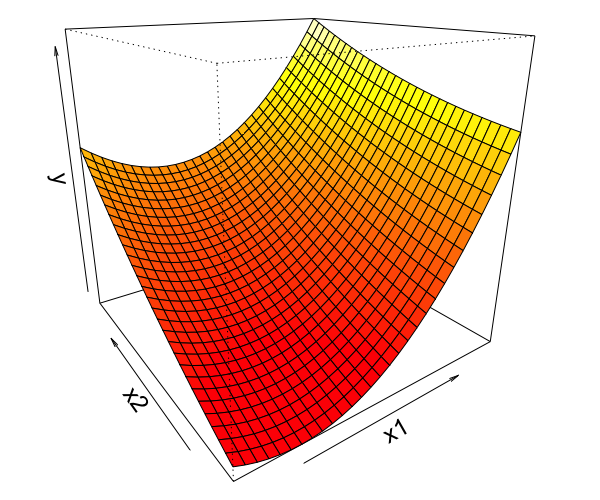
4.2 GAM에서의 상호작용

GAM에서 비선형항과 결과 사이의 관계는 곡선으로 나타난다. 마찬가지로 두 변수의 성호작용은 평활표면으로 나타난다.

\(y = s(x_1,x_2)\)

4.3 GAM에서의 상호작용 구문

GAM에서 상호작용을 나타내는 구문은 매우 직관적이다. 두 변수 사이의 상호작용을 나타내기 위해 다음과 같이 평활함수 s()안에 두변수를 넣어주면 된다.

gam( y ~  s(x1,x2),  # x1,x2 두 변수의 상호작용
     data = 데이터이름, method= "REML")

4.4 상호작용항 과 단순항

상호작용항과 더불어 평활항(비선형항)이나 선형항을 추가할 수 있다. 다음 예는 x1, x2로 이루어진 상호작용 항에 비선형항인 x3를 설명변수로 추가한 예이다.

gam( y ~  s(x1,x2) + s(x3),  ## 비선형항 x3 추가 
     data = 데이터이름, method= "REML")

다음 예는 x1, x2로 이루어진 상호작용 항에 비선형항인 x3와 x4를 설명변수로 추가한 예이다.

gam( y ~  s(x1,x2) + x3 + x4,  ## x3, x4 두 개의 선형항 추가
     data = 데이터이름, method= "REML")

보통 공간자료를 모형으로 다루는 방법은 x, y 좌표를 상호작용항으로 놓고 다른 예측변수들을 추가하는 것이다. 이럴 경우 상호작용항은 데이터의 공간적 구조를 설명하게 된다.

4.5 상호작용 모형의 결과

상호작용이 있는 모형의 결과를 보면 상호작용항이 하나의 평활항으로 나타나는 것을 알 수 있다. 이 상호작용항은 x1과 x2, 그리고 상호작용 세개를 하나의 항으로 나타낸 것으로 선형모형에서 x1, x2, x1:x2 로 나타내는 것과는 다르다. 결과를 보면 상호작용항의 유효자유도(EDF)가 10.82로 높은데 이는 평활선이 아닌 2차원적인 표면을 나타내기 위해 많은 기저함수를 사용한다는 것을 나타낸다.

Family: gaussian 
Link function: identity 

Formula:
y ~ s(x1, x2)

Parametric coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.34256    0.01646   20.82   <2e-16 ***
 ---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Approximate significance of smooth terms:
           edf Ref.df     F p-value    
s(x1,x2) 10.82   14.9 14.37  <2e-16 *** #<-- Interaction
 ---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

R-sq.(adj) =  0.519   Deviance explained = 54.5%
GCV = 0.057564  Scale est. = 0.054161  n = 200

4.6 사용하는 자료

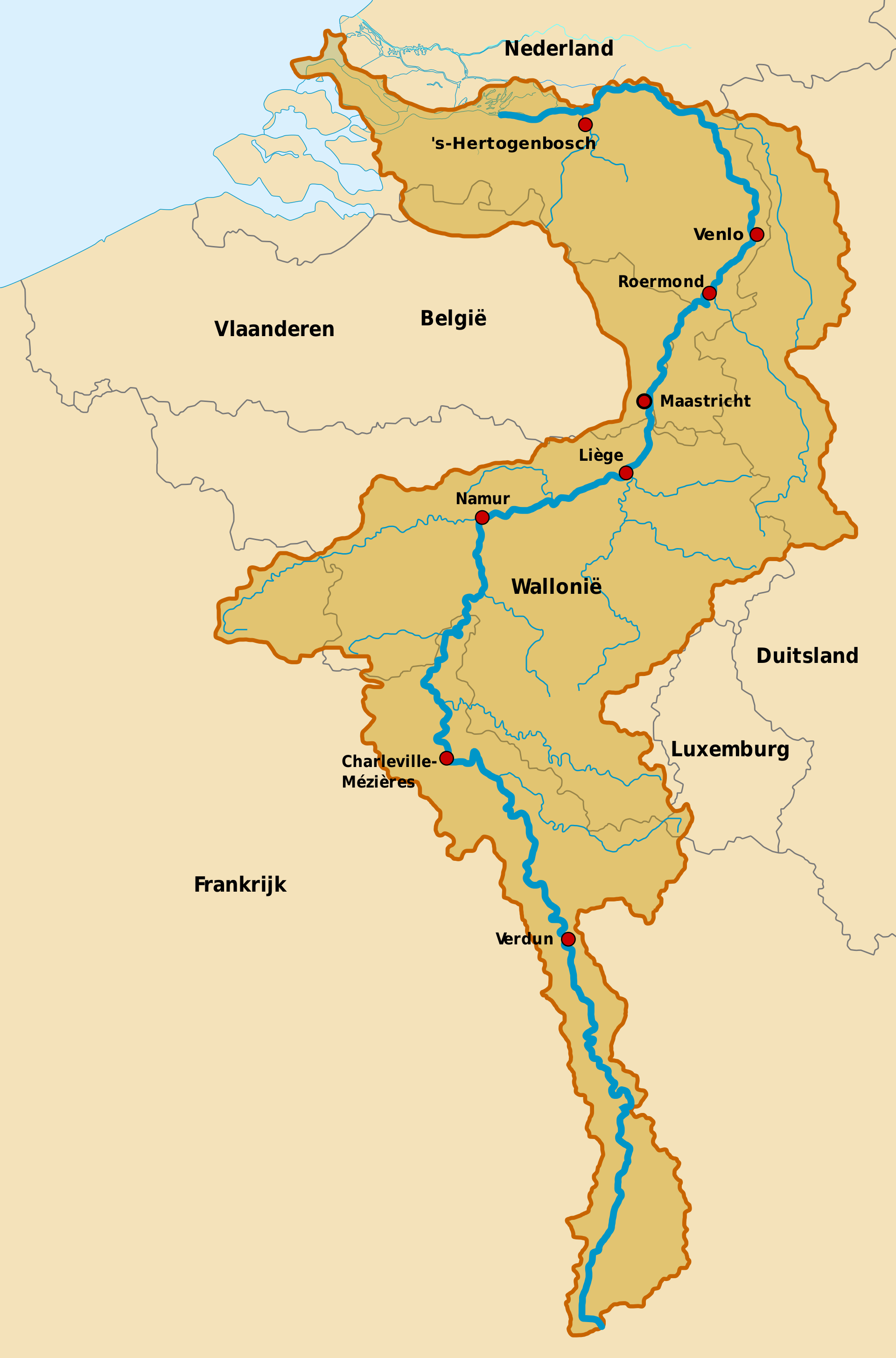
이번 장에서는 예제 데이터로 sp패키지에 있는 meuse 데이터를 사용한다. 이 데이터는 네델란드의 Meuse 강 유역 토양의 중금속 오염에 관한 데이터이다.

데이터를 보면 x,y좌표와 토양 내 중금속의 측정치, 강으로부터의 거리, 고도, 토양의 사용용도 등으로 구성되어 있다.

       x      y cadmium copper lead zinc  elev       dist   om ffreq soil lime
1 181072 333611    11.7     85  299 1022 7.909 0.00135803 13.6     1    1    1
2 181025 333558     8.6     81  277 1141 6.983 0.01222430 14.0     1    1    1
3 181165 333537     6.5     68  199  640 7.800 0.10302900 13.0     1    1    1
4 181298 333484     2.6     81  116  257 7.655 0.19009400  8.0     1    2    0
5 181307 333330     2.8     48  117  269 7.480 0.27709000  8.7     1    2    0
6 181390 333260     3.0     61  137  281 7.791 0.36406700  7.8     1    2    0
  landuse dist.m
1      Ah     50
2      Ah     30
3      Ah    150
4      Ga    270
5      Ah    380
6      Ga    470

4.7 첫번째 모형

토양의 cadmium 농도를 반응변수로 하고 x,y좌표를 설명변수로 하는 모형을 만들어 보면 다음과 같다.


Family: gaussian 
Link function: identity 

Formula:
cadmium ~ s(x, y)

Parametric coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   3.2458     0.1774    18.3   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Approximate significance of smooth terms:
         edf Ref.df     F p-value    
s(x,y) 23.48  27.24 8.667  <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

R-sq.(adj) =  0.607   Deviance explained = 66.7%
-REML = 372.07  Scale est. = 4.8757    n = 155

모형의 요약을 보면 s(x,y)항의 유효자유도는 23.48인 것을 알 수 있고 gam.check()를 해보면 29개의 기저함수가 사용된 것을 알 수 있다.

4.8 설명변수 추가

앞에서 만든 모형에 고도(elev)와 강에서부터의 거리(dist)를 평활항으로 추가해본다.

4.9 GAM 상호작용의 시각화

GAM의 상호작용은 복잡한 공간 데이터를 모형으로 만들 수 있는 강력한 도구이지만 복잡하기 때문에 이해하기 힘들다. 이러한 상호작용을 시각화하는 것이 공간모형을 이해하는데 도움을 주며 mgcv에는 이러한 자료를 2차원, 3차원으로 시각화해주는 강력한 도구가 있다. mgcv 패키지의 plot()함수는 상호작용을 등고선플롯(contour plot)으로 그려준다. 등고선플롯 내부는 지형학적인 지도가 있는데 등고선은 같은 예측 값을 보이는 점들을 연결한 선이며 빨간색과 녹색 점선은 예측이 불확실한 영역으로 예측선에서 표준오차 만큼 높고 낮은 선이다.

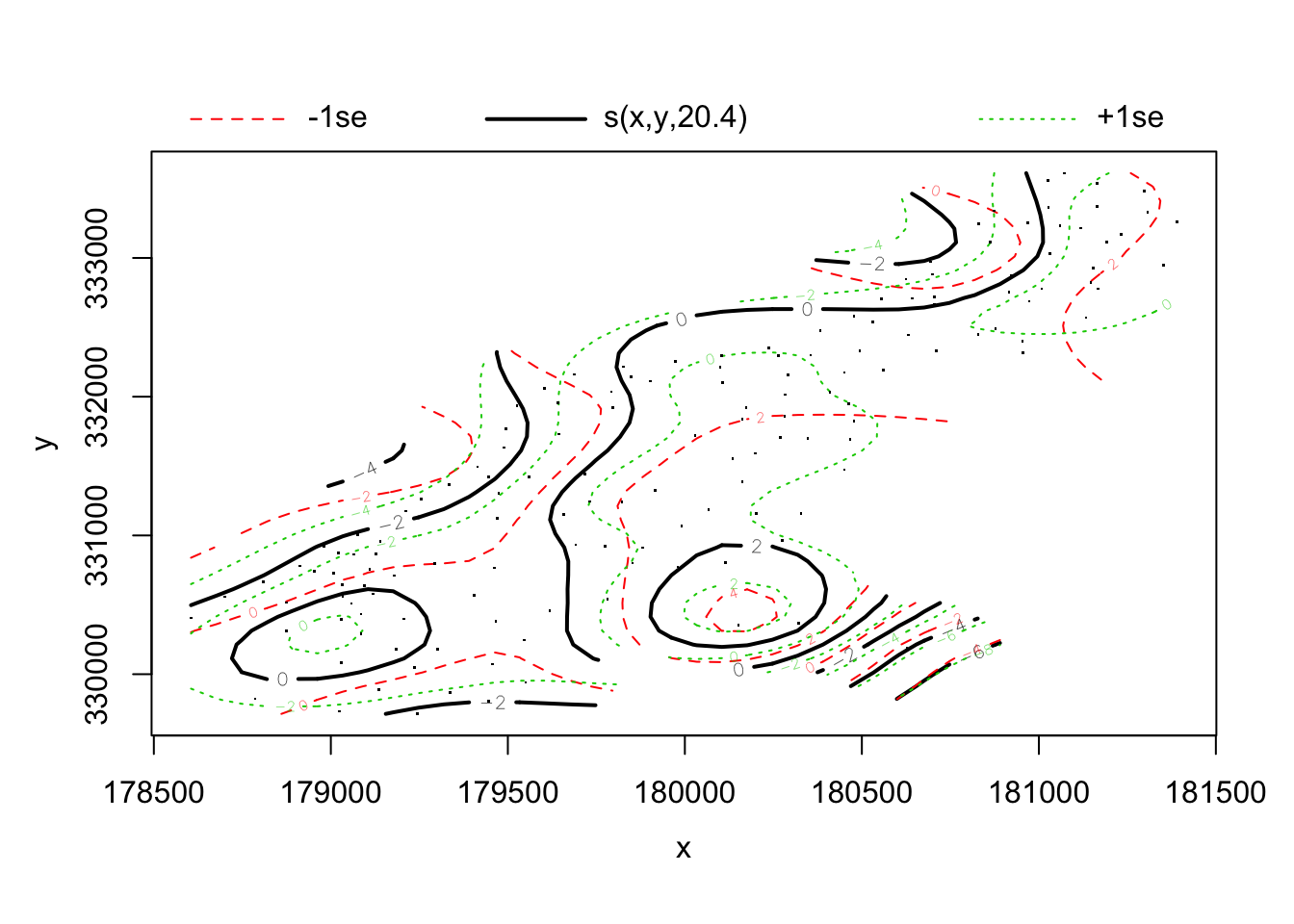
때로는 등고선플롯 보다 삼차원투시도가 더 직관적인 경우도 있다. plot의 scheme인수를 1로 지정하면 3차원 투시도를 얻을 수 있다.

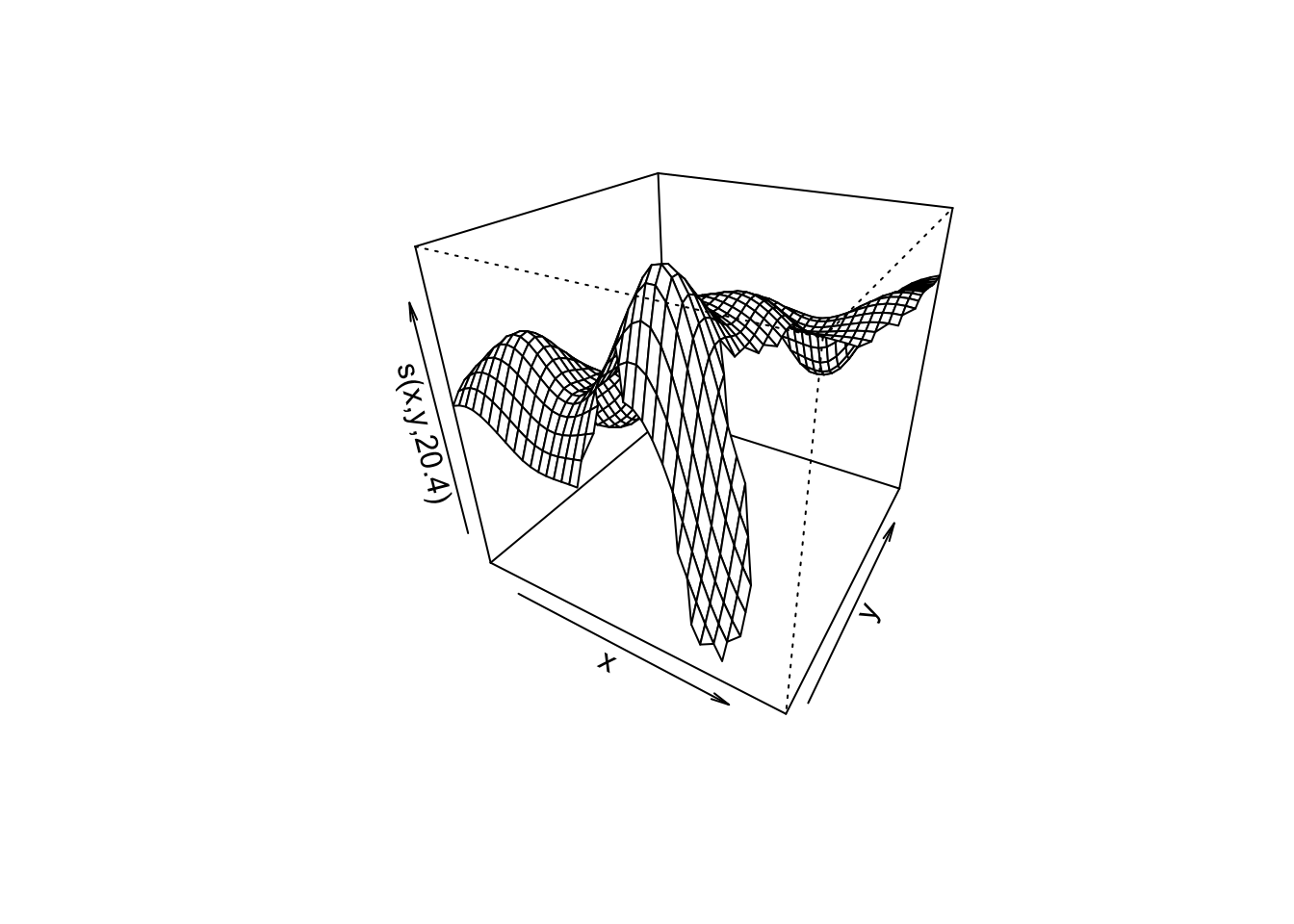
scheme인수를 2로 지정하면 히트맵을 얻을 수 있다. 이 그림은 단순화한 등고선플롯에 색을 더한 것으로 노란색은 큰 예측값을, 붉은 색은 낮은 예측값을 나타낸다.

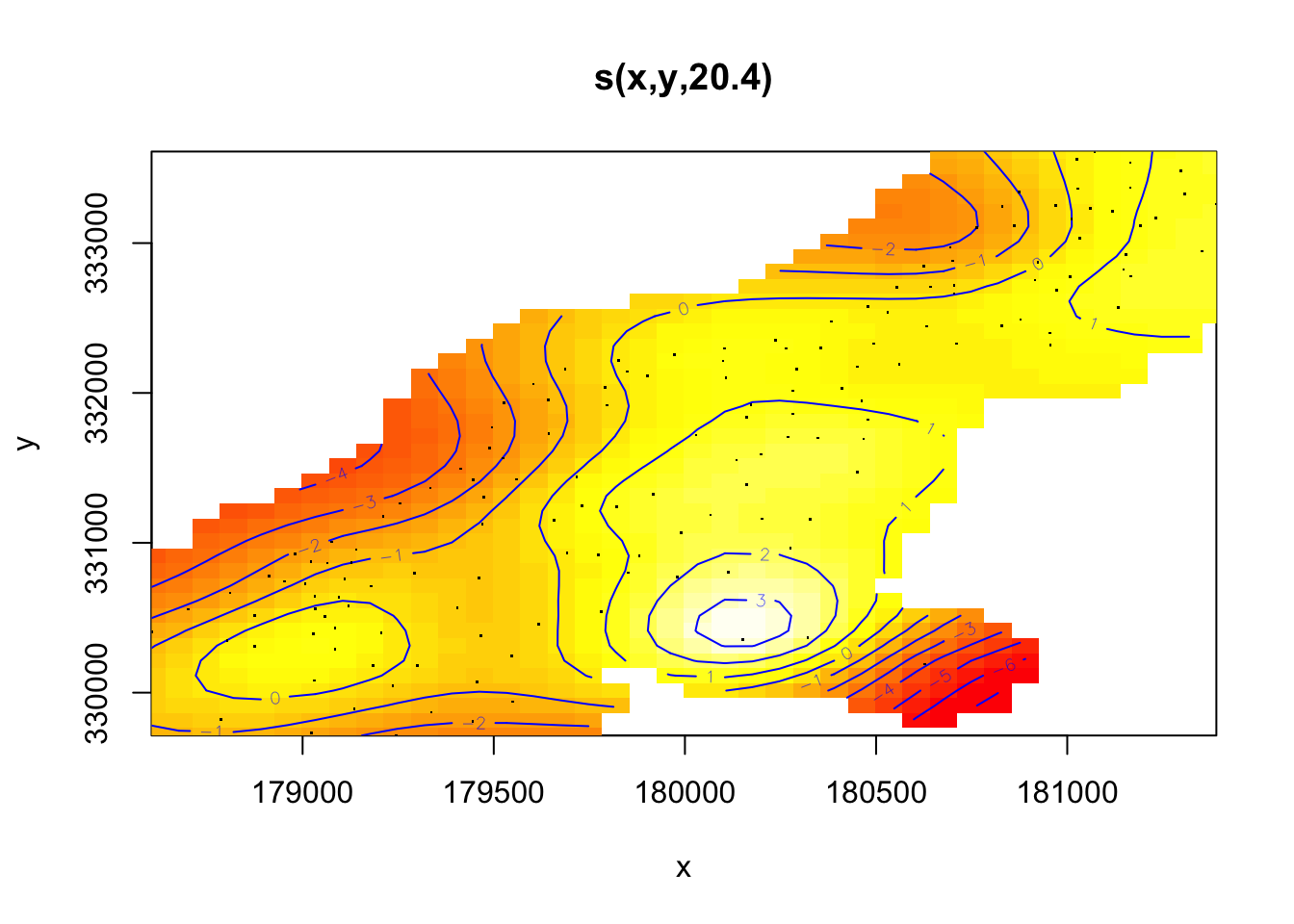
4.10 GAM 상호작용 그림의 사용자화

이들 그림은 우리가 만든 모형의 상호작용을 간편하게 시각화해주는 도구이지만 경우에 따라 그림을 사용자화해야할 때가 있다. 이때 사용할 수 있는 함수가 vis.gam()함수로 많은 옵션을 갖고 있다.

vis.gam(x,
        view = NULL,
        cond = list(),
        n.grid = 30,
        too.far = 0,
        col = NA,
        color = "heat",
        contour.col = NULL,
        se = -1,
        type = "link",
        plot.type = "persp",
        zlim = NULL,
        nCol = 50,
        ...)

vis.gam()함수의 첫번째 인수 x에는 모형이름을 넣어준다. 두번째 view에는 보고자 하는 변수의 이름을 넣어준다. plot.type을 “presp”로 지정해주면 3차원 투시도를 그려준다. 이 그림에서 변수이름을 x,y로 지정했으나 꼭 x,y일 필요는 없고 모형 내의 상호작용을 보고자 하는 임의의 변수 이름 두개를 넣어주면 된다.

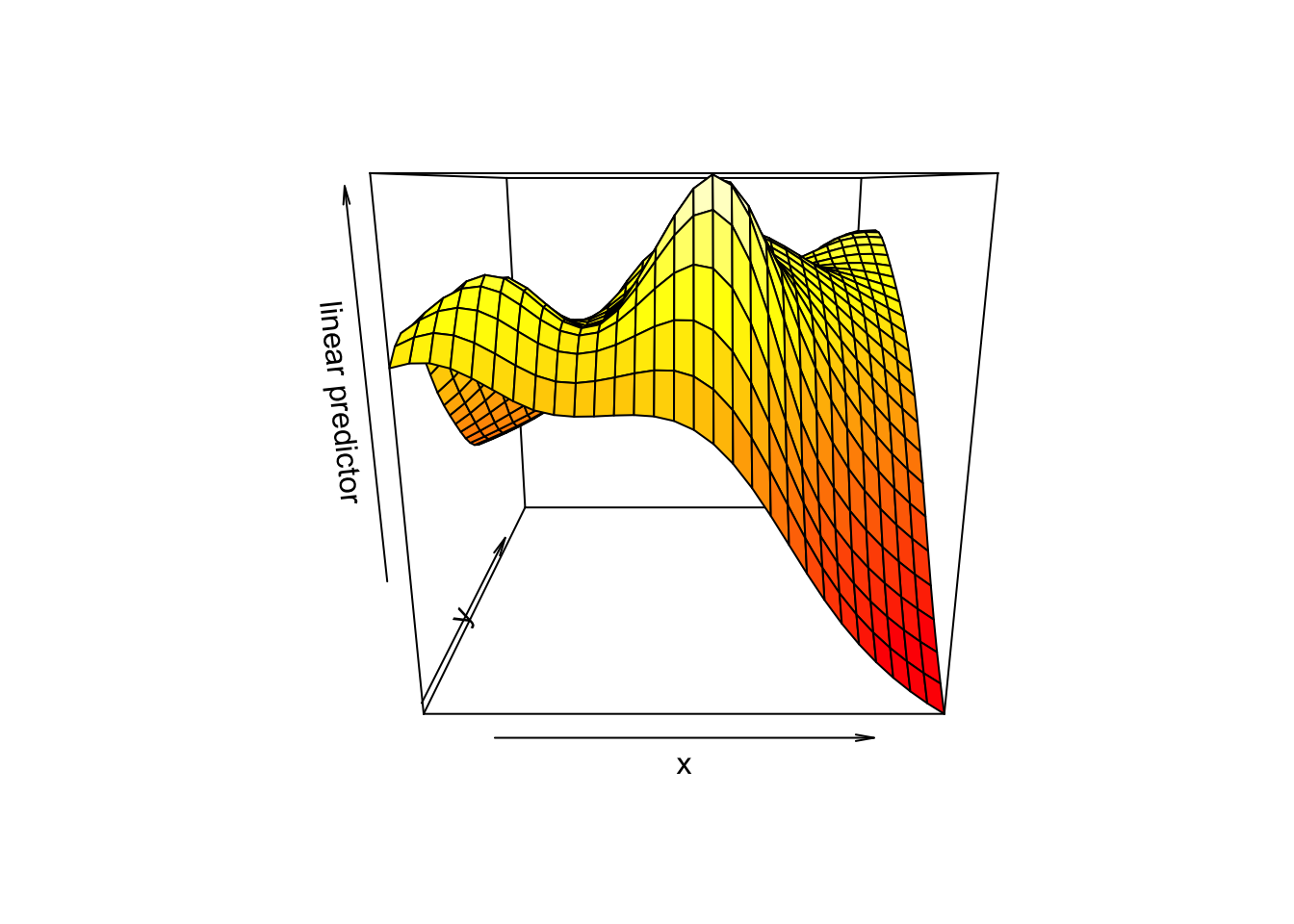
plot.type을 “contour”로 지정해주면 등고선이 있는 히트맵을 그려준다.

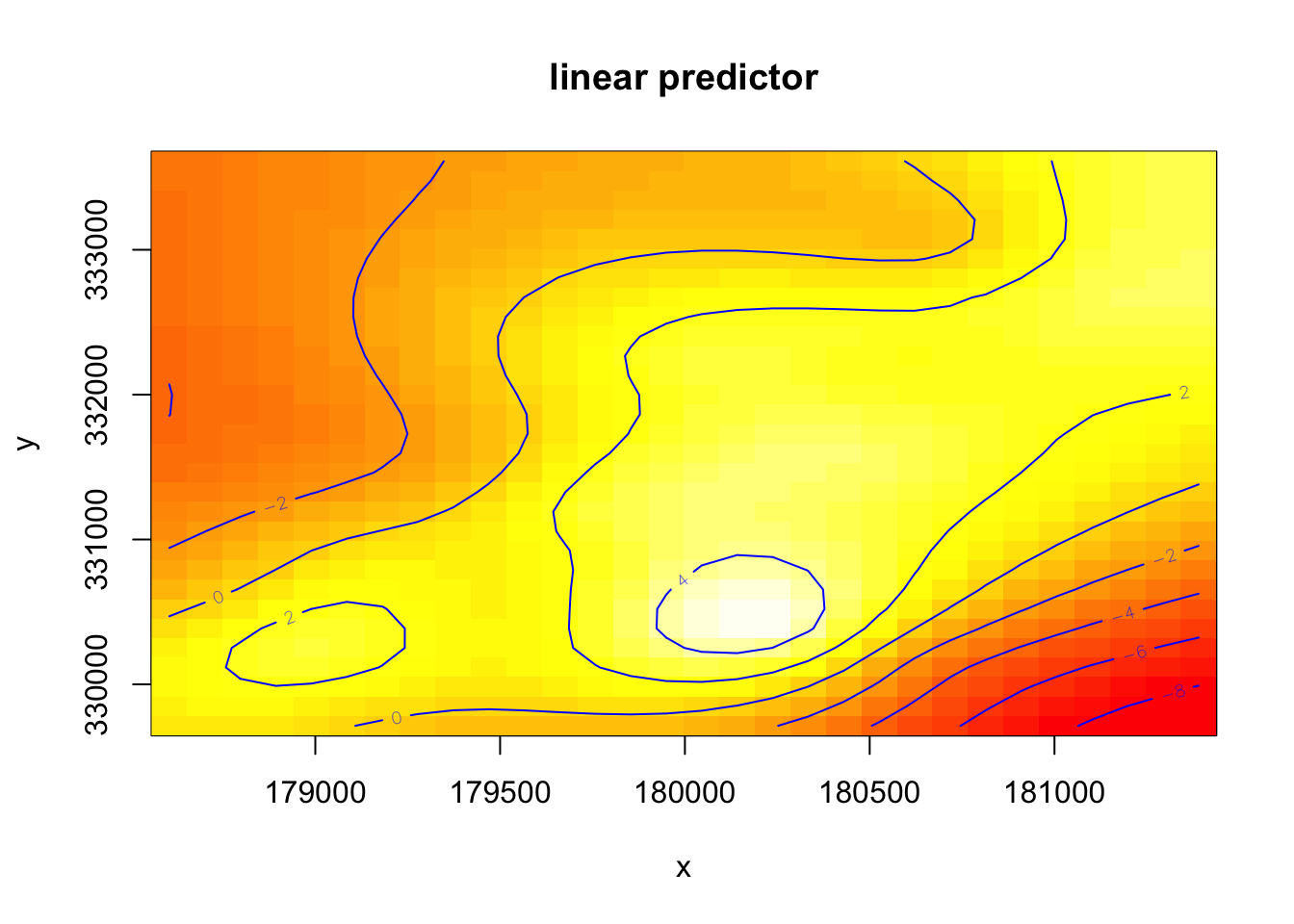
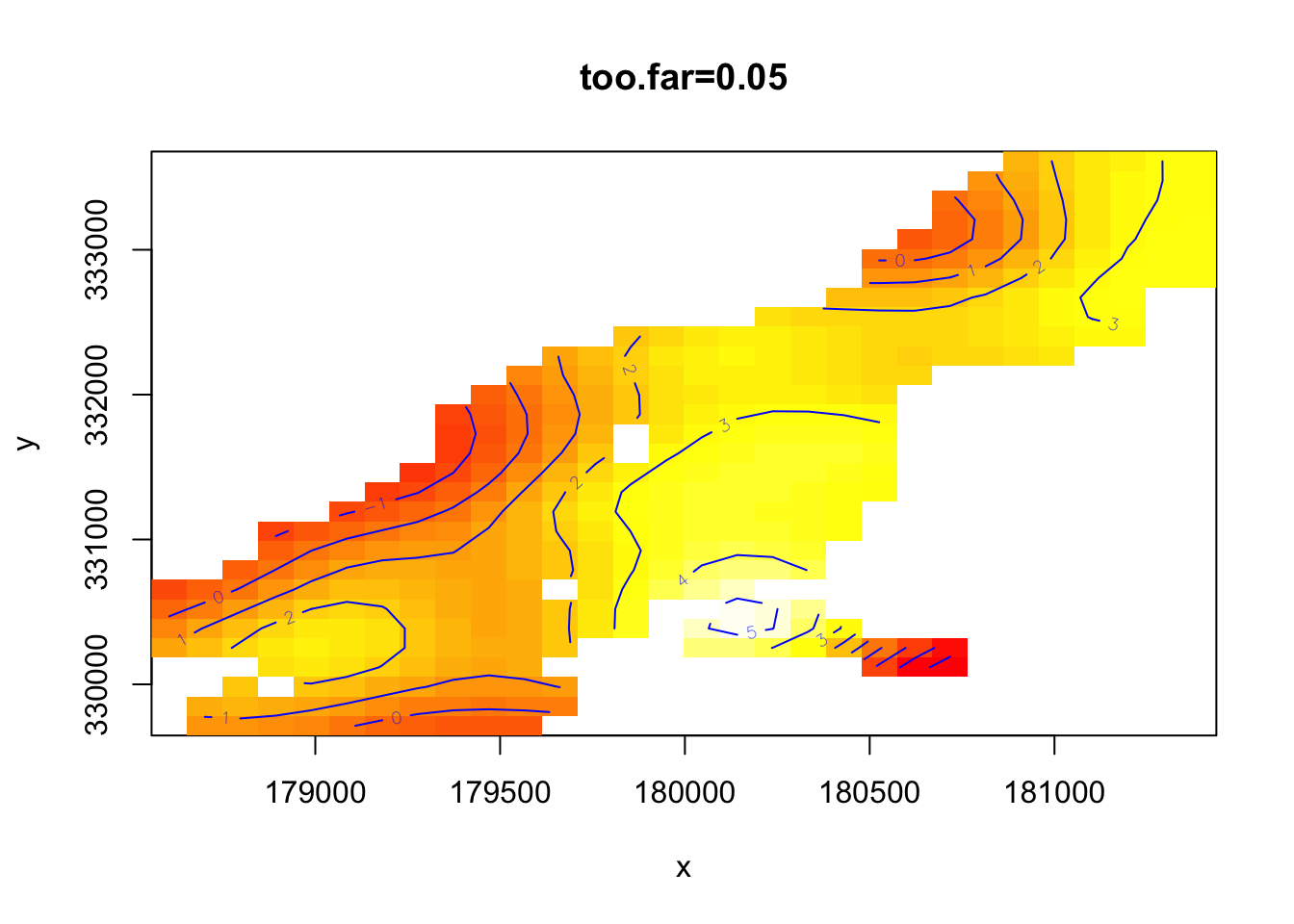
too.far인수는 모형을 검사할떄 중요한 인수이다. too.far인수는 실제 데이터로부터 너무 멀어지므로 그리지 말아야할 예측치를 지정해주는 것이다. 다시 말해 예측치로부터 얼마나 멀어야 먼 것인가를 지정해줌으로써 우리가 가지고 있는 모형 중 어떤 변수의 조합이 나타나지 않는가를 보여줌으로써 예측이 정확하지 않을 조합을 알려준다.

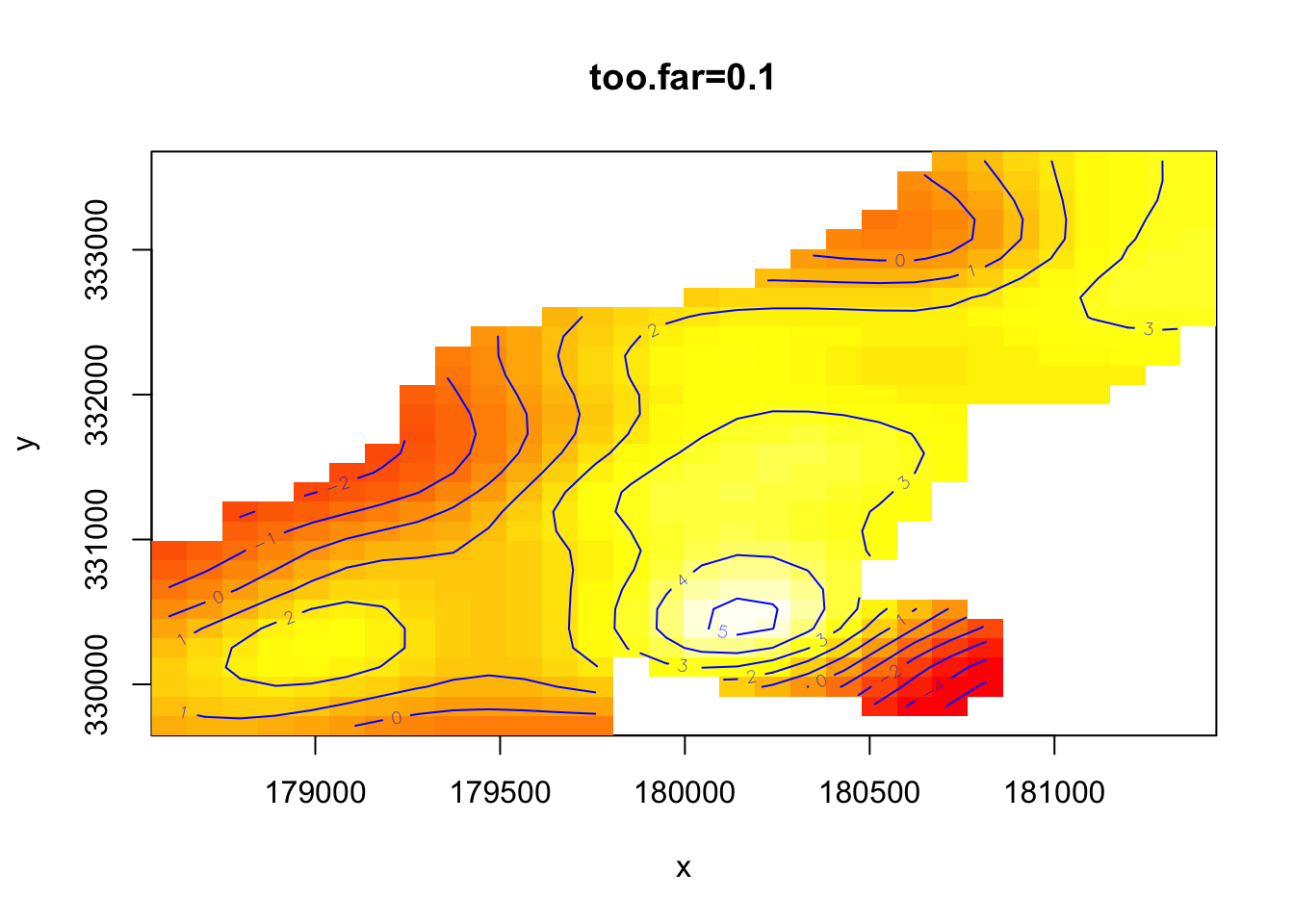
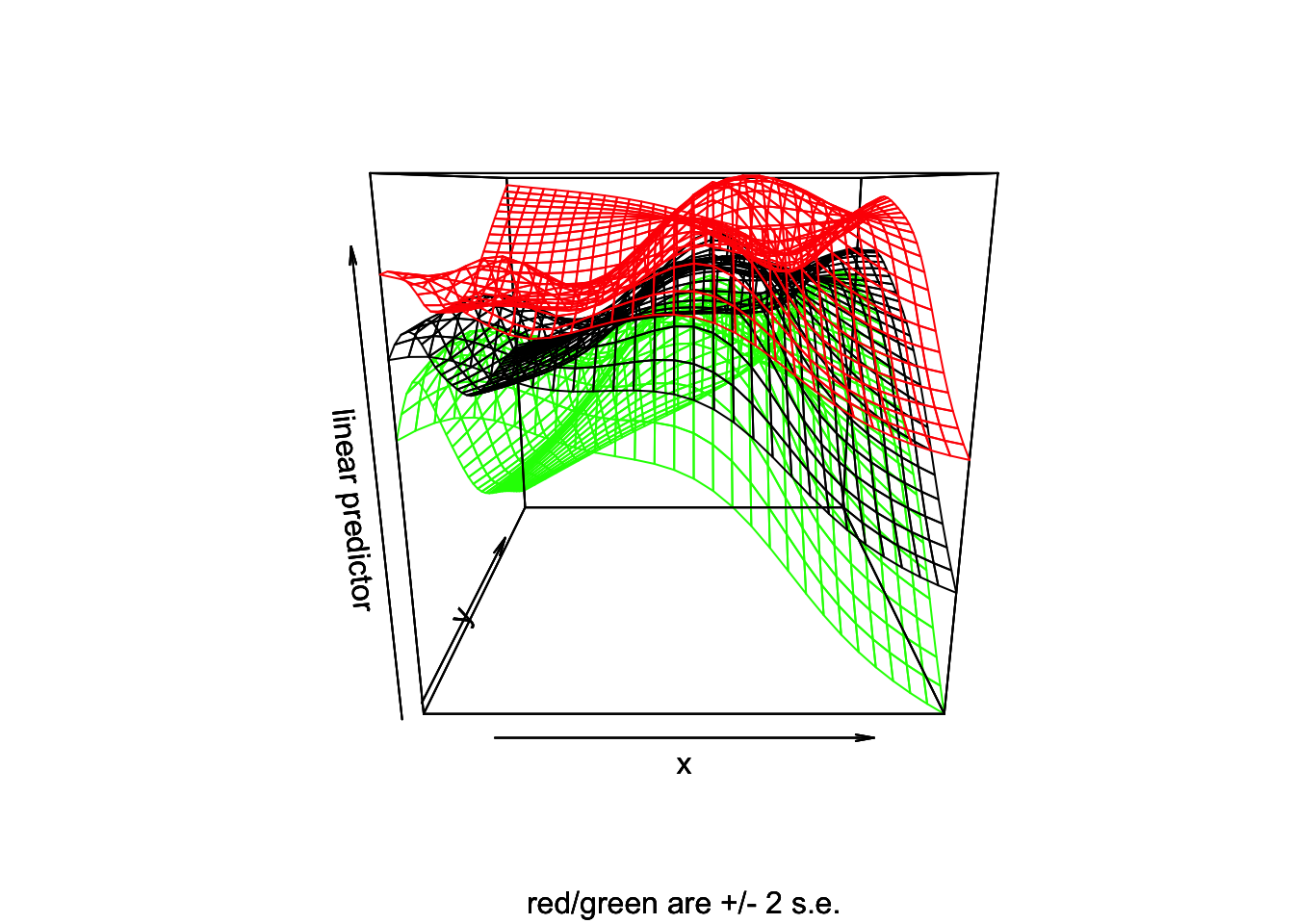
3차원 투시도의 경우 se인수로 신뢰구간을 표시할 수 있다. se인수에 숫자를 지정할 경우 예측표면으로부터 표준오차의 몇배 떨어진 표면을 그릴 것인지 지정해줄 수 있다.

4.11 3차원 투시도의 각도 조절

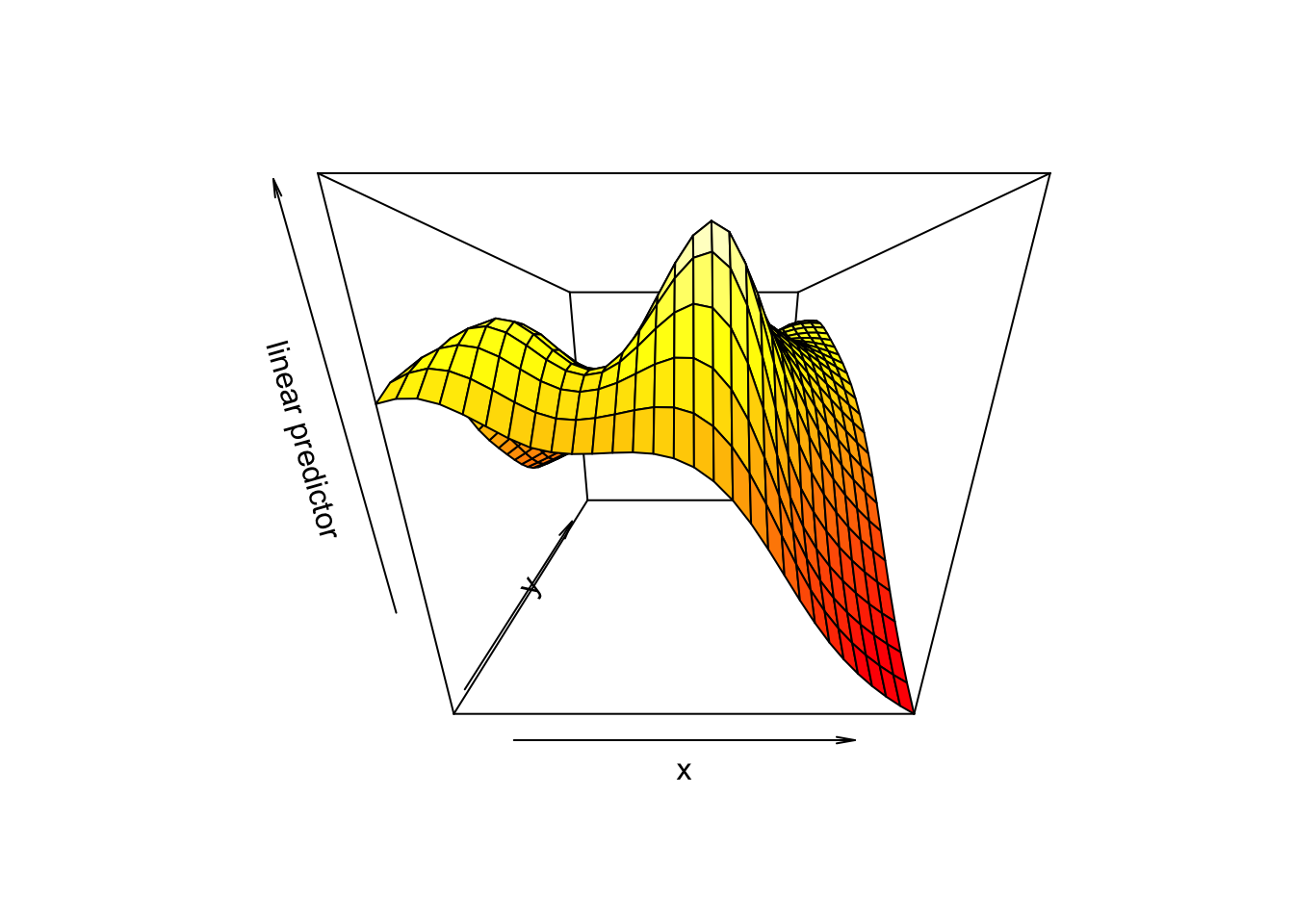
3차원 투시도의 경우 회전각도를 지정할 수 있다. theta는 수평회전, phi는 수직회전을 나타내고 r은 줌을 조절한다. r값이 너무 낮으면 모형이 왜곡되거나 시차가 발생할 수 있고 r값이 너무 클 경우에는 투시도 같은 느낌을 거의 주지 않는다.

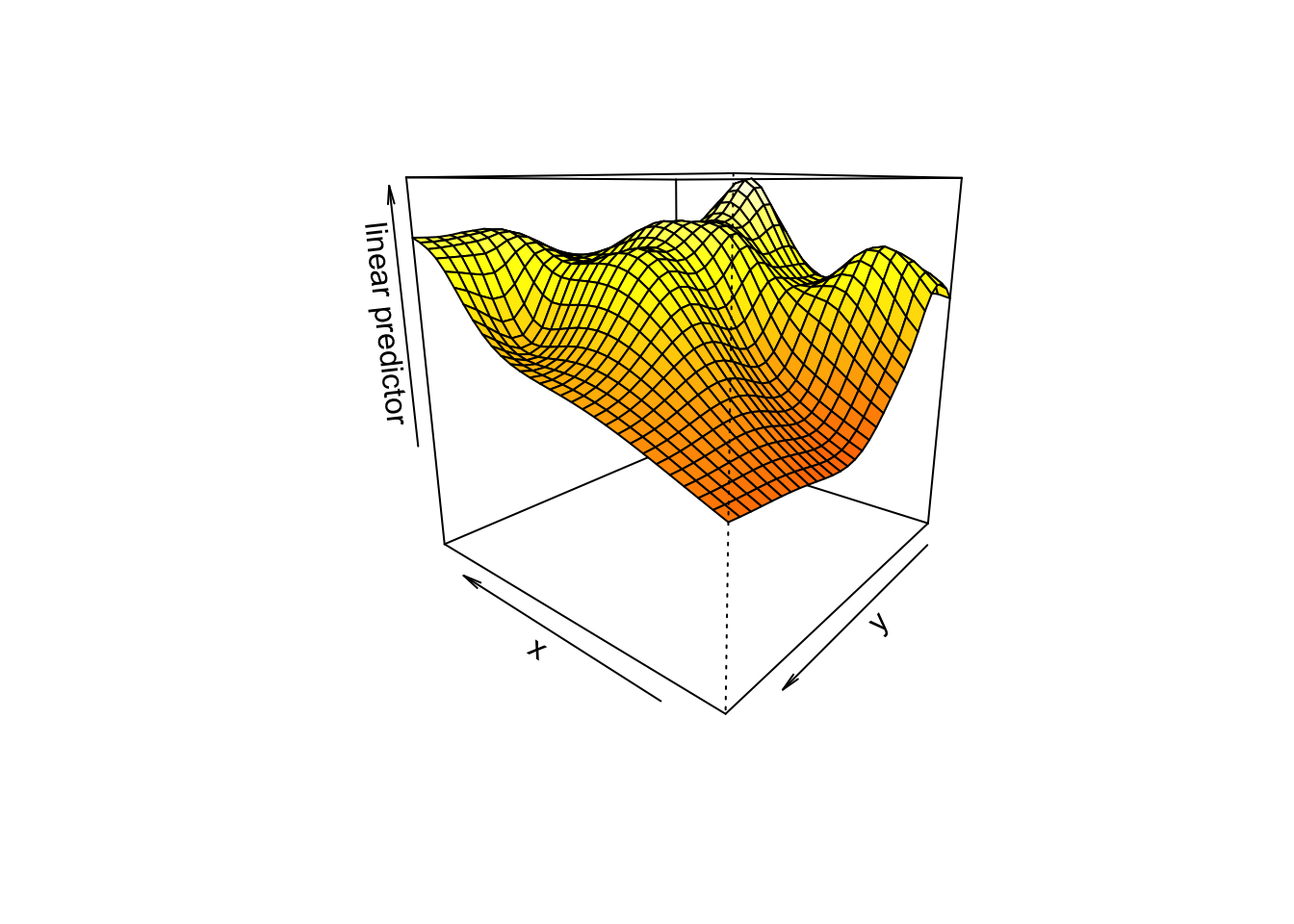
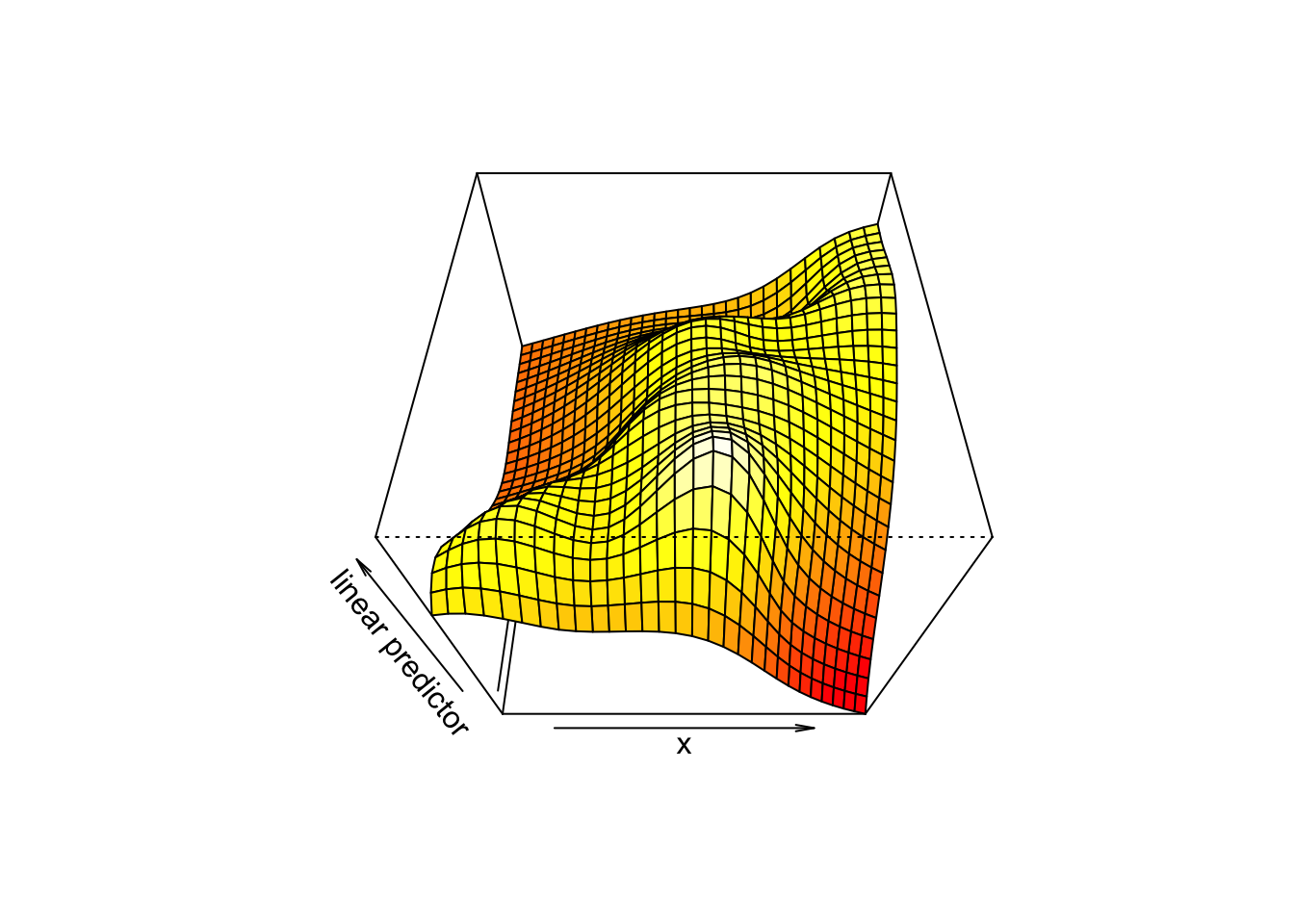
4.12 등고선 플롯의 옵션조절

등고선 플롯의 경우 뚜렷하게 보기 위해서는 색과 대비가 중요하다. 배경색 팔렛트의 조절, 등고선의 색, 등고선의 갯수 등을 조절할 수 있다.

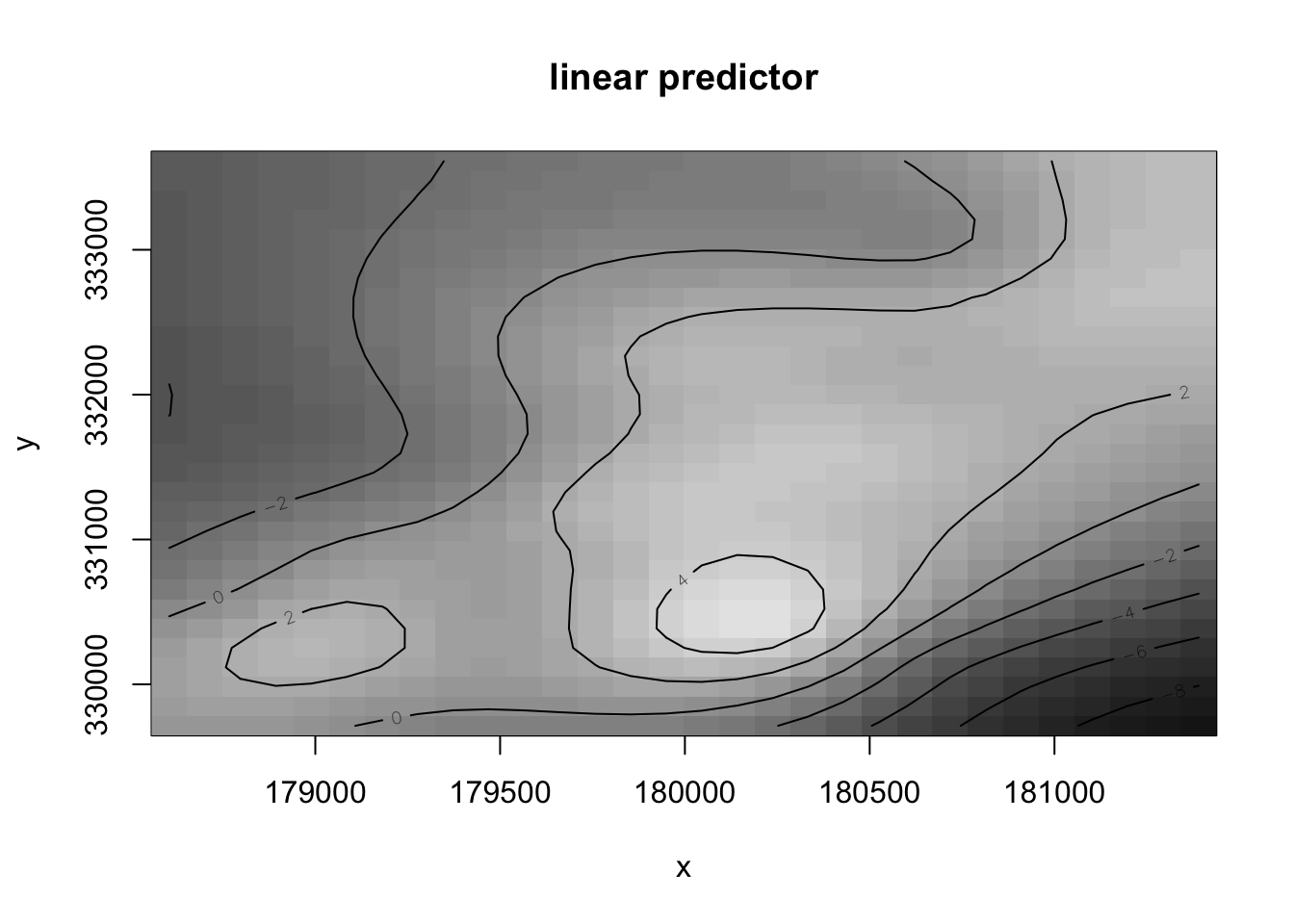
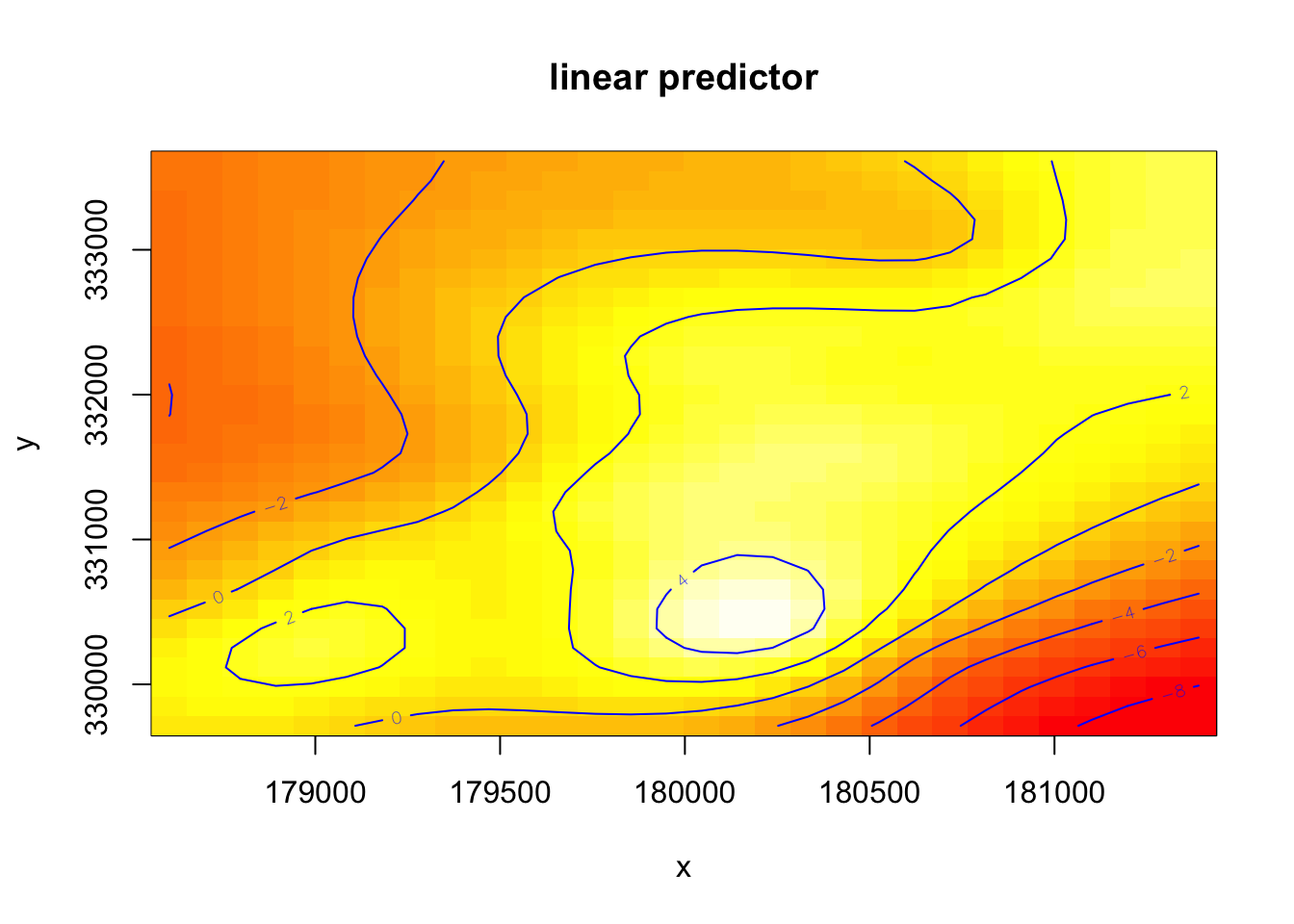
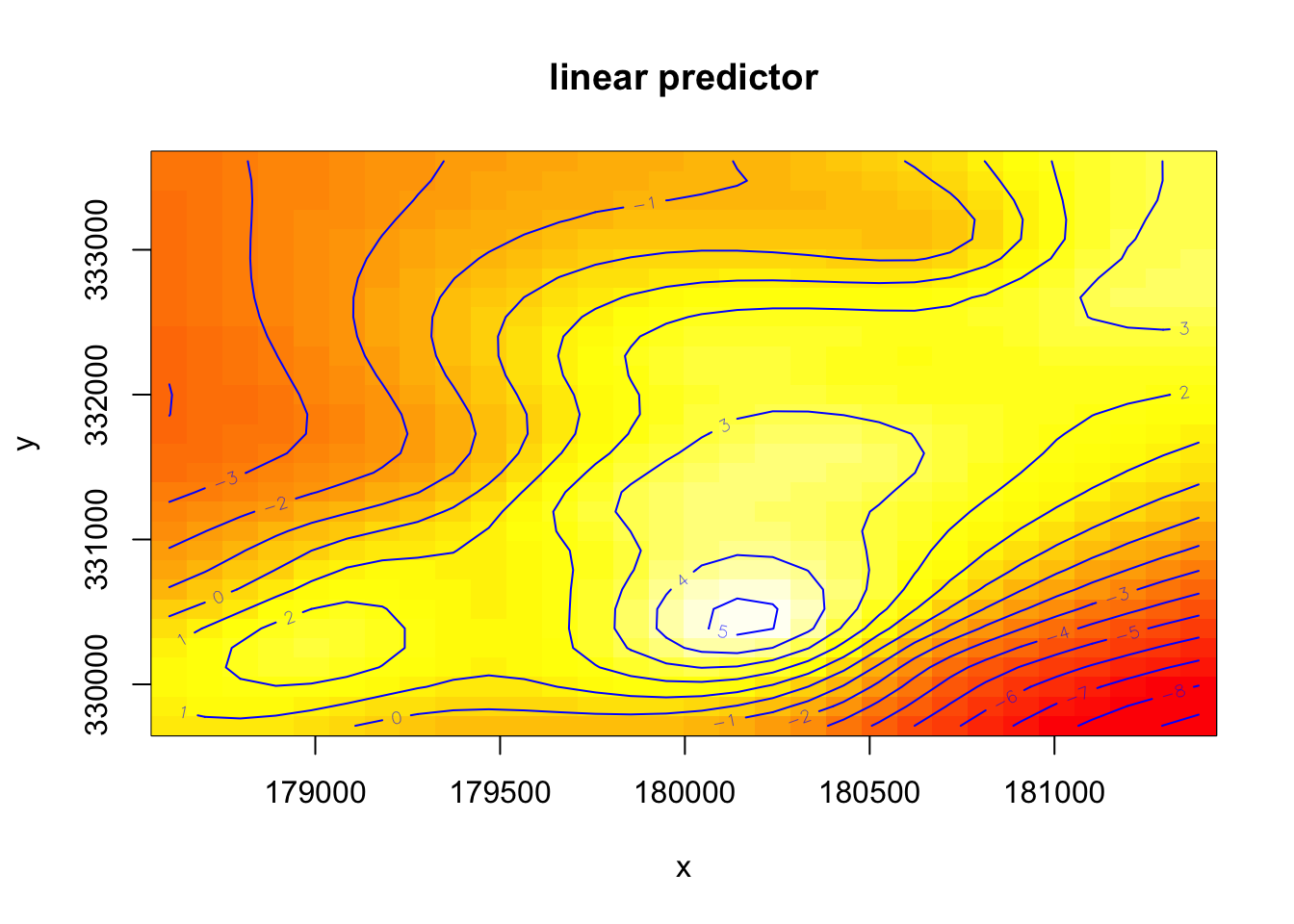
이 외에도 많은 옵션이 있으나 자세한 설명은 도움말 ?vis.gam을 참조한다.

4.13 실습해볼 내용

plot함수를 이용해 모형 mod2의 등고선플롯, 3차원투시도, 히트맵으로 시각화하는 R코드는 다음과 같다. 결과는 표시하지 않았다.

4.14 3차원 투시도 실습

vis.gam()함수를 이용하여 모형 mod의 3차원 투시도를 그리고 se 인수를 이용해 95%신뢰구간을 표시하려면 다음과 같이 한다.

이 3차원 투시도를 수평으로 135도 회전하려면 다음과 같이 한다.

같은 모형에서 등고선플롯을 그리고 데이터의 5%를 외삽에서 제외하려면 다음과 같이 한다.

4.15 범주형-연속형변수 상호작용

GAM에서 다루는 상호작용은 지금까지 보아온 s(x,y)와 같은 상호작용 외에도 여러 상호작용이 있다. 지난 장에서 연속형 변수의 평활항과 범주형변수의 상호작용에 대해 다루었는데 s() 함수 내에 by=“fuel”고 같이 상호작용을 정의하고 선형항을 추가하였다. 이와 같은 방법을 이차원 상호작용 평활항(2D interaction smooth)이라고 한다.

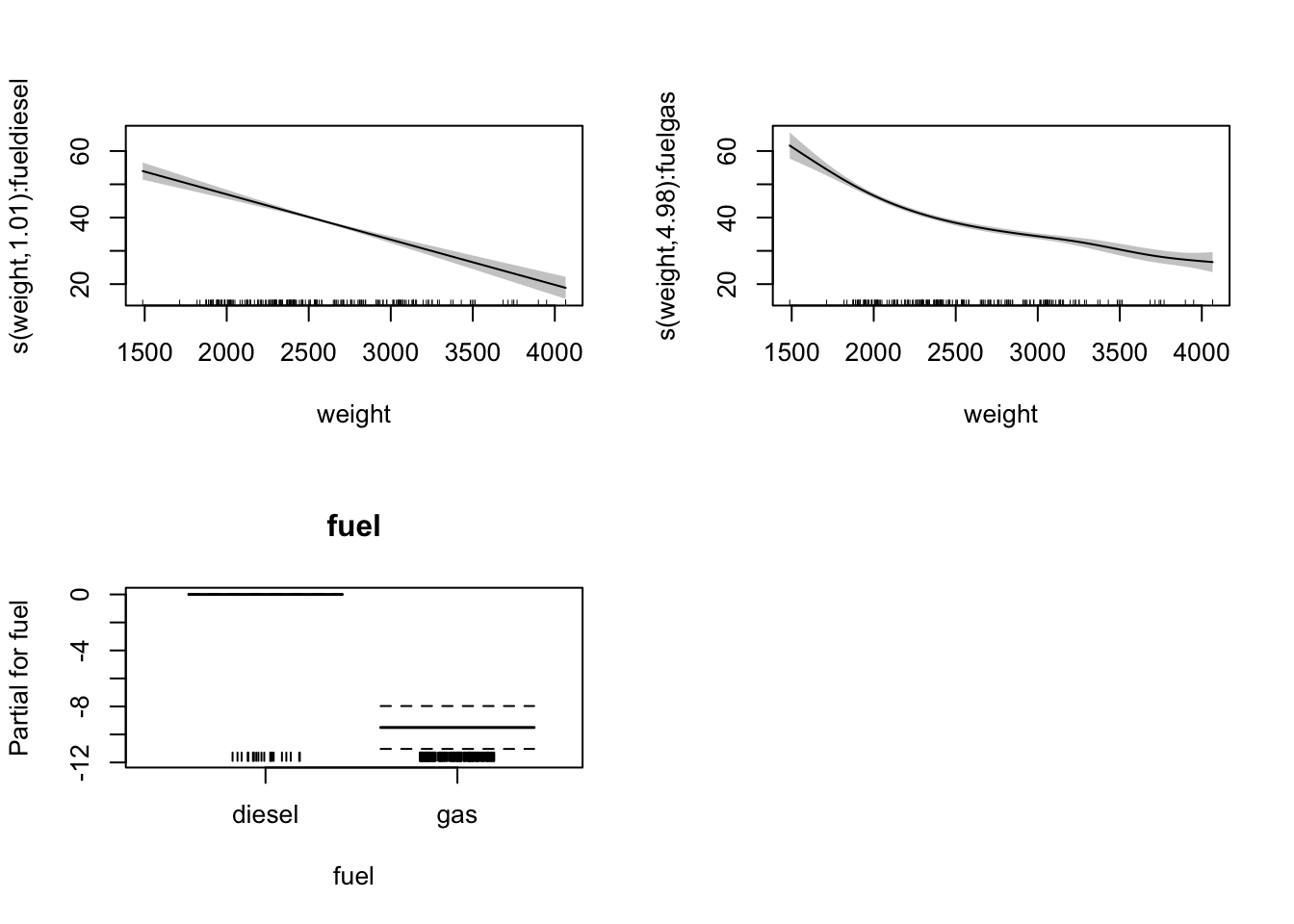
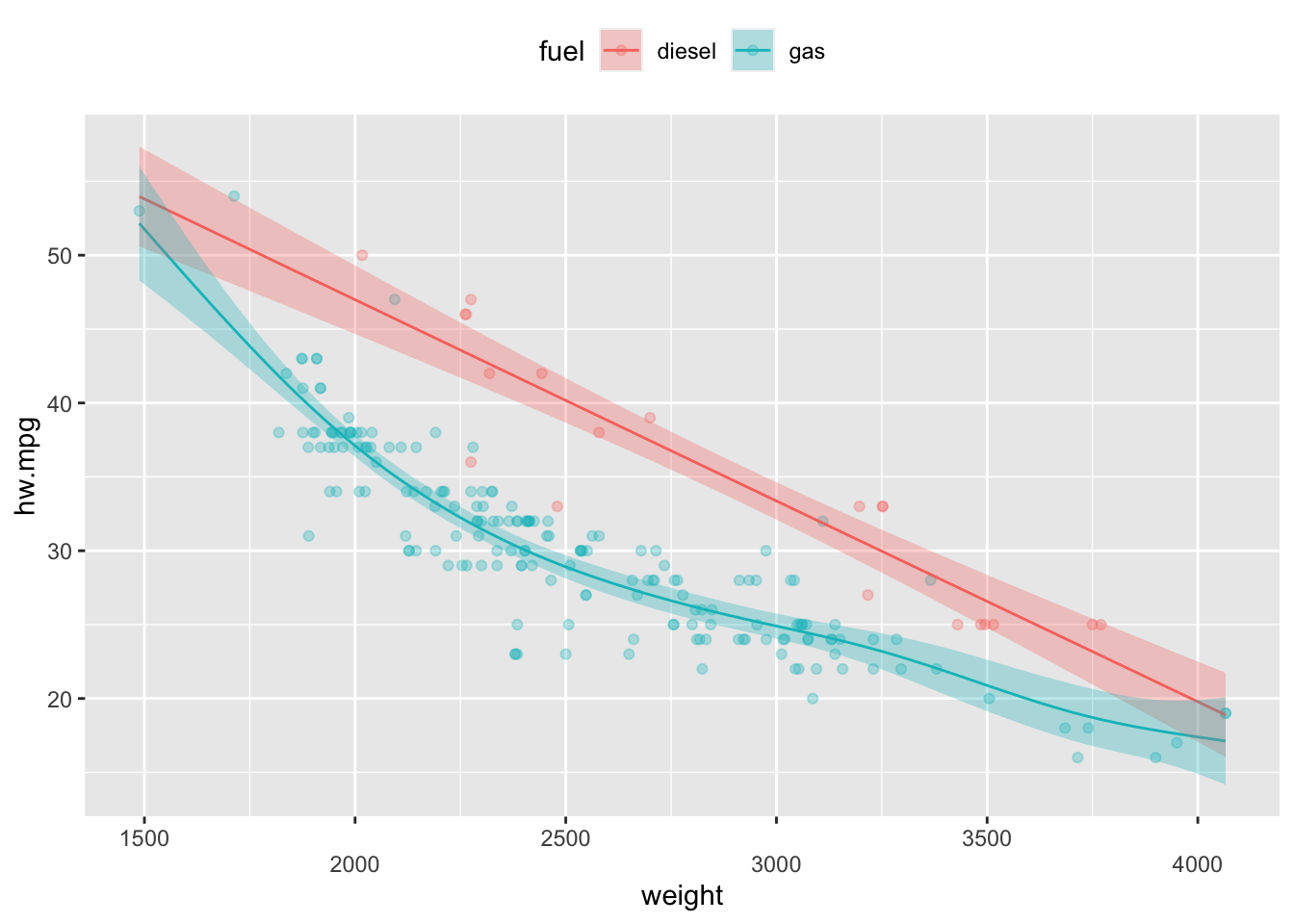
이 방법 외에도 범주평활항(factor-smooth)이라고 불리는 방법이 있다. 이 방법은 s()함수 내에 연속형 변수와 범주형 변수를 넣고 bs=“fs”를 추가해주는 방법이며 이 때에는 선형항을 따로 넣지 않는다.


Family: gaussian 
Link function: identity 

Formula:
hw.mpg ~ s(weight, fuel, bs = "fs")

Parametric coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   28.644      7.615   3.761 0.000223 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Approximate significance of smooth terms:
                edf Ref.df     F p-value    
s(weight,fuel) 7.71     19 53.12  <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

R-sq.(adj) =  0.832   Deviance explained = 83.8%
-REML = 518.54  Scale est. = 7.9735    n = 205

또한 모형의 기술을 보면 모수항에 범주형변수의 수준에 따른 기술이 없고 전체적인 상호작용항 하나만 존재한다. 따라서 범주형 변수의 수준에 따른 효과를 구별하기는 어렵다. 하지만 범주평활항은 우리가 보고자 하는 주요 변수가 아닌 범주형 변수의 영향을 조절하는데 유용하며 특히 범주형변수의 수준이 많거나 일부 범주의 데이터가 적을 때 특히 유용하다. 이러한 범주평활항의 경우 plot()함수로 보면 아주 간단하게 출력되므로 ggGam()함수가 더 유용하다.

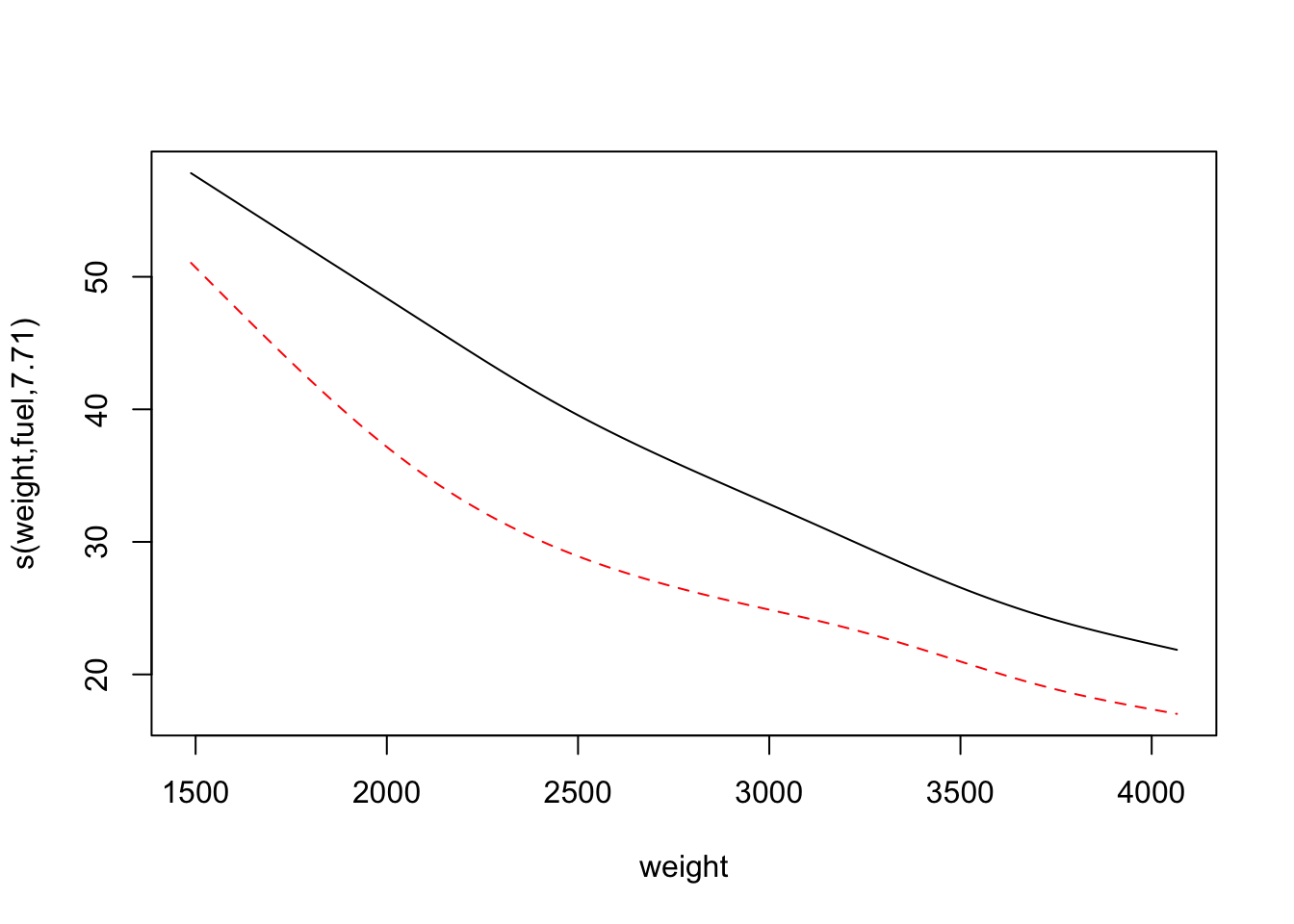
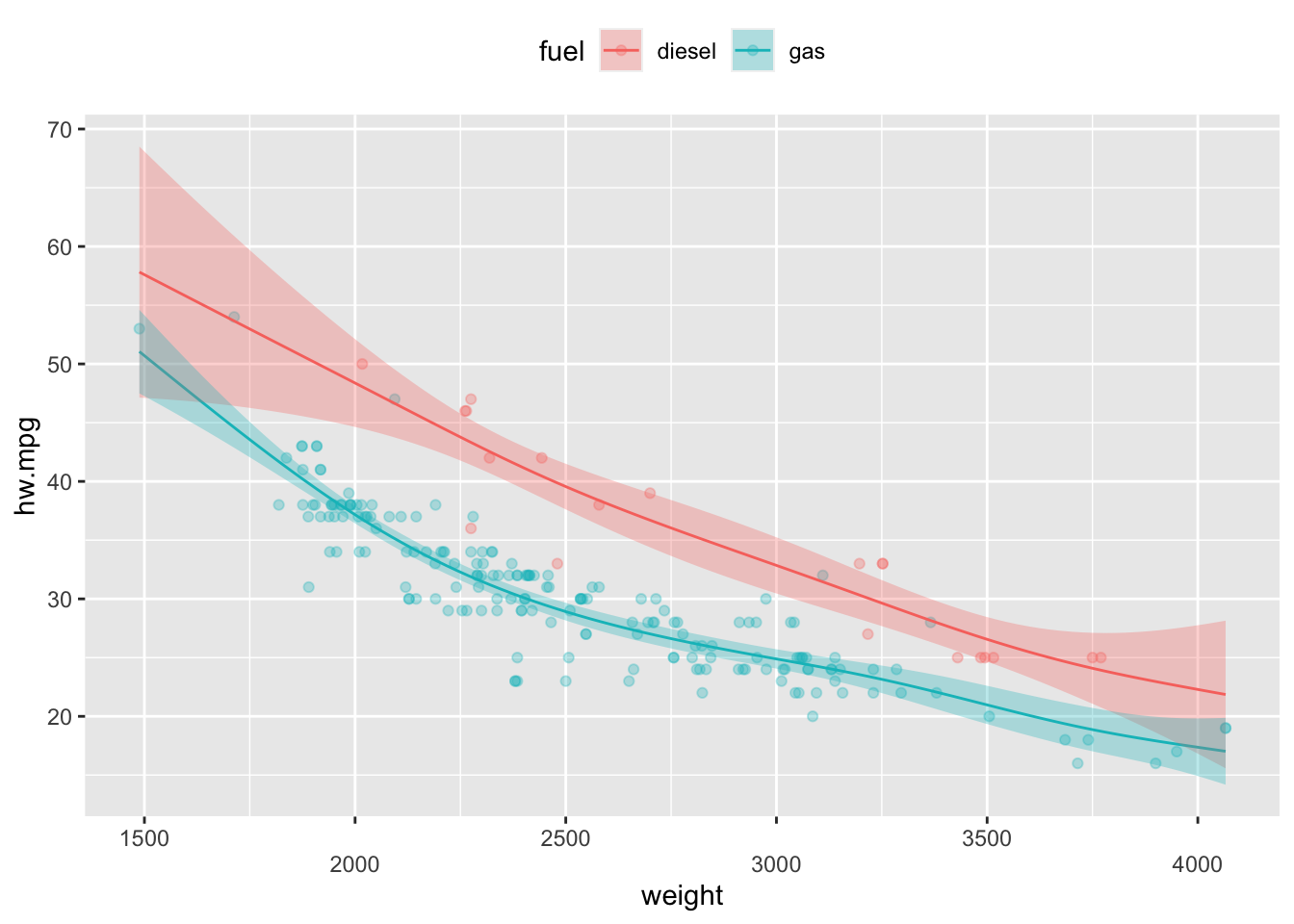
meuse 데이터에서 landuse 에 따른 토양 내 구리의 농도를 반응변수로 하는 GAM모형을 by 및 범주평활항을 이용해 만들면 다음과 같다.

summary()함수로 각 모형의 output을 비교해보자. plot() 함수로 이들 모형을 시각화해보자

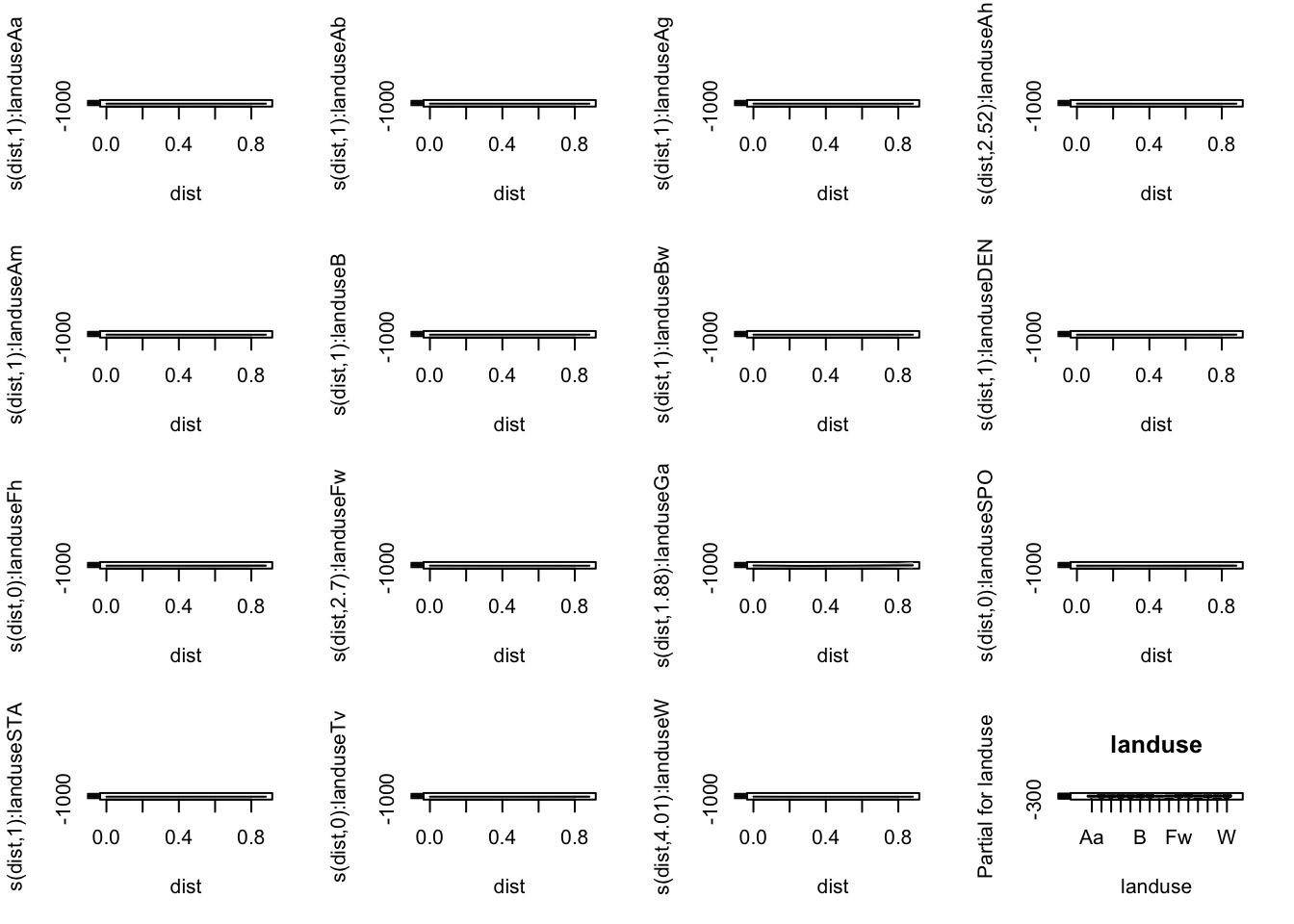
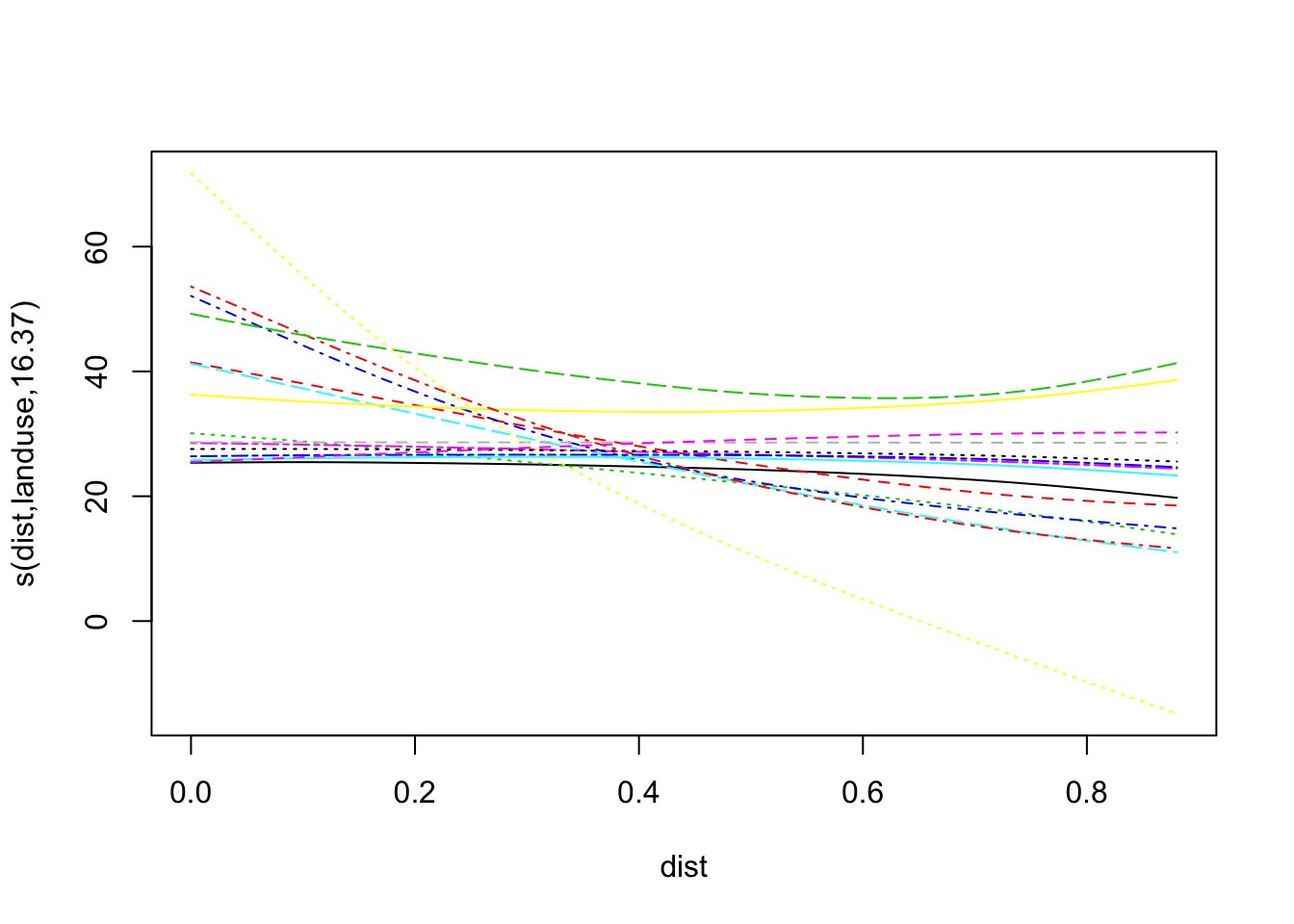
vis.gam()함수로 dist와 landuse의 관계를 3차원투시도로 시각화해보자.

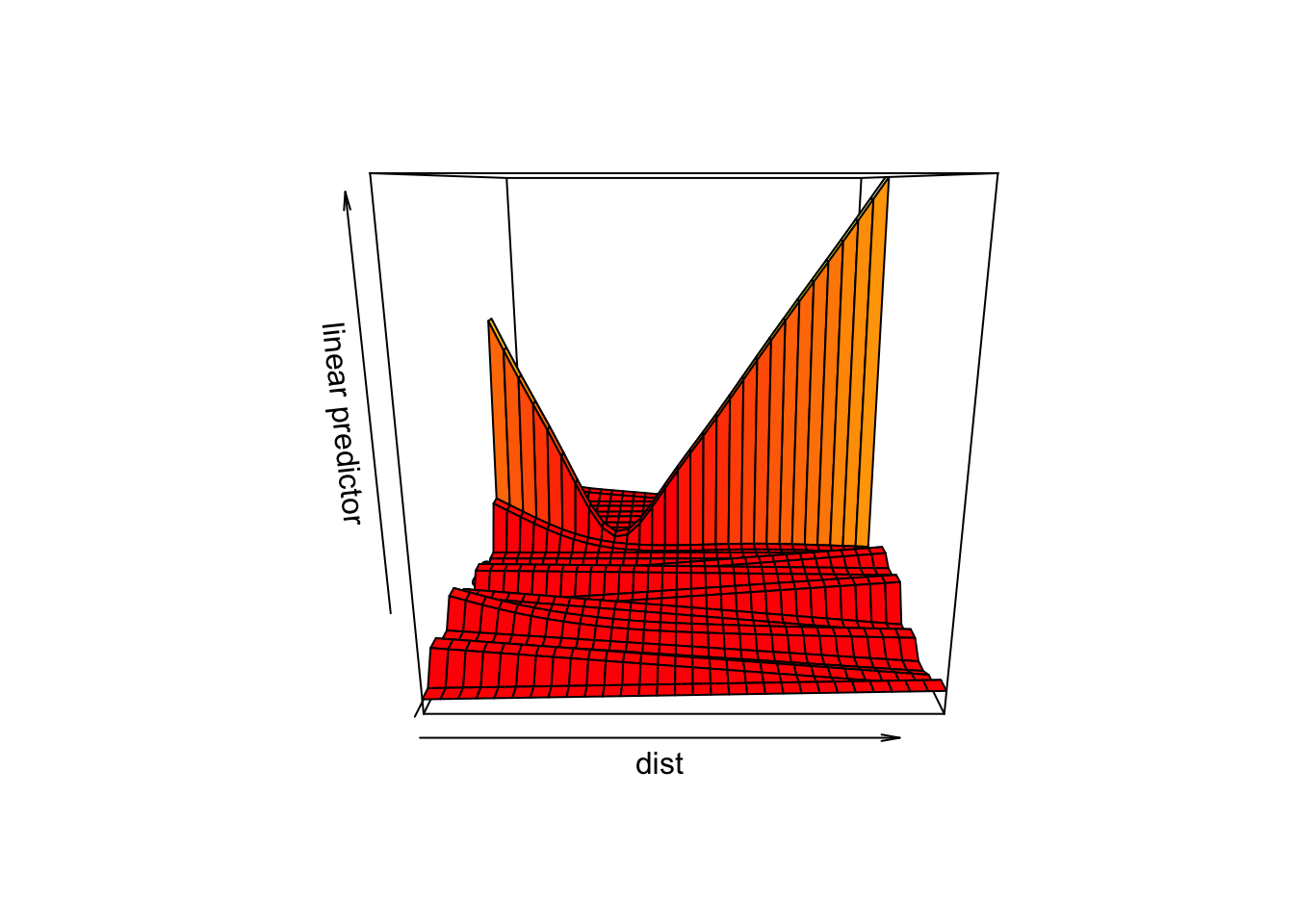
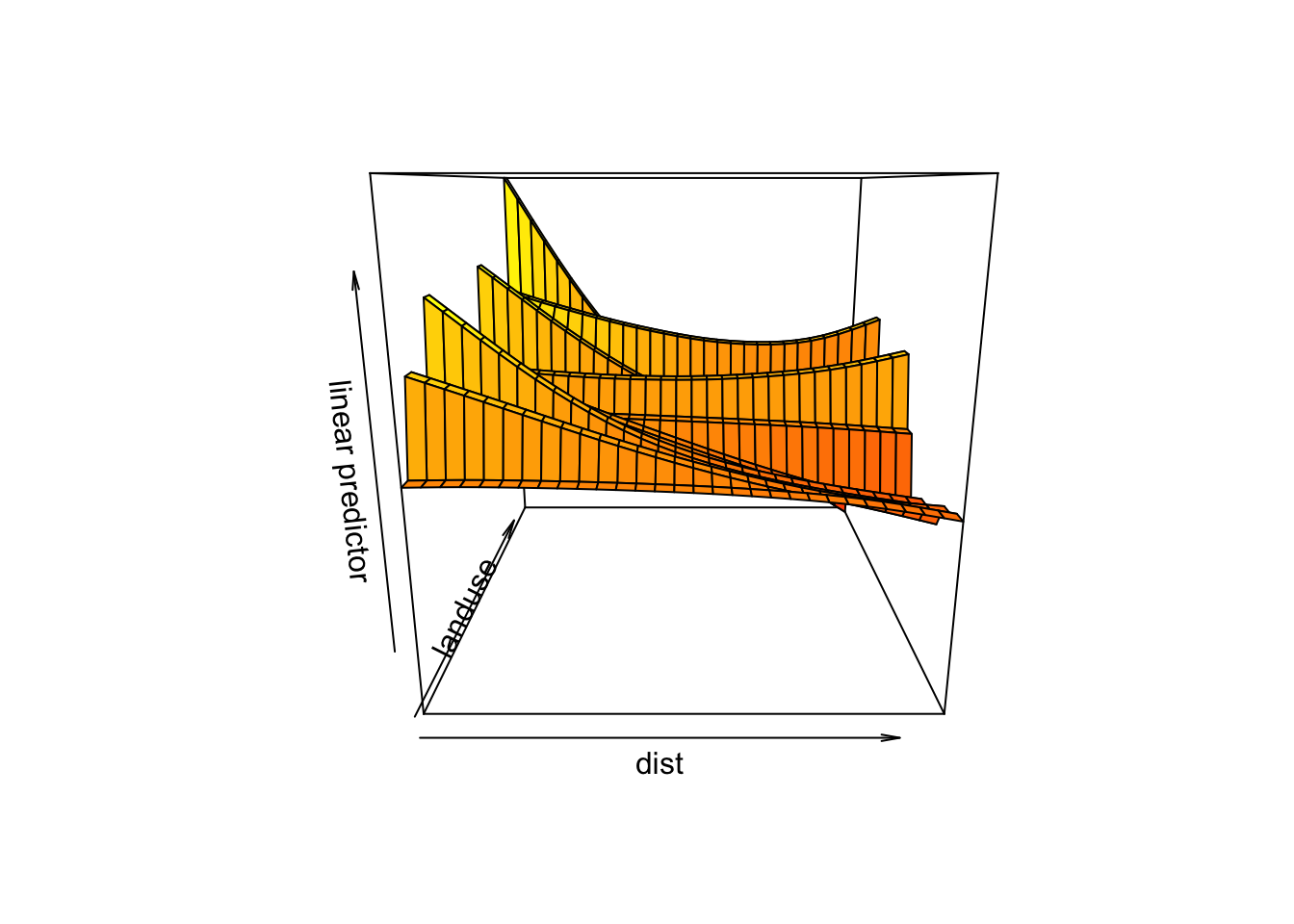
4.16 상호작용의 단위가 다를 때 : 텐서의 사용

지금까지 두가지 형태의 상호작용을 사용해 보았다. 하나는 by를 사용하고 선형항을 추가하는 2차원 상호작용 평활항이고 다른 하나는 bs=“fs”를 사용하는 범주평활항이다. 또 다른 방법은 텐서평활항을 사용하는 방법인데 두 변수가 시간과 공간처럼 사용하는 단위가 다를 때에도 사용할 수 있는 장점이 있다.

4.16.1 2차원 평활항

\(y=s(x_1,x_2)\) with a smoothing parameter \(\lambda\)

처음 다룬 2차원 평활항은 하나의 평활파라미터만 가진다. 하지만 하나의 평활파라미터만으로 해결할 수 없는 경우가 많다. 다음은 우리가 사용하는 meuse 데이터의 일부이다.

       x      y  elev   om
1 181072 333611 7.909 13.6
2 181025 333558 6.983 14.0
3 181165 333537 7.800 13.0
4 181298 333484 7.655  8.0
5 181307 333330 7.480  8.7
6 181390 333260 7.791  7.8

x,y 와 고도(elev)는 모두 미터 단위이다. 수평적으로는 가로와 세로가 비슷한 정도로 움직일 것으로 기대되나 고도는 매우 변동이 작으므로 수평위치의 작은 변화도 고도 입장에서는 매우 큰 변화일 수 있다. 즉 수평위치와 고도는 잔떨림정도(wiggliness)가 다르다. 비슷한 예로 모형 내의 거리(dist)와 유기물질(om)은 단위가 각각 미터(\(m\))와 \(g/kg\)으로 다르므로 측정 단위 자체가 비교불가하다.

4.16.2 텐서평활항(Tensor Smooths)

\(y=te(x_1,x_2)\) with smoothing parameters \(\lambda_1, \lambda_2\)

텐서평활항은 서로 다른 단위를 갖는 두 변수의 상호작용을 다룰 때 유용하다. 텐서평활항은 2차원 평활항과 비슷하지만 평활파리미터를 두 개 갖는다. 사용하는 방법은 s()대신 te()함수를 사용하면 된다. 텐서를 사용할 때는 기저함수의 갯수를 각각 지정할 수 있다.

gam(y ~ te(x1, x2), data = data, method = "REML")
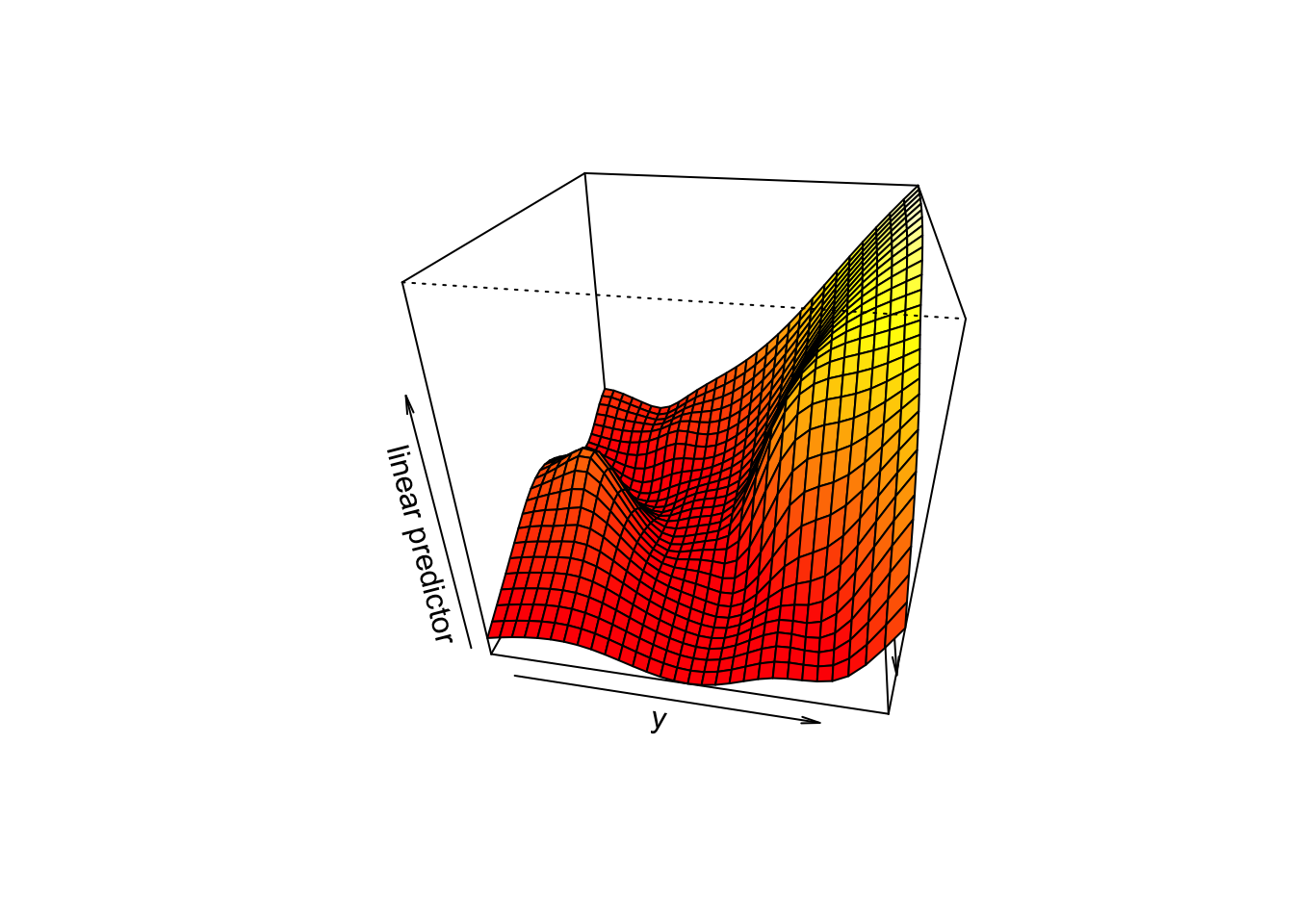
gam(y ~ te(x1, x2, k=c(10,20)), data = data, method = "REML")

아래 그림은 텐서의 사용이 유용한 예이다. 왼쪽의 그림이 두 변수 x1과 x2, 그리고 결과변수의 실제 관계라고 하자. 이떄 x1과 x2의 단위가 상당히 다르다면(예를 들어 x1의 범위가 x2의 5% 미만) s()함수를 시용하여 모형적합을 시도하면 x1과 x2의 변동이 유사하다고 가정하기 때문에 가운데 그림처럼 적합된다. 하지만 텐서평활항을 사용하게 되면 두개의 평활파라미터를 사용하여 오른쪽 모형처럼 보다 적합한 모형을 얻게 된다.

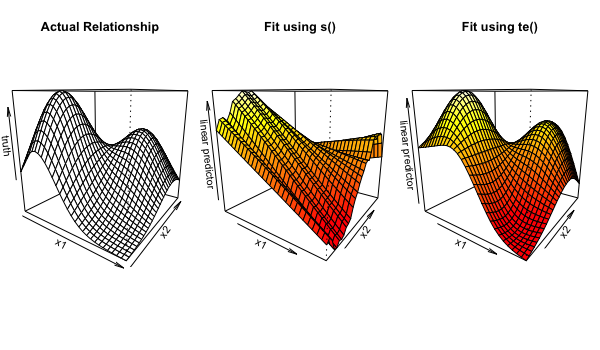
4.16.3 텐서 상호작용(Tensor Interaction)

\(y=s(x_1) +s(x_2) + ti(x_1,x_2)\) with smoothing parameters \(\lambda_1, \lambda_2, \lambda_3, \lambda_4\)

gam(y ~ s(x1) + s(x2) + ti(x1, x2), data = 데이터이름, method = "REML")

텐서평활항의 또다른 큰 장점은 각각의 평활항 밖에서 텐서항을 사용할 수 있다는 점이다. 이렇게 텐서상호작용을 사용할 경우 두 변수의 독립된 효과와는 별개로 두 변수의 상호작용만을 분리해서 평가할 수 있는 장점이 있다. 이렇게 분석하면 보다 많은 항을 분석하게 되지만 당연히 보다 많은 데이터를 필요로 한다.

4.16.4 텐서상호작용의 출력 예

다음은 텐서상호작용을 사용한 GAM 모형의 출력 예이다. 평활항을 보면 각각의 변수와 텐서 상호작용이 따로 분석되므로 각각의 성분의 유의성을 독립적으로 평가할 수 있다. 이것은 텐서의 또다른 장점으로 두 항의 단위가 다르지 않더라도 텐서를 사용하면 두 항과 두 항의 상호작용을 독립적으로 분석할 수 있다.

Family: gaussian 
Link function: identity 

Formula:
y ~ s(x1) + s(x2) + ti(x1, x2)

Parametric coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 0.318698   0.008697   36.65   <2e-16 ***
 ---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Approximate significance of smooth terms:
            edf Ref.df     F  p-value    
te(x1)      4.93  6.009 23.16  < 2e-16 ***    # Separate terms for 
te(x2)      3.42  4.242 10.35 2.75e-08 ***    # each variable and
ti(x1,x2) 10.15 12.763 16.08  < 2e-16 ***     # the interaction
 ---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

R-sq.(adj) =  0.444   Deviance explained = 46.5%
-REML = -85.566  Scale est. = 0.037067  n = 500

이 모형의 플롯 출력 예는 아래 그림과 같다. x1과 x2 각각의 평활항은 부가적인 효과를 보이며 상호작용 또한 두 항의 효과에 더해 부가적인 효과를 보인다. 이와 같이 각각의 효과를 분리해서 생각하면 복잡한 모형도 보다 잘 이해할 수 있게 된다.

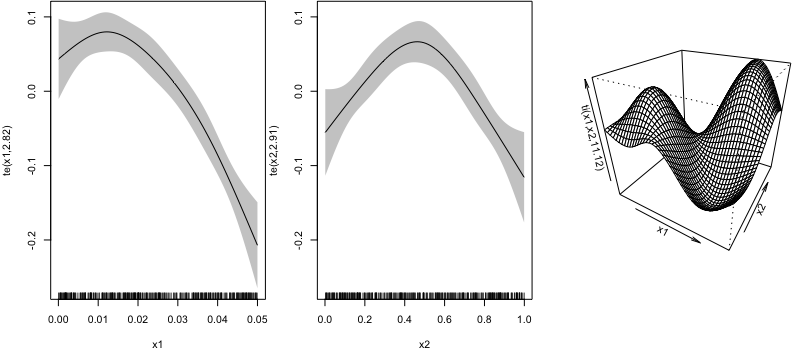
4.16.5 텐서를 사용한 모형

mod4는 이차원 평활항을 사용하여 분석하였기 때문에 적합이 만족스럽지 않았다. 이 모형을 텐서평활항을 이용하여 분석하려면 다음과 같이 할 수 있다.


Family: gaussian 
Link function: identity 

Formula:
cadmium ~ te(x, y, elev)

Parametric coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   3.2458     0.1329   24.43   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Approximate significance of smooth terms:
               edf Ref.df     F p-value    
te(x,y,elev) 38.29  45.86 11.87  <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

R-sq.(adj) =   0.78   Deviance explained = 83.4%
-REML = 318.09  Scale est. = 2.7358    n = 155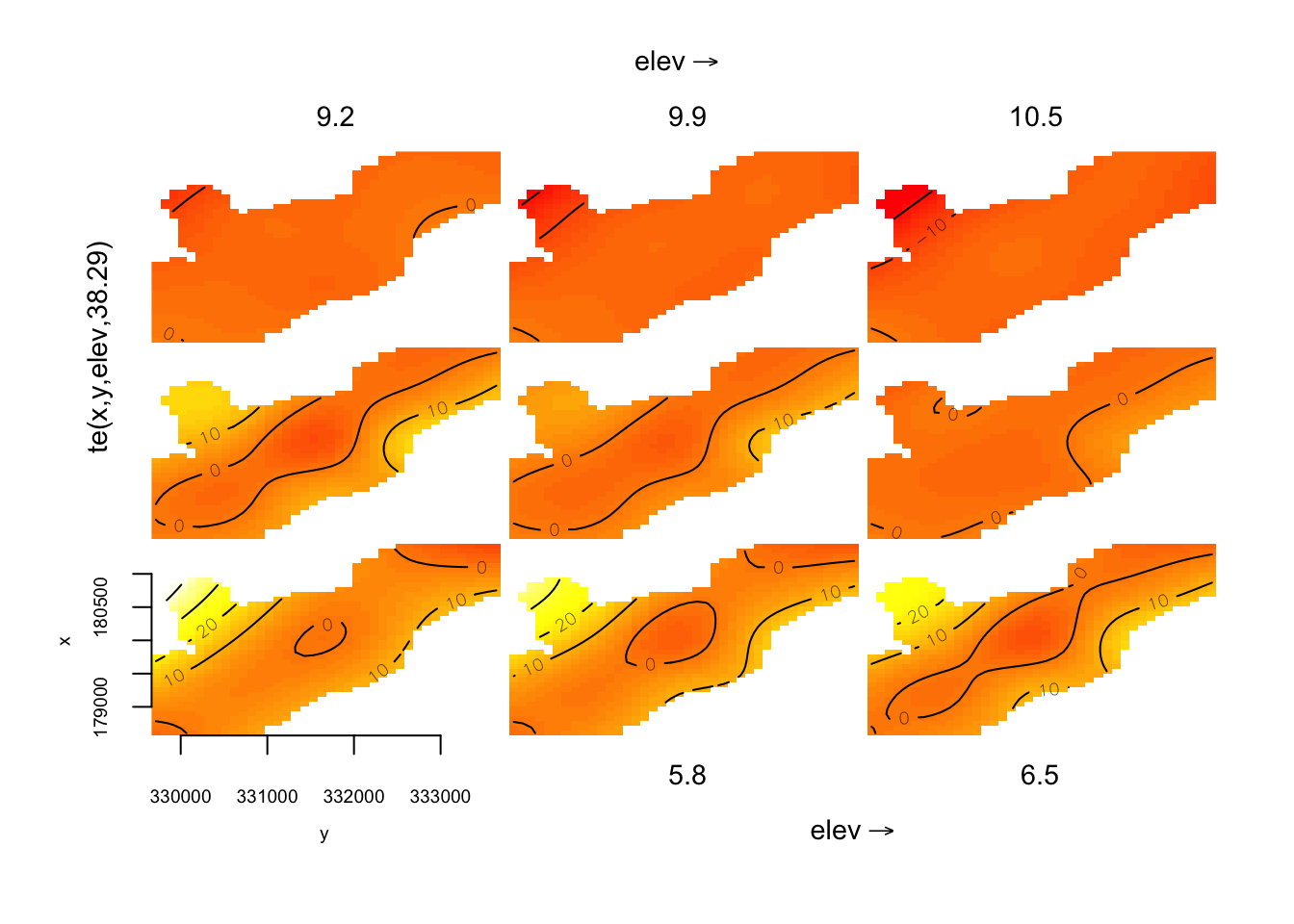

4.16.6 다척도 상호작용의 이용

위의 모형을 s(x,y), s(elev)의 평활항과 별도의 텐서상호작용으로 분리하여 모형을 만들면 다음과 같다.


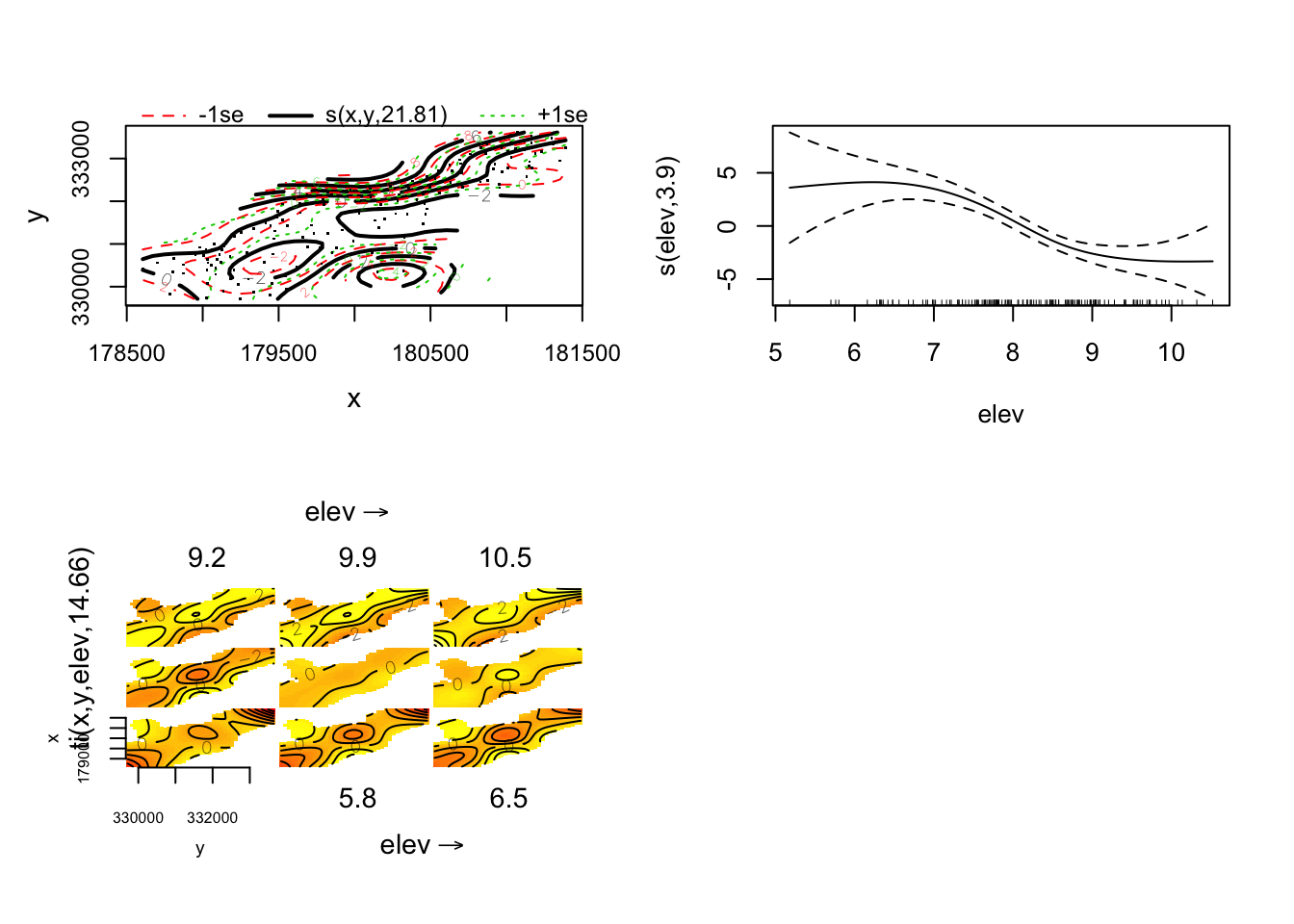
Family: gaussian 
Link function: identity 

Formula:
cadmium ~ s(x, y) + s(elev) + ti(x, y, elev)

Parametric coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   2.7044     0.2244   12.05   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Approximate significance of smooth terms:
                edf Ref.df     F  p-value    
s(x,y)       21.812 25.491 6.386 7.29e-15 ***
s(elev)       3.898  4.688 9.680 1.98e-07 ***
ti(x,y,elev) 14.656 19.180 2.706 0.000516 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

R-sq.(adj) =  0.793   Deviance explained = 84.7%
-REML = 336.62  Scale est. = 2.5755    n = 155