Chapter 5 로지스틱 GAMs
로지스틱 GAM에서는 연속형 변수가 아닌 이분형 변수를 다룬다. 이분형변수는 의학영역에서 많이 다루는 사망과 생존, 토양 속에 샘물체가 존재하는가 여부, 자동차를 살것인가 말것인가 등과 같이 0 또는 1로 나타낼 수 있는 변수를 말한다. 로지스틱 회귀는 반응변수로 이분형변수를 다루며 오즈(odds)의 개념을 이해하여야 한다. 오즈라고 하는 것은 주어진 조건 x에서 성공확률을 p라고 하면 성공확률이 실패확률보다 몇 배 더 높은가를 나타내며 다음과 같이 표현할 수 있다.
\[\begin{equation} odds=\frac{p}{1-p} \end{equation}\]
로짓(logit)은 오즈에 로그를 취한 것으로 로지스틱 회귀식은 다음과 같이 표현된다.
\[\begin{equation} log(\frac{p}{1-p})=\beta_0+\beta_1X_1+\beta_2X_2+ ... + \beta_pX_p \end{equation}\]
GAM에서는 로지스틱회귀를 확장하여 비선형관계를 나타내기 위하여 다음과 같이 확장한다.
\[\begin{equation} log(\frac{p}{1-p})=\beta_0+f_1(X_1)+f_2(X_2)+ ... +f_p(X_p) \end{equation}\]
5.1 로지스틱 함수(Logistic Function)
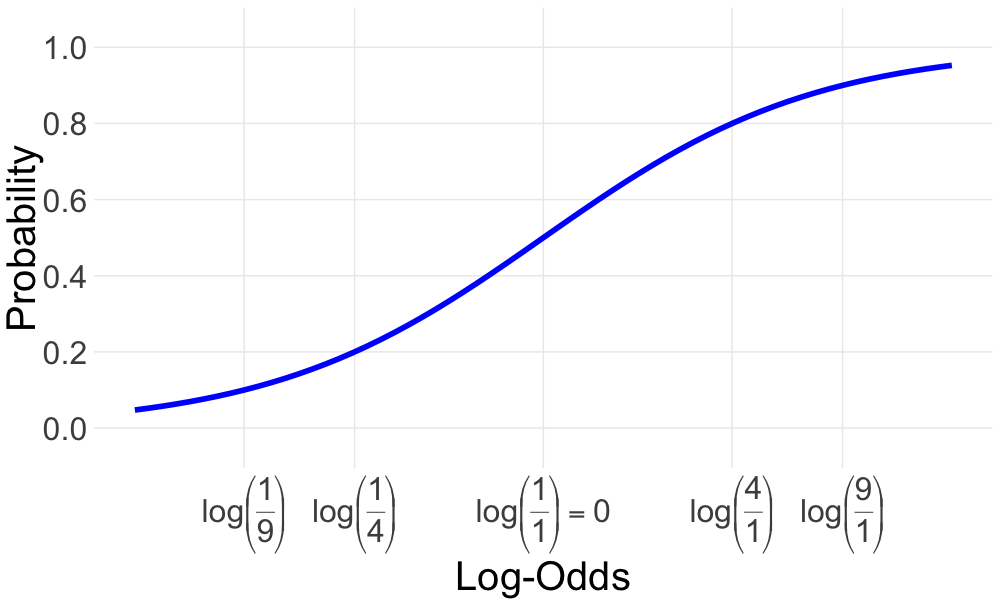
이분형 결과 변수를 다룰 때 우리의 예측은 확률(probability)로써 0과 1 사이에 존재하는 값이다. GAM은 어떠한 숫자도 다룰 수 있으므로 GAM output을 로지스틱 함수를 사용하여 probability로 변환한다. 로지스틱 함수는 어떠한 숫자라도 0과 1사이의 숫자로 변환하여 주므로 이를 이용하여 어떠한 숫자라도 log-odds 즉 양성결과와 음성결과의 비의 로그로 해석할 수 있다.
5.2 로짓함수(Logit Function)
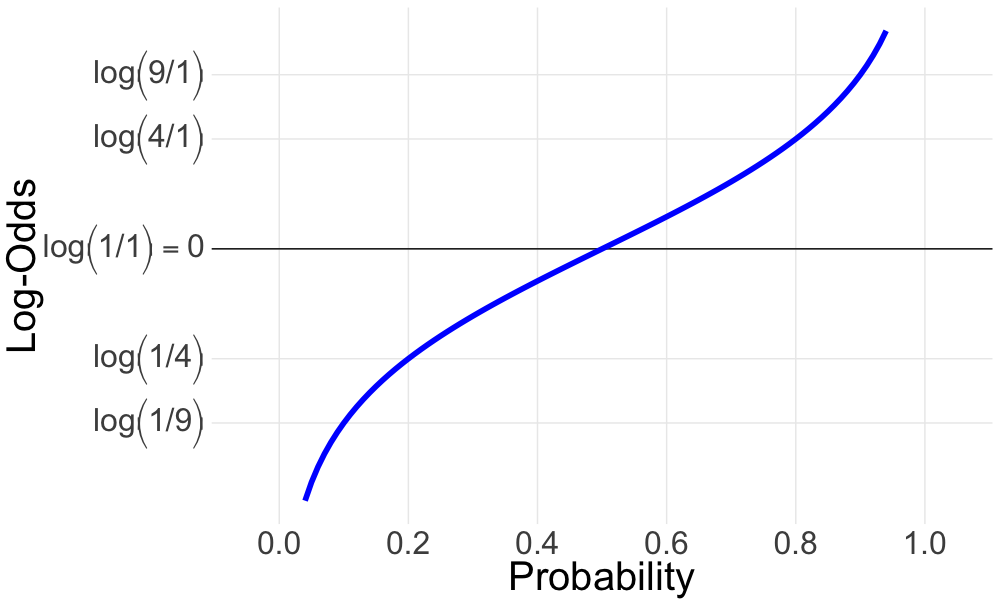
로짓함수는 로지스틱 함수의 역함수로써 0과 1 사이의 확률을 log-odds로 바꾸어준다.
5.3 R 에서 로지스틱과 로짓 함수
R에서 로지스틱함수는 plogis()이고 로짓함수는 logit()이다. 두함수는 역함수이므로 어떤 값의 로지스틱 값을 로짓하면 그 값이 된다.
plogis() # Logistic
qlogis() # Logit[1] 0.5또한 확률(probability)의 로짓 값을 만들면 로그오즈값이 된다. 다음 예를 보면 1/4확률은 오즈로 바꾸면 1/3이 되고 로짓 값은 log(1/3)이 된다.
[1] TRUE5.4 Logistic GAMs with mgcv
이분형변수를 반응변수로 하는 로지스틱 GAM을 시행하는 방법은 gam()함수를 호츨할 때 family인수로 binomial을 지정해주면 된다.
gam( y ~x1 + s(x2), data=데이터이름, family=binomial, method="REML")5.5 Logistic GAM output
로지스틱 GAM의 출력도 보통 GAM의 출력과 유사하다. 보통의 GAM처럼 비모수항이 먼저 나오고 평활항이 나온다. 유효자유도(EDF) 또한 평활항의 복잡함을 나타내고 별 표시는 유의성을 나타낸다. 하지만 여기서의 출력은 모두 로그오즈 스케일로 되어있다. 이것을 확률 개념으로 해석하려면 로지스틱함수를 써서 변환하여야 한다. 출력을 보면 절편이 0.733으로 되어 있다. 이것을 plogis()함수를 써서 바꾸면 절편은 0.675가 된다. 이것의 의미는 이 모형은 기저상태에서 양성 결과를 보일 확률이 67.5% 라는 뜻이다.
Family: binomial
Link function: logit
Formula:
y ~ s(x1) + s(x2)
Parametric coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.7330 0.1208 6.07 1.28e-09 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Approximate significance of smooth terms:
edf Ref.df Chi.sq p-value
s(x1) 1.367 1.646 25.83 1.23e-05 ***
s(x2) 5.754 6.890 51.37 8.12e-09 ***[1] 0.67546335.6 예제 : 당뇨병성 망막병증
5.6.1 필요한 패키지
이번 장의 예제를 분석하기 위해 다음 패키지가 필요하다.
5.6.2 탐색적분석
예제 데이터 wesdr은 gamair 패키지에 포함되어 있는 데이터로 당뇨 환자 중 당뇨병성 망막병증(Diabetic Retinopathy)이 있는 환자와 없는 환자의 예측인자로 질병의 이환기간(dur,단위:년)과 체질량지수(bmi, 단위 \(kg/m^2\)), 당화혈색소(gly, 단위 %) 데이터이다.
'data.frame': 669 obs. of 4 variables:
$ dur: num 10.3 9.9 15.6 26 13.8 31.1 2.6 39.6 7.3 8.3 ...
$ gly: num 13.7 13.5 13.8 13 11.1 11.3 15.1 13.4 14.6 15.4 ...
$ bmi: num 23.8 23.5 24.8 21.6 24.6 24.6 19.3 30.4 24.8 20.7 ...
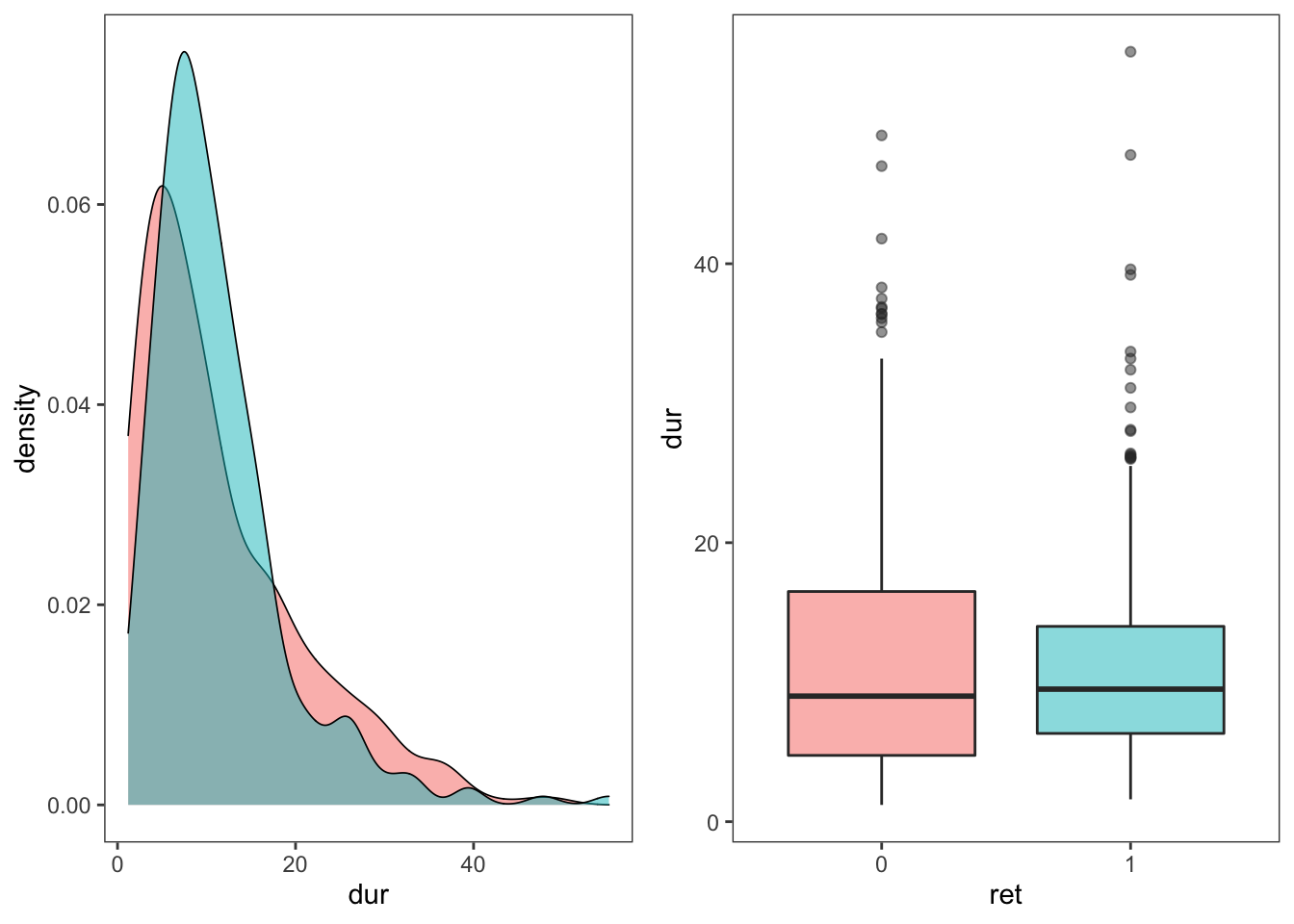
$ ret: int 0 0 0 1 1 1 0 1 1 1 ...먼저 당뇨병성 망막병증(ret) 유무에 따라 이환기간, 체질량지수, 당화혈색소의 분포를 비교해보았다. 비교를 위해 다음과 같은 함수를 만들어 사용하였다.
ggCompare=function(data,y,group){
yvar=as.character(substitute(y))
groupvar=as.character(substitute(group))
if(!is.factor(data[[groupvar]])) data[[groupvar]]=factor(data[[groupvar]])
p1=ggplot(data,aes_string(x=yvar,fill=groupvar))+geom_density(alpha=0.5,size=0.3)+theme_article()+theme(legend.position="None")
p2=ggplot(data,aes_string(x=groupvar,y=yvar,fill=groupvar))+geom_boxplot(alpha=0.5)+theme_article()+theme(legend.position="None")
ggpubr::ggarrange(p1,p2,ncol=2)
}
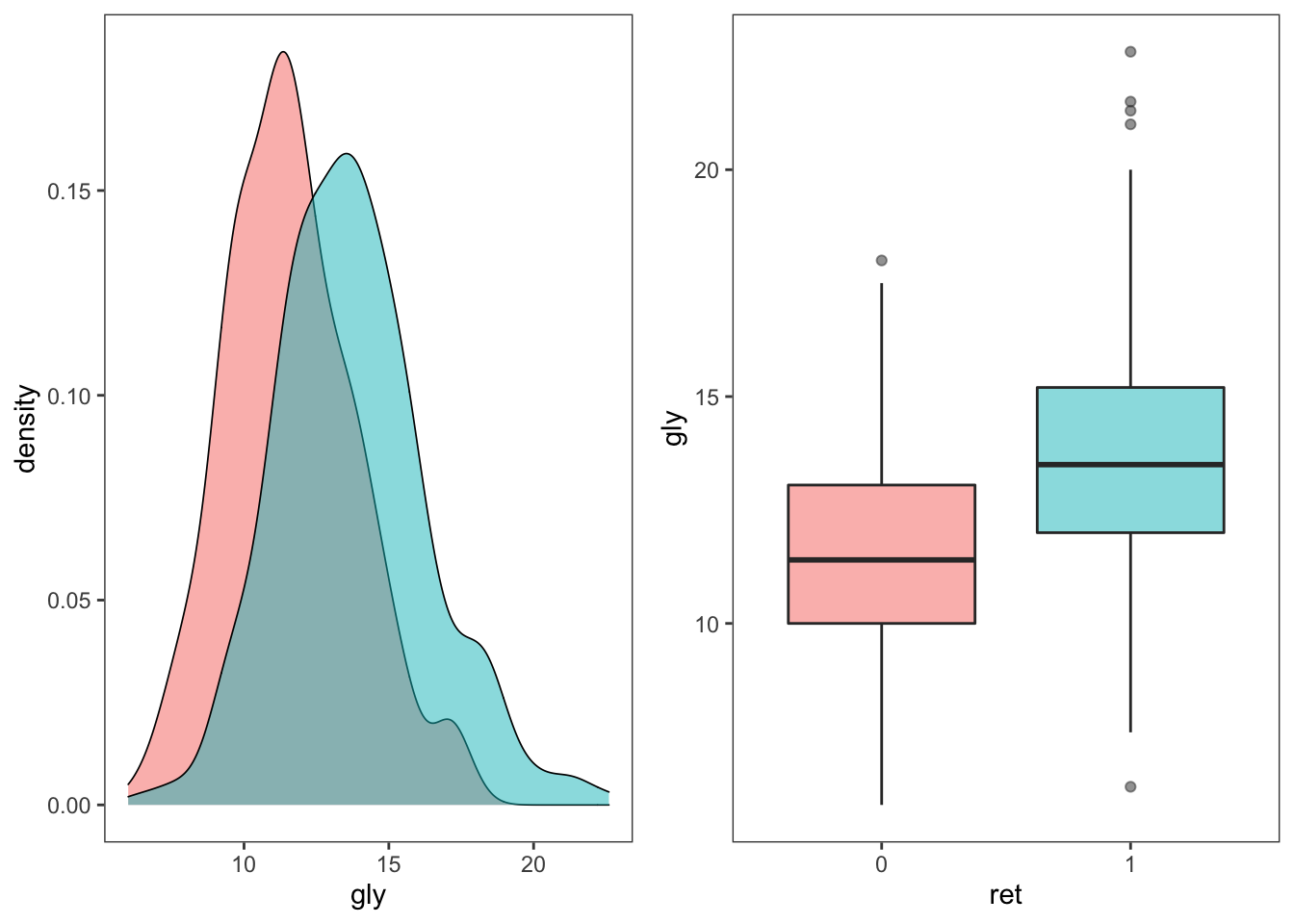
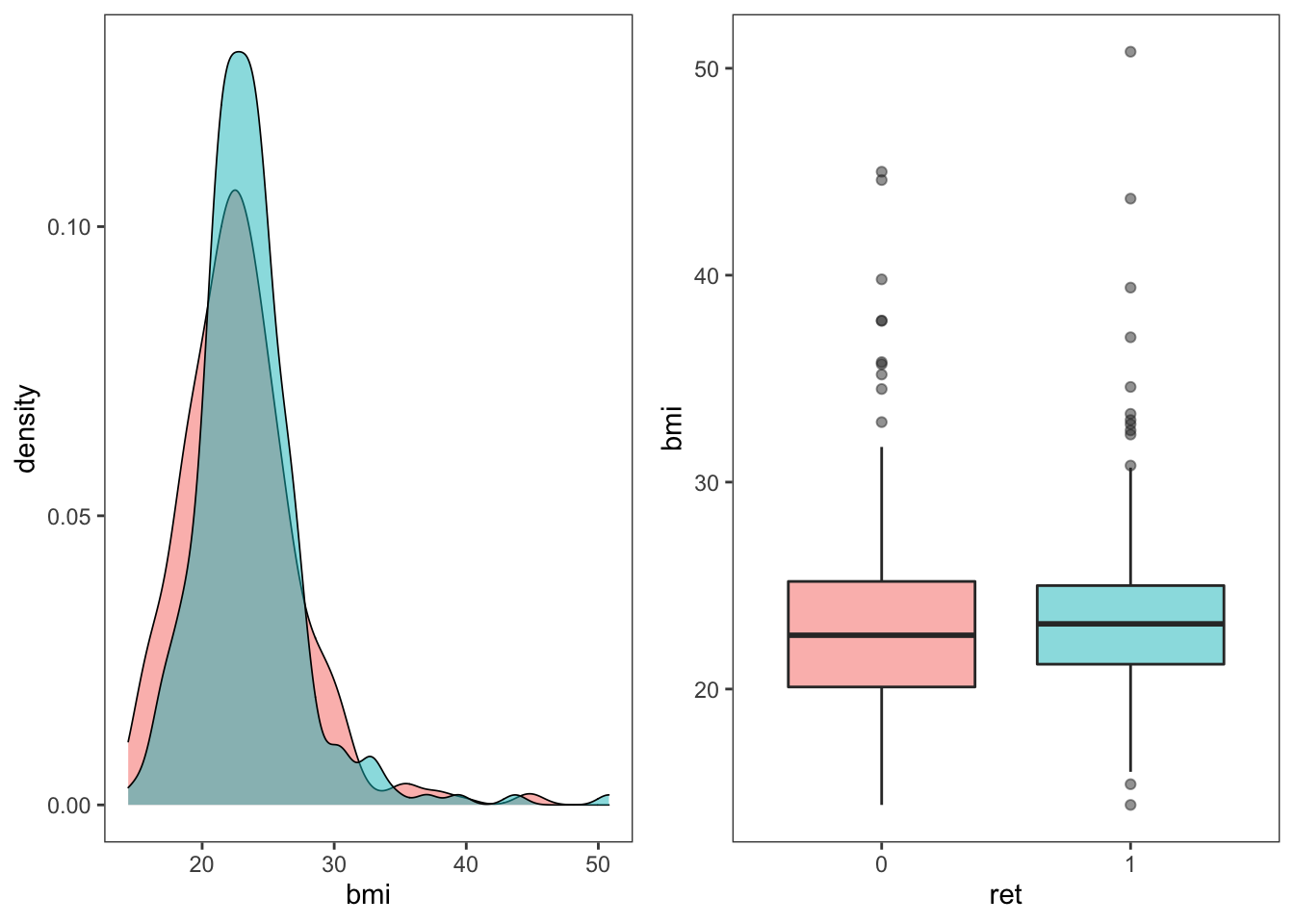
이를 표로 정리해보면 다음과 같다.
| p | |||
|---|---|---|---|
| (N=391) | (N=278) | ||
| dur | 11.6 ± 9.2 | 11.3 ± 7.6 | 0.687 |
즉, 당뇨병성 망막병증이 있는 경우 당화혈색소가 유의하게 높았다. 하지만 다른 변수들과의 관계는 뚜렷하지 않았다.
5.7 모형의 분석
이 데이터의 분석을 위해 로지스틱 일반화가법모형을 사용해 분석하였다. 데이터의 분석을 위해 dur, gly, bmi를 각각 평활항으로 dur,gly,bmi 간의 상호작용을 각각 텐서상호작용으로 투입하였다. 모형 선택에 null space penalty를 사용하였다. 이 모형을 수식으로 나타내보면 다음과 같다.
\[\begin{equation} ret_i \sim binom(1,\mu_i),\\ logit(\mu_i)=f_1(dur_i)+f_2(gly_i)+f_3(bmi_i)+f_4(dur_i,gly_i)+f_5(dur_i,bmi_i)+f_6(bmi_i,gly_i) \end{equation}\]
m <- gam(ret~s(dur)+s(gly)+s(bmi)+ti(dur,gly)+
ti(dur,bmi)+ti(gly,bmi),select=TRUE,
data=wesdr,family=binomial,method="REML")
ow <- options(warn=-1) ## avoid complaint about zlim
plot(m,pages=1,scheme=1,zlim=c(-3,3))
options(ow)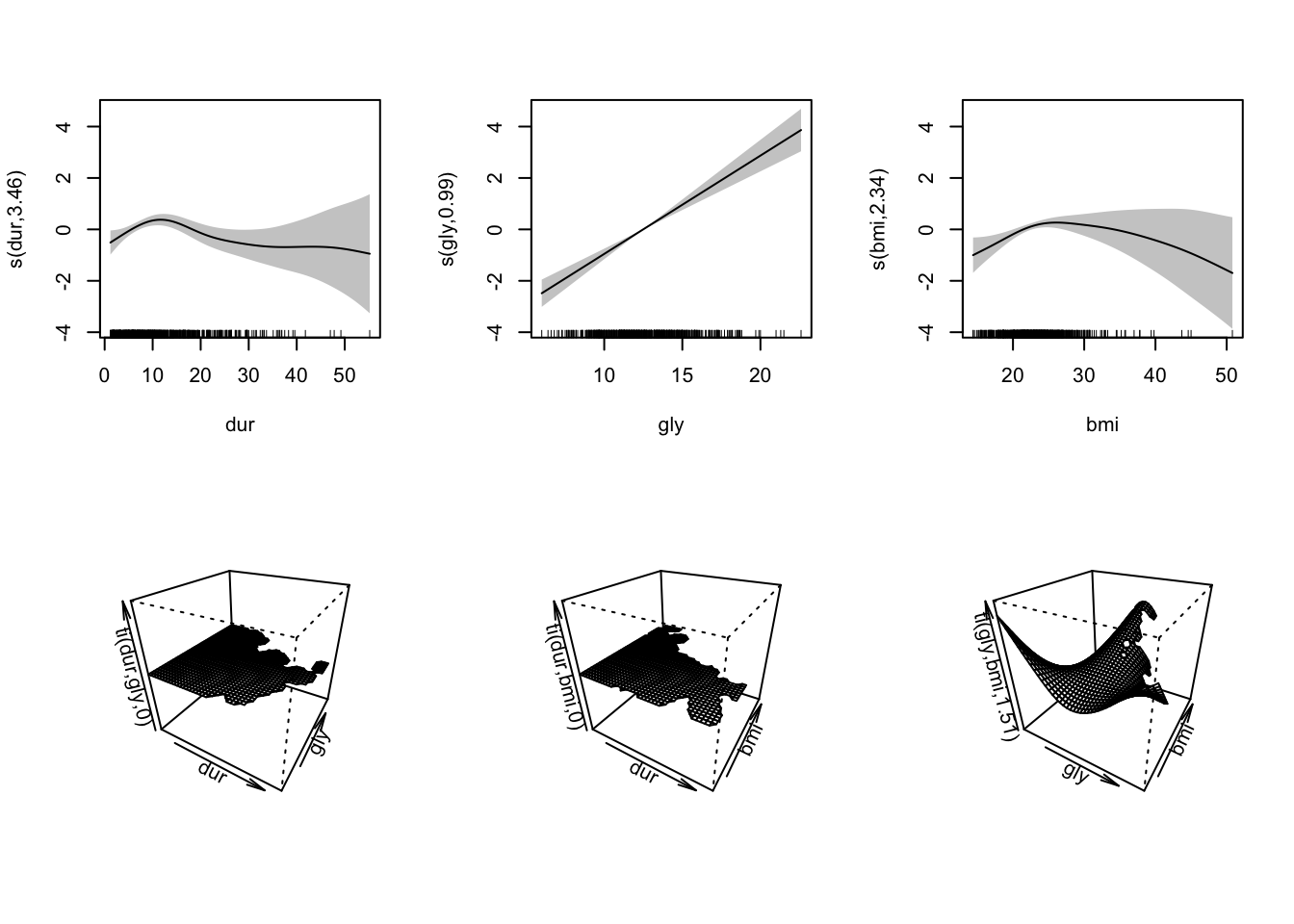
Family: binomial
Link function: logit
Formula:
ret ~ s(dur) + s(gly) + s(bmi) + ti(dur, gly) + ti(dur, bmi) +
ti(gly, bmi)
Parametric coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.40250 0.08976 -4.484 7.33e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Approximate significance of smooth terms:
edf Ref.df Chi.sq p-value
s(dur) 3.4620910 9 15.217 0.00100 **
s(gly) 0.9892167 9 87.624 < 2e-16 ***
s(bmi) 2.3353146 9 11.672 0.00148 **
ti(dur,gly) 0.0001338 16 0.000 0.59122
ti(dur,bmi) 0.0001019 16 0.000 0.81839
ti(gly,bmi) 1.5104273 16 6.957 0.00716 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
R-sq.(adj) = 0.221 Deviance explained = 18.4%
-REML = 387.42 Scale est. = 1 n = 669모형의 출력 내용을 보면 dur, bmi는 비선형곡선을 보이며 유의하였고 gly는 선형관계를 보이나 유의하였다. 위험인자들 간의 상호작용 중에서 gly와 bmi의 상호작용은 비선형관계를 보였으며 통계적으로 유의하였다. gly와 bmi의 상호작용을 다시 시각화해보면 다음과 같다.
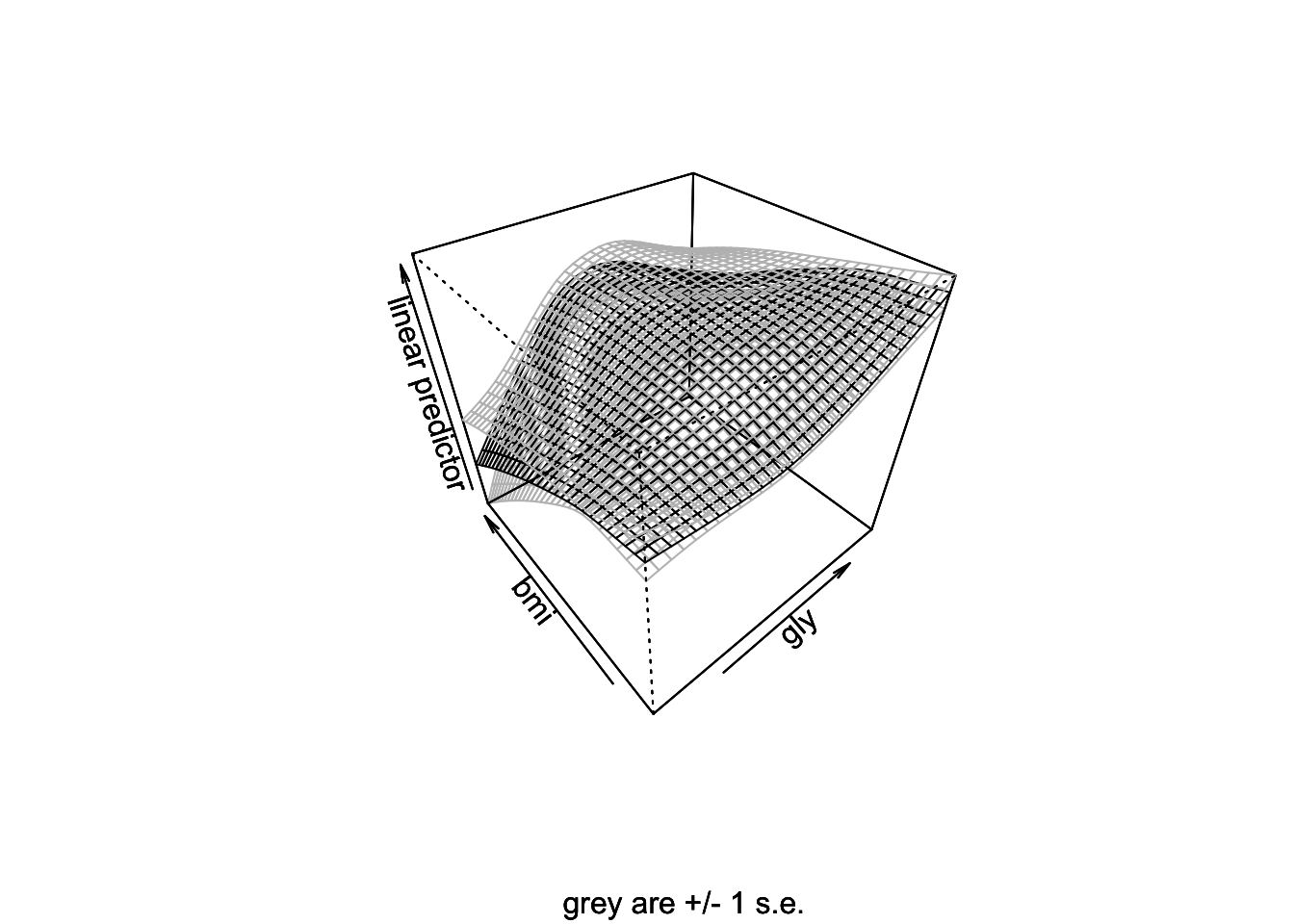
예상대로 당화혈색소가 높은 경우 당뇨병성 망막병증의 위험은 높아지지만 초기에는 체질량지수가 낮은 경우에는 위험의 증가가 가파르지 않았다.
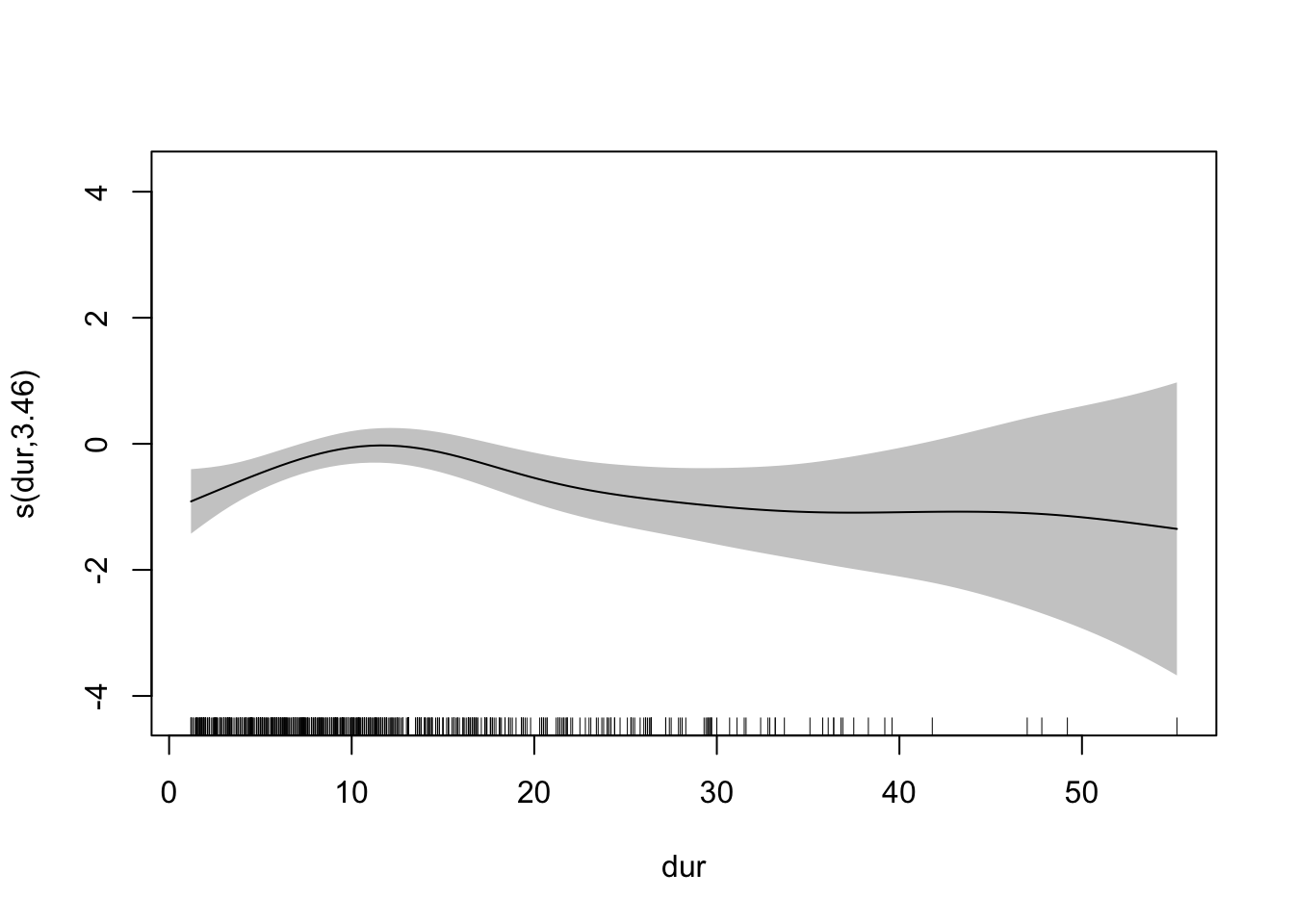 또한 질병의 초기에는 당뇨병성 망막병증의 위험이 증가하지만 그 이후에는 감소하는 증거가 보인다: 가능한 이유로는 당뇨를 잘 조절하는 환자만이 이환기간이 길어질 가능성이 있고 단순히 어떤 환자들에서는 당뇨병성 망막병증이 발생하지 않지만 일부 불운한 환자들에서는 질병의 초기에 당뇨병성 망막병증이 발생하는 것일 수도 있다. 이 모형을 진단해보면 다음과 같다.
또한 질병의 초기에는 당뇨병성 망막병증의 위험이 증가하지만 그 이후에는 감소하는 증거가 보인다: 가능한 이유로는 당뇨를 잘 조절하는 환자만이 이환기간이 길어질 가능성이 있고 단순히 어떤 환자들에서는 당뇨병성 망막병증이 발생하지 않지만 일부 불운한 환자들에서는 질병의 초기에 당뇨병성 망막병증이 발생하는 것일 수도 있다. 이 모형을 진단해보면 다음과 같다.
Method: REML Optimizer: outer newton
full convergence after 16 iterations.
Gradient range [-1.966513e-05,1.366149e-05]
(score 387.415 & scale 1).
Hessian positive definite, eigenvalue range [5.660325e-07,0.9286636].
Model rank = 76 / 76
Basis dimension (k) checking results. Low p-value (k-index<1) may
indicate that k is too low, especially if edf is close to k'.
k' edf k-index p-value
s(dur) 9.00e+00 3.46e+00 1.00 0.520
s(gly) 9.00e+00 9.89e-01 0.96 0.135
s(bmi) 9.00e+00 2.34e+00 0.98 0.290
ti(dur,gly) 1.60e+01 1.34e-04 0.98 0.275
ti(dur,bmi) 1.60e+01 1.02e-04 1.00 0.580
ti(gly,bmi) 1.60e+01 1.51e+00 0.95 0.025 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1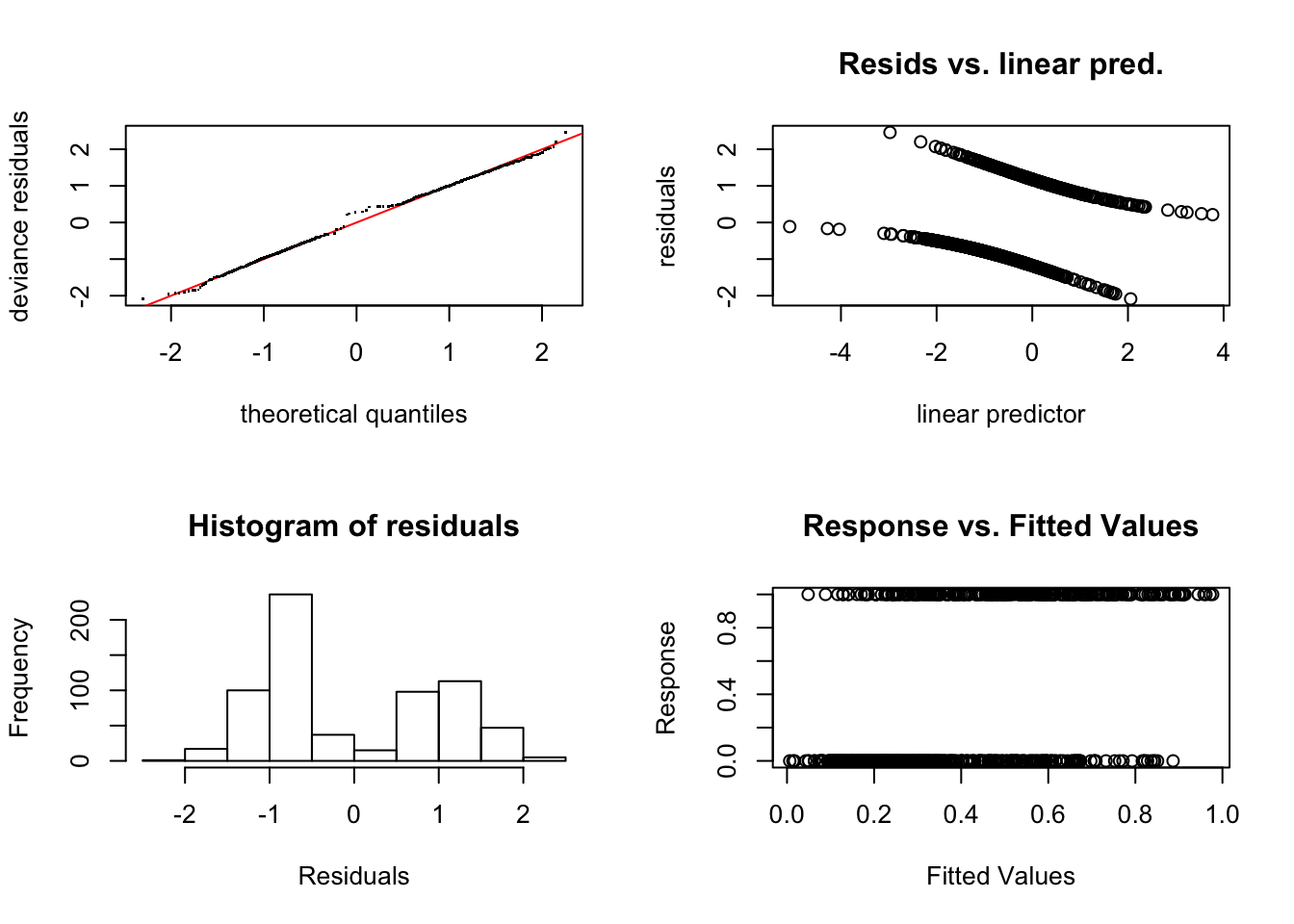 이분형결과변수가 있는 모형에서 모형 진단은 어렵지만 가정된 모형이 유연성을 가지고 있기 때문에 잘못된 결과가 도출될 가능성은 적어보인다.
이분형결과변수가 있는 모형에서 모형 진단은 어렵지만 가정된 모형이 유연성을 가지고 있기 때문에 잘못된 결과가 도출될 가능성은 적어보인다.