Chapter 3 모형 해석하기
이번 장에서는 일반화가법모형에 적합시킨 모형을 어떻게 해석하고 설명하는지 배우고 데이터의 과소적합이나 변수들 사이의 숨겨진 관계 등에 의해 생기는 문제들을 진단하고 이러한 문제들을 반복적으로 수정함으로써 보다 좋은 결과를 얻는 방법을 배울 것이다.
3.1 GAM 출력 해석하기
먼저 mpg데이터를 이용해 다음과 같은 모형을 만들고 summary를 출력한다.
m <- gam(hw.mpg ~ s(weight) + s(rpm) + s(price) + s(comp.ratio) + s(width) + fuel,
data=mpg, method="REML")
summary(m)
Family: gaussian
Link function: identity
Formula:
hw.mpg ~ s(weight) + s(rpm) + s(price) + s(comp.ratio) + s(width) +
fuel
Parametric coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 23.873 3.531 6.760 1.89e-10 ***
fuelgas 7.571 3.922 1.931 0.0551 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Approximate significance of smooth terms:
edf Ref.df F p-value
s(weight) 6.254 7.439 20.909 < 2e-16 ***
s(rpm) 7.499 8.285 8.534 2.07e-09 ***
s(price) 2.681 3.421 1.678 0.155
s(comp.ratio) 1.000 1.001 18.923 2.22e-05 ***
s(width) 1.001 1.001 0.357 0.551
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
R-sq.(adj) = 0.89 Deviance explained = 90.1%
-REML = 464.81 Scale est. = 5.171 n = 1993.1.1 Family와 Link
summary의 첫번째 부분은 Family로 시작한다. Family 부분은 이 모형이 잔차의 분포를 Gaussian 또는 정규분포를 가정한다는 것을 말해준다. Link가 identity라는 것은 이 모형의 예측은 변형(transform)되지 않았다는 것을 말해준다. 변형에 관하여는 logistic GAM 부분에서 다룰 것이다. 그 아랪 부분에 모형의 식(formula)를 볼 수 있다.
Family: gaussian
Link function: identity
Formula:
hw.mpg ~ s(weight) + s(rpm) + s(price) + s(comp.ratio) + s(width) + fuel3.1.2 모형의 모수항
다음으로는 모형의 모수항이 나타난다. 모수항이라는 말은 여기서는 모형의 선형 항을 말한다. 보는 바와 같이 이 부분은 선형회귀의 summary 부분과 동일하다. 모형의 선형 항에 대한 회귀계수와 표준오차, 검정통계량인 t값과 p값을 보여준다. p 값 다음에 보이는 별 표시는 유의수준을 나타내 준다. 이 예에서는 모형의 절편은 유의하게 0과 다르나 fuel이 가솔린인 것은 0.1 수준에서 유의한 것을 보여준다.
Parametric coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 23.873 3.531 6.760 1.89e-10 ***
fuelgas 7.571 3.922 1.931 0.0551 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 13.1.3 모형의 평활항
모수 항 다음에는 평활항에 대한 부분이다. 평활항의 회귀계수는 출력되지 않는데 그 이유는 각 평활항마다 기저함수의 갯수에 따라 회귀계수가 여러개 존재하기 때문이다. 회귀계수 대신 첫번째 열에 edf가 출력되는데 이는 유효자유도(effective degrees of freedom)이다. 이 값은 평활항의 복잡성을 나타내준다. edf가 1인 것은 직선을 뜻하며 edf가 2인 것은 제곱항을 뜻한다. edf가 클수록 곡선은 더욱 복잡해진다. weight 평활항의 edf는 6이 넘으며 곡선은 매우 복잡하고 구불구불하지만 comp.ratio 평활항의 edf는 1로 직선인 것을 알 수 있다. edf 다음은 평활항에 대한 유의성 검정으로 Ref.df와 F는 ANOVA에 사용되는 통계량이며 그 결과 p 값은 오른쪽에 나와 있다. 하지만 이 수치는 근사치로 모형을 시각화하여 점검하는 것이 중요하다. GAM의 평활항의 유의성을 해석하는 좋은 방법은 95% 신뢰구간내에 수평선을 그릴 수 있느냐 하는 것이다. weight와 price에 관한 평활선 그림에서 수평선을 그려보면 price의 경우 95% 신뢰구간 안을 통과하는 수평선을 그릴 수 있다. 또한 유념해야 할 것은 유효자유도(edf)가 높다고 해서 유의하지는 않으며 유의하다고 해서 edf가 높은 것은 아니라는 점이다. 평활항은 선형이면서 유의할 수도 있고, 비선형이고 유의하지 않을 수도 있다. 이 모형에서 price항은 선형이 아니지만 유의하지 않으며 그 해석은 price항은 약간의 복잡성은 있지만 그 효과의 모양이나 방향성은 획실하지 않다고 할 수 있다. Compression ratio는 선형이나 유의하고 width는 선형이고 유의하지도 않다.
Approximate significance of smooth terms:
edf Ref.df F p-value
s(weight) 6.254 7.439 20.909 < 2e-16 ***
s(rpm) 7.499 8.285 8.534 2.07e-09 ***
s(price) 2.681 3.421 1.678 0.155
s(comp.ratio) 1.000 1.001 18.923 2.22e-05 ***
s(width) 1.001 1.001 0.357 0.551
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1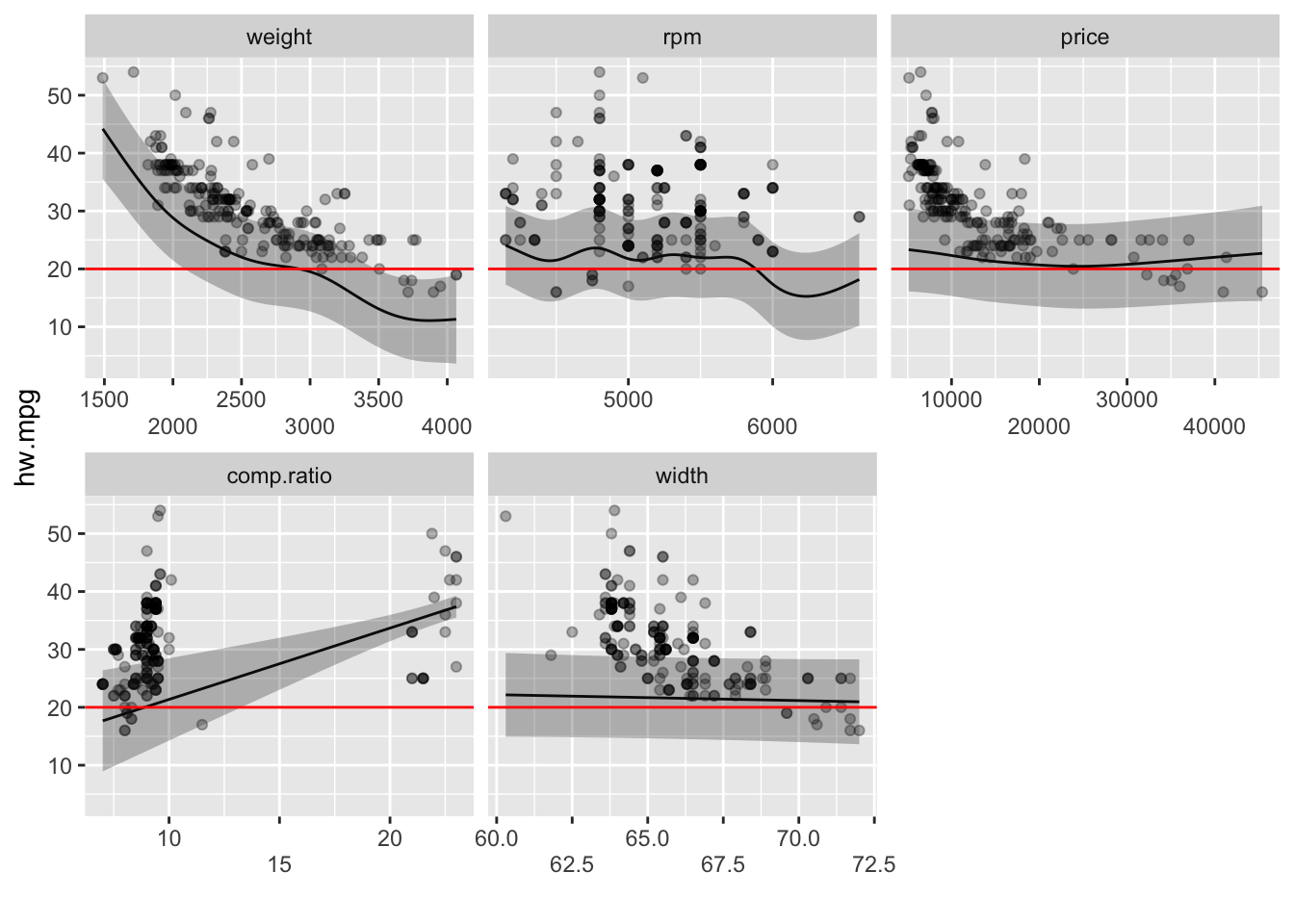
3.2 모형의 진단 : gam.check()
gam()함수로 GAM 모형을 만들고 ggGam()함수로 시각화한 후에는 잘 적합된 모형인지 점검해보아야 한다. GAM 모형을 만들때 몇가지 점검해 봐야 하는 함정들이 있다.
3.2.1 기저 함수의 수 부족
기저함수의 수는 평활항의 곡선이 얼마나 구불구불한지 결정해주며 기저함수의 수가 부족할 경우 두 변수의 관계를 제대로 반영하지 못할 수 있다. 아래에 있는 가상의 데이터 분석에서 보면 4개의 기저함수를 사용하고 있으며 부분효과플롯을 보면 평활곡선이 두 변수의 관계를 제대로 반영하고 있지 못한 것을 알 수 있다. 하지만 부분효과플롯을 통해 항상 기저함수의 수가 충분한지 명확이 드러나지 않을 때도 있다. 이때에는 gam.check()함수를 통해 모형을 점검해 보아야 한다.
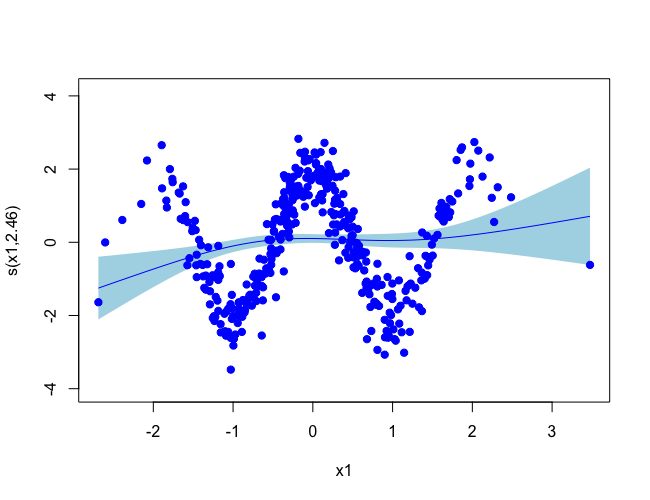gam_check()함수를 실행하면 R console을 통해 글씨가 나오고 plot이 네개 그려진다. 먼저 console output을 살펴보자. 가장 먼저 모형이 수렴(convergence)하는지 보고한다. 이 예에서는 완전수렴한다. 완전수렴한다는 것은 R이 최선의 해답을 찾았다는 뜻이다. 만일 모형이 수렴하지 않으면 그 결과는 정확하지 않다. 모형이 수렴하지 못하는 경우는 데이터가 충분하지 않고 모형이 너무 많은 인수를 포함하고 있을 때 발생한다. 그 아래에는 기저함수 점검표가 나온다. 여기서는 모형의 잔차가 무작위인지 검정을 시행하고 결과를 보여준다. 하나의 평활항마다 한 줄 씩 결과를 보여준다. k’ 값은 기저함수의 수를 나타내며 유효자유도, k-index 통계량과 p값이 보여진다. 여기에서 낮은 p값은 잔차의 분포가 무작위가 아니라는 뜻이며 이는 종종 기저함수의 갯수가 충분하지 않다는 것을 뜻한다. 이 검정 겨로가 또한 근사치로 부분효과플롯으로 확인하여야 하며 p값 뿐만 아니라 k값(기저함수의 갯수)과 유효자유도(edf) 값을 같이 확인하여야 한다. 이 모형에서는 x1의 기저함수의 갯수를 늘려 다시 모형을 적합시켜야 한다.
Method: REML Optimizer: outer newton
full convergence after 9 iterations.
Gradient range [-0.0001467222,0.00171085]
(score 784.6012 & scale 2.868607).
Hessian positive definite, eigenvalue range [0.00014,198.5]
Model rank = 7 / 7
Basis dimension (k) checking results. Low p-value
(k-index<1) may indicate that k is too low, especially
if edf is close to k'.
k' edf k-index p-value
s(x1) 3.00 1.00 0.35 <2e-16 ***
s(x2) 3.00 2.88 1.00 0.52
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1s1의 평활항에 대해 기저함수의 갯수를 늘려 다시 검정한 결과이다. 이제 첫번째 x1 평활항에 대한 검정은 유의하지 않으나 두번째 평활항의 p값이 유의하게 나타났다. 문제 하나를 해결하면 또 다른 문제가 나타날 수 있다. 따라서 모형을 변경한 후에는 반드시 다시 gam.check()를 시행해보아야 한다.
...
k' edf k-index p-value
s(x1) 11.00 10.85 1.05 0.830
s(x2) 3.00 2.98 0.89 0.015 *
...다시 두번째 평활항의 기저함수의 수를 증가시켜 모형을 만든 후 gam.check() 를 다시 시행해본 결과 평활항은 검정에 통과하였다. 두 평활항 모두 잔차에 유의한 양상은 없었고 기저함수의 수도 충분했다.
...
k' edf k-index p-value
s(x1) 11.00 10.86 1.08 0.94
s(x2) 11.00 7.78 0.94 0.12
...3.2.2 진단적그림(Diagnostic plot)
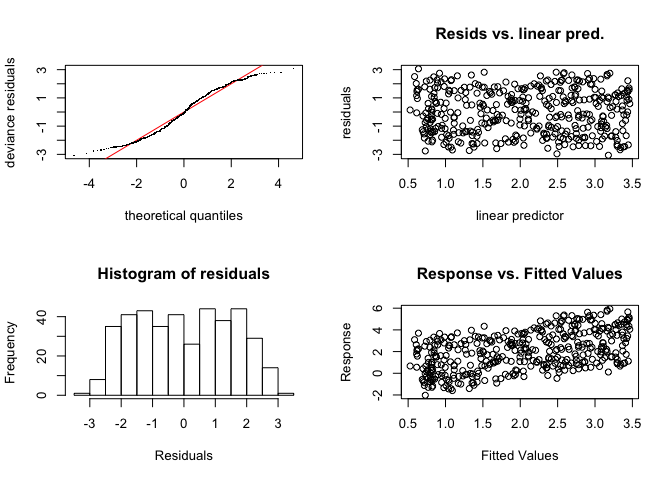
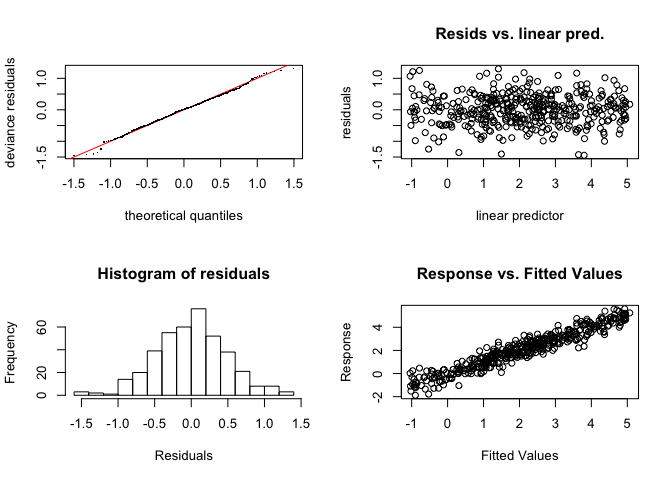
gam.check()함수는 네 개의 plot을 만들어 주는데 이들은 모형의 잔차를 각기 다른 방법으로 보여준다. 아래의 그림은 제대로 적합되지 않은 모형의 diagnostic plot을 보여준다. 왼쪽 위 그림은 Q-Q plot으로 모형의 잔차를 정규분포와 비교해준다. 잘 적합된 모형의 경우 잔차는 직선에 매우 근접한다. 아래 왼쪽은 잔차의 히스토그램으로 잘 적합된 모형의 경우 대칭적인 벨 형태를 기대할 수 있다. 오른쪽 위의 그림은 잔차의 그림으로 0 주위에서 고르게 분포하여야 한다. 마지막으로 오른쪽 아래 그림은 반응변수와 적합된 값을 나타낸 것으로 완벽한 모형인 경우 직선을 형성한다. 우리는 완벽한 모형을 기대하지는 않지만 (0,0)과 (1,1)을 지나는 직선 주위에 모여 있는 양상을 기대한다.
다음 그림은 기저함수의 수를 증가시킨 마지막 모형의 진단적 그림이다. 이 모형의 Q-Q plot은 더이상 곡선이 아닌 직선이며 히스토그램은 벨 모양이고 잔차 그림에서는 0 주위에 고르게 분포하고 있고 반응변수와 적합된 값 그림은 (1,1)을 지나는 직선 주위에 모여있다. 이 모두는 모형적합이 좋아졌다는 것을 말해준다.
3.2.3 Concurvity 점검
3.2.3.1 공선성
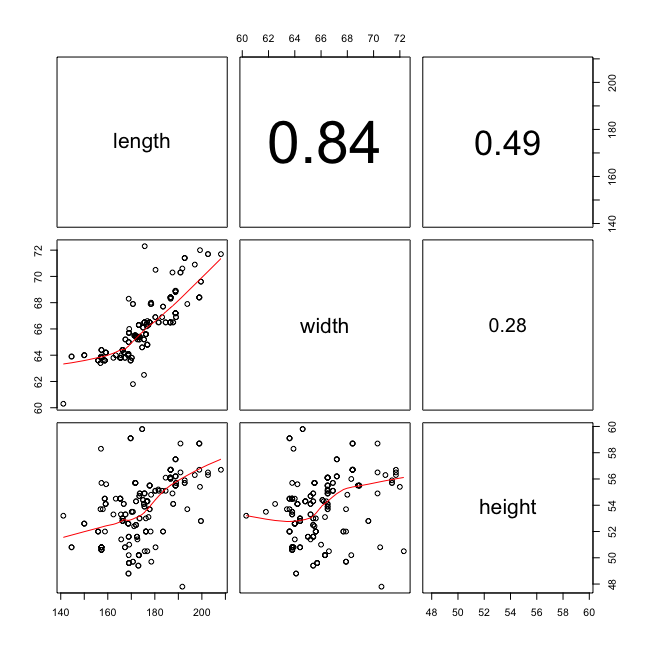
선형모형에서 공선성이라는 개념을 기억해보자. 회귀모형에서 두 개의 설명변수가 높은 상관관계를 보인다면 반응변수두 두 변수 모두에게 반응하기 때문에 모형을 적합시키기 어렵다. 이러한 현상을 공선성이라고 부르며 이러한 경우 큰 신뢰구간을 가진 제대로 적합되지 않은 모형을 만든다. 일반적으로 하나의 모형에 공선성이 있는 설명변수들을 동시에 투입하는 것은 피하여야 한다.
지금까지 다루어 온 mpg 데이터에서 자동차의 length, width 와 height의 상관관계를 살펴보면 왼쪽 그림과 같다. 자동차의 length와 width의 상관관계는 매우 높기 때문에 자동차의 연비에 대한 length와 width의 효과를 구분하기 어렵다.
3.2.3.2 Concurvity
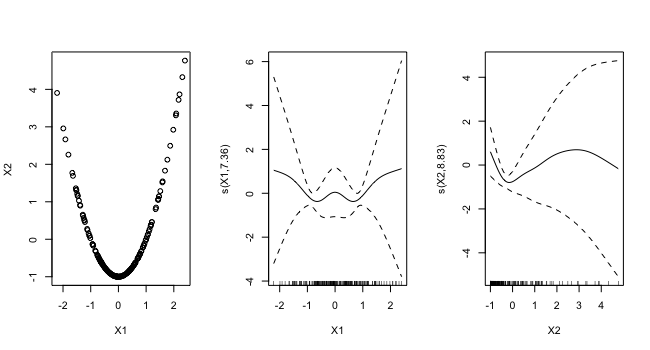
GAM에서는 공선성 이외에도 또 하나의 잠재적인 함정이 있다. 두 개의 변수의 상관관계가 높지 않더라도 두개의 변수의 관계가 곡선 관계인 concurvity를 보일 수 있다. 위의 그림에서 두개의 변수 X1과 X2는 선형관계는 아니지만 완벽한 포물선을 그리기 때문에 이 두개의 변수 X1과 X2를 같은 모형에 예측변수로 사용하는 경우 가운데와 오른쪽 그림과 같은 신뢰구간이 매우 넓은 평활곡선을 얻게 된다.
3.2.3.3 cocurvity() 함수
para s(X1) s(X2)
worst 0 0.84 0.84
observed 0 0.22 0.57
estimate 0 0.28 0.60mgcv패키지의 concurvity() 함수는 모형 내의 설명변수들의 concurvity를 측정해준다. 이 함수도 gam.check() 함수와 마찬가지로 GAM모형의 질을 평가하기 위한 함수이다. 이 함수는 두가지 모드가 있는데 첫번째로 full=TRUE로 지정하면 각 평활항별로 전체 concurvity를 보여준다. 보다 구체적으로 말하면 각 평활항 중 다른 평활항들에 의해 얼마나 미리 결정되어지는지를 수치화해서 보여준다. concurvity는 매우 복잡하므로 이 함수는 세가지 다른 방법으로 concurvity를 측정하여 보여주며 각각의 방법은 경우에 따라 장점을 보여준다. 하지만 가장 나쁜 worst를 주목하여 보아야 하며 worst concurvity가 0.8이상으로 높다면 모형을 주의깊게 검사해보아야 한다. 여기서 보인 예는 약간의 상관관계가 있는 변수들로 만든 모형의 경우이다. worst concurvity가 높으므로 이 모형의 plot을 주의깊게 보아야 하며 해석하는데 주의를 기울여야 한다.
3.2.3.4 쌍별(pairwise) concurvity
full=TRUE로 시행한 concurvity 검사에서 어느 하나라도 높게 나온다면 full=FALSE로 다시 검사를 시행한다. 이때에는 쌍별 concurvity를 볼 수 있다. 이번에는 다른 전체 변수가 아닌 쌍이 되는 다른 한 변수에 의해 얼마나 미리 결정되어지는지를 수치화해서 보여준다. 그 결과 어느 변수들이 밀접한 관계가 있는지 알 수 있다. 전체 모드와 마찬가지로 세 가지 측정 값을 보여주는데 가장 나쁜 worst에 주목하여 높은 값을 보이는 변수의 모양과 신뢰구간을 주의하여 본다.
$worst
para s(X1) s(X2)
para 1 0.00 0.00
s(X1) 0 1.00 0.84
s(X2) 0 0.84 1.00
$observed | $estimate
para s(X1) s(X2) | para s(X1) s(X2)
para 1 0.00 0.00 | para 1 0.00 0.0
s(X1) 0 1.00 0.57 | s(X1) 0 1.00 0.6
s(X2) 0 0.22 1.00 | s(X2) 0 0.28 1.0
3.3 네번째 예제 : 이산화탄소 농도
네번째 예제로 하와이의 Mauna Loa 에서 측정된 이산화탄소 농도 데이터를 분석해 본다. 이번 예제는 http://environmentalcomputing.net/intro-to-gams/ 에서 참조하였다. 이 데이터는 다음 주소에서 다운로드 받을 수 있다.( http://environmentalcomputing.net/wp-content/uploads/2017/10/manua_loa_co2.csv) 데이터를 불러들여 co2라는 이름으로 저장한다.
'data.frame': 665 obs. of 4 variables:
$ year : int 1958 1958 1958 1958 1958 1958 1958 1958 1958 1958 ...
$ co2 : num 316 317 318 317 316 ...
$ month: int 3 4 5 6 7 8 9 10 11 12 ...
$ Date : chr "1/03/1958" "1/04/1958" "1/05/1958" "1/06/1958" ...이 데이터는 날짜가 문자형 변수로 저장되어 있으므로 숫자형 변수로 바꾸어주고 산점도를 그려본다.
co2$time <- as.integer(as.Date(co2$Date,format="%d/%m/%Y"))
ggplot(co2,aes(x=time,y=co2))+geom_line()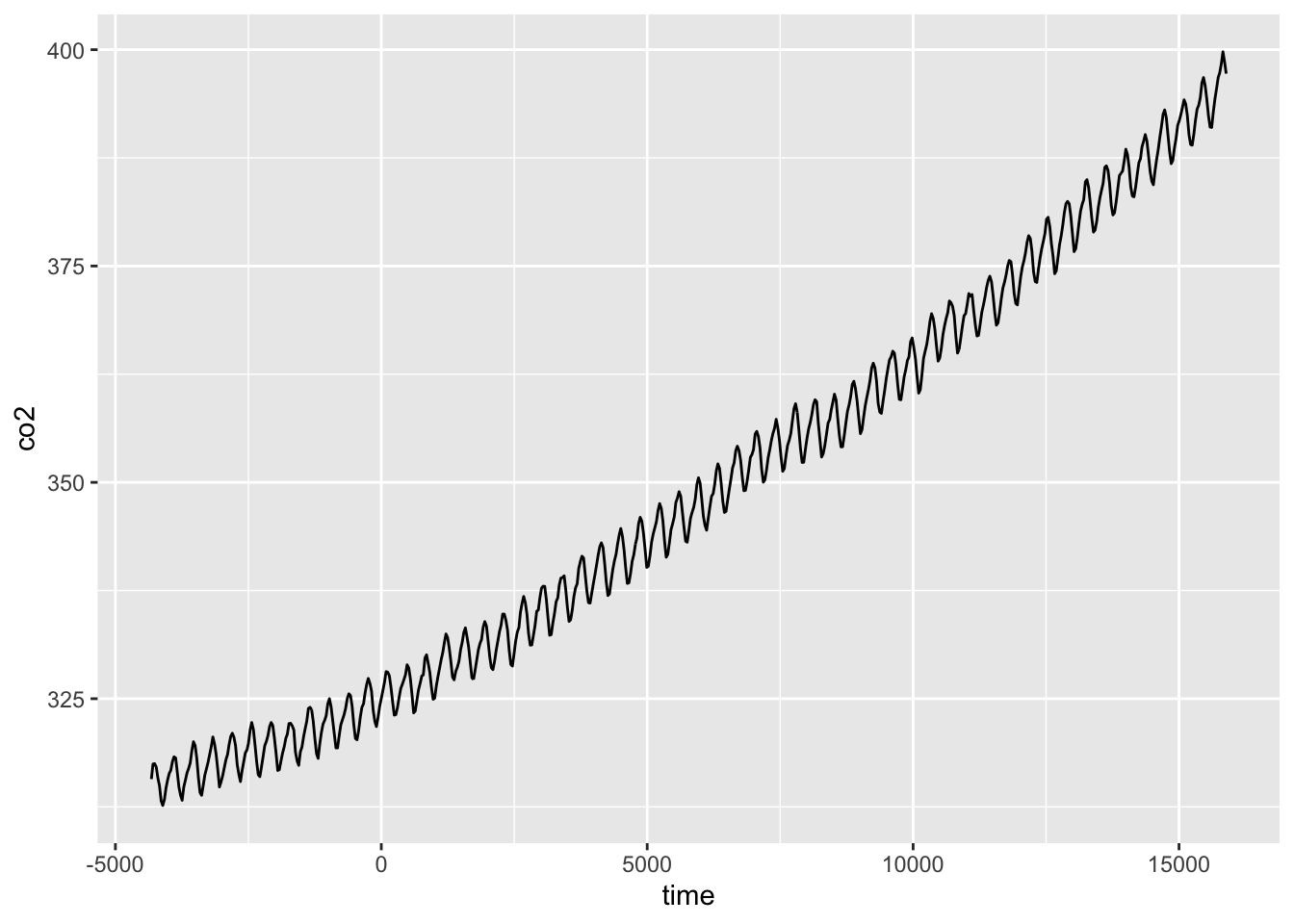
1958년 부터 2013년 까지의 자료중 일단 추세를 보기 위해 2000년 이후의 자료를 분석해본다. 2000년 이후의 자료를 co2df라는 이름으로 저장하고 시간의 흐름에 따른 이산화탄소 농도의 변화를 보기 위해 co2농도를 반응변수로 time을 설명변수로 하여 gam에 적합시킨다.
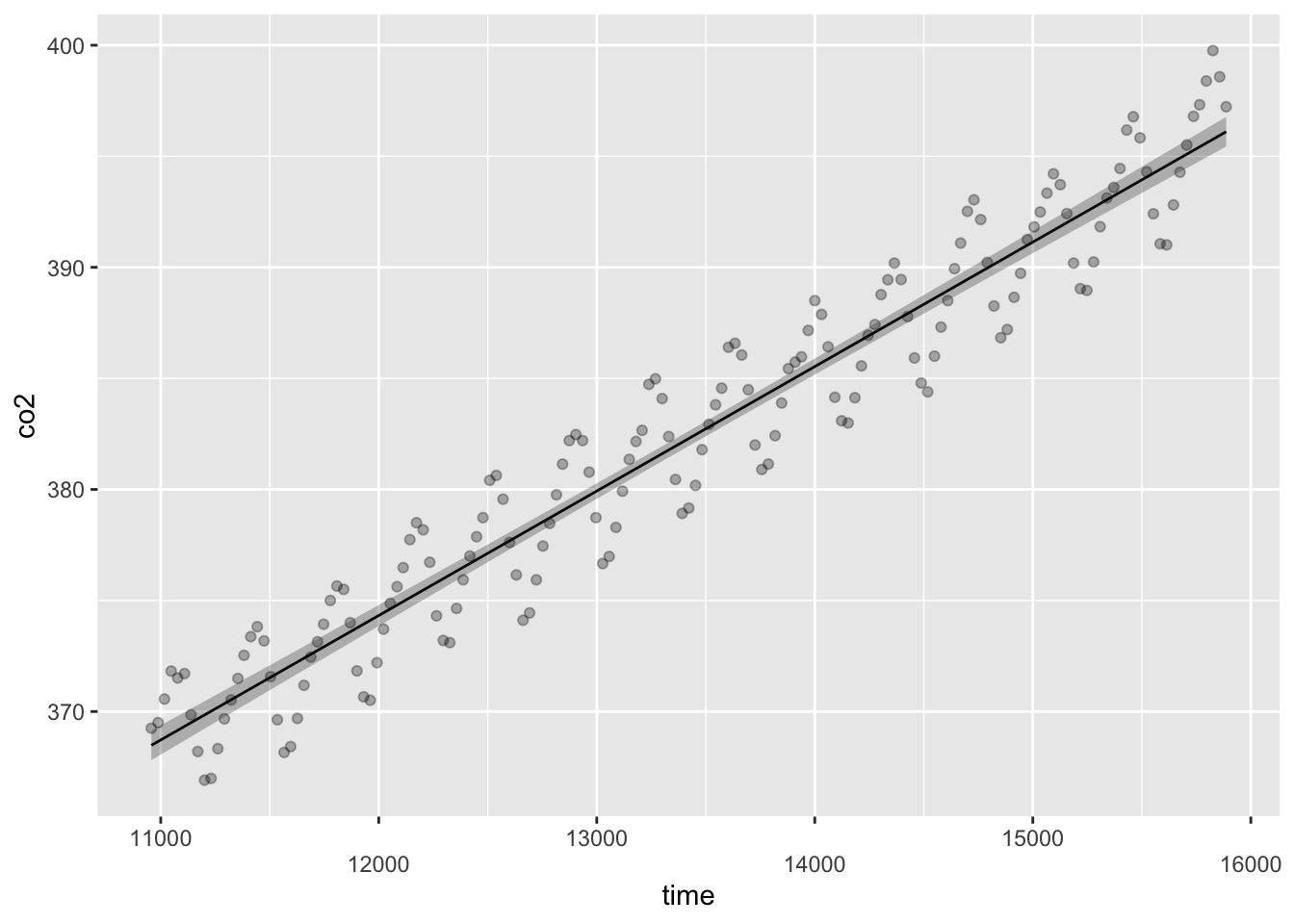
데이터의 전반적인 경향을 볼때 시간의 흐름에 따라 co2의 농도가 높아지는 것은 맞지만 co2의 농도는 계속 변화하는데 적합선은 거의 직선에 가깝게 나타난다. 이 모형의 요약을 본다.
Family: gaussian
Link function: identity
Formula:
co2 ~ s(time)
Parametric coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 382.2928 0.1711 2234 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Approximate significance of smooth terms:
edf Ref.df F p-value
s(time) 1.001 1.001 2196 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
R-sq.(adj) = 0.931 Deviance explained = 93.2%
-REML = 359.38 Scale est. = 4.774 n = 163모형의 요약을 보면 이 모형의 설명력은 0.931로(\(_{adj}R^2=0.931\)) 매우 높게 나타났다. 다음으로 모형의 진단을 해본다.
Method: REML Optimizer: outer newton
full convergence after 8 iterations.
Gradient range [-0.000124547,0.0001953285]
(score 359.3792 & scale 4.773986).
Hessian positive definite, eigenvalue range [0.0001245663,80.4998].
Model rank = 10 / 10
Basis dimension (k) checking results. Low p-value (k-index<1) may
indicate that k is too low, especially if edf is close to k'.
k' edf k-index p-value
s(time) 9 1 0.16 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1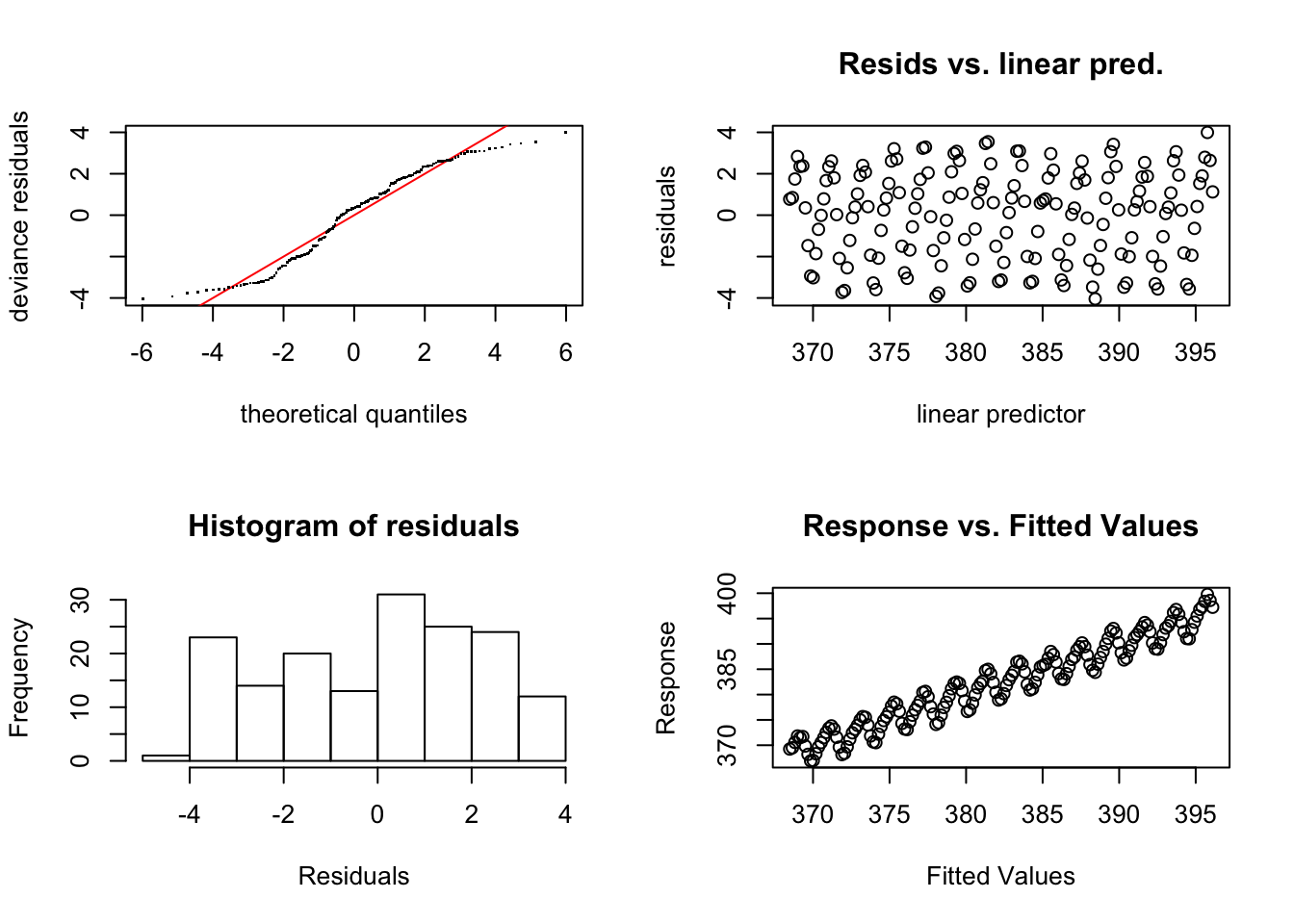
Residual Plot을 보면 매우 이상하게 오르락내리락 하는 양상을 보인다. 이는 이산화탄소 농도가 주기적으로 변화한다는 것을 뜻하므로 설명변수로 month를 추가한다. 이때 기저함수의 base로 cyclic cubic인 “cc”를 선택하고 모두 12개의 달이 있으므로 12개의 기저함수를 선택한다.
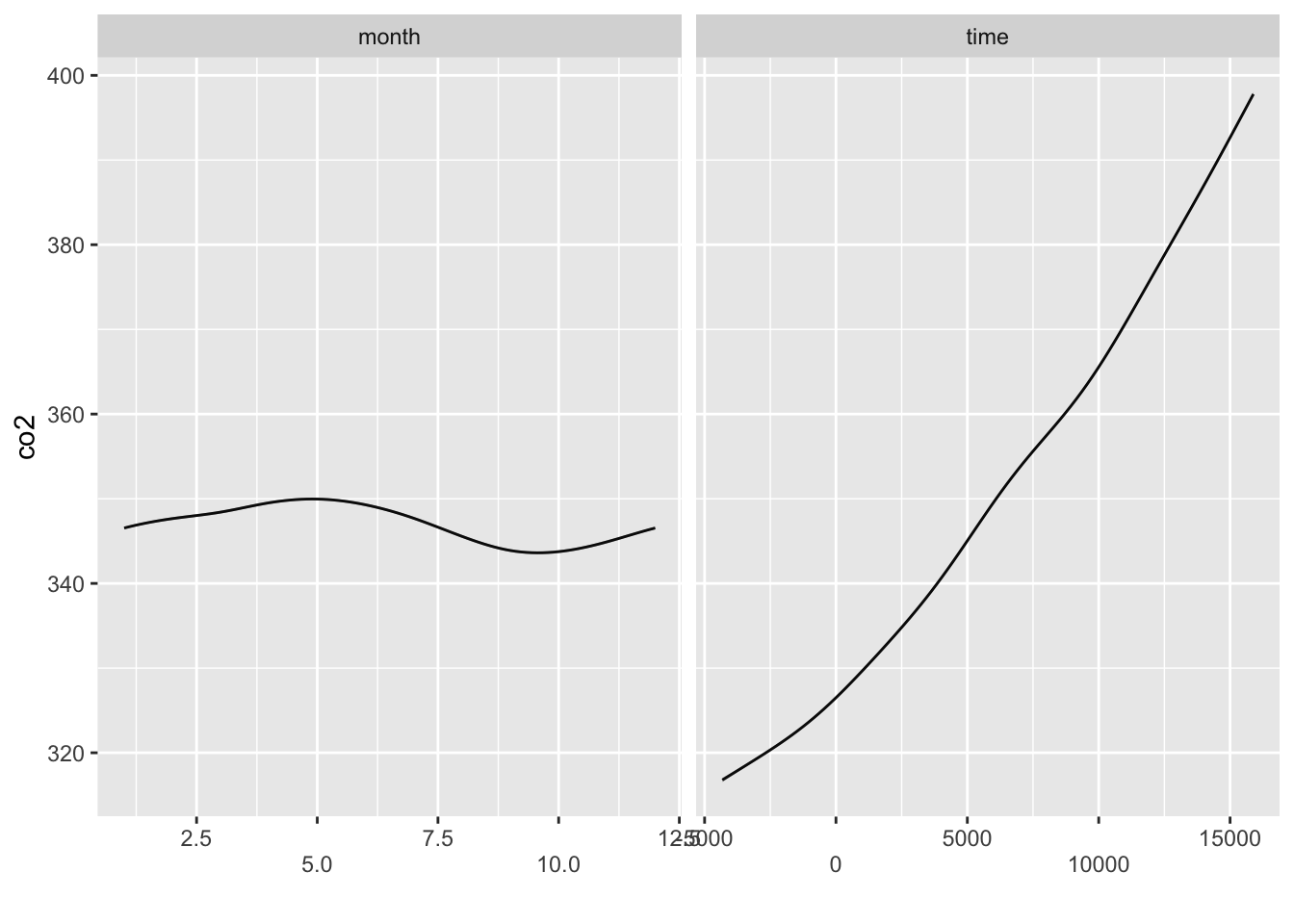모형 적합선을 보면 먼저 month의 변동에 따라 1월부터 상승하여 5월에 최고치를 보이다가 낮아지기 시작하여 9월에 최저치를 보인후 다시 상승한다는 것을 알 수 있다.
Family: gaussian
Link function: identity
Formula:
co2 ~ s(month, bs = "cc", k = 12) + s(time)
Parametric coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 349.0295 0.0198 17624 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Approximate significance of smooth terms:
edf Ref.df F p-value
s(month) 9.367 10.000 1072 <2e-16 ***
s(time) 8.847 8.993 161015 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
R-sq.(adj) = 1 Deviance explained = 100%
-REML = 542.85 Scale est. = 0.26082 n = 665모형의 요약에서 보면 모형의 설명력이 1로(\(_{adj}R^2=1\)) 잔차의 100%를 설명해주는 것으로 나타났다. 다음으로 모형의 진단을 해본다.
Method: REML Optimizer: outer newton
full convergence after 5 iterations.
Gradient range [-8.327572e-08,4.303605e-09]
(score 542.8542 & scale 0.2608165).
Hessian positive definite, eigenvalue range [3.77638,331.6141].
Model rank = 20 / 20
Basis dimension (k) checking results. Low p-value (k-index<1) may
indicate that k is too low, especially if edf is close to k'.
k' edf k-index p-value
s(month) 10.00 9.37 0.65 <2e-16 ***
s(time) 9.00 8.85 0.41 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1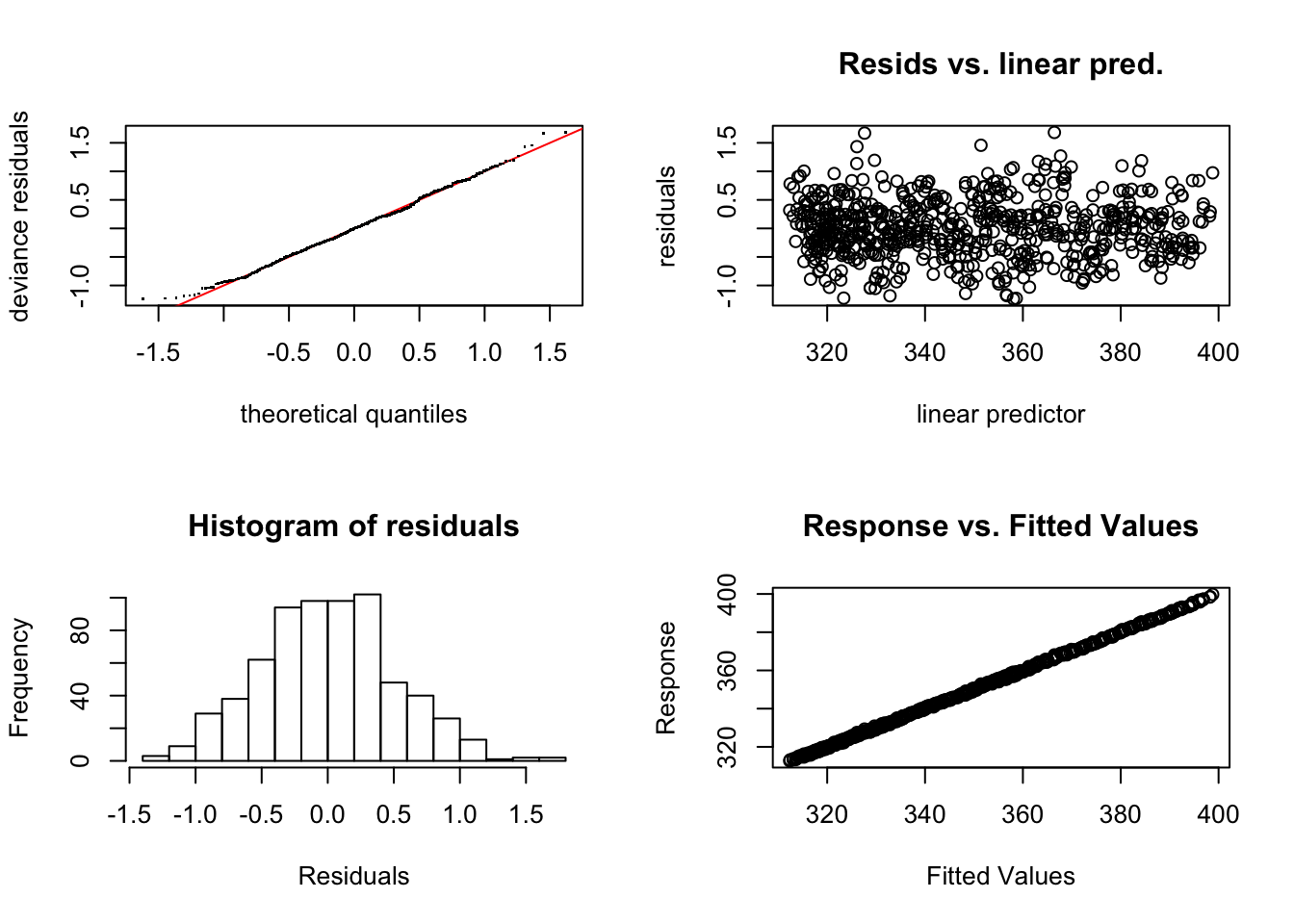
모형진단을 보면 m1 모형에서 보였던 잔차의 주기적인 변동이 모두 사라진 것을 볼 수 있다. ggGam 패키지에 포함되어 있는 gam.Dx()함수를 쓰면 ggplot2을 이용한 진단 그래프르르 볼 수 있다.
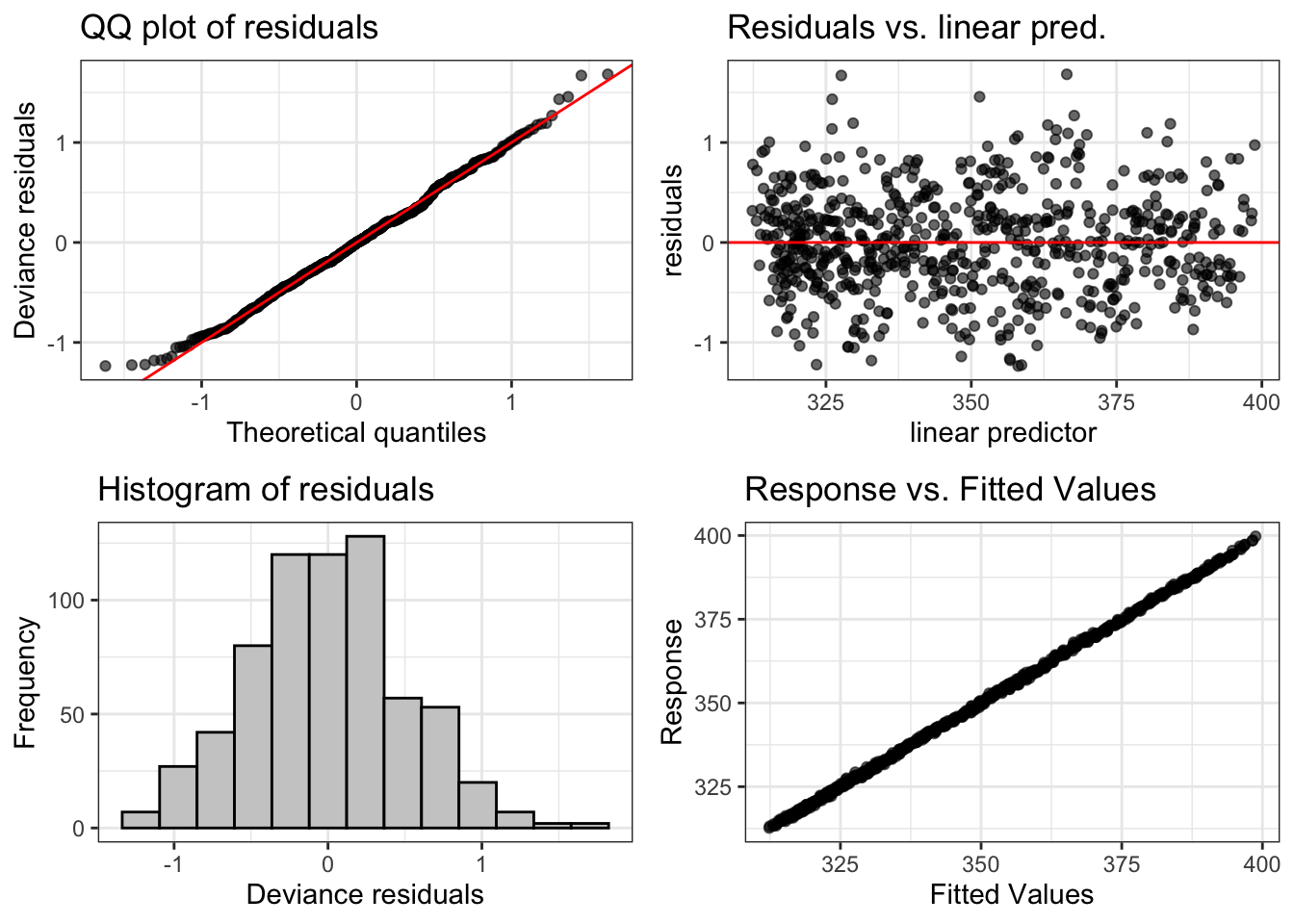
실제 데이터와 모형을 통해 얻어진 co2의 기댓값을 그림으로 그려보면 다음과 같다.
co2$yhat=predict(m2,newdata=co2)
ggplot(co2,aes(x=time,y=co2))+
geom_point()+
geom_line(aes(y=yhat),col="red")