Chapter 6 생존자료분석
이번 장에서 사용하는 R 패키지는 다음과 같다.
6.1 예제데이터
이번 장에서는 일반화가법모형을 이용한 생존데이터분석의 예를 들어보고자 한다. 이번 장의 예제는 Simon N. Wood의 Generalized Additive Models. An Introduction with R(2nd Edition) CRC Press(2017)에 수록되어 있는 예제이다. 예제 데이터는 survival 패키지에 포함되어 있는 pbc 데이터를 사용한다. pbc 데이터는 1974년부터 1984년까지 미국의 Mayo Clinic에서 수행된 원발성 답즙성 간경변증(primary biliary cirrhosis, 이하 PBC) 환자를 대상으로 위약과 D-penicillamin의 효과를 비교한 임상연구 데이터로 모두 418명의 환자의 기저상태의 데이터이다. 환자 중 25명은 간이식 수술을 받아 연구에서 제외되었는데 이들은 중도절단(ceonsored)으로 처리되었다. 환자의 상태(status)는 censored의 경우 0, 이식받은 경우 1, 사망한 경우 2로 기록되어 있다. 데이터를 살펴보면 환자의 일련번호(id), 나이(age), 성별(sex), 치료(trt, treatment)는 D-penicillamin군은 1, 위약은 2로 기록되어 있고 질병의 병기(stage)는 1-4로 구분되어 있는데 4기로 갈수록 심한 상태이다. 다른 변수들은 간기능과 관련된 혈액검사 결과로 albumin, alkaline phosphatase(alk.phos), 빌리루빈(bili), ast, 혈소판(platelet), 프로트롬빈 타임(protime) 등이 기록되어 있다. 데이터에 대한 자세한 설명은 도움말을 참조한다(?pbc).먼저 데이터를 불러들여 구조를 살펴보면 다음과 같다.
'data.frame': 418 obs. of 20 variables:
$ id : int 1 2 3 4 5 6 7 8 9 10 ...
$ time : int 400 4500 1012 1925 1504 2503 1832 2466 2400 51 ...
$ status : int 2 0 2 2 1 2 0 2 2 2 ...
$ trt : int 1 1 1 1 2 2 2 2 1 2 ...
$ age : num 58.8 56.4 70.1 54.7 38.1 ...
$ sex : Factor w/ 2 levels "m","f": 2 2 1 2 2 2 2 2 2 2 ...
$ ascites : int 1 0 0 0 0 0 0 0 0 1 ...
$ hepato : int 1 1 0 1 1 1 1 0 0 0 ...
$ spiders : int 1 1 0 1 1 0 0 0 1 1 ...
$ edema : num 1 0 0.5 0.5 0 0 0 0 0 1 ...
$ bili : num 14.5 1.1 1.4 1.8 3.4 0.8 1 0.3 3.2 12.6 ...
$ chol : int 261 302 176 244 279 248 322 280 562 200 ...
$ albumin : num 2.6 4.14 3.48 2.54 3.53 3.98 4.09 4 3.08 2.74 ...
$ copper : int 156 54 210 64 143 50 52 52 79 140 ...
$ alk.phos: num 1718 7395 516 6122 671 ...
$ ast : num 137.9 113.5 96.1 60.6 113.2 ...
$ trig : int 172 88 55 92 72 63 213 189 88 143 ...
$ platelet: int 190 221 151 183 136 NA 204 373 251 302 ...
$ protime : num 12.2 10.6 12 10.3 10.9 11 9.7 11 11 11.5 ...
$ stage : int 4 3 4 4 3 3 3 3 2 4 ...이 중 환자의 상태(status)는 censored의 경우 0, 이식받은 경우 1, 사망한 경우 2로 기록되어 있으므로 사망한 경우는 1, 그 외에는 0으로 바꾸어 status1 변수에 기록하고 stage는 factor로 바꾸어 저장한다.
6.2 GAM을 이용한 초기 모형 적합
처음 모형에는 모든 변수를 투입한다. 변수들 중 trt, sex, stage는 번주형변수로 선형항으로 투입하고 다른 변수들은 s()함수를 이용하여 평활항으로 만들어 투입한다. protime과 ast는 분포가 비대칭으로 제곱근으로 변환하여 투입하였다. 생존분석을 다루므로 family에는 cox.ph를 넣어준다.
b0 <- gam(time ~ trt + sex +stage+s(sqrt(protime))+s(platelet)+
s(age)+s(bili)+s(albumin)+s(sqrt(ast))+s(alk.phos),
weights=status1, family=cox.ph, data=pbc, method="REML")
anova(b0)
Family: Cox PH
Link function: identity
Formula:
time ~ trt + sex + stage + s(sqrt(protime)) + s(platelet) + s(age) +
s(bili) + s(albumin) + s(sqrt(ast)) + s(alk.phos)
Parametric Terms:
df Chi.sq p-value
trt 1 0.005 0.9433
sex 1 3.686 0.0549
stage 3 5.256 0.1540
Approximate significance of smooth terms:
edf Ref.df Chi.sq p-value
s(sqrt(protime)) 1.000 1.000 12.901 0.000329
s(platelet) 1.000 1.001 2.594 0.107311
s(age) 6.115 7.227 30.217 0.000108
s(bili) 3.605 4.430 45.270 8.97e-09
s(albumin) 1.000 1.000 22.186 2.48e-06
s(sqrt(ast)) 2.197 2.798 4.951 0.167761
s(alk.phos) 1.592 1.957 0.837 0.670138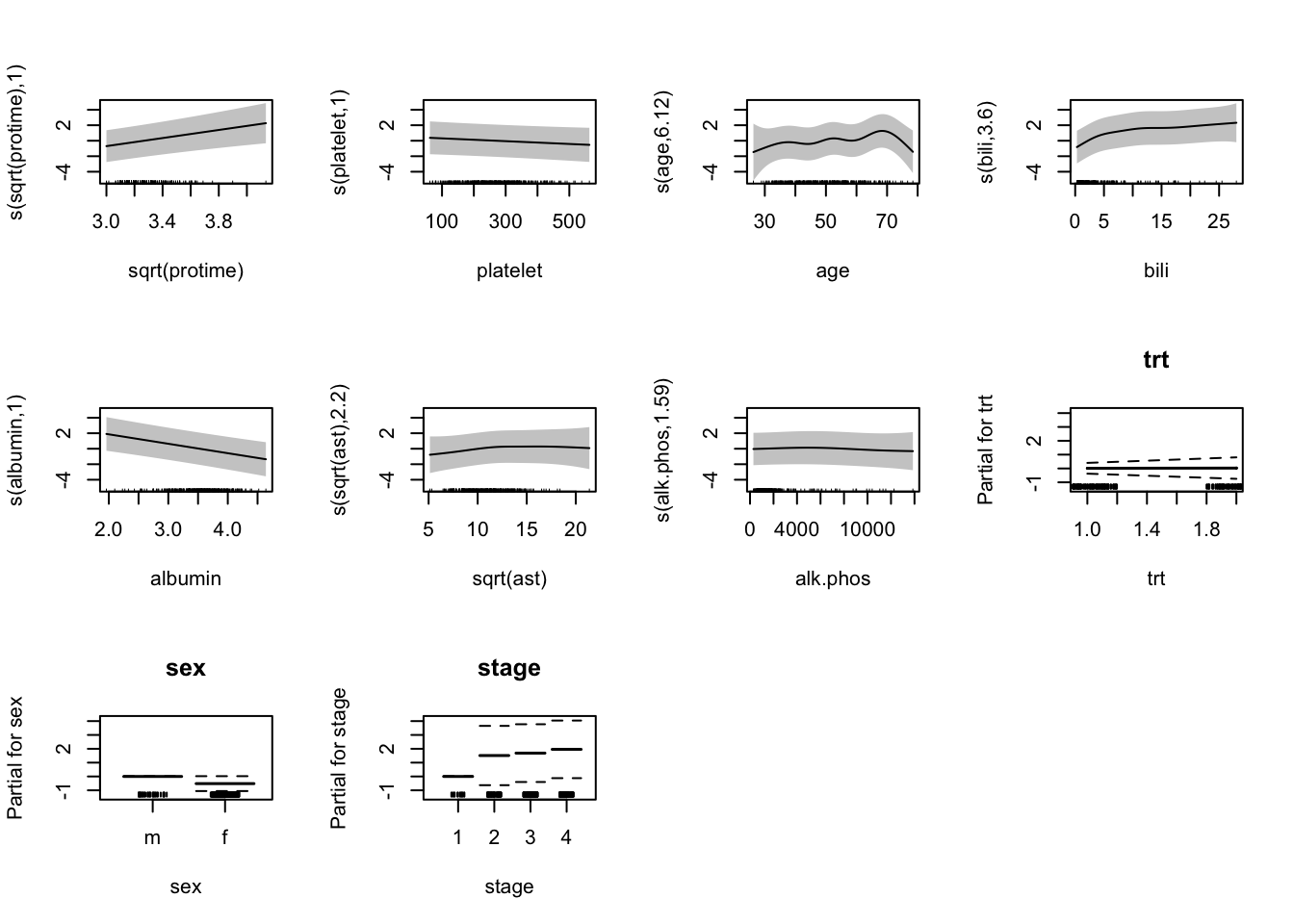
분석 결과에서 alk.phos 및 ast 는 거의 flat하며 p 값이 높아 제외하였다. stage 또한 p값이 높아 제외하였다.
6.3 최종모형
최종적으로 다음 모형을 선택하였다.
6.4 모형진단
이 모형을 다음 R코드를 통해 진단할 수 있다.
Method: REML Optimizer: outer newton
full convergence after 10 iterations.
Gradient range [-5.364015e-05,0.0001458944]
(score 547.2567 & scale 1).
Hessian positive definite, eigenvalue range [3.999032e-05,1.266911].
Model rank = 47 / 47
Basis dimension (k) checking results. Low p-value (k-index<1) may
indicate that k is too low, especially if edf is close to k'.
k' edf k-index p-value
s(sqrt(protime)) 9.00 1.00 1.04 0.81
s(platelet) 9.00 1.00 1.10 0.99
s(age) 9.00 6.04 0.99 0.43
s(bili) 9.00 4.26 0.95 0.14
s(albumin) 9.00 1.00 1.06 0.83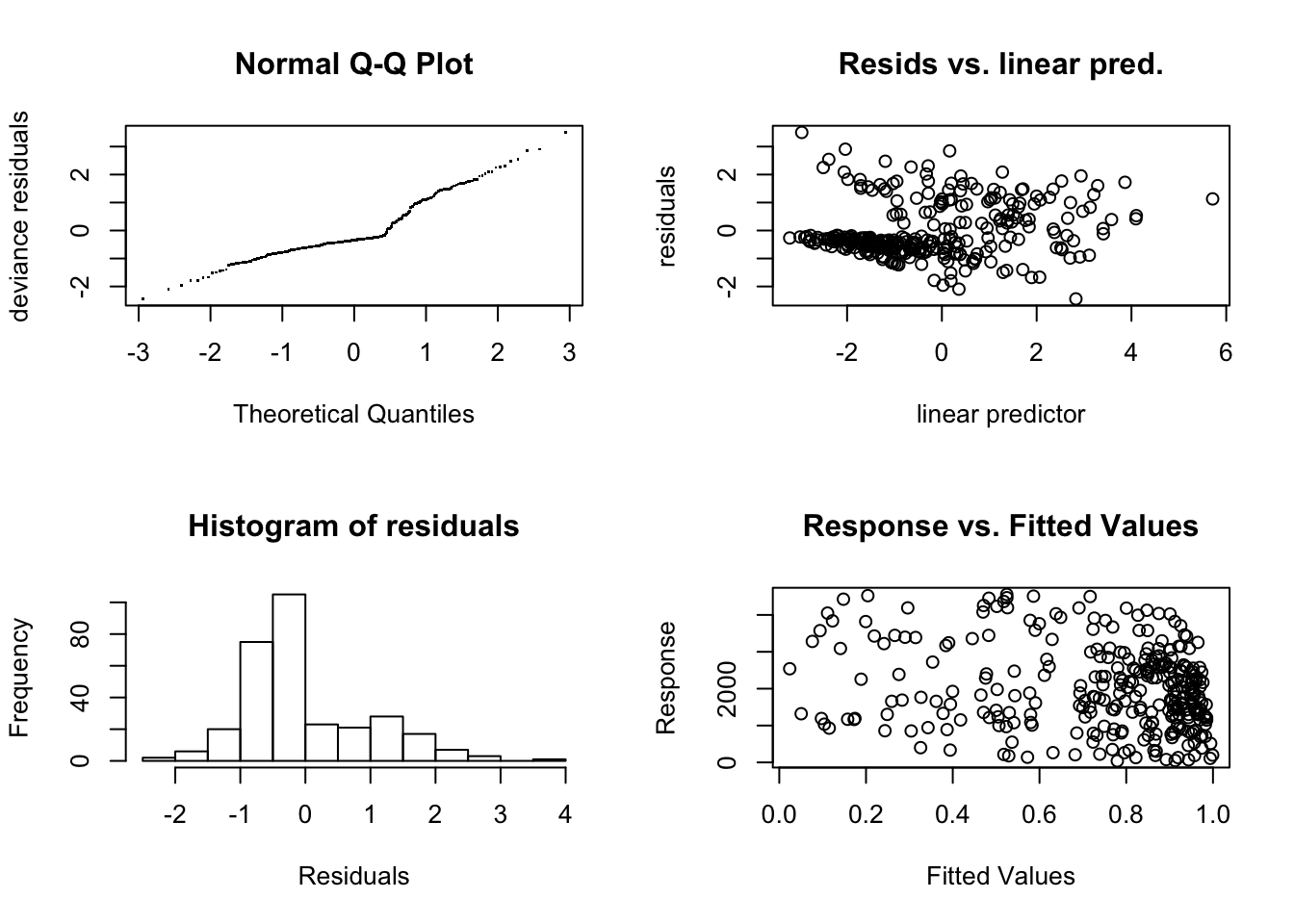
모형진단에서 모형은 완전수렴한다(full convergence). protime, platelet, albumin의 유효자유도는 1로 선형관계인 것을 알 수 있다. 이 중 Residual-linear predictor 을 다시 그려보면 다음과 같다.
df=data.frame(x=b$linear.predictors,y=residuals(b))
ggplot(df,aes(x=x,y=y))+geom_point()+
labs(x="linear predictor",y="residuals")+theme_bw()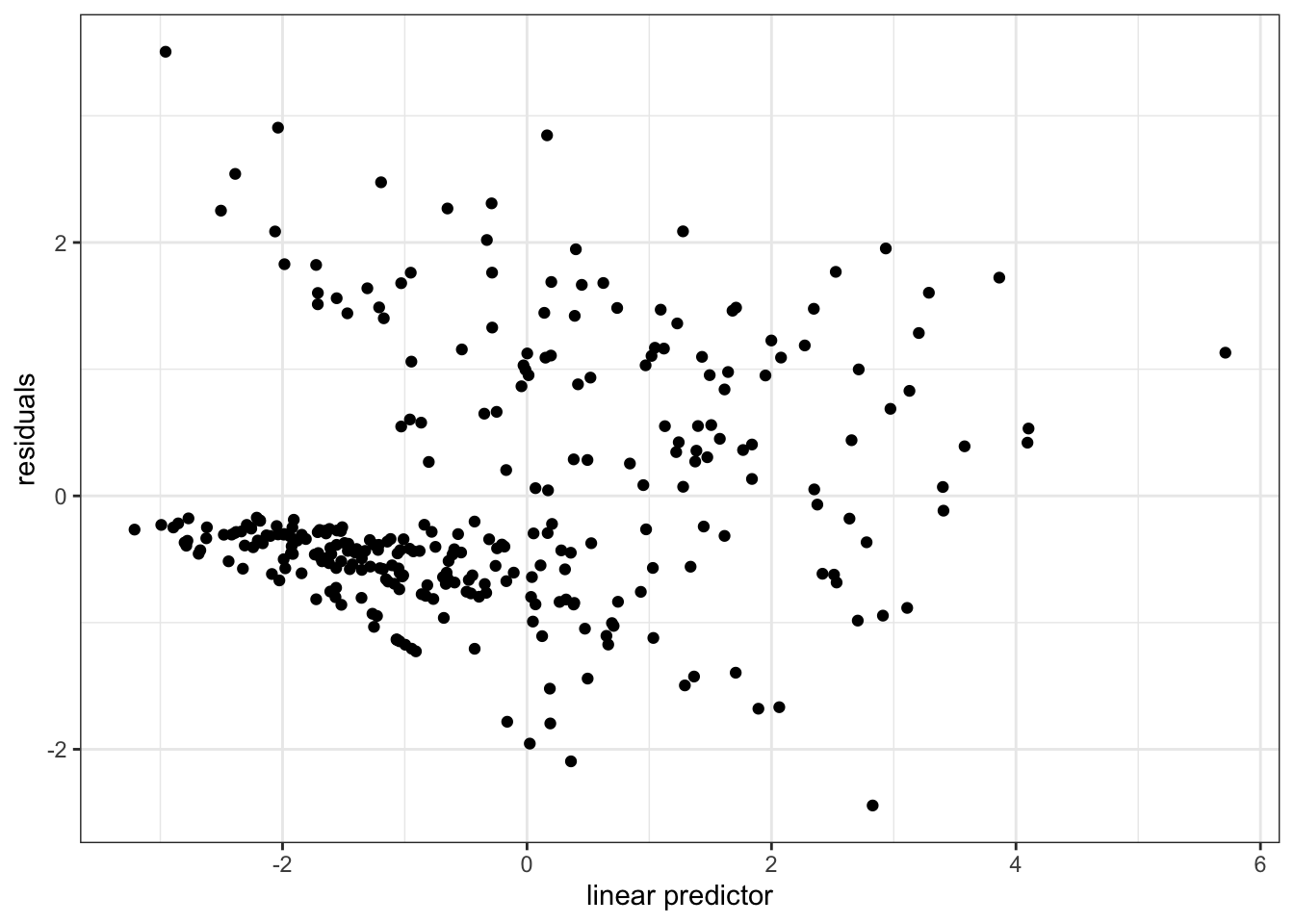
위의 그림에서 왼쪽 아래에 보이는 쐐기모양의 블록(wedge-shaped block)은 중도 절단된 사례들 때문에 나타나는 것으로 전형적인 양상이다. 왼쪽 위에 보이는 높은 점들은 risk score가 낮은데도 불구하고 사망한 환자들로 이상점으로 볼 수 있다. 그 외에는 별 문제가 없어 보인다.
6.5 모형의 결과
모형 결과를 출력해보면 다음과 같다.
Family: Cox PH
Link function: identity
Formula:
time ~ trt + sex + s(sqrt(protime)) + s(platelet) + s(age) +
s(bili) + s(albumin)
Parametric coefficients:
Estimate Std. Error z value Pr(>|z|)
trt 0.06713 0.19407 0.346 0.7294
sexf -0.49516 0.26700 -1.855 0.0637 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Approximate significance of smooth terms:
edf Ref.df Chi.sq p-value
s(sqrt(protime)) 1.000 1.001 13.337 0.000261 ***
s(platelet) 1.001 1.002 5.789 0.016141 *
s(age) 6.043 7.172 29.417 0.000145 ***
s(bili) 4.264 5.223 89.545 < 2e-16 ***
s(albumin) 1.000 1.000 31.086 2.47e-08 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Deviance explained = 30.4%
-REML = 547.26 Scale est. = 1 n = 308이 결과를 그림으로 나타내면 다음과 같다.
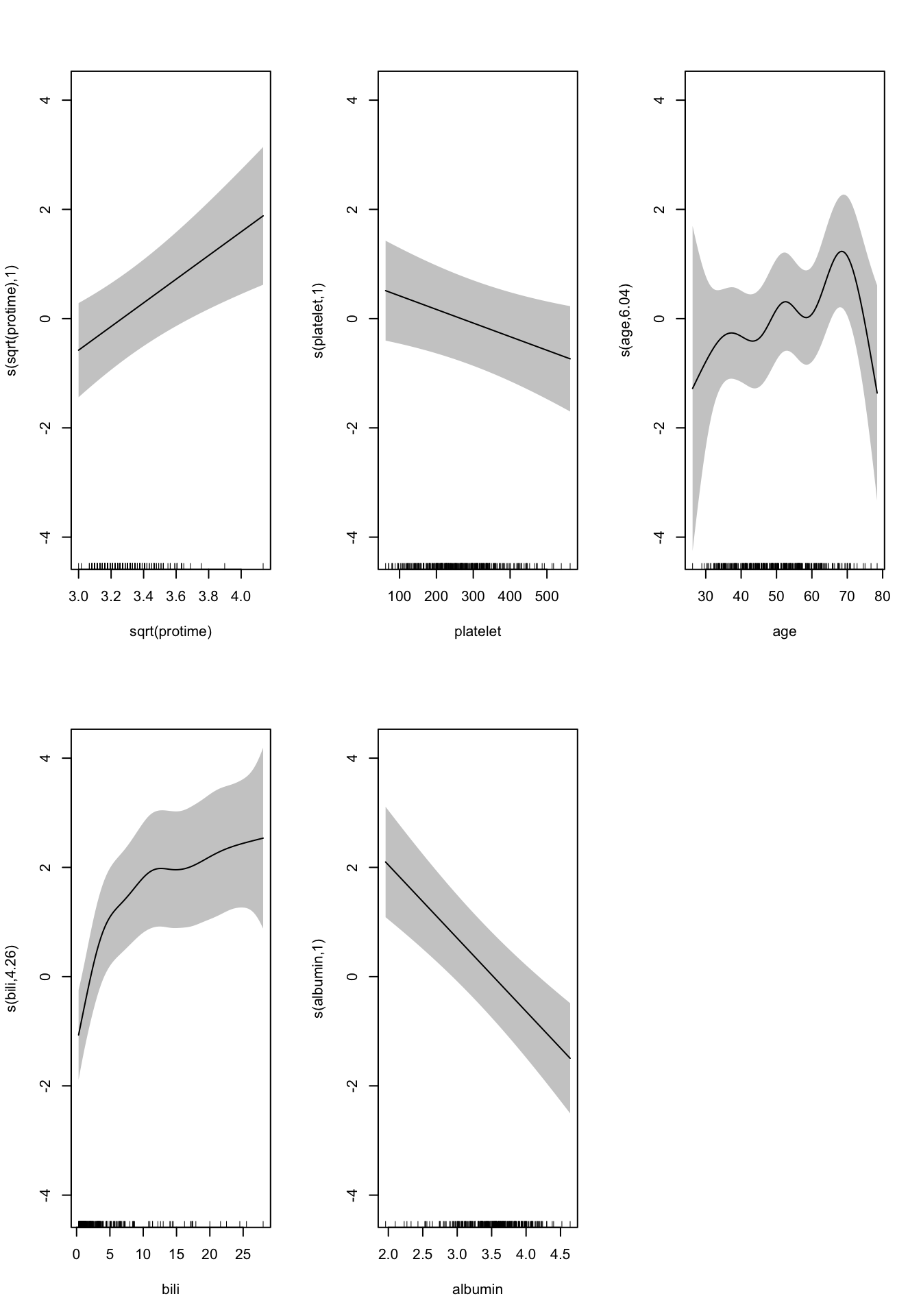
세번째 그림인 나이를 보면 약 70세까지는 나이에 따라 위험이 증가하는 것을 보여준다. 그 이외의 결과는 예상과 비슷하다. 프로트로빈 시간이 길어질수록 위험이 증가하고 혈소판이 낮을수록, 알부민이 낮을수록 위험이 증가한다. 혈중빌리루빈의 경우 약 10mg/dL까지는 위험이 급격히 증가하고 이후에는 서서히 증가하는 양상을 보이는데 이는 간의 기능이 떨어져 빌리루빈을 대사하지 못하기 때문으로 생각된다.
6.6 생존의 예측
predict.gam() 함수를 사용할 경우 만들어진 모형을 이용하여 어떤 변수의 조합이라도 생존의 예측이 가능하다. 이때에는 predict.gam 함수의 type인수를 “response”로 지정해주어야 한다. 다음의 drawSurv() 함수를 이용하면 어떠한 환자의 survival plot 도 그려줄 수 있다.
drawSurv=function(model,data,np=100,timevar="time",until=NULL,id=list()){
if(is.null(until)) until=max(model$model[[timevar]],na.rm=TRUE)
if(length(id)==0) id=list(id=1:nrow(data))
for( i in 1:nrow(data)){
newd <- data.frame(matrix(0,np,0))
for (n in names(data)) newd[[n]] <- rep(data[[n]][i],np)
newd$time <- seq(0,until,length=np)
fv <- predict(model,newdata=newd,type="response",se=TRUE)
newd$fit=fv$fit
# newd$ymax=fv$fit+se*fv$se.fit
# newd$ymin=fv$fit-se*fv$se.fit
se <- fv$se.fit/fv$fit
newd$ymax=exp(log(fv$fit)+se)
newd$ymin=exp(log(fv$fit)-se)
idname=names(id)[1]
newd[[idname]]=id[[1]][i]
if(i==1){
final=newd
} else{
final=rbind(final,newd)
}
}
final[[idname]]=factor(final[[idname]])
final
ggplot(data=final,aes_string(x="time",y="fit",fill=idname,group=idname))+
geom_line(aes_string(color=idname))+
geom_ribbon(aes_string(ymax="ymax",ymin="ymin"),alpha=0.3)+
ylim(c(0,1)) + ylab("cumulative survival")+xlab("days")+
theme_bw()+
theme(legend.position = "top")
}예를 들어 10번, 66번, 25번 환자의 survival plot을 그리려면 다음과 같이 할 수 있다.
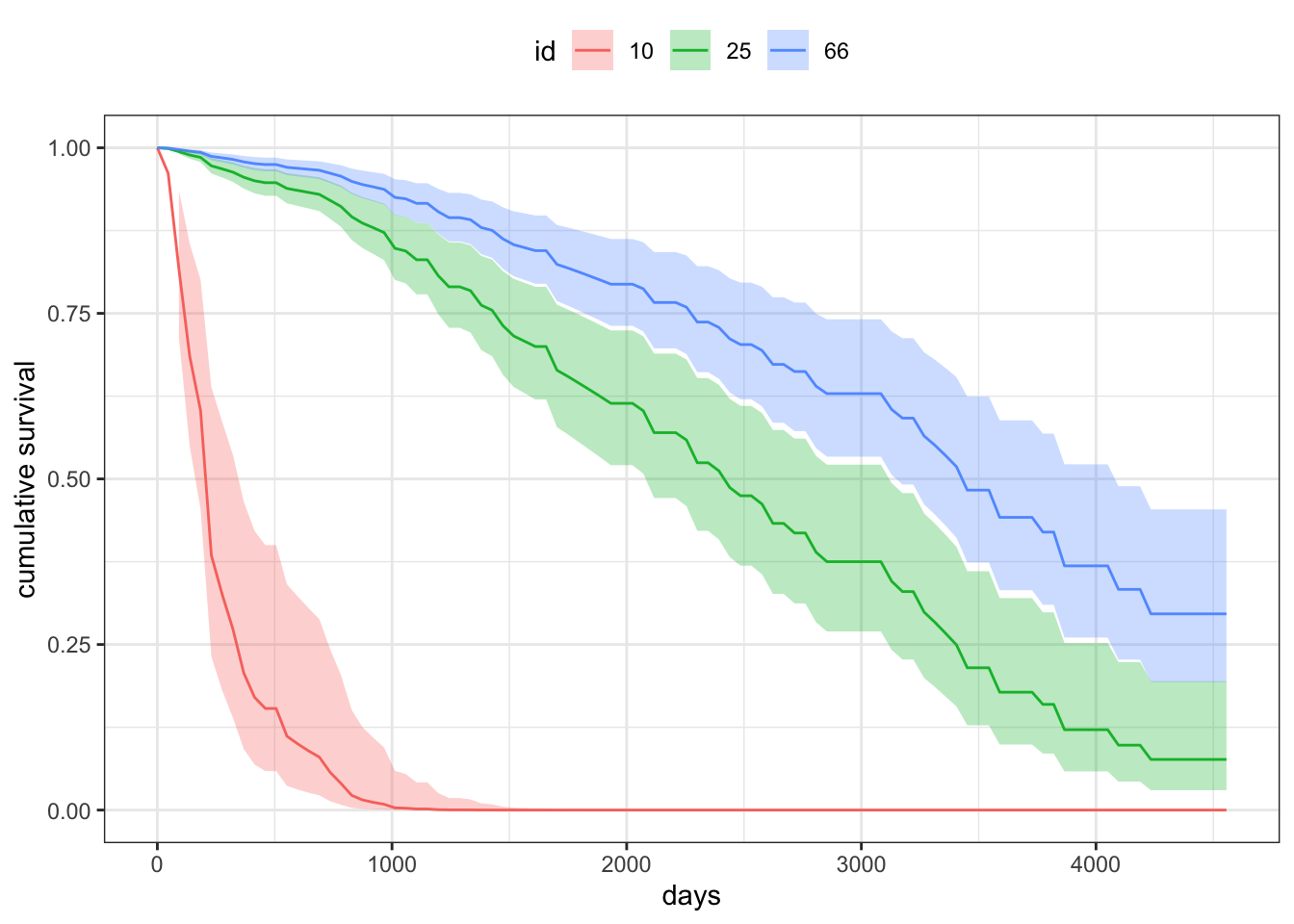
그럼 이 데이터의 평균 환자의 그래프는 어떻게 그릴까? 여기서 평균 환자는 데이터의 변수 중 연속형변수는 평균이고 범주형 변수는 첫번째 범주인 환자를 말한다. 다음과 같은 함수를 만들어 쓸 수 있다.
averageData=function(data){
newd=list()
for(i in 1:ncol(data)){
if(is.numeric(data[[i]])) {
newd[[i]]=mean(data[[i]],na.rm=TRUE)
} else if(is.factor(data[[i]])){
newd[[i]]=levels(data[[i]])[1]
} else{
newd[[i]]=sort(unique(data[[i]]))[1]
}
}
names(newd)=names(data)
df=as.data.frame(newd)
df
}
drawSurv(b,data=averageData(pbc))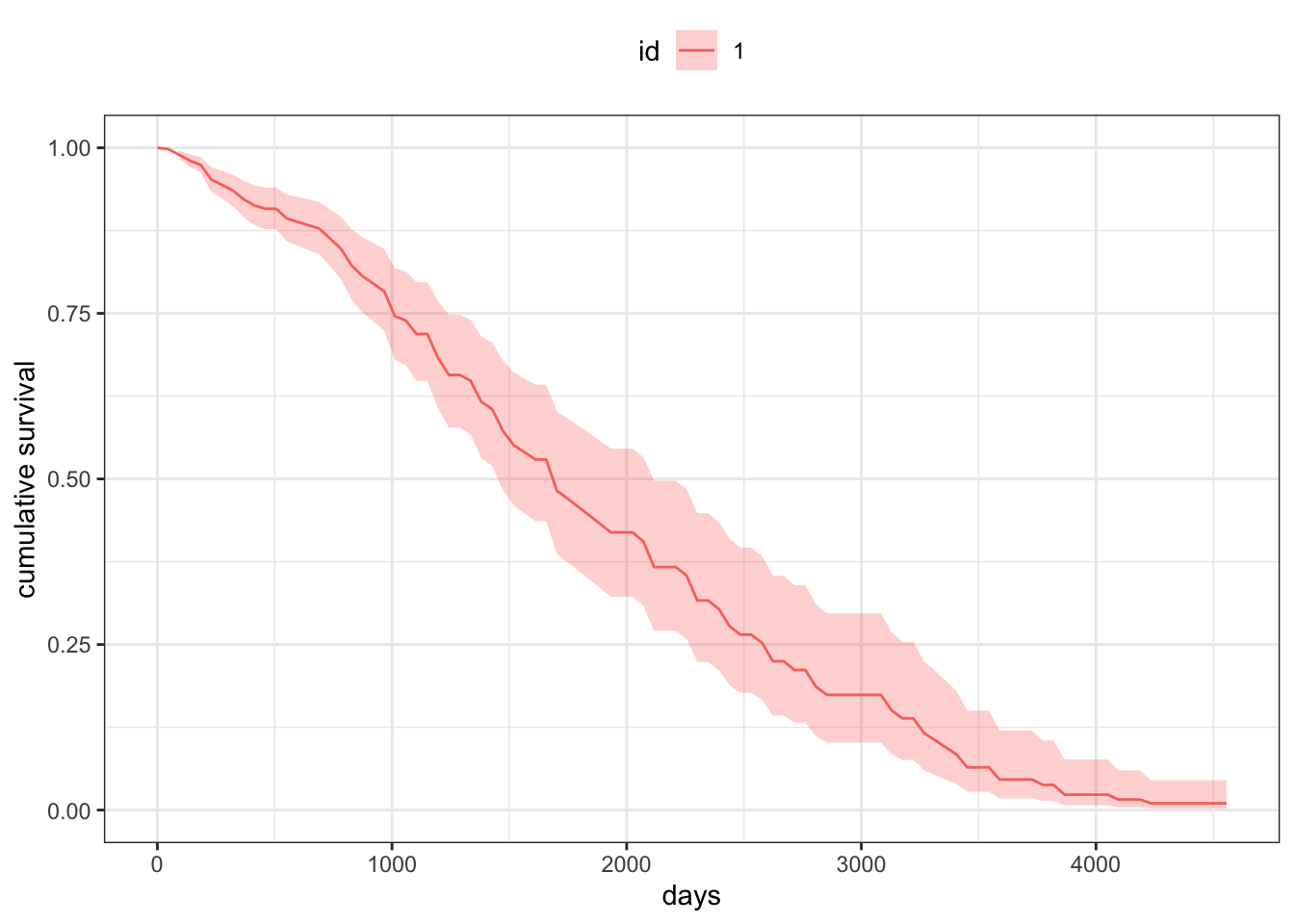
다른 조건은 모두 평균이고 성별만 다른 환자의 자료를 만들고 싶으면 어떻게 할까? 방금 만들었던 averageData 함수를 조금 개선시켜 보자.
averageData=function(data,newValue=list()){
newd=list()
for(i in 1:ncol(data)){
if(is.numeric(data[[i]])) {
newd[[i]]=mean(data[[i]],na.rm=TRUE)
} else if(is.factor(data[[i]])){
newd[[i]]=levels(data[[i]])[1]
} else{
newd[[i]]=sort(unique(data[[i]]))[1]
}
}
names(newd)=names(data)
df=as.data.frame(newd)
df
if(length(newValue)>0){
no=length(newValue[[1]])
for(i in 1:no){
if(i==1) {
final=df
} else{
final=rbind(final,df)
}
}
final[[names(newValue)[1]]]=newValue[[1]]
df=final
}
df
}위의 함수를 사용하는 방법은 다음과 같다. 예를 들어 성별이 각각 “m”,“f”인 환자의 자료를 만들려면 다음과 같이 한다.
id time status trt age sex ascites hepato spiders
1 209.5 1917.782 0.8301435 1.49359 50.74155 m 0.07692308 0.5128205 0.2884615
2 209.5 1917.782 0.8301435 1.49359 50.74155 f 0.07692308 0.5128205 0.2884615
edema bili chol albumin copper alk.phos ast trig
1 0.1004785 3.220813 369.5106 3.49744 97.64839 1982.656 122.5563 124.7021
2 0.1004785 3.220813 369.5106 3.49744 97.64839 1982.656 122.5563 124.7021
platelet protime stage status1
1 257.0246 10.73173 1 0.3851675
2 257.0246 10.73173 1 0.3851675이제 이 데이터로 plot을 그릴 수 있다.
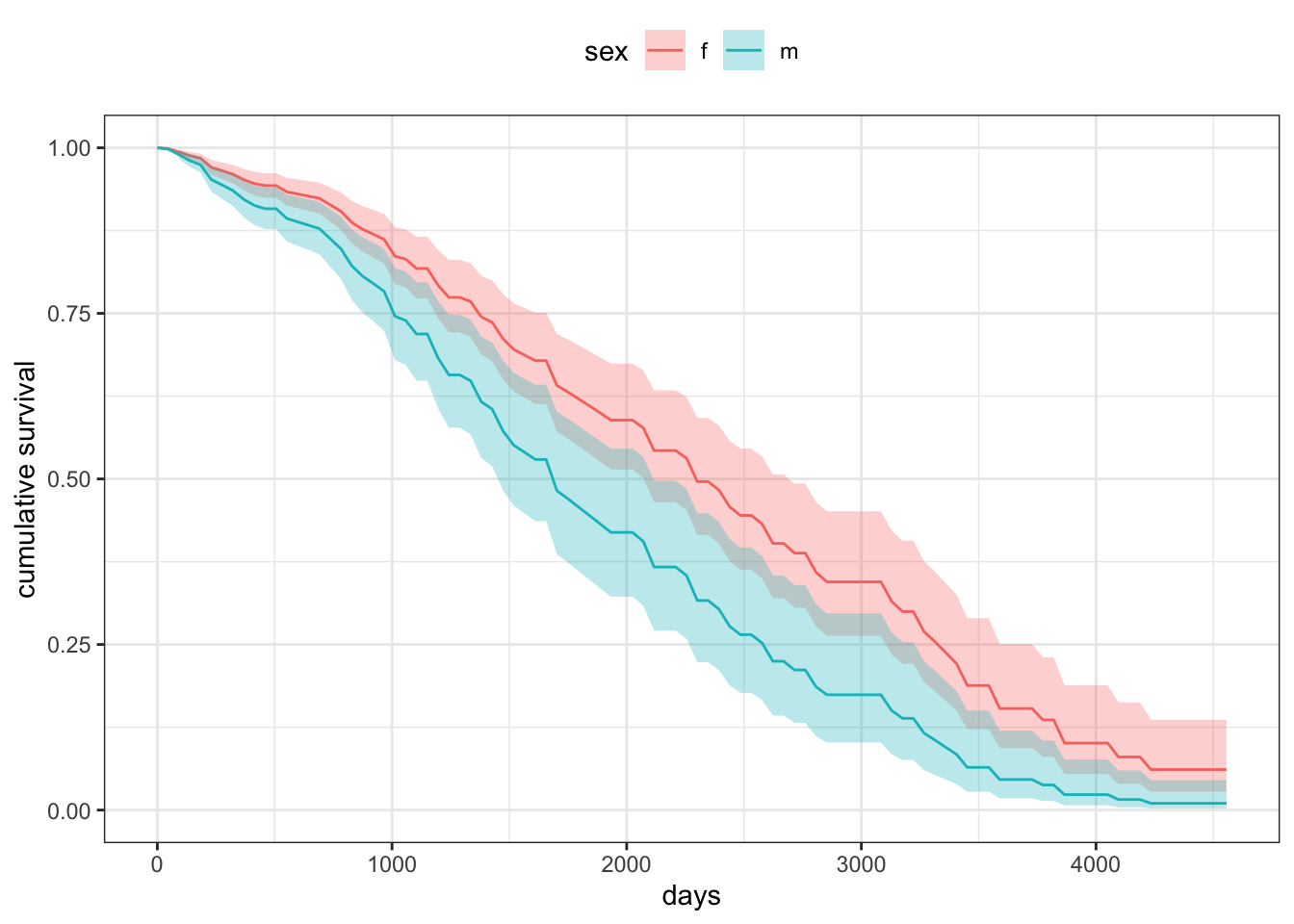다른 예로 혈중 bilirubun 농도가 각각 1 mg/dL, 10 mg/dL인 환자의 plot 을 그리려면 다음과 같이 할 수 있다.
