Chapter 2 일반화가법모형 시작하기
2.1 첫번째 예제 : 외상성뇌손상
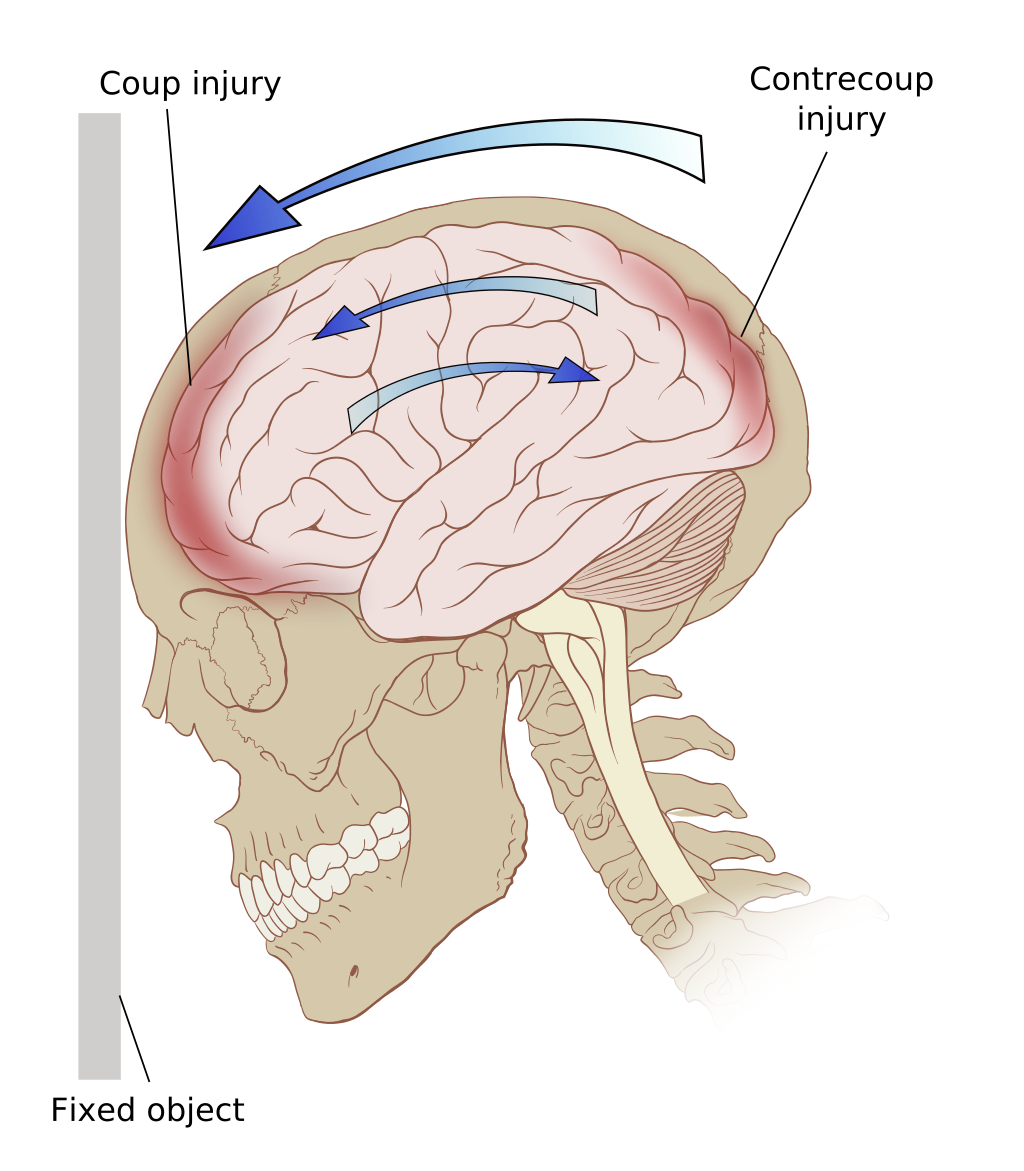
일반화가법모형(Generalized Addtive Model,GAM)에 관한 이론적 설명에 앞서 먼저 간단한 자료를 분석해 보면서 일반회귀모형과의 차이를 보여주고자 한다. 교통사고 등에서 볼수 있는 외상성 뇌손상의 경우 충격을 받은 부위(Coup injury) 뿐 아니라 반대부위(Contrecoup injury)에 더 큰 손상을 입는 경우를 볼 수 있는데 이는 뇌의 가속 및 감속과 관련이 있다.
2.1.1 사용하는 데이터
MASS 패키지에 포함되어 있는 mcycle 데이터는 모터싸이클 사고 모의실험을 통해 머리의 가속과 감속을 측정한 자료이다.
'data.frame': 133 obs. of 2 variables:
$ times: num 2.4 2.6 3.2 3.6 4 6.2 6.6 6.8 7.8 8.2 ...
$ accel: num 0 -1.3 -2.7 0 -2.7 -2.7 -2.7 -1.3 -2.7 -2.7 ...자료의 구조에서 보는 바와 같이 times는 충돌 후 시간(millisecond)이고 accel은 표준중력단위(1g= 9.806 \(m/sec^2\))로 측정된 가속도(g)이다. 시간과 가속도의 관계를 그림으로 나타내 보면 다음과 같다.
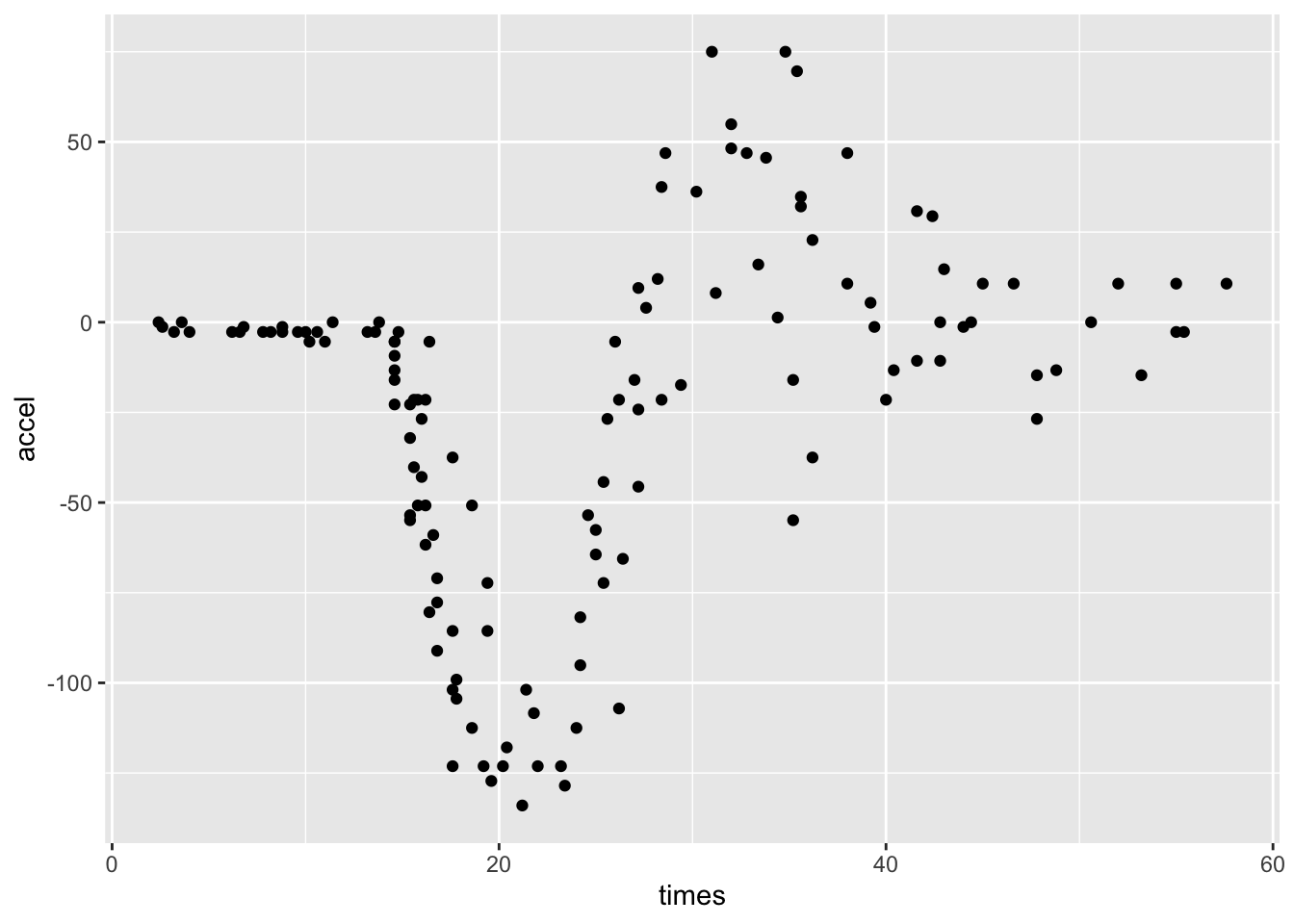 이 자료는 시간 간격이 일정하지 않으면 중복해서 측정된 자료도 있지만 대체적인 관계는 비선형관계인 것을 알 수 있다.
이 자료는 시간 간격이 일정하지 않으면 중복해서 측정된 자료도 있지만 대체적인 관계는 비선형관계인 것을 알 수 있다.
2.1.2 선형회귀모형
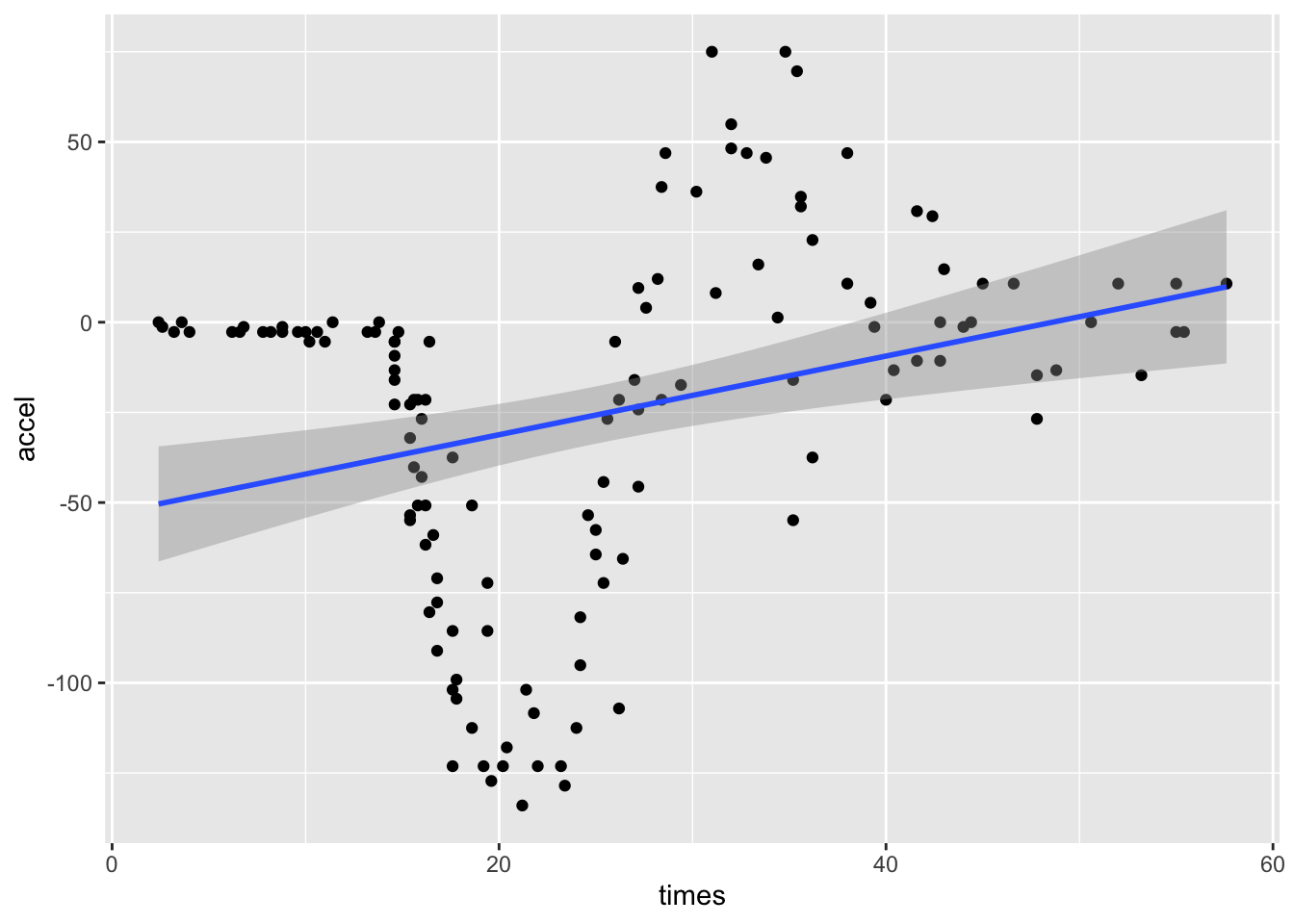
이자료를 시간을 설명변수로 가속도를 반응변수로 하는 선형회귀모형에 적합시키면 다음과 같다.
Call:
lm(formula = accel ~ times, data = mcycle)
Residuals:
Min 1Q Median 3Q Max
-104.114 -25.926 4.582 36.163 94.197
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -53.008 8.713 -6.084 1.2e-08 ***
times 1.091 0.307 3.552 0.000532 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 46.33 on 131 degrees of freedom
Multiple R-squared: 0.08785, Adjusted R-squared: 0.08089
F-statistic: 12.62 on 1 and 131 DF, p-value: 0.0005318이 회귀모형의 설명력은 매우 낮으며(\(R^2 = 0.087\)) 중요한 관계를 놓치고 있다. 이 회귀모형의 진단을 위해 다음 그림을 살펴보자.
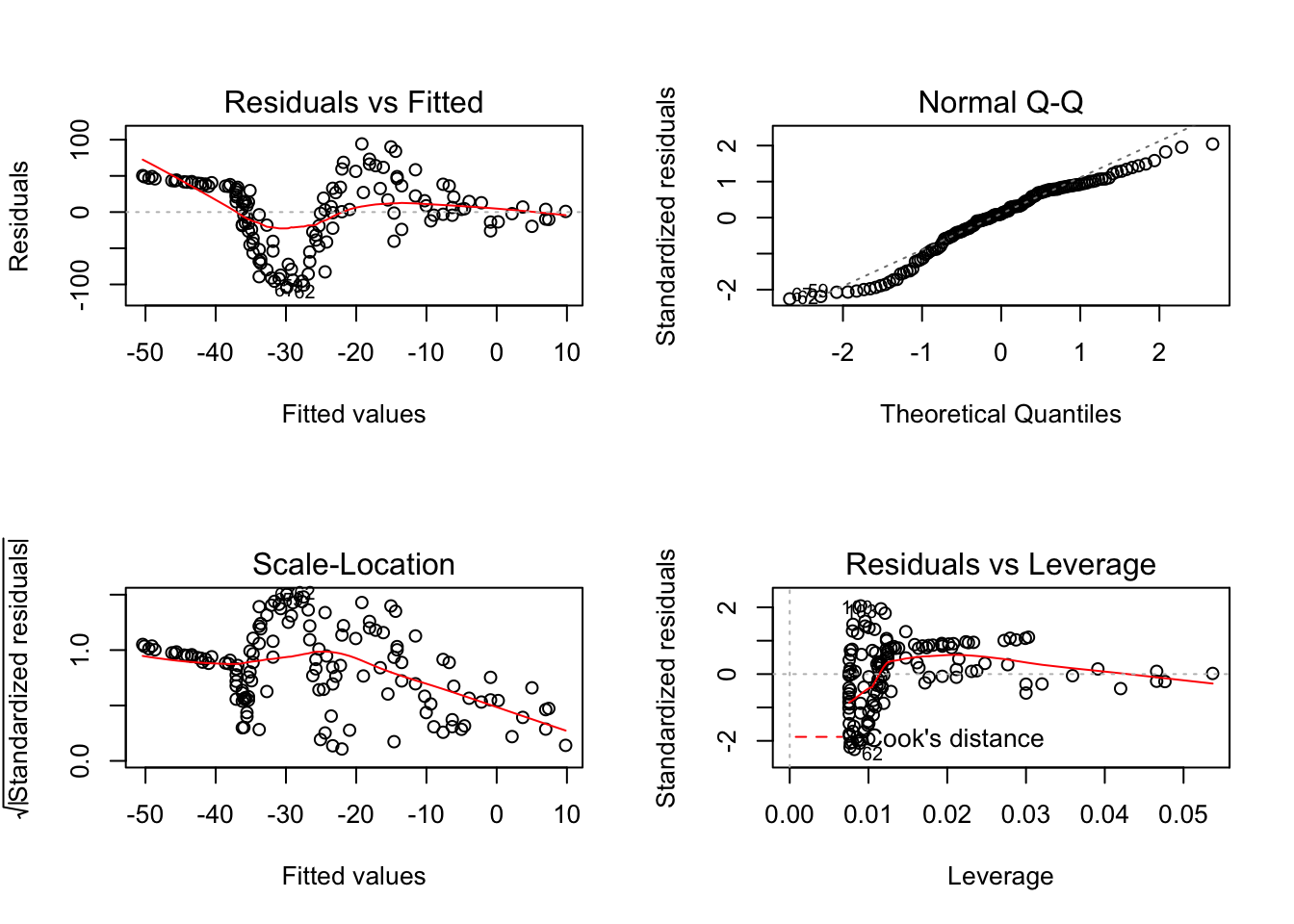
첫번째 잔차를 보면 시간의 흐름에 따라 무작위로 분포되어 있지 않은 것을 알 수 있다.
2.1.3 비선형회귀모형
다음으로 비선형 모형인 일반화가법 모형에 적합시켜보자. GAM은 gam패키지 또는 mgcv패키지를 사용하여 적합시킬 수 있는데 몇가지 장점 때문에 mgcv패키지를 사용한다. 사용하는 방법은 먼저 패키지를 불러오고 선회회귀모형의 lm 대신 gam을 사용하며 설명변수인 times 를 직선이 아닌 곡선(smooth)을 사용하라는 의미로 s(times)를 사용하면 된다.
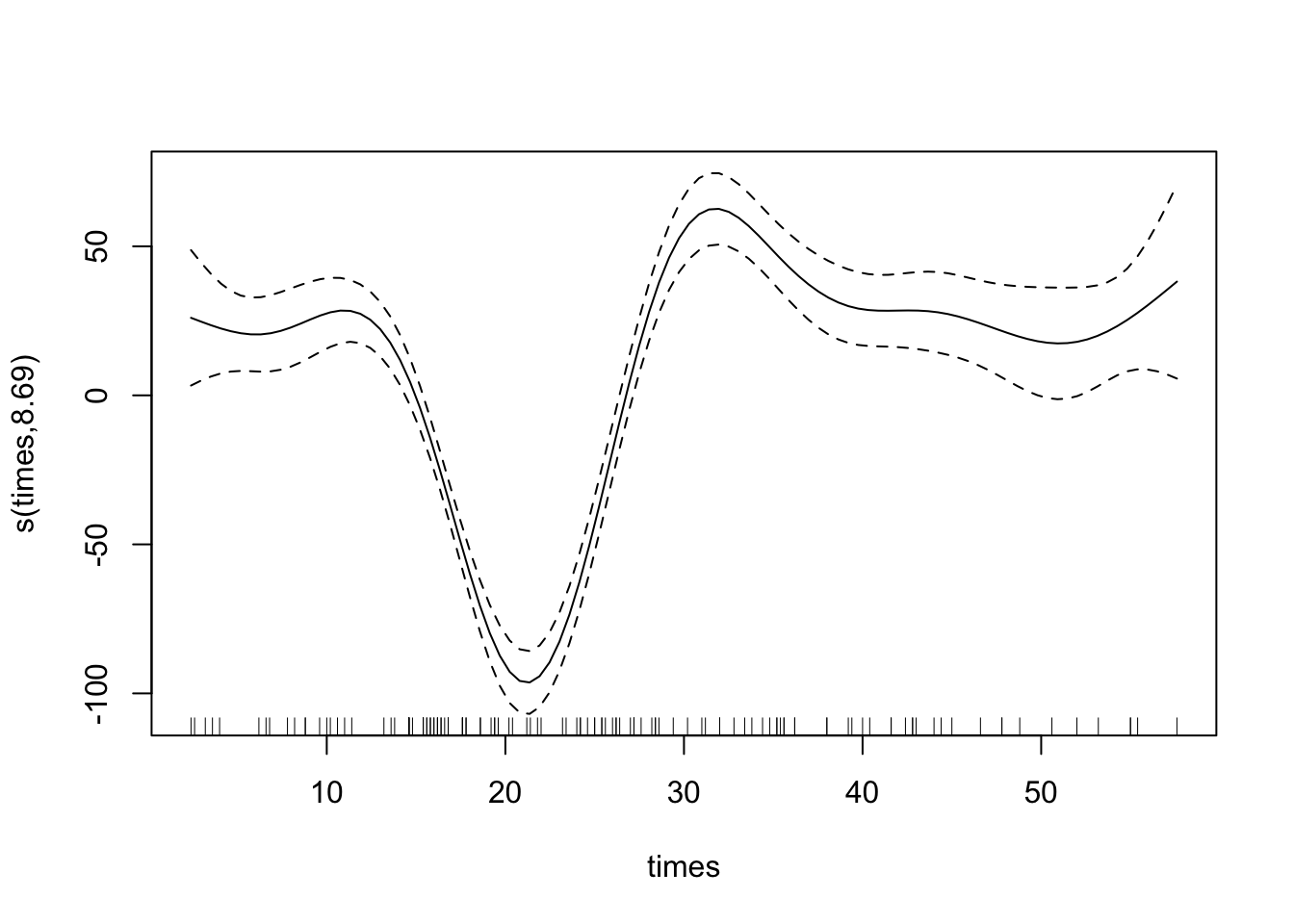 위의 plot은 몇 가지 점에서 불만족스러우므로 다음과 같이 여러가지 옵션을 주면 조금 더 많은 정보를 볼 수 있다.
위의 plot은 몇 가지 점에서 불만족스러우므로 다음과 같이 여러가지 옵션을 주면 조금 더 많은 정보를 볼 수 있다.
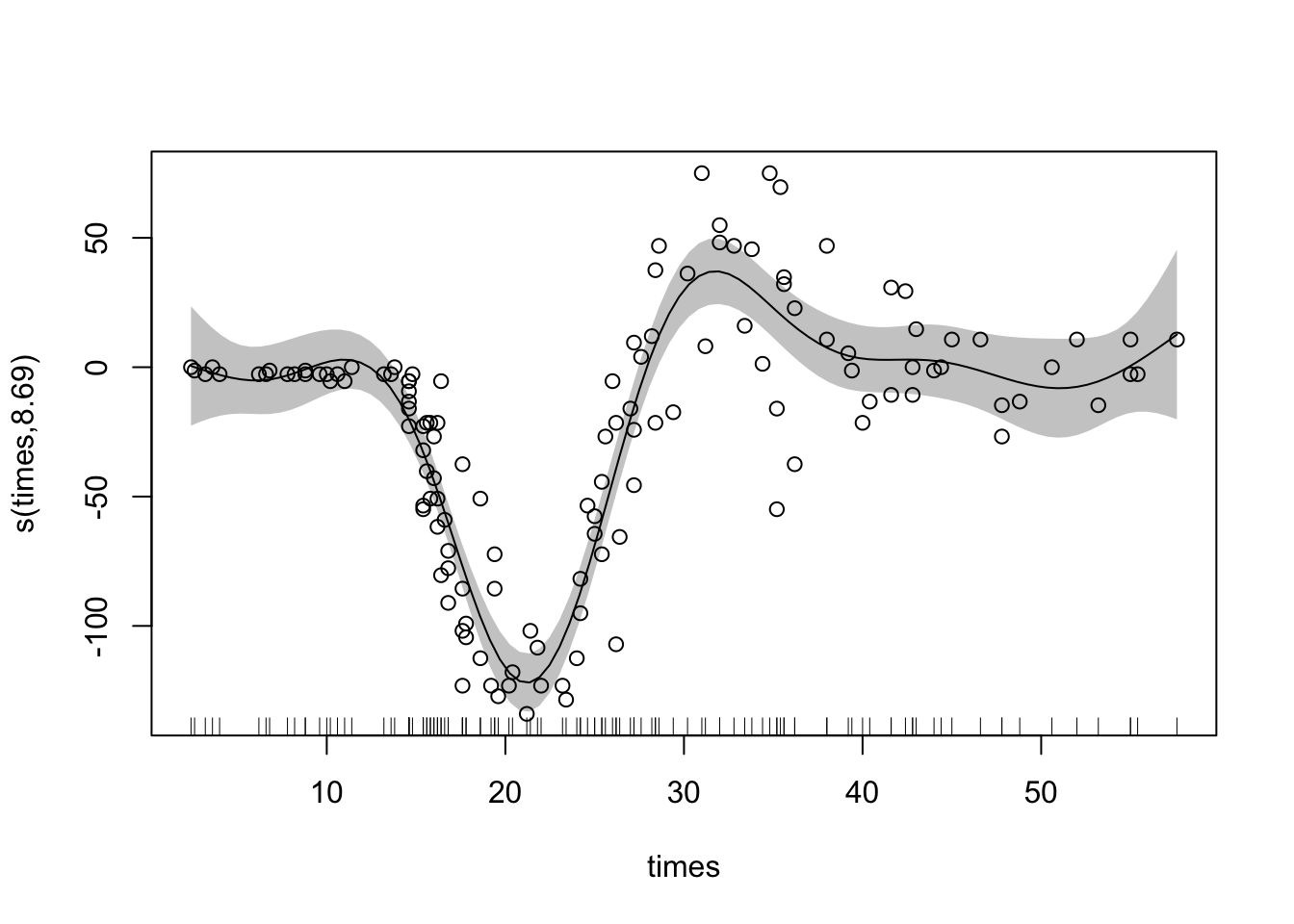 한편 gam모형의 시각화를 위해 저자가 만든 ggGam 패키지를 이용하면 보다 보기 편한 그림을 얻을 수 있다.
한편 gam모형의 시각화를 위해 저자가 만든 ggGam 패키지를 이용하면 보다 보기 편한 그림을 얻을 수 있다.
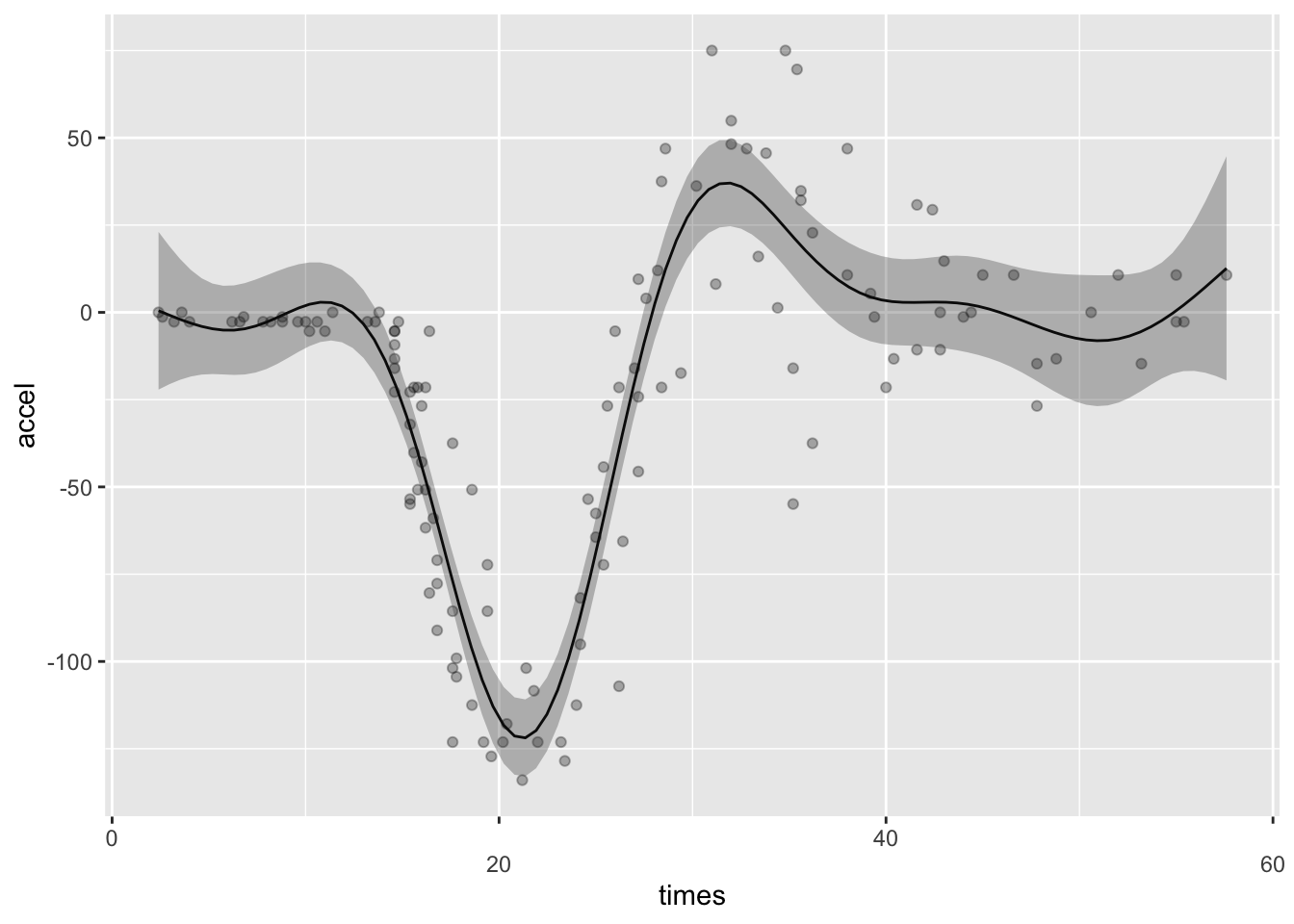 이 모형의 적합선을 보면 먼저 충돌이 있고 난 후 약 12 msec 이후에 감속이 일어나고 이후 약 21msec정도에 최저점에 도달한 후 다시 상승하여 약 31 msec 이후에 최고점에 달하는 것을 알 수 있다. 이러한 결과는 모터싸이클 사고에서 감속-가속에 의한 뇌손상을 설명해준다.
이 모형의 적합선을 보면 먼저 충돌이 있고 난 후 약 12 msec 이후에 감속이 일어나고 이후 약 21msec정도에 최저점에 도달한 후 다시 상승하여 약 31 msec 이후에 최고점에 달하는 것을 알 수 있다. 이러한 결과는 모터싸이클 사고에서 감속-가속에 의한 뇌손상을 설명해준다.
이 모형에 대한 자세한 설명을 보려면 다음과 같이 한다.
Family: gaussian
Link function: identity
Formula:
accel ~ s(times)
Parametric coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -25.546 1.951 -13.1 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Approximate significance of smooth terms:
edf Ref.df F p-value
s(times) 8.693 8.972 53.52 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
R-sq.(adj) = 0.783 Deviance explained = 79.8%
GCV = 545.78 Scale est. = 506 n = 133이 모형의 설명력은 무려 0.78이며(\(_{adj}R^2=0.78\)) 편차(deviance)의 79.8%를 설명해주고 있다. 이 모형의 해석과 모형의 진단에 관하여는 다음절에서 다루기로 한다. 이번 절에서는 직선관계가 아닌 반응변수와 설명변수의 관계를 mgcv패키지의 gam함수를 이용하여 분석하는 방법을 예로 들어 보았다.
2.2 일반화가법모형의 소개
위의 예에서 본 바와 같이 일반화가법모형(GAM)은 생물학, 의학, 환경학 등 여러 분야에서 접할 수 있는 복잡한 비선형관계를 분석할 수 있게 해주는 다재다능한 모형이다. 우리가 통계학적인 모형을 만들 때 모형의 유연성(flexibility)과 해석가능성(interpretability)은 서로 상충하는 관계(trade-off)에 있다.

선형회귀와 같은 단순한 모형은 사용하기 쉽고 해석하기 쉬우며 인수의 뜻도 해석하기 쉽다. 하지만 선형관계로 설명할 수 없는 현상을 설명하려면 보다 복잡한 모형이 필요하다. 신경망과 같은 기계학습 모형은 복잡한 관계를 예측하는 능력은 뛰어나지만 많은 데이터를 필요로 하고 해석하기 어렵고 모형의 결과로부터 추론하는 것이 매우 어렵다. GAM은 선형모형과 기계학습의 중간에 위치하고 있다. 복잡한 비선형관계를 적합시킬 수 있으며 매우 좋은 예측을 할 수 있는 반면 통계적 추론이 가능할 뿐만 아니라 모형의 구조를 이해하고 설명할 수 있으며 예측에 대한 설명도 가능하다.
2.2.1 두번째 예제
이번 예제를 위해 simulation을 통해 다음과 같은 예제 데이터를 만들어 보았다.
set.seed(1)
x <- seq(0, pi * 2, 0.1)
y <- 2*sin(x) + rnorm(n = length(x), mean = 0, sd = sd(2*sin(x) / 2))
data1 <- data.frame(y,x)
ggplot(data1,aes(x=x,y=y))+geom_point()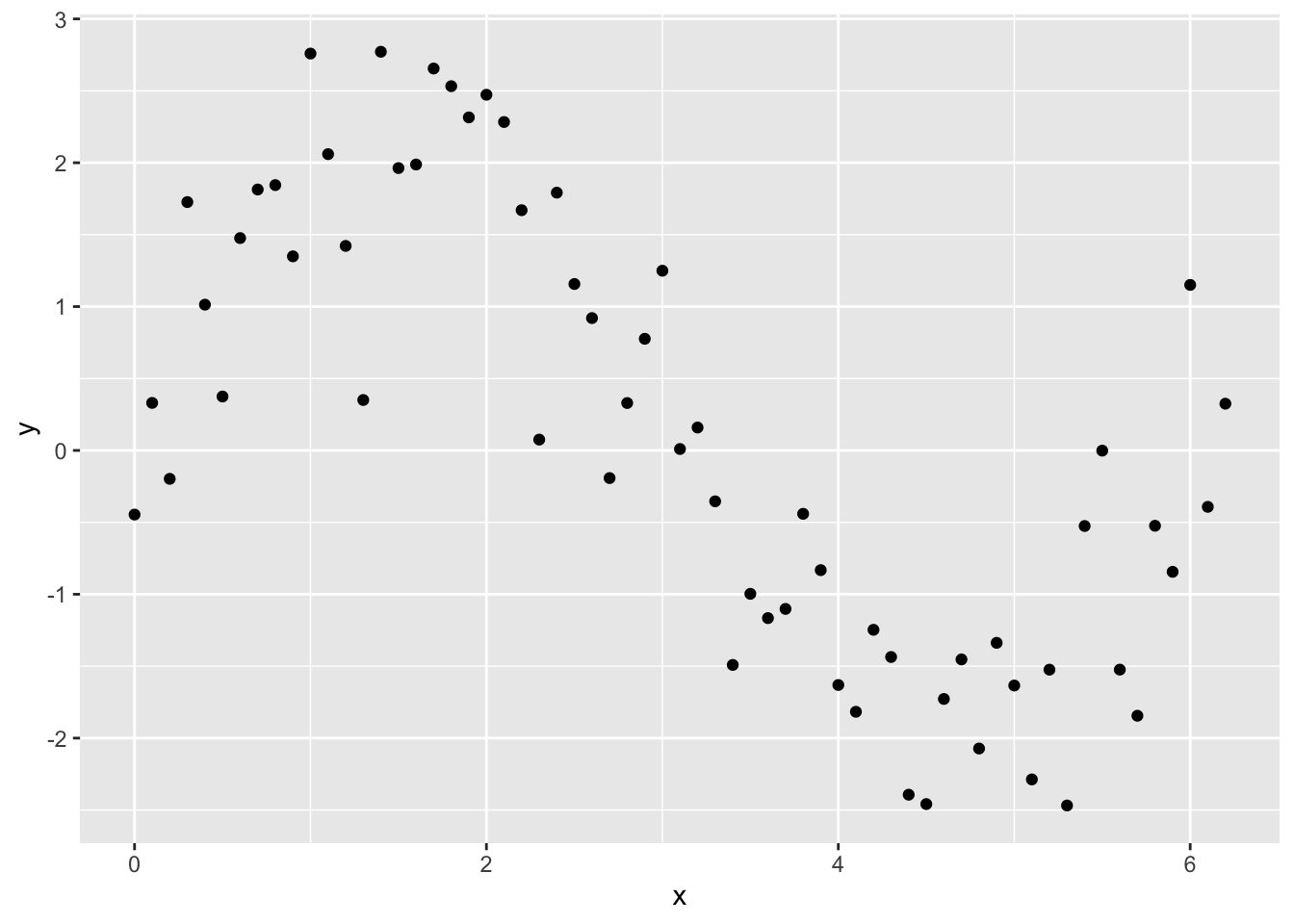 산점도를 통해 두 변수 사이에는 분명히 관계가 있으나 선형적 관계는 아니라는 것을 알 수 있다. 주 변수 사이의 관계를 알기 위해 gam()을 이용해 적합시켜 보면 다음과 같다. 이해를 돕기 위해 smooth 함수를 사용할 때 cyclic cubic regression spline을 사용해(bs=“cc”) 적합시켜 보겠다.
산점도를 통해 두 변수 사이에는 분명히 관계가 있으나 선형적 관계는 아니라는 것을 알 수 있다. 주 변수 사이의 관계를 알기 위해 gam()을 이용해 적합시켜 보면 다음과 같다. 이해를 돕기 위해 smooth 함수를 사용할 때 cyclic cubic regression spline을 사용해(bs=“cc”) 적합시켜 보겠다.
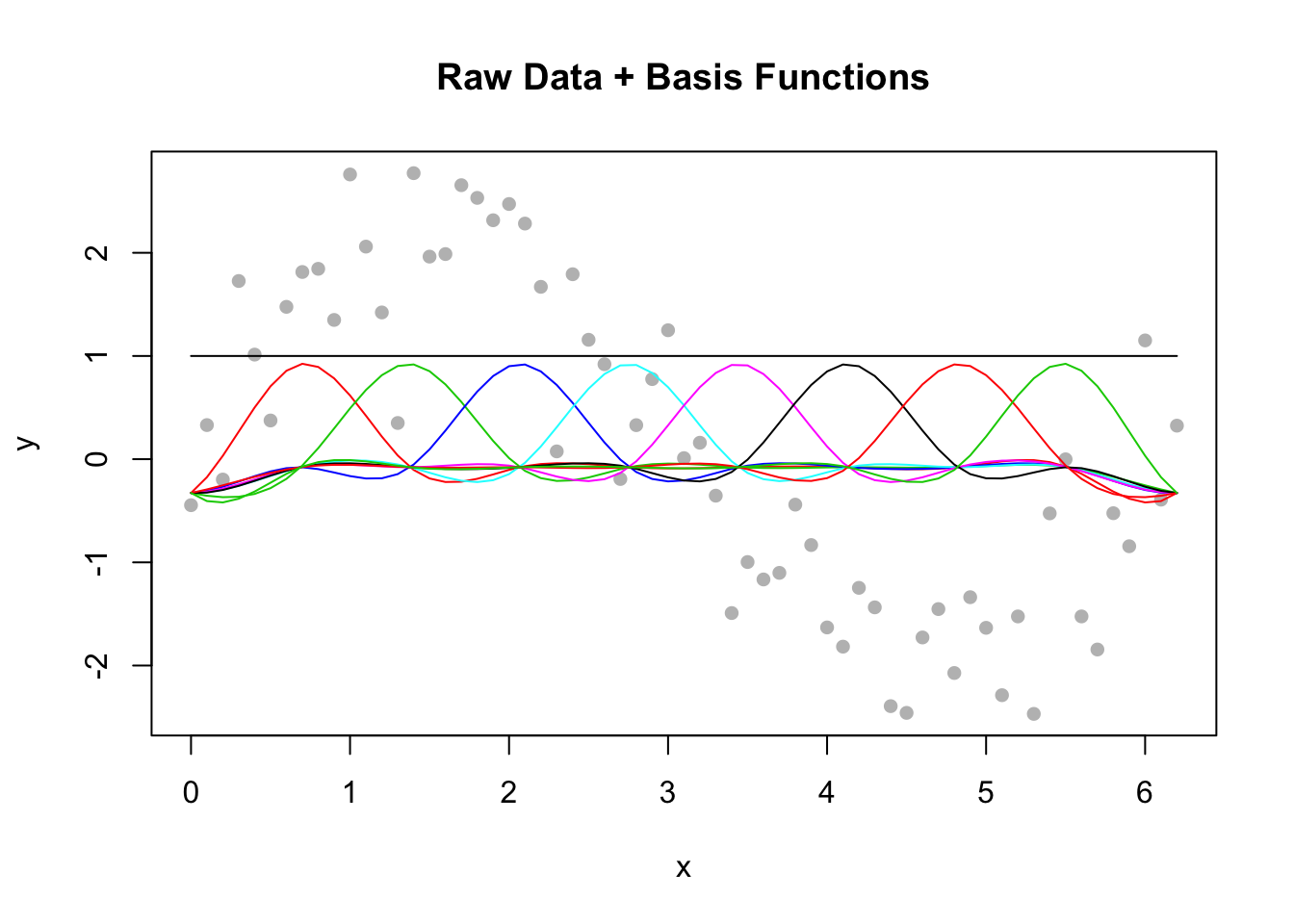
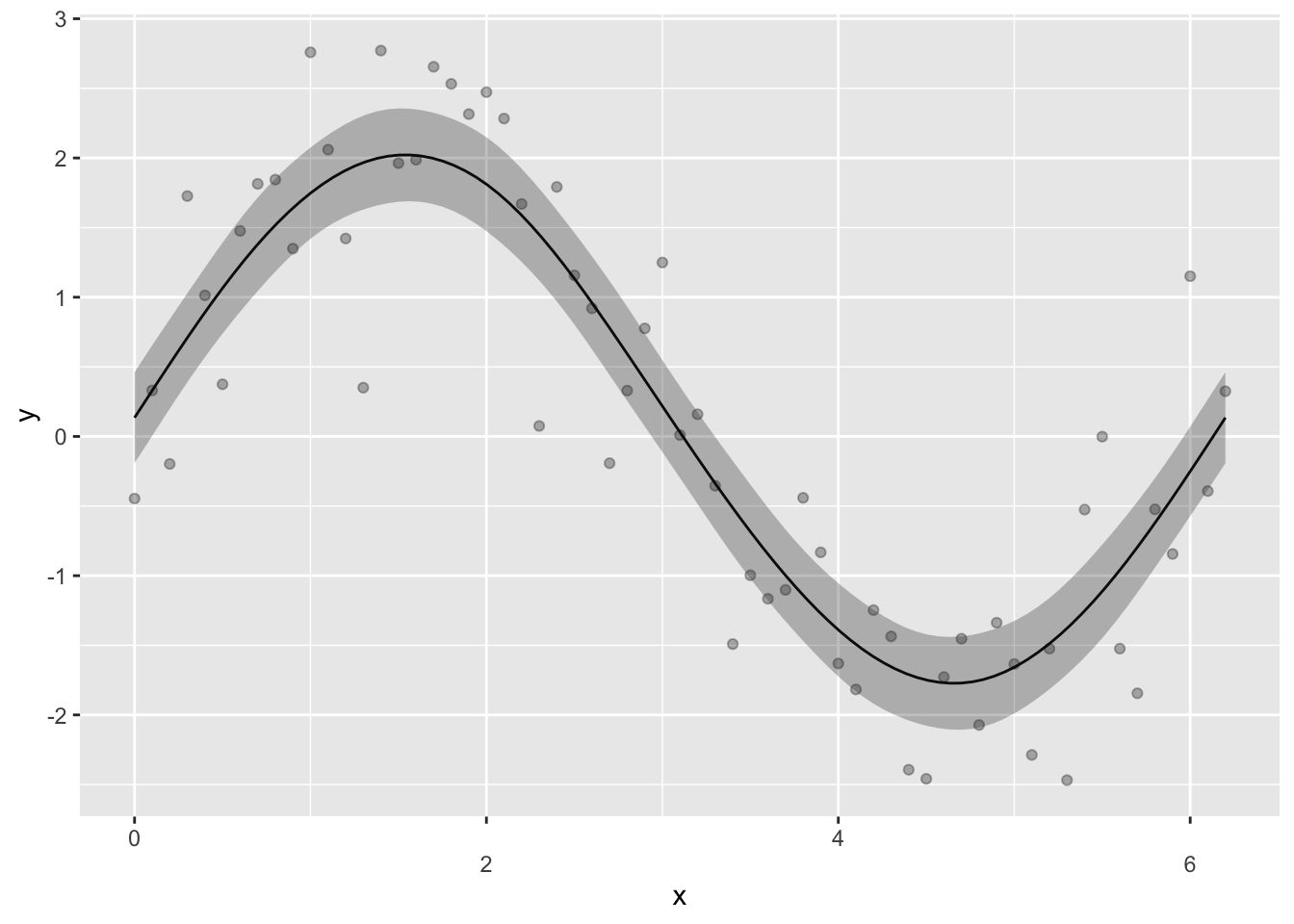 위의 그림에서 보는 gam을 이용한 적합선은 어떻게 만들어지는 것일까? 위의 적합선은 여러 개의 기저함수(basis function)을 이용하여 만들어진다. gam()함수를 이용하면 자동적으로 기저함수의 갯수가 정해지는데 이 모형의 경우 8개의 기저함수가 사용된다(아래 그림의 왼쪽). 8개의 기저함수에 각각의 계수(coefficent)를 곱한 값을 모두 더하면 적합선이 만들어진다(아래 그림의 오른쪽).
위의 그림에서 보는 gam을 이용한 적합선은 어떻게 만들어지는 것일까? 위의 적합선은 여러 개의 기저함수(basis function)을 이용하여 만들어진다. gam()함수를 이용하면 자동적으로 기저함수의 갯수가 정해지는데 이 모형의 경우 8개의 기저함수가 사용된다(아래 그림의 왼쪽). 8개의 기저함수에 각각의 계수(coefficent)를 곱한 값을 모두 더하면 적합선이 만들어진다(아래 그림의 오른쪽).
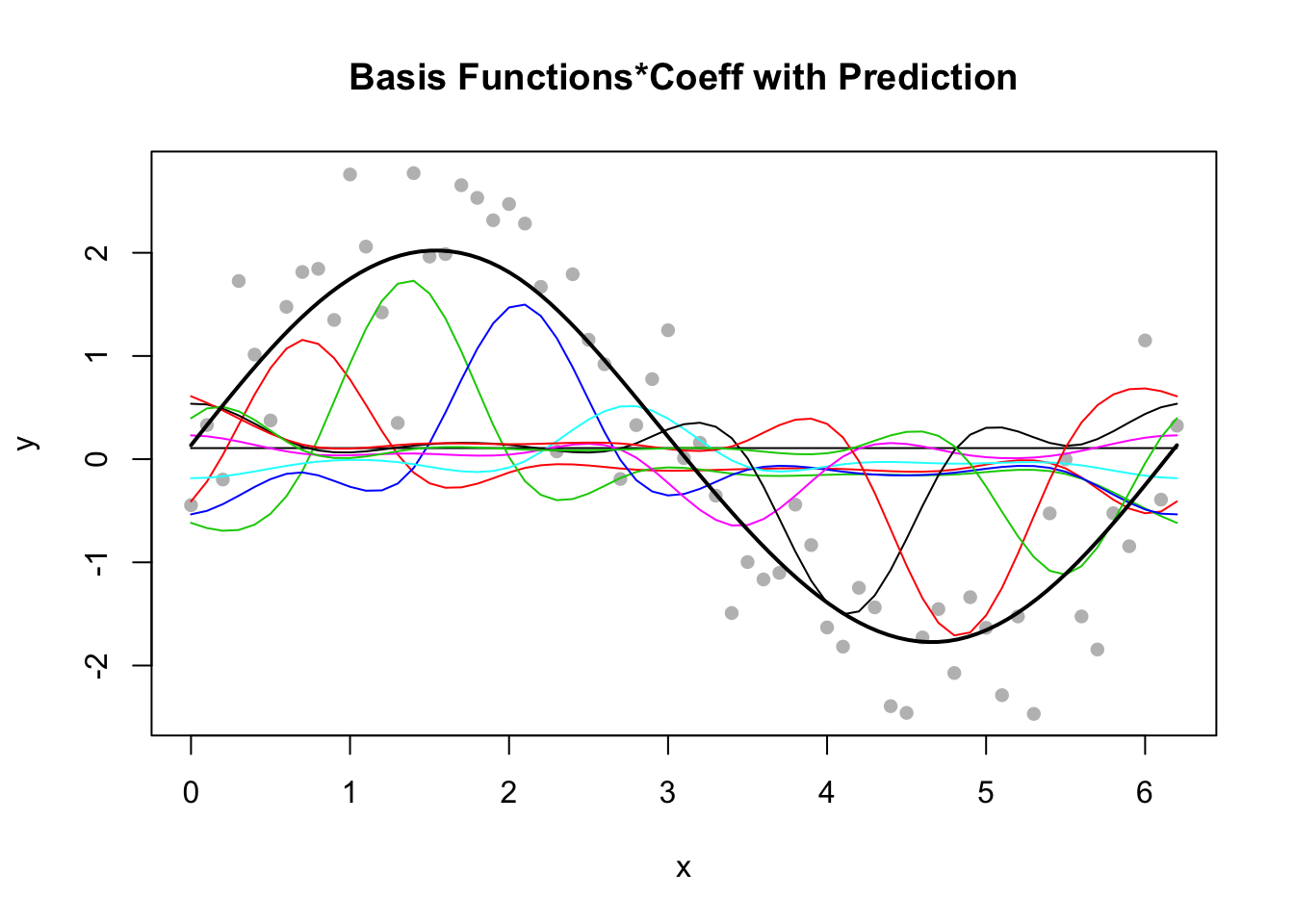 이 모형의 기저함수의 계수들을 보려면 coef()함수를 사용한다.
이 모형의 기저함수의 계수들을 보려면 coef()함수를 사용한다.
(Intercept) s(x).1 s(x).2 s(x).3 s(x).4 s(x).5
0.1072212 1.2501657 1.8832491 1.6322595 0.5622974 -0.7036777
s(x).6 s(x).7 s(x).8
-1.6382503 -1.8604023 -1.2102262 모두 8개의 기저함수의 계수및 절편을 확인할 수 있다.
2.2.2 기저함수와 평활파리미터
비선형모형을 이용하여 모형적합을 할 때 두 가지를 염두에 두어야 한다. 적합한 모형은 데이터에 가까워야 하고(과소적합 방지) 또한 소음(noise)에 적합되는 것을 피해야 한다(과적합 방지). GAM이 데이터의 변동양상을 잘 찾는 정도를 가능도(likelihood)라고 할 수 있고 곡선이 모양을 잘 바꾸는 정도를 잔떨림정도(wiggliness)라고 표현한다면 이 둘은 서로 상충하는 trade-off가 일어나며 평활 파라미터(smoothing parameter) 람다(\(\lambda\))가 균형을 조절하고 있다. GAM을 이용하여 데이터를 적합시킬 때 평활 파라미터는 자동으로 최적화된다.
\[\begin{equation} Fit = Likelihood - \lambda \times Wiggliness \end{equation}\]
평활 파라미터 람다가 너무 큰 경우 적합선은 곡선모양의 데이터를 가로지르는 직선이 되고(왼쪽 그림) 너무 적은 경우 트렌드(trend)가 아닌 소음(noise)에 반응하여 과적합된다(가운데 그림). 가장 적절한 람다의 값은 과적합과 과소적합 사이의 균형을 잡아준다.
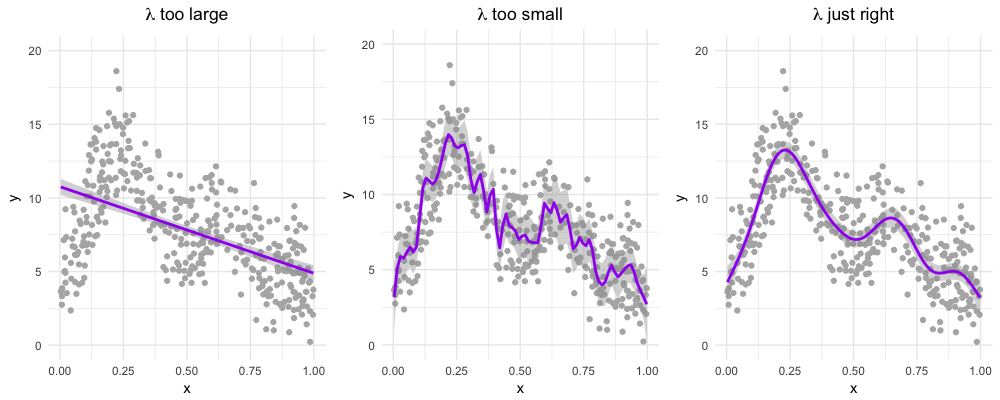
보통 mgcv패키지의 gam() 함수를 통해 모형적합을 할 경우 gam()함수가 제한된 최대가능도(restricted maximum likelihood, REML) 방법으로 적절한 평활 파라미터를 선택하게 된다. 하지만 sp 인수를 통해 평활 파라미터의 값을 지정해 줄 수도 있다. REML방법으로 평활 파라미터를 선택하도록 할 경우 다음과 같이 한다.
고정된 평활 파라미터를 지정할 경우에는 다음과 같이 한다.
평활 파리미터를 선택하는 방법은 REML이외에도 여러가지가 있으며 각 방법에 따라 각각의 잇점이 있으나 REML 방법이 가장 신뢰할만 하고 안정적인 결과를 보여주기 때문에 대부분의 GAM 전문가들은 REML 방법을 추천한다.
2.2.3 기저함수의 갯수와 평활도
평활 파라미터 이외에도 기저함수의 갯수 또한 GAM 함수의 평활도에 영향을 미친다. 같은 데이터에 3개, 7개, 12개의 기저함수를 사용한 경우의 예는 다음과 같다.
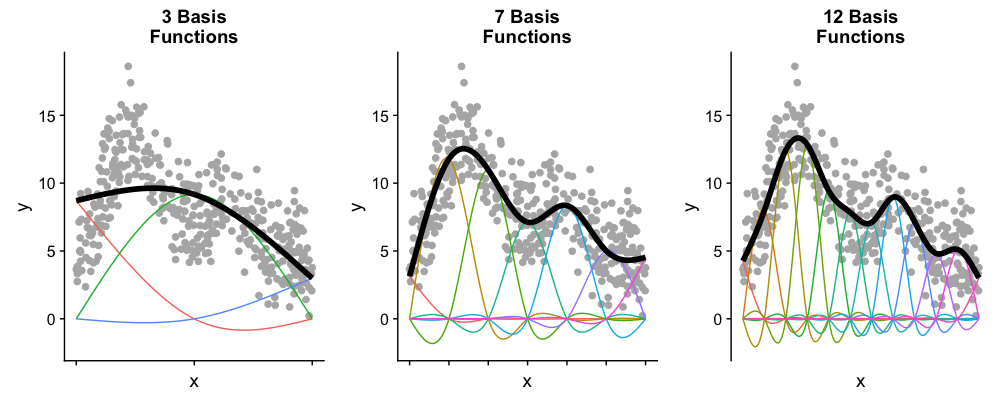 위의 그림과 같이 기저함수의 갯수가 너무 적은 경우 데이터의 변화에 적응시키지 못하며 기저함수의 갯수가 많은 경우 보다 미세한 변화에 적합시킬 수 있다.
위의 그림과 같이 기저함수의 갯수가 너무 적은 경우 데이터의 변화에 적응시키지 못하며 기저함수의 갯수가 많은 경우 보다 미세한 변화에 적합시킬 수 있다.
2.2.4 기저함수 갯수의 조절
mcycle 데이터를 이용하여 GAM 모형을 만들 때 평활함수인 s()함수의 k인수를 이용하여 기저함수의 갯수를 지정할 수 있다. 다음의 예는 기저함수의 갯수를 3개와 20개로 지정하여 차이를 본 것이다.
k3 <- gam(accel ~ s(times, k=3),data=mcycle)
k20 <- gam(accel ~ s(times, k=20),data=mcycle)
ggGam(k3, point=TRUE) + ggtitle("k=3")
ggGam(k20, point=TRUE)+ ggtitle("k=20")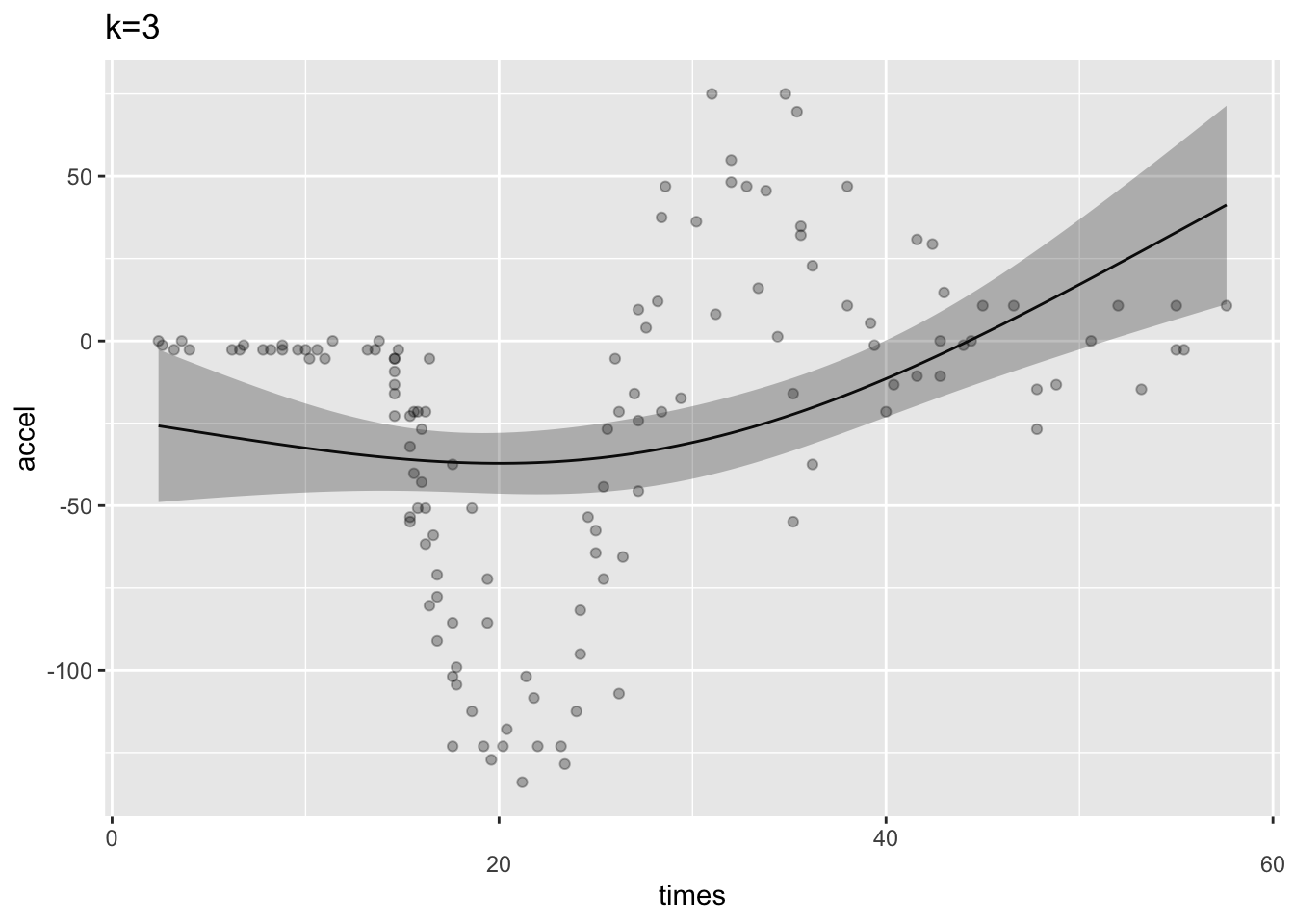
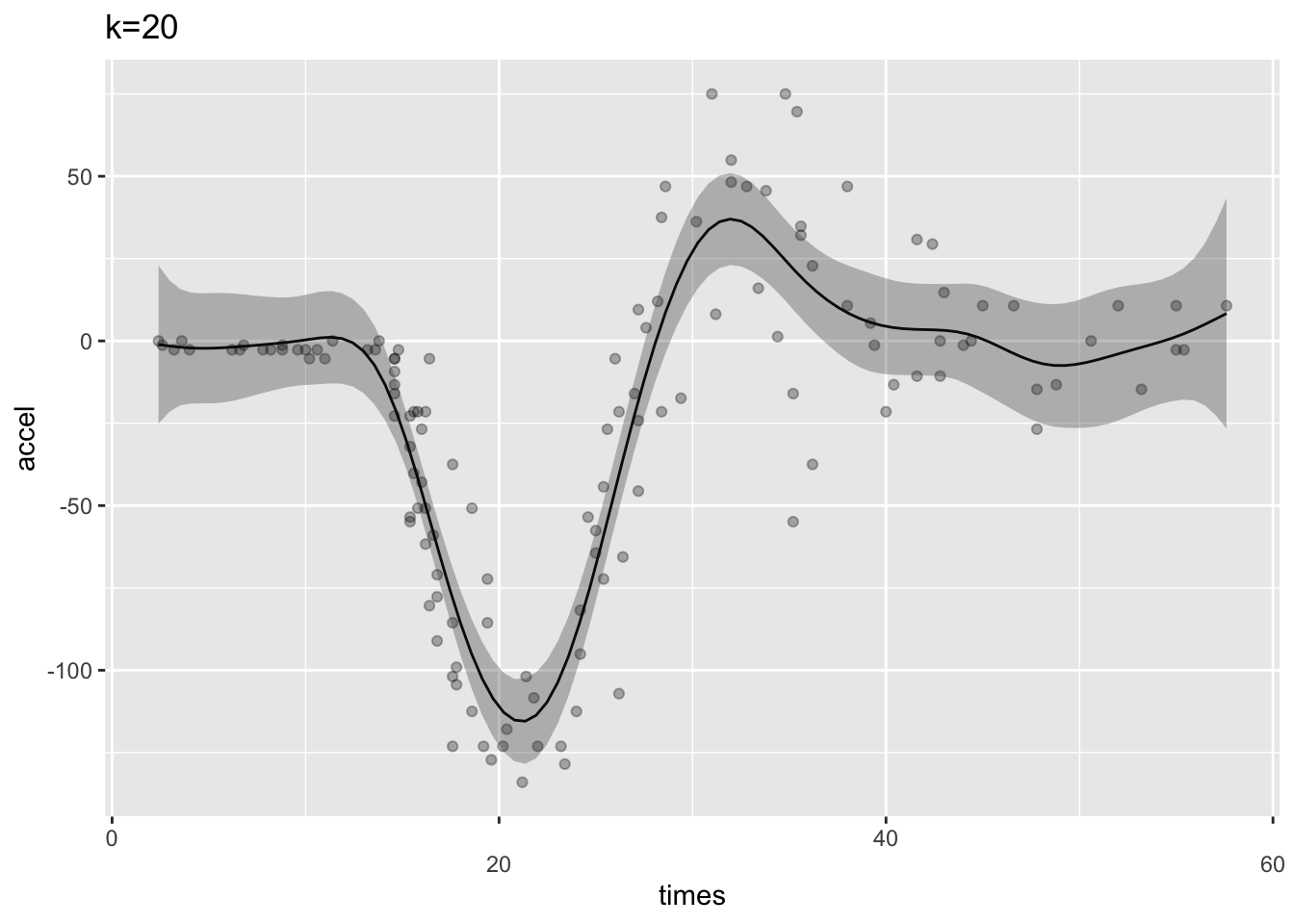
2.2.5 평활 파라미터의 조절
REML 방법으로 평활 파라미터를 자동으로 선택한 경우 다음과 같이 자동선택된 평활 파라미터를 확인할 수 있다.
s(times)
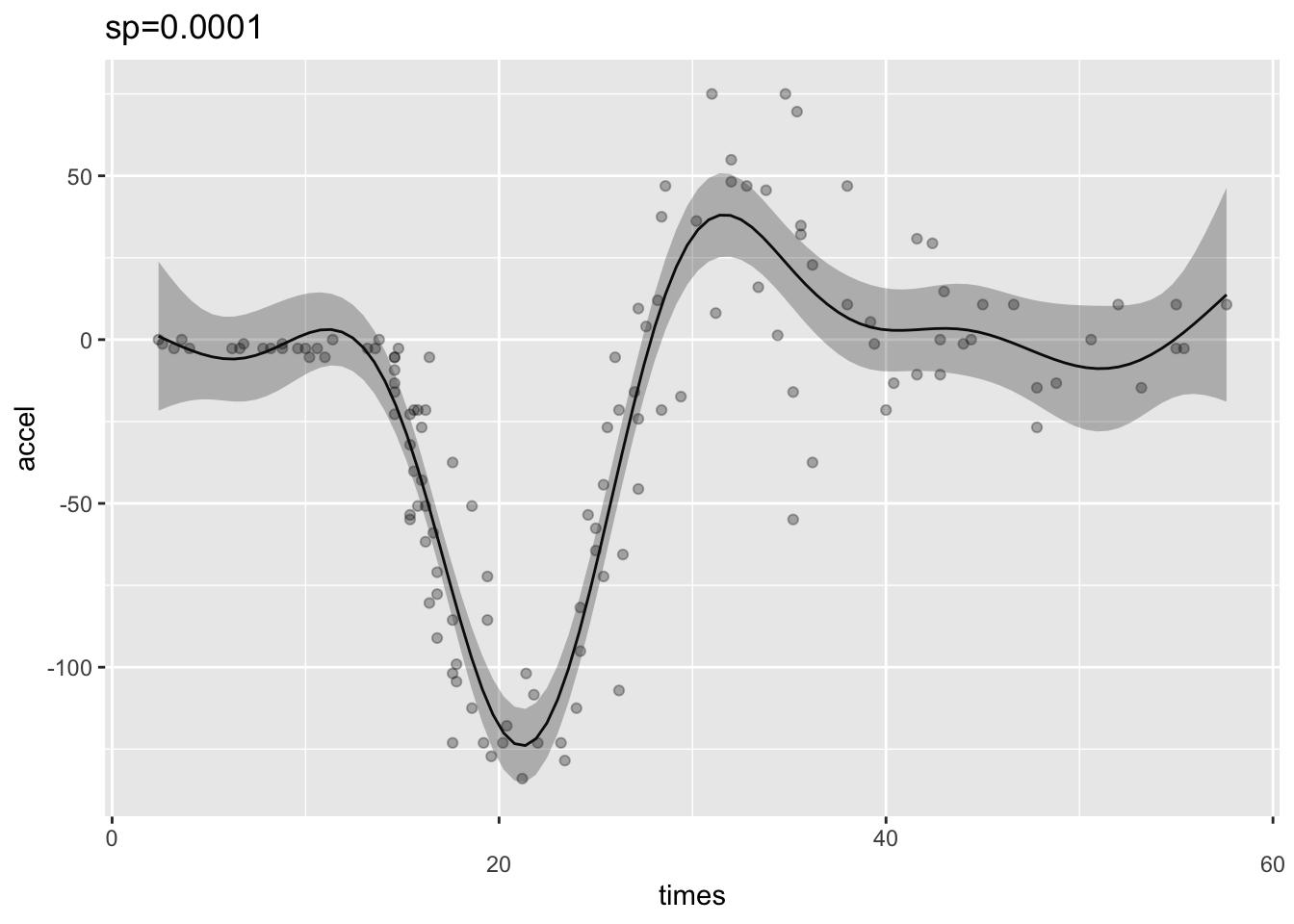
0.0007758036 다음의 예는 평활 파라미터의 값을 0.1과 0.0001로 지정하여 그 차이를 본 것이다.
sp1 <- gam(accel ~ s(times),data=mcycle, sp=0.1)
sp2 <- gam(accel ~ s(times),data=mcycle, sp=0.0001)
ggGam(sp1)+ ggtitle("sp=0.1")
ggGam(sp2)+ ggtitle("sp=0.0001")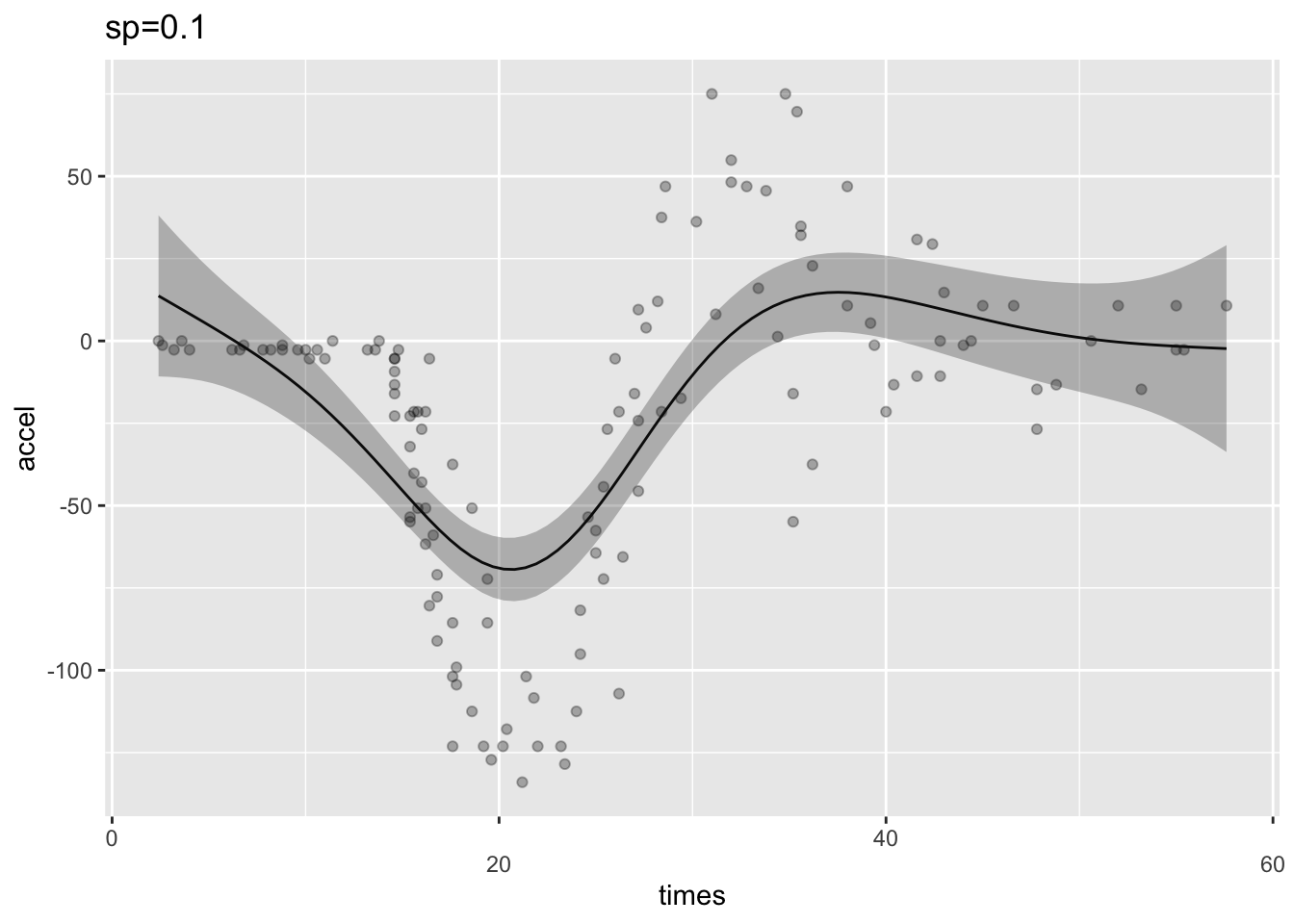
2.3 다중일반화가법모형 (Multiple GAMs)
GAM의 설명변수로 여러 개의 변수를 선택할 수 있으며 연속형 변수인 경우 곡선형태의 비선형효과 또는 선형효과를 선택할 수 있으며 범주형 변수도 선택 가능하며 범주형 변수의 각각의 범주에 따라 서로 다른 비선형 효과를 선택할 수도 있다.
2.3.1 세번째 예제 : mpg 데이터
세번째 예제로는 gamair 패키지의 mpg 데이터를 사용한다. 이 데이터는 미국의 205개 자동차에 대한 자료로 다음과 같은 구조를 갖는다.
2.3.1.1 하나의 평활항을 갖는 GAM
mpg데이터의 고속도로 연비(hw.mpg)를 반응변수로 하고 자동차 무게의 평활 스플라인을 설명변수로 하는 GAM 은 다음과 같이 만들 수 있다.
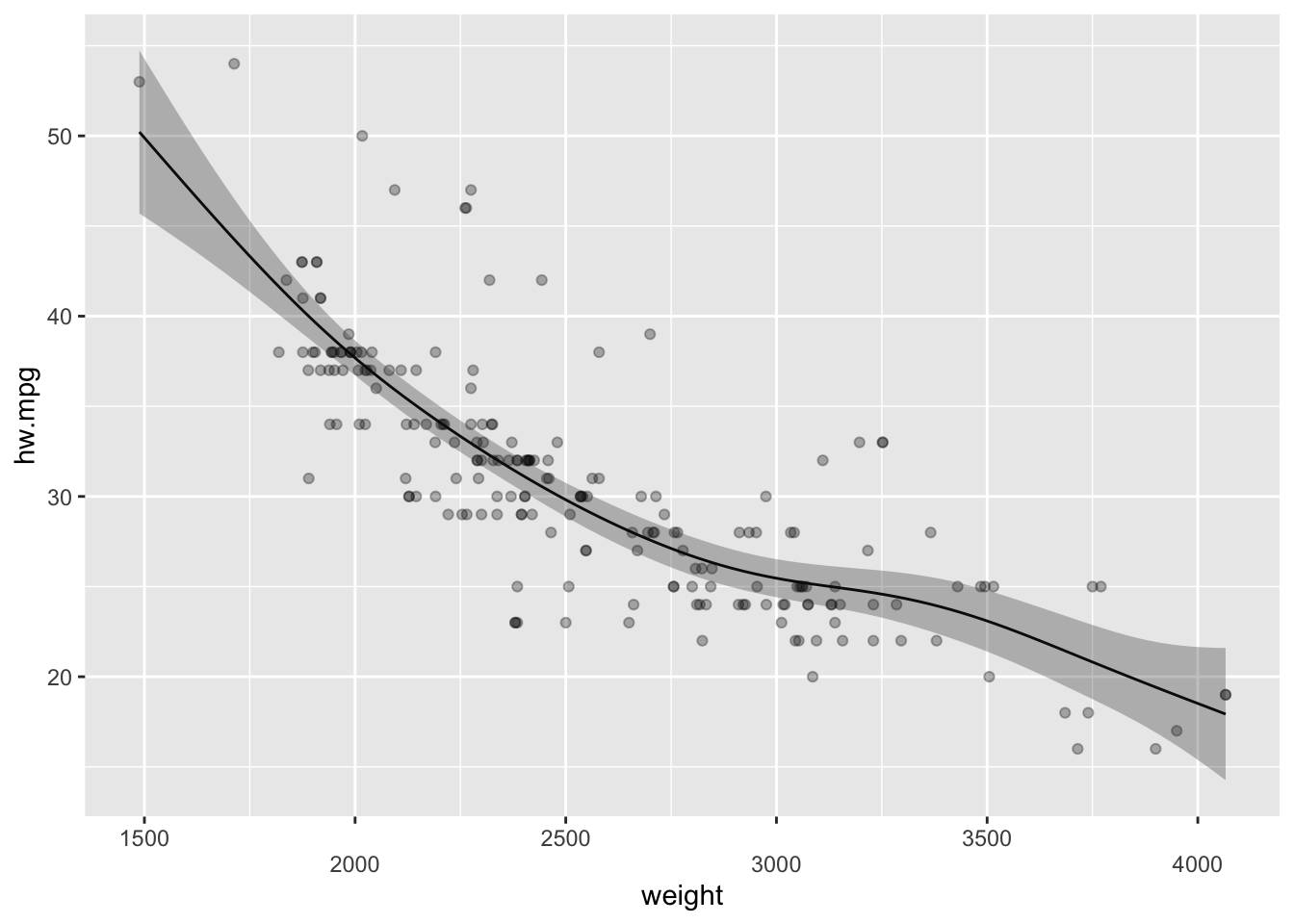
2.3.1.2 두 개의 평활항을 갖는 GAM
이 모형에 자동차 길이의 평활 스플라인을 설명변수로 추가한 모형은 다음과 같다.
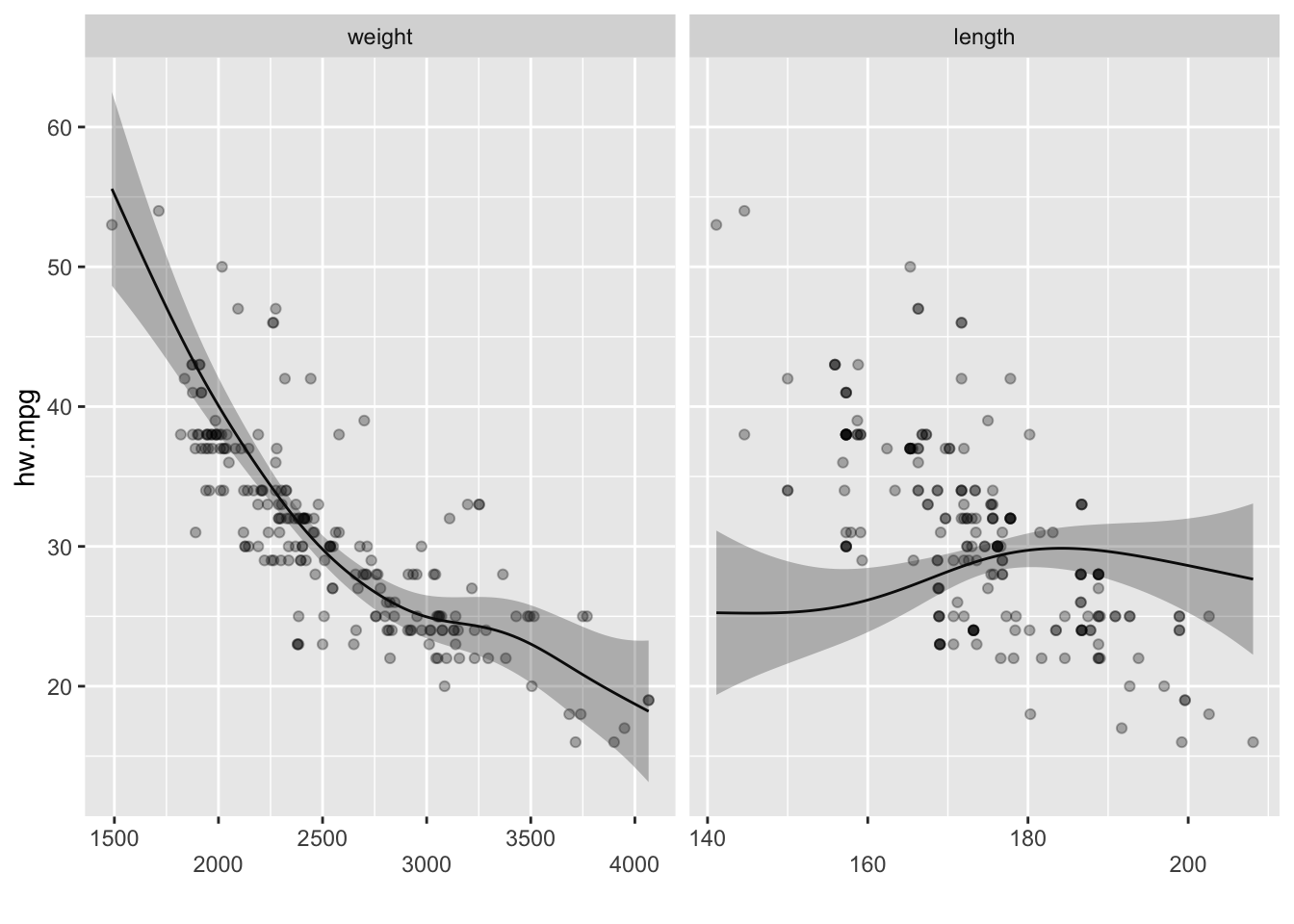
2.3.1.3 평활항과 선형항을 갖는 GAM(1)
GAM의 설명변수 모두가 비선형항인 것은 아니다. 비선형항과 함께 선형항을 설명변수로 사용할 수도 있으며 이때 선형 설명변수는 s()함수를 사용하지 않는다. 이전에 만든 모형에서 자동차 길이를 선형 설명변수로 사용하는 GAM은 다음과 같다.
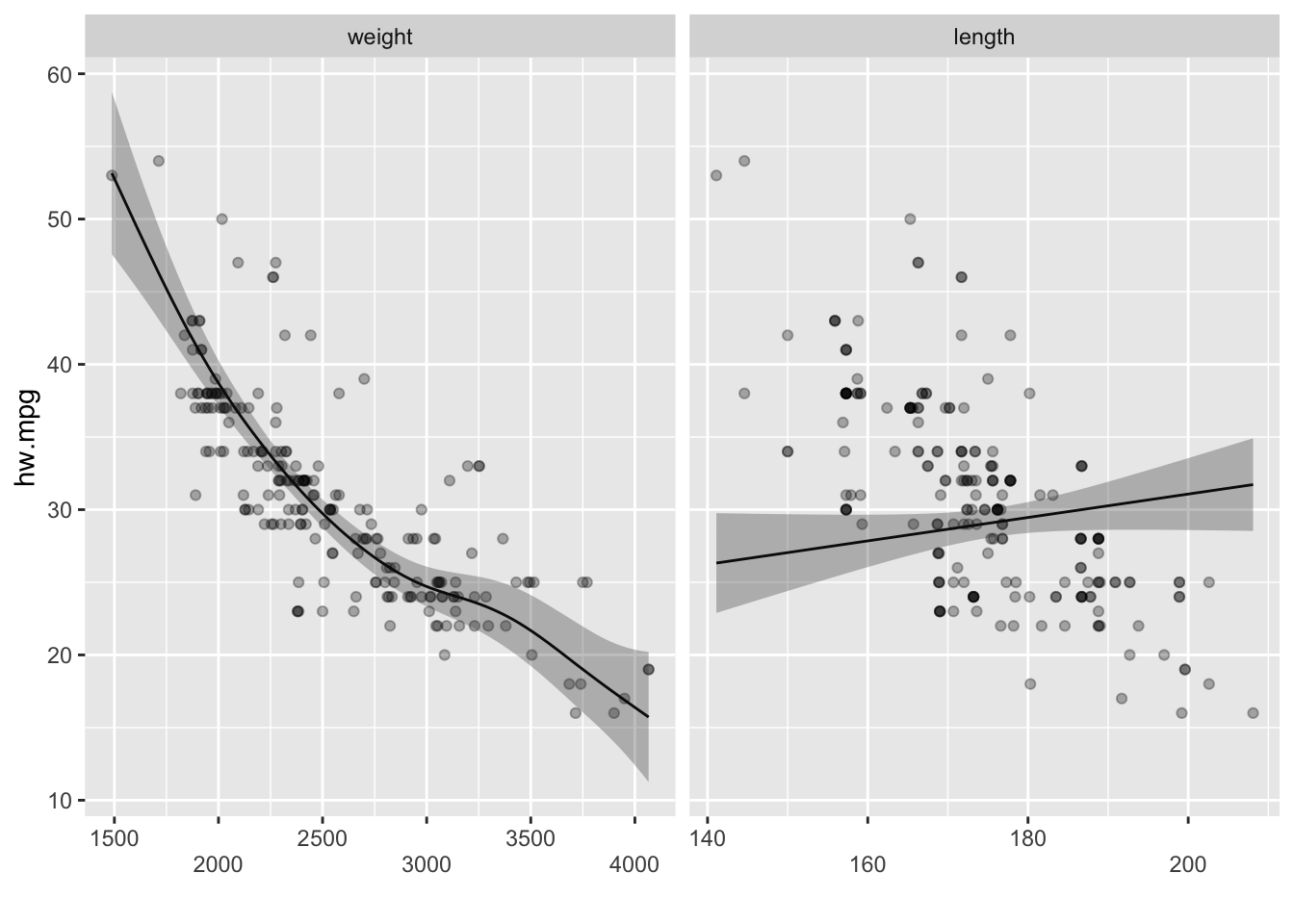 실제로 GAM을 사용할 때에는 선형항을 거의 사용하지 않는다. 만일 두 변수의 관계가 정말로 선형관계라면 자동화된 평활항도 선형 모양을 보이기 때문이다.
실제로 GAM을 사용할 때에는 선형항을 거의 사용하지 않는다. 만일 두 변수의 관계가 정말로 선형관계라면 자동화된 평활항도 선형 모양을 보이기 때문이다.
2.3.1.4 평활항과 선형항을 갖는 GAM(2)
위의 모형과 같은 모형으로 length의 평활항을 만들때 평활 파라미터로 매우 큰 값을 주면 선형모형으로 만들 수 있다.
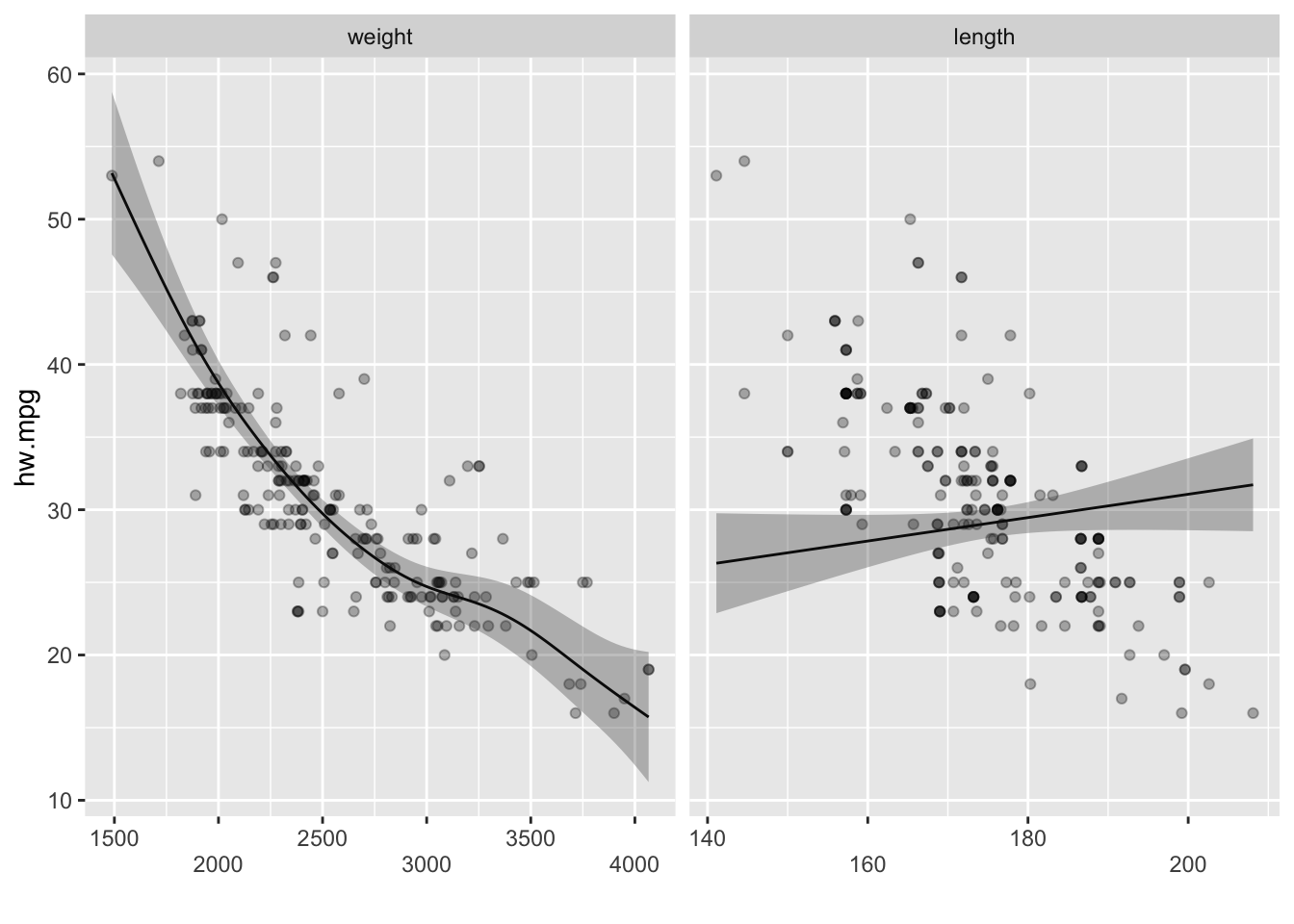
2.3.1.5 평활항과 범주형변수
범주형 변수를 추가할 경우 선형항을 사용하면 된다. mpg 데이터의 fuel변수는 디젤유(diesel)과 가솔린(gas)의 두 개의 범주로 되어 있으며 이 변수를 선형항으로 추가할 경우 gam()함수는 각 범주에 따라 고정효과가 있는 것으로 모형을 적합시킨다. 그 결과 가솔린의 연비가 떨어지는 것을 볼 수 있다. 반대로 디젤 자동차의 연비가 보다 우수하다고 할수 있다. 이 모형에서 자동차의 무게에 의한 비선형효과는 자동차 연료의 종류에 관계 없이 같은 효과를 보인다. 이는 선형회귀모형에서 기울기의 변화 없이 절편만 달라지는 것과 마찬가지이다. 한가지 주의할 점은 범주형 변수를 사용할 때에는 반드시 factor로 사용해야 한다는 점이다. mgcv 패키지에서는 문자형 변수를 사용하지 못한다.
model5 <- gam(hw.mpg ~ s(weight)+fuel, data=mpg, method="REML")
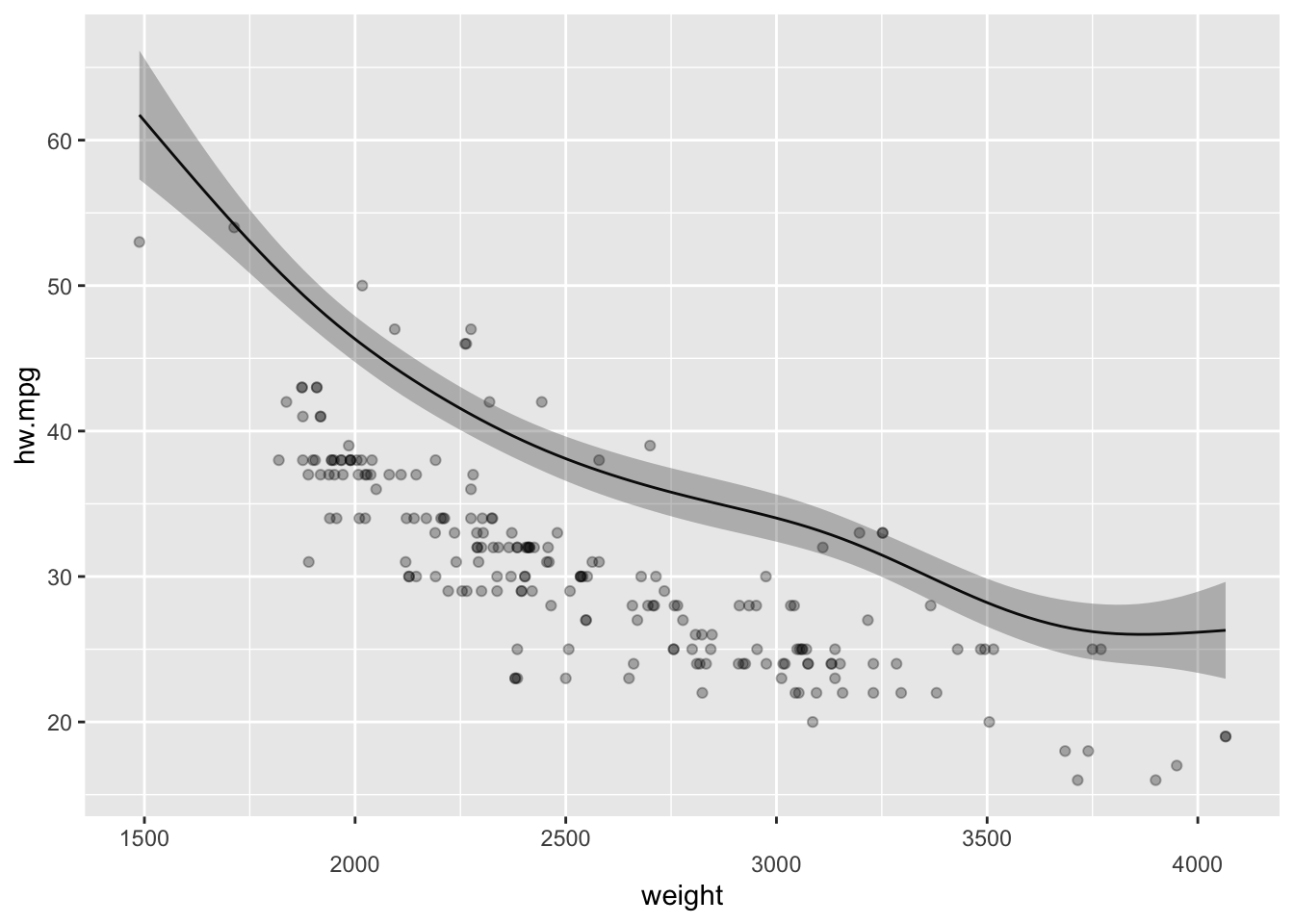
plot(model5,residuals=TRUE,pch=1,shade=TRUE,seWithMean = TRUE,shift=coef(model5)[1],pages=1,all.terms=TRUE)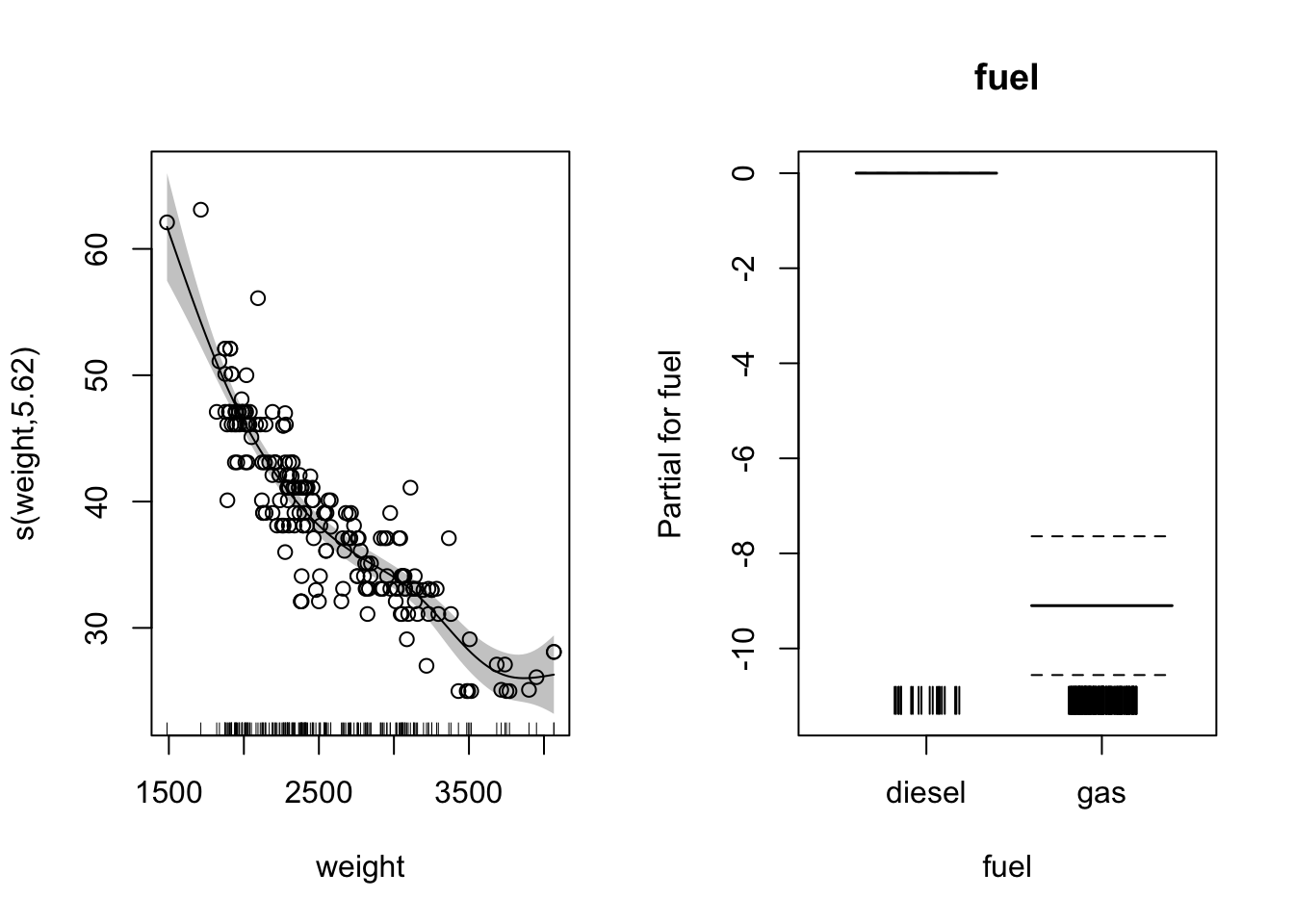 mgcv의 plot.gam 함수와는 달리 ggGam()함수는 by인수에 범주형 변수를 지정해주면 범주별로 분리하여 비선형효과를 시각화해준다.
mgcv의 plot.gam 함수와는 달리 ggGam()함수는 by인수에 범주형 변수를 지정해주면 범주별로 분리하여 비선형효과를 시각화해준다.
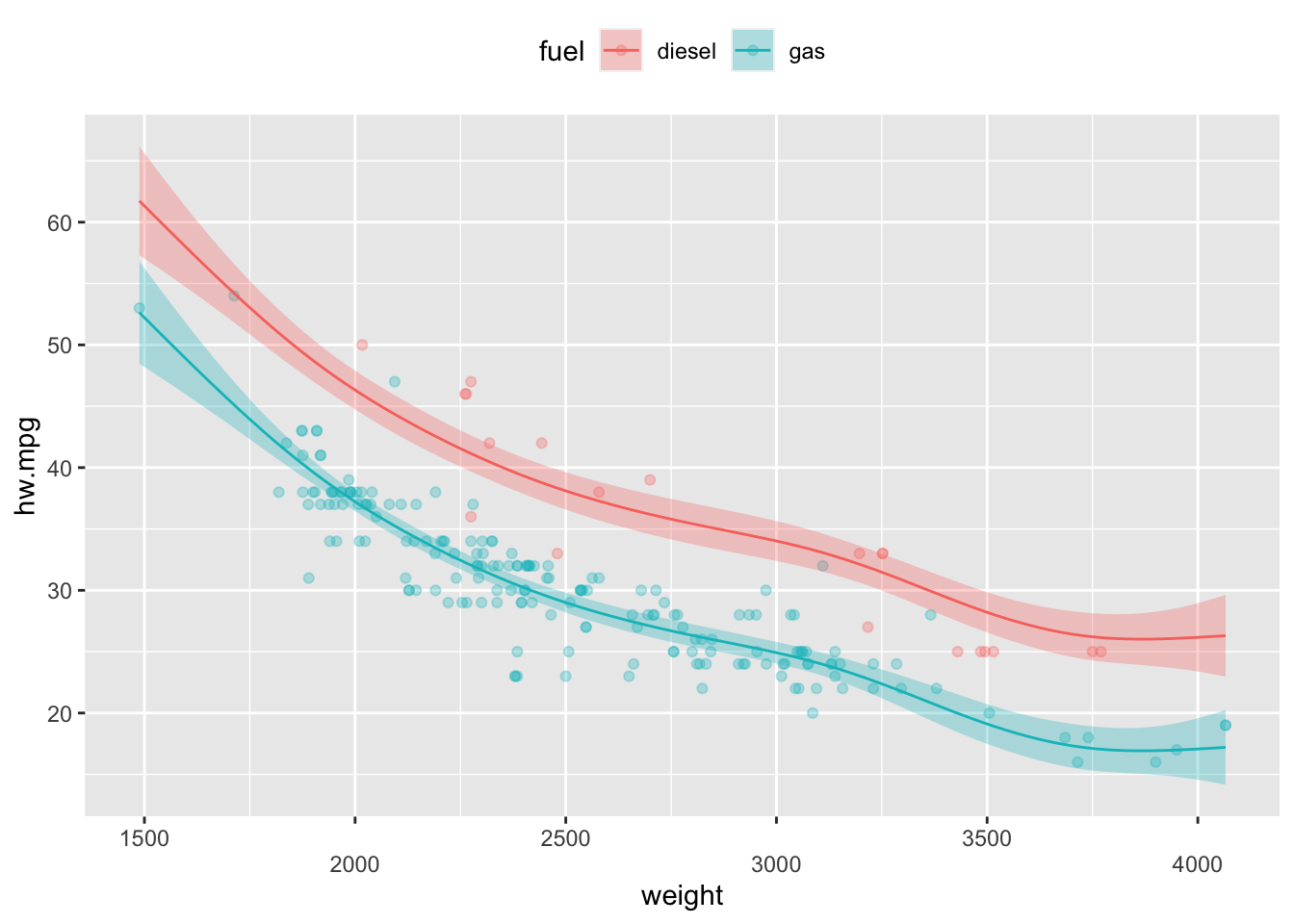
면을 분리하여 별도의 플롯을 만들려면 다음과 같이 할 수 있다.
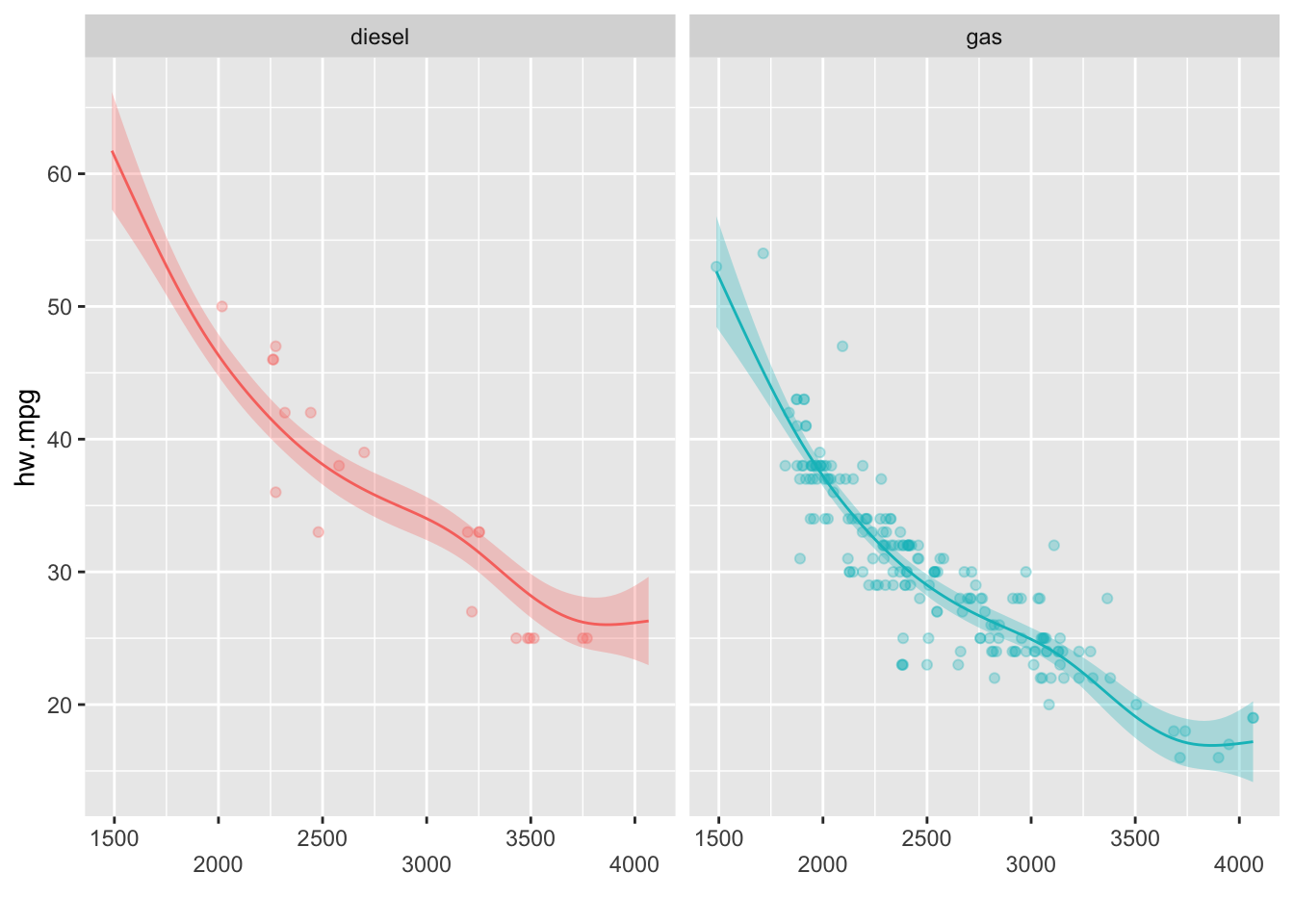
plot.gam()함수와 같은 형태의 출력을 원하는 경우 다음과 같이 사용할 수 있다.
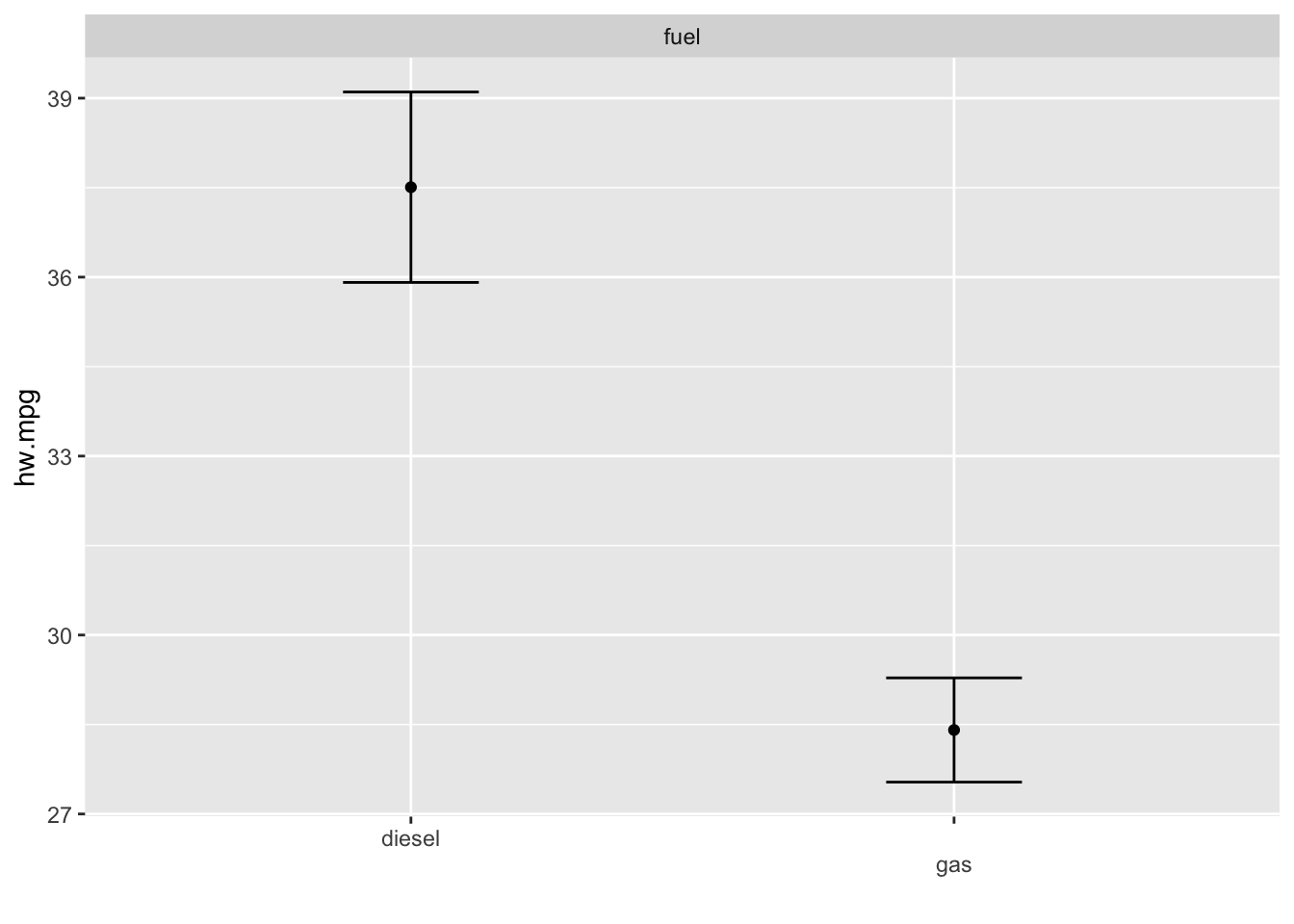
2.3.1.6 범주-평활 상호작용
범주형변수의 범주에 따라 서로 다른 비선형효과를 적합시킬 수 있는데 이를 범주-평활 상호작용(factor-smooth interaction)이라고 한다. 이때에는 s()함수 내부에 by 인수에 범주형 변수를 지정해줌으로써 각각의 범주에 서로 다른 비선형효과를 적합시키도록 한다.
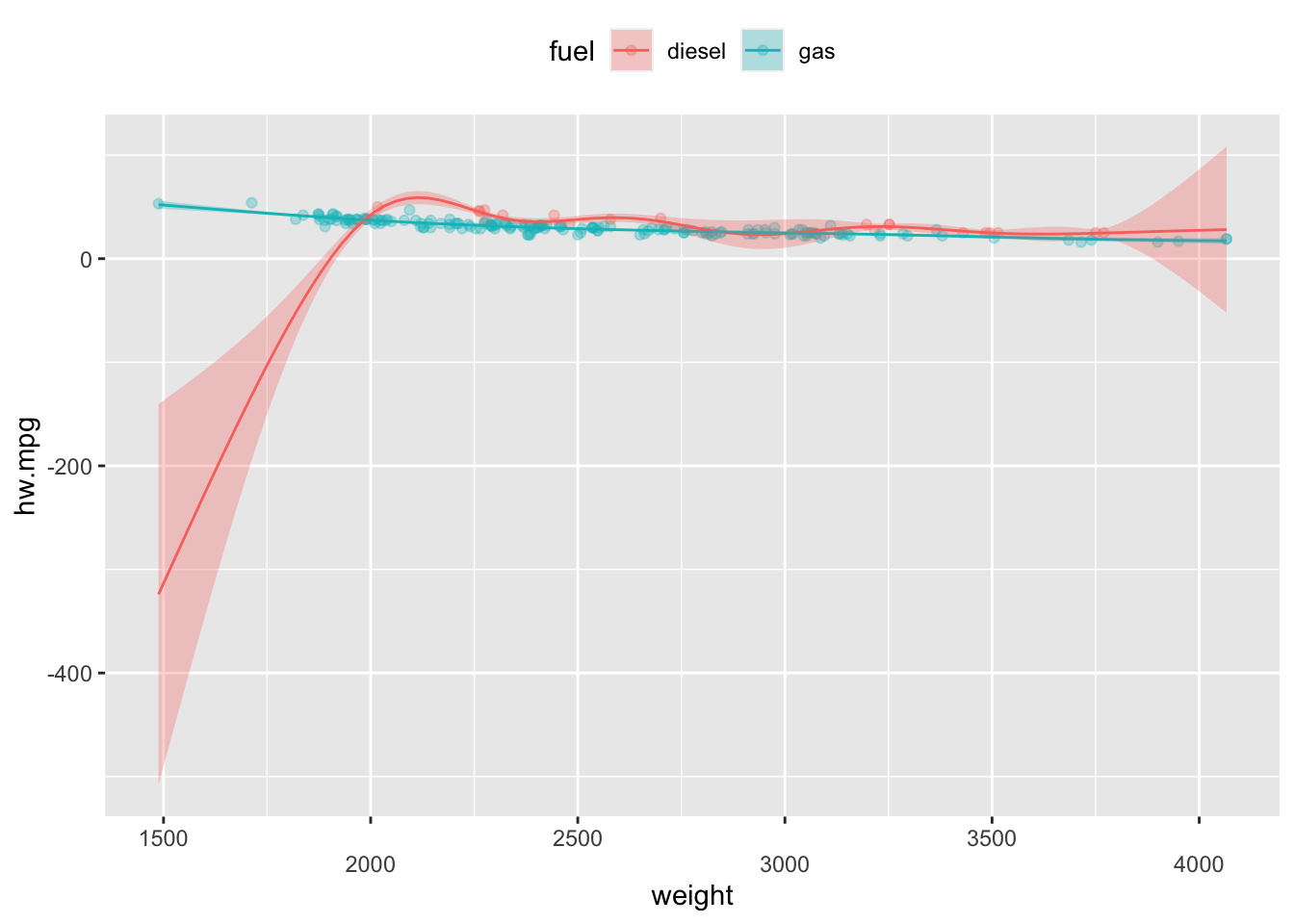 위의 그림에서 디젤과 가솔린은 서로 다른 비선형효과를 보이나 디젤의 경우 비선형효과가 불확실해 보인다.
위의 그림에서 디젤과 가솔린은 서로 다른 비선형효과를 보이나 디젤의 경우 비선형효과가 불확실해 보인다.
2.3.1.7 범주-평활 상호작용(2)
보통 범주-평활 상호작용을 생각하는 경우 비선형효과의 모양 뿐 아니라 절편의 차이도 포함하여야 하므로 범주형 변수를 추가하여 주어야 디젤에 대한 비선형효과의 추정이 개선된다.
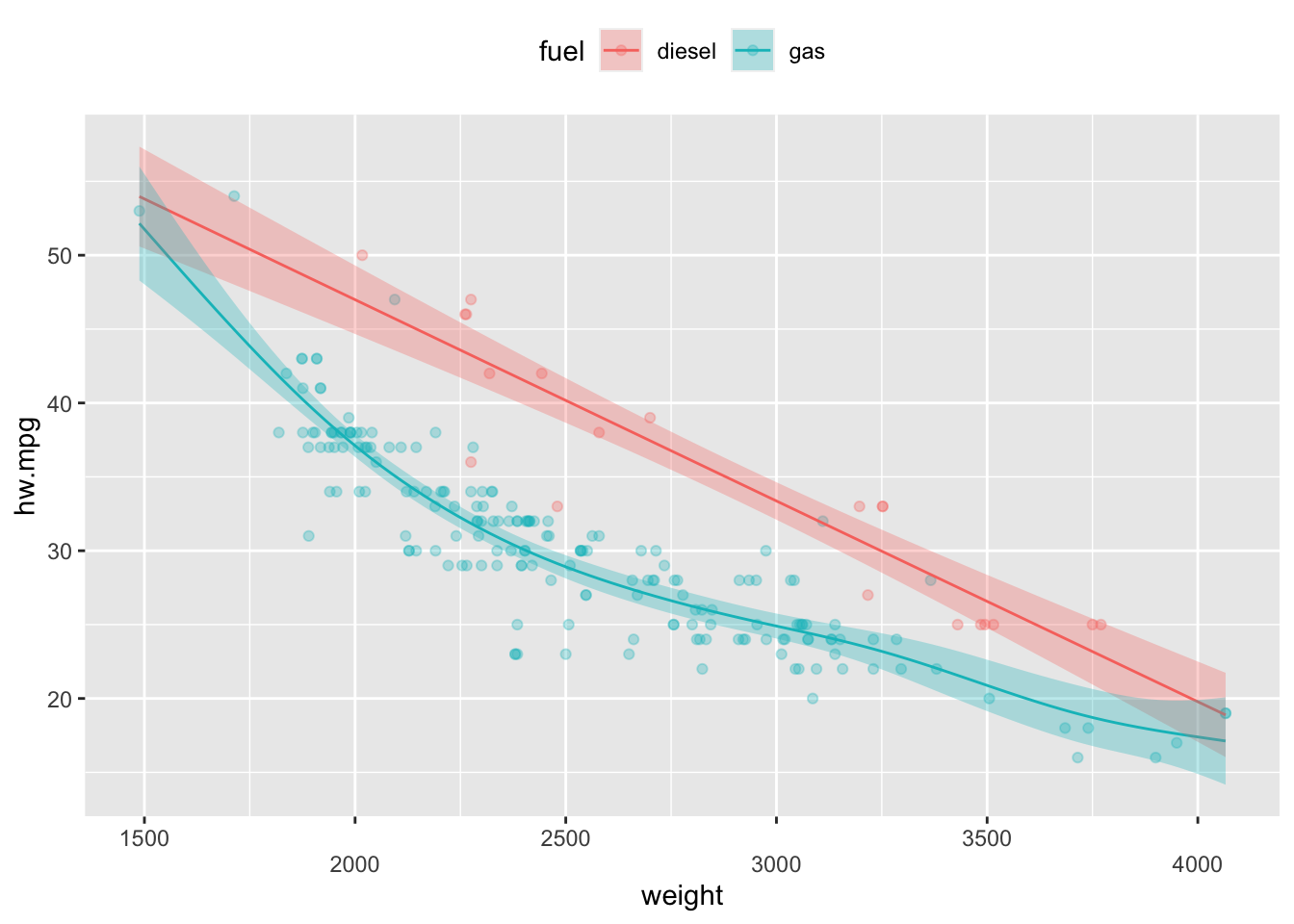
2.3.1.8 다중 평활항을 갖는 GAM
city.mpg를 반응변수로 weight, length, price의 평활함수를 설명변수로 하는 다중 GAM모형을 만들어 보면 다음과 같다.
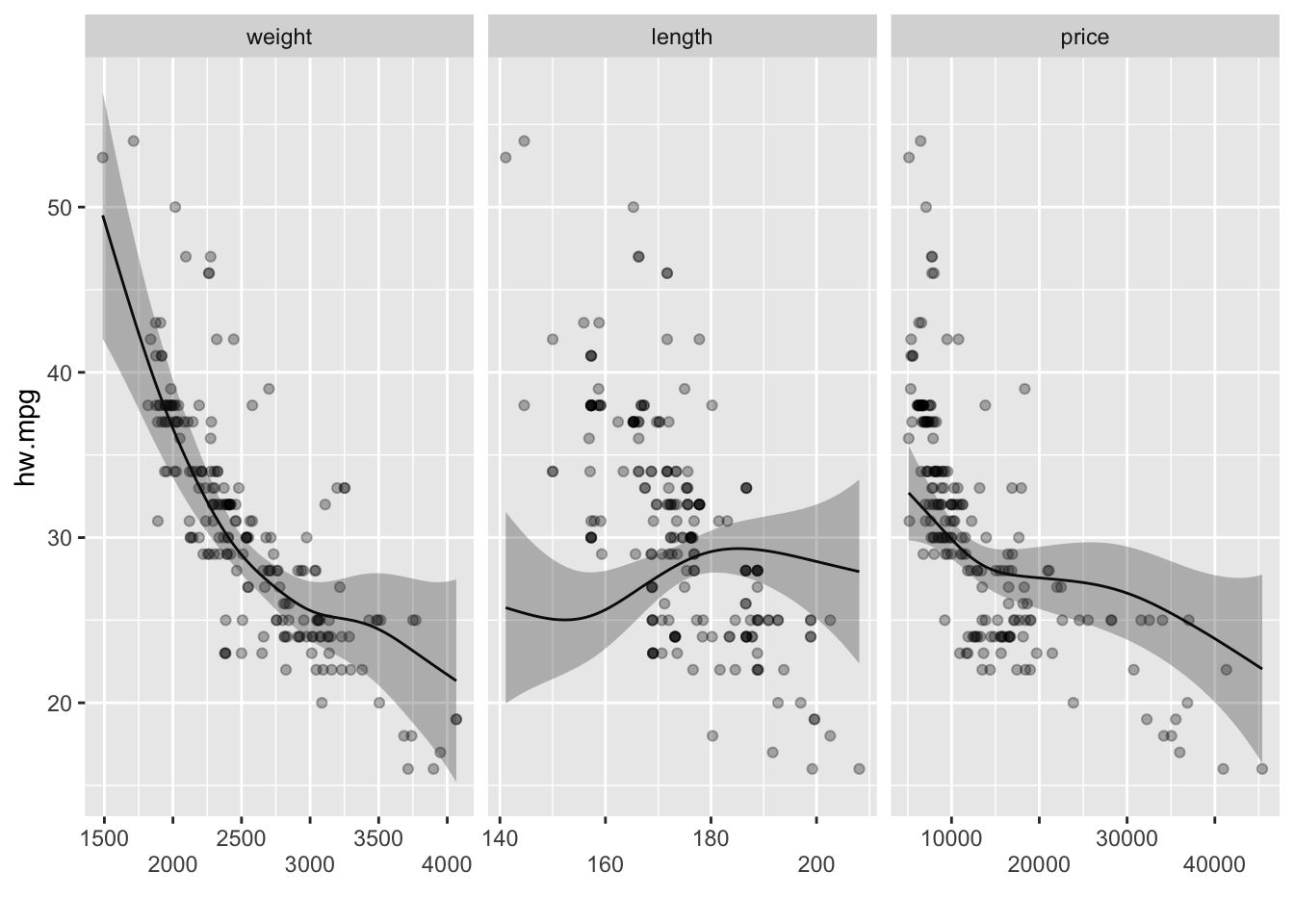
2.3.1.9 다중 평활항과 다중 범주항을 갖는 GAM
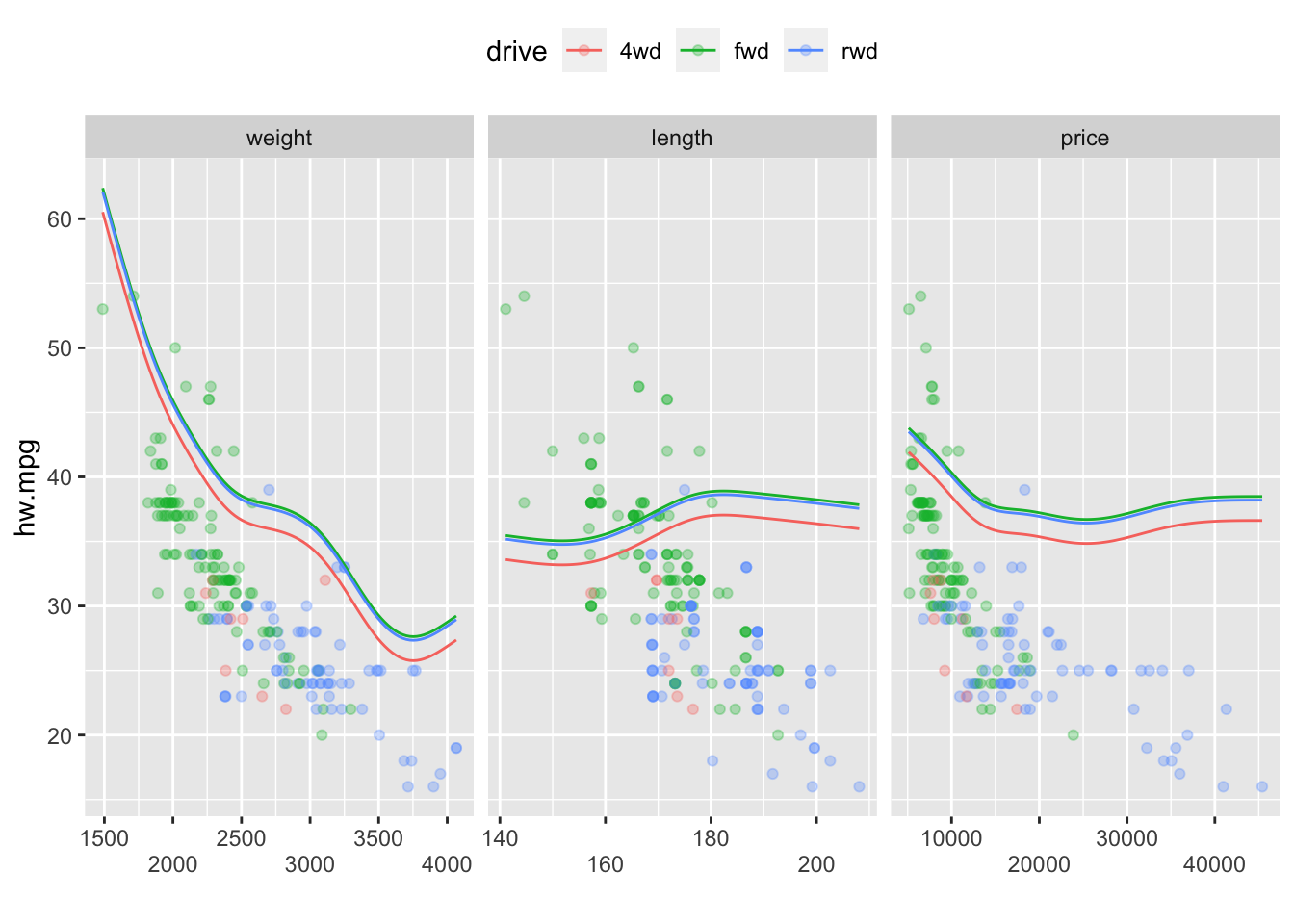
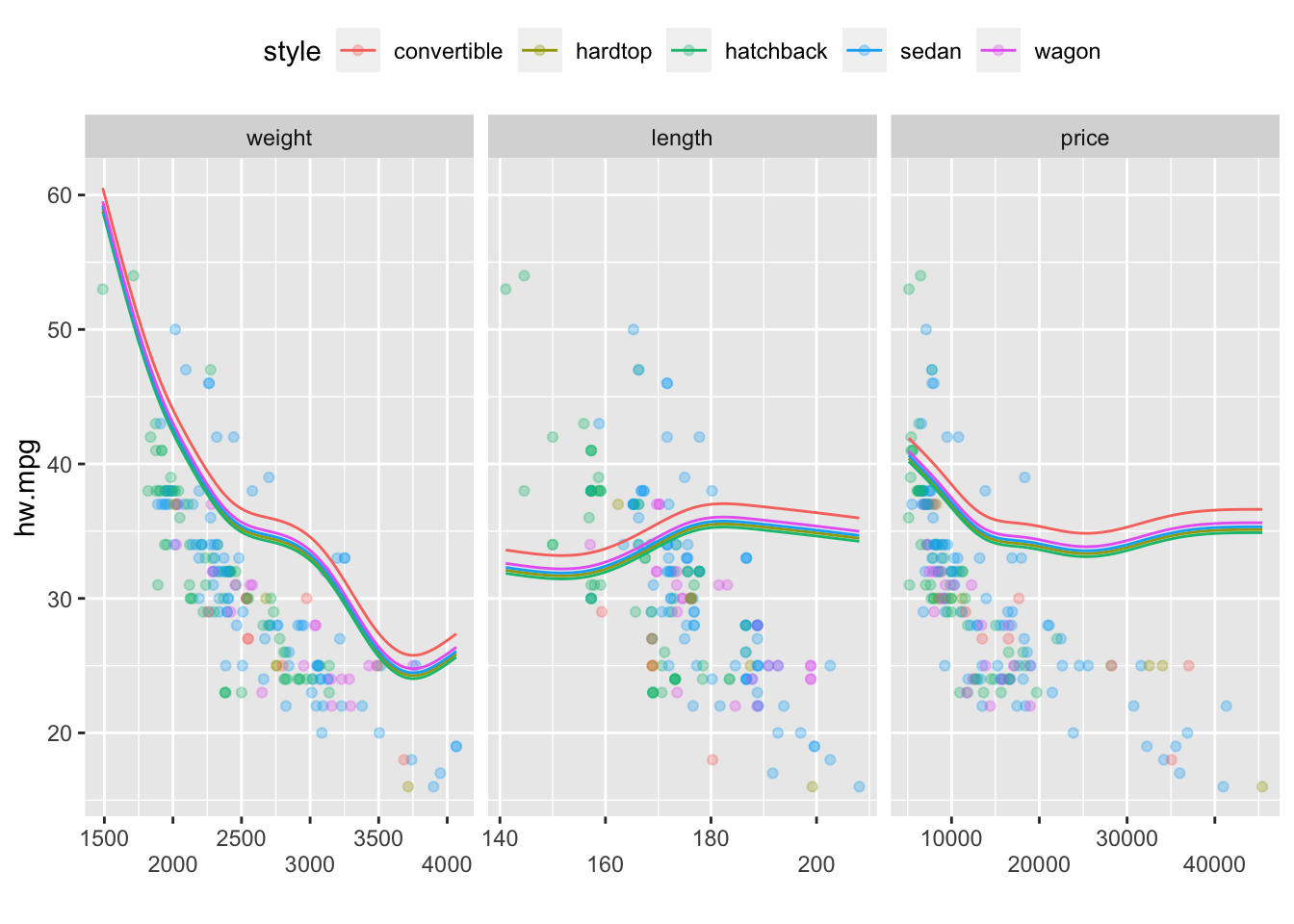
model8에 범주형변수인 fuel, drive, style을 추가하여 GAM을 만들어보면 다음과 같다.
model9 <- gam(hw.mpg ~ s(weight) + s(length) + s(price) + fuel + drive + style,
data=mpg, method="REML")
ggGam(model9)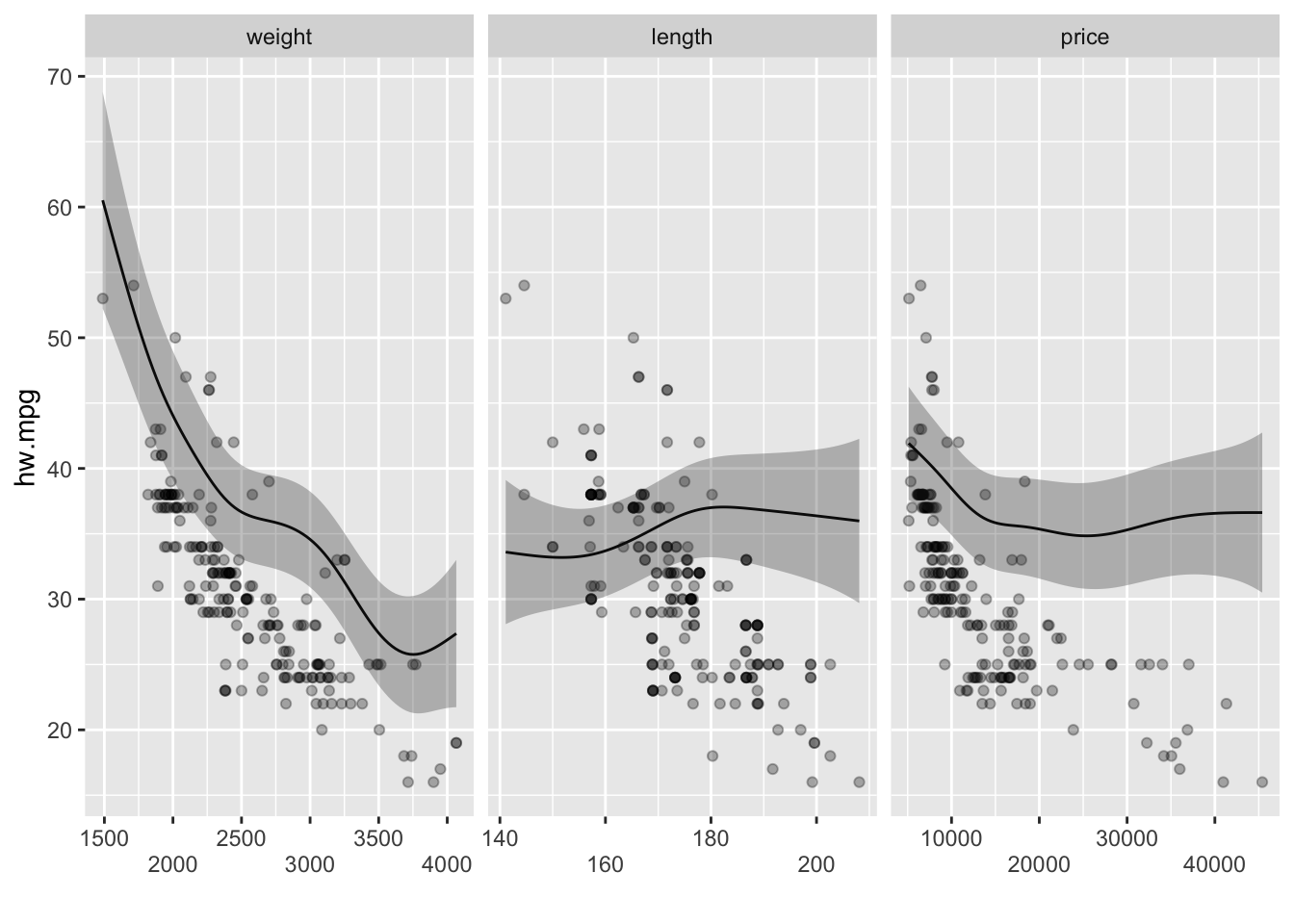
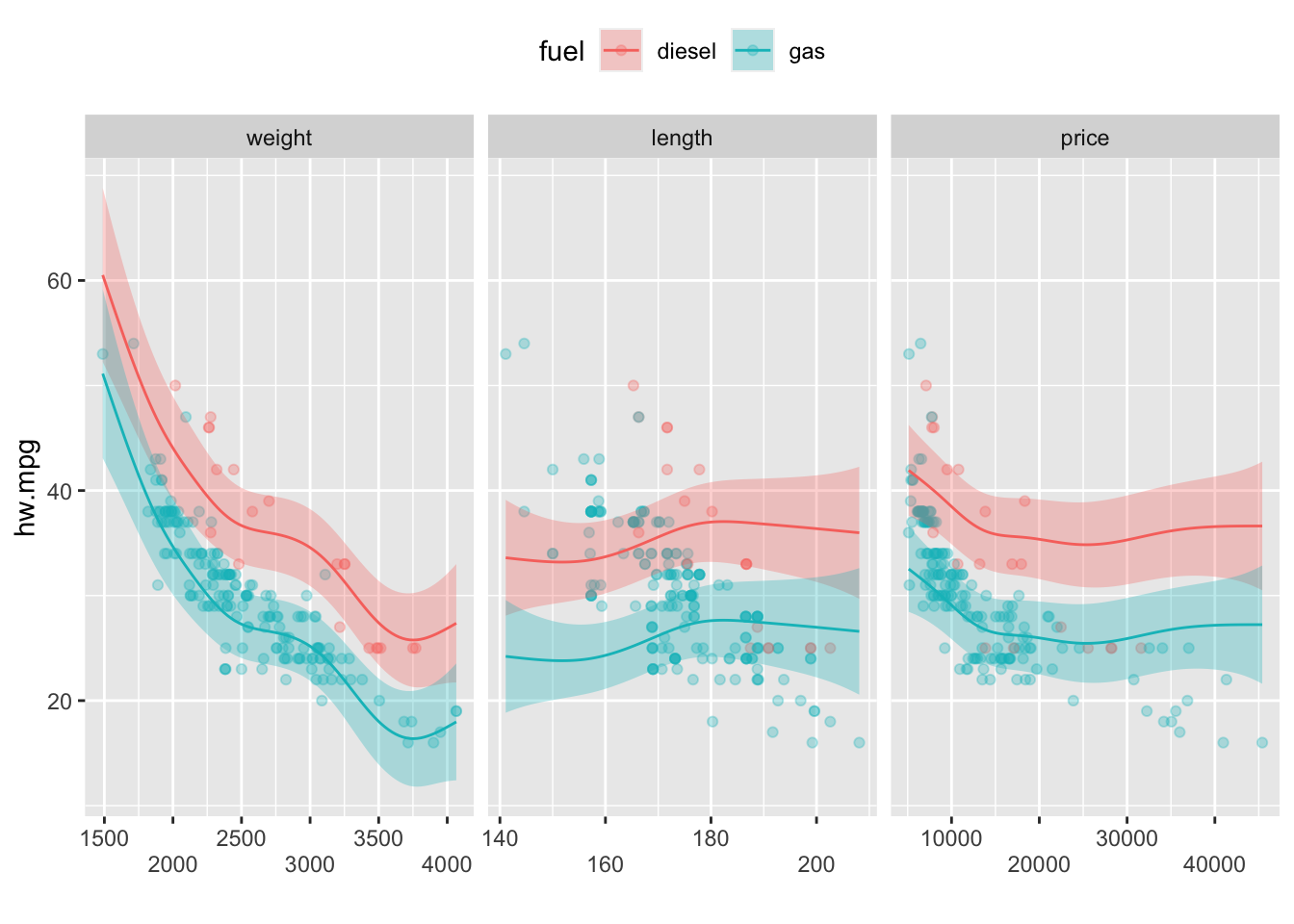
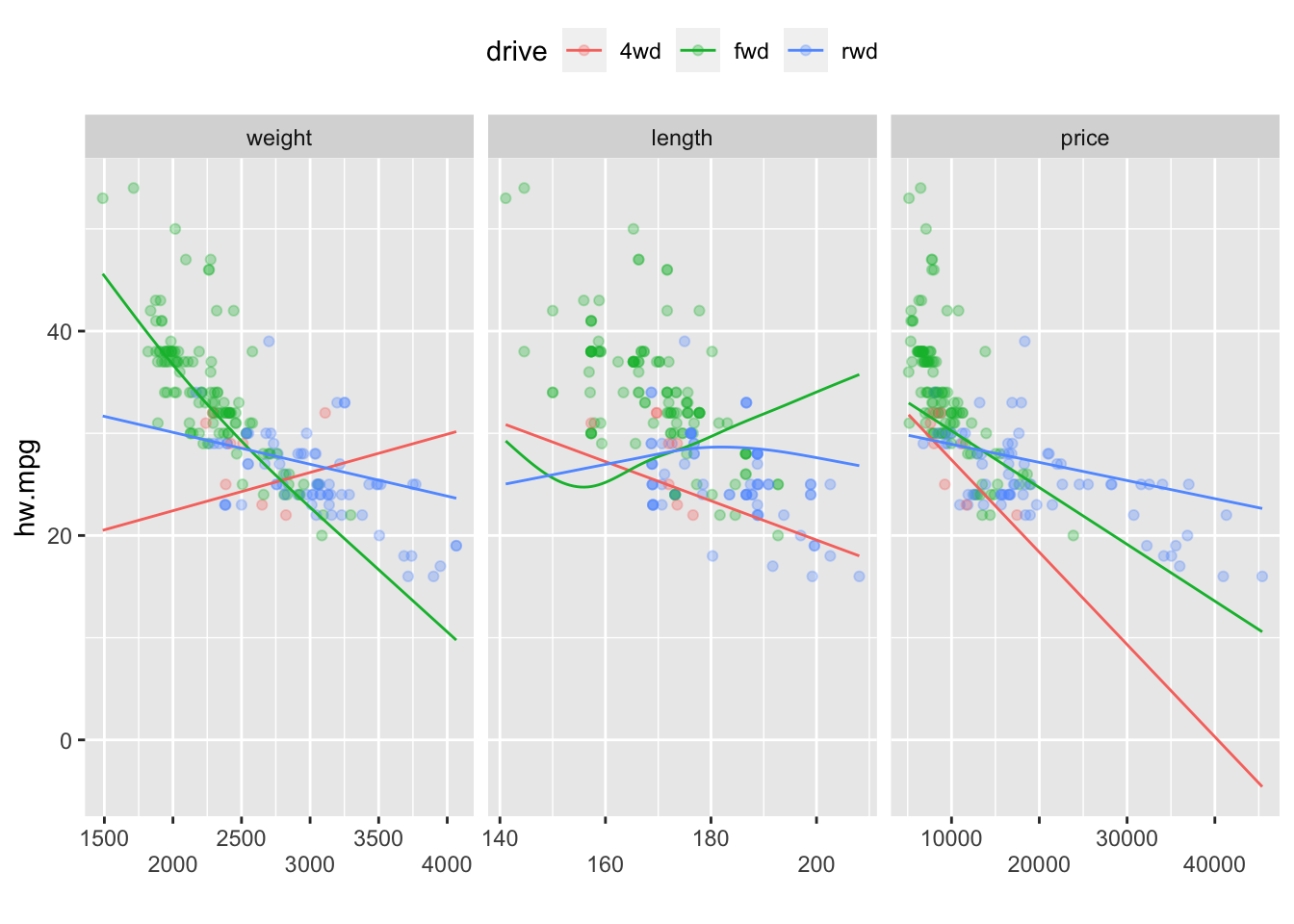
2.3.1.10 범주-다중 평활항 상호작용
다중평활항과 범주형 변수의 상호작용을 갖는 GAM을 다음과 같이 적합시킬 수 있다.
model10 <- gam(hw.mpg ~ s(weight,by = drive) + s(length, by = drive) + s(price, by= drive)+drive,
data=mpg, method="REML")
ggGam(model10,by=drive,se=FALSE)