2.3 Méthodes de tarification
Dans le chapitre 2, nous avons abordé le passage de la modélisaiton d’une variable aléatoire à une prime d’assurance, alors qu’au chapitre 4 nous avions parlé de statistiques compilées par un assureur (telle que la base de données Excel déposée sur Moodle). En réalité, on comprend qu’à une date précise (aujourd’hui), on fait l’exercice de tarification en utilisant des statistiques passés pour estimer la sinistralité future.
On peut probablement mieux expliquer cette situation à l’aide de la flèche du temps suivant:
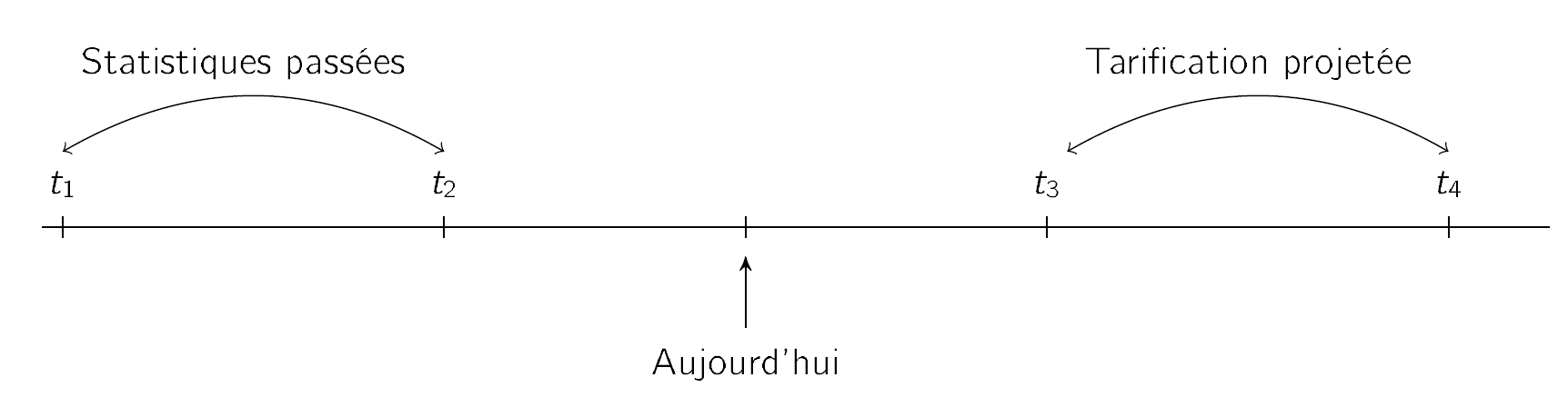
On y voit la période \([t_1, t_2]\), correspondant au moment où les statistiques utilisées pour la tarification ont été collectées et enregistrées. La période \([t_3,t_4]\), dans le futur, correspond au moment où l’exercice de tarification que nous faisons aujourd’hui sera effectif.
Plusieurs éléments valent la peine d’être mentionnées ici:
La tarification, c’est-à-dire l’exercice de calculer une prime pour différents profils d’assurés, s’appliquera à partir du temps \(t_3\), à tous les assurés de l’assureur. On parle ici de nouveaux assurés (qui n’étaient pas dans le portefeuille d’assurance à \(t=t_3 - 1\)) mais aussi aux assurés présents dans le portefeuille d’assurance, lors de leur renouvellement de primes.
On peut donc en conclure qu’il est ainsi important de comprendre la distance entre les deux périodes \([t_1, t_2]\) et \([t_3,t_4]\). La base de données utilisée pour faire l’exercice de tarification est constituée d’assurés qui ne sont probablement plus dans le portefeuille d’assurance en date d’aujourd’hui, ou qui ne le seront plus lors de la période effective de tarification en date \(t_3\).
Plus important encore, entre \([t_1, t_2]\) et \([t_3,t_4]\), le marché de l’assurance a peut-être évolué. En effets, des changements dans le milieu de l’assurance ont peut-être été observés. Mentionnons ainsi:
- Changements dans la loi des assurance, ou changement de jurisprudences;
- Inflation des coûts;
- Changement du contexte économique: fin ou début de récession, par exemple (Lors d’une récession, la sinistralité automobile a tendance à diminuer, alors que la sinistralité reliée aux accidents de travail ou aux incendies a tendance à augmenter).
- Changements à la souscription;
- Changements dans les critères d’indemnisation;
- etc.
En lien avec ces tendances de la fréquence et de la sévérité, on peut d’ailleurs se rappeller des L’évolution de la fréquence et de la sévérité des graphiques fu Groupement des Assureurs Automobiles.
Des techniques de régressions linéaires simples sont souvent proposées pour estimer les facteurs de tendance de la fréquence et de la sévérité. Pour appliquer ces facteurs de tendance, Les actuaires supposeront habituellement une date moyenne de l’expérience passée (comme étant \(\frac{t_1 + t_2}{2}\)) et une date moyenne d’application de la tarification (comme étant \(\frac{t_3 + t_4}{2}\))
2.3.1 Changement de taux
On suppose que vous travaillez dans une compagnie d’assurance existant déjà depuis un moment. L’exercice de tarification nécessite ainsi de calculer de nouvelles primes d’assurance dans un contexte où la compagnie d’assurance propose déjà des taux de primes. On appelle ainsi l’exercice un changement de taux.
Il y a habituellement trois étapes pour un changement de taux:
- On doit déterminer quel est le changement de taux moyen, ou encore le changement de taux global à appliquer aux polices.
- On doit déterminer quels sont les changements à apporter aux différentes relativités liées aux caractéristiques du risque.
- Finalement, nous devrons ajuster les primes pour que les deux exigences plus haut soient simultanément satisfaites.
Pour effectuer ces étapes, il existe deux méthodes classiques en actuariat:
- La méthode du loss cost (ou pure premium), que l’on nommera la méthode de la prime pure;
- La méthode du loss ratio, que l’on nommera la méthode du rapport sinistre-prime.
Ces méthodes sont très vieilles et sont universellement connues dans le domaine de l’assurance non-vie. Les examens professionnels parlent abondamment de ces méthodes, et l’ancienne école de tarification en assurance générale se fonde sur ces techniques. Il convient de les étudier en détails, même si on peut légitemement se demander si ces techniques sont toujours utiles étant donné les données d’assurance transactionelles maintenant disponibles facilement.
2.3.1.1 Méthode des parallélogrammes
Avant d’expliquer les deux méthodes, la technique actuarielle de mise à niveau des primes doit être expliquée. Il convient d’utiliser un exemple pour mieux expliquer cette technique.
Exemple 2.8 On considère les deux tableaux suivants.
Le premier tableau indique le montant total de primes acquises dans les trois dernières années.
| Année calendaire | Primes acquises (en milliers) |
|---|---|
| 2013 | 3853 |
| 2014 | 4600 |
| 2015 | 5125 |
Le second tableau affiche les changements de taux ayant eu lieu dans le passé.
| Taux | Date | Changement de taux |
|---|---|---|
| T1 | 1er juillet 2011 | +0.125 |
| T2 | 15 novembre 2013 | +0.100 |
| T3 | 1er octobre 2014 | +0.080 |
Les taux actuellement en force sont ceux du 1er octobre 2014, et on vous demande de calculer les primes acquises au taux actuels pour les années calendaires 2013, 2014 et 2015.
(Exemple à faire en classe)
Exemple 2.9 (Suite de l’exemple précédent) Au lieu de supposer que nous n’avons que les données agrégées pour la primes acquises de chaque année calendaire, nous avons la liste des polices, de leur date effective de police et de l’acquisition de chaque prime. Dans un tel contexte, calculez les primes acquises au taux actuels pour les années calendaires 2013, 2014 et 2015
| num. police | Date effective | Date de fin | Prime souscrite | Taux |
|---|---|---|---|---|
| 1 | 1er juillet 2012 | 30 juin 2013 | 510 | T1 |
| 2 | 1er décembre 2012 | 15 mai 2013 | 1250 | T1 |
| 3 | 1er décembre 2013 | 31 janvier 2014 | 750 | T2 |
| 4 | 1er novembre 2014 | 1er avril 2015 | 1050 | T3 |
Pour chacune des polices:
- Déterminez la prime acquise pour chaque taux et pour chaque année calendaire;
- Modifiez cette prime acquise pour la mettre au taux actuel.
(Exemple à faire en classe)
(Tableaux)
Il est ainsi assez simple de nos jours, moyennant l’utilisation d’un petit programme informatique, de calculer la prime acquise au taux actuel. On pourrait d’ailleurs faire un petit script R pour effectuer la tâche.
La technique de la prime pure ne fonctionne pas sous ce paradigme. Elle suppose plutôt, comme c’était le cas il y a plus de 30 ans, que nous n’avons pas accès à toutes ces informations transactionnelles. À la place, la technique fonctionne par approximation et par ce qui est appelé la méthode des parallélogrammes.
On utilise de nouveau une flèche du temps pour mesurer l’impact d’un changement de taux sur la prime acquise par année calendaire. En supposant un certain pattern de souscription des polices à travers l’année, il devient possible d’approximer l’impact de la modification des taux sur le portefeuille d’assurance.
Exemple 2.10 En supposant une souscription uniforme des polices dans l’année, montrez, graphiquement, l’impact qu’aurait une modification des taux de primes le 1er juillet 2015 (à mi-année) sur la prime acquise annuelle de 2015 et 2016.
(Exemple à faire en classe)
Exemple 2.11 (Suite de l’exemple) En utilisant la méthode des parallélogrammes, et une illustration graphique de l’impact des taux, calculez les primes acquises au taux actuels pour les années calendaires 2013, 2014 et 2015
(Exemple à faire en classe)
2.3.2 Méthodes de la prime pure et du rapport sinistre/prime
Ayant les primes acquises au taux de prime actuel, il est maintenant possible d’introduire aux techniques de tarification classiques en actuariat, à savoir les méthodes de la prime pure et du rapport sinistre/prime.
Les normes de pratique en actuariat sont parfois confuses au sujet de la différence entre les coûts observés et les coûts projetés, entre les primes observées et les primes projetées ou encore entre les unités acquises (observées) et les futures unités acquises. Pour démêler toutes ces valeurs, des notations plus générales (et plus précises) que celles utilisées dans les notes de examens profesionnelles ont dûes être introduites.
2.3.2.1 Méthode de la prime pure
L’idée de la méthode de la prime pure, pour le calcul du changement de taux moyen, est d’estimer la future prime pure moyenne, et de la comparer avec la prime pure moyenne observée dans le passé. Comme l’encadré précédent l’indiquait, il convient néanmoins de faire attention aux différences entre le observé, le espéré et le projeté.
- Nous calculons d’abord la sinistralité projetée \(S(proj)\), en se basant sur la sinistralité observée \(S(obs)\) :
\[S(proj) = f_S(S(obs))\]
où \(f_S(.)\) est une fonction modifiant la sinistralité observée en sinistralité projetée (en y ajoutant une tendance, par exemple).
- Nous calculons les unités acquises futures et projetées \(UA(proj)\), en se basant sur les unités acquises observées \(UA(obs)\):
\[UA(proj) = f_U(UA(obs))\]
où \(f_U(.)\) est une fonction modifiant les unitées acquises observées en unités acquises projetées (en y incorporant une augmentation ou une diminution de la clientèle, par exemple). On peut toutefois supposer qu’il existe un lien fort entre \(f_S(.)\) inclut déjà la tendance des unités acquises. En ce sens, on peut raisonnablement supposer que \(UA(proj) = UA(obs))\).
- On peut ainsi calculer la prime pure projetée (\(PP(proj)\)), comme:
\[PP(proj) = \frac{S(proj)}{UA(proj)}\]
- On peut estimer les dépenses fixes projetées moyennes par polices (\(\overline{F}(proj)\)) comme
\[\overline{F}(proj) = \frac{F(proj)}{UA(proj)} \]
- En estimant le rapport sinistre/prime admissible projeté (\(PLR(proj) = 1 - V(proj) - Q(proj)\)), on passe ainsi à la prime nette projetée (\(PN(proj)\)):
\[ PN(proj) = \frac{PP(proj)+\overline{F}(proj)}{PLR(proj)} \]
2.3.2.2 Méthode du rapport sinistre/prime
La seconde méthode fonctionne similairement à la première, à la différence que ce sont les rapports sinistre/prime observé et attendu qui sont les bases du calcul. Comme on utilise un rapport, la totalité des variables utilisées dans cette méthode correspond aussi à des rapports.
- On utilise les primes acquises au taux actuel (\(PA(obs)_{act}\)) calculé, par exemple, à l’aide la méthode des parallélogrammes.
- On se base sur le rapport sinistre/prime projeté avec les primes actuelles (\(LR(proj)_{act}\)), défini comme:
\[LR(proj)_{act} = \frac{S(proj)}{PA(obs)_{act}}\]
- En estimant le rapport de dépenses fixes projeté (\(FER(proj)\)) et le rapport sinistre/prime admissible projeté (\(PLR(proj) = 1 - V(proj) - Q(proj)\)), on calcule la modification au taux de primes (, \(IRC\)) comme:
\[IRC = \frac{LR(proj)_{act} + FER(proj)}{PLR(proj)} \]
où nous avons aussi la relation suivante:
\[PN(proj) = PN(act) \times IRC\]
avec \(PN(act)\) représentant la prime nette actuelle définie comme:
\[PN_{act} = \frac{PA(obs)_{act}}{UA(proj)}\]
2.3.2.3 Similitude des deux méthodes
Évidemment, avec des chiffres cohérents, les deux méthodes devraient générer les mêmes indications de modification de primes. C’est d’ailleurs un résultat bien important pour l’association professionnelle de la CAS, qui va jusqu’à utiliser l’expression “théorème” pour montrer cette équivalence.
Proposition 2.2 Les méthodes du rapport sinistre/prime et de la prime pure sont équivalentes.
(Proposition à prouver en classe)
Encore une fois, comme c’est souvent le cas avec les normes de pratiques ou les techniques plus intuitives qui n’ont pas réellement de formaliste mathématique, il est plus simple d’illustrer les méthodes par un exemple numérique.
Exemple 2.12 Voici un exemple tiré d’un livre de référence de la CAS. Nous voulons faire une tarification et un changement de taux en ayant les informations suivantes:
| Information | Valeur |
|---|---|
| Sinistralité attendue (développée et projetée) | 30 000 000 |
| Unités acquises | 1 000 000 |
| Primes acquises au taux actuel | 45 000 000 |
| Dépenses fixes | 5 000 000 |
| Dépense variables | 0.15 |
| Profit et taxes | 0.10 |
Calculez le changement de taux attendu selon les deux méthodes de tarification classiques en actuariat.