2.1 Calcul de la prime

L’une des tâches classiques de l’actuaire est de tarifer les risques à assurer, c’est-à-dire de calculer un prix au contrat d’assurance d’un risque particulier.En d’autres mots, c’est le travail de l’actuaire de déterminer ce que sera la prime d’assurance à charger à un certain profil d’assuré, pour un certain produit d’assurance.

On appelle tarification a priori, la tarification qui se base sur les caractéristiques de l’assuré, mais qui ne se base pas sur l’historique de réclamations de ce dernier. Nous appellons tarification a posteriori, la tarification qui corrige la tarification a priori en considérant l’historique de réclamations d’un assuré.

Le principe d’assurance peut être simple. L’assuré échange son risque $S$ contre une constante $c$ correspondant à une prime d’assurance.

Une manière raisonnable et de déterminer la constante $c$ à substituer à une variable aléatoire serait de choisir la constante la plus proche de la variable aléatoire $S$ correspondant à la charge totale de sinistres. On appelle prime pure la constante $c$ qui approche le plus possible la variable aléatoire $S$.

Il existe plusieurs manières de quantifier l’expression la plus proche. Dans des cours du baccalauréat, vous pourriez être introduits à des notions de distances entre une constante $c$ et une variable aléatoire $S$. Pour le moment, nous serons un peu plus pragmatiques pour éviter d’entrer dans des notions de probabilités qui n’ont pas été vues par tous.

On se rappelle que la tarification habituelle en assurance est prospective, signifiant que l’assureur utilise les données passées de la sinistralité enregistrée pour estimer les réclamations futures. En prenant en exemple la base de données fictives et en supposant que le passé est une bonne image de ce qui pourrait arriver dans le futur, on pourrait ainsi voir comment l’utiliser.

2.1.1 Base de données fictive

L’objectif du calcul de la prime est de trouver une seule valeur $c$ qui pourrait résumer l’historique de réclamations passées des 386,883 contrats que nous avons. Pour chaque contrat de la base de données fictive, on peut calculer la charge pure selon l’équation qui a été donnée au chapitre précédent.

db.fictif$charge.pure <- db.fictif$Tot.Cost/db.fictif$expo

Il peut parfois être difficile de bien visualiser les données en assurance car elles représentent souvent ce qu’on appelle une distribution mixte discrète/continue.

En effet, nous observons deux blocs de contrats: - une importante masse de contrats avec une charge pure nulle, représentant tous les contrats n’ayant pas eu de réclamations d’assurance;
- le restant des contrats portefeuille, composé d’assuré ayant réclamé pendant leur contrat, affiche une charge pure positive représentant la somme de toutes les réclamations qu’ils ont eu dans l’année.

On peut ainsi séparer le portefeuille de contrats selon ces deux blocs. On y voit que 83.58% des contrats du portefeuille ont une charge nulle (323,390 contrats).

db.fictif.0 <- db.fictif[which(db.fictif$charge.pure == 0),]
db.fictif.99 <- db.fictif[which(db.fictif$charge.pure > 0),]

c(nrow(db.fictif.0)/nrow(db.fictif), nrow(db.fictif.99)/nrow(db.fictif))

## [1] 0.8358858 0.1641142

Pour les assurés ayant réclamé au moins une fois, il est possible de faire un histogramme des charges pures:

library(ggplot2)
ggplot()+
  geom_histogram(aes(x=charge.pure), data=db.fictif.99) +
  xlab('Charge pure')+
  ylab('Nombre de contrats')+
  theme_classic()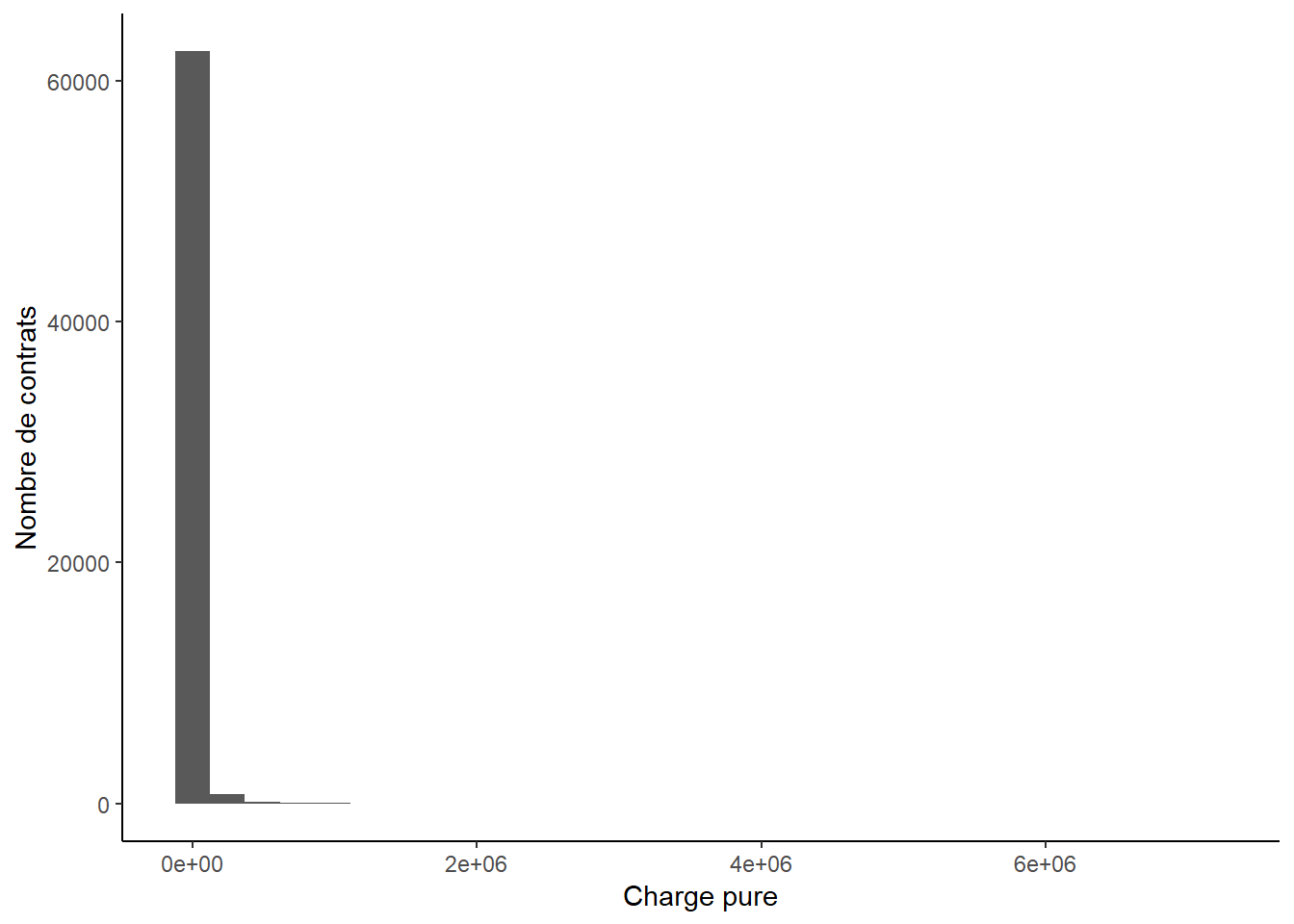

On ne voit pas très bien l’histogramme car certaines valeurs extrêmes ont été observées dans les données. Les 5 plus grandes valeurs de charge pure sont en effet plus grandes que 3.5 millions de dollars.

db.fictif %>%
  arrange(-charge.pure) %>%
  slice(1:5) %>%
  select(charge.pure)

## # A tibble: 5 × 1
##   charge.pure
##         <dbl>
## 1    7151107.
## 2    4770314.
## 3    4078290.
## 4    3996064.
## 5    3696081.

À la place, on peut peut-être simplement faire l’histogramme du logarithme de la charge pure.

ggplot()+
  geom_histogram(aes(x=log(charge.pure)), data=db.fictif.99) +
  xlab('Logarithme de la charge pure')+
  ylab('Nombre de contrats')+
  theme_classic()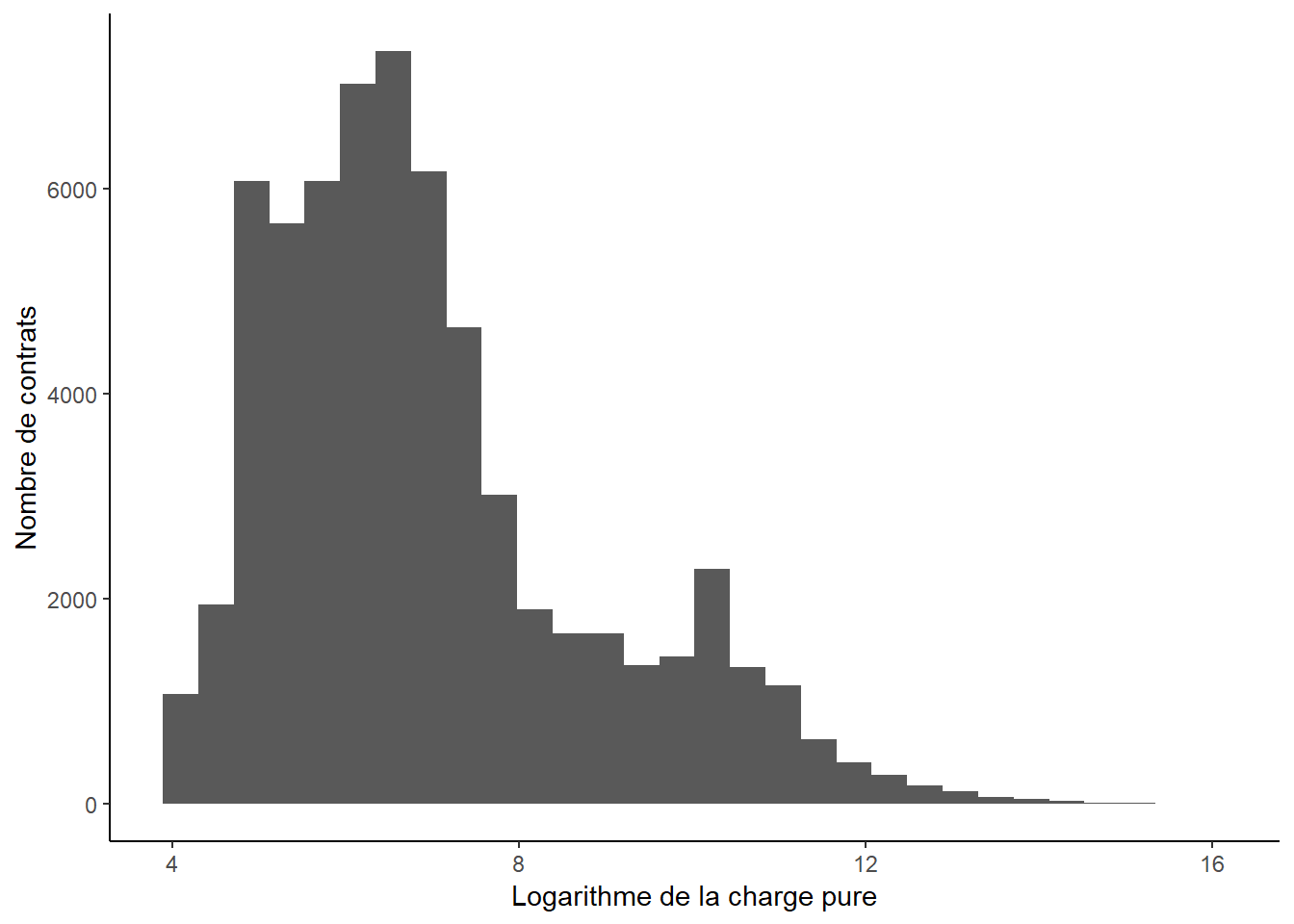

Une autre bonne représentation visuelle de toutes les valeurs possibles est de calculer le nombre de contrats ayant une valeur égale ou plus petite qu’une certaine valeur.

db.fictif %>%
  group_by(charge.pure) %>%
  summarise(nb.contrat = n()) %>%
  ungroup() %>%
  mutate(nb.contrat.cumul = cumsum(nb.contrat)/1000) %>%
  ggplot()+
  geom_line(aes(x=log1p(charge.pure), y=nb.contrat.cumul)) +
  geom_point(aes(x=log1p(0), y=nrow(db.fictif.0)/1000), color='red') +
  xlab('Charge pure')+
  ylab('Nombre de contrats cumuatifs (en milliers)')+
  ylim(0, nrow(db.fictif)/1000)+
  theme_classic()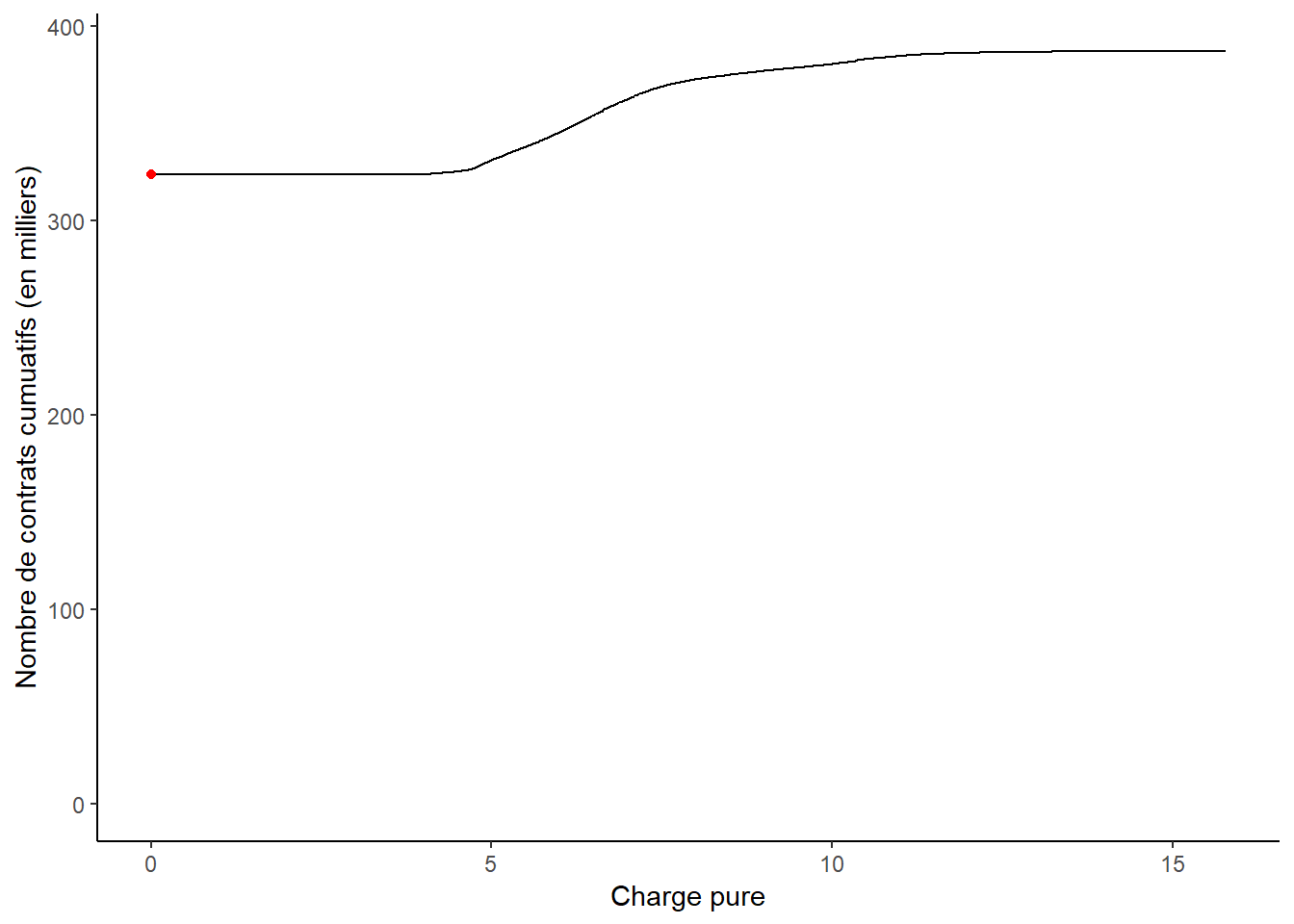

Pour chaque valeur de la charge pure en abscisses, la valeur de la courbe indique le nombre de contrats du portefeuille qui a une valeur de charge pure inférieure. Le point rouge indique ainsi le nombre de contrats ayant une valeur de la charge pure nulle, et la plus grande valeur observée pour la charge pure, (soit 7,151,107, avec log(7,151,107) = 15.78) génère une valeur de 386,883 correspondant au nombre de contrats du portefeuille.

En termes probabilistes, l’expression distribution cumulative empirique est souvent utilisée pour référer à la dernière figure lorsque celle-ci est exprimée en proportion du nombre de contrats total. Le cours MAT1700 Probabilités abordera ce concept.

2.1.2 Candidats pour la prime pure

Dans tous les cas, pour le calcul de la prime pure, on voit ainsi qu’il n’est pas simple de résumer à une seule valeur la distribution de la charge totale de la base de données utilisée. Ce ne sont pas toutes les bases de données en assurance qui ont la même distribution de la charge pure. Certains produits d’assurance ont une masse à zéro plus grande ou plus petite, une proportion différente de petites valeurs de la charge pure est observée, les valeurs maximales ne sont pas les mêmes, etc.

Le calcul de la prime pure a l’objectif de trouver une seule valeur numérique approximant le mieux possible la distribution de la charge pure. Quelques candidats sont intuitivement possibles:

le mode de la distribution (soit la valeur de la charge totale la plus observée dans les données);
la médiane de la distribution (soit la valeur de la charge totale correspond au centre de la série de données, et correspondant ainsi à la valeur de la charge pure qui sépare une distribution en groupes contenant le même nombre de donnée.);
la moyenne de la distribution.

Exemple 2.1 Pour la base de données fictives, quelles sont les valeurs du mode et de la médiane de la charge totale?

(Exemple à faire en classe)

Demander une prime pure de 0$ aux assurés pour leur protection d’assurance n’a aucun sens. La médiane et le mode seraient donc des candidats exclus.

Bien que nous nous basions sur une base de données fictive d’assurance automobile pour illustrer ou encore même justifier que la médiane et le mode ne sont pas des solutions envisageables, la même conclusion s’appliquerait dans la grande majorité des produits d’assurance. En effet, que ce soit en assurance automobile, en assurance habitation ou en assurance des fermes, le mode et la médiane sont presque toujours égaux à 0.

En 2023 par exemple, on pourrait estimer qu’environ 90% des contrats d’assurance automobiles annuels ne génère pas de réclamations. On passerait à environ 95% pour l’assurance habitation.

La moyenne empirique serait donc une bien meilleure candidate pour le calcul de la prime pure. Il faut néanmoins faire attention à l’exposition au risque dans le calcul de la moyenne de la charge totale. Comme on le voit avec le petit calcul plus bas en R, la moyenne de la charge pure pour tous les contrats ne correspond à la somme des pertes totale divisée par l’exposition.

c(mean(db.fictif$charge.pure), sum(db.fictif$Tot.Cost)/sum(db.fictif$expo))

## [1] 1960.531 1439.923

Ce calcul simple fait en sorte qu’une valeur de 1439.92$ serait choisie pour la prime pure d’un contrat avec une exposition au risque de 1.

Exemple 2.2 On suppose trois assurés exposés au risque pendant 0.25, 0.5 et 0.75 années. Quelles seraient leurs primes pures?

(Exemple à faire en classe)

Il devient ainsi possible de calculer la prime pure de tous les contrats du portefeuille.

pp <- sum(db.fictif$Tot.Cost)/sum(db.fictif$expo)

db.fictif$prime.pure <- pp*db.fictif$expo

En faisant un tel exercice, on se rendrait d’une propriété extrêmement importante de la tarification actuarielle: le balancement financier.

Cela signie que la somme des primes de chacun des contrats est égale à la somme des coûts totaux. Cette équivalence est importante car si le passé est comme le futur, l’assureur s’attendra à ce que ce qu’il collecte comme prime pure sera égal à ce qu’il paye.

c(sum(db.fictif$prime.pure), sum(db.fictif$Tot.Cost))

## [1] 488171982 488171982

Exemple 2.3 En utilisant R, calculez: - la prime pure de la composante de fréquence; - la prime pure de la composante de sévérité.

Vérifiez si le principe de balancement fonctionne pour la fréquence et la sévérité, mais aussi lorsque la prime pure de la charge totale correspond au produit de la prime pure de la fréquence et de la prime pure de la sévérité.

Attention: 1) l’exposition au risque doit être considérée pour la fréquence seulement;
2) les colonnes Cost1, Cost2, …, Cost7 indiquent le coût de chacun des réclamation d’un contrat.

(Exemple à faire à la maison)

Au dela de la médiane, du mode et de la moyenne, d’autres formes de primes pures peuvent aussi être utilisés. Toutefois, sauf avis contraire, nous utiliserons toujours la moyenne pour le calcul de la prime pure.

2.1.3 Chargement de sécurité

Dans les étapes suivantes de tarification, un assureur se doit d’ajouter ce qui est appelé un chargement de sécurité.

Exemple 2.4 On suppose un produit d’assurance de réclamation de vols de valises ayant l’historique de réclamations suivants:

75% des contrats ne réclament pas et produisent ainsi une charge pure nulle;
25% des contrats produisent une seule réclamation d’une valeur unique de 5760$.

Calculez la prime pure basée sur le mode, la moyenne et la médiane.

(Exemple à faire à la maison)

Il est intéressant de voir que les deux produits d’assurance, l’assurance automobile de la base de données fictive et l’assurance de vols de valise décrit ci-dessus, ont la même prime pure. Par contre, du point de vue de l’assureur, les produits ne sont vraiment pas équivalents. Alors que la perte maximale pour l’assureur avec le produit d’assurance valise est de 5760$, l’assureur pourrait devoir payer plus de 7 millions de dollars pour l’assurance automobile.

Intuitivement, deux risques de même moyenne, mais ayant des pertes maximales fortement inégales ne devraient certainement pas avoir le même coût. L’un des deux risques est plus dangereux que l’autre. Le but du chargement de sécurité est ainsi de permettre à l’assureur de minimiser son risque d’insolvabilité.

Dans plusieurs ouvrages et articles professionnels, les actuaires n’incluent pas de chargement de sécurité à la prime pure. Dans ce cours, afin de distinguer la prime pure sans chargement de sécurité et la prime pure avec un chargement de sécurité, nous parlerons respectivement de prime pure et de prime pure chargée.

L’objectif de cette partie du chapitre sur l’introduction à la tarification est de proposer certaines quantifications de ce chargement de sécurité. Sans entrer dans des détails trop techniques, l’idée générale serait de pouvoir accorder une prime pure chargée basée sur une certaine forme de calcul du risque d’insolvabilité.

Proposition 2.1 Un principe de calcul de prime est une fonctionnelle $\mathsf{H}$ faisant correspondre une prime pure chargée à un risque $S$. Cette méthode est utilisée pour ajouter un chargement de sécurité à la prime pure.

On peut lister quelques propriétés importantes que doivent satisfaire les principes de calcul de prime:

Afin de ne pas motiver l’assuré à morceler le risque, quels que soient les risques $S$ et $T$, nous avons:

\[\mathsf{H}[S+T] \le \mathsf{H}[S] + \mathsf{H}[T]\]

Nous voulons qu’un contrat offrant plus de protection qu’une autre coûte aussi davantage. Ainsi, quels que soient les risques $S$ et $T$, nous avons:

\[\mathsf{H}[S] \le \mathsf{H}[S] + \mathsf{H}[T]\]

Afin qu’aucun assuré n’ait à payer une prime de montant supérieur au préjudice maximal qu’il pourrait subir, quels que soit le risque $S$ tel qu’il existe une constante $M$ représentant la perte maximale, nous avons:

\[\mathsf{H}[S] \le M\]

Exemples de principes de calcul de primes:

Principe du chargement proportionnel : $\mathsf{H}[S; \rho] = (1+\rho) \overline{S}$;
Principe du chargement additif: $\mathsf{H}[S; \rho] = \overline{S} + \rho$;
Principe de la perte maximale: $\mathsf{H}[S; \rho] = \overline{S} + \rho \max(S)$;
Principe de la valeur au risque à $X$% (VaR, value-at-risk): $\mathsf{H}[S; \rho] = \overline{S} + \rho q_S(X)$.
Principe de l’écart-type : $\mathsf{H}[S; \rho] = \overline{S} + \rho s$;
Principe de la variance : $\mathsf{H}[S; \rho] = \overline{S} + \rho s^2$;

Exemple 2.5 On reprend les deux exemples vus plus tôt, soit celui de l’assurance automobile et celui de l’assurance valise. Calculez la prime pure chargée selon les 4 premiers principes de primes vus plus ci-dessus.

(Exemple à faire à la maison)

Les valeurs des quantiles à 95% et 99% ont été calculées comme:

quantile <- db.fictif %>%
  group_by(charge.pure) %>%
  summarise(nb.contrat = n()) %>%
  ungroup() %>%
  mutate(quantile = cumsum(nb.contrat)/nrow(db.fictif)) 

quantile %>% 
  filter(quantile >= 0.95) %>%
  slice(1) %>%
  select(charge.pure)

## # A tibble: 1 × 1
##   charge.pure
##         <dbl>
## 1       1609.

quantile %>% 
  filter(quantile >= 0.99) %>%
  slice(1)%>%
  select(charge.pure)

## # A tibble: 1 × 1
##   charge.pure
##         <dbl>
## 1      37735.

On peut noter que c’est la colonne cahrge.pure qui a été utilisée dans le calcul du quantile.

Il existe une multitude d’autres principes de prime, surtout basée de la théorie probabiliste avancée. Il existe une vaste littérature scientifique des principes de primes et du risque d’insolvabilité.