第 6 章线性回归分析

这一章我们主要介绍一些如何用R 实现线性回归，线性回归分析主要包括一般线性回归，多元线性回归、广义线性回归分析以及贝叶斯线性回归分析等，线性回归是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，运用十分广泛。其表达形式为\(y= w*x+e\), e为误差服从均值为0的正态分布。回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。跟方差分析类似，我们也可以分为一元线性回归，二元线性回归以及多元线性回归分析，这些线性回归模型主要对于数据程标准正态分布得情况下比较适用，如果数据不符合标准正态分布，则可以选择广义线性回归。这里我们依然使用iris 来进行线性回归举例。比如我们想知道Sepal.Length和Petal.Length线性关系，我们可以做以下运算：

6.1 一元线性回归

我们假设这个一元方程为 \(y=a*Petal.Length +b\),我们用Petal.Length 来对Sepal.Length做线性回归。

#加载数据
data("iris")
m1 <- lm(Sepal.Length ~Petal.Length,data = iris )
## 查看结果
summary(m1)
## 
## Call:
## lm(formula = Sepal.Length ~ Petal.Length, data = iris)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1.24675 -0.29657 -0.01515  0.27676  1.00269 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   4.30660    0.07839   54.94   <2e-16 ***
## Petal.Length  0.40892    0.01889   21.65   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.4071 on 148 degrees of freedom
## Multiple R-squared:   0.76,  Adjusted R-squared:  0.7583 
## F-statistic: 468.6 on 1 and 148 DF,  p-value: < 2.2e-16
##计算模型方差

aov <-anova(m1) 
aov
## Analysis of Variance Table
## 
## Response: Sepal.Length
##               Df Sum Sq Mean Sq F value    Pr(>F)    
## Petal.Length   1 77.643  77.643  468.55 < 2.2e-16 ***
## Residuals    148 24.525   0.166                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#查看预测值
head(fitted(m1),5)
##        1        2        3        4        5 
## 4.879095 4.879095 4.838202 4.919987 4.879095
#查看残差值
head(residuals(m1),5)
##          1          2          3          4          5 
##  0.2209054  0.0209054 -0.1382024 -0.3199868  0.1209054
## 对预测值和实测值进行绘图
plot(fitted(m1),iris$Sepal.Length)
abline(0,1)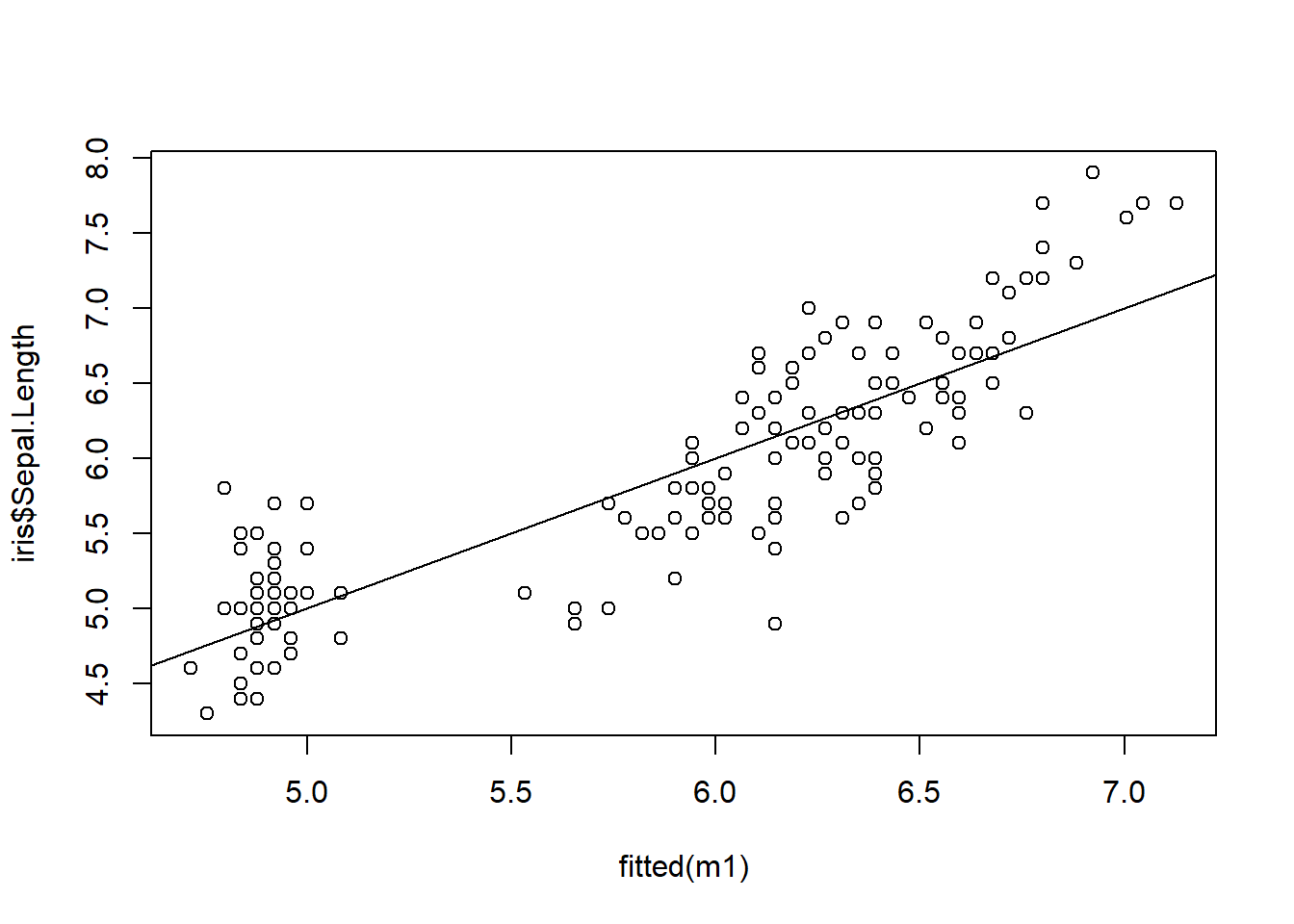

图6.1: 一元线性回归图

##对预测值得残差值绘图
plot(fitted(m1),residuals(m1))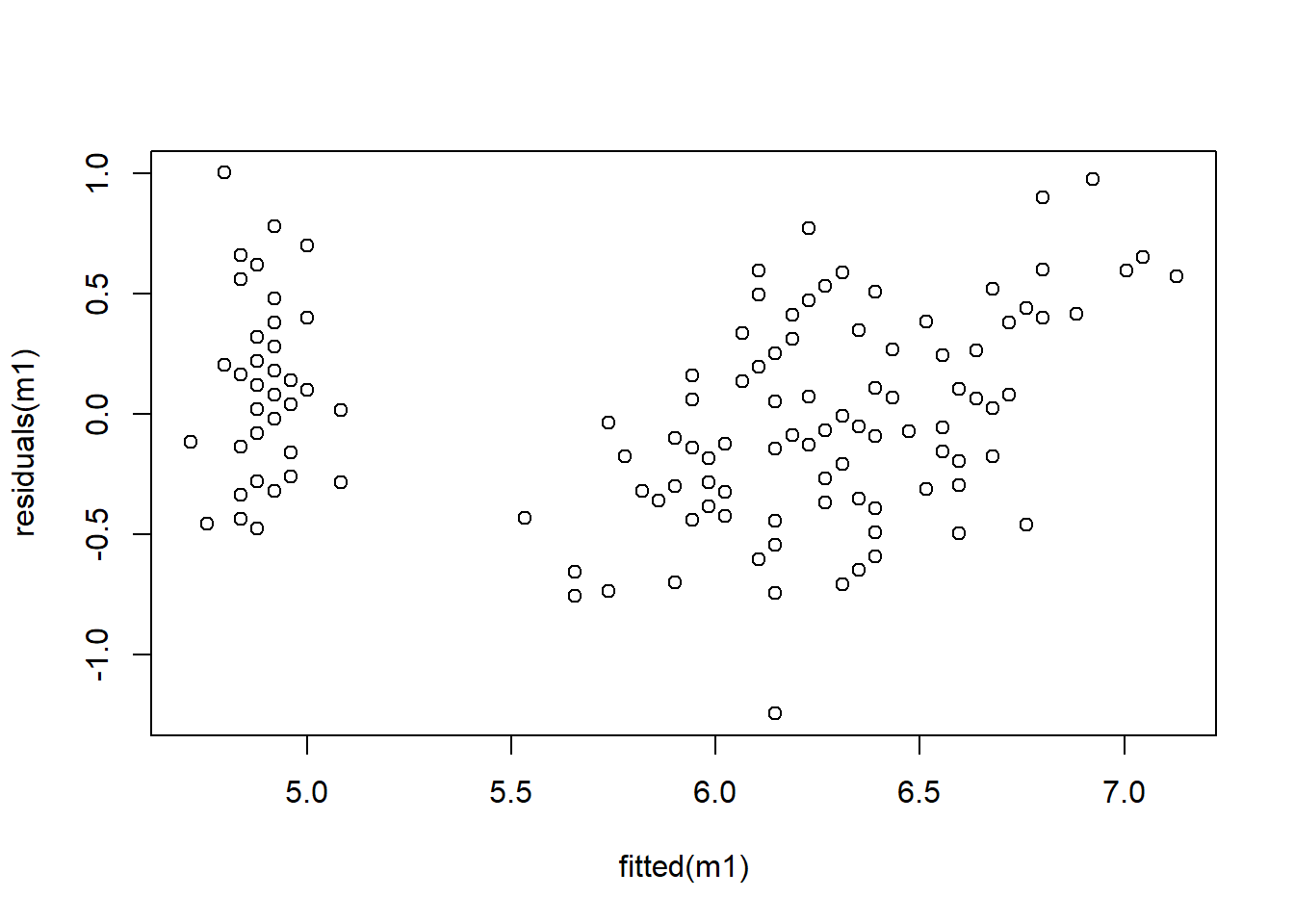

图6.2: 一元线性回归图

这个一元线性方程可以写成\(y=0.40892*Petal.Length + 4.3066\),这里的 summary值里面的Estimate那一列，就是我们要的这个方程的参数。从这个模型看出，这个Petal.Length 对Sepal.Length 有极显著的线性相关性。我们可以将模型的残差与回归模型的预测值以及测量值与预测值进行绘图，查看模型精度。残差范围越小，靠近0，则这个回归模型精度越高。

6.2 多元线性回归

我们也可以根据多个性状对某指定性状进行线性回归分析。

#加载数据
data("iris")
m2 <- lm(Sepal.Length ~Petal.Length + Sepal.Width+Petal.Width,data = iris )
## 查看结果
summary(m2)
## 
## Call:
## lm(formula = Sepal.Length ~ Petal.Length + Sepal.Width + Petal.Width, 
##     data = iris)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.82816 -0.21989  0.01875  0.19709  0.84570 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   1.85600    0.25078   7.401 9.85e-12 ***
## Petal.Length  0.70913    0.05672  12.502  < 2e-16 ***
## Sepal.Width   0.65084    0.06665   9.765  < 2e-16 ***
## Petal.Width  -0.55648    0.12755  -4.363 2.41e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.3145 on 146 degrees of freedom
## Multiple R-squared:  0.8586, Adjusted R-squared:  0.8557 
## F-statistic: 295.5 on 3 and 146 DF,  p-value: < 2.2e-16
##计算模型方差

aov <-anova(m2) 
aov
## Analysis of Variance Table
## 
## Response: Sepal.Length
##               Df Sum Sq Mean Sq F value    Pr(>F)    
## Petal.Length   1 77.643  77.643 784.742 < 2.2e-16 ***
## Sepal.Width    1  8.196   8.196  82.840 6.118e-16 ***
## Petal.Width    1  1.883   1.883  19.035 2.413e-05 ***
## Residuals    146 14.445   0.099                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#查看预测值
fitted(m2)
##        1        2        3        4        5        6        7        8 
## 5.015416 4.689997 4.749251 4.825994 5.080499 5.377194 4.894684 5.021245 
##        9       10       11       12       13       14       15       16 
## 4.624913 4.881642 5.216496 5.092158 4.745645 4.532906 5.199008 5.560786 
##       17       18       19       20       21       22       23       24 
## 5.093541 4.959767 5.367758 5.225932 5.163072 5.105200 4.796847 4.931043 
##       25       26       27       28       29       30       31       32 
## 5.304898 4.831824 4.980862 5.086329 4.950332 4.961991 4.896907 4.909949 
##       33       34       35       36       37       38       39       40 
## 5.532480 5.471002 4.825994 4.678338 4.944503 5.136148 4.619084 5.021245 
##       41       42       43       44       45       46       47       48 
## 4.888854 4.107850 4.749251 4.934649 5.453936 4.634349 5.352493 4.820165 
##       49       50       51       52       53       54       55       56 
## 5.216496 4.885248 6.492521 6.295046 6.513615 5.466023 6.105625 6.146008 
##       57       58       59       60       61       62       63       64 
## 6.446308 5.201659 6.282005 5.599797 5.083151 5.952139 5.567884 6.297270 
##       65       66       67       68       69       70       71       72 
## 5.572873 6.214698 6.164879 5.964216 5.644209 5.636574 6.340841 5.791442 
##       73       74       75       76       77       78       79       80 
## 6.123113 6.343483 6.069265 6.149614 6.303099 6.408148 6.099795 5.473653 
##       81       82       83       84       85       86       87       88 
## 5.500577 5.485312 5.711093 6.339459 6.164879 6.369565 6.371789 5.749676 
##       89       90       91       92       93       94       95       96 
## 5.992523 5.596191 6.000576 6.291440 5.716923 5.136576 5.868185 6.119084 
##       97       98       99      100      101      102      103      104 
## 5.998352 6.069265 4.998355 5.862355 6.867345 6.172514 6.823774 6.712895 
##      105      106      107      108      109      110      111      112 
## 6.697212 7.320166 5.728164 7.209288 6.594387 7.133510 6.442284 6.314340 
##      113      114      115      116      117      118      119      120 
## 6.540121 5.915785 5.959356 6.417166 6.707066 7.856101 7.161275 5.998775 
##      121      122      123      124      125      126      127      128 
## 6.700818 6.040123 7.316560 6.086336 6.877199 7.191799 6.080506 6.281587 
##      129      130      131      132      133      134      135      136 
## 6.480867 7.031102 6.946729 7.754658 6.425219 6.460191 6.740237 6.854304 
##      137      138      139      140      141      142      143      144 
## 6.704424 6.772150 6.210674 6.534292 6.509173 6.210256 6.172514 6.842645 
##      145      146      147      148      149      150 
## 6.654606 6.216085 5.971433 6.383030 6.618246 6.423413
#查看残差值
residuals(m2)
##             1             2             3             4             5 
##  0.0845842387  0.2100028184 -0.0492514176 -0.2259940935 -0.0804994772 
##             6             7             8             9            10 
##  0.0228063193 -0.2946837793 -0.0212452413 -0.2249134657  0.0183576405 
##            11            12            13            14            15 
##  0.1835036110 -0.2921584372  0.0543545524 -0.2329058599  0.6009920509 
##            16            17            18            19            20 
##  0.1392141315  0.3064591029  0.1402325047  0.3322417692 -0.1259318390 
##            21            22            23            24            25 
##  0.2369283669 -0.0051998570 -0.1968466935  0.1689568809 -0.5048980249 
##            26            27            28            29            30 
##  0.1681764266  0.0191380949  0.1136710428  0.2496679547 -0.2619910053 
##            31            32            33            34            35 
## -0.0969072894  0.4900512908 -0.3324795188  0.0289982272  0.0740059065 
##            36            37            38            39            40 
##  0.3216617783  0.5554974346 -0.2361477432 -0.2190839857  0.0787547587 
##            41            42            43            44            45 
##  0.1111457007  0.3921502918 -0.3492514176  0.0653509110 -0.3539363566 
##            46            47            48            49            50 
##  0.1656510844 -0.2524933009 -0.2201646135  0.0835036110  0.1147516706 
##            51            52            53            54            55 
##  0.5074791136  0.1049537714  0.3863847037  0.0339766623  0.3943754392 
##            56            57            58            59            60 
## -0.4460078969 -0.1463080703 -0.3016594803  0.3179951913 -0.3997967395 
##            61            62            63            64            65 
## -0.0831510084 -0.0521392090  0.4321155802 -0.1972697386  0.0271271504 
##            66            67            68            69            70 
##  0.4853024172 -0.5648787967 -0.1642161954  0.5557909307 -0.0365741057 
##            71            72            73            74            75 
## -0.4408410183  0.3085580827  0.1768869993 -0.2434825547  0.3307347790 
##            76            77            78            79            80 
##  0.4503861332  0.4969007814  0.2918517557 -0.0997950808  0.2263466961 
##            81            82            83            84            85 
## -0.0005771938  0.0146877361  0.0889067285 -0.3394585584 -0.7648787967 
##            86            87            88            89            90 
## -0.3695653944  0.3282110955  0.5503238787 -0.3925225451 -0.0961907695 
##            91            92            93            94            95 
## -0.5005755351 -0.1914402587  0.0830772485 -0.1365757643 -0.2681845932 
##            96            97            98            99           100 
## -0.4190840070 -0.2983520251  0.1307347790  0.1016446576 -0.1623551132 
##           101           102           103           104           105 
## -0.5673452231 -0.3725137603  0.2762260566 -0.4128954378 -0.1972124815 
##           106           107           108           109           110 
##  0.2798336852 -0.8281636850  0.0907121908  0.1056130341  0.0664904332 
##           111           112           113           114           115 
##  0.0577159260  0.0856598478  0.2598788402 -0.2157848666 -0.1593561462 
##           116           117           118           119           120 
## -0.0171656678 -0.2070659578 -0.1561009722  0.5387254932  0.0012249512 
##           121           122           123           124           125 
##  0.1991815486 -0.4401228184  0.3834396551  0.2136643655 -0.1771986994 
##           126           127           128           129           130 
##  0.0082006308  0.1194938454 -0.1815867823 -0.0808669238  0.1688979224 
##           131           132           133           134           135 
##  0.4532705646  0.1453420836 -0.0252186578 -0.1601905403 -0.6402373541 
##           136           137           138           139           140 
##  0.8456961968 -0.4044244213 -0.3721496737 -0.2106735864  0.3657083202 
##           141           142           143           144           145 
##  0.1908267264  0.6897444400 -0.3725137603 -0.0426448432  0.0453943647 
##           146           147           148           149           150 
##  0.4839149600  0.3285668674  0.1169701620 -0.4182462955 -0.5234131742
## 对预测值和实测值进行绘图
plot(fitted(m2),iris$Sepal.Length)
abline(0,1)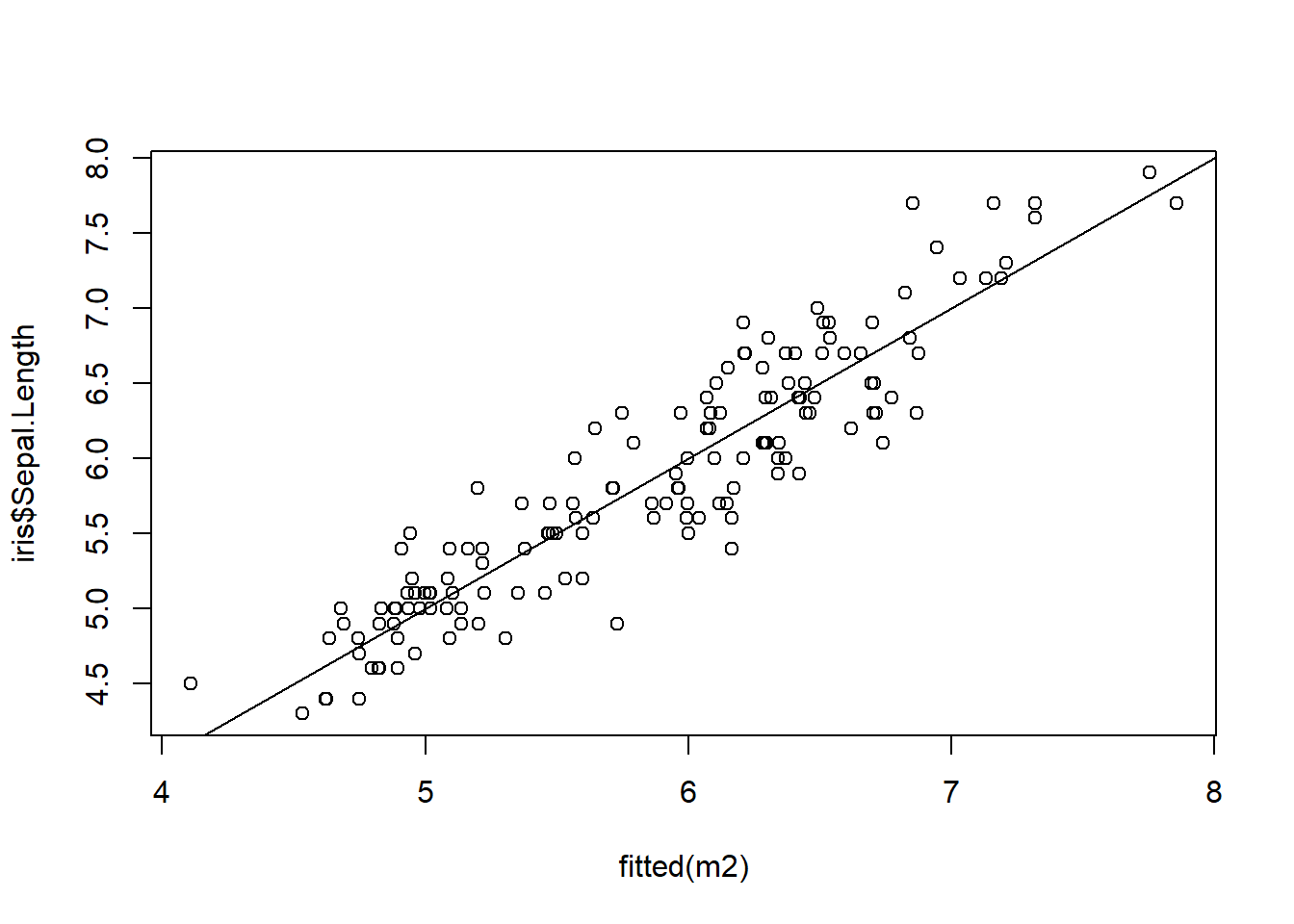

##对预测值得残差值绘图
plot(fitted(m2),residuals(m2))
abline(h=0,lty=2,col='red')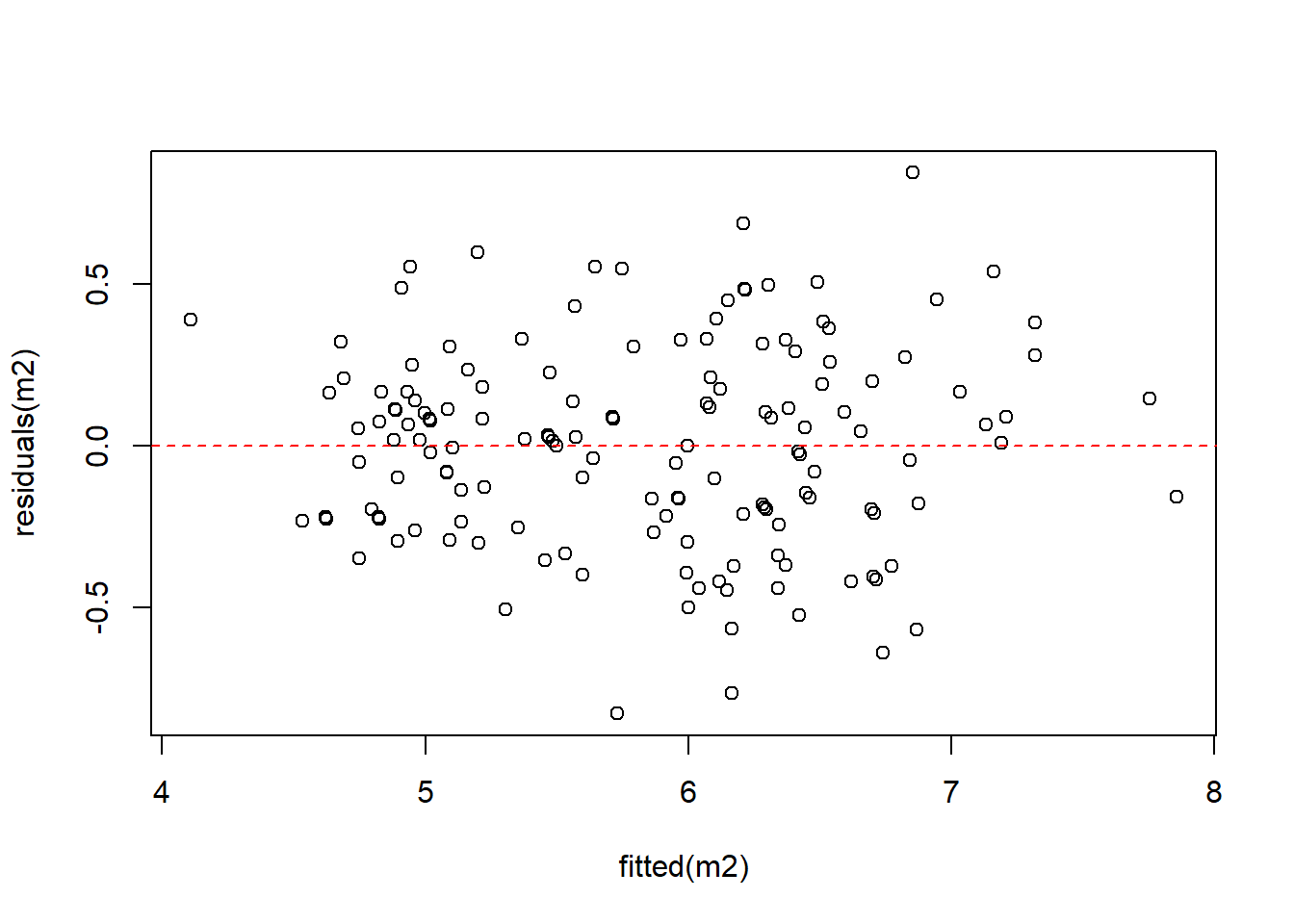

可以看出当我们用多个性状做线性回归的话，模型预测精度要比一个性状的预测精度要高。我们也可以对多个线性模型进行比较，来找出最佳模型。我们也可以将多个性状的交互作用的影响考虑进去。只要将 +替代成 *就好。

library(rcompanion)
##这里面我们创建多个模型
m1 <- lm(Sepal.Length ~Petal.Length,data = iris )
m2 <- lm(Sepal.Length ~Petal.Length + Sepal.Width+Petal.Width,data = iris )

m3 <- lm(Sepal.Length ~Petal.Length + Sepal.Width,data = iris )

m4 <- lm(Sepal.Length ~Sepal.Width+Petal.Width,data = iris )

m5 <- lm(Sepal.Length ~Petal.Length +Petal.Width,data = iris )

m6 <- lm(Sepal.Length ~Petal.Length * Sepal.Width+Petal.Width,data = iris )
m7 <- lm(Sepal.Length ~Petal.Length + Sepal.Width*Petal.Width,data = iris )
m8 <- lm(Sepal.Length ~Petal.Length * Sepal.Width*Petal.Width,data = iris )

compar <- compareLM(m1,m2,m3,m4,m5,m6,m7,m8)
compar
## $Models
##   Formula                                                  
## 1 "Sepal.Length ~ Petal.Length"                            
## 2 "Sepal.Length ~ Petal.Length + Sepal.Width + Petal.Width"
## 3 "Sepal.Length ~ Petal.Length + Sepal.Width"              
## 4 "Sepal.Length ~ Sepal.Width + Petal.Width"               
## 5 "Sepal.Length ~ Petal.Length + Petal.Width"              
## 6 "Sepal.Length ~ Petal.Length * Sepal.Width + Petal.Width"
## 7 "Sepal.Length ~ Petal.Length + Sepal.Width * Petal.Width"
## 8 "Sepal.Length ~ Petal.Length * Sepal.Width * Petal.Width"
## 
## $Fit.criteria
##   Rank Df.res    AIC   AICc   BIC R.squared Adj.R.sq   p.value Shapiro.W
## 1    2    148 160.00 160.20 169.1    0.7600   0.7583 1.039e-47    0.9930
## 2    4    146  84.64  85.06  99.7    0.8586   0.8557 8.588e-62    0.9956
## 3    3    147 101.00 101.30 113.1    0.8402   0.8380 2.933e-59    0.9939
## 4    3    147 191.80 192.10 203.9    0.7072   0.7033 6.151e-40    0.9827
## 5    3    147 158.00 158.30 170.1    0.7663   0.7631 3.997e-47    0.9944
## 6    5    145  84.99  85.57 103.1    0.8602   0.8563 7.234e-61    0.9952
## 7    5    145  85.57  86.16 103.6    0.8596   0.8557 9.576e-61    0.9952
## 8    8    142  85.96  87.25 113.1    0.8648   0.8581 1.923e-58    0.9942
##   Shapiro.p
## 1   0.67670
## 2   0.93490
## 3   0.78560
## 4   0.05653
## 5   0.83740
## 6   0.90360
## 7   0.90290
## 8   0.81390
plot(compar$Fit.criteria$AICc,xlab='Model number', ylab='AICc Value')
lines(compar$Fit.criteria$AICc)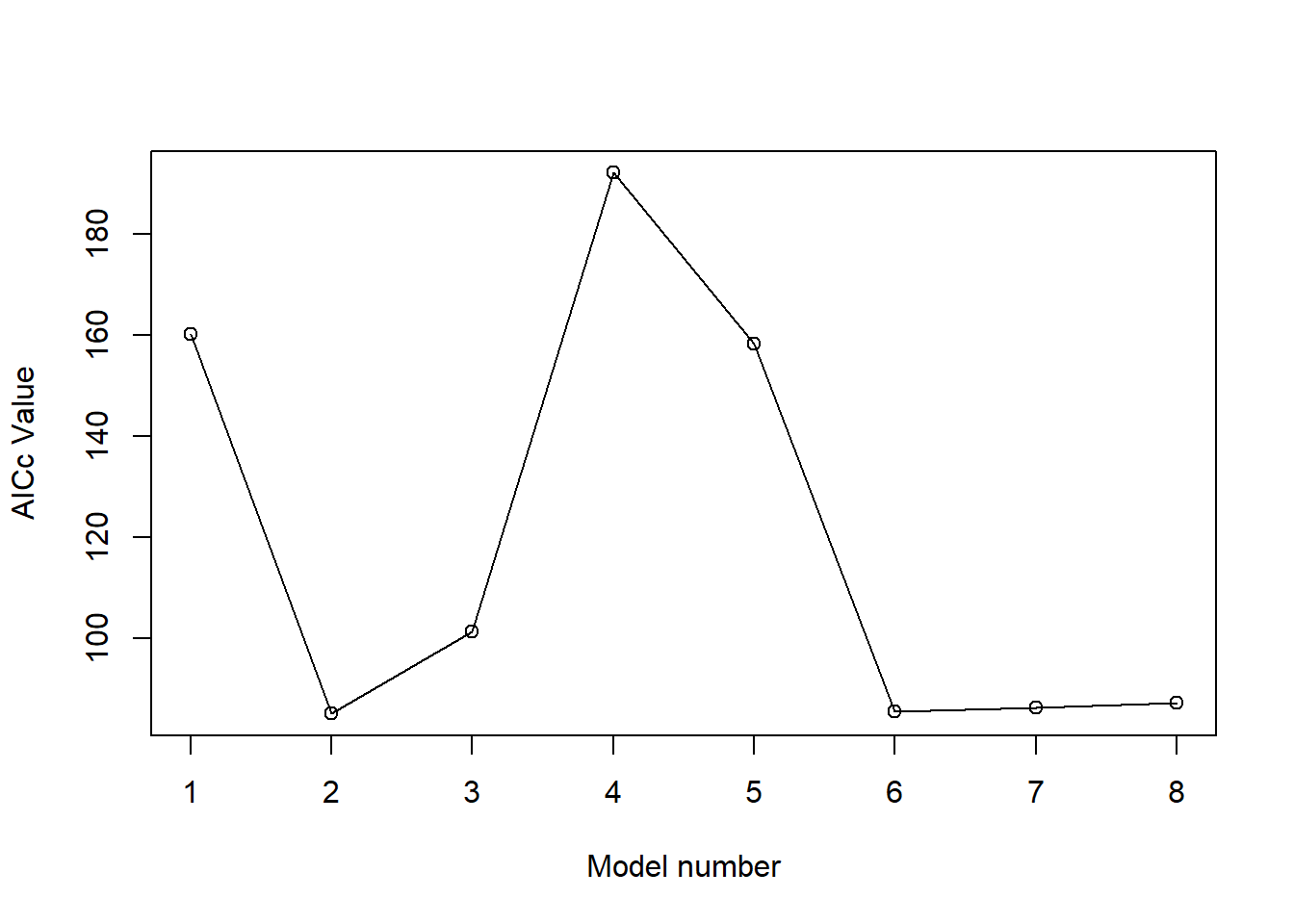


predict <- predict(m6,iris)

# 计算模型R2，MSE,RMSE
actual = iris$Sepal.Length
RSS = sum((actual - predict)^2)
Var = sum((actual - mean(actual))^2)
R2 = 1 - RSS/Var
### Calculate mean square error and rmse
MSE = mean((actual - predict)^2)
RMSE = sqrt(MSE)

R2
## [1] 0.8601633
MSE
## [1] 0.09524586
RMSE
## [1] 0.3086193

可以看出m6模型的 AICc值最小，表示这个回归模型预测准确率最高。所以m6应该是最佳线性回归模型。

m6 <- lm(Sepal.Length ~Petal.Length * Sepal.Width+Petal.Width,data = iris )
summary(m6)

## 
## Call:
## lm(formula = Sepal.Length ~ Petal.Length * Sepal.Width + Petal.Width, 
##     data = iris)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.85716 -0.20637  0.01996  0.21224  0.83426 
## 
## Coefficients:
##                          Estimate Std. Error t value Pr(>|t|)    
## (Intercept)               1.29826    0.50593   2.566   0.0113 *  
## Petal.Length              0.86673    0.13653   6.348 2.63e-09 ***
## Sepal.Width               0.82149    0.15008   5.474 1.89e-07 ***
## Petal.Width              -0.53297    0.12863  -4.144 5.79e-05 ***
## Petal.Length:Sepal.Width -0.05236    0.04128  -1.268   0.2067    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.3139 on 145 degrees of freedom
## Multiple R-squared:  0.8602, Adjusted R-squared:  0.8563 
## F-statistic:   223 on 4 and 145 DF,  p-value: < 2.2e-16

6.3 广义线性回归

当数据不平衡的时候，我们可以也可以使用广义线性回归模型进行运算。百度百科上这样说： > 广义线性模型[generalize linear model]线性模型的扩展，通过联结函数建立响应变量的数学期望值与线性组合的预测变量之间的关系。其特点是不强行改变数据的自然度量，数据可以具有非线性和非恒定方差结构。是线性模型在研究响应值的非正态分布以及非线性模型简洁直接的线性转化时的一种发展<

具体这个广义线性模型是怎么回事，大家可以搜索一下查看具体函数。我们这里只讲怎么实现，在R里面很简单，我们用iris数据进行广义线性建模。

library(dplyr)
library(rcompanion)
data("iris")

set.seed(1234)
##建立一个数据分割程序分成train 和test
create_train_test <- function(data, size = 0.8, train = TRUE) {
    n_row = nrow(data)
    total_row = size * n_row
    train_sample <- 1: total_row
    if (train == TRUE) {
        return (data[train_sample, ])
    } else {
        return (data[-train_sample, ])
    }
}
data_train <- create_train_test(iris, 0.8, train = TRUE)
data_test <- create_train_test(iris, 0.8, train = FALSE)
dim(data_train)

## [1] 120   5

formula <- Sepal.Length ~Petal.Length * Sepal.Width+Petal.Width
logit <- glm(formula, data = data_train)
summary(logit)

## 
## Call:
## glm(formula = formula, data = data_train)
## 
## Deviance Residuals: 
##      Min        1Q    Median        3Q       Max  
## -0.81414  -0.21059   0.01682   0.20426   0.53905  
## 
## Coefficients:
##                          Estimate Std. Error t value Pr(>|t|)    
## (Intercept)               1.30890    0.50950   2.569 0.011479 *  
## Petal.Length              0.92599    0.15052   6.152 1.14e-08 ***
## Sepal.Width               0.81057    0.15107   5.366 4.23e-07 ***
## Petal.Width              -0.68818    0.17133  -4.017 0.000106 ***
## Petal.Length:Sepal.Width -0.05495    0.04492  -1.223 0.223733    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for gaussian family taken to be 0.08989285)
## 
##     Null deviance: 70.699  on 119  degrees of freedom
## Residual deviance: 10.338  on 115  degrees of freedom
## AIC: 58.342
## 
## Number of Fisher Scoring iterations: 2

# 计算模型R2，MSE,RMSE
m1 <- glm(Sepal.Length ~Petal.Length,data = data_train )
m2 <- glm(Sepal.Length ~Petal.Length + Sepal.Width+Petal.Width,data = data_train )

m3 <- glm(Sepal.Length ~Petal.Length + Sepal.Width,data = data_train )

m4 <- glm(Sepal.Length ~Sepal.Width+Petal.Width,data = data_train )

m5 <- glm(Sepal.Length ~Petal.Length +Petal.Width,data = data_train )

m6 <- glm(Sepal.Length ~Petal.Length * Sepal.Width+Petal.Width,data = data_train )
m7 <- glm(Sepal.Length ~Petal.Length + Sepal.Width*Petal.Width,data = data_train )
m8 <- glm(Sepal.Length ~Petal.Length * Sepal.Width*Petal.Width,data = data_train )

compar <- compareGLM(m1,m2,m3,m4,m5,m6,m7,m8)
compar

## $Models
##   Formula                                                  
## 1 "Sepal.Length ~ Petal.Length"                            
## 2 "Sepal.Length ~ Petal.Length + Sepal.Width + Petal.Width"
## 3 "Sepal.Length ~ Petal.Length + Sepal.Width"              
## 4 "Sepal.Length ~ Sepal.Width + Petal.Width"               
## 5 "Sepal.Length ~ Petal.Length + Petal.Width"              
## 6 "Sepal.Length ~ Petal.Length * Sepal.Width + Petal.Width"
## 7 "Sepal.Length ~ Petal.Length + Sepal.Width * Petal.Width"
## 8 "Sepal.Length ~ Petal.Length * Sepal.Width * Petal.Width"
## 
## $Fit.criteria
##   Rank Df.res    AIC   AICc    BIC McFadden Cox.and.Snell Nagelkerke   p.value
## 1    2    118 125.20 125.40 133.60   0.5697        0.7316     0.8123 3.253e-13
## 2    4    116  57.89  58.42  71.83   0.8271        0.8519     0.9459 2.586e-13
## 3    3    117  73.01  73.36  84.16   0.7653        0.8292     0.9207 9.322e-14
## 4    3    117 136.30 136.60 147.40   0.5370        0.7106     0.7890 6.166e-12
## 5    3    117 123.30 123.70 134.50   0.5838        0.7402     0.8219 2.163e-12
## 6    5    115  58.34  59.09  75.07   0.8327        0.8538     0.9480 1.179e-12
## 7    5    115  59.44  60.18  76.16   0.8288        0.8524     0.9465 1.234e-12
## 8    8    112  58.53  60.16  83.61   0.8537        0.8607     0.9557 4.698e-11

plot(compar$Fit.criteria$AICc,xlab='Model number', ylab='AICc Value')
lines(compar$Fit.criteria$AICc)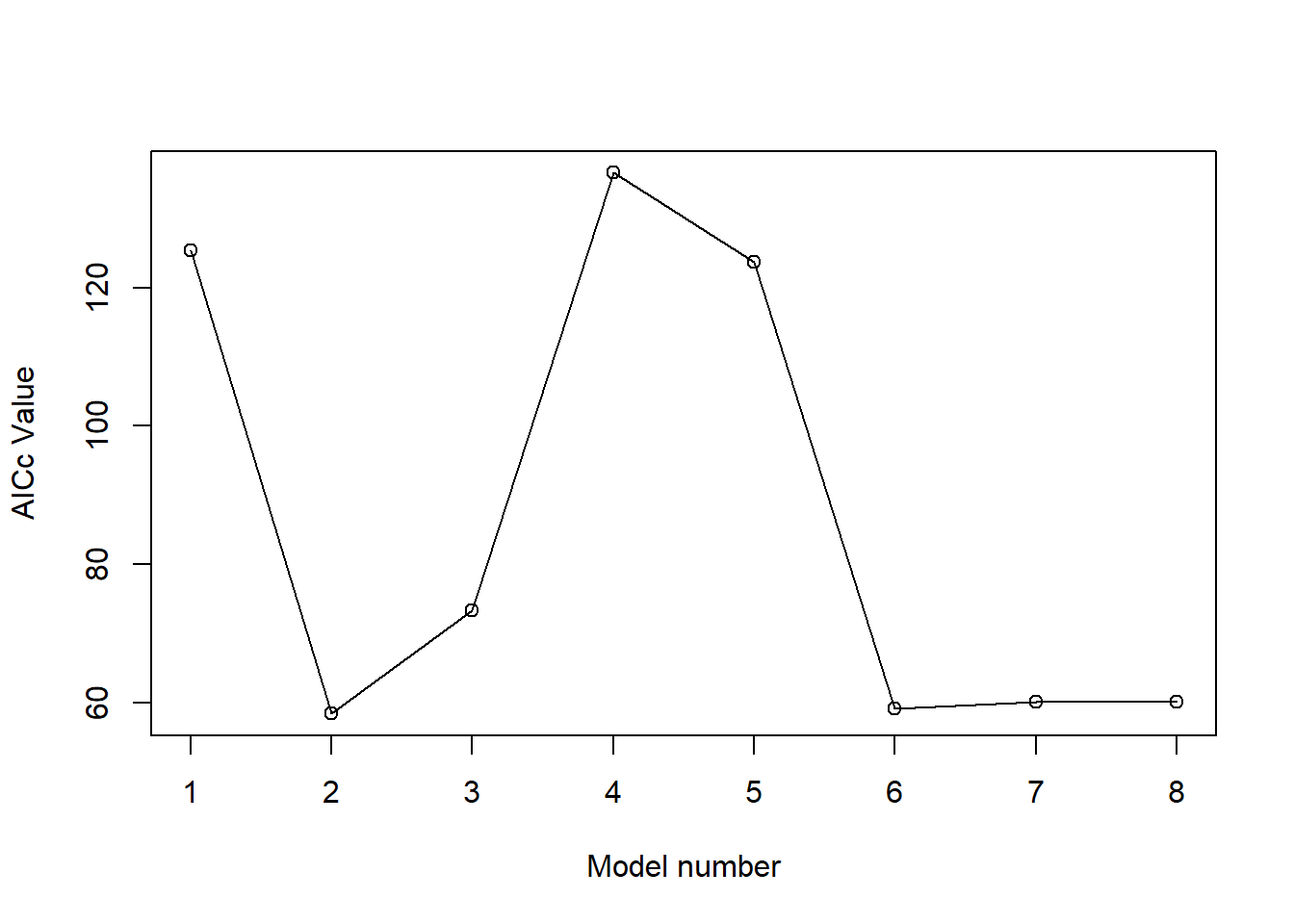

##对test data进行预测
predict <- predict(m2, data_test)
plot(predict,data_test$Sepal.Length)
abline(0,1)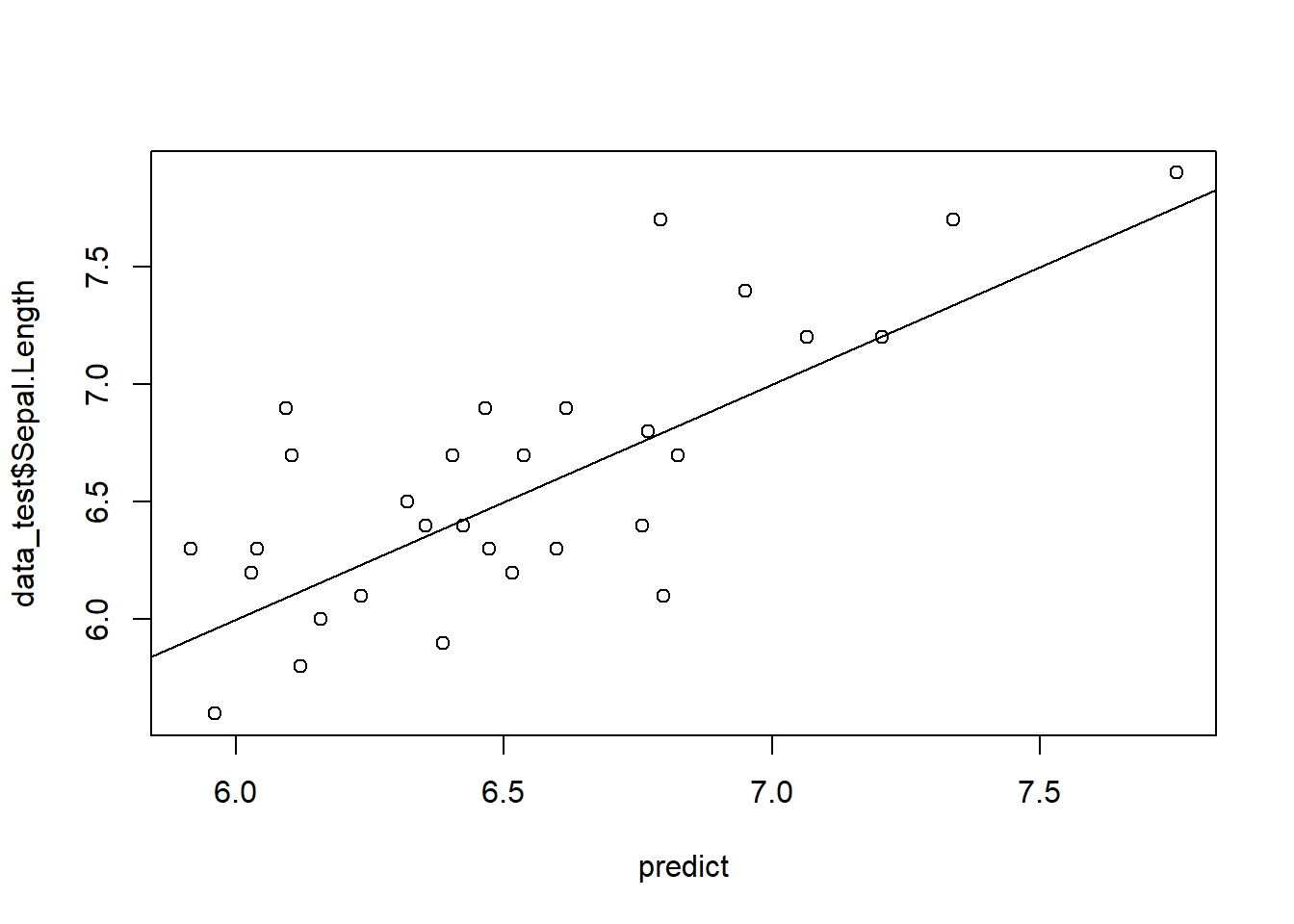

6.4 贝叶斯回归

library(BAS)

m_bay <- bas.lm(Sepal.Length ~Petal.Length * Sepal.Width*Petal.Width,data = data_train,na.action = "na.omit", prior = "BIC", modelprior = uniform() )

image(m_bay, rotate=FALSE)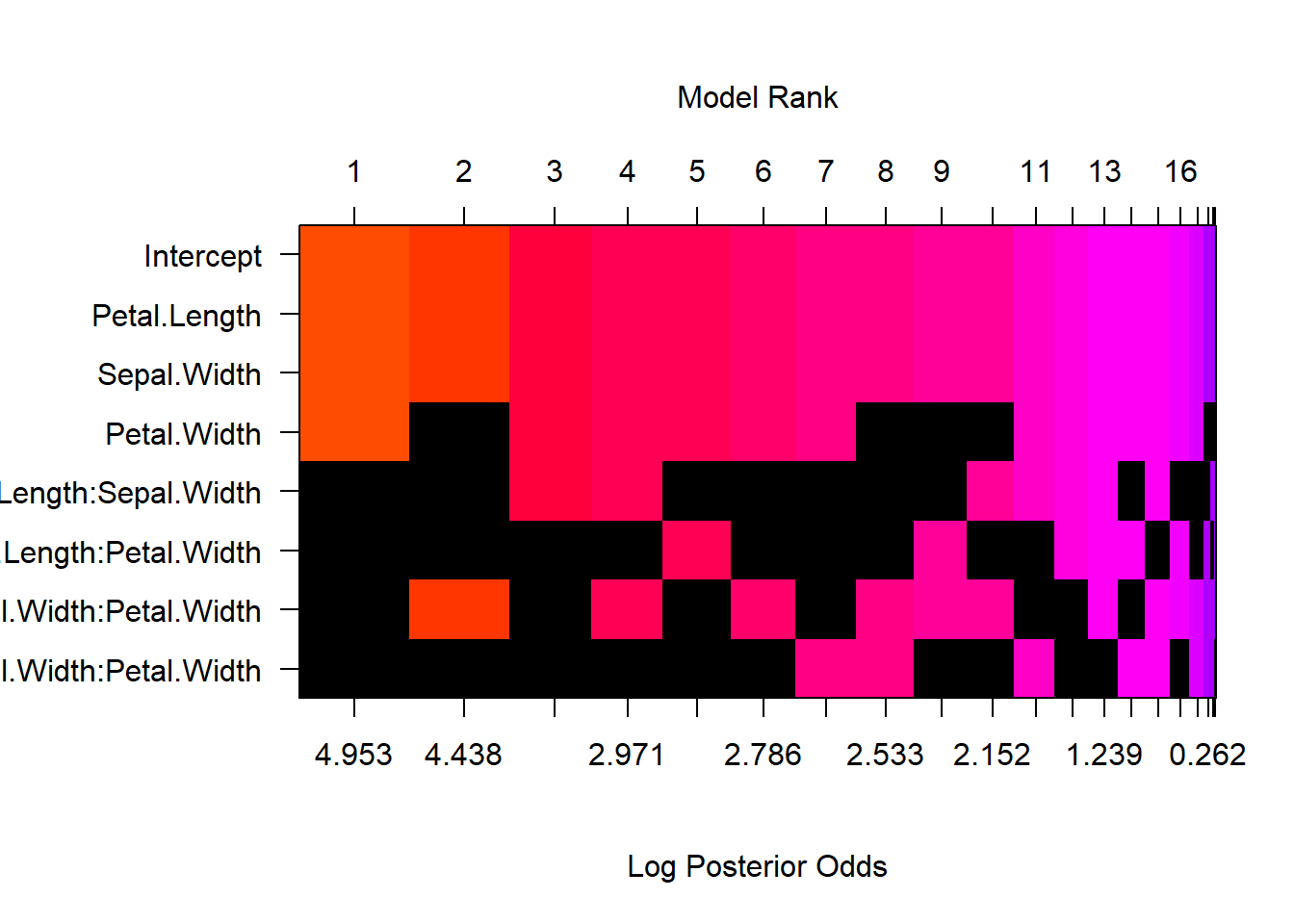

#在模型平均方法下，还可以可视化系数的后验分布。我们在下面绘制iq和sibs系数的后验分布。
pred=  predict(m_bay, data_test,estimator="BMA", interval = "predict", se.fit=TRUE)
plot(pred$fit,data_test$Sepal.Length)
abline(0,1)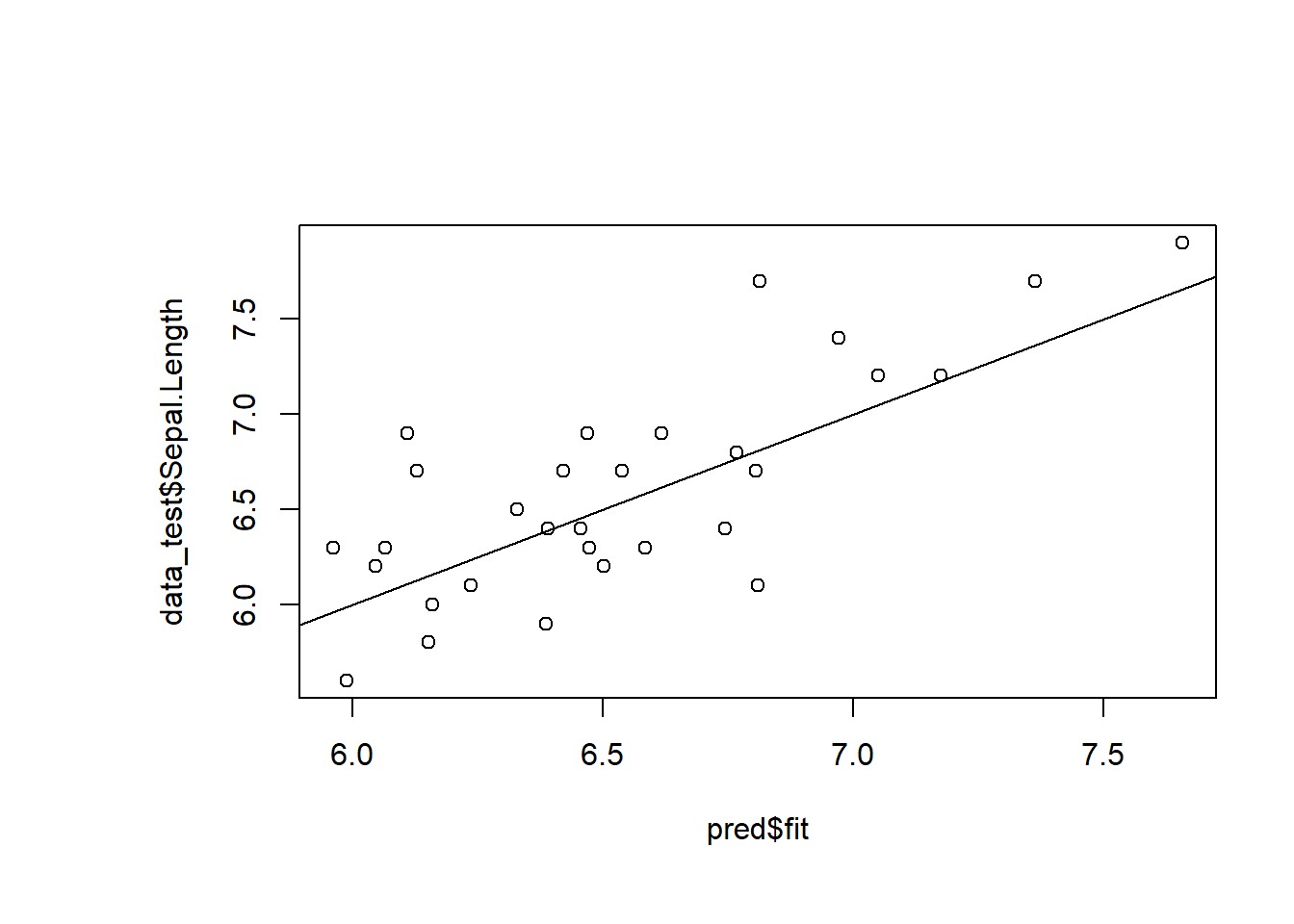

在这里，我们看到了按后验优势比排序的模型，其中黑色正方形表示每个模型遗漏了哪些特征。就像我们先前的stepAIC线性模型特征缩减一样，“检查”可以被认为是对 Sepal.Length 进行预测的不良特征。现在，我们可以比较以下聚合模型的性能： BMA：贝叶斯模型平均（最佳模型的均值） BPM：贝叶斯后验模型（根据某些损失函数（例如平方误差）的最佳预测模型） MPM：中位数概率模型（包括边际概率为非零且大于50％的所有预测变量） HPM：最高概率模型

# Set up matrix to store results in
results = matrix(NA, ncol=4, nrow=1)
colnames(results) = c('BMA', 'BPM', 'MPM', 'HPM')
 
# Make predictions for each aggregated model
for (name in colnames(results)) {
    y_pred = predict(m_bay, data_test, estimator=name)$fit
    results[1, name] = cv.summary.bas(y_pred, data_test$Sepal.Length)
}
 
# Print results
options(digits = 4)
results

##       BMA    BPM    MPM    HPM
## [1,] 0.37 0.3734 0.3753 0.3753

在各种情况下，性能都是相似的，BMA模型似乎是最好的，而MPM和HPM模型是最差的。

.entry{text-indent: 2em;}

第 6 章 线性回归分析

6.1 一元线性回归

6.2 多元线性回归

6.3 广义线性回归

6.4 贝叶斯回归

第 6 章线性回归分析