第 4 章 主成分分析
对于主成分分析的解释,维基百科上是这样说的:
主成分分析(英语:Principal components analysis,PCA)是一种统计分析、简化数据集的方法。它利用正交变换来对一系列可能相关的变量的观测值进行线性变换,从而投影为一系列线性不相关变量的值,这些不相关变量称为主成分(Principal Components)。具体地,主成分可以看做一个线性方程,其包含一系列线性系数来指示投影方向。PCA对原始数据的正则化或预处理敏感(相对缩放)。
那么我们主要将如何在R里面实现,在 R base 或者其他各种安装包里面,都包含主成分分析,我们这里主要介绍R base里面的数据。这里需要用到 prcomp这个方程来实现。这里我们依然用 iris数据来举例。主成分分析的数据里面不能出现 factor或者 character的形式,一般我们要将所有的 numeric数据转换为 matrix形式。
data("iris")
#转换数据
martrix_iris <- as.matrix(iris[-5])
#PCA分析
##可以设置scale. 和center =T, 来对数据进行预处理
pca1<- prcomp(martrix_iris,scale. = T,center = T )
pca1## Standard deviations (1, .., p=4):
## [1] 1.7083611 0.9560494 0.3830886 0.1439265
##
## Rotation (n x k) = (4 x 4):
## PC1 PC2 PC3 PC4
## Sepal.Length 0.5210659 -0.37741762 0.7195664 0.2612863
## Sepal.Width -0.2693474 -0.92329566 -0.2443818 -0.1235096
## Petal.Length 0.5804131 -0.02449161 -0.1421264 -0.8014492
## Petal.Width 0.5648565 -0.06694199 -0.6342727 0.5235971对PCA结果进行可视化。我们这里ggfortify安装包来实现,这个安装包是基于 ggplot2的,所以你的电脑上首先要有ggplot2 这个安装包。
library(ggfortify)
autoplot(pca1,data = iris,col= 'Species',size=2,
loadings =T,loadings.label = TRUE,
frame = TRUE,frame.type='norm',
label = TRUE, label.size = 3
)+
theme_classic()
## Warning: `select_()` was deprecated in dplyr 0.7.0.
## Please use `select()` instead.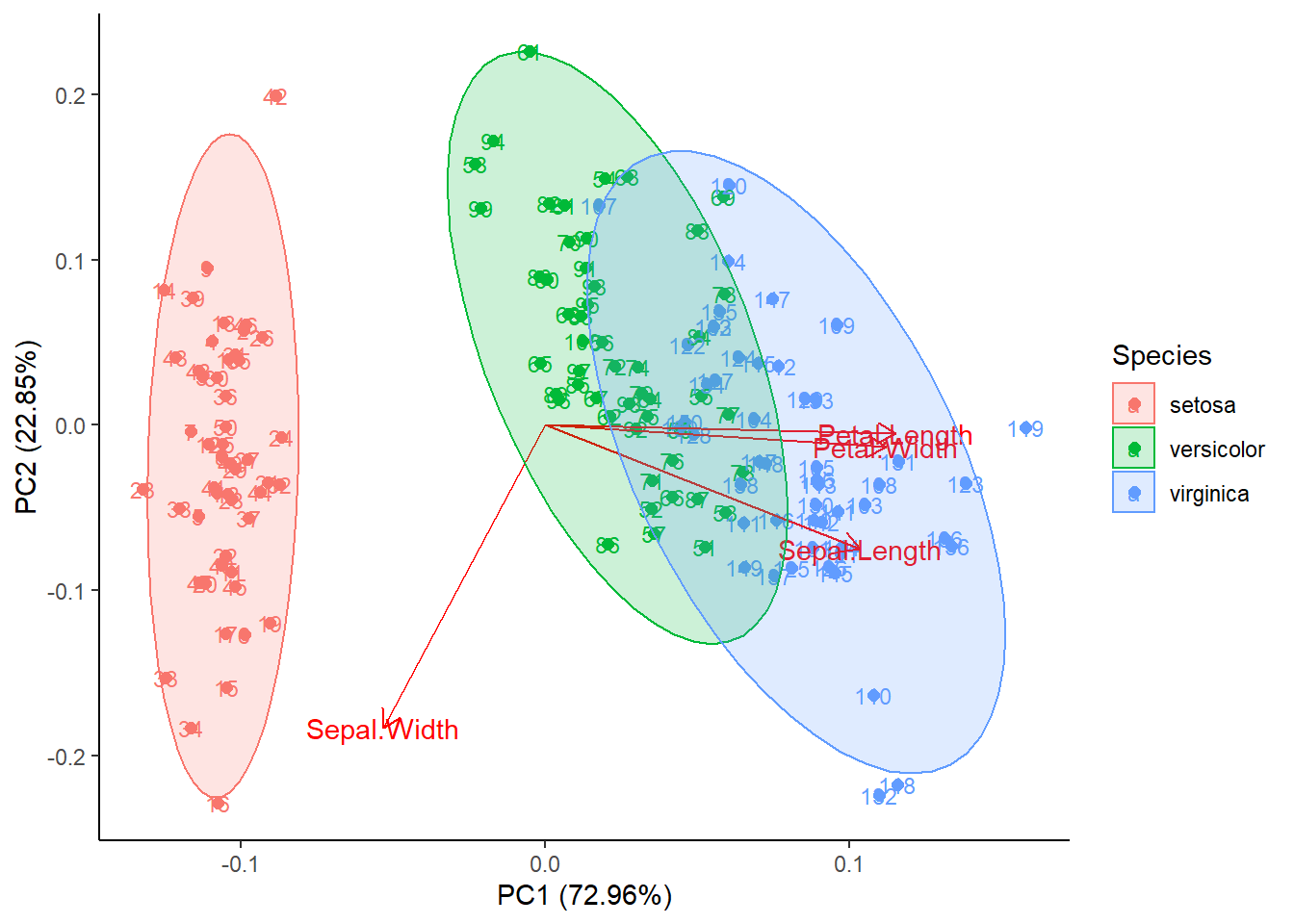
图4.1: PCA plot
你可以根据ggplot相关设置对图像参数进行修改。