5 简单线性模型

以一个简单的贝叶斯线性模型为例，介绍贝叶斯统计中的后验分布。继续以 state_x77 数据为例，以贝叶斯线性模型拟合数据，获得参数的后验分布，Stan 语言编码的贝叶斯线性模型如下：

data {
  int<lower=0> N;   // number of data items
  int<lower=0> K;   // number of predictors
  matrix[N, K] x;   // predictor matrix
  vector[N] y;      // outcome vector
}
parameters {
  real alpha;           // intercept
  vector[K] beta;       // coefficients for predictors
  real<lower=0> sigma;  // error scale
}
model {
  // alpha ~ normal(0, 1);  // prior
  // beta ~ normal(0, 1);   // prior
  y ~ normal(x * beta + alpha, sigma);  // likelihood
}

这里采用汉密尔顿蒙特卡洛算法（HMC）做全贝叶斯推断，下面依次编译模型、准备数据、参数初值和迭代设置。Stan 的 R 语言接口 cmdstanr 包可以让这一切在 R 语言环境里做起来比较顺畅。

library(cmdstanr)
# 编译模型
mod_state_x77 <- cmdstan_model(
  stan_file = "code/state_x77.stan",
  compile = TRUE,
  cpp_options = list(stan_threads = TRUE)
)
# 准备数据
state_x77 <- data.frame(
  x = state.center$x,
  y = state.center$y,
  state_name = state.name,
  state_abb = state.abb,
  state_region = state.region,
  state_division = state.division,
  state.x77, check.names = FALSE
)
state_x77_d <- list(
  N = nrow(state_x77), # 观测记录的条数
  K = 2,               # 协变量个数
  x = state_x77[, c("Income", "Murder")], # N x 2 矩阵
  y = state_x77[, "Life Exp"]             # N 向量
)
nchains <- 4 # 4 条迭代链
# 给每条链设置不同的参数初始值
inits_data <- lapply(1:nchains, function(i) {
  list(
    alpha = runif(1, 0, 1),
    beta = runif(2, 1, 10),
    sigma = runif(1, 1, 10)
  )
})
# 采样拟合模型
fit_state_x77 <- mod_state_x77$sample(
  data = state_x77_d,   # 观测数据
  init = inits_data,    # 迭代初值
  iter_warmup = 1000,   # 每条链预处理迭代次数
  iter_sampling = 2000, # 每条链总迭代次数
  chains = nchains,     # 马尔科夫链的数目
  parallel_chains = 1,  # 指定 CPU 核心数，可以给每条链分配一个
  threads_per_chain = 1, # 每条链设置一个线程
  show_messages = FALSE, # 不显示迭代的中间过程
  refresh = 0,     # 不显示采样的进度
  seed = 20190425  # 设置随机数种子，不要使用 set.seed() 函数
)

模型参数估计结果如下：

表 5.1: 贝叶斯线性模型参数估计结果

variable	mean	median	sd	mad	q5	q95	rhat	ess_bulk	ess_tail
alpha	71.218	71.215	1.015	1.026	69.557	72.883	1.001	2998.845	3565.418
beta[1]	0.000	0.000	0.000	0.000	0.000	0.001	1.001	3335.571	3798.662
beta[2]	-0.270	-0.270	0.034	0.034	-0.326	-0.214	1.000	3365.535	3662.770
sigma	0.849	0.841	0.093	0.089	0.716	1.015	1.001	3192.929	3155.809
lp__	-16.227	-15.869	1.522	1.261	-19.226	-14.467	1.001	2355.608	3560.164

参数的 \(\alpha,\beta_1,\beta_2\) 后验均值估计与普通线性模型的拟合结果非常一致。采样结果可以直接传递给 bayesplot 包(Gabry 等 2019)，绘制参数迭代的轨迹图和后验分布图。

library(ggplot2)
library(bayesplot)
library(patchwork)
# 参数的后验分布
p1 <- mcmc_hist(fit_state_x77$draws(c("alpha", "beta[1]", "beta[2]")),
  facet_args = list(
    labeller = ggplot2::label_parsed,
    strip.position = "top",
    ncol = 1
  )
) + theme_classic()
# 参数的迭代轨迹
p2 <- mcmc_trace(fit_state_x77$draws(c("alpha", "beta[1]", "beta[2]")),
  facet_args = list(
    labeller = ggplot2::label_parsed,
    strip.position = "top",
    ncol = 1
  )
) + theme_classic() + theme(legend.title = element_blank())
# 绘图
p1 | p2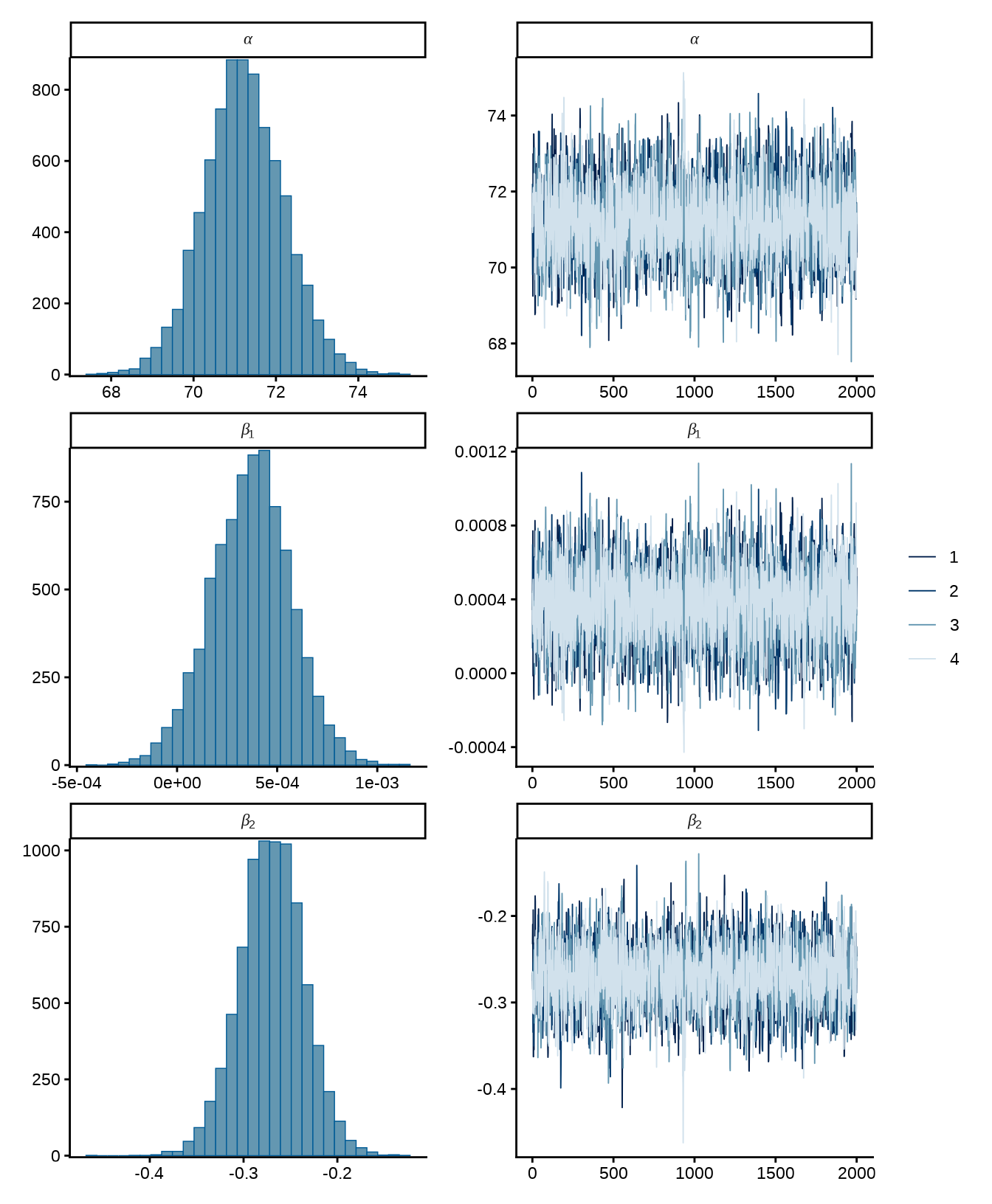

从参数的迭代轨迹可以看出四条马尔可夫链混合得很好，后验分布图主要用来描述参数的迭代结果，后验分布图可以是直方图或密度图的形式。