第四章多个样本均数比较的方差分析

日期: 2020-11-18 作者：wxhyihuan

T检验只能比较两组样本均值，对于多组的样本处理就需要用方差分析(Analysis of variance. ANOVA)。

在进行科学研究时，有时要按实验(对人称为试验)设计将所研究的对象分为多个处理组施加不同的干预(比如治疗某种疾病的方式)，施加的干预为处理，处理因素(Treatment，如用药处理，手术处理，药品剂量等)至少有两个水平(Level，比如药物种类有A，B，C三种，即为3个水平)。这类科研资料的统计分析，是通过所获得的样本信息来推断各处理组均数间的差别是否有统计学意义，即处理有无效果。常采用的统计分析方法为方差分析，由英国统计学家R. A. Fisher 首创，为纪念 Fisher.以F命名，故方差分析又称F检验，也称为 “变异数分析”。

F检验与前面的t检验或者Z检验类似，也有自己的概率分布基础，即方差分析是依靠F-分布为概率分布的依据，利用离均差平方和(Sum of square of deviations from mean,SS)与自由度(Degree of freedom, df)所计算的组间与组内均方(Mean of square,MS)估计出F值和P值，结合检验水准$\alpha=0.05$判断检验结果。若有统计学意义($P值\le0.05$)，则拒绝原假设$H_0(μ_0=μ_1=μ_2=μ_3=\cdots)$，接受$H_1$($μ$不完全相等)，即各样本不是来自不完全相同的总体；反之，若没有统计学意义($P值>0.05$)，则不拒绝原假设$H_0(μ_0=μ_1=μ_2=μ_3=\cdots)$，即还不能确定各样本是来自不完全相同的总体；

4.1 F分布

F分布定义是设$X$、$Y$为两个独立的随机变量，$X$服从自由度为k1的卡方分布， $Y$服从自由度为k2的卡方分布，这两个独立的卡方分布除以各自的自由度后的比率这一统计量的分布，即服从F-分布（F-distribution），即： \[F=\frac{U_1/d_1}{U_2/d_2}\] $U_1$和$U_2$分别是自由度(Degree of freedom, df)为d1和d2的卡方分布，$U_1=\sum_{i=0}^nX_i^2$，$U_2=\sum_{i=0}^nY_i^2$；或者 \[\frac{S_1^2/d_1}{\sigma_1^2}\div\frac{S_2^2/d_2}{\sigma_2^2}\] $S_1^2$为正态分布$N(0,\sigma_1^2)$的$d_1$个随机变量的平方和，$S_2^2$为正态分布$N(0,\sigma_2^2)$的$d_2$个随机变量的平方和。

F-分布对应的概率密度函数是： \[\begin{aligned} f(x,d_1,d_2) &= \frac{\sqrt{\frac{(d_{1}x)^{d_1} d_2^{d_2}}{(d_{1}x+d_2)^{d_1+d2}}}}{xB\left(d_{1}/2,d_{2}/2\right)}\\ &= \frac{1}{B\left(d_{1}/2,d_{2}/2\right)}\left(\frac{d_1}{d_2}\right)^{\frac{d_1}{2}}x^{\frac{d_1}{2}-1}\left(1+\frac{d_1}{d_2}x\right)^{-\frac{d_1+d_2}{2}} \end{aligned}\]

在R语言中。F-分布也有几个与Z分布，t分布基本函数类似的工具函数，分别是df()，pf()，qf()和rf()。

f_val = 2.2
df1 = 10
df2 = 20
q_seq <- c(0.25, 0.5, 0.75, 0.999)

df(f_val, df1 = df1, df2 = df2)
## [1] 0.007858262
pf(f_val, df = df1, df2 = df2, lower.tail = TRUE)
## [1] 0.9944622
qf(q_seq, df1 = df1, df2 = df2, lower.tail = TRUE)
## [1] 0.6563936 0.9662639 1.3994874 5.0752462

x <- rf(100000, df1 = df1, df2 = df2)
hist(x, col="#A8D6FF",
     breaks = 'Scott', freq = FALSE, 
     xlim = c(0,3), ylim = c(0,1),
     xlab = '', main = 'Histogram for a F-distribution with df1=10, df2=20', cex.main=0.9)

curve(df(x, df1 = df1, df2 = df2), from = 0, to = 3, n = 10000, col= 'red', lwd=2, add = T)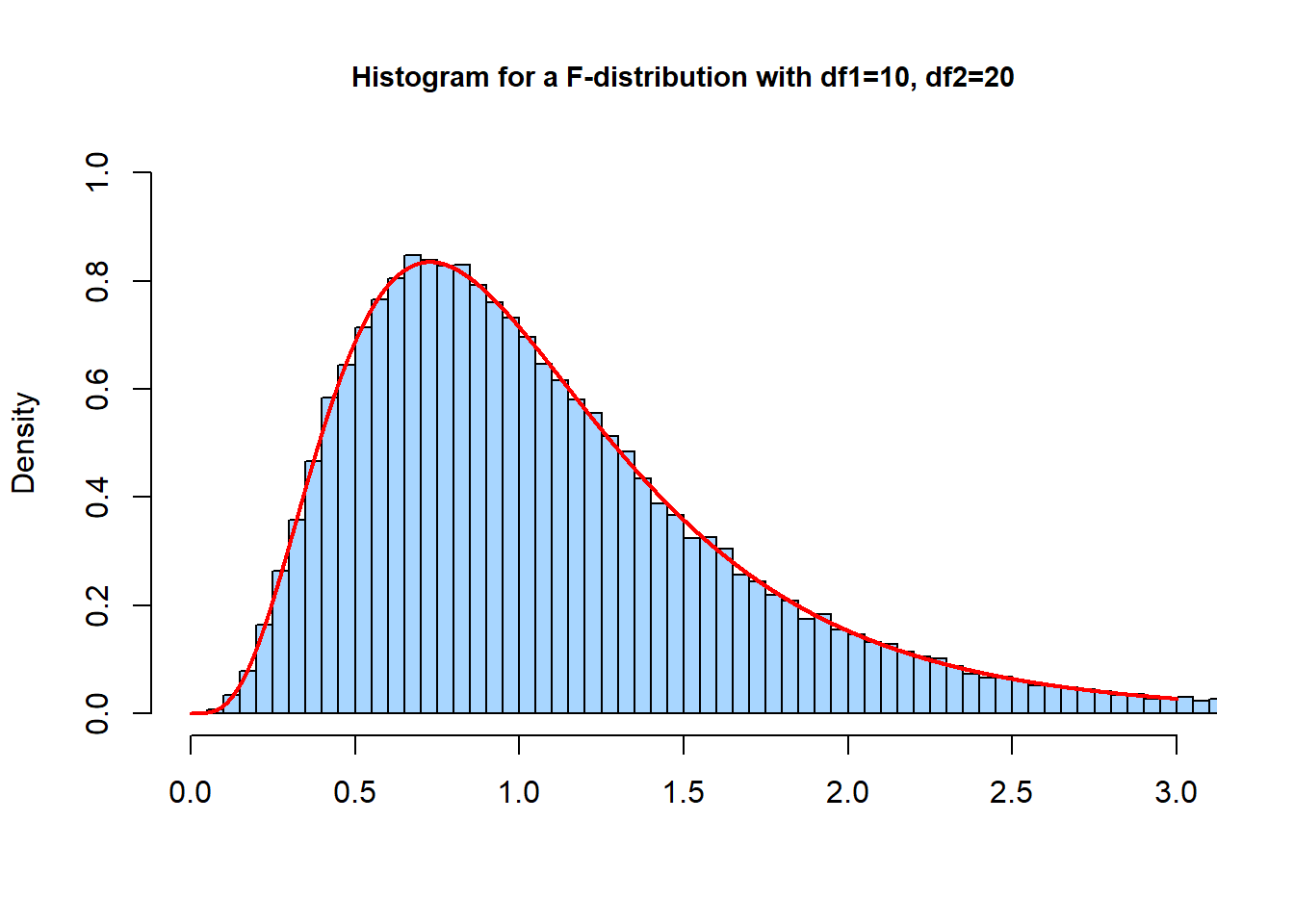

Figure 4.1: F-分布的概率密度曲线测试

4.2 F检验的分类、原理及应用

4.2.1 分类

按方差分析的基本运算概念，依照所感兴趣的因子数量而可分三大类：

单因子方差分析(One-way ANOVA)
双因子方差分析(Two-way ANOVA)
多因子方差分析(Multi-way ANOVA)

如果依照因子的特性不同而有三种型态，分别是：

固定效应方差分析(Fixed-effect ANOVA)
随机效应方差分析(Random-effect ANOVA)
混合效应方差分析(Mixed-effect ANOVA)

一般的，按照因子数量的分类进行区分使用情况比较常见，这里借用单因素方差分析(One-way ANOVA)介绍方差分析的基本思想

4.2.2 原理

ANOVA通过分析方差来推断均值是否和总体有显著性差异(注意：虽然叫做方差分析，但是它的目的是检验每个组的平均数是否相同)。 ANOVA把方差分为处理因素(Treatment effect，真实差异)和误差(Error effect，抽样误差或个体差异)两个来源，两个方差的比值服从F分布，因为方差本身就是个体和均值差平方和，所以对方差组成的分析能够反映均值的差异。处理效应(Treatment effect)是不同组的均值间的差异，误差(Error effect)是组内个体间的差异，习惯性地称前者为组间(Between)差异，后者为组内(Wthin)差异。

例如，在工业生产或实验研究中，为了比较药物X，Y，Z对治疗某疾病的疗效，我们将实验对象分成三组，分别记录服用X，Y，Z三种药物的治疗效果，并依次得到三组样本如下： \[\begin{aligned} & X_1,X_2,X_3,\cdots,X_{n1};\\ & Y_1,Y_2,Y_3,\cdots,Y_{n2};\\ & Z_1,Z_2,Z_3,\cdots,Z_{n3}; \end{aligned}\] 通过这些实验数据，我们希望回答：①三种药物对治疗该疾病有没有显著差异；②如果有差异，哪种药物治疗效果最好？

这个例子中，药物称为处理因素，X，Y，Z称为该因素的水平。这个实验只涉及单个处理因素——“药物”，我们称之为单因素实验，对应的方差分析处理叫单因子方差分析(One-way ANOVA)。此外，如果比较不同的药物和剂量对疗效的影响，这就是双因素实验，对应的方差分析叫双因子方差分析(Two-way ANOVA)，由此类似可推广到多因素实验和多因子方差分析(Multi-way ANOVA)。

示例中，我们记总均数$\bar{M}$，各分组(水平)的均数为$\bar{X}$，$\bar{Y}$，$\bar{Z}$，总样本个数$N=n_1+n_2+n_3$，分组(水平)个数记为g，本例中g=3。 \[\bar{M}=\frac{\sum_{i=0}^{n1}X_{n1}+\sum_{i=0}^{n2}Y_{n2}+\sum_{i=0}^{n3}Z_{n3}}{n_1+n_2+n_3}\]

把所有分组的混在一起，当成一个样本，总的方差的自由度为$v_t=N-1$，($SS_{tol}$总变异)公式为： \[\begin{aligned} SS_{t} &= \sum_{i=1}^g\sum_{j=1}^{n_i}(X_{ij}-\bar{X})\\ &= \sum_{i=1}^g\sum_{j=1}^{n_i}X_{ij}^2-(\sum_{i=1}^g\sum_{j=1}^{n_i}X_{ij})^2/N \end{aligned}\]

组间方差的自由度为$v_b=g-1$，组间方差$SS_{b}$为： \[\begin{aligned} SS_{b} &= \sum_{i=1}^gn_i(X_{i}-\bar{X})\\ &= \sum_{i=1}^g\frac{(\sum_{j=1}^nX_{ij})^2}{n_i}-(\sum_{i=1}^g\sum_{j=1}^{n_i}X_{ij})^2/N \end{aligned}\]

组内方差的自由度为$v_w=N-g$，组内方差SS_{w}(有的也记为SS_{error})为： \[\begin{aligned} SS_{w} &= \sum_{i=1}^g\sum_{j=1}^{n_i}(X_{ij}-\bar{X_i})^2 \end{aligned}\]

总的方差与组间方差和组内方差的关系： \[SS_{t}=SS_{b}+SS_{w}\]

总的方差与组间方差和组内方差各自的自由度之间的关系： \[v_{t}=v_{b}+v_{w}\]

变异程度除与离均差平方和的大小有关外，还与其自由度有关，由于各部分自由度不相等，因此各部分离均差平方和不能直接比较，须将各部分离均差平方和除以相应的自由度，其比值称为均方差，简称均方(Mean of square,MS)。组间均方和组内均方的计算公式为: \[\begin{aligned} MS_{b} &= \frac{SS_b}{v_b}\\ MS_{w} &= \frac{SS_t}{v_t} \end{aligned}\]

组间均方和组内均方的比值，符合F分布，由此可计算F统计量： \[\begin{aligned} F &= \frac{MS_b}{MS_w}\\ &= \frac{\frac{SS_b}{v_b}}{\frac{SS_t}{v_t}} \end{aligned}\]

如果F值接近于1，即组间均方和组内均方越接近的话，就没有理由拒绝$H_0$；反之，F值越大，拒绝$H_0$的理由越充分。数理统计的理论证明，当$H_0$成立时，F统计量服从F分布。方差分析是单侧F检验，可查出按α水准(一般取α = 0.05)F分布的单尾界值F(α,v1,v2)作为判断统计量F大小的标准。若根据实验结果计算的F值偏大，如F≥F(α,v1,v2)时，则P<0.05，拒绝$H_0$，接受$H_1$，说明各样本来自不全相同的总体，即认为各样本的总体均数不全相等。反之，当F<F(α,v1,v2)时，则P>0.05.不拒绝$H_0$，还不能下各样本的总体均数不全相等的结论。

4.2.2.1 F检验的原理示例

上面提到治疗某疾病研究药物处理因素在三种X，Y，Z三种水平的是否有差异，在假设$H_0：μ_0=μ_1=μ_2=μ_3$成立的情况下，我们大概可以做出类似下面这演的示例图。

Figure 4.2: 三种药物来自同一总体的假设模拟及MSb，MSw示例

根据F检验的原理，F值是组间均方$MS_b$和组内均方$MS_w$得比值，由此大概有三种情况：

A. $MS_b≈MS_w$，F≈1

这个时候MSB和MSE比较近似，可能是每组的平均值很集中，且每组方差很小；或者每组的方差较大，平均值也都离的不太远。总之，我们无法很好的剥离出某一组的分布。所以，我们同样无法拒绝$H_0：μ_0=μ_1=μ_2=μ_3$。

Figure 4.3: 三种药物来自同一总体的假设模拟，MSb≈MSw示例

B. $MS_b>>MS_w$，F>1

这个情况说明，至少有一个分布相对其他分布较远，且每个分布都非常集中，即每个分组的分布方差差别较小。所以，我们不能得出三个分布都有相同的均值，于是拒绝$H_0：μ_0=μ_1=μ_2=μ_3$。

Figure 4.4: MSb>>MSw示例

C. $MS_b<<MS_w$，F<1

这个情况有两种可能，当然也可以是这两种可能的混合。一是每组的平均值都相对集中，二是每组的方差很大，导致我们无法把每组分开。所以我们无法拒绝$H_0：μ_0=μ_1=μ_2=μ_3$。两个极端的例子：

Figure 4.5: MSb<<MSw示例

4.2.2.2 F检验的前提和应用

4.2.2.2.1 前提

F-检验是建立在一些假设基础上的，如果你的实验不能满足F-检验的假设，那你需要考虑别的分析方法或者改变实验设计。F-检验有主要有以下3个假设：

方差的齐性，可以理解为每组样本背后的总体(也叫族群)都有相同的方差
族群遵循正态分布
每一次抽样都是独立的，比如每个病人只能提供一个数据。对于一些一个样本需要提供多个数据的情况，有其他相应的F检验方法。

4.2.2.2.2 应用

F检验的主要有如下几种：

4.2.3 单因子方差分析

完全随机设计(Completely random design)是采用完全随机化的分组方法，将全部实验对象分配到g个组(水平组)，各组按照设计因素(单因子方差分析,One-way ANOVA) 分别接受不同水平的处理，实验结束后比较各组均数之间的差别有无统计学意义，推论因素的效应。

注意的是，当方差不齐的是否，可以使用oneway.test()函数进行F检验，设置var.equal为FALSE，此时即为Welch检验。

使用《医学统计学》中的案例4-2 的数据在R中进行完全随机设计资料的方差分析测试。

##案例4-2 
library("memisc")
#读取数据
rdl_sav<-spss.system.file("ExampleData/SavData4MedSta/Exam04-02.sav")
rdl_df<-as.data.frame(as.data.set(rdl_sav))
##简洁地显示任意R对象的结构
str(rdl_df)
## 'data.frame':    120 obs. of  2 variables:
##  $ GROUP: num  1 1 1 1 1 1 1 1 1 1 ...
##  $ LDL_C: num  3.53 4.59 4.34 2.66 3.59 3.13 3.3 4.04 3.53 3.56 ...

##对不规则数组应用指定的函数，快速计算每组的均值，方差，和样本大小
tapply(rdl_df$LDL_C, rdl_df$GROUP, FUN = mean)
##        1        2        3        4 
## 3.430333 2.715333 2.698000 1.966333 

tapply(rdl_df$LDL_C, rdl_df$GROUP, FUN = var)
##         1         2         3         4 
## 0.5114033 0.4072464 0.2471752 0.5571757 

tapply(rdl_df$LDL_C, rdl_df$GROUP, length)
##  1  2  3  4 
## 30 30 30 30 

#boxplot(rdl_df$LDL_C ~ rdl_df$GROUP,col=c(2:5))

## 使用oneway.test()函数进行F检验，注意var.equal 默认是 FALSE，也就是说方差可以不相等(此时即为Welch检验)，但是提供的信息相对较少。
oneway.test(rdl_df$LDL_C ~ rdl_df$GROUP,var.equal=T)
##  One-way analysis of means
## 
## data:  rdl_df$LDL_C and rdl_df$GROUP
## F = 24.884, num df = 3, denom df = 116, p-value = 1.674e-12
oneway.test(rdl_df$LDL_C ~ rdl_df$GROUP,var.equal=F)
##  One-way analysis of means (not assuming equal variances)
## 
## data:  rdl_df$LDL_C and rdl_df$GROUP
## F = 19.665, num df = 3.000, denom df = 63.592, p-value =
## 3.924e-09

#使用aov()函数进行F检验，可以获取完整地参数信息，这里要注意aov()里面提供的group信息
#最好不要是数值形式的分组，否则结果容易当作线性回归处理，导致与预期不一致，可以用
#as.character()将数字转换为字串形式的再使用
aov.out = aov(rdl_df$LDL_C ~ as.character(rdl_df$GROUP))
##                             Df Sum Sq Mean Sq F value   Pr(>F)    
## as.character(rdl_df$GROUP)   3  32.16  10.719   24.88 1.67e-12 ***
## Residuals                  116  49.97   0.431                     
## ---
## Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
## > aov.out
## Call:
##    aov(formula = rdl_df$LDL_C ~ as.character(rdl_df$GROUP))
## 
## Terms:
##                 as.character(rdl_df$GROUP) Residuals
## Sum of Squares                    32.15603  49.96702
## Deg. of Freedom                          3       116
## 
## Residual standard error: 0.6563156
## Estimated effects may be unbalanced
summary(aov.out)
##                             Df Sum Sq Mean Sq F value   Pr(>F)    
## as.character(rdl_df$GROUP)   3  32.16  10.719   24.88 1.67e-12 ***
## Residuals                  116  49.97   0.431                     
## ---
## Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

##其他几个查看aov()对象的工具
summary.aov(aov.out)
summary.lm(aov.out)
TukeyHSD(aov.out)

boxplot(rdl_df$LDL_C ~ rdl_df$GROUP,col=c(2:5),ylab="rdl value",xlab="Group info")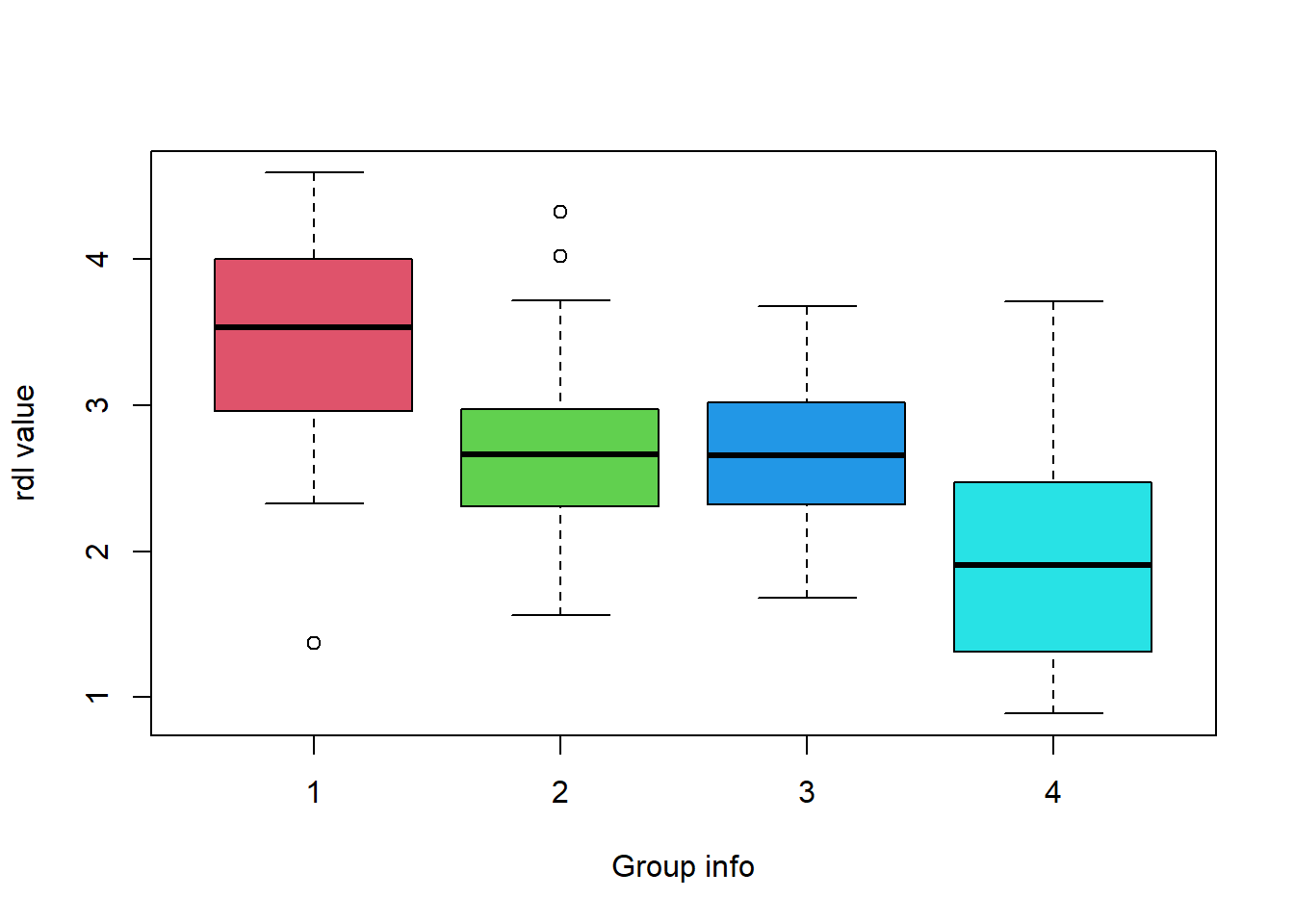

Figure 4.6: 案例 04-02 120例数据的箱线图预览

Table 4.1: 案例04-02 F检验结果
	组间	组内
自由度	3.000	116.0000
SS	32.156	49.9670
MS	10.719	0.4308
F值	24.884
P值	0.000

根据计算结果，F值=24.884>$F_{(0.01,(3,116))}$，P值<0.01<0.05，按照α=0.05的检验水准，拒绝$H_0$，接受 $H_1$，认为4个处理组的总体均数不全相等。

在方差分析的基本操作结束后，我们还可以利用线性回归的工具对方差分析的结果拟合情况进行评估，详细可参考方差分析的诊断图。

4.2.4 双因子方差分析

随机区组设计(Randomized block design)又称为配伍组设计，是配对设计的扩展。具体做法是:先按影响实验结果的非处理因素(如性别、体重、年龄、职业、病情、病程等)将实验对象配成区组(Block)，再分别将各区组内的实验对象随机分配到各处理组或对照组。与完全随机设计相比，随机区组设计的特点是随机分配的次数要重复多次，每次随机分配都对同一个区组内的实验对象进行，且各个处理组的实验对象数量相同，区组内均衡。在进行统计分析时，将区组变异离均差平方和从完全随机设计的组內离均差平和中分离出来，从而减小组内离均差平方和(误差平方和)，提高统计检验效率。若将区组作为另一处理因素的不同水平，随机区组设计等同于无重复观察的两因素设计(双因子方差分析,Two-way ANOVA)。

随机区组设计资料在进行统计分析时，需根据数据的分布特征选择方法，对于正态分布且方差齐同的资料，采用双向分类的方差分析(Two-way classification ANOVA)或配对t检验(g=2)；当不满足方差分析或t检验条件时，可进行变量变换后采用双向分类的方差分析或采用Friedman M检验。

双向ANOVA分析是单向ANOVA的扩展，分析两个因素，我们称之为A和B，假如A有i(1_{g)个水平(或叫区组)，B有j(1}n)个水平(处理因素的水平)，且每个分组的样本数目要一致，则共有$N=ng$样本个体，记总均数为$\bar{X}$，各处理组均数分别是$\bar{X_i}$，各区组均数为$\bar{X_{i}}$，双向ANOVA的实验数据有四个不同的变异：

1. 总变异，它反应所有观测值之间的变异，总离均差平方和：$SS_{total}$

2. 处理组间变异，它反应处理因素的不同水平作用和随机误差产生的变异：$SS_{treat}$

3. 区组间变异，它反应不同区组作用和随机误差产生的变异：$SS_{block}$

4. 误差变异，它是完全由随机误差产生的变异：$SS_{error}$

对总离均差平方和及自由度的分解关系为： \[\begin{aligned} SS_{total} & = SS_{treat}+SS_{block}+SS_{error} \\ v_{total} & = v_{treat}+v_{block}+v_{error} \end{aligned}\]

其中$v_{total}=N-1$，$v_{treat}=g-1$，$v_{block}=n-1$， $v_{error}=v_{treat}v_{block}=(n-1)(g-1)$。

误差变异的均方差即为；$MS_{error}=SS_{error}/v_{error}$，

处理组间变异的均方差即为：$MS_{treat}=SS_{treat}/v_{treat}$，

区组间变异均方差即为：$MS_{block}=SS_{block}/v_{block}$，

处理组间变异的F值公式：$F_{treat}=\frac{MS_{treat}}{MS_{error}}$

区组间变异的F值公式：$F_{block}=\frac{MS_{block}}{MS_{error}}$

双向ANOVA能够同时检验3个零假设：

单独考虑A因素，总体均值间没有差别，这相当于对A因子进行单向ANOVA
单独考虑B因素，总体均值间没有差别，这相当于对B因子进行单向ANOVA
A和B两个因素，没有相互作用，相当于使用二联表进行独立性分析

使用《医学统计学》中的案例4-4 的数据在R中进行双因子方差分析的测试。

library("memisc")
sarc_sav<-spss.system.file("ExampleData/SavData4MedSta/Exam04-04.sav")
sarc_df<-as.data.frame(as.data.set(sarc_sav))
str(sarc_df)
## 'data.frame':    15 obs. of  3 variables:
##  $ GROUP : num  1 2 3 4 5 1 2 3 4 5 ...
##  $ TREAT : num  1 1 1 1 1 2 2 2 2 2 ...
##  $ WEIGHT: num  0.82 0.73 0.43 0.41 0.68 0.65 0.54 0.34 0.21 0.43 ...

sarc_aov.out<-aov(sarc_df$WEIGHT ~ factor(as.character(sarc_df$TREAT))+factor(as.character(sarc_df$GROUP)))
## Call:
##    aov(formula = sarc_df$WEIGHT ~ factor(as.character(sarc_df$TREAT)) + 
##     factor(as.character(sarc_df$GROUP)))
## 
## Terms:
##                 factor(as.character(sarc_df$TREAT)) factor(as.character(sarc_df$GROUP)) Residuals
## Sum of Squares                              0.22800                             0.22836   0.07640
## Deg. of Freedom                                   2                                   4         8
## 
## Residual standard error: 0.0977241
## Estimated effects may be unbalanced
summary(sarc_aov.out)
##                                     Df Sum Sq Mean Sq F value  Pr(>F)   
## factor(as.character(sarc_df$TREAT))  2 0.2280 0.11400  11.937 0.00397 **
## factor(as.character(sarc_df$GROUP))  4 0.2284 0.05709   5.978 0.01579 * 
## Residuals                            8 0.0764 0.00955                   
## ---
## Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

##其他几个查看aov()对象的工具
summary.aov(sarc_aov.out)
summary.lm(sarc_aov.out)
TukeyHSD(sarc_aov.out)

Table 4.2: 案例04-04 双因子f检验结果
	自由度	SS	MS	F值	P值
处理间	2	0.2280	0.1140	11.937	0.0040
区组间	4	0.2284	0.0571	5.978	0.0158
误差	8	0.0764	0.0096

根据计算结果，对于处理组间F值为11.937，对应P值是0.004<0.01<α=0.05，因此拒绝处理组间$H_0: μ_1=μ_2=μ_3$的原假设，接受$H_1$，即认为药物的肿瘤生长有统计学意义。同理，区组间的F值为5.978，对应的P值是0.0158<α=0.05，因此拒绝区组间的$H_0: μ_1=μ_2=μ_3$的原假设，接受$H_1$，即体重对肿瘤生长的影响有统计学意义。

现在有一个问题，是方差分析的结果可以推断多组样本的总体之间的均值是否都相等，如果不都相等，我怎么知道是具体是怎么不相等的呢？详细请看多重比较。

4.2.5 拉丁方设计资料的方差分析

完全随机设计只涉及一个处理因素；随机区组设计涉及一个处理因素、一个区组因素(或称为配伍因素)；倘若实验研究涉及一个处理因素和两个控制因素，每个因素的类别数或水平数相等，此时可采用拉丁方设计(Latin square design)来安排实验，将两个控制因素分别安排在拉丁方设计的行和列上。拉丁方设计是在随机区组设计的基础上发展的，它可多安排一个已知的对实验结果有影响的非处理因素，增加了均衡性，减少了误差，提高了效率。

拉丁方设计资料采用三向分类的方差分析(Three-way classification ANOVA)，总变异可分解为处理组变异、行区组变异、列区组变异和误差4部分，比如对于一个g*g的拉丁方实验设计，用i,j,k分别代表捏区组水平，行区组水平和处理因素的水平，它们和对应的自由度分别是：

1. 总变异，它反应所有观测值之间的变异，总离均差平方和：$SS_{total}$

2. 处理组间变异，它反应处理因素的不同水平作用和随机误差产生的变异：$SS_{treat}$

3. 列区组间变异，它反应不同列区组作用和随机误差产生的变异：$SS_{column}$

4. 行区组间变异，它反应不同行区组作用和随机误差产生的变异：$SS_{row}$

5. 误差变异，它是完全由随机误差产生的变异：$SS_{error}$

对总离均差平方和及自由度的分解关系为： \[\begin{aligned} SS_{total} &= SS_{treat}+SS_{column}+SS_{row}+SS_{error}\\ v_{total} &= v_{treat}+v_{column}+v_{row}+v_{error} \end{aligned}\]

其中$v_{total}=N-1=g^2-1$，$v_{treat}=g-1=$v_{column}=v_{column}=g-1$， $v_{error}=(g-2)(g-1)$。

误差变异的均方差即为；$MS_{error}=SS_{error}/v_{error}$，

处理组间变异的均方差即为：$MS_{treat}=SS_{treat}/v_{treat}$，

列区组间变异均方差即为：$MS_{column}=SS_{column}/v_{column}$，

行区组间变异均方差即为：$MS_{row}=SS_{row}/v_{row}$，

处理组间变异的F值公式：$F_{treat}=\frac{MS_{treat}}{MS_{error}}$

列区组间变异的F值公式：$F_{column}=\frac{MS_{column}}{MS_{error}}$

行区组间变异的F值公式：$F_{row}=\frac{MS_{row}}{MS_{error}}$

拉丁方设计资料采用三向分类的ANOVA，由于比较复杂，在分析之前应该理清楚处理组，列区组。行区组的对应的因素，并理清它们各自的原假设与备择假设，总的来说能够同时检验3个零假设：

处理组之间的总体均数都相等
列区组之间的总体均数都相等
行区组之间的总体均数都相等

使用《医学统计学》中的案例4-5 的数据在R中进行拉丁方实验设计资料的方差分析测试。

library("memisc")
hsv_sav<-spss.system.file("ExampleData/SavData4MedSta/Exam04-05.sav")
hsv_df<-as.data.frame(as.data.set(hsv_sav))
str(hsv_df)
## 'data.frame':    36 obs. of  4 variables:
##  $ 行区组  : num  1 1 1 1 1 1 2 2 2 2 ...
##   ..- attr(*, "label")= chr "<RMC1`:E"
##  $ 列区组  : num  1 2 3 4 5 6 1 2 3 4 ...
##  $ 处理组  : num  3 2 5 4 1 6 2 1 4 3 ...
##   ..- attr(*, "label")= chr "2;M,R)No"
##  $ 实验结果: num  87 75 81 75 84 66 73 81 87 85 ...
##修改一下列名称
colnames(hsv_df)<-c("rg","lg","tg","test_val")
hsv_aov.out <-aov(hsv_df$test_val ~ factor(as.character(hsv_df$tg))+factor(as.character(hsv_df$rg))+factor(as.character(hsv_df$lg)))
summary(hsv_aov.out)
##                                 Df Sum Sq Mean Sq F value Pr(>F)  
## factor(as.character(hsv_df$tg))  5    667   133.4    3.79  0.014 *
## factor(as.character(hsv_df$rg))  5    250    50.1    1.42  0.258  
## factor(as.character(hsv_df$lg))  5     65    13.1    0.37  0.862  
## Residuals                       20    703    35.2                 
## ---
## Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
summary.aov(hsv_aov.out)
summary.lm(hsv_aov.out)
TukeyHSD(hsv_aov.out)

Table 4.3: 案例04-05 拉丁方设计资料采用三向分类的f检验结果
	自由度	SS	MS	F值	P值
处理间	5	667.139	133.428	3.7940	0.0140
家兔间	5	250.472	50.094	1.4244	0.2584
部位间	5	65.337	13.067	0.3716	0.8621
误差	20	703.358	35.168

根据计算结果，对于处理组间F值为3.79402，对应P值是0.014<α=0.05，因此拒绝处理组间$H_0$的原假设，接受$H_1$，即认为 6种药物的对疱疹大小的生长影响有统计学意义。同理，家兔间的F值为1.42444，对应的P值是0.258401>α=0.05，因此暂时不能拒绝家兔间的$H_0$的原假设，即还不能认为疱疹的大小的总体均数不全相等。对于部位间的F值为0.37157，对应的P值是0.862102>α=0.05，因此暂时不能拒绝部位间的$H_0$的原假设，即还不能认为6个部位的疱疹大小的总体均数不全相等。

4.2.6 两阶段交叉设计资料的方差分析

在医学研究中，欲将A、B两种处理先后施加于同一批实验对象，随机地使半数实验对象先接受A后接受B，而另一半实验对象则正好相反，即先接受B再接受A。由于两种处理在全部实验过程中交叉进行，这种设计称为交叉设计(Crossover design)。在交叉设计中，A、B两种处理先后以同等的机会出现在两个实验阶段中，故又称为两阶段交叉设计。当然也可以有多个实验阶段，但本节仅介绍两阶段的交叉设计。虽然交叉实验的处理是单因素，但影响实验结果的因素还有非人为控制的实验对象的个体差异和实验阶段这两个因素。因此，该设计不仅平衡了处理顺序的影响，而且能把处理方法间的差别、时间先后之间的差别和实验对象之间的差别分开来分析。但是该设计有一个较为严格的限制条件：前一个实验阶段的处理效应不能持续作用到下一个实验阶段。为此，有必要在两个阶段之间设一个洗脱(Wash-out)阶段，以消除残留效应(Carry-over effect) 的影响。在医学研究中交叉设计多用于止痛、镇静、降压等药物或治疗方法间疗效的比较。

使用《医学统计学》中的案例4-5 的数据在R中进行两阶段交叉设计资料的方差分析测试。

library("memisc")
gmp_sav<-spss.system.file("ExampleData/SavData4MedSta/Exam04-06.sav")
gmp_df<-as.data.frame(as.data.set(gmp_sav))
str(gmp_df)
## 'data.frame':    20 obs. of  4 variables:
##  $ PERSON: num  1 2 3 4 5 6 7 8 9 10 ...
##   ..- attr(*, "label")= chr "J\\JTU_1`:E"
##  $ TREAT : num  1 2 1 1 2 2 1 2 1 2 ...
##   ..- attr(*, "label")= chr "IAK8R:"
##  $ PHASE : num  1 1 1 1 1 1 1 1 1 1 ...
##   ..- attr(*, "label")= chr "=W6N"
##  $ X     : num  760 860 568 780 960 940 635 440 528 800 ...
##   ..- attr(*, "label")= chr "Q*=,3H-cGMP"
gmp_aov.out <-aov(gmp_df$X ~ factor(as.character(gmp_df$PERSON))+factor(as.character(gmp_df$TREAT))+factor(as.character(gmp_df$PHASE)))
## summary(gmp_aov.out)
##                                     Df Sum Sq Mean Sq F value  Pr(>F)    
## factor(as.character(gmp_df$PERSON))  9 551111   61235 1240.19 1.3e-11 ***
## factor(as.character(gmp_df$TREAT))   1    198     198    4.02   0.080 .  
## factor(as.character(gmp_df$PHASE))   1    490     490    9.93   0.014 *  
## Residuals                            8    395      49                    
## ---
## Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
summary.aov(gmp_aov.out)
summary.lm(gmp_aov.out)
TukeyHSD(gmp_aov.out)

Table 4.4: 案例04-05 两阶段交叉设计资料的f检验结果
	自由度	SS	MS	F值	P值
处理间	1	198.45	198.450	4.0192	0.0799
阶段间	1	490.05	490.050	9.9251	0.0136
受试者间	9	551111.45	61234.606	1240.1945	0.0000
误差	8	395.00	49.375

根据计算结果，还不能认为A和B两种闪烁液的测定结果有差别；可认为测定阶段对测定结果有影响：可认为各受试者的H-cGMP 值不同。交叉试验主要关心处理间的差别，I、II阶段和受试者间通常是已知的控制因素。

4.3 方差分析的诊断图

当我们进行方差分析后，统计软件会输出一堆数字，我们在推断结果是显著的(或不显著的)，你可能认为你已经完成了分析，但我们通常还应该检查方差分析是否适合数据。可以怎么做呢？

这里要补充一点说明线性回归和方差分析的关系。从数学的观点，线性回归和方差分析是相同的：两者将数据的总方差拆分不同的“子方差”，并用检验(F检验)来验证这些“子方差”的相等性。线性回归和方差分析稍有区别的是，在这两种技术中因变量是连续的，但在ANOVA分析中，自变量可以是专有的分类变量，而在回归中，可以使用分类和连续自变量。因此，方差分析可以被认为是线性回归的一个案例，其中所有的预测因子都是分类变量。关于线性回归和方差分析，以后有时间在做更详细的比较说明吧。

所以，我们可以用检查线性回归的模型中用到一些方法来辅助查看方差分析结果。R中线性回归分析的内置诊断图 (Diagnostic Plots，除了内置的基本R函数之外，还有许多其他方法可以探索数据和诊断线性模型)它非常容易运行: 只需在运行分析之后对lm对象或者aov对象使用plot()。然后R将依次向您展示四个残差(估计值与真实值之差)相关的诊断图：

Residuals vs Fitted
Normal Q-Q
Scale-Location
Residuals vs Leverage

下面是用单因子方差分析结果做示例的代码和说明。

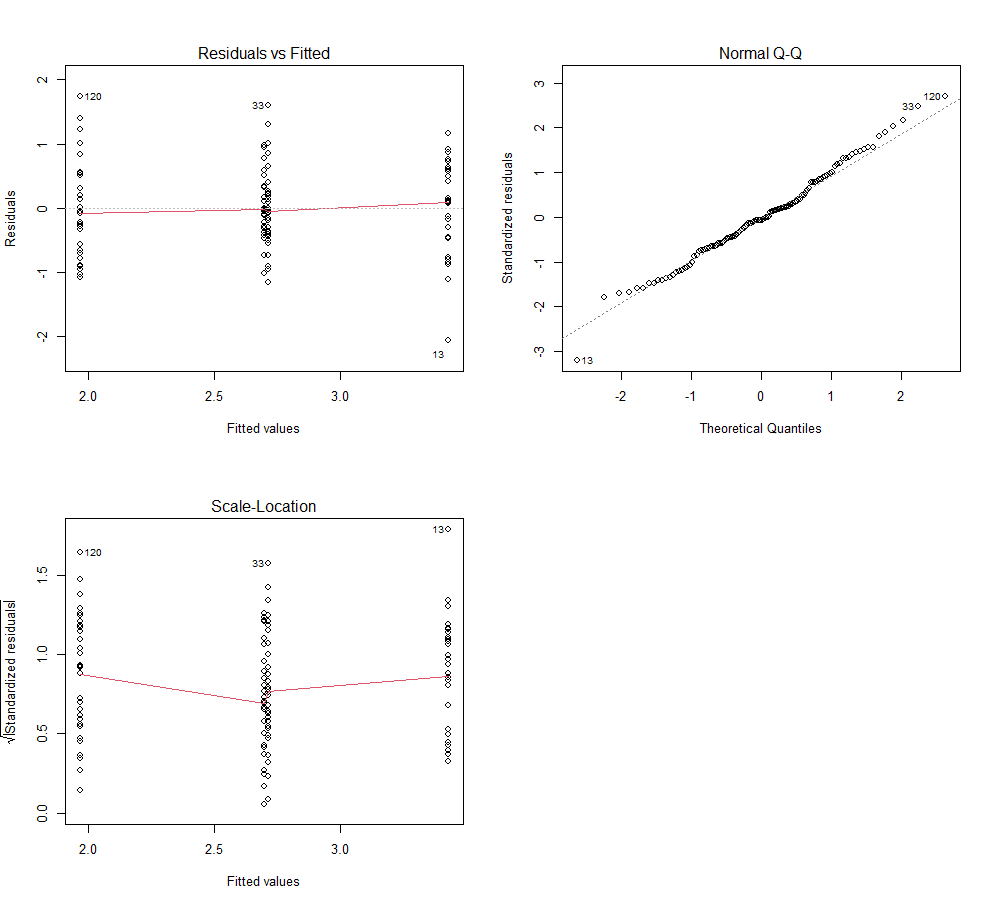
##用aov()的残差诊断图检验方差分析结果
par(mfrow=c(2,2))
plot(aov.out)

Figure 4.7: aov()的残差诊断图

1. Residuals vs Fitted

此图就是残差与真实值之间的关系图。在理想线性模型中有五大假设。其中之一便是残差应该是一个正态分布，与估计值无关。在线性回归当中，如果残差还和估计值有关(即不是一次函数关系，非线性关系)，那就说明模型仍然有值得去改进的地方。对于方差分析，如果残差还和估计值有关，通常说明样本数据均值不同，或者方差不齐等问题。

2. Normal Q-Q

此图是验证残差的正态分布性，即残差是否沿直线良好或严重偏离？如果残差在不是虚线上很好地对齐，则是不是正态分布，表明样本数据可能不符合方差分析的假设前提。

3. Scale-Location

Spread-Location plot，测试残差是否随着拟合值的增加而增加，显示残差是否在预测变量的范围内平均分布。这样可以检查方差齐性(Homoscedasticity,均方差)的假设。如果您看到一条具有相等(随机)分布点的(近似)水平直线，表明各组之间方差齐性。

4. Residuals vs Leverage

本案例中的数据数据比较乖巧，没有特别极端的数据，因此没有画出来。方差分析结果绘制Residuals vs Leverage图类似4.8，可以直观的告诉我们哪一组分组数据拟合的最好。

线性回归分析绘制的Residuals vs Leverage图可以帮助我们找到有影响力的案例(例如受试者)。在线性回归分析中，并非所有的离群值(Outliers) 都有影响。即使数据具有极端值，它们也可能不会对确定回归线产生影响。这意味着，如果我们在分析中包括或排除它们，结果也不会有太大不同。在大多数情况下，它们都是遵循趋势的，它们并不重要，他们没有影响力。另一方面，有些案例可能非常有影响力，即使它们看起来在合理的价值范围内，它们可能是与回归线相反的极端情况，如果我们将它们排除在分析之外，结果可能会发生改变。或者说，在大多数情况下，它们并不认同这种趋势。

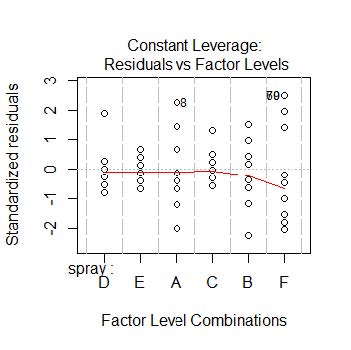
Figure 4.8: aov()的残差诊断图Leverage

4.4 多个样本均数间的多重比较

当方差分析的结果为拒绝$H_0$，接受$H_1$时，只说明g个总体均数不全相等。若想进一步了解哪两个总体均数不等，须进行多个样本均数间的两两比较或称多重比较(Multiple comparison)。这种进一步阐明在ANOVA测试中起重要作用的群体差异的方法，叫做事后测试(Post hoc tests)。如用案例4-2 的两样本均数比较的检验进行多重比较，将会加大犯I型错误(把总体均数间本无差别判为有差别)的概。若用t检验作6次比较，且每次比较的检验水准选为α=0.05，则每次比较不犯I类错误的概率为(1-0.05)，6次均不犯I类错误的概率为(1-0.05)，这时，总的检验水准变为1-(1-0.05)=026，比0.05大多了。因此，样本均数间的多重比较不能用两样本均数比较的检验。

事后测试分析测试非常重要，因为尽管ANOVA提供了很多信息，但它并未提供有关特定研究组之间差异的详细信息，也无法提供有关复杂比较的信息。这些事后测试的进一步分析可能会为研究人员提供该研究的最重要发现。可供我们选择的事后测试统计方法更有10多种，但是目前还没有一种在任何条件下都适用、效果好的方法。因此，选择与数据相匹配的测试方法，进行组间比较有关的信息种类以及必要的分析就非常重要。方法选择不当的后果通常与第Ⅰ类错误有关，但也可能涉及未能发现组之间的重要差异。进一步了解可以阅读：

不同多重比较(Multiple comparison)的比较与他们在R语言中的实现方法，可以参考下面的图表，具体的函数使用和参数设置请查看相应的帮助文档。

Figure 4.9: 多重比较(Multiple comparison)统计方法的比较

多重比较(Multiple comparison)在R中几个示例方法，LSD.test()，scheffe.test()，SNK.test()，HSD.test()和TukeyHSD()，DunnettTest()，代码如下：

##案例4-2 
#install.packages("pacman")
#install.packages("DescTools")
#批量加载包
pacman::p_load(memisc,agricolae,DescTools)
#读取数据
rdl_sav<-spss.system.file("ExampleData/SavData4MedSta/Exam04-02.sav")
rdl_df<-as.data.frame(as.data.set(rdl_sav))
aov.out = aov(rdl_df$LDL_C ~ as.character(rdl_df$GROUP))

##p.adj=c("none","holm","hommel", "hochberg", "bonferroni", "BH", "BY", "fdr")
LSD.test(aov.out,"as.character(rdl_df$GROUP)", p.adj="bonferroni",console = T)
plot(LSD.test(aov.out,"as.character(rdl_df$GROUP)", p.adj="bonferroni",console = F))
## Study: aov.out ~ "as.character(rdl_df$GROUP)"
## 
## LSD t Test for rdl_df$LDL_C 
## P value adjustment method: bonferroni 
## 
## Mean Square Error:  0.4307502 
## 
## as.character(rdl_df$GROUP),  means and individual ( 95 %) CI
## 
##   rdl_df.LDL_C       std  r      LCL      UCL  Min  Max
## 1     3.430333 0.7151247 30 3.193002 3.667664 1.37 4.59
## 2     2.715333 0.6381586 30 2.478002 2.952664 1.56 4.32
## 3     2.698000 0.4971671 30 2.460669 2.935331 1.68 3.68
## 4     1.966333 0.7464421 30 1.729002 2.203664 0.89 3.71
## 
## Alpha: 0.05 ; DF Error: 116
## Critical Value of t: 2.684257 
## 
## Minimum Significant Difference: 0.454874 
## 
## Treatments with the same letter are not significantly different.
## 
##   rdl_df$LDL_C groups
## 1     3.430333      a
## 2     2.715333      b
## 3     2.698000      b
## 4     1.966333      c

#scheffe方法
scheffe.test(aov.out,"as.character(rdl_df$GROUP)",console = T)
## Study: aov.out ~ "as.character(rdl_df$GROUP)"
## 
## Scheffe Test for rdl_df$LDL_C 
## 
## Mean Square Error  : 0.4307502 
## 
## as.character(rdl_df$GROUP),  means
## 
##   rdl_df.LDL_C       std  r  Min  Max
## 1     3.430333 0.7151247 30 1.37 4.59
## 2     2.715333 0.6381586 30 1.56 4.32
## 3     2.698000 0.4971671 30 1.68 3.68
## 4     1.966333 0.7464421 30 0.89 3.71
## 
## Alpha: 0.05 ; DF Error: 116 
## Critical Value of F: 2.682809 
## 
## Minimum Significant Difference: 0.4807537 
## 
## Means with the same letter are not significantly different.
## 
##   rdl_df$LDL_C groups
## 1     3.430333      a
## 2     2.715333      b
## 3     2.698000      b
## 4     1.966333      c

#SNK方法
SNK.test(aov.out,"as.character(rdl_df$GROUP)",console = T)
## Study: aov.out ~ "as.character(rdl_df$GROUP)"
## 
## Student Newman Keuls Test
## for rdl_df$LDL_C 
## 
## Mean Square Error:  0.4307502 
## 
## as.character(rdl_df$GROUP),  means
## 
##   rdl_df.LDL_C       std  r  Min  Max
## 1     3.430333 0.7151247 30 1.37 4.59
## 2     2.715333 0.6381586 30 1.56 4.32
## 3     2.698000 0.4971671 30 1.68 3.68
## 4     1.966333 0.7464421 30 0.89 3.71
## 
## Alpha: 0.05 ; DF Error: 116 
## 
## Critical Range
##         2         3         4 
## 0.3356368 0.4023275 0.4417253 
## 
## Means with the same letter are not significantly different.
## 
##   rdl_df$LDL_C groups
## 1     3.430333      a
## 2     2.715333      b
## 3     2.698000      b
## 4     1.966333      c

#Tukey方法
HSD.test(aov.out,"as.character(rdl_df$GROUP)",console = T)
## Study: aov.out ~ "as.character(rdl_df$GROUP)"
## 
## HSD Test for rdl_df$LDL_C 
## 
## Mean Square Error:  0.4307502 
## 
## as.character(rdl_df$GROUP),  means
## 
##   rdl_df.LDL_C       std  r  Min  Max
## 1     3.430333 0.7151247 30 1.37 4.59
## 2     2.715333 0.6381586 30 1.56 4.32
## 3     2.698000 0.4971671 30 1.68 3.68
## 4     1.966333 0.7464421 30 0.89 3.71
## 
## Alpha: 0.05 ; DF Error: 116 
## Critical Value of Studentized Range: 3.686381 
## 
## Minimun Significant Difference: 0.4417253 
## 
## Treatments with the same letter are not significantly different.
## 
##   rdl_df$LDL_C groups
## 1     3.430333      a
## 2     2.715333      b
## 3     2.698000      b
## 4     1.966333      c

TukeyHSD(aov.out)
##   Tukey multiple comparisons of means
##     95% family-wise confidence level
## 
## Fit: aov(formula = rdl_df$LDL_C ~ as.character(rdl_df$GROUP))
## 
## $`as.character(rdl_df$GROUP)`
##            diff        lwr        upr     p adj
## 2-1 -0.71500000 -1.1567253 -0.2732747 0.0002825
## 3-1 -0.73233333 -1.1740587 -0.2906080 0.0001909
## 4-1 -1.46400000 -1.9057253 -1.0222747 0.0000000
## 3-2 -0.01733333 -0.4590587  0.4243920 0.9996147
## 4-2 -0.74900000 -1.1907253 -0.3072747 0.0001302
## 4-3 -0.73166667 -1.1733920 -0.2899413 0.0001938

#Dunnett，加载DescTools包
DunnettTest(rdl_df$LDL_C, rdl_df$GROUP)
##   Dunnett's test for comparing several treatments with a control :  
##     95% family-wise confidence level
## 
## $`1`
##           diff    lwr.ci     upr.ci    pval    
## 2-1 -0.7150000 -1.118364 -0.3116361 0.00015 ***
## 3-1 -0.7323333 -1.135697 -0.3289694 9.6e-05 ***
## 4-1 -1.4640000 -1.867364 -1.0606361 8.5e-14 ***
## 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

4.5 多样本方差齐性检验

在进行方差分析时要求所对比的各组即各样本的总体方差必须是相等的，这一般需要在作方差分析之前，先对资料的方差齐性进行检验，特别是在样本方差相差悬殊时，应注意这个问题。对两总体方差进行齐性检验的方法前已介绍。本节介绍多样本(也适用于两样本)方差比较的 Bartlett’s 检验和Levene’s 检验。

4.5.1 Bartlett’s 检验

该检验以Maurice Stevenson Bartlett命名的，是基于其抽样分布近似为具有(k-1)自由度的卡方分布的统计量，其中k是随机样本的数量，其大小可能有所不同，并且每个样本均来自独立的正态分布。巴特利特的检验对偏离常态很敏感，如果样本来自非正态分布，那么Bartlett的检验可能就比较差。Levene检验和Brown-Forsythe检验是Bartlett检验的替代方法，对偏离正态性较不敏感。

其统计量和计算公式可以参考《医学统计学》你，或者 Wikipedia。

在R语言中的实现，可以参考下面的代码，以案例4-2数据做测试。根据计算结果，P值=0.1564>0.1，方差齐性检验的通常按照α=-。1 设置，因此不拒绝$H_0$，即不拒绝各组之间的方向都相等。

bartlett.test(rdl_df$LDL_C,rdl_df$GROUP)
## 
##  Bartlett test of homogeneity of variances
## 
## data:  rdl_df$LDL_C and rdl_df$GROUP
## Bartlett's K-squared = 5.2192, df = 3, p-value = 0.1564

4.5.2 Levene’s 检验

Levene’s 检验是Bartlett’s 检验的替代方法，对样本整体数据不必要是正态分布,对偏离正态性较不敏感。与Levene’s 检验相似的还有Brown–Forsythe检验，两者的区别是用来计算各组的中心取得参数不一样，Brown–Forsythe采用的是中位数(median)，Levene’s是均值(mean)。