第七章 $\chi^2$ 检验

日期: 2020-11-28 作者：wxhyihuan

在十九世纪，统计分析方法主要被用于生物数据分析。当时主流意见认为正态分布普遍适用于此类数据，例如乔治·比德尔·艾里以及梅里曼教授，而卡尔·皮尔森在他1900年的论文中就针对了他们的研究数据作出了指正。

直到十九世纪末期，皮尔森指出了部分数据具有明显的偏态，正态分布并不是普遍适用。为了更好地对这些观察数据进行建模，皮尔森在1893年至1916年发表的系列文章中提出了一个包含正态分布以及众多偏态分布的连续概率分布族——皮尔森分布族。同时，他指出数据统计分析的步骤应该是在从皮尔森分布族中选取合适的分布来进行建模后，使用拟合优度检验技术来评价模型和实验数据间的拟合优度(Goodness of fit)。

两个样本率的比较可用前章介绍的u检验，但实际工作中往往更多地应用卡方检验(Chi-square test)。卡方检验是以卡方分布为理论依据，用途颇广的假设检验方法。它在计数资料中的应用主要包括推断两个总体率或构成比之间有无差别、多个总体率或构成比之间有无差别、多个样本率间的多重比较、两个分类变量之间有无关联性、多维列联表的分析和频数分布拟合优度的检验。

7.1 卡方分布

若n个相互独立的随机变量Z₁，Z₂，…,Zv ，均服从标准正态分布，则这n个服从标准正态分布的随机变量的平方和构成一新的随机变量X，其分布规律称为卡方分布(Chi-square distribution)，记作: $X=\sum_{i=1}^vZ_i^2$ 对应卡方分布被称为服从自由度为n的卡方分布，记作： $X \sim X^2(v)$ 。

卡方分布(Chi-square distribution)是一种连续型分布，它只有一个参数，即自由度v。按卡方分布的密度函数f(X)可给出自由度v= 1， 2，3，…的族/分布曲线，且分布的形状依赖于自由度v的大小：

当自由度v≤2 时，曲线呈L形；
随着v的增加，曲线逐渐趋于对称；
当自由度V趋近无穷时，卡方分布趋近正态分布。

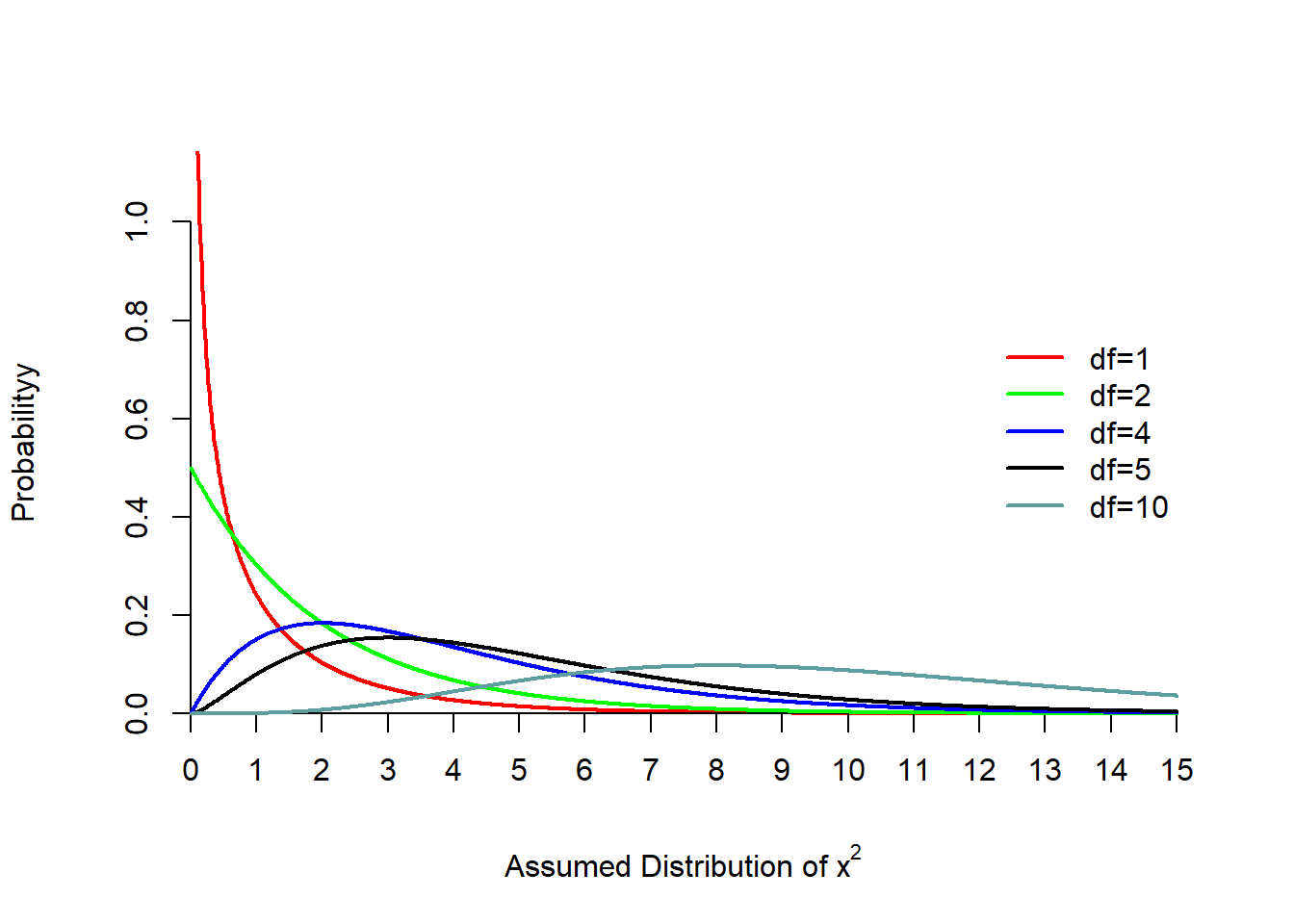
Figure 7.1: 不同自由度情况下的卡方分布概率密度曲线图

7.1.1 概率密度函数

卡方分布的概率密度函数为： $f(x,v)=\frac{x^{v/2-1}e^{-x/2}}{2^{v/2}\Gamma(v/2)}$ 注意的是，当x≤0时， $f(x,v)=0$ ； $\Gamma$ 代表Gamma函数，因此卡方分布也是一种特别的Gamma函数。

卡方分布的均值和方差分别为v，和2v，及自由度和自由度的2倍。

卡方分布的一个基本性质就是可加性，即独立卡方变量之和同样服从卡方分布。如两个独立的卡方分布， $X_1 \sim X^2(v_1)$ 与 $X_2 \sim X^2(v_2)$ ，那么有 $(X_1+X_2) \sim X^2(v_1+v_2)$

在R语言中。卡方分布也有几个与Z分布，t分布基本函数类似的工具函数，分别是dchisq()，pchisq()，qchisq()和rchisq()，对应的检验函数主要是chisq.test()。

7.2 卡方检验

卡方检验(Chi-Squared Test)是一种统计量的分布在零假设成立时近似服从卡方分布的假设检验。在没有其他的限定条件或说明时，卡方检验一般指代的是皮尔森卡方检验。在卡方检验的一般运用中，研究人员将观察量的值划分成若干互斥的分类，且使用一套理论（或零假设）尝试去说明观察量的值落入不同分类的概率分布的模型。而卡方检验的目的就在于去衡量这个假设对观察结果所反映的程度。卡方检验就是统计样本的实际观测值与理论推断值之间的偏离程度，实际观测值与理论推断值之间的偏离程度就决定卡方值的大小，如果卡方值越大，二者偏差程度越大；反之，二者偏差越小；若两个值完全相等时，卡方值就为0，表明理论值完全符合。

卡方检验分为卡方独立性检验和拟合优度的卡方检验。

7.2.1 卡方独立性检验的基本思想

这里使用《医学统计学》中的案例07-01 的数据，介绍 $\chi^2$ 检验的基本思想，详细见四格资料表的卡方检验。

7.2.2 四格资料表的卡方检验

《医学统计学》中的案例07-01 的数据，即四格资料表的比较为例，介绍 $\chi^2$ 检验的基本思想。

Table 7.1: 案例07-01 四格资料表
组别	有效	无效	合计	有效率%
试验组	99(90.48)a	5(13.52)b	104(a+b)	95.20(a/(a+b))
对照组	75(83.52)c	21(12.48)d	96(c+d)	78.13(c/(c+d)))
合计	174(a+c)	26(b+d)	200(n)	87.00((a+c)/n)

案例07-01 的四格资料表有a=99，b=5，c=75和d=21四个基本数据，其余数据都是根据它们计算出来的。现在想知道处理组与对照组两组样本代表总体有无差别，即为两样本率比较的资料，既可以使用二项分布里面的u检验，也可以利用卡方检验。我们设计的原假设 $H_0:$ 处理组与对照组是来自同一总体，即 $P_{treatment}=P_{control}$ 。

u检验方法

下面是用u检验的代码，根据计算结果，P值=0.0003362066<0.01<0.05，所以根据u检验结果，表明拒绝 $H_0$ ，接受备择假设 $H_1$ ，即可以认为两种处理有显著性差异。

n5<-104
n6<-96
x5<-99
x6<-75
binom_twosamplecomp_uAsym(n5,x5,n6,x6)
# [1] 0.0006442179
binom_twosamplecomp_uAsym<-function(n1,x1,n2,x2){
     p1<-x1/n1
     p2<-x2/n2
     S_val<-sqrt((x1+x2)/(n1+n2)*(1-(x1+x2)/(n1+n2))*(1/n1+1/n2))
     p_val<-pnorm((p1-p2)/S_val,lower.tail = F)*2
     return( p_val)
}

卡方检验方法

卡方检验设计的原假设用u检验的一样，即 $H_0:$ 处理组与对照组是来自同一总体， $P_{treatment}=P_{control}$ 。

卡方检验的统计量计算的是 $\chi^2$ ，其计算公式和对应的卡方分布自由度计算方法为： $\chi^2=\sum{\frac{(A-T)^2}{T}} \\ v=(行数-1)(列数-1)$ 此公式也叫做皮尔森卡方检验(Pearson $\chi^2$ )，其中的A代表实际观察频数(Actual frequency)，即上面表格中的abcd四个值；T代表的 $H_0$ 成立时的理论频数(Theoretical frequency)，即假设处理组和对照组是来自同一总体，且总体的有效率的P值根据观察值计算得到为 $p_0=174/200=87%$ 和 $q=1-p_0$ ，然后用p，q与处理组和对照组的样本数分别计算有效，无效的理论频数，计算公式可以换算为： $T_{rc}=\frac{n_r*n_c}{n}$ 其中， $T_{rc}$ 为第r行第c列的理论频数， $n_{r}$ 和 $n_{c}$ 分别是相应第r行的合计样本数，和第c列的合计样本数；n为的行列的总样本数。

对于四格表资料的 $\chi^2$ 检验的卡方值，也可以使用下面专用公式计算： $\chi^2=\frac{(ad-bc)^2n}{(a+b)(c+d)(a+c)(b+d)}$

下面是采用卡方检验的代码，根据计算结果，P值=0.0003362066<0.01<0.05，表明拒绝 $H_0$ ，接受备择假设 $H_1$ ，即可以认为两种处理有显著性差异，同u检验的结论一致。

a<-99
b<-5
c<-75
d<-21

actual_matrix <- matrix(data = c(a,b,c,d), nrow = 2, ncol = 2,byrow = T)

chisquare_fourfoldtable_test<-function(actual_matrix){
     n<-sum(actual_matrix)
     df<-(dim(actual_matrix)[1]-1)*(dim(actual_matrix)[2]-1)
     chi_val<-0
     newmatrix<-matrix(nrow = dim(actual_matrix)[1],ncol = dim(actual_matrix)[2])
     for(i in 1:dim(actual_matrix)[1]){
          for(j in 1:dim(actual_matrix)[2]){
          newmatrix[i,j]=(sum(actual_matrix[i,])*sum(actual_matrix[,j]))/n
          chi_val=chi_val+(actual_matrix[i,j]-newmatrix[i,j])^2/newmatrix[i,j]
          }
     }
     #print(chi_val)
     # [1] 12.85707
    p_val<-pchisq(chi_val,df,,lower.tail = F)
     return (p_val)
}
chisquare_fourfoldtable_test(actual_matrix)
# [1] 0.0003362066

###四格资料卡方检验的专用公式函数
chisquare_fourfoldtable_test1<-function(actual_matrix){
     n<-sum(actual_matrix)
     df<-(dim(actual_matrix)[1]-1)*(dim(actual_matrix)[2]-1)
     chi_val<-(actual_matrix[1,1]*actual_matrix[2,2]-actual_matrix[1,2]*actual_matrix[2,1])^2*n/((actual_matrix[1,1]+actual_matrix[1,2])*(actual_matrix[2,1]+actual_matrix[2,2])*(actual_matrix[1,1]+actual_matrix[2,1])*(actual_matrix[1,2]+actual_matrix[2,2]))
     #print(chi_val)
     # [1] 12.85707
     p_val<-pchisq(chi_val,df,,lower.tail = F)
     return (p_val)
}
chisquare_fourfoldtable_test1(actual_matrix)

##或者可以使用chisq.test()函数
chitest<-chisq.test(actual_matrix,correct = F)
chitest$p.value
# [1] 0.0003362066

7.2.2.1 四格资料表的卡方检验的校正公式

计数资料中的实际频数A为分类资料，是非连续的，由此使用卡方检验的统计量计算的 $\chi^2$ 值也是非连续的，当自由度v特别小，尤其是四格表这样只有1的时候，计算出的卡方值会偏小，导致p值偏大，导致第一类错误的概率增大。为此，美国统计学家F. Yates在1934年提出了一个计算卡方值的连续性校正公式： $\chi^2=\sum\frac{(|A-T|-0.5)^2}{T}$ 或者修正后的专用公式计算为： $\chi^2=\frac{(|ad-bc|-n/2)^2n}{(a+b)(c+d)(a+c)(b+d)}$

在实际工作中，对四格表资料使用卡方检验的规定是：

当n≥40且T≥5时，用 $\chi^2$ 检验的基本公式或专用公式计算；当P值≈α时，改用四格资料的卡方检验的Fisher确切概率法；
当n≥40且5>T≥1时，用 $\chi^2$ 检验的校正公式或校正后的专用公式计算；或改用四格资料的卡方检验的Fisher确切概率法；
当n<40或1>T时，用卡方检验的Fisher确切概率法；

使用《医学统计学》中的案例07-02 的数据，即两样本率比较的 $\chi^2$ 检验为例，

Table 7.2: 案例07-02 四格资料表
组别	有效	无效	合计	有效率%
胞磷胆碱组	46	18	64	88.46
神经节苷脂组	6	8	14	69.23
合计	52	26	78	82.05

在R总的实现代码可以参考下面，采用了经典的计算方法和校正后的计算方法做对比。经典的计算结果显示 $\chi^2$ 值为4.352679，对应的P值为0.03695079<0.05；校正后的计算结果显示 $\chi^2$ 值为3.1448，对应的P值为0.07616886>0.05，两者结果相反。

a<-46
b<-6
c<-18
d<-8

actual_matrix <- matrix(data = c(a,b,c,d), nrow = 2, ncol = 2,byrow = T)

chisquare_fourfoldtable_test<-function(actual_matrix){
     n<-sum(actual_matrix)
     df<-(dim(actual_matrix)[1]-1)*(dim(actual_matrix)[2]-1)
     chi_val<-0
     theoretical_matrix<-matrix(nrow = dim(actual_matrix)[1],ncol = dim(actual_matrix)[2])
     for(i in 1:dim(actual_matrix)[1]){
          for(j in 1:dim(actual_matrix)[2]){
          theoretical_matrix[i,j]=(sum(actual_matrix[i,])*sum(actual_matrix[,j]))/n
          #chi_val=chi_val+(actual_matrix[i,j]-theoretical_matrix[i,j])^2/newmatrix[i,j]
          }
     }
     if(length(which(theoretical_matrix<1))>=1 || n<40){
          print("Fisher 确切检验")
          fisher_out<-fisher.test(actual_matrix)
          return(fisher_out$p.value)
     }else if(length(which(theoretical_matrix<=5))>=1 && n>=40){
          print("校正后的卡方检验")
          chi_val<-chi_val+chisquare_fourfoldtable_updated(actual_matrix,n)
     }else if(length(which(theoretical_matrix<5))==0 && n>=40){
          print("经典的卡方检验")
          chi_val<-chi_val+chisquare_fourfoldtable_classical(actual_matrix,n)
     }
     p_val<-pchisq(chi_val,df,lower.tail=F)
     cat(paste("chi_val",chi_val,"\np_val",p_val,sep="\t"))
     return (p_val)
}

chisquare_fourfoldtable_classical<-function(actual_matrix,n){
     n<-sum(actual_matrix)
     df<-(dim(actual_matrix)[1]-1)*(dim(actual_matrix)[2]-1)
     chi_val<-(actual_matrix[1,1]*actual_matrix[2,2]-actual_matrix[1,2]*actual_matrix[2,1])^2*n/((actual_matrix[1,1]+actual_matrix[1,2])*(actual_matrix[2,1]+actual_matrix[2,2])*(actual_matrix[1,1]+actual_matrix[2,1])*(actual_matrix[1,2]+actual_matrix[2,2]))
     #p_val<-dchisq(chi_val,df)
     return (chi_val)
}

chisquare_fourfoldtable_updated<-function(actual_matrix,n){
     n<-sum(actual_matrix)
     df<-(dim(actual_matrix)[1]-1)*(dim(actual_matrix)[2]-1)
     chi_val<-((abs((actual_matrix[1,1]*actual_matrix[2,2]-actual_matrix[1,2]*actual_matrix[2,1]))-n/2)^2)*n/
     ((actual_matrix[1,1]+actual_matrix[1,2])*(actual_matrix[2,1]+actual_matrix[2,2])*(actual_matrix[1,1]+actual_matrix[2,1])*(actual_matrix[1,2]+actual_matrix[2,2]))
     #p_val<-dchisq(chi_val,df)
     return (chi_val)
}

##print("校正后的卡方检验")
chisquare_fourfoldtable_test(actual_matrix)
# [1] 0.07616886

##print("经典的卡方检验")
chisquare_fourfoldtable_classical(actual_matrix)
# [1] 4.352679
pchisq(chisquare_fourfoldtable_classical(actual_matrix),1,lower.tail = F)
# [1] 0.03695079

7.2.3 配对的四格资料表的卡方检验

计数资料的配对设计常用于两种检验方法、培养方法、诊断方法的比较。其特点是对样本中各观察单位分别用两种方法处理，然后观察两种处理方法的某两分类变量的计数结果。观察结果有四种情况：

两种检测方法皆为阳性数(a);
两种检测方法皆为阴性数(d);
免疫荧光法为阳性，乳胶凝集法为阴性数(b);
乳胶凝集法为阳性，免疫荧光法为阴性数(c)。

可整理成下表的形式，以《医学统计学》中的案例07-07 的数据为例。

Table 7.3: 案例07-07 配对四格资料表
	乳胶凝集法
免疫荧光法	阳性	阴性	合计
阳性	11(a)	2(c)	13(a+c)
阴性	12(b)	33(d)	45(b+d)
合计	23(a+b)	35(c+d)	58(n)

其中，a、d为两法观察结果一致的两种情况，b、c为两法观察结果不一致的两种情况。当两种处理方法无差别时，根据边际同质性的零假设规定，每个结果两个边缘概率是相同的， $p_a + p_b = p_a + p_c$ 并且 $p_c + p_d = p_b + p_d$ ，即两总体率相等 $p_b=p_c$ ，由于在抽样研究中，抽样误差是不可避免的，样本中的b和c往往不等 (b≠c，即两样本率不等: $p_b=p_c$ )。为此，需进行麦克尼马尔假设检验(McNemar’s test)，其检验统计量为：

当 (b+c)≥40 时： $\chi^2=\frac{(b-c)^2}{b+c}, v=1$ 或者当 (b+c)<40 时： $\chi^2=\frac{(|b-c|-1)^2}{b+c}, v=1$ 值得注意的时，麦克尼马尔假设检验一般用于样本含量不太大的资料，因为它只考虑了两种处理不一致的情况(b,c)，而没有考虑样本含量n和两种处理结果一致的情况(a,d)，所以行n很大，且a，d的数值也很大时，b，c相对较小，检验结果的实际意义就不明确了。

使用《医学统计学》中的案例07-07 的数据，做麦克尼马尔假设检验的R实现。

a<-11
b<-12
c<-2
d<-33
actual_matrix <- matrix(data = c(a,b,c,d), nrow = 2, ncol = 2,byrow = T)

chisquare_pairedfourfoldtable_test<-function(actual_matrix){
     n<-sum(actual_matrix)
     df<-(dim(actual_matrix)[1]-1)*(dim(actual_matrix)[2]-1)
     #chi_val<-0
     un_same<-actual_matrix[1,2]+actual_matrix[2,1]
     if(un_same >= 40){
          print("chisquare_pairedfourfoldtable_classical")
          chi_val<-chisquare_pairedfourfoldtable_classical(actual_matrix,n)
     }else if(un_same < 40){
          print("chisquare_fourfoldtable_updated")
          chi_val<-chisquare_pairedfourfoldtable_updated(actual_matrix,n)
     }
     p_val<-pchisq(chi_val,df,lower.tail=F)
     #cat(paste("chi_val",chi_val,"\n p_val ",p_val,sep="\t"))
     return (p_val)
}

chisquare_pairedfourfoldtable_classical<-function(actual_matrix,n){
     n<-sum(actual_matrix)
     df<-(dim(actual_matrix)[1]-1)*(dim(actual_matrix)[2]-1)
     chi_val<-(actual_matrix[1,2]-actual_matrix[2,1])^2/(actual_matrix[1,2]+actual_matrix[2,1])
     #p_val<-dchisq(chi_val,df)
     return (chi_val)
}

chisquare_pairedfourfoldtable_updated<-function(actual_matrix,n){
     n<-sum(actual_matrix)
     df<-(dim(actual_matrix)[1]-1)*(dim(actual_matrix)[2]-1)
     chi_val<-((abs(actual_matrix[1,2]-actual_matrix[2,1])-1)^2)/(actual_matrix[1,2]+actual_matrix[2,1])
          #p_val<-dchisq(chi_val,df)
     return (chi_val)
}
chisquare_pairedfourfoldtable_test(actual_matrix)
#[1] 0.01615693

#或者使用函数mcnemar.test()
mcnemar.test(actual_matrix)
##      McNemar's Chi-squared test with continuity correction
##  
##  data:  actual_matrix
##  McNemar's chi-squared = 5.7857, df = 1, p-value = 0.01616

根据计算结果，P值=0.01615693<0.05，按α=0.05的检验水准，拒绝 $H_0$ ，接受 $H_1$ ，即可认为两种方法的检验效率不一样。

7.2.4 四格资料表的Fisher确切概率法

四格表的Fisher确切概率法，即Fisher精确检验(Fisher’s exact test)又称四格表概率的直接计算，常用于四格表资料的假设检验的补充，即通常对四格表中出现n<40或T<1，或用经典计算卡方值后的 P值≈α的情况，需改用Fisher确切概率法计算。其基本思想是：在四格表的周边合计不变的条件下，直接计算表内四个实际频数(a,b,c,d)的所有组合的概率 $P_i$ ，并且有 $\sum{P_i}$ =1。各组合的概率服从超几何分布，按检验假设取单侧或双侧的累计概率P，即可按所取检验水准作出推断结论。

使用《医学统计学》中的案例07-04 的数据，做四格表的Fisher确切概率法的R实现。

Table 7.4: 案例07-04 Fisher确切概率法四格资料表
组别	阳性	阴性	合计	感染率(%)
预防注射组	4 \| a	18 \| b	22 \| a+b	18.18
非预防组	5 \| c	6 \| d	11 \| c+d	45.45
合计	9 \| a+c	24 \| b+d	33 \| n	27.27

第一步：计算实际频数(a,b,c,d)的所有组合的概率 $P_i$

在四格表的周边合计不变的条件下，实际频数(a,b,c,d)的所有组合的的可能性共有“周边合计最小数+1”个，如案例07-04的实际频数组合情况有min(a+c,a+b,c+d,b+d)+1=9+1=10种，详细见下图：

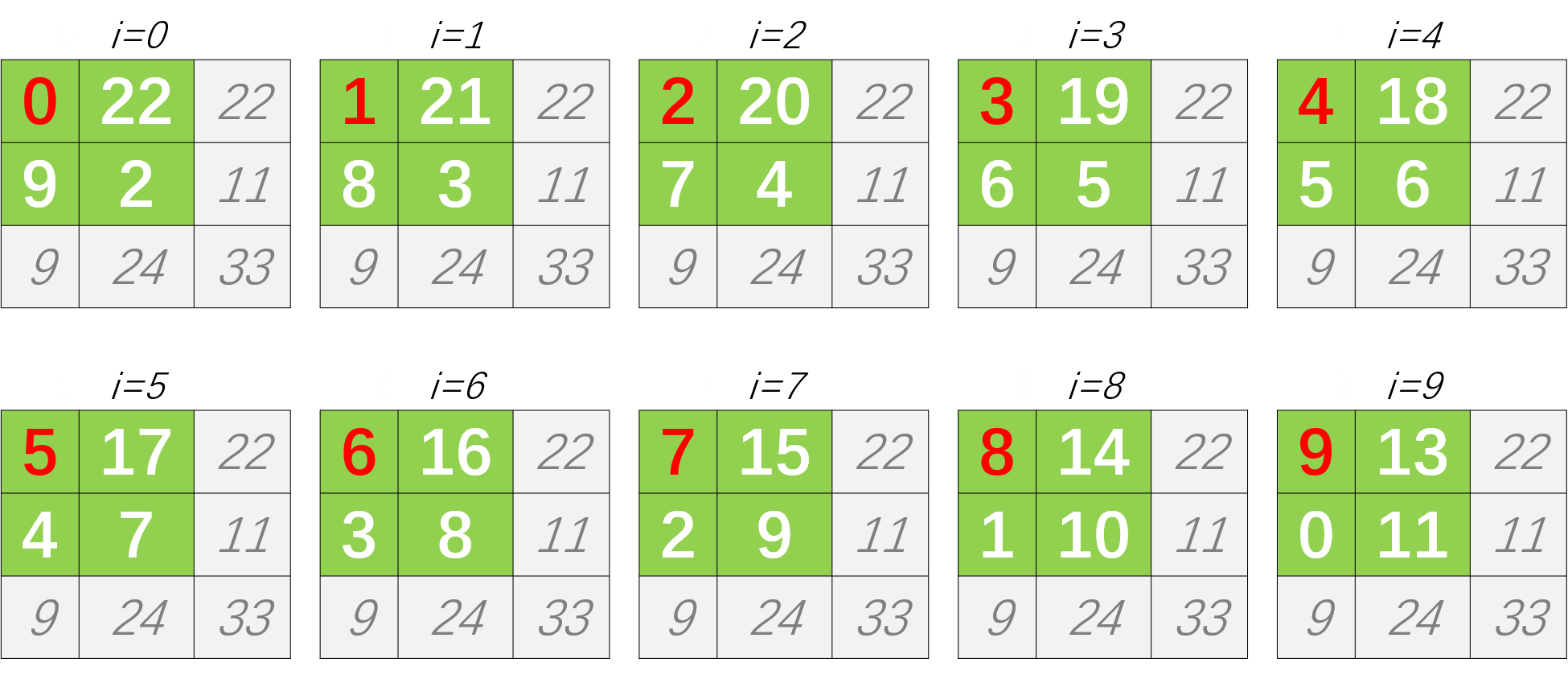
Figure 7.2: 案例 07-04的实际频数组合情况

各组合的概率 $P_i$ 服从超几何分布， $P_i$ 的计算公式为： $P_i=\frac{(a+c)!(a+b)!(c+d)!(b+d)!}{a!b!c!d!n!}$

第二步：计算累积概率的P值

一般的规定， $P_i$ (i=1,2,3,…)对应a从小到大的概率，那么各种组合下累计概率的计算，分单、双侧检验两种情况：

单侧检验：现有样本的实际观察频率(记作 $P_a$ )的左侧为左侧概率(记作 $P_l$ )，备择假设 $H_1$ 为 $p_1 > p_2$ ；现有样本的实际观察频率(记作 $P_a$ )的右侧为右侧概率(记作 $P_r$ )，备择假设 $H_1$ 为 $p_1 < p_2$ ；
双侧检验：若遇到a+b=c+d或a+c=b+d时，四格表各组序列呈对称分布，此时只计算 $P_i≤P_a$ 的单侧概率，然后乘以2即算的双侧的累积概率值。

注意的是，Fisher精确检验依赖的时超几何分布(Hypergeometric distribution)， R语言中与超几何分布相关的主要函数有dhyper(),phyper(),qhyper()和rhyper()。

超几何分布：从一个有限的总体中进行不放回抽样，设其中包含有n个黑球(阳性/成功)，m个白球(阴性/失败)，若从中不放回地随机抽取k个( $k\in[0,m+n]$ )，其中含有的不白球的个数为x(x=1,2,3,…,k)，则X的个数对应的概率即是服从超几何分布，记为X~h(k, n, m)。案例07-04的数据可以视作：从一个总体为33的数据中进行不放回抽样，设其中包含有24个黑球(阳性/成功)，9个白球(阴性/失败)，若从中不放回地随机抽取22个( $k\in[0,m+n]$ )，其中含有的白球的个数为x=1:9(m=9 < k=22)，则X的个数对应的概率即是服从超几何分布，记为X~h(22, 24, 9)。

假设预防组和非预防组的来自同一总体，即 $H_0:p_1=p_2=9/33$ ， $H_1:p_1≠p_2$ ，同二项分布的应用中类似，主要是回答“有无差别”，及备择假设是 $p≠p_0$ 是否成立，因此计算的是实际样本“成功”x次(实际频数,A=a)出现的概率，与更背离原假设的事件出现的概率和。

a<-4;b<-18;
c<-5;d<-6;
actual_matrix <- matrix(data = c(a,b,c,d), nrow = 2, ncol = 2,byrow = T)

m<-a+c;n<-b+d;k<-a+b;

##使用dhyper()计算不同x值得p值
dhyper(x=0:9, m=m, n=n, k=k)
dhyper(x=a, m=m, n=n, k=k)
#0.08762728

#计算出现4次各情况的累计概率值
p4<-dhyper(x=a, m=m, n=n, k=k)
#0.08762728
#计算出现更背离原假设的事件及概率，即：
p4_1<-sum(dhyper(0:m, m=m, n=n, k=k)[which(dhyper(0:m, m=m, n=n, k=k)<dhyper(x=a, m=m, n=n, k=k))])
# [1] 0.03341747
#双侧检验的p值为：
p4+p4_1
# [1] 0.1210448

#或者直接用which()函数一并计算
sum(dhyper(0:m, m=m, n=n, k=k)[which(dhyper(0:m, m=m, n=n, k=k)<=dhyper(x=a, m=m, n=n, k=k))])
# [1] 0.1210448

#或者使用fisher.test()
fisher.test(actual_matrix,alternative = "two.sided")
##      Fisher's Exact Test for Count Data
##  
##  data:  actual_matrix
##  p-value = 0.121
##  alternative hypothesis: true odds ratio is not equal to 1
##  95 percent confidence interval:
##   0.03974151 1.76726409
##  sample estimates:
##  odds ratio 
##   0.2791061

根据计算结果，p值=0.1210448>0.05，不拒绝 $H_0: p_1=p_1$ ，即还不能认为两种处理得感染率不同。

使用《医学统计学》中的案例07-05 的数据，做四格表的Fisher确切概率法的R实现。

a<-6;b<-4;
c<-1;d<-9;
actual_matrix <- matrix(data = c(a,b,c,d), nrow = 2, ncol = 2,byrow = T)

m<-a+c;n<-b+d;k<-a+b;
sum(dhyper(0:m, m=m, n=n, k=k)[which(dhyper(0:m, m=m, n=n, k=k)<=dhyper(x=a, m=m, n=n, k=k))])
# [1] 0.05727554

#或者使用fisher.test()
fisher.test(actual_matrix,alternative = "two.sided")
##      Fisher's Exact Test for Count Data
##  
##  data:  actual_matrix
##  p-value = 0.05728
##  alternative hypothesis: true odds ratio is not equal to 1
##  95 percent confidence interval:
##     0.9487882 684.4235629
##  sample estimates:
##  odds ratio 
##     11.6367

根据计算结果，p值=0.05727554>0.05，不拒绝 $H_0: p_1=p_1$ ，记即还不能认为两种肿瘤中 $P_{53}$ 基因的表达率不同。

注意的是，如果专业上有理由肿瘤A中的 $P_{53}$ 基因的表达率高于肿瘤B中，那么这里应该进行单侧检验， $H_1: p_1>p_2$ ，计算P值应该是 $P_r$ ，反之可以计算 $P_l$ 。

7.3 行列资料表的卡方检验

行x列表资料的卡方检验用于多个样本率的比较、两个或多个构成比的比较以及双向无序分类资料的关联性检验。其基本数据有以下3种情况:

多个样本率比较时，有R行2列，称为Rx2表；
两个样本的构成比比较时，有2行C列，称2xC表；
多个样本的构成比比较以及双向无序分类资料关联性检验时，有R行C列，称为RxC表。

以上3种情况可统称为行×列表资料。行x列表资料的检验仍用 Pearsony $\chi^2$ 公式计算检验统计量值。因该式需先计算理论频数 $T_{rc}$ ，化简后得行×列表资料检验的专用公式和自由度为： $\chi^2=n(\sum\frac{A^2}{n_{r}n_{c}}-1)，v=(行数-1)(列数-1)$

其中的A代表实际观察频数(Actual frequency)，n_{r} $和$ n_{c}$分别是相应第r行的合计样本数和第c列的合计样本数。

7.3.1 多个样本率的比较( $R \times 2$ 表)

使用《医学统计学》中的案例07-06 的数据，做多个样本率的比较的卡方检验和R实现。

Table 7.5: 案例07-06 3x2 表资料的多个样本率的比较测试数据
疗法	有效	无效	合计	有效率(%)
物理疗法组	199	7	206	96.60
药物疗法组	164	18	182	90.11
外用膏药组	118	26	144	81.94
合计	481	51	532	90.41

设置的原假设 $H_0: p_1=p_2=p_3$ ，即三种疗法的治疗的有效率是一样的；相应的备择假设$H_1:$3种治疗方法的有效率不都一样。

actual_matrix <- matrix(data = as.numeric( c("199","164","118","7","18","26")), 
nrow = 3, ncol = 2,byrow = F)

chisquare_rctable_multiratio_test<-function(actual_matrix){
     n=sum(actual_matrix)
     df<-(dim(actual_matrix)[1]-1)*(dim(actual_matrix)[2]-1)
     chi_val<-n*(-1)
     for(i in 1:dim(actual_matrix)[1]){
          for(j in 1:dim(actual_matrix)[2]){
               chi_val<-chi_val+n*(actual_matrix[i,j]^2/(sum(actual_matrix[i,])*sum(actual_matrix[,j])))
          }
     }
     #cat("chi_val: ",chi_val)
     p_val<-pchisq(chi_val,df,lower.tail=F)*2 
     return(p_val)
}
chisquare_rctable_multiratio_test(actual_matrix)
# [1] 5.404583e-05

根据计算结果，p值=5.404583e-05<0.001<0.01<0.05，即拒绝原假设 $H_0$ ，接受 $H_1$ ，认为三种治疗方法的有效率不都一样。 注意，这里同方差分析类似，我们后面还会进一步讨论这种情况的多组比较，即探讨三种疗法具体谁比较好，谁比较差。

7.3.2 样本构成比的比较( $2 \times C$ 表)

Table 7.6: 案例07-07 2x3 表资料的多个样本率的比较测试数据
组别	DD	ID	II	合计
DN组	42	48	21	111
无DN组	30	72	36	138
合计	72	120	57	249

设置的原假设 $H_0:$ 即在某疾病的两组亚型涉及的基因A的基因型的总体构成比是一样的；相应的备择假设 $H_1:$ 某疾病的两组亚型涉及的基因A的基因型的总体构成比不都一样。

actual_matrix <- matrix(data = as.numeric( c("42","30","48","72","21","36")), 
nrow = 2, ncol = 3,byrow = F)

chisquare_rctable_multiratio_test<-function(actual_matrix){
     n=sum(actual_matrix)
     df<-(dim(actual_matrix)[1]-1)*(dim(actual_matrix)[2]-1)
     chi_val<-n*(-1)
     for(i in 1:dim(actual_matrix)[1]){
          for(j in 1:dim(actual_matrix)[2]){
               chi_val<-chi_val+n*(actual_matrix[i,j]^2/(sum(actual_matrix[i,])*sum(actual_matrix[,j])))
          }
     }
     #cat("chi_val: ",chi_val)
     p_val<-pchisq(chi_val,df,lower.tail=F)*2 
     return(p_val)
}
chisquare_rctable_multiratio_test(actual_matrix)
# [1] 0.01913288

根据计算结果，p值=0.01913288<0.05，即拒绝原假设 $H_0$ ，接受 $H_1$ ，认为两组亚型涉及的基因A的基因型的总体构成比不都一样。

7.3.3 双向无序分组资料的关联性检验

对于两个分类变量皆为 无序分类变量 的行x列表资料料，又称为双向无序RxC表资料。若是一个样本的双向无序 RxC表资料，常常分析两个分类变量之间有无关系?关系的密切程度如何? 此时可用行x列表资料 $\chi^2$ 检验来推断两个分类变量之间有无关系(或关联); 在有关系的前提下，若须进一步分析关系的密切程度时，可计算 Pearson 列联系数C，其计算公式为： $C=\sqrt{\frac{\chi^2}{n+\chi^2}}$

式中 $\chi^2$ 为行×列表资料的 $\chi^2$ 值，n为样本含量。列联系数C取值范围在0~1之间，愈接近于0，关系愈不密切;愈接近于1，关系愈密切。

Table 7.7: 案例07-08 rxc 表资料的双向无序分组资料的关联性检验测试数据
	MN血型
ABO血型	M	N	MN	合计
O	431	490	902	1823
A	388	410	800	1598
B	495	587	950	2032
AB	137	179	32	348
合计	1451	1666	2684	5801

设置的原假设 $H_0:$ 两种血型系统之间没有关联；相应的备择假设 $H_1:$ 两种血型系统之间有关联。


actual_matrix <- matrix(data = as.numeric( c("431","388","495","137","490","410","587","179","902","800","950","32")), 
nrow = 4, ncol = 3,byrow = F)

chisquare_rctable_multiratio_test<-function(actual_matrix){
     n=sum(actual_matrix)
     df<-(dim(actual_matrix)[1]-1)*(dim(actual_matrix)[2]-1)
     chi_val<-chisquare_chivaler(actual_matrix)
     cat("chi_val: ",chi_val,"\n df: ",df)
     p_val<-pchisq(chi_val,df,lower.tail=F)*2 
     return(p_val)
}

chisquare_rctable_pearsonC<-function(actual_matrix){
     n=sum(actual_matrix)
     chi_val<-chisquare_chivaler(actual_matrix)
     pearsonC<-sqrt(chi_val/(n+chi_val))
     return(pearsonC)
}

chisquare_chivaler<-function(actual_matrix){
     n=sum(actual_matrix)
     chi_val<-n*(-1)
     for(i in 1:dim(actual_matrix)[1]){
          for(j in 1:dim(actual_matrix)[2]){
               chi_val<-chi_val+n*(actual_matrix[i,j]^2/(sum(actual_matrix[i,])*sum(actual_matrix[,j])))
          }
     }
     return(chi_val)
}

chisquare_rctable_multiratio_test(actual_matrix)
# [1] 5.971112e-43
chisquare_rctable_pearsonC(actual_matrix)
# [1] 0.1882638

##或者可以用chisq.test()计算，但是p值函数使用的最小p值有关，
##默认情况返回的P值与上面的计算不一致
chisq.test(actual_matrix)
##      Pearson's Chi-squared test
##  
##  data:  actual_matrix
##  X-squared = 213.16, df = 6, p-value < 2.2e-16

##列联系数也可以用DescTools包中的ContCoef()计算
DescTools::ContCoef(actual_matrix)
# [1] 0.1882638

根据计算结果，p值=5.971112e-43<0.01<0.05，因此拒绝原假设 $H_0$ 。接受 $H_1$ ，即认为两种血型系统之间有关联。其关联程度按照列联系数C=0.1882638，数值较小，虽然有统计学意义，但是关系不大，关于统计显著与专业意义的关系可以参考参数估计与假设检验的联系的内容。

分类变量可分为无序变量和有序变量两大类：

无序分类变量，指所分类别zhi或属性之间无程度和dao顺序的差别。无序分类又可分为：
- 二项分类，如性别（男、女），药物反应（阴性，阳性）等；
- 多项分类，如血型（O、A、B、AB），职业（工、农、商、学、兵）等。对于无序分类变量的分析，应先按类别分组，清点各组的观察单位数，编制分类变量的频数表，所得资料为无序分类资料，亦称计数资料。
有序分类变量，指各类别之间有程度的差别。如尿糖化验结果按-、±、+、++、+++分类；疗效按治愈、显效、好转、无效分类。对于有序分类变量，应先按等级顺序分组，清点各组的观察单位个数，编制有序变量的频数表，所得资料称为等级资料。

7.3.4 双向有序分组资料的线性趋势检验

对双向有序属性不同的RxC表资料，除可推断两个分类变量是否存在相关关系外，还可通过分解推断其相关是否为线性相关。其基本思想是：首先计算RxC表资料的值，然后将总的值分解成线性回归分量与偏离线性回归分量。若两分量均有统计学意义，说明两个分类变量存在相关关系，但关系不是简单的直线关系；若线性回归分量有统计学意义，偏离线性回归分量无统计学意义时，说明两个分类变量存在直线相关关系。

计算过程如大致下： 1. 按照先前介绍的行×列表资料检验的专用公式 $\chi_{tol}^2=n(\sum\frac{A^2}{n_{r}n_{c}}-1)$ 计算中的 $\chi^2$ 值，自由度为 $v_{tol}=(行数-1)\times(列数-1)$ 。 2. 计算线性回归分量 $\chi_{reg}^2$ 先给两个有序变量分别赋值(如X变量有-，+，++，其对应赋值1,2,3,···；Y变量有治愈、显效、好转、无效+对应赋值1,2,3,4···)，再计算线性回归的 $\chi_{reg}^2$ 恒量： $\chi_{reg}^2=\frac{b^2}{S_b^2}, v_{reg}=1，v_{reg}=1$ 其中b为回归系数， $S_b^2$ 为b的方差， $b=l_{xy}/l_{xx}$ ， $S_b^2=l_{yy}/(n*l_{xx})$ ， $l_{xx}，l_{yy}$ 分别是变量X，Y的离差平方和； $l_{xy}$ 是变量X，Y的离均差积和，f为样本观察频率即： $l_{xx}=\sum fx^2-\frac{(\sum fx)^2}{\sum f}$ $l_{yy}=\sum fy^2-\frac{(\sum fy)^2}{\sum f}$ $l_{xy}=\sum f(xy)-\frac{(\sum fx)(\sum fy)}{\sum f}$ 3. 计算偏离线性回归分量 $\chi_{wide}^2$ ，公式为： $\chi_{wide}^2=\chi_{tol}^2-\chi_{reg}^2，v_{wide}=v_{tol}-v_{reg}$

使用《医学统计学》中的案例07-09 的数据，做双向有序分组资料的线性趋势检验的R实现。

Table 7.8: 案例07-09 rxc 双向有序分组资料的线性趋势检验测试数据
	冠状动脉硬化等级(Y)
年龄(岁)X	-	+	++	+++	合计
20~	70	22	4	2	98
30~	27	24	9	3	62
40~	16	23	13	7	59
≤50	9	20	15	14	58
合计	122	89	41	26	278

设置的原假设 $H_0:$ 年龄与动脉硬化等级之间没有线性关系；相应的备择假设 $H_1:$ 年龄与动脉硬化等级之间有线性关系。

actual_matrix <- matrix(data = as.numeric( c("70","27","16","9","22","24","23","20","4","9","13","15","2","3","7","14")), 
nrow = 4, ncol = 4,byrow = F)

#计算总的卡方
chisquare_chivaler<-function(actual_matrix){
     n=sum(actual_matrix)
     chi_val<-n*(-1)
     for(i in 1:dim(actual_matrix)[1]){
          for(j in 1:dim(actual_matrix)[2]){
               chi_val<-chi_val+n*(actual_matrix[i,j]^2/(sum(actual_matrix[i,])*sum(actual_matrix[,j])))
          }
     }
     return(chi_val)
}

#计算线性回归分量对应的卡方
chisquare_chivaler_4reg<-function(actual_matrix){
     n=sum(actual_matrix)
     actual_matrix_squ<-actual_matrix^2
     fsum=n
     fXsum<-sum(apply(actual_matrix, 1, sum)*(1:dim(actual_matrix)[1]))
     fXXsum<-sum(apply(actual_matrix, 1, sum)*(1:dim(actual_matrix)[1])^2)
     fYsum<-sum(apply(actual_matrix, 2, sum)*(1:dim(actual_matrix)[2]))
     fYYsum<-sum(apply(actual_matrix, 2, sum)*(1:dim(actual_matrix)[2])^2)
     fXYsum<-0
     for(x in 1:dim(actual_matrix)[1]){
          for(y in 1:dim(actual_matrix)[2]){
               fXYsum<-fXYsum+actual_matrix[x,y]*x*y
          }
     }
     #cat("fsum=",fsum,"fXsum=",fXsum,"fXXsum=",fXXsum,"fYsum=",fYsum,"fYYsum=",fYYsum,"fXYsum=",fXYsum)
     l_xx<-fXXsum-fXsum^2/fsum
     l_yy<-fYYsum-fYsum^2/fsum
     l_xy<-fXYsum-fXsum*fYsum/fsum
     b<-l_xy/l_xx
     SS_b<-l_yy/(l_xx*fsum)
     chi_val<-b^2/SS_b
     #cat("b=",b,"SS_b=",SS_b)
     return(chi_val)
}

chi_tol<-chisquare_chivaler(actual_matrix)
# [1] 71.43249
chi_reg<-chisquare_chivaler_4reg(actual_matrix)
# [1] 63.61832
chi_wide<-chi_tol-chi_reg
# [1] 7.814174
pchisq(chi_tol,(4-1)*(4-1),lower.tail=F)
# [1] 7.969604e-12
pchisq(chi_reg,1,lower.tail=F)
# [1] 1.510182e-15
pchisq(chi_wide,(4-1)*(4-1)-1,lower.tail=F)
# [1] 0.4518296

##或者可以用chisq.test()计算总的卡方和p值
chisq.test(actual_matrix)

Table 7.9: 双向有序分组资料的线性趋势检验测试结果
变异来源	$\chi^2$	自由度	P值
总变异	71.43249	9	7.969604e-12
线性回归分量	63.61832	1	1.510182e-15
偏离线性回归分量	7.814174	8	0.4518296

根据计算结果，线性回归分量的卡方P值=1.510182e-15<0.005<0.05，具有统计学意义；偏离线性回归分量的卡方P值=0.4518296>0.05，pchisq 不具有同继续意义，因此可以认为年龄与冠状动脉硬化之间存在线性相关的关系，结合资料表说明时随年龄增加动脉硬化风险升高。

7.3.5 卡方检验的注意事项与选择思路

7.3.5.1 注意事项

一般认为，行×列表资料中各格的理论频数不应小于1，并且1<7<5的格子数不宜超过格子总数的1/5。若出现上述情况，可通过以下方法尝试解决：
- 最好是增加样本含量，使理论频数增大;
- 根据专业知识，考虑能否删去理论频数太小的行或列，能否将理论频数太小的行或列与性质相近的邻行或邻列合并;
- 改用双向无序R×C表资料的 Fisher 确切概率法。
多个样本率比较，若所得统计推断为拒绝日，接受 $H_0$ 时，只能认为各总休率之间总的来说有差別，但不能说明任两个总体率之间均有差别。要进一步推断哪两两总体字之间有差别，需进一步做多个样本率的多重比较。
医学期刊中常见这样的情况:不管RxC表资料中的两个分类变量是有序还是无序，均用 $\chi^2$ 检验分析。这种做法是不妥的。对于有序的R×C表资料不宜用 $\chi^2$ 检验，因为行×列表资料的 $\chi^2$ 检验与分类变量的顺序无关，当有序变量的R×C表资料中的分类顺序固定不变时，无论将任何两行(或两列)频数互换，所得值皆不变，其结论相同，这显然是不妥的。因此在实际应用中，对于RxC表资料要根据其分类类型和研究目的选用恰当的检验方法。

7.3.5.2 选择思路

RxC表资料可以分为双向无序、单向有序、双向有序属性相同和双向有序属性不同4类。

双向无序RxC表资料 RxC表资料中两个分类变量皆为无序分类变量。对于该类资料，
- 若研究目的为多个样本率(或构成比)的比较，可用RxC表资料的 $\chi^2$ 检验;
- 若研究目的为分析两个分类变量之间有无关联性以及关系的密切程度时，可用RxC表资料的 $\chi^2$ 检验以及Pearson 列联系数进行分析。
单向有序RxC表资料对于该类资料，有两种形式，
- 若RxC表资料中的分组变量(如年龄)是有序的，而指标变量(如传染病的类型)是无序的。其研究目的通常是分析不同年龄组各种传染病的构成情况，此种单向有序RxC表资料可用行x列表资料的 $\chi^2$ 检验进行分析。
- 若RxC表资料中的分组变量 (如疗法)为无序的，而指标变量(如疗效按等级分组)是有序的。其研究目的为比较不同疗法的疗效，此种向有序RXC表资料宜用秩转换的非参数检验进行分析。
双向有序属性相同的RxC表资料 RxC表资料中的个分类变量皆为有序且属性相同。实际上是配对四格表资料的扩展，即水平数≥3 的配伍资料，如用两种检测方法同时对同一批样品的测定结果。其研究目的通常是分析两种检测方法的一致性，此时宜用一致性检验或称Kappa 检验;也可用特殊模型分析方法。
双向有序属性不同的RxC表资料 RxC表资料中两个分类变量皆为有序的，但属性不同。对于该类资料，
- 若研究目的为分析不同年龄组患者疗效之间有无差别时，可把它视为单向有序 RxC表资料，选用秩转换的非参数检验；
- 若研究目的为分析两个有序分类变量间是否存在相关关系，宜用等级相关分析;
- 若研究目的为分析两个有序分类变量间是否存在线性变化趋势，可用前述的双向有序分组资料的线性趋势检验(Test for linear trend)。

7.3.6 多个样本率的多重比较

当多个样本率比较的RxC表资料 $\chi^2$ 检验，推断结论为拒绝 $H_0$ ，接受 $H_1$ 时，只能认为各总体率之间总的来说有差别，但不能说明任两个总体率之间有差别。要进一步推断哪两两总体率有差别，即事后分析/析因分析(Post-hoc analysis)。若直接用四格表资料的检验进行多重比较，将会加大犯第一类错误的概率。因此，样本率间的多重比较不能直接用四格表资料的检验。多个样本率间的多重比较的方法有 $\chi^2$ 分割法(Partitions of method)、 Scheffe’可信区间法和SNK法。《医学统计学》中本节仅介绍一种基于 $\chi^2$ 分割法(Partitions of method)的多个样本率间多重比较的方法。

7.3.6.1 卡方分割法

多个样本率比较的资料可整理成2 × k表资料，经行×列表资料 $\chi^2$ 检验的结论为拒绝 $H_0$ ，接受 $H_1$ 时，若不经任何处理，而直接用分割法把2 × k表 $\chi^2$ 分成多个独立的四格表/进行两两比较，必须重新规定检验水准α’，其目的是为保证检验假设中第一类错误 α 的概率不变。因分析目的不同，k个样本率两两比较的次数不同，故重新规定的检验水准α’的估计方法亦不同。通常有两种情况：

多个实验组间的两两比较分析目的是k个实验组间，任两个率均进行比较情况；对于这种情况的检验水准α’用以下公式校验： $\alpha'=\frac{\alpha}{k(k-1)/2+1}$
实验组与同一个对照组的比较分析目的是k个实验组与同一个对照组的比较，不同实验组之间不需要比较；对于这种情况的检验水准α’用以下公式校验： $\alpha'=\frac{\alpha}{2(k-1)}$

使用《医学统计学》中的案例07-06 的数据，做多个样本率的的卡方分割法多重比较。

actual_matrix <- matrix(data = as.numeric( c("199","164","118","7","18","26")), nrow = 3, ncol = 2,byrow = F)
rownames(actual_matrix)<-c("物理","药物","膏药")
colnames(actual_matrix)<-c("有效","无效")

a_adjust_pairwise<-function(alpha=0.05,k){
     alpha_adj<-alpha/(k*(k-1)/2+1)
     return(alpha_adj)
}

a_adjust_TC<-function(alpha=0.05,k){
     alpha_adj<-alpha/(2*(k-1))
     return(alpha_adj)
}

FUN = function(i,j){
     chisq.test(matrix(c(actual_matrix[i,1], actual_matrix[i,2],
     actual_matrix[j,1], actual_matrix[j,2]),
     nrow=2,
     byrow=TRUE),correct=F)$p.value
     }
comp<-pairwise.table(FUN,rownames(actual_matrix),p.adjust.method="none")
##               物理       药物
##  药物 9.343461e-03         NA
##  膏药 3.880885e-06 0.03213982
comp<a_adjust_pairwise(alpha = 0.05,k=3)
##       物理  药物
##  药物 TRUE    NA
##  膏药 TRUE FALSE
comp<a_adjust_TC(alpha = 0.05,k=3)
##       物理  药物
##  药物 TRUE    NA
##  膏药 TRUE FALSE

##查看不同处理组的残差
chisq.test(actual_matrix,correct = F)$residuals
##              有效       无效
##  物理  0.93410527 -2.8686877
##  药物 -0.04308075  0.1323033
##  膏药 -1.06881180  3.2823787

按照计算结果，实验组间的两两比较的目的下，物理疗法与药物组的 P值<α’，物理疗法与膏药组的 P值<α’，表明拒绝它们的原假设 $H_0$ ，接受 $H_1$ ；而药物组与膏药组的 P值>α’，因此不拒绝它的原假设 $H_0$ 。根据实验数据和卡方检验的残差，我们可以判断物理疗法的有效率显著优于其他两组，还不能认为药物与膏药之间的有效率有显著差异。

按照计算结果，实验组(物理疗法与膏药组)与同一个对照组(药物组)比较的目的下，物理疗法与药物组的 P值<α’，药物组与膏药组的 P值>α’，因此不拒绝它的原假设 $H_0$ 。根据实验数据和卡方检验的残差，我们可以判断物理疗法的有效率显著优于药物组，还不能认为药物与膏药之间的有效率有显著差异。

与方差分析类似，多个样本率的多重比较的事后分析/析因分析也有很多种方法，这里补充介绍一下R中 rcompanion包中的pairwiseNominalIndependence()函数。矫正α值的方法非常多，适用条件也不尽相同，可以参考多个样本均数间的多重比较(#多个样本均数间的多重比较)。

actual_matrix <- matrix(data = as.numeric( c("199","164","118","7","18","26")), nrow = 3, ncol = 2,byrow = F)
rownames(actual_matrix)<-c("物理","药物","膏药")
colnames(actual_matrix)<-c("有效","无效")
#rownames(actual_matrix)<-c("20","30","40","50")
#colnames(actual_matrix)<-c("-","+","++","+++")

##使用rcompanion包中的pairwiseNominalIndependence()函数
if(!require(rcompanion)){install.packages("rcompanion")}
#method should be one of “holm”, “hochberg”, “hommel”, “bonferroni”, “BH”, “BY”, “fdr”, “none”
posthoc<-pairwiseNominalIndependence(actual_matrix,fisher = FALSE,gtest  = FALSE,chisq  = TRUE,method = "fdr")
##     Comparison  p.Chisq p.adj.Chisq
##  1 物理 : 药物 1.68e-02    0.025200
##  2 物理 : 膏药 9.34e-06    0.000028
##  3 药物 : 膏药 4.78e-02    0.047800

##使用rpairwise.table()函数工具
FUN = function(i,j){
     chisq.test(matrix(c(actual_matrix[i,1], actual_matrix[i,2],
     actual_matrix[j,1], actual_matrix[j,2]),
     nrow=2,
     byrow=TRUE))$ p.value
     }
pairwise.table(FUN,rownames(actual_matrix),p.adjust.method="fdr")
#               物理       药物
#  药物 2.513146e-02         NA
#  膏药 2.803385e-05 0.04776377

7.4 Cochran-Mantel-Haenszel卡方统计量检验

Cochran-Mantel-Haenszel卡方统计量检验，简称CMH检验，是Mantel-Haenszel卡方关联检验 ( $\chi_{MH}^2=(n-1)r^2$ , r为行列变量的Pearson相关系数)的扩展，它在2 x 2 表格数据的基础上，引入了第三个(某一个或几个)分类变量，称之为混杂因素(或分层变量)，分层变量的引入使得该检验可以用于分析分层样本，即实现对三维(高维)数据表的卡方检验。CMH检验在生物统计学领域，常用于疾病对照研究。

该检验的 $H_0$ 为任一层的行变量X与列变量Y均不相关， $H_1$ 为至少有一层X与Y存在统计学关联。当 $H_0$ 成立时， CMH统计量渐近 $\chi^2$ 分布。需要注意的是，当各层间行变量与列变量相关的方向不一致时，CMH统计量的检验效能较低。

根据行变量X和列变量Y的类型不同， CMH统计量包括:

相关统计量(Correlation statistic)：适用于X和Y均为有序分类变量的资料。对一维RxC列联表，CMH统计量即为 $\chi_{MH}^2$ ；当考虑分层变量时(高维RxC列联表)， $\chi_{CMH}^2$ 是校正了分层变量影响后的检验统计量。一维和高维RxC列联表相关统计量 $\chi_{CMH}^2$ 的自由度均为1。
方差分析统计量：也称行平均得分统计量(Row mean scores statistic)，适用于列变量Y为有序分类变量的资料。此时，可求各行中列变量Y的平均得分， $H_0$ 为所有层的各行Y变量平均得分均相等，且为至少有一层各行间Y变量平均得分不等。对于一维的RxC列联表，该检验等价于对各行Y变量平均得分的方差分析;若得分用秩计算，则等价于 Kruskal-Wallis 检验。对高维RxC列联表，该检验可看作校正了分层变量影响后的方差分析或Kruskal-Wallis 检验。此类的自由度为(R-1)。
一般关联统计量(General association statistic)：适用于行变量X和列变量Y均为无序分类变量的资料，目的是检验X与Y是否存在关联性。对于一维RxC列联表， $\chi_{CMH}^2$ 等于 $(n-1/n)\chi_P^2$ ， $\chi_P^2$ 为 Pearson $\chi^2$ 统计量；对于高维RxC列联表， $\chi_{CMH}^2$ 相当于用分层变量校正的 Pearson $\chi^2$ 统计量。此类 $\chi_{CMH}^2$ 的自由度为(C-1)。

以上各 $\chi_{CMH}^2$ 统计量的计算公式较为复杂，可参阅相关参考书。实际应用中的计算过程通常需借助统计软件来完成。下面仅介绍R语言中的几个工具。

使用《医学统计学》中的案例07-12 的数据，做CMH检验测试。设置的

$H_0$ ：各年龄组的心肌梗死的发生均与口服避孕药无关；

$H_1:$ 至少有一个年龄组的心肌梗死的发生与口服避孕药有关。

Table 7.10: 按年龄分成的心肌梗死于近期使用口服避孕药的病例对照数据
		近期使用口服避孕药
年龄	心肌梗死	是	否	合计
$\lt40$ 岁	病例	17	47	64
	对照	121	944	1065
	小计	138	991	1129
$\geq40$ 岁	病例	12	158	170
	对照	14	663	677
	小计	26	821	847
合计		164	1812	1976


data_arr<-array(as.numeric(c("17","12","121","14","47","158","944","663")),
                   dim = c(2,2,2),
                   dimnames =
                   list(Age = c("<40", "≥40" ),
                        Mi = c("Case", "contral"),
                        Pill = c("Yes", "No")))
data_ftab<-as.table(data_arr)
ftable(as.table(data_arr))
##              Pill Yes  No
##  Age Mi                  
##  <40 Case          17  47
##      contral      121 944
##  ≥40 Case          12 158
##      contral       14 663

##使用Breslow-Day Test()或者Woolf-test判断数据是否适合使用CMH卡方检验
library("DescTools")
BreslowDayTest(data_ftab, correct = T)
##      Breslow-Day Test on Homogeneity of Odds Ratios (with Tarone correction)
##  
##  data:  data_ftab
##  X-squared = 0.23387, df = 1, p-value = 0.6287
library(vcd)
woolf_test(data_ftab)
##      Woolf-test on Homogeneity of Odds Ratios (no 3-Way assoc.)
##  
##  data:  data_ftab
##  X-squared = 0.23358, df = 1, p-value = 0.6289

#进行CMH卡方检验，使用的是mantelhaen.test()工具
mantelhaen.test(data_ftab)
##      Mantel-Haenszel chi-squared test with continuity correction
##  
##  data:  data_ftab
##  Mantel-Haenszel X-squared = 107.43, df = 1, p-value < 2.2e-16
##  alternative hypothesis: true common odds ratio is not equal to 1
##  95 percent confidence interval:
##   0.1482944 0.2821464
##  sample estimates:
##  common odds ratio 
##            0.20455

根据计算结果，Breslow-Day检验和伍尔夫测试都显示测试数据可以采用CHM检验分析，使用mantelhaen.test()工具计算，P值< 2.2e-16<0.05，因此拒绝原假设 $H_0$ ，接受 $H_1$ ，可认为在控制年龄因素否，心肌梗死与近期服用口服避孕药物相关。

注意的是：这里的计算结果与《医学统计学》教材上的结论相同，但是卡方值和P值并不一致，这可能有一些问题还没搞明白。

进一步的，我们可以用R中rcompanion包中的析因分析工具groupwiseCMH()进一步探讨控制不同因素后组之间的关系。

library(rcompanion)

groupwiseCMH(data_ftab,group= 2,fisher= FALSE,gtest= FALSE,chisq= TRUE,
              method = "fdr",correct = "none",digits  = 3)
##   Group       Test  p.value    adj.p
## 1   Yes Chi.square 1.10e-04 1.10e-04
## 2    No Chi.square 6.16e-22 1.23e-21
groupwiseCMH(data_ftab,group= 2,fisher= FALSE,gtest= FALSE,chisq= TRUE,
              method = "fdr",correct = "none",digits  = 3)
##     Group       Test  p.value    adj.p
## 1    Case Chi.square 1.37e-04 1.37e-04
## 2 contral Chi.square 2.96e-12 5.92e-12
groupwiseCMH(data_ftab,group= 1,fisher= FALSE,gtest= FALSE,chisq= TRUE,
              method = "fdr",correct = "none",digits  = 3)
##   Group       Test  p.value   adj.p
## 1   <40 Chi.square 0.000651 0.00130
## 2   ≥40 Chi.square 0.001780 0.00178

7.5 频数分布的拟合优度检验

拟合优度检验(Goodness-of-Fit Tests)用于将名义变量的水平比例与理论比例进行比较。常见的拟合优度检验是似然比卡方检验(Likelihood ratio Chi-Square，或似然比检验，Likelihood ratio test)，卡方检验和二项式或多项式精确检验。

通常，关于这些观察到的抽样数据有两种情况：

观察数据的分布并无预期，对于这种情况：如果出现理论频数(预期频数)较低(比如<5)，则卡方检验和似然比卡方检验的结果可能会不准确。对于卡方检验和似然比卡方检验，所有统计上理论频数(预期频数)均应≥5。对于理论频数(预期频数)数的小于5的情况，可以精确的测试，这些测试不会因理论频数太小而困扰。但是，如果实际观察频数和理论频数都不低，则使用G检验或卡方检验是没问题的，而且卡方检验可能更被人们熟悉。
观察数据的分布有预期，对于这种情况：一般目的是检验数据是否服从某个指定分布，一般使用卡方拟合优度检验。

使用《医学统计学》中的07-13的数据测试不同拟合优度是检验数据。

Table 7.11: 某克山病去的克山病空间分布抽样数据与经验概率
取样单位内的病例数X	观察频数	经验概率
0	26	0.0854
1	51	0.2102
2	75	0.2585
3	63	0.2120
4	38	0.1304
5	17	0.0641
6	5	0.0263
7	3	0.0092
$\geq8$	1	0.0039
	279(n)	1

7.5.1 观察数据的无分布预期

卡方拟合优度检验

gof_tib<- tibble(
  'sample' = c(seq(0, 7, 1),"≥8" ), 
  'observed' = c("26","51","75","63","38","17","5","3","1" ), 
  'theoreticalP' = c("0.0854","0.2102","0.2585","0.2120","0.1304","0.0641","0.0263","0.0092","0.0039"), 
  )
observed<-as.numeric(gof_tib$observed)
theoreticalP<-as.numeric(gof_tib$theoreticalP)

csqtest_gof<-chisq.test(observed, p = theoreticalP)
csqtest_gof$expected
# [1] 23.8266 58.6458 72.1215 59.1480 36.3816 17.8839  7.3377  2.5668  1.0881
str(csqtest_gof)
## List of 9
##   $ statistic: Named num 2.5
##    ..- attr(*, "names")= chr "X-squared"
##   $ parameter: Named num 8
##    ..- attr(*, "names")= chr "df"
##   $ p.value  : num 0.962
##   $ method   : chr "Chi-squared test for given probabilities"
##   $ data.name: chr "observed"
##   $ observed : num [1:9] 26 51 75 63 38 17 5 3 1
##   $ expected : num [1:9] 23.8 58.6 72.1 59.1 36.4 ...
##   $ residuals: num [1:9] 0.445 -0.998 0.339 0.501 0.268 ...
##   $ stdres   : num [1:9] 0.466 -1.123 0.394 0.564 0.288 ...
##   - attr(*, "class")= chr "htest"

似然比拟合优度检验


if(!require(DescTools)){install.packages("DescTools")}
gtest_gof<-GTest(observed, p = theoreticalP, correct="none")
gtest_gof$expected
#  [1] 23.8266 58.6458 72.1215 59.1480 36.3816 17.8839  7.3377  2.5668  1.0881
str(gtest_gof)

二项式或多项式精确检验

二项式或多项式精确检验是通过检查样本数据的形态来验证总体数据是否符合二项或多项分布，其零假设是样本来自的总体与预设的二项或多项分布没有显著差异。二项或多项分布检验，常用于小样本数据的精确检验方法，而对大样本数据则主要采用近似检验方法(如卡方检验或似然比检验)。

gof_tib<- tibble(
  'sample' = c(seq(0, 7, 1),"≥8" ), 
  'observed' = c("26","51","75","63","38","17","5","3","1" ), 
  'theoreticalP' = c("0.0854","0.2102","0.2585","0.2120","0.1304","0.0641","0.0263","0.0092","0.0039"), 
  )
observed<-as.numeric(gof_tib$observed)
theoreticalP<-as.numeric(gof_tib$theoreticalP)

if(!require(EMT)){install.packages("EMT")}
mtest_gof<-multinomial.test(observed, p = theoreticalP,MonteCarlo = TRUE)
##   WARNING: Number of simulated withdrawels is lower than the number of possible outcomes. 
##                  This might yield unreliable results!
##  
##  
##   Monte Carlo Multinomial Test, distance measure: f
##  
##         Events    fObs    p.value
##   1.034643e+15       0          0

7.5.2 观察数据的有预期分布

泊松分布的拟合优化检验 使用《医学统计学》中的07-13的数据测试检验数据是否服从某个指定分布。设置 $H_0:$ 抽样数据符合泊松分布，并根据抽样计算出均值和方差和 $\lambda$ ，并计算相应观察值对应的理论概率。

gof_tib<- tibble(
  'sample' = c(seq(0, 7, 1),"≥8" ), 
  'observed' = c("26","51","75","63","38","17","5","3","1" ), 
  'theoreticalP' = c("0.0854","0.2102","0.2585","0.2120","0.1304","0.0641","0.0263","0.0092","0.0039"), 
  )
observed<-as.numeric(gof_tib$observed)
theoreticalP<-as.numeric(gof_tib$theoreticalP)
observed_mg<-c(observed[which(observed>5)],sum(observed[which(observed<=5)]))

theoreticalP_mg<-c(theoreticalP[which(observed>5)],sum(theoreticalP[which(observed<=5)]))

csqtest_gof<-chisq.test(observed_mg, p = theoreticalP_mg)
chi_val<-sum((observed_mg-csqtest_gof$expected)^2/observed_mg)

pchisq(chi_val,df=5,lower.tail = F)
#[1] 0.8164961

根据计算结果P值>0.1，按照α=0.1的水准不拒绝 $H_0$ ，即可认为数据符合假设的分布(泊松分布)。

二项分布的拟合优化检验

使用《医学统计学》中的06-08的数据测试不同拟合优度是检验数据是否服从某个二项分布，设置 $H_0:$ 抽样数据符合二项分布，并根据抽样计算的阳性和阴性对应的概率。

Table 7.12: 患病数据资料与二项分布拟合优度测试数据
X	观察频数	经验概率
0	26	0.13265
1	10	0.38235
2	28	0.36735
3	18	0.11765
合计	82

gof_tib<- tibble(
  'sample' = c(seq(0, 3, 1),"合计"), 
  'X' = as.numeric(c("26","10","28","18","82")), 
  'theoreticalP' = -as.numeric(c("0.13265","0.38235","0.36735","0.11765","1"))
  )
n<-3*sum(gof_tib$X[1:4])
neg_no<-sum(as.numeric(gof_tib$sample[1:4])*gof_tib$X[1:4])
p<-neg_no/n
##这里类似重复抽取四次，n最大值3
theoreticalP<-dbinom(0:3,3,p)
observed_mg<-sum(gof_tib$X[1:4])*theoreticalP

chi_val<-sum(((gof_tib$X[1:4])-observed_mg)^2/gof_tib$X[1:4])
pchisq(chi_val,df=2,lower.tail = F)
#[1] 1.610495e-13

根据计算结果P值<0.005<0.1，按照α=0.1的水准拒绝 $H_0$ ，接受 $H_1$ ，即还不能认为数据符合假设的分布(二项分布)，即该疾病具有家族遗传性。

注意的是，按照《医学统计学》上的表格，theoreticalP的和是不为1的，因此在计算式没有使用书上提供的高铝数值，计算的卡方检验值(58.91413)也与书上相差有点大。

第七章 χ2\chi^2检验