第九章 双变量回归与相关
日期: 2020-12-05 作者:wxhyihuan
前面几章讨论了单变量(Univariate)计量资料的统计分析方法,着重于描述某一变量的统计特征或比较该变 量的组间差别。但是在大量的医学科研与实践中,经常会遇到对两个变量(Bivariate)之间关系的研究,例如糖尿病患者 的血糖与其胰岛素水平的关系如何,某人群年龄的变化与其收缩压的关系怎样等,此时常用线性回归(Linear Regression)与相关分(Correlation) 析。本章介绍两个数值变量呈直线或曲线关系的分析方法,及可用于有序分类变量(等级变量)的秩相关 的非参数统计方法。
9.1 直线回归
在定量描述Y与X数量上的依存关系时,将X称为自变量(Independent variable);Y称为应变量(Dependent variable)。 当Y随X变化而变化且呈直线趋势,但并非自变量全部都恰好全都在这个直线上(即与两变量间严格的直线函数关系不 同), 称为直线回归(Linear regression)或简单回归(Simple regression),用以下直线回归方程(Linear regression equation) 表示: \[ \hat {Y} = a+bX \tag{9-1}\]
方程\((9-1)\) 被称为经验回归方程或样本回归方程,它是对X、Y两变个量总体间线性关系的一个估计。 根据散点图可以假定,对于X各个取值,相应Y的总体均数\(\mu_{Y|X}\)在一条直线上,表示为:
\[\mu_{Y|X}= \alpha +\beta X +\epsilon_i\]
\(\epsilon_i\)被称为残差,即。除了图中所示两变量呈直线关系外,一般还假定每个X对应Y的总体为正态分布,各个正态分布的总 体方差相等且各次观测相互独立。这样,公式(9-1)中\(\bar{Y}\)的实际上是X所对应Y的总体均数 \(\mu_{Y|X}\)的一个样 本估计值,称为回归方程的预测值(Predicted value),而a,b分别为\(\alpha\)和 \(\beta\)的样本估计。其中a称为常数项 (Constant term),是回归直线在Y轴上的截距(Intercept), 其统计意义是当X取值为0时相应Y的均数估计值;b称为回归系数(Coefficient of regression), 是直线的斜率(Slope),其统计意义是当X变化一个单位时Y的平均改变的估计值,并且: - b>0时直线从左下方走向右上方,Y随X的增大而增大; - b<0时直线从左上方走向右下方,Y随X的增大而减小; - b=0时直线与X轴平行,Y与X无直线关系。
如果能够从样本数据中求得a、b的数值,回归方程即可唯一确定。求解 a、b实际上就是 怎样“合理地”找到一条能最好地代表数据点分布趋势的直线。将实测值Y与假定回归线上的估计值$ {Y}\(的纵向距 离\)Y-{Y}$称为残差(Residual)或剩余值,一个自然的想法就是各点残差要尽可能的小。由于考虑所有点之残差有 正有负,所以通常取各点残差平方和最小的直线为所求,这就是所谓“最小二乘方拟合”(Least squares fitting,LSF)原则。 在一定假没条件下,如此得到的回归系数最为理想。按照这一原则,数学上可以容易地得到残差平方和最小计算公式为: \[\sum_{i=1}^n\epsilon_i^2=\sum_{i=1}^n(\hat Y_i-\alpha-\beta x_i)^2\] 此时对应的斜率b(回归系数)值为: \[b=\frac{\sum_{i=1}^n(Y-\bar Y)(X-\bar X)}{\sum_{i=1}^n(X-\bar X)^2}\] 此时对应的截距a(常数项)值为: \(a=\bar Y-b\bar X\)
R种的直线回归方程的主要工具是lm()工具,这里使用《医学统计学》中的案例9-1的数据来估计尿肌酐含量与年龄的直线回归方程。
| 编号 | 年龄(X) | 尿肌酐(Y) |
|---|---|---|
| 1 | 13 | 3.54 |
| 2 | 11 | 3.01 |
| 3 | 9 | 3.09 |
| 4 | 6 | 2.48 |
| 5 | 8 | 2.56 |
| 6 | 10 | 3.36 |
| 7 | 12 | 3.18 |
| 8 | 7 | 2.65 |
library("dplyr")
library("kableExtra")
library("haven")
#使用haven包种的read_sav()的函数读取数据
Creatinine_df<-read_sav(file="ExampleData/SavData4MedSta/Exam09-01.sav")
colnames(Creatinine_df)<-c("No.","Age","CreatiC")
lmod<-lm(Creatinine_df$CreatiC~Creatinine_df$Age)
# Call:
# lm(formula = Creatinine_df$CreatiC ~ Creatinine_df$Age)
#
# Coefficients:
# (Intercept) Creatinine_df$Age
# 1.6617 0.1392
lmod_summary <- summary(lmod)
# Call:
# lm(formula = Creatinine_df$CreatiC ~ Creatinine_df$Age)
# Residuals:
# Min 1Q Median 3Q Max
# -0.21500 -0.15937 -0.00125 0.09583 0.30667
#
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 1.66167 0.29700 5.595 0.00139 **
# Creatinine_df$Age 0.13917 0.03039 4.579 0.00377 **
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
# Residual standard error: 0.197 on 6 degrees of freedom
# Multiple R-squared: 0.7775, Adjusted R-squared: 0.7404
# F-statistic: 20.97 on 1 and 6 DF, p-value: 0.003774
pf(lmod_summary$fstatistic[1],lmod_summary$fstatistic[2],lmod_summary$fstatistic[3],lower.tail = F)根据计算结果,常项数a=1.6617,回归系数b=0.1392,因此\(\hat Y=1.6617+0.1392X\)。
9.2 直线回归中的统计推断
建立样本直线回归方程,只是完成了统计分析中两变量关系的统计描述,研究者还必须回答它所来自 总体的直线回归关系是否确实存在,即是否对总体有β≠0? 当无论X如何取值,\(\mu_{Y|X}\) 总在一条 水平线上,即β=0,总体直线回归方程并不成立,意即 Y与X无直线关系,此时\(\mu_{Y|X}\)。然而在一次随机 抽样中,如果所得样本为实心圆点所示,则会得到一个并不等于0的样本回归系数b。b与0相差到多大可以认为具有统计学意义?一般可以用用方差分析或与其等价的t检验来回答这一问题。
9.2.1 方差分析
将应变量Y的离均差平方和(\(SS_{tol}\))分解为估计值的离均差方和(\(SS_{reg}\))与残差平方和\(SS_{res}\),即\(SS_{tol}=SS_{reg}+SS_{res}\): \[\sum{(Y-\bar Y)^2}=\sum{(\hat Y-\bar Y)^2}+\sum{(Y-\hat Y)^2}\] \(SS_{tol},SS_{reg},SS_{res}\)各自的自由度\(v\),并有: \[v_{tol}=v_{reg}+v_{res}=n-1,v_{reg}=1,v_{res}=n-2\]
根据方差分析,计算F值计算公式为: \[F=\frac{SS_{reg}/v_{res}}{SS_{res}/v_{res}}=\frac{MS_{reg}}{MS_{res}},v_{reg}=1,v_{res}=n-2\]
在计算\(SS_{reg}\)计算的简化公式为: \[SS_{reg}=b^2*l_{XX}=b^2*(\sum X^2-(\sum X)^2/n)\]
9.2.2 t检验
对β=0这一假设是否进行t检验:
\[\begin{aligned} t &= \frac{b-0}{S_b}\\ S_b &= \frac{S_{Y|X}}{\sqrt{l_{XX}}}\\ S_{Y|X} &=\sqrt{\frac{SS_{res}}{n-2}} \end{aligned}\] 公式中的\(S_b\)为样本回归系数标准误,\(S_{Y|X}\)为回归的剩余标准差(Standed deviation of residuals)。
9.2.3 总体回归系数β的可信区间
利用对回归系数的t检验,可以的到β的1-α的可信区间为: \[b ± S_b*t_{\alpha/2,v}\]
根据计算结果,β的95%可信区间为(0.06480131,0.213532),要注意的是,此区间不包含0值!
9.2.4 利用回归方程进行估计和预测
9.2.4.1 总体均数\(\mu_{Y|X}\)的可信区间
给定X的数值\(X_0\),由样本回归方程计算出的\(\hat Y_0\)只是相应总体均数\(\mu_{Y|X_0}\)的一个点估计。由于 存在抽样误差,\(\hat Y_0\)会因样本而不同。反应其抽样误差大小的标准误的计算公式为: \[S_{\hat Y_0}=S_{Y|X}\sqrt{1/n+\frac{(X_0-\bar X)^2}{\sum(X-\bar X)^2}}\] \(\hat Y_0\)的标准误与回归的剩余标准差\(S_{Y|X}\)成正比。当\(X=X_0\)时,达到其最小值\(S_{Y|X}/\sqrt{n}\),相差越大,则\(S_{\hat Y_0}\)越大。
给定\(X=X_0\)时,总体均数\(\mu_{Y|X_0}\)的1-α可信区间为: \[\hat Y_0 ± S_{\hat Y_0}*t_{\alpha/2,v}\]
在直角坐标系中,总体均数\(\mu_{Y|X_0}\)的1-α可信区间通常被表示为一条中间窄,两端宽的带子(边缘一般是实线),其中最窄处对应的就是\(X=X_0\)。
9.2.4.2 个体Y值的预测区间
将预报因子(自变量X)代入回归方程对总体中预报量(因变量Y)的个体值进行估计。给定X的数值\(X_0\),对应的个体Y值 也存在一个波动范围,其标准差\(S_{Y_0}\)(注意:不要与样本观察值Y的标准差相混淆)的计算公式为: \[S_{Y_0}=S_{Y|X}*\sqrt{1+1/n+\frac{(X-\bar X)^2}{\sum (X-\bar X)^2}}\] 给定\(X=X_0\)时的个体Y值的1-α得预测区间为: \[\hat Y_0 ± S_{Y_0}*t_{\alpha/2,v}\]
在直角坐标系中,个体Y值的1-α得预测区间通常被比表示为一条比总体均数\(\mu_{Y|X_0}\)的1-α可信区间带更宽的带子, 其中最窄处对应的也是\(X=X_0\)。
应注意的是,给定\(X=X_0\)时,相应Y的均数的可信区间与其个体Y值的预测区间的含义是不同的:前者表示在固定的\(X_0\)处, 如果反复抽样100次,可算出100个相应Y的总体均数的可信区间,平均有100x(1-α)个可信区间包含总体均数;后者表示的是一 个预测值的取值范围,即预测100个个体值中,平均将有100x(1-α)个个体值在求出的范围内。
library("dplyr")
library("haven")
library("ggplot2")
Creatinine_df<-read_sav(file="ExampleData/SavData4MedSta/Exam09-01.sav")
colnames(Creatinine_df)<-c("No.","Age","CreatiC")
lmod<-lm(Creatinine_df$CreatiC~Creatinine_df$Age)
meanX<-mean(Creatinine_df$Age)
meanY<-mean(Creatinine_df$CreatiC)
n<-length(Creatinine_df$CreatiC)
##用离均差平方和计算不同的变异量
SS_tol<-sum((Creatinine_df$CreatiC-meanY)^2)
SS_reg<-sum((lmod$fitted.values-meanY)^2)
SS_res<-sum((Creatinine_df$CreatiC-lmod$fitted.values)^2)
##计算不同的离均差平方和(Sum of square of deviations from mean,SS),离均差积和
DAS_xx<-sum(Creatinine_df$Age^2)-(sum(Creatinine_df$Age))^2/n
DAS_yy<-sum(Creatinine_df$CreatiC^2)-(sum(Creatinine_df$CreatiC))^2/n
DAS_xy<-sum(Creatinine_df$Age*Creatinine_df$CreatiC)-(sum(Creatinine_df$Age)*sum(Creatinine_df$CreatiC))/n
#计算回归系数b与常项数a
b<-DAS_xy/DAS_xx
# [1] 0.1391667
a<-meanY-b*meanX
# [1] 1.661667
#计算回归方程的剩余标准差SDR_xy
SDR_xy<-sqrt(SS_res/(n-2))
#计算样本回归系数的标准误Se_rc
Se_b<-SDR_xy/sqrt(DAS_xx)
F_val<-SS_reg*(n-2)/SS_res
# [1] 20.96842
t_val<-b/Se_b
# [1] 4.579129
# 计算回归系数Beta(b)的95%可信区间
alpha<-0.05
t_alphaval<-qt(alpha/2,n-2,lower.tail = F)
# [1] 2.446912
lci<-b-t_alphaval*Se_b
uci<-b+t_alphaval*Se_b
#根据计算的回归系数和b和常项数a计算Y的预测值
pred.y <- b * Creatinine_df$Age + a
#根据抽样误差大小的标准误计算公式计算总体均数的可信区间
pred.y_se<-SDR_xy*sqrt(1/n+(Creatinine_df$Age-meanX)^2/sum((Creatinine_df$Age-meanX)^2))
pred.y_uci<-pred.y+t_alphaval*pred.y_se
pred.y_lci<-pred.y-t_alphaval*pred.y_se
#根据抽样观察值的波动标准差计算公式计算观察值的预测区间
y_se<-SDR_xy*sqrt(1+1/n+(Creatinine_df$Age-meanX)^2/sum((Creatinine_df$Age-meanX)^2))
y_uci<-pred.y+t_alphaval*y_se
y_lci<-pred.y-t_alphaval*y_se
pred.y_df<-cbind(Creatinine_df$Age,
predict(lmod,interval = "confidence")[,2],
predict(lmod,interval = "confidence")[,3], pred.y)
y_df<-cbind(Creatinine_df$Age, y_lci, y_uci, pred.y)
#plot(Creatinine_df$Age,Creatinine_df$CreatiC, cex = 1.75, pch = 21, bg = 'gray')
#lines(pred.y_df[order(pred.y_df[,1]),][,1],pred.y_df[order(pred.y_df[,1]),][,4],col="green")
#lines(pred.y_df[order(pred.y_df[,1]),][,1],pred.y_df[order(pred.y_df[,1]),][,2],col="red")
#lines(pred.y_df[order(pred.y_df[,1]),][,1],pred.y_df[order(pred.y_df[,1]),][,3],col="red")
#lines(y_df[order(y_df[,1]),][,1],y_df[order(y_df[,1]),][,2],col="blue")
#lines(y_df[order(y_df[,1]),][,1],y_df[order(y_df[,1]),][,3],col="blue")
colnames(pred.y_df)<-c("Age","LCI","UCI","predy")
colnames(y_df)<-c("Age","LCI","UCI","predy")
o <- ggplot(Creatinine_df, aes(Age, CreatiC))+
xlab("年龄(岁)|Age(Years)")+ ylab("尿肌酐浓度(mmol/24h)|Creatic concentration(mmol/24h)")+
geom_point(shape=21,size=3.5, colour = "black",fill="red",alpha=0.5)+
geom_smooth(method="lm", se=TRUE, colour = "blue",fill="blue",alpha=0.3,size=1.1)+
geom_path(data=as.data.frame(y_df[order(y_df[,1]),]),aes(Age,UCI),lineend="butt",linejoin="round",linemitre=1,
color="red",size=1.1,alpha=0.5,linetype=2)+
geom_path(data=as.data.frame(y_df[order(y_df[,1]),]),aes(Age,LCI),lineend="butt",linejoin="round",linemitre=1,
color="red",size=1.1,alpha=0.5,linetype=2)+
theme_classic()
print(o)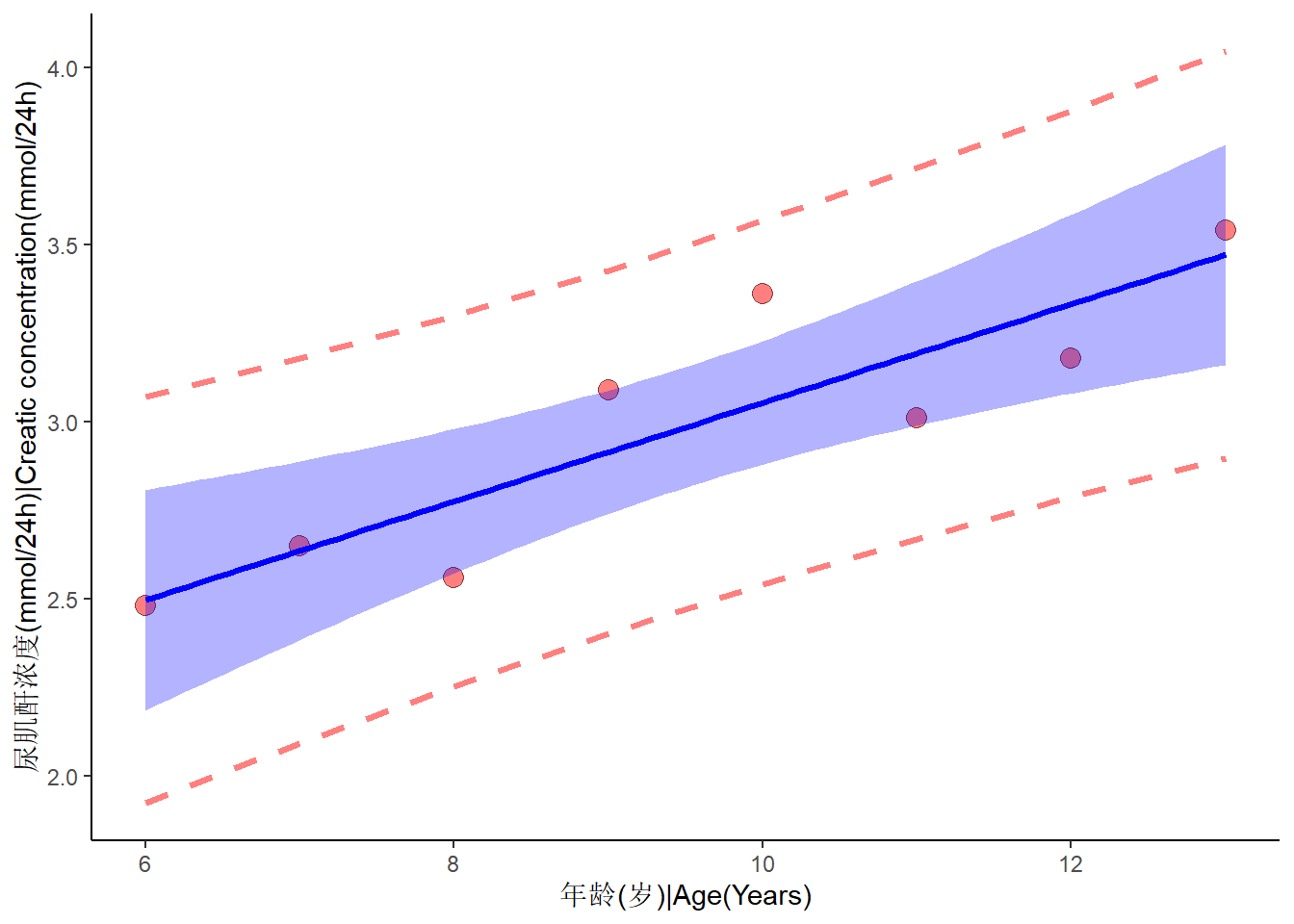
Figure 9.1: 8名正常儿童的年龄X(岁)与尿肌酐含量Y*(mmol/24h)的线性回归模拟
9.3 直线相关
直线相关(Linear correlation)又称简单相关(Simple correlation),用于双变量正态分布(Bivariate normal distribution)资料。 直线相关的性质可由散点图直观的说明,一般有下面几种情况:
若两变量X、Y同时增大或减小,变化趋势是同向的,称为正相关(Positive correlation);
若两变量X、Y间呈反向变化,称为负相关(Negative correlation);
若X、Y是同向变化,称为完全正相关(Perfect positive correlation);
若X、Y呈反向变化,称为完全负相关(Perfect negative correlation)。
若散点分布为圆形等一些形状,两变量间没有直线相关关系,称为零相关(Zero correlation)。
正相关或负相关并不一定表示一个变量的改变是另一个变量变化的因,有可能同受另一个因素的影响。因此,相关关系并不一定是因果关系。
9.3.1 相关系数
相关系数(Coefficient of correlation)又称 Pearson 积差相关系数(Coefficient of product-moment correlation),以符号r表示样本相关系数, 符号p表示其总体相关系数。它用来说明具有直线关系的两变 量间相关的密切程度与相关方向。样本相关系数的计算公式为: \[r=\frac{\sum{(X-\bar X)(Y-\bar Y)}}{\sqrt{\sum(X-\bar X)^2}*\sqrt{\sum(Y-\bar Y)^2}}=\frac{l_{xy}}{\sqrt{l_{xx}l_{yy}}}\] 其中\(l_{xx}=\sum X^2-(\sum X)^2/n,l_{yy}=\sum Y^2-(\sum Y)^2/n,l_{xy}=\sum XY-(\sum X)(\sum Y)/n\)
相关系数没有单位,其值为 -1<r<1。r值为正表示正相关,r值为负表示负相关,r的绝对值等于1为完全相关,r= 0为零相关。在生物界由于影响因素众多,因此很少完全相关。
注意:这里的r实际上是就总体相关系数p来说的,r是p的估计值。
library("dplyr")
library("haven")
library("ggplot2")
bulkv_df<-read_sav(file="ExampleData/SavData4MedSta/Exam09-05.sav")
colnames(bulkv_df)<-c("No.","Weight","Bulkv")
meanW<-mean(bulkv_df$Weight)
meanB<-mean(bulkv_df$Bulkv)
n<-length(bulkv_df$Weight)
##计算不同的离均差平方和(Sum of square of deviations from mean,SS),离均差积和
DAS_xx<-sum(bulkv_df$Weight^2)-(sum(bulkv_df$Weight))^2/n
DAS_yy<-sum(bulkv_df$Bulkv^2)-(sum(bulkv_df$Bulkv))^2/n
DAS_xy<-sum(bulkv_df$Weight*bulkv_df$Bulkv)-(sum(bulkv_df$Weight)*sum(bulkv_df$Bulkv))/n
#计算样本的相关系数
r<-DAS_xy/sqrt(DAS_xx*DAS_yy)
#[1] 0.8754315
wb <- ggplot(bulkv_df, aes(Weight, Bulkv))+
xlab("体重|Weight/kg X")+ ylab("双肾体积|Bulkv/ml Y")+
geom_point(shape=21,size=3.5, colour = "black",fill="red",alpha=0.5)+
geom_smooth(method="lm", se=TRUE, colour = "blue",fill="blue",alpha=0.3,size=1.1)+
geom_vline(aes(xintercept = mean(Weight)),linetype=2)+
geom_hline(aes(yintercept = mean(Bulkv)),linetype=2)+
geom_point(aes(mean(Weight),mean(Bulkv)),shape=16,size=3.5, colour="green",alpha=0.5)+
theme_classic()
print(wb)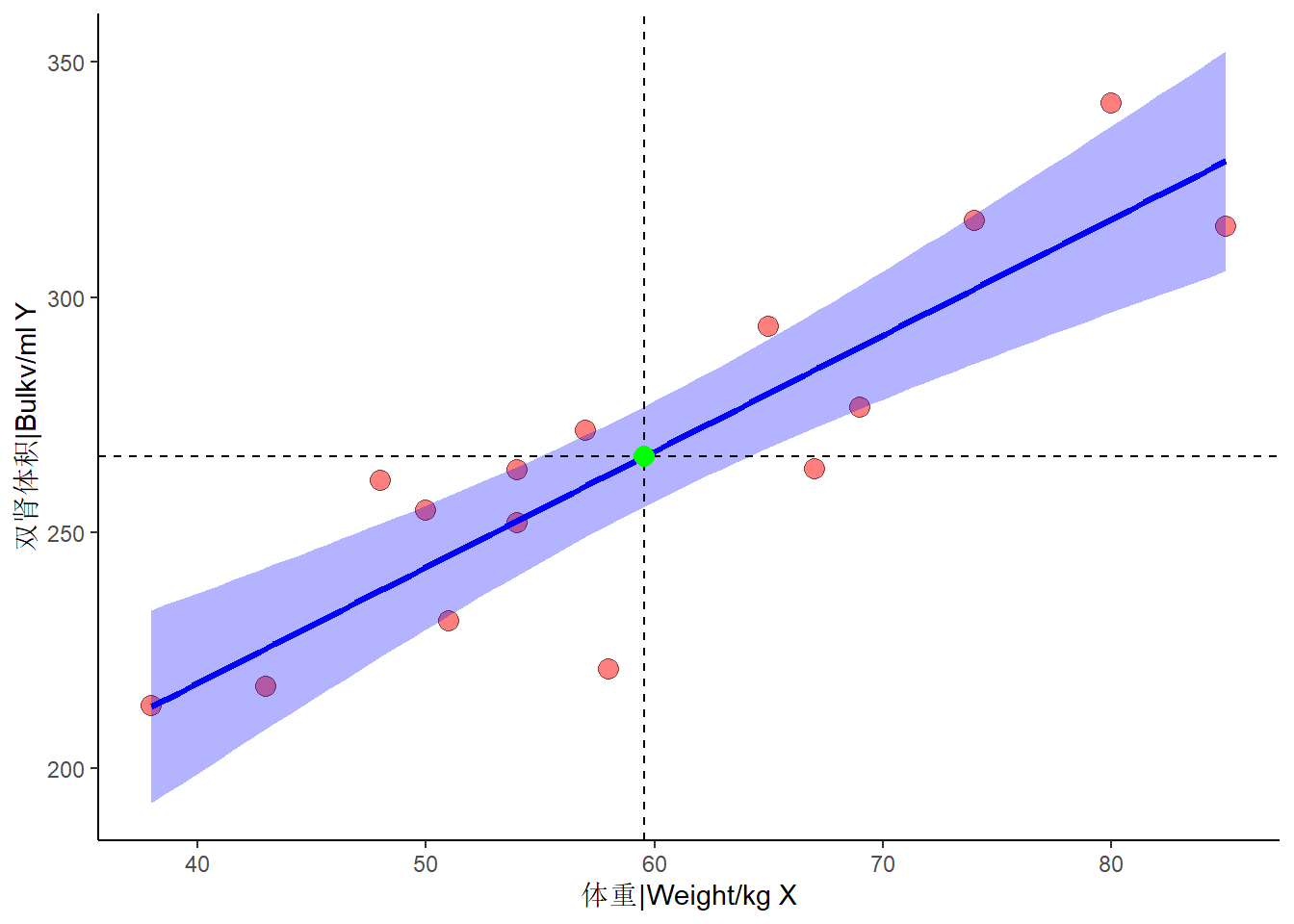
Figure 9.2: 15例正常成年人体重与双肾总体积的散点图
9.4 直线相关的假设推断
9.4.1 相关系数的假设检验
从同一总体抽出的不同样本会得到不同的样本相关系数,所以要判断X、Y间是否确有直线相关关系,就要检验r是否来自ρ≠0的总体。 因为即使从ρ=0的总体作随机抽样,由于抽样误差的影响,所得r值也常不等于零。故当计算出r值后,接着做p=0的假设检验。常用t检验, 检验统计量1值的计算公式如下: \[t=\frac{r-0}{S_r}=\frac{r}{\sqrt{\frac{1-r^2}{n-2}}},v=n-2\] 公式中\(S_r\)为相关系数的标准误,求得t值后可查t界值表判断P值,按检验水准判断结果。
9.4.2 总体相关系数的可信区间
由于相关系数的抽样分布在ρ不等于零时呈偏态分布(大样本情况下亦如此),所以ρ的可信区间不 能简单地按照前述回归系数一样用t分布去解决,而需要先将其进行某种变量变换,使变换后变量服从正 态分布,然后再估计其可信区间。具体步骤如下:
- 首先对r作如下z变换: \[z=tanh^{-1} \text{或者} z=1/2*ln\frac{1+r}{1-r}\]
- 按下式根据正态近似原理计算z的1-α的可信区间: \[(z±u_{a/2}/\sqrt{n-3}) \]
- 根据计算的z的上限和下限做如下变换,得到r的1-α的可信区间: \[r=tanhz \text{或者} r=\frac{e^{2z}-1}{e^{2z}+1}\]
9.4.3 决定系数
直线回归与相关中,为了更直观得反应Y的总变异中回归关系所能解释的百分比,产生了决定系数(Coeddicient of determination)这一统计量, 定义为回归平方与总平方和之比,计算公式为: \[R^2=SS_{reg}/SS_{tol}=\frac{l_{xy}^2}{l_{xx}*l_{yy}}\]
\(R^2\in[0,1]\)之间,其值大小反映了回归共享的相对程度,即回归关系所能解释的总变异百分比。 注意,在双变量分析和多变量分析中,决定系数都用\(R^2\)表示,但是在双变量分析中\(R^2=r^2\)是一样的。 比如体重与肾脏体积的案例中\(R^2=r^2=\) 0.76638。
决定系数还可以用作对直线回归或相关作假设检验,其中对只想回归的拟合有毒就等价于对总体回归系数的假设检验,统计量为: \[F=R^2/(1-R^2)(n-2)\]
9.4.4 直线回归与相关引用的注意事项
根据分析目的选择自/应变量和统计方法
进行直线回归和相关分析前绘制散点图,离群值处理
用残差图考察数据是否符合模型假设条件:自变量与因变量关系为线性,误差服从均数为0的正态分布且方差相等, 各观测独立(残差图横坐标为\(\hat Y\)或者X,纵坐标为残差),一般有以下几种情况:
- 正常情况: 残差图中的点近乎对称的分布在直线y=0两侧,并且左右对称
- 出现离群值: 残差图中的绝大部分点近乎对称的分布在直线y=0两侧,并且左右对称,但是有个别/极少数点会与它们远离
- 方差不齐: 残差图中的点左右不对称,呈喇叭状分散,说明数据方差不齐,须进行方差稳定化处理
- 不符合直线模型: 残差图中的点大致呈曲线分布,则说明直线回归不适合该数据,可能是符合曲线模型
- 呈直线相关分布:残差图中的点大致呈直线相关分布,说明残差之间不独立,与横轴存在相关,直线回归模型不适合该数据,
结果的解释与正确应用
- 相关系数或回归系数的绝对值反映密切程度
- 假设检验的P值越小,越有理由认为变量间的直线关系存在(而不能说广义越密切或越“显著”)