第二章 计量资料的统计描述
日期: 2020-11-10 作者:wxhyihuan
2.1 描述统计
描述统计学(广义上的描述统计学,Descriptive statistics)是统计学的一个分支,旨在概括、描述和呈现一系列值或数据集(比如对单样本的分析)。 由于难以识别数据中的任何模式,没有任何准备或没有任何汇总度量的长系列值通常无法提供信息。
描述统计通常是统计分析的第一步,也是统计分析的重要组成部分。它允许通过检测潜在的异常值(即似乎与其他数据分离的数据点)、 收集或编码错误来检查数据的质量。它还有助于“理解”数据,如果表述得当,描述性统计是进一步分析的一个很好的起点。
位置与离散度量是两种不同的总结数据的测量方法。其中一些给出了关于数据位置的理解,另一些给出了关于数据分散性的理解。 在实践中,这两种度量方法经常一起使用,以便以最简洁和完整的方式总结数据。
位置度量允许查看数据位于“何处”,围绕哪个值。换句话说,位置度量可了解什么是总体趋势,即数据整体的“位置”。 它主要包括:平均值,中位数,四分位数,第三、四分位数,众数,最大值,最小值等。
常见的离散度量,它有助于了解离散度和数据的可变性(在何种程度上分布被压缩或拉伸):范围,标准偏差,方差,四分位间距,变异系数。
2.2 测试数据
| V1 | V2 | V3 | V4 | V5 | V6 | V7 | V8 | V9 | V10 | V11 | V12 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 3.96 | 4.23 | 4.42 | 3.59 | 5.12 | 4.02 | 4.32 | 3.72 | 4.76 | 4.16 | 4.61 | 4.26 |
| 3.77 | 4.20 | 4.36 | 3.07 | 4.89 | 3.97 | 4.28 | 3.64 | 4.66 | 4.04 | 4.55 | 4.25 |
| 4.63 | 3.91 | 4.41 | 3.52 | 5.03 | 4.01 | 4.30 | 4.19 | 4.75 | 4.14 | 4.57 | 4.26 |
| 4.56 | 3.79 | 3.89 | 4.21 | 4.95 | 3.98 | 4.29 | 3.67 | 4.69 | 4.12 | 4.56 | 4.26 |
| 4.66 | 4.28 | 3.83 | 4.20 | 5.24 | 4.02 | 4.33 | 3.76 | 4.81 | 4.17 | 3.96 | 3.27 |
| 4.61 | 4.26 | 3.96 | 4.23 | 3.76 | 4.01 | 4.29 | 3.67 | 3.39 | 4.12 | 4.27 | 3.61 |
| 4.98 | 4.24 | 3.83 | 4.20 | 3.71 | 4.03 | 4.34 | 4.69 | 3.62 | 4.18 | 4.26 | 4.36 |
| 5.28 | 4.21 | 4.42 | 4.36 | 3.66 | 4.02 | 4.31 | 4.83 | 3.59 | 3.97 | 3.96 | 4.49 |
| 5.11 | 4.20 | 4.36 | 4.54 | 3.72 | 3.97 | 4.28 | 4.76 | 3.21 | 4.04 | 4.56 | 4.25 |
| 4.92 | 4.23 | 4.47 | 3.60 | 5.23 | 4.02 | 4.32 | 4.68 | 4.76 | 3.69 | 4.61 | 4.26 |
| 3.89 | 4.21 | 4.36 | 3.42 | 5.01 | 4.01 | 4.29 | 3.68 | 4.71 | 4.13 | 4.57 | 4.26 |
| 4.03 | 5.46 | 4.16 | 3.64 | 4.16 | 3.76 |
2.3 数据输入和频率统计
2.3.1 读取数据,并将数据转换成单列形式
2.3.3 确定组段数和组距
可以参考PAST软件中的the zero-stage rule of Wand 1997方式计算分段“最佳”个数。\(h=3.49min(s,IQ/1.349)n^{1/3}\),其中s是样本标准差,IQ是四分位数范围。
2.3.4 计算频数分布
根据计算的短组段数(h=8),极差值(rge=2.39))和组距(i=rge/h=0.3164)计算各组段的频数。
breaks = seq(min(RBC_v), max(RBC_v), length.out = 8)
RBC_v.cut = cut(RBC_v, breaks, right=T,include.lowest=T)
RBC_v.freq = table(RBC_v.cut)
## [3.07,3.41) [3.41,3.75) [3.75,4.09) [4.09,4.44) [4.44,4.78)
## 4 17 29 51 23
## [4.78,5.12) [5.12,5.46)
## 9 4
hist(RBC_v, right=FALSE,
breaks = breaks, labels =TRUE,
freq = TRUE, col = "#A8D6FF",
border = "white", ylim=c(0, max(RBC_v.freq)))
hist(RBC_v, right=FALSE,
breaks = breaks, labels =TRUE,
freq = FALSE, col = "#A8D6FF",
border = "white", ylim=c(0,1))
lines(density(RBC_v),col="red",lwd=2)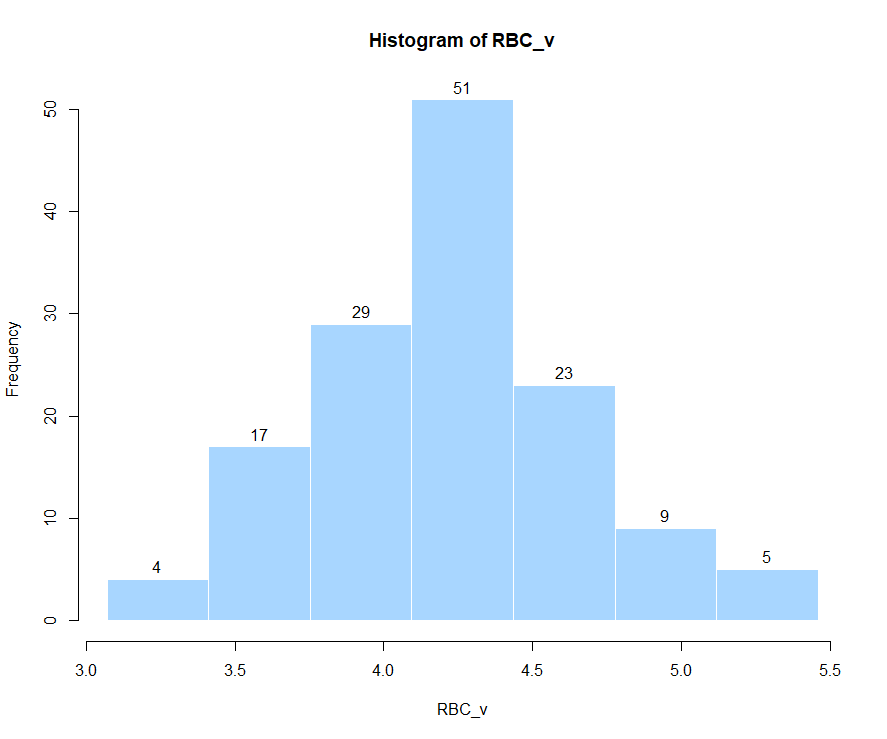
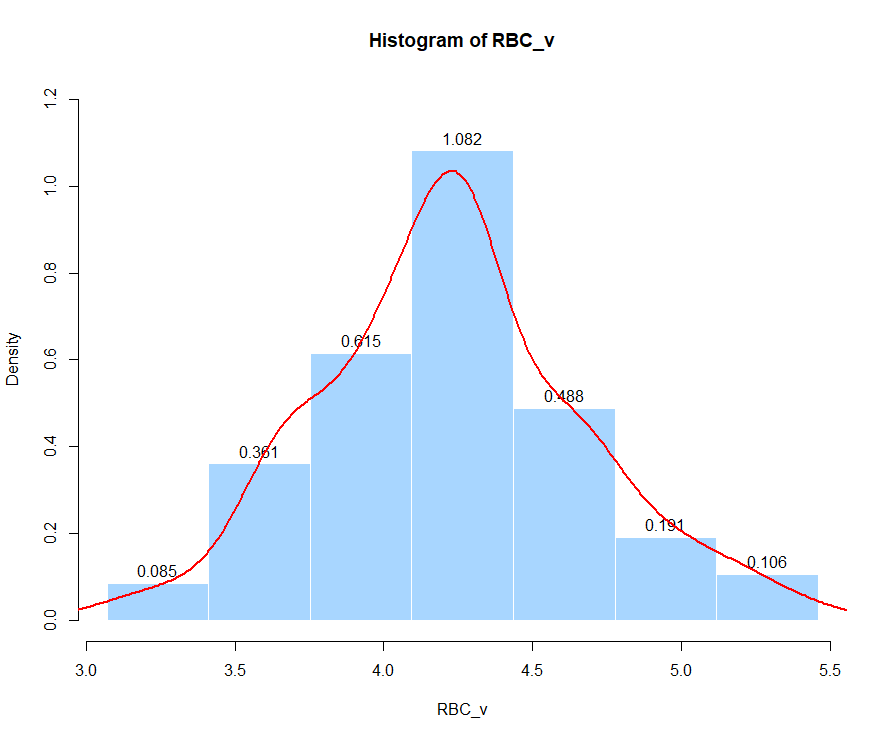
Figure 2.1: 红细胞含量的频数分布
2.4 描述性统计的度量
2.4.2 几何平均值
几何均数(geometric mean)可用于反映一组经 对数转换 后呈对称分布的变量值在数量上的平均水平。
2.4.3 中位数与百分位数
中位数(median)是将n个变量值从小到大排列,位置居于中间的那个数。当为奇数时取位次居中 的变量值,当n为偶数时取位次居中的两个变量值的均数。 它适用于各种分布类型的资料,尤其是偏态分 布资料和一端或两端无确切数值的资料。
2.4.5 四分位间距
四分位数(quartile)是把全部变量值分为四部分的分位数,即第1四分位数(Q .=Ps)、第2四分位数 M=P)、第3四分位数 (Qu=Ps)。 四分位数间距(quartile range)是由第3四分位数和第1四分位数相减行得, 记为 R.它般和中位数起描述偏态分们资料的分布特征
2.4.6 方差与标准差
方差(variance,var)也称均方差(mean Square deviation),反映一组数据的平均离散水平。 标准差(standard deviation,sd)是方差的正平方根,其单位与原变量值的单位相同。
2.4.7 变异系数
变异系数(Cefficient of variation,CV),当进行两个或多个资料变异程度的比较时,如果度量单位与平均数相同, 可以直接利用标准差来比较。如果单位和(或)平均数不同时,比较其变异程度就不能采用标准差, 而需采用标准差与平均数的比值(相对值)来比较。标准差与平均数的比值称为变异系数,。 变异系数可以消除单位和(或)平均数不同对两个或多个资料变异程度比较的影响。
2.4.8 其他的描述统计
2.4.8.1 Summary
R语言中,可以使用summary()来计算最小,第1四分位数,中位数,平均值,第3,4分位数和最大值的数据集的所有数值变量。
dat <- iris
summary(dat)
## Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## Min. :4.300 Min. :2.000 Min. :1.000 Min. :0.100 setosa :50
## 1st Qu.:5.100 1st Qu.:2.800 1st Qu.:1.600 1st Qu.:0.300 versicolor:50
## Median :5.800 Median :3.000 Median :4.350 Median :1.300 virginica :50
## Mean :5.843 Mean :3.057 Mean :3.758 Mean :1.199
## 3rd Qu.:6.400 3rd Qu.:3.300 3rd Qu.:5.100 3rd Qu.:1.800
## Max. :7.900 Max. :4.400 Max. :6.900 Max. :2.500 2.4.8.2 众数
众数(Mode)是指在统计分布上具有明显集中趋势点的数值,代表数据的一般水平。 也是一组数据中出现次数最多的数值,有时众数在一组数中有好几个。 可以利用table()和sort()来寻找数据集中的众数。
# 计算每个元素的出现的次数
RBC_t <- table(RBC_v)
# 对计算的次数进行排序
sort(RBC_t, decreasing = TRUE)
## 4.26 4.36 3.96 4.02 4.2 3.76 3.97 4.01 4.16 4.21 4.23 4.28 4.29 4.56 4.61 4.76
## 7 5 4 4 4 3 3 3 3 3 3 3 3 3 3 3
## 3.59 3.64 3.67 3.72 3.83 3.89 4.03 4.04 4.12 4.25 4.32 4.42 4.57 4.66 4.69 3.07
## 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1
## 3.21 3.27 3.39 3.42 3.52 3.6 3.61 3.62 3.66 3.68 3.69 3.71 3.77 3.79 3.91 3.98
## 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
## 4.13 4.14 4.17 4.18 4.19 4.24 4.27 4.3 4.31 4.33 4.34 4.41 4.47 4.49 4.54 4.55
## 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
## 4.63 4.68 4.71 4.75 4.81 4.83 4.89 4.92 4.95 4.98 5.01 5.03 5.11 5.12 5.23 5.24
## 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
## 5.28 5.46
## 1 1
#或者结合 which()函数确定众数和其次数
RBC_t[which(((RBC_t==max(RBC_t))==T))]
## 4.26
## 7 2.5 正态分布和标准正态分布
正态分布(Normal distribution)又名高斯分布(Gaussian distribution),是一个非常常见的连续概率分布。 正态分布在统计学上十分重要,经常用在自然和社会科学来代表一个不明的随机变量。 可以说,弄懂正态分布是灵活运用统计学中各种假设检验方法、理解p值,均数置信区间的前提。 R包含有很丰富的正态分布相关的函数功能, 比如概率密度函数dnorm(),概率累积分布函数pnorm(),正态分位函数qnorm()和用来生成特定正态分布数据序列的函数rnorm(), 以及检测数据时候符合正态分布的方法,这里主要做下面一些介绍。
2.5.1 概率密度函数dnorm()
概率密度函数(Probability density function),R中即为dnorm(), 它可以给出了指定均值和标准差下每个点的概率分布的高度, 越高就代表着这个点/区间的概率越密集(大)。概率密度函数有时也被称为概率分布函数,但这种称法可能会和累积分布函数pnorm()混淆。
#在-10~10区间等分的 100个 数据集x
x <- seq(-10, 10, by = .1)
#创建一个均值是2.5,标准差是0.5正态分布 y
y <- dnorm(x, mean = 2.5, sd = 0.5)
#将 y 中的落在x数据集上的数据画出来
plot(x,y,col="red",pch=20)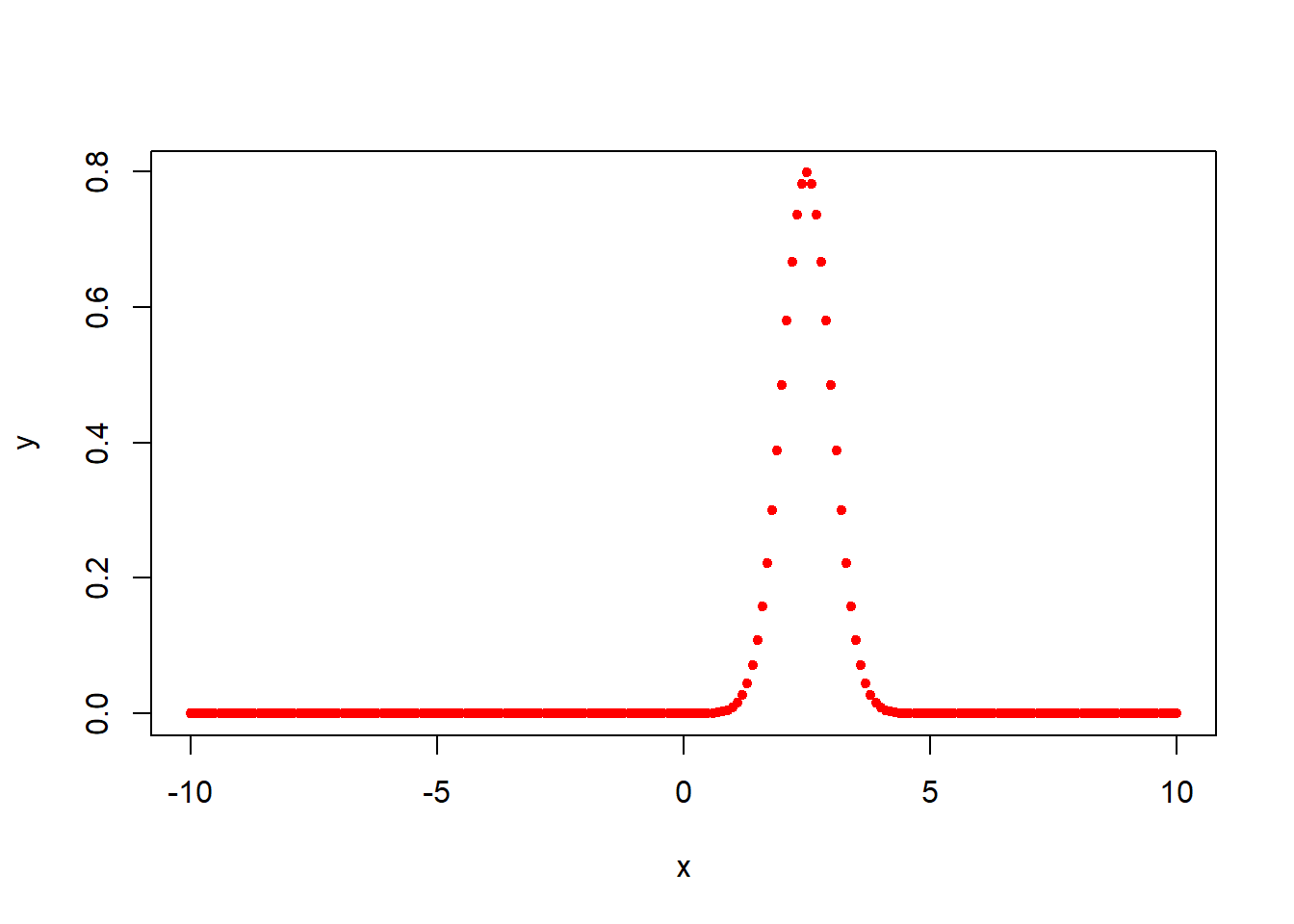
Figure 2.2: 概率密度函数示例
2.5.2 概率累积分布函数pnorm()
累积分布函数(Cumulative Distribution Function),R中即为pnorm(), 又叫分布函数,是概率密度函数的积分,能完整描述一个实随机变量X的概率分布,它给出一个正态分布中小于一个给定数字的累计概率(即指定定点的左边范围的曲线面积)。
#在-10~10区间等分的 40个 数据集x
x <- seq(-10, 10, by = .5)
#创建一个均值是2.5,标准差是0.5正态分布 y
y <- pnorm(x, mean = 2.5, sd = 0.5)
#将 y 中的落在x数据集上的累计概率画出来
plot(x,y,col="red",pch=20)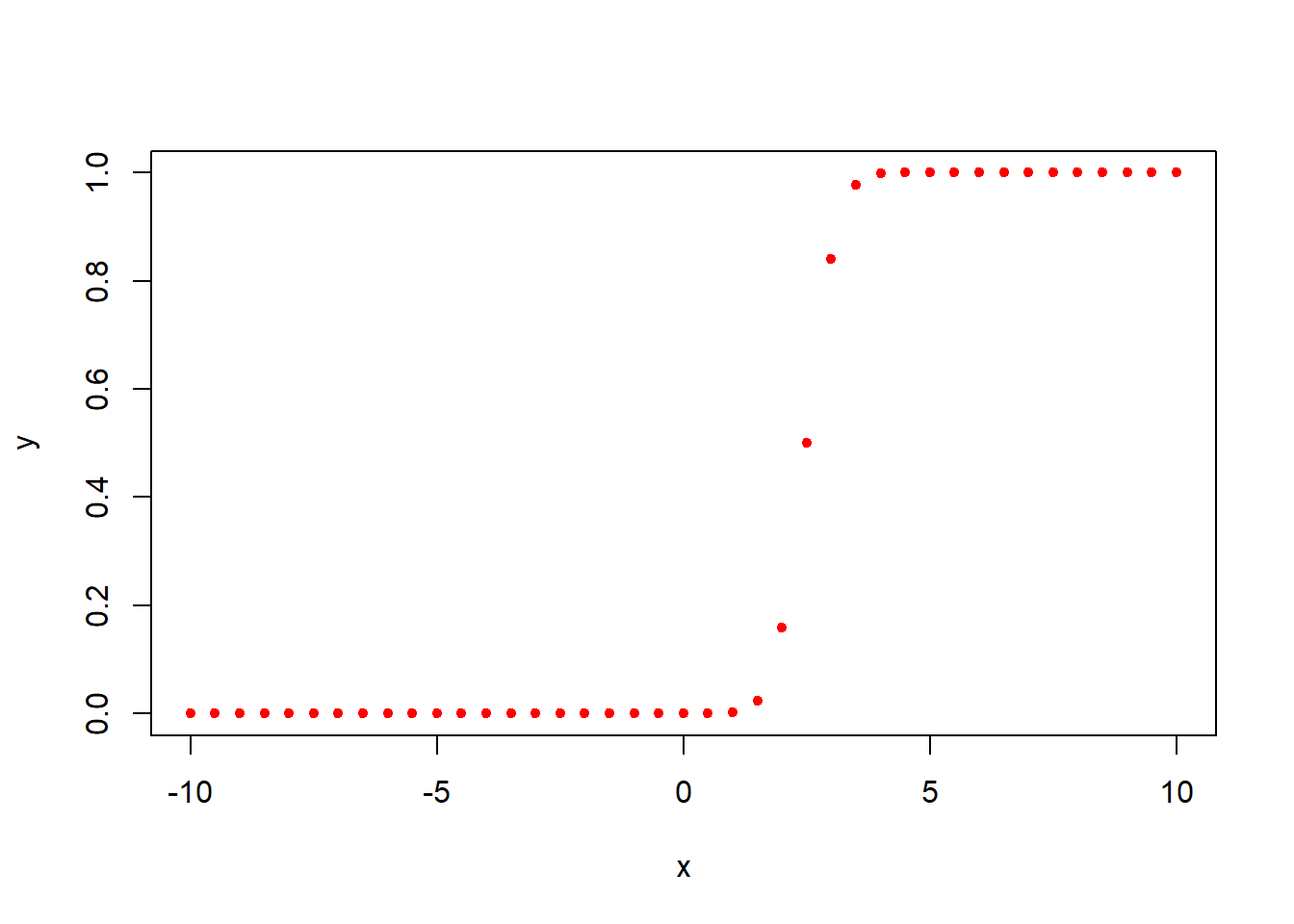
Figure 2.3: 累积分布函数示例
2.6 正态分布检验
许多计量资料的分析方法要求数据分布是正态或近似正态,因此对原始独立测定数据进行正态性检验是十分必要的。通过绘制数据的频数分布直方图来定性地判断数据分布正态性。
以下正态检验的资料整理自:
正态性检验主要有三类方法:
计算综合统计量 如动差法、夏皮罗-威尔克Shapiro-Wilk 法(W 检验) 、达戈斯提诺D′Agostino 法(D 检验) 、Shapiro-Francia 法(W′检验)。
正态分布的拟合优度检验
如皮尔逊χ2 检验 、对数似然比检验 、柯尔莫哥洛夫Kolmogorov-Smirov 法检验。
图示法(正态概率图Normal Probability plot)
如分位数图(Quantile Quantileplot ,简称QQ 图) 、百分位数(Percent Percent plot ,简称PP 图) 和稳定化概率图(Stablized Probability plot , 简称SP 图) 等。
统计软件中常用的正态性检验方法
用偏态系数和峰态系数检验数据正态性
偏态系数Sk,它用于检验不对称性;峰态系数Ku,它用于检验峰态。 S k= 0, K u= 0 时, 分布呈正态, S k> 0 时, 分布呈正偏态,S k < 0 时, 分布呈负偏态。适用条件:样本含量应大于200
用夏皮罗-威尔克(Shapiro-Wilk)法检验数据正态性 即W检验,1965 年提出,适用于样本含量n ≤50 时的正态性检;。
用达戈斯提诺(D′Agostino)法检验数据正态性 即D检验,1971提出,正态性D检验该方法效率高,是比较精确的正态检验法。
Shapiro-Francia 法 即W′检验,于1972 年提出,适用于50 < n < 100 时的正态性检验。
QQ图或PP图 散点聚集在固定直线的周围,可以认为数据资料近似服从正态分布
常用的规则:
SPSS 规定:当样本含量3 ≤n ≤5000 时,结果以Shapiro - Wilk (W 检验) 为难,当样本含量n > 5000 结果以Kolmogorov - Smirnov 为准。
SAS 规定:当样本含量n ≤2000 时,结果以Shapiro - Wilk (W 检验) 为准,当样本含量n >2000 时,结果以Kolmogorov - Smirnov (D 检验) 为准。
参考:
刘庆武,胡志艳,如何用SPSS、SAS 统计软件进行正态性检验,湘南学院学报(自然科学版),2005 朱红兵,何丽娟,在SPSS10.0 中进行数据资料正态性检验的方法,首都体育学院学报,2004
2.6.1 直方图
直方图显示了分布的分布范围和形状,因此它是评估正态性的一个很好的起点。本文开始测试的红细胞浓度遵循正态曲线,因此数据似乎遵循正态分布。
hist(RBC_v, right=FALSE,
breaks = breaks, labels =TRUE,
freq = FALSE, col = "#A8D6FF",
border = "white", ylim=c(0,1))
lines(density(RBC_v),col="red",lwd=2)
Figure 2.6: 正态分布检验与直方图
2.6.2 概率密度图
概率密度图图提供了关于数据是否服从正态分布的直观判断。它们类似于直方图,因为它们也允许分析分布的传播和形状。但是,它们是直方图的平滑版本。
maintxt<-paste("N=",length(RBC_v),",","Mean=",round(mean(RBC_v),3),",","Sd=",round(s,3))
plot(density(RBC_v),col="red",lwd=2,main = maintxt)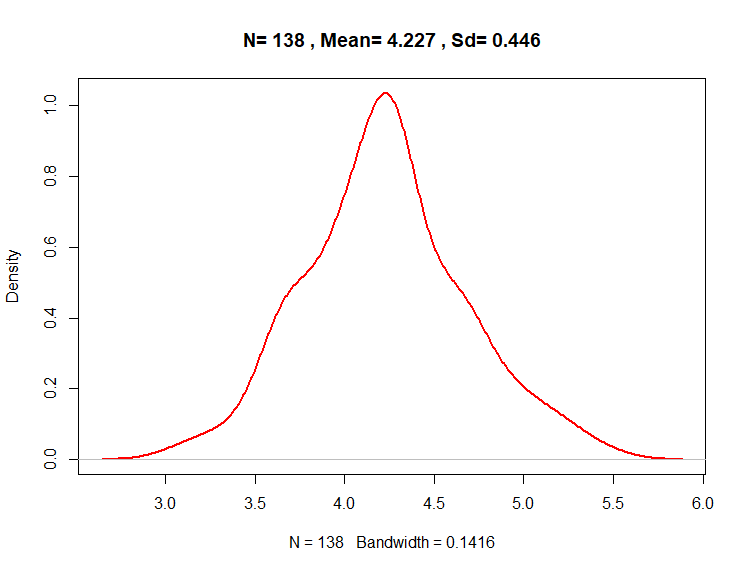
Figure 2.7: 正态分布检验与密度图
2.6.3 QQ-plot
有的数据从直方图和密度图很难检验正态性,因此建议用qq图来确证这些图。QQ-plot,又称正态图。在QQ-plots中, 我们只需要确定数据点是否沿着直线(有时也称为Henry’s line),而不是查看数据的扩散情况(如直方图和密度图)。 如果点靠近参考线并且在置信区间内,则认为满足了正态性假设。点与参考线之间的偏差越大,偏离置信区间越远, 满足正态条件的可能性就越小。这12个成年人的身高似乎服从正态分布,因为所有的点都在置信区间内。
如果qq图所示的非正态分布(系统地偏离参考线)时,通常第一步是对数据进行对数变换, 并重新检查对数变换后的数据是否正态分布。可以应用log()函数进行对数变换。
另外,qq图也是评估回归分析的残差是否服从正态分布的一种方便的方法。
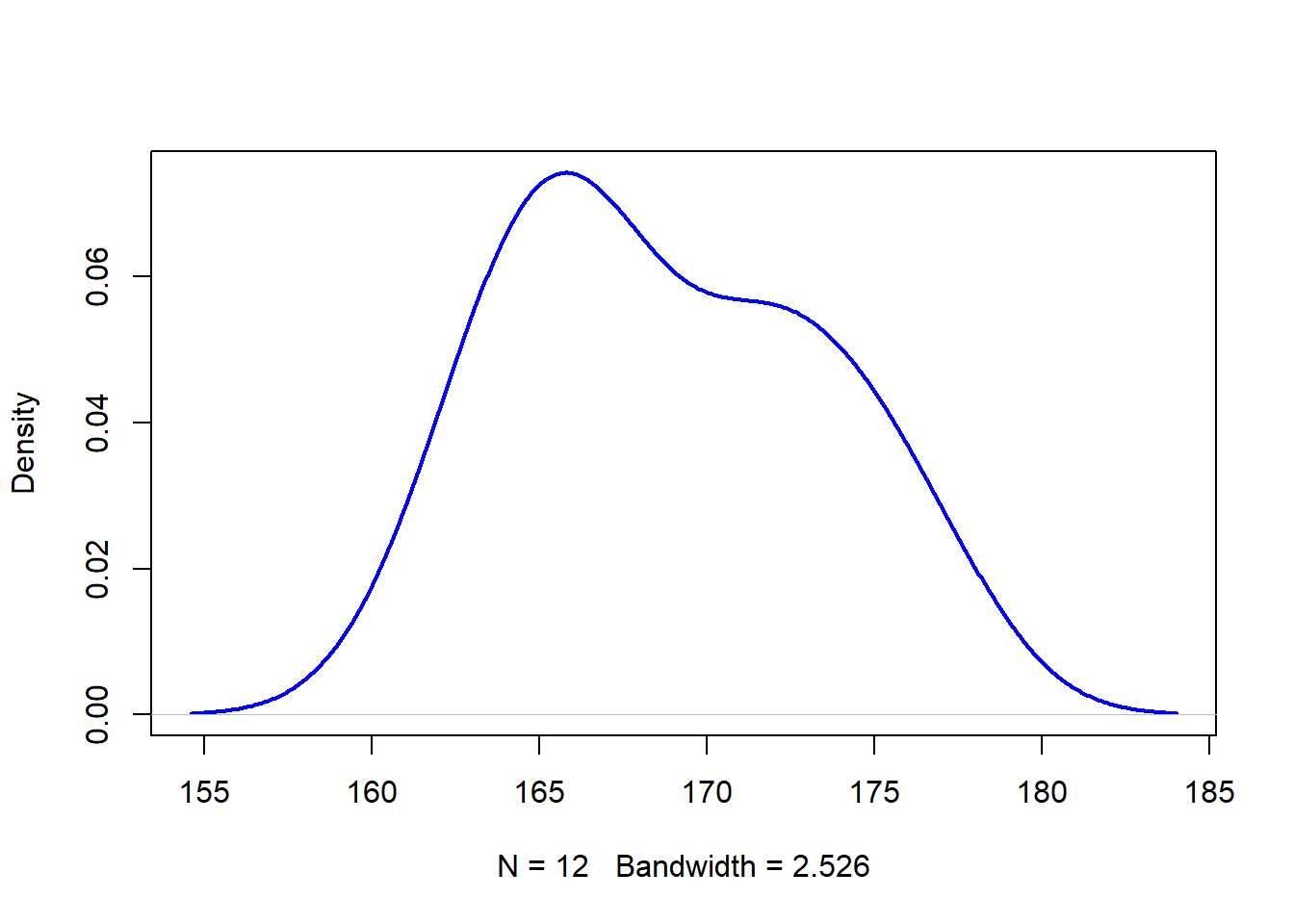
Figure 2.8: 难以判断正态分布的密度图
#qqPlot是car包中的函数,因此需要载入包,可以使用groups参数,同时对多组数据分别处理
library(car)
set.seed(42)
dat_hist <- data.frame( value = rnorm(12, mean = 165, sd = 5))
qqPlot(dat_hist$value)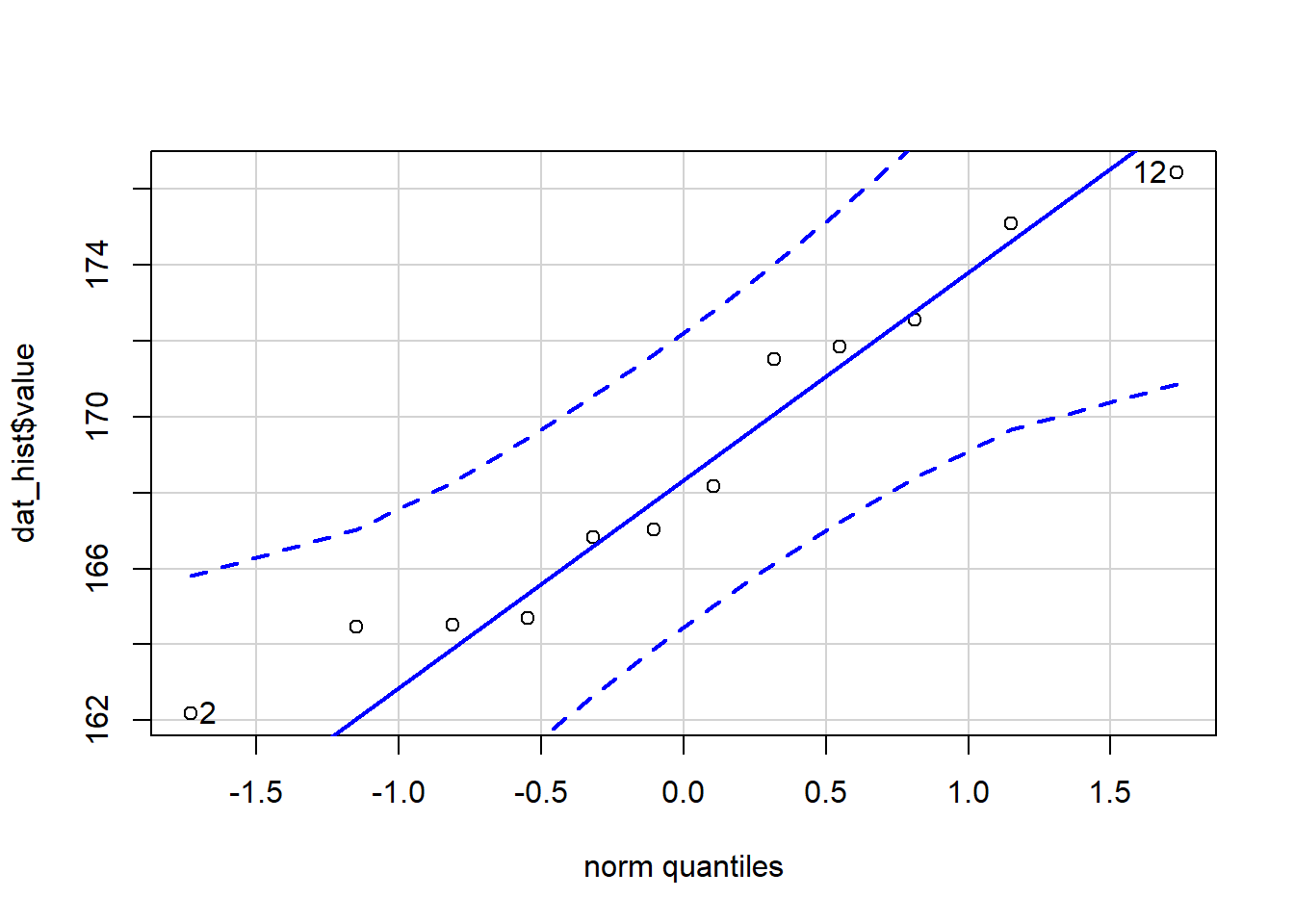
Figure 2.9: 正态分布检验与QQ-plot (1)
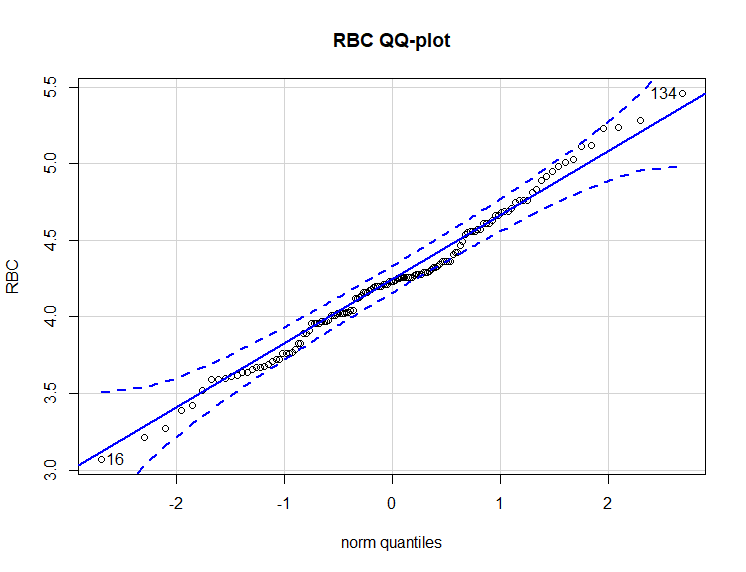
Figure 2.10: 正态分布检验与QQ-plot (2)
2.6.4 正态检验
上述3种方法是对常态的目视检查。然而,目测有时可能不可靠,因此也有可能通过统计检验正式检验数据是否服从正态分布。 这些正态性检验将数据的分布与正态分布进行比较,以评估观察结果是否显示出偏离正态性的重要偏差。 最常用的两种正态性检验是Shapiro-Wilk检验(K检验)和Kolmogorov-Smirnov检验(D检验)。两种测试都有相同的假设,即:
H0 : 数据服从正态分布
H1 : 数据不服从正态分布
正态性检验推荐使用Shapiro-Wilk检验,因为它比Kolmogorov-Smirnov检验提供更好的效用。 在R中,正态性的Shapiro-Wilk检验可以通过函数shapiro.test()进行。
set.seed(42)
dat_hist <- data.frame( value = rnorm(12, mean = 165, sd = 5))
shapiro.test(dat_hist$value)
## Shapiro-Wilk normality test
##
## data: dat_hist$value
## W = 0.9, p-value = 0.5从输出中,我们看到p-value>0.05意味着我们不拒绝数据服从正态分布的原假设。 该检验与qq图的方向相同,qq图与正态性没有显著偏差(因为所有点都在置信区间内)。
shapiro.test(RBC_v)
## Shapiro-Wilk normality test
##
## data: as.numeric(RBC_v)
## W = 1, p-value = 0.4对RBC数据同样的结果。
注意的是,在实践中,正态检验通常被认为过于保守,因为对于大样本(n>50),对正态条件的一个 小偏差可能会导致违反正态判断的条件。由于正态性检验是一种假设检验,所以随着样本量的增加,其检测较小差 异的能力也会增加。因此,随着观测数的增加,Shapiro-Wilk检验变得非常敏感,甚至对正态性的一个 微小偏差也非常敏感。所以,根据正态性检验,数据不服从正态分布,尽管偏离正态分布的情况可以忽略不计,但数据 实际上服从正态分布。因此,通常情况下,正态性条件的验证是基于本文所介绍的所有方法的组合,即目视检验 (使用直方图和q-q图)和正式化检验(例如使用shapio-wilk检验)。
R中还有其他一些正态检验的方法,比如 ks.test() 函数实现Kolmogorov-Smirnov Test(D检验), 是对经验分布的拟合检验,检验的是经验分布函数和假设总体分布函数的差异,适应于大样本(n>5000)。 另外有一些package包含了丰富的检验函数,比如fBasics,nortest等。