第三章 总体均数的估计与假设检验
日期: 2020-11-14 作者:wxhyihuan
3.1 推论统计
推论统计(或称统计推断,Statistical inference),指统计学中,研究如何根据样本数据去推断总体数量特征的方法。 它是在对样本数据进行描述的基础上,对统计总体的未知数量特征做出以概率形式表述的推断。更概括地说, 是在一段有限的时间内,通过对一个随机过程的观察来进行推断的。统计学中,统计推断与描述统计相对应。
推论统计(Statistical inferences)是借助抽样调查,从局部推断总体,以对不肯定的事物做出决策的一种统计。 有总体参数估计与假设检验两种。前者以一次性抽样实验为依据,对整个总体的某个数字特征做出估计。后者则是对 某种假设进行检验,根据计算结果推断所做的假设是否可以接受。如平均数、标准差、相关系数、回归系数等特征的 总体估计及差异显著性检验。推断统计的理论基础是概率论,它更多地需要借助抽样理论与方法。
3.1.1 参数估计与假设检验
参数估计背后的思想是通过对从总体中抽取的样本进行统计显著性检验(如t检验),为研究人员提供关于总体的统计推断。 最常用的就是t检验,其参数检验是基于W.S.Gosset的t统计量,该统计数据假设变量来自正态总体。t检验统计量中的总体均值是已知的。 这种分布称为t分布,其形状与正态分布类似,即钟形曲线。t检验用于检验那些样本小于30的样本比正态分布要好, 在大样本上做的和正态分布一样好。
假设检验(Hypothesis test)过去也叫做显著性检验(Significance test),是利用小概率反证法思想,从问题的对立面(\(H_0\))出发, 间接判断解决问题(\(H_1\))是否成立。即在假设\(H_0\)成立的条件下,计算检验统计量(Test static),然后根据\(P\)值(P-value)来判断。
3.1.2 统计量与标准误
样本是总体的代表和反映,也是统计推断的依据,为了对总体的分布或数字特征进行各种统计推断,还需要对样本作加工处理, 把样本中应关心的事物和信息集中起来,针对不同的问题构造出样本的不同函数(如均值,方差,极差,标准差,中位数,众数等),这种样本的函数我们称其为统计量。
样本统计量的标准差即为标准误(Stand error,SE),反映了抽样的统计量的离散程度或误差大小。如样本均数的标准差也称为均数标准误 (Stand error of mean, SEM),反映了样本均数的离散程度。
3.2 t 分布
若某一随机变量X服从总体均数为μ,总体标标准差为σ的正态分布\(N(μ,σ^2)\),通过u变换(也称Z变换)可将一般正态分布 转化为标准正态分布\(N(0,1^2)\),即u分布(也称Z分布)。同理,若样本含量为n的样本均数 \(\bar{X}\) 服从总体均数为μ, 总体标准差为\(σ_\bar{x}\)的正态分布\(N(μ,σ_\bar{x}^2)\),则可通过u变换(\(\frac{\bar{X}-μ}{σ_\bar{x}}\))将其转换为标准正态分布。 但是,实际中总体标准差( \(σ_\bar{x}\) )是未知的,所以用均数标准误的估计值(\(S_\bar{x}=\frac{S}{\sqrt{n}}\),其中S为样本标准差)代替, 这就使得(\(\frac{\bar{X}-μ}{S_\bar{x}}\))不再是标准正态分布,而是服从t-分布(t-distribution), 即: \[t=\frac{\bar{X}-μ}{S_\bar{x}}=\frac{\bar{X}-μ}{\frac{S}{\sqrt{n}}}\]
t-分布 对应的概率密度函数是: \[f(x)=\frac{\Gamma(\frac{v+1}{2})}{\sqrt{v\pi}\Gamma(\frac{v}{2})}{\left(1+\frac{x^2}{v}\right)^\frac{-v+1}{2}}\]
其中\(\Gamma\)是伽马函数(Gamma function),\(v\)是自由度(Degree of freedom,df)。
自由度(df)在数学上只能自由取值的变量个数,如\(X+Y+Z=1\),有3个变量,但是能够自由取值的自由两个,故其自由度\(v=2\)。 在统计学中,自由度计算方式为: \[v=n-m\]
其中n为计算某一统计量是用到的数据个数,m为计算该统计量是用到的其他独立统计量个数。比如根据肿瘤位置,大小,组织活检,生化指标 判断肿瘤的类型是A,也可能是B,这里有\(n=4\)个独立的信息,和\(m=2\)个估计,所以自由度就是\(df=4-2=2\)。一般的希望估计(推测)的越可靠, 当然是自由度越大越好了。
t分布是一簇曲线,其形态变化与n(即其自由度)大小有关。自由度n越小,t分布曲线越低平;自由度n越大,t分布曲线越接近标准正态分布(u分布) 曲线,当自由度无限大时,t分布就成了正态分布。
3.2.1 概率密度函数dt()
R中,t分布的概率密度函数为dt(),它可以给出了指定均值和标准差下每个点的概率分布的高度, 越高就代表着这个点/区间的概率越密集(大)。从下免得概率密度图见,当df=20时,t分布曲线已经非常接近标准正态曲线了。
curve(dnorm(x),xlim=c(-5,5),ylim=c(0,0.45),ylab="Student's t Density",col="red",lty=1,lwd=2)
abline(v=0,lwd=1,col="black")
curve(dt(x,1),col="green",lty=2,add=TRUE)
curve(dt(x,2),col="brown",lty=3,add=TRUE)
curve(dt(x,5),col="blue",lty=4,add=TRUE)
curve(dt(x,20),col="dark green",lty=5,add=TRUE)
legend(2,0.38,c("normal","df=1","df=2","df=5","df=20"),
col=c("red","green","brown","blue","dark green"),lty=1:5)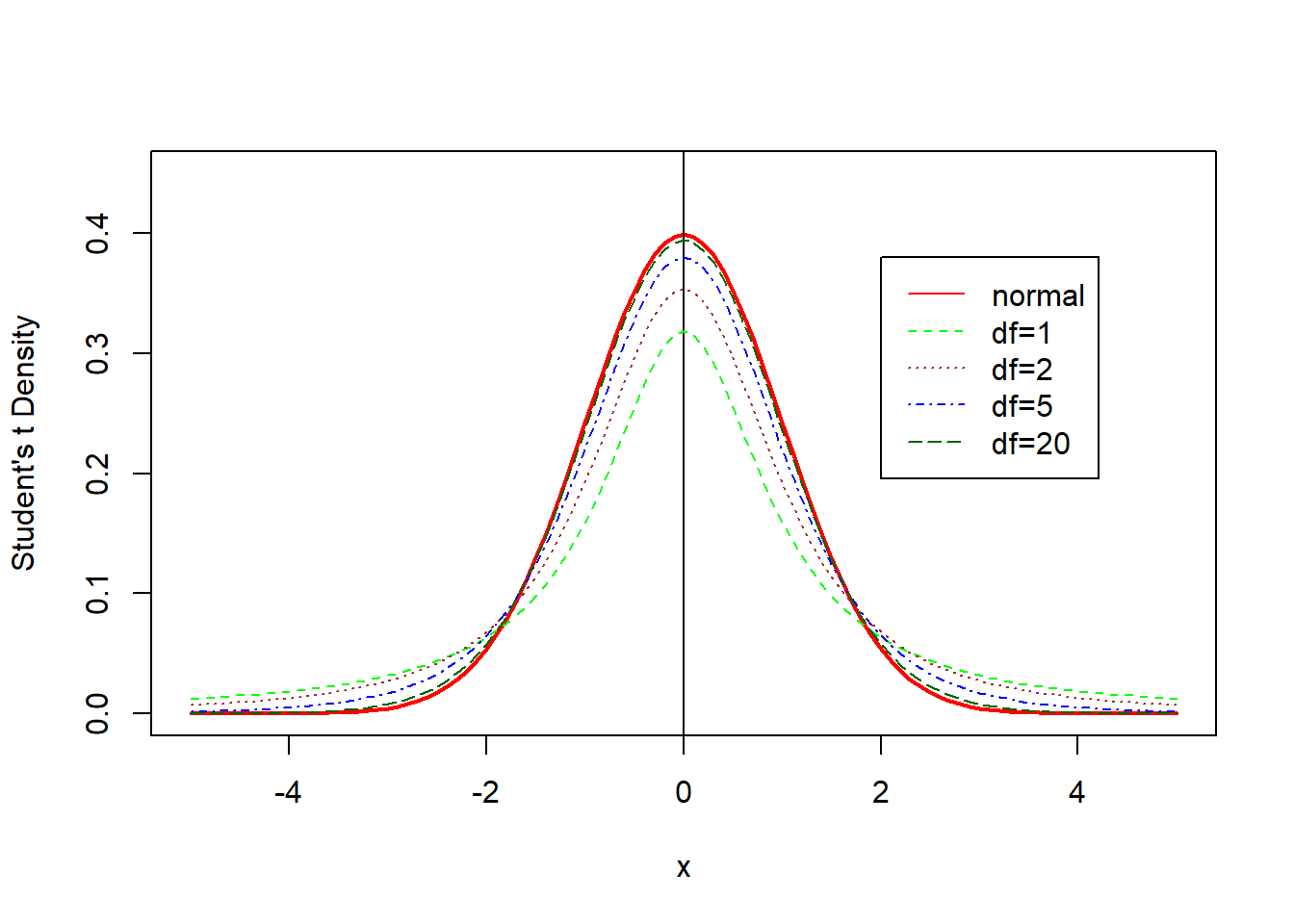
Figure 3.1: t分布检验与正态分布
3.2.2 概率累积分布函数pt()
同所有连续数值型分布一样,统计应用中最关心的是分布曲线下的尾部面积(即概率\(P\)或α)与横轴间的关系。 R中即为pt(),它给出一个正态分布中小于一个给定数字的累计概率(即指定定点的左边范围的曲线面积)。 一侧尾部面积称为单侧概率或单尾概率(one-tailed probability,\(t_{α,v}\)),两侧尾部的面积之和称为双侧概率或双尾概率 (two-tailes probability,\(t_{α/2,v}\))。
单侧的p值计算
双侧的p值计算
## 双侧 p-value
## 两边对称单侧相加
pt(q=1.9, df=5, lower.tail = F) + pt(q=-1.9, df=5, lower.tail = T)
## 0.1158633
## 单侧p值*2,对称性
pt(q=1.9, df=5, lower.tail = F)*2
## 0.1158633# x坐标序列向量
x_pt <- seq(- 5, 5, by = 0.1)
# 用pt()函数获取df=5的x累计密度值
y_pt <- pt(x_pt, df = 5)
# Plotting
plot(y_pt, type = "l", main = "t-distribution cumulative function example", las=1, col="red",lwd=2)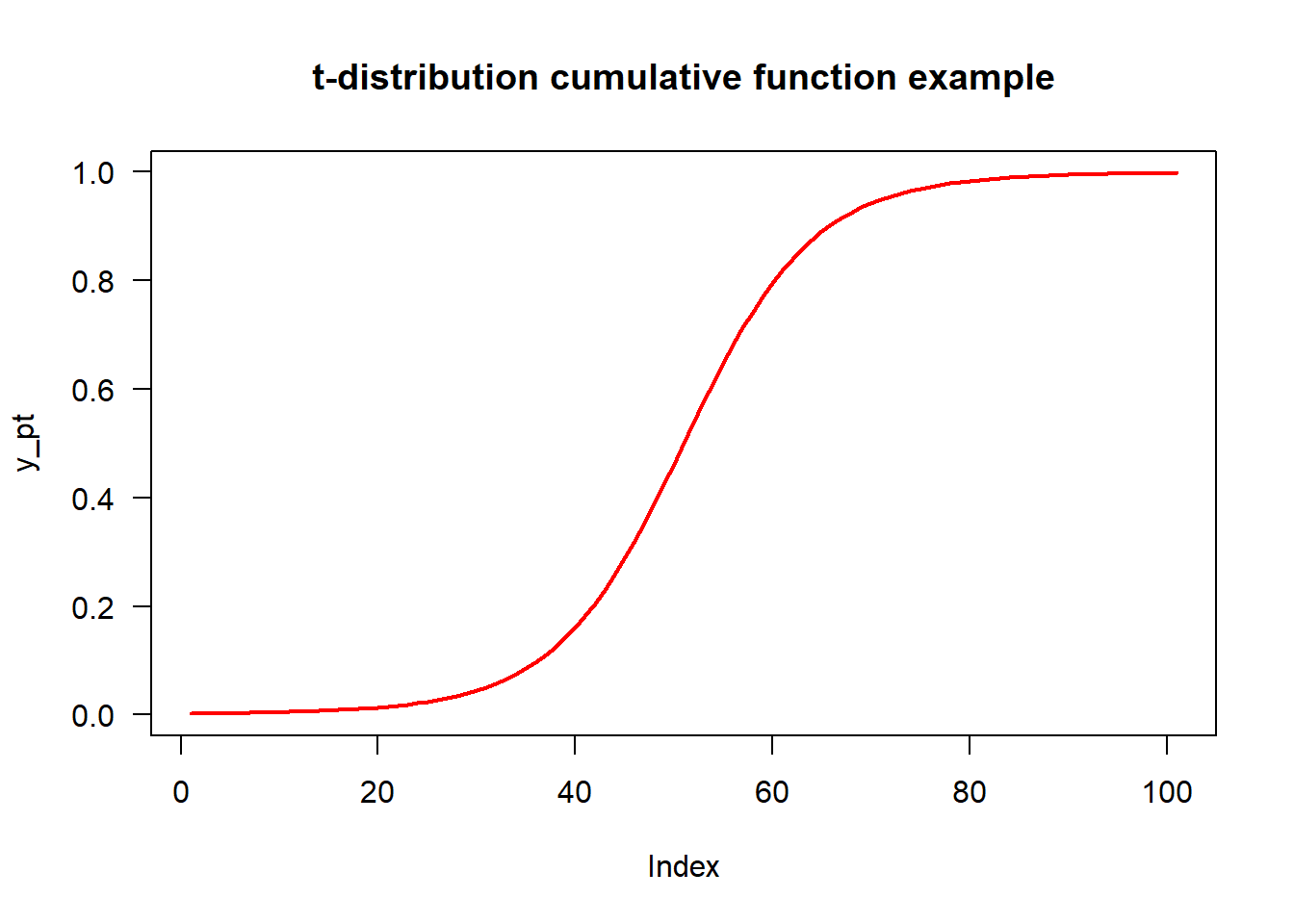
Figure 3.2: t分布的pt()
3.2.3 求置信区间的qt()
t分布分位函数,R中即为qt(),它可以给出一个累积分布概率达到指定值的数字。
# find t for 95% confidence interval value of t with 2.5% in each tail
qt(p=0.025, df = 5, lower.tail = T)
## -2.570582# Specifyin the x-values
x_qt <- seq(0.1, by = 0.01)
# Applying the qt() function
y_qt <- qt(x_qt, df = 5)
# Plotting
plot(y_qt, main = "t quantile function example", las = 1,col="red",lwd=2)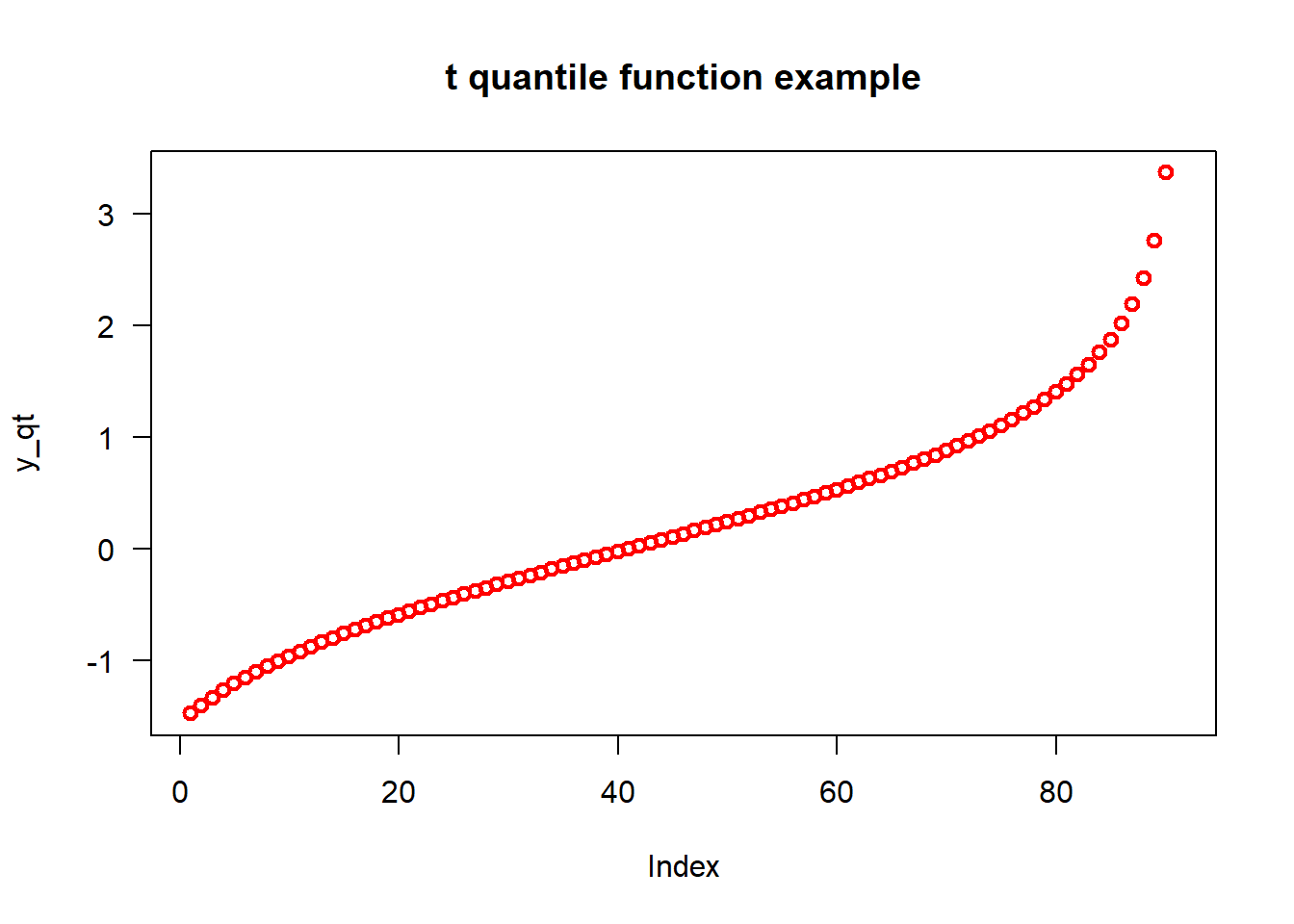
Figure 3.3: t分布的qt()
3.2.4 指定t分布函数rt()
rt()函数用于生成符合指定观测数目和自由度的t分布的随机数,默认是。
set.seed(61)
# Setting sample size
n <- 10000
# Using rt() to drawing N log normally distributed values
y_rt <- rt(n, df = 5)
# Plotting a histogram of y_rt
hist(y_rt, breaks = 100, main = "Randomly drawn t density", freq=FALSE,
col="#A8D6FF",xlim=c(-10,10),ylim=c(0,0.4))
lines(density(y_rt), col="red", lwd=2)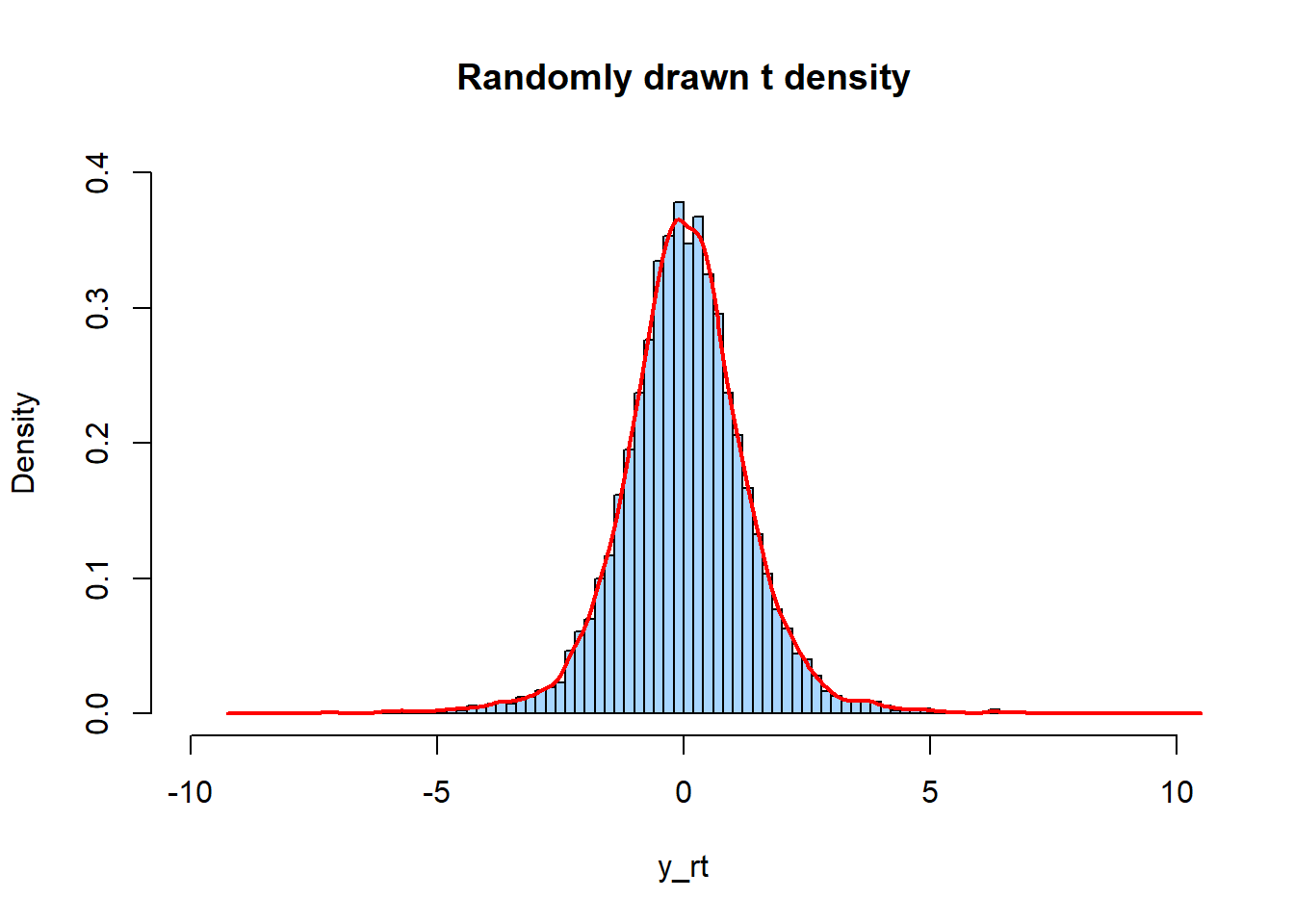
Figure 3.4: t分布的rt()
3.2.5 参数估计
参数估计是指用样本参数(统计量)推断总体参数,有点值估计(Point estimation)和区间估计(Interval estimation)两种。
点值估计就是用相应样本统计量简单直接的作为总体参数的估计值,如用\(\bar{X}\)估计\(μ\),用\(S\)估计\(\sigma\)。 案例 某开发团队对开发App进行了改版迭代,现在有以下两个版本 + 版本1: 首页为一屏课程列表 + 版本2:首页为信息流 如果我们想区分两个版本,哪个版本用户更喜欢,转化率会更高。我们就需要对总体(全部用户)进行评估, 但是并不是全部存量用户都会访问App,并且每天还会新增很多用户,所以我们无法对总体(全部用户)进行评估, 我们只能从总体的用户中随机抽取样本(访问App)的用户进行分析,用样本数据表现情况来充当总体数据表现情况, 以此来评估哪个版本转化率更高。
区间估计是按预先给定概率(\(1-\alpha\)),通过特定的分布函数来计算确定的未知总体参数的范围。该范围称为参数的可信区间或
置信区间(Confidence bound/Confidence interval,CI),预先设定的概率\((1-\alpha)\)称为可信度或置信度(Confidence level), 通常取值95%或99%,如果特殊说明,一般是双侧95%。可信区间是两个字确定的范围,其中较小的值称为可信下限(Lower limit,L), 较大值称为可行上限(Upper limit,U),表示为开区间(L,U)。
3.2.6 假设检验
从总体中随机抽样,由样本信息推断总体特征,除前面所讲的参数估计方法外,在实际应用中还会遇到这样的问题:某一样本均数是 否来自于某已知数的总体?两个不同样本均数是否来自均数不相等的总体等要回答这类问题,除可用前面参数估计的方法外, 更多的是用统计推断的另一方面——假设检验 (Hypothesis test)来解决,比如下面两个案例:
案例3-5 某医生测量了36名从事铅作业男性工人的血红蛋白含量,算得其均数为130.83 g/L,标准差为25.74 g/L。问: 从事铅作业男性工人的血红蛋白含量均数(μ)是否不等于正常成年男性的均数 140 g/L (\(μ_0\))?
针对问题一,其目的是判断是否\(μ≠μ_0\),以给出的条件看\(\bar{X}\)与已知总体均数\(μ_0\)不相等, 造成两者不等的原因有两种情况:
①从事前作业的样品血红含量确实与正常样品不一样,即非同一总体(\(μ≠μ_0\));
②因为抽样误差导致的两者不相等,两者实际为同一总体(\(μ=μ_0\))。
要判断第一种情况很困难,但可以利用反正思想从第②种出发,间接判断是否\(μ≠μ_0\):假设\(μ=μ_0\),判断由于抽样误 差造成不相等的可能行有多大?
如果\(\bar{X}\)与\(μ_0\)接近,其差别可用抽样误差解释,即可认为\(\bar{X}\)来自\(μ_0\)总体。反之,相差很大, 则难以说明\(\bar{X}\)来自\(μ_0\)总体。那么,\(\bar{X}\)与\(μ_0\)相差多大算是抽样误差造成的呢?若假设(\(μ=μ_0\))成立, 且样本总体符合正态分布(本案例未进行进一步判断,针对实际数据情况,做假设检验前应该情况进行分布判断或转换处理,选择合适的检验方法), 则可以用t分布(\(t=\frac{\bar{X}-μ}{S/\sqrt{n}}\))或正态分布(\(u=\frac{\bar{X}-μ}{\sigma/\sqrt{n}}\)) 来计算t值或者u值。然后根据t值或u值求得P值(P-value)来判断。如果\(\bar{X}\)与\(μ_0\)相差很大,那么t或者u值就很大, 对应P值就小;当P值小于或等于预先规定的概率值α(如0.05)时,则为小概率事件,这有理由怀疑原假设(\(μ=μ_0\))可能不成立, 认为其对立面(\(μ≠μ_0\))成立,该结论的正确性冒着5%的错误风险。
3.2.6.1 假设检验的步骤
1. 建立检验假设,确定检验水准
有两种假设,即\(H_0\)和\(H_1\):
(1)\(μ=μ_0\),即检验假设(Hypothsis under test),称为无效假设,也叫做零假设,原假设(Null hypothsis), 用\(H_0\)表示,原假设的设置一般为:等于=、大于等于>=、小于等于<=。
(2)\(μ≠μ_0\),即备择假设(Alternative test),也称为对立假设,用\(H_1\)表示,备择假设的设置一般为:不等于、大于>、小于<。
对检验假设,需要注意以下几点
①. 检验假设针对的是总体,而不是样本;
②. \(H_0\)和\(H_1\)是相互联系,对你的假设,后面的统计推断的结论是根据\(H_0\)和\(H_1\)作出的,二者缺一不可;
③. \(H_0\)为无效假设,其假定通常是:某两个(或多个)总体的参数相等,或两个总体参数之差为0,或某资料服从某一特定分布 (如正态分布,Poisson分布等),或\(\cdots\cdots\)无效等;
④. \(H_1\)的内容直接反映呢检验的单双侧。比如案例3-5中,如果\(μ≠μ_0\),则此检验为双侧检验(Two-sided test);若\(H_1\)为 \(μ>μ_0\)或\(μ小于μ_0\),则检验为单侧检验(One-sided test),不仅考虑差异,而且考虑差异的方向。单双侧检验的确定, 首先需要根据专业知识,其次是根据需要解决的问题来确定。
- 检验水准α,也称显著性水准(Singnificance level),它属于Ⅰ型错误的范畴,是预先规定的概率值,它确定了 小概率事件的标准。实际中常取\(\alpha=0.05\),可根据不同研究目的给予不同设置。
第I类错误和第Ⅱ类错误
为什么统计者想要拒绝的假设放在原假设呢?因为原假设备被拒绝如果出错的话,只能犯第I类错误,而犯第I类错误的概率已经 被规定的显著性水平所控制。
我们通过样本数据来判断总体参数的假设是否成立,但样本是随机抽取的,因而有可能出现小概率的错误。这种小概率错误有两种, 一种是第I类错误(也叫弃真错误,Type Ⅰ error),另一种是第Ⅱ类错误(也叫取伪错误,Type Ⅱ error)。
第I类错误或α错误:它是指\(H_0\)实际上是真的,但通过假设检验后,拒绝了原假设。这是错误的, 我们拒绝了真实的原假设,所以叫弃真错误,这个错误的概率我们记为α,也就是检验水准。在假设检验之前我们会规定这个概率的大小,从而控制检验功效。
第II类错误或β错误:它是指\(H_0\)实际上假的,但通过假设检验显示,不拒绝原假设。这也是错误的,我们接受的原假设实际上是假的,所以叫取伪错误,这个错误的概率我们记为β。
1-β称为检验效能(Power of test),过去称把握度。其意义为当两总体确有差异,按规定检验水准α所能发现该差异的能力。 和B一样,1-β只取单尾。如1-β = 0.90,意味着若两总体确有差别,则理论上平均每100 次检验中,有90 次能够得出差异 有统计学意义的结论。从图中可看出,α愈小,B愈大; 反之α愈大,β愈小。若要同时减小型错误a以及1型错误B,唯一的方法 就是增加样本含量n。若重点是减少第I类错误α(如一般的假设检验),一般取 a=0.05。 若重点是减少第II类错误(如方差齐性检验,正态性检验或想用一种方法代替另一种方法的检验等), 一般取 a = 0.10 或0.20,甚至更高。注意:拒绝\(H_0\),只可能犯第I类错误,不可能第II类错误。 不拒绝\(H_0\),只可能犯第II类错误,不可能犯第I类错误。
因此,原假设一般都是想要拒绝的假设,如果原假设备被错误拒绝的话,只能犯弃真错误,而犯弃真错误的概率可以用 检验水准\(\alpha\)控制,对统计者来说更容易控制,将错误影响降到最小。
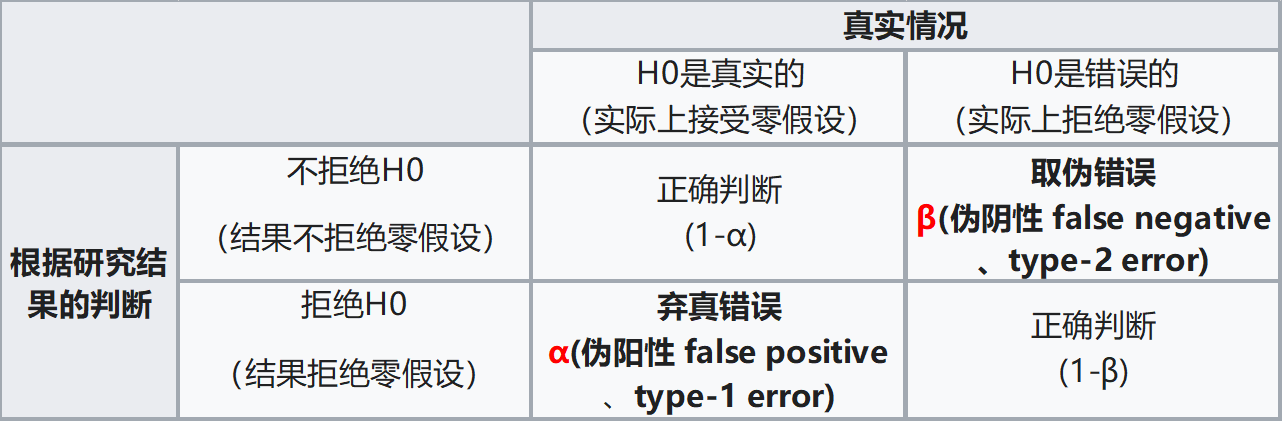
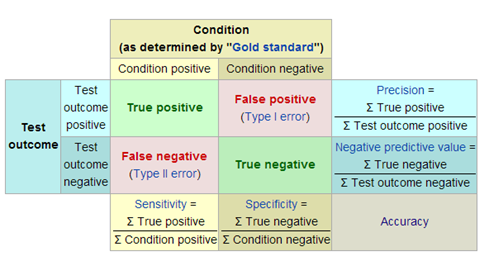
Figure 3.5: 第I类错误和第Ⅱ类错误
2. 计算检验统计量
应该根据变量或资料的类型,设计方案,统计推断的目的,方法的适用条件等选择检验统计量。如成组设计两样本均数的比较可根据 资料特点选用检验统计量\(t,t',u\)等;而成组设计两样本翻查的比较一般先用检验统计量\(F\)。计算这些统计量都是在\(H_0\)(\(μ=μ_0\)), 即假定是比较的数据来自同一总体的成立前提下算出来的。
- 有的检验方法无需计算检验统计量,如四个表资料。
3. 确定\(P\)值,做出推断结论
\(P\)的含义是指从\(H_0\)规定的总体中随机抽样,抽得等于及大于或(和)等于及小于现有样本获得的统计量(如\(t\)、\(u\)等)值的概率。 根据获得的时候概率\(P\)值,与之相规定的检验水准\(\alpha\)进行比较,看其是否为小概率事件二得出结论。 一般来说,推断结论应包含统计结论和专业结论两部分,前者只说明差异是否有统计学意义(Statistical Significance), 后者这是结合专业内容给出的结论解释:
\(P\leq\alpha\),则发生小概率事件,拒绝\(H_0\),接受\(H_1\),差异具有统计学意义。
- \(P>\alpha\),则不拒绝\(H_0\),差异无统计学意义。\(P>\alpha\)也成为“无显著性”(Non-Significance,NS),即阴性结果。
注意的是:
① 不拒绝\(H_0\)不等于接受\(H_0\),虽然在逻辑上否定的否定为肯定,但在统计上是按照检验水准\(\alpha\)不拒绝\(H_0\),若接受\(H_0\) 则因为范Ⅱ型错误的概率\(\beta\)未知而证据不足,以决策的观点,之客认为展示有条件“接受”,或“阴性待诊”。
② 作结论是,对\(H_0\)只能说拒绝(Reject)或者不拒绝(Not reject)\(H_0\)。而对\(H_1\)只能说接受\(H_1\),其他说法俱不妥当。
③ 差异有无统计学意义,是对样本统计量和总体参数(如\(\bar{X}\)和\(μ_0\)),或两个,多个样本统计量(如\(\bar{X_1}\)和\(\bar{X_2}\))而言, 对推断两个总体参数(如\(μ_1\)和\(μ_0\),或\(μ_1\)和\(μ_2\))而言,只能说是否相等。
拒绝域 拒绝域是由显著性水平围成的区域。拒绝域的功能主要用来判断假设检验是否拒绝原假设的。如果样本观测计算出来的 检验统计量(如t,u值)的具体数值落在拒绝域内,就拒绝原假设,否则不拒绝原假设。给定检验水准\(\alpha\)后,查表就可以得到具体 临界值,将检验统计量与临界值进行比较,判断是否拒绝原假设。
3.3 t 检验的分类及应用
连续性数值变量资料在假设检验,最简单,常用的方法就是t检验(t-test/Student’s t-test),实际应用时, 理清各种检验方法的用途和使用条件及注意事项。 参数检验用于在假设检验中进行具有统计意义的检验。
3.3.1 t检验与Z检验
当\(\sigma\)未知且样本量n较小时(如n<60),理论上要求t检验的样本随机抽取自正态分布的总体;如果是独立两小样本量的均数比较,还要求 多对应的两总体的方差相等(\(\sigma_1^2=\sigma_2^2\))。即方差齐性。在实际应用中,路与上述条件有略偏离,对结果影响不大。当样本含量n 较大时,t值近似u值,即可适用正态分布的u检验(或Z检验)。
如果两独立样本的方差不相等(方差不齐),可采用数据变换(如两样本几何均数的t检验,就是将原始数据对数转换后进行t检验)处理, 或采用近似t检验(Separate variance estimation t-test),即t‘检验或秩转换的非参数检验,比如常用的Cochran&Cox法和Satterthwaite法两种,还有Welch法。
t检验基本上有三种类型:
单样本t检验(One sample/gourp t-test)
配对样本t检验(Paired/matched t-test)
两种独立样本t检验(Two sample/gourp t-test)
R的stats包提供了t.test(),可以用于各种t检验,如果只提供一组数据,则进行单样本t检验,如果提供两组数据, 则进行两样本t检验,主要的相关的参数是:
- paired参数,TRUE则进行配对t检验,FALSE 则进行两独立样本t检验。
- var.equal参数,对于两独立样本t检验,还要注意方差是否齐性,TRUE则进行经典方法,FALSE则采用近似t检验, 将数据取对数处理后进行t检验,t.test()中是采用Welch t检验。
- alternative参数,用来指定检验方式,默认是双侧检验(“two.sided”),还可以是左侧检验(“less”)和右侧检验(“greater”)。
t.test()为什么用Welch t检验
配对数据我们可以把配对信息扔了,放在一起做两独立样本t检验;当然还是成对T检验好,比如病人在使用某药 物前后的指标,如果不用配对信息,则病人之间的 variance 也混进去,方差估计会大一些,使得t检验的检验效能减弱。
方差齐性样本数据,理论上我们也可以把它当做不齐的样本用t’方法处理,但是用经典方法可以检验出更小的差别。 所以如果不确定方差齐性与否的情况下(最好时进行方差齐性检验),就用Welch t检验。因为与经典方法相比, Welch t检验的自由度会比方差齐性的经典方法要小,根据t分布特征,自由度越小,中心越平, 而尾巴越长,要观察到同样一个t值,自由度越小所计算出来的p值会越大,换句话说,自由度越小,t检验就越保守。
在方差非齐性的处理方法中,Welch 法检验又可以给出相对较高的自由度,因此t.tes()默认使用Welch t 检验的原因估计就是因为它较为保守。
3.3.2 单样本t检验
单样本t检验(One sample/gourp t-test)即已知样本均数\(\bar{X}\)(代表未知总体均数\(μ\))与已知总体\(μ_0\)的比较。比如 使用《医学统计学》中的 案例3-5 的数据在R中进行单样本t检验测试。
#使用memic包读取spss的数据格式
#install.packages('memisc')
library("memisc")
#读取数据
home_sav<-spss.system.file("ExampleData/SavData4MedSta/Exam03-05.sav")
#将数据形式转换为数据框
home_df<-as.data.frame(as.data.set(home_sav))
#直接使用t.test()进行计算
t.test(home_df$hb, mu=140)
## One Sample t-test
##
## data: bfc_df
## t = -2.1367, df = 35, p-value = 0.03969
## alternative hypothesis: true mean is not equal to 140
## 95 percent confidence interval:
## 122.1238 139.5428
## sample estimates:
## mean of x
## 130.8333
#左侧检验
t.test(home_df$hb, mu=140, alternative = "less")
#右侧检验
t.test(home_df$hb, mu=140, alternative = "greater")
#直接计算出t值后,使用pt函数计算p值的方式
t.value <- mean(home_df$hb - 140) /
sd(home_df$hb) * sqrt(nrow(home_df))
#-2.136668
#双侧检验,概率值乘以2
p.value <- pt(t.value,
df=nrow(home_df)-1,
lower.tail=T)*2
## [1] 0.03969288计算显示\(P=0.03969288<\alpha=0.05\),可以认为一次抽样发生了小概率事件,因此拒绝原假设\(H_0\), 接受\(H_1\),差异有统计意义;结合案例数据意义,可以认为从事铅作业的工人的平均血红蛋白含量低于 (因为给出样本均值是小于总体均值的)正常值。
我们还可以通过绘制拒绝域和t值落点,更直观的发现t值落在左侧和右侧的拒绝域内的。
#l使用scales包中alpha函数改变颜色透明度
library("scales")
t.value<--2.136668
df=35
x <- seq(-5,5,by=0.01)
y <- dt(x,df=df)
#右侧p值0.95对应的t值
right <- qt(0.95,df=df)
#左p值0.05对应的t值
left <- qt(0.05,df=df,lower.tail=T)
#绘制密度曲线
plot(x,y,type="l",xaxt="n",ylab="Probabilityy",
xlab=expression(paste('Assumed Distribution of ',bar(x))),
axes=FALSE,ylim=c(0,max(y)*1.1),xlim=c(min(x),max(x)),
frame.plot=FALSE)
#添加坐标轴
axis(1,at=c(-5,left,right,0,5),
pos = c(0,0),
labels=c(expression(' '),expression(bar(x)[cil]),
expression(bar(x)[cir]),expression(mu[0]),expression('')))
axis(2,pos = c(-5,0))
#标记左侧和右侧的拒绝域
xRiReject <- seq(right,5,by=0.01)
yRiReject <- dt(xRiReject,df=df,)
xLeReject <- seq(left,-5,by=-0.01)
yLeReject <- dt(xLeReject,df=df)
#用poltgon()绘制拒绝域
polygon(c(xRiReject,xRiReject[length(xRiReject)],xRiReject[1]),
c(yRiReject,0, 0), col=alpha("red",0.4),border=NA)
polygon(c(xLeReject,xLeReject[length(xLeReject)],xLeReject[1]),
c(yLeReject,0, 0), col=alpha("red",0.4),border=NA)
#在坐标轴上添加t值标记
axis(1,at=c(t.value,-1*(t.value)),
pos = c(0,0),lwd.ticks=1,
labels=c( round(t.value,2),round(-1*(t.value),2)))
arrows(-1*(t.value),0, -1*(t.value), 0.4, length = 0,lty =2,col="blue")
arrows(t.value,0, t.value, 0.4, length = 0,lty =2,col="blue")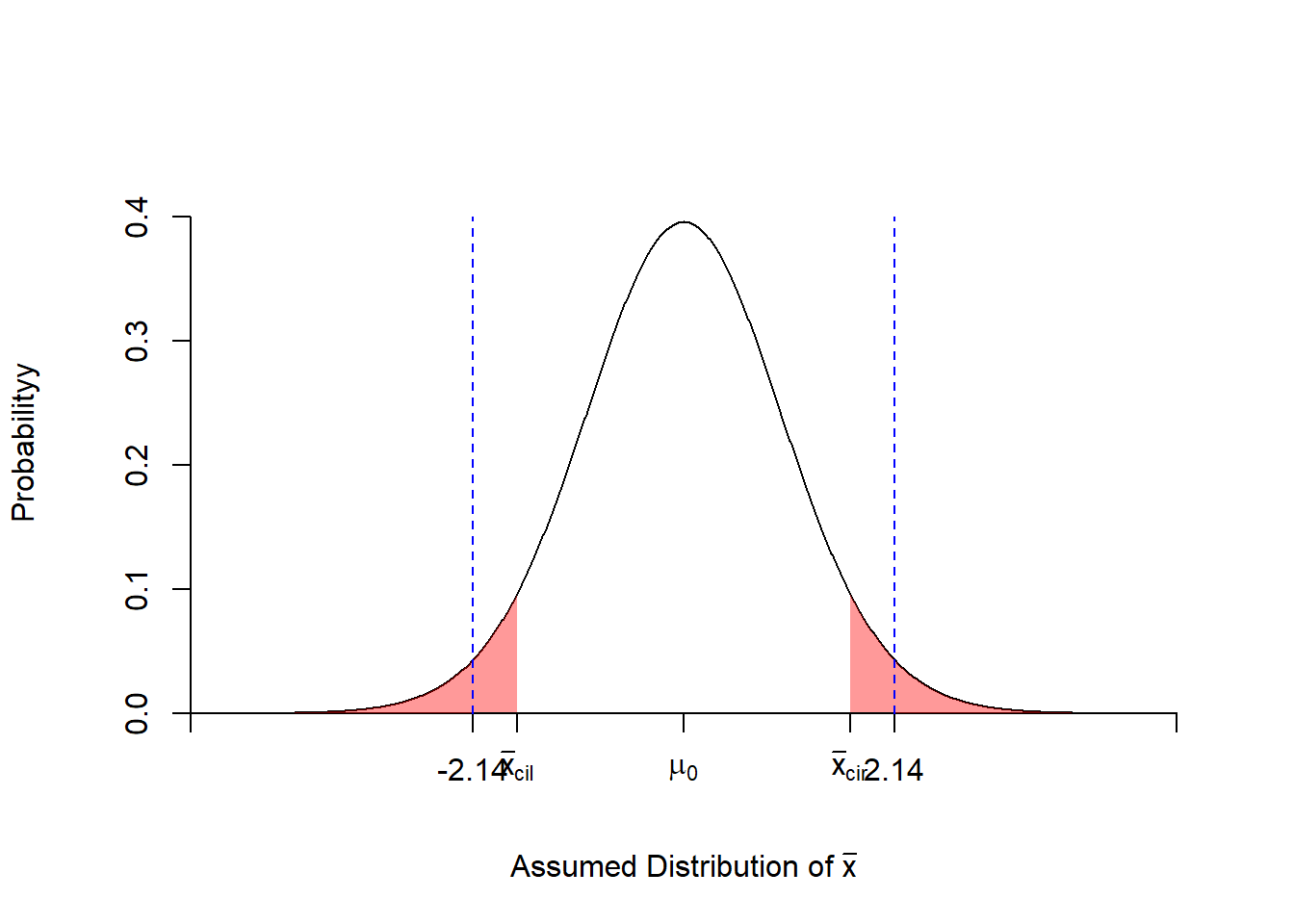
Figure 3.6: 血红蛋白样本的单样本t检验
3.3.3 配对样本t检验
简称配对t检验(Paired/matched t-test),也称成对t检验(注意区别于成组t检验),适用于配对设计的计量资料。配对设计是将受试对象按照某些重要特征特征配成对子,再见没对中的 两个受试对象随机分配到两处理组。常见的配对设计主要有:
两通志受试对象配成对子,分别接受两种不同的处理;
同一受试对象分别接受两种不同处理;
同一受试对象接受一种处理前后。
使用《医学统计学》中的 案例3-6 的数据在R中进行配对样本t检验测试,案例3-6属于第2种配对设计情况。
#使用memic包读取spss的数据格式
#install.packages('memisc')
library("memisc")
#读取数据
bfc_sav<-spss.system.file("ExampleData/SavData4MedSta/Exam03-06.sav")
#将数据形式转换为数据框
bfc_df<-as.data.frame(as.data.set(bfc_sav))
#直接使用t.test()进行计算,注意paired=TRUE
t.test(bfc_df$x1, bfc_df$x2, paired=TRUE)
## Paired t-test
##
## data: bfc_df$x1 and bfc_df$x2
## t = 7.926, df = 9, p-value = 2.384e-05
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## 0.1946542 0.3501458
## sample estimates:
## mean of the differences
## 0.2724 计算显示\(P=2.384e-05<\alpha=0.05\),可以认为一次抽样发生了小概率事件,因此拒绝原假设\(H_0\), 接受\(H_1\),差异有统计意义;结合案例数据意义,可认为两种方法对脂肪含量的测定结果不同, 而且第一种方法的鉴定结果数值较高(mean of the differences=0.27224 > 0)。
同样,可以通过绘制拒绝域和t值落点,更直观的发现t值落在左侧和右侧的拒绝域内的。
#l使用scales包中alpha函数改变颜色透明度
library("scales")
t.value<-7.926
df=9
x <- seq(-9,9,by=0.01)
y <- dt(x,df=df)
#右侧p值0.95对应的t值
right <- qt(0.95,df=df)
#左p值0.05对应的t值
left <- qt(0.05,df=df,lower.tail=T)
#绘制密度曲线
plot(x,y,type="l",xaxt="n",ylab="probabilityy",
xlab=expression(paste('Assumed Distribution of ',bar(x))),
axes=FALSE,ylim=c(0,max(y)*1.1),xlim=c(min(x),max(x)),
frame.plot=FALSE)
#添加坐标轴
axis(1,at=c(-9,left,right,0,9),
pos = c(0,0),
labels=c(expression(' '),expression(bar(x)[cil]),
expression(bar(x)[cir]),expression(mu[0]),expression('')))
axis(2,pos = c(-9,0))
#标记左侧和右侧的拒绝域
xRiReject <- seq(right,9,by=0.01)
yRiReject <- dt(xRiReject,df=df,)
xLeReject <- seq(left,-9,by=-0.01)
yLeReject <- dt(xLeReject,df=df)
#用poltgon()绘制拒绝域
polygon(c(xRiReject,xRiReject[length(xRiReject)],xRiReject[1]),
c(yRiReject,0, 0), col=alpha("red",0.4),border=NA)
polygon(c(xLeReject,xLeReject[length(xLeReject)],xLeReject[1]),
c(yLeReject,0, 0), col=alpha("red",0.4),border=NA)
#在坐标轴上添加t值标记
axis(1,at=c(t.value,-1*(t.value)),
pos = c(0,0),lwd.ticks=1,
labels=c( round(t.value,2),round(-1*(t.value),2)))
arrows(-1*(t.value),0, -1*(t.value), 0.4, length = 0,lty =2,col="blue")
arrows(t.value,0, t.value, 0.4, length = 0,lty =2,col="blue")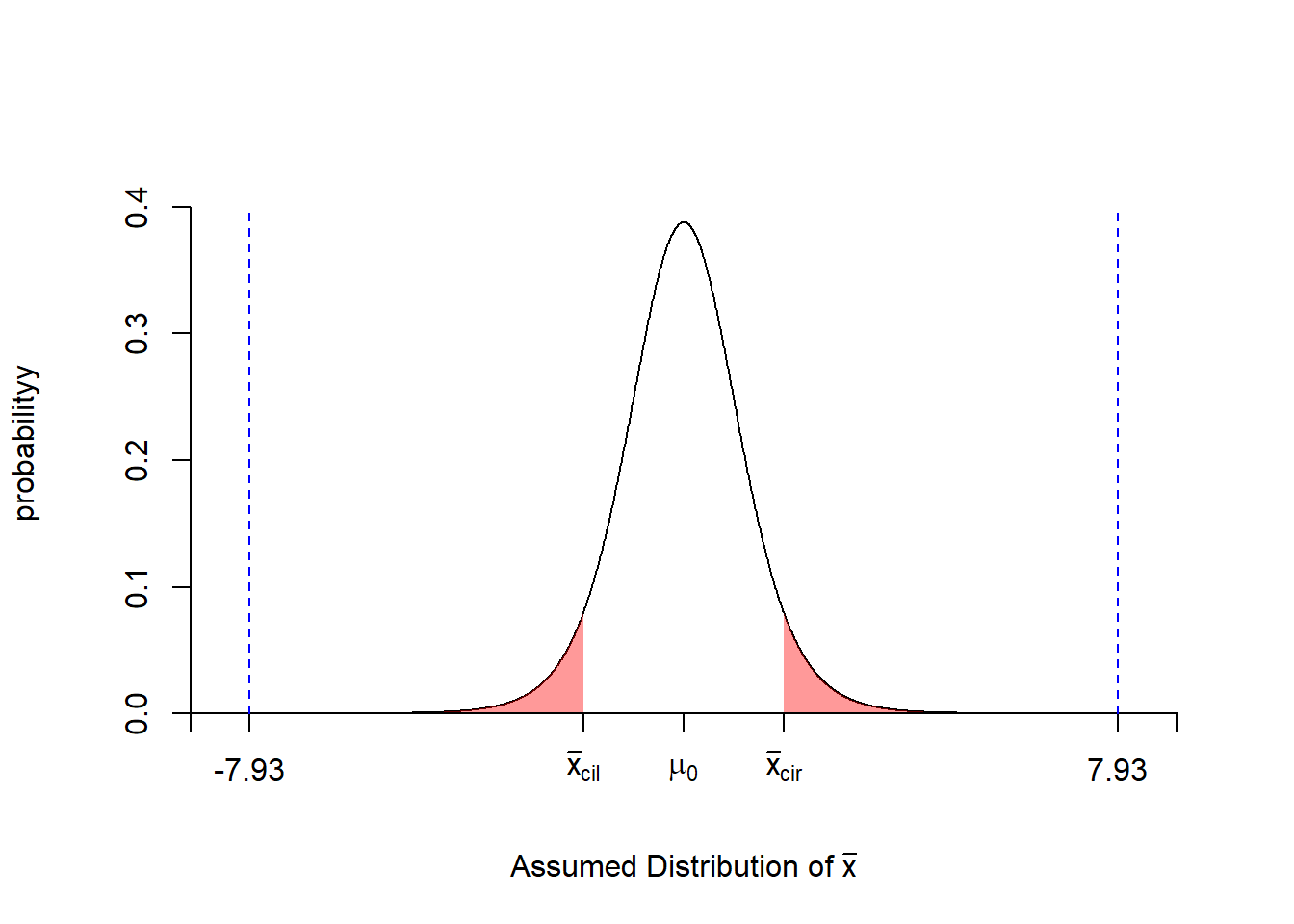
Figure 3.7: 两种方法对饮料中的脂肪含量检测的配对t检验
3.3.4 两种独立样本t检验
两种独立样本t检验又称为成组t检验((Two sample/gourp t-test),适用于完全随机设计两样本均数比较, 通常是比较两样本所代表的总体的均数是否不同。两组完全随机设计是将受试对象完全随机分配到两个不同处理组。
当两样本含量较小(\(n_1\leq60,或(和)n_2\leq60\)),且各自的总体符合正态分布(正态分布检验)时,再根据两组 数据的方差是否一样(方差齐性,方差齐性检验)来采用不同t检验方法。
3.3.4.1 总体方差相等的t检验
library("memisc")
#读取数据
bfg_sav<-spss.system.file("ExampleData/SavData4MedSta/Exam03-07.sav")
#将数据形式转换为数据框
bfg_df<-as.data.frame(as.data.set(bfg_sav))
x <- bfg_df$result[which(bfg_df$group==1)]
y <- bfg_df$result[which(bfg_df$group==2)]
#直接使用t.test()进行计算,注意 var.equal=TRUE
t.test(x,y,var.equal=TRUE)
## Two Sample t-test
##
## data: x and y
## t = -0.64187, df = 38, p-value = 0.5248
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -2.326179 1.206179
## sample estimates:
## mean of x mean of y
## 2.065 2.625 计算显示 \(P=0.5248>\alpha=0.05\),因此不拒绝原假设\(H_0\),差异无统计意义;结合案例数据意义, 还不能认为两种方法的预后效果不同。
3.3.4.2 t’检验
t’检验,用于总体方差不相等的t检验。当两独立小样本的均数比较,如果方差不相等(方差不齐),可采用数据变换(如两样本几何均数的t检验, 就是将原始数据对数转换后进行t检验)处理,或采用近似t检验(Separate variance estimation t-test),即t’检验或秩转换的非参数检验,比如常用的 Cochran&Cox法 和 Satterthwaite法 两种, 还有t.teet()里面使用的Welch法。注意的是,我了解的资料显示,似乎R语言中还没有具体实现Cochran&Cox法 和 Satterthwaite法的函数实现,需根据公式写代码实现,可以参考下面的代码。另外,Satterthwaite法和Welch法都是在 Cochran&Cox法的检验统计量t’的基础上,进行的自由度矫正,然后得到矫正自由度后对应的t’值代替t值。
使用《医学统计学》中的 案例3-8 的数据在R中进行总体方差不相等的t检验测试。
mean_x <- 1.46
mean_y <- 1.13
stdev_x <- 1.36
stdev_y <- 0.7
nx <- 20
ny <- 20
#Cochran&Cox法的检验统计量*t'*的
cochran_test<-function(mean_x,mean_y,stdev_x,stdev_y,nx,ny) {
t_vul <- (mean_x-mean_y)/sqrt(stdev_x^2/nx+stdev_y^2/ny)
return(t_vul)
}
#计算t'值
cochran_t<-cochran_test(mean_x,mean_y,stdev_x,stdev_y,nx,ny)
## [1] 0.9648463
#计算P值
pt(cochran_t,df=nx-1,lower.tail=F)*2
## 0.3467427
#Satterthwaite法来矫正Cochran&Cox法的检验统计量*t'*的自由度
sattw_df<-function(stdev_x,stdev_y,nx,ny){
satt_df<-(stdev_x^2/nx+stdev_y^2/ny)^2/
(((stdev_x^2/nx)^2/(nx-1))+
((stdev_y^2/ny)^2/(ny-1)))
return(satt_df)
}
satt_df<-sattw_df(stdev_x,stdev_y,nx,ny)
#这里注意的是cochran_t>0,我们要计算cochran_t相关的双侧拒绝域面积,需要指定 lower.tail=F,并加倍
pt(cochran_t,satt_df,lower.tail=F)*2
#[1] 0.3427644
#Welch法来矫正Cochran&Cox法的检验统计量*t'*的自由度
welch_df<-function(stdev_x,stdev_y,nx,ny){
welch_df<-(stdev_x^2/nx+stdev_y^2/ny)^2/
(((stdev_x^2/nx)^2/(nx+1))+
((stdev_y^2/ny)^2/(ny+1)))-2
return(welch_df)
}
wel_df<-welch_df(stdev_x,stdev_y,nx,ny)
pt(cochran_t,wel_df,lower.tail=F)*2
#[1] 0.3424925从上面的计算过程可知,三种t’检验显示了都不拒绝原假设\(H_0\),可以认为差异物统计学意义,尚不能认为两种药物 对患者的干预效果不同。但是三种发放给出的效能是不一样的,其中Welch法的最小,Cochran&Cox法的最大,也就是说 Cochran&Cox法更为保守。
3.3.4.3 参数估计与假设检验的联系
可信区间与假设检验的区别和联系可信区间用于说明量的大小即推断总体参数(如总体均数)的范围,而假设检验用于推断 质的不同即判断两总体参数是否不等。两者既相互联系,又有区别。
一方面,可信区间亦可回答假设检验的问题,算得的可信区间若包含了\(H_0\)则按检验水准a,不拒绝\(H_0\):若不包含\(H_0\),则按检验水准a,拒绝\(H_0\),接受\(H_1\)。
另一方面,可信区间不但能回答差别是否有统计学意义,而且还能提供比假设检验更多的信息,即提示差別有无实际的专业意义。’ Figure 3.8中的 a b c 均有统计学意义(因可信区间未包含\(H_0\))。但其中:a提示有实际的专业意义(因可信区间高于有实际专业意义的值), 值得重视:b提示可能有实际专业意义;c提示无实际专业意义,该图中d、e提示差异均无统计学意义,但其中: d因可信区间较宽,样本含量过小,抽样误差太大,难于得出结论;e提示以决策的观点,可“接受”\(H_0\),因为即使增加 样本含量,得到差异有统计学意义义,也无实际专业意义。
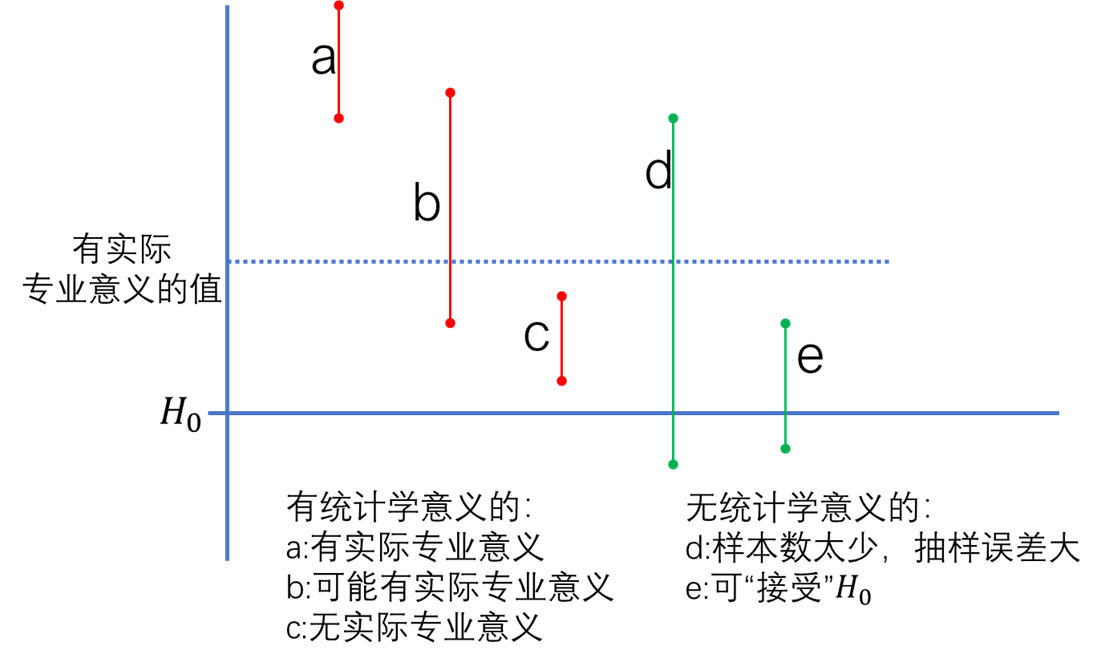
Figure 3.8: 参数估计与假设检验的联系
3.3.5 两样本方差齐性检验
前面已经提到,在进行两样本检验尤其是两小样本均数的比较时,要求相应的两总体均服从正态分布且两总体方差相等,即方差齐性: 而配对,检验则要求每对数据差值的总体服从正态分布即可。因此进行两小样本检验时,一般应先对资料进行方差齐性检验Hmogeneity of variance test), 特别是发现两样本方差相差悬殊时,要判断两样本所代表的两总体方差是否不等。若方差齐,采用一般的t检验;若方差不齐, 则采用近似t检验(如Cochran&Cox 的检验等)。必要时,也可对资料进行 正态性检验(Normality test),但正态性检 验更多用于采用正态分布法制定参考值范围时。
两总体方差是否不等的判断过去多采用F检验(F-test),由于该检验理论上要求资料服从正态分布,但很多资料方差不齐时, 往往不服从正态分布。因此,近年来多采用更为稳健,不依赖总体分布具体形式Levene检验(Levene’s test,1960)。 Levene检验实质上是将原始观测值\(X_{ij}\)转换为相应的离差\(z_{ij}\)(有多种去可选), 然后再作方差分析, 它既可用于对两个总体方差进行齐性检验,也可用于对个总体方差进行齐性检验。这里仅介绍两样本方差比较的F检验。
F检验与前面介绍到的利用正态分布进行Z检验,利用t分布进行t检验一样,它是利用F分布来进行检验的。 在R中,F分布同样拥有与正态分布,t分布类似的几个函数,分别是df(),pf(),qf()和rf(), 不过F分布主要收两组样品的自由度共同影响。R中用F检验来比较两组样本方差的函数是var.test()。
注意的是,方差齐性检验中的第一类错误的控制水准一般选择0.1,即\(\alpha=0.1\),而且一般约定取较大的方差作为分子,较小的方差作为分母, 这样计算出来的[公式],缩小了范围,这样可以方便查表做出结论。
使用《医学统计学》中的 案例3-6 和 案例3-8 的数据在R中进行总体方差齐性检验测试。
##案例3-6
library("memisc")
#读取数据
bfc_sav<-spss.system.file("ExampleData/SavData4MedSta/Exam03-06.sav")
bfc_df<-as.data.frame(as.data.set(bfc_sav))
x <- bfg_df$result[which(bfg_df$group==1)]
y <- bfg_df$result[which(bfg_df$group==2)]
var.test(x,y)
## F test to compare two variances
##
## data: x and y
## F = 1.5984, num df = 19, denom df = 19, p-value = 0.3153
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
## 0.6326505 4.0381795
## sample estimates:
## ratio of variances
## 1.598361
##方法2
#用F公式来计算F值
f_val1<-var(x)/var(y)
## [1] 1.598361
p_val1 <- pf(f_val1, df1=length(x)-1, df2=length(y)-1, lower.tail=FALSE)*2
## [1] 0.3152554
#将分子分母调换,需要注意lower.tail=TRUE/FALSE的设定
pf(var(y)/var(x), df1=length(y)-1, df2=length(x)-1, lower.tail=TRUE)*2
##案例3-8
mean_x <- 1.46
mean_y <- 1.13
stdev_x <- 1.36
stdev_y <- 0.7
nx <- 20
ny <- 20
#根据F分布公式,计算F值
f_val<-stdev_x^2/stdev_y^2
## [1] 3.774694
p_val <- pf(f_val, df1=nx-1, df2=ny-1, lower.tail=FALSE)*2
## [1] 0.005732012根据计算结果,案例3-6的P值 0.3153>0.1,按照α=0.1的水准,不拒绝\(H_0\),差异不具有统计学意义,两组数据的方差相等,应该采用经典的t检验。 案例3-8的P值 0.0057<0.1,按照α=0.1的水准,拒绝\(H_0\),差异具有统计学意义,两组数据的方差不相等,应该采用t’检验。
3.4 变量转换
在主要的处理以前对数据进行的一些预处理,比如数据清洗,数据整合,数据变换)等。这里主要关注统计背景下的数据转换 (Transformation),也叫变量转换,从更广泛的意义上讲,变量转换是一种更改分布或关系的形状的替换。
实际资料若不满足正态性或(和)方差齐性的假定,尤其是小样本资料时,如用一般的,检验可能会导致偏离真实结果较远。 对于明显偏离上述应用条件的资料,可通过变量变换的方法加以改善。所谓变量变换(Variable transformation)是将原始 数据作某种函数转换,如转换为对数值等。它可使各组方差齐同, 亦可使偏态資料正态化,以满足,检验或其他统计分析方法对 资料的要求。通常情况下,适当的变显变换可同时达到上述两个目的。但变量变换后,在结果解释上不如原始观测变量直观, 比如地震震级是能量释放的数据的对数转换的结果,但是震级每相差1.0级,能量相差大约32倍; 每相差2.0级,能量相差约1000倍!
常用的变量变换有:
- 对数变换(Logarithm)
- 平方根变换(Square root)
- 平方根反正弦变换(Arcsine, Arcsine-square)
- 倒数变换(Reciprocal)
- 指数变换(Exponential)
其他的(如立方根等)应根据资料性质选择适当的变量变换方法。
关于变量转换的困惑?
转换的主要动机是更易于描述会和挖掘数据信息。 尽管转换的处理看起来不太自然,但这在很大程度上是心理上的反对。 拥有丰富的转换经验后会减少这种感觉,因为转换通常效果很好。 实际上,许多熟悉的测量单位也是转换后的数据,比如分贝, pH和地震震级的里氏标度都是为对数转换后的数据。但是,在经验丰富的数据分析人员中,转换也引起了争论。 有些人经常使用它们,其他人则少得多。
所有观点都是可以辩驳的,或者至少是可以理解的。
常用的变量变换及其适用的数据分布,或者可以参考示例图3.9:
- 变换前数据分布,集中前面, 使用倒数变换(Reciprocal);
- 变换前数据分布,偏前, 使用对数变换(Logarithm)
- 变换前数据分布,偏中前的, 使用平方根变换(Square root)
- 变换前数据分布,偏中后, 使用平方变换(Square),或平方根反正弦变换(Arcsine, Arcsine-square)
- 变换前数据分布,偏后, 使用指数变换(Exponential)
- 变换前,数据接近正态分布, 直接标准化
![不同转换数据大致适应的数据分布情况, 右图来自Stevens J P. Applied multivariate statistics for the social sciences[M]. Routledge, 2012.](image/Datatransfromsuit.png)
![不同转换数据大致适应的数据分布情况, 右图来自Stevens J P. Applied multivariate statistics for the social sciences[M]. Routledge, 2012.](image/Distributional%20transformations.png)
Figure 3.9: 不同转换数据大致适应的数据分布情况, 右图来自Stevens J P. Applied multivariate statistics for the social sciences[M]. Routledge, 2012.
下面以介绍最常用的 对数变换做一个比较详细的示例,其他转换的逻辑是相同的,只是具体形式有所差别罢,故不累述。
3.4.1 对数变换
对数是指对变量x的作10,或者2,或者自然对数e 为底的对数,对分布形状有很大影响的强变换。 它通常用于减少右偏斜,并且通常适用于测量变量(一般是正态分布的连续型资料),不能应用于零或负值。 对数刻度上的一个单 位表示与所使用的对数的底数相乘,数增长或下降。
对数变换适用于: ①对数正态分布资料,即原始数据的效应是相乘时,如抗体滴度;食品、蔬菜、水果 中农药的残留量;环境中某些有毒有害物质的含量;某些疾病的潜伏期等资料;②各样本标准差与均数成 比例或变异系数是常数或接近某一常数的资料。基本形式有:
\[ X'= \lg X \]
\[X'= \lg(X+K) , (当原始数据较小或有0值时,k=1;K还可以是负数)\]
在R中进行日志记录的基本方法是使用log()函数,格式为log(value,base), 该函数返回以base为底的value的对数。 默认情况下,此函数产生自然对数值(即默认base=e)。以2为底和以10为底的函数分别为log2(),log10()。
下面是单样本数据的对数转换示例:
#install.packages("openintro","e1071","pryr")
#使用mammals数据集测试
library(openintro)
#e1071包中的skewness()计算偏斜度
library(e1071)
#使用pryr包中的绘图对象保存方案
library(pryr)
library("dplyr")
skewness(mammals$body_wt)
#使用log()对body_wt数据进行转换
loged_bd_wt <- log(mammals$body_wt)
#skewness()计算偏斜度
skewness(loged_bd_wt)
##[1] 0.1453599
p1.pryr %<a-% {
hist(mammals$body_wt,breaks = 200,freq=FALSE,
xlim=c(min(mammals$body_wt),max(mammals$body_wt)),main="Bodt wt. 数据分布")
lines(density(mammals$body_wt), col="red", lwd=1)
}
p2.pryr %<a-% {
hist(loged_bd_wt,breaks = 200,freq=FALSE,
xlim=c(min(loged_bd_wt),max(loged_bd_wt)),main="经过Log转换后Bodt wt. 数据分布")
lines(density(loged_bd_wt), col="red", lwd=1)
}
split.screen(c(1, 2))
screen(1)
p1.pryr
screen(2)
p2.pryr下面是两组样本数据的对数转换示例,在mammals$body_wt数据上结合mammals$brain_wt数据:
#使用log()对brain_wt数据进行转换
loged_br_wt <- log(mammals$brain_wt)
p3.pryr %<a-% {
plot(mammals$body_wt,mammals$brain_wt,main="body_wt vs brain_wt",col="red",pch=16)
}
p4.pryr %<a-% {
plot(loged_bd_wt,loged_br_wt,main="body_wt vs brain_wt after both loged",col="red",pch=16)
}
split.screen(c(1, 2))
screen(1)
p3.pryr
screen(2)
p4.pryr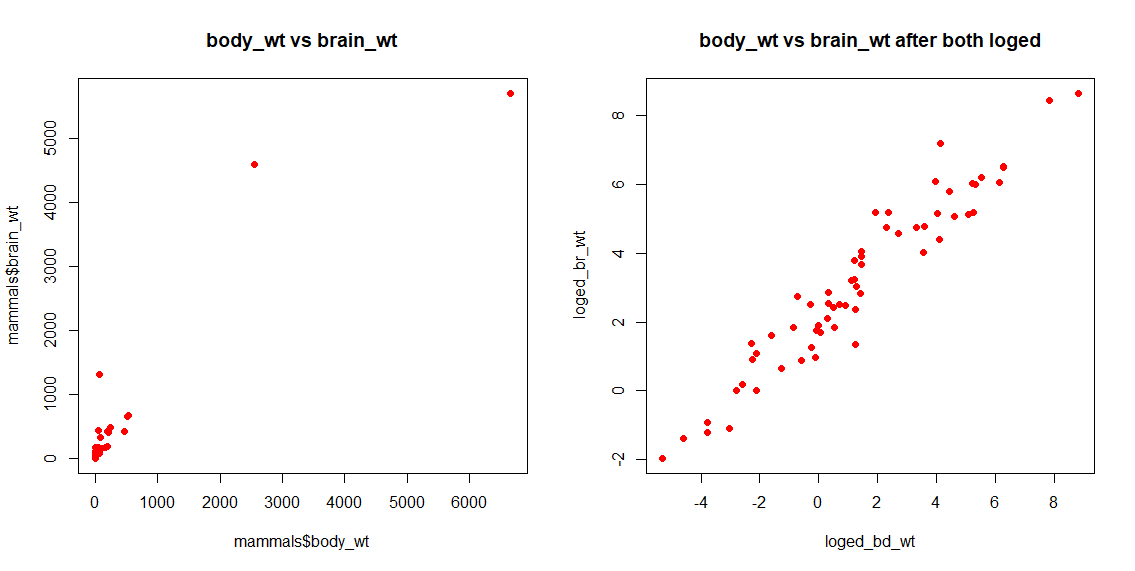
Figure 3.10: log转换前后的body_wt vs brain_wt
在建立预测模型时,数据转换也可以起到很大效果。我们可以看看用mammals$body_wt和mammals$brain_wt来构建线性模型时,使用对数转换前后的残差(Residual standard error)变化。 计算结果显示,数据转换前的预测模型的残差是334.7,对数转换后的预测模型的残差是0.6943,相比转换前的要小非常多了。
lm.model <- lm(mammals$brain_wt ~ mammals$body_wt)
lm_log.model <- lm(loged_br_wt ~ loged_bd_wt)
summary(lm.model)
## Call:
## lm(formula = mammals$brain_wt ~ mammals$body_wt)
##
## Residuals:
## Min 1Q Median 3Q Max
## -810.07 -88.52 -79.64 -13.02 2050.33
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 91.00440 43.55258 2.09 0.0409 *
## mammals$body_wt 0.96650 0.04766 20.28 <2e-16 ***
## ---
## Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
##
## Residual standard error: 334.7 on 60 degrees of freedom
## Multiple R-squared: 0.8727, Adjusted R-squared: 0.8705
## F-statistic: 411.2 on 1 and 60 DF, p-value: < 2.2e-16
summary(lm_log.model)
## Call:
## lm(formula = loged_br_wt ~ loged_bd_wt)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.71550 -0.49228 -0.06162 0.43597 1.94829
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.13479 0.09604 22.23 <2e-16 ***
## loged_bd_wt 0.75169 0.02846 26.41 <2e-16 ***
## ---
## Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
##
## Residual standard error: 0.6943 on 60 degrees of freedom
## Multiple R-squared: 0.9208, Adjusted R-squared: 0.9195
## F-statistic: 697.4 on 1 and 60 DF, p-value: < 2.2e-16