4 Modelización de Series Univariantes: (G)ARCH
 |
| Robert F. Engle III (1942-) Fue laureado con el Premio del Banco de Suecia en Ciencias Económicas en memoria de Alfred Nobel el año 2003, compartido con Clive W. J. Granger, por sus métodos de análisis de series temporales económicas con volatilidad variable en el tiempo ARCH. Los valores de los instrumentos financieros varían aleatoriamente en el tiempo en función del riesgo; el grado de variación se conoce como volatilidad. La volatilidad muestra períodos turbulentos, con cambios bruscos, seguidos por otros períodos de calma con apenas fluctuaciones. Engle propuso los modelos ARCH (modelos de heteroscedasticidad autorregresiva condicional) que ayudan a describir las propiedades de muchas series temporales y desarrolló métodos para hacer modelos de las variaciones de volatilidad a lo largo del tiempo. Estos modelos se han hecho indispensables para todos los interesados en el análisis de los mercados financieros. |
Tomado de varias fuentes:
- “Penn State University Applied Time Series Analysis” (2021)
Librerías usadas:
fGarchquantmodPerformanceAnalyticshighcharter
4.1 Introducción
Usamos el modelo ARMA para la media condicional.
Usamos el modelo ARCH para la varianza condicional.
Los modelos ARMA y ARCH se pueden usar juntos para describir tanto la media condicional como la varianza condicional.
Un modelo ARCH (autorregresivo condicionalmente heterocedástico) es un modelo para la varianza de una serie de tiempo.
Los modelos ARCH se utilizan para describir una varianza que cambia y es posiblemente volátil.
Los modelos ARCH se crearon en el contexto de problemas econométricos y financieros relacionados con inversiones o acciones que aumentan (o disminuyen) en el tiempo, por lo que existe una tendencia a describirlos como modelos para ese tipo de variable. Por esa razón, la variable de interés en estos problemas podría ser \(y_t=(x_{t}-x_{t-1})/x_{t-1}\), la proporción ganada o perdida desde la última vez \(log (x_t / x_{t-1})=log(x_t)-log(x_{t-1})\), o el logaritmo de la relación entre el valor de este tiempo y el valor de la última vez.
Un modelo ARCH podría usarse para cualquier serie que tenga períodos de varianza aumentada o disminuida. Esto podría, por ejemplo, ser una propiedad de los residuos después de que un modelo ARIMA se haya ajustado a los datos.
4.2 ARCH(1)
Supongamos que estamos modelizando la varianza de una serie \(y_t\). El modelo \(ARCH(1)\) para la varianza del modelo \(y_t\) es que, condicionada a \(y_{t-1}\), la varianza en el tiempo es:
\[ \text{Var}(y_t | y_{t-1}) = \sigma^2_t = \alpha_0 + \alpha_1 y^2_{t-1} \] Imponemos las restricciones \(\alpha_0\geq 0\) y \(\alpha_1\geq 0\) para evitar varianza negativa.
Si asumimos que la serie tiene media = 0 (esto siempre se puede hacer centrando la serie), el modelo \(ARCH\) podría escribirse como:
\[\begin{eqnarray} y_t = \sigma_t \epsilon_t,\tag{4.1}\\ \sigma_t = \sqrt{\alpha_0 + \alpha_1y^2_{t-1}},\\ \epsilon_t \overset{iid}{\sim} (\mu=0,\sigma^2=1) \end{eqnarray}\]
Para la inferencia (y la estimación de máxima verosimilitud) también podemos suponer que \(\epsilon_t\) se distribuyen normalmente.
4.2.1 Propiedades
Dos propiedades útiles del modelo \(ARCH (1)\), como está escrito en la línea de ecuación (4.1) anterior, son las siguientes:
\(y^2_t\) tiene el modelo \(AR (1)\) \(y^2_t = \alpha_0 +\alpha_1y^2_{t-1}+error\).
\(y_t\) es ruido blanco cuando \(0 \leq \alpha_1\leq 1\).
4.2.1.1 Ejemplo
Simulemos el modelo \(\text{Var}(y_t | y_{t-1}) = \sigma^2_t = 5+ 0.5y^2_{t-1}\).
library(fGarch)
spec = garchSpec(model = list(alpha = c(0.5), beta = 0,mu = 5))
set.seed(1985)
serie <- garchSim(spec, n = 300)
plot(serie)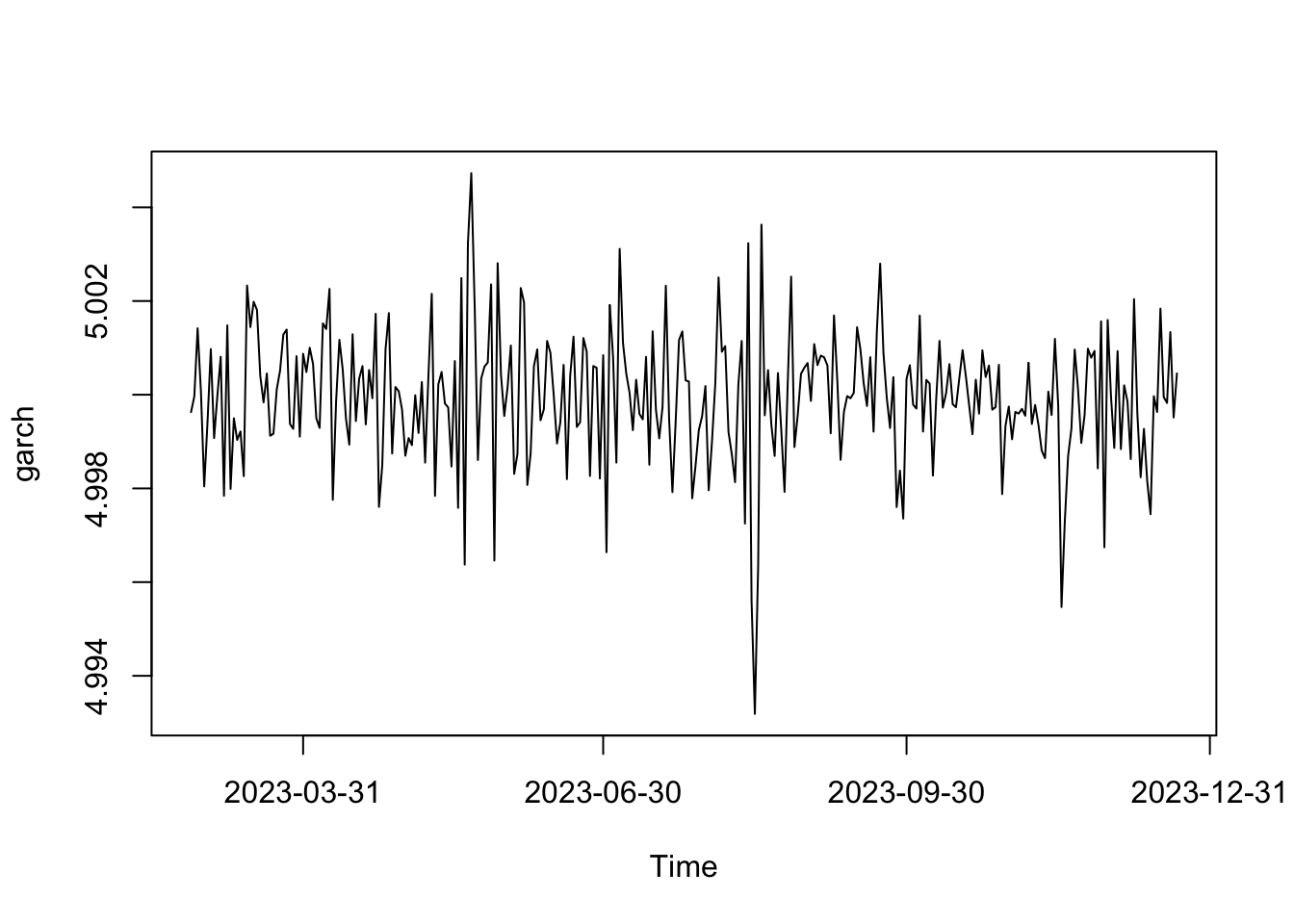
mm <- mean(serie) # nota la resta para cumplir con el supuesto teórico
serie <- (serie-mm)
plot(serie)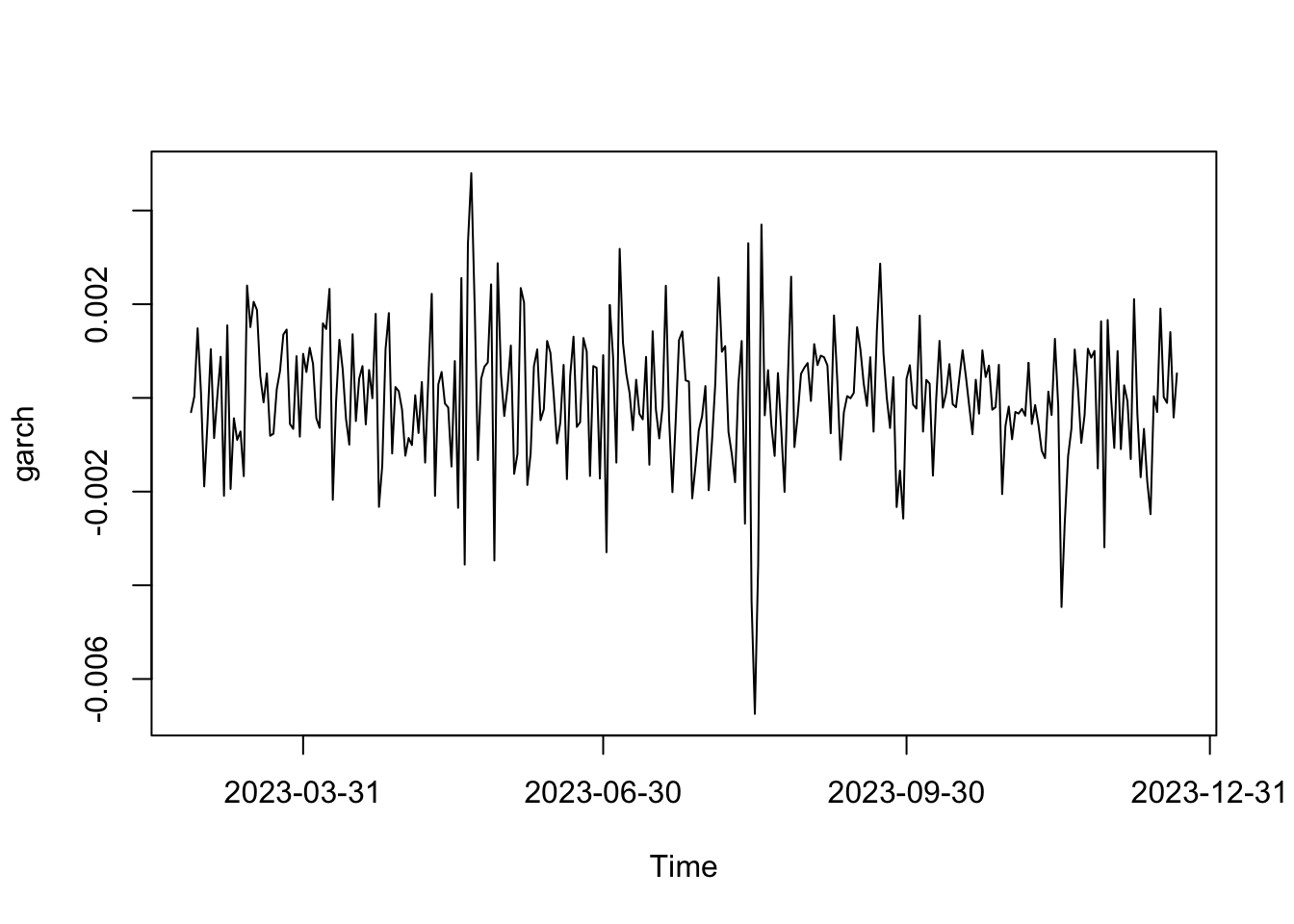
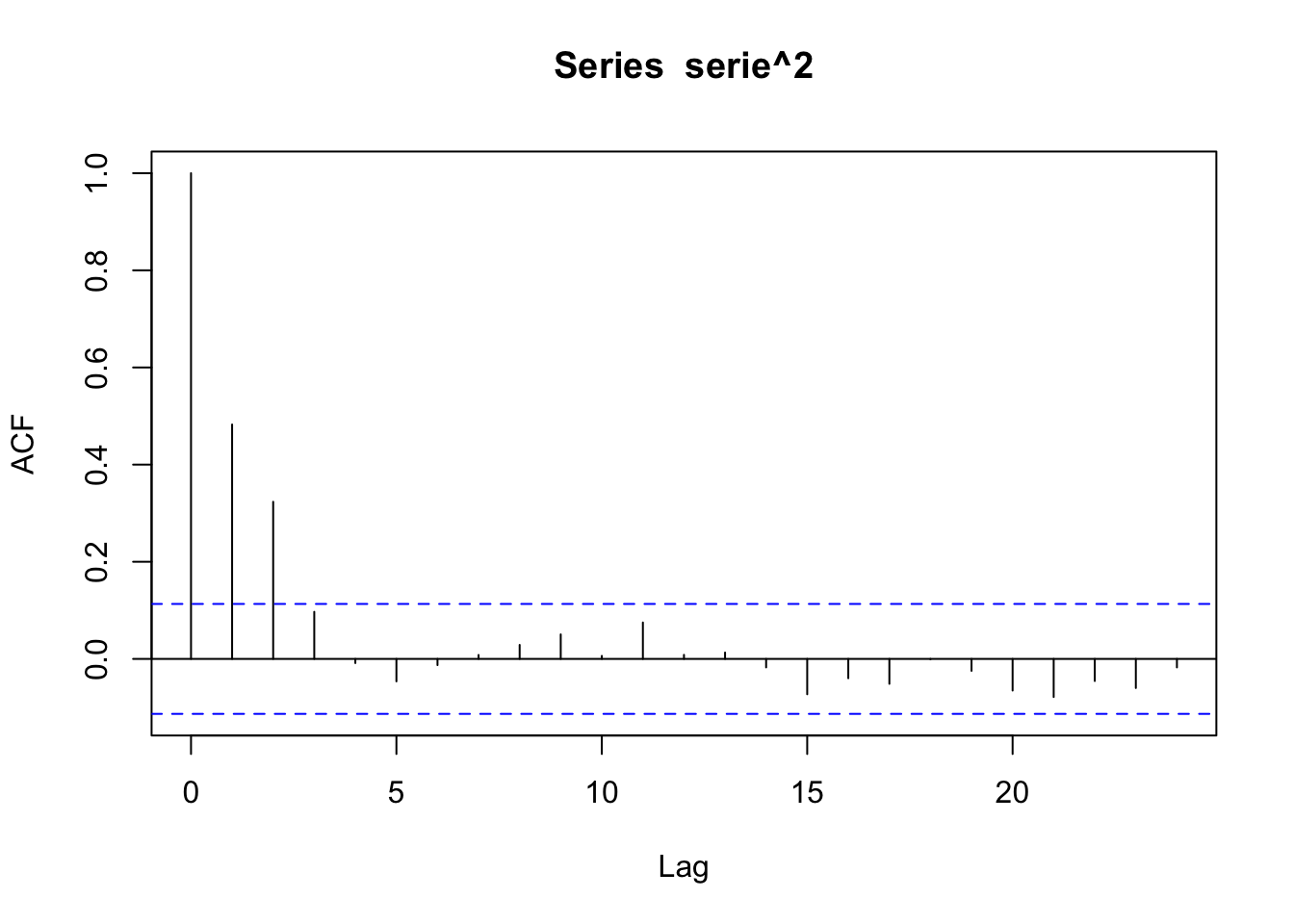
El ACF de la serie a continuación muestra que la serie parece ser ruido blanco.
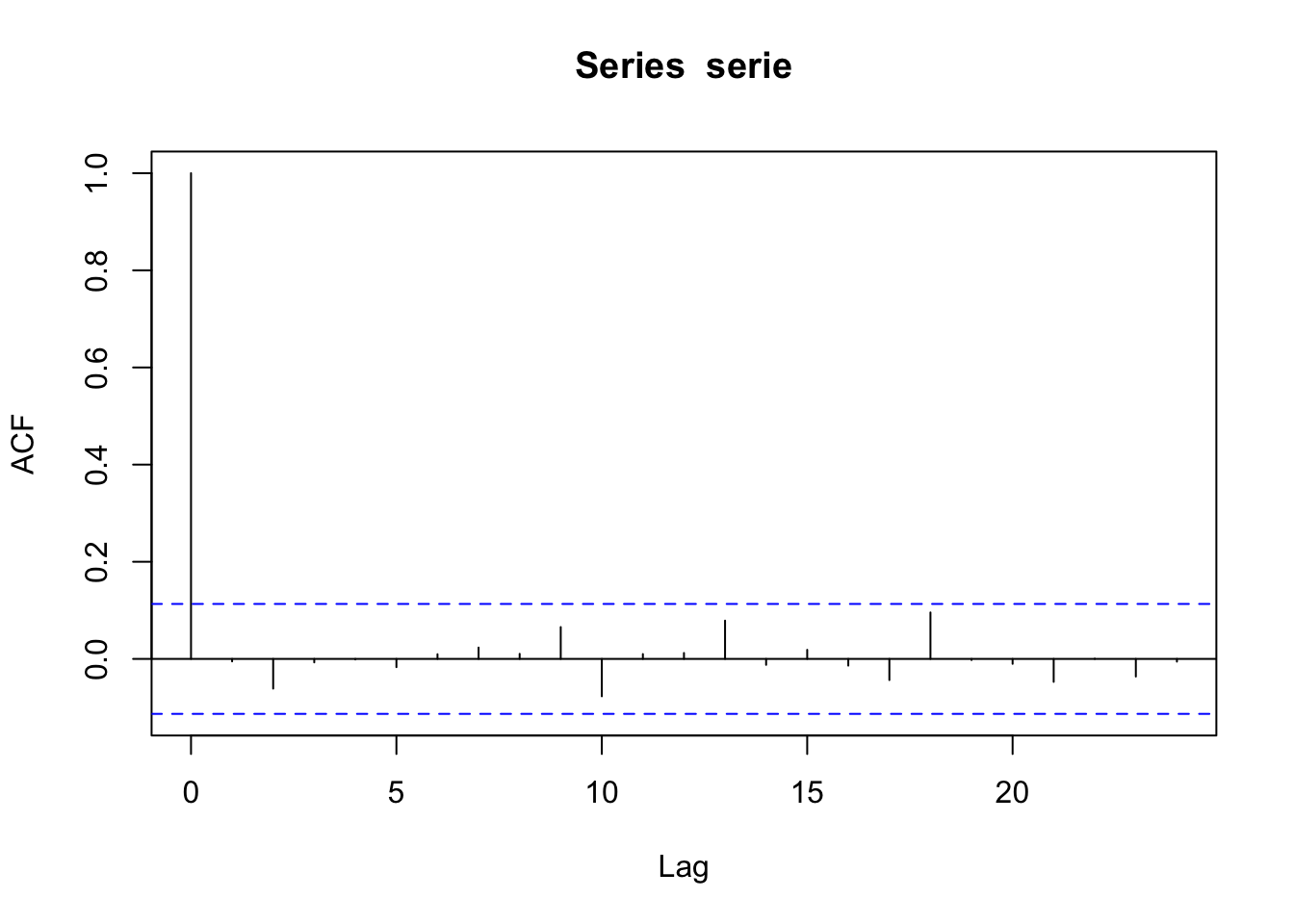
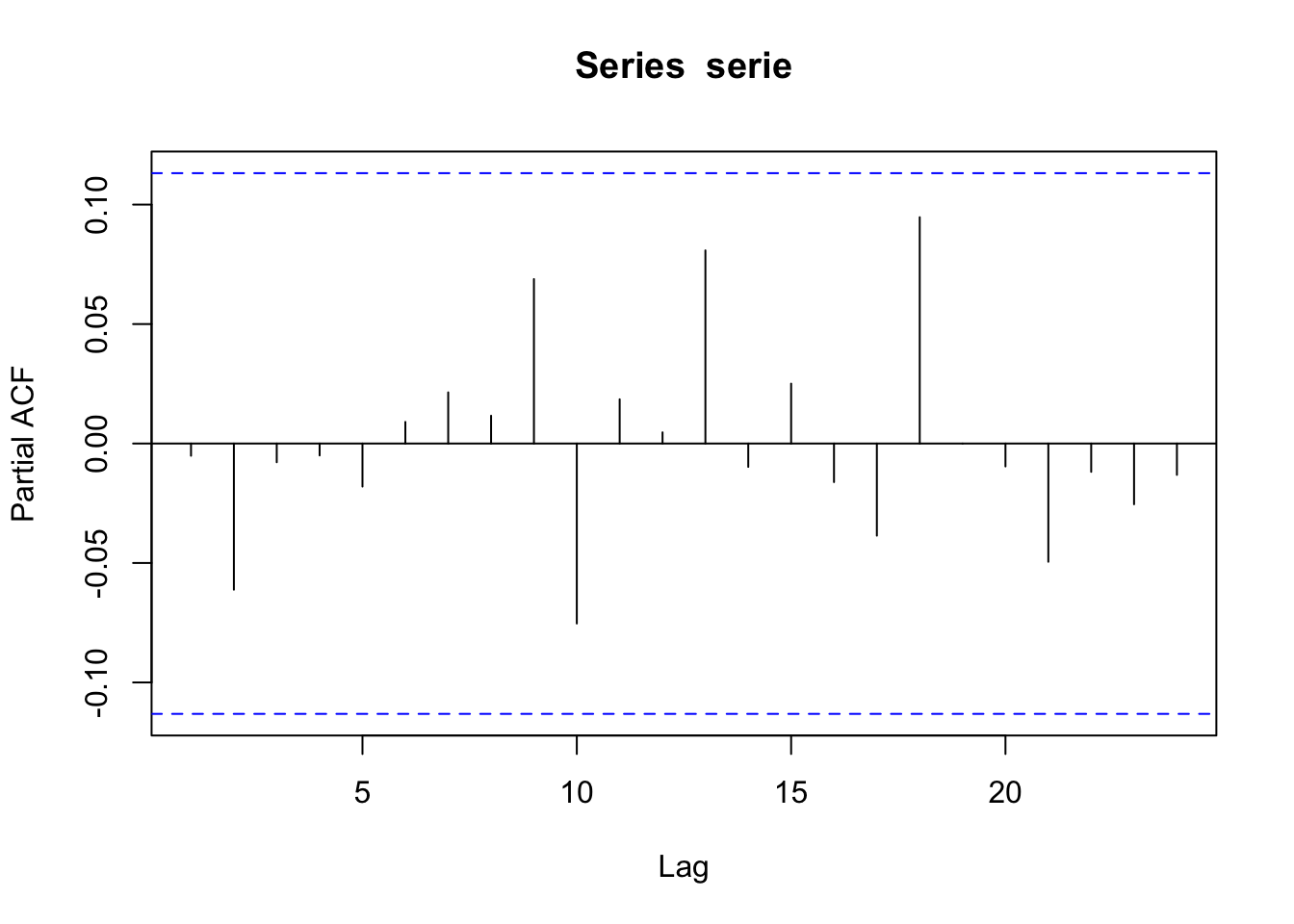
El ACF de la serie al cuadraro sigue un patrón ARMA debido a figura que muestran tanto el ACF como el PACF. Esto sugiere un modelo \(GARCH (2,0)\).
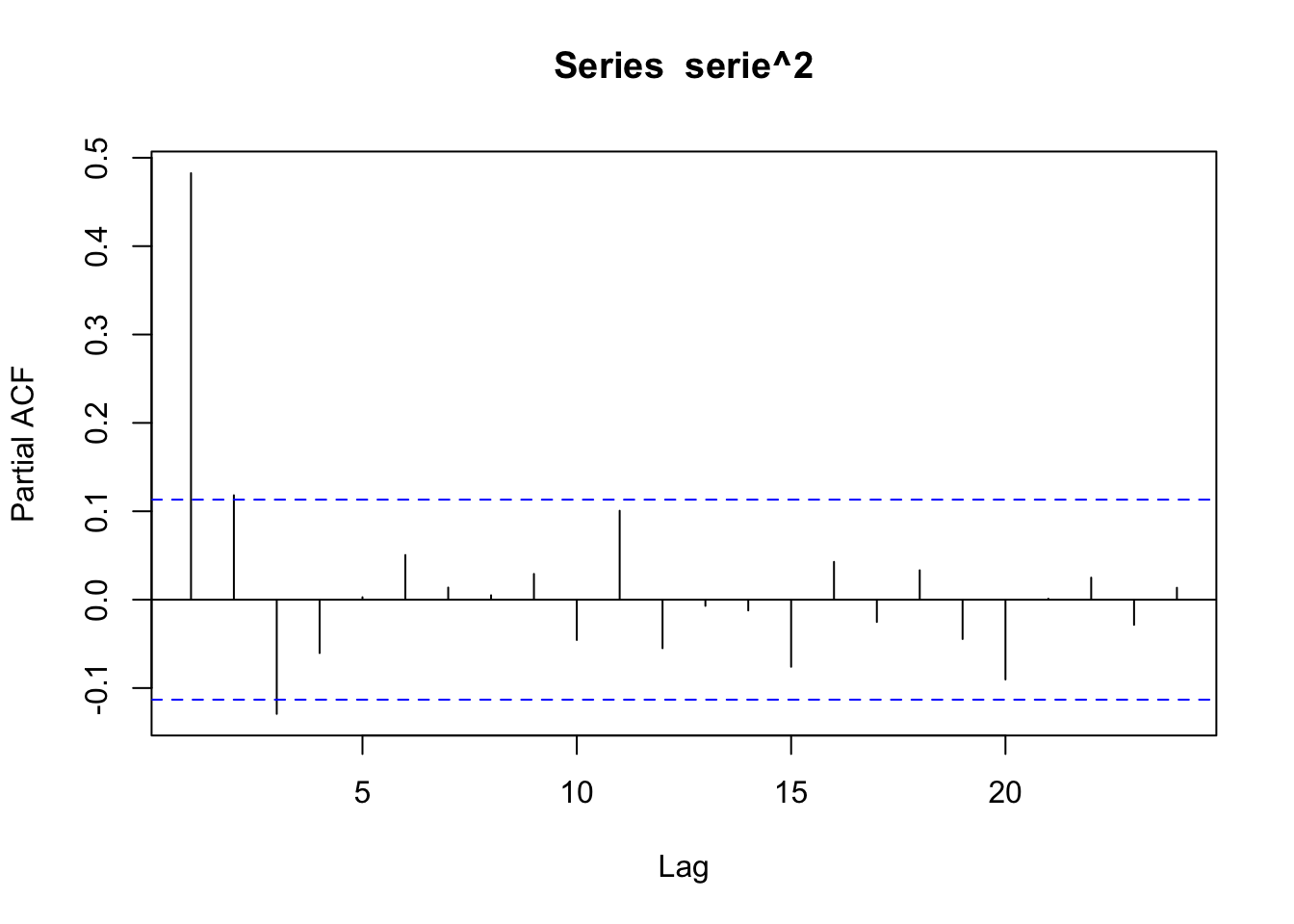
4.3 ARCH(q)
Un proceso \(ARCH (q)\) es aquel para el cual la varianza en el tiempo \(t\) está condicionado a las observaciones en los \(m\) tiempos anteriores, y la relación es
\[ \text{Var}(y_t | y_{t-1}, \dots, y_{t-m}) = \sigma^2_t = \alpha_0 + \alpha_1y^2_{t-1} + \dots + \alpha_my^2_{t-m} = \alpha_{0}+\sum_{i = 1}^{q}\alpha_i y^2_{t-i}. \]
Con ciertas restricciones impuestas a los coeficientes, la serie \(y_t\) al cuadrado teóricamente será \(AR (m)\).
4.4 GARCH
Un modelo GARCH (autorregresivo generalizado condicionalmente heterocedástico) utiliza valores de las observaciones pasadas al cuadrado y varianzas pasadas para modelizar la varianza en el tiempo \(t\). Por ejemplo, un \(GARCH (1,1)\) es
\[ \sigma^2_t = \alpha_0 + \alpha_1 y^2_{t-1} + \beta_1\sigma^2_{t-1} \]
En la notación \(GARCH\), el primer subíndice se refiere al orden de los términos \(y^2\) en el lado derecho, y el segundo subíndice se refiere al orden de los términos \(\sigma^2\).
En general, un modelo GARCH(p,q)
\[ \text{Var}(y_t | y_{t-1}, \dots, y_{t-m}) = \sigma^2_t = \omega + \alpha_1y^2_{t-1} + \dots + \alpha_my^2_{t-m}+\beta_1\sigma^2_{t-1}+\cdots +\beta_p\sigma^2_{t-p} = \omega+\sum_{i = 1}^{q}\alpha_i y^2_{t-i}+\sum_{i = 1}^{p}\beta_i \sigma^2_{t-i} \]
4.5 Identificación
La mejor herramienta de identificación puede ser un gráfico de la serie de tiempo. Por lo general, es fácil detectar periodos de mayor variación esparcidos a lo largo de la serie.
Puede resultar útil examinar el ACF y el PACF de \(y_t\) y \(y^2_t\). Por ejemplo,
si \(y_t\) parece ser ruido blanco y parece ser \(AR (1)\), se sugiere un modelo \(ARCH (1)\) para la varianza.
Si el PACF de sugiere \(AR (p)\), entonces \(ARCH (m)\) puede funcionar.
Los modelos \(GARCH\) pueden ser sugeridos por una estructura de tipo ARMA en el ACF y PACF de \(y^2_t\).
En la práctica, es posible que tengas que experimentar con varias estructuras ARCH y GARCH después de detectar que es necesario aborar el problema con este tipo de modelos.
4.5.0.1 Ejemplo
Simulemos el modelo \(\text{Var}(x_t | x_{t-1}) = \sigma^2_t = 0.3x^2_{t-1} + 0.5\sigma^2_{t-1}\).
spec = garchSpec(model = list(alpha = c(0.3), beta = c(0.5),mu = 0))
set.seed(85)
serie <- garchSim(spec, n = 300)
plot(serie)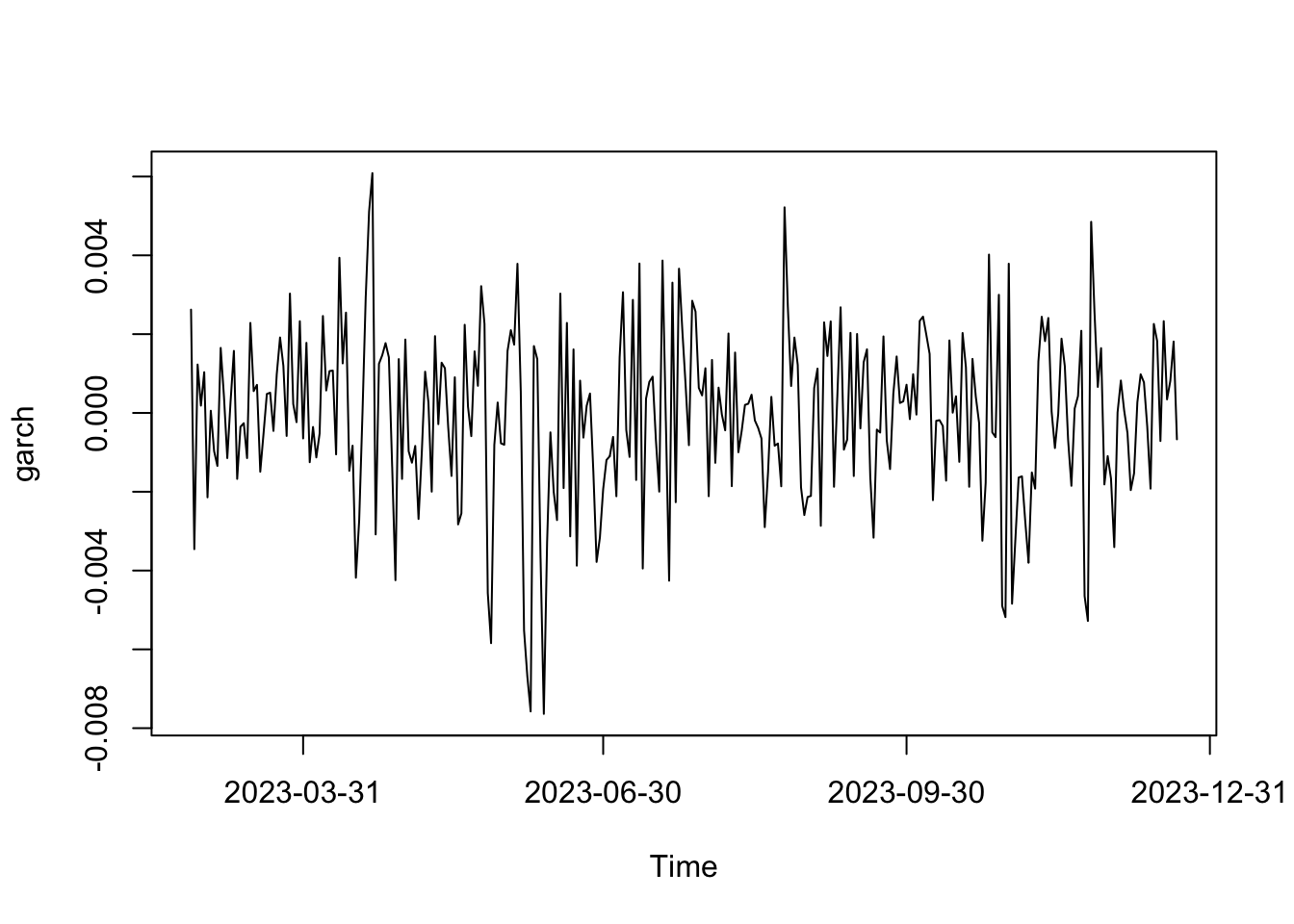
alpha: el valor o vector de coeficientes autorregresivos.beta: el valor o vector de los coeficientes de varianza.mu: el valor promedio (constante)omega: el coeficiente de la constante en la ecuación de varianza.
El ACF de la serie parece ser ruido blanco.
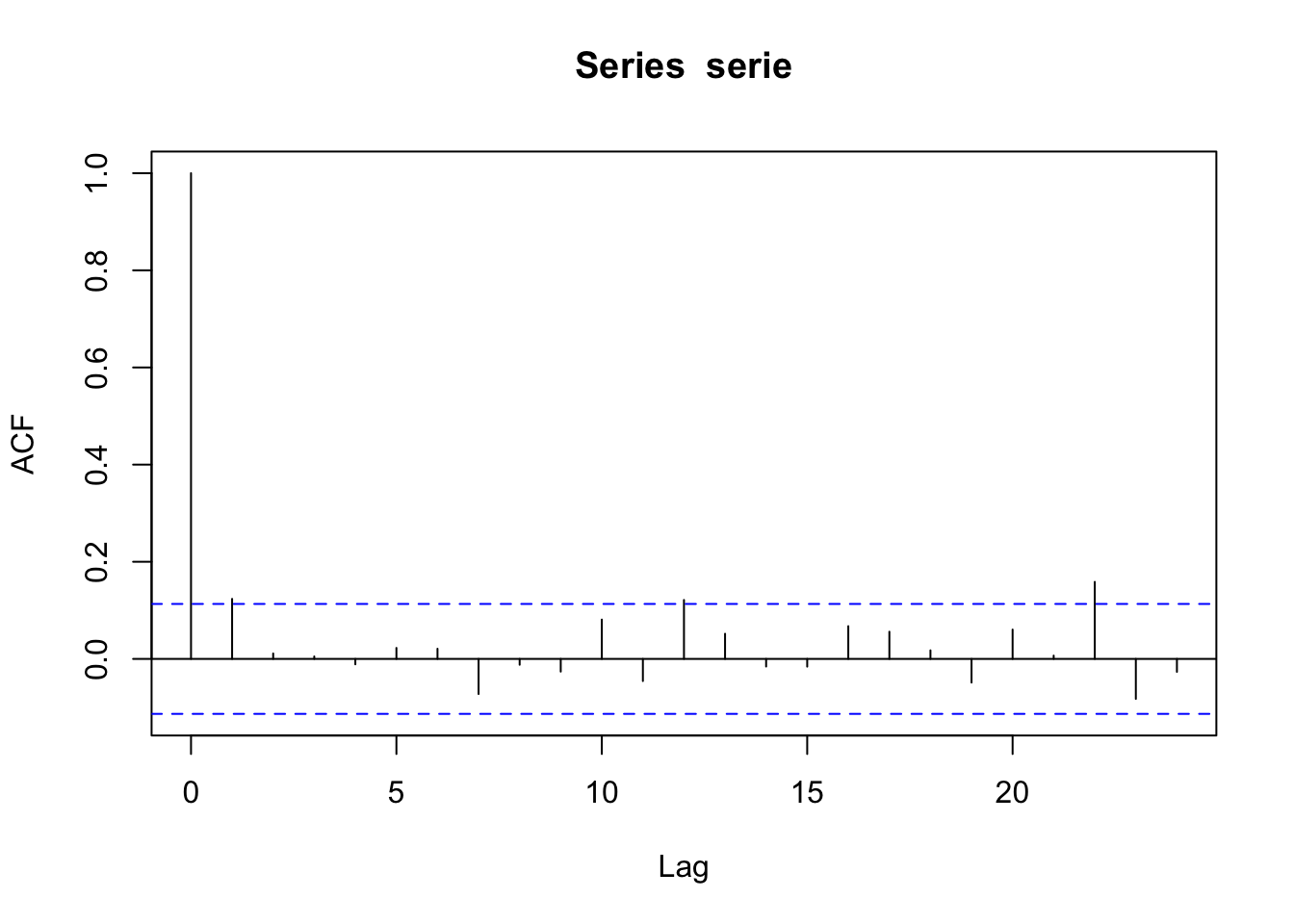
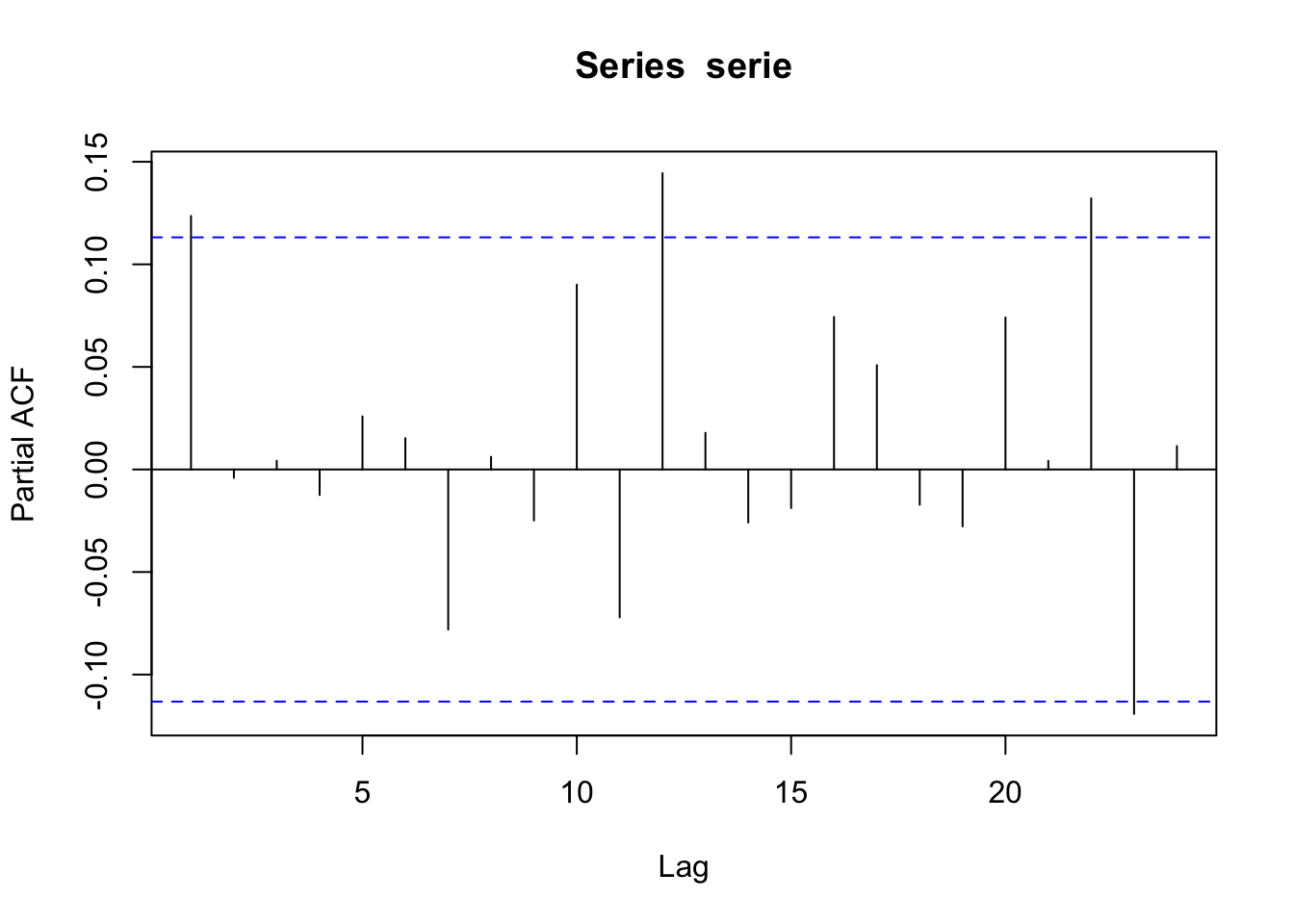
El ACF de la serie al cuadraro sigue un patrón ARMA debido a figura que muestran tanto el ACF como el PACF. Esto sugiere un modelo \(GARCH (1,0)\).
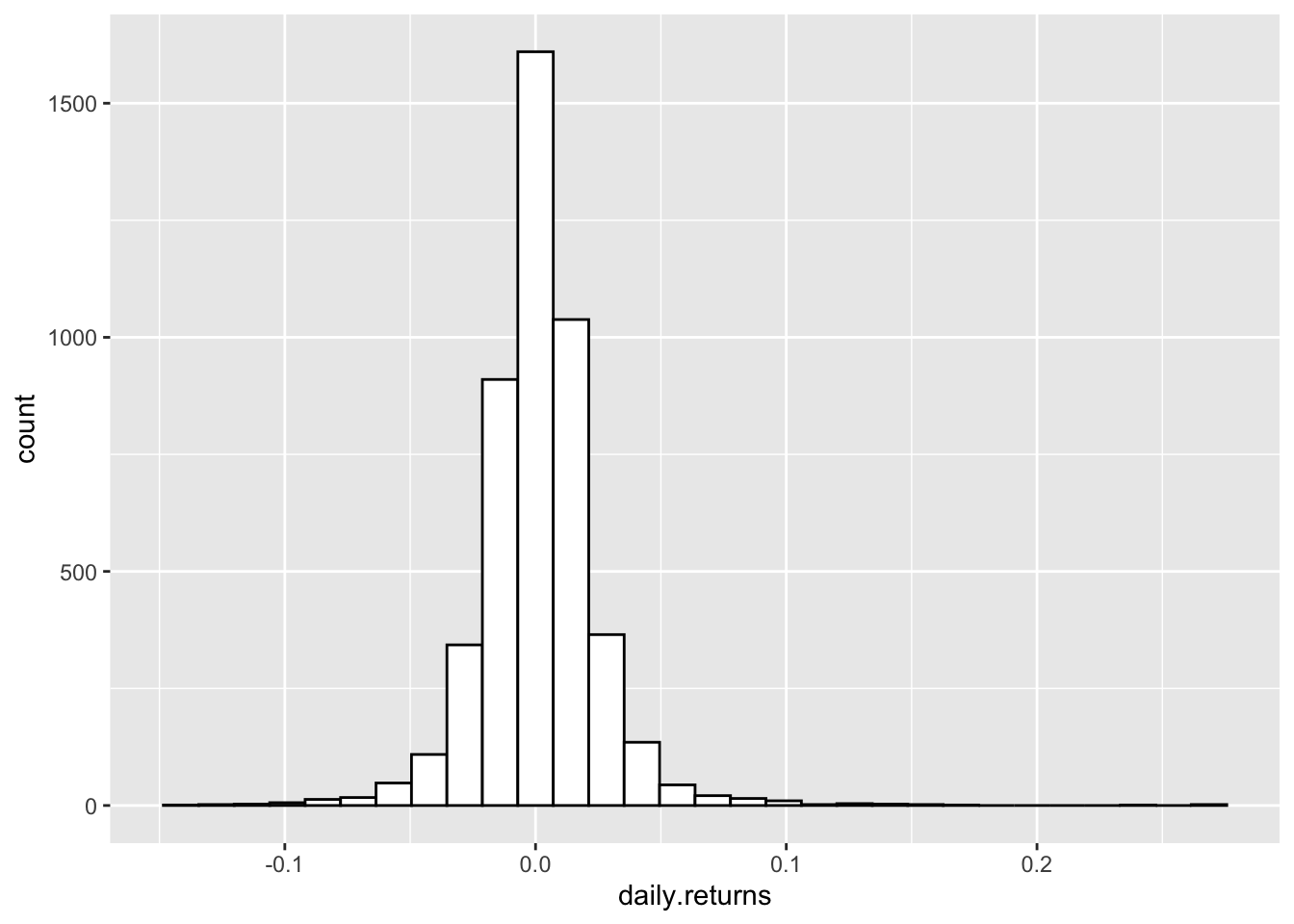
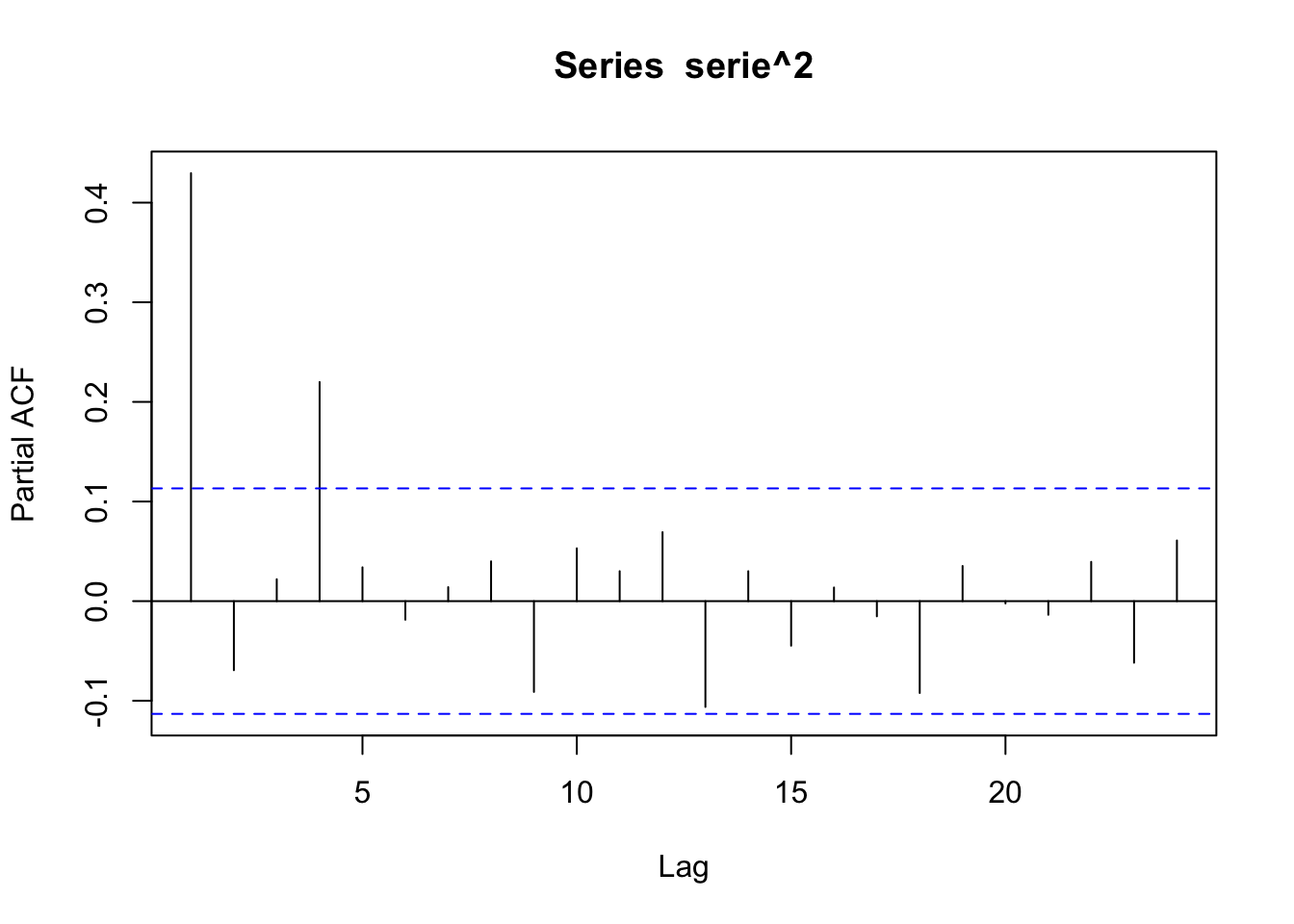Ajustamos un modelo \(GARCH(1,0)\) a los datos:
x <- serie
y = x - mean(x) #centramos x
x.g = garchFit(~garch(1,0), y, include.mean=F,trace = FALSE)
print(x.g)##
## Title:
## GARCH Modelling
##
## Call:
## garchFit(formula = ~garch(1, 0), data = y, include.mean = F,
## trace = FALSE)
##
## Mean and Variance Equation:
## data ~ garch(1, 0)
## <environment: 0x7fb1a2b687c8>
## [data = y]
##
## Conditional Distribution:
## norm
##
## Coefficient(s):
## omega alpha1
## 2.6750e-06 4.1904e-01
##
## Std. Errors:
## based on Hessian
##
## Error Analysis:
## Estimate Std. Error t value Pr(>|t|)
## omega 2.675e-06 3.347e-07 7.991 1.33e-15 ***
## alpha1 4.190e-01 1.048e-01 3.998 6.39e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Log Likelihood:
## 1436.056 normalized: 4.786853
##
## Description:
## Sat Dec 23 06:32:43 2023 by user:Ajustamos un modelo \(GARCH(2,0)\) a los datos:
##
## Title:
## GARCH Modelling
##
## Call:
## garchFit(formula = ~garch(2, 0), data = y, include.mean = F,
## trace = FALSE)
##
## Mean and Variance Equation:
## data ~ garch(2, 0)
## <environment: 0x7fb19f290908>
## [data = y]
##
## Conditional Distribution:
## norm
##
## Coefficient(s):
## omega alpha1 alpha2
## 2.5013e-06 4.1879e-01 4.7495e-02
##
## Std. Errors:
## based on Hessian
##
## Error Analysis:
## Estimate Std. Error t value Pr(>|t|)
## omega 2.501e-06 3.981e-07 6.282 3.34e-10 ***
## alpha1 4.188e-01 1.071e-01 3.911 9.17e-05 ***
## alpha2 4.749e-02 6.992e-02 0.679 0.497
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Log Likelihood:
## 1436.189 normalized: 4.787295
##
## Description:
## Sat Dec 23 06:32:43 2023 by user:Se puede elegir el modelo con mayor valor de verosimilitud. No obstante, en este caso podemos observar que pese a que la verosimilitud es mayo en el \(GARCH(2,0)\), la ganancia es muy poca ante el costo de incorporar un nuevo parámetro. Entonces en este caso se recomienda el modelo \(GARCH(1,0)\).
Una manera automática de estimación:
# http://www.quintuitive.com/2012/08/22/arma-models-for-trading/
# https://www.r-bloggers.com/2013/03/automatic-armagarch-selection-in-parallel/
# https://gist.github.com/ivannp/5198580
garchAutoTryFit = function(
ll,
data,
trace=FALSE,
forecast.length=1,
with.forecast=TRUE,
ic="AIC",
garch.model="garch" )
{
xxx = paste( sep="",
"~ arma(", ll$order[1], ",", ll$order[2], ")+",
garch.model,
"(", ll$order[3], ",", ll$order[4], ")" )
formula = formula(paste0(xxx,collapse = "") )
fit = tryCatch( suppressWarnings(garchFit( formula=formula,
data=data,
trace=FALSE,
cond.dist=ll$dist )),
error=function( err ) TRUE
# ,warning=function( warn ) FALSE
)
# print(fit)
pp = NULL
if( !is.logical( fit ) ) {
if( with.forecast ) {
pp = tryCatch( predict( fit,
n.ahead=forecast.length,
doplot=FALSE ),
error=function( err ) FALSE,
warning=function( warn ) FALSE )
if( is.logical( pp ) ) {
fit = NULL
}
}
} else {
fit = NULL
}
if( trace ) {
if( is.null( fit ) ) {
cat( paste( sep="",
" Analyzing (", ll$order[1], ",", ll$order[2],
",", ll$order[3], ",", ll$order[4], ") with ",
ll$dist, " distribution done.",
"Bad model.\n" ) )
} else {
if( with.forecast ) {
cat( paste( sep="",
" Analyzing (", ll$order[1], ",", ll$order[2], ",",
ll$order[3], ",", ll$order[4], ") with ",
ll$dist, " distribution done.",
"Good model. ", ic, " = ", round(fit@fit$ics[[ic]],6),
", forecast: ",
paste( collapse=",", round(pp[,1],4) ), "\n" ) )
} else {
cat( paste( sep="",
" Analyzing (", ll[1], ",", ll[2], ",", ll[3], ",", ll[4], ") with ",
ll$dist, " distribution done.",
"Good model. ", ic, " = ", round(fit@fit$ics[[ic]],6), "\n" ) )
}
}
}
return( fit )
}
garchAuto = function(
xx,
min.order=c(0,0,1,1),
max.order=c(5,5,1,1),
trace=FALSE,
cond.dists="sged",
with.forecast=TRUE,
forecast.length=1,
arma.sum=c(0,1e9),
cores=1,
ic="AIC",
garch.model="garch" )
{
require( fGarch )
require( parallel )
len = NROW( xx )
models = list( )
for( dist in cond.dists )
for( p in min.order[1]:max.order[1] )
for( q in min.order[2]:max.order[2] )
for( r in min.order[3]:max.order[3] )
for( s in min.order[4]:max.order[4] )
{
pq.sum = p + q
if( pq.sum <= arma.sum[2] && pq.sum >= arma.sum[1] )
{
models[[length( models ) + 1]] = list( order=c( p, q, r, s ), dist=dist )
}
}
res = mclapply( models,
garchAutoTryFit,
data=xx,
trace=trace,
ic=ic,
garch.model=garch.model,
forecast.length=forecast.length,
with.forecast=TRUE,
mc.cores=cores )
best.fit = NULL
best.ic = 1e9
for( rr in res )
{
if( !is.null( rr ) )
{
current.ic = rr@fit$ics[[ic]]
if( current.ic < best.ic )
{
best.ic = current.ic
best.fit = rr
}
}
}
if( best.ic < 1e9 )
{
return( best.fit )
}
return( NULL )
}## data ~ arma(0, 0) + garch(1, 1)
## attr(,"data")
## [1] "data = data"
## <environment: 0x7fb1979d54c0>La función garchAuto indica que el mejor modelo para nuestros datos es: \(GARCH(1,1)\)
4.5.0.2 Ejemplo: acciones de Amazon
Importamos los datos directamente con la librería quantmod
library(quantmod)
library(PerformanceAnalytics)
library(highcharter)
prices1 <- Ad(getSymbols("AMZN",auto.assign = FALSE))
head(prices1)## AMZN.Adjusted
## 2007-01-03 1.9350
## 2007-01-04 1.9450
## 2007-01-05 1.9185
## 2007-01-08 1.8750
## 2007-01-09 1.8890
## 2007-01-10 1.8575Hacemos un gráfico de la cotización de las acciones de Amazon:
Calculamos el retorno según la fórmula:
\[ Retorno = \frac{X_t}{X_{t-1}}-1 \]
## daily.returns
## 2007-01-03 0.000000000
## 2007-01-04 0.005168015
## 2007-01-05 -0.013624733
## 2007-01-08 -0.022673937
## 2007-01-09 0.007466698
## 2007-01-10 -0.016675543## Index daily.returns
## Min. :2007-01-03 Min. :-0.1404944
## 1st Qu.:2011-03-30 1st Qu.:-0.0099654
## Median :2015-06-29 Median : 0.0008005
## Mean :2015-06-28 Mean : 0.0013122
## 3rd Qu.:2019-09-25 3rd Qu.: 0.0124223
## Max. :2023-12-22 Max. : 0.2694973Veamos ahora el histograma de los retornos:
library(ggplot2)
p <- ggplot(rets1, aes(x=daily.returns)) +
geom_histogram(color="black", fill="white")
p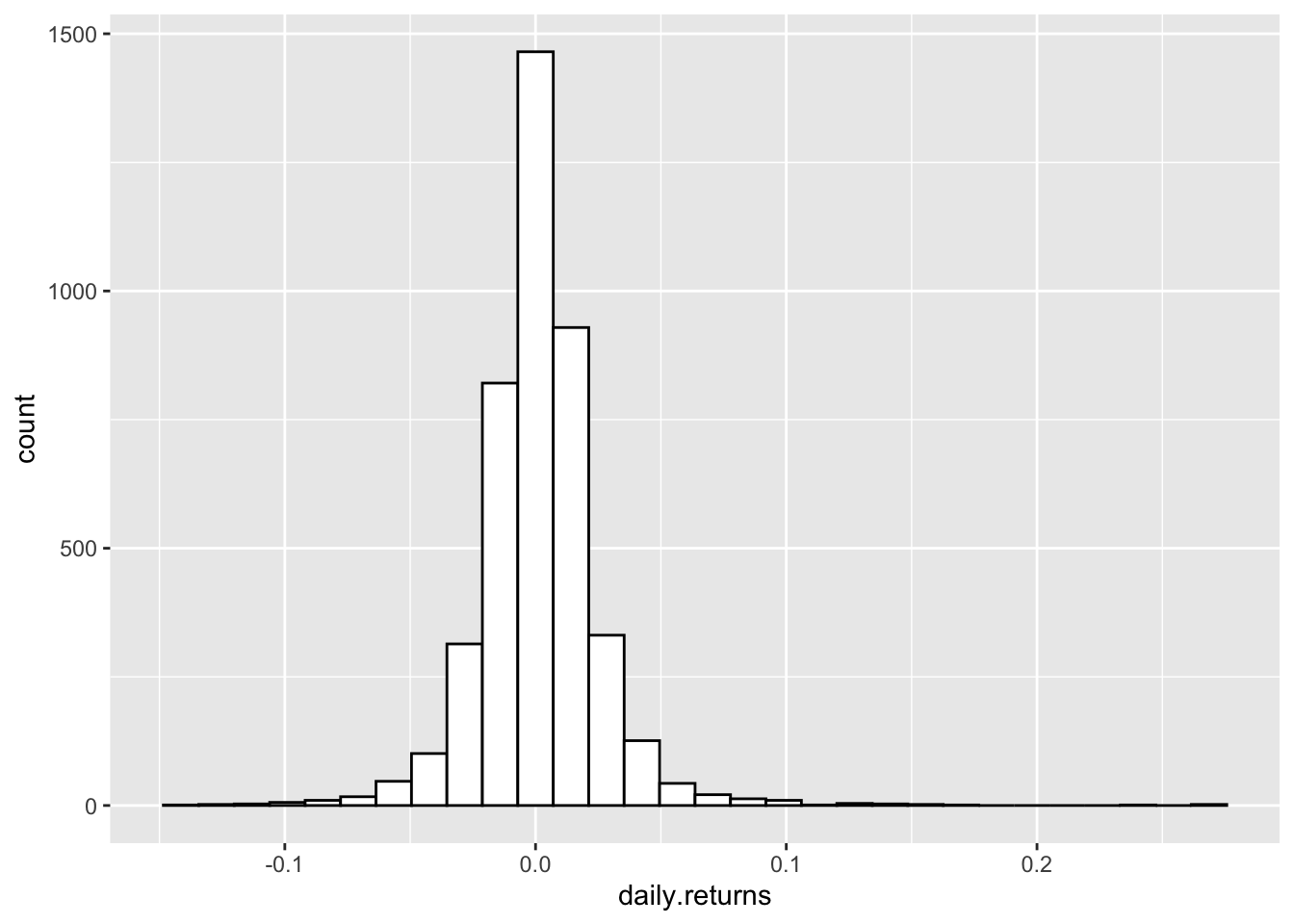
Calculamos el \(VaR\) (value at risk) con el método histórico para niveles de confianza de \(0.95\), \(0.999\), \(0.999\):
## daily.returns
## VaR -0.03308532## daily.returns
## VaR -0.05992208## daily.returns
## VaR -0.1104962Calculamos el \(CVaR\) (conditional value at risk) con el método histórico para niveles de confianza de \(0.95\), \(0.999\), \(0.999\):
## daily.returns
## ES -0.05145315## daily.returns
## ES -0.08432025## daily.returns
## ES -0.1250984Comparemos el ACF de los retornos y los retornos al cuadrado:
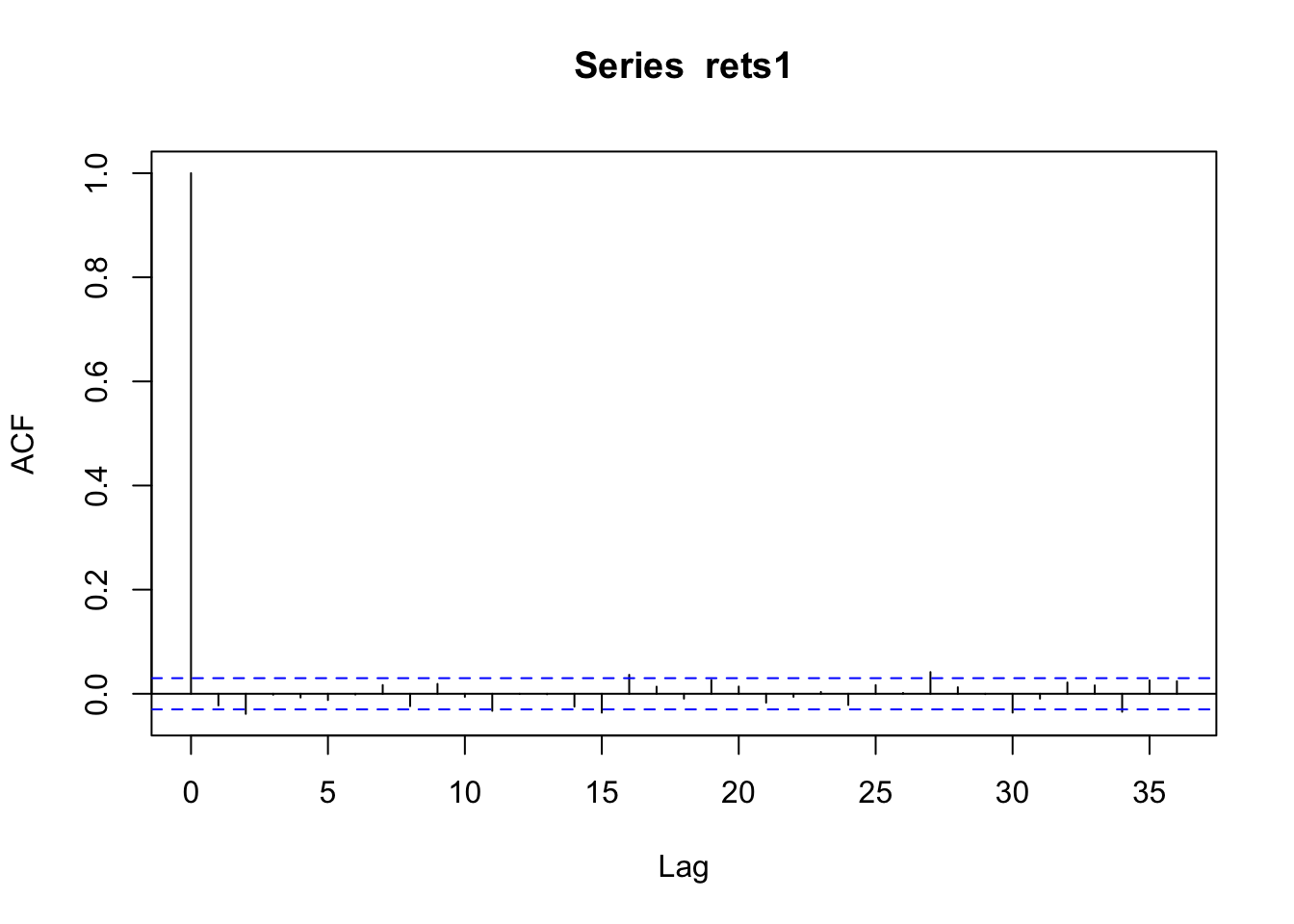
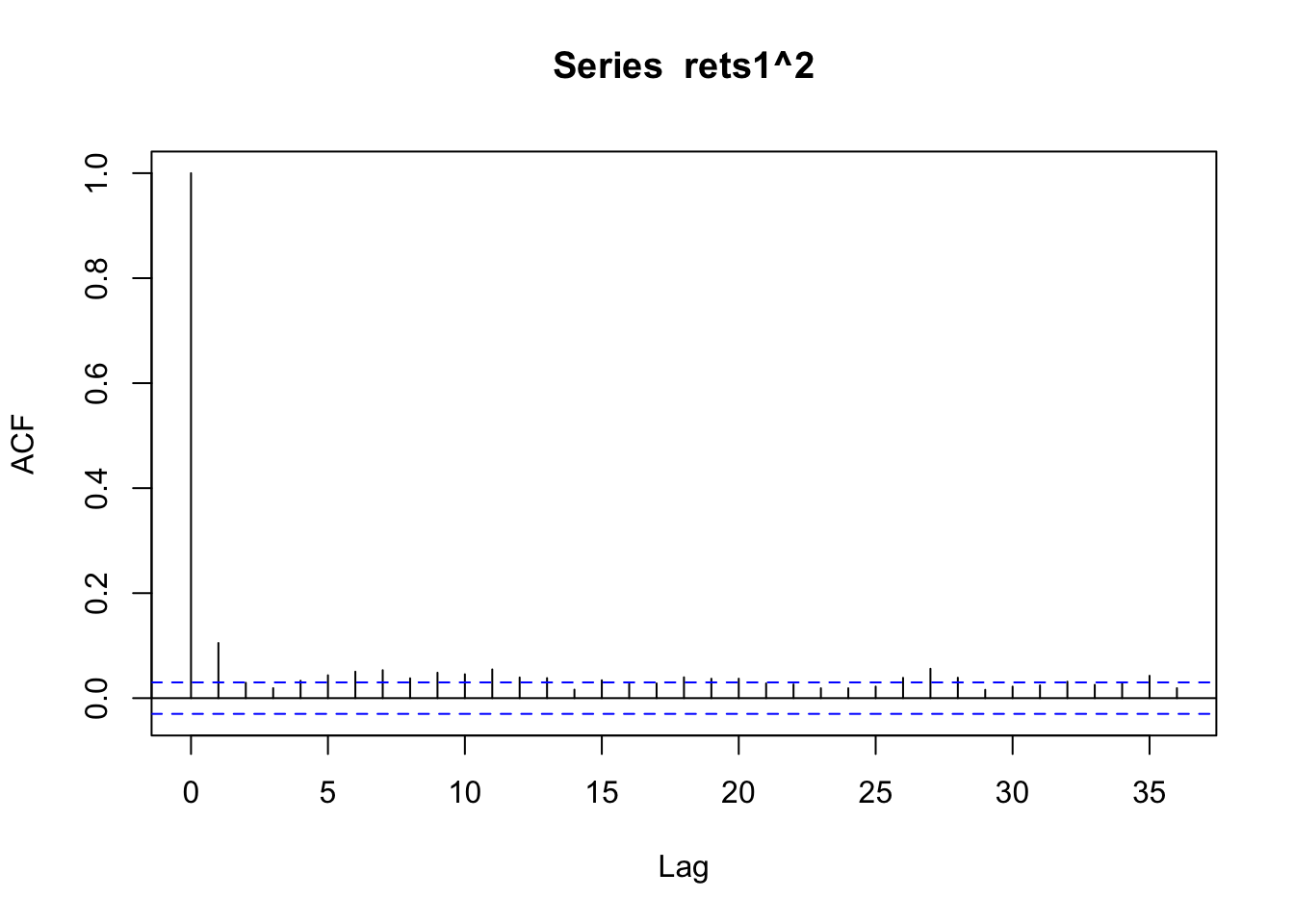
Podemos observar que los retornos parecen ser independientes mientras sus valores al cuadrado (volatilidad) se aroxima a un proceso \(ARMA(p,q)\).
y = rets1$daily.returns
garchAuto(y$daily.returns,cond.dists = "norm",max.order = c(0,0,4,4),cores = 8)##
## Title:
## GARCH Modelling
##
## Call:
## garchFit(formula = formula, data = data, cond.dist = ll$dist,
## trace = FALSE)
##
## Mean and Variance Equation:
## data ~ arma(0, 0) + garch(1, 3)
## <environment: 0x7fb1a4e1e7b8>
## [data = data]
##
## Conditional Distribution:
## norm
##
## Coefficient(s):
## mu omega alpha1 beta1 beta2 beta3
## 0.00153248 0.00001210 0.08998884 0.00000001 0.04720173 0.84808694
##
## Std. Errors:
## based on Hessian
##
## Error Analysis:
## Estimate Std. Error t value Pr(>|t|)
## mu 1.532e-03 3.123e-04 4.907 9.24e-07 ***
## omega 1.210e-05 2.761e-06 4.382 1.18e-05 ***
## alpha1 8.999e-02 1.341e-02 6.712 1.92e-11 ***
## beta1 1.000e-08 NaN NaN NaN
## beta2 4.720e-02 8.414e-03 5.610 2.02e-08 ***
## beta3 8.481e-01 NaN NaN NaN
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Log Likelihood:
## 10172.19 normalized: 2.380016
##
## Description:
## Sat Dec 23 06:32:49 2023 by user:4.6 Ejercicios
Analizar el índice S&P 500 desde 2000-12-28 a 2011-01-01 y estimar un modelo para su volatilidad.
A partir del índice de precios al consumidor (variación porcentual mensual nacional por dominios), determine el mejor modelo GARCH para el producto flores.