1 Características de una serie de Tiempo
 |
| George E.P.Box (1919-2013) Estadístico británico. Trabajó durante ocho años en Inglaterra para una empresa química y en ese periodo inventó la operación evolutiva y el análisis de las superficies de respuesta. En 1956 emiga a EEUU, donde funda el departamento de Estadística de la Universidad de Wisconsin en Madison, que se convierte en poco tiempo en uno de los principales centros de investigación estadística en el mundo. Creador con G. Jenkins (1932-1982) de la metodologías más usada actualmente para el análisis de series temporales, sus contribuciones a todos los campos de la estadística le han convertido en uno de los científicos más influyentes del siglo XX. |
Tomado de Peña-Sanchez (2005), sección cap 1 & 2.
Librerías usadas:
xtsquantmodlatticelatticeExtraRColorBrewer
1.2 Ejemplos de series univariantes
Cuando observamos una variable durante un periodo de tiempo (cada día, cada mes, cada año, etc) estamos ante la presencia de una serie de tiempo o serie temporal.
Los principales objetivos del análisis y modelización de series de tiempo son i) entender la dinámica o la estructura tiempo-dependiente en una serie (univariante) y ii) determinar las relaciones principales, rezagadas y de retroalimentación entre varias series (multivariante).
Las series temporales tienen diferentes características que nos ayudan a entenderlas y estudiarlas. Por ejemplo, existen series estacionarias, no estacionarias, estacionales, entre otras.
Series estacionarias
Las siguientes figuras 1.1 y 1.2 muestran casos de series estacionarias.
La serie 1.1 representa las leguas diarias recorridas por la flota de Cristóbal Colón en su primer viaje a América desde la isla de la Gomera a la de San Salvador.
uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/AST/colon.dat"
colon <- read.csv(uu,header = FALSE,sep = "")
colon.ts <- ts(colon$V2, st = c(1492,9), freq = 365)
plot(colon.ts)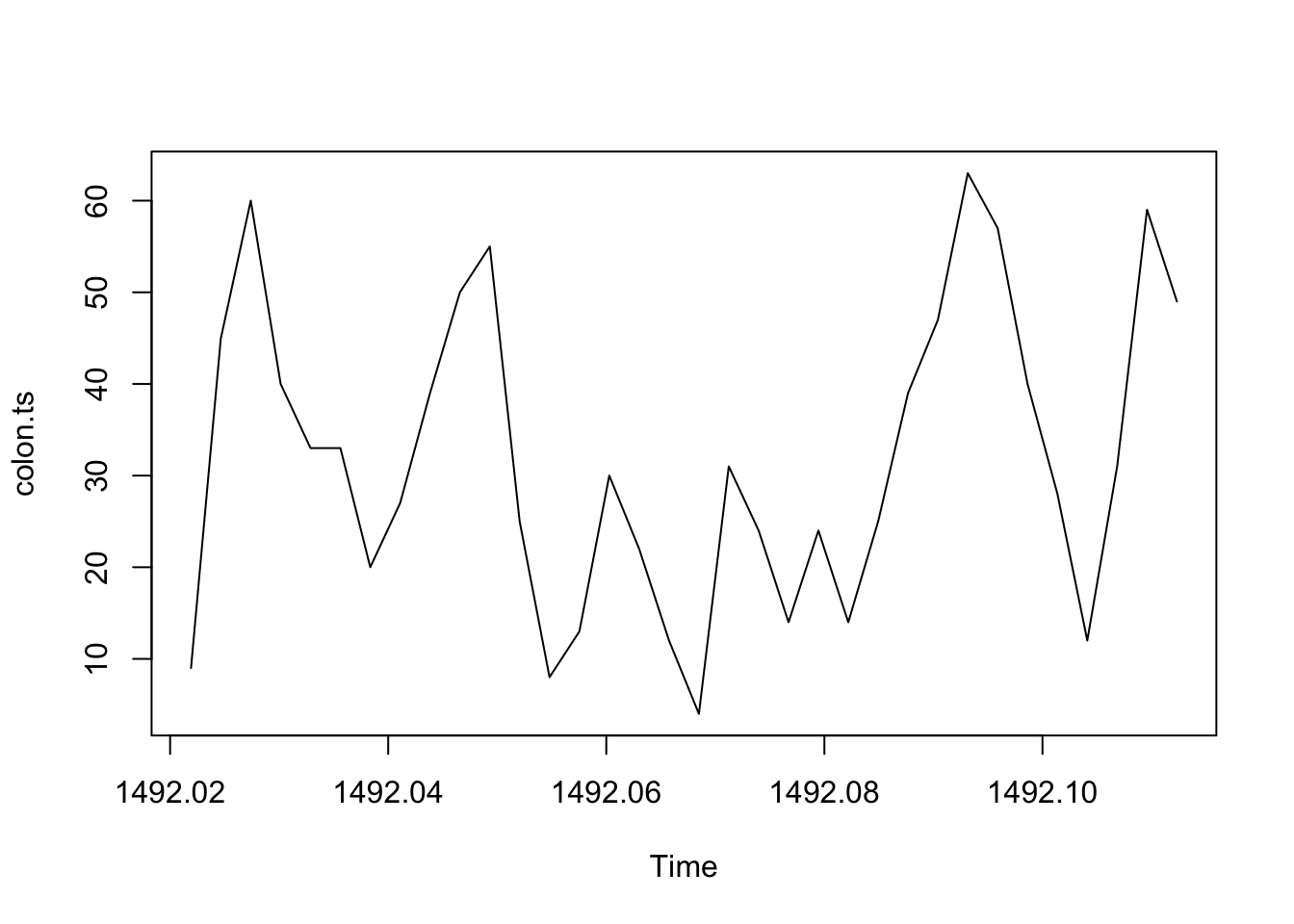
Figure 1.1: Leguas diarias recorridas por la flota de Cristóbal Colón en su primer viaje a América desde la isla de la Gomera a la de San Salvador
En general usaremos objetos ts para estudiar series de tiempo. No obstante, otros paquetes como xts (Ryan and Ulrich (2020)) o zoo (Zeileis and Grothendieck (2005)) son también especializados en series de tiempo.
library(xts)
inds <- seq(as.Date("1492-09-08"), as.Date("1492-10-11"), by = "day")
colon.xts <- xts(x = colon$V2, order = inds)
plot(colon.xts,main = "Leguas diarias recorridas por CC")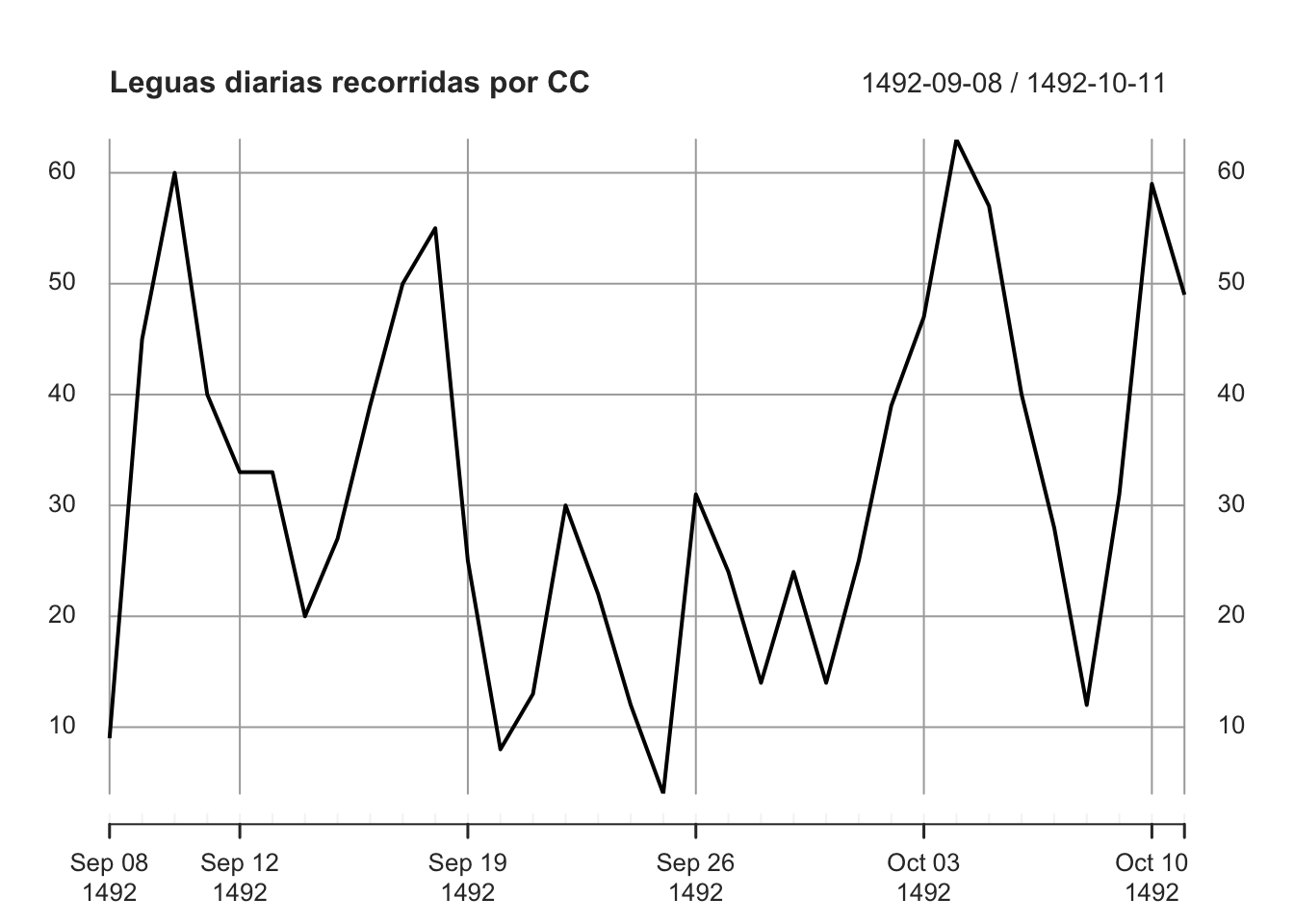
Veamos un resumen estadístico de los datos
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 4.00 20.50 30.50 31.82 43.75 63.00Podemos observar en 1.1 que los valores de la serie oscilan al rededor de un recorrido promedio estable de unas 32 leguas. El gráfico no muestra una clara tendencia creciente o decreciente.
La serie 1.2 muestra la evolución de precios de las acciones de Apple entre enero 2015 y diciembre 2020.
library(quantmod)
# Apple .............................
getSymbols("AAPL", src = "yahoo", from = '2015-01-01',
to = "2020-12-31",warnings = FALSE,
auto.assign = TRUE)## [1] "AAPL"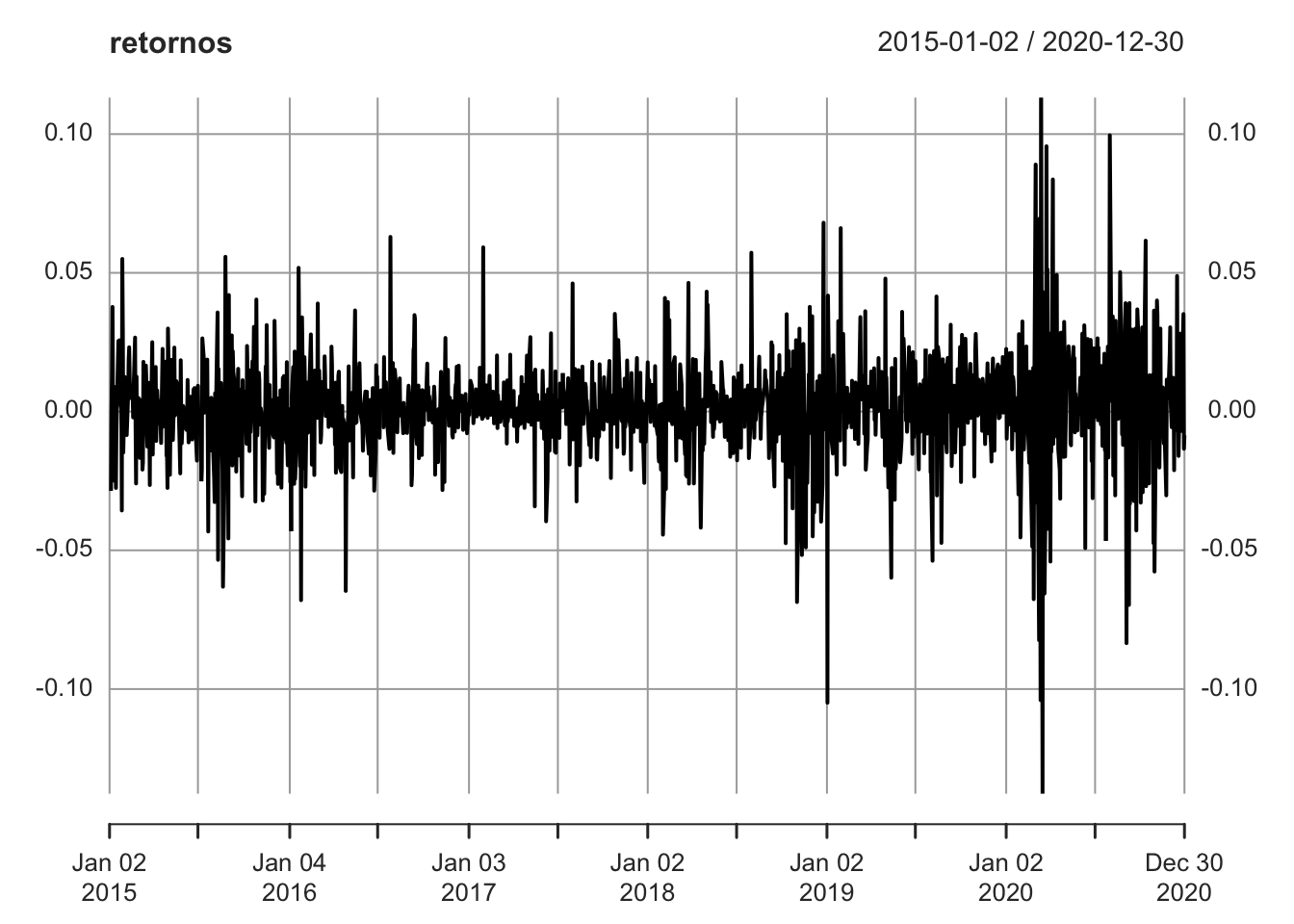
Figure 1.2: Retornos de las acciones de Apple entre 2015 y 2020
Veamos su resumen estadístico
## Index AAPL.Adjusted
## Min. :2015-01-02 Min. :-0.1377081
## 1st Qu.:2016-07-02 1st Qu.:-0.0063592
## Median :2017-12-31 Median : 0.0009403
## Mean :2017-12-31 Mean : 0.0011139
## 3rd Qu.:2019-07-02 3rd Qu.: 0.0100208
## Max. :2020-12-30 Max. : 0.1131577
## NA's :1Notamos que los retornos de las acciones de Apple oscilan al rededor de 0.0011139, equivalente al 1.34 por cierto anual. Como en el caso anterior, esta serie tiene un nivel fijo, sin ninguna tendencia clara a crecer o decrecer con el tiempo.
Series no estacionarias
La figura 1.3 presenta una serie que no es estable en el tiempo, esto se debe a que su nivel aumenta con el tiempo (tiene tendencia). La serie representa a la población mayor de 16 años en españa desde el primer cuatrimestre de 1977 hasta el cuarto del 2000. Este tipo de serie es no estacionaria.
uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/AST/pobmay16.dat"
pobmay16 <- read.csv(uu,header = FALSE,sep = "")
pobmay16.ts <- ts(pobmay16$V2, st = c(1977,1), freq = 4)
plot(pobmay16.ts)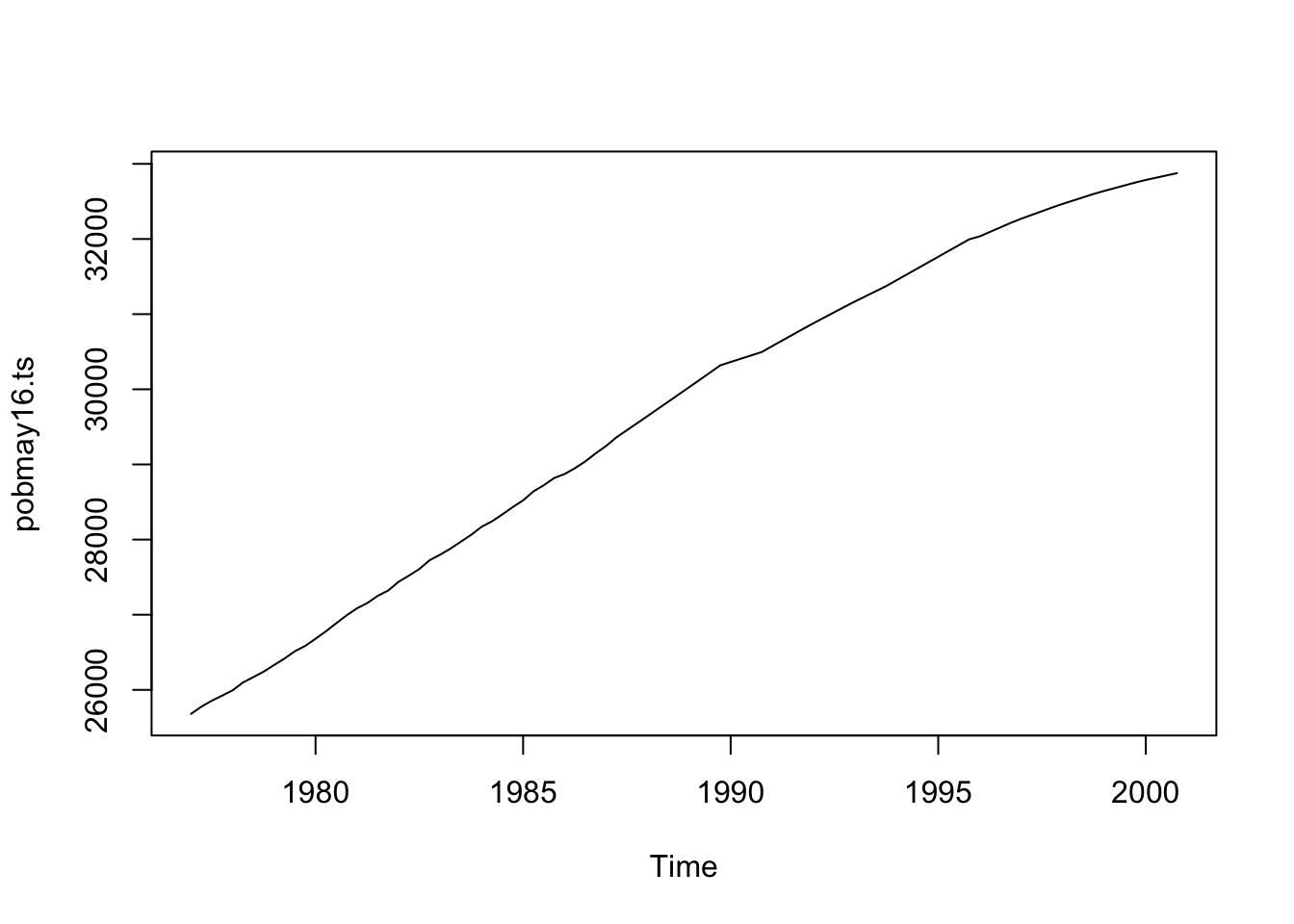
Figure 1.3: Población mayor de 16 años en españa desde el primer cuatrimestre de 1977 hasta el cuarto del 2000
Notemos también que la serie tiene una clara tendencia positiva. La mayoría de series sociales y económicas no son estacionarias y presentan tendencias más o menos constantes en el tiempo.
En este caso la tendencia es bastante lineal, aunque en una primera ventana de tiempo se tiene una pendiente más pronunciada que la segunda. Esto sugiere que el crecimiento anual de la población puede ser decreciente en el tiempo. Cuanto esto sucede se dice que existe una tendencia variable en el tiempo, no constante. De hecho, no es común observar tendencias constantes en periodos lagos de observación.
La figura 1.4 muestra los nacimientos anuales en España, entre 1946 y 2000.
uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/AST/nacidos.dat"
nacidos <- read.csv(uu,header = FALSE,sep = "")
nacidos.ts <- ts(nacidos$V2, st = c(1946,1), freq = 1)
plot(nacidos.ts)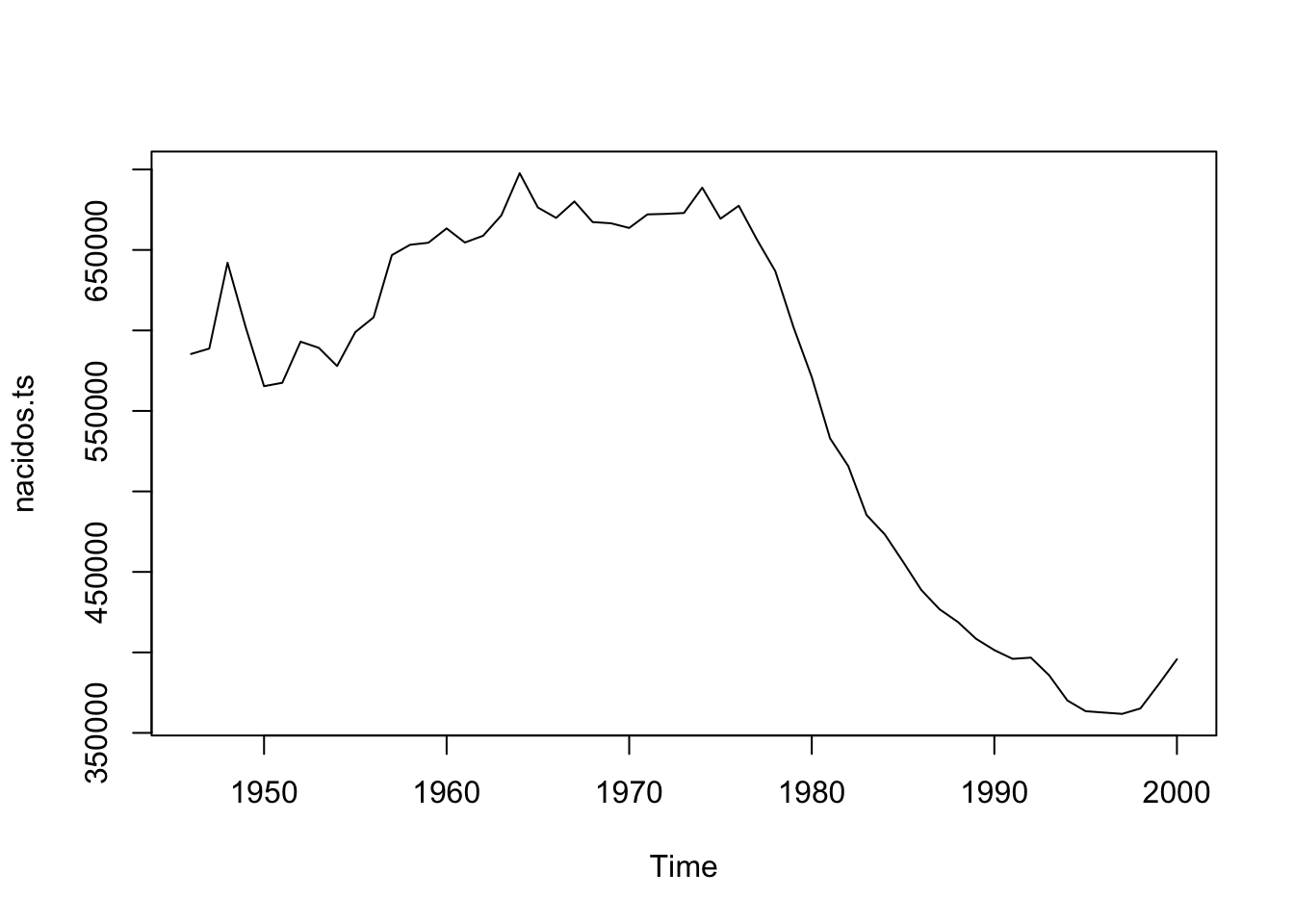
Figure 1.4: Nacimientos anuales en España, entre 1946 y 2000
Esta serie no es estable ya que no oscila al rededor de ningún nivel fijo. La serie no muestra una única tendencia creciente en todo el periodo. Los nacimientos crecen entre los 50 y 60, luego tienen un periodo más o menos estable hasta los 70 y luego decrecen. Esta serie presenta una tendencia evolutiva o cambiante en el tiempo.
Estacionalidad
Las figuras 1.5 y 1.6 muestran los datos del precio del trigo en Valladolid en periodo julio 1880- diciembre 1890 y de Lluvia en Cumbayá desde mayo 2000 a julio 2019 respectivamente.
uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/AST/trigo.dat"
trigo <- read.csv(uu,header = FALSE,sep = "")
trigo.ts <- ts(trigo$V2, st = c(1880,7), freq = 12)
plot(trigo.ts)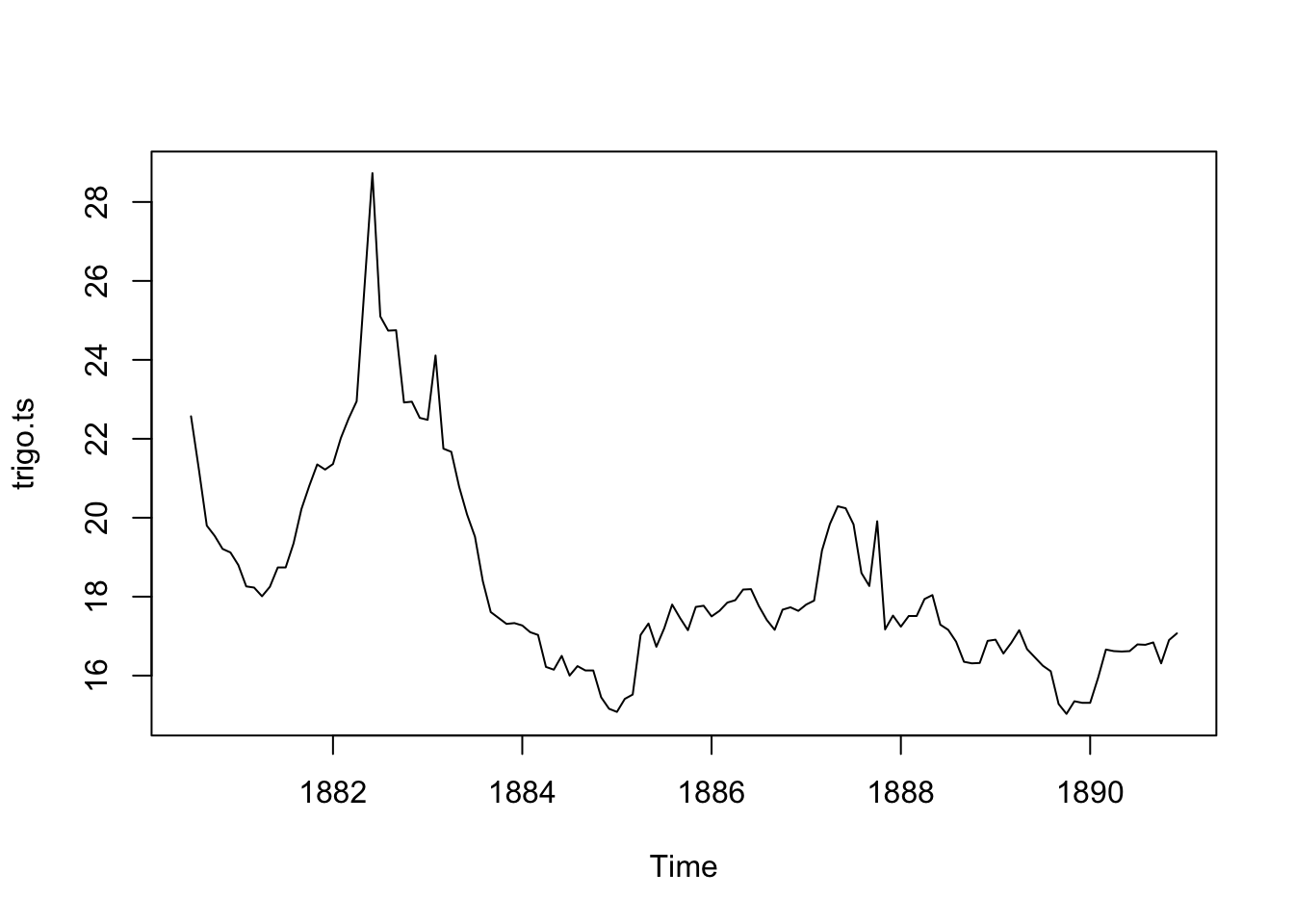
Figure 1.5: Precio del trigo en Valladolid en periodo julio 1880- diciembre 1890
El precio del trigo no muestra una evolución al rededor de un nivel fijo y tiene un nivel variable en el tiempo. Presenta un gran crecimiento a finales de 1882 y luego decrece para luego mostrar menores fluctuaciones en los últimos años.
uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/precipEstacionesEC.csv"
lluviaSC <- read.csv(uu,header = TRUE,sep = ",")
lluviaSC.ts <- ts(lluviaSC$P13, st = c(2000,5), freq = 12)
plot(lluviaSC.ts)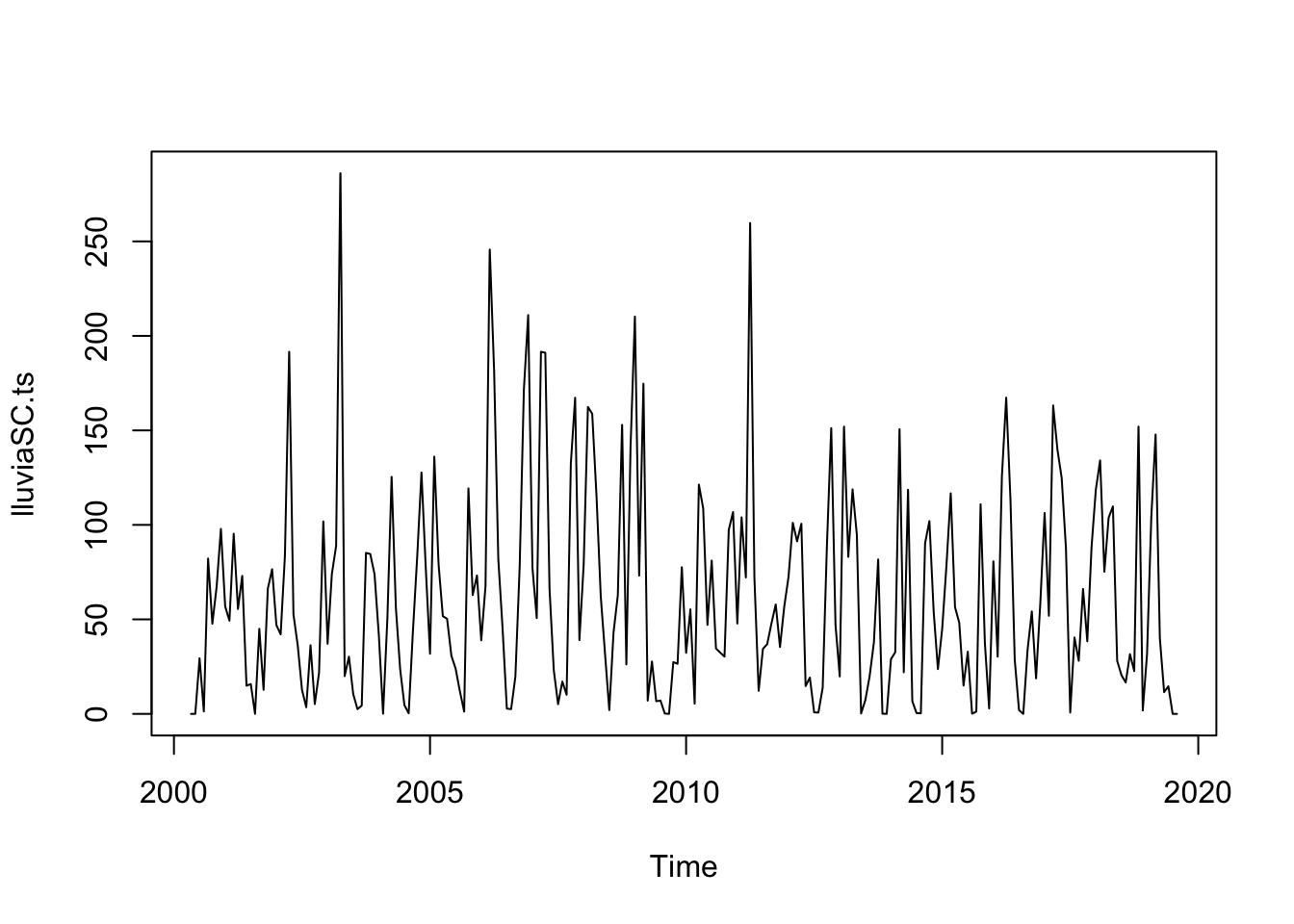
Figure 1.6: Lluvia en Cumbayá desde mayo 2000 a julio 2019
En la serie de lluvia vemos que los valores oscilan al rededor de un valor fijo pero algunos meses tienen sistemáticamente más lluvia que otros. Agosto es el mes que presenta menos luvia y abril el que muestra más lluvia.
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.00 19.77 47.75 61.72 89.03 286.10Veamos los datos de agosto y abril:
plot(window(lluviaSC.ts,start = c(2001,4),freq = 1)) # abril
lines(window(lluviaSC.ts,start = c(2000,8),freq = 1),lty = 2) # agosto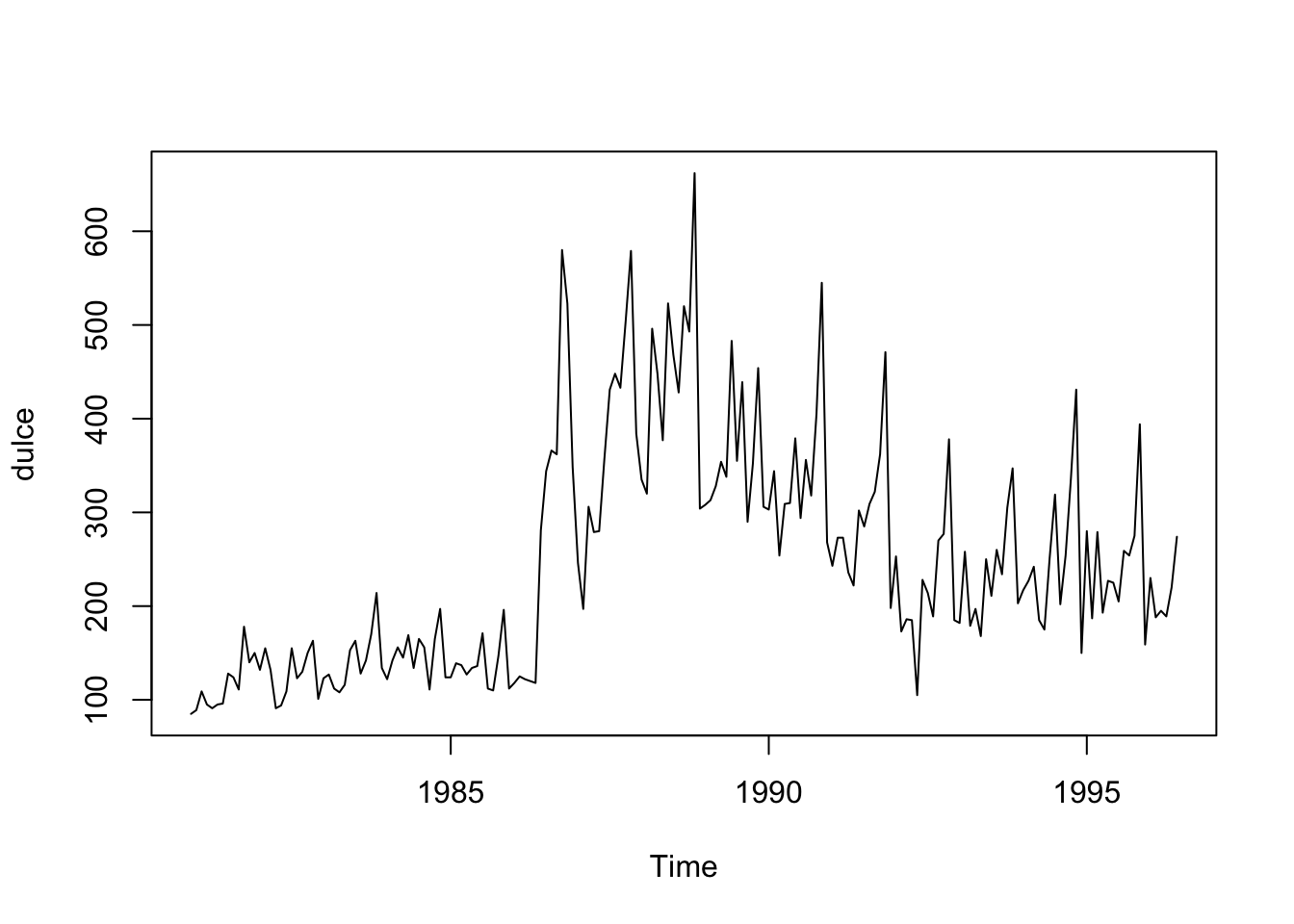
En efecto, vemos que las lluvias de los meses de agosto y abril están muy por debajo y por arriba respecto a la media histórica.
En resumen, las series temporales pueden tener o no un nivel estable en el tiempo, y si lo tienen, pueden presentar tendencias más o menos constantes.
Cuando el nivel de la serie no es estable decimos que la serie no es estacionaria. Un caso particular de no estacionariedad es cuando el nivel varía siguiendo un ciclo.
1.3 Ejemplos de series multivariantes
Además de estudiar la evolución histórica de una serie, los modelos de series temporales nos permiten estudiar la relación dinámica entre dos o más series.
Por ejemplo, la figura 1.7 muestra las series de número de vehículos matriculados y del consumo de gasolina en España en el periodo 1960 a 1999.
uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/AST/gasolauto.dat"
gasolauto <- read.csv(uu,header = FALSE,sep = "")
gasolauto.ts <- ts(gasolauto$V2, st = c(1945,1), freq = 12)
uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/AST/matricul.dat"
matricula <- read.csv(uu,header = FALSE,sep = "")
matricula.ts <- ts(matricula$V1, st = c(1960,1), freq = 12)
aux <- window(gasolauto.ts,st = c(1960,1))
ts.plot(cbind(log(aux),log(matricula.ts)),col = c(3,4))
legend("bottomright",c("Consumo de gasolina","Matriculaciones"), lty = 1,col = c(3,4))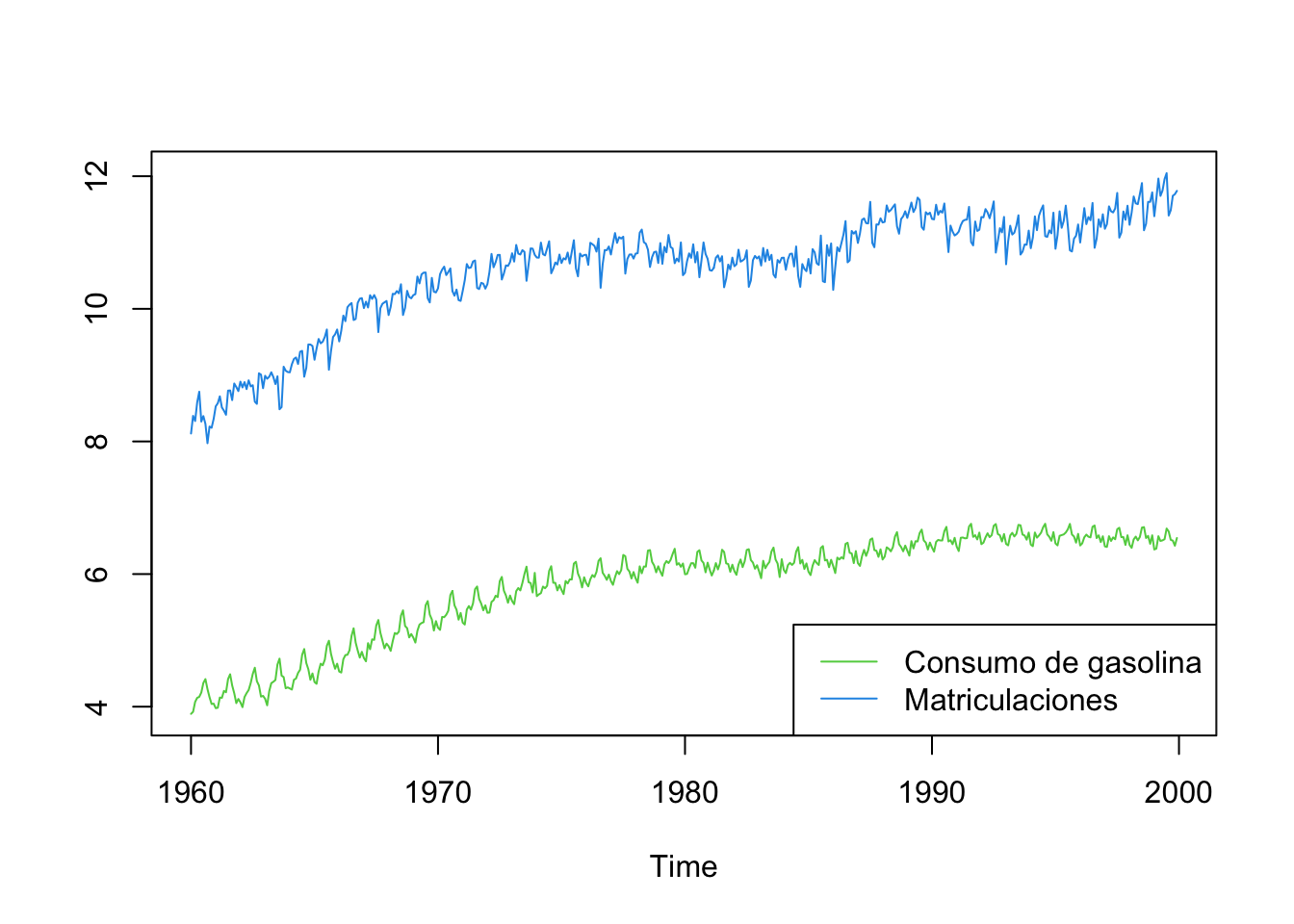
Figure 1.7: Logaritmos del número de vehículos matriculados y del consumo de gasolina en España en el periodo 1960 a 1999
Ambas series son no estacionarias y estacionales, con pautas marcadas a lo largo del año.
Entre estas dos series es esperable que exista una relación donde aumentos en las matriculaciones de automóviles produzca aumentos en el consumo de gasolina, aunque el gráfico sugiere que esta relación puede ir variando en el tiempo.
No obstante, no es esperable una relación que vaya en el sentido contrario, del consumo de gasolina a las matriculaciones.
Las relaciones entre las variables dinámicas pueden ser en ambas direcciones. Por ejemplo, la figura 1.8 presenta la evolución de la cuota de mercado de los dentífricos Crest y Colgate medida en semanas entre el 1 de enero de 1958 y abril de 1963.
uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/AST/crestcolgate.dat"
crestcolgate <- read.csv(uu,header = FALSE,sep = "")
colnames(crestcolgate) <- c("cuotaCrest","cuotaColgate","precioCrest","precioColgate")
crestcolgate <- na.omit(crestcolgate)
crestcolgate.ts <- ts(crestcolgate, st = c(1958,1), freq = 48)
ts.plot(scale(crestcolgate.ts[,1:2]),col = c(3,4))
legend("bottomright",c("Crest","Colgate"), lty = 1,col = c(3,4))
abline(v = time(crestcolgate.ts)[136])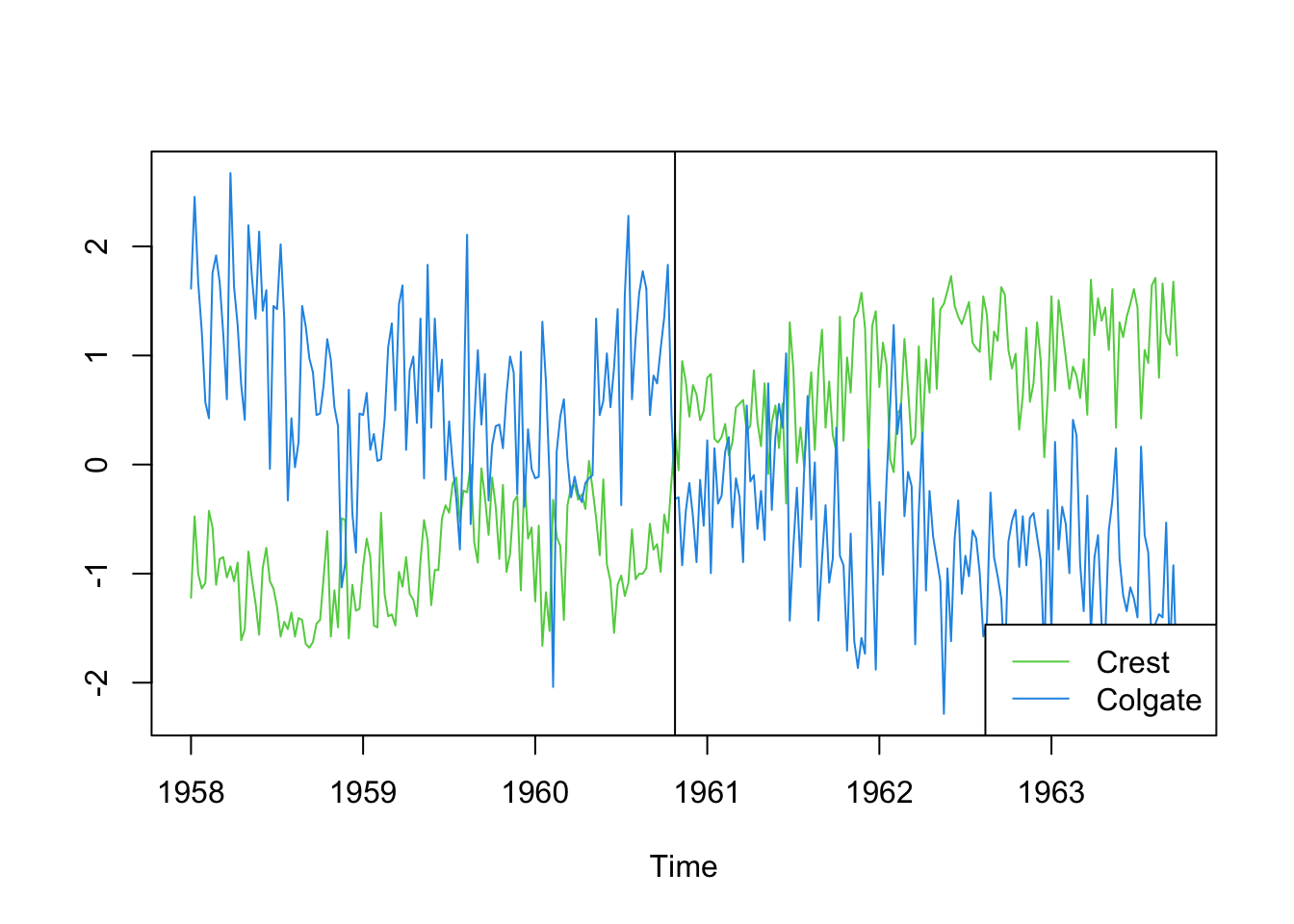
Figure 1.8: Cuota de mercado de los dentífricos Crest y Colgate
Ambas series son no estacionarias con un nivel que cambia en el tiempo. También apreciamos que existe una relación bidireccional o de retroalimentación: una subida de Crest produca una bajada d Colgate, pero también los cambios en Colgate afectan a la evolución de la cuota de Crest.
Además existen intervenciones externas (shocks) que afectan a las series y explican el cambio brusco en la cuota de mercado de Crest. En esa semana se da una declaración formal del Gobierno de EEUU que indica que el fluor es efectivo para combatir las caries, y Crest lo tenía.
Un problema importante es modelizar estos efectos externos o efectos de intervención (shocks) dentro de la relación dinámica entre las series.
1.4 Ejercicios
Determinar catacterísticas de las series de tiempo (estacionaria o no, si tiene estacionalidad, si es de niveles constantes o variables).
Descargue los datos del IPC de Ecuador y describa las caracterísitcas del IPC General Nacional mensual desde el 2001. (ver tabulados y series históricas Excel)
Del conjunto de datos anterior, grafique cada uno de los meses en series de tiempo separadas, 12 series en total. Comente el resultado.