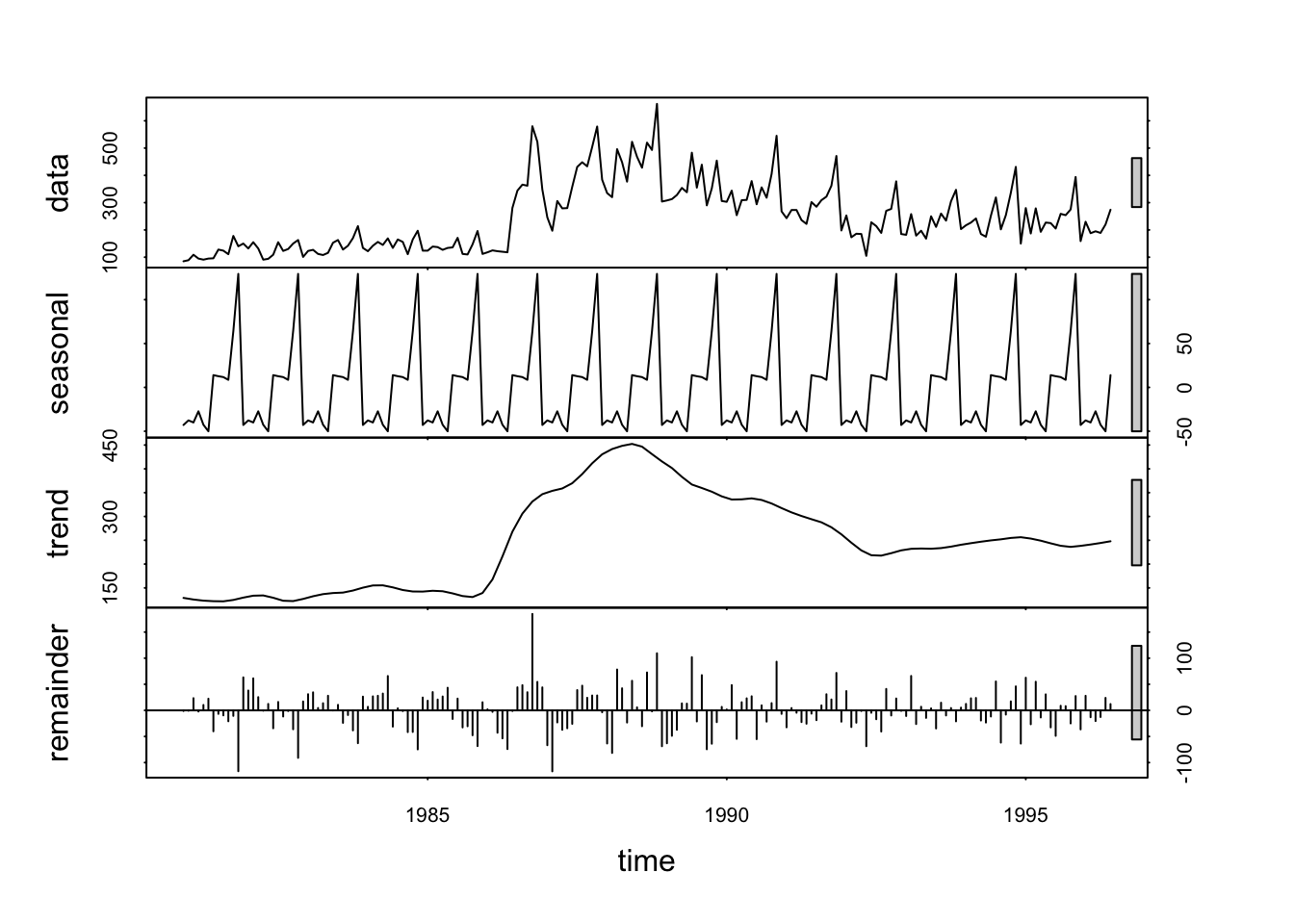
2 Análisis descriptivo de una serie temporal

FlorenceNightingaleDavid
Florence Nightingale (1820-1910) Estadística británica. Fue la primera mujer en ser miembro de la Royal Statistical Society en 1858. Fue pionera en el uso de gráficos circulares. Nightingale realizó un estudio estadístico completo sobre el saneamiento en la vida rural de la India y fue la figura principal en la introducción de una mejor atención médica y servicios de salud pública en la India. Fue pionera en estadística médica e influyó en Francis Galton y Karl Pearson.

2.1 Rezagos y operadores en diferencia

2.1.1 Operadores de rezagos

Definición:

\[ \Delta Y_{t-i} = Y_t-Y_{t-i} \]

Ejemplos:

\[ \Delta Y_{t} = Y_t-Y_{t-1} \]

Caso general:

\[ L^{j}Y_t=Y_{t-j} \]

Ejemplos:

\[ L^1Y_t=LY_t=Y_{t-1} \] \[ L^2Y_t=Y_{t-2} \]

\[ L^{-2}Y_t=Y_{t+2} \]

\[ L^{i}L^{j}=L^{i+j}=Y_{t-(i+j)} \]

2.2 Manipulando ts en R

  • Abrir IPCEcuador.csv
  • Se puede ver una inflación variable
uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/IPCEcuador.csv"
datos <- read.csv(url(uu),header=T,dec=".",sep=",")
IPC <- ts(datos$IPC,start=c(2005,1),freq=12)
plot(IPC)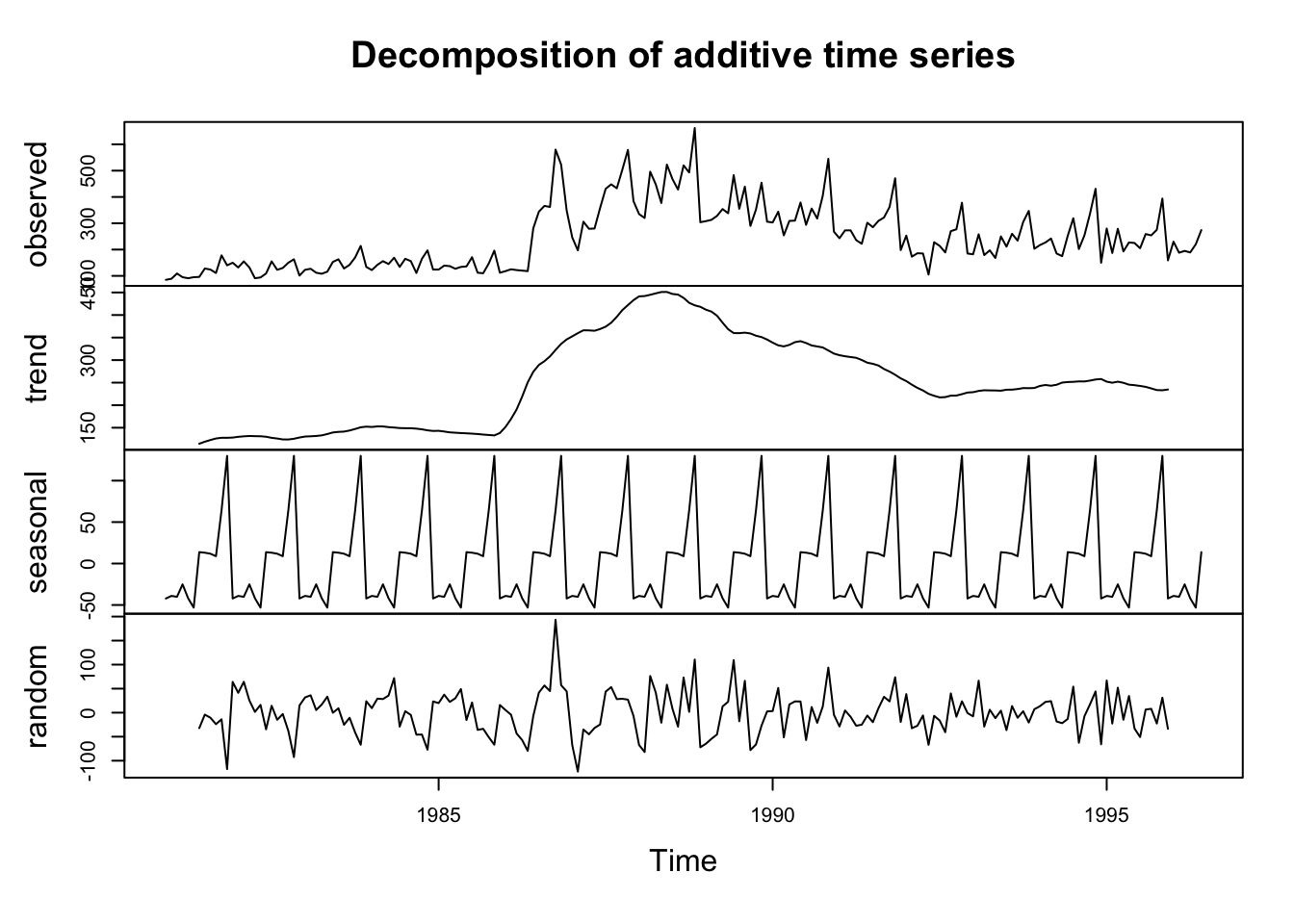

La serie tiene tendencia creciente. Tratemos de quitar esa tendencia:

plot(diff(IPC)) # Se puede ver una inlfacion estable
abline(h=0)

Se ha estabilizado, pero podemos hacerlo aún más con el logaritmo de la diferencia:

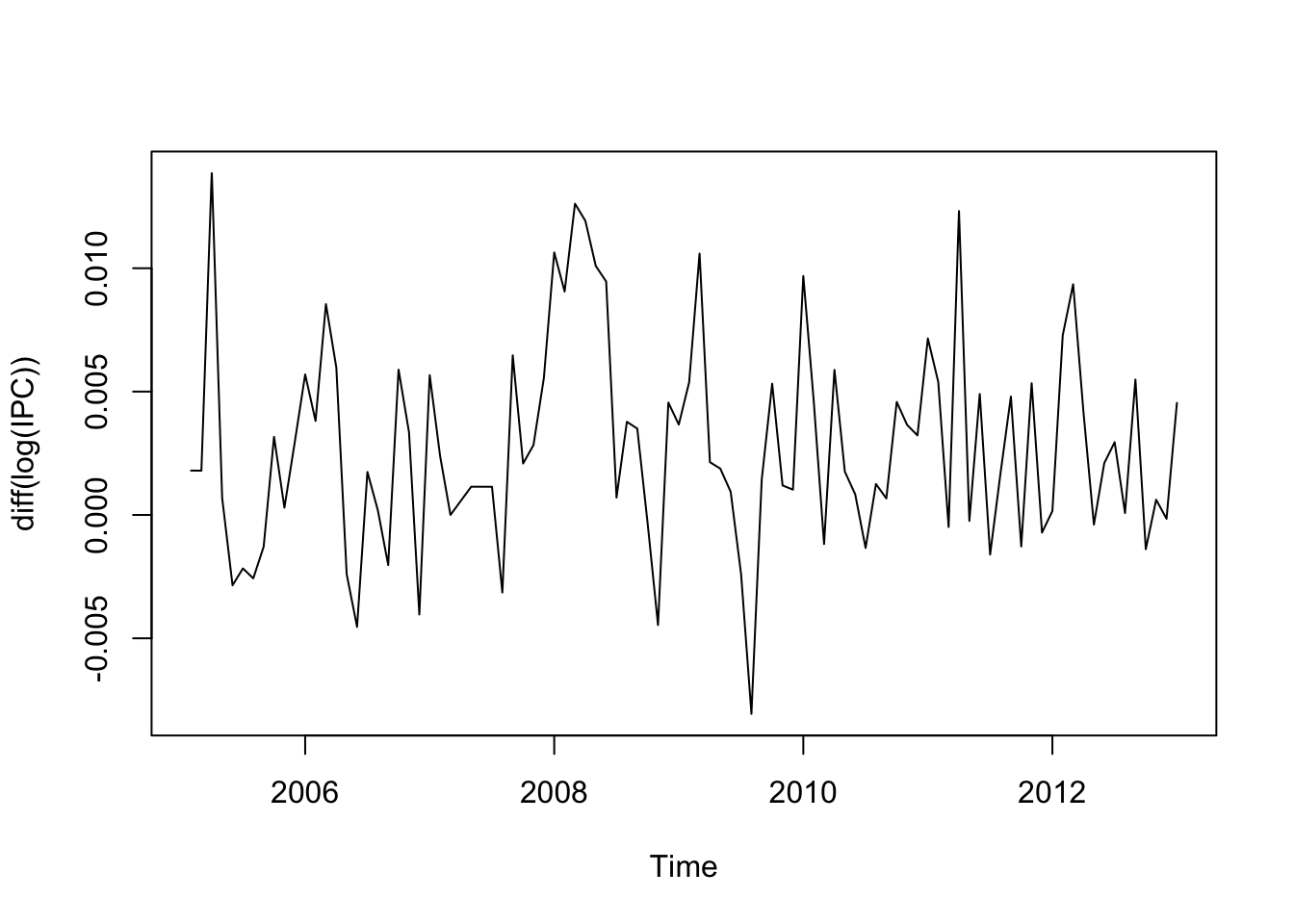
plot(diff(log(IPC))) #Tasa de variacion del IPC

La serie no tiene tendencia y es estable. Ahora, si deseo trabajar con un subconjunto de datos, puedo…

# Solo quiero trabajar con los datos de agosto 2008
IPC2 <- window(IPC,start=c(2008,8),freq=1)
plot(IPC2)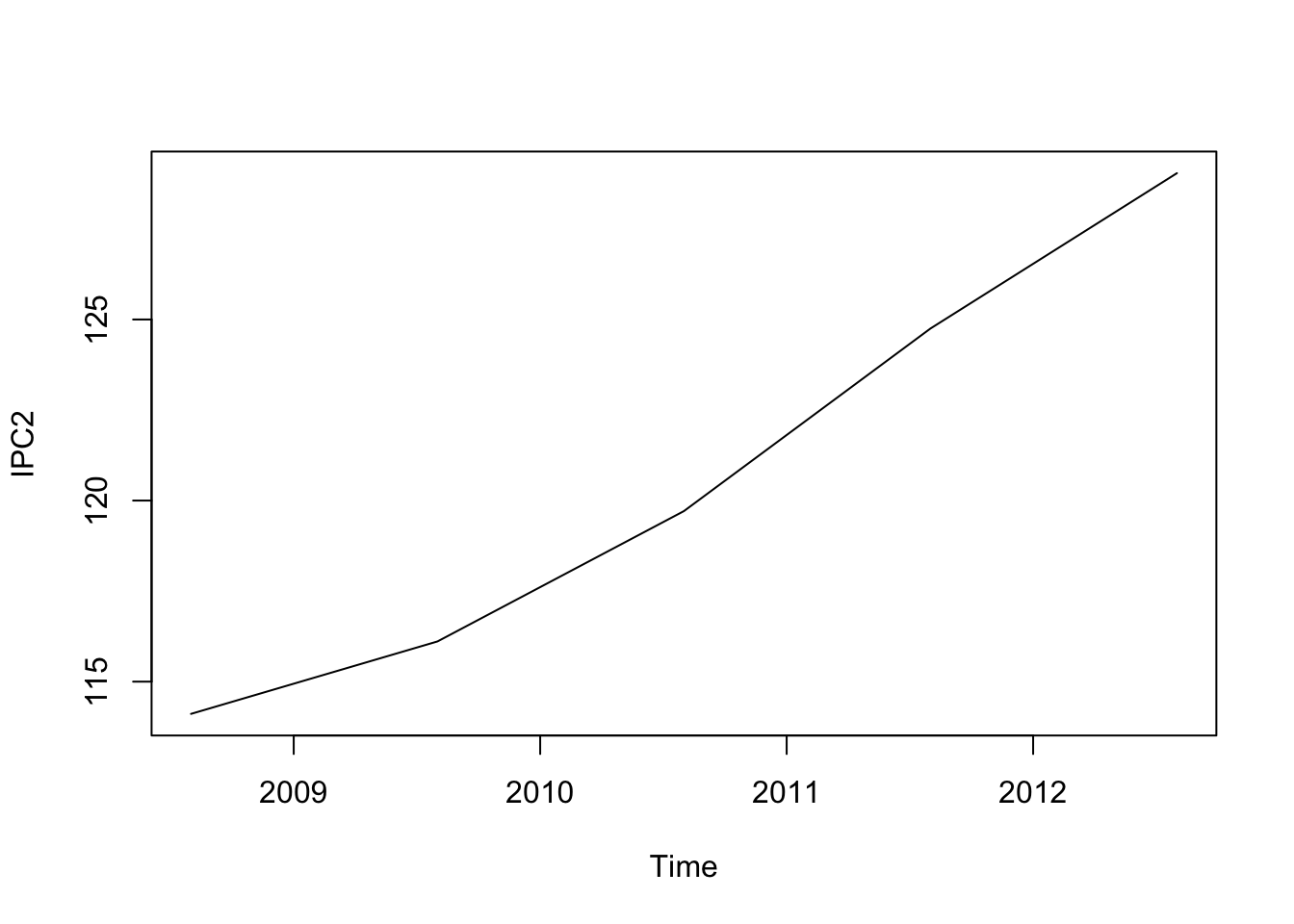

# IPC de todos los diciembres
IPC.dic <- window(IPC,start=c(2005,12),freq=T)
plot(IPC.dic)
points(IPC.dic)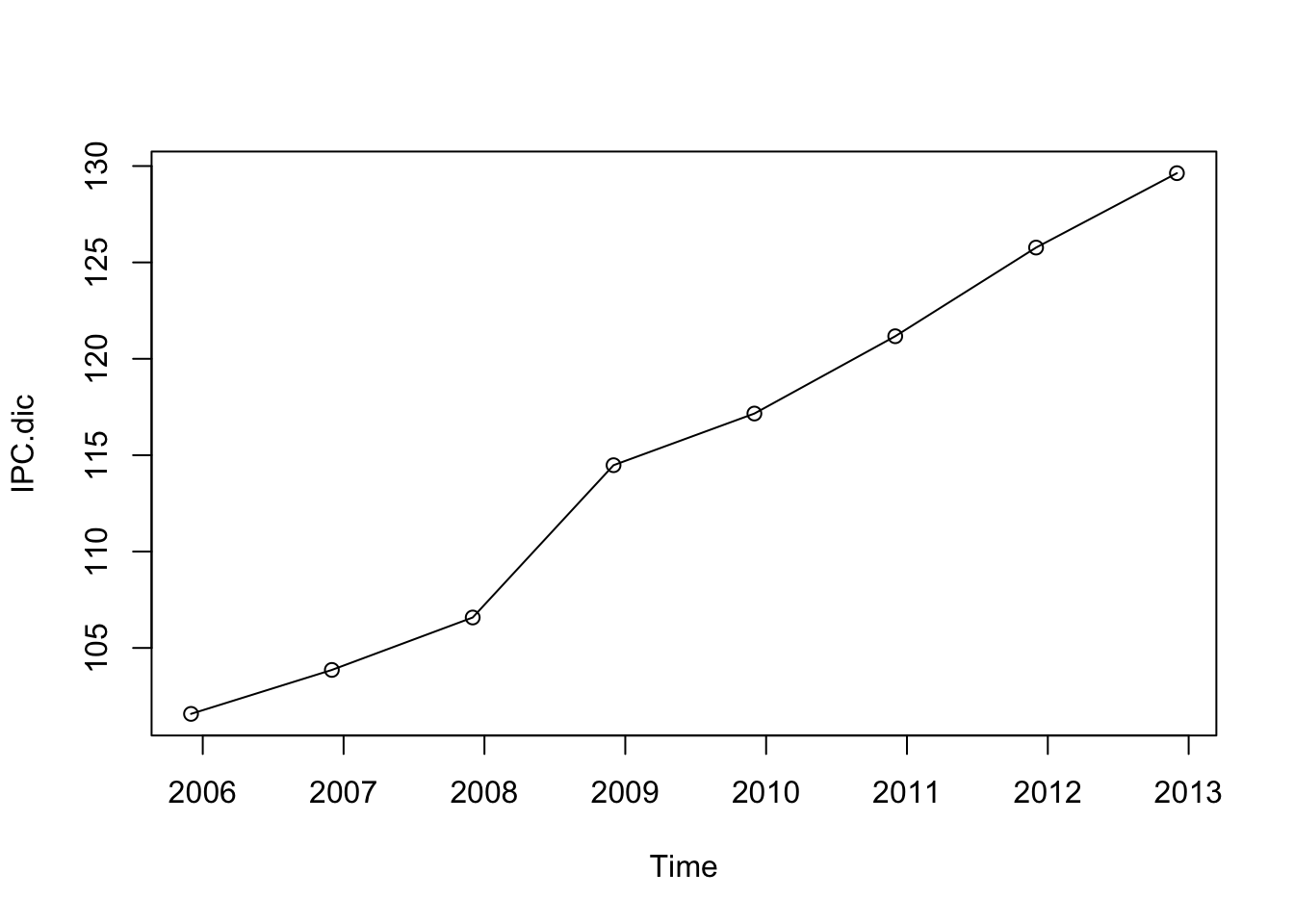

Si tengo mensuales y necesito trabajar con el IPC anual:

aggregate(IPC)
## Time Series:
## Start = 2005 
## End = 2012 
## Frequency = 1 
## [1] 1213.09 1241.75 1262.13 1349.24 1399.26 1435.96 1491.87 1542.53

A continuación algunas transformaciones frecuentes y su interpretación:

Transformación Interpretación
\(z_t=\nabla y_t=y_t-y_{t-1}\) Cambio en \(y_t\). Es un indicador de crecimiento absoluto.
\(z_t=ln(y_t)-ln(y_{t-1})\approx \frac{y_t-y_{t-1}}{y_{t-1}}\) Es la tasa logarítmica de variación de una variable. Es un indicador de crecimiento relativo. Si se multiplica por 100 es la tasa de crecimiento porcentual de la variable
\(z_t=\nabla[ln(y_t)-ln(y_{t-1})]\) Es el cambio en la tasa logarítmica de variación de una variable. Es un indicador de la aceleración de la tasa de crecimiento relativo de una variable.

Ejemplo

Veamos un gráfico más interesante usando un conjunto de datos anterior, vamos a:

  • Abrir la base estadísticas Turismo.csv
  • Agregar de manera mensual
  • Convertir a ts y graficar
uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/estadisticas%20Turismo.csv"
datos <- read.csv(url(uu),header=T,dec=".",sep=";")


# Visitas a Areas Naturales Protegidas

# Sumar por mes y año

mensual <- aggregate(datos$TOTALMENSUAL,by=list(datos$mesnum,datos$Year),FUN="sum") # Los datos sin mes es el total de ese anio

TOTALmensual <- ts(mensual[,3],start=c(2006,1),freq=12)
plot(TOTALmensual)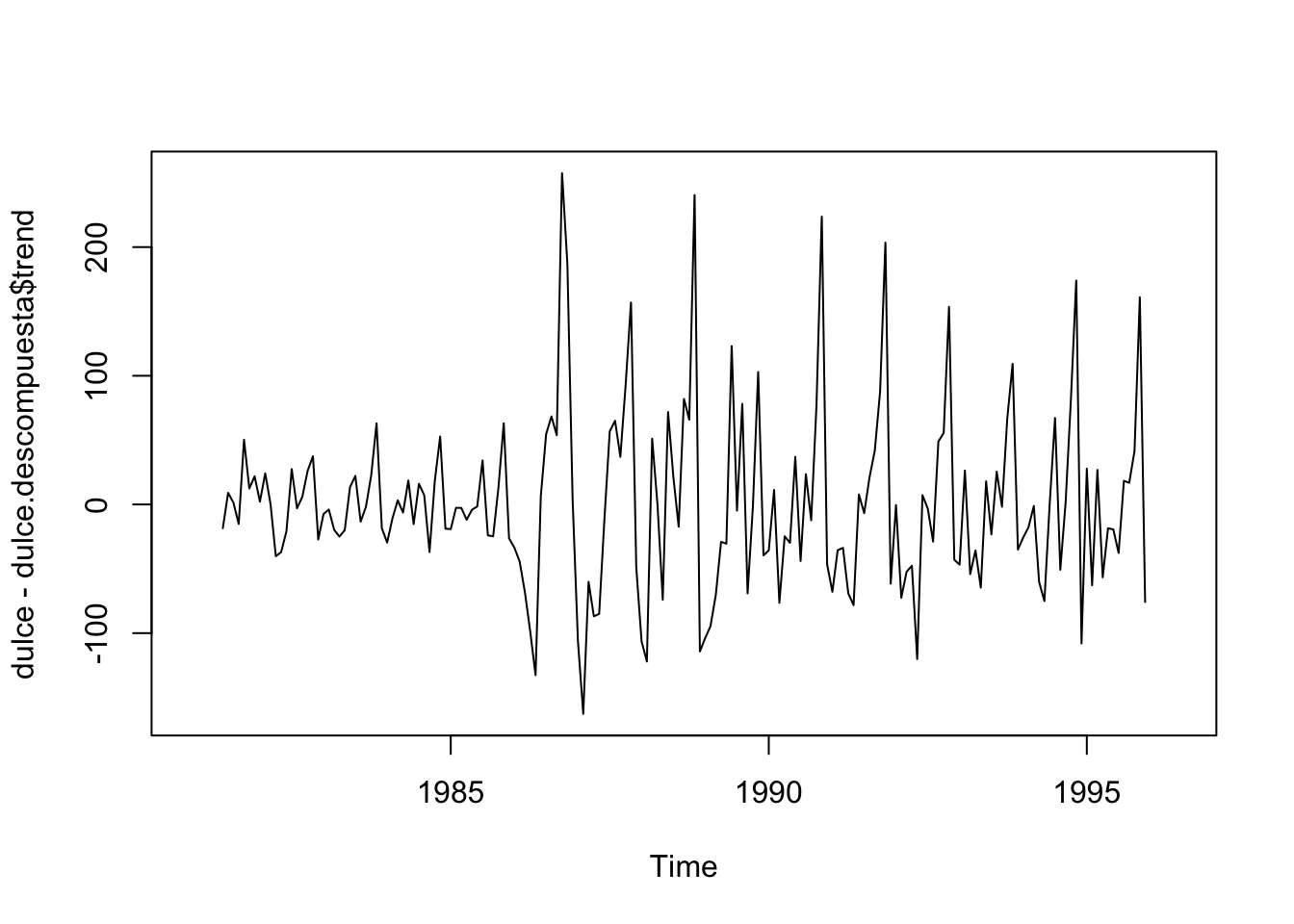

Se ve una tendencia creciente y también una cierta estacionalidad. Veamos la misma serie en gráficos más atractivos:

library(latticeExtra)
library(RColorBrewer)
library(lattice)
xyplot(TOTALmensual)

asTheEconomist(xyplot(TOTALmensual,
                      main="TOTAL VISITAS MENUSALES \n AREAS PROTEGIDAS")
               ,xlab="Year_mes",ylab="Visitantes")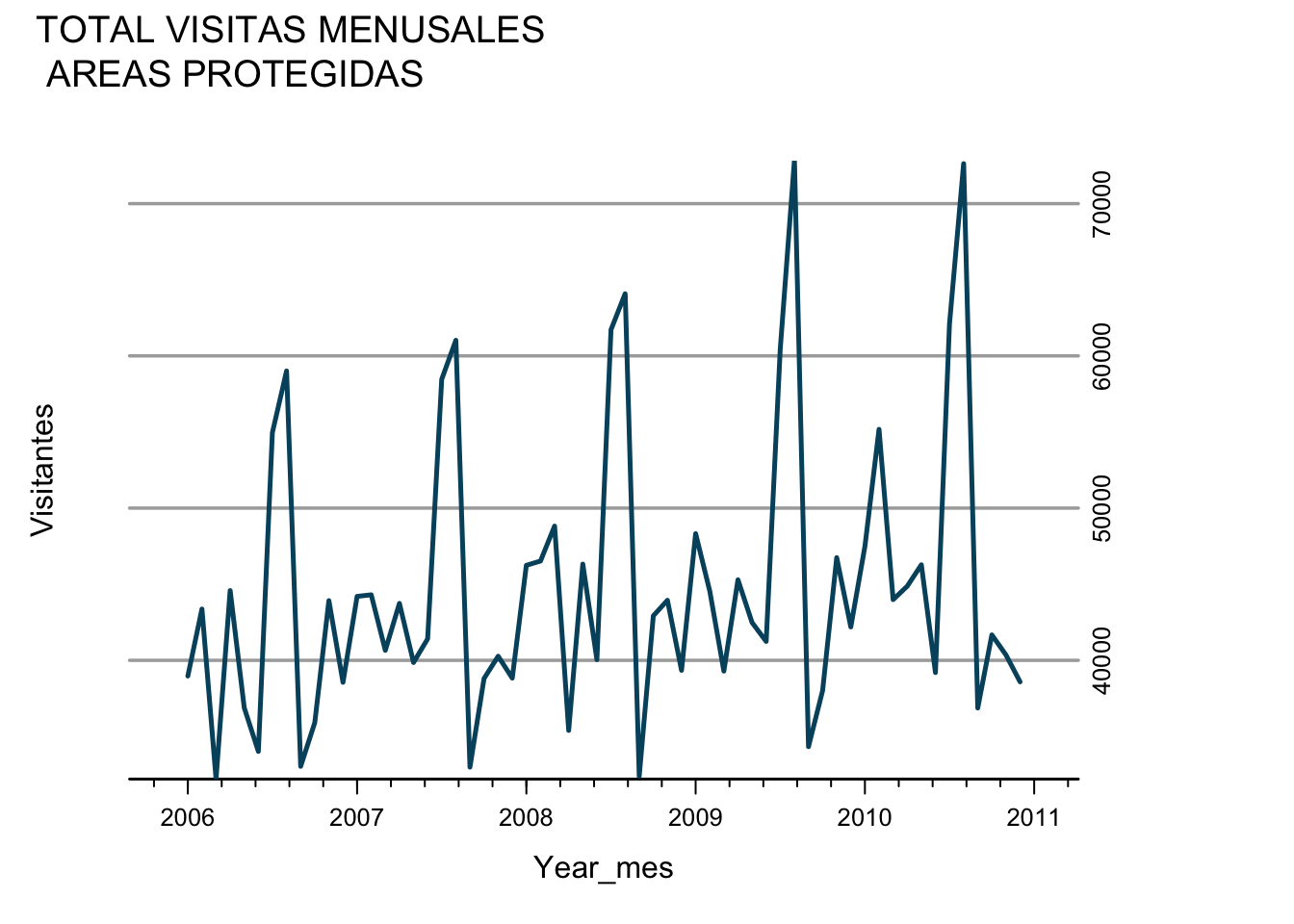

2.3 Descomposición de una serie de tiempo

Componentes

  • Tendencia-ciclo: representa los cambios de largo plazo en el nivel de la serie de tiempo
  • Estacionalidad: Caracteriza fluctuaciones periódicas de longitud constante causadas por factores tales como temperatura, estación del año, periodo vacacional, políticas, etc.

\[ Y_t = f(S_t,T_t,E_t) \] donde \(Y_t\) es la serie observada, \(S_t\) es el componente estacional, \(T_t\) es la tendencia y \(E_t\) es el término de error.

La forma de \(f\) en la ecuación anterior determina tipos de descomposiciones:

Descomposición Expresión
Aditiva \(Y_t = S_t +T_t+E_t\)
Multiplicativa \(Y_t = S_t *T_t*E_t\)
Transformación logaritmica \(log(Y_t) = log(S_t) +log(T_t)+log(E_t)\)
Ajuste estacional \(Y_t - S_t =T_t+E_t\)

Ejemplo

visitas.descompuesta<-decompose(TOTALmensual, type="additive")
plot(visitas.descompuesta)

Dentro de visitas.decompuesta tenemos los siguientes elementos:

  • $x = serie original
  • $seasonal = componente estacional de los datos EJ: en marzo hay un decremento de 2502 (para cada dato)
  • $trend = tendencia
  • $random = visitas no explicadas por la tendencia o la estacionalidad
  • $figure = estacionalidad (mismo que seasonal pero sin repetición)

2.3.1 Descomposición: ¿aditiva o multiplicativa?

Visualmente:

  • Aditivo:
    • las fluctuaciones estacionales lucen aproximadamente constantes en tamaño con el tiempo y
    • no parecen depender del nivel de la serie temporal,
    • y las fluctuaciones aleatorias también parecen ser más o menos constantes en tamaño a lo largo del tiempo
  • Multiplicativo:
    • Si el efecto estacional tiende a aumentar a medida que aumenta la tendencia
    • la varianza de la serie original y la tendencia aumentan con el tiempo.

Forma alternativa de elegir: ver cuál es la que tiene un componente aleatorio menor.

Ejemplo

Los datos en el archivo wine.dat son ventas mensuales de vino australiano por categoría, en miles de litros, desde enero de 1980 hasta julio de 1995. Las categorías son blanco fortificado (fortw), blanco seco (dryw), blanco dulce (sweetw), rojo (red), rosa (rose) y espumoso (spark).

direccion <- "https://raw.githubusercontent.com/dallascard/Introductory_Time_Series_with_R_datasets/master/wine.dat"
wine <- read.csv(direccion,header=T,sep="")
dulce <- ts(wine$sweetw,start=c(1980,12), freq=12)
plot(dulce)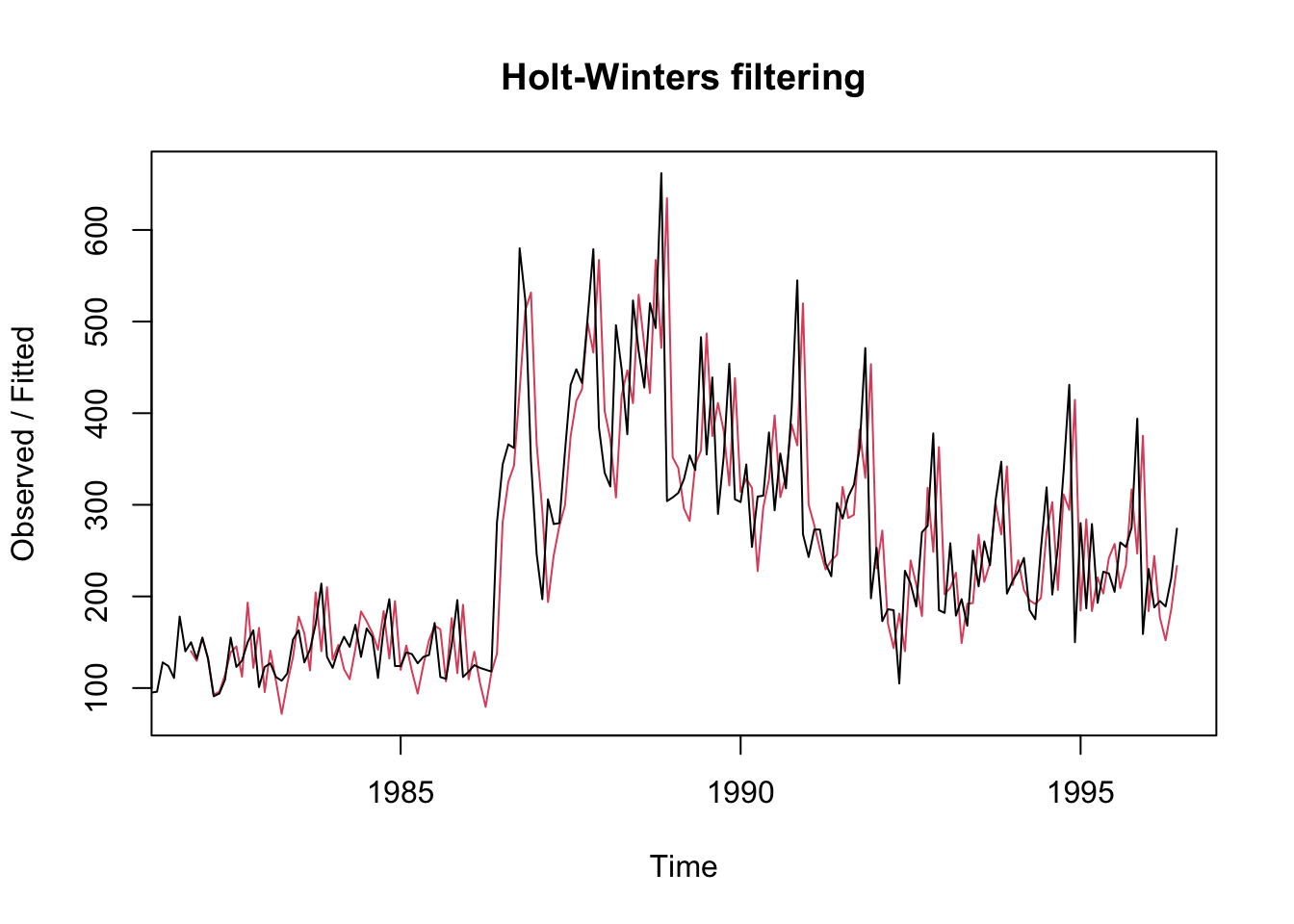

Tratemos la serie como un caso aditivo:

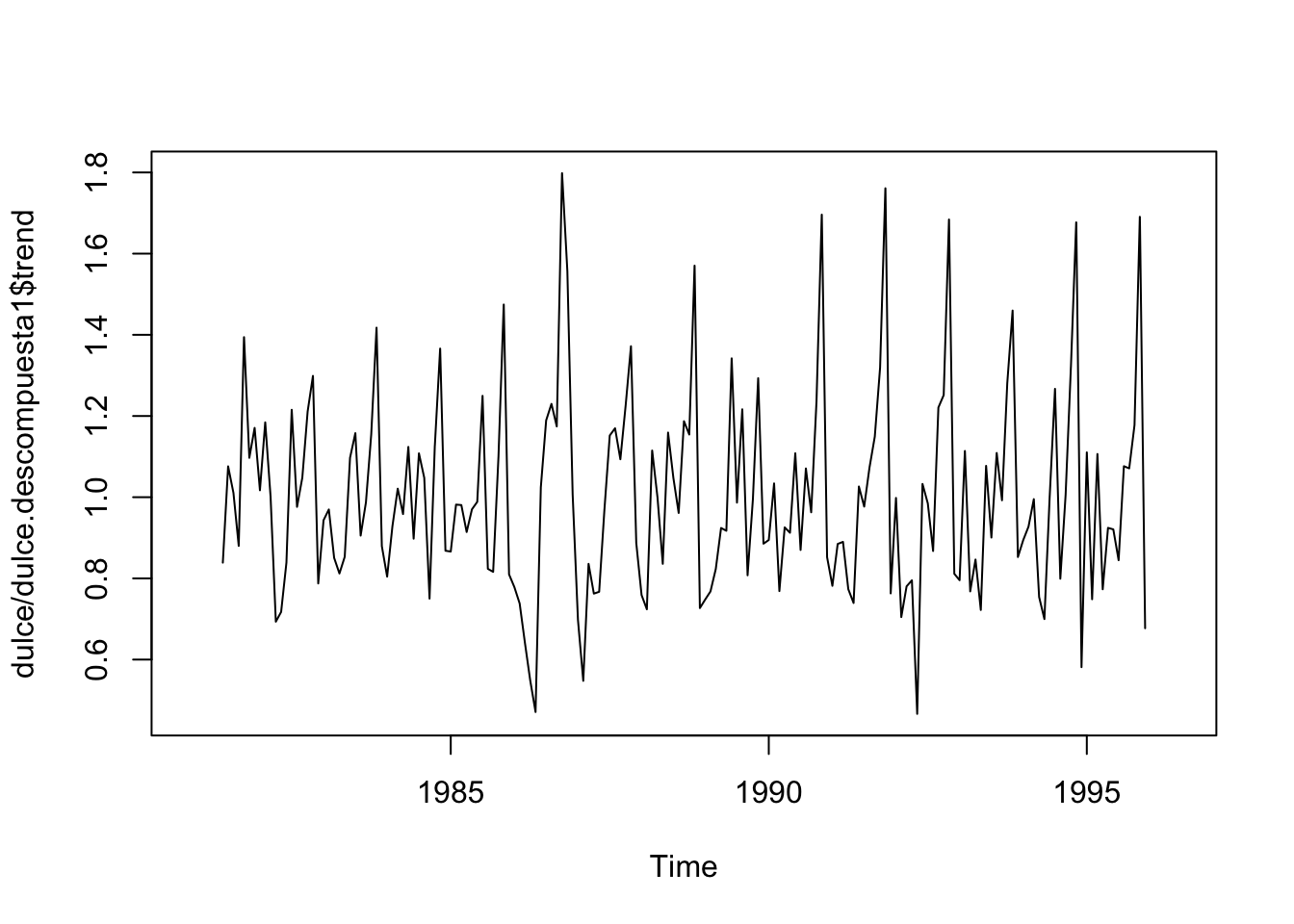
En funcion del gráfico de la variable, se decide el type de la descomposición La estacionalidad tiene valores negativos porque se plantea respecto de la tendencia

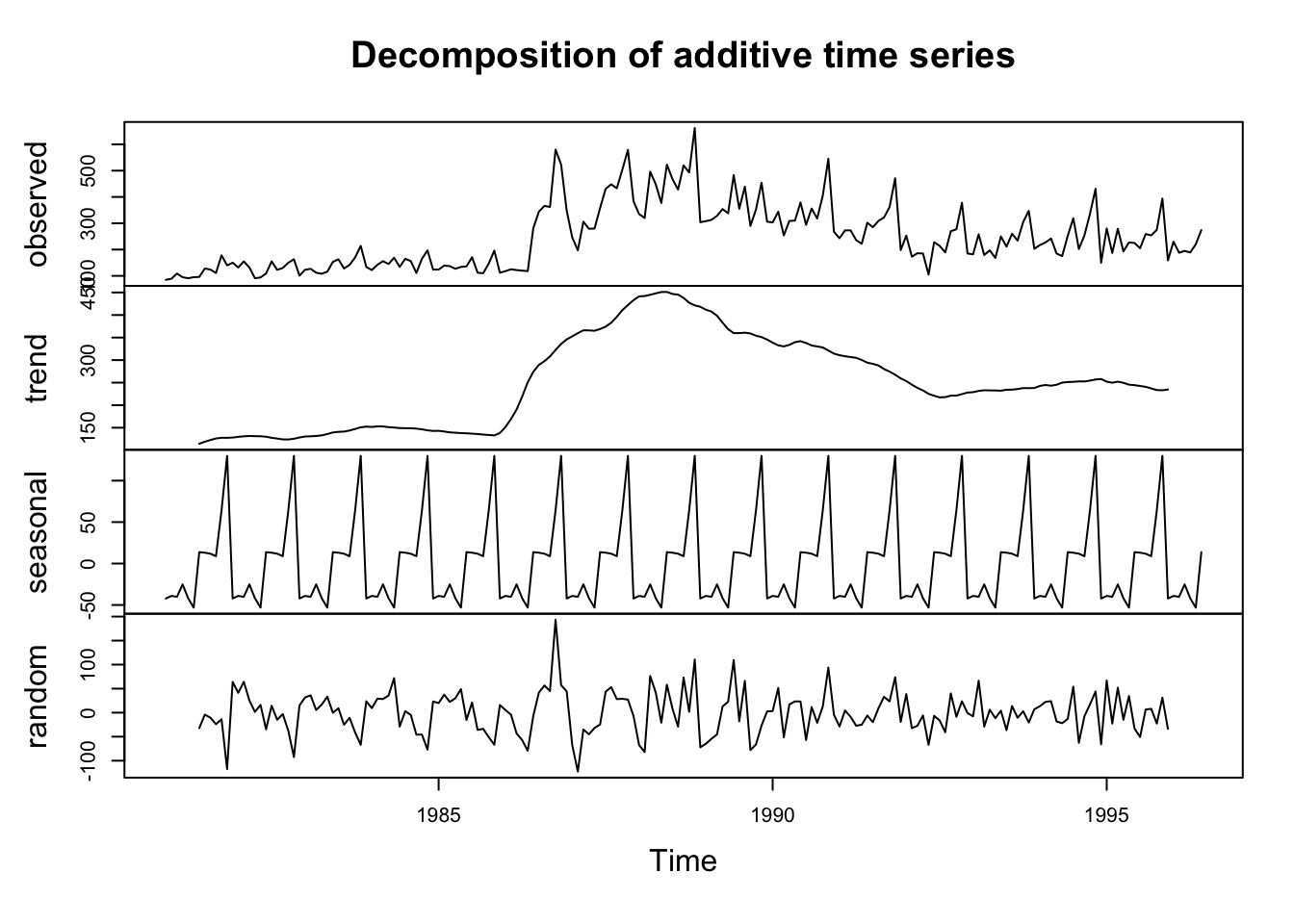
dulce.descompuesta<-decompose(dulce, type="additive") 
plot(dulce.descompuesta)

a <- dulce.descompuesta$trend[27] # La tendencia era de 130 en mayo del 82
b <- dulce.descompuesta$seasonal[27] # El componente de la estacionalidad era este
c <- dulce.descompuesta$random[27]  # Es el componente aleatorio

a+b+c # La sumatoria de la descomposicion de la serie da el valor real, si es aditiva
## [1] 127

Veamos el caso multiplicativo:

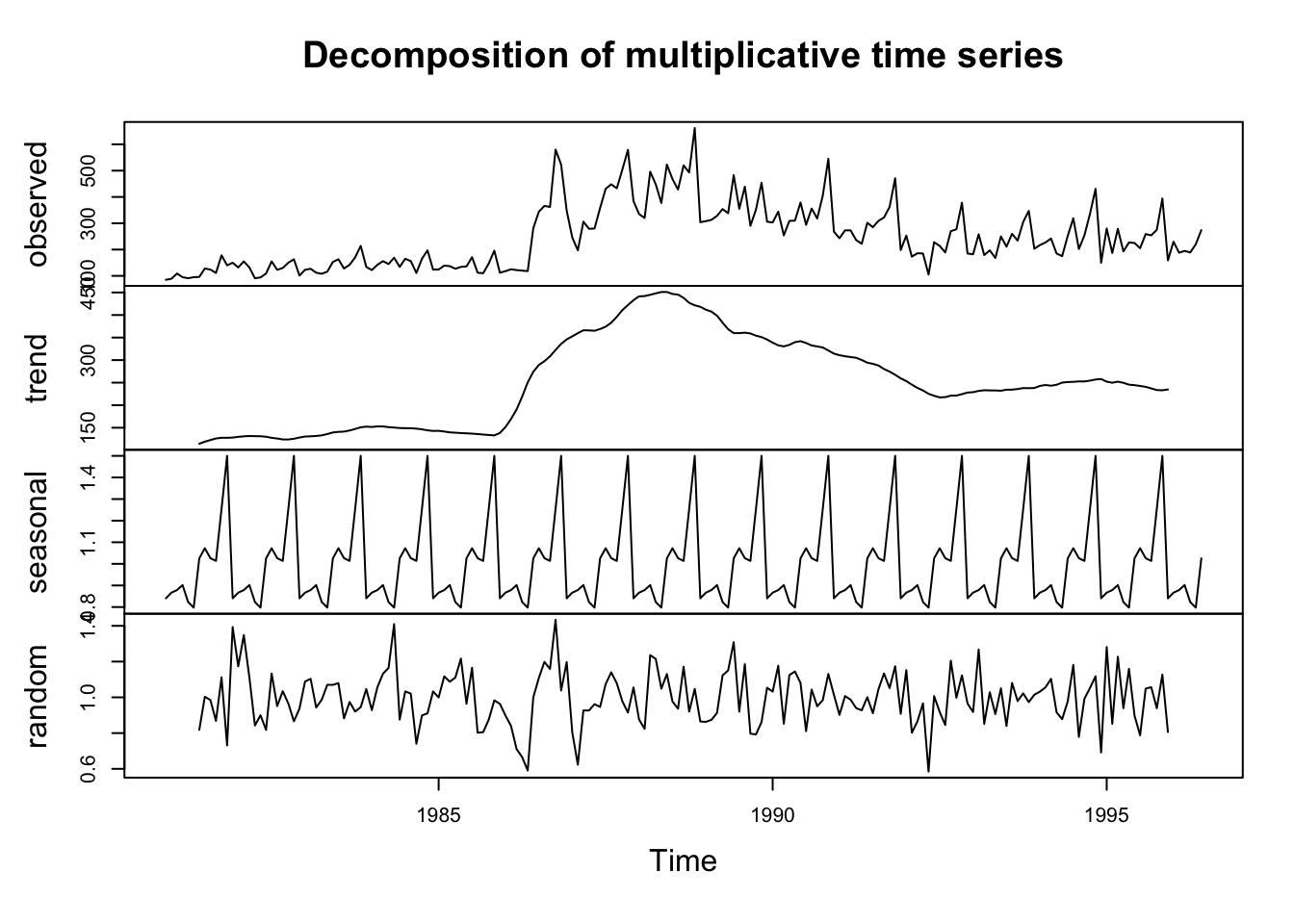
# Multiplicativa
dulce.descompuesta1<-decompose(dulce, type="multiplicative")
plot(dulce.descompuesta1)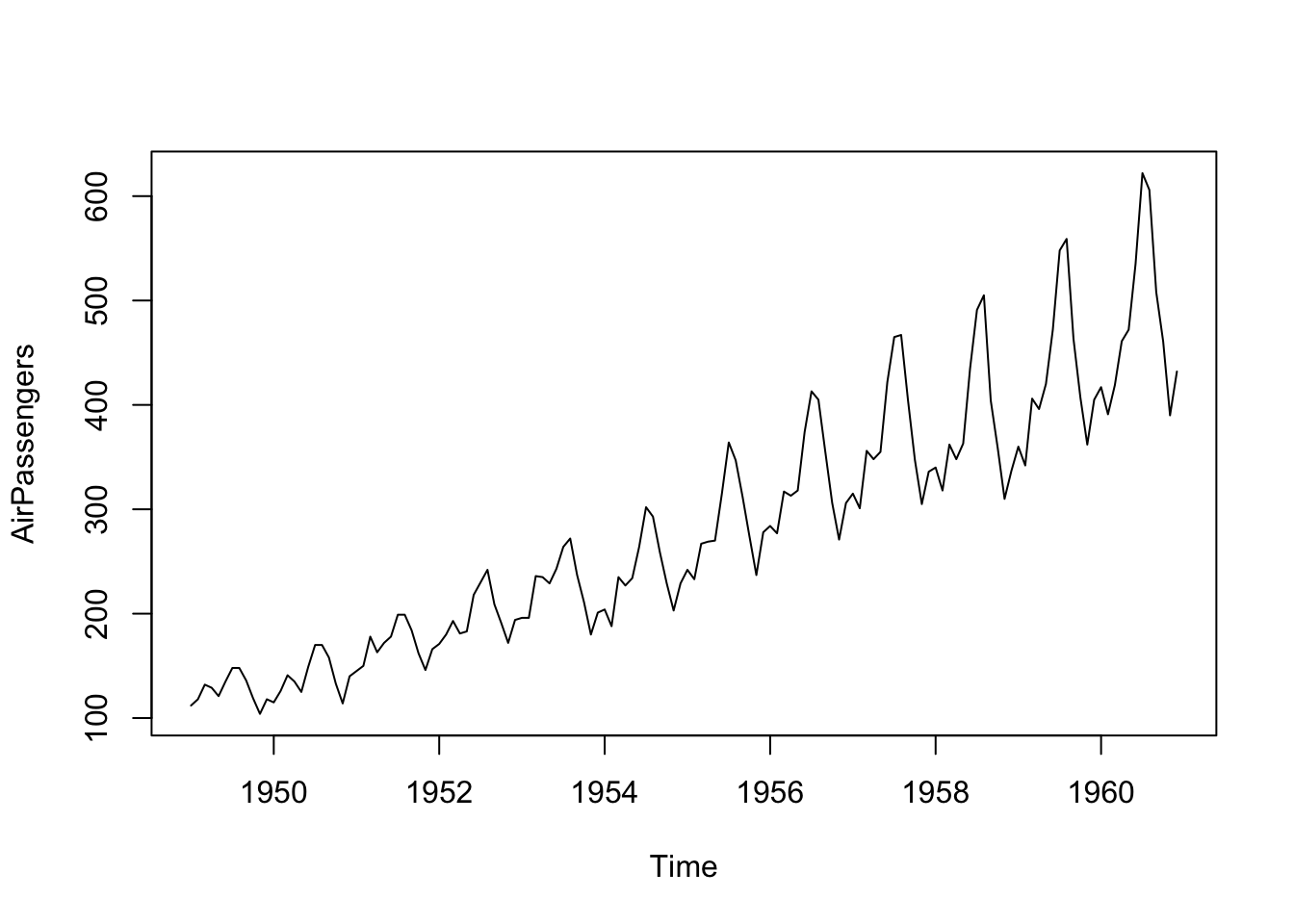

a <- dulce.descompuesta1$trend[27] # La tendencia era de 130 en mayo del 82
b <- dulce.descompuesta1$seasonal[27] # El componente de la estacionalidad era este
c <- dulce.descompuesta1$random[27]  # Es el componente aleatorio

a*b*c # La sumatoria de la descomposicion de la serie da el valor real, si es aditiva
## [1] 127

Veamos la forma alternativa de elección:

u1 <- var(dulce.descompuesta$random,na.rm=T)
u2 <- var(dulce.descompuesta1$random,na.rm=T)
cbind(u1,u2)
##            u1         u2
## [1,] 1970.235 0.02247602

Se escoge la multiplicativa en este caso.

2.3.2 Detrend:

Las series se ofrecen generalmente sin tendencia ni estacionalidad. Veamos la serie sin tendencia:

dulce.detrended <- dulce-dulce.descompuesta$trend
plot(dulce.detrended)
abline(h=0)

Parece ser que hay un cambio en la varianza desde el 85.

Si descomponemos multiplicativamente en vez de restar se debe dividir.

plot(dulce-dulce.descompuesta$trend)

plot(dulce/dulce.descompuesta1$trend)

Existen formas de descomponer más sofisticadas, por ejemplo, usando la función stl.

dulce.stl <- stl(dulce,s.window="per")
plot(dulce.stl)

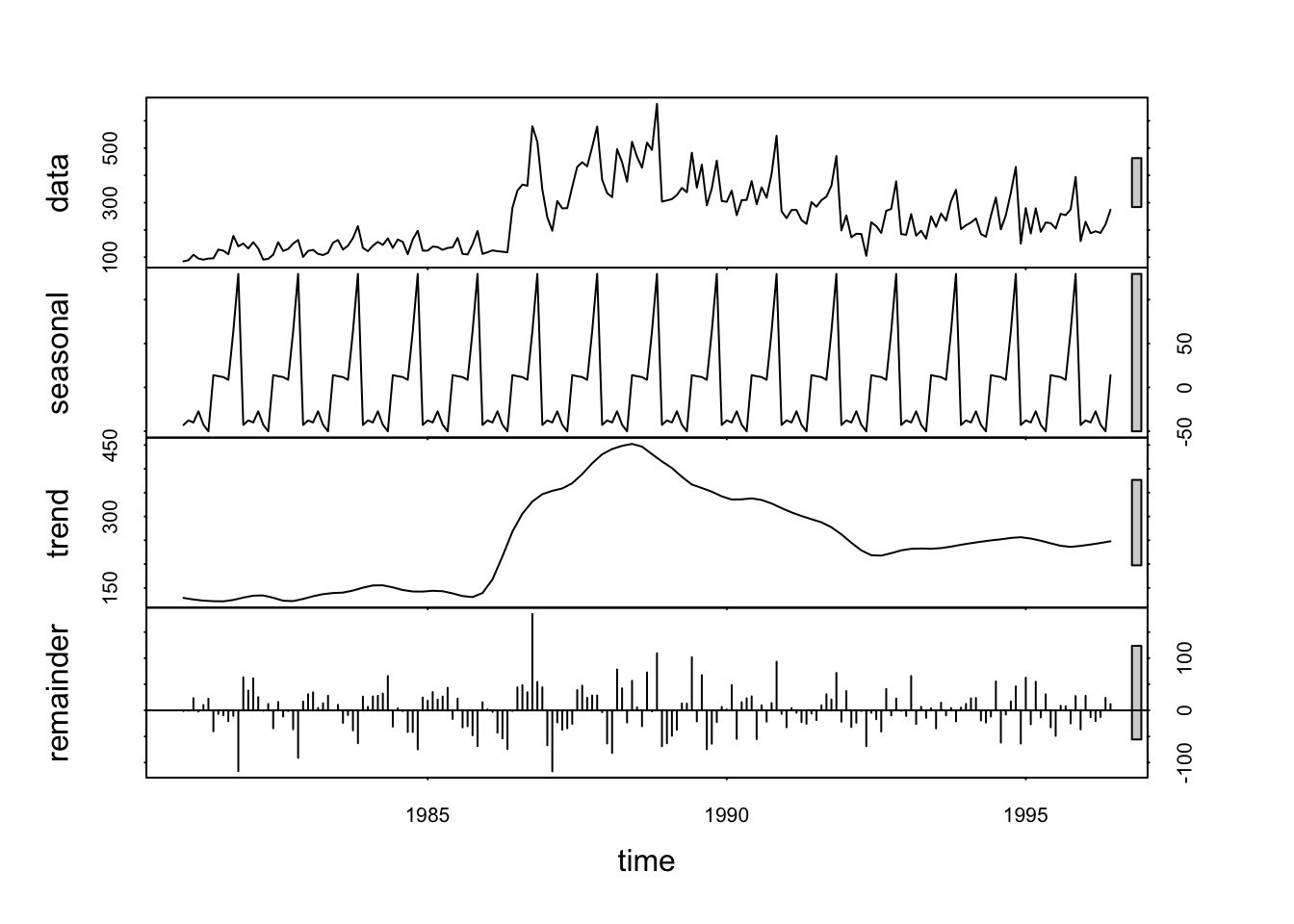
En este caso el cálculo de la tendencia cambia, se calcula con formas no paramétricas. La barra del final es la desviación estándar.

2.4 Suavizamiento: Holt-Winters

El método se resume en las fórmulas siguientes:

\[\begin{eqnarray} a_{t} &=& \alpha(x_{t}-s_{t-p})+(1-\alpha)(a_{t-1}+b_{t-1}) \nonumber \\ b_{t} &=& \beta(a_{t}-a_{t-1})+(1-\beta)b_{t-1} \nonumber \\ s_{t} &=& \gamma(x_{t}-a_{t})+(1-\gamma)s_{t-p} \nonumber \end{eqnarray}\]

donde

  • \(0\leq\alpha\leq1\) es el factor de suavizamiento de los datos,
  • \(0\leq\beta\leq1\) es el factor de suavizamiento de la tendencia,
  • \(0\leq\gamma\leq1\) es el factor de suavizamiento del cambio estacional.

Con \(x_0 = a_0\), la predicción se define como

\[ F_{t+m} = a_t+mb_t+c_{t-L+1+((m+1)\mod L)} \]

El método de Holt-Winters generaliza el método de suavizamiento exponencial.

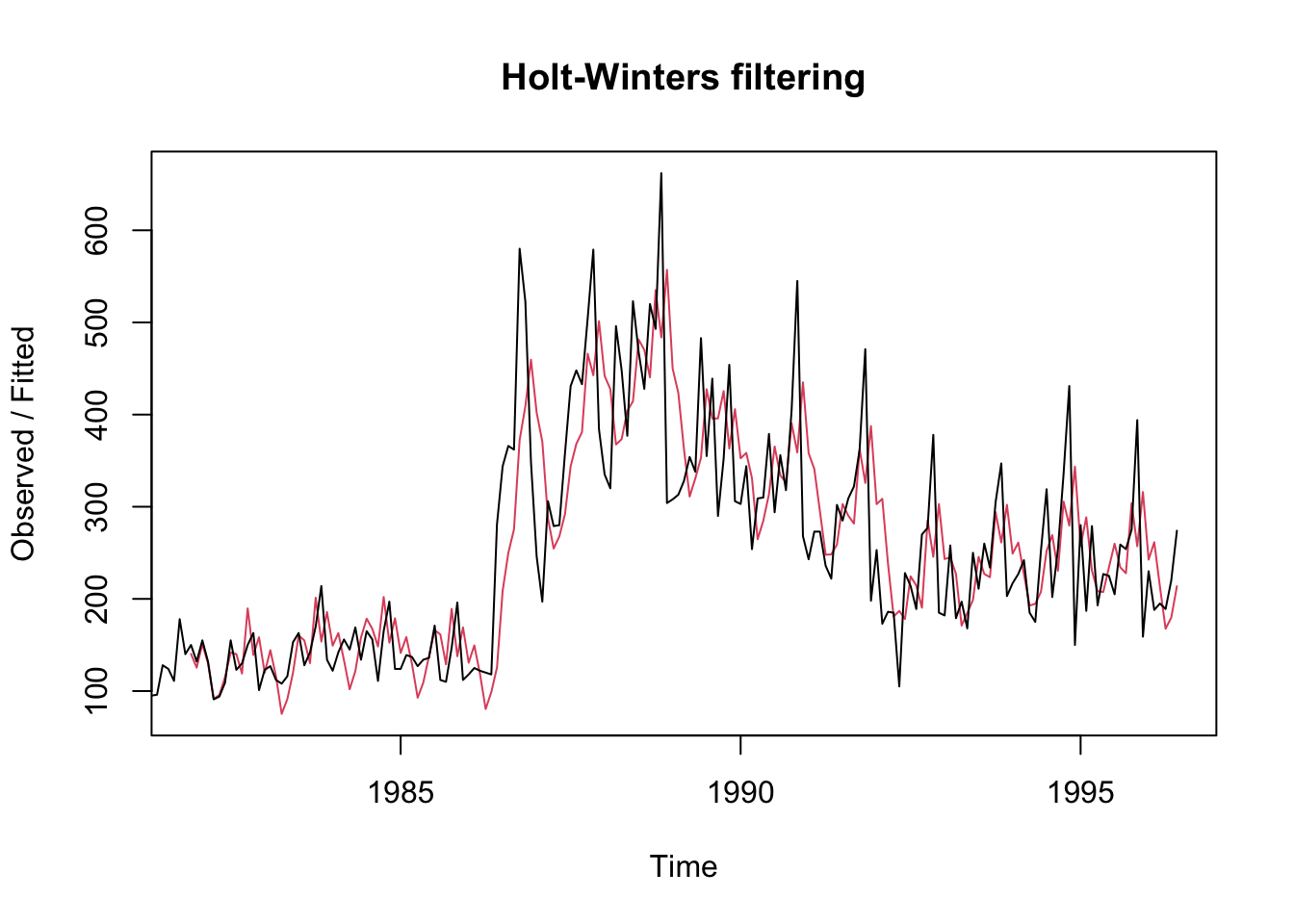
Ejemplo

Veamos un modelo más sencillo:

\[\begin{eqnarray} x_{t} &=& \mu_{t}+w_{t} \nonumber \\ \mu_{t}=a_{t}&=& \alpha x_{t} + (1-\alpha) a_{t-1} \nonumber \end{eqnarray}\]

donde \(x_0 = a_0\)

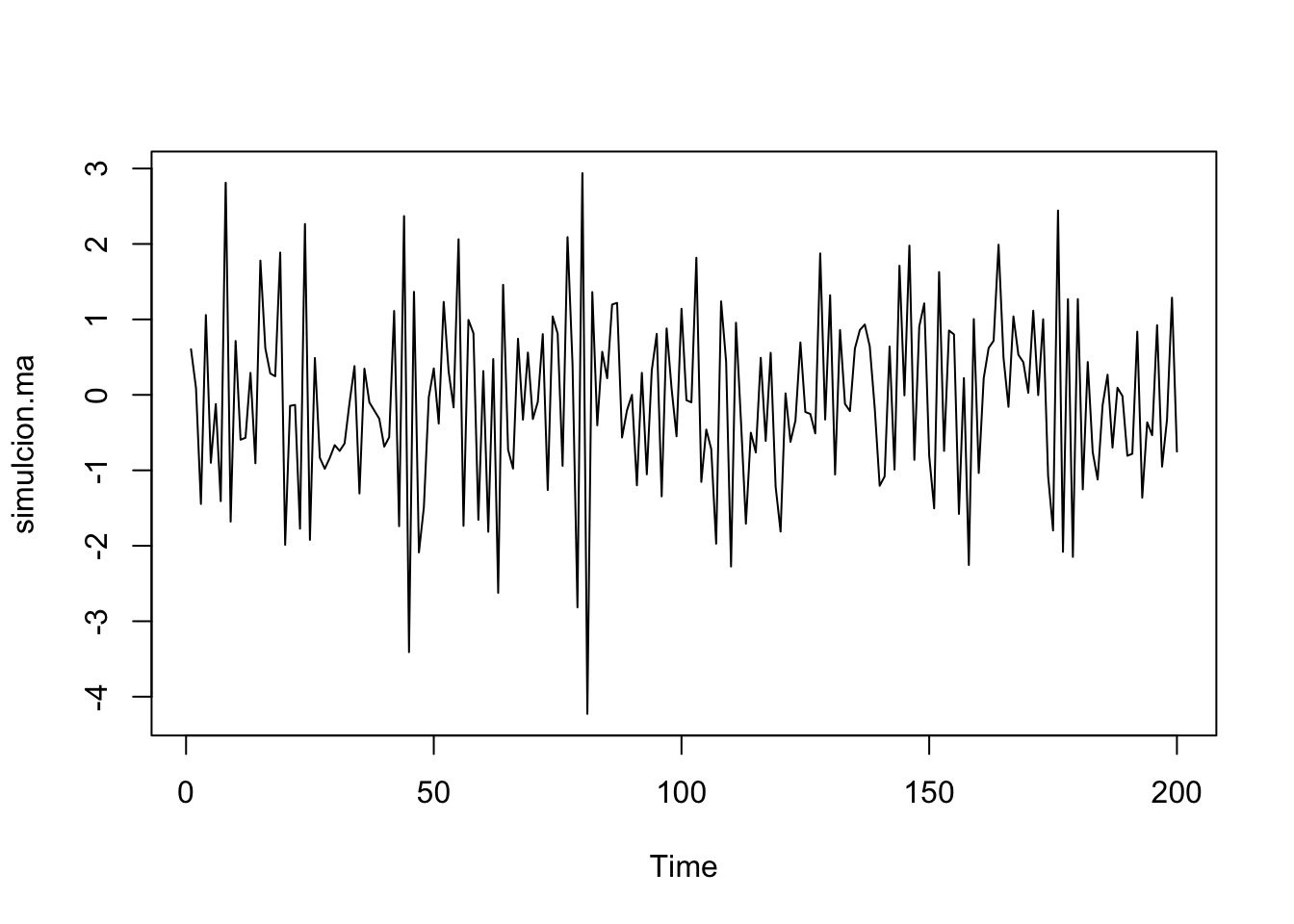
dulce.se <- HoltWinters(dulce,beta=0,gamma=0)
plot(dulce.se)

Es un suavizamiento HW sin tendencia y sin componente estacional. La serie roja son los datos con suavizamiento exponencial y la negra son los observados. R buscó el alpha que le pareció apropiado.

Usemos un alpha deliberado:

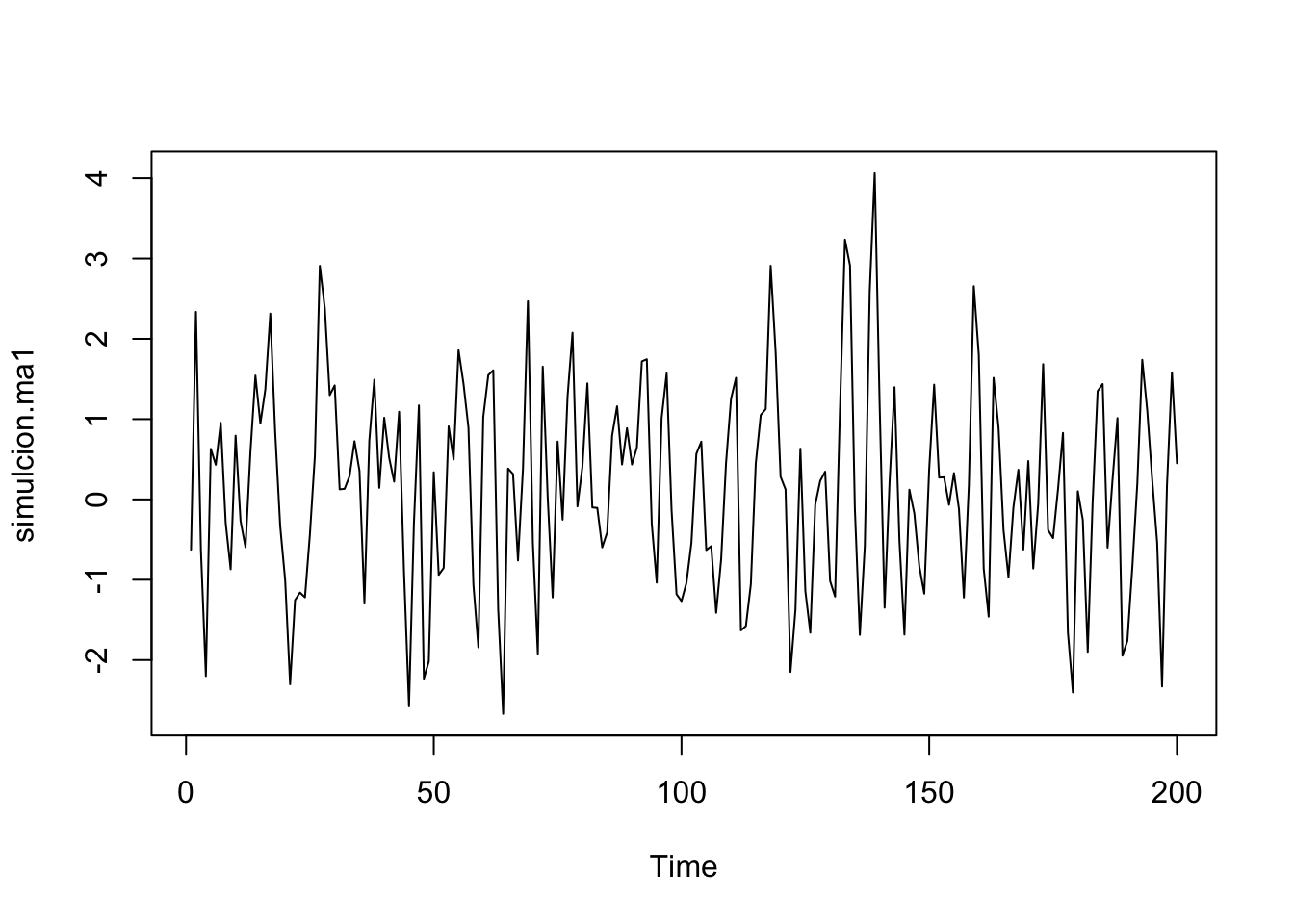
dulce.se1 <- HoltWinters(dulce,alpha=0.8,beta=0,gamma=0)
plot(dulce.se1)

¿Qué pasó con los errores?

dulce.se$SSE # Suma de los residuos al cuadrado (de un paso)
## [1] 963408.2
dulce.se1$SSE # Suma de los residuos al cuadrado (de un paso)
## [1] 1132577

Es decir, el criterio para la busqueda de los parámetros es la minimización del SSE.

Ejemplo

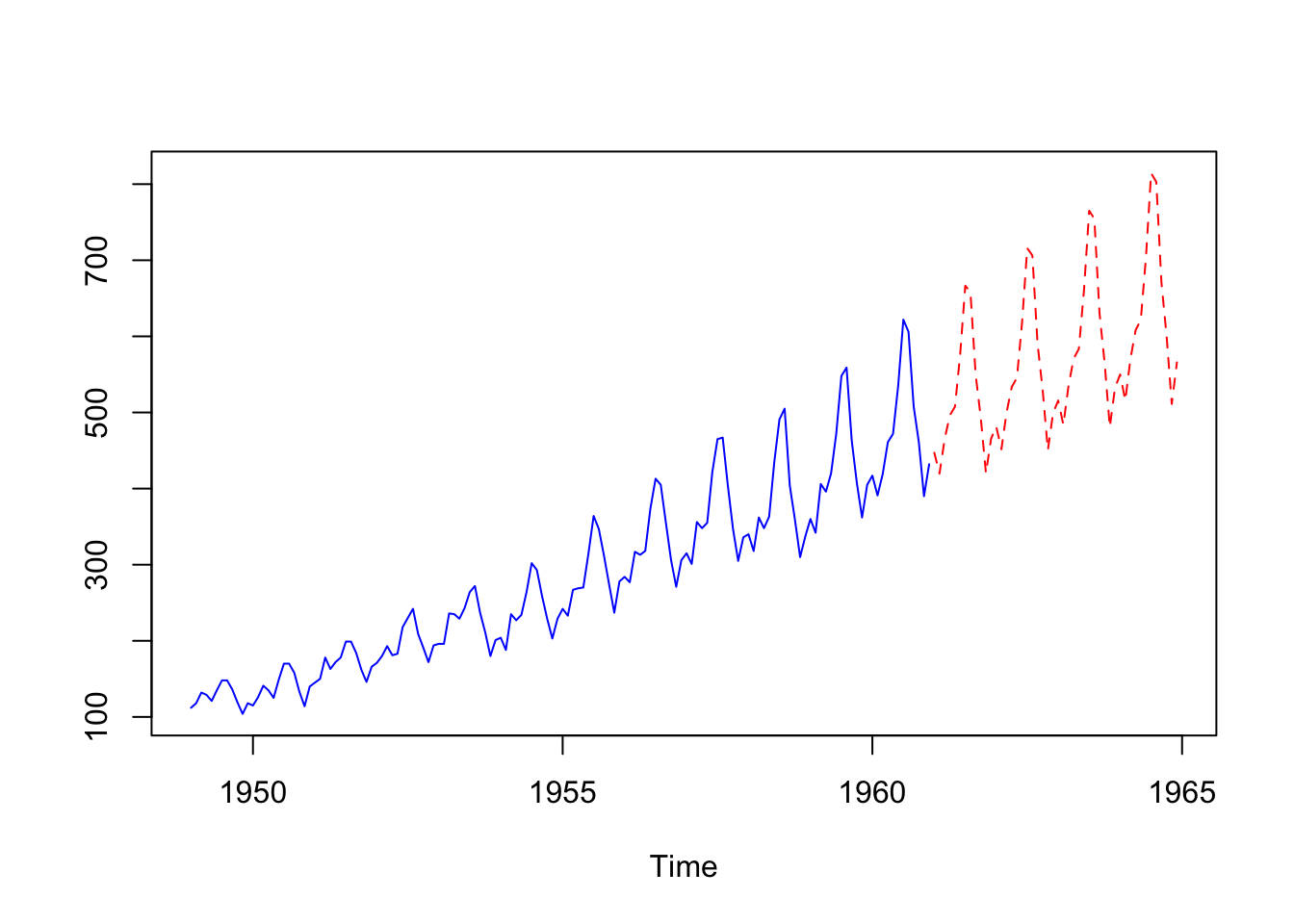
Total mensual de pasajeros (en miles) de líneas aéreas internacionales, de 1949 a 1960.

data(AirPassengers)
str(AirPassengers)
##  Time-Series [1:144] from 1949 to 1961: 112 118 132 129 121 135 148 148 136 119 ...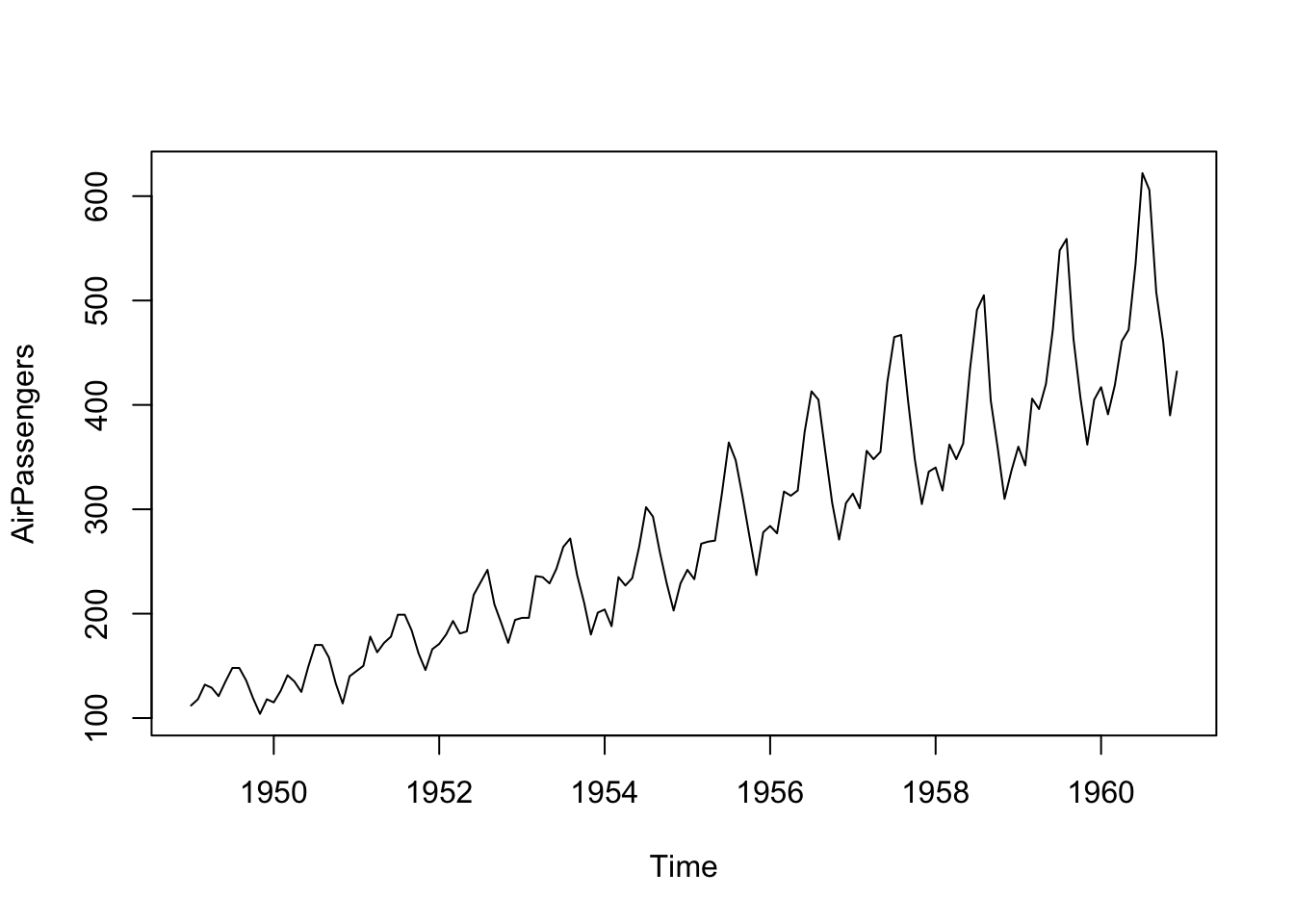
plot(AirPassengers)

Se aprecia tendencia y variabilidad. Podemos usar HW para predicción:

ap.hw <- HoltWinters(AirPassengers,seasonal="mult")
plot(ap.hw)

ap.prediccion <- predict(ap.hw,n.ahead=48)
ts.plot(AirPassengers,ap.prediccion,lty=1:2, col=c("blue","red"))

2.5 Ejercicios

  1. Analiza los datos de lluvia en Cumbayá y determina los 2 meses donde hay más lluvia y menos lluvia. Justifica tu respuesta usando la descomposición de la serie de tiempo.

  2. Usando el método de HoltWinters, realiza una predicción 3 periodos del IPC Nacional General de Ecuador.