5 Modelización de Series Multivariantes: VAR & VEC

Greta M. Ljung (1941-) Greta Marianne Ljung es una estadística estadounidense de origen finlandés. La prueba de Ljung-Box para datos de series de tiempo lleva el nombre de ella y su asesor de la escuela de posgrado, George E. P. Box. Ha escrito libros de texto sobre análisis de series de tiempo y su trabajo ha sido publicado en varias de las principales revistas estadísticas, incluidas Biometrika y Journal of the Royal Statistical Society.

Tomado de varias fuentes:

• Colonescu (2016)
• Novales-Cinca (1993)

Librerías usadas:

• tseries
• vars

5.1 Cointegración

• Una serie de tiempo no es estacionaria si su distribución, en particular su media, varianza o covarianza cambian con el tiempo.

• Las series temporales no estacionarias no se pueden usar en los modelos de regresión porque pueden crear una regresión espuria, una relación falsa debido, por ejemplo, a una tendencia común en variables que de otro modo no estarían relacionadas.

• Dos o más series no estacionarias aún pueden ser parte de un modelo de regresión si están cointegradas, es decir, están en una relación estacionaria de algún tipo.

Definición

Dos series \(y\) y \(x\) están cointegradas si las dos condiciones siguientes se cumplen:

1. \(y\) es no estacionaria, \(x\) es no estacionaria.
2. Existe una combinación lineal de \(y\) y \(x\) que si es estacionaria.

En resumen, dos series son cointegradas si son no estacionarias y relacionadas.

5.1.1 Estacionariedad

Hasta ahora hemos realizado procedimientos para averiguar si una serie es estacionaria. Recordemos, por ejemplo, el proceso \(AR(1)\):

\[ y_t = \phi y_{t-1}+\epsilon_t \]

Este proceso es estacionario si \(|\phi|<1\); cuando \(\phi=1\) el proceso se llama caminata aleatoria.

El siguiente código genera procesos \(AR(1)\):

• con y sin constante
• con y sin tendencia
• \(\phi\) menor que 1.

La ecuación genérica para la simulación es:

\[ y_t = \alpha-\lambda t+\phi y_{t-1}+\epsilon_t \]

N <- 500
a <- 1
l <- 0.01
rho <- 0.7

set.seed(246810)
v <- ts(rnorm(N,0,1))

par(mfrow = c(3,2))

y <- ts(rep(0,N))
for (t in 2:N){
  y[t]<- rho*y[t-1]+v[t]
}
plot(y,type='l', ylab="rho*y[t-1]+v[t]",main= "Sin tendencia")
abline(h=0)

y <- ts(rep(0,N))
for (t in 2:N){
  y[t]<- a+rho*y[t-1]+v[t]
}
plot(y,type='l', ylab="a+rho*y[t-1]+v[t]", main= "Con constante")
abline(h=0)

y <- ts(rep(0,N))
for (t in 2:N){
  y[t]<- a+l*time(y)[t]+rho*y[t-1]+v[t]
}
plot(y,type='l', ylab="a+l*time(y)[t]+rho*y[t-1]+v[t]", main = "Con tendencia y constante")
abline(h=0)

y <- ts(rep(0,N))
for (t in 2:N){
  y[t]<- y[t-1]+v[t]
}
plot(y,type='l', ylab="y[t-1]+v[t]", main = "Caminata aleatoria")
abline(h=0)

a <- 0.1
y <- ts(rep(0,N))
for (t in 2:N){
  y[t]<- a+y[t-1]+v[t]
}
plot(y,type='l', ylab="a+y[t-1]+v[t]", main = "Caminata aleatoria con constante")
abline(h=0)

y <- ts(rep(0,N))
for (t in 2:N){
  y[t]<- a+l*time(y)[t]+y[t-1]+v[t]
}
plot(y,type='l', ylab="a+l*time(y)[t]+y[t-1]+v[t]", main = "Caminata aleatoria con constante y tendencia")
abline(h=0)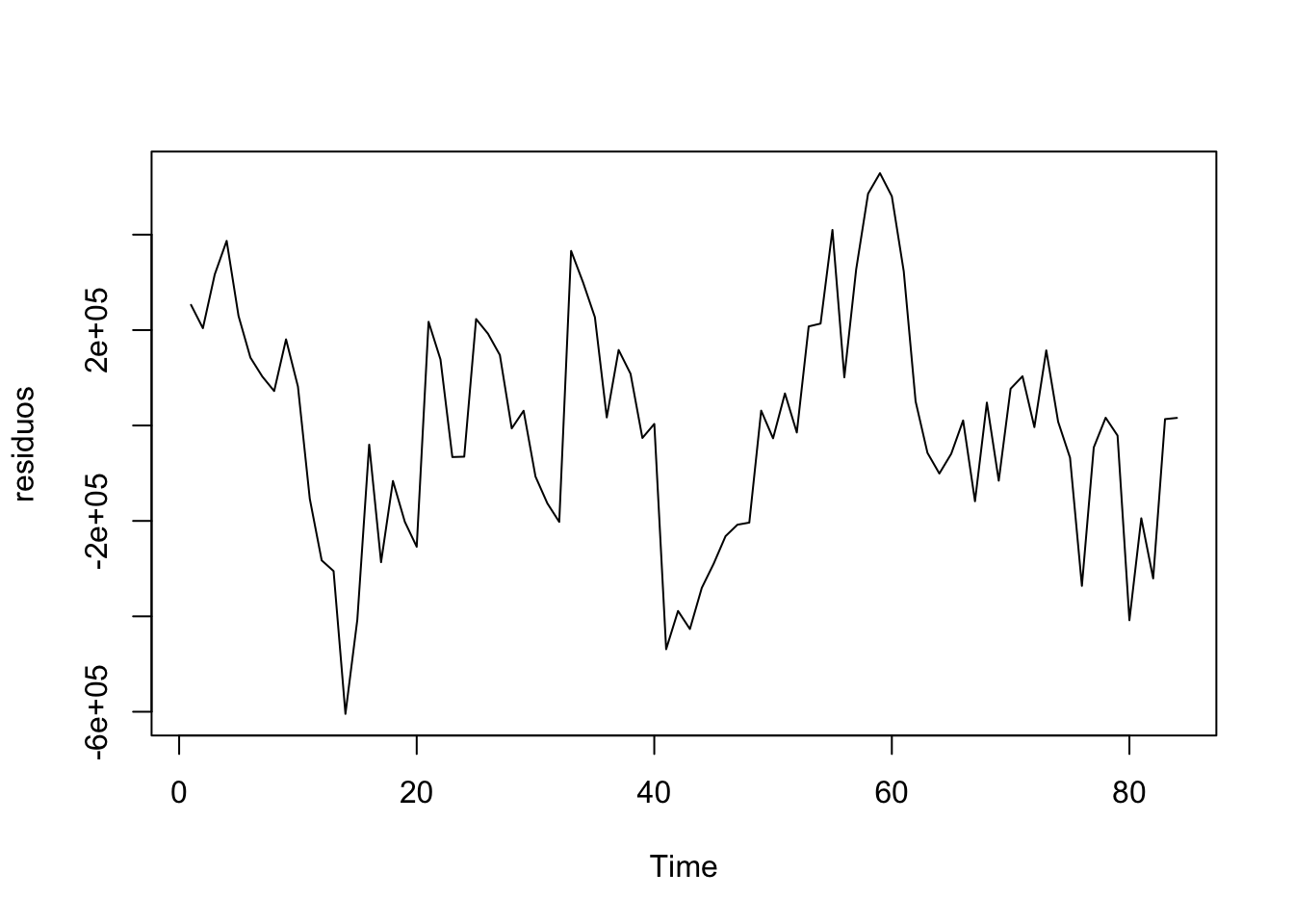

5.1.2 Regresión espúrea

La no estacionariedad puede conducir a una regresión espuria, una aparente relación entre variables que, en realidad, no están relacionadas. La siguiente secuencia de código genera dos procesos de paseo aleatorio independientes, \(y\) y \(x\), hacemos la regresión \(y_t=\beta_o+\beta_1x_t\).

Veamos las series y su gráfica de dispersión:

T <- 1000
set.seed(1357)
y <- ts(rep(0,T))
vy <- ts(rnorm(T))
for (t in 2:T){
  y[t] <- y[t-1]+vy[t]
}

set.seed(4365)
x <- ts(rep(0,T))
vx <- ts(rnorm(T))
for (t in 2:T){
  x[t] <- x[t-1]+vx[t]
}
y <- ts(y[300:1000])
x <- ts(x[300:1000])

par(mfrow = c(1,2))
ts.plot(y,x, ylab="y & x")
plot(x, y, type="p", col="grey")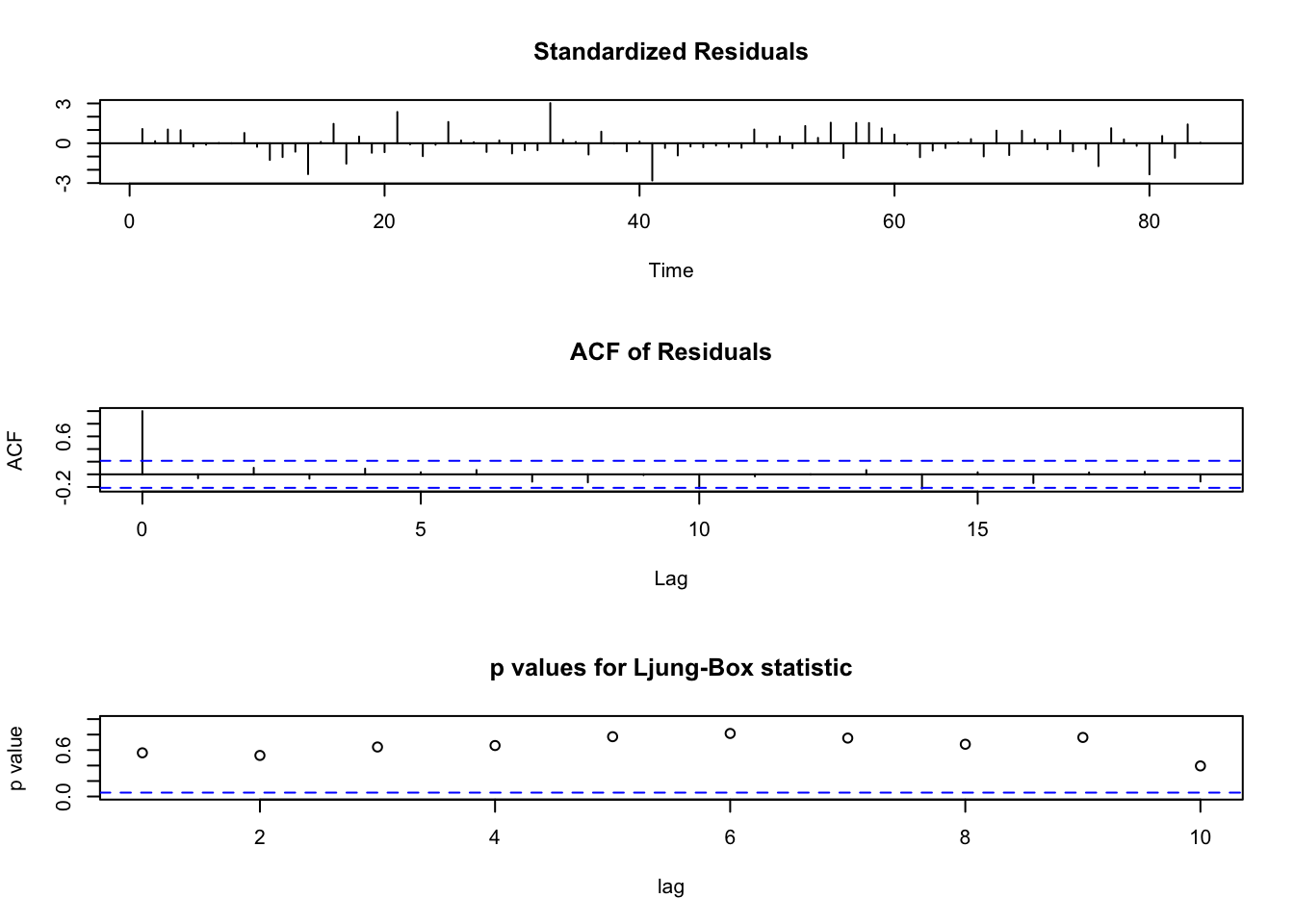

spurious.ols <- lm(y~x)
summary(spurious.ols)

## 
## Call:
## lm(formula = y ~ x)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -12.554  -5.973  -2.453   4.508  24.678 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -20.38711    1.61958 -12.588  < 2e-16 ***
## x            -0.28188    0.04331  -6.508 1.45e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 7.954 on 699 degrees of freedom
## Multiple R-squared:  0.05713,    Adjusted R-squared:  0.05578 
## F-statistic: 42.35 on 1 and 699 DF,  p-value: 1.454e-10

El resumen muestra una fuerte correlación entre las dos variables, aunque se han generado de forma independiente. (Sin embargo, no es necesario que ninguno de los dos procesos generados aleatoriamente genere una regresión espuria).

Comprueba siempre la estacionariedad del residuo. La regresión es espuria si el residuo no es estacionario.

El hecho de que dos series se muevan juntas no significa que estén relacionadas.

5.1.3 Estacionariedad

Ya hemos trabajado con la prueba de Dickey-Fuller para determinar si una serie es estacionaria. Recuerda que la \(H_o\) de esta prueba es no estacionariedad. Es decir, si rechazamos la hipótesis nula, la serie es estacionaria.

Un concepto que está estrechamente relacionado con la estacionalidad es el orden de integración, que es cuántas veces necesitamos diferenciar una serie hasta que se vuelva estacionaria.

Una serie es \(I(0)\), es decir, integrada de orden \(0\) si ya es estacionaria (es estacionaria en niveles, no en diferencias); una serie es \(I(1)\) si es no estacionara en niveles, pero estacionaria en sus primeras diferencias.

5.1.3.1 Prueba de Phillips-Perron

La hipótesis nula es que la serie tiene una raíz unitaria, usaremos el comando pp.test.

5.1.3.2 Ejemplo

Serie trimestral (2020:1 - 2020:4) de Ecuador de las siguientes variables:

• PIB: P.I.B.
  
• IMPOR: Importaciones de bienes y servicios (fob)
  
• OF: Oferta final
  
• DI: Demanda interna
  
• GCFH: Gasto de Consumo final Hogares (*)
• GCFGC: Gasto de Consumo final Gobierno General
  
• FBKF
  
• VE: Variación de existencias
  
• EXPOR: Exportaciones de bienes y servicios (fob)
  
• UF: Utilización final

uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/pib_ec_const.csv"
datos <- read.csv(uu,sep = ";")
ts.datos <- ts(datos[,2:ncol(datos)],st = c(2000,1),freq =4)

Analicemos Oferta Final (OF) y el Gasto de Consumo final Hogares GCFH:

y <- (ts.datos[,"OF"])
x <- (ts.datos[,"GCFH"])

ggplot2::autoplot(cbind(y,x),main ="",ylab = "USD")

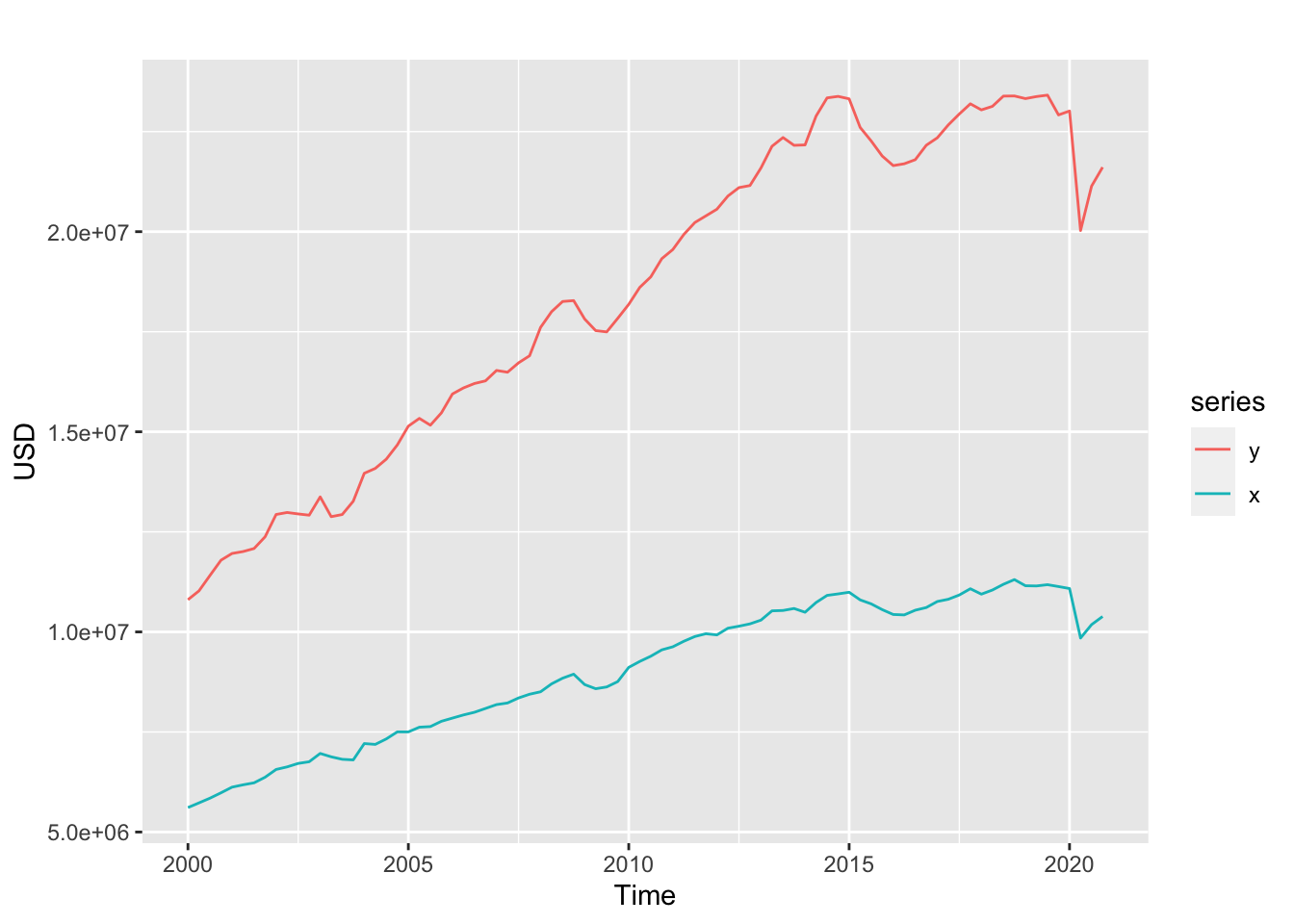
Veamos la estacionariedad de las series:

library(tseries)
pp.test(y)

## 
##  Phillips-Perron Unit Root Test
## 
## data:  y
## Dickey-Fuller Z(alpha) = -2.0923, Truncation lag parameter = 3,
## p-value = 0.9644
## alternative hypothesis: stationary

pp.test(x)

## 
##  Phillips-Perron Unit Root Test
## 
## data:  x
## Dickey-Fuller Z(alpha) = -0.90319, Truncation lag parameter = 3,
## p-value = 0.9872
## alternative hypothesis: stationary

Las series no son estacionarias. Analicemos sus diferencias

pp.test(diff(y))

## 
##  Phillips-Perron Unit Root Test
## 
## data:  diff(y)
## Dickey-Fuller Z(alpha) = -86.34, Truncation lag parameter = 3,
## p-value = 0.01
## alternative hypothesis: stationary

pp.test(diff(x))

## 
##  Phillips-Perron Unit Root Test
## 
## data:  diff(x)
## Dickey-Fuller Z(alpha) = -81.513, Truncation lag parameter = 3,
## p-value = 0.01
## alternative hypothesis: stationary

Las series en diferencias son estacionarias.

5.1.3.3 Prueba de Cointegración: Phillips-Ouliaris

Peter C. B. Phillips y Sam Ouliaris (1990) muestran que las pruebas de raíz unitaria basadas en residuos aplicadas a los residuos de cointegración estimados no tienen las distribuciones habituales de Dickey-Fuller bajo la hipótesis nula de no cointegración.

Debido al fenómeno de regresión espuria bajo la hipótesis nula, la distribución de estas pruebas tiene distribuciones asintóticas que dependen de

1. el número de términos de tendencias deterministas y
2. el número de variables con las que se prueba la cointegración.

Estas distribuciones se conocen como distribuciones de Phillips-Ouliaris.

bfx <- as.matrix(cbind(y,x))
bfx <- as.matrix(cbind(x,y))
po.test(bfx)

## 
##  Phillips-Ouliaris Cointegration Test
## 
## data:  bfx
## Phillips-Ouliaris demeaned = -24.975, Truncation lag parameter =
## 0, p-value = 0.02113

Recordemos que la hipótesis nula en el test de Phillips-Ouliaris es que las series no son cointegradas. En este caso rechazamos la hipótesis nula, existe evidencia para sostener que las series son cointegradas, es decir que hay una tendencia a largo plazo.

mm <- lm(y~x)
summary(mm)

## 
## Call:
## lm(formula = y ~ x)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -604462 -159909    9193  157619  528899 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -2.429e+06  1.385e+05  -17.53   <2e-16 ***
## x            2.313e+00  1.508e-02  153.35   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 238000 on 82 degrees of freedom
## Multiple R-squared:  0.9965, Adjusted R-squared:  0.9965 
## F-statistic: 2.352e+04 on 1 and 82 DF,  p-value: < 2.2e-16

Una relación entre las variables \(I(1)\) cointegradas es una relación a largo plazo, mientras que una relación entre las variables \(I(0)\) es a corto plazo.

residuos <- resid(mm)
ts.plot(residuos)

pp.test(residuos)

## 
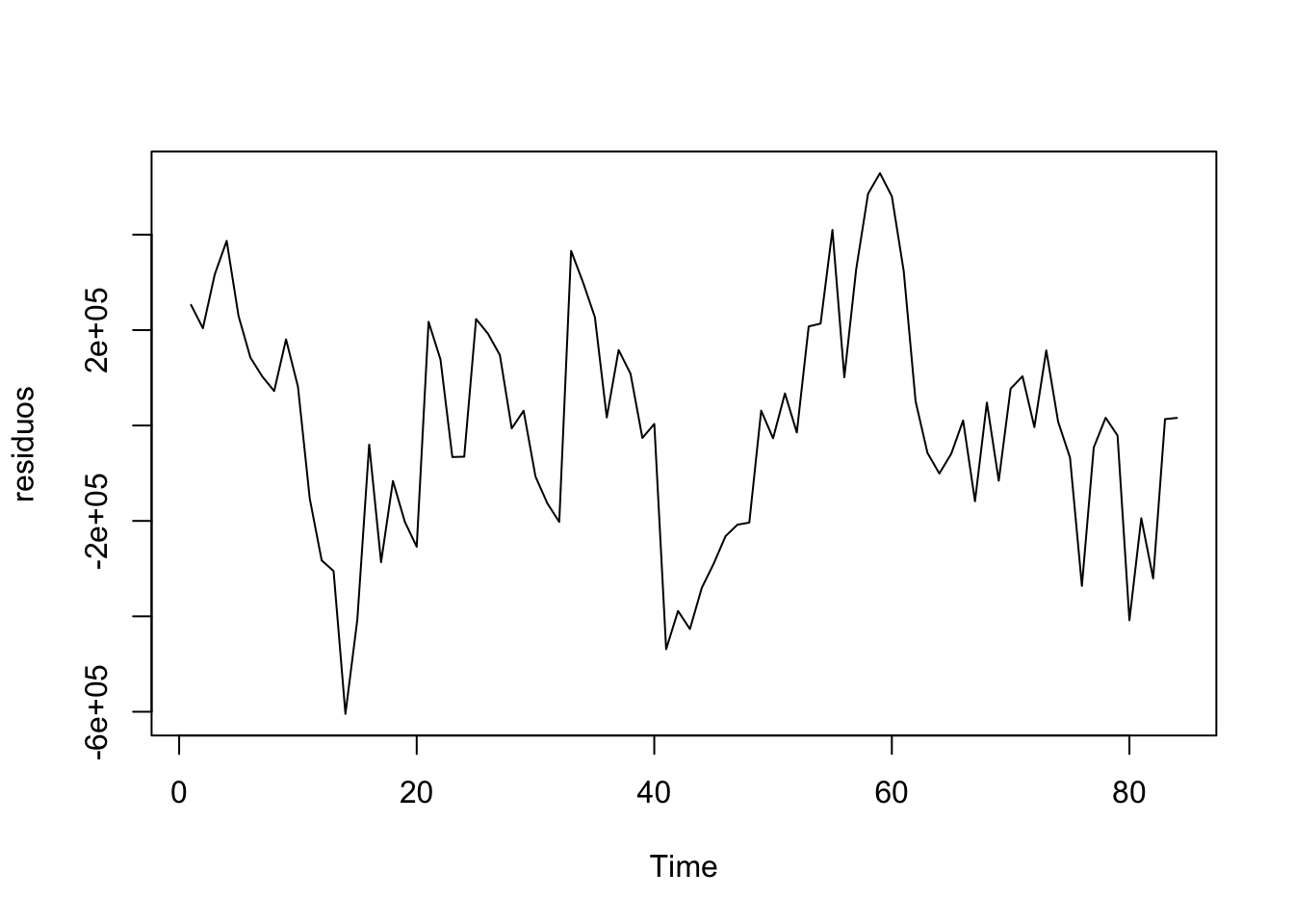
##  Phillips-Perron Unit Root Test
## 
## data:  residuos
## Dickey-Fuller Z(alpha) = -23.904, Truncation lag parameter = 3,
## p-value = 0.02206
## alternative hypothesis: stationary

Presentan una estructura, debemos modelizarlos.

arma11 <- forecast::auto.arima(residuos)
arma11

## Series: residuos 
## ARIMA(1,0,0) with zero mean 
## 
## Coefficients:
##          ar1
##       0.7013
## s.e.  0.0766
## 
## sigma^2 = 2.817e+10:  log likelihood = -1129.61
## AIC=2263.21   AICc=2263.36   BIC=2268.07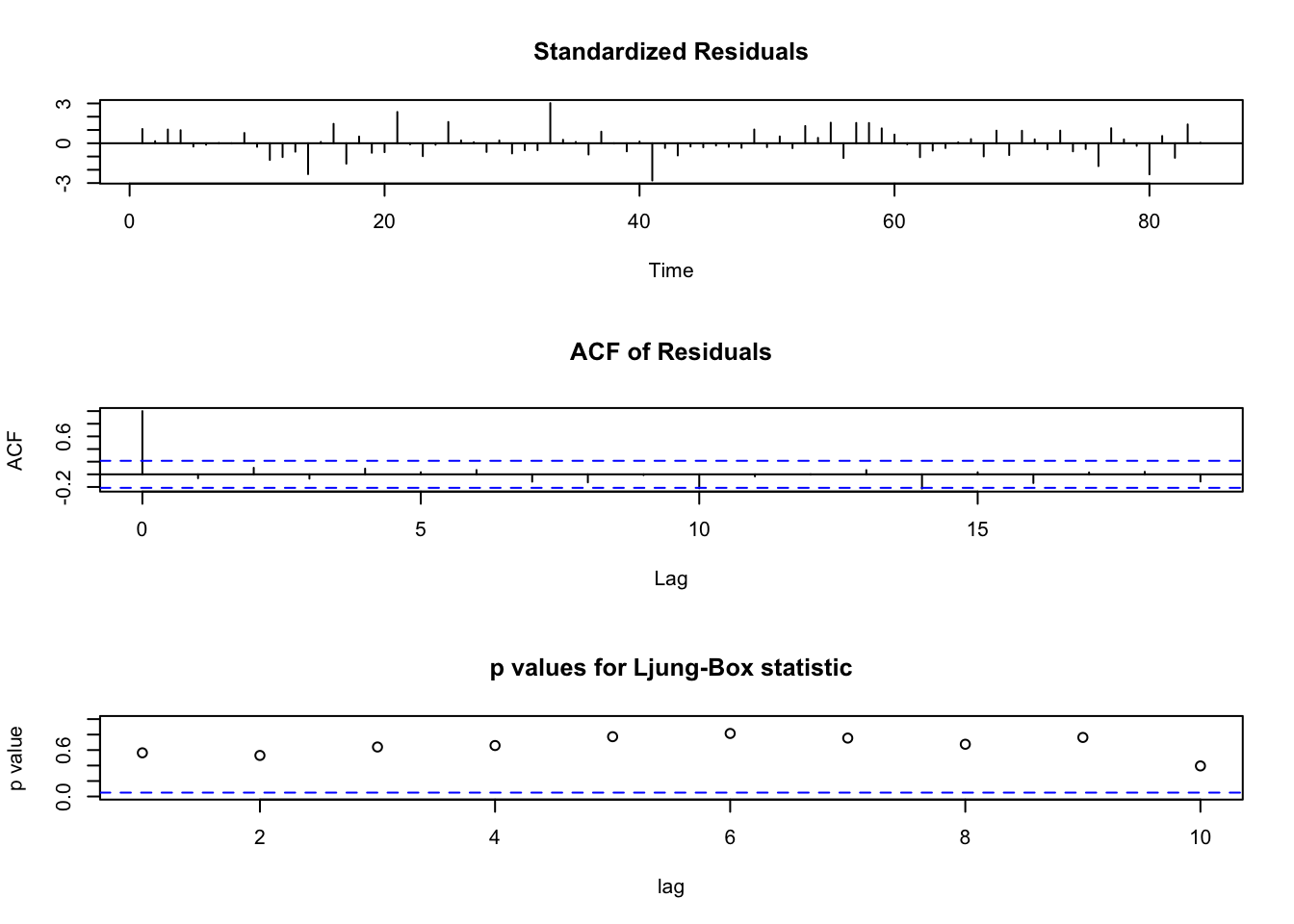

tsdiag(arma11)

Encontramos un modelo en los errores que si es estacionario, la relación a largo plazo entonces es el coeficiente de la regresión: \(2.3\).

5.1.3.4 Ejemplo 2

Datos: tasas de cambio mensuales de Estados Unidos, Inglaterra y Nueva Zelanda desde 2004.

uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/us_rates.txt"
datos <- read.csv(url(uu),sep="",header=T)

# Tasas de cambio, datos mensuales
uk.ts <- ts(datos$UK,st=2004,fr=12)
eu.ts <- ts(datos$EU,st=2004,fr=12)
ggplot2::autoplot(cbind(uk.ts,eu.ts))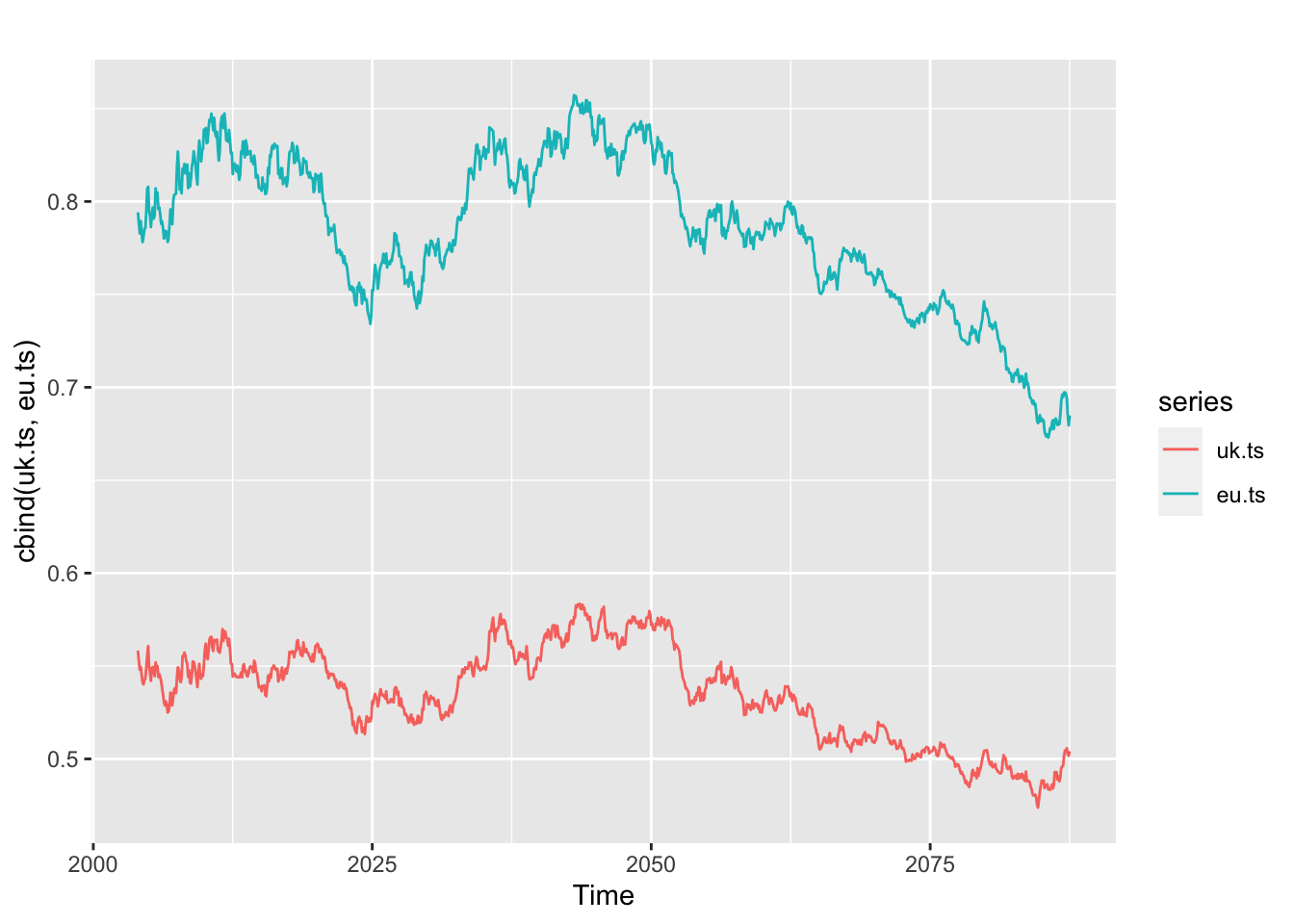

Revisemos si las series en diferencias son estacionarias:

# Tets de Phillips Perron
pp.test(diff(uk.ts))

## 
##  Phillips-Perron Unit Root Test
## 
## data:  diff(uk.ts)
## Dickey-Fuller Z(alpha) = -949.71, Truncation lag parameter = 7,
## p-value = 0.01
## alternative hypothesis: stationary

pp.test(diff(eu.ts))

## 
##  Phillips-Perron Unit Root Test
## 
## data:  diff(eu.ts)
## Dickey-Fuller Z(alpha) = -970.03, Truncation lag parameter = 7,
## p-value = 0.01
## alternative hypothesis: stationary

No tienen raíces unitarias.

Objetivo: Se piensa que la libra esterlina y el euro tienen alguna relación

#Test de Phillips Ouliaris
po.test(cbind(uk.ts,eu.ts))

## 
##  Phillips-Ouliaris Cointegration Test
## 
## data:  cbind(uk.ts, eu.ts)
## Phillips-Ouliaris demeaned = -21.662, Truncation lag parameter =
## 10, p-value = 0.04118

La \(Ho\): NO COINTEGRADAS.

Si son cointegradas, es decir que hay una tendencia a largo plazo.

Veamos la relación:

reg <- lm(uk.ts~eu.ts)
summary(reg)

## 
## Call:
## lm(formula = uk.ts ~ eu.ts)
## 
## Residuals:
##        Min         1Q     Median         3Q        Max 
## -0.0216256 -0.0068351  0.0004963  0.0061439  0.0284938 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 0.074372   0.004983   14.92   <2e-16 ***
## eu.ts       0.587004   0.006344   92.53   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.008377 on 1001 degrees of freedom
## Multiple R-squared:  0.8953, Adjusted R-squared:  0.8952 
## F-statistic:  8561 on 1 and 1001 DF,  p-value: < 2.2e-16

Analicemos los resíduos:

residuos = resid(reg)
plot(resid(reg),t="l")

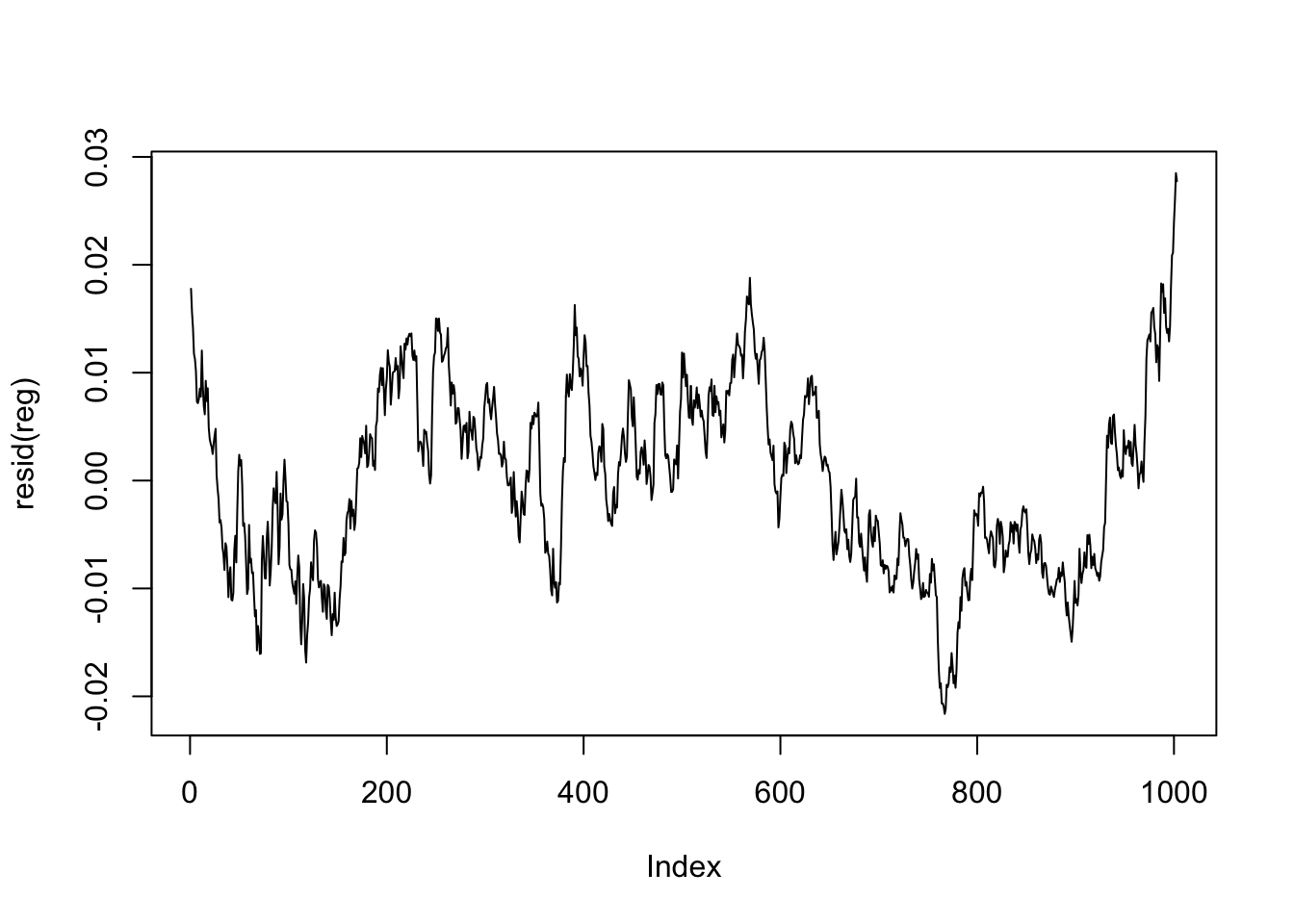
Presentan una estructura, debemos modelizarlos.

arma11 <- forecast::auto.arima(residuos)
arma11

## Series: residuos 
## ARIMA(1,1,2) 
## 
## Coefficients:
##          ar1      ma1      ma2
##       0.9225  -0.8383  -0.1052
## s.e.  0.0473   0.0567   0.0327
## 
## sigma^2 = 3.053e-06:  log likelihood = 4942.14
## AIC=-9876.29   AICc=-9876.25   BIC=-9856.65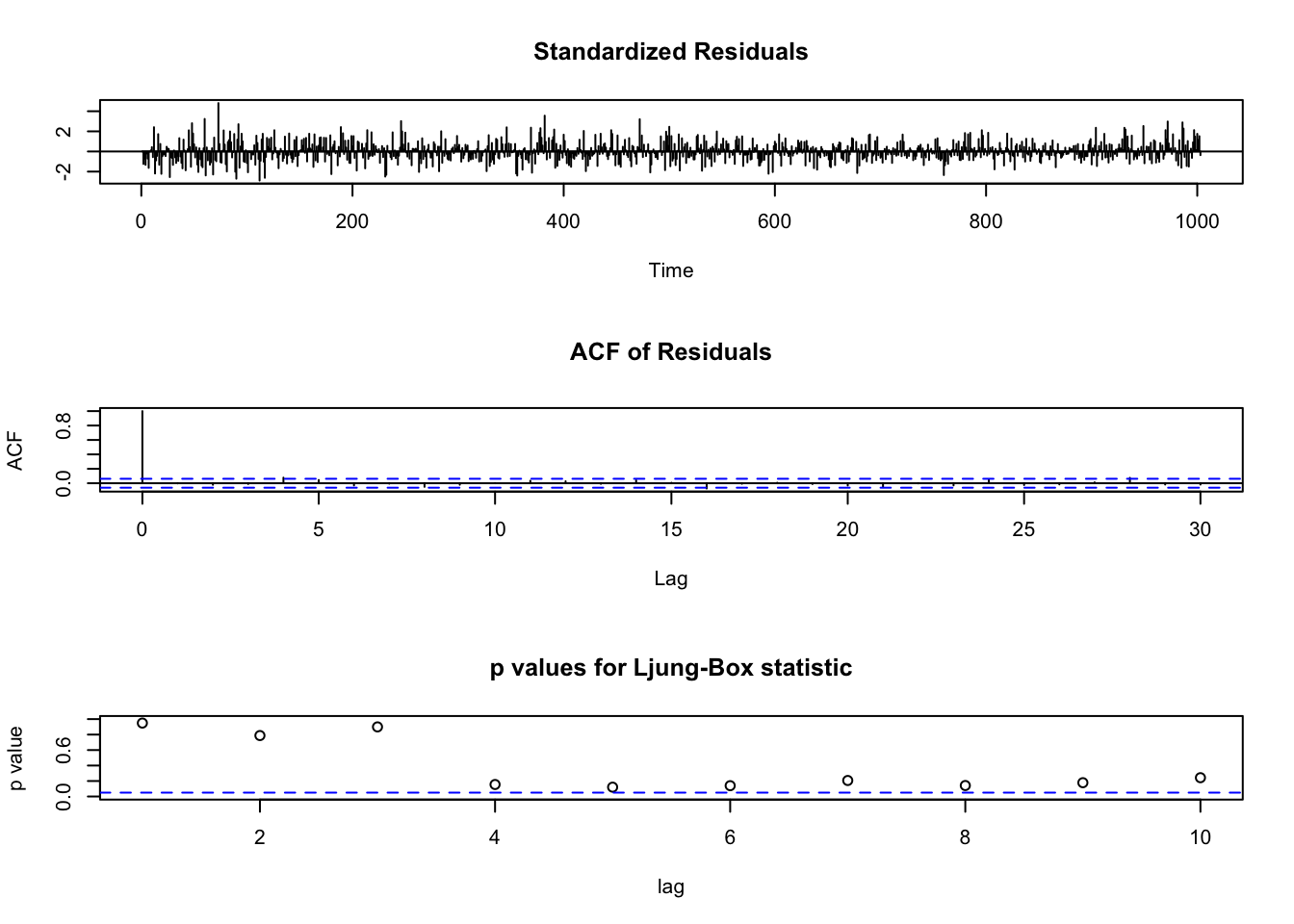

tsdiag(arma11)

Encontramos un modelo en los errores que si es estacionario, la relación a largo plazo entonces es el coeficiente de la regresión: \(0.58\).

5.2 Modelo de corrección de errores

Necesitamos aplicar el modelo vectorial de corrección de errores si las series no son estacionarias y están cointegradas.

Los Modelos de Corrección de Errores o (ECM por sus siglas en inglés) se abordan principalmente, luego de verificar que los residuos de la regresión de largo plazo son estacionarios, aún puede resultar que:

• \(cov(x_t,u_t)\neq 0\).

Exploremos los errores del modelo anterior, en la regresión en niveles \(y_t\) y \(x_t\) son no estacionarias o \(I(p)\) (generalmente \(I(1)\)):

\[ y_t = \pi_1+\pi_2x_t +v_t \]

Su residuo puede escribirse:

\[ v_t = y_t-\pi_1-\pi_2x_t \]

• Si \(v_t\) es estacionario, entonces \(y_t\) y \(x_t\) son cointegradas.
• Si dos variables están cointegradas, tienden a moverse juntas en el tiempo y están acotadas por un efecto de largo plazo en el tiempo.
• Notemos que \(v_t\) es una función lineal de \(y_t\) y \(x_t\).

Pero pese a que \(v_t\) sea estacionario, aún puede presentar autocorrelación. Una posible solución es incluir términos rezagados para obtener residuos que no tengan autocorrelación. Por ejemplo:

\[\begin{eqnarray} y_t = \beta_{10}+\beta_{20}x_t+\alpha_1y_{t-1}+\beta_{21}x_{t-1}+\epsilon_t\\ y_t-y_{t-1}=\beta_{10}+\beta_{20}(x_t-x_{t-1})+(\alpha_1-1)y_{t-1}+(\beta_{21}+\beta_{20})x_{t-1}+\epsilon_t\\ \Delta y_t = \delta_{20}\Delta x_t +\psi(y_{t-1}-\pi_1-\pi_2x_{t-1})+\epsilon_t \tag{5.1} \end{eqnarray}\]

donde

• \(\delta_{20} = \beta_{20}\), \(\psi = \alpha_1-1\)
• \(\pi_1=\frac{\beta_{10}}{(1-\alpha_1)}\)
• \(\pi_2=\frac{\beta_{21}+\beta_{20}}{(1-\alpha_1)}\)

El modelo (5.1) se conoce como Modelo de Corrección de Errores.

El término \(\Delta x_t\):

• representa la dinámica de corto plazo.
• contiene información de la influencia que cambios en \(x_t\) generan en \(y_t\).
• cómo \(\Delta x_t\) influencia en \(\Delta y_t\).

El término \(\psi(y_{t-1}-\pi_1-\pi_2x_{t-1})\):

• también se puede representar como \(\psi (v_{t_1})\)
• se conoce como el mecanismo de corrección de errores.

Recuerda que \(y_t = \pi_1+\pi_2x_t +v_t\) representa el equilibrio de largo plazo:

• si \(v_t=y_t-\pi_1+\pi_2x_t>0\), \(y_t\) está sobre el punto de equilibrio en \(t-1\).
• si \(v_t=y_t-\pi_1+\pi_2x_t<0\), \(y_t\) está debajo el punto de equilibrio en \(t-1\).

5.2.0.1 Ejemplo

Usaremos los datos del ejemplo 5.1.3.2.

Hemos visto que OF y GCFH son \(I(1)\), el primer paso es estimar el modelo

\[ OF = \pi_1 + \pi_2GCFH + v_t \]

uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/pib_ec_const.csv"
datos <- read.csv(uu,sep = ";")
ts.datos <- ts(datos[,2:ncol(datos)],st = c(2000,1),freq =4)

y <- (ts.datos[,"OF"])
x <- (ts.datos[,"GCFH"])

m1 <- lm(y~x)
summary(m1)

## 
## Call:
## lm(formula = y ~ x)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -604462 -159909    9193  157619  528899 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -2.429e+06  1.385e+05  -17.53   <2e-16 ***
## x            2.313e+00  1.508e-02  153.35   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 238000 on 82 degrees of freedom
## Multiple R-squared:  0.9965, Adjusted R-squared:  0.9965 
## F-statistic: 2.352e+04 on 1 and 82 DF,  p-value: < 2.2e-16

El segundo paso es determinar si los residuos del modelo son \(I(0)\):

resm1 <- resid(m1)
pp.test(resm1)

## 
##  Phillips-Perron Unit Root Test
## 
## data:  resm1
## Dickey-Fuller Z(alpha) = -23.904, Truncation lag parameter = 3,
## p-value = 0.02206
## alternative hypothesis: stationary

Los residuos son estacionarios pero, ¿son ruido blanco?

Box.test(resm1,type = "Ljung-Box",lag = 5) #Ho: independencia

## 
##  Box-Ljung test
## 
## data:  resm1
## X-squared = 87.588, df = 5, p-value < 2.2e-16

Ahora estimamos el modelo

\[ \Delta OF_t = \delta_{20}\Delta GCFH_t +\psi(v_{t-1})+\epsilon_t \]

n <- length(y)
ecm1 <- lm(diff(y)~diff(x)+lag(resm1[2:(n)],1))
ecm1 <- lm(diff(y)~diff(x)+lag(resm1[1:(n-1)],1))
summary(ecm1)

## 
## Call:
## lm(formula = diff(y) ~ diff(x) + lag(resm1[1:(n - 1)], 1))
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -459962 -104487  -19632  109106  543392 
## 
## Coefficients:
##                            Estimate Std. Error t value Pr(>|t|)    
## (Intercept)               3.578e+02  2.090e+04   0.017   0.9864    
## diff(x)                   2.265e+00  1.086e-01  20.857   <2e-16 ***
## lag(resm1[1:(n - 1)], 1) -1.667e-01  8.394e-02  -1.986   0.0506 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 180900 on 79 degrees of freedom
##   (1 observation deleted due to missingness)
## Multiple R-squared:  0.8471, Adjusted R-squared:  0.8432 
## F-statistic: 218.8 on 2 and 79 DF,  p-value: < 2.2e-16

Box.test(resid(ecm1))

## 
##  Box-Pierce test
## 
## data:  resid(ecm1)
## X-squared = 9.3356, df = 1, p-value = 0.002247

Se ha corregido la estructura de correlación de los residuos.

Tenemos que el efecto de largo plazo es 2.3132057 y el de corto plazo es 2.2654903.

Usando el paquete ecm llegamos al siguiente resultado:

library(ecm)
trn <- data.frame(y = as.numeric(y),x = as.numeric(x))
xeq <- xtr <- data.frame(trn$x)
(ecm2 <- ecm(trn$y, xeq,xtr ))

## 
## Call:
## lm(formula = dy ~ ., data = x, weights = weights)
## 
## Coefficients:
## (Intercept)   deltatrn.x    trn.xLag1        yLag1  
##  -7.543e+05    2.317e+00    6.974e-01   -3.005e-01

5.3 Introducción a los modelos de vectores autorregresivos: VAR

Veamos el modelo estructural dinámico (Novales (2011)):

\[\begin{eqnarray} y_{1t} = \alpha_{10} + \alpha_{11}y_{2t}+\alpha_{12}y_{1t-1}+\alpha_{13}y_{2t-1}+\gamma_1'z_t+\varepsilon_{1t}\tag{5.2}\\ y_{2t} = \alpha_{20} + \alpha_{21}y_{1t}+\alpha_{22}y_{1t-1}+\alpha_{23}y_{2t-1}+\gamma_2'z_t+\varepsilon_{2t} \end{eqnarray}\]

donde \(y_{1t}\), \(y_{2t}\), son variables estacionarias, y \(\epsilon_{1t}\), \(\epsilon_{2t}\) son procesos ruido blanco con esperanza cero y varianzas \(\sigma_{\epsilon_1}^2\), \(\sigma_{\epsilon_2}^2\) y covarianza \(\sigma_{12}\).

El modelo (5.2) es de ecuaciones simultáneas con dos variables endógenas \(y_{1t}\) y \(y_{2t}\) y un vector \(z_t\) de variables exógenas.

Un shock sobre \(y_{2t}\), en la forma de un valor no nulo de la innovación estructural \(\varepsilon_{2t}\), afecta directamente a \(y_{2t}\), pero también influye a \(y_{1t}\) a través de la presencia de \(y_{2t}\) como variable explicativa en la primera ecuación.

Además, este efecto se propaga en el tiempo, debido a la presencia de los valores rezagados de ambas variables como variables explicativas.

Las variables explicativas exógenas \(z_t\) también pueden aparecer con rezagos en el modelo. Por ejemplo, \(z_t\) podría ser una tendencia determinista o que recoja la estacionalidad. \(z_t\) también puede representar variables tal que \(E(z_{t-s}\varepsilon_{1t})=E(z_{t-s}\varepsilon_{2t})=0\) \(\forall s\). Por ejemplo, el precio de barril de petróleo que se determina en mercados internacionales mientras \(y_{1t}\) y \(y_{2t}\) son variables de la macroeconmía ecuatoriana.

De manera matricial, el modelo (5.2) puede representarse:

\[ By_t=\Gamma_0+\Gamma_1y_{t-1}+Gz_t+\varepsilon_t \]

En el caso del modelo de dos ecuaciones, las matrices son:

\[ B = \begin{pmatrix} 1 & -\alpha_{11} \\ -\alpha_{21} & 1 \end{pmatrix}; \Gamma_0 = \begin{pmatrix} \alpha_{10} \\ \alpha_{20} \end{pmatrix}; \Gamma_1 = \begin{pmatrix} \alpha_{12} & \alpha_{13} \\ \alpha_{22} & \alpha_{23} \end{pmatrix}; G = \begin{pmatrix} \gamma'_{1} \\ \gamma'_{2} \end{pmatrix}. \]

Este modelo se conoce como VAR estructural y presenta dos problemas:

1. la simultaneidad, al aparecer cada una de las dos variables como variable explicativa en la ecuación de la otra, lo que genera inconsistencia del estimador MCO. 1.1. podría resolverse estimando por variables instrumentales, siempre que contemos con instrumentos adecuados, lo cual no es sencillo de justificar. Además, el segundo problema podría persistir.

2. si los términos de error tuviesen autocorrelación, las estimaciones MCO serían inconsistentes, al tratarse de un modelo dinámico. 2.1. se resuelve tratando de ampliar la estructura dinámica del modelo hasta lograr que los términos de error carezcan de autocorrelación.

Supongamos que la matriz \(B\) tiene inversa (\(det(B)\neq 0\)), tenemos entonces:

\[ y_t = B^{-1}\Gamma_0+B^{-1}\Gamma_1y_{t-1}+B^{-1}Gz_{t}+B^{-1}\varepsilon_t=A_0+A_1y_{t-1}+Mz_t+u_t \tag{5.3} \]

donde \(A_0= B^{-1}\Gamma_0\), \(A_1=B^{-1}\Gamma_1\), \(M=B^{-1}G\), \(u_t=B^{-1}\varepsilon_t\).Así hemos pasado a la forma reducida, o modelo vectorial autoregresivo (VAR) en el cual:

\[\begin{eqnarray} y_{1t} = \beta_{10}+\beta_{11}y_{1t-1}+\beta_{12}y_{2t-1}+m_{11}z_t+u_{1t}\tag{5.4}\\ y_{2t} = \beta_{20}+\beta_{21}y_{1t-1}+\beta_{22}y_{2t-1}+m_{21}z_t+u_{2t} \end{eqnarray}\]

5.3.1 El modelo VAR (1)

El orden de los modelos VAR está dado por el número de rezagos que se usa en cada ecuación. El modelo descrito anteriormente es entonces un \(VAR(1)\), para denotar también el número de variables se usa \(VAR_2(1)\).

La relación de parámetros de la forma reducida y de la forma estructural es:

\[\begin{eqnarray} B^{-1} =\frac{1}{1-\alpha_{11}\alpha_{21}} \begin{pmatrix} 1 & \alpha_{11} \\ \alpha_{21} & 1 \end{pmatrix},\\ A_1 =\begin{pmatrix} \beta_{11} & \beta_{12} \\ \beta_{21} & \beta_{22} \end{pmatrix} = \frac{1}{1-\alpha_{11}\alpha_{21}}\begin{pmatrix} \alpha_{12}+\alpha_{11}\alpha_{22} & \alpha_{13}+\alpha_{11}\alpha_{23} \\ \alpha_{22}+\alpha_{21}\alpha_{12} & \alpha_{23}+\alpha_{13}\alpha_{21} \end{pmatrix} ,\tag{5.5}\\ A_0 =\begin{pmatrix} \beta_{10} \\ \beta_{20} \end{pmatrix} = \frac{1}{1-\alpha_{11}\alpha_{21}}\begin{pmatrix} \alpha_{10}+\alpha_{11}\alpha_{20} \\ \alpha_{20}+\alpha_{21}\alpha_{10} \end{pmatrix} ,\tag{5.6}\\ M =\begin{pmatrix} \beta_{10} \\ \beta_{20} \end{pmatrix} = \frac{1}{1-\alpha_{11}\alpha_{21}}\begin{pmatrix} \gamma'_{1}+\alpha_{11}\gamma'_{2} \\ \alpha_{21}\gamma'_{1}+\gamma'_{2} \end{pmatrix} ,\tag{5.7}\\ u_t =\begin{pmatrix} u_{1t} \\ u_{2t} \end{pmatrix} = B^{-1}\varepsilon_t=B^{-1}\begin{pmatrix} \varepsilon_{1t} \\ \varepsilon_{2t} \end{pmatrix}=\frac{1}{1-\alpha_{11}\alpha_{21}}\begin{pmatrix} \varepsilon_{1t}+\alpha_{11}\varepsilon_{2t} \\ \alpha_{21}\varepsilon_{1t}+\varepsilon_{2t} \end{pmatrix}.\tag{5.8} \end{eqnarray}\]

Aunque esta es la versión más general del modelo \(VAR\), es habitual hacer supuestos simplificadores (uno de ellos es que \(B\) sea diagonal).

Podemos suponer que \(G=0_k\), también que la matriz de covarianzas de las innovaciones \(\varepsilon_t\) del modelo \(VAR\), \(\Sigma_\varepsilon\), es diagonal, es decir que las innovaciones asociadas a distintas variables tienen covarianza nula, puesto que la correlación entre \(y_{1t}\) e \(y_{2t}\) ya está recogida por la presencia de cada una de estas variables en la ecuación de la otra variable en el modelo estructural.

Usando estos supuestos podemos tener un modelo estructural dinámico de la forma:

\[ y_{1t} = \alpha_{10}+\alpha_{11}y_{2t}+\alpha_{12}y_{t-1}+\alpha_{13}y_{2t-1}+\varepsilon_{1t} \\ y_{2t} = \alpha_{20}+\alpha_{21}y_{1t}+\alpha_{22}y_{t-1}+\alpha_{23}y_{2t-1}+\varepsilon_{2t} \]

y su forma reducida o \(VAR_2(1)\):

\[ y_{1t} = \beta_{10}+\beta_{11}y_{t-1}+\beta_{12}y_{2t-1}+u_{1t}\\ y_{2t} = \beta_{20}+\beta_{21}y_{t-1}+\beta_{22}y_{2t-1}+u_{2t} \]

o, en forma matricial

\[ \begin{pmatrix}y_{1t}\\y_{2t}\end{pmatrix}={\begin{pmatrix}\beta_{10}\\\beta_{20}\end{pmatrix}}+{\begin{pmatrix}\beta_{11}&\beta_{12}\\\beta_{21}&\beta_{22}\end{pmatrix}}{\begin{pmatrix}y_{1t-1}\\y_{2t-1}\end{pmatrix}}+{\begin{pmatrix}u_{1t}\\u_{2t}\end{pmatrix}} \]

o, de forma más compacta:

\[ y_t = A_0+ A_1y_{t-1}+u_t \]

donde los términos de error satisfacen

\[ E(u_{1t}) = E(u_{2t}) = 0, \forall t \] \[ E(u_{1t}u_{1s}) = E(u_{2t}u_{2s}) = E(u_{1t}u_{2s}) =0, \forall t \neq s \]

\[ u_t = \begin{pmatrix} u_{1t} \\u_{2t} \end{pmatrix} = B^{-1}\begin{pmatrix} \varepsilon_{1t} \\ \varepsilon_{2t} \end{pmatrix} = \frac{1}{(1-\alpha_{11}\alpha_{21})}\begin{pmatrix} \varepsilon_{1t}+\alpha_{11}\varepsilon_{2t} \\ \varepsilon_{2t}+\alpha_{21}\varepsilon_{1t} \end{pmatrix} \] \[ \Sigma_u = Var\begin{pmatrix} u_{1t} \\u_{2t} \end{pmatrix} = \begin{pmatrix} \sigma_{1}^2 & \sigma_{12} \\ \sigma_{12} & \sigma_{2}^2 \end{pmatrix} = \frac{1}{(1-\alpha_{11}\alpha_{21})^2}\begin{pmatrix} \sigma_{\varepsilon_1}^2+\alpha_{11}^2\sigma_{\varepsilon_2}^2 & \alpha_{21}\sigma_{\varepsilon_1}^2+\alpha_{11}\sigma_{\varepsilon_2}^2 \\ \alpha_{21}\sigma_{\varepsilon_1}^2+\alpha_{11}\sigma_{\varepsilon_2}^2 & \alpha_{21}^2\sigma_{\varepsilon_1}^2+\sigma_{\varepsilon_2}^2 \end{pmatrix} \]

Es importante observar que las innovaciones del modelo VAR estarán correlacionadas entre si, \(\sigma_{u_1u_2}\neq 0\), incluso si las innovaciones del modelo estructural están incorrelacionadas, \(\sigma_{\varepsilon_1\varepsilon_2}=0\), como hemos supuesto en la expresión anterior. La única excepción requeriría \(\alpha_{11}=\alpha_{21}=0\), el caso en que no hay efectos contemporáneos de ninguna variable sobre la otra. Únicamente en este caso limite tendríamos \(\sigma_{u_1u_2}=0\).

En este modelo \(VAR\), valores negativos de \(\beta_{12}\) y \(\beta_{21}\) tienden a inducir correlación negativa entre \(y_{1t}\) y \(y_{2t}\) si bien no la garantizan, y valores positivos de \(\beta_{12}\) y \(\beta_{21}\) tienden a generar correlación positiva.

Un shock inesperado en \(y_{2t}\), en la forma de un valor no nulo de la innovación \(u_{2t}\), además de afectar a \(y_{2t}\), también influye sobre \(y_1\) en periodos futuros, debido a la presencia del rezago \(y_{2t-1}\) como variable explicativa en la ecuación de \(y_{1t}\).

Por otra parte, dada la correlación existente entre ambos términos de error, un valor no nulo de \(u_{2t}\) vendrá habitualmente acompañado de un valor positivo o negativo (según sean los signos de \(u_{2t}\) y de \(\sigma_{12}\)) de \(u_{1t}\), por lo que la reacción de \(y_{1t}\) vendrá acompañada también de una reacción de \(y_{2t}\).

Dada la relación existente entre los vectores \(\varepsilon_t\) y \(u_t\), si los términos de error del modelo estructural eran ruido blanco, los términos de error del modelo \(VAR\) también tendrán estructura de ruido blanco: \(E(u_{1t}u_{1t-s}) = 0\quad \forall s\neq 0\).

Es asimismo importante examinar las relaciones entre los parámetros de ambos modelos, que son, en el caso del modelo \(VAR(1)\), las \(6\) relaciones entre los parámetros \(\beta\) y los parámetros que aparecen en (5.5) y (5.6), más las 3 relaciones entre los elementos de las respectivas matrices de covarianzas,

\[ \sigma_{u_1}^2=\frac{1}{(1-\alpha_{11}\alpha_{21})^2}(\sigma_{\varepsilon_1}^2+\alpha_{11}^2\sigma_{\varepsilon_2}^2)\\ \sigma_{u_2}^2=\frac{1}{(1-\alpha_{11}\alpha_{21})^2}(\sigma_{\varepsilon_2}^2+\alpha_{21}^2\sigma_{\varepsilon_1}^2)\\ \sigma_{u_1u_2}=\frac{1}{(1-\alpha_{11}\alpha_{21})^2}(\alpha_{21}\sigma_{\varepsilon_1}^2+\alpha_{11}\sigma_{\varepsilon_2}^2) \]

Básicamente, que todo depende de todo.

5.3.2 El modelo VAR(n)

En general, un modelo VAR de orden \(n\), con variables endógenas, se especifica,

\[ Y_t = A_0+\sum_{s=1}^{n} A_sY_{t-s}+GW_t+u_t \] donde \(Y_t\) es un vector columna \(k\times 1\), \(n\) es el orden del modelo \(VAR\) (número de rezagos en cada variable en cada ecuación), y \(u_t\) es el vector \(k\times 1\) de innovaciones, es decir, procesos sin autocorrelación, con \(Var(u_t)=\Sigma\), constante. \(W_t\) es un vector de variables exógenas.

5.3.2.1 Ejemplo

Empecemos simulando un proceso VAR (2)

set.seed(123) # Misma semilla para tener los mismos resultados

# Generamos muestra
t <- 200 # tamaño de la serie
k <- 2 # Número de variables endogenas
p <- 2 # numero de rezagos

# Generamos matriz de coeficientes
A.1 <- matrix(c(-.3, .6, -.4, .5), k) # Matriz de coeficientes del rezago 1
A.2 <- matrix(c(-.1, -.2, .1, .05), k) # Matriz de coeficientes del rezago 2
A <- cbind(A.1, A.2) # Forma compuesta

# Generamos las series
series <- matrix(0, k, t + 2*p) # Inicio serie con ceros
for (i in (p + 1):(t + 2*p)){ # Generamos los errores e ~ N(0,0.5)
  series[, i] <- A.1%*%series[, i-1] + A.2%*%series[, i-2] + rnorm(k, 0, .5)
}

series <- ts(t(series[, -(1:p)])) # Convertimos a formato ts
names <- c("V1", "V2") # Renombrar variables
plot.ts(series) # Graficos de la serie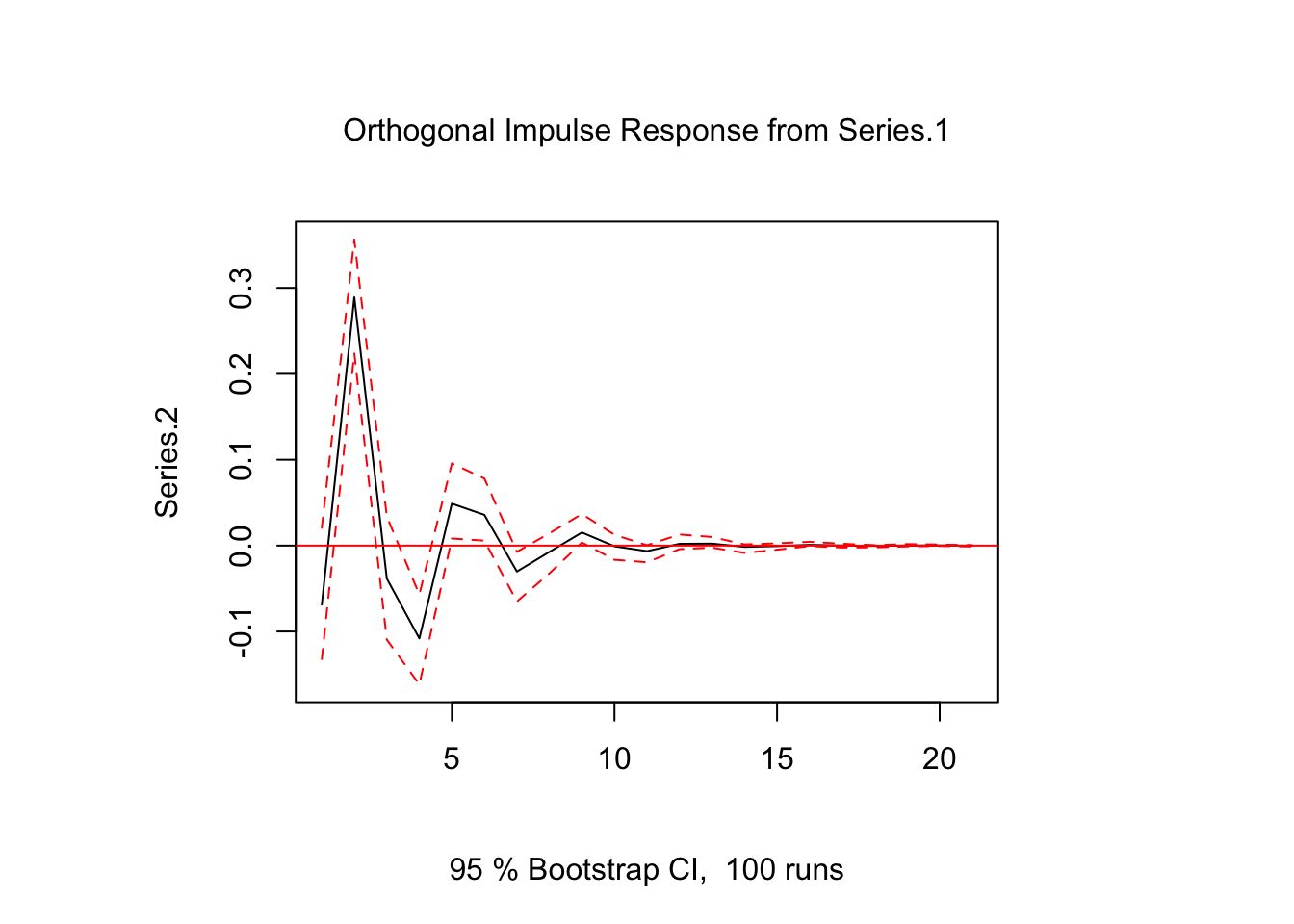

5.3.3 Estimación

La función relevante es VAR y su uso es directo. Solo tienes que cargar el paquete y especificar los datos (y), el orden (n) y el tipo del modelo. El tipo de opción determina si se debe incluir un término de intercepción, una tendencia o ambos en el modelo. Como los datos artificiales que hemos generado no contienen términos determinísticos, elegimos no tomarlo en cuenta en la estimación al establecer type = "none".

library(vars) # Cargamos el paquete
var.1 <- VAR(series, 2, type = "none") # Estimamos el modelo
var.1

## 
## VAR Estimation Results:
## ======================= 
## 
## Estimated coefficients for equation Series.1: 
## ============================================= 
## Call:
## Series.1 = Series.1.l1 + Series.2.l1 + Series.1.l2 + Series.2.l2 
## 
## Series.1.l1 Series.2.l1 Series.1.l2 Series.2.l2 
## -0.19749787 -0.32015115 -0.23210384  0.04687272 
## 
## 
## Estimated coefficients for equation Series.2: 
## ============================================= 
## Call:
## Series.2 = Series.1.l1 + Series.2.l1 + Series.1.l2 + Series.2.l2 
## 
## Series.1.l1 Series.2.l1 Series.1.l2 Series.2.l2 
##  0.67380854  0.34135611 -0.18429803  0.06903447

Algunas consideraciones sobre la estimación de un modelo VAR:

• El modelo tiene tantas ecuaciones como variables, y los valores rezagados de todas las ecuaciones aparecen como variables explicativas en todas las ecuaciones.

• Una vez estimado el modelo, puede procederse a excluir algunas variables explicativas, en función de su significación estadística, pero hay razones para no hacerlo.

• En el modelo \(VAR\) pueden estimarse con bastante precisión los elementos globales del modelo, como el \(R^2\); la desviación típica residual, y los mismos residuos, o el efecto global de una variable sobre otra, lo que se resume en los contrastes de causalidad que veremos más adelante. Sin embargo, no cabe hacer interpretaciones de coeficientes individuales en distintos rezagos, ni llevar a cabo contrastes de hipótesis sobre coeficientes individuales.

• El número de parámetros crece muy rápidamente. Por ejemplo, en un \(VAR_2(1)\), las variables explicativas de cada ecuación son: una constante, más un rezago de cada una de las variables del modelo, más \(3\) parámetros en la matriz de covarianzas, con un total de \(9\) parámetros para explicar el movimiento conjunto de \(2\) variables. En un \(VAR_3(1)\) habrían 18 parámetros en total, en un \(VAR_4(3)\), ¿cuántos parámetros tendríamos?

5.3.4 Comparación: escoger el número de rezagos.

Un problema central en el análisis de modelos \(VAR\) es encontrar el número de rezagos que produce los mejores resultados. La comparación de modelos generalmente se basa en criterios de información como el Akaike AIC, Bayesiano BIC o Hannan-Quinn HQ, buscando que se minimice el valor del criterio de información.

\[ AIC = -2\frac{l}{T}+2\frac{p}{T} \]

\[ BIC = -2\frac{l}{T}+2\frac{ln(T)}{T} \]

\[ HQ = -2\frac{l}{T}+2\frac{kln(ln(T))}{T} \]

donde \(l=-\frac{Tk}{2}(1+ln(2\pi))-\frac{T}{2}ln(|\hat{\Sigma}|)\), y \(p=k(d+nk)\) el número de parámetros estimados en el modelo \(VAR\), siendo \(d\) es el número de variables exógenas, \(n\) el orden del VAR, \(k\) el número de variables endógenas.

Por lo general, el AIC es preferible a otros criterios, debido a sus características favorables de pronóstico de muestras pequeñas. El BIC y HQ, sin embargo, funcionan bien en muestras grandes y tienen la ventaja de ser un estimador consistente, es decir, converge a los valores verdaderos.

El parámetro clave es lag.max = 5 en el código siguiente:

var.aic <- VAR(series, type = "none", lag.max = 5, ic = "AIC")

Veamos los resultados:

summary(var.aic)

## 
## VAR Estimation Results:
## ========================= 
## Endogenous variables: Series.1, Series.2 
## Deterministic variables: none 
## Sample size: 200 
## Log Likelihood: -266.065 
## Roots of the characteristic polynomial:
## 0.6611 0.6611 0.4473 0.03778
## Call:
## VAR(y = series, type = "none", lag.max = 5, ic = "AIC")
## 
## 
## Estimation results for equation Series.1: 
## ========================================= 
## Series.1 = Series.1.l1 + Series.2.l1 + Series.1.l2 + Series.2.l2 
## 
##             Estimate Std. Error t value Pr(>|t|)    
## Series.1.l1 -0.19750    0.06894  -2.865  0.00463 ** 
## Series.2.l1 -0.32015    0.06601  -4.850 2.51e-06 ***
## Series.1.l2 -0.23210    0.07586  -3.060  0.00252 ** 
## Series.2.l2  0.04687    0.06478   0.724  0.47018    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## 
## Residual standard error: 0.4638 on 196 degrees of freedom
## Multiple R-Squared: 0.2791,  Adjusted R-squared: 0.2644 
## F-statistic: 18.97 on 4 and 196 DF,  p-value: 3.351e-13 
## 
## 
## Estimation results for equation Series.2: 
## ========================================= 
## Series.2 = Series.1.l1 + Series.2.l1 + Series.1.l2 + Series.2.l2 
## 
##             Estimate Std. Error t value Pr(>|t|)    
## Series.1.l1  0.67381    0.07314   9.213  < 2e-16 ***
## Series.2.l1  0.34136    0.07004   4.874 2.25e-06 ***
## Series.1.l2 -0.18430    0.08048  -2.290   0.0231 *  
## Series.2.l2  0.06903    0.06873   1.004   0.3164    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## 
## Residual standard error: 0.4921 on 196 degrees of freedom
## Multiple R-Squared: 0.3574,  Adjusted R-squared: 0.3443 
## F-statistic: 27.26 on 4 and 196 DF,  p-value: < 2.2e-16 
## 
## 
## 
## Covariance matrix of residuals:
##          Series.1 Series.2
## Series.1  0.21417 -0.03116
## Series.2 -0.03116  0.24154
## 
## Correlation matrix of residuals:
##          Series.1 Series.2
## Series.1    1.000   -0.137
## Series.2   -0.137    1.000

Notemos que:

• Con muchos rezagos perdemos bastantes grados de libertad.
• Pocos rezagos pueden hacer que el modelo sea poco preciso. Por ejemplo podría causar autocorrelación en el error que indiquen significancias de parámetros que no son reales.

5.3.5 Condición de estabilidad

En un modelo de la forma

\[ Y_t = A_0+\sum_{s=1}^{n} A_sY_{t-s}+GW_t+u_t \]

Las raíces del polinomio característico de cada matriz \(A\), es decir que las raíces del polinomio característico de la matriz \(|I-\lambda A|=0\) caigan fuera del círculo unitario.

VAR representado como un MA(\(\infty\))

Si resolvemos recursivamente el VAR(k) tenemos:

\[ Y_t = A_0+A_1Y_{t-1}+u_t \] \[ Y_t = A_0+A_1(A_0+A_1Y_{t-2}+u_{t-1})+u_t \]

\[ Y_t = (I_k+A_1)A_0+A_1^2Y_{t-2}+(A_1u_{t-1}+u_{t}) \] \[ Y_t = (I_k+A_1+A_1^2+\cdots+A_1^{n-1})A_0+A_1^nY_{t-n}+\sum_{i=0}^{n-1}A_1^iu_{t-i} \] Cuando se cumplen las condiciones de estabilidad, tomando límites, tenemos

\[ Y_t = \mu+\sum_{i=0}^{\infty}A_1^iu_{t-i} = \mu+\Phi(L)u_t \] donde \(\mu = (I_k-A_1)^{-1}A_0\).

5.3.6 Causalidad de granger

Es probable que, cuando un \(VAR\) incluye muchos rezagos de variables, sea difícil ver qué conjuntos de variables tienen efectos significativos en cada variable dependiente y cuáles no.

Veamos por ejemplo un \(VAR(3)\)

\[ \begin{pmatrix}y_{1t}\\y_{2t}\end{pmatrix}={\begin{pmatrix}\beta_{10}\\\beta_{20}\end{pmatrix}}+{\begin{pmatrix}\beta_{11}&\beta_{12}\\\beta_{21}&\beta_{22}\end{pmatrix}}{\begin{pmatrix}y_{1t-1}\\y_{2t-1}\end{pmatrix}} +{\begin{pmatrix}\gamma_{11}&\gamma_{12}\\\gamma_{21}&\gamma_{22}\end{pmatrix}}{\begin{pmatrix}y_{1t-2}\\y_{2t-2}\end{pmatrix}}+ {\begin{pmatrix}\delta_{11}&\delta_{12}\\\delta_{21}&\delta_{22}\end{pmatrix}}{\begin{pmatrix}y_{1t-3}\\y_{2t-3}\end{pmatrix}} +{\begin{pmatrix}u_{1t}\\u_{2t}\end{pmatrix}} \] Es decir:

\[ y_{1t} = \beta_{10}+\beta_{11}y_{1t-1}+\beta_{12}y_{2t-1}+\gamma_{11}y_{1t-2}+\gamma_{12}y_{2t-2}+\delta_{11}y_{1t-3}+\delta_{12}y_{2t-3}+u_{1t}\\ y_{2t} = \beta_{20}+\beta_{21}y_{1t-1}+\beta_{22}y_{2t-1}+\gamma_{21}y_{1t-2}+\gamma_{22}y_{2t-2}+\delta_{21}y_{1t-3}+\delta_{22}y_{2t-3}+u_{2t} \] En el test de (Granger (1969)) tenemos las siguientes hipótesis:

Hipótesis	Restricción implícita
Rezagos de \(y_{1t}\) no explican \(y_{2t}\)	\(\beta_{21}=0\) y \(\gamma_{21}=0\) y \(\delta_{21} = 0\)
Rezagos de \(y_{1t}\) no explican \(y_{1t}\)	\(\beta_{11}=0\) y \(\gamma_{11}=0\) y \(\delta_{11} = 0\)
Rezagos de \(y_{2t}\) no explican \(y_{1t}\)	\(\beta_{12}=0\) y \(\gamma_{12}=0\) y \(\delta_{12} = 0\)
Rezagos de \(y_{2t}\) no explican \(y_{2t}\)	\(\beta_{22}=0\) y \(\gamma_{22}=0\) y \(\delta_{22} = 0\)

• Cada una de estas cuatro hipótesis conjuntas se puede probar dentro del marco de la prueba \(F\), ya que cada conjunto de restricciones contiene solo parámetros extraídos de una ecuación.

• Las pruebas de causalidad de Granger buscan responder preguntas como ¿Los cambios en \(y_1\) causan cambios en \(y_2\)?.

• si \(y_1\) causa \(y_2\), los rezagos de \(y_1\) deberían ser significativos en la ecuación para \(y_2\). Si este es el caso, decimos que \(y_1\) causa en el sentido de Granger a \(y_2\).

• si \(y_2\) causa \(y_1\), los rezagos de \(y_2\) deberían ser significativos en la ecuación para \(y_1\).

• si ambos conjuntos de rezagos son significativos, hay una causalidad bidireccional.

causality(var.aic,"Series.1")

## $Granger
## 
##  Granger causality H0: Series.1 do not Granger-cause Series.2
## 
## data:  VAR object var.aic
## F-Test = 49.674, df1 = 2, df2 = 392, p-value < 2.2e-16
## 
## 
## $Instant
## 
##  H0: No instantaneous causality between: Series.1 and Series.2
## 
## data:  VAR object var.aic
## Chi-squared = 3.8312, df = 1, p-value = 0.05031

Causalidad de Granger: \(y_1\) granger causa \(y_2\) si un modelo que usa valores actuales \(y_2\) pasados de \(y_1\) y valores actuales y pasados de \(y_2\) para predecir valores futuros de \(y_2\) tiene un error de pronóstico menor que un modelo que solo usa valores actuales y pasados de \(y_2\) para predecir \(y_2\). En otras palabras, la causalidad de Granger responde a la siguiente pregunta: ¿ayuda el pasado de la variable \(y_1\) a mejorar la predicción de los valores futuros de \(y_2\)?

Causalidad instantánea: \(y_1\) causa \(y_2\) (en el sentido de Granger instantáneo) si un modelo que usa valores actuales, pasados y futuros de \(y_1\) y valores actuales y pasados de \(y_2\) para predecir \(y_2\) tiene un error de pronóstico menor que un modelo que solo usa valores actuales y pasados de \(y_1\) y valores actuales y valores pasados de \(y_2\). En otras palabras, la causalidad instantánea de Granger responde a la pregunta: ¿conocer el futuro de \(y_1\) me ayuda a predecir mejor el futuro de \(y_2\)? Si sé que va a hacer \(y_1\), ¿me ayuda a saber lo que va a saber \(y_2\)?

5.3.7 Impulso respuesta

–>

Dado que todas las variables en un modelo \(VAR\) dependen unas de otras, las estimaciones de coeficientes individuales solo brindan información limitada sobre la reacción del sistema a un choque.

Para obtener una mejor idea del comportamiento dinámico del modelo, se utilizan respuestas de impulso (IR). El punto de partida de cada función de respuesta implícita para un modelo \(VAR\) lineal es su representación de media móvil (MA), que también es la función de error de impulso-respuesta(FEIR). Matemáticamente, el FEIR \(\Phi_i\) para el \(i\)-ésimo período después del choque se obtiene por

\[ \Phi_i = \sum_{j = 1}^{i} \Phi_{i - j} A_j, \ \ i = 1, 2, \ldots \] donde \(\Phi_0 = I_{K}\) y \(A_j = 0 \text{ para } j>n\) para \(j>n\), donde \(K\) es el número de variables endógenas y \(n\) es el orden del modelo \(VAR\).

En R, la función irf del paquete vars se puede utilizar para obtener los errores predichos por la función de impulso-respuesta. El siguiente código calcula y traza la respuesta estimada de Series.1 a un impulso en Series.2 con bandas bootstrap.

ir.1 <- irf(var.1, impulse = "Series.1", response = "Series.2", n.ahead = 20, ortho = FALSE)
plot(ir.1)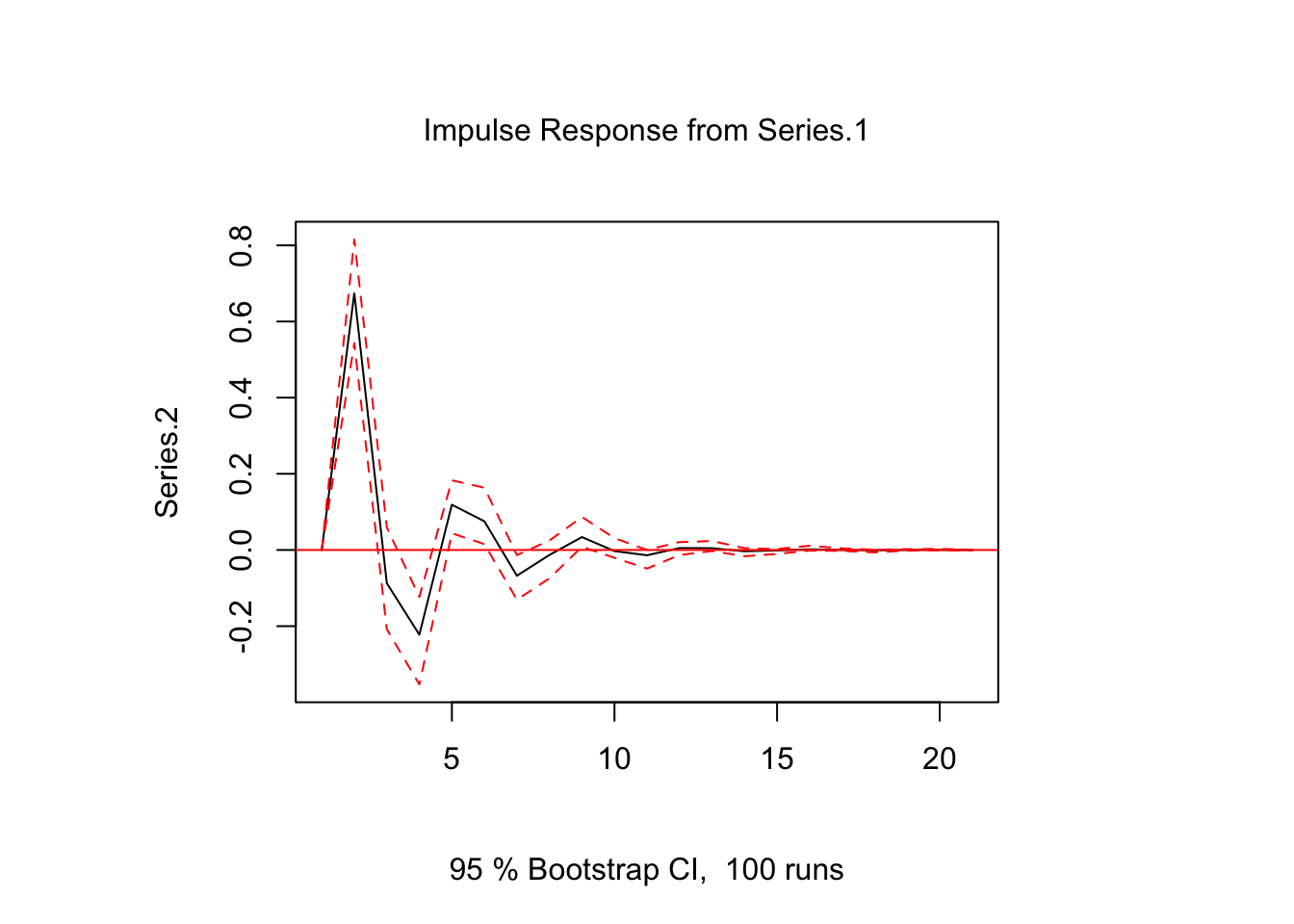

Una advertencia de los FEIR es que no se pueden utilizar para evaluar reacciones contemporáneas de variables. Esto se puede ver en el gráfico anterior, donde el FEIR es cero en el primer período.

Matemáticamente, esto puede explicarse por el hecho de que para la construcción de \(\Phi_i\) solo se utilizan las matrices de coeficientes \(A_j\), que no contienen información sobre relaciones contemporáneas. La información no esta última está más bien contenida en los elementos fuera de la diagonal de la matriz simétrica de varianza-covarianza \(\Sigma\). Para el conjunto de datos utilizado, se estima que

sm <- summary(var.1)
sm$covres #Sigma

##             Series.1    Series.2
## Series.1  0.21417107 -0.03115646
## Series.2 -0.03115646  0.24153934

Dado que los elementos fuera de la diagonal de la matriz de varianza-covarianza estimada no son cero, podemos asumir que existe una correlación contemporánea entre las variables en el modelo VAR. Esto se confirma con la matriz de correlación, que corresponde a \(\Sigma\):

sm$corres #Rho

##            Series.1   Series.2
## Series.1  1.0000000 -0.1369852
## Series.2 -0.1369852  1.0000000

Sin embargo, esas matrices solo describen la correlación entre los errores, pero no está claro en qué dirección van las causalidades. Identificar estas relaciones causales es uno de los principales desafíos de cualquier análisis \(VAR\).

Independientemente de los métodos específicos utilizados para identificar los choques de un modelo VAR lineal, se puede introducir más información sobre las relaciones contemporáneas en el FEIR simplemente multiplicándolo por una matriz \(F\)

\[ \Theta_i = \Phi_i F \]

para \(i=0,1,\ldots\). A continuación, se presentan algunos métodos para encontrar \(F\) y sus correspondientes respuestas de impulso.

5.3.7.1 Impulso-respuesta ortogonal

Un enfoque común para identificar los choques de un modelo \(VAR\) es utilizar respuestas de impulso ortogonales.

La idea básica es descomponer la matriz de varianza-covarianza de modo que \(\Sigma = PP'\), donde \(P\) es una matriz triangular inferior con elementos diagonales positivos, que a menudo se obtiene mediante una descomposición de Choleski. Dada la matriz de varianza-covarianza estimada \(P\), la descomposición se puede obtener mediante

t(chol(sm$covres))

##             Series.1  Series.2
## Series.1  0.46278620 0.0000000
## Series.2 -0.06732365 0.4868335

De esta matriz, se puede ver que Series.1 tiene un efecto contemporáneo en Series.2, pero no vice versa. La función de impulso respuesta es

\[ \Theta^o_i = \Phi_i P. \]

En R, la función irf del paquete vars se puede usar para obtener los resultados mediante el argumento orto = TRUE:

ir.1 <- irf(var.1, impulse = "Series.1", response = "Series.2", n.ahead = 20, ortho = TRUE)
plot(ir.1)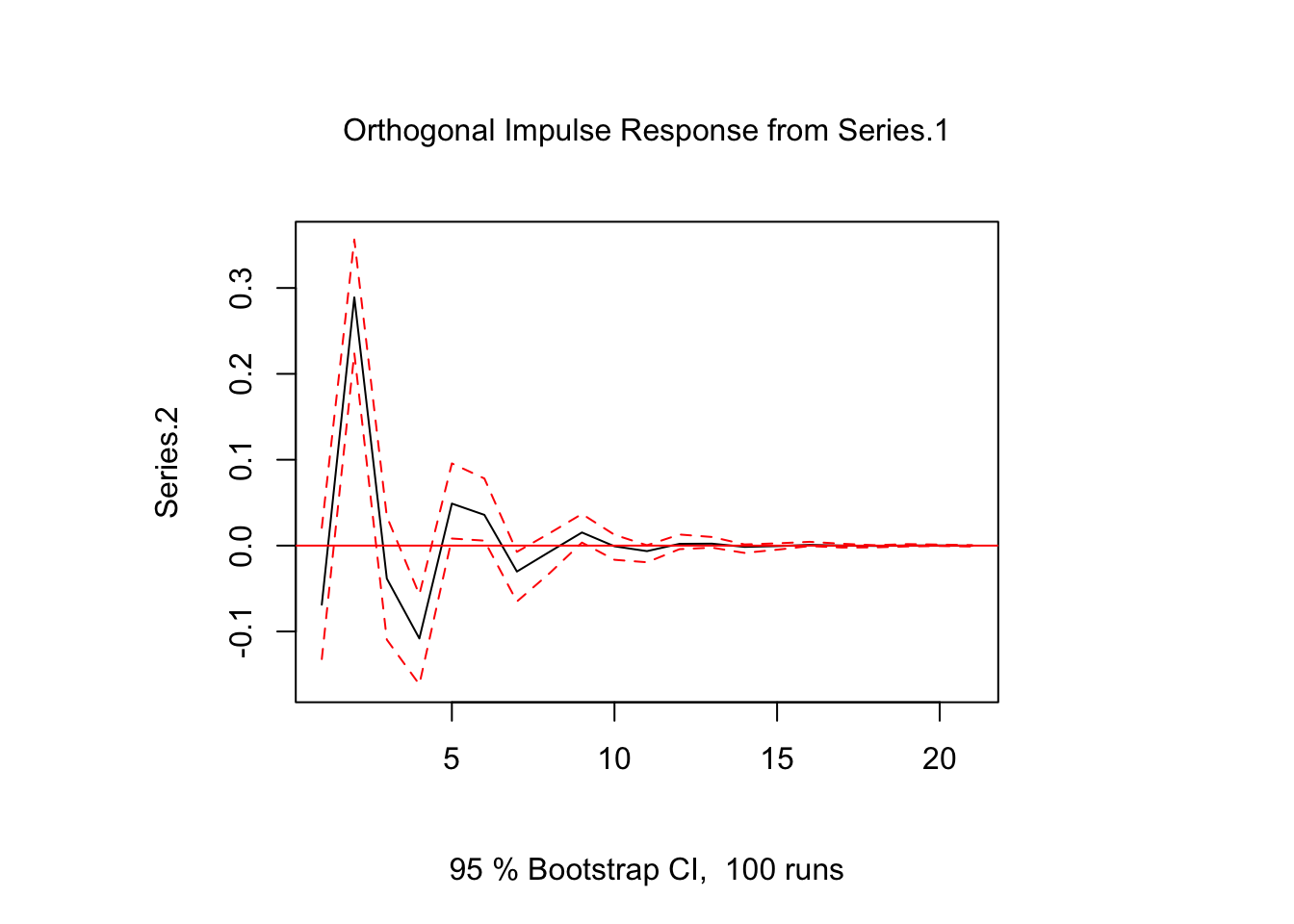

Tenga en cuenta que la salida de la descomposición de Choleski es una matriz triangular inferior, de modo que la variable de la primera fila nunca será sensible a un choque contemporáneo de cualquier otra variable y la última variable del sistema será sensible a los choques de todas las demás variables. Por lo tanto, los resultados de un impulso-respuesta ortogonal pueden ser sensibles al orden de las variables y se recomienda estimar el modelo VAR anterior con diferentes órdenes para ver qué tan fuertemente los impulso-respuesta ortogonal resultantes se ven afectados por eso.

5.3.7.2 Impulso-respuesta estructural

Las respuestas de impulso estructural (SIR) ya tienen en cuenta el problema de identificación durante la estimación del modelo VAR. Para el modelo autorregresivo de vector estructural (SVAR)

\[ A_0 y_t = v + \sum_{i = 1}^{2} A_i y_{t-i} + \epsilon_t, \]

donde \(\epsilon_t \sim N(0, \Omega)\) con \(\Omega\) siendo la matriz diagonal de varianzas y \(A_0\) como una matriz triangular inferior con unos en su diagonal principal, la función de impulso respuesta estructural es

\[ \Theta^s_i = \Phi_i A_0^{-1}. \]

A veces es importante obtener el efecto a largo plazo. Para esto se calcula el gráfico de la función impulso-respuesta acumulada:

ir.2 <- irf(var.1,impulse="Series.1",response="Series.2",n.ahead = 20,ortho = TRUE,
cumulative = TRUE)
plot(ir.2)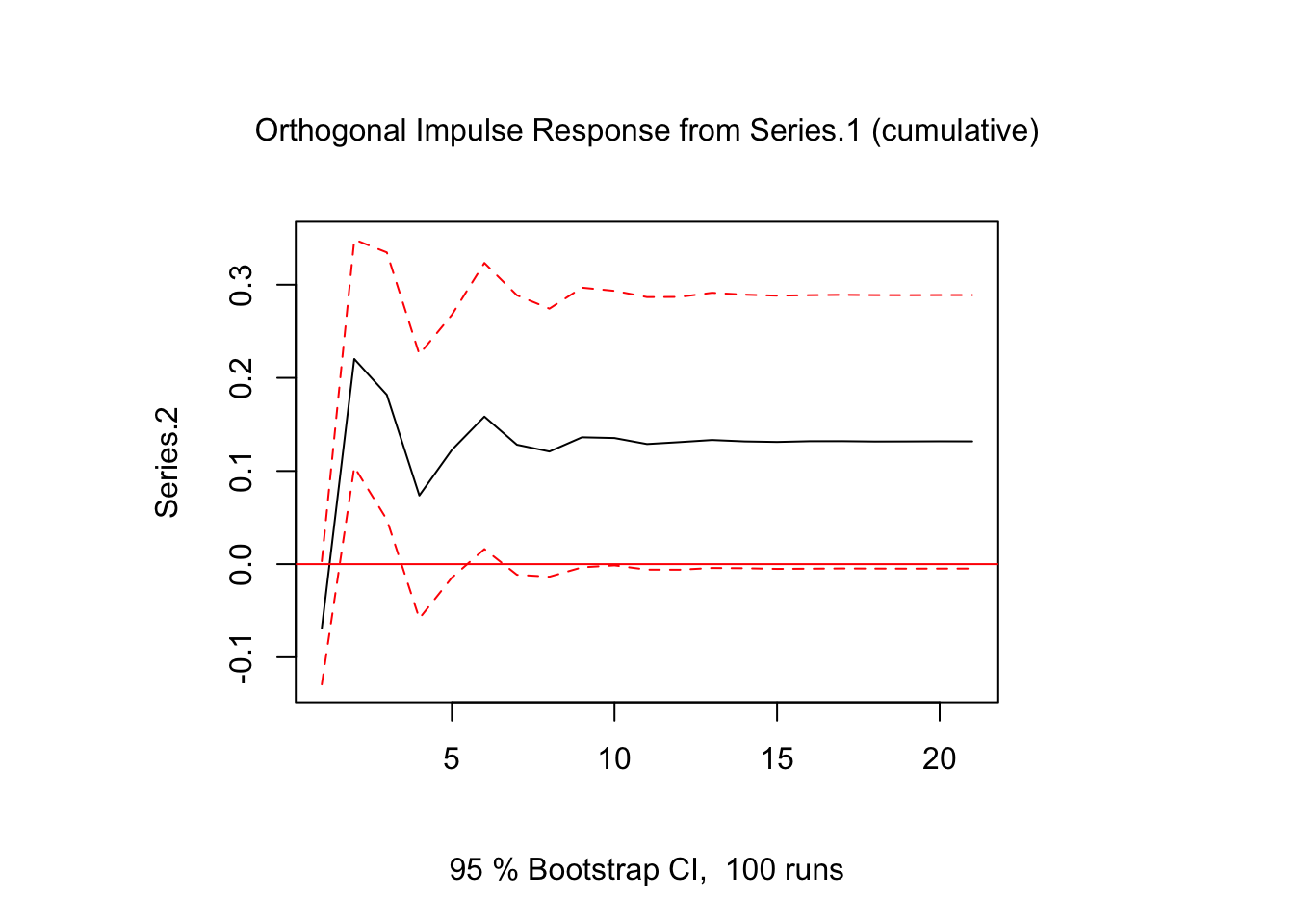

Vemos que, pese a variaciones negativas en algunos períodos, en el largo plazo el efecto es positivo.

5.3.7.3 Ejemplo

Usaremos los datos del artículo Carrillo Maldonado (2017). Para la estimación se utilizaron datos con frecuencia mensual entre enero del 2003 y noviembre del 2013. Las fuentes de información fueron el Banco Central del Ecuador (BCE) y el Servicio de Rentas Internas (SRI).

De acuerdo con la literatura, las variables que ingresaron al modelo fueron: ingresos petroleros (exportaciones y venta de derivados), no petroleros (impuestos, contribuciones a la seguridad social, superávit de empresas públicas y otros), gasto público e Índice de Actividad Empresarial No Petrolera (IAE-NP) como proxy del PIB a nivel mensual.

Las variables fiscales pertenecen al sector público no financiero.

uu <- "https://github.com/vmoprojs/DataLectures/raw/master/datosCarrillo2017.RData"
load(url(uu))

plot(datosBU,main = "Series en niveles")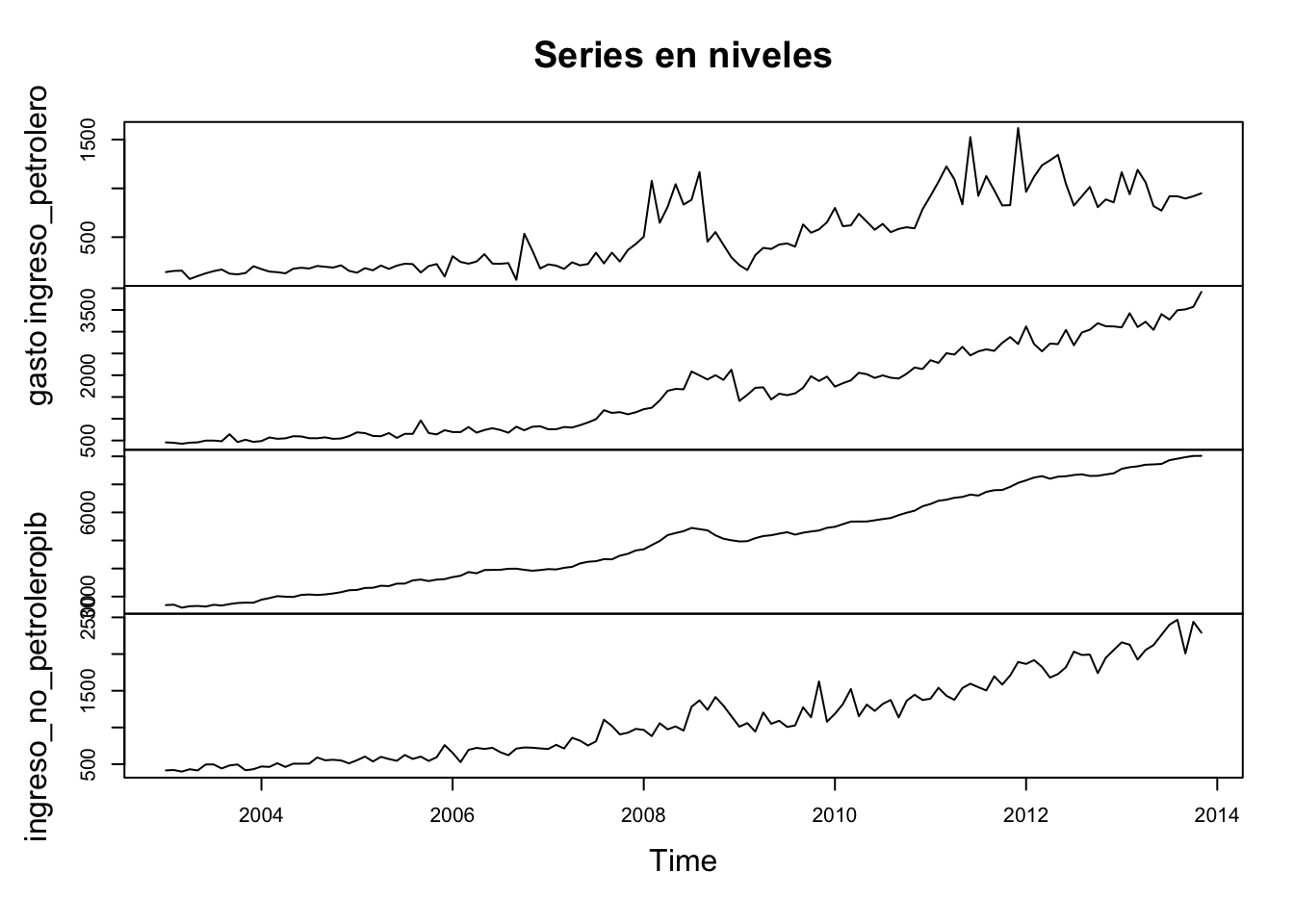

Las series no son estacionarias, veamos si las tasas de crecimiento lo son:

datosCrec <- diff(log(datosBU))
ggplot2::autoplot(datosCrec,main = "Series como tasas de crecimiento")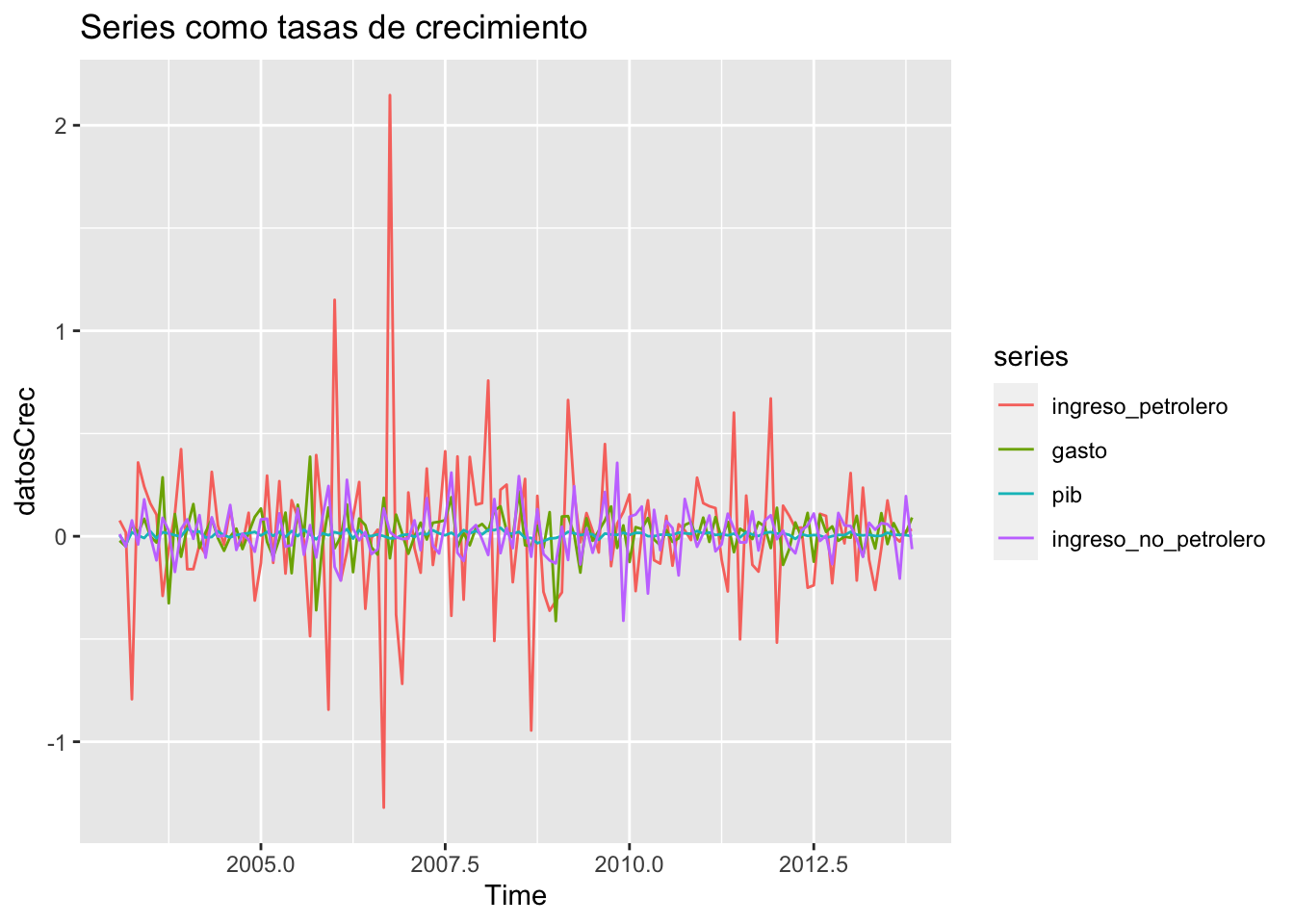

sol <- NULL
for(i in 1:ncol(datosCrec))
{
  # i = 1
  aux <- pp.test(datosCrec[,i]) #Ho: non stationarity
  sol <- c(sol,aux$p.value)
}
names(sol) <- colnames(datosCrec)
sol

##    ingreso_petrolero                gasto                  pib 
##                 0.01                 0.01                 0.01 
## ingreso_no_petrolero 
##                 0.01

En efecto, las tasas de crecimiento son estacionarias.

Escogemos el mejor modelo:

VARselect(datosCrec, type = "none", lag.max = 5)

## $selection
## AIC(n)  HQ(n)  SC(n) FPE(n) 
##      2      2      2      2 
## 
## $criteria
##                    1             2             3             4
## AIC(n) -1.993900e+01 -2.032775e+01 -2.031822e+01 -2.023732e+01
## HQ(n)  -1.979193e+01 -2.003361e+01 -1.987701e+01 -1.964904e+01
## SC(n)  -1.957698e+01 -1.960370e+01 -1.923215e+01 -1.878923e+01
## FPE(n)  2.190991e-09  1.486188e-09  1.502928e-09  1.634912e-09
##                    5
## AIC(n) -2.015797e+01
## HQ(n)  -1.942262e+01
## SC(n)  -1.834785e+01
## FPE(n)  1.779595e-09

Los criterios de información sugieren un \(VAR_4(2)\):

modVar <- VAR(datosCrec, 2, type = "none")
summary(modVar)

## 
## VAR Estimation Results:
## ========================= 
## Endogenous variables: ingreso_petrolero, gasto, pib, ingreso_no_petrolero 
## Deterministic variables: none 
## Sample size: 128 
## Log Likelihood: 602.74 
## Roots of the characteristic polynomial:
## 0.7834 0.628 0.628 0.5893 0.586 0.586 0.4564 0.4564
## Call:
## VAR(y = datosCrec, p = 2, type = "none")
## 
## 
## Estimation results for equation ingreso_petrolero: 
## ================================================== 
## ingreso_petrolero = ingreso_petrolero.l1 + gasto.l1 + pib.l1 + ingreso_no_petrolero.l1 + ingreso_petrolero.l2 + gasto.l2 + pib.l2 + ingreso_no_petrolero.l2 
## 
##                         Estimate Std. Error t value Pr(>|t|)    
## ingreso_petrolero.l1    -0.56885    0.08446  -6.735 5.99e-10 ***
## gasto.l1                 0.56004    0.31168   1.797   0.0749 .  
## pib.l1                   1.02387    1.93942   0.528   0.5985    
## ingreso_no_petrolero.l1  0.21771    0.26378   0.825   0.4108    
## ingreso_petrolero.l2    -0.37305    0.08335  -4.476 1.74e-05 ***
## gasto.l2                -0.12990    0.31333  -0.415   0.6792    
## pib.l2                   4.78778    1.98108   2.417   0.0172 *  
## ingreso_no_petrolero.l2  0.25001    0.26530   0.942   0.3479    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## 
## Residual standard error: 0.3068 on 120 degrees of freedom
## Multiple R-Squared: 0.3697,  Adjusted R-squared: 0.3277 
## F-statistic: 8.798 on 8 and 120 DF,  p-value: 2.054e-09 
## 
## 
## Estimation results for equation gasto: 
## ====================================== 
## gasto = ingreso_petrolero.l1 + gasto.l1 + pib.l1 + ingreso_no_petrolero.l1 + ingreso_petrolero.l2 + gasto.l2 + pib.l2 + ingreso_no_petrolero.l2 
## 
##                         Estimate Std. Error t value Pr(>|t|)    
## ingreso_petrolero.l1     0.05601    0.02531   2.213  0.02878 *  
## gasto.l1                -0.56646    0.09341  -6.065 1.58e-08 ***
## pib.l1                   1.70551    0.58121   2.934  0.00401 ** 
## ingreso_no_petrolero.l1  0.07032    0.07905   0.890  0.37551    
## ingreso_petrolero.l2     0.04972    0.02498   1.991  0.04880 *  
## gasto.l2                -0.22201    0.09390  -2.364  0.01967 *  
## pib.l2                   0.67370    0.59370   1.135  0.25874    
## ingreso_no_petrolero.l2  0.05256    0.07951   0.661  0.50982    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## 
## Residual standard error: 0.09195 on 120 degrees of freedom
## Multiple R-Squared: 0.3136,  Adjusted R-squared: 0.2678 
## F-statistic: 6.852 on 8 and 120 DF,  p-value: 2.143e-07 
## 
## 
## Estimation results for equation pib: 
## ==================================== 
## pib = ingreso_petrolero.l1 + gasto.l1 + pib.l1 + ingreso_no_petrolero.l1 + ingreso_petrolero.l2 + gasto.l2 + pib.l2 + ingreso_no_petrolero.l2 
## 
##                          Estimate Std. Error t value Pr(>|t|)    
## ingreso_petrolero.l1     0.005014   0.003499   1.433  0.15441    
## gasto.l1                -0.006962   0.012911  -0.539  0.59072    
## pib.l1                   0.210360   0.080337   2.618  0.00997 ** 
## ingreso_no_petrolero.l1  0.001074   0.010927   0.098  0.92186    
## ingreso_petrolero.l2     0.008499   0.003452   2.462  0.01524 *  
## gasto.l2                -0.002175   0.012979  -0.168  0.86720    
## pib.l2                   0.410522   0.082062   5.003 1.96e-06 ***
## ingreso_no_petrolero.l2 -0.004555   0.010990  -0.414  0.67927    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## 
## Residual standard error: 0.01271 on 120 degrees of freedom
## Multiple R-Squared: 0.3443,  Adjusted R-squared: 0.3006 
## F-statistic: 7.878 on 8 and 120 DF,  p-value: 1.785e-08 
## 
## 
## Estimation results for equation ingreso_no_petrolero: 
## ===================================================== 
## ingreso_no_petrolero = ingreso_petrolero.l1 + gasto.l1 + pib.l1 + ingreso_no_petrolero.l1 + ingreso_petrolero.l2 + gasto.l2 + pib.l2 + ingreso_no_petrolero.l2 
## 
##                          Estimate Std. Error t value Pr(>|t|)    
## ingreso_petrolero.l1     0.011153   0.028904   0.386  0.70028    
## gasto.l1                 0.087538   0.106666   0.821  0.41346    
## pib.l1                   0.999707   0.663719   1.506  0.13464    
## ingreso_no_petrolero.l1 -0.560666   0.090272  -6.211 7.85e-09 ***
## ingreso_petrolero.l2     0.013163   0.028523   0.461  0.64528    
## gasto.l2                -0.007495   0.107230  -0.070  0.94439    
## pib.l2                   0.672705   0.677978   0.992  0.32309    
## ingreso_no_petrolero.l2 -0.302464   0.090794  -3.331  0.00115 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## 
## Residual standard error: 0.105 on 120 degrees of freedom
## Multiple R-Squared: 0.2652,  Adjusted R-squared: 0.2162 
## F-statistic: 5.414 on 8 and 120 DF,  p-value: 7.938e-06 
## 
## 
## 
## Covariance matrix of residuals:
##                      ingreso_petrolero      gasto       pib
## ingreso_petrolero            0.0928509 -0.0032213 5.371e-04
## gasto                       -0.0032213  0.0084063 1.573e-04
## pib                          0.0005371  0.0001573 1.483e-04
## ingreso_no_petrolero        -0.0004028  0.0025694 9.944e-05
##                      ingreso_no_petrolero
## ingreso_petrolero              -4.028e-04
## gasto                           2.569e-03
## pib                             9.944e-05
## ingreso_no_petrolero            1.094e-02
## 
## Correlation matrix of residuals:
##                      ingreso_petrolero   gasto     pib
## ingreso_petrolero              1.00000 -0.1153 0.14472
## gasto                         -0.11530  1.0000 0.14090
## pib                            0.14472  0.1409 1.00000
## ingreso_no_petrolero          -0.01264  0.2680 0.07808
##                      ingreso_no_petrolero
## ingreso_petrolero                -0.01264
## gasto                             0.26799
## pib                               0.07808
## ingreso_no_petrolero              1.00000

Revisamos los residuos del modelo:

rr <- resid(modVar)
Box.test(rr[,1]);Box.test(rr[,2]);Box.test(rr[,3]);Box.test(rr[,4])

## 
##  Box-Pierce test
## 
## data:  rr[, 1]
## X-squared = 0.054457, df = 1, p-value = 0.8155

## 
##  Box-Pierce test
## 
## data:  rr[, 2]
## X-squared = 0.20881, df = 1, p-value = 0.6477

## 
##  Box-Pierce test
## 
## data:  rr[, 3]
## X-squared = 1.6416, df = 1, p-value = 0.2001

## 
##  Box-Pierce test
## 
## data:  rr[, 4]
## X-squared = 0.95738, df = 1, p-value = 0.3278

5.3.8 Función de impulso respuesta

variables <- colnames(datosCrec)
i = 1
j = 3
ir.1 <- irf(modVar, impulse = variables[i], response = variables[j], n.ahead = 20, ortho = FALSE)
plot(ir.1)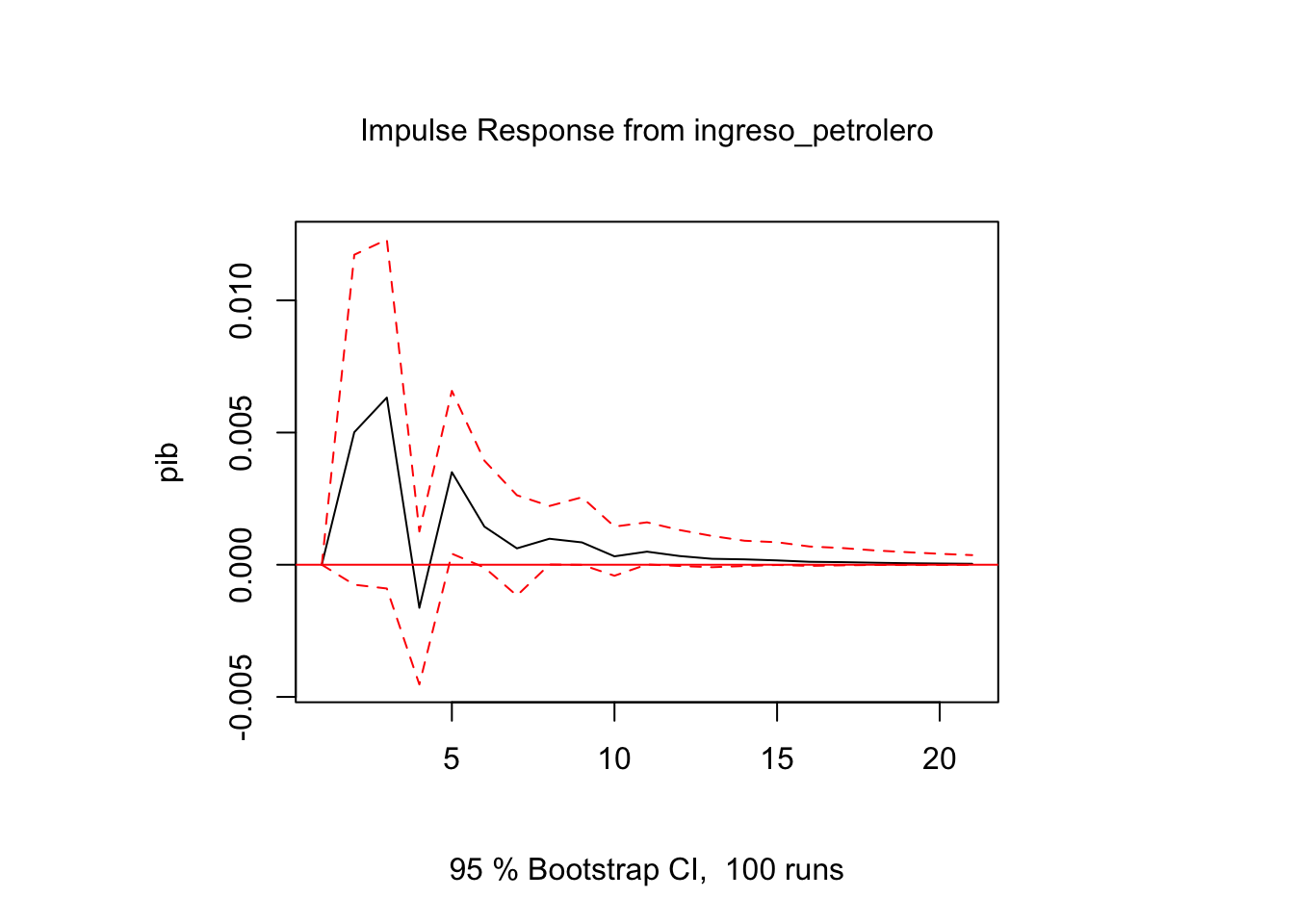

i = 1
j = 3
ir.2 <- irf(modVar,impulse=variables[i],response=variables[j],n.ahead = 20,ortho = FALSE,
cumulative = TRUE)
plot(ir.2)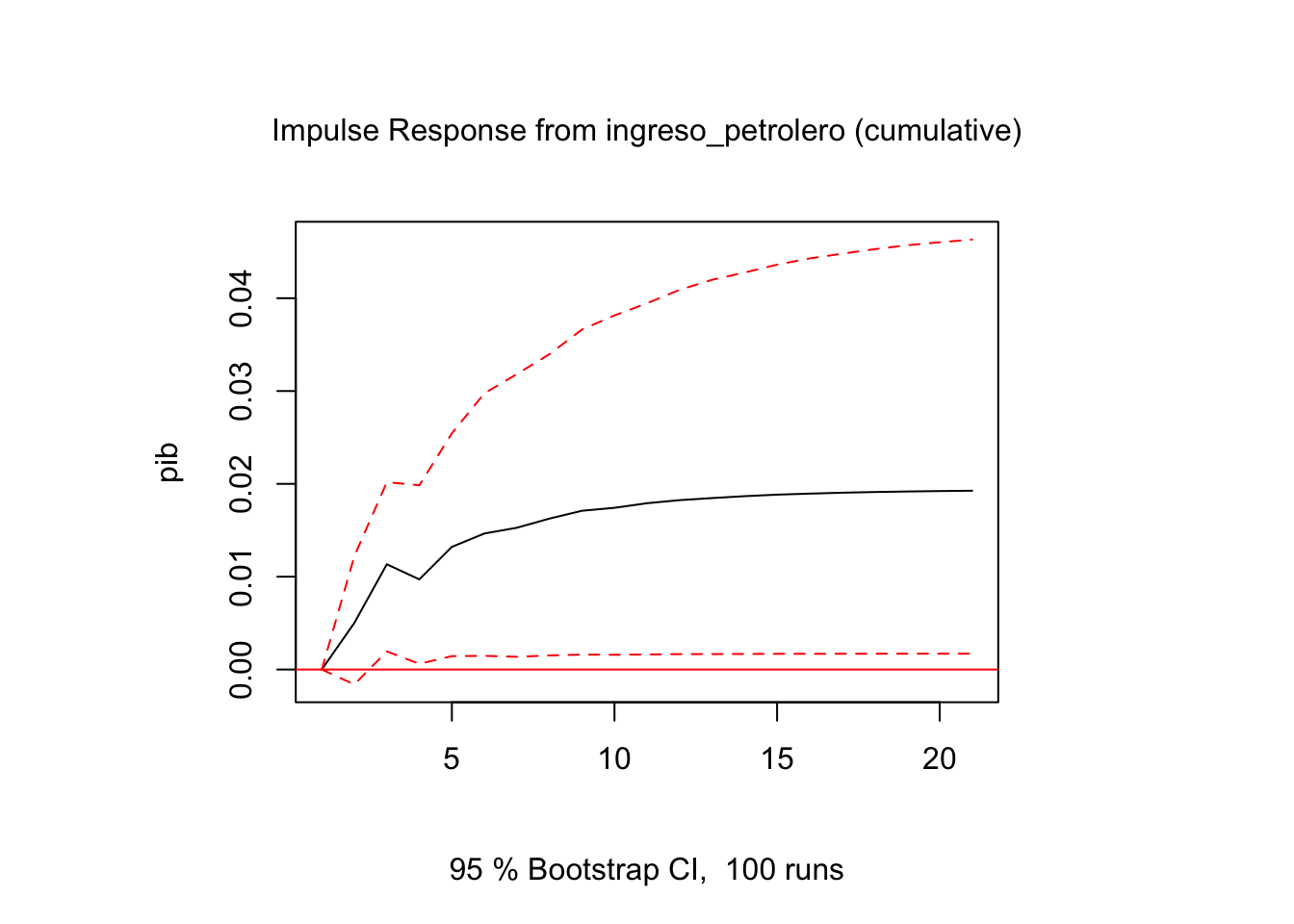

5.3.9 Causalidad de granger

i = 1
for(i in 1:ncol(datosCrec))
{
  variable = colnames(datosCrec)[i]
  cat("\n-------",variable,"--------\n")
 print(causality(modVar,cause = variable)) 
}

## 
## ------- ingreso_petrolero --------
## $Granger
## 
##  Granger causality H0: ingreso_petrolero do not Granger-cause gasto
##  pib ingreso_no_petrolero
## 
## data:  VAR object modVar
## F-Test = 1.8876, df1 = 6, df2 = 480, p-value = 0.08122
## 
## 
## $Instant
## 
##  H0: No instantaneous causality between: ingreso_petrolero and
##  gasto pib ingreso_no_petrolero
## 
## data:  VAR object modVar
## Chi-squared = 3.8219, df = 3, p-value = 0.2813
## 
## 
## 
## ------- gasto --------
## $Granger
## 
##  Granger causality H0: gasto do not Granger-cause ingreso_petrolero
##  pib ingreso_no_petrolero
## 
## data:  VAR object modVar
## F-Test = 1.1226, df1 = 6, df2 = 480, p-value = 0.3479
## 
## 
## $Instant
## 
##  H0: No instantaneous causality between: gasto and
##  ingreso_petrolero pib ingreso_no_petrolero
## 
## data:  VAR object modVar
## Chi-squared = 12.545, df = 3, p-value = 0.005732
## 
## 
## 
## ------- pib --------
## $Granger
## 
##  Granger causality H0: pib do not Granger-cause ingreso_petrolero
##  gasto ingreso_no_petrolero
## 
## data:  VAR object modVar
## F-Test = 3.8683, df1 = 6, df2 = 480, p-value = 0.0008809
## 
## 
## $Instant
## 
##  H0: No instantaneous causality between: pib and ingreso_petrolero
##  gasto ingreso_no_petrolero
## 
## data:  VAR object modVar
## Chi-squared = 5.3232, df = 3, p-value = 0.1496
## 
## 
## 
## ------- ingreso_no_petrolero --------
## $Granger
## 
##  Granger causality H0: ingreso_no_petrolero do not Granger-cause
##  ingreso_petrolero gasto pib
## 
## data:  VAR object modVar
## F-Test = 0.44941, df1 = 6, df2 = 480, p-value = 0.8454
## 
## 
## $Instant
## 
##  H0: No instantaneous causality between: ingreso_no_petrolero and
##  ingreso_petrolero gasto pib
## 
## data:  VAR object modVar
## Chi-squared = 9.261, df = 3, p-value = 0.02601

5.4 Ejercicios

1. Los están datos ubicados en: https://raw.githubusercontent.com/vmoprojs/DataLectures/master/MonetarioBCE.csv.

• DepositosVista: Se refiere a depósitos en cuenta corriente recibidos por las entidades bancarias, exigibles mediante la presentación de cheques u otros mecanismos de pago y registro.

• M1: La oferta monetaria se define como la cantidad de dinero a disposición inmediata de los agentes para realizar transacciones; contablemente el dinero en sentido estricto, es la suma de las especies monetarias en circulación y los depósitos en cuenta corriente.

• Cuasidinero: Corresponde a las captaciones de las Otras Sociedades de Depósito, que sin ser de liquidez inmediata, suponen una segunda línea de medios de pago a disposición del público. Está formado por los depósitos de ahorro, plazo, operaciones de reporto, fondos de tarjetahabientes y otros depósitos.

• M2: La liquidez total o dinero en sentido amplio incluye la oferta monetaria y el cuasidinero.

Formula y estima un modelo de correción de errores.

2. Use los datos del ejemplo 5.1.3.4 y estime un modelo de corrección de errores.

3. Formula y estima un modelo \(VAR\) para los datos del ejercicio 1.