3 Modelización de Series Univariantes: (S)ARIMA
 |
| Maurice Bartlett (1910-2002) Estadístico británico. Fue profesor en Manchester, donde fundó el Departamento de Estadística, en University College de Londres, y, finalmente, en Oxford hasta su jubilación. Hizo contribuciones fundamentales a los procesos estocásticos, especialmente a la inferencia de las autocorrelaciones y el espectro. Fue elegido en 1961 miembro de la Royal Society. |
Tomado de varias fuentes:
- Peña-Sanchez (2005)
- Gujarati and Porter (2010)
- Novales-Cinca (1993)
Librerías usadas:
AERtseriesforecast
Antes de empezar con la modelización ARIMA debemos revisar algunos conceptos necesarios para una adecuada compresión:
- Proceso estocástico
- Ruido blanco
- Proceso estacionario
3.1 Proceso estocástico
Entenderemos un proceso estocástico como una familia de variables aleatorias, denotada por \(Y_t\), \(t\in T\) definidas por un espacio muestral \(\Omega\) y que toman valores en un conjunto \(E\) (suele ser \(\mathbb{R}\), pero también pueden ser \(\mathbb{C}\), \(\mathbb{R}^k\) o \(\mathbb{C}^k\)). \(T\) es el espacio de tiempos; por lo general es \(\mathbb{R}\) o un subconjunto de este, como \(\mathbb{N}\) o \(\mathbb{Z}\). Mientas no se especifique lo contrario, se asumirá que \(T=\mathbb{Z}\): conjunto de números enteros y que el proceso es real (toma valores en \(\mathbb{R}\)) (Capa-Santos (2021)),
En otras palabras, un proceso estocástico \(\left\{y_{t} \right \}_ {t =-\infty}^{\infty}\) es un modelo que describe la estructura de probabilidad de una secuencia de observaciones a lo largo del tiempo. Una serie de tiempo \(y_{t}\) es una realización de un proceso estocástico que se observa solo para un número finito de períodos, indexado por \(t = 1, \dots, T\).
3.2 Ruido blanco
Una serie \((w_t,t\in \mathbb{Z)}\) se dice que es Ruido Blanco si cumple
- \(E(w_t)=0\) (media cero)
- \(Var(w_t)=\sigma^2\) (varianza constante)
- \(\forall k\neq 0\), \(Cov(w_t,w_{t+k})=0\) (sin correlación)
Si además cumple que \(w_t\sim N(0,\sigma^2)\) se dice que \(w_t\) es Ruido Blanco Gaussiano (RBG).
El ruido blanco es un ejemplo de proceso estacionario ??.
3.2.1 Detección de ruido blanco
¿Cómo sé si algo es un ruido blanco? Analizo la función de autocorrelación muestral.
3.2.1.1 Función de autocorrelación muestral
Es una función (acf en R) que para instante \(t\), y cada entero \(k\) toma un valor \(\hat\rho_k(t)\)
\[ \hat\rho_k(t) = \frac{\hat\gamma_k(t)}{\hat\gamma_0} \]
donde \(k\) identifica el rezago \(Y_{t-k}\)
\[ \hat\gamma_k = \frac{\sum(Y_t-\bar{Y})(Y_{t-k}-\bar{Y})}{n} \] \[ \hat\gamma_0 = \frac{\sum(Y_t-\bar{Y})^2}{n} \]
Se asume que \(\hat\rho_k \sim N(0,1/n)\). Es decir, si:
\[ \hat\rho_k = \frac{\sum_{t=k+1}^{T}(Y_t-\bar{Y})(Y_{t-k}-\bar{Y})}{\sum_{t=1}^{T}(Y_t-\bar{Y})^2} \] presenta valores fuera de las bandas \(\pm 2(\frac{1}{\sqrt{n}})\) (ver líneas entre cortadas en gráfico), es evidencia de la presencia de autocorrelación.
Calculamos la función de autocorrelación (ACF por sus siglas en inglés):
Si el valor del ACF se sale de las franjas, si hay correlación significativa y no hay ruido blanco.
3.2.2 Paseo aleatorio (random walk)
Un paseo aleatorio es un proceso estocástico \(Y_t\) cuyas primeras diferencias forman un proceso de ruido blanco, es decir.
\[ Y_t = Y_{t-1}+w_{t};\quad t = -\infty,\ldots,-2-1,0,1,2,\ldots \]
donde \(w_t\) es un ruido blanco.
El paseo aleatorio no es un proceso estacionario ya que puede escribirse:
\[ y_t = y_{t-1}+\epsilon_t = y_{t-2}+\epsilon_{t-1}+\epsilon_t = y_{t-3}+\epsilon_{t-2}+\epsilon_{t-1}+\epsilon_t+\cdots \]
Lo cual hace que no se pueda definir su esperanza ni su varianza, tampoco la distribución marginal de cada \(Y_t\).
3.2.3 Prueba de Ljung-Box
La prueba de Ljung-Box para determinar si una serie es o no un proceso de ruido blanco. Tiene las siguientes hipótesis:
\(H_0\): Los datos se distribuyen de forma independiente (es decir, las correlaciones en la población de la que se toma la muestra son \(0\), de modo que cualquier correlación observada en los datos es el resultado de la aleatoriedad del proceso de muestreo).
\(H_a\): Los datos no se distribuyen de forma independiente.
El estadístico de prueba es:
\[ Q=n\left(n+2\right)\sum _{k=1}^{h}{\frac {{\hat {\rho }}_{k}^{2}}{(n-k)}} \]
donde \(n\) es el tamaño de la muestra, \(\hat\rho_{k}\) es la autocorrelación de la muestra en el retraso \(k\) y \(h\) es el número de retardos que se están probando. Por nivel de significación \(\alpha\), la región crítica para el rechazo de la hipótesis de aleatoriedad es
\[ Q>\chi _{1-\alpha ,h}^{2} \]
donde \(\chi _{1-\alpha ,h}^{2}\) es el \(\alpha\)-cuantil de la distribución chi-cuadrado con \(h\) (número de rezagos que se está probando) grados de libertad.
Ejemplo
##
## Box-Ljung test
##
## data: w
## X-squared = 0.00027958, df = 1, p-value = 0.9867En este caso no se rechaza la hipótesis nula de independencia. Destaquemos algunos parámetros:
lag: el estadístico se basará en coeficientes de autocorrelación de rezago (\(k\) en \(\hat\rho_k\)).
3.3 Serie estacionaria (en covarianza)(#estac)
Una serie \((Y_t, t \in Z)\) se dice estacionaria en covarianza o estacionaria de segundo orden si cumple:
\[\begin{eqnarray} \textrm{E}\, (Y_t) = \mu < \infty \\ E (Y_t - \mu)^2 = \gamma_0 < \infty \\ Cov(Y_{t},Y_{s})=E (Y_t - \mu) (Y_s - \mu) = \gamma_{\vert t-s\vert} \qquad \forall t, s \quad t \neq s \end{eqnarray}\]
Es decir, la covarianza entre \(Y_{t}\) y \(Y_{s}\) depende únicamente de la distancia entre los tiempos \(t\) y \(s\), \(|t-s|\).
La estacionariedad de segundo orden significa que las propiedades de segundo orden (medias y covarianzas) de las variables aleatorias permanecen constantes en el tiempo. Cabe señalar que, a diferencia de la estacionariedad fuerte, la distribución conjunta de las variables aleatorias puede cambiar con el tiempo.
3.3.1 Prueba de estacionariedad: Test de Dickey Fuller
La Prueba de Dickey-Fuller busca determinar la existencia o no de raíces unitarias en una serie de tiempo. La hipótesis nula de esta prueba es que existe una raíz unitaria en la serie (si existen, el proceso no es estacionario).
##
## Augmented Dickey-Fuller Test
##
## data: w
## Dickey-Fuller = -4.8889, Lag order = 5, p-value = 0.01
## alternative hypothesis: stationaryEn este caso se rechaza la hipótesis nula de raíz unitaria, el proceso es estacionario. Destaquemos algunos parámetros:
k: el orden del rezago para calcular el estadístico. Por defecto el valor es \((n-1)^\frac{1}{3}\), donde \(n\) es el número de observaciones de la serie.
3.4 Procesos ARMA(p,q)
En los modelos de descomposición \(Y_t = T_t + S_t + \epsilon_t\), \(t = 1, 2,\ldots\) se estima \(\hat\epsilon_t\) y se determina si es o no ruido blanco mediante, por ejemplo, las pruebas LjungBox y Durbin Watson.
En caso de encontrar que \(\hat\epsilon_t\) no es ruido blanco, el siguiente paso es modelizar esta componente mediante tres posibles modelos:
- Medias Móviles de orden \(q\), \(MA(q)\).
- Autorregresivos de orden \(p\), \(AR(p)\).
- Medias Móviles Autorregresivos, \(ARMA(p, q)\).
Si se encuentra que \(\hat\epsilon_t\) es un ruido blanco, se puede analizar el vector mediante estadística clásica asumiendo independencia.
3.4.1 Proceso de Medias Móviles (MA)
Recordemos el polinomio de rezagos:
\[ B_p{(L)} = \beta_0+\beta_1L+\beta_2L^2+\cdots++\beta_pL^p \]
combinados con una serie de tiempo:
\[ B_p{(L)}(Y_t) = (\beta_0+\beta_1L+\beta_2L^2+\cdots++\beta_pL^p)(Y_t) \]
\[ B_p{(L)}(Y_t) =\sum_{j=0}^{p}\beta_jL^jY_t \] \[ B_p{(L)}(Y_t) =\sum_{j=0}^{p}\beta_jL^jY_t \]
Definición
Se dice que una serie \(Y_t\) sigue un proceso \(MA(q)\), \(q =1, 2,\ldots\) de media móvil de orden \(q\), si se cumple que
\[ Y_t = \epsilon_t+\theta_1\epsilon_{t-1}+\cdots+\theta_q\epsilon_{t-q} \]
para constantes \(\theta_1,\ldots,\theta_p\) y \(\epsilon_t\sim N(0,\sigma^2)\). La expresión con el operador \(L\) es, si se define el polinomio.
\[ \theta_p(L) = 1+\theta_1L+\cdots+\theta_qL^q \]
entonces la ecuación se puede escribir en términos de su polinomio de rezagos:
\[ Y_t = \theta_q(L)(\epsilon_t) \]
Propiedades
- \(E(Y_t)=0\)
- \(Var(Y_t)= (1+\theta_1^2+\cdots+\theta_q^2)\sigma^2\)
luego \(Var(Y_t) > Var(\epsilon_t)\), en general.
- \(Cov(Y_t,Y_{t+k}) = \rho(k)\), donde
\[ \rho(K) = \sigma^2\sum_{j=0}^{q-k}\theta_j\theta_{j+k} \tag{3.1} \]
donde \(\theta_0=1\) y \(k<q+1\). \(\rho(K)=0\) si \(k\geq q+1\).
- Un \(MA(q)\) siempre es un proceso estacionario con ACF, \(p(k)=\frac{\rho(k)}{\rho(0)}\)
La ecuación (3.1) se puede interpretar como una indicación de que un \(MA(q)\) es un proceso débilmente correlacionado, ya que su autocovarianza es cero a partir de un valor. Por esta razón se puede ver los procesos \(MA(q)\) como alternativas al Ruido Blanco completamente incorrelacionado.
Ejemplo
Sea \(Y_t\sim MA(2)\) dado por:
\[ y_t = \epsilon_t+\theta_1\epsilon_{t-1}+\theta_2\epsilon_{t-2} \] donde \(\epsilon_{t} \sim N(0,9)\), con \(\theta_1=-0.4\),\(\theta_2=0.4\).
De acuerdo con (3.1), si la fac muestral de una serie \(Y_t\) termina abruptamente puede tratarse de un \(MA(q)\).
Simulemos un modelo:

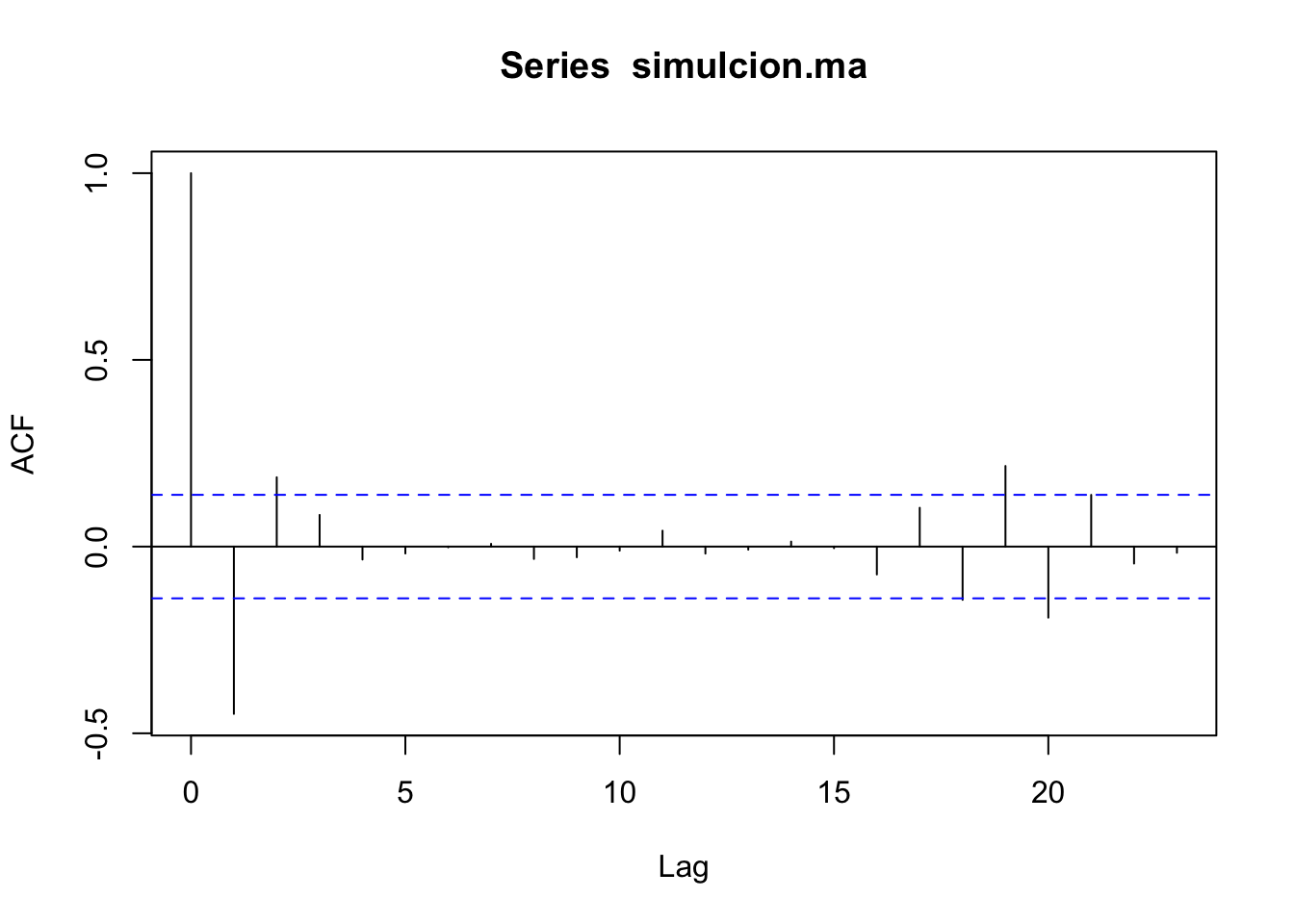
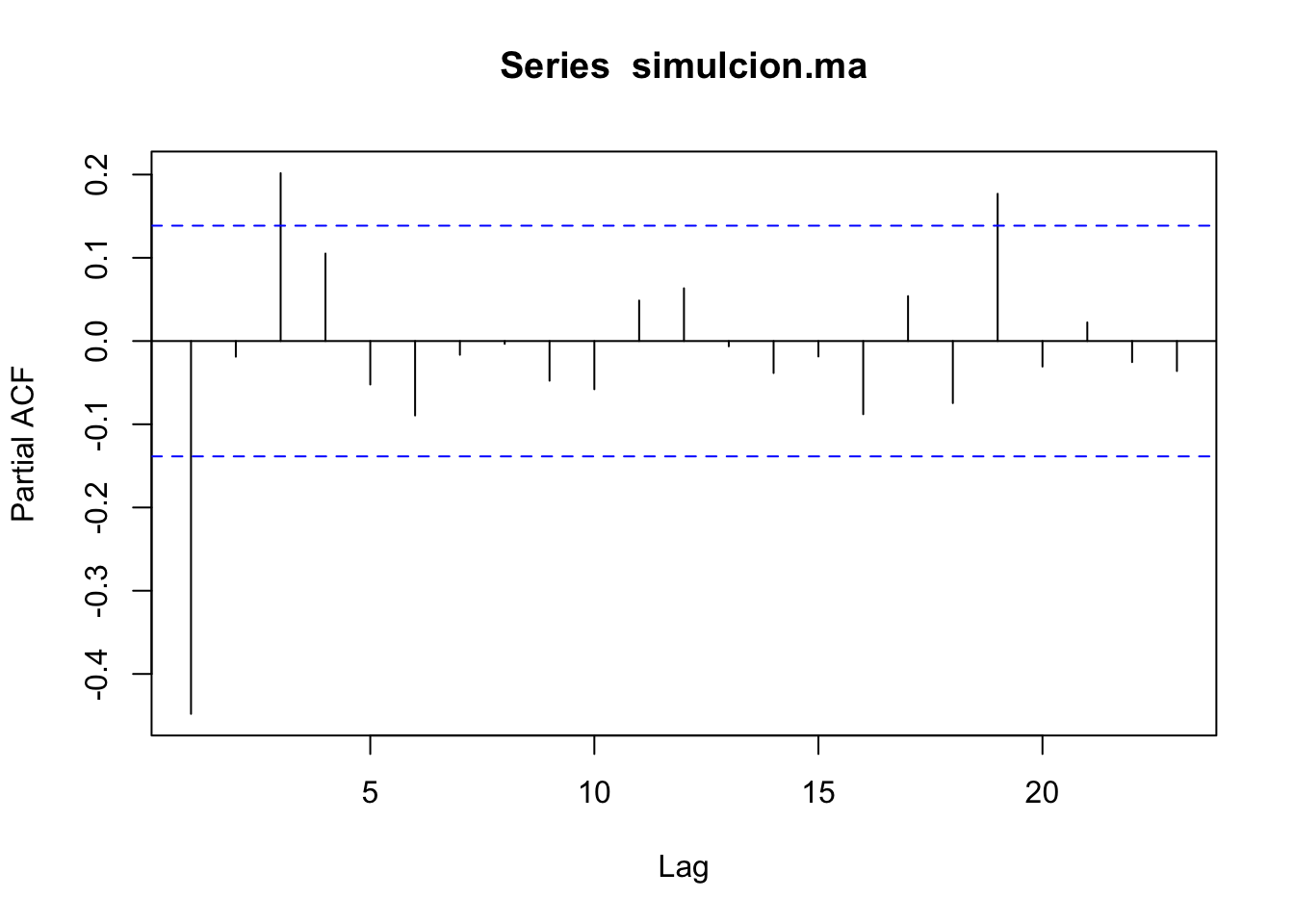
- Las \(p\) primeras autocorrelaciones van a ser diferentes de cero.
- La autocorrelación parcial decae exponencialmente.
Veamos otro ejemplo \(Y_t = \epsilon_t+0.6\epsilon_{t-1}-0.3\epsilon_{t-2}-0.1\epsilon_{t-3}\)
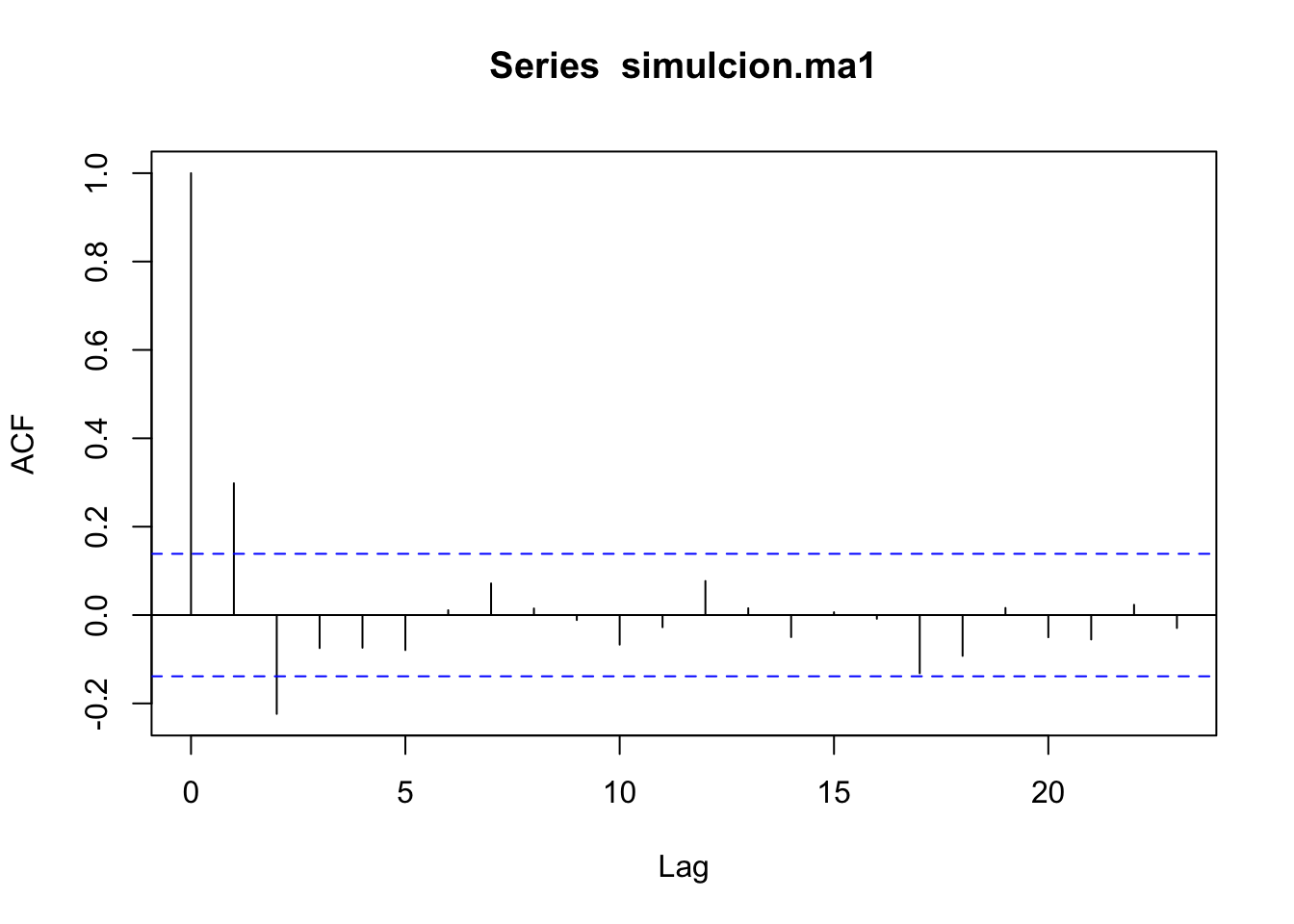
3.4.1.1 Autocorrelación parcial
Suponga que \((Y_t, t \in Z)\) es estacionaria. La pacf muestral es una función de \(k\),
- \(\hat{\alpha}(1)=\hat\rho(1)\)
- \(\hat{\alpha}(2)\): se regresa \(Y_t\) sobre \(Y_{t-1}\) y \(Y_{t-2}\) tal que \(Y_t=\phi_{21}Y_{t-1}+\phi_{22}Y_{t-2}+\epsilon_t\) entonces \(\hat{\alpha}(2)=\phi_{22}\)
- \(\hat{\alpha}(k)\): se regresa \(Y_t\) sobre \(Y_{t-1}\ldots Y_{t-k}\) tal que \(Y_t=\phi_{k1}Y_{t-1}+\ldots+\phi_{kk}Y_{t-2}+\epsilon_t\) entonces \(\hat{\alpha}(k)=\phi_{kk}\)
En los datos de series de tiempo, una gran proporción de la correlación entre \(Y_t\) y \(Y_{t-k}\) puede deberse a sus correlaciones con los rezagos intermedios \(Y_1,Y_2,\ldots,Y_{t-k+1}\). La correlación parcial elimina la influencia de estas variables intermedias.
La facp de un proceso \(Y_t\sim MA(q)\) se puede encontrar si se asume la condición de invertibilidad para un \(MA(q)\).
3.4.1.2 Condición de invertibilidad de un proceso \(MA(q)\)
Dado un proceso \(MA(q)\), \(Y_t = \theta q(L)(\epsilon_t)\) donde \(\theta_q(L) = 1+\theta_1L+\theta_2L^2+\cdots+\theta_qL^q\), entonces considerando el polinomio en \(z\in \mathbb{C}, \theta_q(z) = 1+\theta_1z+\cdots+\theta_qz^q\) y sus \(q\) raíces \((z_1, z_2,\ldots,z_q)\in \mathbb{C}\), es decir, valores \(z \in \mathbb{C}\) tales que \(\theta_q(z) = 0\), se dice que el proceso \(Y_t\) es invertible si se cumple
\[ |z_j|>1, \quad \forall j = 1,\ldots,q \tag{3.2} \] o también, si \(\theta_q(z) \neq 0,\forall z, |z|\leq 1\). Note que (3.2) es equivalente a
\[ \frac{1}{z_j}<1, \quad \forall j = 1,\ldots,q \]
es decir, los inversos de las raíces deben caer dentro del círculo unitario complejo.
Ejemplo
Determina si el proceso \(Y_t = \epsilon_t+0.6\epsilon_{t-1}-0.3\epsilon_{t-2}-0.1\epsilon_{t-3}\) es invertible.
## [1] -1.223462+0i -3.882021+0i 2.105483+0i## [1] 1.223462 3.882021 2.105483Se cumple que \(|z_j|>1\), por lo tanto el proceso \(Y_t\) es invertible.
3.4.2 El modelo Autorregresivo AR(p)
Se dice que \(Y_t\), \(t \in \mathbb{Z}\) sigue un proceso \(AR(p)\) de media cero si
\[ Y_t = \phi_1Y_{t-1}+\phi_2Y_{t-2}+\cdots+\phi_pY_{t-p}+\epsilon_t \tag{3.3} \]
donde \(\epsilon_t\sim RB(0,\sigma^2)\) y \(p = 1,2,\ldots\). Usando el operador de rezago \(L\) se puede escribir como:
\[ \phi_p(L)(Y_t) =\epsilon_t \]
con \(\phi_p(z)=1-\phi_1z-\phi_2z^2-\cdots-\phi_pz^p\), \(z\in \mathbb{C}\) el polinomio autorregresivo.
Condición Suficiente para que un \(AR(p)\) sea Estacionario en Covarianza
La condición suficiente para que \(Y_t \sim AR(p)\) sea estacionario en covarianza es que las \(p\) raíces de la ecuación \(\phi_p(z) = 0\), \(z_i\), \(i =1,2,\ldots,p\) cumplan
\[ |z_i|>1. \tag{3.4} \]
Nótece que si \(z_i = a_i +ib_i\) entonces \(|z_i|=\sqrt{a_i^2 +b_i^2}\), \(z_i\in \mathbb{Z}\).
En otras palabras, la condición (3.4) se describe como para que un proceso autorregresivo de orden \(p\) sea estacionario en covarianza, es suficiente que las raíces del polinomio autorregresivo estén por fuera del círculo unitario
Si el proceso \(Y_t\) es estacionario en covarianza se cumple que su media es constante, \(E(Y_t) = \mu\). El proceso definido en (3.3) cumple las siguientes propiedades:
Propiedades
- \(E(Y_t) = 0\)
- \(Var(Y_t) = \sigma^2\sum_{j=0}^{\infty}\phi_j^2\)
- La función de autocovarianza \(R(k)=\sum_{j=1}^{p}=\phi_j R(k-j)\), \(k=1,2,\ldots\). También conocida como ecuación de Yule-Walker.
Trabajaremos con datos de \(M1\) (WCURRNS dinero en circulación fuera de los Estados Unidos) semanales de los Estados Unidos desde enero de 1975.
uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/WO/WCURRNS.csv"
datos <- read.csv(url(uu),header=T,sep=";")
names(datos)## [1] "DATE" "VALUE"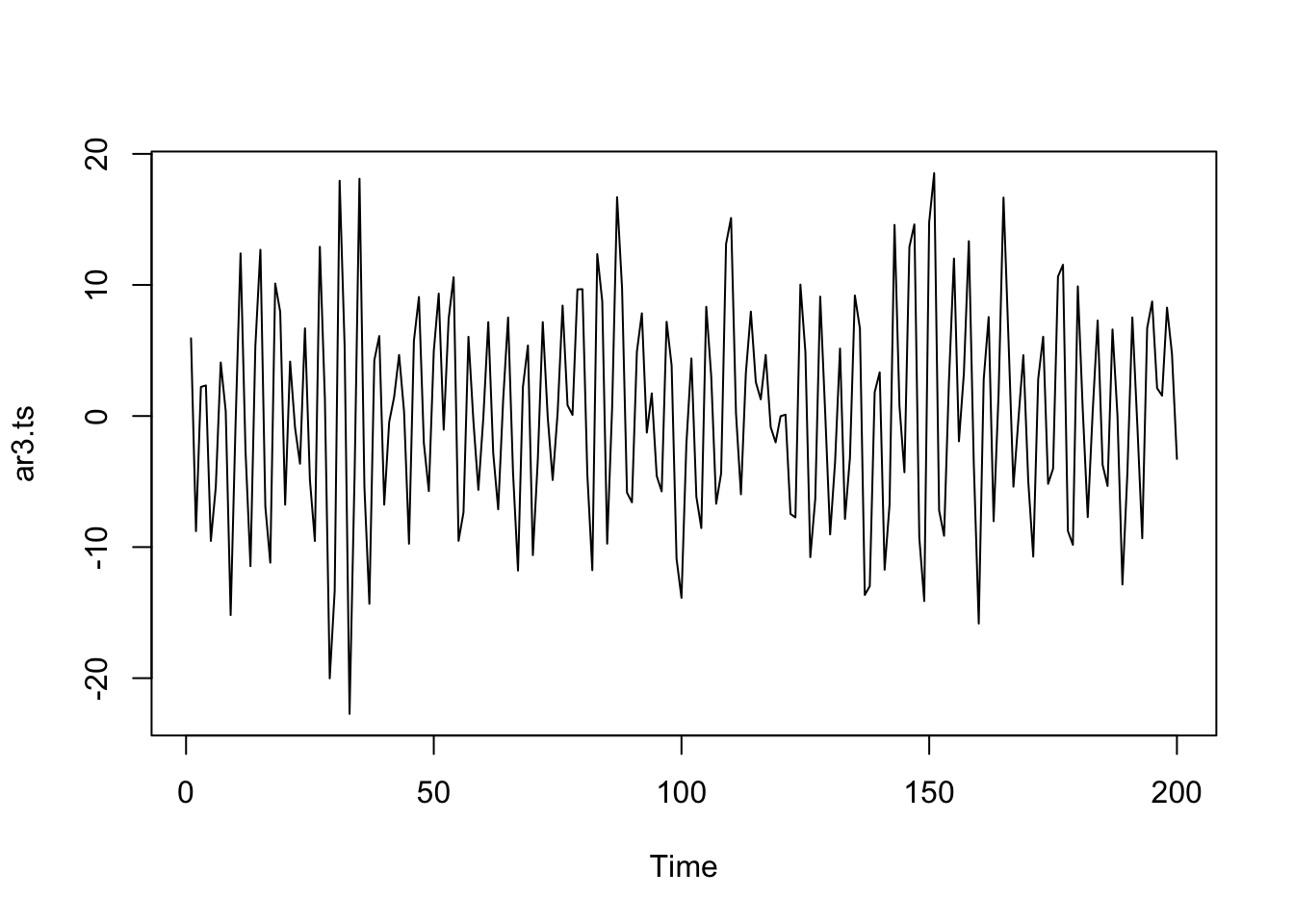
Estacionariedad: La serie es estacionaria si la varianza no cambia
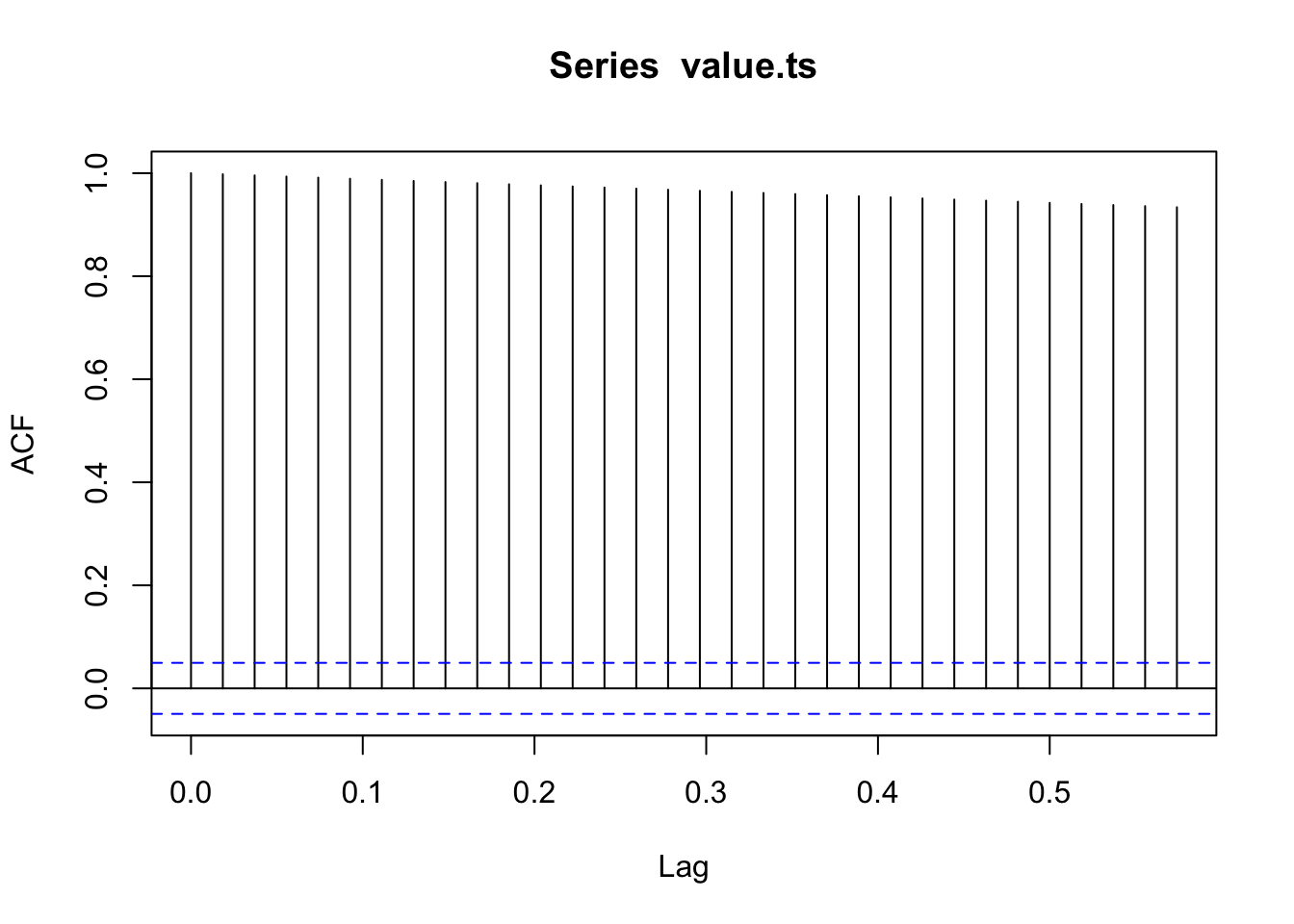
##
## Augmented Dickey-Fuller Test
##
## data: value.ts
## Dickey-Fuller = 1.111, Lag order = 11, p-value = 0.99
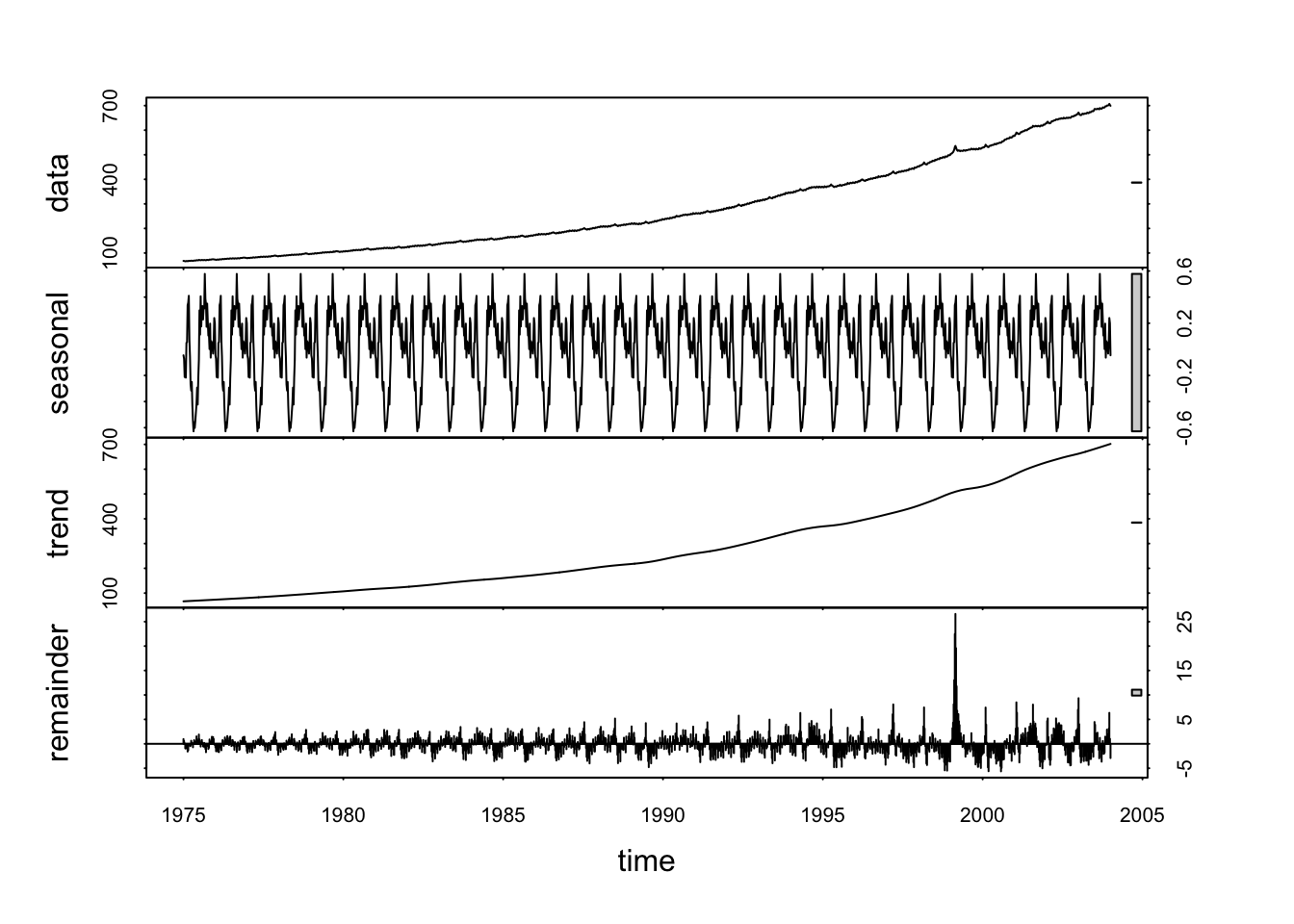
## alternative hypothesis: stationaryEsta es la marca de una serie que NO es estacionaria, dado que la autocorrelación decrece muy lentamente y el test también refuerza esta conclusión.
Una forma de trabajar con una serie estacionaria es quitarle el trend
Reminder es lo que queda sin tendencia ni estacionalidad
Veamos cómo quedo la serie:
##
## Augmented Dickey-Fuller Test
##
## data: valuereminder
## Dickey-Fuller = -10.399, Lag order = 11, p-value = 0.01
## alternative hypothesis: stationarySe puede decir que la hicimos una serie estacionaria, tanto la función de autocorrelación como la prueba estadística lo comprueban.
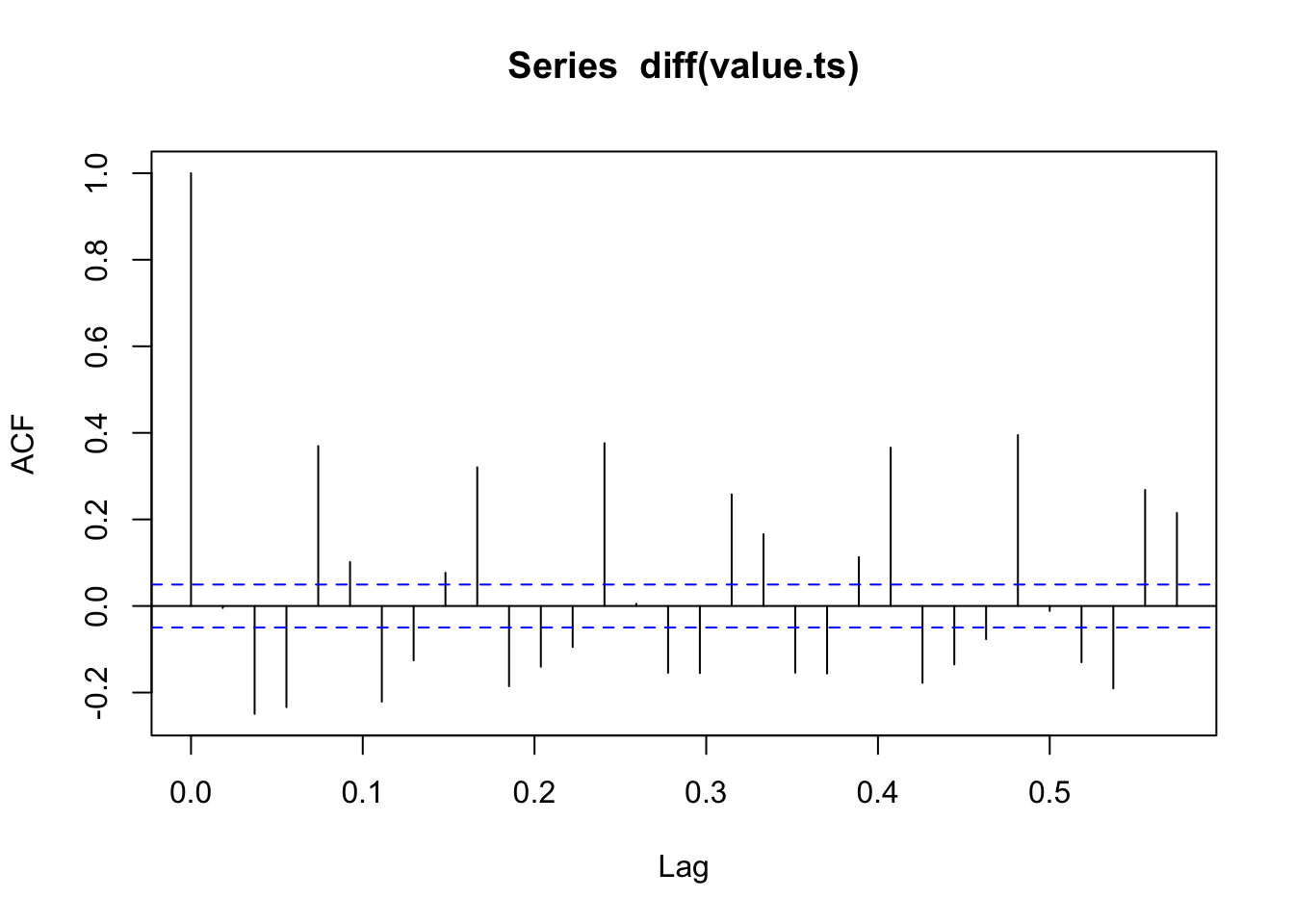
Otra forma de hacer estacionaria una serie es trabajar con las diferencias
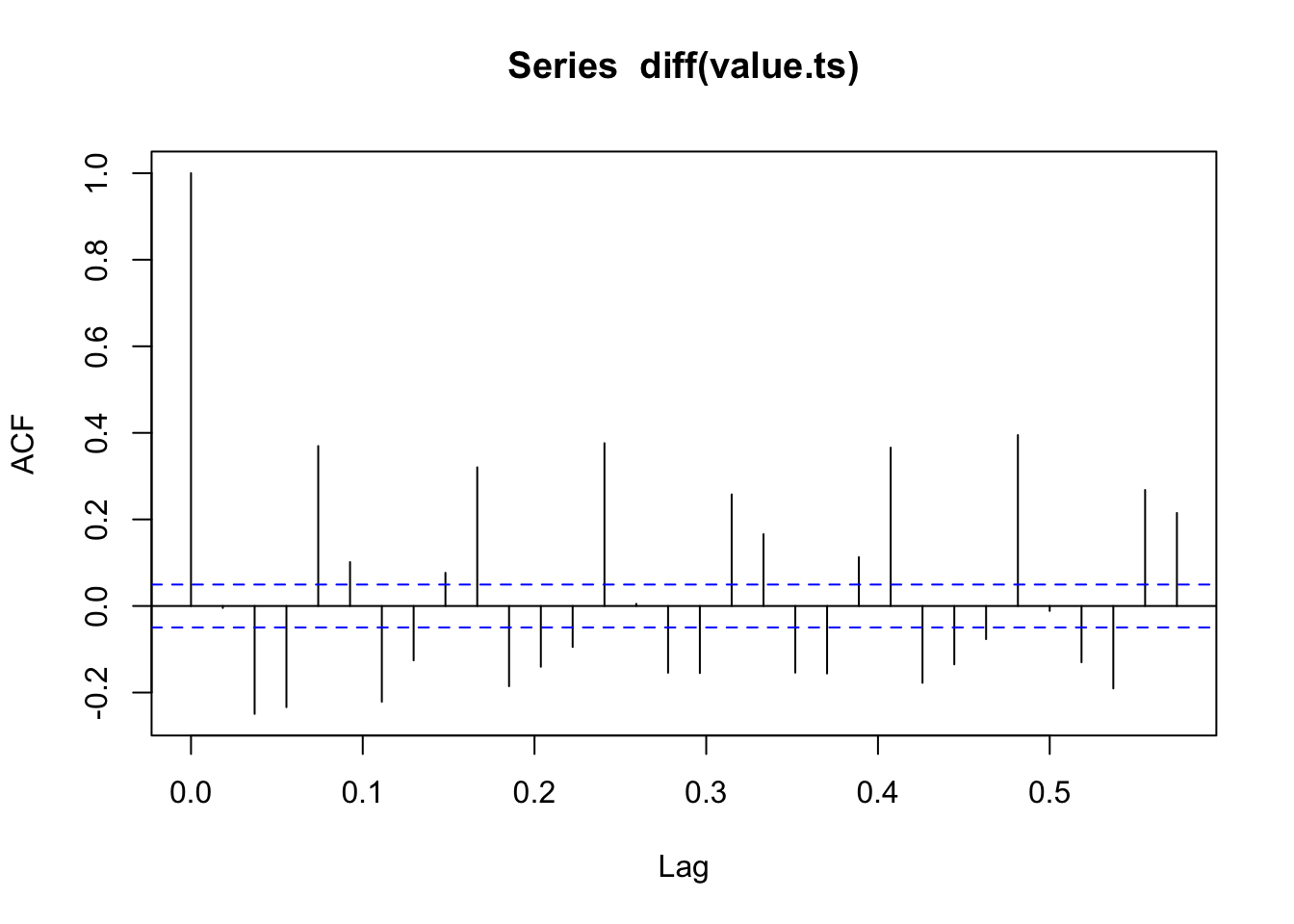
##
## Augmented Dickey-Fuller Test
##
## data: diff(value.ts)
## Dickey-Fuller = -15.255, Lag order = 11, p-value = 0.01
## alternative hypothesis: stationaryNos indica que hay una estructura en la serie que no es ruido blanco pero SI estacionaria (cae de \(1\) a casi cero)
3.4.2.1 Simulación:
El siguiente paso es modelizar esta estructura. Un modelo para ello es un modelo autorregresivo. Simular un \(AR(1)\).
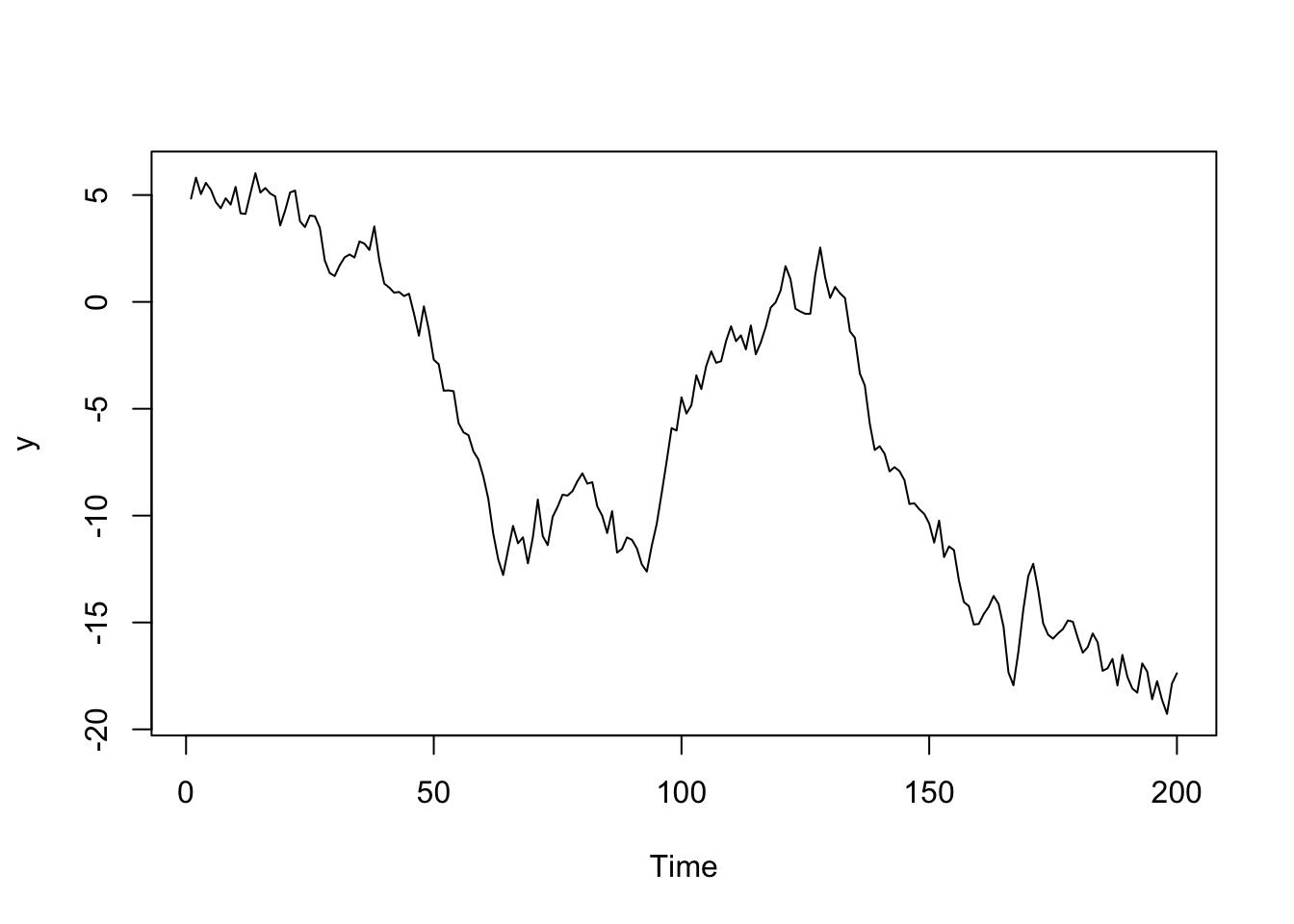
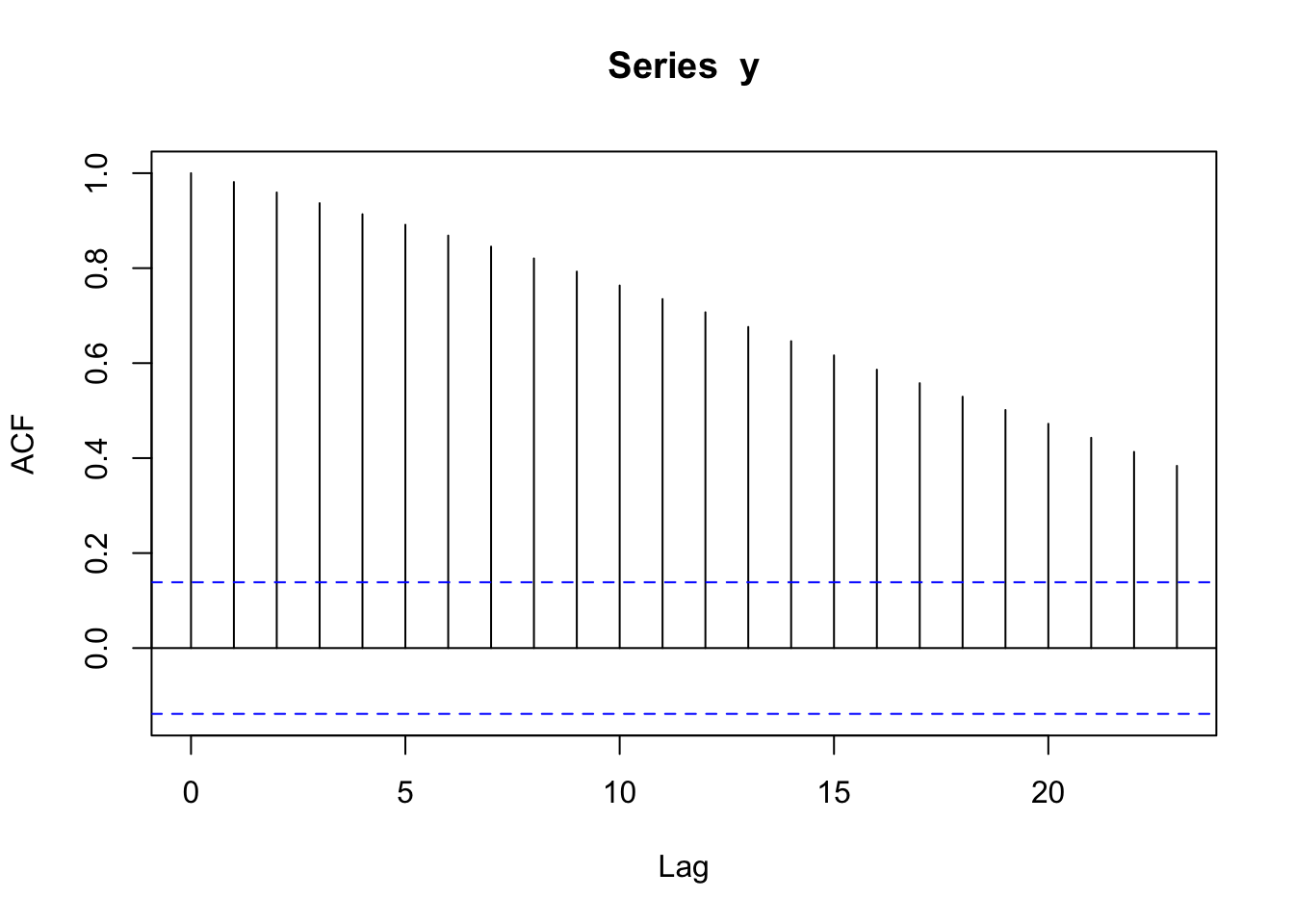
¿Cuáles son los parámetros del arima.sim? Hemos simulado \(Y_t = \phi_{0}+\phi_{1}Y_{t-1} = \phi_{0}+0.99Y_{t-1}\). Si \(\phi_{0}\approx 1\), el proceso es inestable, se aproxima a un paseo aleatorio.
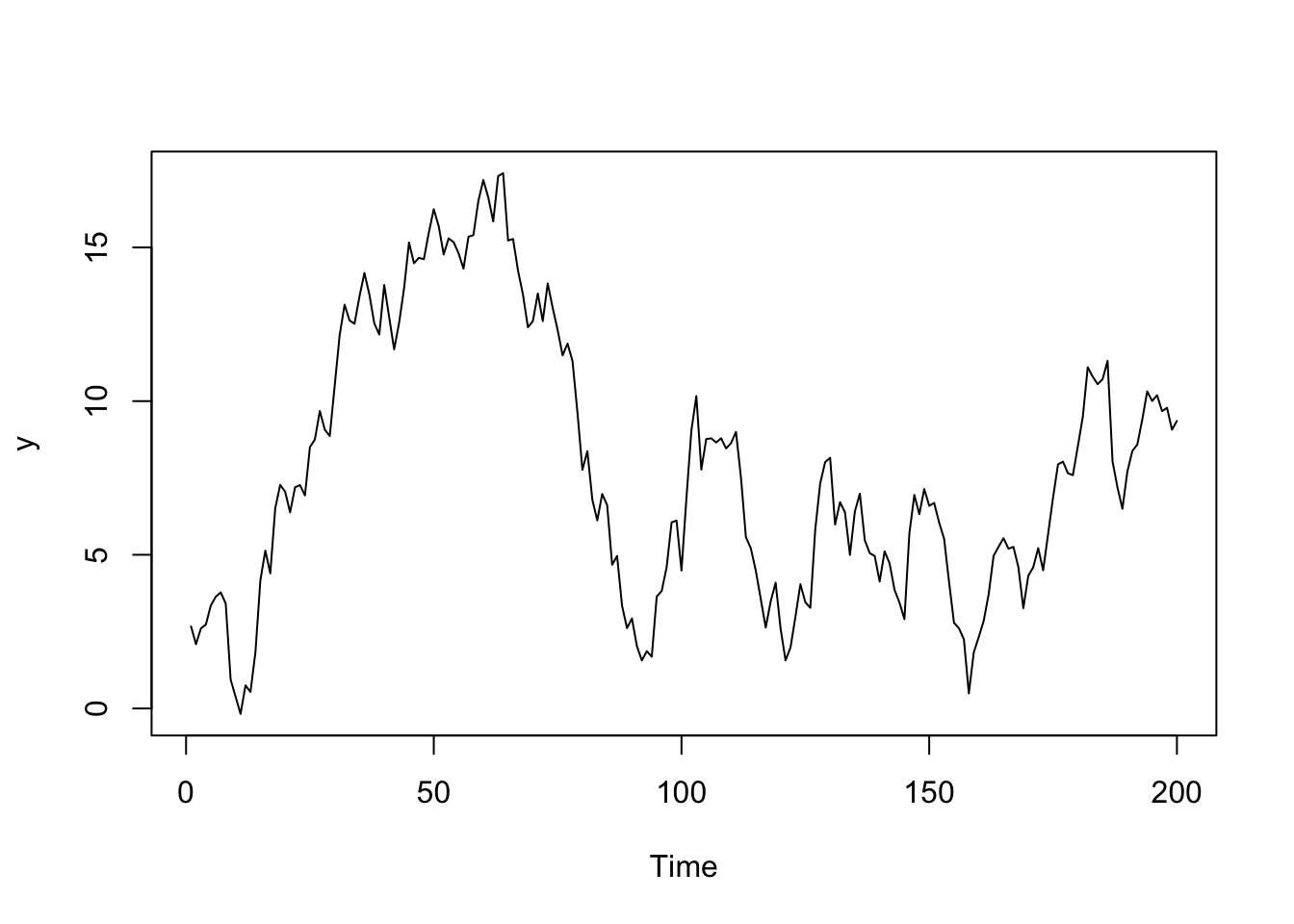
## [1] -1.010101+0i## [1] 1.010101Simulemos el modelo: \(Y_t = 0.5Y_{t-1} - 0.7Y_{t-2} + 0.6Y_{t-3}\)
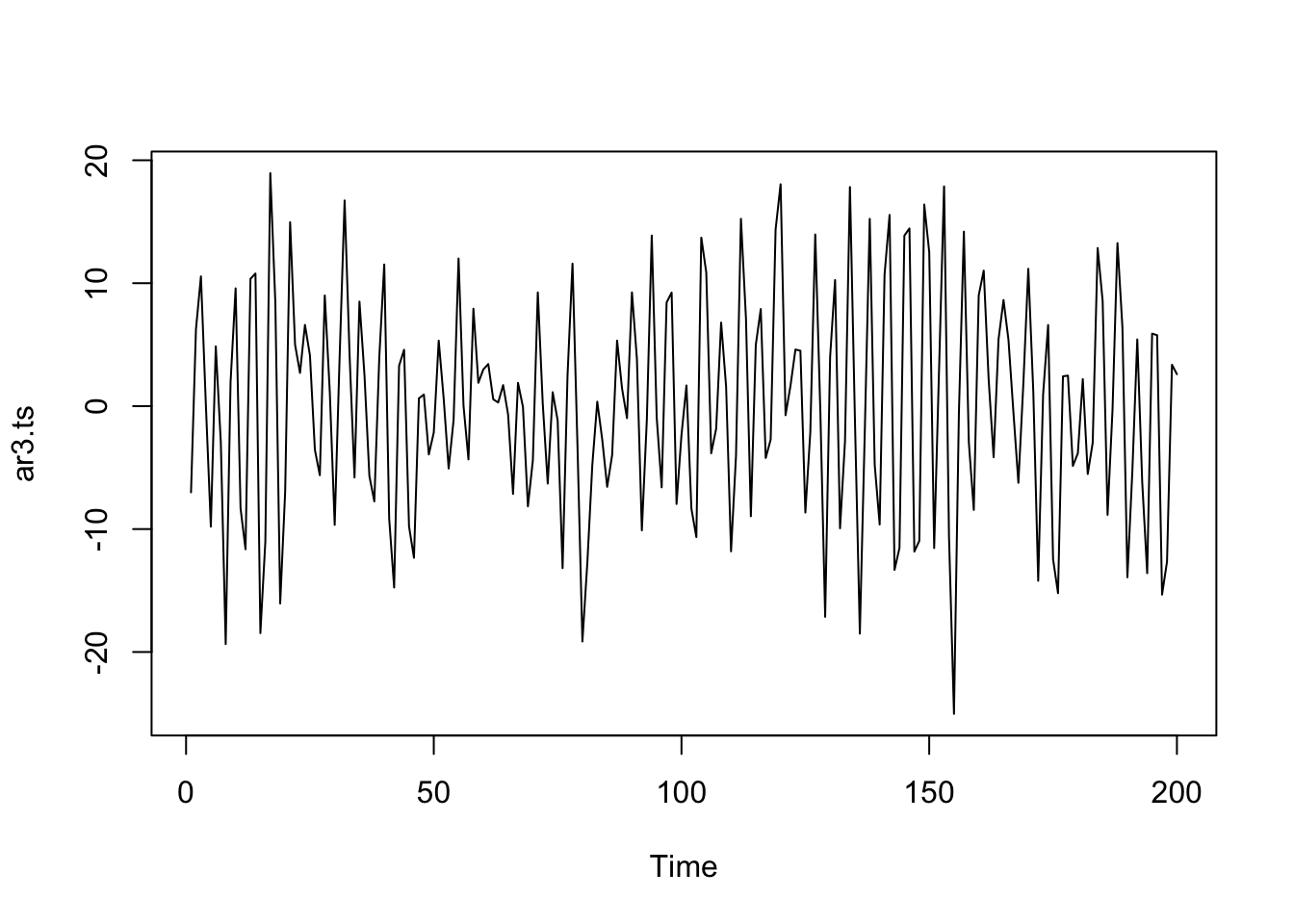
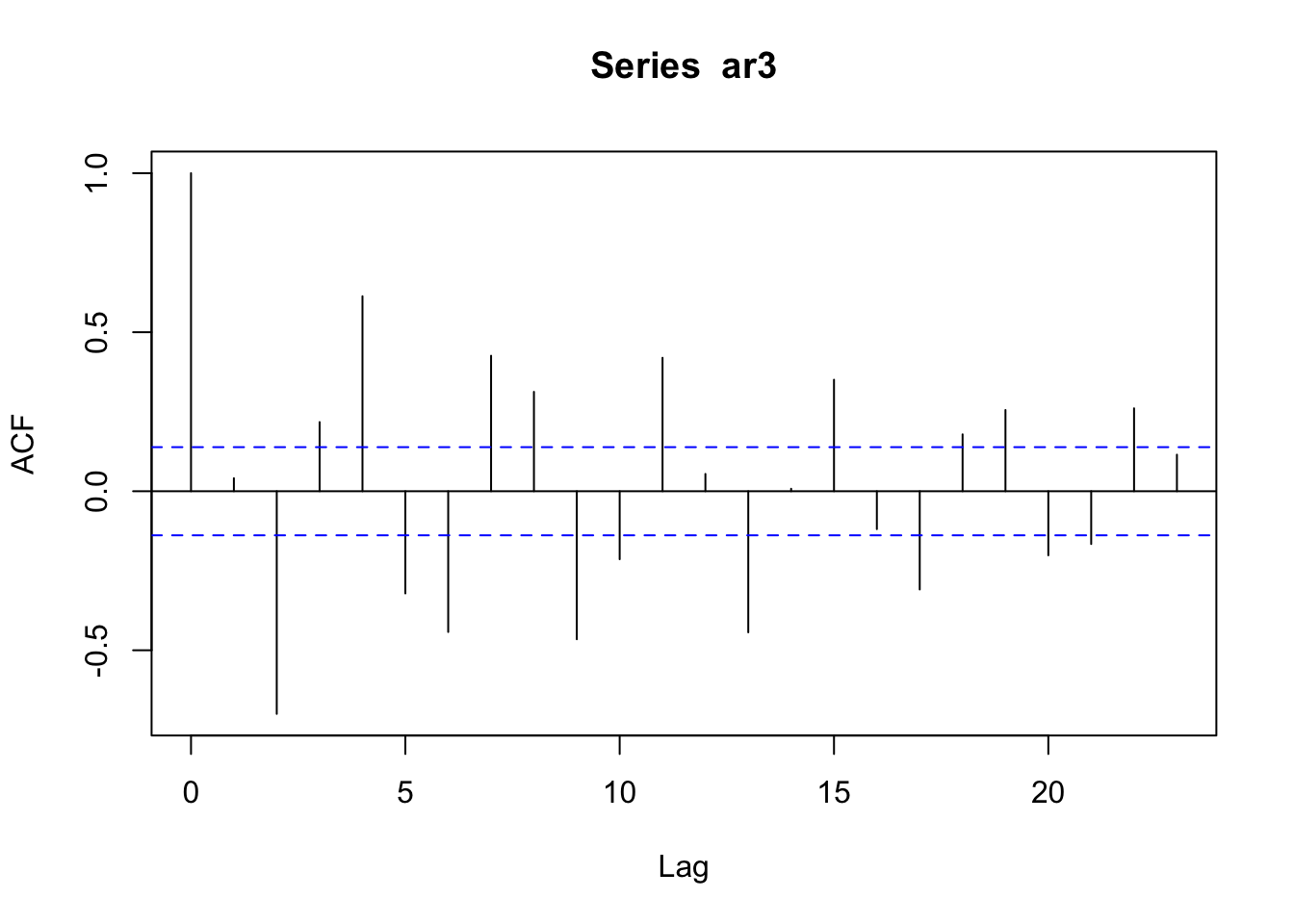
Las autocorrelaciones decaen exponencialmente a cero.
## [1] -0.122790+1.079387i -0.122790-1.079387i 1.412247+0.000000i## [1] 1.086348 1.086348 1.412247Autocorrelaciones parciales: nos ayudan a determinar el orden del modelo.
La autocorrelación parcial es la correlación entre \(Y_t\) y \(Y_{t-k}\) después de eliminar el efecto de las \(Y\) intermedias.
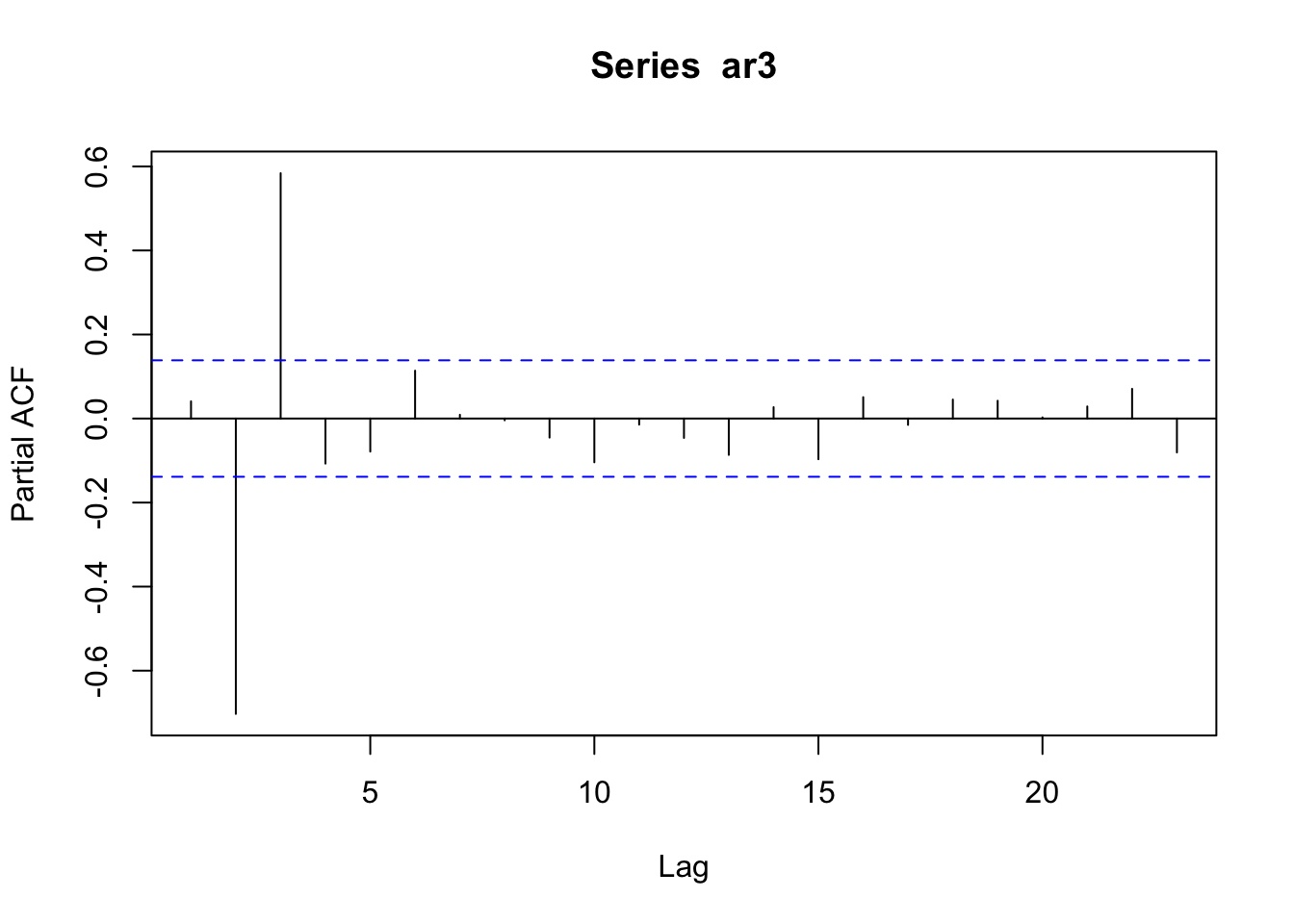
## 0 1 2 3 4 5
## 214.2962026 215.9605122 81.7168386 0.3161484 0.0000000 0.7604714
## 6 7 8 9 10 11
## 0.1479566 2.1319143 4.1282844 5.7166840 5.5328922 7.4911755
## 12 13 14 15 16 17
## 9.0651162 9.5623719 11.4158169 11.5321854 13.0141281 14.9684525
## 18 19 20 21 22 23
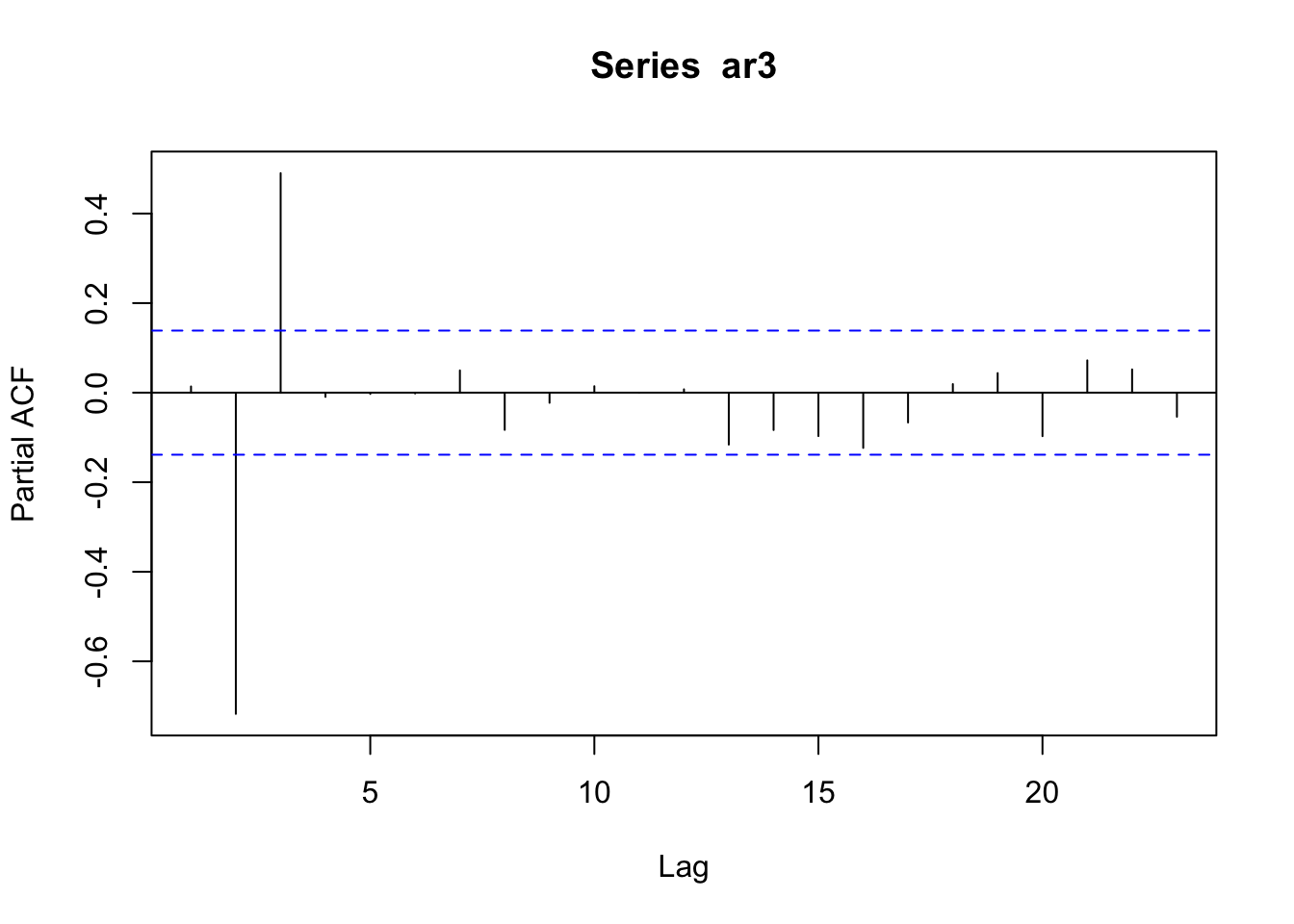
## 16.5600954 18.2016313 20.2001532 22.0341818 23.0318203 23.7241581La tercera autocorrelación es la que está fuera de las bandas, esto indica que el modelo es un \(AR(3)\).
Ejemplo
Datos: precio de huevos desde 1901
uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/PrecioHuevos.csv"
datos <- read.csv(url(uu),header=T,sep=";")
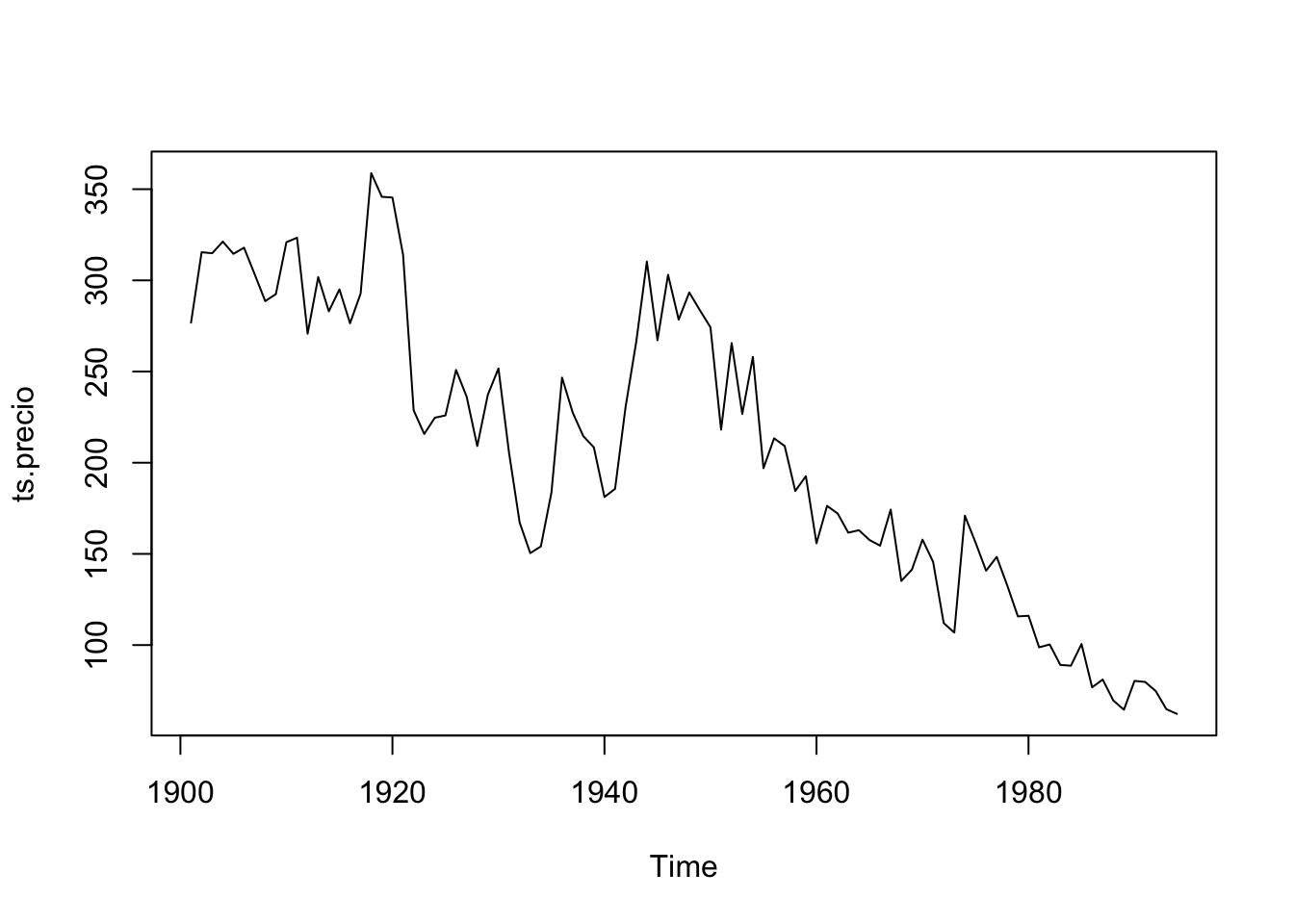
ts.precio <- ts(datos$precio,start=1901)
plot(ts.precio)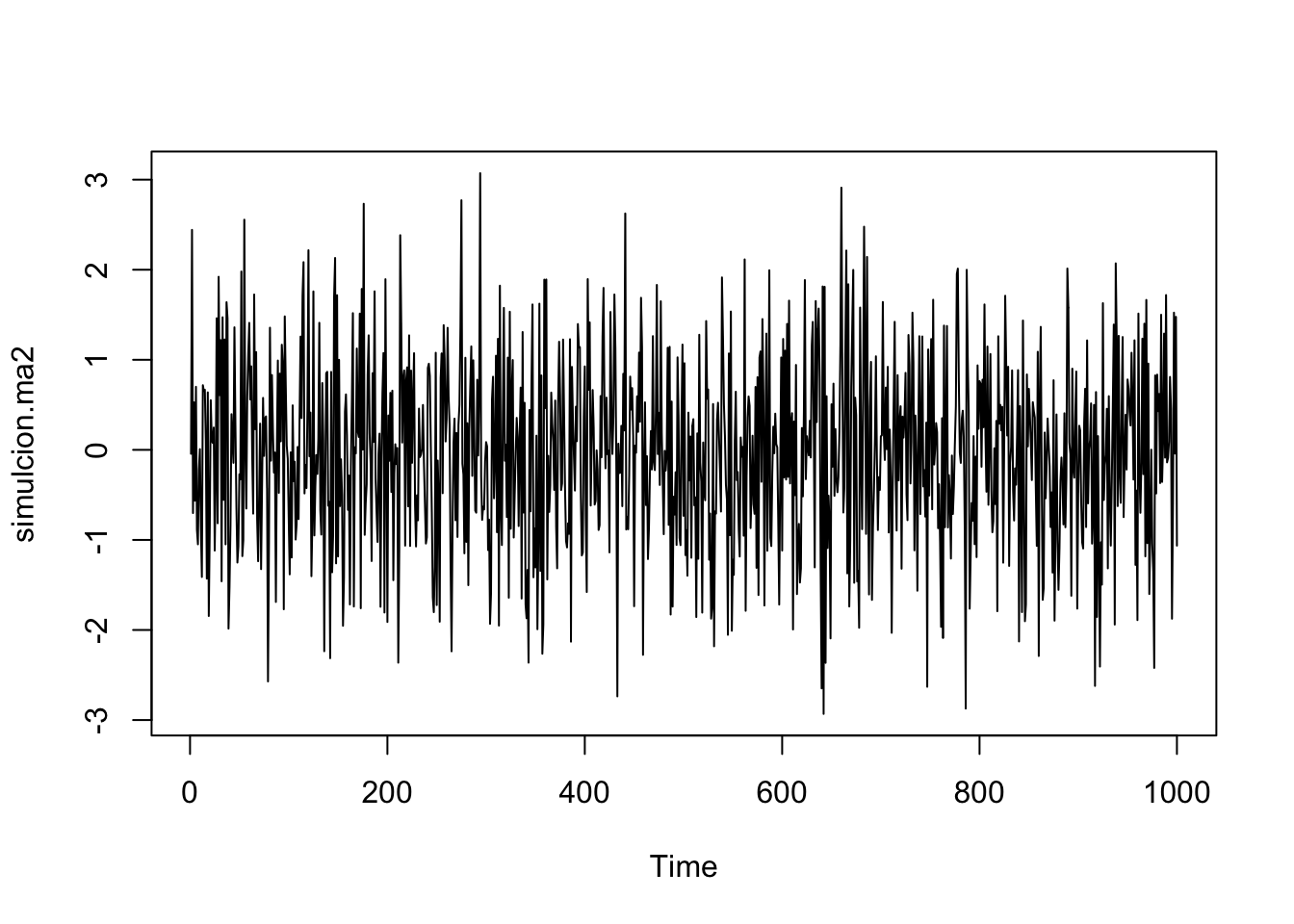
Veamos las autocorrelaciones:
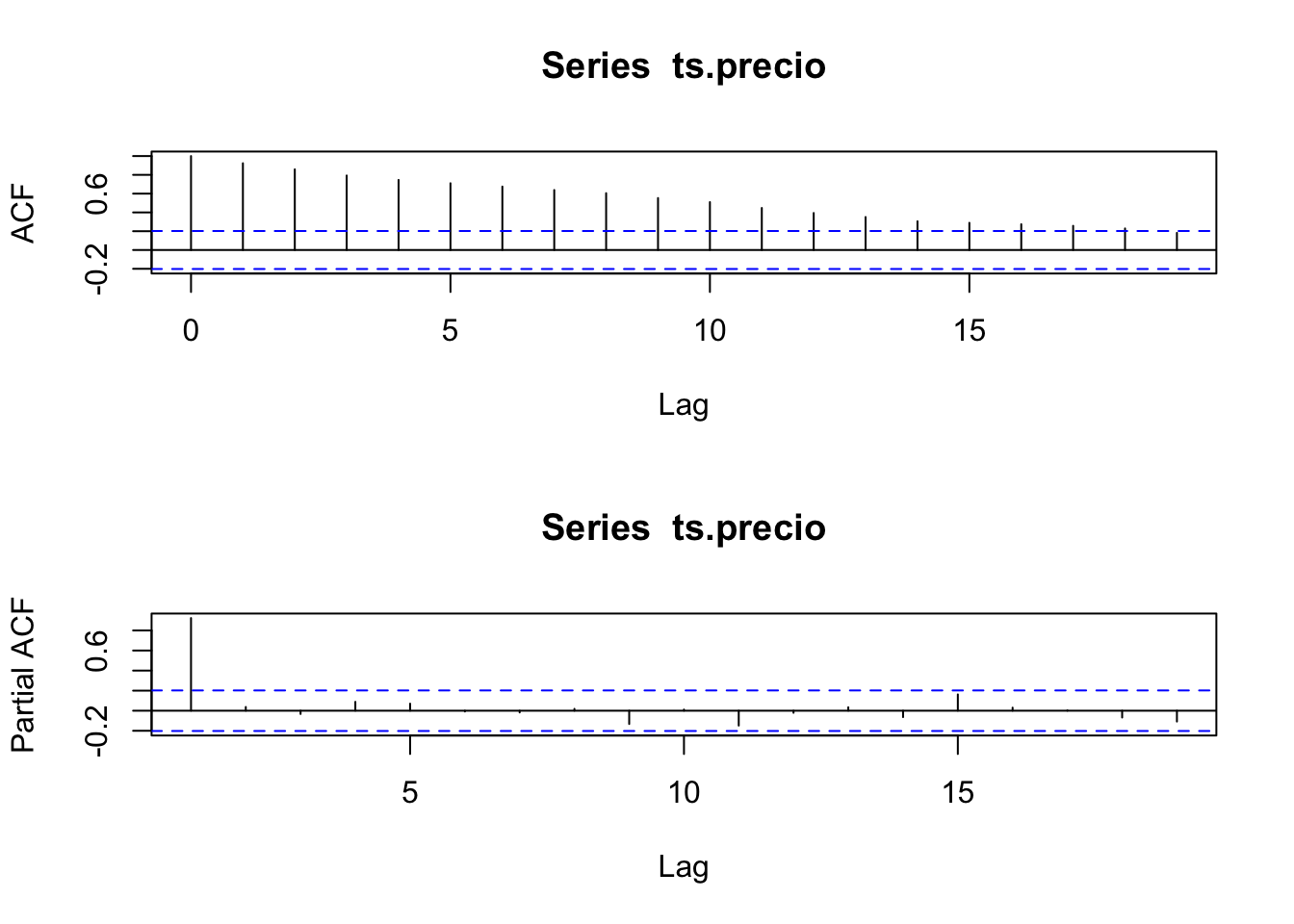
##
## Augmented Dickey-Fuller Test
##
## data: ts.precio
## Dickey-Fuller = -2.3934, Lag order = 4, p-value = 0.414
## alternative hypothesis: stationaryLas autocorrelaciones si decaen, no lo hacen tan rápido. No se puede decir si es estacionario o no. Pero la prueba de estacionariedad es clara, el proceso no es estacionario.
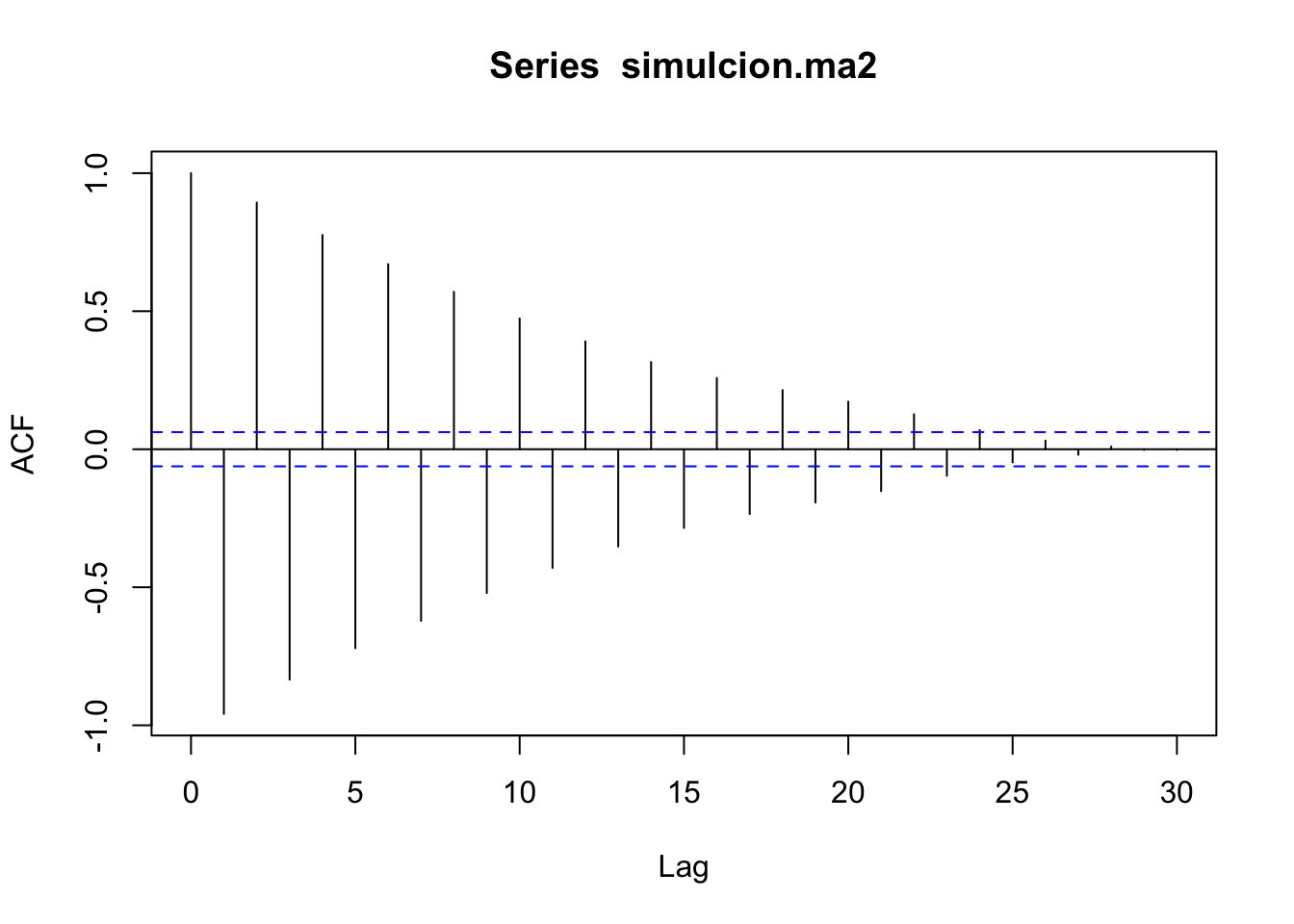
##
## Augmented Dickey-Fuller Test
##
## data: diff(ts.precio)
## Dickey-Fuller = -5.8255, Lag order = 4, p-value = 0.01
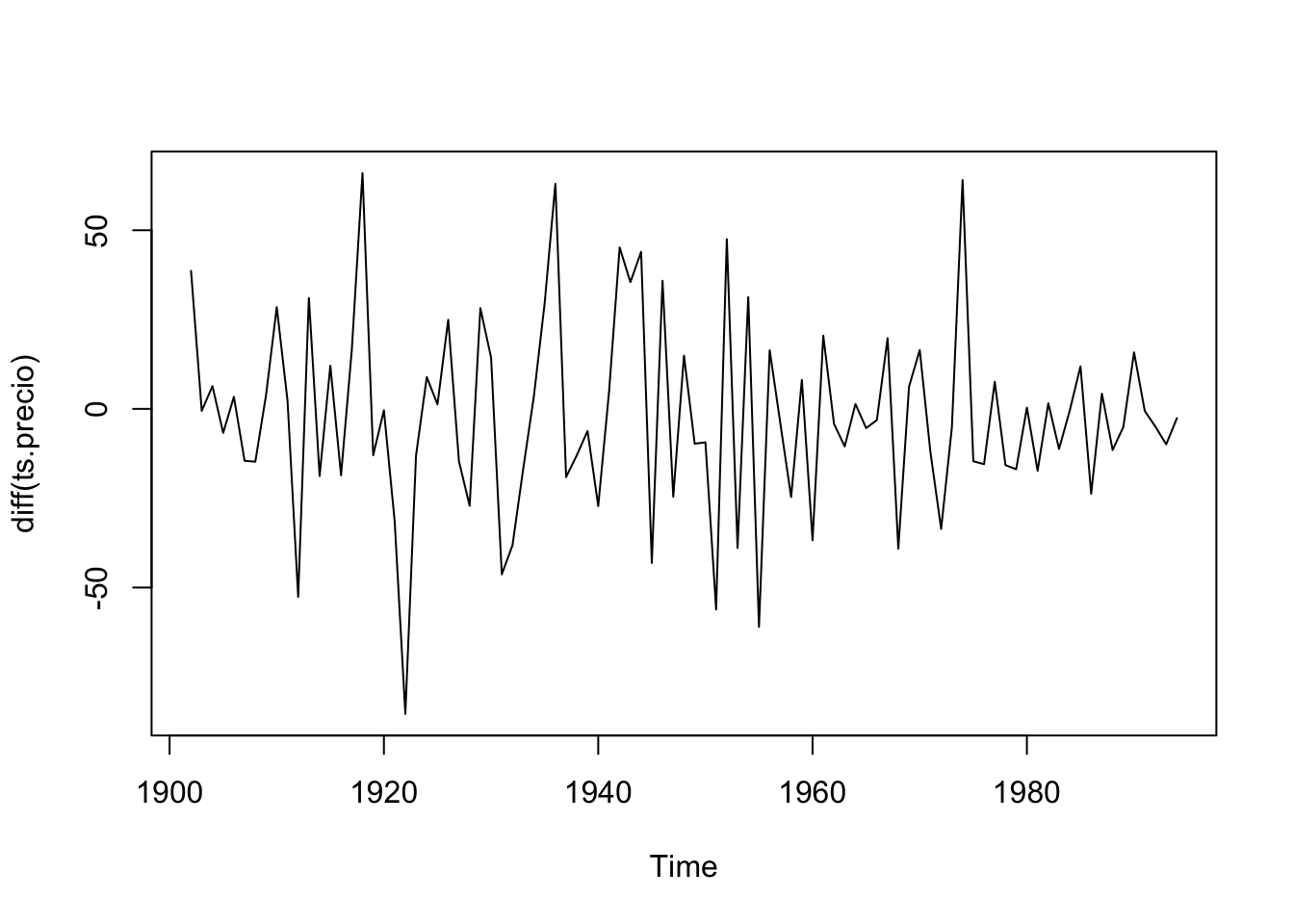
## alternative hypothesis: stationaryLa primera diferencia sí es estacionaria. Evaluemos un modelo:
##
## Call:
## arima(x = diff(ts.precio), order = c(1, 0, 0))
##
## Coefficients:
## ar1 intercept
## -0.1488 -2.3634
## s.e. 0.1033 2.4024
##
## sigma^2 estimated as 706.2: log likelihood = -437.01, aic = 880.02## ar1 intercept
## ar1 0.010667969 0.003553029
## intercept 0.003553029 5.771602581¿Qué nos recomienda R?
##
## Call:
## ar(x = diff(ts.precio))
##
## Coefficients:
## 1
## -0.1466
##
## Order selected 1 sigma^2 estimated as 722.2Analicemos los residuos
residuos = ar.precio$resid
# Los residuos debe estar sin ninguna estructura
par(mfrow = c(2,1))
plot(residuos)
abline(h=0,col="red")
abline(v=1970,col="blue")
acf(residuos,na.action=na.pass)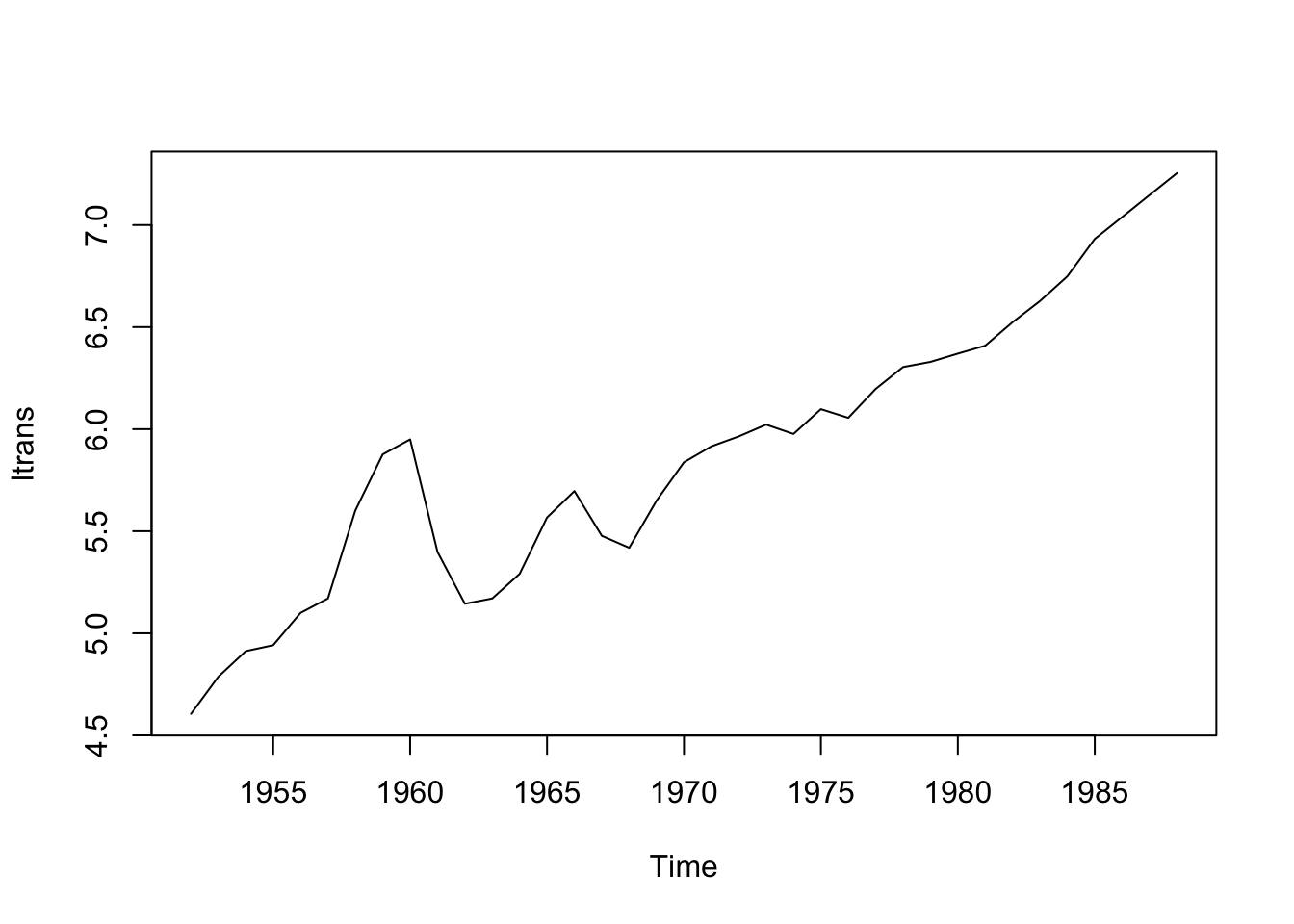
La prueba de Ljung-Box se utiliza comúnmente en un modelo autorregresivo integrado de media móvil de modelado (ARIMA).
Ten en cuenta que se aplica a los residuos de un modelo ARIMA, no en la serie original, y en tales aplicaciones, la hipótesis es que los residuos del modelo ARIMA no tienen autocorrelación.
Al probar los residuos de un modelo ARIMA estimado, los grados de libertad deben ser ajustados para reflejar la estimación de parámetros. Por ejemplo, para un modelo \(ARIMA (p,0,q)\), los grados de libertad se debe establecer en \((h-p-q)\).
##
## Box-Ljung test
##
## data: residuos
## X-squared = 25.118, df = 20, p-value = 0.1969\(Ho\): Ruido Blanco ¿Es ruido blanco?
Probemos un segundo modelo
##
## Call:
## arima(x = diff(ts.precio), order = c(2, 0, 0))
##
## Coefficients:
## ar1 ar2 intercept
## -0.1495 -0.005 -2.3651
## s.e. 0.1045 0.104 2.3908
##
## sigma^2 estimated as 706.2: log likelihood = -437.01, aic = 882.02Comparemos los resultados:
##
## Call:
## ar(x = diff(ts.precio), aic = FALSE, order.max = 2)
##
## Coefficients:
## 1 2
## -0.1472 -0.0042
##
## Order selected 2 sigma^2 estimated as 730.2## [1] 882.0161## [1] 880.0184Se escoge el modelo de menor AIC. En este caso, el modelo \(AR(1)\).
3.4.3 Proceso ARMA
Definición
Un proceso \(Y_t \sim ARMA(p, q)\) se define mediante
\[ \phi_p(L)(Y_t)=\theta_q(L)\epsilon_t \] donde \(\epsilon_t\sim RB(0,\sigma^2)\) y \(\phi_p(z)=1-\sum_{j=1}^{p}\phi_jz^j\), \(\theta_q(z)=1+\sum_{j=1}^q\theta_jz^j\) son los polinomios autorregresivo y de media móvil respectivamente.
Se asume que las raíces de las ecuaciones \(\phi_p(z) = 0\) y \(\theta_q(z) = 0\) están fuera del círculo unitario. Además se asume que estos polinomios no tienen raíces en común. Si se cumplen estas condiciones el proceso \(Y_t \sim ARMA(p, q)\) es estacionario e identificable.
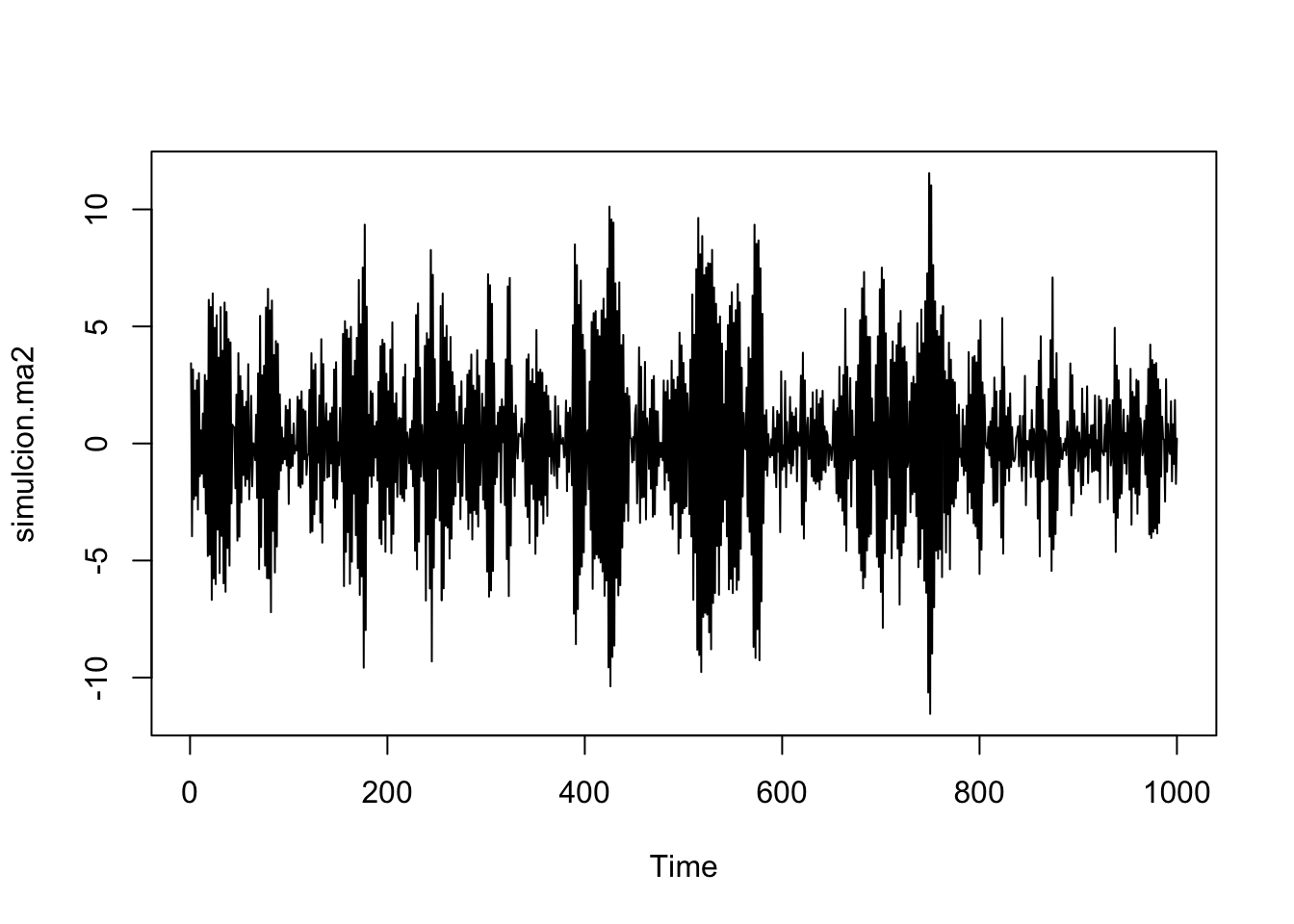
Simulemos el proceso \(Y_t = 0.1Y_{t-1}+0.1\epsilon_{t-1}+\epsilon_{t}\):
simulcion.ma2 <- arima.sim(1000, model=list(order=c(1,0,1),ar=c(-0.1),ma=c(0.1)))
plot(simulcion.ma2)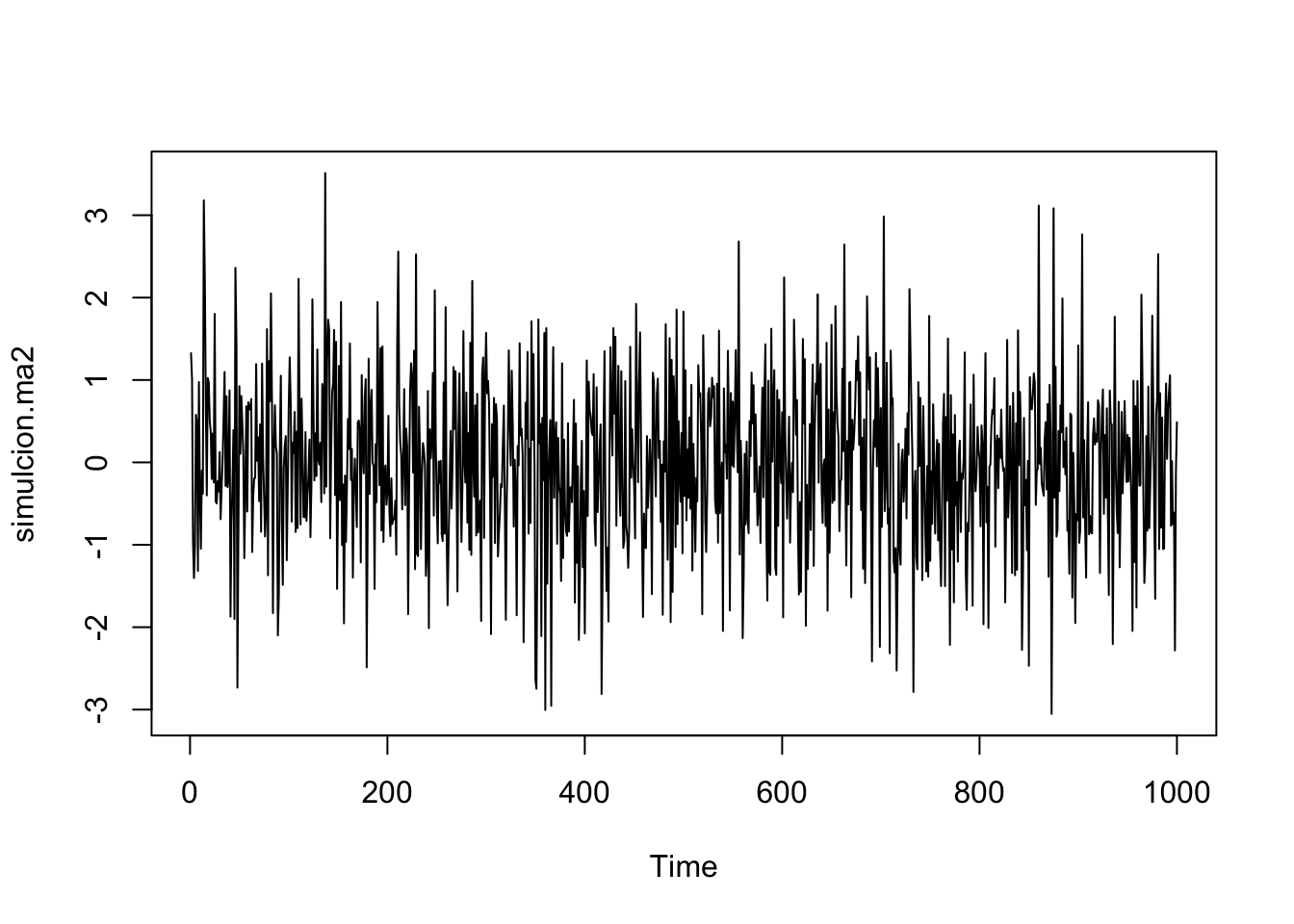
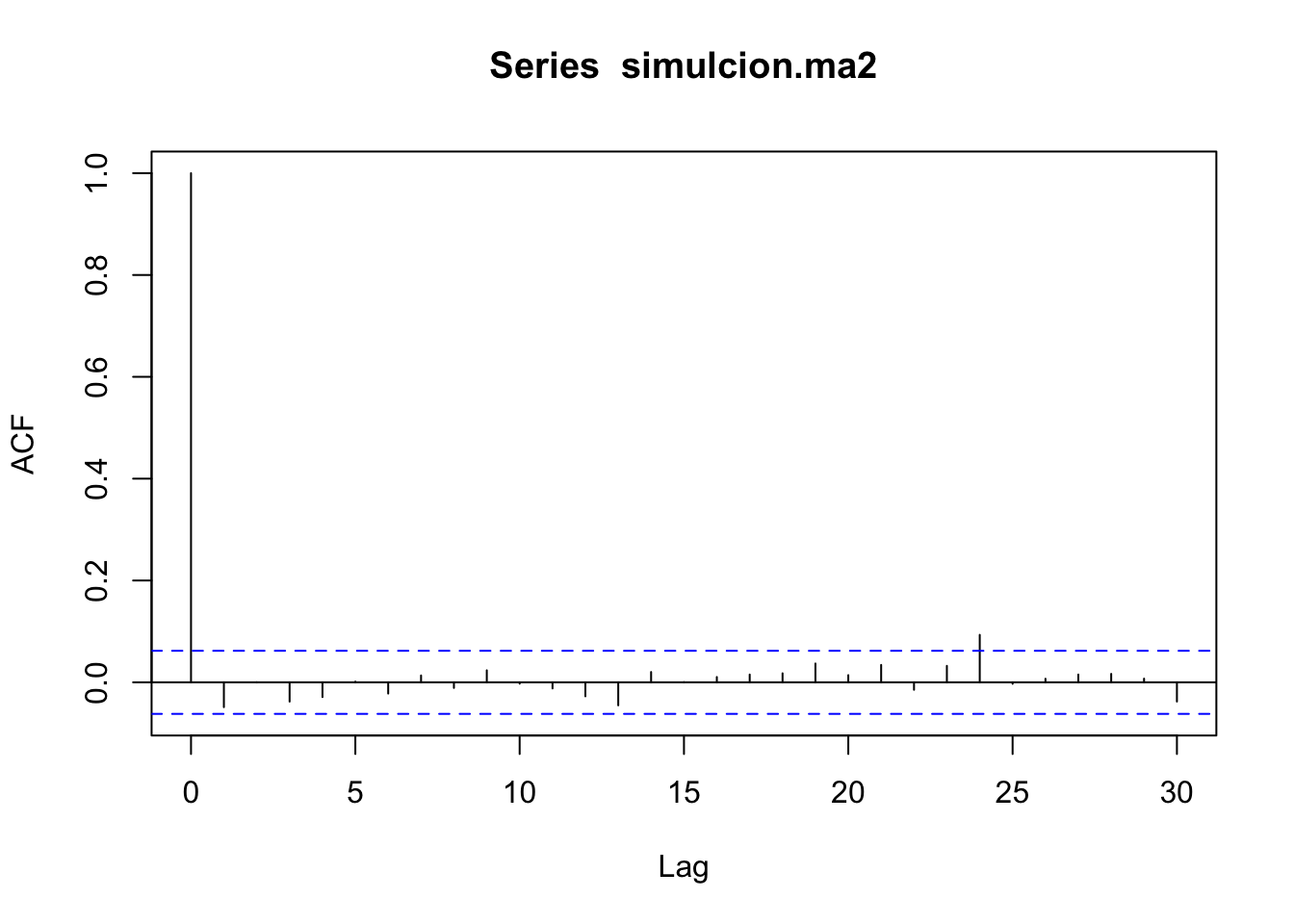
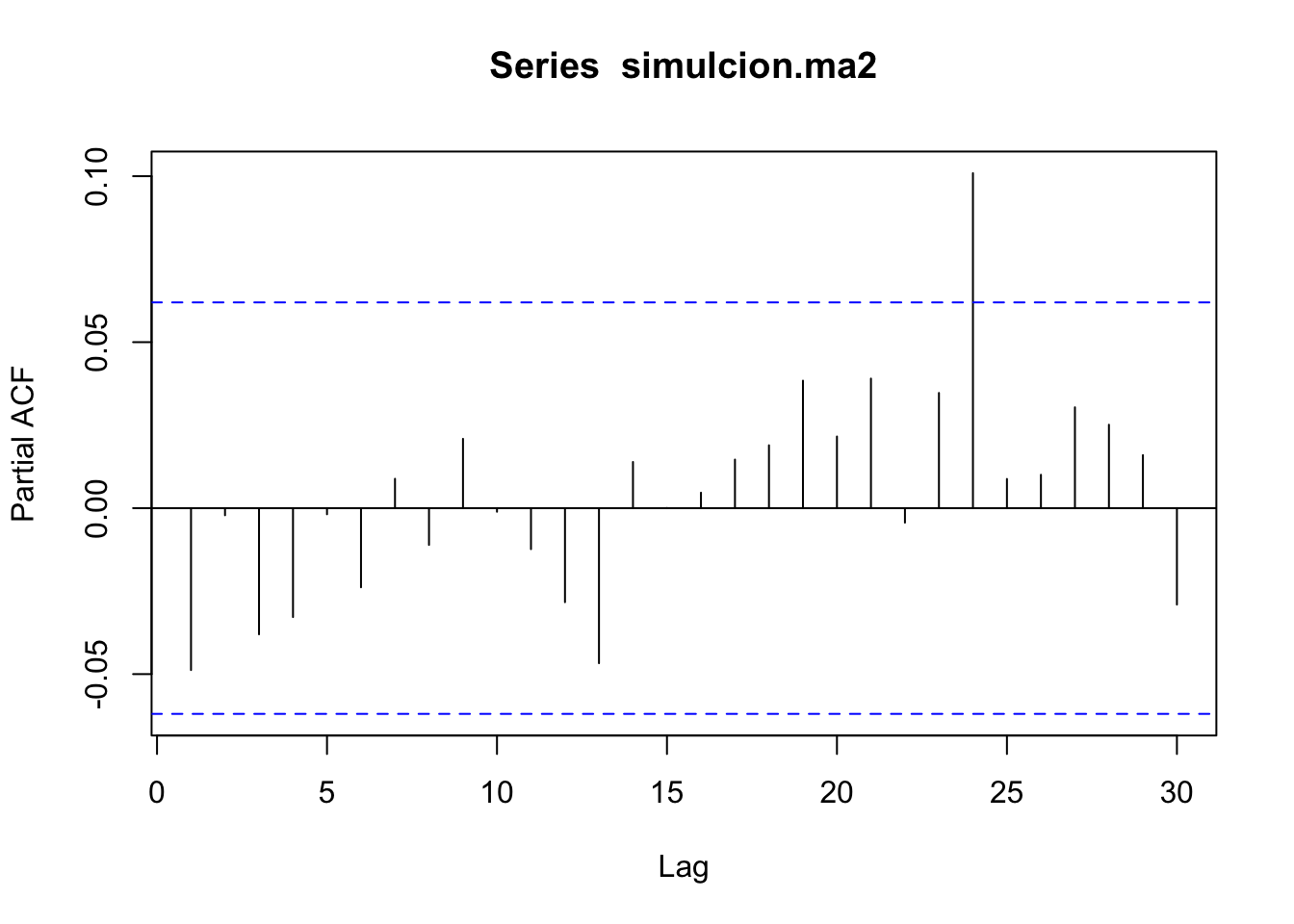
z.ar <- polyroot(c(1,-0.1)) # Estacionario (Las raíces son |x|>1)
z.ma <- polyroot(c(1,0.1)) # condicion de invertibilidad
Mod(z.ar) ## [1] 10## [1] 10Notemos que se cumple que las raíces están fuera del círculo unitario, pero no se cumple que no tengan raíces en común.
Simulemos el proceso \(Y_t = 0.9Y_t-0.4\epsilon_{t-1}+\epsilon_{t}\):
simulcion.ma2 <- arima.sim(1000, model=list(order=c(1,0,1),ar=c(-0.9),ma=c(-0.4)))
plot(simulcion.ma2)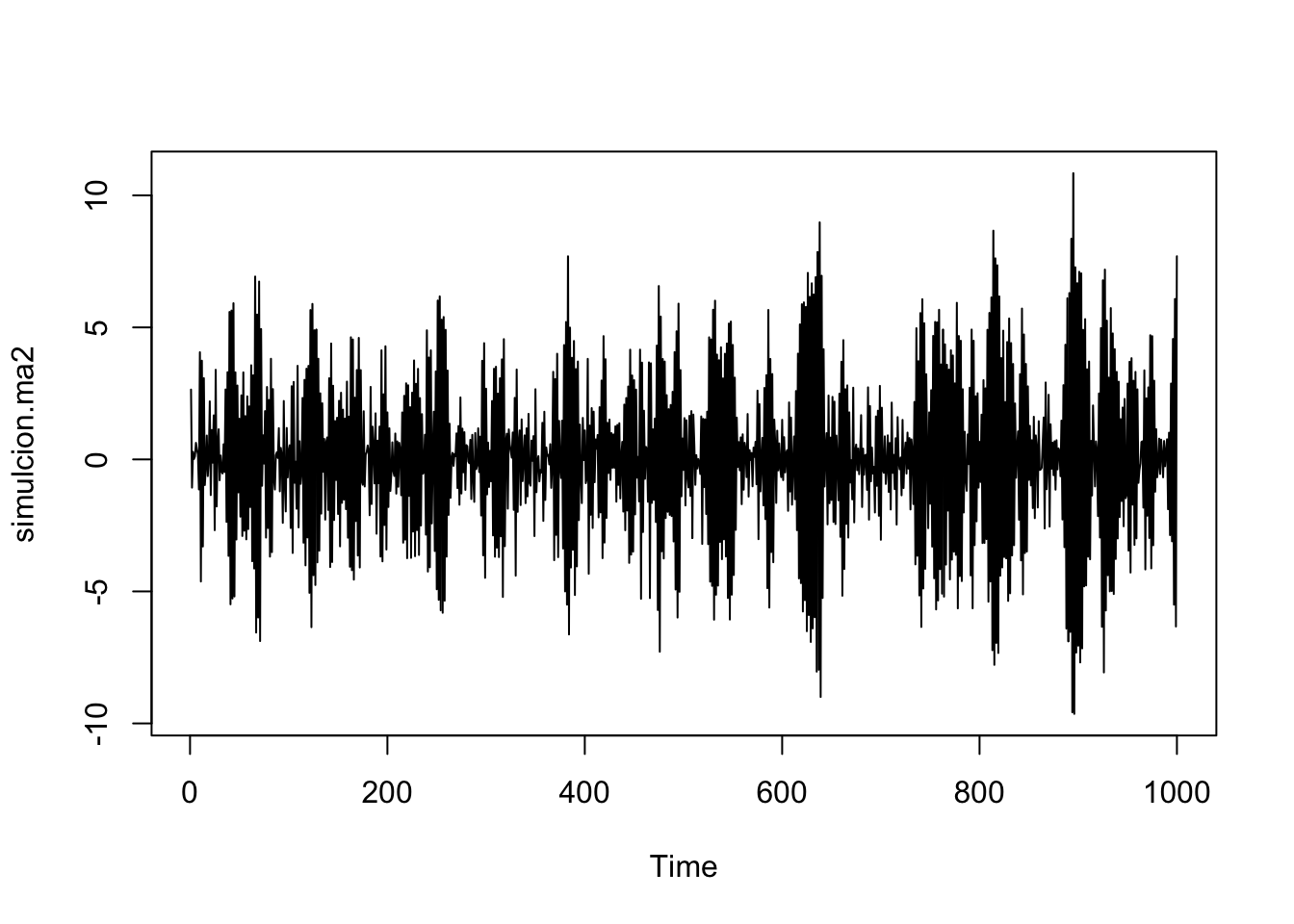
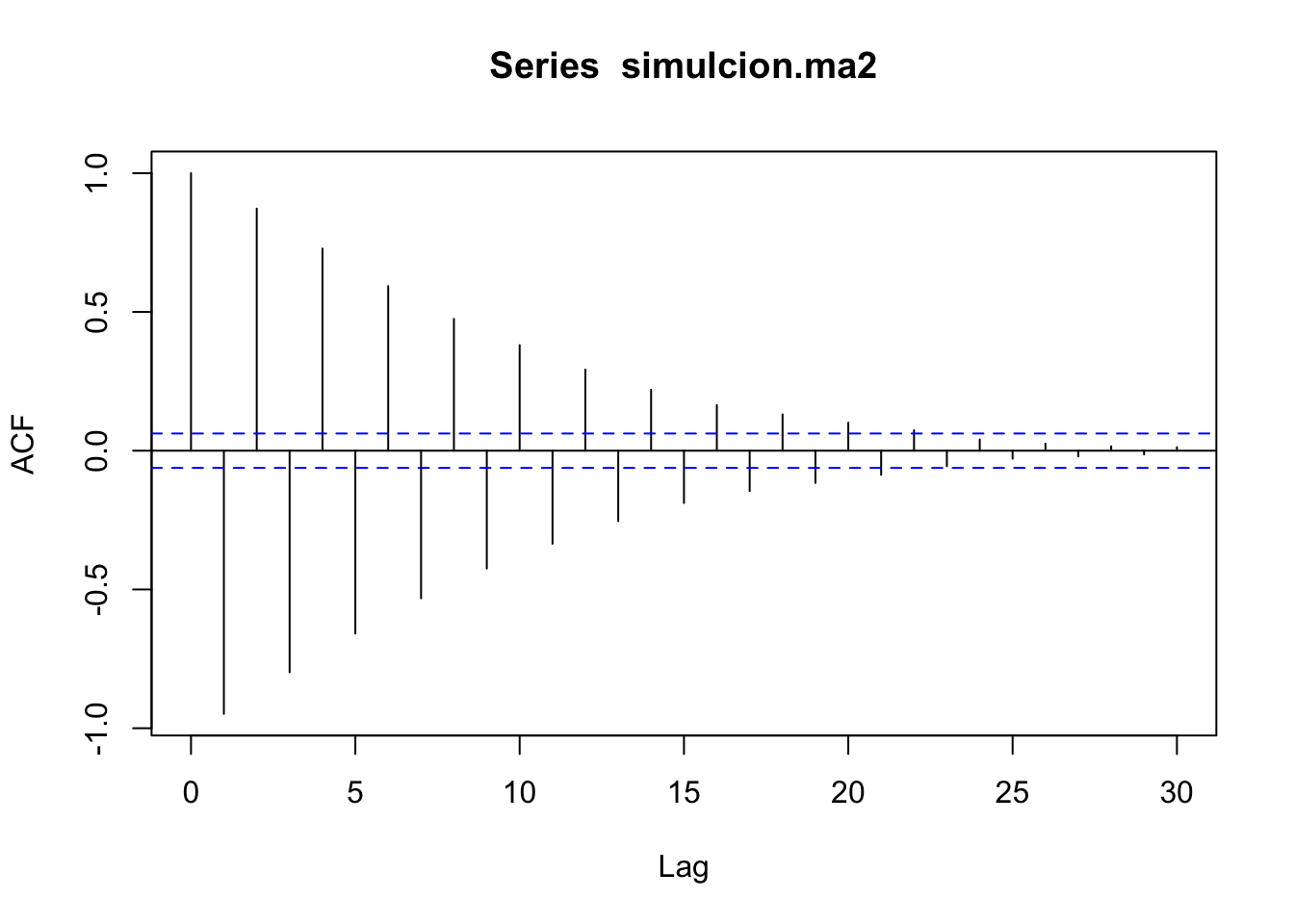
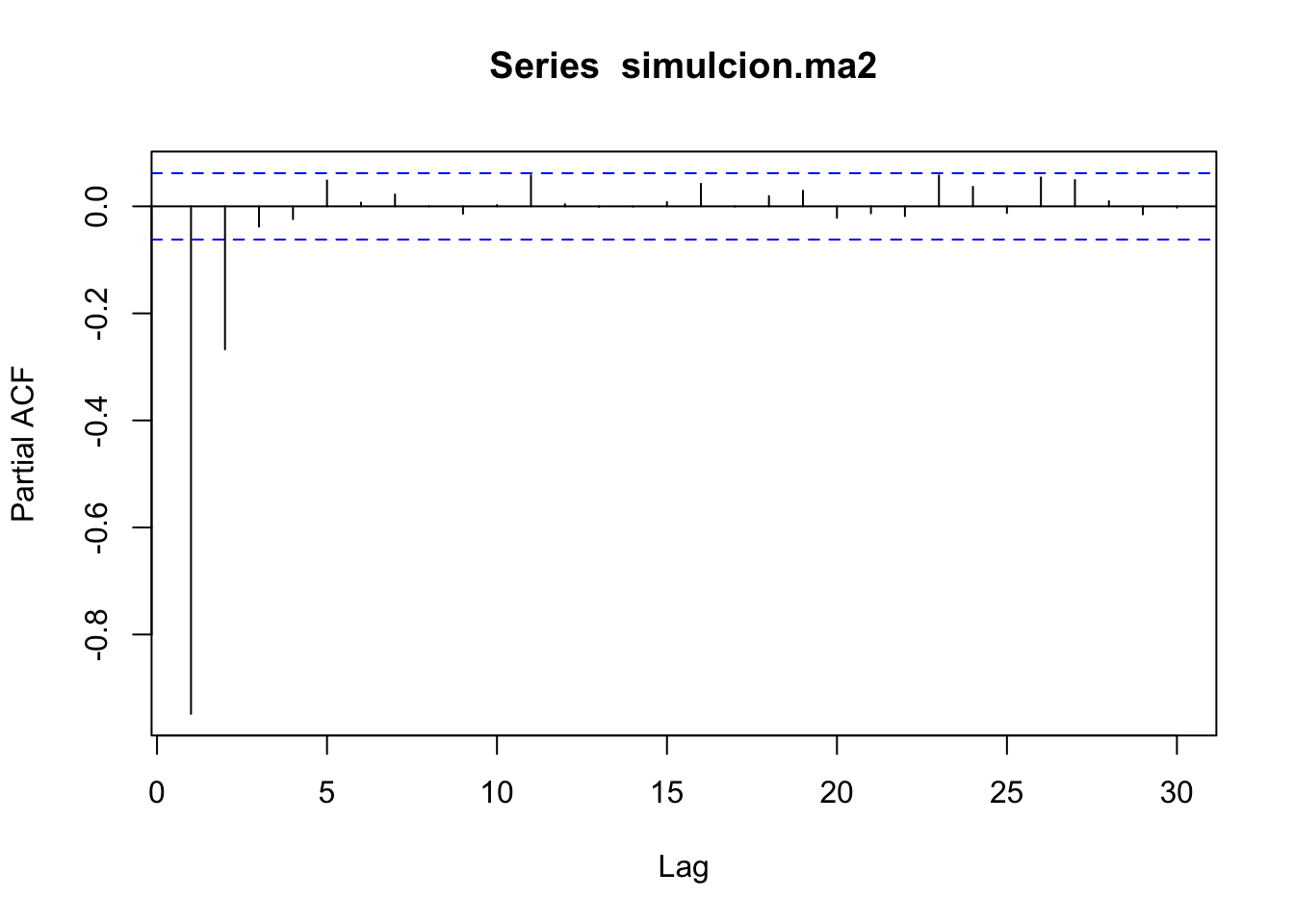
z.ar <- polyroot(c(1,0.9)) # Estacionario (Las raíces son |x|>1)
z.ma <- polyroot(c(1,-0.4)) # condicion de invertibilidad
Mod(z.ar) ## [1] 1.111111## [1] 2.5Notemos que se cumple que las raíces están fuera del círculo unitario y no tiene raíces en común, entonces el proceso \(Y_t = 0.9Y_t-0.4\epsilon_{t-1}+\epsilon_{t}\) es estacionario.
3.4.4 Buscando el mejor modelo
Ejemplo 1
Datos: Serie de tiempo (1952-1988) del ingreso nacional real en China por sector (año base: 1952)
## Time-Series [1:37, 1:5] from 1952 to 1988: 100 102 103 112 116 ...
## - attr(*, "dimnames")=List of 2
## ..$ : NULL
## ..$ : chr [1:5] "agriculture" "commerce" "construction" "industry" ...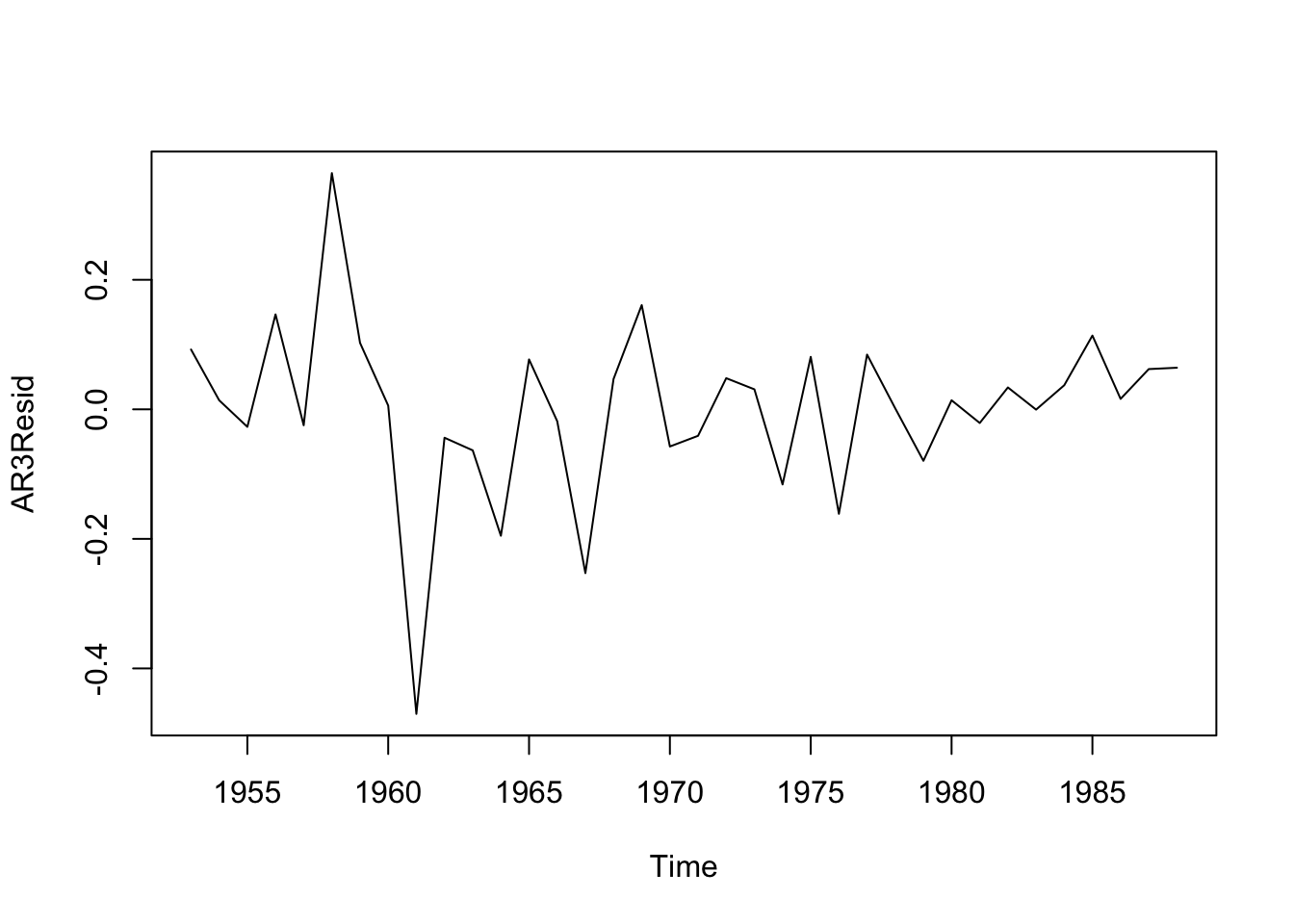
Parece no ser estacionario. Hacemos una transformación para tratar de confirmar la estacionariedad.
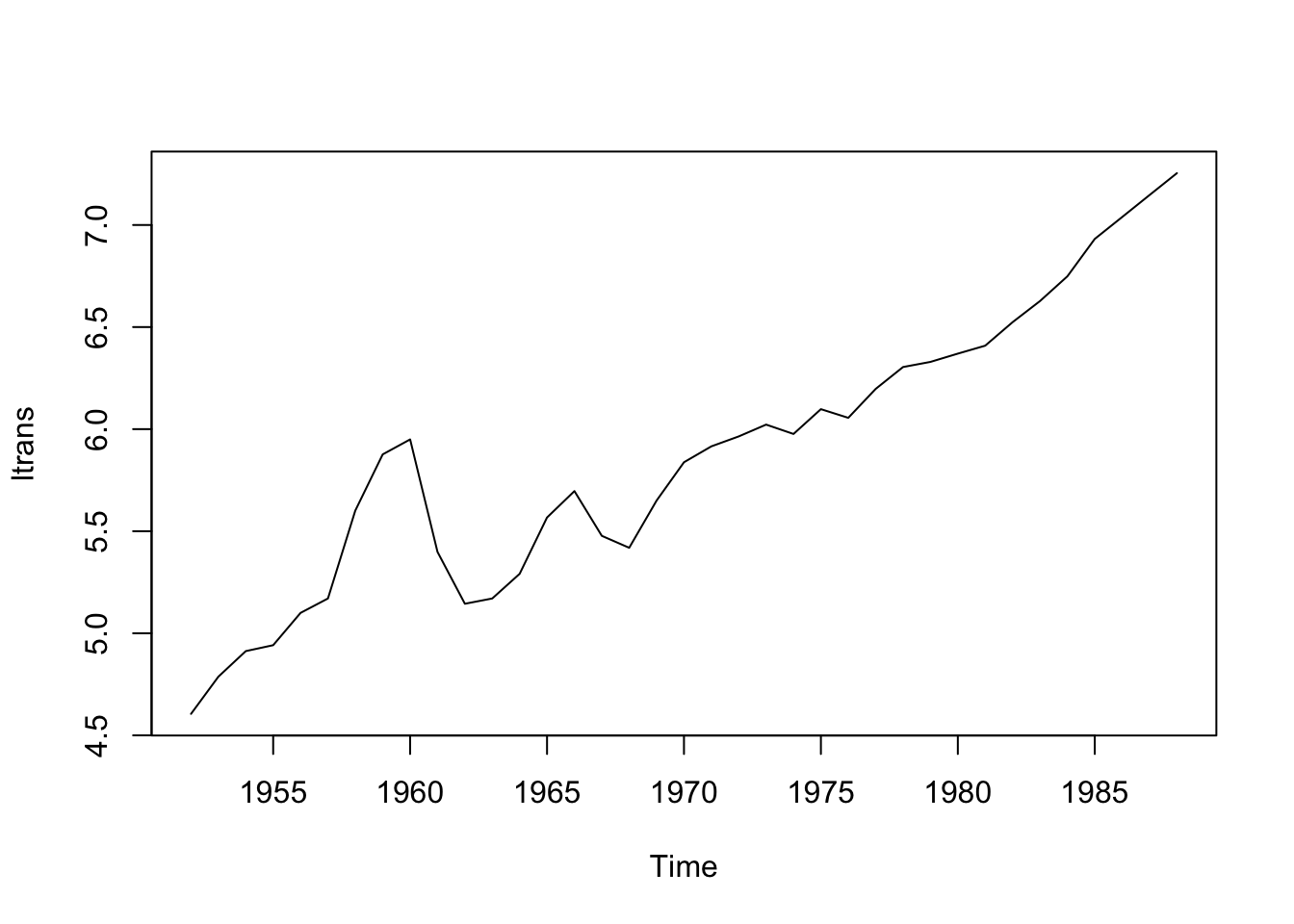
Notamos que persiste el problema, sigue sin ser estacionario. Probemos con la diferencia:
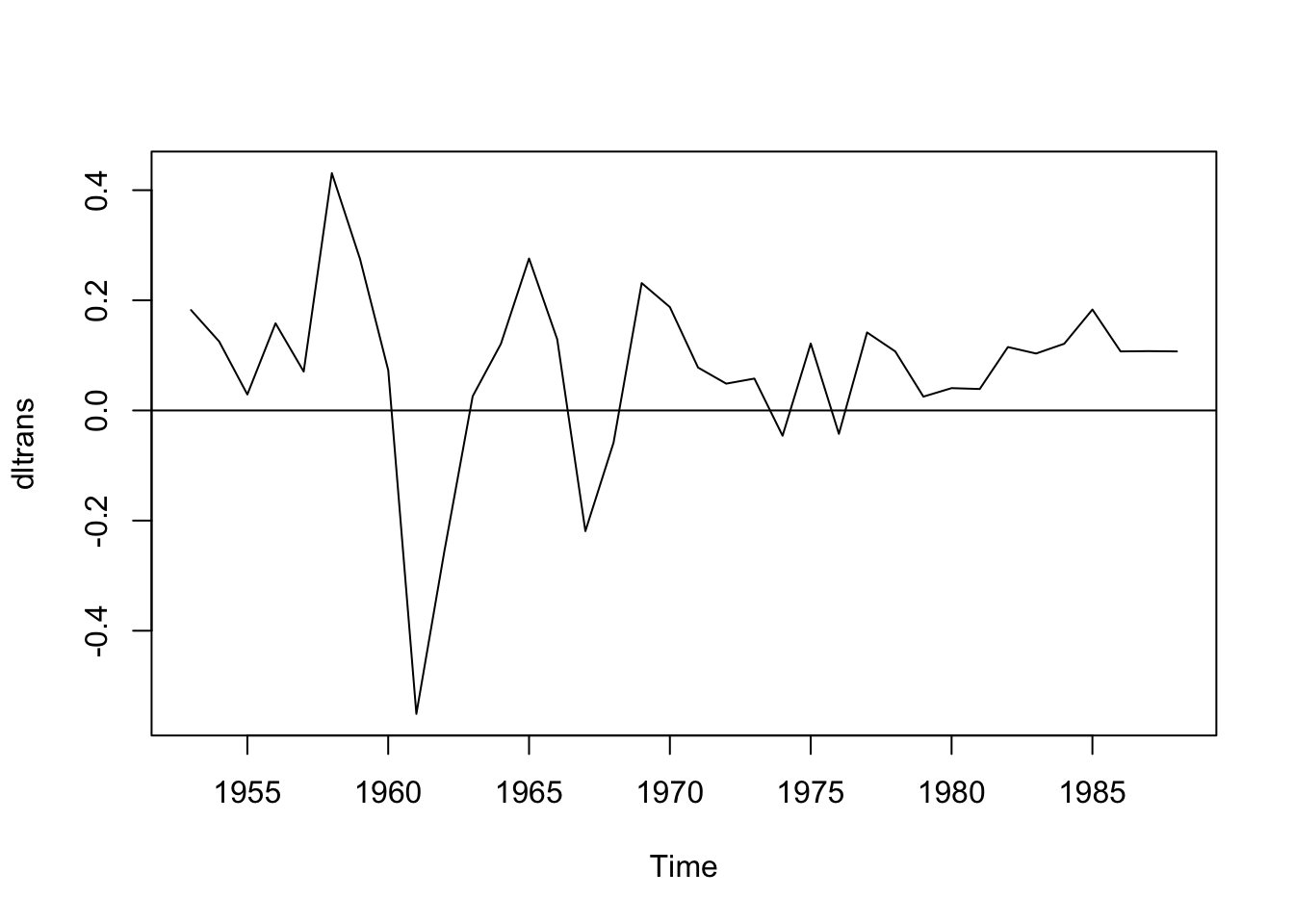
Asumamos estacionariedad (después haremos una prueba específica para verificar estacionariedad) y busquemos el mejor modelo.
Usaremos el acf y el pacf para evaluar si es \(MA\) o \(AR\).
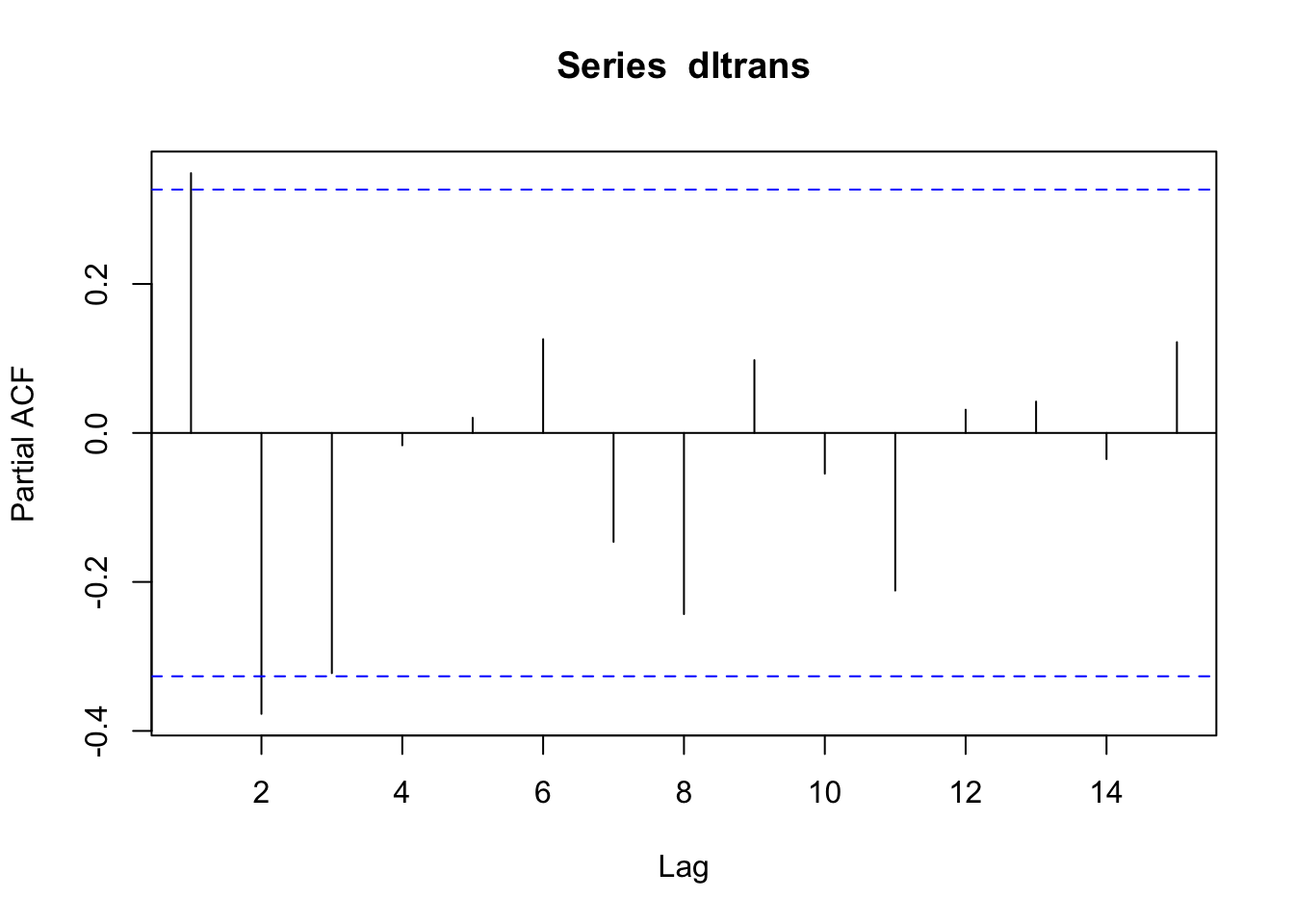
Ajustando según la gráfica, tendríamos un proceso \(MA(2)\)
¿Qué recomienda R?
## 0 1 2 3 4 5 6
## 8.140754 5.473906 1.951624 0.000000 1.990078 3.975236 5.400529
## 7 8 9 10 11 12 13
## 6.622877 6.428684 8.083145 9.975465 10.326488 12.291432 14.227677
## 14 15
## 16.183322 17.644775Según esta recomendación, estamos ante un proceso \(AR(3)\).
## [1] -32.75694Ajustemos el \(MA(2)\) y comparemos:
## [1] -28.01574Recuerda: Un menor AIC es mejor. ¿Con qué modelo te quedas?
Ajustemos un \(MA(3)\):
##
## Call:
## arima(x = dltrans, order = c(0, 0, 3))
##
## Coefficients:
## ma1 ma2 ma3 intercept
## 0.1763 -0.4596 -0.7167 0.0621
## s.e. 0.1883 0.1640 0.1925 0.0053
##
## sigma^2 estimated as 0.01625: log likelihood = 21.26, aic = -32.53## [1] -32.52547Este modelo es mejor que el \(MA(2)\), pero peor que \(AR(3)\).
Probemos algunas combinaciones:
## [1] -27.49033## [1] -32.45195## [1] -29.86264Nos quedamos con el \(AR(3)\). Revisemos los residuos:
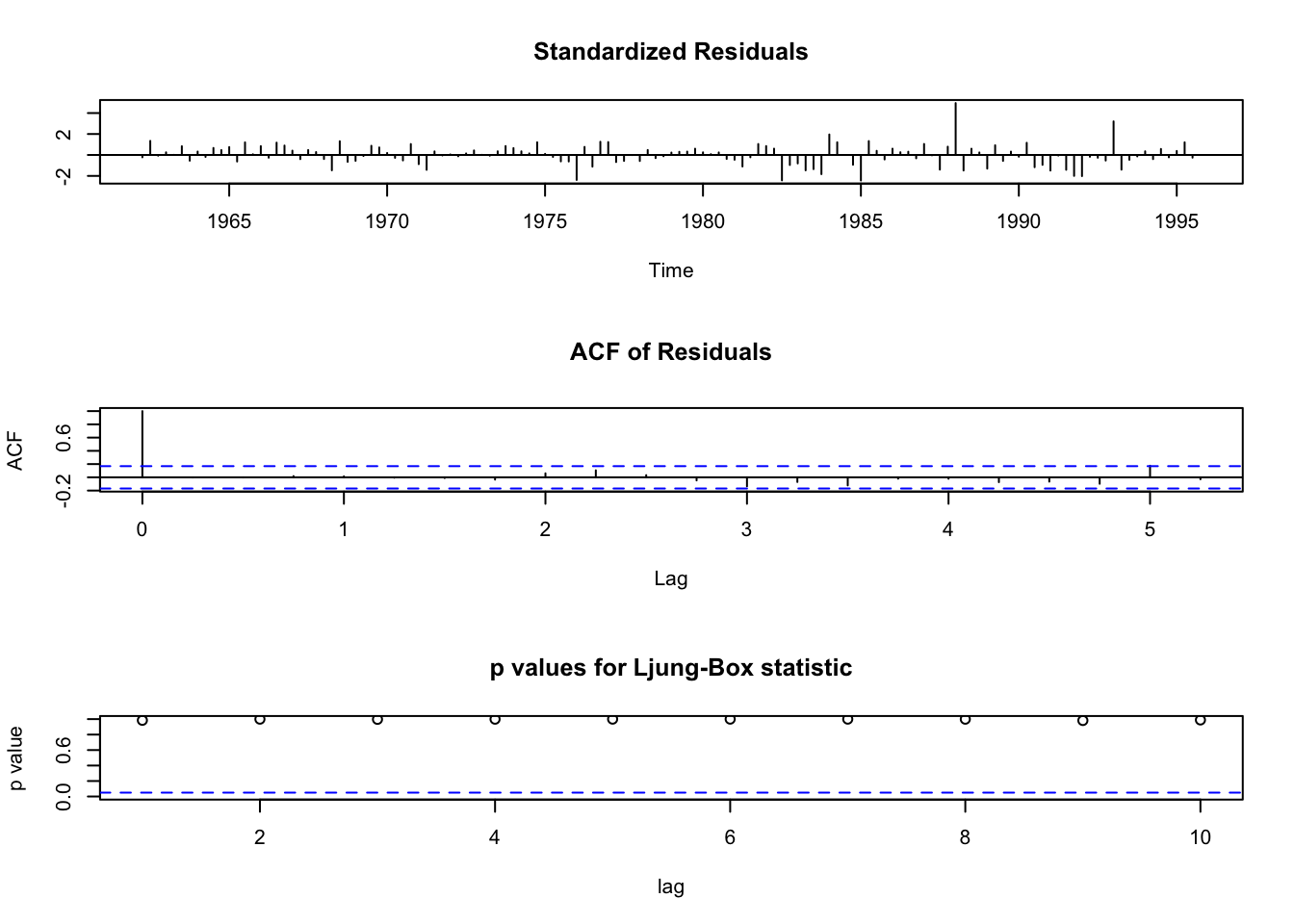
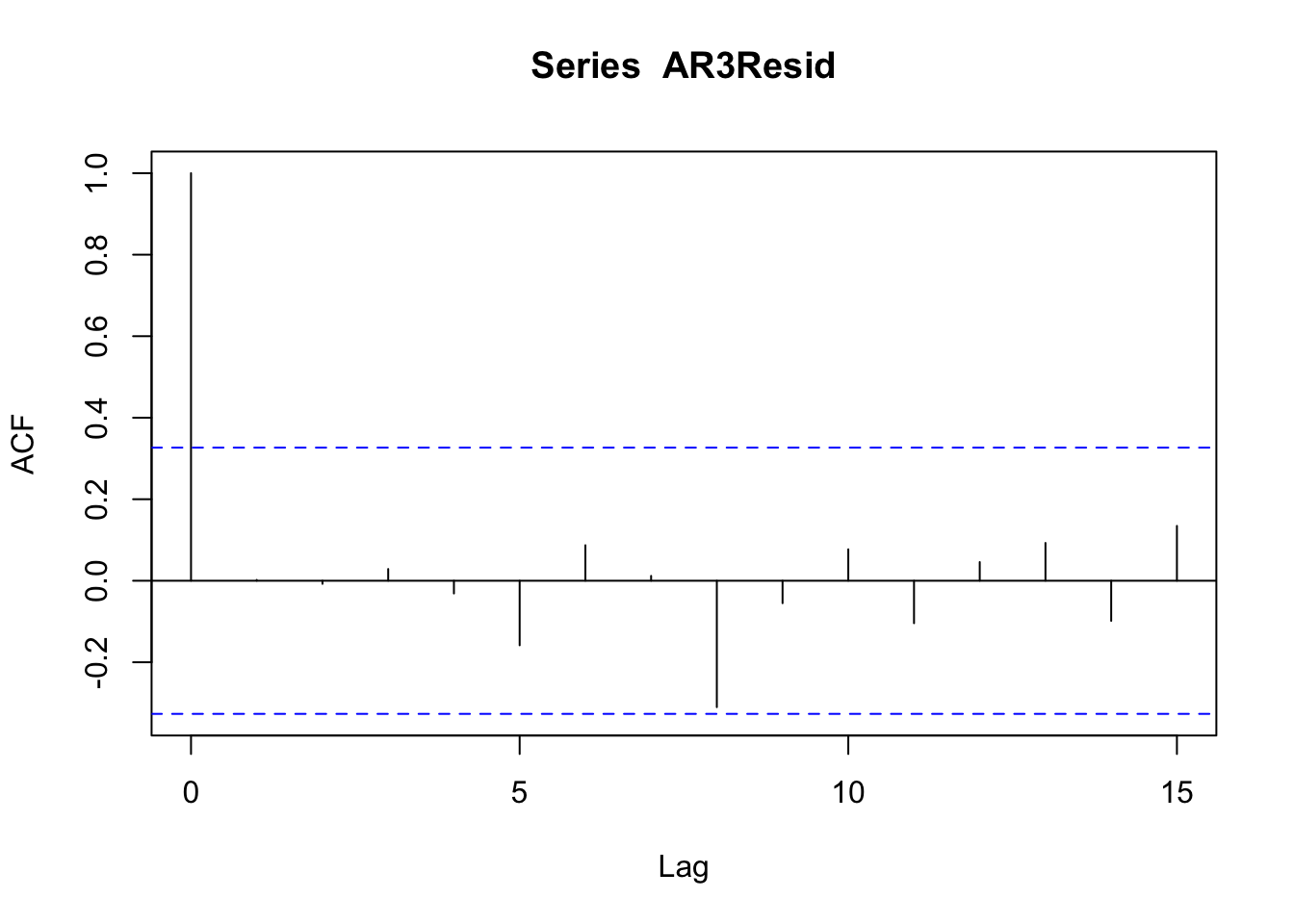
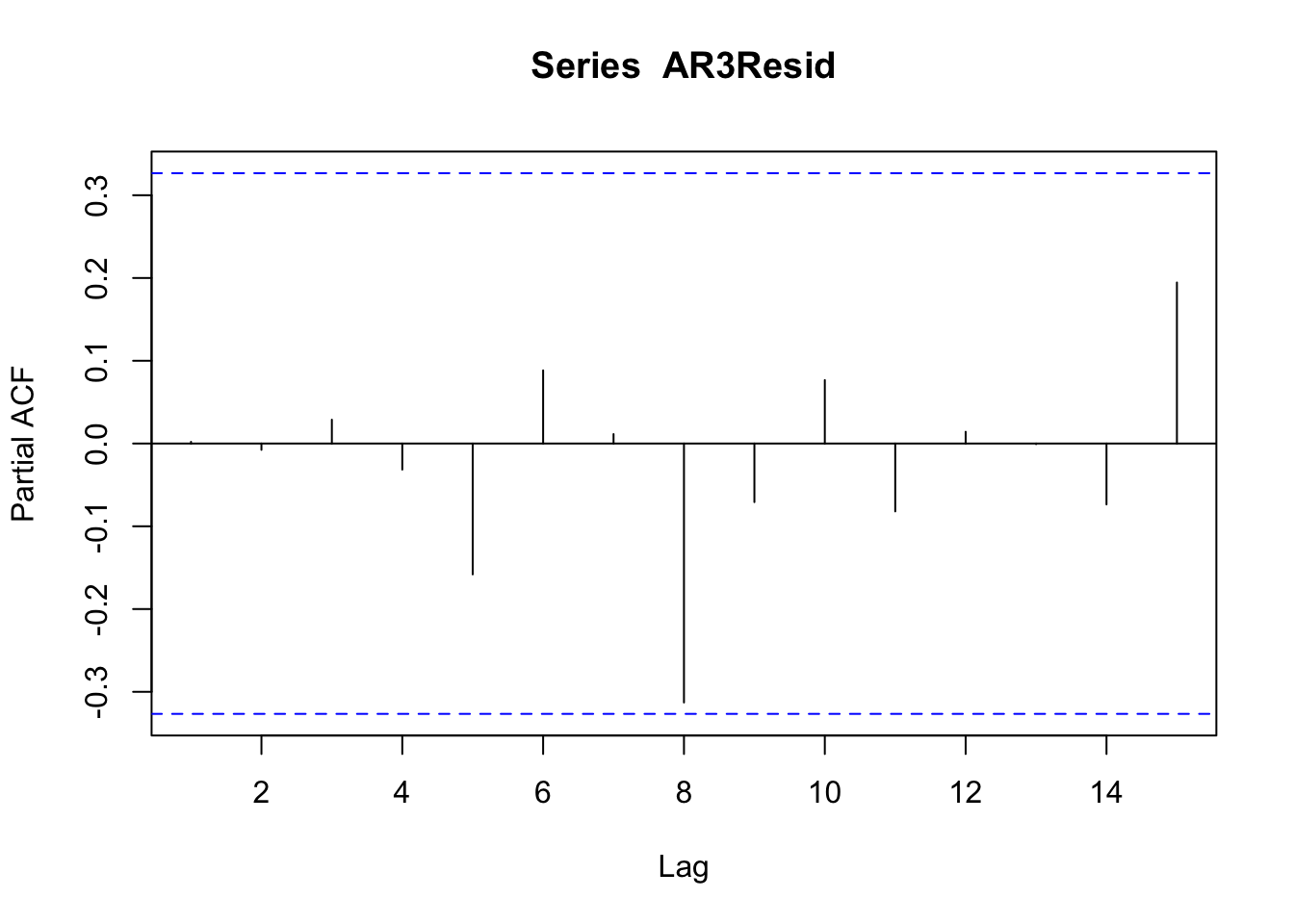
No hay autocorrelación, no hay autocorrelación parcial.
Veamos si se trata de un ruido blanco
##
## Box-Pierce test
##
## data: AR3Resid
## X-squared = 0.00015103, df = 1, p-value = 0.9902¿Es ruido blanco?
Realicemos una proyección a 5 años:
intervalos de confianza:
n <- (length(dltrans))
ic = pred5$pred + cbind(-2*pred5$se,2*pred5$se)
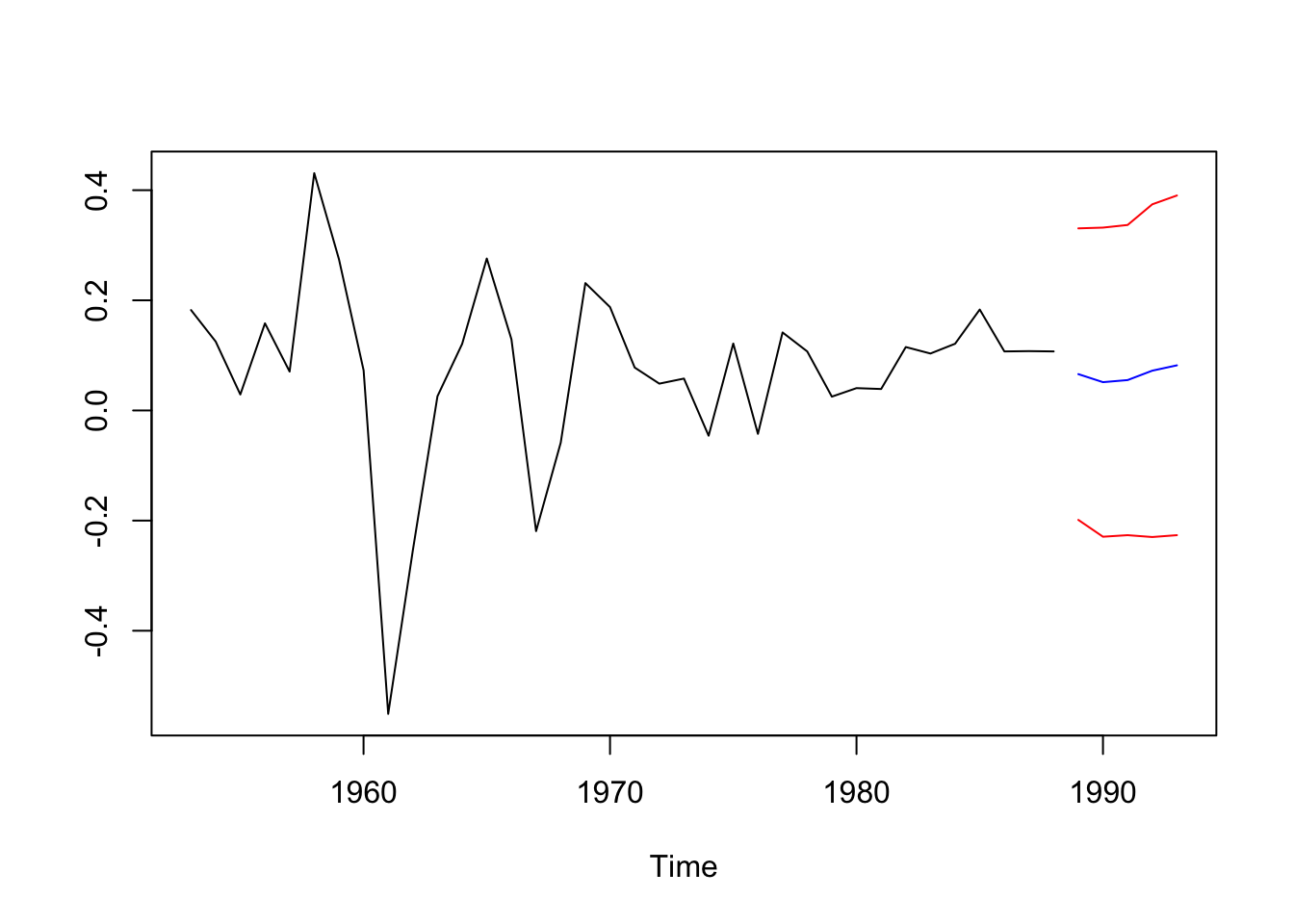
ts.plot(dltrans,pred5$pred,ic,
col=c("black","blue","red","red"))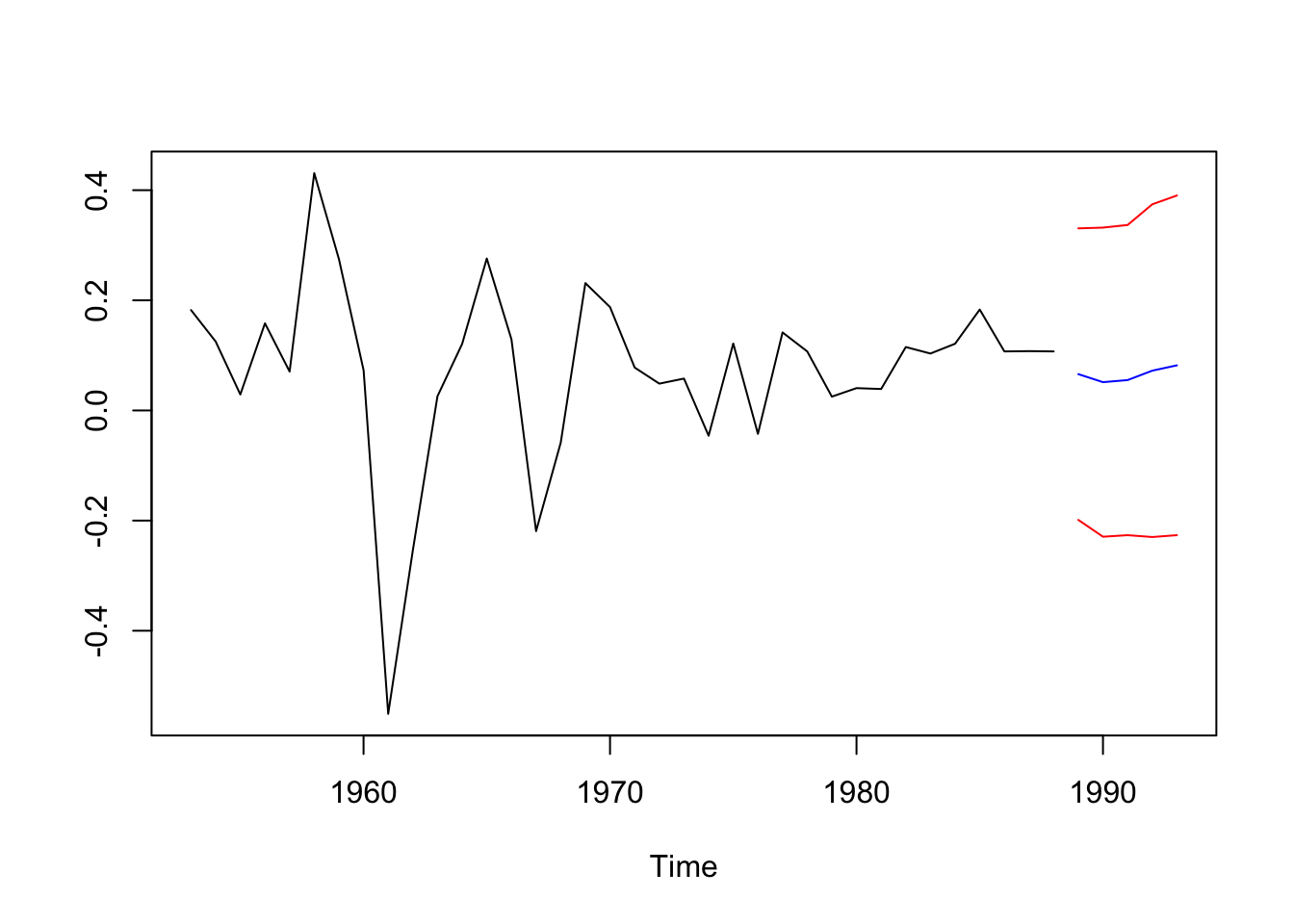
Los intervalos son grandes, podría ser por la cantidad de datos.
A continuación se usa el modelo estimado para realizar la predicción de una sub ventana de la serie analizada:
mp <- forecast::Arima(dltrans[1:(length(dltrans)-5)], model=modelo1)
# comparamos la prediccion con lo observado:
ss <- cbind(dltrans[(length(dltrans)-4):length(dltrans)],predict(mp,n.ahead = 5)$pred)
colnames(ss) <- c("Observado","Predicción")
ss## Time Series:
## Start = 32
## End = 36
## Frequency = 1
## Observado Predicción
## 32 0.1211453 0.08394945
## 33 0.1832397 0.05625961
## 34 0.1071942 0.05423808
## 35 0.1077345 0.06537286
## 36 0.1072015 0.07821377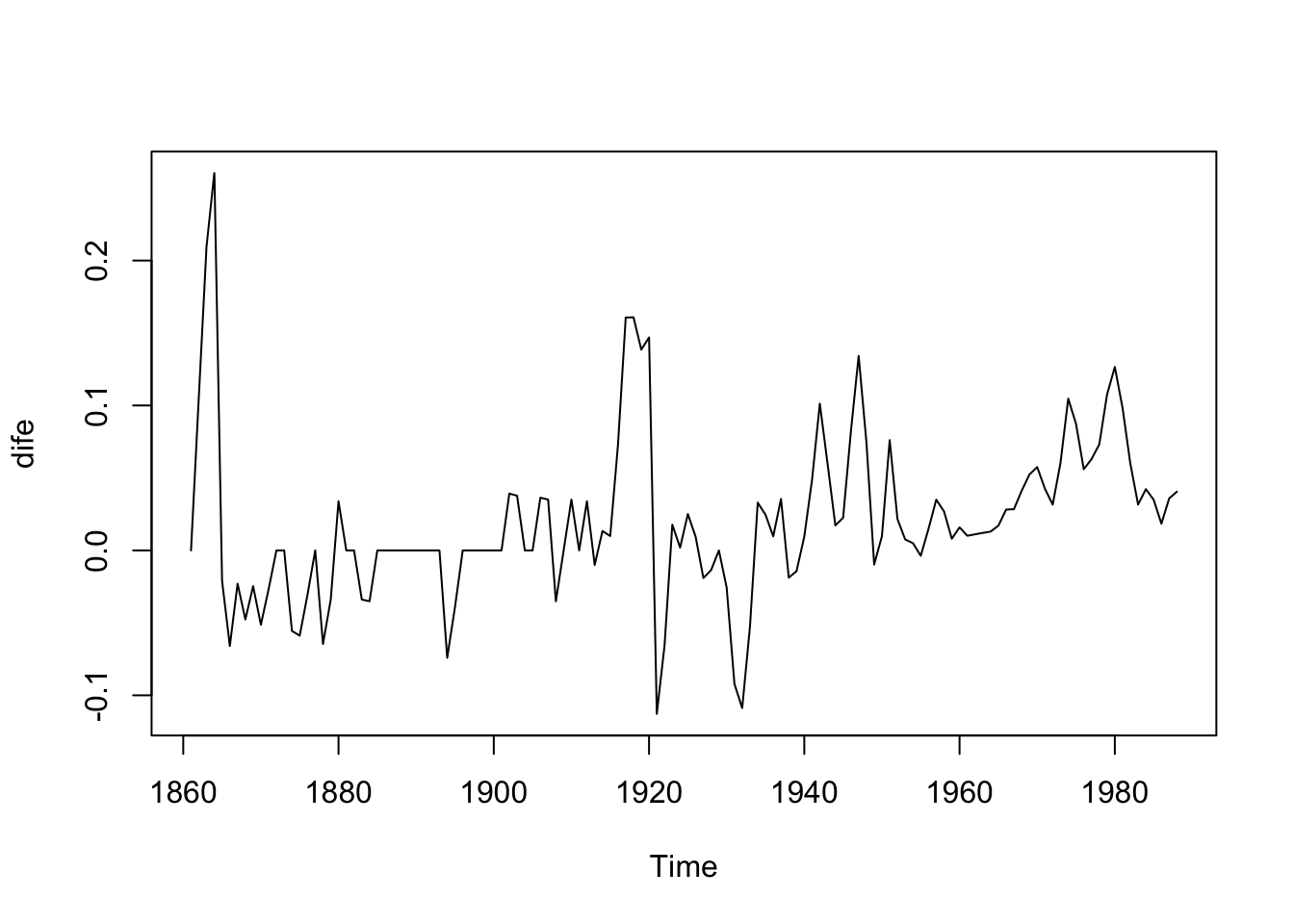
Ejemplo 2
Datos: Índice de desempleo trimestral en Canadá desde 1962.
uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/CAEMP.DAT"
datos <- read.csv(url(uu),sep=",",header=T)
emp.ts <- ts(datos,st=1962,fr=4)
plot(emp.ts)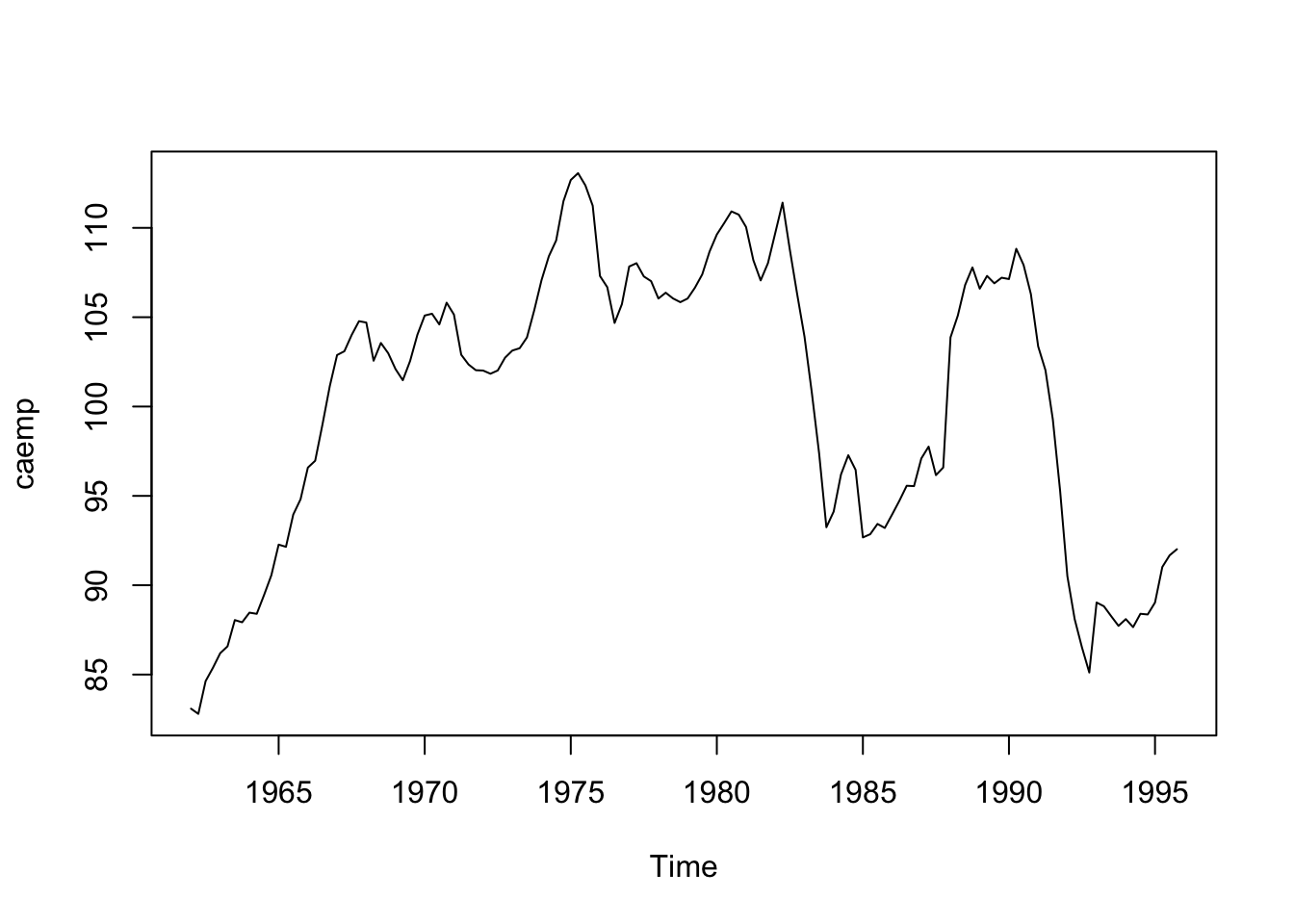
La serie no es estacionaria, probemos con sus diferencias:
Veamos sus autocorrelaciones y AIC:
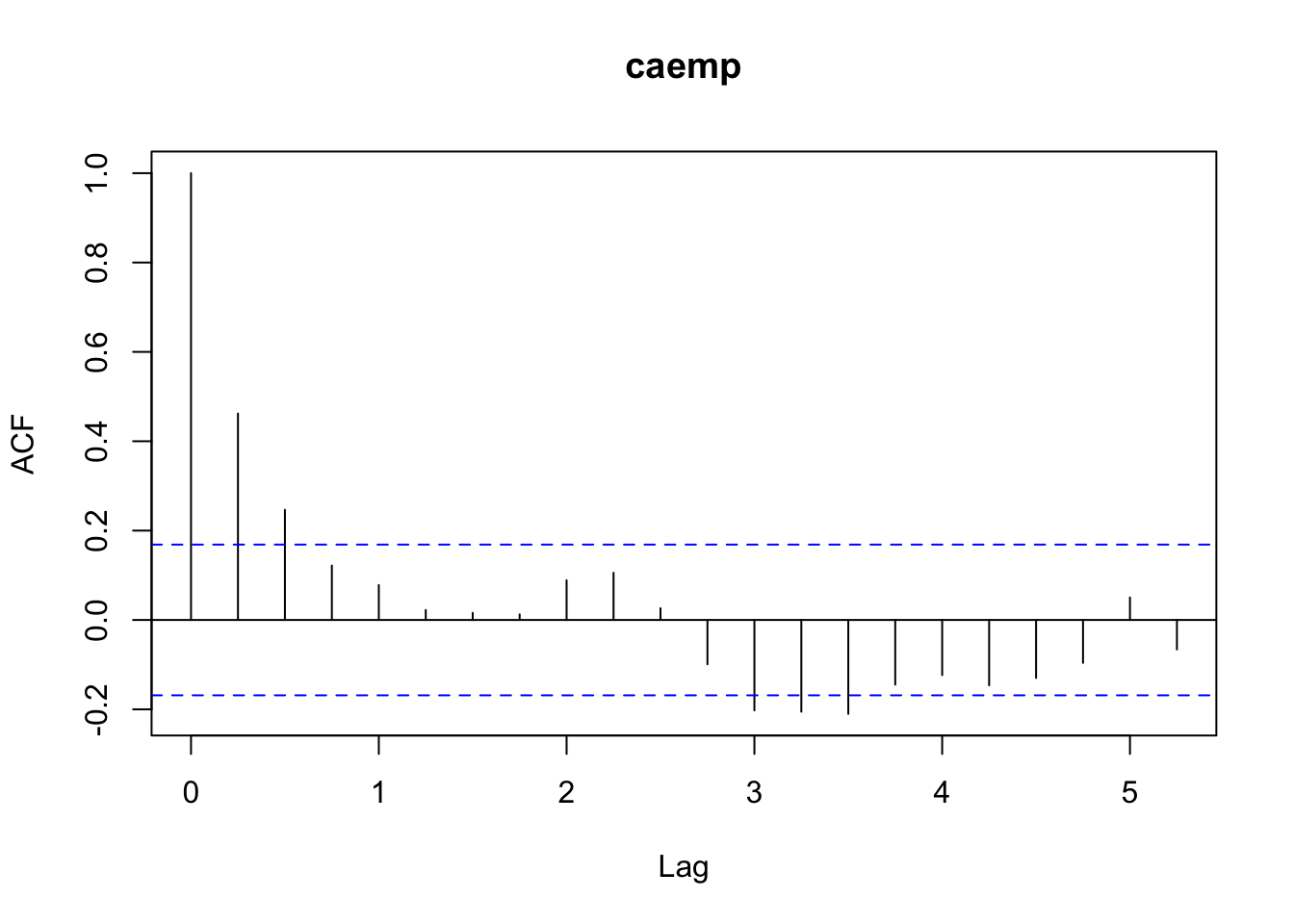
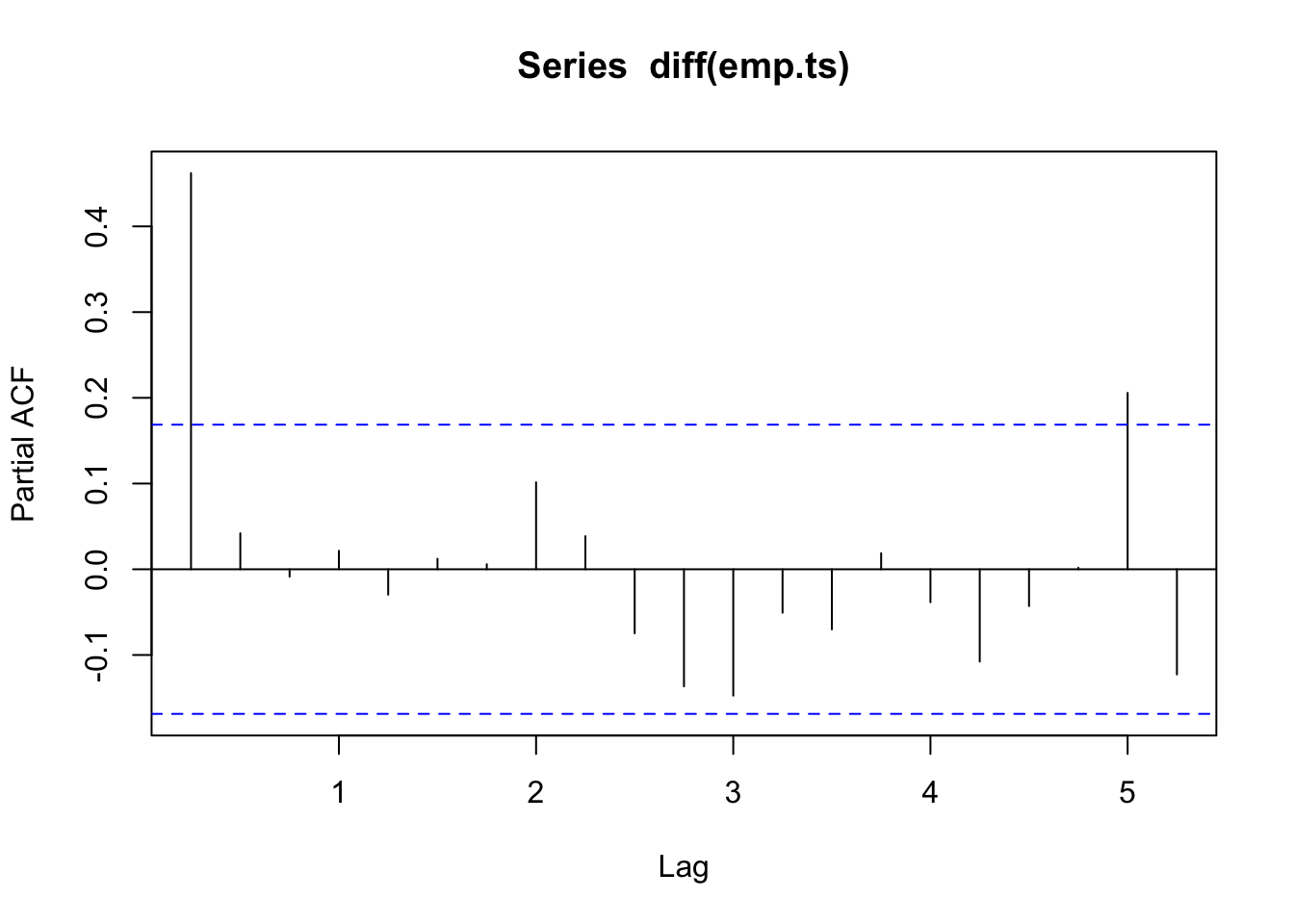
##
## Augmented Dickey-Fuller Test
##
## data: diff(emp.ts)
## Dickey-Fuller = -4.0972, Lag order = 5, p-value = 0.01
## alternative hypothesis: stationary## 0 1 2 3 4 5
## 347.493734 8.048336 0.000000 1.386627 2.471906 4.195572
## 6 7 8 9 10 11
## 6.015058 7.925583 9.390454 10.273560 10.989316 12.924608
## 12 13 14 15 16 17
## 14.892737 16.870041 18.803523 20.117383 22.114279 23.215372
## 18 19 20 21
## 25.038216 26.186319 28.019605 29.975609Las diferencias de la serie sí son estacionarias.
Comparemos modelos:
mode1 <- arima(diff(emp.ts),order=c(2,0,0))
mode2 <- arima(diff(emp.ts),order=c(0,0,4))
Box.test(mode1$resid,t="Ljung",lag=20)##
## Box-Ljung test
##
## data: mode1$resid
## X-squared = 17.165, df = 20, p-value = 0.6423##
## Box-Ljung test
##
## data: mode2$resid
## X-squared = 17.086, df = 20, p-value = 0.6474Ambos modelos muestran residuos independientes, sin autocorrelación. Analicemos los residuos con tsdiag:
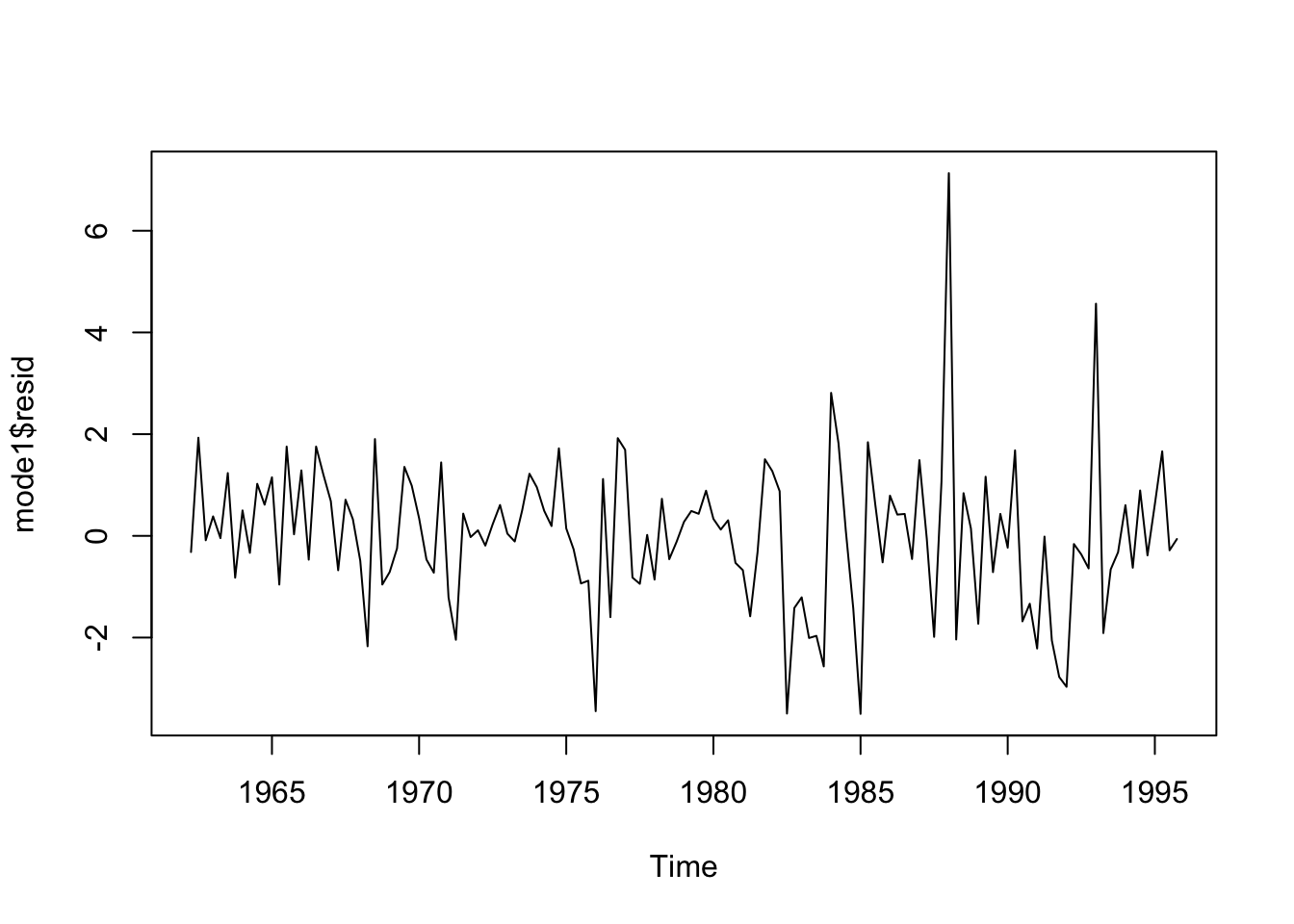
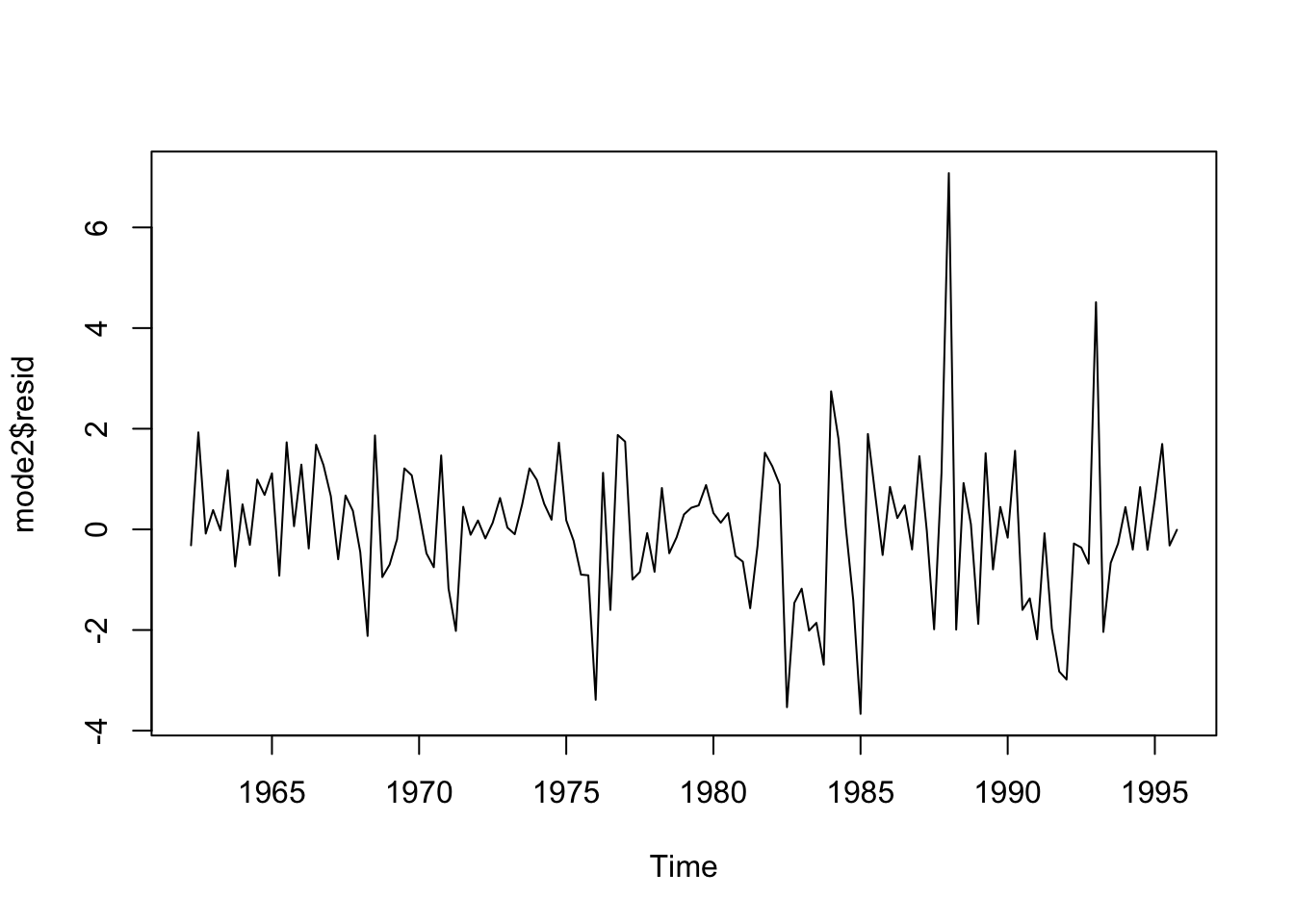
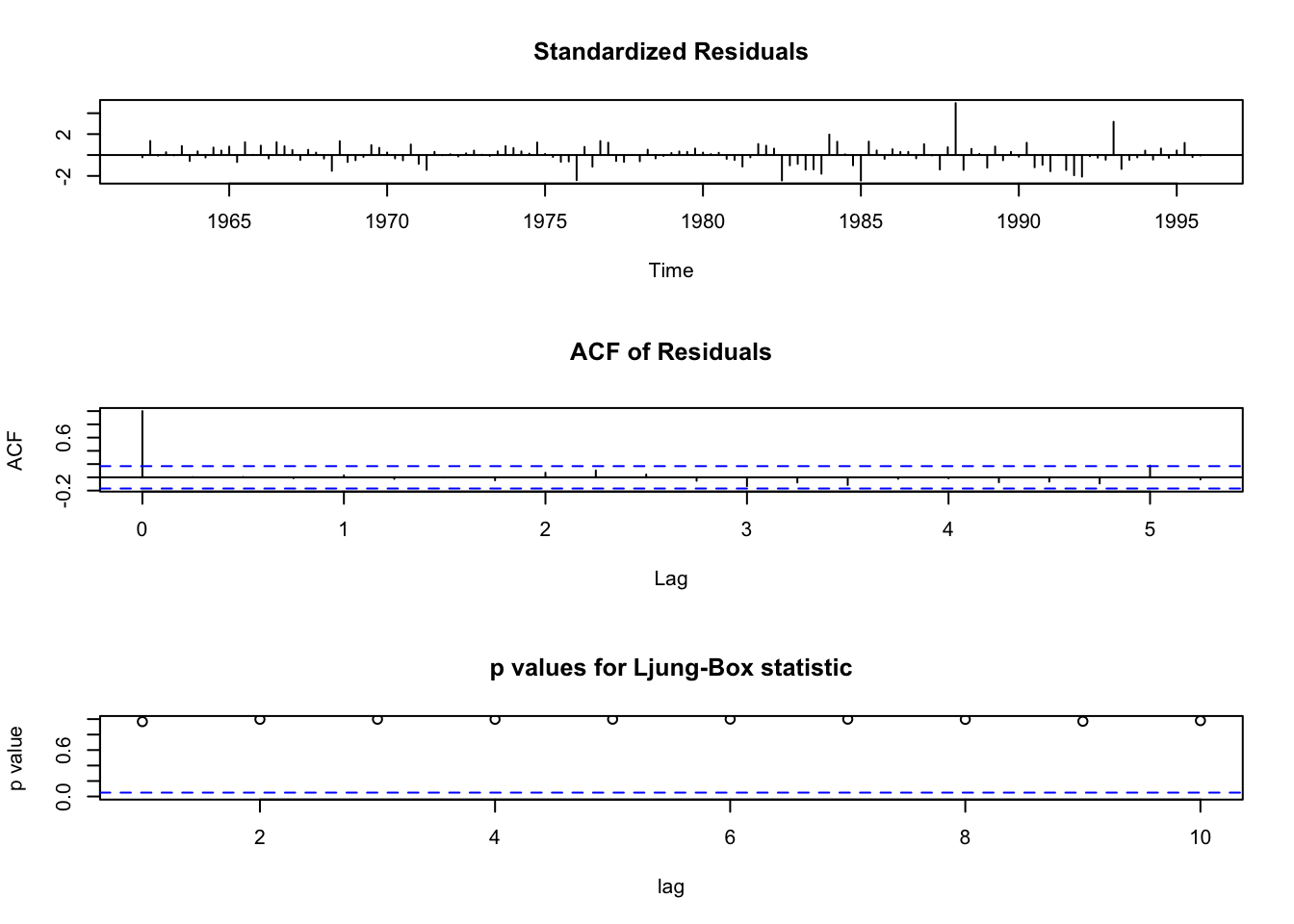
Probemos un modelo ARMA:
## [1] 490.9171##
## Call:
## arima(x = diff(emp.ts), order = c(2, 0, 1))
##
## Coefficients:
## ar1 ar2 ma1 intercept
## -0.3413 0.3950 0.7880 0.0715
## s.e. 0.5997 0.2552 0.6146 0.2319
##
## sigma^2 estimated as 2.06: log likelihood = -240.46, aic = 490.92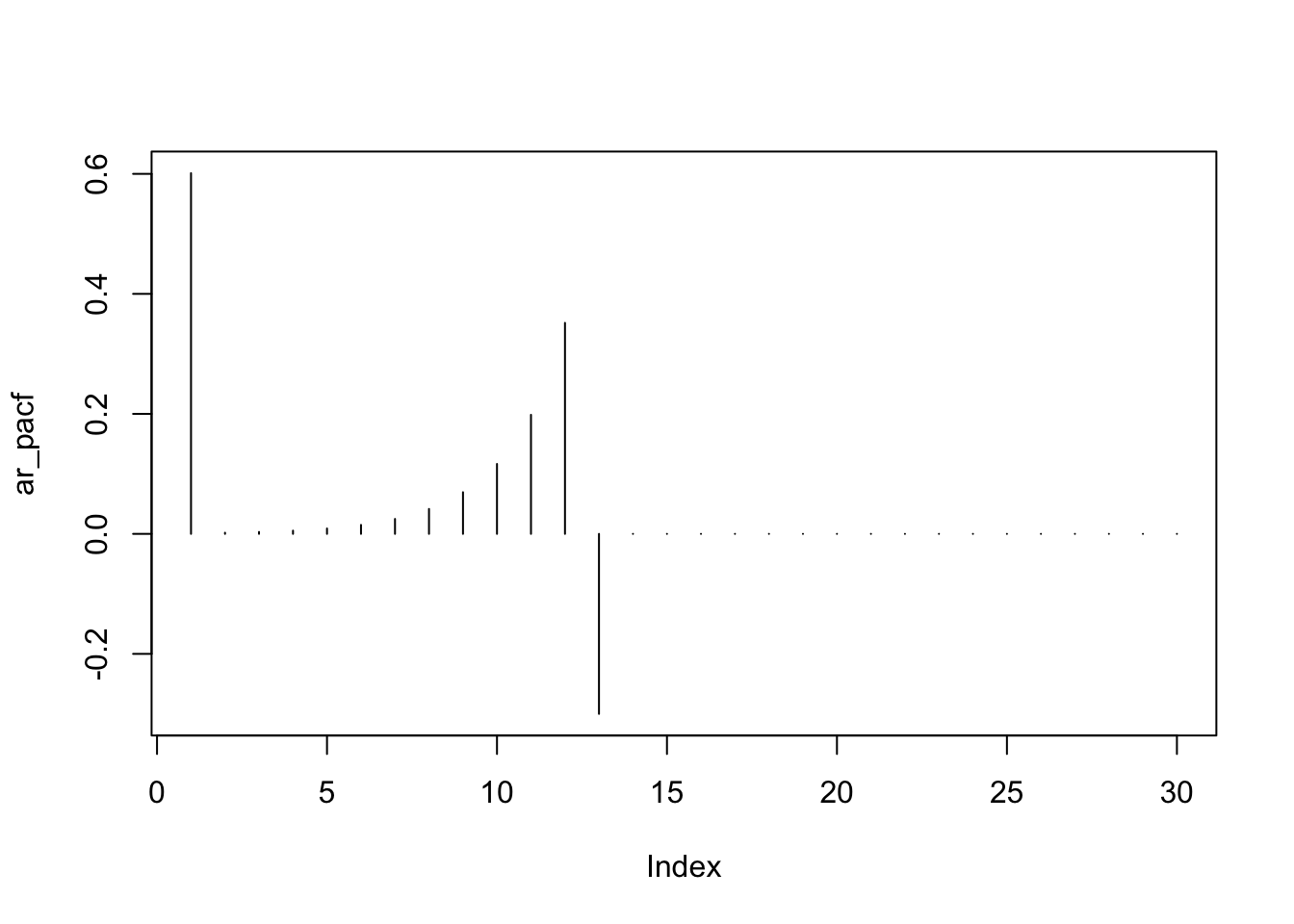
## ar1 ar2 ma1 intercept
## -0.34125663 0.39500196 0.78804111 0.07147069## ar1 ar2 ma1 intercept
## ar1 0.3595826088 -0.1408034638 -0.3653406111 -0.0007833386
## ar2 -0.1408034638 0.0651151395 0.1491243653 0.0005246816
## ma1 -0.3653406111 0.1491243653 0.3776951226 0.0008752775
## intercept -0.0007833386 0.0005246816 0.0008752775 0.0537596113z.ar <- polyroot(c(1,0.3413,-0.3950)) # Estacionario (Las raíces son |x|>1)
z.ma <- polyroot(c(1,0.7880)) # condicion de invertibilidad
Mod(z.ar) ## [1] 2.080750 1.216699## [1] 1.269036Se cumple que \(|z_j|>1\) por lo que el proceso ARMA es estacionario.
Ejemplo 3
Datos: 14 series macroeconómicas:
- indice de precios del consumidor (
cpi), - producción industrial (
ip), - PNB Nominal (
gnp.nom), - Velocidad (
vel), - Empleo (
emp), - Tasa de interés (
int.rate), - Sueldos nominales (
nom.wages), - Deflactor del PIB (
gnp.def), - Stock de dinero (
money.stock), - PNB real (
gnp.real), - Precios de stock (
stock.prices), - PNB per cápita (
gnp.capita), - Salario real (
real.wages), y - Desempleo (
unemp).
Tienen diferentes longitudes pero todas terminan en 1988. Trabajaremos con cpi
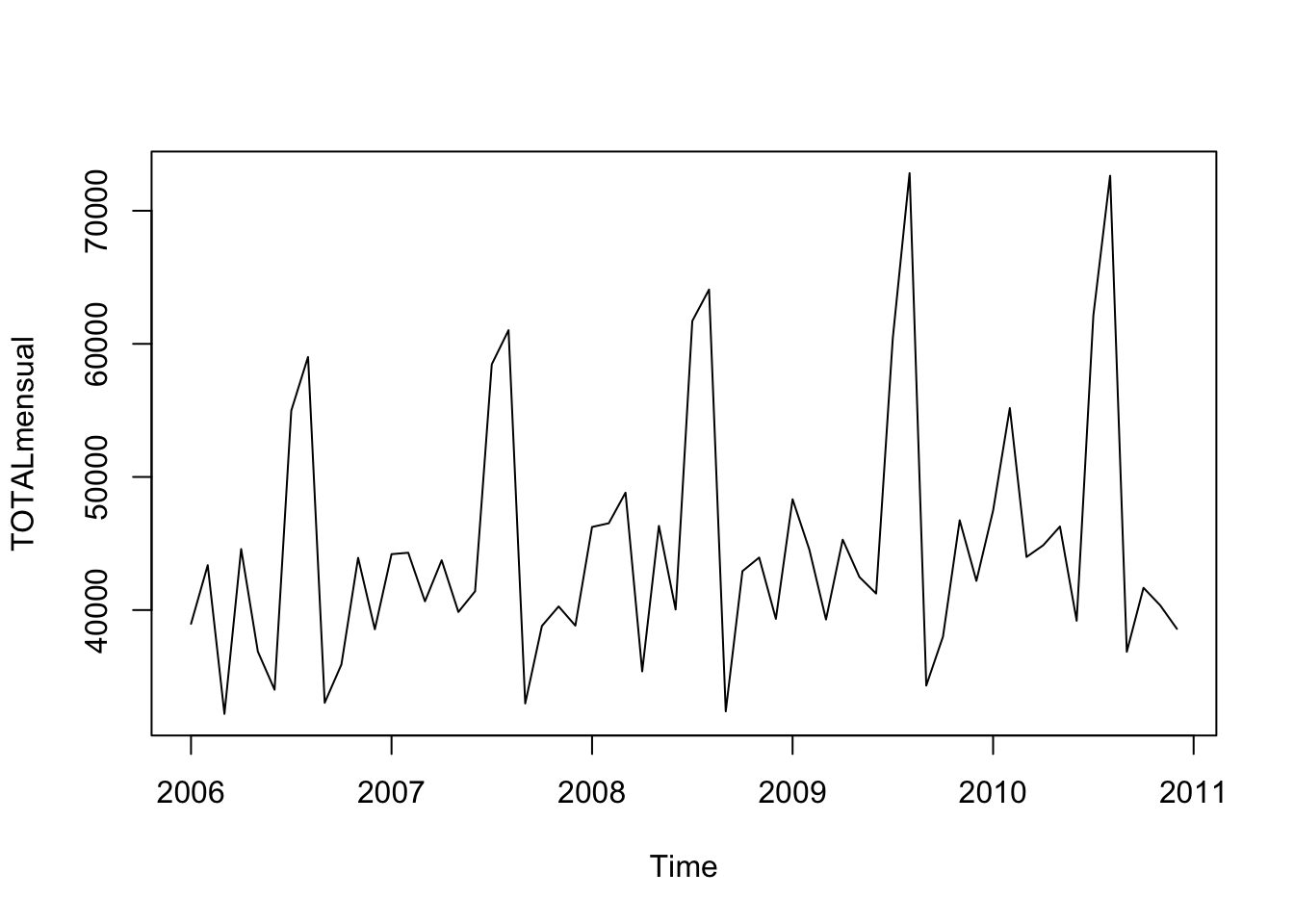
La serie parece no ser estacionaria ni lineal.
Veamos las raíces unitarias:
##
## Augmented Dickey-Fuller Test
##
## data: cpi
## Dickey-Fuller = -1.6131, Lag order = 5, p-value = 0.7374
## alternative hypothesis: stationary¿Es estacionaria?
Probemos con las diferencias
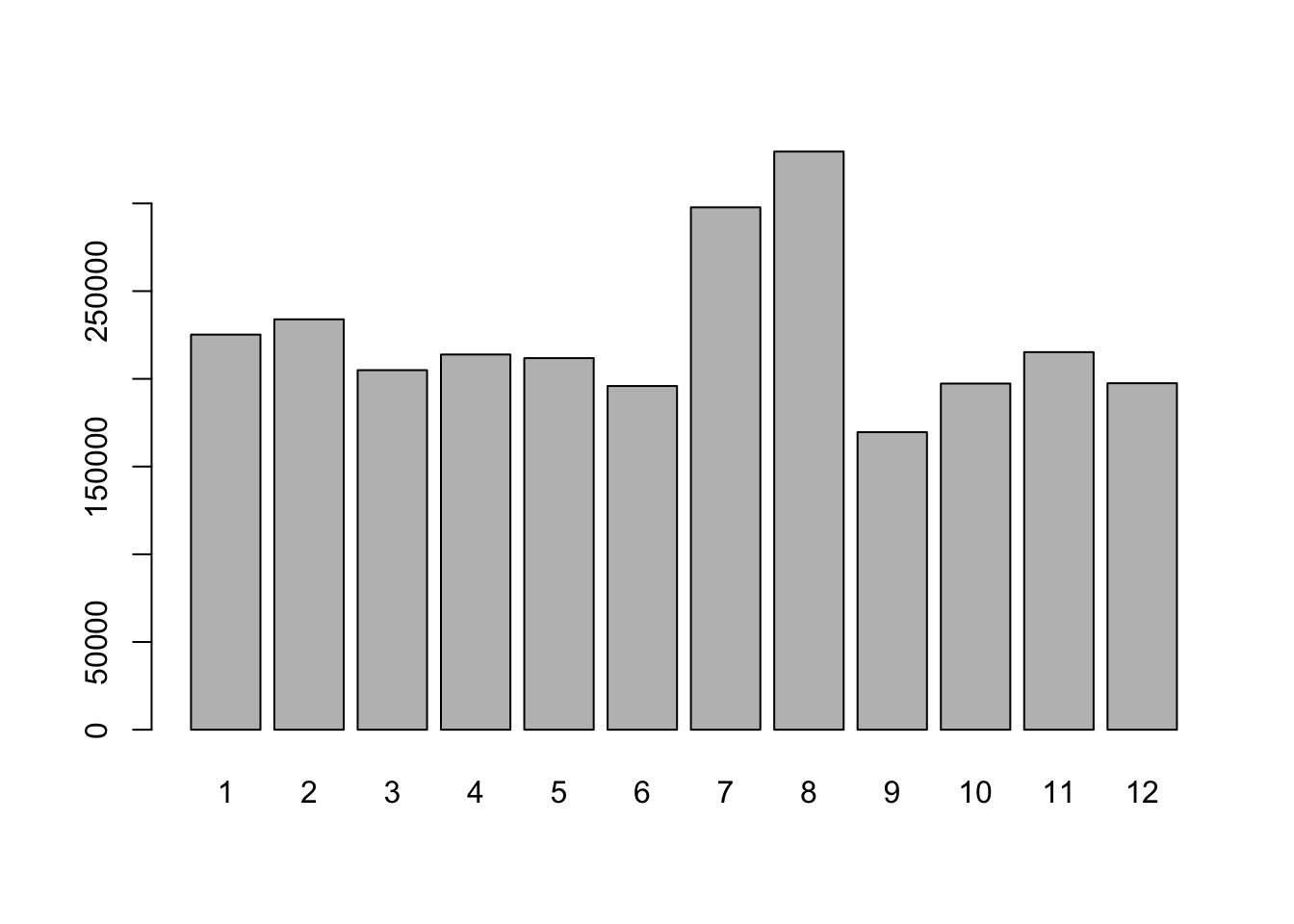
##
## Augmented Dickey-Fuller Test
##
## data: dife
## Dickey-Fuller = -4.4814, Lag order = 5, p-value = 0.01
## alternative hypothesis: stationaryLa serie en diferencias si es estacionaria. Veamos qué modelo sugiere R:
##
## Call:
## ar(x = dife)
##
## Coefficients:
## 1 2 3
## 0.8067 -0.3494 0.1412
##
## Order selected 3 sigma^2 estimated as 0.001875Hasta mi última revisión, no existe una función ma como ar, pero:
#### Busquemos el mejor MA #####
N=10
AICMA=matrix(0,ncol=1,nrow=N)
for (i in 1:N){
AICMA[i] = arima(diff(cpi),order=c(0,0,i))$aic
}
which.min(AICMA)## [1] 3## [,1]
## [1,] -432.7692
## [2,] -435.4208
## [3,] -436.1922
## [4,] -434.4117
## [5,] -432.4410
## [6,] -432.1389
## [7,] -432.3631
## [8,] -430.4594
## [9,] -428.4612
## [10,] -429.8065Se sugiere un \(MA(3)\).
Evaluemos el modelo \(MA\) con una diferencia:
##
## Call:
## arima(x = cpi, order = c(0, 1, 3))
##
## Coefficients:
## ma1 ma2 ma3
## 0.8782 0.3754 0.1898
## s.e. 0.0876 0.1172 0.0890
##
## sigma^2 estimated as 0.00185: log likelihood = 220.67, aic = -433.34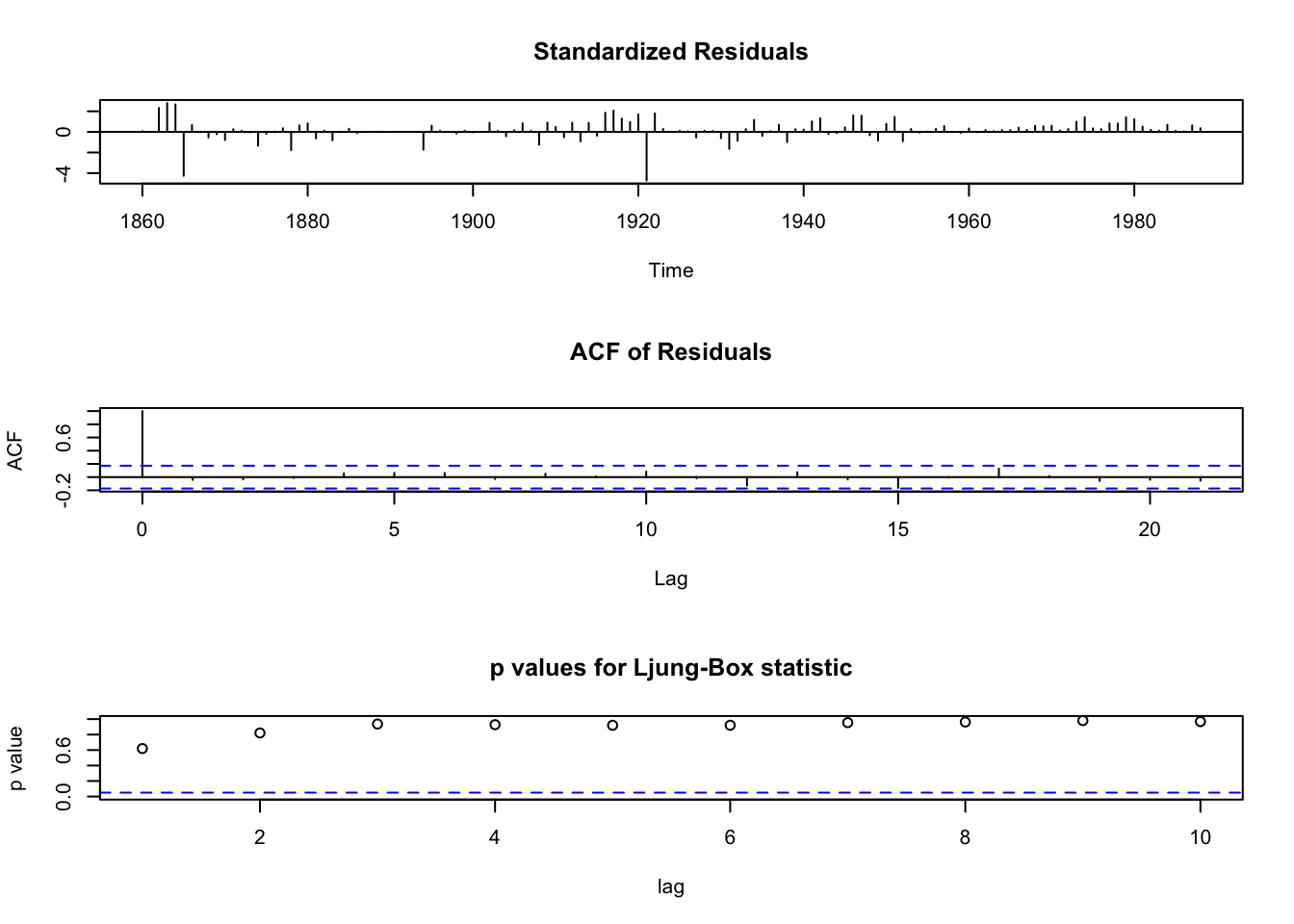
Para identificar el mejor ARMA se puede usar:
3.5 Procesos SARIMA
Esta sección fue tomada de “Penn State University Applied Time Series Analysis” (2021)
La estacionalidad en una serie de tiempo es un patrón regular de cambios que se repite durante \(S\) períodos de tiempo, donde \(S\) define el número de períodos de tiempo hasta que el patrón se repite nuevamente.
Por ejemplo, existe una estacionalidad en los datos mensuales para los cuales los valores altos tienden a ocurrir siempre en algunos meses en particular y los valores bajos tienden a ocurrir siempre en otros meses en particular. En este caso, \(S = 12\) (meses por año) es el lapso del comportamiento estacional periódico. Para los datos trimestrales, \(S = 4\) períodos de tiempo por año.
En un modelo \(ARIMA\) estacional o \(SARIMA\), los términos \(AR\) y \(MA\) estacionales predicen utilizando valores de datos y errores en momentos con rezagos que son múltiplos de \(S\) (el intervalo de la estacionalidad).
Con datos mensuales (y \(S = 12\)), se utilizaría un modelo autorregresivo de primer orden estacional para predecir
Por ejemplo, si vendiéramos ventiladores de refrigeración, podríamos predecir las ventas de agosto utilizando las ventas de agosto pasado. (Esta relación de predicción utilizando los datos del año pasado se mantendría para cualquier mes del año).
Un modelo autorregresivo estacional de segundo orden utilizaría \(x_{t-12}\) y \(x_{t-24}\) para predecir \(x_t\). Aquí predeciríamos los valores de agosto a partir de los dos últimos agosto.
Un modelo \(MA(1)\) de primer orden estacional (con \(S=12\)) usaría \(w_{t-12}\) como predictor. Un modelo \(MA(2)\) de segundo orden estacional usaría \(w_{t-12}\) y \(w_{t-24}\).
3.5.1 Diferenciación
Casi por definición, puede ser necesario examinar datos diferenciados cuando tenemos estacionalidad. La estacionalidad generalmente hace que la serie no sea estacionaria porque los valores promedio en algunos momentos particulares dentro del intervalo estacional (meses, por ejemplo) pueden ser diferentes de los valores promedio en otros momentos. Por ejemplo, nuestras ventas de ventiladores de refrigeración siempre serán más altas en los meses de verano.
3.5.1.1 Diferenciación estacional
La diferenciación estacional se define como una diferencia entre un valor y un valor con rezago que es un múltiplo de \(S\).
- Con \(S = 12\), que puede ocurrir con datos mensuales, una diferencia estacional es \((1-B^{12})x_t = x_t-x_{t-12}\).
Las diferencias (con respecto al año anterior) pueden ser aproximadamente las mismas para cada mes del año, lo que nos da una serie estacionaria.
- Con \(S = 4\), que puede ocurrir con datos trimestrales, una diferencia estacional es \((1-B^{4})x_t = x_t-x_{t-4}\).
3.5.1.2 Diferenciación no estacional
Si la tendencia está presente en los datos, es posible que también necesitemos una diferenciación no estacional. A menudo (no siempre) una primera diferencia (no estacional) desviará la tendencia de los datos. Es decir, usamos \((1-B)x_t = x_t-x_{t-1}\) en presencia de tendencia.
3.5.1.3 Diferenciación para tendencia y estacionalidad
Cuando están presentes tanto la tendencia como la estacionalidad, es posible que debamos aplicar una primera diferencia no estacional y una diferencia estacional.
Es decir, es posible que debamos examinar el ACF y el PACF de \((1-B^{12})(1-B)x_t=(x_t-x_{t-1})-(x_{t-12}-x_{t-13})\).
Eliminar la tendencia no significa que hayamos eliminado la dependencia. Es posible que hayamos eliminado la media, \(\mu_t\), parte de la cual puede incluir un componente periódico. De alguna manera, estamos dividiendo la dependencia en cosas recientes que han sucedido y cosas a largo plazo que han sucedido.
El comportamiento no estacional seguirá siendo importante …
Con datos estacionales, es probable que los componentes no estacionales a corto plazo sigan contribuyendo al modelo. En las ventas mensuales de ventiladores de refrigeración mencionadas anteriormente, por ejemplo, las ventas en el mes anterior o dos, junto con las ventas del mismo mes hace un año, pueden ayudar a predecir las ventas de este mes.
Tendremos que observar el comportamiento de \(ACF\) y \(PACF\) durante los primeros rezagos (menos de \(S\)) para evaluar qué términos no estacionales podrían funcionar en el modelo.
3.5.2 El modelo
El modelo ARIMA estacional (\(SARIMA\)) incorpora factores estacionales y no estacionales en un modelo multiplicativo. Una notación abreviada para el modelo es
\(ARIMA(p,d,q)\times (P,D,Q)_s\)
con
- \(p=\texttt{orden AR no estacional}\),
- \(d=\texttt{orden de diferencias no estacional}\),
- \(q=\texttt{orden MA no estacional}\),
- \(P=\texttt{orden AR estacional}\),
- \(D=\texttt{orden de diferencia estacional}\),
- \(Q=\texttt{orden MA estacional}\) y
- \(S=\texttt{ventana de tiempo del patrón estacional}\).
Sin operaciones de diferenciación, el modelo podría escribirse más formalmente como
\[ \Phi(B^s)\phi(B)(x_t-\mu) ) = \Theta(B^s)\theta(B)w_t \]
Los componentes no estacionales son:
- AR: \(\phi(B)=1-\phi_1B-\ldots-\phi_pB^p\).
- MA: \(\theta(B) = 1+ \theta_1B+ \ldots + \theta_qB^q\).
Los componentes estacionales son:
- AR estacional: \(\Phi(B^S) = 1- \Phi_1 B^S - \ldots - \Phi_PB^{PS}\).
- MA estacional: \(\Theta(B^S) = 1 + \Theta_1 B^S + \ldots + \Theta_Q B^{QS}\).
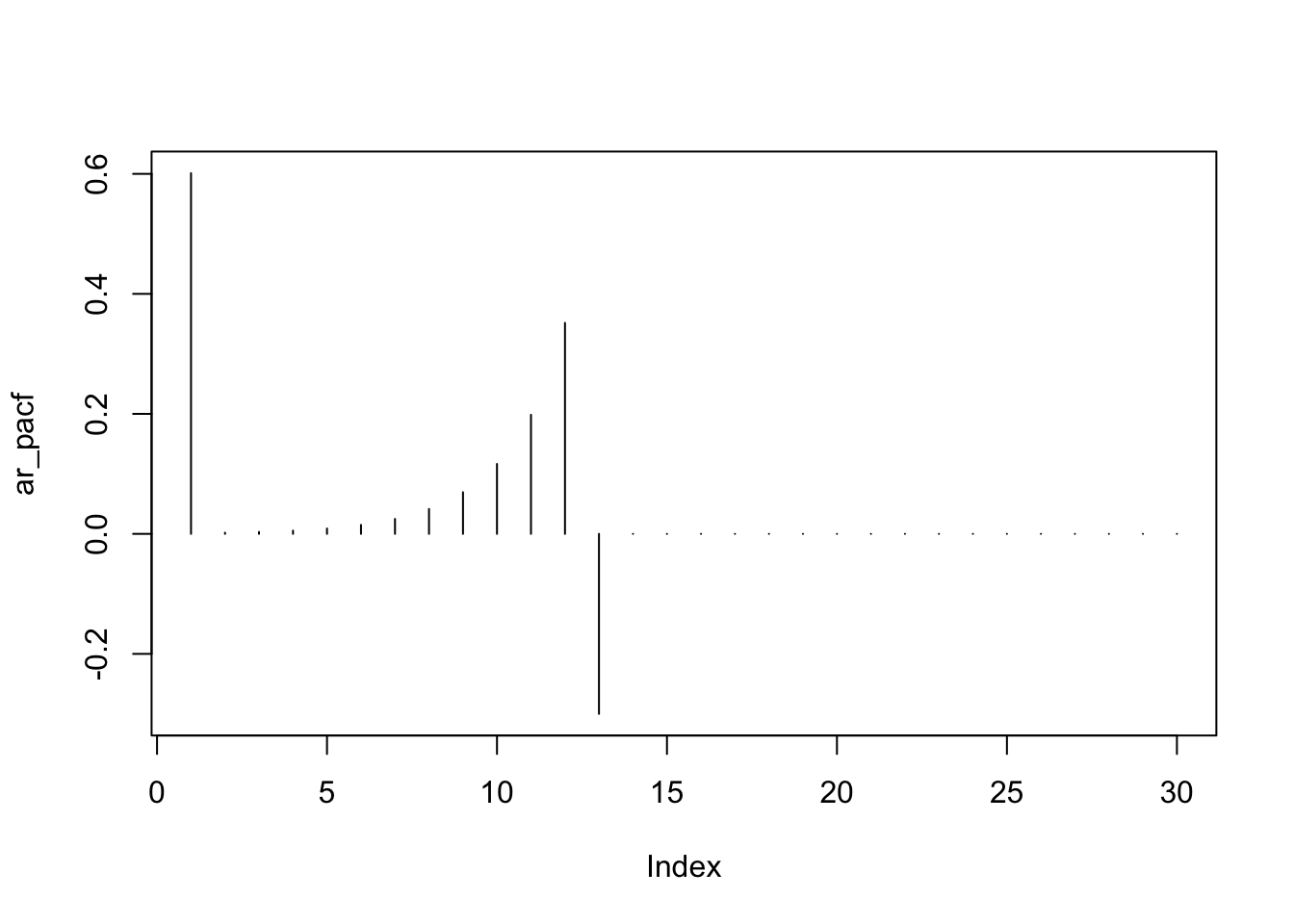
Ejemplo \(ARIMA(1,0,0)\times (1,0,0)_{12}\)
El modelo incluye un término \(AR(1)\) no estacional, un \(AR(1)\) estacional, sin diferenciación, sin términos \(MA\) y un periodo estacional \(S=12\).
El modelo es
\[ (1-\phi_1B)(1-\Phi_1B^{12})(x_t-\mu) = w_t \] Sea \(z_t = x_t -\mu\) por simplicidad, multiplicamos los dos componentes \(AR\) y despejamos \(z_t\) obtenemos:
\[ z_{t} = \phi_1 z_{t-1} + \Phi_1 z_{t-12} + \left( - \phi_1\Phi_1 \right) z_{t-13} + w_t \]
Este es un modelo \(AR\) con predictores en los rezagos 1, 12 y 13.
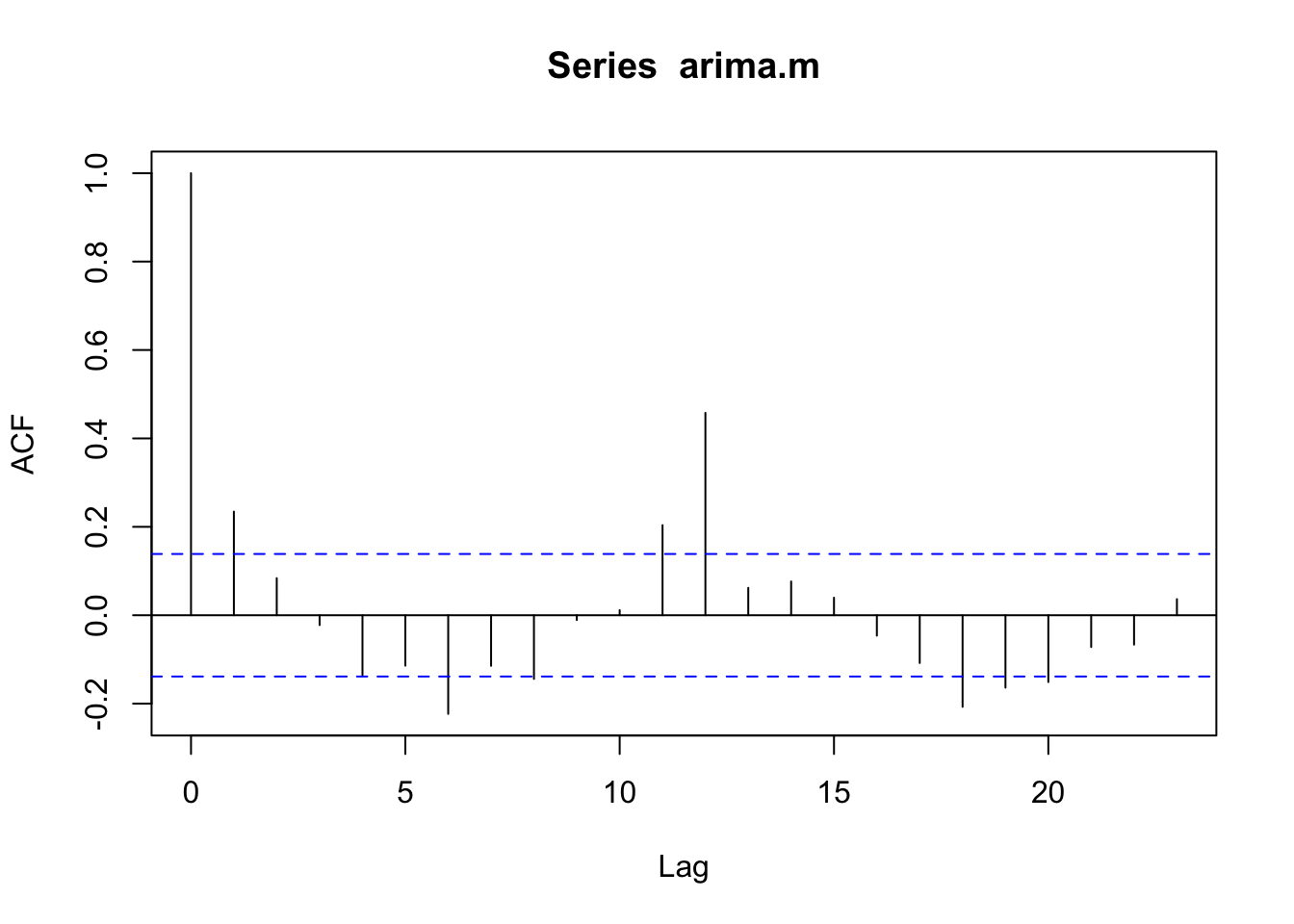
Ejemplo \(ARIMA(0,0,1)\times (0,0,1)_{12}\)
El modelo incluye términos \(MA (1)\) estacionales y no estacionales, sin diferenciación ni términos \(AR\), y el período estacional es \(S = 12\). Por lo tanto, este modelo tiene términos MA en los rezagos 1, 12 y 13. También hay autocorrelación en el rezago 11.
Ejemplo con datos reales
Paso 1: exploración gráfica de los datos
Tomemos las visitas mensuales a parques nacionales en Ecuador desde enero 2006 hasta diciembre 2010.
uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/estadisticas%20Turismo.csv"
datos <- read.csv(url(uu),header=T,dec=".",sep=";")
# Visitas a Areas Naturales Protegidas
# Sumar por mes y año
mensual <- aggregate(datos$TOTALMENSUAL,by=list(datos$mesnum,datos$Year),FUN="sum") # Los datos sin mes es el total de ese anio
TOTALmensual <- ts(mensual[,3],start=c(2006,1),freq=12)
plot(TOTALmensual)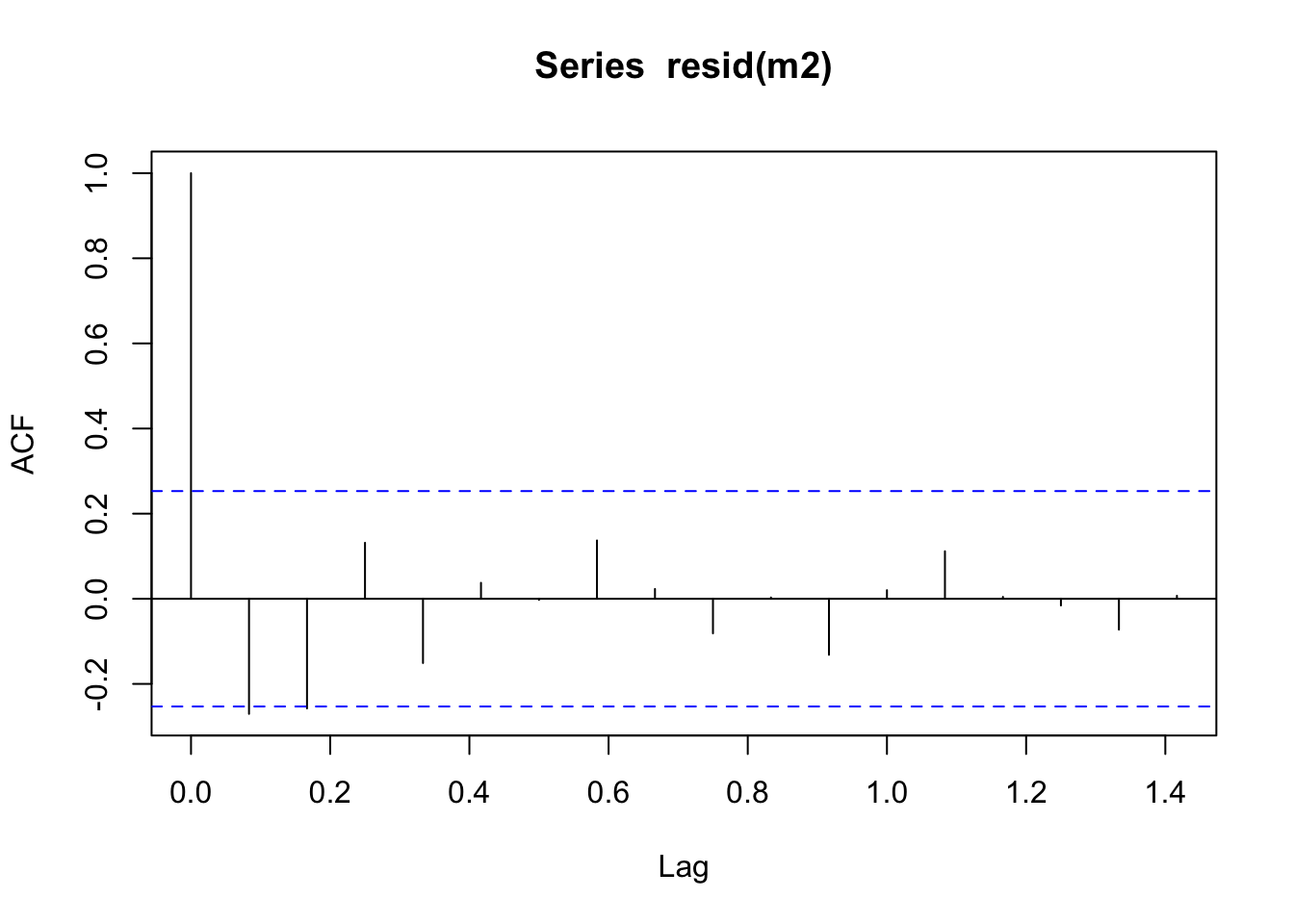
En ocasiones el componente estacional se puede observar directamente de la serie como en este caso. De lo contrario, podemos apoyarnos en una descomposición de la serie o mediante el gráfico de la autocorrelación (como sucedió en la serie del índice de desempleo en Canadá).
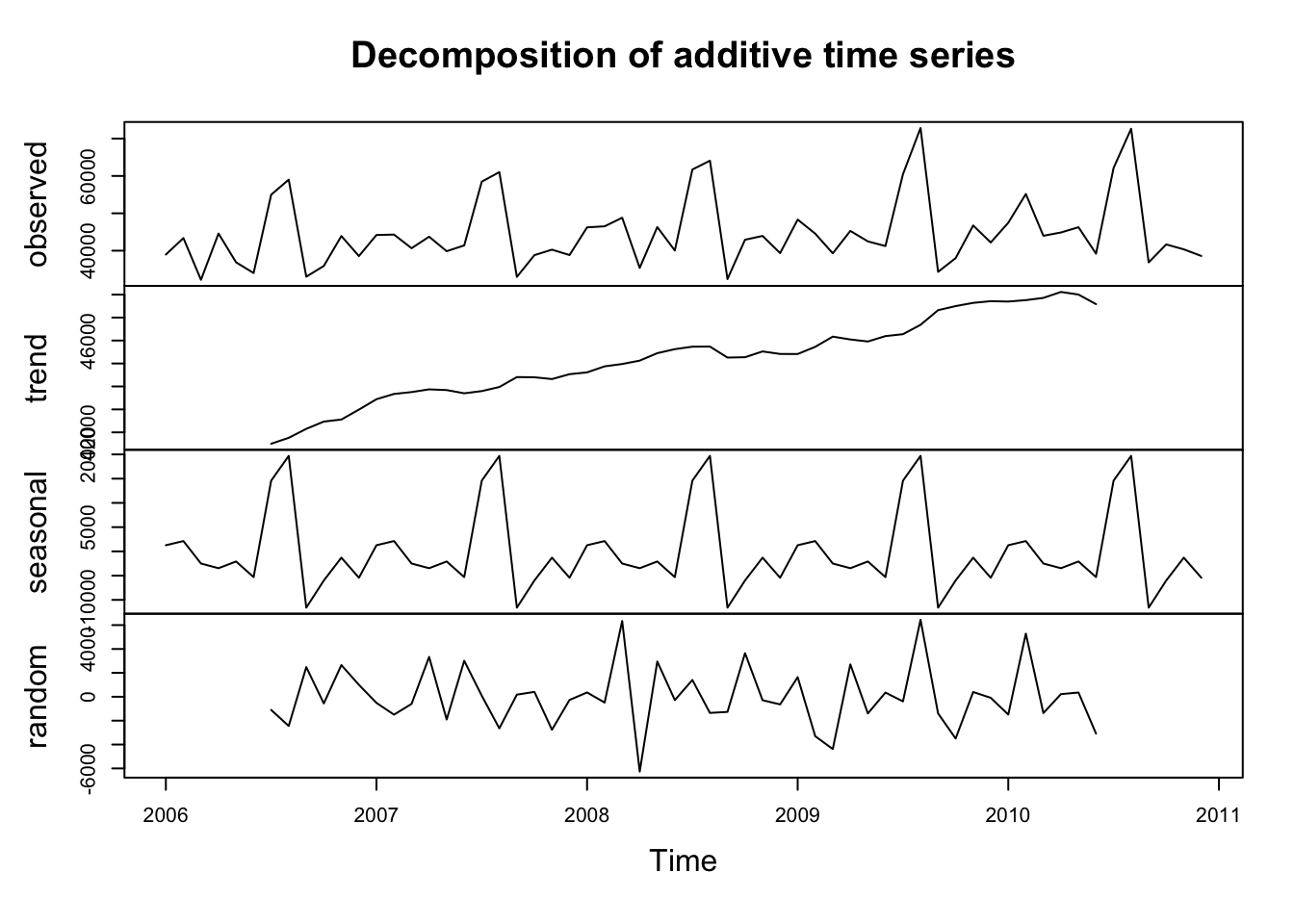
Vemos que los meses de agosto alcanza su mayor valor. Esto sugiere que \(S=12\).
Otro gráfico que nos ayuda a determinar la estacionalidad es determinar valores por mes del año:
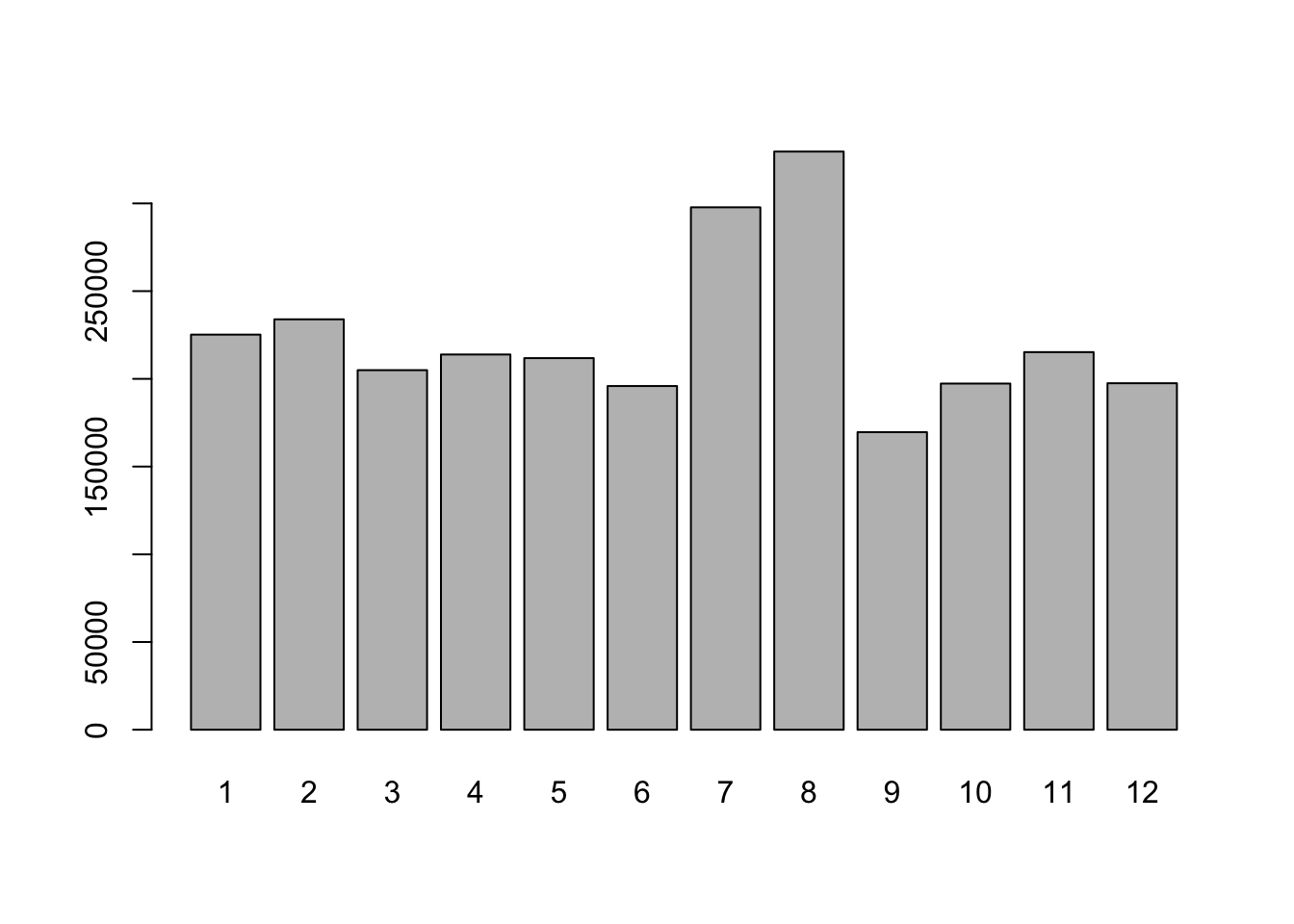 Paso 2
Paso 2
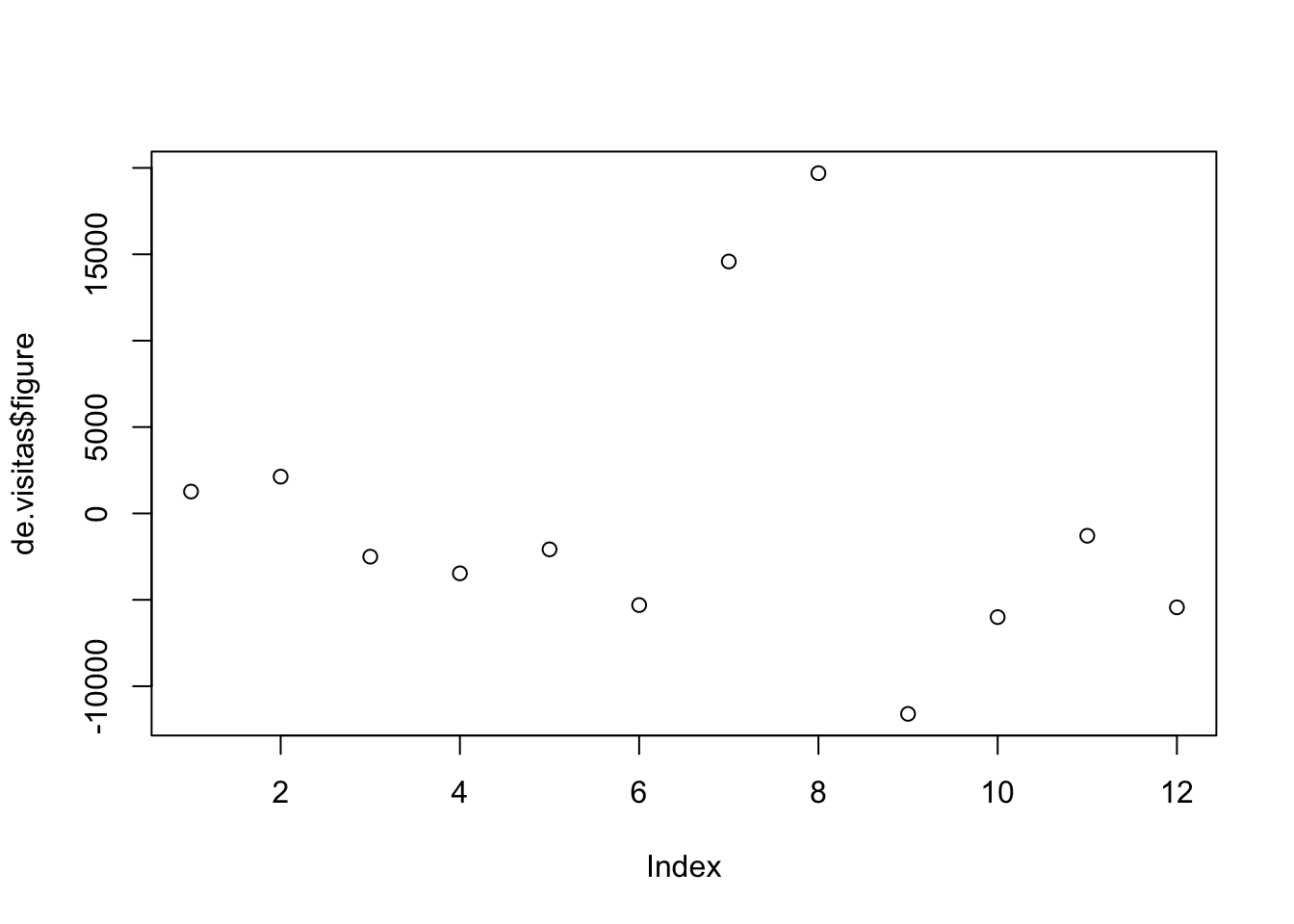
Se observa que hay tendencia en los datos por lo que se trabajará con la serie en diferencias:
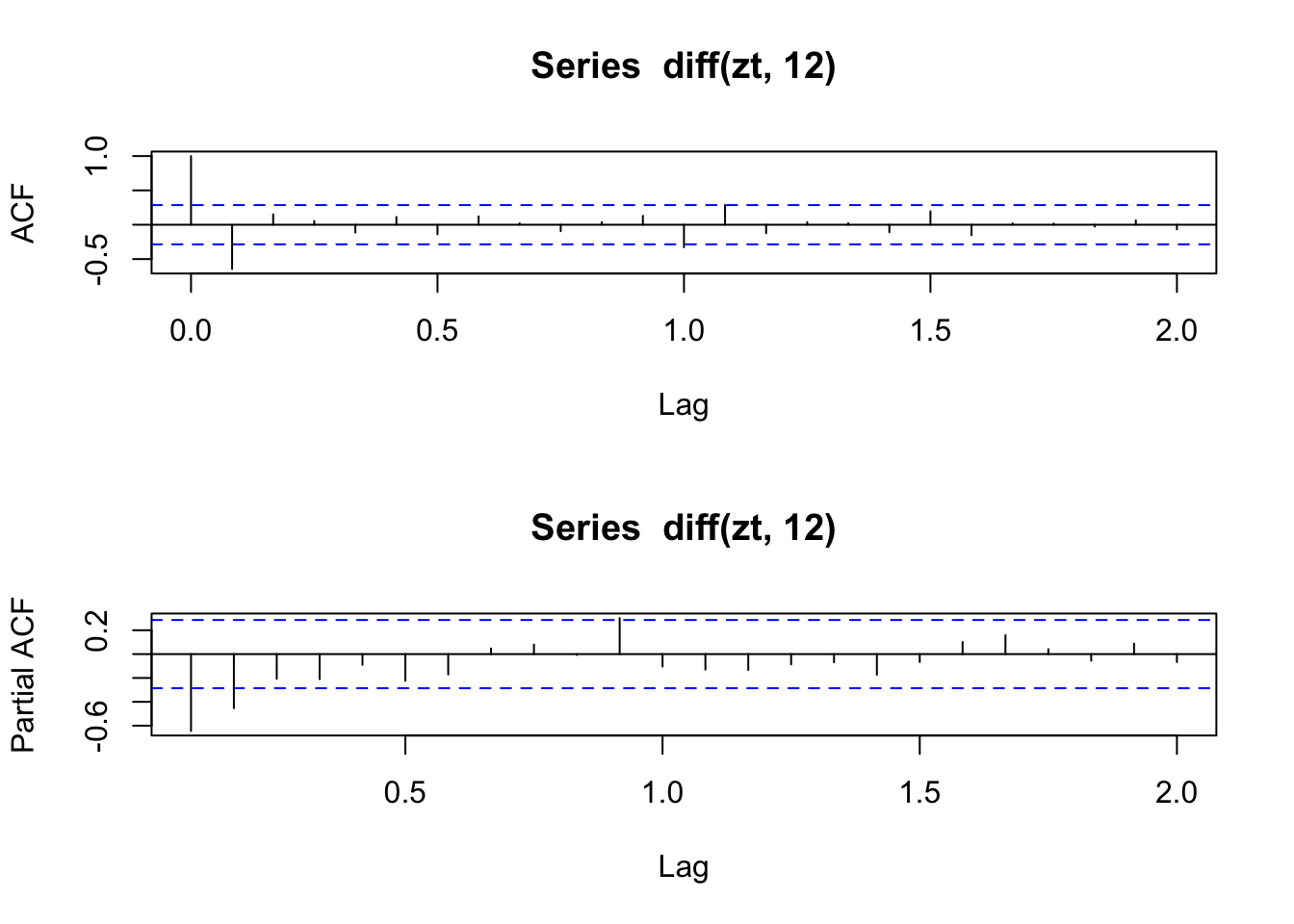
Ajustamos un ARIMA estacional \(( 0,1,1 ) \times ( 0,1,1 )_{ 12 }\) sobre \(x_t\), TOTALmensual
##
## Call:
## arima(x = TOTALmensual, order = c(0, 1, 1), seasonal = list(order = c(0, 1,
## 1), period = 12))
##
## Coefficients:
## ma1 sma1
## -0.9670 -0.6485
## s.e. 0.1634 0.2823
##
## sigma^2 estimated as 14069655: log likelihood = -458.44, aic = 922.87Veamos el ACF de los residuos:
## [1] -458.4369Ahora ajustamos el modelo \(( 1,1,0 ) \times ( 0,1,1 )_{ 12 }\) sobre \(x_t\), TOTALmensual
##
## Call:
## arima(x = TOTALmensual, order = c(1, 1, 0), seasonal = list(order = c(0, 1,
## 1), period = 12))
##
## Coefficients:
## ar1 sma1
## -0.6288 -0.7273
## s.e. 0.1115 0.3439
##
## sigma^2 estimated as 18790957: log likelihood = -464.78, aic = 935.56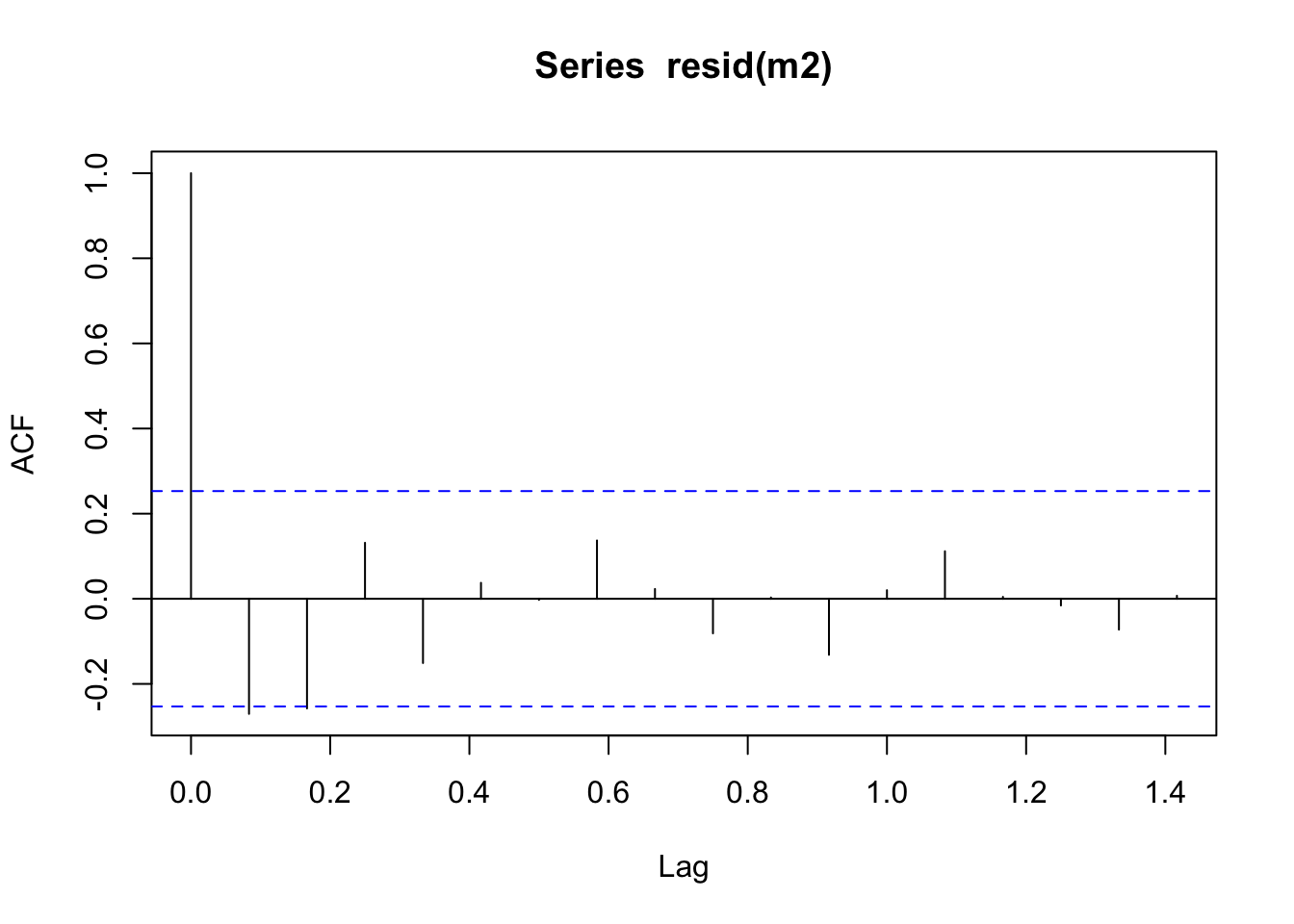
## [1] -464.7806## [1] 922.8739## [1] 935.5612Usando los criterios AIC y de máxima verosimilitud, vemos que el AIC del modelo \(( 0,1,1 ) \times ( 0,1,1 )_{ 12 }\) es menor, así como su verosimilitud es mayor. Esto indica que es un mejor modelo.
Ejemplo
Veamos la serie mensual de depósitos a la vista de Ecuador desde enero 2010.
datos <- read.csv(("https://raw.githubusercontent.com/vmoprojs/DataLectures/master/MonetarioBCE.csv"),sep = ";",dec = ".")
i = 3
tsdat <- ts((datos[,i]), st = c(2010,1),fr = 12)
plot(tsdat)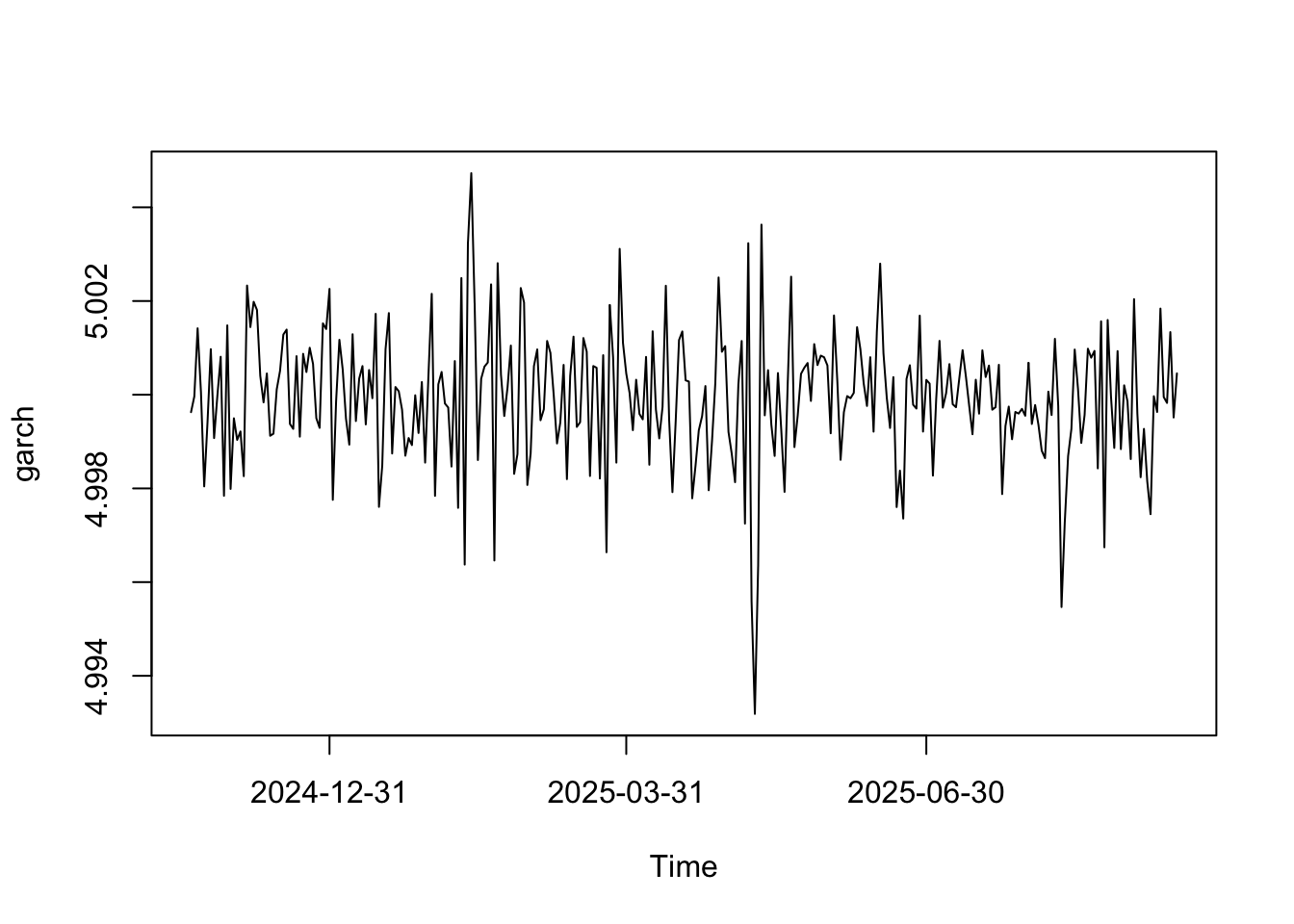
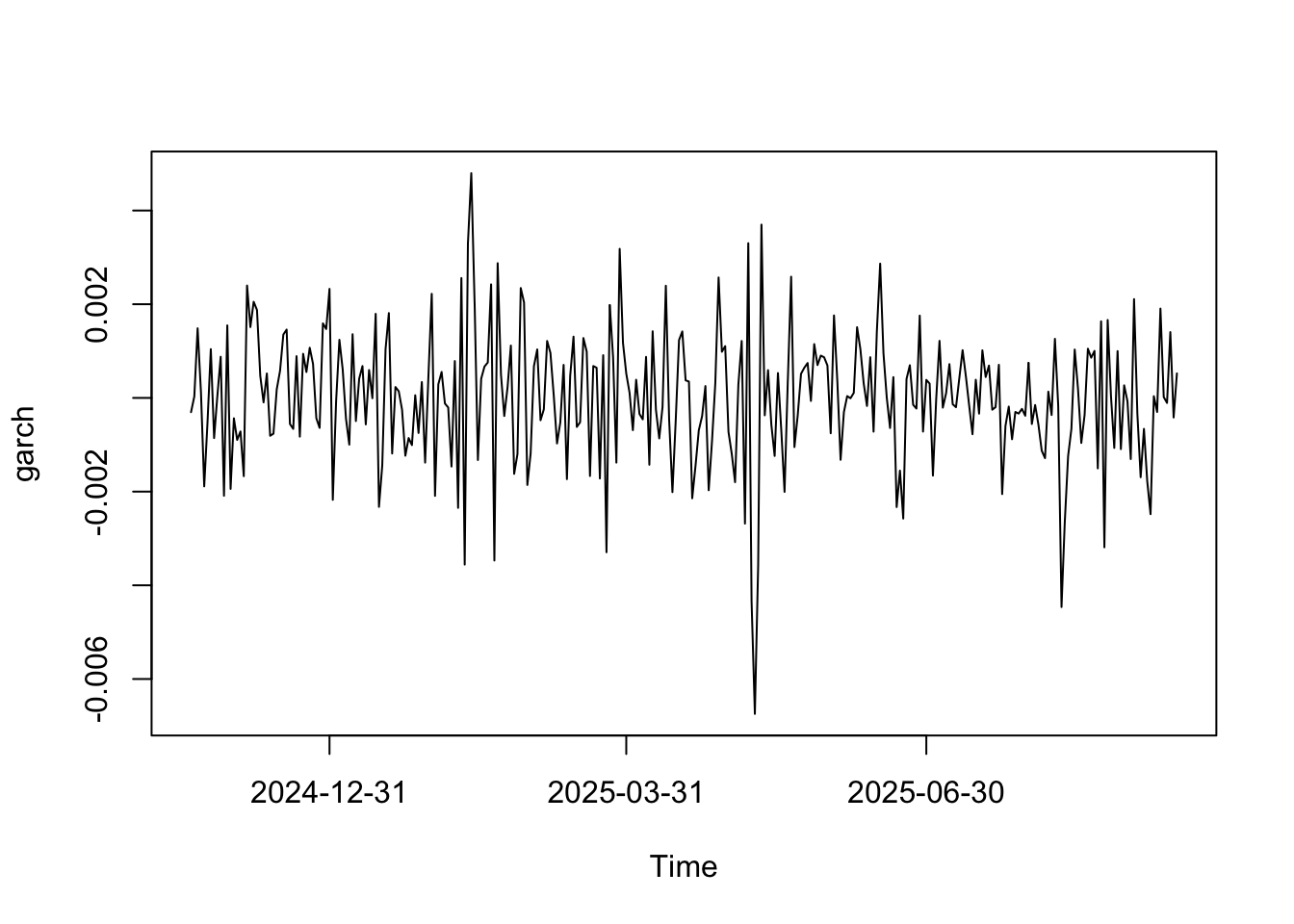
## Warning in adf.test(serie): p-value smaller than printed p-value##
## Augmented Dickey-Fuller Test
##
## data: serie
## Dickey-Fuller = -5.4564, Lag order = 5, p-value = 0.01
## alternative hypothesis: stationaryLa serie en primeras diferencias es estacionaria. Ajustamos un modelo para la serie:
## Series: serie
## ARIMA(0,0,0)(2,0,0)[12] with zero mean
##
## Coefficients:
## sar1 sar2
## 0.3374 0.267
## s.e. 0.0834 0.086
##
## sigma^2 = 49423: log likelihood = -929.24
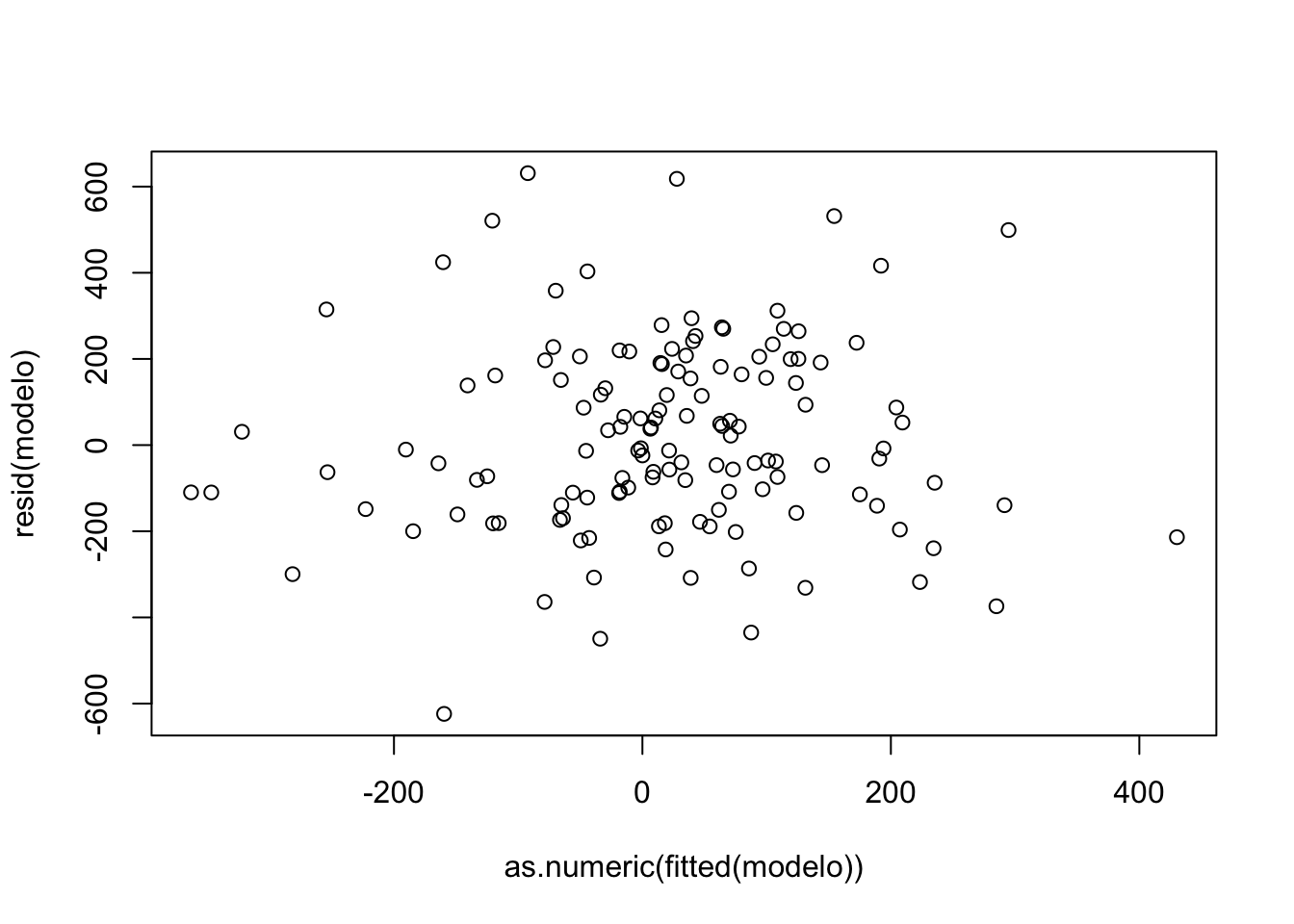
## AIC=1864.48 AICc=1864.66 BIC=1873.22Veamos los residuos del modelo:
##
## Box-Pierce test
##
## data: resid(modelo)
## X-squared = 0.18963, df = 1, p-value = 0.6632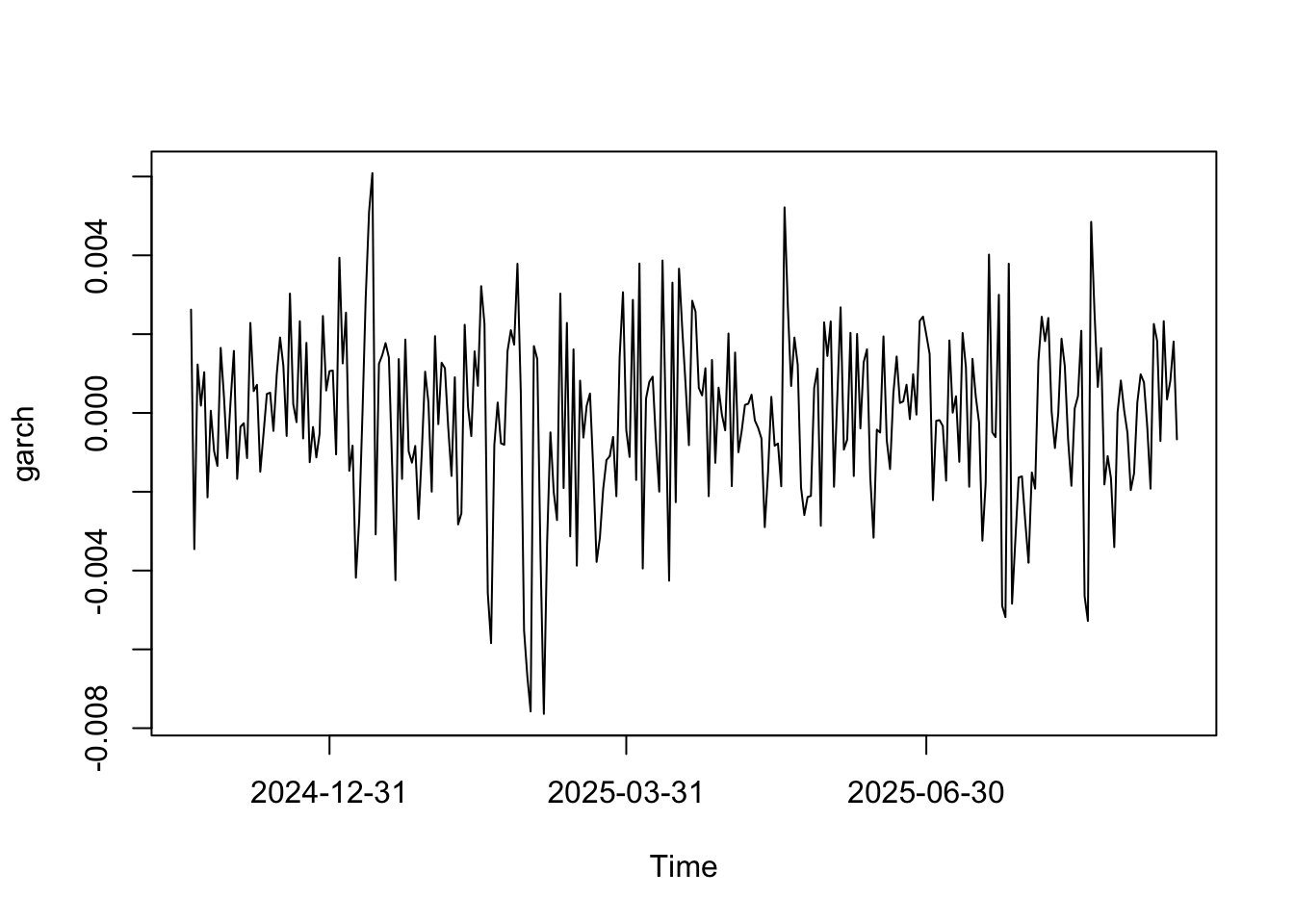
##
## Pearson's product-moment correlation
##
## data: as.numeric(fitted(modelo)) and resid(modelo)
## t = 0.49756, df = 134, p-value = 0.6196
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## -0.1263030 0.2097595
## sample estimates:
## cor
## 0.042942883.6 Ejercicios
- En cada una de las series de la Oferta-Utilización de bienes y servicios en este link, cuyas variables son:
PIB: P.I.B.
IMPOR: Importaciones de bienes y servicios (fob)
OF: Oferta final
DI: Demanda interna
GCFH: Gasto de Consumo final Hogares (*)GCFGC: Gasto de Consumo final Gobierno General
FBKF
VE: Variación de existencias
EXPOR: Exportaciones de bienes y servicios (fob)
UF: Utilización final
Realizar:
- Identificar y comentar la estacionalidad de la serie.
- Identificar si la serie es multiplicativa o aditiva.
- Modelizar la serie con un proceso SARIMA y escribir el modelo estimado.
- Realiza la predicción a cuatro períodos usando HoltWinters. Compara y comenta los resultados de la predicción SARIMA vs HoltWinters.
¿El proceso \(Y_t = \epsilon_t+2.1\epsilon_{t-1}-0.9\epsilon_{t-2}-4.7\epsilon_{t-3}\) es invertible?
Los están datos ubicados en: https://raw.githubusercontent.com/vmoprojs/DataLectures/master/MonetarioBCE.csv.
DepositosVista: Se refiere a depósitos en cuenta corriente recibidos por las entidades bancarias, exigibles mediante la presentación de cheques u otros mecanismos de pago y registro.M1: La oferta monetaria se define como la cantidad de dinero a disposición inmediata de los agentes para realizar transacciones; contablemente el dinero en sentido estricto, es la suma de las especies monetarias en circulación y los depósitos en cuenta corriente.Cuasidinero: Corresponde a las captaciones de las Otras Sociedades de Depósito, que sin ser de liquidez inmediata, suponen una segunda línea de medios de pago a disposición del público. Está formado por los depósitos de ahorro, plazo, operaciones de reporto, fondos de tarjetahabientes y otros depósitos.M2: La liquidez total o dinero en sentido amplio incluye la oferta monetaria y el cuasidinero.
Realizar en cada una de las series:
- Identificar y comentar la estacionalidad de la serie.
- Identificar si la serie es multiplicativa o aditiva.
- Modelizar la serie con un proceso SARIMA y escribe el modelo estimado.
- Realiza la predicción a tres períodos usando HoltWinters. Compara y comenta los resultados de la predicción SARIMA vs HoltWinters.
- Los siguientes datos contienen información de el saldo en mora (numerador) y el saldo total de una entidad financiera (denominador). Construye una serie con datos semanales (puedes usar la función
apply.weeklydel paquetexts). Esa es la serie de estudio.
Realizar:
- Identificar y comentar la estacionalidad de la serie.
- Identificar si la serie es multiplicativa o aditiva.
- Modelizar la serie con un proceso SARIMA y escribe el modelo estimado.
- Realiza la predicción a cuatro períodos usando HoltWinters. Compara y comenta los resultados de la predicción SARIMA vs HoltWinters.
Datos: https://raw.githubusercontent.com/vmoprojs/DataLectures/master/AST/tasaMoraTotalEntidadEC.csv
- Los siguientes datos presentan información de facturación de ventas de una tienda online. Para cada fecha, agrega (con la función suma) la iformación de cantidad ventida. Usando esta serie debes hacer la predicción del stock total que requiere la tienda. Específicamente:
- Identificar y comentar la estacionalidad de la serie.
- Identificar si la serie es multiplicativa o aditiva.
- Modelizar la serie con un proceso SARIMA y escribe el modelo estimado.
- Realiza la predicción a cuatro períodos usando HoltWinters. Compara y comenta los resultados de la predicción SARIMA vs HoltWinters.