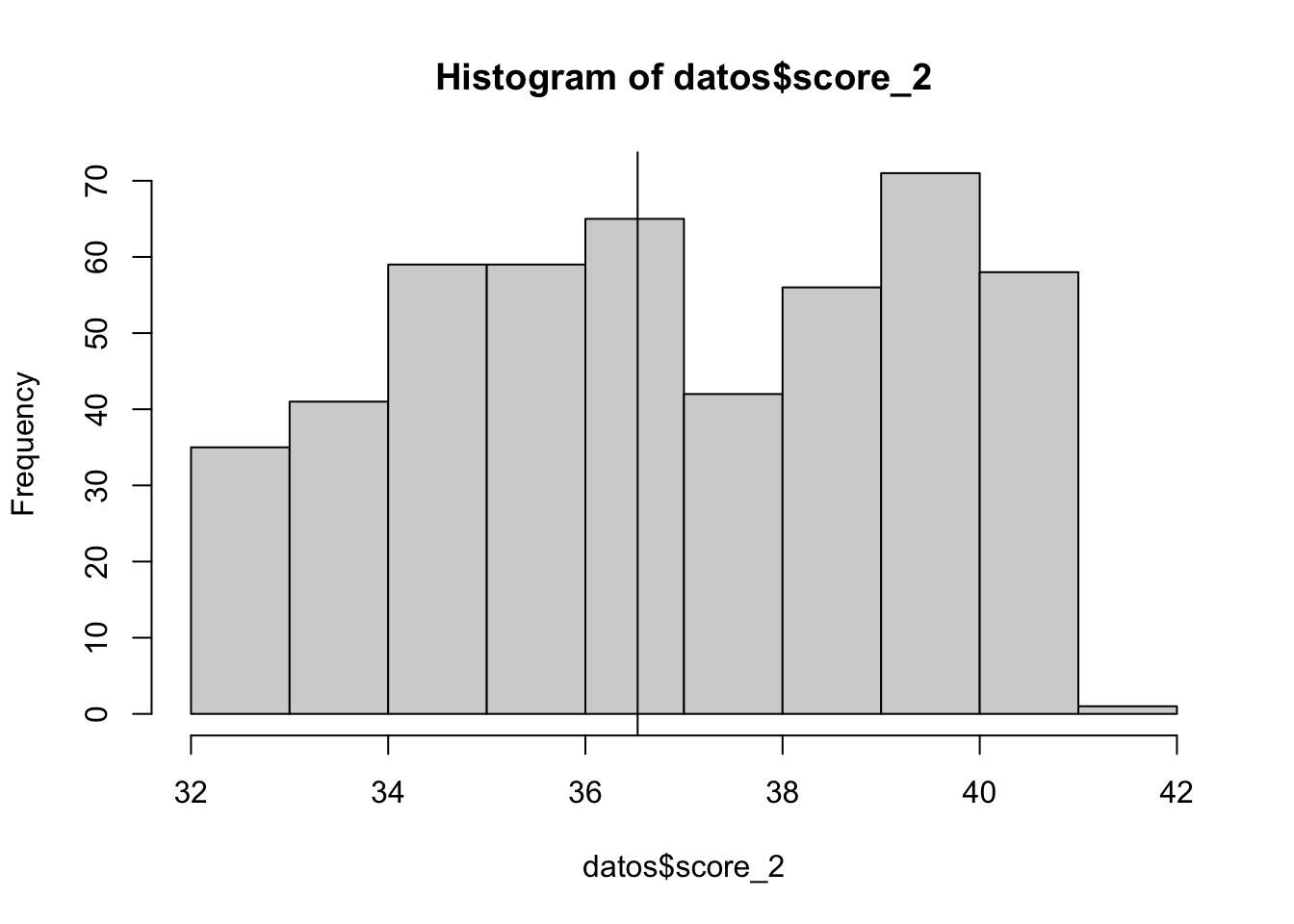
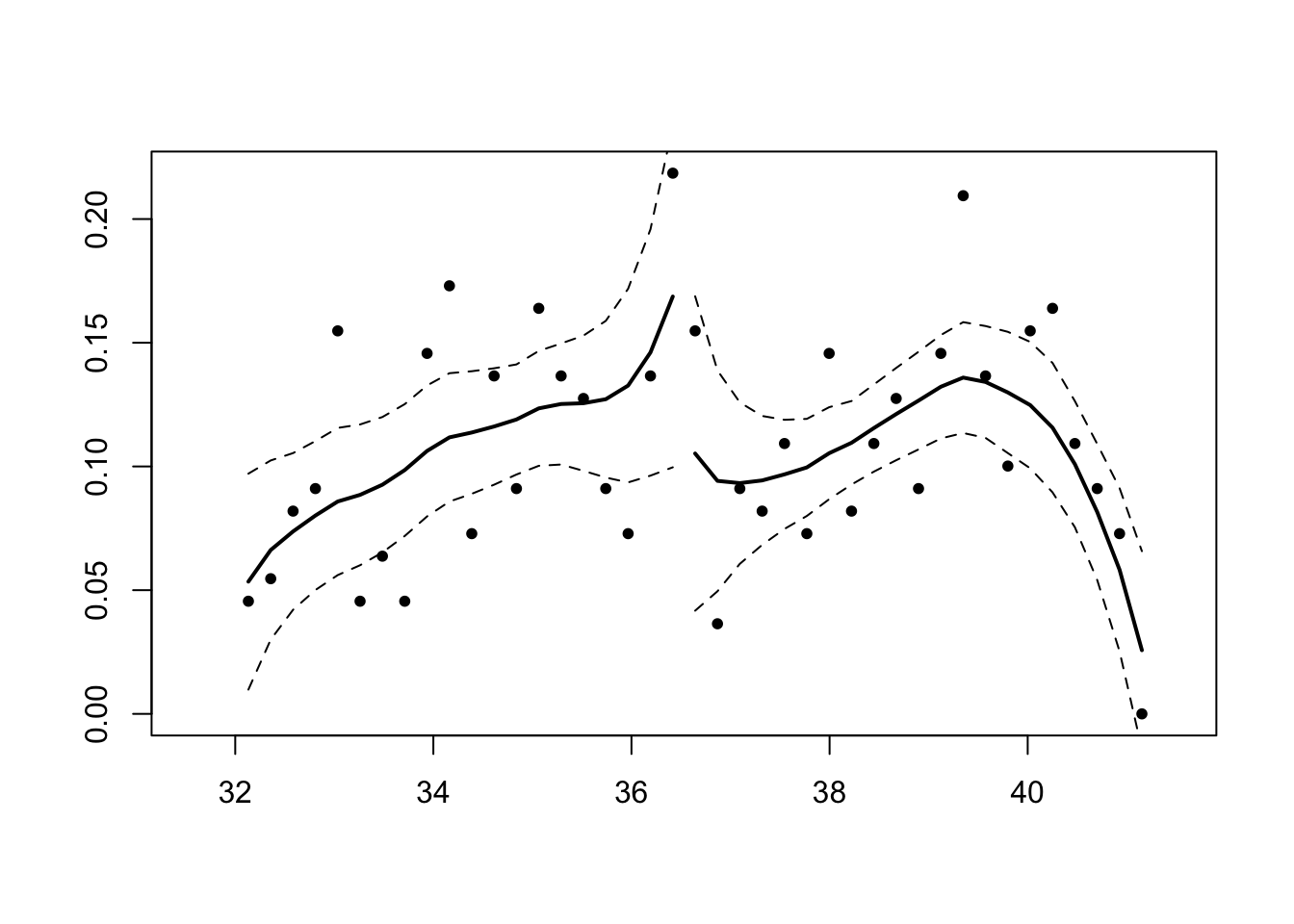
5 Regresión discontinua
Es un mecanismo de selección de participación cuando hay un índice. Por ejemplo, con el índice SELBEN. Tiene un punto de corte que determina quienes participan y quienes no participan del programa.
Se busca comparar individuos que están en la vecindad del punto de corte.
Otras variables donde puede haber este tipo de métodos son: puntaje en pruebas, edad, etc.
Condiciones
Variable continua con la cual se hace la selección.
Punto de corte que discrimina quien participa o no.
5.1 Limitaciones e interpretación.
Si no hay impacto, significa que debemos recomendar que se mueva el umbral, casi siempre hacia abajo.
Se debe mostrar varias bandas en la definición de la vecindad para estudiar la robustez.
Hay que tener cuidado teniendo claro el efecto mínimo detectable con el que estoy trabajando.
5.2 Supuestos
Condición de exclusión: no hay otra discontinuidad alrededor del punto de corte.
Continuidad: Establece que \(E[Y^0_i\mid W=w_0]\) y \(E[Y_i^1\mid W=w_0]\) son funciones continuas (suaves) de \(W\) incluso a través del umbral \(w_0\). En otras palabras, sin el tratamiento, los resultados potenciales esperados no habrían aumentado; habrían seguido siendo funciones suaves de \(W\). No se puede testear este supuesto, se debe argumentar.
Se asume la relación \(f(\cdot)\) entre la variable de resultado y la variable que determina el tratamiento.
5.3 Tipos de Regresión discontinua (RD)
5.3.2 Fuzzy RD
La regla de asignación no se cumple de manera determinista, hay otras variables ue inciden en la participación en el programa. Es decir, la variable \(W\) determina el cambio de \(D=0\) a \(D=1\) exactamente en \(w_0\) tal que \(\text{Prob}(D=1|W=w_0)\).
Se analiza con regresión de variables instrumentales.
5.5 Fuzzy RD
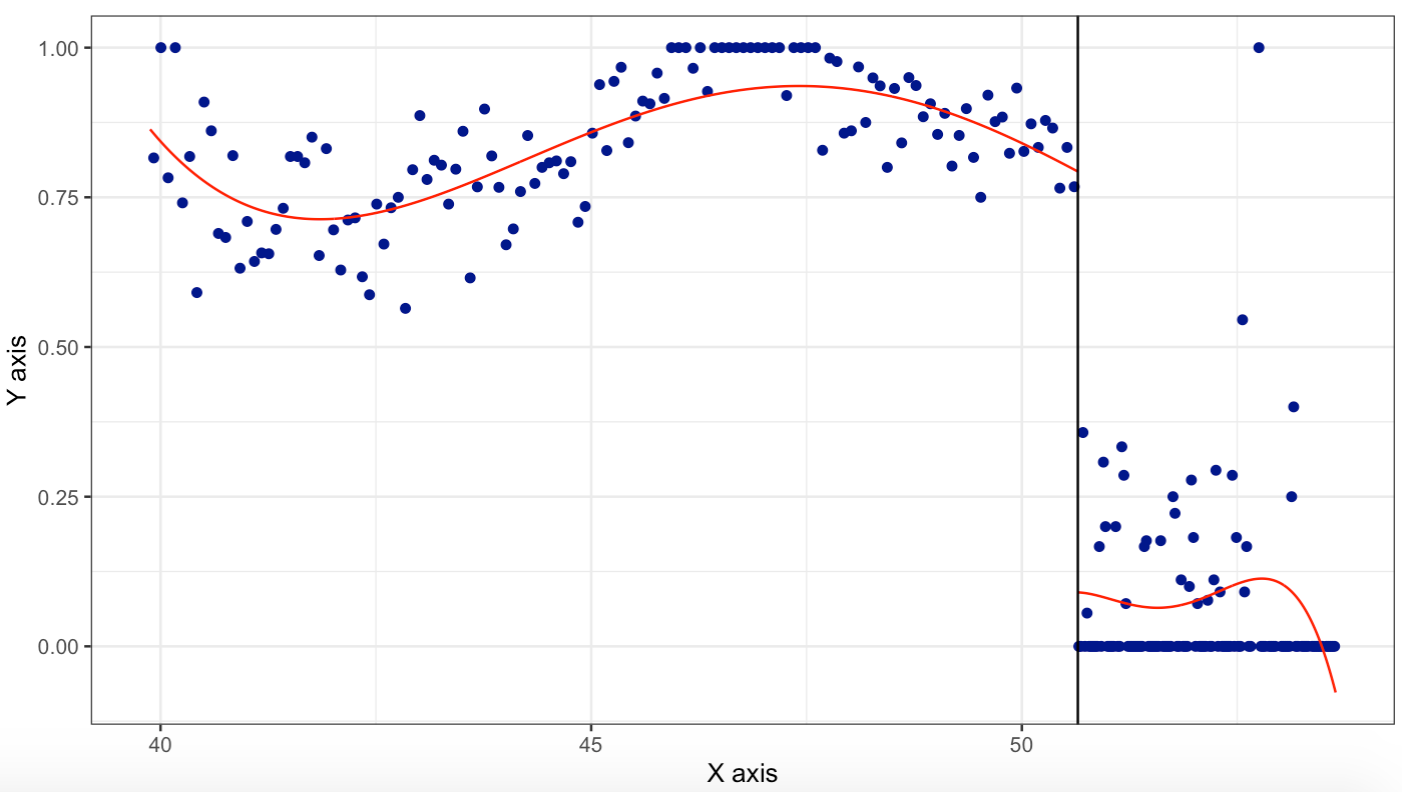
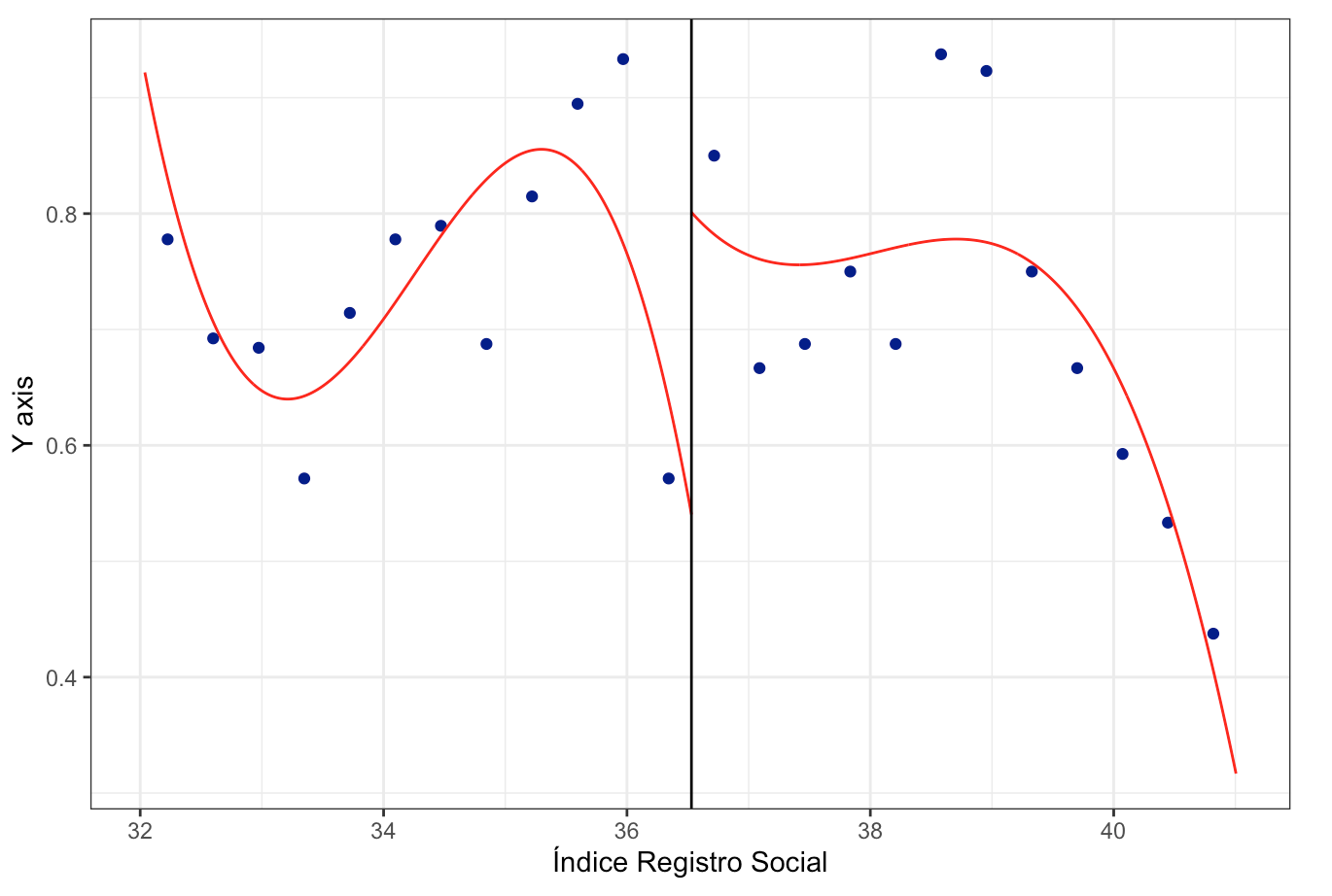
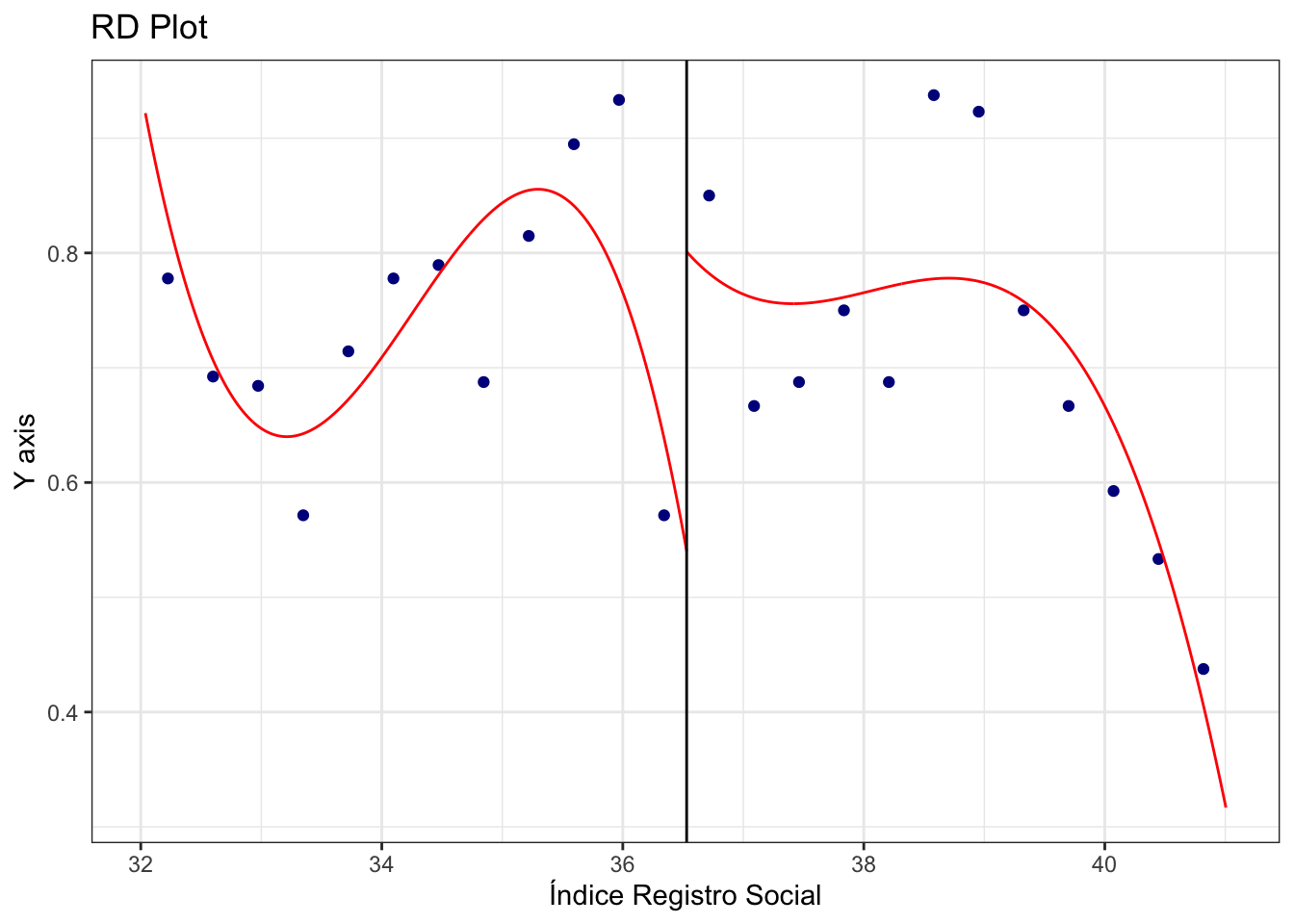
Figure 5.3: Variable W (cuasi) determina D
En este diseño se tiene que \(W\) determina parcialmente a \(D\).
Debemos estimar el modelo mediante el método de Variable Instrumental.
El instrumento será la predicción de lo que realmente sucedió \(D\) regresado en la aleatorización inicial \(\hat{D}\).
Primera etapa
\[ Z_i = \begin{cases} 1 \text{ if } & W_i<{w_0} \\ 0 \text{ if } & W_i \geq w_0 \end{cases} \]
\[ \hat{D}_i = X_i\beta+\rho Z_i+f(W_i)+\epsilon_i \]
\[ Y_i = X_i\beta+\lambda \hat{D}_i+f(W_i)+u_i \]
Donde el efecto del tratamiento es \(\lambda\).
Ejemplo
Se desea estimar si el Bono de Desarrollo Humano tiene un impacto en la tasa de matrícula escolar.
las variables que terminan en 0 son de la linea base y las 1 son de la segunda toma.
los datos están en formato horizontal.
la variable de respuesta es \(Y=\text{Cenroll1}\).
\(D=\text{D}\) representa la aleatorización inicial del experimento.
\(D=\text{D_hat}\) representa lo que terminó sucediendo.
Leemos los datos y limpiamos la base
library(haven)
uu <- "https://github.com/vmoprojs/DataLectures/raw/master/complete_panel.dta"
datos <- read_dta(uu)
datos <- data.frame(datos)
# se generan variables en linea de base que se usarán como controles
datos$tot0_5_0 <- datos$M0t50+datos$F0t50
datos$tot6_17_0 <- datos$M6t170+datos$F6t170
datos$tot18_44_0 <- datos$M18t440+datos$F18t440
datos$tot45_64_0 <- datos$M45t640+datos$F45t640
datos$tot65p_0 <- datos$M65p0+datos$F65p0
datos$log_cons_0=log(datos$Epcexp0)
datos$D <- (datos$b2==1)*1 #tratados reales
datos$D[datos$b2==0]=0
datos$D_hat <-( datos$g2==2 |datos$g2==4 )*1 # aleatorizacion inicial, Z en la clase
datos$D_hat[datos$g2==1 |datos$g2==3] = 0
# g2 es el grupo inicial aleatorizado A, B regresion discontinua, C, D experimental
# b2 reciben o no reciben efectivamente
datos$puntaje2 <- datos$puntaje^2
datos$puntaje3 <- datos$puntaje^3
datos$DCenroll <- datos$Cenroll1-datos$Cenroll0#cambio en la matricula entre tomas
#limpio la base
fil <- !is.na(datos$Cage0) & !is.na(datos$Cenroll1) & !is.na(datos$D_hat)
table(fil)## fil
## FALSE TRUE
## 5653 9585datos <- datos[which(fil),]
datos$EXP <- (datos$gr_def==3|datos$gr_def==4)*1 #Diseño experimental
datos$RDD <-(datos$gr_def==1|datos$gr_def==2) *1 # Diseño RDD
vlist0 <- c("log_cons_0" ,"Cfhome0", "HHmale0" ,"HHindi0" ,"HHlit0", "Hhsize0" ,"tot0_5_0", "tot6_17_0", "tot18_44_0" ,"tot45_64_0", "area1")Veamos la contaminación del experimento:
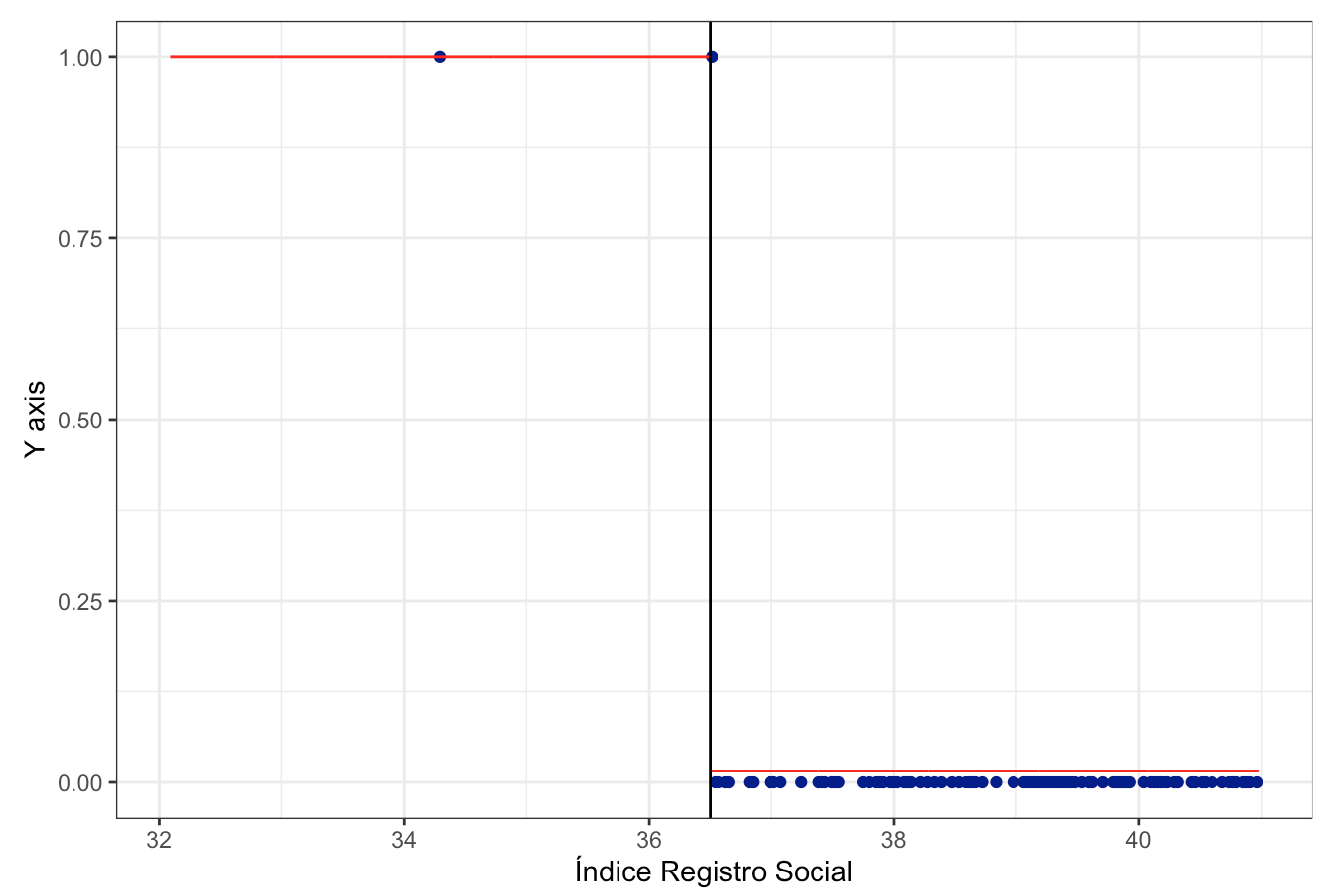
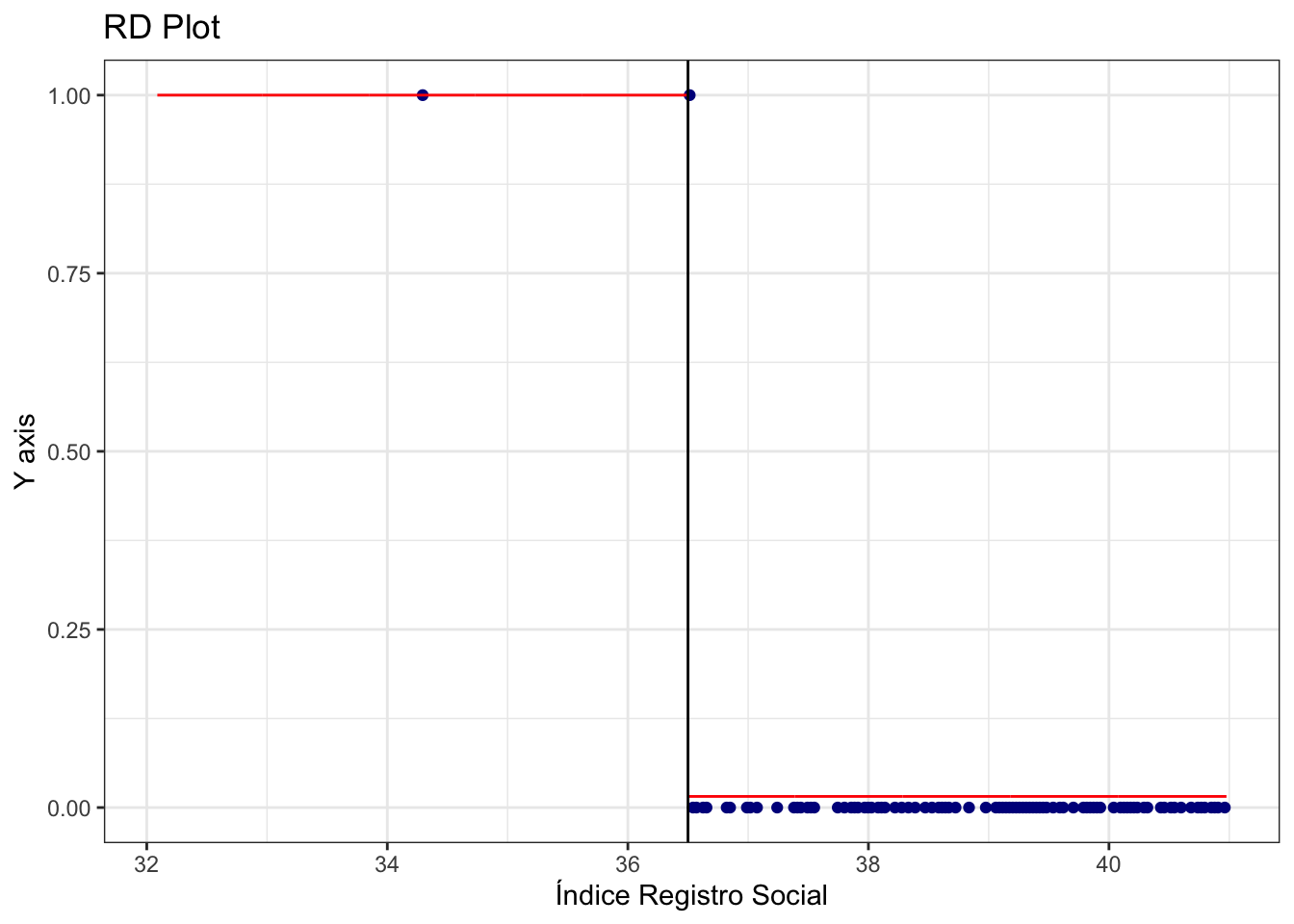
rdplot(datos$D,datos$puntaje,c= 50.65)## [1] "Mass points detected in the running variable."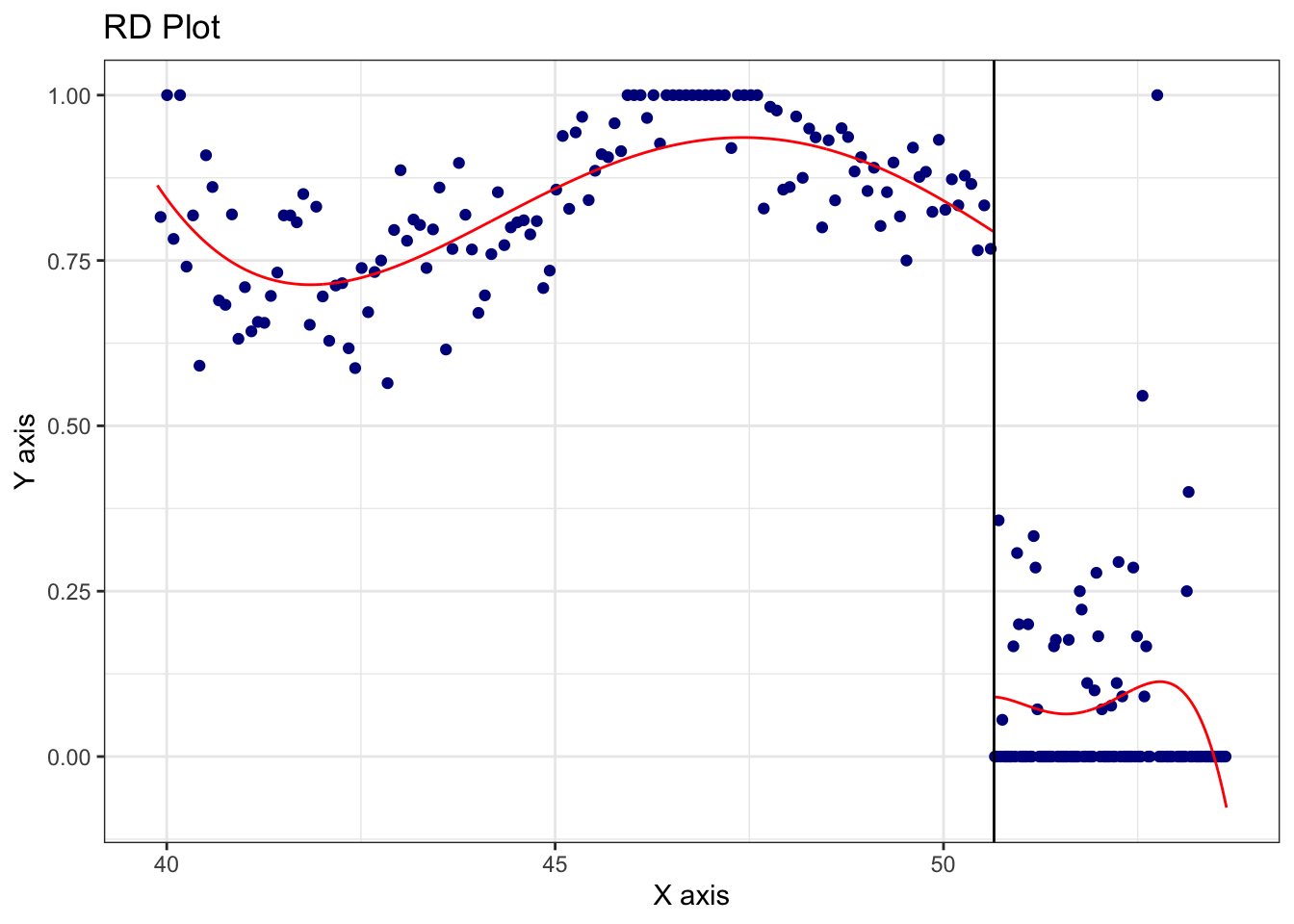
Comparacion de medias en linea de base para tratamiento y control
# comparacion de medias en linea de base para tratamiento y control
aux <- subset(datos,datos$EXP==1)
for(i in 1:length(vlist0))
{
cat("-----",vlist0[i],"------\n")
print(tapply(aux[,vlist0[i]],aux$D,summary) )
}## ----- log_cons_0 ------
## $`0`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 1.136 2.357 2.698 2.721 3.083 4.622
##
## $`1`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.7661 2.3414 2.6484 2.6494 2.9631 5.5600
##
## ----- Cfhome0 ------
## $`0`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.0000 1.0000 1.0000 0.8234 1.0000 1.0000
##
## $`1`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.0000 1.0000 1.0000 0.7876 1.0000 1.0000
##
## ----- HHmale0 ------
## $`0`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.0000 1.0000 1.0000 0.8705 1.0000 1.0000
##
## $`1`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.000 1.000 1.000 0.845 1.000 1.000
##
## ----- HHindi0 ------
## $`0`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.0000 0.0000 0.0000 0.1427 0.0000 1.0000
##
## $`1`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.0000 0.0000 0.0000 0.1593 0.0000 1.0000
##
## ----- HHlit0 ------
## $`0`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.0000 1.0000 1.0000 0.8441 1.0000 1.0000
##
## $`1`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.0000 1.0000 1.0000 0.8566 1.0000 1.0000
##
## ----- Hhsize0 ------
## $`0`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 2.000 5.000 6.000 6.217 7.000 14.000
##
## $`1`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 2.000 5.000 6.000 6.354 7.000 14.000
##
## ----- tot0_5_0 ------
## $`0`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.0000 0.0000 0.0000 0.5413 1.0000 4.0000
##
## $`1`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.0000 0.0000 0.0000 0.5649 1.0000 5.0000
##
## ----- tot6_17_0 ------
## $`0`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 1.000 2.000 3.000 3.011 4.000 6.000
##
## $`1`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 1.000 2.000 3.000 3.176 4.000 8.000
##
## ----- tot18_44_0 ------
## $`0`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.000 1.000 2.000 1.908 2.000 6.000
##
## $`1`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.000 1.000 2.000 1.864 2.000 6.000
##
## ----- tot45_64_0 ------
## $`0`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.0000 0.0000 0.0000 0.6766 1.0000 3.0000
##
## $`1`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.0000 0.0000 0.0000 0.6475 1.0000 3.0000
##
## ----- area1 ------
## $`0`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 1.000 1.000 1.000 1.942 3.000 3.000
##
## $`1`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 1.000 1.000 2.000 2.033 3.000 3.000# mismo análisis sobre aleatorización inicial
aux <- subset(datos,datos$EXP==1)
for(i in 1:length(vlist0))
{
cat("-----",vlist0[i],"------\n")
print(tapply(aux[,vlist0[i]],aux$D_hat,summary) )
}## ----- log_cons_0 ------
## $`0`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.7661 2.3398 2.6510 2.6558 2.9537 4.6291
##
## $`1`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 1.136 2.355 2.686 2.694 3.029 5.560
##
## ----- Cfhome0 ------
## $`0`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.0000 1.0000 1.0000 0.7803 1.0000 1.0000
##
## $`1`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.0000 1.0000 1.0000 0.8277 1.0000 1.0000
##
## ----- HHmale0 ------
## $`0`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.0000 1.0000 1.0000 0.8352 1.0000 1.0000
##
## $`1`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.0000 1.0000 1.0000 0.8813 1.0000 1.0000
##
## ----- HHindi0 ------
## $`0`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.0000 0.0000 0.0000 0.1479 0.0000 1.0000
##
## $`1`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.0000 0.0000 0.0000 0.1659 0.0000 1.0000
##
## ----- HHlit0 ------
## $`0`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.0000 1.0000 1.0000 0.8582 1.0000 1.0000
##
## $`1`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.0000 1.0000 1.0000 0.8443 1.0000 1.0000
##
## ----- Hhsize0 ------
## $`0`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 2.000 5.000 6.000 6.289 7.000 14.000
##
## $`1`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 2.000 5.000 6.000 6.358 7.000 14.000
##
## ----- tot0_5_0 ------
## $`0`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.0000 0.0000 0.0000 0.5549 1.0000 5.0000
##
## $`1`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.0000 0.0000 0.0000 0.5635 1.0000 4.0000
##
## ----- tot6_17_0 ------
## $`0`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 1.000 2.000 3.000 3.125 4.000 7.000
##
## $`1`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 1.000 2.000 3.000 3.135 4.000 8.000
##
## ----- tot18_44_0 ------
## $`0`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.000 1.000 2.000 1.841 2.000 6.000
##
## $`1`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.000 1.000 2.000 1.936 2.000 6.000
##
## ----- tot45_64_0 ------
## $`0`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.0000 0.0000 0.0000 0.6652 1.0000 3.0000
##
## $`1`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.0000 0.0000 0.0000 0.6401 1.0000 2.0000
##
## ----- area1 ------
## $`0`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 1.000 1.000 2.000 2.019 3.000 3.000
##
## $`1`
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 1.000 1.000 2.000 1.986 3.000 3.000Se tiene contaminzación, por lo que se procede con Fuzzy RD. Estimamos el instrumento D_hat en la primera etapa:
# Primera etapa:
m1 <- lm(D_hat~ D ,data = datos)
m2 <- lm(D_hat~ D +puntaje,data = datos)
f <- paste("D_hat ~D+puntaje+puntaje2+puntaje3+",paste0(vlist0,collapse = "+"))
m3 <- lm(f,data = datos)
export_summs(m1, m2,m3)| Model 1 | Model 2 | Model 3 | |
|---|---|---|---|
| (Intercept) | 0.26 *** | 0.08 | 221.24 *** |
| (0.01) | (0.06) | (11.26) | |
| D | 0.07 *** | 0.08 *** | 0.01 |
| (0.01) | (0.01) | (0.01) | |
| puntaje | 0.00 ** | -14.53 *** | |
| (0.00) | (0.73) | ||
| puntaje2 | 0.32 *** | ||
| (0.02) | |||
| puntaje3 | -0.00 *** | ||
| (0.00) | |||
| log_cons_0 | 0.07 *** | ||
| (0.01) | |||
| Cfhome0 | -0.01 | ||
| (0.02) | |||
| HHmale0 | 0.11 *** | ||
| (0.02) | |||
| HHindi0 | -0.01 | ||
| (0.01) | |||
| HHlit0 | 0.00 | ||
| (0.01) | |||
| Hhsize0 | -0.04 ** | ||
| (0.01) | |||
| tot0_5_0 | 0.06 *** | ||
| (0.01) | |||
| tot6_17_0 | 0.05 *** | ||
| (0.01) | |||
| tot18_44_0 | 0.04 ** | ||
| (0.01) | |||
| tot45_64_0 | 0.02 | ||
| (0.01) | |||
| area1 | 0.01 ** | ||
| (0.00) | |||
| N | 9585 | 9585 | 9585 |
| R2 | 0.00 | 0.01 | 0.07 |
| *** p < 0.001; ** p < 0.01; * p < 0.05. | |||
datos$T_hat <- predict(m3)Ahora usamos la estimación en la segunda etapa:
# Segunda etapa:
m4 <- lm(Cenroll1~ T_hat ,data = datos)
m5 <- lm(D_hat~ T_hat +puntaje,data = datos)
f <- paste("D_hat ~T_hat+puntaje+puntaje2+",paste0(vlist0,collapse = "+"))
m6 <- lm(f,data = datos)
export_summs(m4, m5,m6)| Model 1 | Model 2 | Model 3 | |
|---|---|---|---|
| (Intercept) | 0.66 *** | 0.00 | 0.00 |
| (0.01) | (0.06) | (0.99) | |
| T_hat | 0.32 *** | 1.00 *** | 1.00 *** |
| (0.04) | (0.04) | (0.05) | |
| puntaje | 0.00 | 0.00 | |
| (0.00) | (0.04) | ||
| puntaje2 | 0.00 | ||
| (0.00) | |||
| log_cons_0 | 0.00 | ||
| (0.01) | |||
| Cfhome0 | 0.00 | ||
| (0.02) | |||
| HHmale0 | 0.00 | ||
| (0.02) | |||
| HHindi0 | 0.00 | ||
| (0.01) | |||
| HHlit0 | 0.00 | ||
| (0.01) | |||
| Hhsize0 | 0.00 | ||
| (0.01) | |||
| tot0_5_0 | 0.00 | ||
| (0.01) | |||
| tot6_17_0 | 0.00 | ||
| (0.01) | |||
| tot18_44_0 | 0.00 | ||
| (0.01) | |||
| tot45_64_0 | 0.00 | ||
| (0.01) | |||
| area1 | 0.00 | ||
| (0.00) | |||
| N | 9585 | 9585 | 9585 |
| R2 | 0.01 | 0.07 | 0.07 |
| *** p < 0.001; ** p < 0.01; * p < 0.05. | |||
Se puede apreciar que el BDH aumenta la tasa de matrícula.