3 Regresión

3.1 Causa-efecto con OLS

Una regresión simple

$$Y_i = \beta_0+\beta_1D_i+u_i$$

donde $Y$ es la variable dependiente (ingresos), $D=1$ si tiene título universitario y $D=0$ en otro caso, y $u$ es el término de error que contiene lo que no podemos observar.

OLS estima el efecto de $D$ en $Y$:

$$\hat{\beta}_1=\frac{\text{cov}(Y_i,D_i)}{\text{var}(D_i)} = \beta_1+\frac{\text{cov}(D_i,u_i)}{\text{var}(D_i)}$$

$\hat{\beta}_1$ consiste de dos partes. La primera parte $\beta_1$ mide el efecto en el que estamos interesados. La segunda parte es el sesgo.

$\hat{\beta}_1$ es igual a $\beta_1$ solo si $D_i$ y $u_i$ no están correlacionados ($\text{cov}(D_i,u_i)=0$).

Resultados potenciales	Análogo en regresión
$E[Y_1|D=1]-E[Y_0|D=1]$	$\beta_1$
$E[Y_1|D=1]-E[Y_0|D=0]$	$\hat{\beta}_1$
$E[Y_0|D=1]-E[Y_0|D=0]$	$\frac{\text{cov}(D,u)}{\text{var}(D)}$

Ejemplo

La siguiente tabla detalla una versión simplificada de la estrategia de emparejamiento de Dale y Krueger, en una configuración que llamamos la “matriz de emparejamiento de universidades.” Esta tabla enumera las solicitudes, admisiones y decisiones de matriculación para una lista (inventada) de nueve estudiantes, cada uno de los cuales postuló a hasta tres escuelas elegidas de una lista imaginaria de seis. Tres de las seis escuelas enumeradas en la tabla son públicas (All State, Tall State y Altered State) y tres son privadas (Ivy, Leafy e Smart). Cinco de nuestros nueve estudiantes (números 1, 2, 4, 6 y 7) asistieron a escuelas privadas. Las ganancias promedio en este grupo son USD 92000. Los otros cuatro, con ingresos promedio de USD 72500, fueron a una escuela pública. La brecha de casi USD 20000 entre estos dos grupos sugiere una gran ventaja para las escuelas privadas.

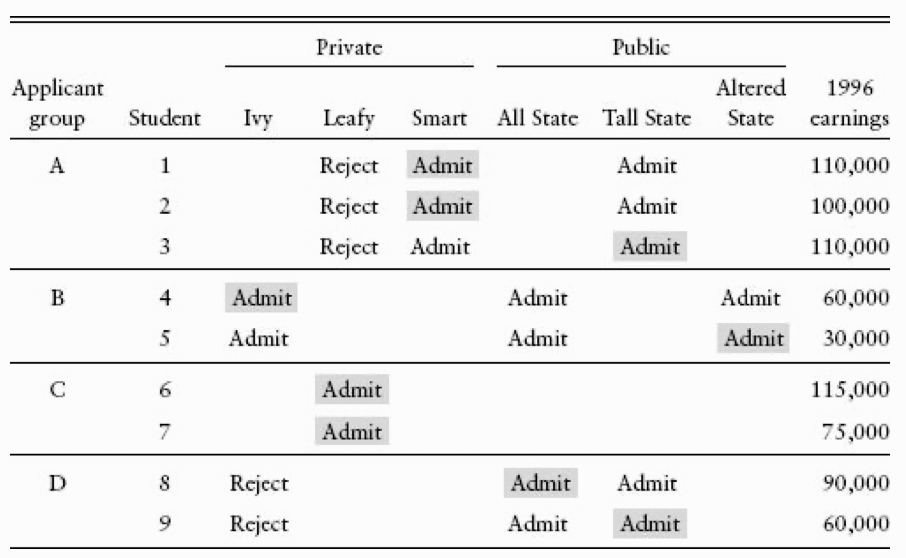
Figure 3.1: Número de valores posibles para el vector de asignación por diseño y tamaño de muestra

Los estudiantes de la tabla están organizados en cuatro grupos definidos por el conjunto de escuelas a las que postularon y fueron admitidos. Dentro de cada grupo, es probable que los estudiantes tengan ambiciones profesionales similares, mientras que el personal de admisiones de las escuelas a las que postularon también consideró que tenían una capacidad similar. Por lo tanto, las comparaciones dentro de los grupos deberían ser considerablemente más equivalentes a las comparaciones no controladas que involucran a todos los estudiantes.

1. $E(Y|\text{Private})-E(Y|\text{Public})= ((110+100+60+115+75)/5-(110+30+90+60)/4)\times 1000 = 19500$

2. $E(Y|\text{Private},\text{A o B})-E(Y|\text{Public},\text{A o B})= ((110+100+60)/3-(110+30)/2)\times 1000 = 20000$

3. $E(Y|\text{Private},\text{A})-E(Y|\text{Public},\text{A})= ((110+100)/2-(110)/1)\times 1000 = -5000$

4. $E(Y|\text{Private},\text{B})-E(Y|\text{Public},\text{B})= ((60)/1-(30)/1)\times 1000 = 30000$

El promedio ponderado de 3 y 4 es $9000$ (3/5*(-5000)+2/5*(30000)), no ponderado es $12500$. Esta diferencia es mucho menor a la que tendríamos sin control alguno. Este método es un match en el grupo aplicante.

Los grupos C y D no son informativos, porque, desde la perspectiva de nuestro esfuerzo por estimar el efecto del tratamiento de una escuela privada, cada uno está compuesto por individuos que han recibido todos los tratamientos o que están totalmente controlados.

3.1.1 Sesgo de variable omitida (OVB)

Regresión completa:

$$Y_i = \alpha'+\beta'P_i+\gamma A_i+e'_i$$

Regresión corta:

$$Y_i = \alpha^s+\beta^sP_i+e^s_i$$ Regresión auxiliar

$$A_i = \pi_0+\pi_1P_i+u_i$$ De lo cual tenemos:

$$\text{OVB} = \beta^s-\beta'= \pi\times \gamma$$

Por ejemplo, si tenemos el siguiente modelo:

$$Y_i = \alpha'+0.152\text{Privada}+0.051\text{SAT}+e'_i$$ $$Y_i = \alpha^s+0.212\text{Privada}+e^s_i$$ Entonces $\beta'=0.152$,$\beta^s=0.212$ y

$$\text{OVB} = 0.212\times 0.152=0.06$$

3.2 Malos controles

No siempre incluir más controles es mejor.

• Algunas variables son malos controles y no deben incluirse en un modelo de regresión incluso si su inclusión cambia el coeficiente de interés.

• Los malos controles son variables que son en sí mismas variables de resultado.

• Los buenos controles son variables que se han fijado en el momento en que se determinó el regresor de interés.

3.2.1 Ejemplo

• Supongamos que estamos interesados en los efectos de un **título universitario en los ingresos** y que las personas pueden trabajar en una de dos ocupaciones, cuello blanco y cuello azul.

• Un título universitario claramente abre la puerta a trabajos administrativos (cuello blanco) mejor pagados. Por tanto, ¿debería considerarse la **ocupación como una variable omitida en una regresión de los salarios según la escolaridad**?

• Veamos el efecto de la universidad en los salarios de quienes están dentro de una ocupación, digamos sólo de cuello blanco.

• El problema es que si la universidad afecta la ocupación, las comparaciones de salarios por estado de título universitario dentro de una ocupación ya no son equivalentes, incluso si la finalización del título universitario se asigna al azar.

• Modelo de resultados potenciales

$$Y_i = C_iY_{1i}+(1-C_i)Y_{0i}$$ $$W_i = C_iW_{1i}+(1-C_i)W_{0i}$$ donde $W$ indica un trabajador de cuello blanco, $Y$ denota ingresos y $C$ es un indicador para graduados universitarios.

• Los subíndices $1$ y $0$ indican resultados potenciales con y sin universidad. Suponemos que $C$ se asigna aleatoriamente.

• Los efectos causales de $C$ sobre $Y$ o $W$ son sencillos (debido a la independencia que estamos suponiendo).

$$E[Y_i|C_i=1]-E[Y_i|C_i=0]=E[Y_{1i}-Y_{0i}]$$ $$E[W_i|C_i=1]-E[W_i|C_i=0]=E[W_{1i}-W_{0i}]$$ - Un mal control significa que una comparación de ganancias condicionada a $W_i$ no tiene una interpretación causal.

• Considere la diferencia en los ingresos medios entre los graduados universitarios y otras personas condicionadas a trabajar en un trabajo administrativo (cuello blanco).

• Podemos calcular esto en un modelo de regresión que incluye $W_i$ o regresando $Y_i$ sobre $C_i$ en la muestra donde $W_i = 1$:

$$E[Y_i|W_i=1,C_i=1]-E[Y_i|W_i=1,C_i=0]=E[Y_{1i}|W_{1i}=1,C_i=1]-E[Y_{0i}|W_{0i}=1,C_i=0]$$ - Mediante la independencia conjunta de los resultados potenciales y $C_i$, tehemos:

$$E[Y_{1i}|W_{1i}=1,C_i=1]-E[Y_{0i}|W_{0i}=1,C_i=0]=E[Y_{1i}|W_{1i}=1]-E[Y_{0i}|W_{0i}=1]$$

• Esta expresión ilustra la naturaleza de **comparar manzanas con naranjas** del problema del mal control:

$$E[Y_{1i}|W_{1i}=1]-E[Y_{0i}|W_{0i}=1]=E[Y_{1i}-Y_{0i}|W_{1i}=1]+(E[Y_{0i}|W_{1i}=1]-E[Y_{0i}|W_{0i}=1])$$ donde el primer término en el lado derecho es el efecto causal en los graduados universitarios, y el segundo término es el sesgo de selección.

set.seed(123)

n <- 300000
habilidad <- rnorm(n)
universidad <- runif(n)>0.5 # asigna universidad aleatoriamente a la mitad

cuelloBlanco <- (0.5*universidad+0.5*habilidad+0.5*rnorm(n))>0

lnsalario <- log(10000)+0.2*universidad+0.8*cuelloBlanco+0.4*habilidad+rnorm(n)

m1 <- lm(lnsalario~universidad)
m2 <- lm(lnsalario~universidad+cuelloBlanco)
m3 <- lm(lnsalario~universidad+cuelloBlanco+habilidad)
m4 <- lm(cuelloBlanco~universidad)

library(jtools)
export_summs(m1, m2,m3,m4)

Table 3.1:

	Model 1	Model 2	Model 3	Model 4
(Intercept)	9.61 ***	8.98 ***	9.21 ***	0.50 ***
	(0.00)	(0.00)	(0.00)	(0.00)
universidadTRUE	0.40 ***	0.08 ***	0.20 ***	0.26 ***
	(0.00)	(0.00)	(0.00)	(0.00)
cuelloBlancoTRUE		1.26 ***	0.80 ***
		(0.00)	(0.00)
habilidad			0.40 ***
			(0.00)
N	300000	300000	300000	300000
R2	0.03	0.26	0.33	0.07
*** p < 0.001; ** p < 0.01; * p < 0.05.