1 Introducción

Papers

Experimentos aleatorios

De Ree et al. (2018)
Ashraf, Berry, and Shapiro (2010)
Jayachandran et al. (2017)

Regresión

DiNardo and Pischke (1997)
Leuven and Oosterbeek (2008)

Matching

Ichino, Mealli, and Nannicini (2008)
Imbens (2015)

Diferencias en diferencias

Card and Krueger (2000)
Marie and Zölitz (2017)

Regresión discontinua

Pop-Eleches and Urquiola (2013)
Angrist and Lavy (1999)

1.1 ¿Qué es la inferencia causal?

Es el apalacamiento entre teoría y un conocimiento profundo de los detalles institucionales para estimar el impacto de eventos y decisiones sobre una variable de interés (Cunningham (2021))

La inferencia causal compara resultados potenciales, descripciones del mundo cuando se toman caminos alternativos (Angrist and Pischke (2014))

La inferencia causal siempre ha sido el nombre del juego en la econometría aplicada. El estadístico Paul Holland (1986) advierte que no puede haber causalidad sin manipulación, una máxima que parecería descartar la inferencia causal a partir de datos no experimentales. Los observadores menos reflexivos recurren a que la correlación no es causalidad. Como la mayoría de las personas que trabajan con datos para ganarse la vida, creemos que la correlación a veces puede proporcionar una evidencia bastante buena de una relación causal, incluso cuando la variable de interés no ha sido manipulada por un investigador o experimentador (Angrist and Pischke (2008)).

Uno de los pioneros en la inferencia causal es Ronald Fisher (Fisher (1935)) gracias a su libro The Design of experiments. Hoy es usual encontrar temas de inferencia causal como evaluación de programas.

1.2 Correlación no es causalidad

El efecto Mozart (Stock, Watson, and others (2015), p.186)

Imagínese que tenemos datos sobre el coeficiente intelectual de los niños a los 12 años y si estuvieron expuestos (sí/no) a Mozart cuando eran bebés.

Si tomamos los puntajes de CI promedio en ambos grupos, y simplemente tomamos la diferencia.

¿Qué esperas? ¿Qué significa eso?

Estadísticamente, significa que existe una asociación positiva entre la exposición a Mozart y el coeficiente intelectual.

¿Podemos darle a esta asociación una interpretación causal?

¿Escuchar a Mozart (causa) te hace más inteligente (efecto)? O ¿Hay algo más que impulse esta asociación?

Salario y Educación

Ahora tenemos información sobre los ingresos de las personas y si tienen un título universitario (sí/no)

Si comparamos las ganancias promedio en ambos grupos, ¿qué encontramos?

¿Podemos darle a esta asociación una interpretación causal?

¿Ganarías menos (efecto) si no hubieras ido a la universidad (causa)?

A veces hay correlaciones causales aún sin haber correlaciones observables.

Imaginemos un Banco Central que consulta al oráculo de delfos si se aproxima una recesión. Al tener una respuesta afirmativa el BC compra bonos inyectando liquidez a la economía. Estas operaciones de mercado abierto no mostrarán correlación con el resultado.

Los seres humanos muy rara vez actúan de manera aleatoria, y es la principal razón del por qué a correlación no implica causalidad. De hecho, la presencia de aleatoriedad es cricial para identificar efectos causales.

Existen dos grandes grupos de datos en términos generales: experimentales y no experimentales (también llamamos observacionales).

En datos observacionales, la regla es que correlación no implica causalidad, no la excepción. En parte esto se debe a que somos seres humanos quienes decidimos qué variables serán necesarias para tomar la mejor decisión, lo cual genera endogeneidad.

La elección o tratamiento que se estudia debe ser independiente de los potenciales resultados que se desea evaluar, solo así puede considerarse como un efecto causal.

Análisis Empírico: uso de datos para probar una teoría o estimar alguna relación entre variables.

1.3 Un repaso de regresión lineal

1.3.1 El valor esperado, esperanza

Suponga que la variable $X$ puede tomar valores $x_1,x_2,\ldots,x_k$, cada uno con probabilidad $f(x_1), f(x_2), \ldots, f(x_k)$ respectivamente. Se define el valor esperado como

\[ \begin{align} E(X) & = x_1f(x_1)+x_2f(x_2)+\dots+x_kf(x_k) \\ & = \sum_{j=1}^k x_jf(x_j) \end{align} \] Veamos un ejemplo numérico. Si $X$ toma valores $-1,0,2$ con probabilidades $0.3$, $0.3$ y $0.4$ respectivamente, entonces el valor esperado de $X$ es

\[ \begin{align} E(X) & = (-1)(0.3)+(0)(0.3)+(2)(0.4) \\ & = 0.5 \end{align} \]

De hecho, se puede tomar la esperanza de una función de a variable $X$, por ejemplo de $X^2$. En este caso $X^2$ toma valores $1,0,4$ con las mismas probabilidades:

\[ \begin{align} E(X^2) & = (-1)^2(0.3)+(0)^2(0.3)+(2)^2(0.4) \\ & = 1.9 \end{align} \] Propiedades

Para cualquier constante $c$, $E(c)=c$.
Para cualquier par de constantes $a$ y $b$, $E(aX+ b)=E(aX)+E(b)=aE(X)+b$.
Si tenemos las constantes $a_1, \dots, a_n$ y las variables aletorias $X_1, \dots, X_n$, entonces:

\[ \begin{align} E(a_1X_1+\dots+a_nX_n)=a_1E(X_1)+\dots+a_nE(X_n) \end{align} \] \[ \begin{align} E\bigg(\sum_{i=1}^na_iX_i\bigg)=\sum_{i=1}a_iE(X_i) \end{align} \]

El operador de esperanza $E(\cdot)$ es un concepto poblacional. Se refiere a todo el grupo de interés, no solo a la muestra que tenemos disponible.

Sean $W$ y $H$ dos variables aleatorias y $a$ y $b$ dos constantes:

\[ \begin{align} E(aW+b) & = aE(W)+b\ \text{para cualquier constantes $a$, $b$} \\ E(W+H) & = E(W)+E(H) \\ E\Big(W - E(W)\Big) & = 0 \end{align} \]

1.3.2 Varianza

La varianza de una variable aleatoria $W$ está dada por

\[ \begin{align} V(W)=\sigma^2=E\Big[\big(W-E(W)\big)^2\Big]\ \text{en la población} \end{align} \] Podemos mostrar que

\[ V(W)=E(W^2) - E(W)^2 \]

En una muestra dada de datos, podemos estimar la varianza mediante:

\[ \begin{align} \widehat{S}^2=(n-1)^{-1}\sum_{i=1}^n(x_i - \overline{x})^2 \end{align} \]

Propiedades

La varianza de $aX+b$ es $V(aX+b)=a^2V(X)$
$V(c) = 0$ para cualquier constante $c$
La varianza de la suma de dos variables aleatorias $X$ y $Y$ es

\[ V(X+Y)=V(X)+V(Y)+2\Big(E(XY) - E(X)E(Y)\Big) \tag{1.1} \]

Si las dos variables son independientes, entonces $E(XY)=E(X)E(Y)$ y $V(X+Y)$ es igual a la suma de $V(X)+V(Y)$.

1.3.3 Covarianza

La parte final de la ecuación \tag{1.1} es la covarianza. La covarianza mide la cantidad de dependencia lineal entre dos variables aleatorias. Lo representamos con el operador $C (X, Y)$.

La expresión $C (X, Y)> 0$ indica que dos variables se mueven en la misma dirección, mientras que $C (X, Y) <0$ indica que se mueven en direcciones opuestas. Por tanto, podemos reescribir la ecuación \tag{1.1} como:

\[ \begin{align} V(X+Y)=V(X)+V(Y)+2C(X,Y) \end{align} \]

Si bien es tentador decir que una covarianza cero significa que dos variables aleatorias no están relacionadas, eso es incorrecto. Podrían tener una relación no lineal. La definición de covarianza es

\[ C(X,Y)=E(XY) - E(X)E(Y) \tag{1.2} \]

Como dijimos, si $X$ e $Y$ son independientes, entonces $C (X, Y) = 0$ en la población. La covarianza entre dos funciones lineales es:

\[ \begin{align} C(a_1+b_1X, a_2+b_2Y)=b_1b_2C(X,Y) \end{align} \]

Las dos constantes, $a_1$ y $a_2$, se hacen cero porque su media son ellas mismas y, por lo tanto, la diferencia es igual a 0.

Interpretar la magnitud de la covarianza puede ser complicado. Para eso, estamos mejor si analizamos la correlación. Sea $W=\dfrac{X-E(X)}{\sqrt{V(X)}}$ y $Z=\dfrac{Y - E(Y)}{\sqrt{V(Y)}}$, entonces:

\[ \text{Corr}(X,Y) = \text{Cov}(W,Z)=\dfrac{C(X,Y)}{\sqrt{V(X)V(Y)}} \]

El coeficiente de correlación está limitado por $-1$ y $1$. Una correlación positiva (negativa) indica que las variables se mueven de la misma manera (opuesta). Cuanto más cerca esté el coeficiente de $1$ o $-1$, más fuerte será la relación lineal.

1.3.4 El modelo poblacional

Suponga que hay dos variables, $x$ e $y$, y queremos ver cómo varía $y$ con los cambios en $x$.

Hay tres preguntas que surgen de inmediato:

¿qué pasa si $y$ se ve afectado por factores distintos de $x$? ¿Cómo manejaremos eso?
¿cuál es la forma funcional que conecta estas dos variables?
si estamos interesados en el efecto causal de $x$ sobre $y$, ¿cómo podemos distinguir eso de una correlación?

Comencemos con un modelo específico:

\[ y=\beta_0+\beta_1x+u \tag{1.2} \]

Se supone que este modelo es el que sigue la población. La ecuación (1.2) define un modelo de regresión lineal bivariado. Los términos del lado izquierdo generalmente se consideran el efecto, y los términos del lado derecho se consideran las causas.

Respuestas a nuestras preguntas:

La ecuación (1.2) permite explícitamente que otros factores afecten a $y$ al incluir una variable aleatoria llamada término de error, $u$.
Esta ecuación también modela explícitamente la forma funcional asumiendo que y es linealmente dependiente de $x$. Llamamos al coeficiente $\beta_0$ el parámetro de intersección y al coeficiente $\beta_1$ el parámetro de la pendiente.

Estos describen una población, y nuestro objetivo en el trabajo empírico es estimar sus valores. Nunca observamos directamente estos parámetros, porque no son datos. Sin embargo, lo que podemos hacer es estimar estos parámetros utilizando datos y supuestos. Para hacer esto, necesitamos supuestos creíbles para estimar con precisión estos parámetros con datos.

En este marco de regresión simple, todas las variables no observadas que determinan y están absorbidas por el término de error $u$.

Aún debemos elaborar más para poder responder a esta pregunta.

Sin pérdida de generalidad, sea el valor esperado de $u$ igual a cero en la población:

\[ E(u)=0 \tag{1.3} \] Si normalizamos la variable aleatoria $u$ para que sea $0$, no tiene importancia. ¿Por qué? Porque la presencia de $\beta_0$ (el término de intersección) siempre nos permite esta flexibilidad. Si el promedio de $u$ es diferente de $0$, por ejemplo, digamos que es $\alpha_0$, entonces ajustamos la intersección. Sin embargo, ajustar la intersección no tiene ningún efecto sobre el parámetro de pendiente $\beta_1$. Por ejemplo:

\[ \begin{align} y=(\beta_0+\alpha_0)+\beta_1x+(u-\alpha_0) \end{align} \]

donde $\alpha_0 = E(u)$. El nuevo término de error es $(u-\alpha_0)$, y el nuevo intercepto es $\beta_0+ \alpha_0$. Pero notemos que si cambia al intercepto, $\beta_1$ no cambia.

1.3.5 Independencia en media

Se define como:

\[ E(u\mid x)=E(u)\ \text{para todo $x$} \tag{1.4} \]

donde $E(u\mid x)$ significa el valor esperado de $u$ dado $x$. Si (1.4) es verdadera, entonces $u$ es independiente en media de $x$.

Un ejemplo podría ayudar aquí. Supongamos que estamos estimando el efecto de la escolaridad en los salarios y $u$ es una habilidad no observada. La independencia en media requiere que $E(\text{habilidad}\mid x=8)=E(\text{habilidad}\mid x=12)=E(\text{habilidad}\mid x=16)$. Debido a que las personas eligen en cuánta educación invertir en función de sus propias habilidades y atributos no observados, es probable que se viole la ecuación (1.4), al menos en este ejemplo.

Pero digamos que estamos dispuestos a hacer este supuesto. Luego, combinando esta nueva suposición, $E(u\mid x)=E(u)$ (supuesto nada trivial), con $E (u) = 0$, se obtiene el siguiente nuevo supuesto:

\[ \begin{align} E(y\mid x)=\beta_0+\beta_1x \end{align} \]

que muestra que la función de regresión poblacional es una función lineal de $x$, que también se conoce como función de esperanza condicional. Esta relación es crucial para la intuición del parámetro, $\beta_1$, como parámetro causal.

1.3.6 Mínimos cuadrados ordinarios (OLS)

Dados los datos de $x$ y $y$, ¿cómo podemos estimar los parámetros poblacionales, $\beta_0$ y $\beta_1$? Sean $\big\{(x_i,\ \textrm{and}\ y_i): i=1,2,\dots,n \big\}$ muestras aleatorias de tamaño $n$ de la población. Al insertarlas en la ecuación poblacional tenemos:

\[ \begin{align} y_i=\beta_0+\beta_1x_i+u_i \end{align} \]

donde $i$ indica una observación particular. Observamos $y_i$ y $x_i$ pero no $u_i$. Solo sabemos que $u_i$ está ahí. Luego usamos las dos restricciones de población que discutimos anteriormente:

\[ \begin{align} E(u) & =0 \\ E(u\mid x) & = 0 \end{align} \]

para obtener ecuaciones para estimar $\beta_0$ y $\beta_1$. Usando lo muestral tenemos:

\[ \begin{align} \dfrac{1}{n}\sum_{i=1}^n\Big(y_i-\widehat{\beta_0}-\widehat{\beta_1}x_i\Big) & =0 \tag{1.5} \\ \dfrac{1}{n}\sum_{i=1}^n \Big(x_i\Big[y_i-\widehat{\beta_0}-\widehat{\beta_1}x_i \Big]\Big) & =0 \tag{1.6} \end{align} \]

resolviendo el sistema tenemos

\[ \begin{align} \widehat{\beta_0}=\overline{y}-\widehat{\beta_1} \overline{x} \end{align} \] y

\[ \begin{align} \widehat{\beta}_1 & = \dfrac{\sum_{i=1}^n (x_i-\overline{x}) (y_i-\overline{y})}{\sum_{i=1}^n(x_i-\overline{x})^2 } \\ & =\dfrac{\text{Covarianza muestral}(x_i,y_i) }{\text{Varianza muestral}(x_i)} \end{align} \]

Para cualquier estimación de $\widehat{\beta}_0, \widehat{\beta}_1$, definimos un valor ajustado para cada $i$ como:

\[ \begin{align} \widehat{y_i}=\widehat{\beta}_0+\widehat{\beta}_1x_i \end{align} \] Recuerde que $i=\{1, \ldots, n\}$, entonces tenemos $n$ de estas ecuaciones. Este es el valor que predecimos para $y_i$ dado que $x = x_i$. Pero hay un error de predicción porque $y\neq y_i$. Llamamos a ese error el residuo, y aquí usamos la notación $\widehat{u_i}$ para ello. Entonces el residuo es igual a:

\[ \begin{align} \widehat{u_i} & = y_i-\widehat{y_i} \\ \widehat{u_i} & = y_i-\widehat{\beta_0}-\widehat{\beta_1}x_i \end{align} \] Veamos una simulación:

library(tidyverse)

set.seed(1)
tb <- tibble(
  x = rnorm(10000),
  u = rnorm(10000),
  y = 5.5*x + 12*u
) 

reg_tb <- tb %>% 
  lm(y ~ x, .) %>%
  print()

## 
## Call:
## lm(formula = y ~ x, data = .)
## 
## Coefficients:
## (Intercept)            x  
##    -0.04991      5.55690

reg_tb$coefficients

## (Intercept)           x 
## -0.04990882  5.55690164

tb <- tb %>% 
  mutate(
    yhat1 = predict(lm(y ~ x, .)),
    uhat1 = residuals(lm(y ~ x, .)),
  )

summary(tb[-1:-3])

##      yhat1               uhat1         
##  Min.   :-20.45096   Min.   :-51.5275  
##  1st Qu.: -3.79189   1st Qu.: -8.1520  
##  Median : -0.13842   Median : -0.1727  
##  Mean   : -0.08624   Mean   :  0.0000  
##  3rd Qu.:  3.71578   3rd Qu.:  7.9778  
##  Max.   : 21.12342   Max.   : 44.7176

cc <- coef(lm(y ~ x, tb))

tb %>% 
  lm(y ~ x, .) %>% 
  ggplot(aes(x=x, y=y)) + 
  ggtitle("Línea de regresión OLS") +
  geom_point(size = 0.05, color = "black", alpha = 0.5) +
  geom_smooth(method = lm, color = "black") +
  annotate("text", x = -1.5, y = 30, color = "red", 
           label = paste("y-intercepto = ", round(cc[1],5))) +
  annotate("text", x = 1.5, y = -30, color = "blue", 
           label = paste("Pendiente =", round(cc[2],5)))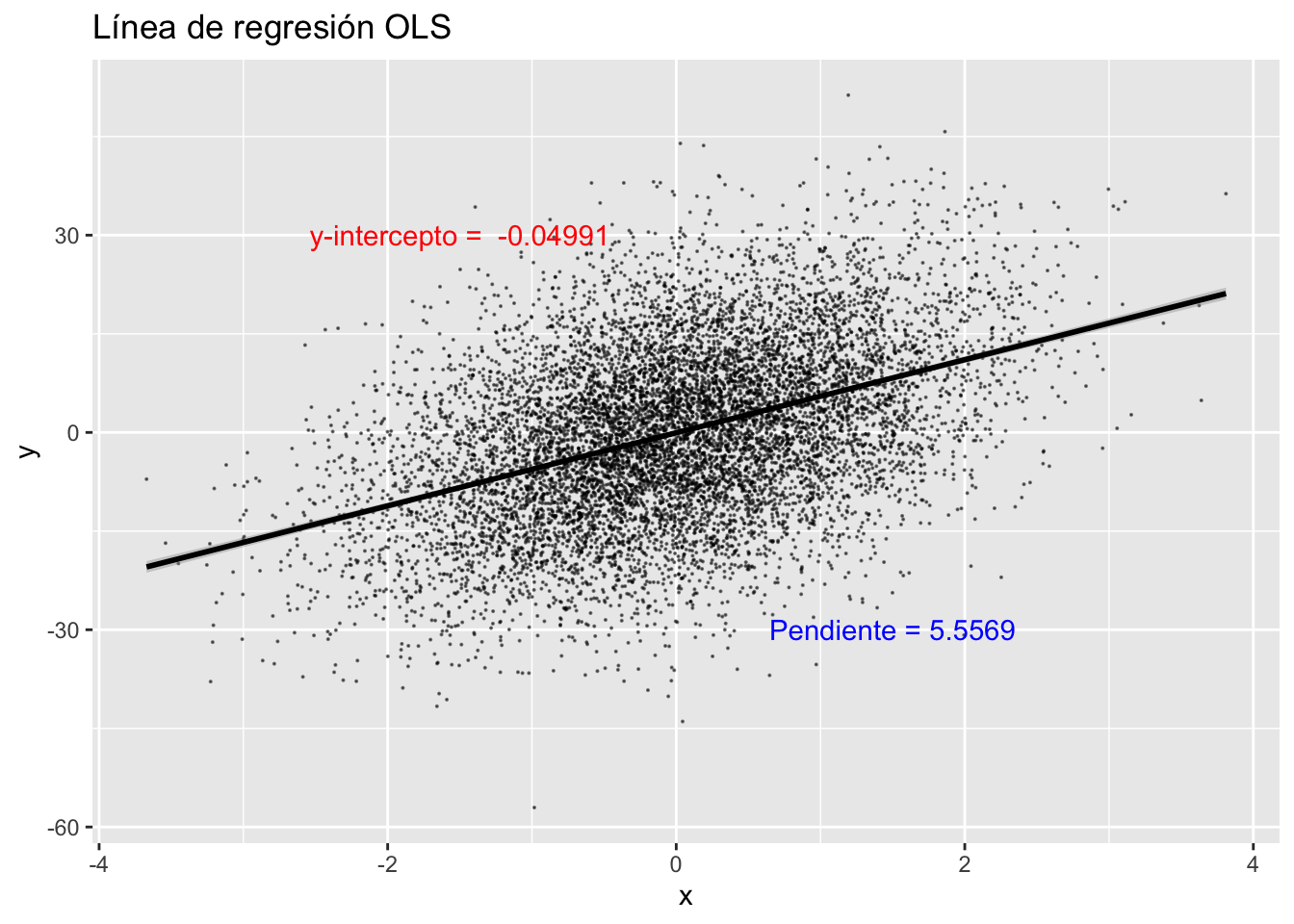

1.3.7 Propiedades de OLS

¿Recuerdas cómo obtuvimos $\beta_0$ y $\beta_1$? Cuando se incluye una intersección, tenemos:

\[ \begin{align} \sum_{i=1}^n\Big(y_i-\widehat{\beta}_0 -\widehat{\beta}_1x_i\Big) =0 \end{align} \]

El residuo de OLS siempre suma cero, por construcción.

\[ \sum_{i=1}^n \widehat{u_i}=0 \tag{1.6} \]

La covarianza muestral (y por tanto la correlación muestral) entre las variables explicativas y los residuos es siempre cero:

\[ \begin{align} \sum_{i=1}^n x_i \widehat{u_i}=0 \tag{1.7} \end{align} \] Debido a que $\widehat{y_i}$ son funciones lineales de $x_i$, los valores ajustados y los residuos tampoco están correlacionados:

\[ \begin{align} \sum_{i=1}^n \widehat{y_i} \widehat{u_i}=0 \tag{1.8} \end{align} \]

Ambas propiedades ((1.7) y (1.8)) se dan por construcción. En otras palabras, se seleccionaron $\widehat{\beta}_0$ y $\widehat{\beta}_1$ para que así sea.

Una tercera propiedad es que si sustituimos el promedio de x, predecimos el promedio de la muestra para y. Es decir, el punto $(\overline{x}, \overline{y})$ está en la línea de regresión OLS, o:

\[ \begin{align} \overline{y}=\widehat{\beta}_0+\widehat{\beta}_1 \overline{x} \end{align} \]

1.3.8 Bondad de ajuste

Para cada observación, escribimos

\[ \begin{align} y_i=\widehat{y_i}+\widehat{u_i} \end{align} \]

Definimos la suma total de cuadrados (SST), la suma de cuadrados explicada (SSE) y la suma de cuadrados residual (SSR) como

\[ \begin{align} SST & = \sum_{i=1}^n (y_i - \overline{y})^2 \tag{1.9} \\ SSE & = \sum_{i=1}^n (\widehat{y_i} - \overline{y})^2 \tag{1.10} \\ SSR & = \sum_{i=1}^n \widehat{u_i}^2 \tag{1.11} \end{align} \] que, divididas para $n-1$, son varianzas muestrales de $y_i$, $\widehat{y_i}$ y $\widehat{u_i}$ respectivamente.

Dado que la ecuación (1.8) muestra que los valores ajustados no están correlacionados con los residuos, podemos escribir la siguiente ecuación:

\[ \begin{align} SST=SSE+SSR \end{align} \]

Suponiendo que $SST> 0$, podemos definir la fracción de la variación total en $y_i$ que se explica por $x_i$ (o la línea de regresión OLS) como

\[ \begin{align} R^2=\dfrac{SSE}{SST}=1-\dfrac{SSR}{SST} \end{align} \]

Sin embargo, te animo a que no te fijes en $R$-cuadrado en proyectos de investigación donde el objetivo es estimar algún efecto causal. Es una medida de resumen útil, pero no nos informa sobre causalidad. Recuerda, no estás tratando de explicar la variación en $y$ si estás tratando de estimar algún efecto causal. El $R^2$ nos dice qué parte de la variación en $y_i$ se explica por las variables explicativas. Pero si estamos interesados en el efecto causal de una sola variable, $R^2$ es irrelevante. Para la inferencia causal, necesitamos la ecuación (1.4) (independencia en media).

1.3.9 Esperanza de OLS

Los residuos siempre promedian a cero cuando aplicamos OLS a una muestra, independientemente de cualquier modelo subyacente. Pero nuestro trabajo se vuelve más difícil. Ahora tenemos que estudiar las propiedades estadísticas del estimador OLS, refiriéndonos a un modelo poblacional y asumiendo un muestreo aleatorio.

El campo de la estadística matemática se ocupa de cuestiones tipo ¿cómo se comportan los estimadores en diferentes muestras de datos? En promedio, por ejemplo, ¿obtendremos la respuesta correcta si muestreamos repetidamente? Necesitamos encontrar el valor esperado de los estimadores de OLS — en efecto, el resultado promedio en todas las muestras aleatorias posibles — y determinar si estamos en lo cierto, en promedio. Esto conduce naturalmente a que queramos que sea insesgado, una propiedad que es deseable para todos los estimadores.

\[ E(\widehat{\beta})=\beta \tag{1.12} \] Hay varios supuestos necesarios para que OLS sea insesgado

La primera suposición se llama lineal en los parámetros.
Nuestro segundo supuesto es el muestreo aleatorio. Tenemos una muestra aleatoria de tamaño $n$, $\{ (x_i, y_i){:} i=1, \dots, n\}$, siguiendo el modelo poblacional. Sabemos cómo utilizar estos datos para estimar $\beta_0$ y $\beta_1$ por OLS. Debido a que cada $i$ es una extracción de la población, podemos escribir, para cada $i$:

\[ \begin{align} y=\beta_0+\beta_1 x+u \end{align} \]

Observa que $u_i$ aquí es el error no observado para la observación $i$. No es el residuo lo que calculamos a partir de los datos.

El tercer supuesto se llama variación muestral en la variable explicativa. Es decir, los resultados de la muestra en $x_i$ no tienen el mismo valor. Esto es lo mismo que decir que la varianza muestral de $x$ no es cero.
Se llama supuesto de media condicional igual a cero y es probablemente la suposición más crítica en la inferencia causal. En la población, el término de error tiene media cero dado cualquier valor de la variable explicativa:

\[ \begin{align} E(u\mid x)=E(u)=0 \end{align} \] Este es el supuesto clave para mostrar que OLS es insesgado, y que el valor cero no tiene importancia una vez que asumimos que $E (u∣x)$ no cambia con $x$. Ten en cuenta que podemos calcular estimaciones de OLS independientemente de que este supuesto se cumpla o no, incluso si existe un modelo poblacional subyacente.

Con estos supuestos en mente, demostremos (1.12) paso a paso.

Paso 1

Escribamos $\widehat{\beta_1}$ como $\dfrac{C(x,y)}{V(x)}$:

\[ \begin{align} \widehat{\beta_1}=\dfrac{\sum_{i=1}^n (x_i - \overline{x})y_i}{\sum_{i=1}^n (x_i - \overline{x})^2} \end{align} \] Sea $\sum_{i=1}^n (x_i - \overline{x})^2=SST_x$ (variación total de $x_i$), entonces:

\[ \begin{align} \widehat{\beta_1}=\dfrac{ \sum_{i=1}^n (x_i - \overline{x})y_i}{SST_x} \end{align} \] Paso 2

Reemplazar cada $y_i$ con $y_i= \beta_0+\beta_1 x_i+u_i$ (que usa el primer y segundo supuesto). El numerado sería:

\[ \begin{align} \sum_{i=1}^n (x_i - \overline{x})y_i & =\sum_{i=1}^n (x_i - \overline{x})(\beta_0+\beta_1 x_i+u_i) \\ & = \beta_0 \sum_{i=1}^n (x_i - \overline{x})+\beta_1 \sum_{i=1}^n (x_i - \overline{x})x_i+\sum_{i=1}^n (x_i+\overline{x}) u_i \\ & =0+\beta_1 \sum_{i=1}^n (x_i - \overline{x})^2+ \sum_{i=1}^n (x_i - \overline{x})u_i \\ & = \beta_1 SST_x+\sum_{i=1}^n (x_i - \overline{x}) u_i \end{align} \]

Notemos que usamos $\sum_{i=1}^n (x_i-\overline{x})=0$ y $\sum_{i=1}^n (x_i - \overline{x})x_i=\sum_{i=1}^n (x_i - \overline{x})^2$. Se ha demostrado que:

\[ \begin{align} \widehat{\beta_1} & = \dfrac{ \beta_1 SST_x+ \sum_{i=1}^n (x_i - \overline{x})u_i }{SST_x} \nonumber \\ & = \beta_1+\dfrac{ \sum_{i=1}^n (x_i - \overline{x})u_i }{SST_x} \end{align} \]

Ten en cuenta que la última pieza es el coeficiente de pendiente de la regresión OLS de $u_i$ en $x_i$, $i: 1, \dots, n$. No podemos hacer esta regresión porque las $u_i$ no se observan. Ahora define $w_i=\dfrac{(x_i - \overline{x})}{SST_x}$para que tengamos lo siguiente:

\[ \begin{align} \widehat{\beta_1}=\beta_1+\sum_{i=1}^n w_i u_i \end{align} \]

Esto nos ha mostrado lo siguiente: es una función lineal de los errores no observados, $u_i$. Las $w_i$ son todas funciones de $\{ x_1, \dots, x_n \}$.

Paso 3

Encuentrar $E(\widehat{\beta_1})$. Bajo el supuesto de muestreo aleatorio y el supuesto de media condicional cero, $E(u_i \mid x_1, \dots, x_n)=0$, esto es, condicional a cada una de las $x$ variables:

\[ \begin{align} E\big(w_iu_i\mid x_1, \dots, x_n\big) = w_i E\big(u_i \mid x_1, \dots, x_n\big)=0 \end{align} \]

porque $w_i$ es una función de $\{x_1, \dots, x_n\}$. Notemos que esta expresión es cierta debido a que $E(u_i \mid x_1, \dots, x_n)=0$, no porque sea un supuesto en sí mismo.

Ahora podemos completar la prueba: condicional en $\{x_1, \dots, x_n\}$:

\[ \begin{align} E(\widehat{\beta_1}) & = E \bigg(\beta_1+\sum_{i=1}^n w_i u_i \bigg) \\ & =\beta_1+\sum_{i=1}^n E(w_i u_i) \\ & = \beta_1+\sum_{i=1}^n w_i E(u_i) \\ & =\beta_1 +0 \\ & =\beta_1 \end{align} \]