6 Diferencias en diferencias
En cuasiexperimentos, la fuente de aleatoriedad como si en la asignación de tratamientos a menudo no puede evitar por completo las diferencias sistemáticas entre los grupos de control y de tratamiento.
Este problema fue encontrado por Card & Krueger (1994) quienes usan la geografía como la asignación de tratamiento aleatorio como si para estudiar el efecto sobre el empleo en restaurantes de comida rápida causado por un aumento en el salario mínimo estatal en Nueva Jersey en el año de 1992.
Su idea era utilizar el hecho de que el aumento del salario mínimo se aplicaba a los empleados de Nueva Jersey (grupo de tratamiento) pero no a los que vivían en la vecina Pensilvania (grupo de control).
Es bastante concebible que tal aumento salarial no esté correlacionado con otros determinantes del empleo. Sin embargo, todavía puede haber algunas diferencias específicas de cada estado y, por tanto, diferencias entre el grupo de control y el grupo de tratamiento. Esto haría que el estimador de diferencias fuera sesgado e inconsistente.
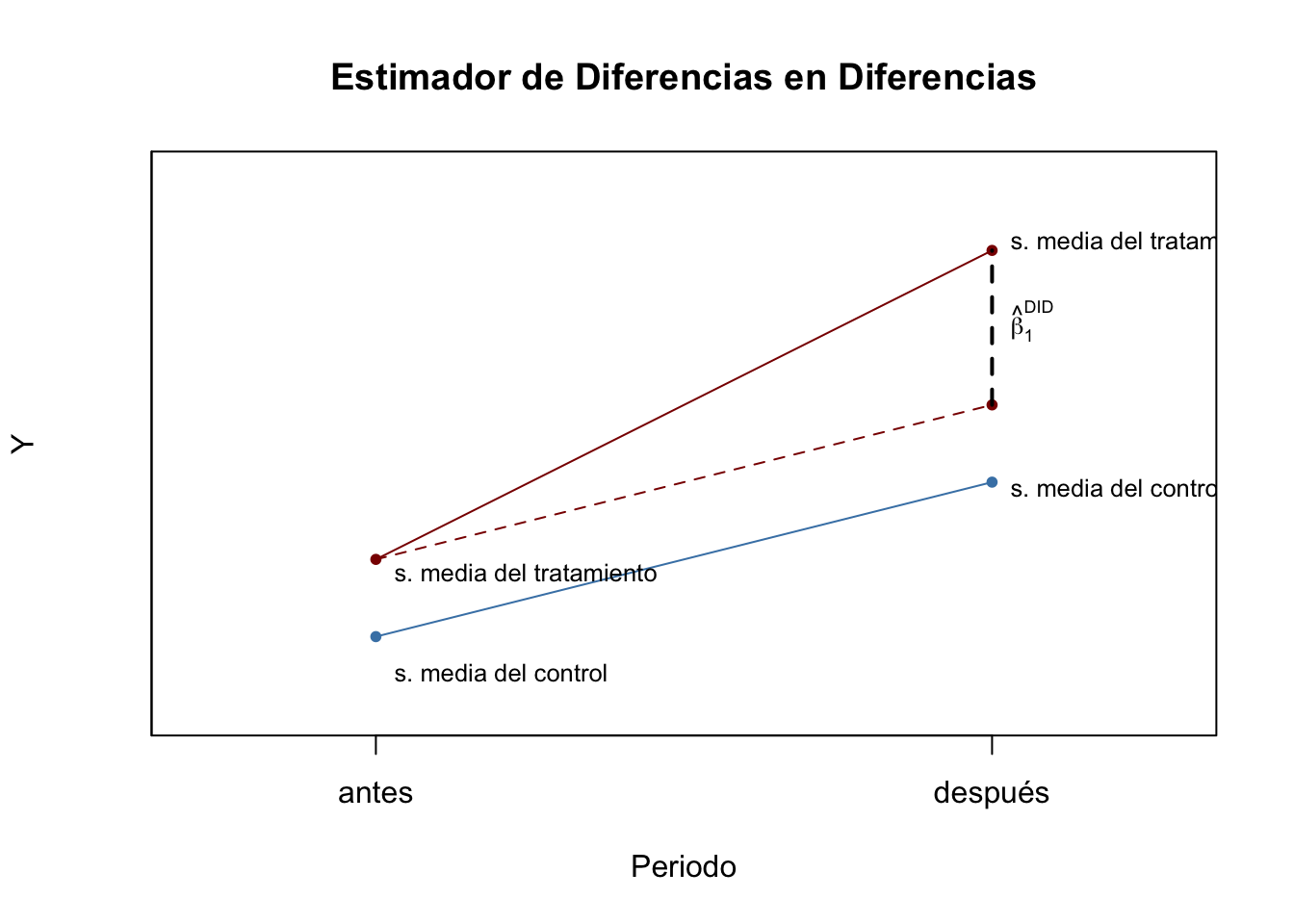
Card y Krueger (1994) resolvieron esto usando un estimador DID: recolectaron datos en febrero de 1992 (antes del tratamiento) y noviembre de 1992 (después del tratamiento) para los mismos restaurantes y estimaron el efecto del aumento salarial analizando las diferencias en el diferencias en el empleo para Nueva Jersey y Pensilvania antes y después del aumento. El estimador DID es
\[ \begin{align} \widehat{\beta}_1^{\text{diffs-in-diffs}} =& \, (\overline{Y}^{\text{tratamiento,después}} - \overline{Y}^{\text{tratamiento,antes}}) - (\overline{Y}^{\text{control,después}} - \overline{Y}^{\text{control,antes}}) \\ =& \Delta \overline{Y}^{\text{tratamiento}} - \Delta \overline{Y}^{\text{control}} \end{align} \] con
\(\overline{Y}^{\text{tratamiento,antes}}\): promedio de la muestra en el grupo de tratamiento antes del tratamiento.
\(\overline{Y}^{\text{tratamiento,después}}\): promedio de la muestra en el grupo de tratamiento después del tratamiento.
\(\overline{Y}^{\text{tratamiento,antes}}\): promedio de la muestra en el grupo de control antes del tratamiento.
\(\overline{Y}^{\text{tratamiento,después}}\): promedio de la muestra en el grupo de control después del tratamiento.
El estimador DID también se puede escribir en notación de regresión: \(\widehat{\beta}_1^{\text{DID}}\) es el estimador MCO de \(\beta_1\) en
\[ \begin{align} \Delta Y_i = \beta_0 + \beta_1 X_i + u_i, \end{align} \]
donde \(\Delta Y_i\) denota la diferencia en los resultados previos y posteriores al tratamiento del individuo \(i\) y \(X_i\) es el indicador de tratamiento.
Añadiendo covariables adicionales que miden las características previas al tratamiento obtenemos:
\[ \begin{align} \Delta Y_i = \beta_0 + \beta_1 X_i + \beta_2 W_{1i} + \dots + \beta_{1+r} W_{ri} + u_i, \end{align} \]
el estimador de diferencias en diferencias con covariables adicionales. Las covariables adicionales pueden conducir a una estimación más precisa de \(\beta_1\).
Debemos enfocarnos en la estimación del efecto del tratamiento usando DID en el caso más simple, es decir, un grupo de control y un grupo de tratamiento observados durante dos períodos de tiempo, uno antes y otro después del tratamiento.
Ejemplo
fte: equivalente al empleo total (variable continua), variable de resultadot: tiempo, denota el antes y el después.
uu <- "https://github.com/vmoprojs/DataLectures/raw/master/cardkrueger1994.dta"
datos <- read_dta(uu)
std <- function(x) sd(na.omit(x))/sqrt(length(na.omit(x)))
datos %>%
group_by(treated, t) %>%
summarize(means = mean(fte,na.rm=TRUE),std = std(fte))## # A tibble: 4 x 4
## # Groups: treated [2]
## treated t means std
## <dbl+lbl> <dbl> <dbl> <dbl>
## 1 0 [PA] 0 19.9 1.32
## 2 0 [PA] 1 17.5 0.901
## 3 1 [NJ] 0 17.1 0.483
## 4 1 [NJ] 1 17.6 0.491tval <- (17.57266-17.06518)-(17.54221-19.94872)
tval## [1] 2.91399El impacto del programa es 2.9 empleos.
Usando OLS:
datos$TY <- datos$treated*datos$t
m1 <- lm(fte~TY+ treated +t,data = datos)
m2 <- lm(fte~TY +treated +t +bk+ kfc+ roys,data = datos)
export_summs(m1,m2)| Model 1 | Model 2 | |
|---|---|---|
| (Intercept) | 19.95 *** | 21.16 *** |
| (1.02) | (1.14) | |
| TY | 2.91 | 2.94 * |
| (1.61) | (1.46) | |
| treated | -2.88 * | -2.32 * |
| (1.13) | (1.03) | |
| t | -2.41 | -2.40 |
| (1.45) | (1.31) | |
| bk | 0.92 | |
| (0.89) | ||
| kfc | -9.20 *** | |
| (1.01) | ||
| roys | -0.90 | |
| (0.97) | ||
| N | 801 | 801 |
| R2 | 0.01 | 0.19 |
| *** p < 0.001; ** p < 0.01; * p < 0.05. | ||
Ventajas de OLS
Manera conveniente de obtener errores estándar.
Fácil de agregar regresores adicionales que varían en el tiempo.
La variable de tratamiento puede ser continua.
6.1 Supuestos
Supuesto principal: En ausencia de intervención, los grupos de tratamiento y control tendrían tendencias comunes.
No se necesita datos de panel para aplicar DID.
La composición de los grupos de tratamiento y control no cambia con el tiempo.
Respecto al supuesto de tendencia común: en principio este supuesto no es comprobable, especialmente con 2 períodos de tiempo.
Con múltiples períodos de tiempo, se puede testear: investigar las tendencias previas a la intervención.
6.1.1 Solución al supuesto de tendencia común
Incluir covariables que varían en el tiempo y/o tendencias de tiempo específicas de grupo.
Diferencia en diferencia en diferencias.
Enfoque de grupo de control sintético.
Enfoque de diferencia en diferencias + variable instrumental.
Cambios en cambios (dif-en-dif no lineal).