2 Experimentos aleatorios (modelo de resultado potencial)
Empecemos con un ejemplo, donde \(Y\) representa el estado de salud, que es nuestra variable de resultado de interés. \(Y_i\) es el estado de salud de la persona \(i\). El resultado \(Y_i\) está registrado en nuestros datos. Pero, frente a la opción de pagar por un seguro, la persona \(i\) tiene dos resultados potenciales, de los cuales solo uno se observa.
Para distinguir un resultado potencial de otro, añadimos otro subíndice: no comprar el seguro es \(Y_{0i}\) para la persona \(i\) mientras que comprar el seguro es \(Y_{1i}\) para la persona \(i\). Los resultados potenciales son lo que habría pasado al tomar esa decisión. El efecto causal de comprar el seguro en el estado de salud es \(Y_{1i}-Y_{0i}\).
Pensemos en dos estudiantes que les ofrecen un seguro en la universidad, Esteban y Constanza. Esteban, luego de pensarlo, llega a la conclusión que el seguro vale la pena. Digamos que \(Y_{0i}=3\) y \(Y_{1i}=4\) para \(i=\text{Esteban}\). Para él, el efecto causal en el estado de salud es:
\[ Y_{1,\text{Esteban}}-Y_{0,\text{Esteban}} = 1. \] La siguiente tabla resume la información:
| Esteban | Constanza | |
|---|---|---|
| Resultado potencial sin seguro: \(Y_{0i}\) | 3 | 5 |
| Resultado potencial con seguro: \(Y_{1i}\) | 4 | 5 |
| Tratamiento (seguro elegido): \(D_{i}\) | 1 | 0 |
| Resultado en salud: \(Y_i\) | 4 | 5 |
| Efecto del tratamiento: \(Y_{1i}-Y_{0i}\) | 1 | 0 |
Notemos que esta tabla es imaginaria, pues Esteban puede comprar el seguro, revelándonos \(Y_{1i}\), o no comprarlo \(Y_{0i}\).
La información de Constanza también se muestra en la tabla. Digamos que Esteban si compra el seguro y Constanza no, entonces
\[ Y_{\text{Esteban}} = Y_{1,\text{Esteban}}=4 \]
\[ Y_{\text{Constanza}} = Y_{0,\text{Constanza}}=5 \]
La diferencia entre ellos es
\[ Y_{\text{Esteban}}-Y_{\text{Constanza}} =-1 \]
Usando este valor (que de hecho si observamos), la decisión de Esteban de comprar el seguro es contraproducente: la salud de Esteban que si está asegurado es peor que la de Constanza que no está asegurada.
De hecho, la comparación entre Esteban (se salud frágil) y Constanza (de salud fuerte) nos dice poco acerca de los efectos causales de sus elecciones. Esto puede verse de mejor manera en conjunto con los resultados potenciales:
\[ Y_{\text{Esteban}}-Y_{\text{Constanza}} = Y_{1,\text{Esteban}}-Y_{0,\text{Constanza}} \] \[ =(Y_{1,\text{Esteban}}-Y_{0,\text{Esteban}})+(Y_{0,\text{Esteban}}-Y_{0,\text{Constanza}}) \] \[ =(1)+(-2) \] Se introdujo \(Y_{0,\text{Esteban}}\) sumando y restando en la ecuación, generando dos comparaciones ocultas que determinan la que terminamos observando.
La primera comparación \((Y_{1,\text{Esteban}}-Y_{0,\text{Esteban}})\) es el efecto causal de la compra del seguro en la salud de Esteban, que es igual a \(1\).
La segunda comparación \((Y_{0,\text{Esteban}}-Y_{0,\text{Constanza}})\) es el estado de salud de dos estudiantes que no compraron el seguro. Este valor, que es igual a \(-2\) refleja la fragilidad del estado de salud de Esteban. El segundo término se conoce como sesgo de selección.
En resumen:
Queremos calcular el efecto del tratamiento binario \(D_i\) en la variable de resultado \(Y_i\).
Para cada individuo \(i\) el modelo postula dos resultados potenciales: \(Y_{0i}\) y \(Y_{1i}\).
\(Y_{0i}\) es el resultado del individuo \(i\) sin tratamiento (\(D_i=0\)), \(Y_{1i}\) es el resultado del individuo \(i\) con tratamiento (\(D_i=1\)).
Dado que \(i\) solo puede elegir una de las dos opciones, el resultado bajo la otra opción (el contrafactual), no se observa.
El resultado observado \(Y_i\) se relaciona con los resultados potenciales de la siguiente manera:
\[ Y_i = Y_i(D_i) = Y_{0i}(1-D_i)+Y_{1i}D_i. \] El modelo de resultados potenciales separa los efectos causales del mecanismo de asignación y los supuestos de la forma funcional, y hace que la naturaleza del tratamiento (\(D_i\)) sea muy explícita.
2.1 Efectos de tratamiento
Average treatment effect
\[ ATE= E[Y_{1i} - Y_{0i} ] \] Average treatment effect on the treated
\[ ATT = E[Y_{1i} - Y_{0i}| D_i = 1] \]
Conditional average treatment effect
\[ CATE = E[Y_{1i} - Y_{0i} |X_i = x] \]
Local average treatment effect
\[ LATE = E[Y_{1i} - Y_{0i} |\text{Compliers}] \]
2.2 Causa y efecto
Supongamos que estamos interesados en el regreso a la educación universitaria para las personas con un título universitario (un \(ATT\)), es decir:
\[ E[Y_{1i}| D_i = 1]-E[Y_{0i}| D_i = 1] \] Problema: no hay personas con titulación universitaria que no tengan titulación universitaria. Es decir, no se observa el contrafactual \(E[Y_{0i}| D_i = 1]\).
Solo observamos \(Y_{0i}\) para aquellas personas que no fueron a la universidad. La diferencia entre las ganancias de ambos grupos es:
\[ E[Y_{1i}| D_i = 1]-E[Y_{0i}| D_i = 0] \]
Sumamos y restamos \(E[Y_{0i}| D_i = 1]\):
\[ E[Y_{1i}| D_i = 1]-E[Y_{0i}| D_i = 1]+E[Y_{0i}| D_i = 1]-E[Y_{0i}| D_i = 0] \] que es igual a
\[ E[Y_{1i}-Y_{0i}| D_i = 1]+(E[Y_{0i}| D_i = 1]-E[Y_{0i}| D_i = 0]) \]
La primera parte \(E[Y_{1i}-Y_{0i}| D_i = 1]+E[Y_{0i}| D_i = 1]\) mide el ATT.
La idea es que tome la diferencia entre individuos que son intrínsecamente idénticos, excepto por su educación y su impacto en los ingresos.
La segunda parte \((E[Y_{0i}| D_i = 1]-E[Y_{0i}| D_i = 0])\) mide el sesgo de selección. Esto es, las personas con y sin título universitario pueden ser intrínsecamente diferentes.
- El sesgo de selección captura diferencias en capacidad y/o motivación.
- El sesgo de selección casi siempre está presente siempre que la elección de los individuos influya en \(D\).
- \(D\) es endógeno.
- La mayoría de los problemas al plantear cuestiones causales importantes surgen cuando el sesgo de selección o de endogeneidad no es ignorable.
2.2.1 ¿Qué hacer?
Hacer experimentos aleatrios.
Suponer que, condicional a los observables, el sesgo no existe (unconfoundedness). Esta es la base para los métodos matching (incluido OLS).
Aplicar un método que imite los experimentos aleatorios.
- Diferencias en diferencias.
- Diferencias en diferencias.
- Regresión discontinua.
Aceptar que no podemos dar una estimación (puntual) precisa y calcular los límites superior e inferior.
2.3 Ensayos aleatorizados
La asignación aleatoria a los grupos de tratamiento y control asegura que las unidades tratadas y no tratadas sean, en promedio, las mismas. Sin sesgo de selección.
Ampliamente usado en la economía hoy en día (Banerjee, Duflo, Karlan, Kremer, pero criticado por Deaton)
Costoso, lleva tiempo, validez externa limitada, restringe la atención a las intervenciones que pueden ser aleatorias
2.3.1 Stable Unit Treatment Value Assumption
Evaluar el efecto causal de un tratamiento (binario) requiere observar más de una unidad.
Imbens and Rubin (2015) definen \(SUTVA\) de la siguiente manera:
Los resultados potenciales para cualquier unidad no varían con los tratamientos asignados a otras unidades y, para cada unidad, no existen diferentes formas o versiones de cada nivel de tratamiento, lo que lleva a diferentes resultados potenciales Imbens and Rubin (2015).
Sin interferencia. A menudo no es creíble el efecto encontrado en estudios a nivel de aula/escuela; por lo tanto, aleatorizar a nivel de tipos de escuelas/escuelas en lugar de estudiantes.
Sin variaciones ocultas de tratamientos. Por ejemplo: no debería importar si el tratamiento fue asignado por el investigador o elegido por la persona.
\(SUTVA\) es solo una posible restricción de exclusión para modelizar interacciones entre unidades y el conjunto de niveles de tratamiento en un experimento en particular.
En muchos entornos, \(SUTVA\) es la opción líder.
2.3.2 Ensayos aleatorios
- Ventaja: la asignación aleatoria de \(D_i\) es independiente de las características de los participantes.
- justifica el uso de OLS sin variables de control (esto es, \(E(u_i|D_i)=0\)).
- La aleatorización puede estar basada en covariables \(X_i\) pre-tratamiento.
- justifica el uso de OLS con variables de control (esto es, \(E(u_i|D_i,X)=E(u_i|X)\) ).
- \(D_i\) puede ser de varios niveles, no solo binaria.
2.3.3 Ensayos aleatorios clásicos
Ensayos de Bernoulli: las asignaciones para todas las unidades son independientes.
Experimentos completamente aleatorios: todas las unidades obtienen un número aleatorio; las unidades con números \(P\) más bajos reciben tratamiento.
Experimentos aleatorizados estratificados.
Experimentos aleatorizados emparejados.
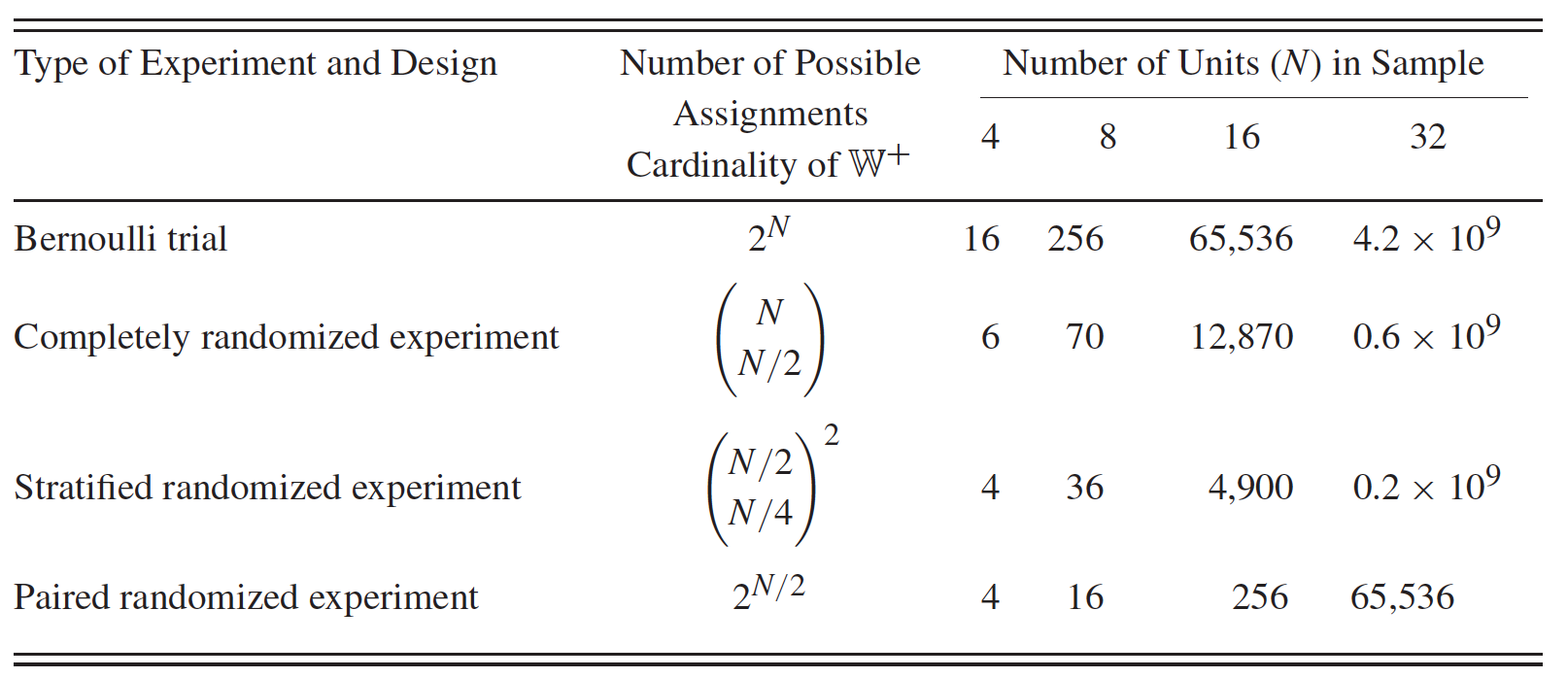
Figure 2.1: Número de valores posibles para el vector de asignación por diseño y tamaño de muestra
2.3.4 Asignación aleatoria
La aleatorización puede depender de las covariables (previas al tratamiento) \(X_i\)
Ejemplo: El efecto de la finalización de la escuela de medicina en los ingresos Ketel et al. (2016).
seis categorías de lotería basadas en el GPA en la escuela secundaria.
los estudiantes con un GPA más alto tienen mayor probabilidad de ser admitidos.
si el GPA tiene un efecto en los ingresos, el efecto de la escuela de medicina se sobrestimará si no se controla (es decir, \(E (u_i |D_i) = 0\) no se cumple, pero \(E (u_i |D_i, GPA_i) = E (u_i |GPA_i)\) sí).
2.4 Poder y tamaño de la muestra
2.4.1 Medias
Considere un estudio de las calificaciones de matemáticas del examen SER Bachiller (SB). A los investigadores les gustaría probar si un nuevo programa de entrenamiento aumenta el puntaje promedio de matemáticas del SB en 20 puntos en comparación con el promedio nacional en un año determinado de 514.
No anticipan que la desviación estándar de los puntajes sea mayor que el valor nacional de 117. Los investigadores planean probar las diferencias entre los puntajes mediante el uso de una prueba \(t\) de una muestra.
Antes de realizar el estudio, a los investigadores les gustaría estimar el tamaño de la muestra requerido para detectar la diferencia anticipada mediante el uso de una prueba de dos colas con \(\alpha=5\%\) con un poder de \(90\%\).
Podemos usar el comando power.t.test para estimar el tamaño de la muestra para este estudio; consulte la ayuda para obtener más ejemplos. Notemos que el comando recibe la diferencia entre la media referencial y la que se desea probar.
medias <- c(514 ,534)
# Tamaño de la muestra
power.t.test(delta = dist(medias),sd = (117), power = 0.9,alternative = "two.sided",type = "one.sample")##
## One-sample t test power calculation
##
## n = 361.5165
## delta = 20
## sd = 117
## sig.level = 0.05
## power = 0.9
## alternative = two.sidedLos investigadores no tienen suficientes recursos para inscribir a tantos sujetos. Les gustaría estimar la potencia correspondiente a una muestra más pequeña de \(300\) personas. Para calcular la potencia, reemplazamos la opción de potencia (\(0.9\)) con la opción \(n=300\)) en el comando anterior.
# Poder
power.t.test(delta = dist(medias),sd = (117), n = 300,alternative = "two.sided",type = "one.sample")##
## One-sample t test power calculation
##
## n = 300
## delta = 20
## sd = 117
## sig.level = 0.05
## power = 0.8392265
## alternative = two.sidedEfecto mínimo detectable
A los investigadores también les gustaría estimar la diferencia mínima detectable entre las puntuaciones de una muestra de 300 personas y una potencia del \(90\%\). Para calcular la diferencia estandarizada entre las puntuaciones, o el tamaño del efecto, especificamos tanto la potencia como el tamaño de la muestra.
# MDE
power.t.test(delta = NULL, n = 300,power = 0.9,alternative = "two.sided",type = "one.sample")##
## One-sample t test power calculation
##
## n = 300
## delta = 0.1877525
## sd = 1
## sig.level = 0.05
## power = 0.9
## alternative = two.sidedLa diferencia estandarizada mínima detectable dada la potencia solicitada y el tamaño de la muestra es \(0.19\), lo que corresponde a un puntaje promedio de matemáticas de aproximadamente \(536\) y una diferencia entre los puntajes de \(22\).
2.4.2 Proporciones
Considere un estudio de osteoporosis en mujeres posmenopáusicas. El término osteoporosis se refiere a la disminución de la masa ósea que es más frecuente en mujeres posmenopáusicas.
Las mujeres diagnosticadas con osteoporosis tienen una densidad ósea vertebral más del \(10\%\) por debajo de la densidad ósea promedio de las mujeres con características demográficas similares, como edad, altura, peso y raza.
La Organización Mundial de la Salud (OMS) define la osteoporosis como un valor de densidad ósea inferior a \(2.5\) desviaciones estándar por debajo de los niveles máximos de masa ósea en mujeres jóvenes.
Suponga que los investigadores desean evaluar el efecto de un nuevo tratamiento sobre el aumento de la densidad ósea en mujeres diagnosticadas con osteoporosis. El tratamiento se considera exitoso si la densidad ósea de un sujeto mejora en más de una desviación estándar de la densidad ósea medida.
Suponga que los estudios anteriores han informado una tasa de respuesta del \(30\%\) para las mujeres con mayor densidad ósea después del tratamiento. Los investigadores esperan que el nuevo tratamiento genere una tasa de respuesta más alta de aproximadamente el \(50\%\).
El objetivo es obtener el tamaño de muestra mínimo requerido para detectar una proporción alternativa de \(0.5\) usando la prueba de \(H_0: p = 0.3\) versus \(Ha: p \neq 0.3\) con \(80\%\) de potencia y \(5\%\) de nivel de significancia.
Para calcular el tamaño de la muestra:
p <- 0.5
p0 <- 0.3
alpha <- 0.05
beta <- 0.20
n <- p*(1-p)*((qnorm(1-alpha/2)+qnorm(1-beta))/(p-p0))^2
ceiling(n) # 50## [1] 50z <- (p-p0)/sqrt(p*(1-p)/n)
(Power <- pnorm(z-qnorm(1-alpha/2))+pnorm(-z-qnorm(1-alpha/2)))## [1] 0.800001Para más especificaciones podemos visitar: http://powerandsamplesize.com/