Chapter 12 The basics of machine learning

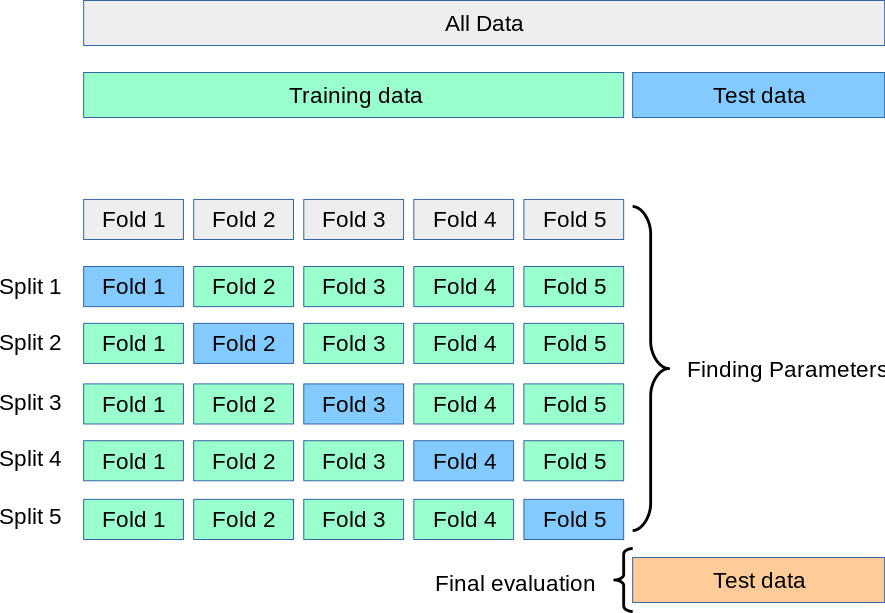
The machine learning flow. source: mlr3 manual

Data: $$(y_i,\bf{x}_i)_{i=1,\dots,N}$$ where $\bf{x}\in\mathbb{R}^D$.

Want to predict $y$ from $\bf{x}$.

Model for prediction: $$f(\bf{x})=\theta^T\bf{x}+\theta_0$$

12.1 Training vs prediction

12.1.1 Training vs testing (predicting) sets

• The entire sample $\mathcal{S}=(y_i,\bf{x}_i)_{i=1,\dots,N}$ is randomly separatedly to two disjoint sets of sample, say $\mathcal{S}_t$ and $\mathcal{S}_p$, so that

$$\mathcal{S}_t\cup\mathcal{S}_p=\mathcal{S},\ \mathcal{S}_t\cap\mathcal{S}_p=\mathcal{S}$$

• Model training phase: when you are estimating parameters using $\mathcal{S}_t$.

• Model testing phase: when you are evaluating your model performance using $\mathcal{S}_p$.

12.2 How to train a model

• some measure of quality:

  • empirical risk minimization: such as SSE

$$\min_{\theta,\theta_0}\ \sum_{(y_i,\bf{x}_i)\in\mathcal{S}_t}(y_i-f(\bf{x_i}|\theta,\theta_0))^2/N$$

• Bayesian inference

12.3 Training while avoiding over/under-fitting

• Training without proper reigning will lead to a trained model that performs well in $\mathcal{S}_t$, but poorly in $\mathcal{S}_p$.

You want to predict head or tail from a coin tossing. You collect a sample of $(H,T,H,H,H)$. Randomly separate it into $\mathcal{S}_t=(H,H,H)$ and $\mathcal{S}_p=(H,T)$.

• What is your model?

• What is your measure of quality?

• What is your parameter estimate?

12.3.1 Reigning while training

• Regularization: add penalty term (call regularizer) to our loss function, such as $\left\Vert \bf{\theta}\right\Vert^2$, with a tunning parameter $\lambda$. For example,

$$\min_{ \bf{\theta}}\ \sum_{(y_i,\bf{x}_i)\in\mathcal{S}_t}(y_i-f(\bf{x_i}| \bf{\theta}))^2/N + \lambda\left\Vert \bf{\theta}\right\Vert^2, \ or$$ $$\min_{ \bf{\theta}}\ \left\Vert \bf{y}-f(\bf{x}| \bf{\theta})\right\Vert^2/N + \lambda\left\Vert \bf{\theta}\right\Vert^2,$$ where $\lambda>0$ is called a tunning parameter that needs to be chosen in the training phase as well.

• Addinng a prior

12.3.2 Cross-validation to choose tunning parameter

12.4 Python example

Intall the basic Python machine learning package:

conda_install("m-team","scikit-learn")
# conda_install("m-team","h2o")

• cross-validation: https://scikit-learn.org/stable/model_selection.html#model-selection

• Regularization of Linear Regression Model:
  • Ridge regression
    $$\min_{w} || X w - y||_2^2 + \alpha ||w||_2^2$$
    

  linear_model.Ridge(alpha=0.5) # instance initiation
  linear_model.RidgeCV()

  • Lasso regression
    $$\min_{w} { \frac{1}{2n_{\text{samples}}} ||X w - y||_2 ^ 2 + \alpha ||w||_1}$$
    

  linear_model.Lasso() # instance initiation

• Stochastic Gradient Descent:
  • SGDRegressor:
    a batch size of 1, stochastic gradient descent algorithm.

  SGDRegressor(
    loss="squared_loss", # OLS Loss function
    panelty="l2", # squared norm of parameters
    alpha=0.0001
    )

  其他參數還有max_it（全部data可pass through的次數，即epoch，上限），

  $$Sample\ size(1000) / Batch\ size (250) = Iteration\ times (4)$$ One epoch is one complete sample size passing through, which requires four iterations to complete.

## choose your model class
from sklearn.linear_model import LinearRegression, Ridge, RidgeCV, Lasso, LassoCV, SGDRegressor

## choose your metrics
from sklearn.metrics import mean_squared_error, r2_score

## training-test split
from sklearn.model_selection import train_test_split

import numpy as np                                     
import matplotlib.pyplot as plt      
rng=np.random.default_rng(seed=2019) # initiate a random generator with seed 2019, for replication purpose
x = rng.normal(size=30)

y = 0 +0.1* x + 0.33*rng.normal(size=x.shape)    


X=np.column_stack(
  (np.ones(x.shape),x,x**2,x**3)
)

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42)

12.4.1 模型設定

# Linear regression
Linear1=LinearRegression()
# Ridge regression
Ridge1=Ridge(alpha=0.5)
Ridge2=RidgeCV(alphas=np.linspace(0.1,3,10), cv=5) # 5-fold cv
# Lasso regression
Lasso1=Lasso(alpha=0.5)
Lasso2=LassoCV(alphas=np.linspace(0.1,3,10), cv=5) # 5-fold cv
# SGD regression
SGD1=SGDRegressor()
SGD2=SGDRegressor()

12.4.2 Training

# Linear regression
Linear1.fit(X_train,y_train)
# Ridge regression

## LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)

Ridge1.fit(X_train,y_train)

## Ridge(alpha=0.5, copy_X=True, fit_intercept=True, max_iter=None,
##       normalize=False, random_state=None, solver='auto', tol=0.001)

Ridge2.fit(X_train,y_train) # 5-fold cv
# Lasso regression

## RidgeCV(alphas=array([0.1       , 0.42222222, 0.74444444, 1.06666667, 1.38888889,
##        1.71111111, 2.03333333, 2.35555556, 2.67777778, 3.        ]),
##         cv=5, fit_intercept=True, gcv_mode=None, normalize=False, scoring=None,
##         store_cv_values=False)
## 
## //anaconda3/envs/m-team/lib/python3.7/site-packages/sklearn/model_selection/_search.py:814: DeprecationWarning: The default of the `iid` parameter will change from True to False in version 0.22 and will be removed in 0.24. This will change numeric results when test-set sizes are unequal.
##   DeprecationWarning)

Lasso1.fit(X_train,y_train)

## Lasso(alpha=0.5, copy_X=True, fit_intercept=True, max_iter=1000,
##       normalize=False, positive=False, precompute=False, random_state=None,
##       selection='cyclic', tol=0.0001, warm_start=False)

Lasso2.fit(X_train,y_train) # 5-fold cv
# SGD regression

## LassoCV(alphas=array([0.1       , 0.42222222, 0.74444444, 1.06666667, 1.38888889,
##        1.71111111, 2.03333333, 2.35555556, 2.67777778, 3.        ]),
##         copy_X=True, cv=5, eps=0.001, fit_intercept=True, max_iter=1000,
##         n_alphas=100, n_jobs=None, normalize=False, positive=False,
##         precompute='auto', random_state=None, selection='cyclic', tol=0.0001,
##         verbose=False)

SGD1.fit(X_train,y_train)


### mini-batch SGD for one epoch

## SGDRegressor(alpha=0.0001, average=False, early_stopping=False, epsilon=0.1,
##              eta0=0.01, fit_intercept=True, l1_ratio=0.15,
##              learning_rate='invscaling', loss='squared_loss', max_iter=1000,
##              n_iter_no_change=5, penalty='l2', power_t=0.25, random_state=None,
##              shuffle=True, tol=0.001, validation_fraction=0.1, verbose=0,
##              warm_start=False)

n_batches = 3
(n, m)=X_train.shape
split_index=np.arange(0,n,1)
rng.shuffle(split_index) # 洗牌
for slice_index in np.array_split(split_index, n_batches):
    SGD2.partial_fit(X_train[slice_index,:],y_train[slice_index])

## SGDRegressor(alpha=0.0001, average=False, early_stopping=False, epsilon=0.1,
##              eta0=0.01, fit_intercept=True, l1_ratio=0.15,
##              learning_rate='invscaling', loss='squared_loss', max_iter=1000,
##              n_iter_no_change=5, penalty='l2', power_t=0.25, random_state=None,
##              shuffle=True, tol=0.001, validation_fraction=0.1, verbose=0,
##              warm_start=False)
## SGDRegressor(alpha=0.0001, average=False, early_stopping=False, epsilon=0.1,
##              eta0=0.01, fit_intercept=True, l1_ratio=0.15,
##              learning_rate='invscaling', loss='squared_loss', max_iter=1000,
##              n_iter_no_change=5, penalty='l2', power_t=0.25, random_state=None,
##              shuffle=True, tol=0.001, validation_fraction=0.1, verbose=0,
##              warm_start=False)
## SGDRegressor(alpha=0.0001, average=False, early_stopping=False, epsilon=0.1,
##              eta0=0.01, fit_intercept=True, l1_ratio=0.15,
##              learning_rate='invscaling', loss='squared_loss', max_iter=1000,
##              n_iter_no_change=5, penalty='l2', power_t=0.25, random_state=None,
##              shuffle=True, tol=0.001, validation_fraction=0.1, verbose=0,
##              warm_start=False)

12.4.3 Predict

# Linear regression
y_predictLinear1=Linear1.predict(X_test)
# Ridge regression
y_predictRidge1=Ridge1.predict(X_test)
y_predictRidge2=Ridge2.predict(X_test) # 5-fold cv
# Lasso regression
y_predictLasso1=Lasso1.predict(X_test)
y_predictLasso2=Lasso2.predict(X_test) # 5-fold cv
# SGD regression
y_predictSGD1=SGD1.predict(X_test)
y_predictSGD2=SGD2.predict(X_test)

12.4.4 accuracy

mseLinear1=mean_squared_error(y_test,y_predictLinear1)
# Ridge regression
mseRidge1=mean_squared_error(y_test,y_predictRidge1)
mseRidge2=mean_squared_error(y_test,y_predictRidge2) # 5-fold cv
# Lasso regression
mseLasso1=mean_squared_error(y_test,y_predictLasso1)
mseLasso2=mean_squared_error(y_test,y_predictLasso2) # 5-fold cv
# SGD regression
mseSGD1=mean_squared_error(y_test,y_predictSGD1)
mseSGD2=mean_squared_error(y_test,y_predictSGD2)

{"mseLinear1": mseLinear1,
# Ridge regression
 "mseRidge1": mseRidge1,
 "mseRidge2": mseRidge2,
# Lasso regression
"mseLasso1": mseLasso1,
"mseLasso2": mseLasso2,
# SGD regression

"mseSGD1": mseSGD1,
"mseSGD2": mseSGD2
}

## {'mseLinear1': 0.23913965444458862, 'mseRidge1': 0.22923260522059308, 'mseRidge2': 0.20688285341153212, 'mseLasso1': 0.164949079025128, 'mseLasso2': 0.17400205980219802, 'mseSGD1': 0.18901352025558144, 'mseSGD2': 0.15951178277143552}