Chapter 2 Working with vectors, matrices, and arrays

2.1 Data objects in R

2.1.1 Atomic vs. recursive data objects

The analysis of data in R involves creating, naming, manipulating, and operating on data objects using functions. Data in R are organized as objects and have been assigned names. We have already been introduced to several R data objects. Now we make further distinctions. Every data object has a mode and length. The mode of an object describes the type of data it contains and is available by using the mode function. An object can be of mode character, numeric, logical, list, or function.

#> [1] "character"
#> [1] "numeric"
#> [1] FALSE  TRUE
#> [1] "logical"
#> [1] "list"
#> [1] "list"
#> [1] 25
#> [1] "function"

Data objects are further categorized into atomic or recursive objects. An atomic data object can only contain elements from one, and only one, of the following modes: character, numeric, or logical. Vectors, matrices, and arrays are atomic data objects. A recursive data object can contain data objects of any mode. Lists, data frames, and functions are recursive data objects. We start by reviewing atomic data objects.

A vector is a collection of like elements without dimensions.14 The vector elements are all of the same mode (either character, numeric, or logical). When R returns a vector the [n] indicates the position of the element displayed to its immediate right.

#> [1] "Pedro" "Paulo" "Maria"
#> [1] 1 2 3 4 5
#> [1]  TRUE  TRUE FALSE FALSE FALSE

Remember that a numeric vector can be of type double precision or integer. By default R does not use single precision numeric vectors. The vector type is not apparent by inspection (also see Table 2.1).

#> [1] 3 4 5
#> [1] "double"
#> [1] 3 4 5
#> [1] "integer"
TABLE 2.1: Summary of numeric vectors
vector example mode(x) typeof(x) class(x)
x <- c(3, 4, 5) numeric double numeric
x <- c(3L, 4L, 5L) numeric integer integer

A matrix is a collection of like elements organized into a 2-dimensional (tabular) data object with r rows and c columns. We can think of a matrix as a vector re-shaped into a \(r \times c\) table. When R returns a matrix the [i,] indicates the ith row and [,j] indicates the jth column.

#>      [,1] [,2]
#> [1,] "a"  "c" 
#> [2,] "b"  "d"

An array is a collection of like elements organized into a z-dimensional data object. We can think of an array as a vector re-shaped into a \(n_1 \times n_2 \times n_3 \ldots n_z\) table. For example, when R returns a 3-dimensional array the [i,,] indicates the ith row and [,j,] indicates the jth column, and “, , k” indicates the kth depth.

#> , , 1
#> 
#>      [,1] [,2] [,3]
#> [1,]    1    3    5
#> [2,]    2    4    6
#> 
#> , , 2
#> 
#>      [,1] [,2] [,3]
#> [1,]    7    9   11
#> [2,]    8   10   12

If we try to include elements of different modes in an atomic data object, R will coerce the data object into a single mode based on the following hierarchy: character \(>\) numeric \(>\) logical. In other words, if an atomic data object contains any character element, all the elements are coerced to character.

#> [1] "hello" "4.56"  "FALSE"
#> [1] 4.56 0.00

A recursive data object can contain one or more data objects where each object can be of any mode. Lists, data frames, and functions are recursive data objects. Lists and data frames are of mode list, and functions are of mode function (Table 2.2).

A list is a collection of data objects without any restrictions. Think of a list of length \(k\) as \(k\) “bins” in which each bin can contain any type of data object.

#> [[1]]
#> [1] 1 2 3
#> 
#> [[2]]
#> [1] "Male"   "Female" "Male"  
#> 
#> [[3]]
#>      [,1] [,2]
#> [1,]    1    3
#> [2,]    2    4

A data frame is a special list with a 2-dimensional (tabular) structure. Epidemiologists are very experienced working with data frames where each row usually represents data collected on individual subjects (also called records or observations) and columns represent fields for each type of data collected (also called variables).

#>   subjno age    sex case
#> 1      1  34   Male  Yes
#> 2      2  56   Male   No
#> 3      3  45 Female   No
#> 4      4  23   Male  Yes
#> [1] "list"

A tibble “is a modern reimagining of the data.frame, keeping what time has proven to be effective, and throwing out what is not. Tibbles are data.frames that are lazy and surly: they do less (i.e. they don’t change variable names or types, and don’t do partial matching) and complain more (e.g. when a variable does not exist). This forces you to confront problems earlier, typically leading to cleaner, more expressive code. Tibbles also have an enhanced print() method which makes them easier to use with large datasets containing complex objects.” To learn more see https://tibble.tidyverse.org.

2.1.2 Assessing the structure of data objects

TABLE 2.2: Summary of six types of data objects in R
Data object Possible mode Default class
Atomic
  vector character, numeric, logical NULL
  matrix character, numeric, logical NULL
  array character, numeric, logical NULL
Recursive
  list list NULL
  data frame list data.frame
  function function NULL

Summarized in Table 2.2 are the key attributes of atomic and recursive data objects. Data objects can also have class attributes. Class attributes are just a way of letting R know that an object is ‘special,’ allowing R to use specific methods designed for that class of objects (e.g., print, plot, and summary methods). The class function displays the class if it exists. For our purposes, we do not need to know any more about classes.

Frequently, we need to assess the structure of data objects. We already know that all data objects have a mode and length attribute. For example, let’s explore the infert data set that comes with R. The infert data comes from a matched case-control study evaluating the occurrence of female infertility after spontaneous and induced abortion.

#> [1] "list"
#> [1] 8

At this point we know that the data object named ‘infert’ is a list of length 8. To get more detailed information about the structure of infert use the str function (str comes from ’str’ucture).

#> 'data.frame':    248 obs. of  8 variables:
#>  $ education     : Factor w/ 3 levels "0-5yrs","6-11yrs",..: 1 1 1 1 2 2 2 2 2 2 ...
#>  $ age           : num  26 42 39 34 35 36 23 32 21 28 ...
#>  $ parity        : num  6 1 6 4 3 4 1 2 1 2 ...
#>  $ induced       : num  1 1 2 2 1 2 0 0 0 0 ...
#>  $ case          : num  1 1 1 1 1 1 1 1 1 1 ...
#>  $ spontaneous   : num  2 0 0 0 1 1 0 0 1 0 ...
#>  $ stratum       : int  1 2 3 4 5 6 7 8 9 10 ...
#>  $ pooled.stratum: num  3 1 4 2 32 36 6 22 5 19 ...

Great! This is better. We now know that infert is a data frame with 248 observations and 8 variables. The variable names and data types are displayed along with their first few values. In this case, we now have sufficient information to start manipulating and analyzing the infert data set.

Additionally, we can extract more detailed structural information that becomes useful when we want to extract data from an object for further manipulation or analysis (Table 2.3). We will see extensive use of this when we start programming in R.

To get practice calling data from the console, enter data() to display the available data sets in R. Then enter data(data_set) to load a dataset. Study the examples in Table 2.3 and spend a few minutes exploring the structure of the data sets we have loaded. To display detailed information about a specific data set use ?data_set at the command prompt (e.g., ?infert).

TABLE 2.3: Useful functions for assessing R data objects
Function Returns
str summary of data object structure
attributes list with data object attributes
mode mode of object
typeof type of object; similar to mode but includes double and integer, if applicable
length length of object
class class of object, if it exists
dim vector with object dimensions, if applicable
nrow number of rows, if applicable
ncol number of columns, if applicable
dimnames list containing vectors of names for each dimension, if applicable
rownames vector of row names of a matrix-like object
colnames vector of column names of a matrix-like object
names vector of names for the list (for a data frame returns field names)
row.names vector of row names for a data frame

2.2 A vector is a collection of like elements

2.2.1 Understanding vectors

A vector15 is a collection of like elements (i.e., the elements all have the same mode). There are many ways to create vectors (see Table 2.6). The most common way of creating a vector is using the c function:

#> [1] 136 219 176 214 164
#> [1] "Mateo" "Mark"  "Luke"  "Juan"
#> [1]  TRUE  TRUE FALSE  TRUE FALSE

A single element is also a vector; that is, a vector of length = 1. Try, for example, is.vector('Zoe'). In mathematics, a single number is called a scalar; in R, it is a numeric vector of length = 1. When we execute a math operation between a scalar and a vector, in the background, the scalar expands to the same length as the vector in order to execute a vectorized operation. For example, these two calculation are equivalent:

#> [1]  50 100 150
#> [1]  50 100 150

A note of caution: when vector lengths differ, the shorter vector will recyle its elements to enable a vectorized operation. For example,

#>      x  y   z
#> [1,] 3 10  30
#> [2,] 5 20 100
#> [3,] 3 30  90
#> [4,] 5 40 200

In effect, x expanded from c(3, 5) to c(3, 5, 3, 5) in order to execute a vectorized operation. This expansion of x is not apparent from the math operation; that is, no warning was produced. Therefore, be aware: math operations with vectors of different lengths may not produce a warning.

2.2.1.1 Boolean queries and subsetting of vectors

In R, we use relational and logical operators (Table 2.4) and (Table 2.5) to conduct Boolean queries. Boolean operations is a methodological workhorse of data analysis. For example, suppose we have a vector of female movie stars and a corresponding vector of their ages (as of January 16, 2004), and we want to select a subset of actors based on age criteria. Let’s select the actors who are in their 30s. This is done using logical vectors that are created by using relational operators (<, >, <=, >=, ==, !=). Study the following example:

#> [1]  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE FALSE
#> [1] FALSE FALSE  TRUE  TRUE  TRUE  TRUE  TRUE
#> [1] FALSE FALSE  TRUE  TRUE  TRUE  TRUE FALSE
#> [1] "Amanda"    "Jennifer"  "Winona"    "Catherine"
TABLE 2.4: Using relational operators with vectors
Operator Description Try these examples
< Less than pos <- c('p1', 'p2', 'p3', 'p4')
x <- c(1, 2, 3, 4)
y <- c(5, 4, 3, 2)
x < y
pos[x < y]
> Greater than x > y
pos[x > y]
<= Less than or equal to x <= y
pos[x <= y]
>= Greater than or equal to x >= y
pos[x >= y]
== Equal to x == y
pos[x == y]
!= Not equal to x != y
pos[x != y]
TABLE 2.5: Using logical operators with vectors
Operator Description Try these examples
! Element-wise NOT x <- c(1, 2, 3, 4)
x > 2
!(x > 2)
pos[!(x > 2)]
& Element-wise AND (x > 1) & (x < 5)
pos[(x > 1) & (x < 5)]
\(\mid\) Element-wise OR (x <= 1) \(\mid\) (x > 4)
pos[(x <= 1) \(\mid\) (x > 4)]
xor Exclusive OR: only TRUE if one xx <- x <= 1
or other element is true, not both yy <- x > 4
xor(xx, yy)

To summarize:

  • Logical vectors are created using Boolean comparisons,
  • Boolean comparisons are constructed using relational and logical operators
  • Logical vectors are commonly used for indexing (subsetting) data objects

Before moving on, we need to be sure we understand the previous examples, then study the examples in the Table 2.4 and Table 2.5. For practice, study the examples and spend a few minutes creating simple numeric vectors, then

  1. generate logical vectors using relational operators,
  2. use these logical vectors to index the original numerical vector or another vector,
  3. generate logical vectors using the combination of relational and logical operators, and
  4. use these logical vectors to index the original numerical vector or another vector.

Notice that the element-wise exclusive or operator (xor) returns TRUE if either comparison element is TRUE, but not if both are TRUE. In contrast, the | returns TRUE if either or both comparison elements are TRUE.

2.2.1.2 Integer queries and subsetting of vectors

TODO - which function

2.2.2 Creating vectors

TABLE 2.6: Common ways of creating vectors de novo
Function Description Try these examples
c Concatenate a collection x <- c(1, 2, 3, 4, 5)
y <- c(6, 7, 8, 9, 10)
z <- c(x, y)
scan Scan a collection xx <- scan()
(press enter twice 1 2 3 4 5
after last entry) yy <- scan(what = '')
'Javier' 'Miguel' 'Martin'
xx; yy # Display vectors
: Make integer sequence 1:10
10:(-4)
seq Sequence of numbers seq(1, 5, by = 0.5)
seq(1, 5, length = 3)
zz <- c('a', 'b', 'c')
seq(along = zz)
rep Replicate argument rep('Juan Nieve', 3)
rep(1:3, 4)
rep(1:3, 3:1)
paste Paste character strings paste(c('A','B','C'),1:3,sep='')

Vectors are created directly, or indirectly as the result of manipulating an R object. The c function for concatenating a collection has been covered previously. Another, possibly more convenient, method for collecting elements into a vector is with the scan function.

This method is convenient because we do not need to type c, parentheses, and commas to create the vector. The vector is created after executing a newline twice.

To generate a sequence of consecutive integers use the : function.

#>  [1] -9 -8 -7 -6 -5 -4 -3 -2 -1  0  1  2  3  4  5  6  7  8

However, the seq function provides more flexibility in generating sequences. Here are some examples:

#> [1] 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0
#> [1] 1.000000 1.571429 2.142857 2.714286 3.285714 3.857143
#> [7] 4.428571 5.000000
#> [1] 1.000000 1.571429 2.142857 2.714286 3.285714 3.857143
#> [7] 4.428571 5.000000

These types of sequences are convenient for plotting mathematical equations.16 For example, suppose we wanted to plot the standard normal curve using the normal equation. For a standard normal curve \(\mu = 0\) (mean) and \(\sigma = 1\) (standard deviation)

\[\begin{equation} f(x) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left\{\frac{-(x - \mu)^2}{2 \sigma^2} \right\} \end{equation}\]

Here is the R code to plot this equation:

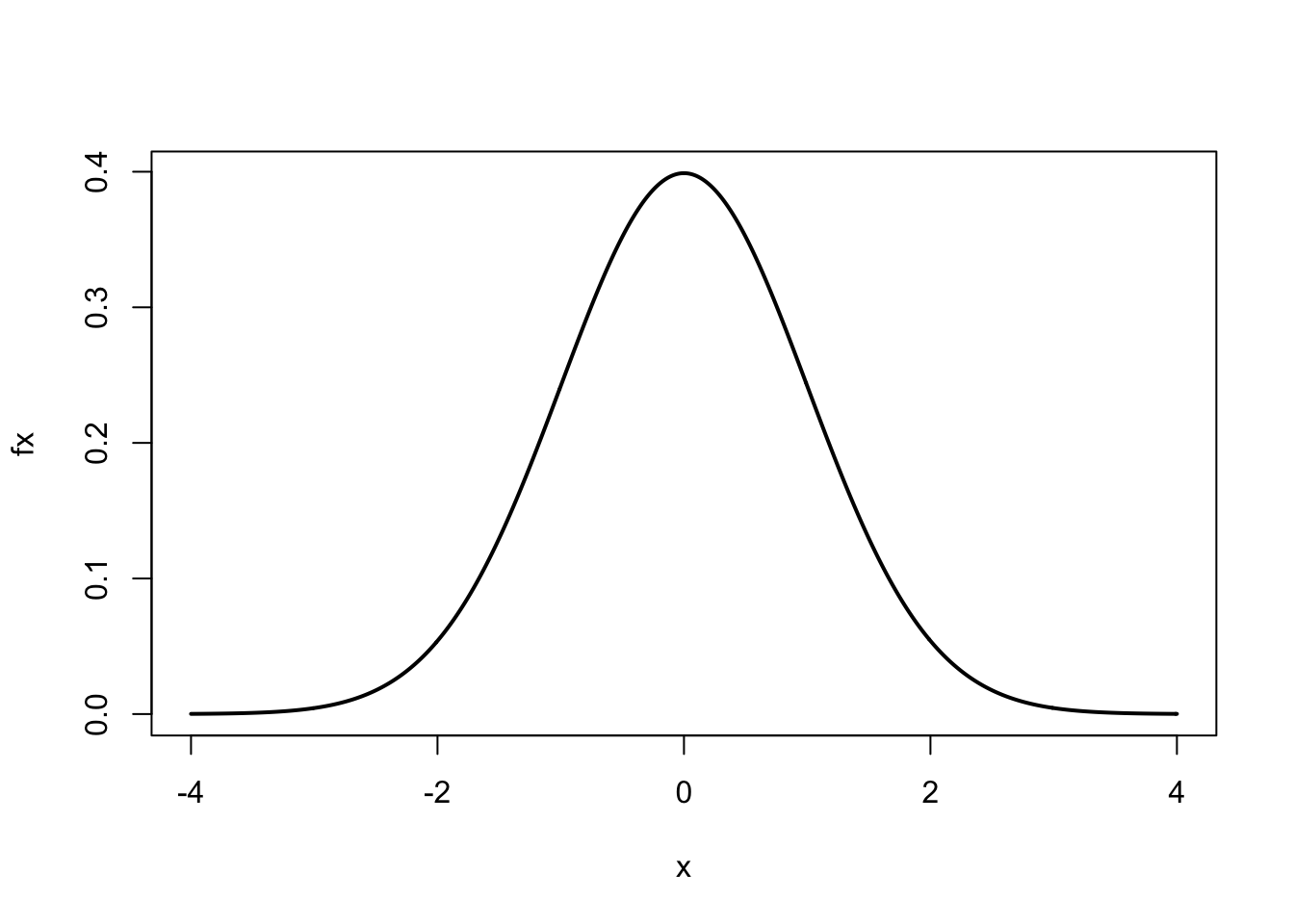
After assigning values to mu and sigma, we assigned to x a sequence of numbers from \(-4\) to 4 by intervals of 0.01. Using the normal curve equation, for every value of \(x\) we calculated \(f(x)\), represented by the numeric vector fx. We then used the plot function to plot \(x\) vs. \(f(x)\). The optional argument type='l' produces a ‘line’ and lwd=2 doubles the line width.

The rep function is used to replicate its arguments. Study the examples that follow:

#> [1] 5 5
#>  [1] 1 2 1 2 1 2 1 2 1 2
#>  [1] 1 1 1 1 1 2 2 2 2 2
#>  [1] 1 1 1 1 1 2 2 2 2 2
#>  [1] 1 1 1 1 1 2 2 2 2 3 3 3 4 4 5

The paste function pastes character strings:

#> [1] "John Snow"        "Kenneth Rothman"  "Sander Greenland"
#> [1] "var1" "var2" "var3" "var4" "var5" "var6" "var7"

Indexing (subsetting) an object often results in a vector. To preserve the dimensionality of the original object use the drop option.

#>      [,1] [,2] [,3] [,4]
#> [1,]    1    3    5    7
#> [2,]    2    4    6    8
#> [1] 2 4 6 8
#>      [,1] [,2] [,3] [,4]
#> [1,]    2    4    6    8

Up to now we have generated vectors of known numbers or character strings. On occasion we need to generate random numbers or draw a sample from a collection of elements. First, sampling from a vector returns a vector:

#> [1] "H" "T" "H" "T" "T" "H" "T" "H"
#>  [1] 1 3 4 3 1 3 4 6 4 6

Second, generating random numbers from a probability distribution returns a vector:

#>  [1] 23 29 27 22 27 27 27 22 21 28
#> [1] -1.4143248  0.3112364 -0.6454943 -2.3003939  0.1891422

There are additional ways to create vectors. To practice creating vectors study the examples in Table 2.6 and spend a few minutes creating simple vectors. If we need help with a function remember enter ?function_name or help(function_name).

Finally, notice that we can use vectors as arguments to functions:

2.2.3 Naming vectors

Each element of a vector can be labeled with a name at the time the vector is created or later. The first way of naming vector elements is when the vector is created:

#> chol  sbp  dbp  age 
#>  234  148   78   54

The second way is to create a character vector of names and then assign that vector to the numeric vector using the names function:

#> [1] 234 148  78  54
#> chol  sbp  dbp  age 
#>  234  148   78   54

The names function, without an assignment, returns the character vector of names, if it exist. This character vector can be used to name elements of other vectors.

#> [1] "chol" "sbp"  "dbp"  "age"
#> [1] 250 184  90  45
#> chol  sbp  dbp  age 
#>  250  184   90   45

The unname function removes the element names from a vector:

#> [1] 250 184  90  45

For practice study the examples in Table 2.7 and spend a few minutes creating and naming simple vectors.

TABLE 2.7: Common ways of naming vectors
Function Description Try these examples
c Name elements at creation x <- c(a = 1, b = 2, c = 3)
names Name elements by assignment; y <- 1:3
Returns names if they exist names(y) <- c('a', 'b', 'c')
names(y) # return names
unname Remove names (if they exist) y <- unname(y)
names(y) <- NULL #equivalent

2.2.4 Indexing (subsetting) vectors

Indexing a vector is subsetting or extracting elements from a vector. A vector is indexed by position, by name (if it exist), or by logical value (TRUE vs FALSE). Positions are specified by positive or negative integers.

#> sbp age 
#> 148  54
#> chol  dbp 
#>  234   78

Although indexing by position is concise, indexing by name (when the names exists) is better practice in terms of documenting our code. Here is an example:

#> sbp age 
#> 148  54

A logical vector indexes the positions that corresponds to the TRUEs. Here is an example:

#>  chol   sbp   dbp   age 
#>  TRUE FALSE  TRUE  TRUE
#> chol  dbp  age 
#>  234   78   54

Any expression that evaluates to a valid vector of integers, names, or logicals can be used to index a vector.

#> [1] 1 2 3 3 4 4 1
#> chol  sbp  dbp  dbp  age  age chol 
#>  234  148   78   78   54   54  234
#> [1] "dbp"  "dbp"  "age"  "chol" "age"  "dbp"  "dbp"
#>  dbp  dbp  age chol  age  dbp  dbp 
#>   78   78   54  234   54   78   78

Notice that when we indexed by position or name we indexed the same position repeatly. This will not work with logical vectors. In the example that follows NA means ‘not available.’

#> [1] FALSE FALSE  TRUE  TRUE  TRUE  TRUE FALSE
#>  dbp  age <NA> <NA> 
#>   78   54   NA   NA

We have already seen that a vector can be indexed based on the characteristics of another vector.

#> [1] FALSE    NA  TRUE  TRUE    NA
#> [1] NA         "Luisito"  "Angelita" NA
#> [1] "Tomasito" "Luisito"  "Angelita"
#> [1] "Luisito"  "Angelita"

In this example, NA represents missing data. The is.na function returns a logical vector with s at NA positions. To generate a logical vector to index values that are not missing use !is.na.

For practice study the examples in Table 2.8 and spend a few minutes creating, naming, and indexing simple vectors.

TABLE 2.8: Common ways of indexing vectors
Indexing Try these examples
By logical x < 100
x[x < 100]
(x < 150) & (x > 70)
bp <- (x < 150) & (x > 70)
x[bp]
By position x <- c(chol = 234, sbp = 148, dbp = 78)
x[2] # positions to include
x[c(2, 3)]
x[-c(1, 3)] # positions to exclude
x[which(x<100)]
By name (if exists) x['sbp']
x[c('sbp', 'dbp')]
Unique values samp <- sample(1:5, 25, replace = TRUE)
unique(samp)
Duplicated values duplicated(samp) # generates logical
samp[duplicated(samp)]

2.2.4.1 The which function

A Boolean operation that returns a logical vector contains TRUE values where the condition is true. To identify the position of each TRUE value we use the which function. For example, using the same data above:

#> [1] 3 4
#> [1] "Luisito"  "Angelita"

Notice that is was unnecessary to remove the missing values.

2.2.5 Replacing vector elements (by indexing and assignment)

If a vector element can be indexed, it can be replaced. Therefore, to replace vector elements we combine indexing and assignment. Replacing vector elements is one method of recoding a variable. In this example, we recode a vector of ages into age categories:

#> agecat
#>  >=65 15-24 25-44 45-64 
#>   424   121   234   221

First, we made a copy of the numeric vector age and named it agecat. Then, we replaced elements of agecat with character strings for each age category, creating a character vector (agecat) from a numeric vector (age).

Review the results of table(agecat). What’s wrong? Age categories have a natural ordering which was loss in our recoding. This would be fine if this were a nominal variable where there is no ordering. (Later we will learn how to use the cut function for discretizing continous data into a factor.) Another problem is that the category “<15” is not included in our table with the value of 0.

Let’s try replacement with integers to preserve the natural ordering, and convert it to a factor and set the possible levels to preserve the “<15” category for tracking and reporting.

#> agecat2
#>   2   3   4   5 
#> 121 234 221 424
#> agecat2
#>   2   3   4   5 
#> 121 234 221 424
#> agecat2
#>   <15 15-24 25-44 45-64  >=65 
#>   121   234   221   424     0

Notice that transforming the numeric vector agecat2 into a factor is not sufficient, we must also specify the possible levels with the levels function. Do not assume that all possible levels of responses appear in the data. Note that setting levels can occur as an option to the factor function.

For practice study the examples in Table 2.9 and spend a few minutes replacing vector elements.

TABLE 2.9: Common ways of replacing vector elements
Replacing Try these examples
By logical x[x<100]
x[x<100] <- NA; x
By position x <- c(chol = 234, sbp = 148, dbp = 78)
x[1]
x[1] <- 250; x
By name (if exists) x['sbp']
x['sbp'] <- 150; x

2.2.6 Operating on vectors

Operating on vectors is very common in epidemiology and statistics. In this section we cover common operations on single vectors (Table 2.10) and multiple vectors (Table 2.11).

2.2.6.1 Operating on single vectors

TABLE 2.10: Selected operations on single vectors
Function Description Function Description
sum summation rev reverse order
cumsum cumulative sum order order
diff x[i+1]-x[i] sort sort
prod product rank rank
cumprod cumulative product sample random sample
mean mean quantile percentile
median median var variance, covariance
min minimum sd standard deviation
max maximum table tabulate character vector
range range xtabs tabulate factor vector

First, we focus on operating on single numeric vectors (Table 2.10). This also gives us the opportunity to see how common mathematical notation is translated into simple R code.

To sum elements of a numeric vector \(x\) of length \(n\), (\(\sum_{i=1}^{n}{x_i}\)), use the sum function:

#> [1] 9.128177

To calculate a cumulative sum of a numeric vector \(x\) of length \(n\), (\(\sum_{i=1}^{k}{x_i}\), for \(k=1,\ldots,n\)), use the cumsum function which returns a vector:

#>  [1] 2 2 2 2 2 2 2 2 2 2
#>  [1]  2  4  6  8 10 12 14 16 18 20

To multiply elements of a numeric vector \(x\) of length \(n\), (\(\prod_{i=1}^{n}{x_i}\)), use the prod function:

#> [1] 40320

To calculate the cumulative product of a numeric vector \(x\) of length \(n\), (\(\prod_{i=1}^{k}{x_i}\), for \(k=1,\ldots,n\)), use the cumprod function:

#> [1]     1     2     6    24   120   720  5040 40320

To calculate the mean of a numeric vector \(x\) of length \(n\), (\(\frac{1}{n} \sum_{i=1}^{n}{x_i}\)), use the sum and length functions, or use the mean function:

#> [1] 0.1594427
#> [1] 0.1594427

To calculate the sample variance of a numeric vector \(x\) of length \(n\), use the sum, mean, and length functions, or, more directly, use the var function.

\[\begin{equation} S_X^2 = \frac{1}{n-1} \left[ \sum_{i = 1}^n{(x_i - \bar{x})^2} \right] \end{equation}\]

#> [1] 0.9736283
#> [1] 0.9736283

This example illustrates how we can implement a formula in R using several functions that operate on single vectors (sum, mean, and length). The var function, while available for convenience, is not necessary to calculate the sample variance.

When the var function is applied to two numeric vectors, \(x\) and \(y\), both of length \(n\), the sample covariance is calculated:

\[\begin{equation} S_{XY} = \frac{1}{n-1} \left[ \sum_{i = 1}^n{(x_i - \bar{x}) (y_i - \bar{y})} \right] \end{equation}\]

#> [1] 0.03298182
#> [1] 0.03298182

The sample standard deviation, of course, is just the square root of the sample variance (or use the sd function):

\[\begin{equation} S_X = \sqrt{\frac{1}{n-1} \left[ \sum_{i = 1}^n{(x_i - \bar{x})^2} \right]} \end{equation}\]

#> [1] 0.9826895
#> [1] 0.9826895

To sort a numeric or character vector use the sort function.

#> [1] 4 7 8

However, to sort one vector based on the ordering of another vector use the order function.

#> [1] "Angela" "Luis"   "Tomas"
#> [1] 2 3 1

Notice that the order function does not return the data, but rather indexing integers in new positions for sorting the vector age or another vector. For example, order(ages) returned the integer vector c(2, 3, 1) which means “move the 2nd element (age = 4) to the first position, move the 3rd element (age = 7) to the second position, and move the 1st element (age = 8) to the third position.” Verify that sort(ages) and ages[order(ages)] are equivalent.

To sort a vector in reverse order combine the rev and sort functions.

#> [1]  1  3  3  5 12 14
#> [1] 14 12  5  3  3  1

In contrast to the sort function, the rank function gives each element of a vector a rank score but does not sort the vector.

#> [1] 5.0 2.5 6.0 2.5 4.0 1.0

The median of a numeric vector is that value which puts 50% of the values below and 50% of the values above, in other words, the 50% percentile (or 0.5 quantile). For example, the median of c(4, 3, 1, 2, 5) is 3. For a vector of even length, the middle values are averaged: the median of c(4, 3, 1, 2) is 2.5. To get the median value of a numeric vector use the median or quantile function.

#> [1] 39
#> 50% 
#>  39

To return the minimum value of a vector use the min function; for the maximum value use the max function. To get both the minimum and maximum values use the range function.

#> [1] 20
#> [1] 20
#> [1] 77
#> [1] 77
#> [1] 20 77
#> [1] 20 77

To sample from a vector of length \(n\), with each element having a default sampling probability of \(1/n\), use the sample function. Sampling can be with or without replacement (default). If the sample size is greater than the length of the vector, then sampling must occur with replacement.

#>  [1] "T" "H" "T" "T" "T" "H" "T" "T" "H" "T"
#>  [1] 86 10 69 13 26  6 93 51 14 36 80 32 45 62 33

2.2.6.2 Operating on multiple vectors

TABLE 2.11: Selected operations on multiple vectors
Function Description
c Concatenates into vectors
append Appends a vector to another vector
cbind Column-bind vectors or matrices
rbind Row-bind vectors or matrices
table Creates contingency table from 2 or more vectors
xtabs Creates contingency table from 2 or more factors in a data frame
ftable Creates flat contingency table from 2 or more vectors
outer Outer product
tapply Applies a function to strata of a vector
<, > Relational operators
<=, >=
==, !=
!, |, xor Logical operators

Next, we review selected functions that work with one or more vectors. Some of these functions manipulate vectors and others facilitate numerical operations.

In addition to creating vectors, the c function can be used to append vectors.

#>  [1]  6  7  8  9 10 20 21 22 23 24

The append function also appends vectors; however, one can specify at which position.

#>  [1]  6  7  8  9 10 20 21 22 23 24
#>  [1]  6  7 20 21 22 23 24  8  9 10

In contrast, the cbind and rbind functions concatenate vectors into a matrix. During the outbreak of severe acute respiratory syndrome (SARS) in 2003, a patient with SARS potentially exposed 111 passengers on board an airline flight. Of the 23 passengers that sat ‘close’ to the index case, 8 developed SARS; among the 88 passengers that did not sit ‘close’ to the index case, only 10 developed SARS [8]. Now, we can bind 2 vectors to create a \(2 \times 2\) table (matrix).

#>           case noncase
#> exposed      8      15
#> unexposed   10      78
#>         exposed unexposed
#> case          8        10
#> noncase      15        78

For the example that follows, let’s recreate the SARS data as two character vectors.

#>      exposure  outcome
#> [1,] "exposed" "case" 
#> [2,] "exposed" "case" 
#> [3,] "exposed" "case" 
#> [4,] "exposed" "case"

Now, use the table function to cross-tabulate one or more vectors.

#>          exposure
#> outcome   exposed unexposed
#>   case          8        10
#>   noncase      15        78

The ftable function creates a flat contingency table from one or more vectors.

#>         exposure exposed unexposed
#> outcome                           
#> case                   8        10
#> noncase               15        78

This will come in handy later when we want to display a 3 or more dimensional table as a ‘flat’ 2-dimensional table.

The outer function applies a function to every combination of elements from two vectors. For example, create a multiplication table for the numbers 1 to 5.

#>      [,1] [,2] [,3] [,4] [,5]
#> [1,]    1    2    3    4    5
#> [2,]    2    4    6    8   10
#> [3,]    3    6    9   12   15
#> [4,]    4    8   12   16   20
#> [5,]    5   10   15   20   25

The tapply function applies a function to strata of a vector that is defined by one or more ‘indexing’ vectors. For example, to calculate the mean age of females and males:

#>    F    M 
#> 54.0 42.6
#>    F    M 
#> 54.0 42.6

The tapply function is an important and versatile function because it allows us to apply any function that can be applied to a vector, to be applied to strata of a vector. Moveover, we can use our user-created functions as well.

2.2.7 Converting vectors into factors (categorical variables)

The Williams Institute recommends a two-step approach for asking survey questions for gender identity [9]:

  1. [sex] What sex were you assigned at birth, on your original birth certificate? (select one)
    \(\bigcirc\) Male
    \(\bigcirc\) Female
  2. [gender] How do you describe yourself? (select one)
    \(\bigcirc\) Male
    \(\bigcirc\) Female
    \(\bigcirc\) Transgender
    \(\bigcirc\) Do not identify as female, male, or transgender

Suppose you conduct a survey of 100 subjects and the gender variable is represented by a character vector. Here is the tabulation of your data:

#> [1] "Male"   "Male"   "Female" "Male"   "Female"
#> gender
#> Female   Male 
#>     43     57

What is wrong with this tabulation? The tabulation does not have all the possible reponse levels (“Female”, “Male”, “Transgender”, “Neither.FMT”). This is because the first 100 respondents identified only as female and male. The character vector only contains the actual reponses without keeping track of the possible responses. To remedy this we use the factor function to convert vectors into a categorical variable that can keep track of possible response levels. Factors is how R manages categorical variables.

#> [1] Male   Male   Female Male   Female
#> Levels: Female Male Transgender Neither.FMT
#> gender.fac
#>      Female        Male Transgender Neither.FMT 
#>          43          57           0           0

How does the display of factors differ from the display of character vectors? This was our first introduction to factors. Later, we cover factors in more detail.

Note: factors are actually integer (numeric) vectors with labels called levels. Try unclass(gender.fac) followed by table(unclass(gender.fac)).

2.3 A matrix is a 2-dimensional table of like elements

2.3.1 Understanding matrices

A matrix is a 2-dimensional table of like elements. Matrix elements can be either numeric, character, or logical. Contingency tables in epidemiology are represented in R as numeric matrices or arrays. An array is the generalization of matrices to 3 or more dimensions (commonly known as stratified tables). We cover arrays later, for now we will focus on 2-dimensional tables.

Consider the \(2\times 2\) table of crude data in Table 2.12 [10]. In this randomized clinical trial (RCT), diabetic subjects were randomly assigned to receive either tolbutamide, an oral hypoglycemic drug, or placebo. Because this was a prospective study we can calculate risks, odds, a risk ratio, and an odds ratio. We will do this using R as a calculator.

TABLE 2.12: Deaths among subjects who received tolbutamide and placebo in the Unversity Group Diabetes Program (1970)
Treatment
Outcome status Tolbutamide Placebo
  Deaths 30 21
  Survivors 174 184 
#>           Tolbutamide Placebo
#> Deaths             30      21
#> Survivors         174     184
#>            Tolbutamide   Placebo
#> risks        0.1470588 0.1024390
#> risk.ratio   1.4355742 1.0000000
#> odds         0.1724138 0.1141304
#> odds.ratio   1.5106732 1.0000000

Now let’s review each line briefly to understand the analysis in more detail.

We used the rownames and the colnames functions to assign row and column names to the matrix dat. The row names and the column names are both character vectors.

We used the apply function to sum the columns; it is a versatile function for applying any function to matrices or arrays. The second argument is the MARGIN option: in this case, MARGIN=2, meaning apply the sum function to the columns. To sum the rows, set MARGIN=1.

Using the definition of the odds, we calculated the odds of death for each treatment group. Then we calculated the odds ratios using the placebo group as the reference.

Finally, we display the dat table we created. We also created a table of results by row binding the vectors using the rbind function.

In the sections that follow we will cover the necessary concepts to make the previous analysis routine.

2.3.2 Creating matrices

There are several ways to create matrices (Table 2.13). In general, we create or use matrices in the following ways:

  • Contingency tables (cross tabulations)
  • Spreadsheet calculations and display
  • Collecting results into tabular form
  • Results of 2-variable equations
TABLE 2.13: Common ways of creating a matrix
Function Description Try these examples
cbind Column-bind x <- 1:3; y <- 3:1; cbind(x, y)
rbind Row-bind vectors rbind(x, y)
matrix Generates matrix matrix(1:4, nrow=2, ncol=2)
dim Assign dimensions mtx2 <- 1:4
dim(mtx2) <- c(2, 2)
table Cross-tabulate table(infert$educ, infert$case)
xtabs Cross-tabulate xtabs(~education + case, data = infert)
ftable Creates 2-D flat table ftable(infert$educ, infert$spont, infert$case)
array Creates 2-D array array(1:4, dim = c(2, 2))
as.matrix Coercion as.matrix(1:3)
outer Outer product outer(1:5, 1:5, '*')
x[r,,] Indexing an array x <- array(1:8, c(2, 2, 2))
x[,c,] x[1, , ]
x[,,d] x[ ,1, ]
x[ , ,1]

2.3.2.1 Contingency tables (cross tabulations)

In the previous section we used the matrix function to create the \(2 \times 2\) table for the UGDP clinical trial:

#>           Tolbutamide Placebo
#> Deaths             30      21
#> Survivors         174     184

Alternatively, we can create a 2-way contingency table using the table function with fields from a data set;

#> [1] "Status"    "Treatment" "Agegrp"
#>           
#>            Placebo Tolbutamide
#>   Death         21          30
#>   Survivor     184         174

Alternatively, the xtabs function cross tabulates using a formula interface. An advantage of this function is that the field names are included.

#>           Treatment
#> Status     Placebo Tolbutamide
#>   Death         21          30
#>   Survivor     184         174

Finally, a multi-dimensional contingency table can be presented as a 2-dimensional flat contingency table using the ftable function. Here we stratify the above table by the variable Agegrp.

#> , , Agegrp = <55
#> 
#>           Treatment
#> Status     Placebo Tolbutamide
#>   Death          5           8
#>   Survivor     115          98
#> 
#> , , Agegrp = 55+
#> 
#>           Treatment
#> Status     Placebo Tolbutamide
#>   Death         16          22
#>   Survivor      69          76
#>                      Agegrp <55 55+
#> Status   Treatment                 
#> Death    Placebo              5  16
#>          Tolbutamide          8  22
#> Survivor Placebo            115  69
#>          Tolbutamide         98  76

However, notice that ftable, while preserving the order of the variables, does provide the equivalent, namely, Status vs. Treatment, by Agegrp. We can fix this by reversing the order of the variables within the xtabs function:

#>                 Treatment Placebo Tolbutamide
#> Agegrp Status                                
#> <55    Death                    5           8
#>        Survivor               115          98
#> 55+    Death                   16          22
#>        Survivor                69          76

2.3.2.2 Spreadsheet calculations and display

Matrices are commonly used to display spreadsheet-like calculations. In fact, a very efficient way to learn R is to use it as our spreadsheet. For example, assuming the rate of seasonal influenza infection is 10 infections per 100 person-years, let’s calculate the individual cumulative risk of influenza infection at the end of 1, 5, and 10 years. Assuming no competing risk, we can use the exponential formula:

\[\begin{equation} R(0, t) = 1 - e^{-\lambda t} \end{equation}\]

where , \(\lambda\) = infection rate, and \(t\) = time.

#>      rate years cumulative.risk
#> [1,]  0.1     1      0.09516258
#> [2,]  0.1     5      0.39346934
#> [3,]  0.1    10      0.63212056

Therefore, the cumulative risk of influenza infection after 1, 5, and 10 years is 9.5%, 39%, and 63%, respectively.

2.3.2.3 Collecting results into tabular form

A 2-way contingency table from the table or xtabs functions does not have margin totals. However, we can construct a numeric matrix that includes the totals. Using the UGDP data again,

#>          Placebo Tolbutamide Total
#> Death         21          30    51
#> Survivor     184         174   358
#> Total        205         204   409

This table (tab2b) is primarily for display purposes.

2.3.2.4 Results of 2-variable equations

When we have an equation with 2 variables, we can use a matrix to display the answers for every combination of values contained in both variables. For example, consider this equation:

\[\begin{equation} z = x y \end{equation}\]

And suppose \(x = \{1, 2, 3, 4, 5 \}\) and \(y = \{6, 7, 8, 9, 10 \}\).

Here’s the long way to create a matrix for this equation:

#>    6  7  8  9 10
#> 1  6  7  8  9 10
#> 2 12 14 16 18 20
#> 3 18 21 24 27 30
#> 4 24 28 32 36 40
#> 5 30 35 40 45 50

Okay, but the outer function is much better for this task:

#>    6  7  8  9 10
#> 1  6  7  8  9 10
#> 2 12 14 16 18 20
#> 3 18 21 24 27 30
#> 4 24 28 32 36 40
#> 5 30 35 40 45 50

In fact, the outer function can be used to calculate the ‘surface’ for any 2-variable equation (more on this later).

2.3.3 Naming matrix components

We have already seen several examples of naming components of a matrix. Table 2.14 summarizes the common ways of naming matrix components. The components of a matrix can be named at the time the matrix is created, or they can be named later. For a matrix, we can provide the row names, column names, and field names.

TABLE 2.14: Common ways of naming matrix components
Function Try these examples
matrix # name rows and columns only
dat <- matrix(c(178, 79, 1411, 1486), 2, 2,
dimnames = list(c('TypeA','TypeB'), c('Y','N')))
# name rows, columns, and fields
dat <- matrix(c(178, 79, 1411, 1486), 2, 2,
dimnames = list(Behavior = c('TypeA','TypeB'),
'Heart attack' = c('Y','N')))
rownames dat <- matrix(c(178, 79, 1411, 1486), 2, 2)
rownames(dat) <- c('TypeA','TypeB')
colnames colnames(dat) <- c('Y','N') # col names
dimnames # name rows and columns only
dat <- matrix(c(178, 79, 1411, 1486), 2, 2)
dimnames(dat) <- list(c('TypeA','TypeB'), c('Y','N'))
# name rows, columns, and fields
dat <- matrix(c(178, 79, 1411, 1486), 2, 2)
dimnames(dat) <- list(Behavior = c('TypeA','TypeB'),
'Heart attack' = c('Y','N'))
names # add field to row \& col names
`dat <- matrix(c(178, 79, 1411, 1486), 2, 2,
dimnames = list(c('TypeA','TypeB'), c('Y','N')))
names(dimnames(dat)) <- c('Behavior', 'Heart attack')

For example, the UGDP clinical trial \(2 \times 2\) table can be created de novo:

#>            Treatment
#> Outcome     Tolbutamide Placebo
#>   Deaths             30      21
#>   Survivors         174     184

In the ‘Treatment’ field, the possible values, ‘Tolbutamide’ and ‘Placebo,’ are the column names. Similarly, in the ‘Status’ field, the possible values, ‘Death’ and ‘Survivor,’ are the row names.

If a matrix does not have field names, we can add them after the fact, but we must use the names and dimnames functions together. Having field names is necessary if the row and column names are not self-explanatory, as this example illustrates.

#>     Yes  No
#> Yes  30  21
#> No  174 184
#>      Tolbutamide
#> Death Yes  No
#>   Yes  30  21
#>   No  174 184

Study and test the examples in Table 2.14.

2.3.4 Indexing (subsetting) a matrix

Similar to vectors, a matrix can be indexed by position, by name, or by logical. Study and practice the examples in (Table 2.15). An important skill to master is indexing rows of a matrix using logical vectors.

TABLE 2.15: Common ways of indexing a matrix
Indexing Try these examples
By logical dat[, 1] > 100
dat[dat[, 1] > 100, ]
dat[dat[, 1] > 100, , drop = FALSE]
By position dat <- matrix(c(178, 79, 1411, 1486), 2, 2)
dimnames(dat) <- list(Behavior = c('Type A',
'Type B'), 'Heart attack' = c('Yes', 'No'))
dat[1, ]
dat[1,2]
dat[2, , drop = FALSE]
By name (if exists) dat['Type A', ]
dat['Type A', 'Type B']
dat['Type B', , drop = FALSE]

Consider the following matrix of data, and suppose I want to select the rows for subjects age less than 60 and systolic blood pressure less than 140.

#>      age chol sbp
#> [1,]  45  145 124
#> [2,]  56  168 144
#> [3,]  73  240 150
#> [4,]  44  144 134
#> [5,]  65  210 112
#> [1]  TRUE  TRUE FALSE  TRUE FALSE
#> [1]  TRUE FALSE FALSE  TRUE  TRUE
#> [1]  TRUE FALSE FALSE  TRUE FALSE
#>      age chol sbp
#> [1,]  45  145 124
#> [2,]  44  144 134

Notice that the tmp logical vector is the intersection of the logical vectors separated by the logical operator &.

2.3.5 Replacing matrix elements

Remember, replacing matrix elements is just indexing plus assignment: anything that can be indexed can be replaced. Study and practice the examples in (Table 2.16).

TABLE 2.16: Common ways of replacing matrix elements
Replacing Try these examples
By logical qq <- dat[, 1] < 100 # logic vector
dat[qq, ] <- 99; dat
dat[dat[, 1] < 100, ] <- c(79, 1486); dat
By position dat <- matrix(c(178, 79, 1411, 1486), 2, 2)
dimnames(dat) <- list(c('Type A','Type B'),
c('Yes','No'))
dat[1, ] <- 99; dat
By name (if exists) dat['Type A', ] <- c(178, 1411); dat

2.3.6 Operating on a matrix

In epidemiology books, authors have preferences for displaying contingency tables. Software packages have default displays for contingency tables. In practice, we may need to manipulate a contingency table to facilitate further analysis. Consider the following 2-way table:

#>            Treatment
#> Outcome     Tolbutamide Placebo
#>   Deaths             30      21
#>   Survivors         174     184

We can transpose the matrix using the t function.

#>              Outcome
#> Treatment     Deaths Survivors
#>   Tolbutamide     30       174
#>   Placebo         21       184

We can reverse the order of the rows and/or columns.

#>            Treatment
#> Outcome     Tolbutamide Placebo
#>   Survivors         174     184
#>   Deaths             30      21
#>            Treatment
#> Outcome     Placebo Tolbutamide
#>   Deaths         21          30
#>   Survivors     184         174

In short, we need to be able to manipulate and execute operations on a matrix. Table 2.17 summarizes key functions (apply and sweep) for passing other functions to execute operations on a matrix. Table 2.18 summarizes additional convenience functions for operating on a matrix.

TABLE 2.17: Common ways of operating on a matrix
Function Description Try these examples
t Transpose matrix dat=matrix(c(178,79,1411,1486),2,2)
t(dat)
apply Apply a function to apply(X = dat, MARGIN=2, FUN=sum)
margins of a matrix apply(dat, 1, FUN=sum)
apply(dat, 1, mean)
apply(dat, 2, cumprod)
sweep Sweeping out a rsum <- apply(dat, 1, sum)
summary statistic rdist <- sweep(dat, 1, rsum, '/')
rdist
csum <- apply(dat, 2, sum)
cdist <- sweep(dat, 2, csum, '/')
cdist
TABLE 2.18: Alternative ways of operating on a matrix (with equivalents)
Function Description Try these examples
margin.table, Marginal sums dat <- matrix(5:8, 2, 2)
rowSums, margin.table(dat)
colSums margin.table(dat, 1)
rowSums(dat) # equivalent
apply(dat, 1, sum) # equivalent
margin.table(dat, 2)
colSums(dat) # equivalent
apply(dat, 2, sum) # equivalent
addmargins Marginal totals addmargins(dat)
rowMeans, Marginal means rowMeans(dat)
colMeans apply(dat, 1, mean) # equivalent
colMeans(dat)
apply(dat, 2, mean) # equivalent
prop.table Marginal prop.table(dat)
distributions dat/sum(dat) # equivalent
prop.table(dat, 1)
sweep(dat, 1, apply(y,1,sum), '/')
prop.table(dat, 2)
sweep(y, 2, apply(y, 2, sum), '/')

2.3.6.1 The apply function

The apply function is an important and versatile function for conducting operations on rows or columns of a matrix, including user-created functions. The same functions that are used to conduct operations on single vectors (Table 2.10) can be applied to rows or columns of a matrix.

To calculate the row or column totals use the apply with the sum function:

#>            Treatment
#> Outcome     Tolbutamide Placebo
#>   Deaths             30      21
#>   Survivors         174     184
#>    Deaths Survivors 
#>        51       358
#> Tolbutamide     Placebo 
#>         204         205

These operations can be used to calculate marginal totals and have them combined with the original table into one table.

#>            Treatment
#> Outcome     Tolbutamide Placebo
#>   Deaths             30      21
#>   Survivors         174     184
#>           Tolbutamide Placebo Total
#> Deaths             30      21    51
#> Survivors         174     184   358
#>           Tolbutamide Placebo Total
#> Deaths             30      21    51
#> Survivors         174     184   358
#> Total             204     205   409

For convenience, R provides some functions for calculating marginal totals, and calculating row or column means (margin.table, rowSums, colSums, rowMeans, and colMeans). However, these functions just use the apply function.17

Here’s an alternative method to calculate marginal totals:

#>            Treatment
#> Outcome     Tolbutamide Placebo
#>   Deaths             30      21
#>   Survivors         174     184
#>           Tolbutamide Placebo Total
#> Deaths             30      21    51
#> Survivors         174     184   358
#> Total             204     205   409

For convenience, the addmargins function calculates and displays the marginals totals with the original data in one step.

#>            Treatment
#> Outcome     Tolbutamide Placebo
#>   Deaths             30      21
#>   Survivors         174     184
#>            Treatment
#> Outcome     Tolbutamide Placebo Sum
#>   Deaths             30      21  51
#>   Survivors         174     184 358
#>   Sum               204     205 409

The power of the apply function comes from our ability to pass many functions (including our own) to it. For practice, combine the apply function with functions from Table 2.10 to conduct operations on rows and columns of a matrix.

2.3.6.2 The sweep function

The sweep function is another important and versatile function for conducting operations across rows or columns of a matrix. This function ‘sweeps’ (operates on) a row or column of a matrix using some function and a value (usually derived from the row or column values). To understand this, we consider an example involving a single vector. For a given integer vector x, to convert the values of x into proportions involves two steps:

#> [1] 0.06666667 0.13333333 0.20000000 0.26666667 0.33333333

To apply this equivalent operation across rows or columns of a matrix requires the sweep function.

For example, to calculate the row and column distributions of a 2-way table we combine the apply (step 1) and the sweep (step 2) functions:

#>            Treatment
#> Outcome     Tolbutamide Placebo
#>   Deaths             30      21
#>   Survivors         174     184
#>            Treatment
#> Outcome     Tolbutamide   Placebo
#>   Deaths      0.5882353 0.4117647
#>   Survivors   0.4860335 0.5139665
#>            Treatment
#> Outcome     Tolbutamide  Placebo
#>   Deaths      0.1470588 0.102439
#>   Survivors   0.8529412 0.897561

Because R is a true programming language, these can be combined into single steps:

#>            Treatment
#> Outcome     Tolbutamide   Placebo
#>   Deaths      0.5882353 0.4117647
#>   Survivors   0.4860335 0.5139665
#>            Treatment
#> Outcome     Tolbutamide  Placebo
#>   Deaths      0.1470588 0.102439
#>   Survivors   0.8529412 0.897561

For convenience, R provides prop.table. However, this function just uses the apply and sweep functions.

2.4 An array is a n-dimensional table of like elements

2.4.1 Understanding arrays

An array is the generalization of matrices from 2 to \(n\)-dimensions. Stratified contingency tables in epidemiology are represented as array data objects in R. For example, the randomized clinical trial previously shown comparing the number deaths among diabetic subjects that received tolbutamide vs. placebo is now also stratified by age group (Table 2.19):

TABLE 2.19: Deaths among subjects who received tolbutamide (TOLB) and placebo in the Unversity Group Diabetes Program (1970) stratifying by age
Age<55 Age>=55 Combined
TOLB Placebo TOLB Placebo TOLB Placebo
Deaths 8 5 22 16 30 21
Survivors 98 115 76 69 174 184
Total 106 120 98 85 204 205

This is 3-dimensional array: outcome status vs. treatment status vs. age group. Let’s see how we can represent this data in R.

#> , , Age group = Age<55
#> 
#>            Treatment
#> Outcome     Tolbutamide Placebo
#>   Deaths              8       5
#>   Survivors          98     115
#> 
#> , , Age group = Age>=55
#> 
#>            Treatment
#> Outcome     Tolbutamide Placebo
#>   Deaths             22      16
#>   Survivors          76      69

R displays the first stratum (tdat[,,1]) then the second stratum (tdat[,,2]). Our goal now is to understand how to generate and operate on these types of arrays. Before we can do this we need to thoroughly understand the structure of arrays.

Let’s study a 4-dimensional array. Displayed in Table 2.20 is the year 2000 population estimates for Alameda and San Francisco Counties by age, ethnicity, and sex. The first dimension is age category, the second dimension is ethnicity, the third dimension is sex, and the fourth dimension is county. Learning how to visualize this 4-dimensional sturcture in R will enable us to visualize arrays of any number of dimensions.

TABLE 2.20: Year 2000 population estimates by age, ethnicity, sex, and county
County, Sex, & Age White Black AsianPI Latino Multirace AmInd
Alameda
   Female, Age
   <=19 58,160 31,765 40,653 49,738 10,120 839
   20–44 112,326 44,437 72,923 58,553 7,658 1,401
   45–64 82,205 24,948 33,236 18,534 2,922 822
   65+ 49,762 12,834 16,004 7,548 1,014 246
   Male, Age
   <=19 61,446 32,277 42,922 53,097 10,102 828
   20–44 115,745 36,976 69,053 69,233 6,795 1,263
   45–64 81,332 20,737 29,841 17,402 2,506 687
   65+ 33,994 8,087 11,855 5,416 711 156
San Francisco
   Female, Age
   <=$19 14355 6986 23265 13251 2940 173
   20–44 85766 10284 52479 23458 3656 526
   45–64 35617 6890 31478 9184 1144 282
   65+ 27215 5172 23044 5773 554 121
   Male, Age
   <=19 14881 6959 24541 14480 2851 165
   20–44 105798 11111 48379 31605 3766 782
   45–64 43694 7352 26404 8674 1220 354
   65+ 20072 3329 17190 3428 450 76
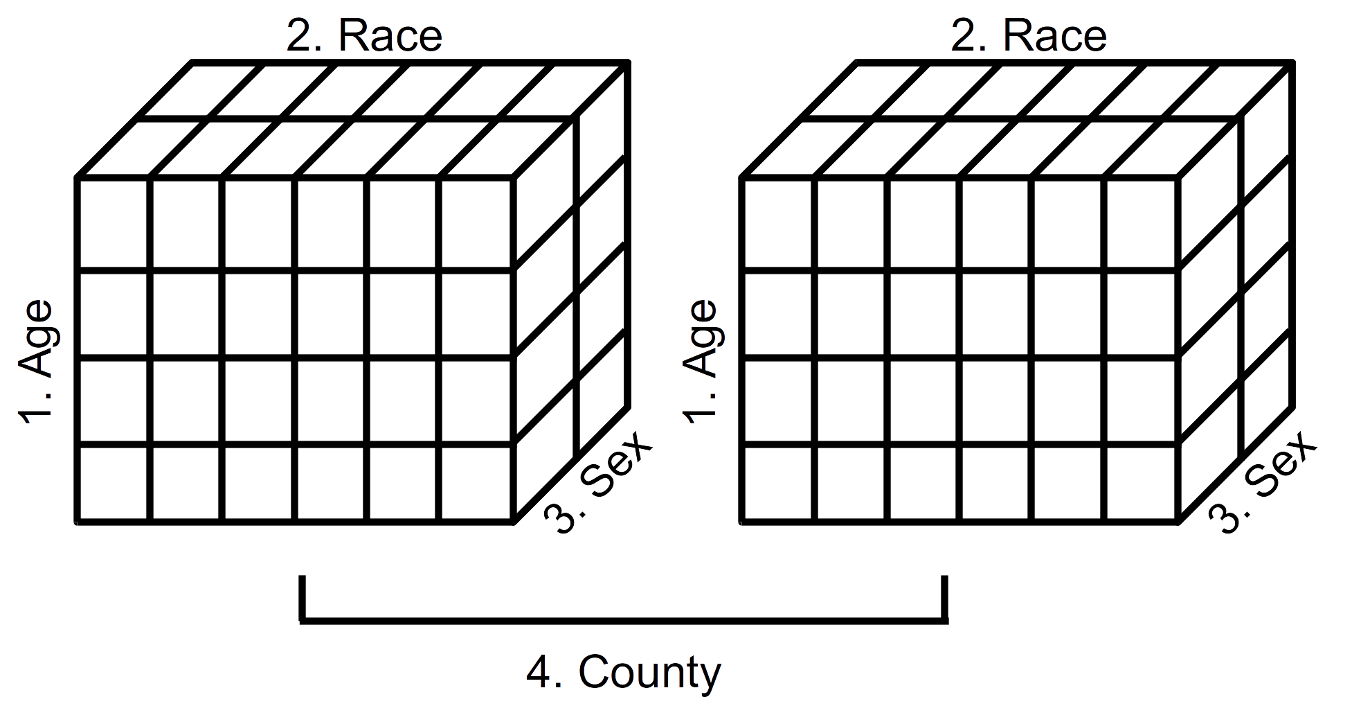
Schematic representation of a 4-dimensional array (Year 2000 population estimates by age, race, sex, and county)

FIGURE 2.1: Schematic representation of a 4-dimensional array (Year 2000 population estimates by age, race, sex, and county)

Displayed in Figure 2.1 is a schematic representation of the 4-dimensional array of population estimates in Table 2.20. The left cube represents the population estimates by age, race, and sex (dimensions 1, 2, and 3) for Alameda County (first component of dimension 4). The right cube represents the population estimates by age, race, and sex (dimensions 1, 2, and 3) for San Francisco County (second component of dimension 4). We see, then, that it is possible to visualize data arrays in more than three dimensions.

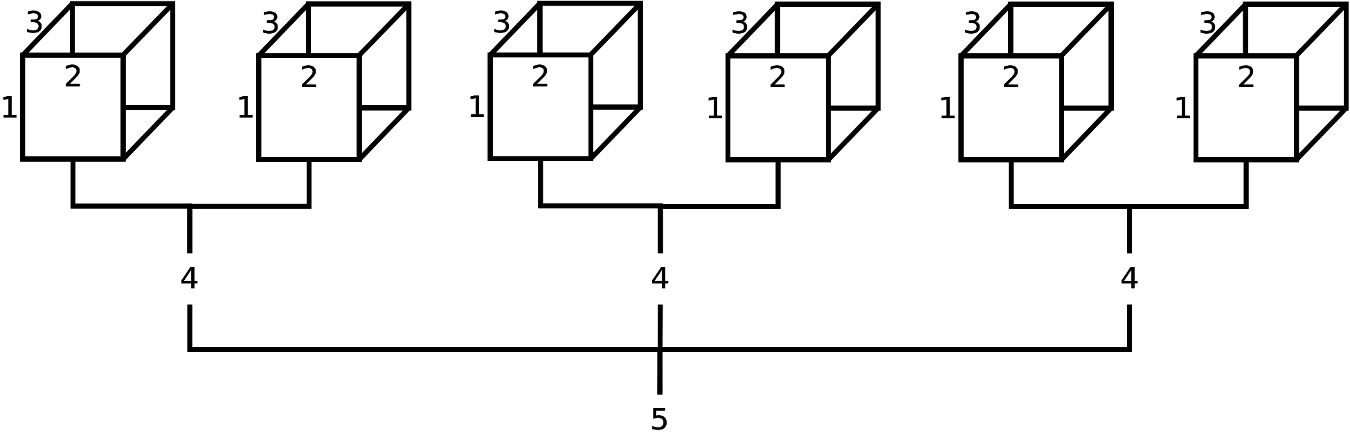
Schematic representation of a theoretical 5-dimensional array (possibly population estimates by age (1), race (2), sex (3), party affiliation (4), and state (5)). From this diagram, we can infer that the field 'state' has 3 levels, and the field 'party affiliation' has 2 levels; however, it is not apparent how many age levels, race levels, and sex levels have been created. Although not displayed, age levels would be represented by row names (along 1st dimension), race levels would be represented by column names (along 2nd dimension), and sex levels would be represented by depth names (along 3rd dimension).

FIGURE 2.2: Schematic representation of a theoretical 5-dimensional array (possibly population estimates by age (1), race (2), sex (3), party affiliation (4), and state (5)). From this diagram, we can infer that the field ‘state’ has 3 levels, and the field ‘party affiliation’ has 2 levels; however, it is not apparent how many age levels, race levels, and sex levels have been created. Although not displayed, age levels would be represented by row names (along 1st dimension), race levels would be represented by column names (along 2nd dimension), and sex levels would be represented by depth names (along 3rd dimension).

To convince ourselves further, displayed in Figure 2.2 is a theorectical 5-dimensional data array. Suppose this 5-D array contained data on age (‘Young’, ‘Old’), ethnicity (‘White’, ‘Nonwhite’), sex (‘Male’, ‘Female’), party affiliation (‘Democrat’, ‘Republican’), and state (‘California’, ‘Washington State’, ‘Florida’). For practice, using fictitious data, try the following R code and study the output:

2.4.2 Creating arrays

In R, arrays are most often produced with the array, table, or xtabs functions (Table 2.21). As in the previous example, the array function works much like the matrix function except the array function can specify 1 or more dimensions, and the matrix function only works with 2 dimensions.

#> [1] 1
#>      [,1]
#> [1,]    1
#> , , 1
#> 
#>      [,1]
#> [1,]    1
TABLE 2.21: Common ways of creating arrays
Function Description Try these examples
array Reshapes vector aa<-array(1:12,dim=c(2,3,2))
table Cross-tabulate vectors data(infert) # load infert
table(infert$educ, infert$spont, infert$case)
xtabs Cross-tabulate data frame xtabs(~education + case + parity, data = infert)
as.table Coercion ft <- ftable(infert$educ, infert$spont, infert$case)
as.table(ft)
dim Assign dimensions to object x <- 1:12
dim(x) <- c(2, 3, 2)

The table and xtabs functions cross tabulate two or more categorical vectors, except that xtabs only works with data frames. In R, categorical data are represented by character vectors or factors.18 First, we cross tabulate character vectors using table and xtabs.

#> 'data.frame':    409 obs. of  3 variables:
#>  $ Status   : chr  "Death" "Death" "Death" "Death" ...
#>  $ Treatment: chr  "Tolbutamide" "Tolbutamide" "Tolbutamide" "Tolbutamide" ...
#>  $ Agegrp   : chr  "<55" "<55" "<55" "<55" ...
#> , ,  = <55
#> 
#>           
#>            Placebo Tolbutamide
#>   Death          5           8
#>   Survivor     115          98
#> 
#> , ,  = 55+
#> 
#>           
#>            Placebo Tolbutamide
#>   Death         16          22
#>   Survivor      69          76

The as~is option assured that character vectors were not converted to factors, which is the default. Notice that the table function produced an array with no field names (i.e., Status, Treatment, Agegrp). This is not ideal. A better option is to use xtabs, which uses a formula interface (~ V1 + V2):

#> , , Agegrp = <55
#> 
#>           Treatment
#> Status     Placebo Tolbutamide
#>   Death          5           8
#>   Survivor     115          98
#> 
#> , , Agegrp = 55+
#> 
#>           Treatment
#> Status     Placebo Tolbutamide
#>   Death         16          22
#>   Survivor      69          76

Notice that xtabs includes the field names. For practice with cross tabulating factors, repeat the above expressions with read in the data setting option as is to FALSE.

Although table does not generate the field names, they can be added manually:

#> , , Age = <55
#> 
#>           Therapy
#> Outcome    Placebo Tolbutamide
#>   Death          5           8
#>   Survivor     115          98
#> 
#> , , Age = 55+
#> 
#>           Therapy
#> Outcome    Placebo Tolbutamide
#>   Death         16          22
#>   Survivor      69          76

Recall that the ftable function creates a flat contingency from categorical vectors. The as.table function converts the flat contingency table back into a multidimensional array.

#>                 Outcome Death Survivor
#> Age Therapy                           
#> <55 Placebo                 5      115
#>     Tolbutamide             8       98
#> 55+ Placebo                16       69
#>     Tolbutamide            22       76
#> , , Outcome = Death
#> 
#>      Therapy
#> Age   Placebo Tolbutamide
#>   <55       5           8
#>   55+      16          22
#> 
#> , , Outcome = Survivor
#> 
#>      Therapy
#> Age   Placebo Tolbutamide
#>   <55     115          98
#>   55+      69          76

2.4.3 Naming arrays

Naming components of an array is an extension of naming components of a matrix (Table 2.14). Study and implement the examples in Table 2.22.

TABLE 2.22: Common ways of naming arrays
Function Study and try these examples
array x <- c(140, 11, 280, 56, 207, 9, 275, 32)
rn <- c('>=1 cups per day', '0 cups per day')
cn <- c('Cases', 'Controls')
dn <- c('Females', 'Males')
x <- array(x, dim = c(2, 2, 2),
dimnames = list(Coffee = rn,
Outcome = cn, Gender = dn)); x
dimnames x <- c(140, 11, 280, 56, 207, 9, 275, 32)
rn <- c('>=1 cups per day', '0 cups per day')
cn <- c('Cases', 'Controls')
dn <- c('Females', 'Males')
x <- array(x, dim = c(2, 2, 2))
dimnames(x) <- list(Coffee = rn, Outcome = cn,
Gender = dn); x
names x <- c(140, 11, 280, 56, 207, 9, 275, 32)
rn <- c('>=1 cups per day', '0 cups per day')
cn <- c('Cases', 'Controls')
dn <- c('Females', 'Males')
x <- array(x, dim = c(2, 2, 2))
dimnames(x) <- list(rn, cn, dn)
x # display w/o field names
names(dimnames(x))<-c('Coffee', 'Case status', 'Sex')
x # display w/ field names

2.4.4 Indexing (subsetting) arrays

Indexing an array is an extension of indexing a matrix (Table 2.15). Study and implement the examples in (Table 2.23).

TABLE 2.23: Common ways of indexing arrays
Indexing Try these examples
By logical zz <- x[ ,1,1]>50; zz
x[zz, , ]
By position x[1, , ]
x[ ,2 , ]
By name (if exists) x[ , , 'Males']
x[ ,'Controls', 'Females']

2.4.5 Replacing array elements

Replacing elements of an array is an extension of replacing elements of a matrix (Table 2.16). Study and implement the examples in (Table 2.24).

TABLE 2.24: Common ways of replacing array elements
Replacing Try these examples
By logical x > 200
x[x > 200] <- 999
x
By position # use x from Table 2.22
x[1, 1, 1] <- NA
x
By name (if exists) x[ ,'Controls', 'Females'] <- 99; x

2.4.6 Operating on an array

With the exception of the aperm function, operating on an array (Table 2.25) is an extension of operating on a matrix (Table 2.17). The second group of functions, such as margin.table, are shortcuts provided for convenience. In other words, these operations are easily accomplished using apply and/or sweep.

TABLE 2.25: Common ways of operating on an array
Function Description
aperm Transpose an array by permuting its dimensions
apply Apply a function to the margins of an array
sweep Sweep out a summary statistic from an array
These short-cuts function use apply and/or sweep
margin.table For array, sum of table entries for a given index
rowSums Sum across rows of an array
colSums Sum down columns of an array
addmargins Calculate and display marginal totals of an array
rowMeans Calculate means across rows of an array
colMeans Calculate means down columns of an array
prop.table Generates distribution

The aperm function is a bit tricky so we illustrated its use.

#> , , Gender = Females
#> 
#>                   Outcome
#> Coffee             Cases Controls
#>   >=1 cups per day   140      280
#>   0 cups per day      11       56
#> 
#> , , Gender = Males
#> 
#>                   Outcome
#> Coffee             Cases Controls
#>   >=1 cups per day   207      275
#>   0 cups per day       9       32
#> , , Coffee = >=1 cups per day
#> 
#>          Outcome
#> Gender    Cases Controls
#>   Females   140      280
#>   Males     207      275
#> 
#> , , Coffee = 0 cups per day
#> 
#>          Outcome
#> Gender    Cases Controls
#>   Females    11       56
#>   Males       9       32
TABLE 2.26: Example of 3-dimensional array with marginal totals: Primary and secondary syphilis morbidity by age, race, and sex, United State, 1989 (Source: CDC Summary of Notifiable Diseases, United States, 1989, MMWR 1989;38(54))
Age (yrs) Sex White Black Other Total
<=19 Male 90 1,443 217 1,750
Female 267 2,422 169 2,858
Total 357 3,865 386 4,608
20–29 Male 957 8,180 1,287 10,424
Female 908 8,093 590 9,591
Total 1,865 16,273 1,877 20,015
30–44 Male 1,218 8,311 1,012 10,541
Female 559 4,133 316 5,008
Total 1,777 12,444 1,328 15,549
45+ Male 539 2,442 310 3,291
Female 79 484 55 618
Total 618 2,926 365 3,909
Total (by sex & ethnicity) Male 2,804 20,376 2,826 26,006
Female 1,813 15,132 1,130 18,075
Total (by ethnicity) 4617 35508 3956 44081

Consider the number of primary and secondary syphilis cases in the United State, 1989, stratified by sex, ethnicity, and age (Table 2.26). This table contains the marginal and joint distribution of cases. Let’s read in the original data and reproduce the table results.

#> 'data.frame':    44081 obs. of  3 variables:
#>  $ Sex : Factor w/ 2 levels "Female","Male": 2 2 2 2 2 2 2 2 2 2 ...
#>  $ Race: Factor w/ 3 levels "Black","Other",..: 3 3 3 3 3 3 3 3 3 3 ...
#>  $ Age : Factor w/ 4 levels "<=19","20-29",..: 1 1 1 1 1 1 1 1 1 1 ...
#> $Sex
#> [1] "Female" "Male"  
#> 
#> $Race
#> [1] "Black" "Other" "White"
#> 
#> $Age
#> [1] "<=19"  "20-29" "30-44" "45+"

In R, categorical data are converted into factors. The possible values for each factor are called levels. We used lapply to pass the levels function and display the levels for each factor. In order to match the table display we need to reorder the levels for Sex and Race, and we recode Age into four levels.

#> $Sex
#> [1] "Male"   "Female"
#> 
#> $Race
#> [1] "White" "Black" "Other"
#> 
#> $Age
#> [1] "<=19"  "20-29" "30-44" "45+"

We used the factor function and the levels option to reorder the levels. Now we are ready to create an array and calculate the marginal totals to replicate Table 2.26.

#> , , Age = <=19
#> 
#>         Race
#> Sex      White Black Other
#>   Male      90  1443   217
#>   Female   267  2422   169
#> 
#> , , Age = 20-29
#> 
#>         Race
#> Sex      White Black Other
#>   Male     957  8180  1287
#>   Female   908  8093   590
#> 
#> , , Age = 30-44
#> 
#>         Race
#> Sex      White Black Other
#>   Male    1218  8311  1012
#>   Female   559  4133   316
#> 
#> , , Age = 45+
#> 
#>         Race
#> Sex      White Black Other
#>   Male     539  2442   310
#>   Female    79   484    55

To get marginal totals for one dimension, use the apply function and specify the dimension for stratifying the results.

#> [1] 44081
#>   Male Female 
#>  26006  18075
#> White Black Other 
#>  4617 35508  3956
#>  <=19 20-29 30-44   45+ 
#>  4608 20015 15549  3909

To get the joint marginal totals for 2 or more dimensions, use the apply function and specify the dimensions for stratifying the results. This means that the function that is passed to apply is applied across the other, non-stratified dimensions.

#>         Race
#> Sex      White Black Other
#>   Male    2804 20376  2826
#>   Female  1813 15132  1130
#>         Age
#> Sex      <=19 20-29 30-44  45+
#>   Male   1750 10424 10541 3291
#>   Female 2858  9591  5008  618
#>        Race
#> Age     White Black Other
#>   <=19    357  3865   386
#>   20-29  1865 16273  1877
#>   30-44  1777 12444  1328
#>   45+     618  2926   365

In R, arrays are displayed by the 1st and 2nd dimensions, stratified by the remaining dimensions. To change the order of the dimensions, and hence the display, use the aperm function. For example, the syphilis case data is most efficiently displayed when it is stratified by race, age, and sex:

#> , , Sex = Male
#> 
#>        Age
#> Race    <=19 20-29 30-44  45+
#>   White   90   957  1218  539
#>   Black 1443  8180  8311 2442
#>   Other  217  1287  1012  310
#> 
#> , , Sex = Female
#> 
#>        Age
#> Race    <=19 20-29 30-44  45+
#>   White  267   908   559   79
#>   Black 2422  8093  4133  484
#>   Other  169   590   316   55

Using aperm we moved the 2nd dimension (race) into the first position, the 3rd dimension (age) into the second position, and the 1st dimension (sex) into the third position.

Another method for changing the display of an array is to convert it into a flat contingency table using the ftable function. For example, to display Table 2.26 as a flat contingency table in R (but without the marginal totals), we use the following code:

#>              Race White Black Other
#> Age   Sex                          
#> <=19  Male           90  1443   217
#>       Female        267  2422   169
#> 20-29 Male          957  8180  1287
#>       Female        908  8093   590
#> 30-44 Male         1218  8311  1012
#>       Female        559  4133   316
#> 45+   Male          539  2442   310
#>       Female         79   484    55

This ftable object can be treated as a matrix, but it cannot be transposed. Also, notice that we can combine the ftable with addmargins:

#>              Race White Black Other   Sum
#> Age   Sex                                
#> <=19  Male           90  1443   217  1750
#>       Female        267  2422   169  2858
#>       Sum           357  3865   386  4608
#> 20-29 Male          957  8180  1287 10424
#>       Female        908  8093   590  9591
#>       Sum          1865 16273  1877 20015
#> 30-44 Male         1218  8311  1012 10541
#>       Female        559  4133   316  5008
#>       Sum          1777 12444  1328 15549
#> 45+   Male          539  2442   310  3291
#>       Female         79   484    55   618
#>       Sum           618  2926   365  3909
#> Sum   Male         2804 20376  2826 26006
#>       Female       1813 15132  1130 18075
#>       Sum          4617 35508  3956 44081

To share the U.S. syphilis data in a universal format, we could create a text file with the data in a tabular form. However, the original, individual-level data set has over 40,000 observations. Instead, it would be more convenient to create a group-level, tabular data set using the as.data.frame function on the data array object.

#> 'data.frame':    24 obs. of  4 variables:
#>  $ Sex : Factor w/ 2 levels "Male","Female": 1 2 1 2 1 2 1 2 1 2 ...
#>  $ Race: Factor w/ 3 levels "White","Black",..: 1 1 2 2 3 3 1 1 2 2 ...
#>  $ Age : Factor w/ 4 levels "<=19","20-29",..: 1 1 1 1 1 1 2 2 2 2 ...
#>  $ Freq: int  90 267 1443 2422 217 169 957 908 8180 8093 ...
#>      Sex  Race   Age Freq
#> 1   Male White  <=19   90
#> 2 Female White  <=19  267
#> 3   Male Black  <=19 1443
#> 4 Female Black  <=19 2422
#> 5   Male Other  <=19  217
#> 6 Female Other  <=19  169
#> 7   Male White 20-29  957
#> 8 Female White 20-29  908

The group-level data frame is practical only if all the fields are categorical data, as is the case here. For additional practice, study and implement the examples in Table 2.25.

2.5 Selected applications

2.5.1 Probabilistic reasoning with Bayesian networks

A Bayesian network (BN) is a graphical model for representing probabilistic, but not necessarily causal, relationships between variables called nodes [11,12]. The nodes are connected by lines called edges which, for our purposes, are always directed with an arrow. Consider this noncausal BN:

Smelling smoke increases the probability of a fire burning nearby, but obviously smoke alone does not cause a fire. In other words, does knowing \(X\) (smell smoke) change the credibility of \(Y\) (fire nearby)? In contrast, now consider this causal BN:

This causal BN depicts fire causing smoke. Notice that both noncausal and causal BNs have probabilistic dependence which we will use for probabilistic reasoning. Noncausal BNs are commonly used in influence diagrams for decision analysis which we cover later in the book.

A two-node causal BN has two types of proabilistic reasoning (Table ).

Probabilistic reasoning for 2-node causal BN
Probabilistic reasoning Conditional probability
Causal (predictive) reasoning \(P(\text{Effect}\mid\text{Cause})\)
Evidential (diagnostic) reasoning \(P(\text{Cause}\mid\text{Effect})\)

When a causal effect is not firmly established, the BN asserts this concept:

Bayesian network involving a hypothesis and evidence
Conditional probability Probabilistic reasoning
\(P(\text{Evidence}\mid\text{Hypothesis})\) Causal reasoning
\(P(\text{Hypothesis}\mid\text{Evidence})\) Evidential reasoning

Evidential reasoning requires Bayes Theorem.

\[\begin{align*} P(H \mid E) &= \frac{P(E \mid H)P(H)}{P(E)}\\ &= \frac{P(E \mid H)P(H)}{P(E \mid H)P(H)+P(E \mid \neg H)P(\neg H)} \end{align*}\]

\(P(H)\) is the prior (old) belief, \(P(H \mid E)\) is the posterior (new) belief, and \(P(E \mid H)\) is called the likelihood. The likelihood is critical because it is usually measurable. The challenge is that we need Bayes Theorem for two reasons:

  1. to use evidence and theory to update our belief from \(P(H)\) to \(P(H \mid E)\), and
  2. to avoid the fallacy of the transposed conditional; i.e., confusing \(P(E \mid H)\) with \(P(H \mid E)\).

2.5.1.1 Example: HIV testing

For example, from Neapolitan (p. 491, [13]), suppose Sam takes a test (evidence) to determine whether he has HIV infection (hypothesis). Here is the BN:

In diagnostic testing we use Bayes Theorem to calculate the post-test probability from the test results, pre-test probability (prevalence of infection), and test characteristics (sensitivity, specificity). Table displays the data we need for applying Bayes Theorem.

Probabilities for using Bayes Theorem in diagnostic testing
Name Probabilities Value
Pre-test (prior) probability of \(\text{HIV}+\) \(P(\text{HIV}+)\) 0.00001
Sensitivity \(P(\text{Test}+\mid\text{HIV}+)\) 0.999
Specificity \(P(\text{Test}-\mid\text{HIV}-)\) 0.998
Post-test (posterior) probability \(P(\text{HIV}\mid\text{Test})\) TBD

For illustrative purposes, we calculate the “positive predictive value” (PPV).

\[ P(H+ \mid T+) = \frac{P(T+ \mid H+)P(H+)}{P(T+ \mid H+)P(H+) + P(T+ \mid H-)P(H-)} \]

This is easy to calculate in R.

#> [1] 0.004970223

Calculating the PPV (or NPV) is evidential reasoning and it requires applying Bayes Theorem. Our brains cannot calculate posterior probabilities reliably; we need computational tools. In other words, for the simplest 2-node graph, our brains are not able to “flip the arrow” from \(P(\text{Evidence}\mid\text{Hypothesis})\) to \(P(\text{Hypothesis}\mid \text{Evidence})\) and make valid Bayesian calculations.

2.5.2 Causal graphs—the story behind the data

2.5.2.1 Example: A retrospective observation study

A vector (one variable) is represented by a single node. A matrix (cross-tabulation of two variables) is represented by two nodes. A 3-dimensional array (cross-tabulation of two variables) is represented by three nodes. And, an n-dimensional array is represented by n nodes. Therefore, we can think of these arrays as stratified contigency tables.

The story is how the data was generated (data generating process) and how the data was measured (study design). With a causal graph we encode the salient parts of the story that can only come from human knowledge. Data, by themselves, cannot tell us how they were generated.

In 1986, Charig published a retrospective observational study comparing open surgery (Treatment A) to percutaneous nephrolithotomy (Treatment B) for the treatment of kidney stones [14,15]. Treatment B is noninvasive. Success was defined as no stones at three months. The data are presented in Table 2.27.

TABLE 2.27: Comparison of Treatment A to B for kidney stones, by size
Stone size Treatment A Success (%) Treatment B Success (%)
Small stones 81/87 93 234/270 87
Large stones 192/263 73 55/80 69
Combined 273/350 78 289/350 83

If you believe in “data-driven” decision-making then you have a big problem! When you stratify the data and know the stone size, Treatment A is better for both size. However, if you do not stratify and do not know the stone size, Treatment B is better. Which is correct? No amount of data or data analysis will answer this question—that’s why it’s call a paradox—in this case, Simpson’s paradox. We need more information (the story) and we need a method (causal graphs) to encode this story.

We have three variables: \(X\): treatment (A, B), \(Y\): success (yes, no), \(Z\): stone size (small, large). How are they related? The obvious relationship is the causal effect of Treatment on Success.

Causal graph of treatment (X) and success (Y)

FIGURE 2.3: Causal graph of treatment (X) and success (Y) 

#>            Treatment (X)
#> Success (Y)   A   B
#>         Yes 273 289
#>         No   77  61
#>            Treatment (X)
#> Success (Y)    A         B
#>         Yes 0.78 0.8257143
#>         No  0.22 0.1742857

Now, here is the missing story: It turns out that urologists select open surgery (Treatment A) for more severe cases, and larger stones are considered more severe. In other words, severity causes a selection of treatment, and we can see the resulting association in the data.

#>              Stone.Size (Z)
#> Treatment (X) Small Large
#>             A    87   263
#>             B   270    80
#>              Stone.Size (Z)
#> Treatment (X)     Small     Large
#>             A 0.2436975 0.7667638
#>             B 0.7563025 0.2332362

Of course, stone size (i.e., severity) has a causal effect on success. We now have enough information to construct the full causal graph (Figure 2.4).

Causal graph of treatment (X), success (Y), and stone size (Z).

FIGURE 2.4: Causal graph of treatment (X), success (Y), and stone size (Z).

Figure 2.4 depicts the three possible patterns we can observe with three nodes:

  1. chain (sequential cause): \(Z \rightarrow X \rightarrow Y\)
  2. fork (common cause): \(X \leftarrow Z \rightarrow Y\)
  3. collider (common effect): \(X \rightarrow Y \leftarrow Z\)

In this causal graph (Figure 2.4), the stone size (\(Z\)) is a common cause (fork) and is also called a confounder because it distorts the causal effect of treatment (\(X\)) on success (\(Y\)).

Later we will learn how to use the causal graph to derive an adjustment formula to de-confound the causal effect of treatment on success. This is not possible with the data table alone; the causal graph encodes the story, allowing us to adjust for confounding.

KEY IDEA: All causal graphs, regardless of complexity, are constructed from the three core patterns: chain (sequential cause), fork (common cause), and collider (common effect). The causal graph encodes the “story” of the data generating process. By itself the data tables never tell the full story—we need a causal graph.

2.5.2.2 Conditional probability tables in R

A directed acyclic graph (DAG) is a causal Bayesian network (BN). A BN is a probabilistic graphical model where nodes are conditional probability tables and connecting arrows encode probabilistic dependence. Depending on the probabilistic assessment, in BNs arrows can “flip.” However, in DAGs the arrows cannot flip because they represent causal effects, yet we can still evaluate a DAG as a probabilistic graphical model.

For example, Figure 2.4 represents data that has a joint probability distribution. Using product decomposition we can rewrite it as a product of conditional probabilities that we read directly from the DAG.

\[ \Pr(X,Y,Z) = \Pr(Z) \Pr(X \mid Z) \Pr(Y \mid X, Z) \]

There are no arrows into node \(Z\) so this is represented by the marginal probability \(\Pr(Z)\). There is an arrow from parent node \(Z\) to child node \(X\); therefore, we have the conditional probability \(\Pr(X \mid Z)\). Finally, we have an arrow from \(X\) to \(Y\) and from \(Z\) to \(Y\); therefore, we have the conditional probability \(\Pr(Y \mid X, Z)\).

Using the data from Table 2.27, let’s use R to construct these conditional probability tables. We start with \(\Pr(Y \mid X, Z)\).

#> , , Stone.size (Z) = Small
#> 
#>            Treatment (X)
#> Success (Y)  A   B
#>         Yes 81 234
#>         No   6  36
#> 
#> , , Stone.size (Z) = Large
#> 
#>            Treatment (X)
#> Success (Y)   A  B
#>         Yes 192 55
#>         No   71 25
#> , , Stone.size (Z) = Small
#> 
#>            Treatment (X)
#> Success (Y)          A         B
#>         Yes 0.93103448 0.8666667
#>         No  0.06896552 0.1333333
#> 
#> , , Stone.size (Z) = Large
#> 
#>            Treatment (X)
#> Success (Y)        A      B
#>         Yes 0.730038 0.6875
#>         No  0.269962 0.3125

Notice what the option margin = c(2, 3) accomplished: “Stratified by dimensions 2 (\(X\)) and 3 (\(Z\)), provide the distribution along the remaining dimension(s) (in this case, dimension 1 or \(Y\)).” This enables us to assess the probability of success given treatment, stratified by stone size (severity).

Now, let’s construct \(\Pr(X \mid Z)\). Recall, we already constructed this two-way table de novo, but now we use the apply function instead.

#>              Stone.size (Z)
#> Treatment (X) Small Large
#>             A    87   263
#>             B   270    80
#>              Stone.size (Z)
#> Treatment (X)     Small     Large
#>             A 0.2436975 0.7667638
#>             B 0.7563025 0.2332362

This table is the crude, combined or unstratified table.

Finally, let’s construct \(\Pr(Z)\), again using apply.

#> Small Large 
#>   357   343
#> Small Large 
#>  0.51  0.49

Consider DAGs (Figure 2.4) and data (Table 2.27) two sides of the same coin. They both give us different but complementary information. Causal models represent our beliefs or hypotheses of how the world works (the story). As the world unfolds it generates data which we can measure and analyze. Because one particular instance of data (e.g., a stratified contingency table) can be generated from many different data generating processes we need a causal model to guide us. For now, we are learning to use R to encode this information (data) and knowledge (DAG).

2.6 Exercises

Exercise 2.1 (Find file path to working directory) From RStudio main menu, select File \(\rightarrow\) New Project \(\rightarrow\) New Directory \(\rightarrow\) Empty Project. Name the new directory ph251d-hwk. At the R console, use R to display the file path to the work directory containing .RData?

Exercise 2.2 (Recreate 2 x 2 Table) The Whickham data set is “Data on age, smoking, and mortality from a one-in-six survey of the electoral roll in Whickham, a mixed urban and rural district near Newcastle upon Tyne, in the UK. The survey was conducted in 1972–1974 to study heart disease and thyroid disease. A follow-up on those in the survey was conducted twenty years later. This dataset contains a subset of the survey sample: women who were classified as current smokers or as never having smoked.” (source: mosaicData package)

A data frame with 1314 observations on women for the following variables:

  • outcome: survival status after 20 years: a factor with levels Alive Dead
  • smoker: smoking status at baseline: a factor with levels No Yes
  • age: age (in years) at the time of the first survey
Using the counts in Table 2.28 recreate the table using any combination of the matrix, cbind, rbind, dimnames, or names functions.
TABLE 2.28: Risk of death in a 20-year period among women in Whickham, England, according to smoking status at the beginning of the period [10]
Outcome Smoker
Yes No
Dead 139 230
Alive 443 502
Exercise 2.3 (Create table marginal totals) Starting with the 2x2 matrix object we created in Table 2.28, using any combination of apply, cbind, rbind, names, and dimnames functions, recreate the Table 2.29.
TABLE 2.29: Risk of death in a 20-year Period among women in Whickham, England, according to smoking status at the beginning of the period
Outcome Smoker
Yes No Total
Dead 139 230 329
Alive 443 502 945
Total 582 732 1314
Exercise 2.4 (Create marginal and joint probability distributions) Using the \(2 \times 2\) data from Table 2.28, use the sweep and apply functions to calculate row, column, and joint probability distributions (i.e., create three tables with proportions).
Exercise 2.5 (Create measures of association) Using the data from the previous problems, recreate Table 2.30 and interpret the results.
TABLE 2.30: Risk ratio and odds ratio of death in a 20-year period among women in Whickham, England, according to smoking status at the beginning of the period
Measure Smoker
Yes No
Risk 0.24 0.31
Risk Ratio 0.76 1.00
Odds 0.31 0.46
Odds Ratio 0.68 1.00
Exercise 2.6 (Conduct analyses) Install the mosaicData R package using install.packages("mosaicData"). Load the Whickham data set. Using the xtabs function create two-way and three-way contingency tables. Calculate “measures of associations.” What is your interpretation? Here is some R code to get you started.
Exercise 2.7 (Practice tapply) Use the tapply function to calculate the mean age at study entry comparing
  1. smokers to non-smokers,
  2. dead vs. alive,
  3. smoker status stratified by outcome status (2 x 2 table).
Exercise 2.8 (California home prices, July, 2019) Read into R the median prices for single family homes in selected California counties for July, 2019. The R code is provided. The data object will be a data frame, but can be manipulated like a matrix.
  1. Create a character vector of the county names.
  2. Create a numeric vector of the home prices.
  3. Which county has the lowest price?
  4. Which county has the highest price?
  5. What is the median price for California counties? (i.e., the median of the median prices)
  6. What is the mean price? (i.e., the mean of the median prices)
  7. The data frame (hp) can be treated like a matrix. Sort the data frame by county name (hint: use the order function).
  8. Sort the data frame by home price (hint: use the order function).
  9. List the counties that have medican home prices between the 25% and 75% percentiles (hint: use the quantile function and index using a Boolean query).

References

8. Olsen SJ, Chang H-L, Cheung TY-Y, Tang AF-Y, Fisk TL, Ooi SP-L, et al. Transmission of the severe acute respiratory syndrome on aircraft. N Engl J Med. 2003 Dec;349(25):2416–22.

9. The GenIUSS Group. Best practices for asking questions to identify transgender and other gender minority respondents on population-based surveys [Internet]. The Williams Institute; 2014. Available from: https://williamsinstitute.law.ucla.edu/wp-content/uploads/geniuss-report-sep-2014.pdf

10. Rothman K. Epidemiology: An introduction. 2nd ed. New York, NY: Oxford University Press; 2012.

11. Scutari M, Denis J-B. Bayesian networks: With examples in r. Boca Raton: Chapman; Hall; 2014.

12. Fenton N, Neil M. Risk assessment and decision analysis with bayesian networks. Chapman; Hall/CRC; 2 edition; 2019.

13. Neapolitan R, Jiang X, Ladner DP, Kaplan B. A primer on Bayesian decision analysis with an application to a kidney transplant decision. Transplantation. 2016 Mar;100(3):489–96.

14. Charig CR, Webb DR, Payne SR, Wickham JE. Comparison of treatment of renal calculi by open surgery, percutaneous nephrolithotomy, and extracorporeal shockwave lithotripsy. Br Med J (Clin Res Ed). 1986 Mar;292(6524):879–82.

15. Julious SA, Mullee MA. Confounding and simpson’s paradox. BMJ. 1994 Dec;309(6967):1480–1.

  1. In other programming languages, vectors are either row vectors or column vectors. R does not make this distinction until it is necessary. Do not confuse a vector, as discussed in this section, with the vector function which can create atomic or recursive objects.↩

  2. In other programming languages, vectors are either row vectors or column vectors. R does not make this distinction until it is necessary. Do not confuse a vector, as discussed in this section, with the vector function which can create atomic or recursive objects.↩

  3. See also the curve function for graphing mathematical equations.↩

  4. More specifically, rowSums,colSums, rowMeans, and colMeans are optimized for speed.↩

  5. For now, consider factors as character vectors where the possible values (called levels) have been specified. We cover factors later.↩