3 Elements of Set Theory for Probability

test

_The beaverduck_ from [Tenso Graphics](https://cargocollective.com/tensographics)

Figure 3.1: The beaverduck from Tenso Graphics

In order to formalise the theory of probability, our first step consists in formulating events with uncertain outcomes as mathematical objects. To do this, we take advantage of Set Theory.

In this chapter, we will overview some elements of Set Theory, and link them with uncertain outcomes.

3.1 Random Experiments, Events and Sample Spaces

Let us start our journey with some definitions:

Definition 3.1 (Random Experiment) A Random Experiment is a process that can result in two or more different outcomes with uncertainty as to which will be observed.

We perform Random Experiments almost every day in our everyday life. Some are very deliberate, such as the referee flipping a coin to decide who gets to kick the ball first in a football game. However, some are less deliberate, such as the rise or fall of the price of a Stock which, as we have illustrated in the introductory lecture, falls within this definition.

Definition 3.2 (Event) An Event is an uncertain outcome of a random experiment.

An event can be:

Elementary: it includes only one particular outcome of the experiment
Composite: it includes more than one elementary outcome in the possible sets of outcomes.

For instance, in some card games, you have to draw more than one card, and in some dice games, (such as the Bolivian game of “Cacho Alalay”), you have to throw more 5 dice. The result of your throw is therefore the composition of elementary events (the result of each die).

Definition 3.3 (Sample Space) The Sample Space is the complete listing of the elementary events that can occur in a random experiment. We will denote the sample space by $S$.

Example 3.1 (A simple card game) To illustrate all these definitions, we will use a game of cards.

Let us suppose that the game requires drawing one card at random from a full deck of 52 playing cards. This draw consitutes a Random Experiment
The Sample Space $S$ consists of the values of the cards of all colors and suits.

S = {A♣, 2♣, …,K♣,A♦, 2♦, … ,K♦ , A♥, 2♥, … ,K♥, A♠, 2♠, … ,K♠}

Here, we can define Events as subsets of the sample space, To keep it simple, let’s consider Elementary Events:
- $K$: drawing a King
  K = {K♣, K♦, K♥, K♠}
- $H$: Event of drawing a Heart
  H = {A♥, 2♥, … ,K♥}
- $J$: drawing a Jack or higher
  J = {J♣, Q♣,K♣,J♦, Q♦, K♦ , J♥, Q♥, K♥, J♠, Q♠, K♠}
- $Q$: drawing a Queen
  Q = {Q♣, Q♦, Q♥, Q♠}

With a game of cards, we can also illustrate Composite Events, e.g. drawing 4 Aces

Figure 1.1: Someone is lucky!

Example 3.2 (Flipping Coins) Flipping a set of two coins can be characterised as another random experiment allowing for composite events. In this case, let us denote the outcomes for each coin are $H$ for Head and $T$ for Tail.

Hence, the sample space of the experiment “flipping two coins” contains the following four points:

\[S = \{ (HH),(HT),(TH),(TT) \}.\]

Example 3.3 (Time on your phone) Say you are interested in measuring the time of your life spent on your phone. The measure of the time (in hours) can be considered as the outcome of a random experiment, and every measure of the time, an event.

When you take a measure, you will be counting fractions of the hour spent on your phone (e.g. 20 minutes = 1/3 h). Therefore, the possible outcomes of this experiment are are durations measured in fractions ranging from 0 to infinity. Hence, the sample space consists of all nonnegative real numbers: \[ S = \{x: 0 \leq x < \infty \}\] or, equivalently, $S\equiv \mathbb{R}^+$.

3.2 Some definitions from set theory

The following definitions from set theory will be useful to deal with events.

Definition 3.4 If every element of a set $A$ is also an element of a set $B$, then $A$ is a subset of $B$.

We write this as : \[A \subset B\] and we read it as “$A$ is contained in $B$”

Definition 3.5 Two sets $A$ and $B$ are said to be equal if \[A \subset B \text{ and } B \subset A;\]

Definition 3.6 If a set $A$ contains no points, it will be called the null set, or empty set, and it is typically denoted by $\varnothing$.

3.3 The Venn diagram

The Venn diagram is an elementary schematic representation of sets and helps displaying their properties. As you might remember from your elementary mathematics classes, a Venn diagram represents a set with a closed figure and it is assumed that the set elements are in the surface contained by the figure. They are very useful to illustrate inclusion and equality as well as more abstract notions.

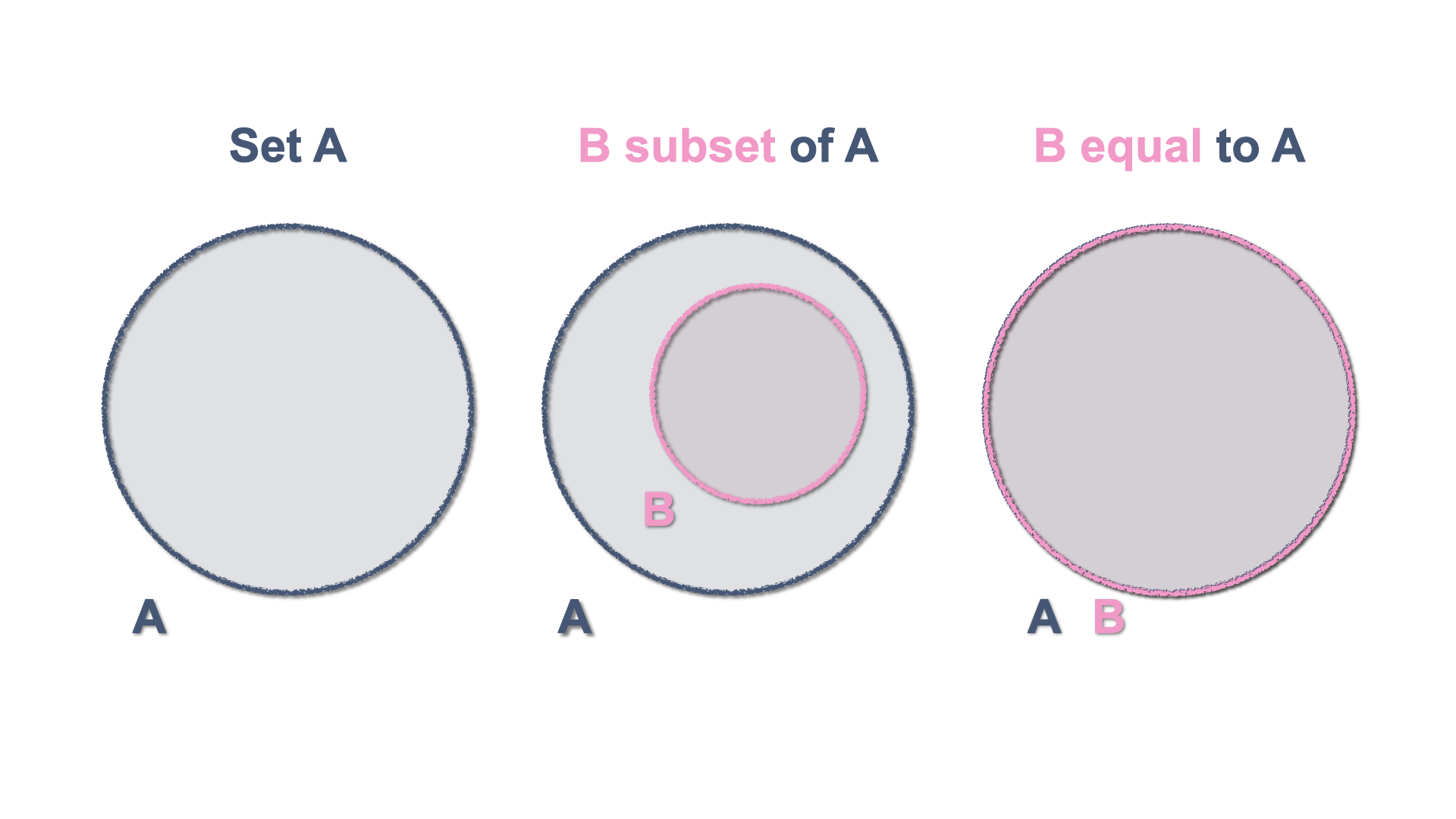
Figure 1.2: Inclusion and Equality of sets with Venn Diagrams

3.3.1 Sample Space and Events

By definition, an event or several events, constitute a subset of the sample space. This can be represented in a Venn Diagram with a figure enclosed within the Sample Space.

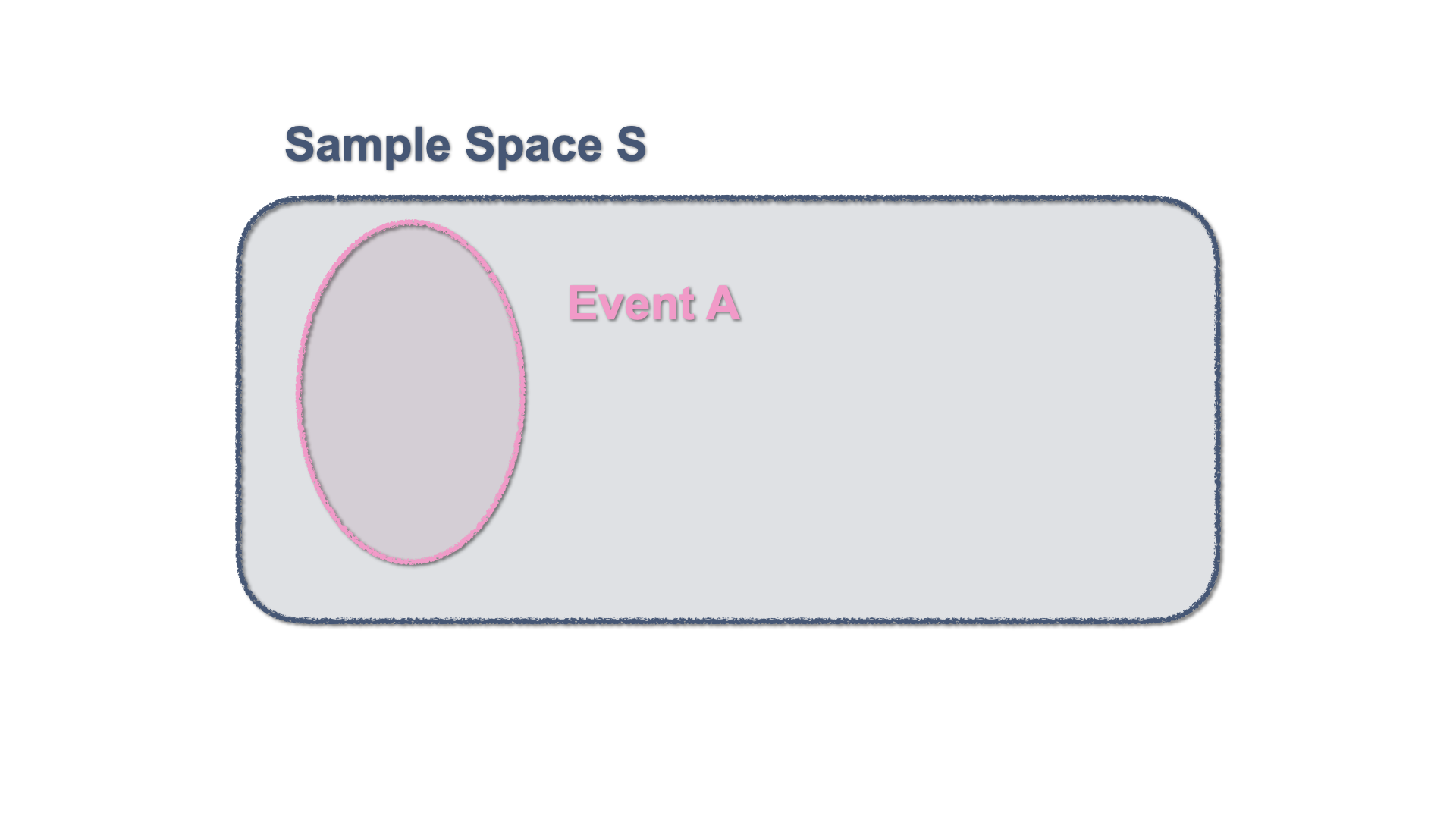
Figure 3.2: Venn Diagram - An event within the Sample Space

3.3.2 Exclusive and Non-Exclusive Events

Two events are mutually exclusive is they cannot occur jointly. This is represented by two separate enclosed surfaces within the sample space.

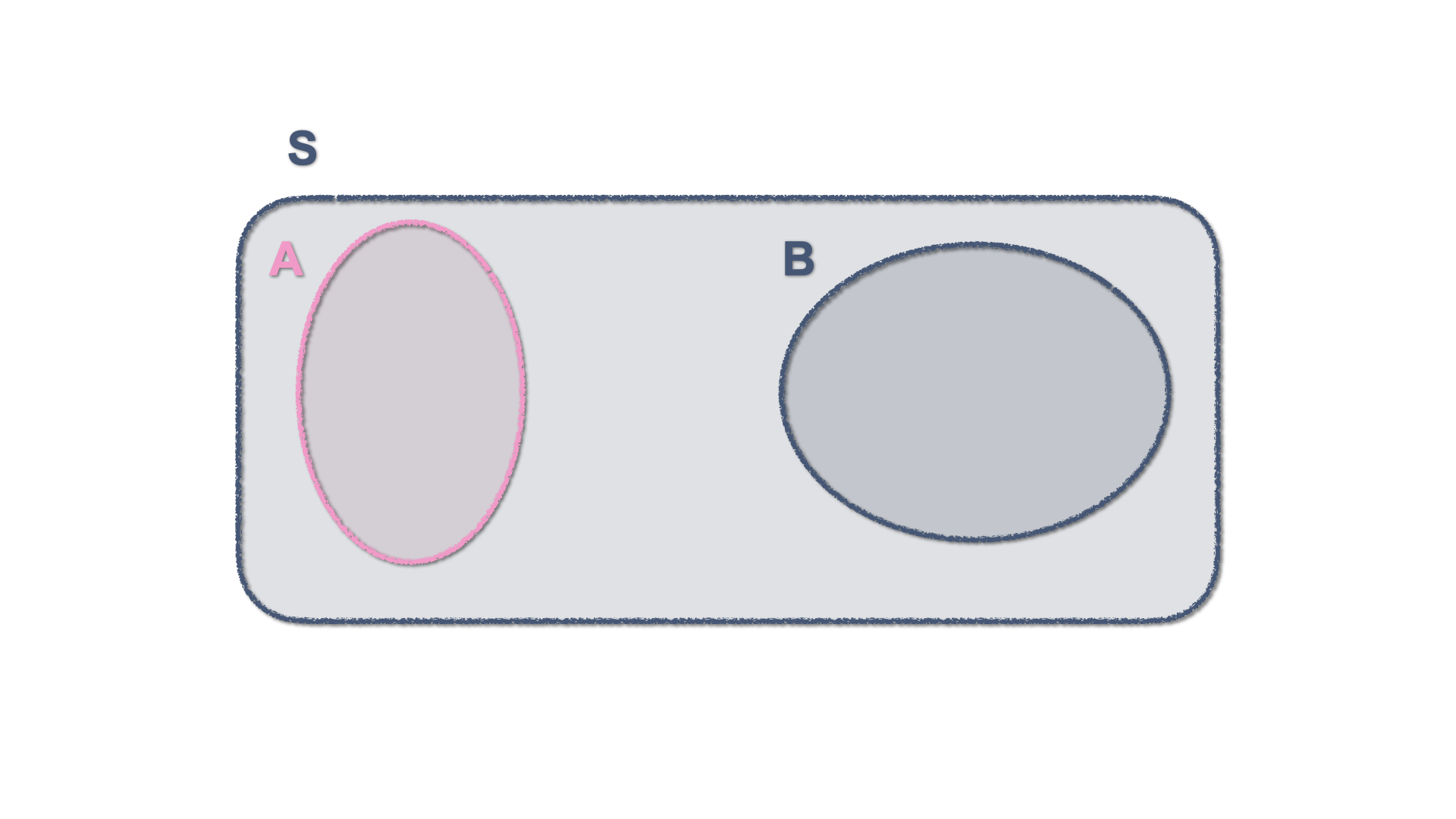
Figure 3.3: Venn Diagram - Two mutually exclusive events

Exercise 3.1 Consider our simple card game example. Build Venn Diagrams of the events “drawing a King” and “drawing a Queen.” Do they have element in common? What does that say about these events?

Events that are not mutually exclusive have a shared area, which in set theory constitutes an intersection and gets shown in a Venn diagram by two figures that share some of their areas.

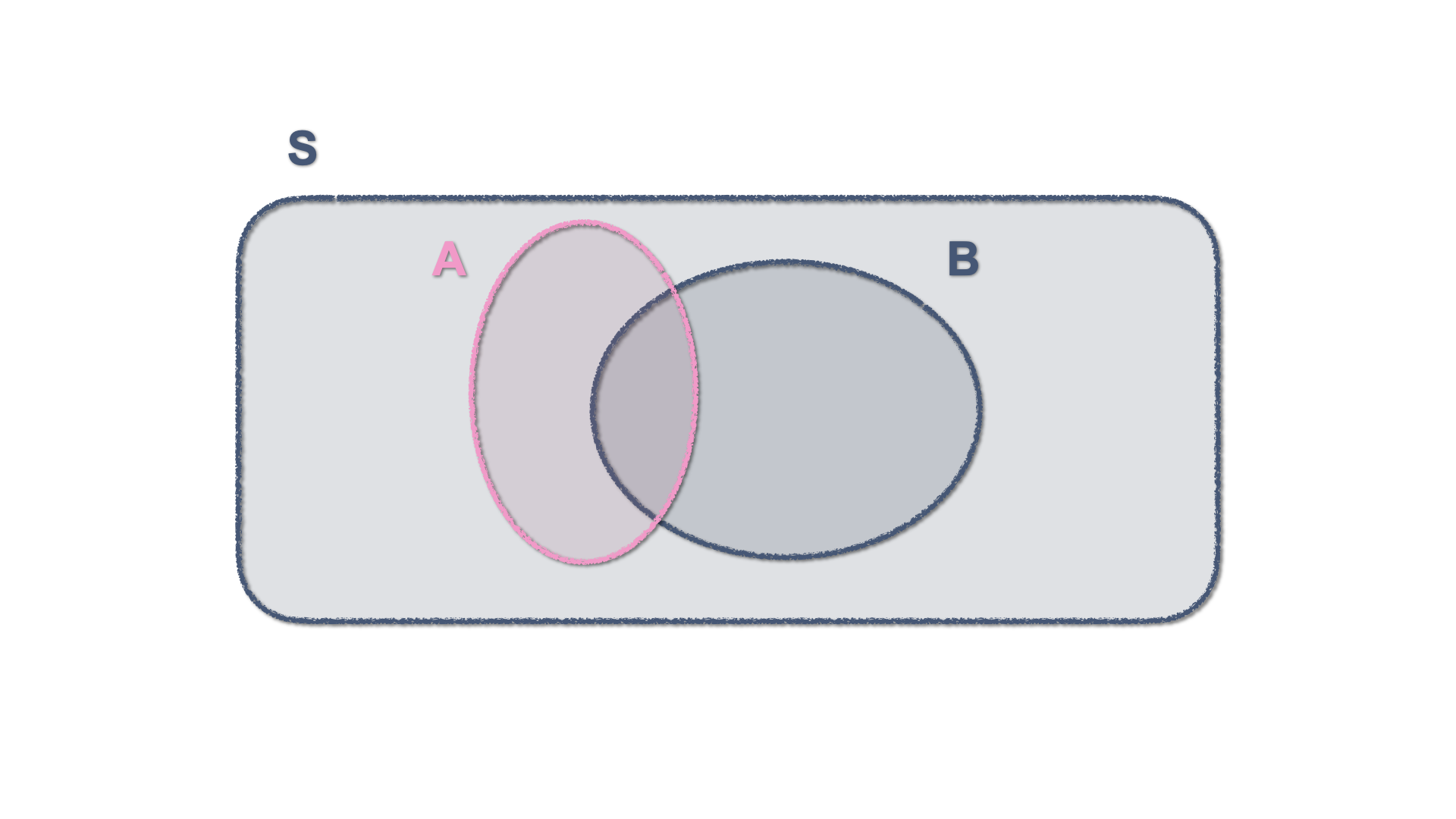
Figure 3.4: Venn Diagram - Two Non-mutually exclusive events

Exercise 3.2 Coming back to our example with the card game, build Venn diagrams for the events “drawing a King” and “drawing a Heart.” Do they have element in common? What does that say about these events?

3.3.3 Union and Intersection of Events

The union of the events $A$ and $B$ is the event which occurs when either $A$ or $B$ occurs: $A \cup B$. In a Venn diagram, we can illustrate this by shading the area enclosed by both sets.

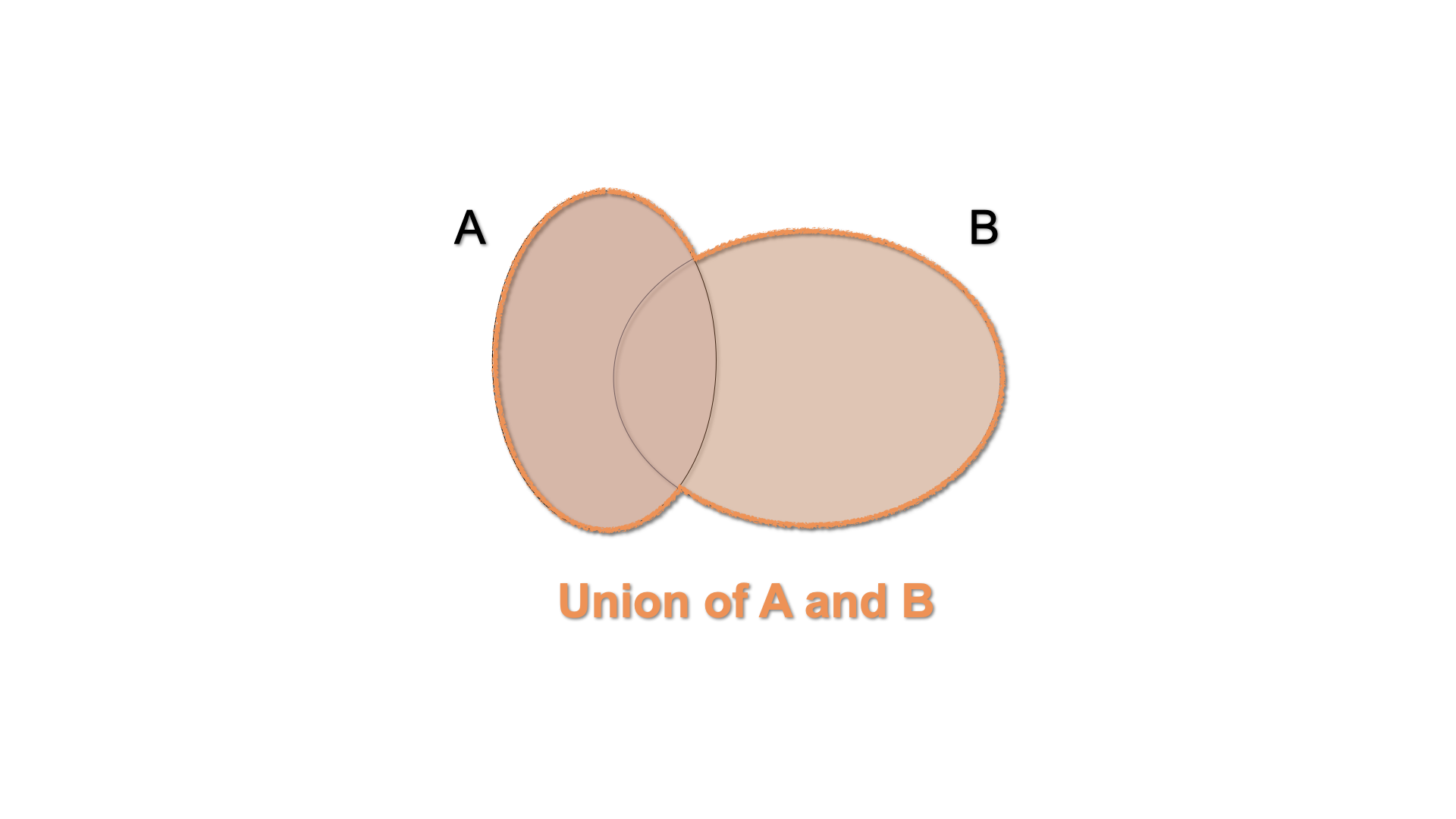
$Venn Diagram - $A\cup B$$

Figure 3.5: Venn Diagram - $A\cup B$

The intersection of the events $A$ and $B$ is the event which occurs when both $A$ and $B$ occur: $A \cap B$. In a Venn diagram, we can illustrate this by shading the area shared by both sets.

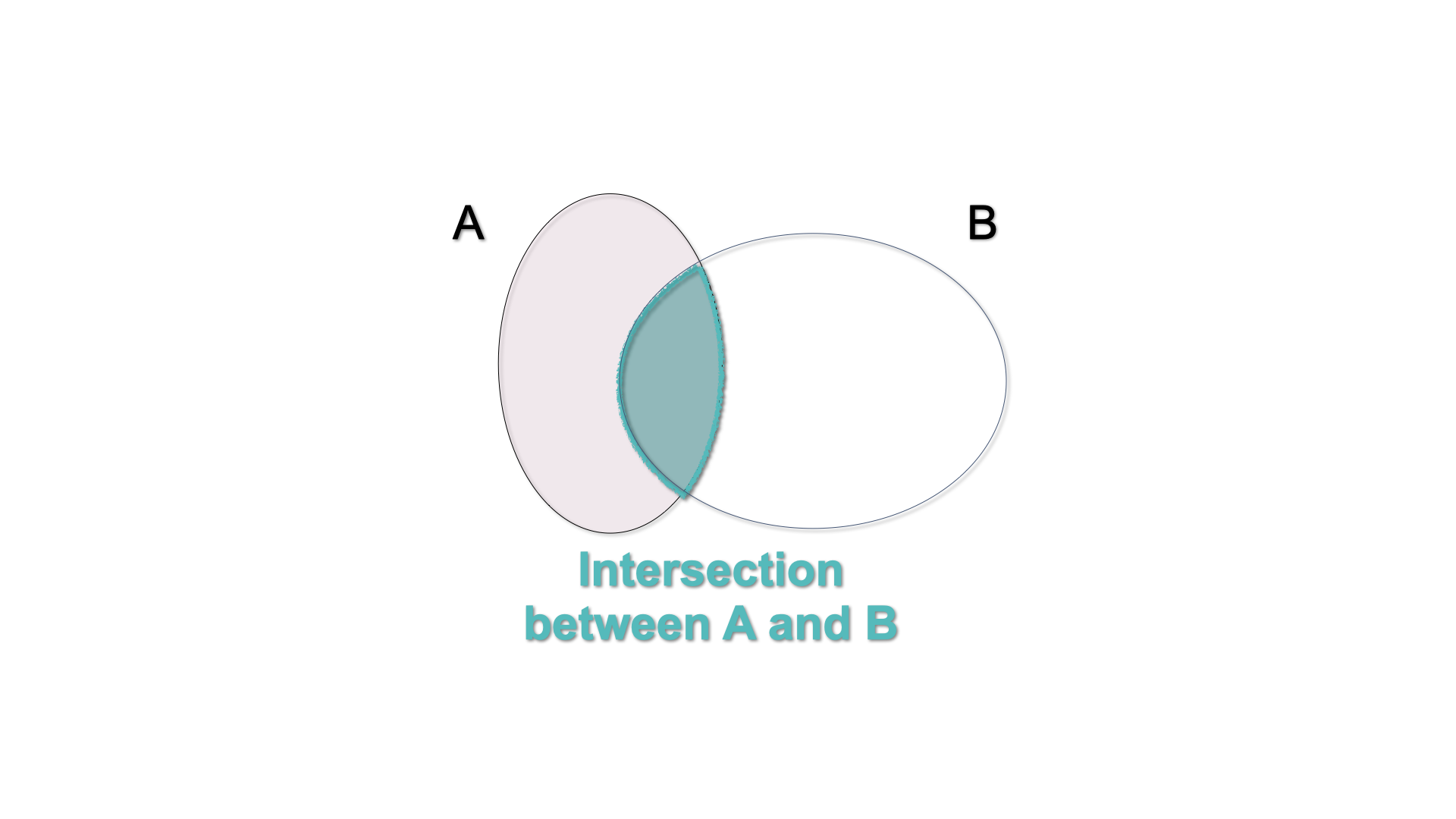
$Venn Diagram - $A\cap B$$

Figure 3.6: Venn Diagram - $A\cap B$

3.3.4 Complement

The complement of an event $A$ is the event that occurs when $A$ does not occur: We write $A^{c}$ or $\overline{A}$. A Venn diagram illustrates this by shading the area outside the set that defines the event $A$.

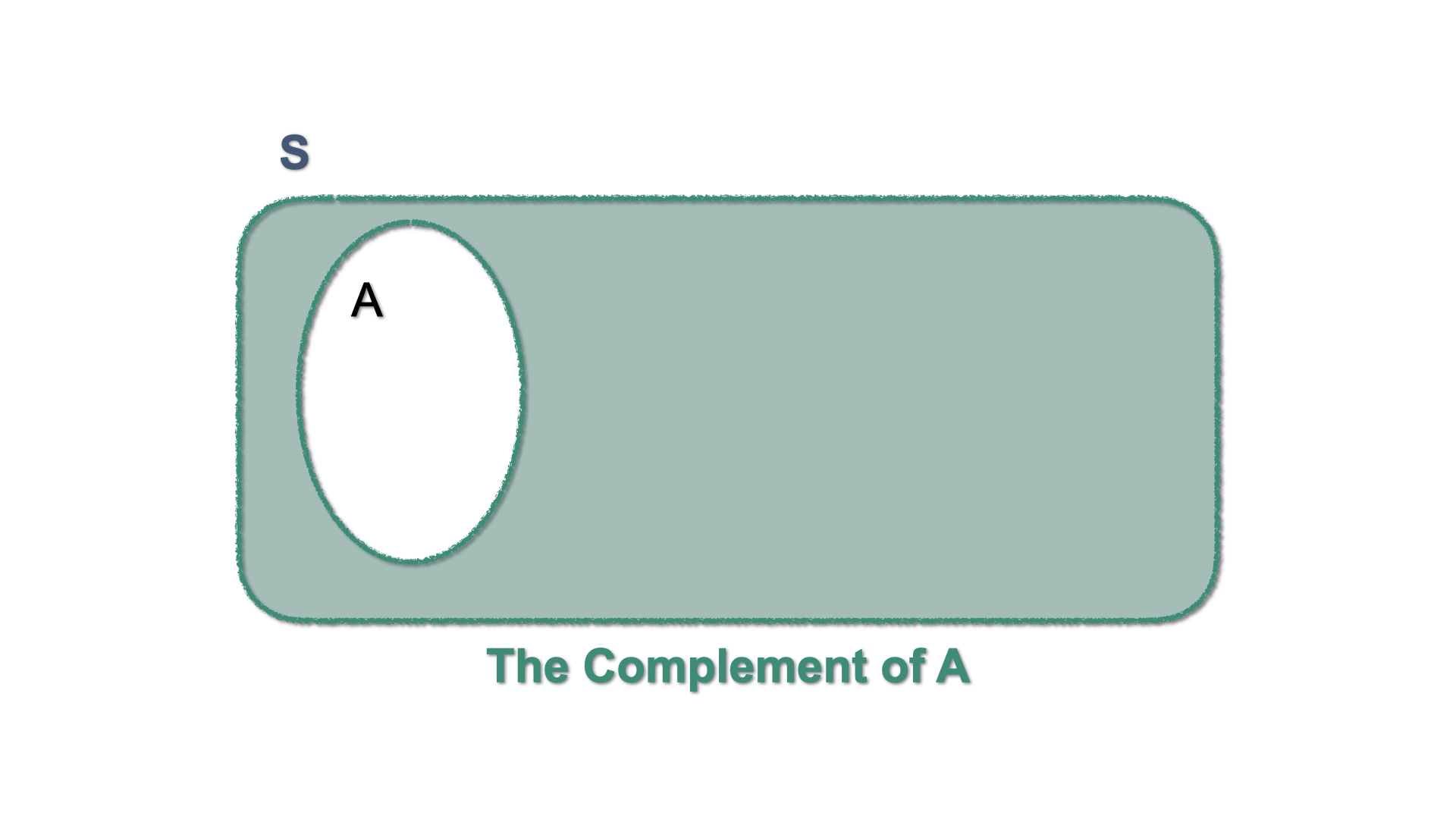
$Venn Diagram - $A^{c}$$

Figure 3.7: Venn Diagram - $A^{c}$

Let $S$ be the complete set of all possible events, i.e. the Sample Space. In such case, $A^c$ can be written as: \[A^c = S \setminus A = S-A.\] and is such that \[A \cup A^c = S.\]

3.3.5 Some Properties of union and intersection

Let $A$, $B$, and $D$ be sets. The following laws hold:

Commutative laws: Union and Intersection of sets are commutative, i.e. they produce the same outcome irrespective of the order in which the sets are written. \[\begin{eqnarray*} A \cup B = B \cup A \\ A \cap B = B \cap A \end{eqnarray*}\]
Associative laws: Union and Intersection of more than two sets operate irrespective of the order. \[\begin{eqnarray*} A \cup (B \cup C) = (A \cup C) \cup C \\ A \cap (B \cap C) = (A \cap C) \cap C \end{eqnarray*}\]
Distributive laws
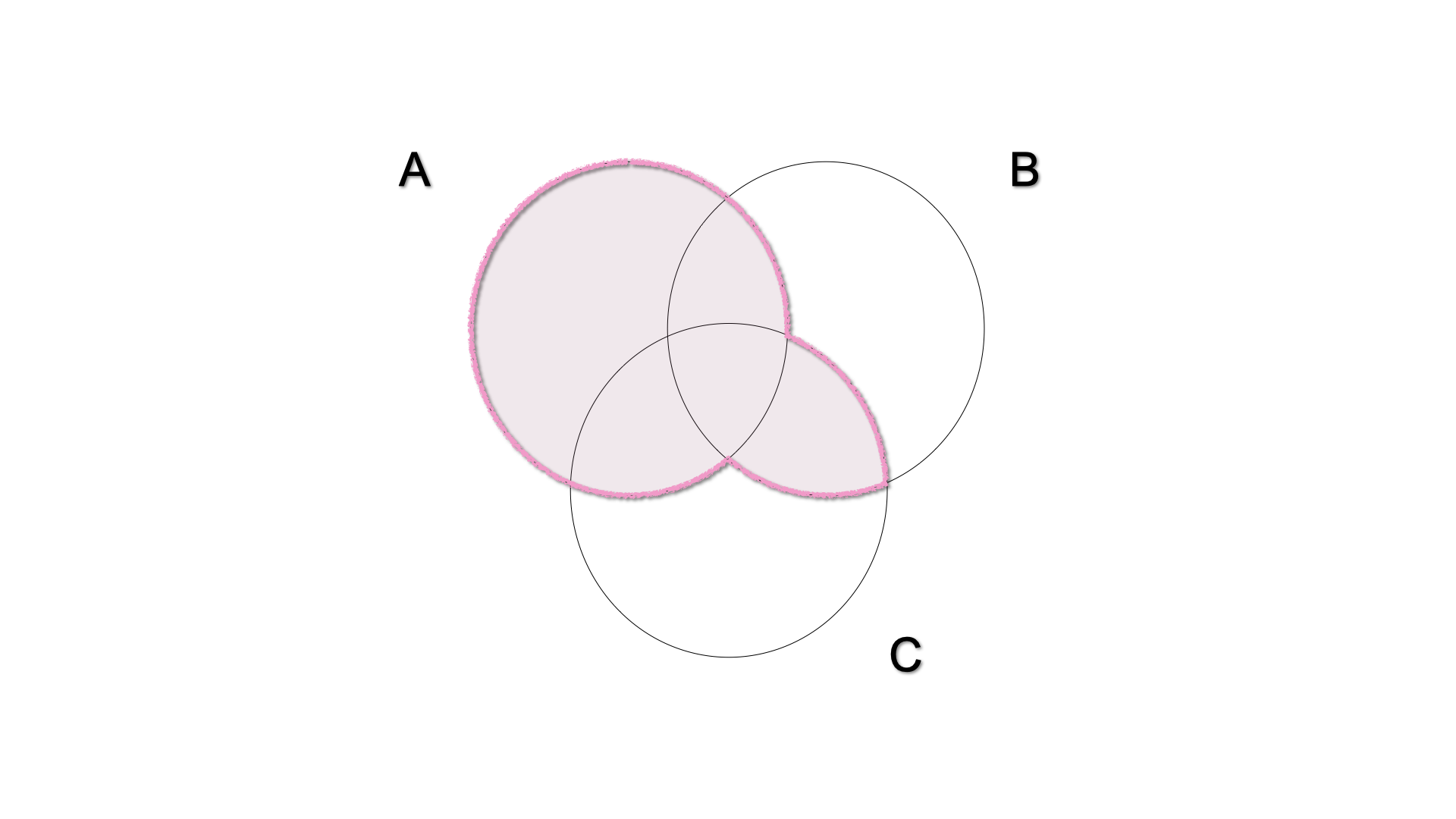
- The intersection is distributive with respect to the union, i.e. the intersection between a set ($A$) and the union of two other sets ($B$ and $C$) is the union of the intersections. \[ A \cap (B \cup C) = (A \cap B) \cup (A\cap C)\]
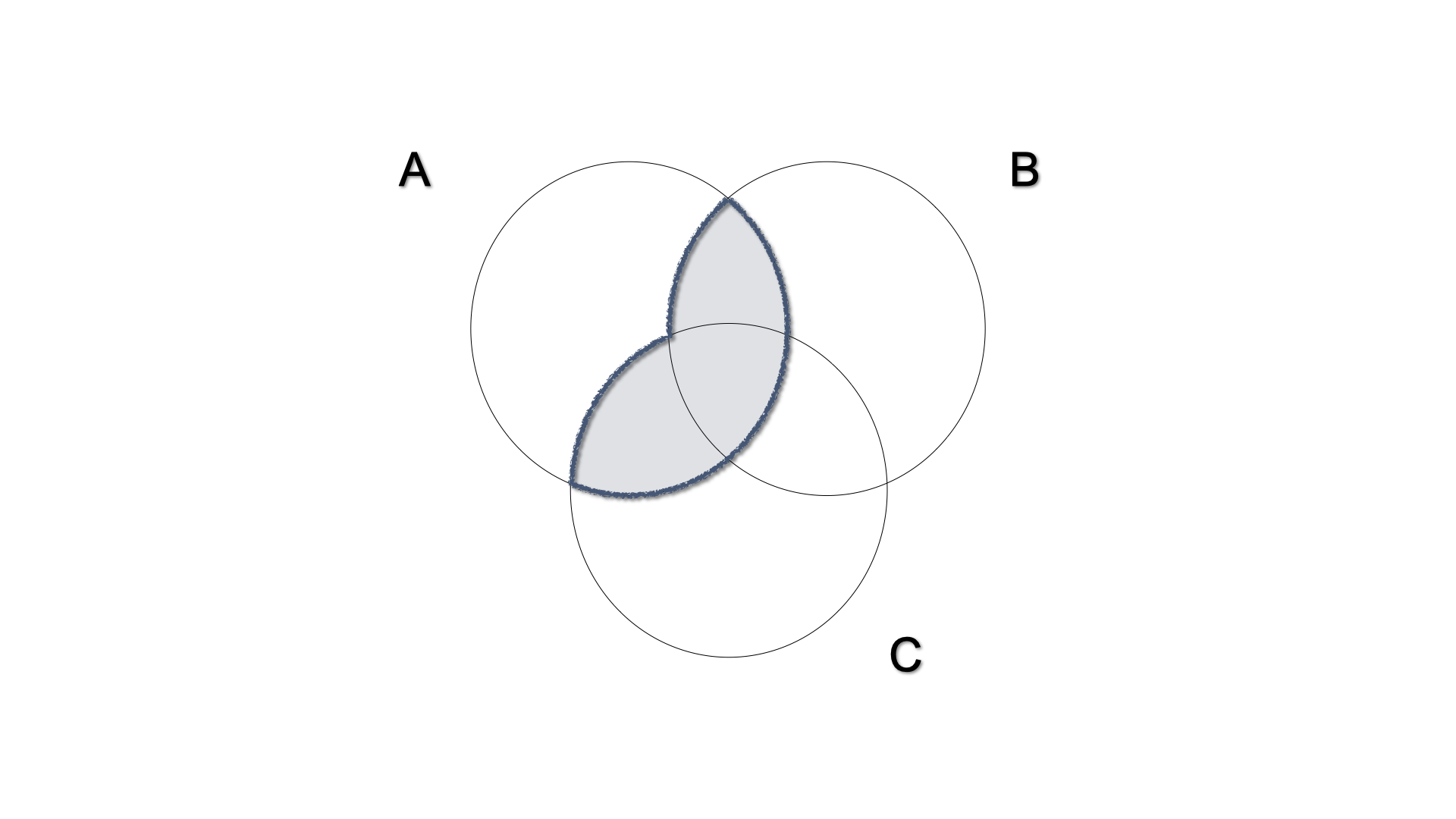
- The union is distributive with respect to the intersection, i.e. the union between a set ($A$) and an intersection of two others is the intersection of the unions. \[A \cup (B \cap C) = (A\cup C) \cap (A \cup C)\]

Exercise 3.3 Let $A$ and $B$ be two non-exclusive Events in the Sample Space $S$. Use Venn diagrams to represent:

$\overline{A\cap B} = (A\cap B)^{c}$
$B-A$

3.4 Countable and Uncountable sets

Events can be represented by means of sets and sets can be either countable or uncountable.

In mathematics, a Countable Set is a set with the same cardinality (number of elements) as some subset of the set of natural numbers $\mathbb{N}= \{0, 1, 2, 3, \dots \}$.

A countable set can be countably finite or countably infinite. Whether finite or infinite, the elements of a countable set can always be counted one at a time and, although the counting may never finish, every element of the set is associated with a natural number. Roughly speaking one can count the elements of the set using $1,2,3,..$

Example 3.4 (Our deck of cards and Finite Countable Sets) Let’s come back to our example with the deck of cards and the event. The following events can be considered countably finite sets as they have a limited and countable number of elements:

$K \cup H$ = {K♣, K♦, K♥, K♠, A♥, 2♥, … , Q♥}
$J \cup H$ = {J♣, Q♣, K♣, J♦, Q♦, K♦, J♥, Q♥, K♥, J♠, Q♠, K♠, A♥, 2♥, … , 10♥}
$H^{c}$ = {A♣, 2♣, …,K♣,A♦, 2♦, … ,K♦ ,A♠, 2♠, … ,K♠}

Exercise 3.4 (Illustrations within an Uncountable Set) Any segment of the Real line is an Uncountable set. Consider the segment ranging from (but excluding) 0 to 1 the Sample Space \[S = \{x : 0 <x <1\}\] and the sets \[\begin{align*} A &= \{x \in S : 0.4<x<0.8\} \text{and}\\ B &= \{x \in S : 0.6<x<1\} \end{align*}\]

Using these definitions, compute:

$A^c$
$B^c$
$B^c \cup A$
$B^c \cup A^c$
$A \cup B$
$A \cap B$
$B \cup A^c$
$A^c \cup A$

Exercise 3.5 (flipping coins again) Let us come back to the experiment where we flip two coins. For each coin we have $H$ for Head and $T$ for Tail. Remember that the sample space contains the following four points:

\[ S = \{ (HH),(HT),(TH),(TT) \}.\]

Then, let us consider the events:

$A= H$ is obtained at least once = $\Big\{ (HH),(HT),(TH) \Big\}$
$B=$ the second toss yields $T$ = $\Big\{ (HT),(TT) \Big\}$

Using these definitions of $A$ and $B$ compute:

$A^c$
$B^c$
$B^c \cup A$
$A \cup B$
$A \cap B$
$B \cup A^c$

Proposition 3.1 Let $A$ be a set in $S$ and let $\varnothing$ denote the empty set¹. The following relations hold:

$A \cap S = A$;
$A \cup S = S$;
$A \cap \varnothing = \varnothing$;
$A \cup \varnothing = A$;
$A \cap A^c = \varnothing$;
$A \cup A^c = S$;
$A \cap A = A$;
$A \cup A = A$;

Exercise 3.6 Use Venn Diagrams to illustrate these relationships

The identities in proposition 3.1 are helpful to define some other relations between sets/events.

Example 3.5 Let $A$ and $B$ be two sets in $S$. Then we have: \[B = (B \cap A) \cup (B \cap A^c).\]

To check it, we can proceed as follows:

\[\begin{eqnarray*} B & = & S \cap B \\ & = & (A \cup A^c) \cap B \\ & = & (B \cap A) \cup (B \cap A^c). \end{eqnarray*}\]

That concludes the argument.

3.5 De Morgan’s Laws

Operations of union and intersection of sets have interesting interactions with complementarity. These properties are formulated under the name of De Morgan’s laws.

For simplicity, let us illustrate these laws in the case of two sets $A$ and $B$ both included in the Sample Space $S$. Just keep in mind that they can be generalized for an infinite amount of sets.

3.5.1 First Law

Let $A$ and $B$ be two sets in $S$, then \[\begin{eqnarray} (A\cap B)^{c} =A^c \cup B^c, \end{eqnarray}\]

where:

Left hand side: $(A\cap B)^{c}$ represents the set of all elements that are not both $A$ and $B$;
Right hand side: $A^c \cup B^c$ represents all elements that are not $A$ (namely they are $A^c$) and not $B$ either (namely they are $B^c$) $\Rightarrow$ set of all elements that are not both $A$ and $B$.

Put in words, the firs law says that

the complement of the intersection between two sets is the union of their complements.

Exercise 3.7 It is easy to see this graphically using Venn Diagrams. Try it, as an exercise.

3.5.2 Second Law

Let $A$ and $B$ be two sets in $S$. Then:

\[\begin{eqnarray} (A\cup B)^{c} =A^c \cap B^c, \end{eqnarray}\]

where:

Left hand side: $(A\cup B)^{c}$ represents the set of all elements that are neither $A$ nor $B$;
Right hand side: $\color{blue}{A^c \cap B^c}$ represents the intersection of all elements that are not in $A$ (namely they are $A^c$) and not $B$ either (namely they are $B^c$) $\Rightarrow$ set of all elements that are neither $A$ nor $B$.

Put in words, this law says that

the complement of the union between two sets is the intersection of their complements.

Exercise 3.8 Once again, it is easy to see this graphically with Venn Diagrams. Try it, as an exercise.

3.5.3 De Morgan’s Theorem

We can extend these laws to three sets. Let us consider three sets $A_{1}$, $A_{2}$ and $A_{3}$ in $S$, and use the overline notation to denote the complement of a set, (i.e. $A^{c}_{1} = \overline{A_{1}})$,

The First law then becomes: \[\overline{\left(A_{1}\cup A_{2}\cup A_{3}\right)} = \overline{A_{1}} \cap \overline{A_{2}} \cap \overline{A_{3}}\]
While the Second Law becomes: \[\overline{\left(A_{1}\cap A_{2}\cap A_{3}\right)} = \overline{A_{1}} \cup \overline{A_{2}} \cup \overline{A_{3}}\]

Exercise 3.9 Show this using Venn diagrams.

More generally, this can be extended to the union of an infinite amount of sets in a theorem that we present without demonstration. Consider the following notation for the union of an infinity of sets :

\[\bigcup_{i \in \mathbb{N}} A_{i} = A_{1} \cup A_{2} \cup A_{3} \cup \dots \]

and the intersection of an infinite but countable amount of sets

\[\bigcap_{i \in \mathbb{N}} A_{i} = A_{1} \cap A_{2} \cap A_{3} \cap \dots\]

Theorem 3.1 (De Morgan’s Theorem) Let $\mathbb{N}$ be the set of natural number and $\{A_{i}\}$ a collection (indexed by $i \in \mathbb{N}$) of subsets of $S$. Then:

the complement of the union of all $A_i$ is the intersection of their complements. \[\begin{eqnarray} \overline{\bigcup_{i \in \mathbb{N}} A_i} &=& \bigcap_{i \in \mathbb{N}} \overline{A}_i; \end{eqnarray}\]
the complement of the intersection of all $A_i$ is the union of their complements. \[\begin{eqnarray} \overline{\bigcap_{i \in \mathbb{N}} A_i} &=& \bigcup_{i \in \mathbb{N}} \overline{A}_i. \end{eqnarray}\]

3.6 Probability as Frequency

When assessing any experiment with an uncertain outcome the, primary interest is not necessarily in the events itself (as they may or may not happen) but in the degree of likelihood that it can happen. That is, we are interested in the probability of the event happening

Intuitively, the probability of an event is a value associated with the event: \[\text{event} \rightarrow \text{pr(event)}\] and it is such that:

the probability is positive or more generally non-negative (it can be zero);
the $\text{pr}(S)=1$, where $S$ is the sample space and $\text{pr}(\varnothing)=0$;
the probability of two (or more) mutually exclusive events is the sum of the probabilities of each event.

In many experiments, it is natural to assume that all outcomes in the sample space ($S$) are equally likely to occur. Think of when you throw a well balanced die, for example. If the die is well balanced, you would assume that all 6 numbers have an equal chance of happening.

Let us apply this logic in the abstract with an experiment whose sample space is a finite set, say, $S = \{1, 2, 3, \dots N\}$. If you believe that all outcomes are equally likely to occur, you are assuming that the probability of every event, every subset with one element has the same probability:

\[P(\{1\})=P(\{2\})=...=P(\{N\})\] or equivalently $P(\{i\})= 1/N$, for $i=1,2,...,N$.

Now, if we define a composite event $A$, a subset of $S$, composed of $N_A$ realizations i.e. elements of $S$ having the same likelihood (namely, the same probability). Then, the probability of the event $A$ becomes the ratio of the outcomes in $A$ with respect to the total possible outcomes.

\[\begin{equation} \boxed{P(A)=\frac{N_A}{N}=\frac{\mbox{# of favorable outcomes}}{\mbox{total # of outcomes}}=\frac{\mbox{# of outcomes in $A$}}{\mbox{# of outcomes in $S$}}} \tag{3.1} \end{equation}\]

where the “hash” ‘$\#$’ stands for “number.”

Example 3.6 (An even number among 6 dice) We roll a fair die and we define the event \[A=\text{the outcome is an even number}=\{2,4,6\}.\] What is the probability of $A$?

First, we identify the sample space as \[S=\{1,2,3,4,5,6\}.\]

Then, we have that

\[P(A)=\frac{N_A}{N} = \frac{\mbox{3 favorable outcomes}}{\mbox{6 total outcomes}} = \frac{1}{2}. \]

Building on the intuition gained in the last example and formula (3.1), we state a first informal definition, which establishes the probability of an event in terms of relative frequency.

Definition 3.7 (Informal definition of probability) Suppose that an experiment, whose sample space is $S$, is repeatedly performed under exactly the same conditions.

For each event, say $A$, of the sample space, we define $n(A)$ to be the number of times in the first $n$ repetitions of the experiment that the event $A$ occurs.

Then, $P(A)$, namely the probability of the event $A$, is defined as:

\[\begin{equation} P(A)=\lim_{n \to \infty} \frac{n(A)}{n}, \tag{3.2} \end{equation}\]

put in words:

$P(A)$ is the limiting proportion/frequency of time that $A$ occurs. $P(A)$ is the limit of relative frequency of $A$.

Example 3.7 (Tossing a well-balanced coin) In tossing a well-balanced coin, there are 2 mutually exclusive equiprobrable outcomes: “Heads” $H$ and “Tails” $T$.

Let $A$ be the event of $H$. Since the coin is fair, we have $P(A)=1/2$. To confirm this intuition/conjecture we can toss the coin a large number of times (each under identical conditions) and count the times we spot $H$.

Let $n$ be the total number of repetitions while $n(A)$ is the number of times in which we observe $A$. Then, the relative frequency: \[\lim_{n \to \infty} \frac{n(A)}{n},\] converges to $P(A)$.

So, \[P(A) \sim \frac{n(A)}{n}, \quad \text{for large $n$}.\]

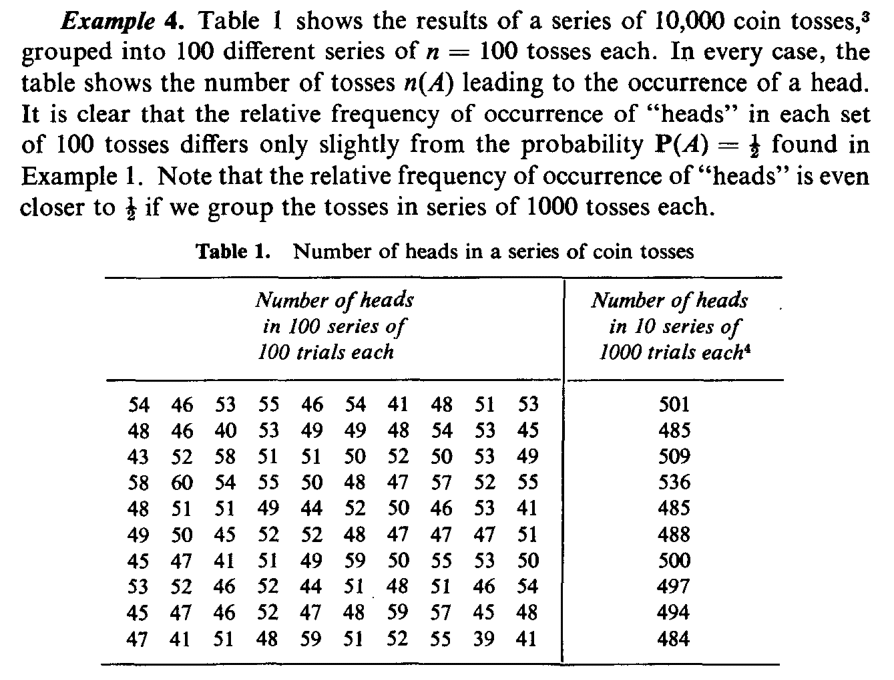
The taable shon in Figure 3.8 , taken from Ross (2014) illustrates this point.

Figure 3.8: Taken from Ross (2014)

Clearly, \[0 \leq n(A) \leq n, \quad \text{so} \quad 0 \leq P(A) \leq 1.\] Thus, we say that the probability is a set function (it is defined on sets) and it associates to each set/event a number between zero and one.

Remark. One can provide a more rigorous definition of probability, as a real-valued function which defines a mapping between sets/events and the interval $[0,1]$.

\[P : A \subseteq \mathbb{R} \longrightarrow [0,1]\]

However, to provide this formal definition we need to introduce the concept of sigma-algebra (which represents the domain of the probability), a concept that narrowly escapes the frame of our course.

We will proceed without presenting it, with the very unfortunate cost of losing the mathematical rigour in the following sections and chapters.

To express the probability, we need to impose some additional conditions, that we are going to call axioms.

We here briefly state the ideas, then we will formalize them:

When we define the probability we would want the have a domain such that it includes the sample space $S$ and $P(S)=1$.
Moreover, for the sake of completeness, if $A$ is an event and we can talk about the probability that $A$ happens, then it is suitable for us that $A^c$ is also an event, so that we can talk about the probability that $A$ does not happen.
Similarly, if $A_1$ and $A_2$ are two events (so we can say something about their probability of happening), so we should be able to say something about the probability of the event $A_1 \cup A_2$.

3.7 Some references

The interested reader can find some additional info in Rozanov (2013) and Hogg, McKean, and Craig (2019).

2 TP0

4 Probability Axioms