Chapter 8 Generalized Linear Models in JAGS
8.1 Background to GLMs
Recall the linear model, which has the feature of modeling a response variable that is assume to come from a normal distribution and have normally-distributed errors. Once we can adopt different error structures, we have generalized the linear model, and the name reflects this. Generalized linear models are not hierarchical, but they are still of great interest because the ability to modify the error structure on the response variable greatly increases the type of data we can model. GLMs were introduced in the early 1970s (McCullagh and Nelder 1972) and have become very popular in recent decades.
8.2 Components of a GLM
A transformation of the expectation of the response (\(E(y)\))is expressed as a linear combination of covariate effects, and distributions other than the normal can be used for the random part of the model.
- A statistical distribution is used to describe the random variation in response \(y\)
- A link-function \(g\) is applied to the expectation of the response \(E(y)\)
- A linear predictor is the linear combination of covariate effects thought to make up \(E(y)\)
8.2.1 Common GLMs
Technically a normal distribution is considered a special case of the GLM, but practically speaking the binomial and Poisson GLM are the most common. Note that the Bernoulli distribution is also common, but is just a special case of the Binomial where the parameter \(N=1\). Each distributional family in a GLM has a default link function, which is very likely the link function you will want to use. However, note that other link functions are available and with some digging, you may find a link function that is better for your data than the detault link function.

Figure 8.1: Family calls and default link functions for GLMs in R
Although it is not considered in the family of GLMs, recall the Beta distribution can be used for Beta regression, which is appropriate when your response variable takes on a proportion (\(0>y<1\)).
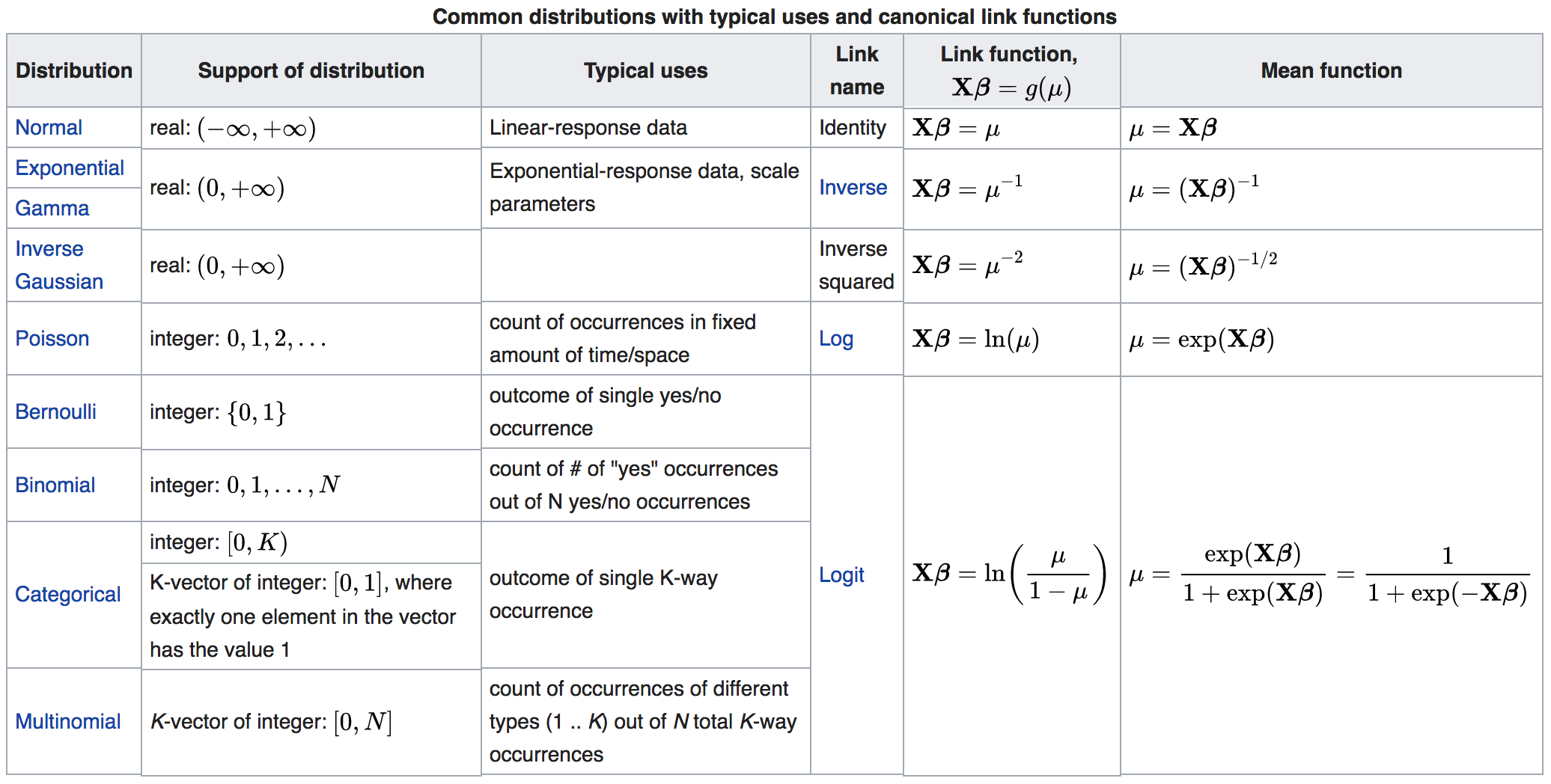
Figure 8.2: Common statistical distributions, their description, use, and default link function information.