Chapter 4 Spatial data operations

Note: this is the first edition of Geocomputation with R, first published in 2019 and with minor updates since then until summer 2021. For the Second Edition of Geocomputation with R, due for publication in 2022, see geocompr.robinlovelace.net.

Prerequisites

• This chapter requires the same packages used in Chapter 3:

library(sf)
library(raster)
library(dplyr)
library(spData)

4.1 Introduction

Spatial operations are a vital part of geocomputation. This chapter shows how spatial objects can be modified in a multitude of ways based on their location and shape. The content builds on the previous chapter because many spatial operations have a non-spatial (attribute) equivalent. This is especially true for vector operations: Section 3.2 on vector attribute manipulation provides the basis for understanding its spatial counterpart, namely spatial subsetting (covered in Section 4.2.1). Spatial joining (Section 4.2.3) and aggregation (Section 4.2.5) also have non-spatial counterparts, covered in the previous chapter.

Spatial operations differ from non-spatial operations in some ways, however. To illustrate the point, imagine you are researching road safety. Spatial joins can be used to find road speed limits related with administrative zones, even when no zone ID is provided. But this raises the question: should the road completely fall inside a zone for its values to be joined? Or is simply crossing or being within a certain distance sufficient? When posing such questions, it becomes apparent that spatial operations differ substantially from attribute operations on data frames: the type of spatial relationship between objects must be considered. These are covered in Section 4.2.2, on topological relations.

Another unique aspect of spatial objects is distance. All spatial objects are related through space, and distance calculations can be used to explore the strength of this relationship. These are covered in Section 4.2.6.

Spatial operations also apply to raster objects. Spatial subsetting of raster objects is covered in Section 4.3.1; merging several raster ‘tiles’ into a single object is covered in Section 4.3.8. For many applications, the most important spatial operation on raster objects is map algebra, as we will see in Sections 4.3.2 to 4.3.6. Map algebra is also the prerequisite for distance calculations on rasters, a technique which is covered in Section 4.3.6.

It is important to note that spatial operations that use two spatial objects rely on both objects having the same coordinate reference system, a topic that was introduced in Section 2.4 and which will be covered in more depth in Chapter 6.

4.2 Spatial operations on vector data

This section provides an overview of spatial operations on vector geographic data represented as simple features in the sf package before Section 4.3, which presents spatial methods using the raster package.

4.2.1 Spatial subsetting

Spatial subsetting is the process of selecting features of a spatial object based on whether or not they in some way relate in space to another object. It is analogous to attribute subsetting (covered in Section 3.2.1) and can be done with the base R square bracket ([) operator or with the filter() function from the tidyverse.

An example of spatial subsetting is provided by the nz and nz_height datasets in spData. These contain projected data on the 16 main regions and 101 highest points in New Zealand, respectively (Figure 4.1). The following code chunk first creates an object representing Canterbury, then uses spatial subsetting to return all high points in the region:

canterbury = nz %>% filter(Name == "Canterbury")
canterbury_height = nz_height[canterbury, ]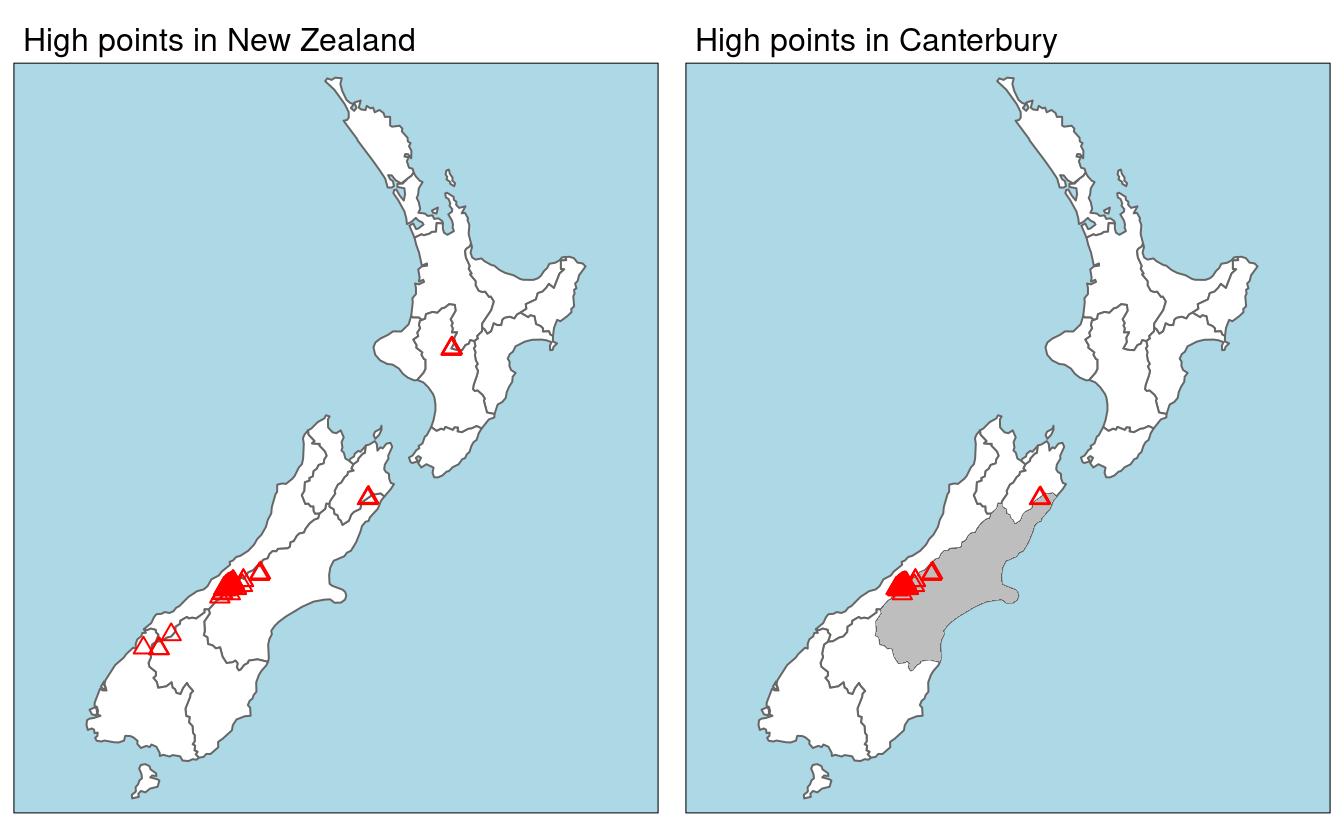

FIGURE 4.1: Illustration of spatial subsetting with red triangles representing 101 high points in New Zealand, clustered near the central Canterbuy region (left). The points in Canterbury were created with the [ subsetting operator (highlighted in gray, right).

Like attribute subsetting x[y, ] subsets features of a target x using the contents of a source object y. Instead of y being of class logical or integer — a vector of TRUE and FALSE values or whole numbers — for spatial subsetting it is another spatial (sf) object.

Various topological relations can be used for spatial subsetting. These determine the type of spatial relationship that features in the target object must have with the subsetting object to be selected, including touches, crosses or within (see Section 4.2.2). Intersects is the default spatial subsetting operator, a default that returns TRUE for many types of spatial relations, including touches, crosses and is within. These alternative spatial operators can be specified with the op = argument, a third argument that can be passed to the [ operator for sf objects. This is demonstrated in the following command which returns the opposite of st_intersects(), points that do not intersect with Canterbury (see Section 4.2.2):

nz_height[canterbury, , op = st_disjoint]

Note the empty argument — denoted with , , — in the preceding code chunk is included to highlight op, the third argument in [ for sf objects. One can use this to change the subsetting operation in many ways. nz_height[canterbury, 2, op = st_disjoint], for example, returns the same rows but only includes the second attribute column (see sf:::`[.sf` and the ?sf for details).

For many applications, this is all you’ll need to know about spatial subsetting for vector data. In this case, you can safely skip to Section 4.2.2.

If you’re interested in the details, including other ways of subsetting, read on. Another way of doing spatial subsetting uses objects returned by topological operators. This is demonstrated in the first command below:

sel_sgbp = st_intersects(x = nz_height, y = canterbury)
class(sel_sgbp)
#> [1] "sgbp" "list"
sel_logical = lengths(sel_sgbp) > 0
canterbury_height2 = nz_height[sel_logical, ]

In the above code chunk, an object of class sgbp (a sparse geometry binary predicate, a list of length x in the spatial operation) is created and then converted into a logical vector sel_logical (containing only TRUE and FALSE values). The function lengths() identifies which features in nz_height intersect with any objects in y. In this case 1 is the greatest possible value but for more complex operations one could use the method to subset only features that intersect with, for example, 2 or more features from the source object.

Note: another way to return a logical output is by setting sparse = FALSE (meaning ‘return a dense matrix not a sparse one’) in operators such as st_intersects(). The command st_intersects(x = nz_height, y = canterbury, sparse = FALSE)[, 1], for example, would return an output identical to sel_logical. Note: the solution involving sgbp objects is more generalisable though, as it works for many-to-many operations and has lower memory requirements.

It should be noted that a logical can also be used with filter() as follows (sparse = FALSE is explained in Section 4.2.2):

canterbury_height3 = nz_height %>%
  filter(st_intersects(x = ., y = canterbury, sparse = FALSE))

At this point, there are three versions of canterbury_height, one created with spatial subsetting directly and the other two via intermediary selection objects. To explore these objects and spatial subsetting in more detail, see the supplementary vignettes on subsetting and tidyverse-pitfalls.

4.2.2 Topological relations

Topological relations describe the spatial relationships between objects. To understand them, it helps to have some simple test data to work with. Figure 4.2 contains a polygon (a), a line (l) and some points (p), which are created in the code below.

# create a polygon
a_poly = st_polygon(list(rbind(c(-1, -1), c(1, -1), c(1, 1), c(-1, -1))))
a = st_sfc(a_poly)
# create a line
l_line = st_linestring(x = matrix(c(-1, -1, -0.5, 1), ncol = 2))
l = st_sfc(l_line)
# create points
p_matrix = matrix(c(0.5, 1, -1, 0, 0, 1, 0.5, 1), ncol = 2)
p_multi = st_multipoint(x = p_matrix)
p = st_cast(st_sfc(p_multi), "POINT")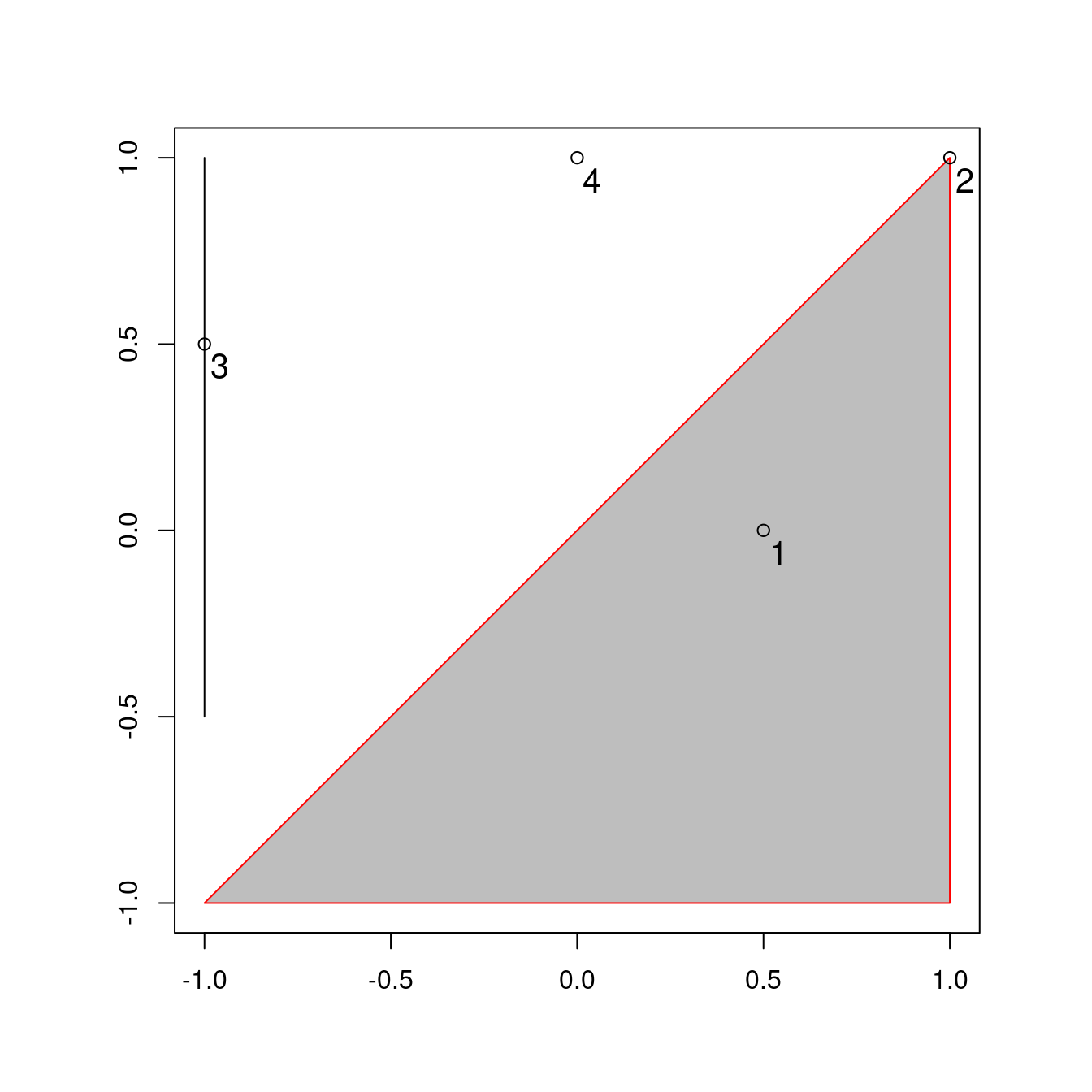

FIGURE 4.2: Points (p 1 to 4), line and polygon objects arranged to illustrate topological relations.

A simple query is: which of the points in p intersect in some way with polygon a? The question can be answered by inspection (points 1 and 2 are over or touch the triangle). It can also be answered by using a spatial predicate such as do the objects intersect? This is implemented in sf as follows:

st_intersects(p, a)
#> Sparse geometry binary ..., where the predicate was `intersects'
#> 1: 1
#> 2: 1
#> 3: (empty)
#> 4: (empty)

The contents of the result should be as you expected: the function returns a positive (1) result for the first two points, and a negative result (represented by an empty vector) for the last two. What may be unexpected is that the result comes in the form of a list of vectors. This sparse matrix output only registers a relation if one exists, reducing the memory requirements of topological operations on multi-feature objects. As we saw in the previous section, a dense matrix consisting of TRUE or FALSE values for each combination of features can also be returned when sparse = FALSE:

st_intersects(p, a, sparse = FALSE)
#>       [,1]
#> [1,]  TRUE
#> [2,]  TRUE
#> [3,] FALSE
#> [4,] FALSE

The output is a matrix in which each row represents a feature in the target object and each column represents a feature in the selecting object. In this case, only the first two features in p intersect with a and there is only one feature in a so the result has only one column. The result can be used for subsetting as we saw in Section 4.2.1.

Note that st_intersects() returns TRUE for the second feature in the object p even though it just touches the polygon a: intersects is a ‘catch-all’ topological operation which identifies many types of spatial relation.

The opposite of st_intersects() is st_disjoint(), which returns only objects that do not spatially relate in any way to the selecting object (note [, 1] converts the result into a vector):

st_disjoint(p, a, sparse = FALSE)[, 1]
#> [1] FALSE FALSE  TRUE  TRUE

st_within() returns TRUE only for objects that are completely within the selecting object. This applies only to the first object, which is inside the triangular polygon, as illustrated below:

st_within(p, a, sparse = FALSE)[, 1]
#> [1]  TRUE FALSE FALSE FALSE

Note that although the first point is within the triangle, it does not touch any part of its border. For this reason st_touches() only returns TRUE for the second point:

st_touches(p, a, sparse = FALSE)[, 1]
#> [1] FALSE  TRUE FALSE FALSE

What about features that do not touch, but almost touch the selection object? These can be selected using st_is_within_distance(), which has an additional dist argument. It can be used to set how close target objects need to be before they are selected. Note that although point 4 is one unit of distance from the nearest node of a (at point 2 in Figure 4.2), it is still selected when the distance is set to 0.9. This is illustrated in the code chunk below, the second line of which converts the lengthy list output into a logical object:

sel = st_is_within_distance(p, a, dist = 0.9) # can only return a sparse matrix
lengths(sel) > 0
#> [1]  TRUE  TRUE FALSE  TRUE

Functions for calculating topological relations use spatial indices to largely speed up spatial query performance. They achieve that using the Sort-Tile-Recursive (STR) algorithm. The st_join function, mentioned in the next section, also uses the spatial indexing. You can learn more at https://www.r-spatial.org/r/2017/06/22/spatial-index.html.

4.2.3 Spatial joining

Joining two non-spatial datasets relies on a shared ‘key’ variable, as described in Section 3.2.3. Spatial data joining applies the same concept, but instead relies on shared areas of geographic space (it is also known as spatial overlay). As with attribute data, joining adds a new column to the target object (the argument x in joining functions), from a source object (y).

The process can be illustrated by an example. Imagine you have ten points randomly distributed across the Earth’s surface. Of the points that are on land, which countries are they in? Random points to demonstrate spatial joining are created as follows:

set.seed(2018) # set seed for reproducibility
(bb_world = st_bbox(world)) # the world's bounds
#>   xmin   ymin   xmax   ymax 
#> -180.0  -89.9  180.0   83.6
random_df = tibble(
  x = runif(n = 10, min = bb_world[1], max = bb_world[3]),
  y = runif(n = 10, min = bb_world[2], max = bb_world[4])
)
random_points = random_df %>% 
  st_as_sf(coords = c("x", "y")) %>% # set coordinates
  st_set_crs(4326) # set geographic CRS

The scenario is illustrated in Figure 4.3. The random_points object (top left) has no attribute data, while the world (top right) does. The spatial join operation is done by st_join(), which adds the name_long variable to the points, resulting in random_joined which is illustrated in Figure 4.3 (bottom left — see 04-spatial-join.R). Before creating the joined dataset, we use spatial subsetting to create world_random, which contains only countries that contain random points, to verify the number of country names returned in the joined dataset should be four (see the top right panel of Figure 4.3).

world_random = world[random_points, ]
nrow(world_random)
#> [1] 4
random_joined = st_join(random_points, world["name_long"])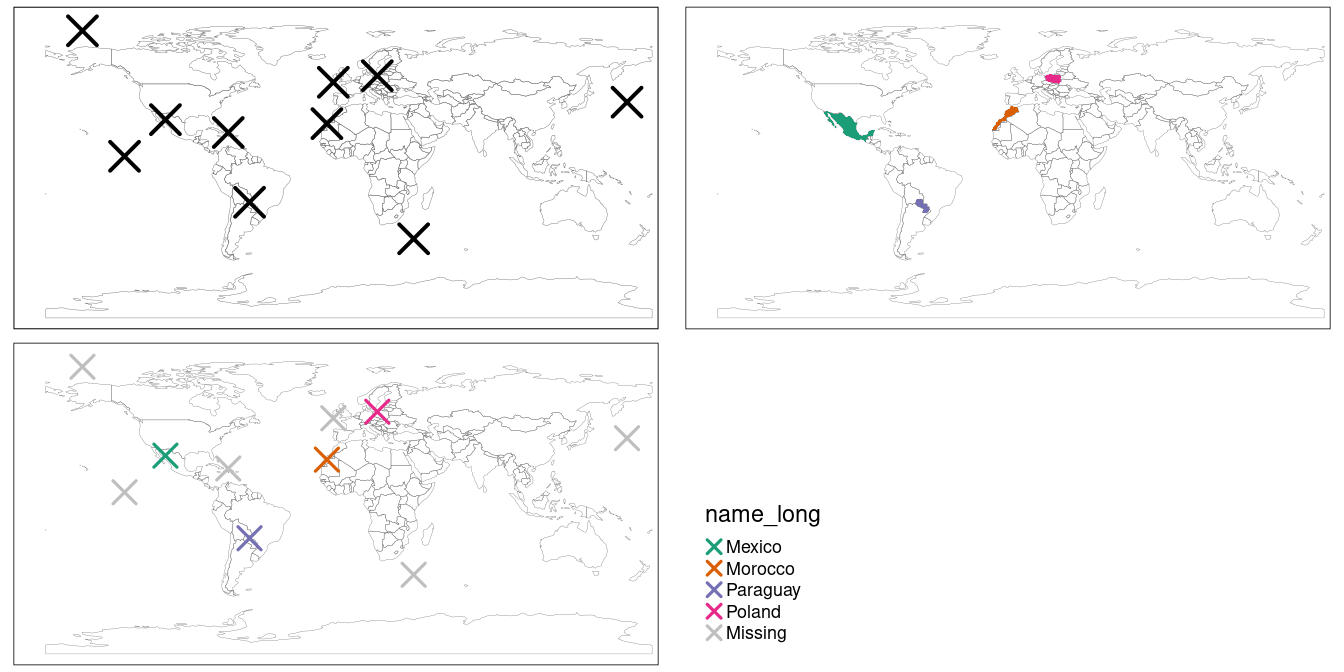

FIGURE 4.3: Illustration of a spatial join. A new attribute variable is added to random points (top left) from source world object (top right) resulting in the data represented in the final panel.

By default, st_join() performs a left join (see Section 3.2.3), but it can also do inner joins by setting the argument left = FALSE. Like spatial subsetting, the default topological operator used by st_join() is st_intersects(). This can be changed with the join argument (see ?st_join for details). In the example above, we have added features of a polygon layer to a point layer. In other cases, we might want to join point attributes to a polygon layer. There might be occasions where more than one point falls inside one polygon. In such a case st_join() duplicates the polygon feature: it creates a new row for each match.

4.2.4 Non-overlapping joins

Sometimes two geographic datasets do not touch but still have a strong geographic relationship enabling joins. The datasets cycle_hire and cycle_hire_osm, already attached in the spData package, provide a good example. Plotting them shows that they are often closely related but they do not touch, as shown in Figure 4.4, a base version of which is created with the following code below:

plot(st_geometry(cycle_hire), col = "blue")
plot(st_geometry(cycle_hire_osm), add = TRUE, pch = 3, col = "red")

We can check if any points are the same st_intersects() as shown below:

any(st_touches(cycle_hire, cycle_hire_osm, sparse = FALSE))
#> [1] FALSE

FIGURE 4.4: The spatial distribution of cycle hire points in London based on official data (blue) and OpenStreetMap data (red).

Imagine that we need to join the capacity variable in cycle_hire_osm onto the official ‘target’ data contained in cycle_hire. This is when a non-overlapping join is needed. The simplest method is to use the topological operator st_is_within_distance() shown in Section 4.2.2, using a threshold distance of 20 m. Note that, before performing the relation, both objects are transformed into a projected CRS. These projected objects are created below (note the affix _P, short for projected):

cycle_hire_P = st_transform(cycle_hire, 27700)
cycle_hire_osm_P = st_transform(cycle_hire_osm, 27700)
sel = st_is_within_distance(cycle_hire_P, cycle_hire_osm_P, dist = 20)
summary(lengths(sel) > 0)
#>    Mode   FALSE    TRUE 
#> logical     304     438

This shows that there are 438 points in the target object cycle_hire_P within the threshold distance of cycle_hire_osm_P. How to retrieve the values associated with the respective cycle_hire_osm_P points? The solution is again with st_join(), but with an addition dist argument (set to 20 m below):

z = st_join(cycle_hire_P, cycle_hire_osm_P,
            join = st_is_within_distance, dist = 20)
nrow(cycle_hire)
#> [1] 742
nrow(z)
#> [1] 762

Note that the number of rows in the joined result is greater than the target. This is because some cycle hire stations in cycle_hire_P have multiple matches in cycle_hire_osm_P. To aggregate the values for the overlapping points and return the mean, we can use the aggregation methods learned in Chapter 3, resulting in an object with the same number of rows as the target:

z = z %>% 
  group_by(id) %>% 
  summarize(capacity = mean(capacity))
nrow(z) == nrow(cycle_hire)
#> [1] TRUE

The capacity of nearby stations can be verified by comparing a plot of the capacity of the source cycle_hire_osm data with the results in this new object (plots not shown):

plot(cycle_hire_osm["capacity"])
plot(z["capacity"])

The result of this join has used a spatial operation to change the attribute data associated with simple features; the geometry associated with each feature has remained unchanged.

4.2.5 Spatial data aggregation

Like attribute data aggregation, covered in Section 3.2.2, spatial data aggregation can be a way of condensing data. Aggregated data show some statistics about a variable (typically average or total) in relation to some kind of grouping variable. Section 3.2.2 demonstrated how aggregate() and group_by() %>% summarize() condense data based on attribute variables. This section demonstrates how the same functions work using spatial grouping variables.

Returning to the example of New Zealand, imagine you want to find out the average height of high points in each region. This is a good example of spatial aggregation: it is the geometry of the source (y or nz in this case) that defines how values in the target object (x or nz_height) are grouped. This is illustrated using the base aggregate() function below:

nz_avheight = aggregate(x = nz_height, by = nz, FUN = mean)

The result of the previous command is an sf object with the same geometry as the (spatial) aggregating object (nz).¹⁷ The result of the previous operation is illustrated in Figure 4.5. The same result can also be generated using the ‘tidy’ functions group_by() and summarize() (used in combination with st_join()):

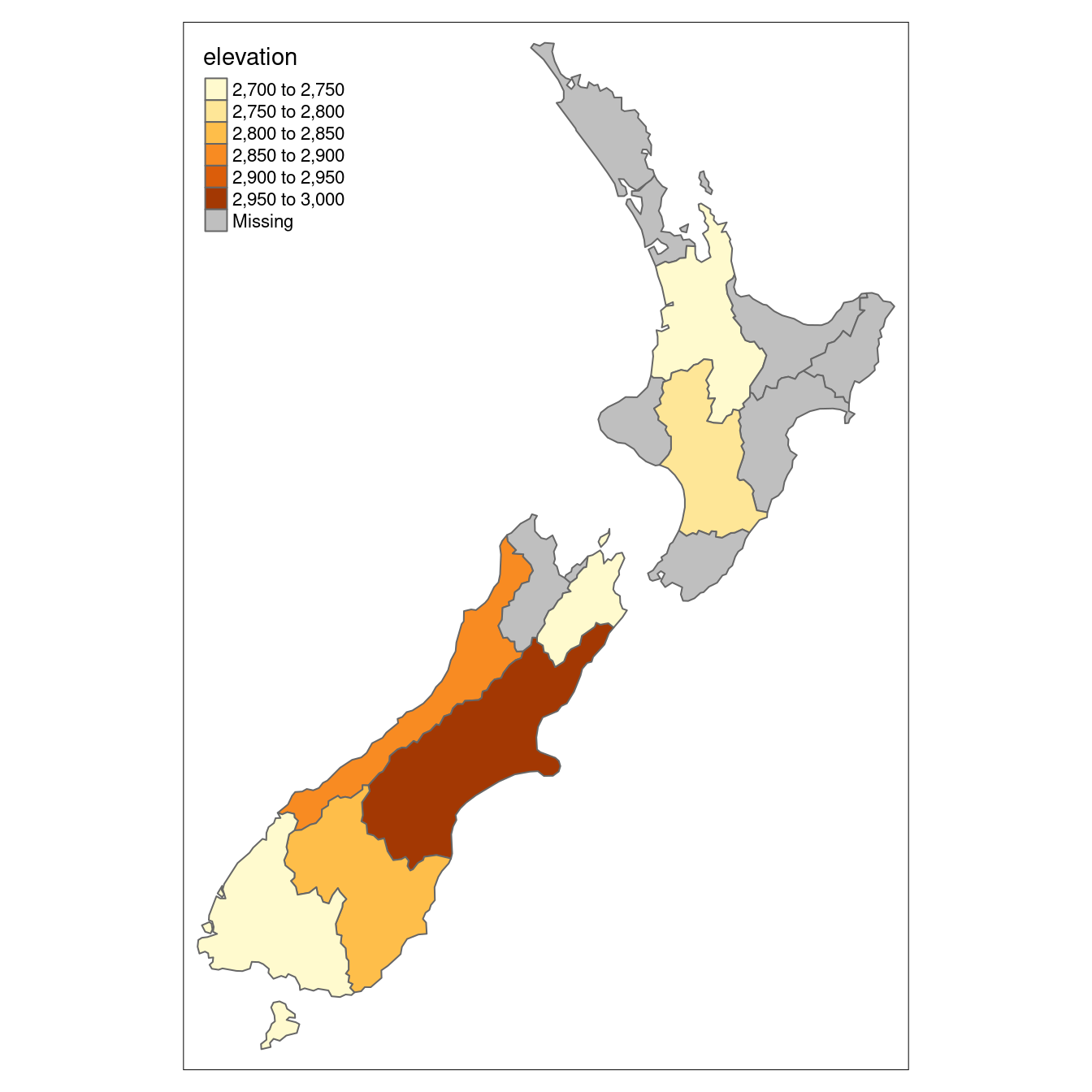
FIGURE 4.5: Average height of the top 101 high points across the regions of New Zealand.

nz_avheight2 = nz %>%
  st_join(nz_height) %>%
  group_by(Name) %>%
  summarize(elevation = mean(elevation, na.rm = TRUE))

The resulting nz_avheight objects have the same geometry as the aggregating object nz but with a new column representing the mean average height of points within each region of New Zealand (other summary functions such as median() and sd() can be used in place of mean()). Note that regions containing no points have an associated elevation value of NA. For aggregating operations which also create new geometries, see Section 5.2.6.

Spatial congruence is an important concept related to spatial aggregation. An aggregating object (which we will refer to as y) is congruent with the target object (x) if the two objects have shared borders. Often this is the case for administrative boundary data, whereby larger units — such as Middle Layer Super Output Areas (MSOAs) in the UK or districts in many other European countries — are composed of many smaller units.

Incongruent aggregating objects, by contrast, do not share common borders with the target (Qiu, Zhang, and Zhou 2012). This is problematic for spatial aggregation (and other spatial operations) illustrated in Figure 4.6. Areal interpolation overcomes this issue by transferring values from one set of areal units to another. Algorithms developed for this task include area weighted and ‘pycnophylactic’ areal interpolation methods (Tobler 1979).

FIGURE 4.6: Illustration of congruent (left) and incongruent (right) areal units with respect to larger aggregating zones (translucent blue borders).

The spData package contains a dataset named incongruent (colored polygons with black borders in the right panel of Figure 4.6) and a dataset named aggregating_zones (the two polygons with the translucent blue border in the right panel of Figure 4.6). Let us assume that the value column of incongruent refers to the total regional income in million Euros. How can we transfer the values of the underlying nine spatial polygons into the two polygons of aggregating_zones?

The simplest useful method for this is area weighted spatial interpolation. In this case values from the incongruent object are allocated to the aggregating_zones in proportion to area; the larger the spatial intersection between input and output features, the larger the corresponding value. For instance, if one intersection of incongruent and aggregating_zones is 1.5 km² but the whole incongruent polygon in question has 2 km² and a total income of 4 million Euros, then the target aggregating zone will obtain three quarters of the income, in this case 3 million Euros. This is implemented in st_interpolate_aw(), as demonstrated in the code chunk below.

agg_aw = st_interpolate_aw(incongruent[, "value"], aggregating_zones,
                           extensive = TRUE)
#> Warning in st_interpolate_aw.sf(incongruent[, "value"], aggregating_zones, :
#> st_interpolate_aw assumes attributes are constant or uniform over areas of x
# show the aggregated result
agg_aw$value
#> [1] 19.6 25.7

In our case it is meaningful to sum up the values of the intersections falling into the aggregating zones since total income is a so-called spatially extensive variable. This would be different for spatially intensive variables, which are independent of the spatial units used, such as income per head or percentages. In this case it is more meaningful to apply an average function when doing the aggregation instead of a sum function. To do so, one would only have to set the extensive parameter to FALSE.

4.2.6 Distance relations

While topological relations are binary — a feature either intersects with another or does not — distance relations are continuous. The distance between two objects is calculated with the st_distance() function. This is illustrated in the code chunk below, which finds the distance between the highest point in New Zealand and the geographic centroid of the Canterbury region, created in Section 4.2.1:

nz_heighest = nz_height %>% top_n(n = 1, wt = elevation)
canterbury_centroid = st_centroid(canterbury)
st_distance(nz_heighest, canterbury_centroid)
#> Units: [m]
#>        [,1]
#> [1,] 115540

There are two potentially surprising things about the result:

• It has units, telling us the distance is 100,000 meters, not 100,000 inches, or any other measure of distance
• It is returned as a matrix, even though the result only contains a single value

This second feature hints at another useful feature of st_distance(), its ability to return distance matrices between all combinations of features in objects x and y. This is illustrated in the command below, which finds the distances between the first three features in nz_height and the Otago and Canterbury regions of New Zealand represented by the object co.

co = filter(nz, grepl("Canter|Otag", Name))
st_distance(nz_height[1:3, ], co)
#> Units: [m]
#>        [,1]  [,2]
#> [1,] 123537 15498
#> [2,]  94283     0
#> [3,]  93019     0

Note that the distance between the second and third features in nz_height and the second feature in co is zero. This demonstrates the fact that distances between points and polygons refer to the distance to any part of the polygon: The second and third points in nz_height are in Otago, which can be verified by plotting them (result not shown):

plot(st_geometry(co)[2])
plot(st_geometry(nz_height)[2:3], add = TRUE)

4.3 Spatial operations on raster data

This section builds on Section 3.3, which highlights various basic methods for manipulating raster datasets, to demonstrate more advanced and explicitly spatial raster operations, and uses the objects elev and grain manually created in Section 3.3. For the reader’s convenience, these datasets can be also found in the spData package.

4.3.1 Spatial subsetting

The previous chapter (Section 3.3) demonstrated how to retrieve values associated with specific cell IDs or row and column combinations. Raster objects can also be extracted by location (coordinates) and other spatial objects. To use coordinates for subsetting, one can ‘translate’ the coordinates into a cell ID with the raster function cellFromXY(). An alternative is to use raster::extract() (be careful, there is also a function called extract() in the tidyverse) to extract values. Both methods are demonstrated below to find the value of the cell that covers a point located 0.1 units from the origin.

id = cellFromXY(elev, xy = c(0.1, 0.1))
elev[id]
# the same as
raster::extract(elev, data.frame(x = 0.1, y = 0.1))

It is convenient that both functions also accept objects of class Spatial* Objects. Raster objects can also be subset with another raster object, as illustrated in Figure 4.7 (left panel) and demonstrated in the code chunk below:

clip = raster(xmn = 0.9, xmx = 1.8, ymn = -0.45, ymx = 0.45,
              res = 0.3, vals = rep(1, 9))
elev[clip]
#> [1] 18 24
# we can also use extract
# extract(elev, extent(clip))

Basically, this amounts to retrieving the values of the first raster (here: elev) falling within the extent of a second raster (here: clip).

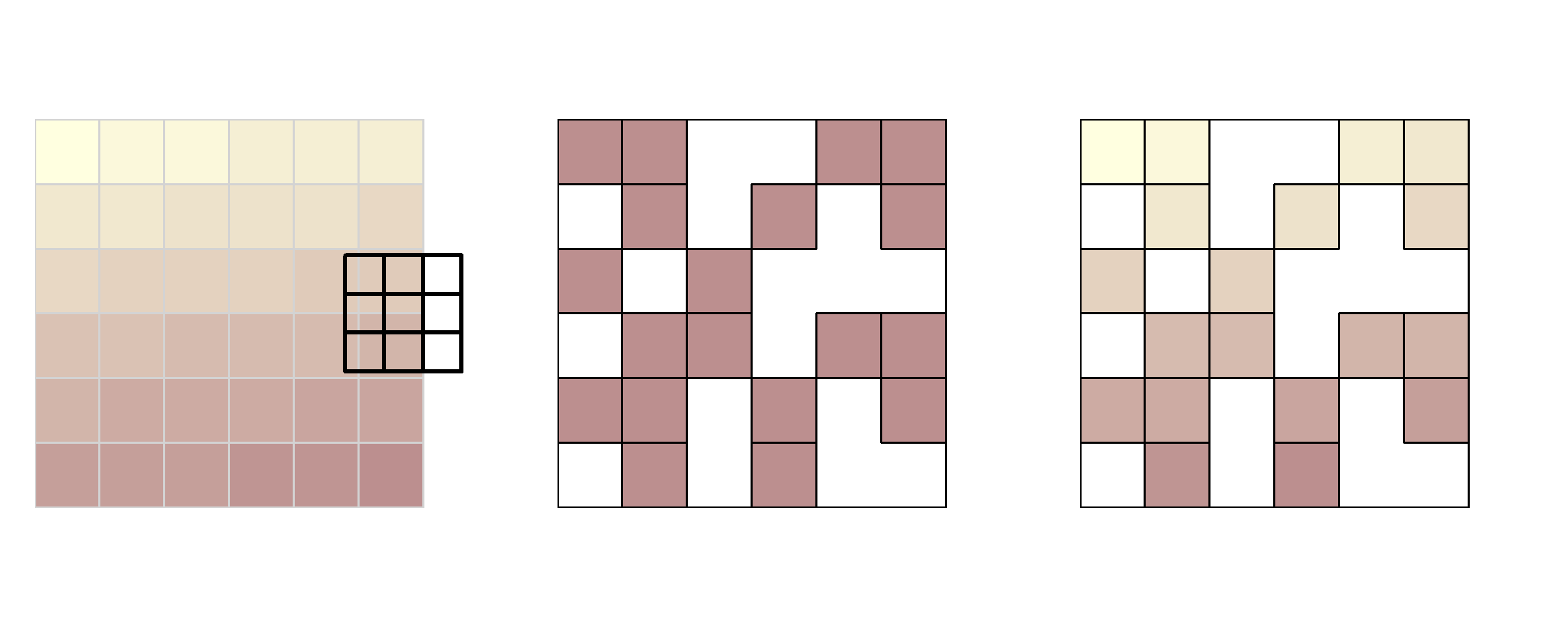
FIGURE 4.7: Subsetting raster values with the help of another raster (left). Raster mask (middle). Output of masking a raster (right).

So far, the subsetting returned the values of specific cells, however, when doing spatial subsetting, one often also expects a spatial object as an output. To do this, we can use again the [ when we additionally set the drop parameter to FALSE. To illustrate this, we retrieve the first two cells of elev as an individual raster object. As mentioned in Section 3.3, the [ operator accepts various inputs to subset rasters and returns a raster object when drop = FALSE. The code chunk below subsets the elev raster by cell ID and row-column index with identical results: the first two cells on the top row (only the first 2 lines of the output is shown):

elev[1:2, drop = FALSE]    # spatial subsetting with cell IDs
elev[1, 1:2, drop = FALSE] # spatial subsetting by row,column indices
#> class       : RasterLayer 
#> dimensions  : 1, 2, 2  (nrow, ncol, ncell)
#> ...

Another common use case of spatial subsetting is when a raster with logical (or NA) values is used to mask another raster with the same extent and resolution, as illustrated in Figure 4.7, middle and right panel. In this case, the [, mask() and overlay() functions can be used (results not shown):

# create raster mask
rmask = elev 
values(rmask) = sample(c(NA, TRUE), 36, replace = TRUE)

# spatial subsetting
elev[rmask, drop = FALSE]           # with [ operator
mask(elev, rmask)                   # with mask()
overlay(elev, rmask, fun = "max")   # with overlay

In the code chunk above, we have created a mask object called rmask with values randomly assigned to NA and TRUE. Next, we want to keep those values of elev which are TRUE in rmask. In other words, we want to mask elev with rmask. These operations are in fact Boolean local operations since we compare cell-wise two rasters. The next subsection explores these and related operations in more detail.

4.3.2 Map algebra

Map algebra makes raster processing really fast. This is because raster datasets only implicitly store coordinates. To derive the coordinate of a specific cell, we have to calculate it using its matrix position and the raster resolution and origin. For the processing, however, the geographic position of a cell is barely relevant as long as we make sure that the cell position is still the same after the processing (one-to-one locational correspondence). Additionally, if two or more raster datasets share the same extent, projection and resolution, one could treat them as matrices for the processing. This is exactly what map algebra is doing in R. First, the raster package checks the headers of the rasters on which to perform any algebraic operation, and only if they are correspondent to each other, the processing goes on.¹⁸ And secondly, map algebra retains the so-called one-to-one locational correspondence. This is where it substantially differs from matrix algebra which changes positions when for example multiplying or dividing matrices.

Map algebra (or cartographic modeling) divides raster operations into four subclasses (Tomlin 1990), with each working on one or several grids simultaneously:

1. Local or per-cell operations.
2. Focal or neighborhood operations. Most often the output cell value is the result of a 3 x 3 input cell block.
3. Zonal operations are similar to focal operations, but the surrounding pixel grid on which new values are computed can have irregular sizes and shapes.
4. Global or per-raster operations; that means the output cell derives its value potentially from one or several entire rasters.

This typology classifies map algebra operations by the number/shape of cells used for each pixel processing step. For the sake of completeness, we should mention that raster operations can also be classified by discipline such as terrain, hydrological analysis or image classification. The following sections explain how each type of map algebra operations can be used, with reference to worked examples (also see vignette("Raster") for a technical description of map algebra).

4.3.3 Local operations

Local operations comprise all cell-by-cell operations in one or several layers. A good example is the classification of intervals of numeric values into groups such as grouping a digital elevation model into low (class 1), middle (class 2) and high elevations (class 3). Using the reclassify() command, we need first to construct a reclassification matrix, where the first column corresponds to the lower and the second column to the upper end of the class. The third column represents the new value for the specified ranges in column one and two. Here, we assign the raster values in the ranges 0–12, 12–24 and 24–36 are reclassified to take values 1, 2 and 3, respectively.

rcl = matrix(c(0, 12, 1, 12, 24, 2, 24, 36, 3), ncol = 3, byrow = TRUE)
recl = reclassify(elev, rcl = rcl)

We will perform several reclassifactions in Chapter 13.

Raster algebra is another classical use case of local operations. This includes adding, subtracting and squaring two rasters. Raster algebra also allows logical operations such as finding all raster cells that are greater than a specific value (5 in our example below). The raster package supports all these operations and more, as described in vignette("Raster") and demonstrated below (results not shown):

elev + elev
elev^2
log(elev)
elev > 5

Instead of arithmetic operators, one can also use the calc() and overlay() functions. These functions are more efficient, hence, they are preferable in the presence of large raster datasets. Additionally, they allow you to directly store an output file.

The calculation of the normalized difference vegetation index (NDVI) is a well-known local (pixel-by-pixel) raster operation. It returns a raster with values between -1 and 1; positive values indicate the presence of living plants (mostly > 0.2). NDVI is calculated from red and near-infrared (NIR) bands of remotely sensed imagery, typically from satellite systems such as Landsat or Sentinel. Vegetation absorbs light heavily in the visible light spectrum, and especially in the red channel, while reflecting NIR light, explaining the NVDI formula:

\[ \begin{split} NDVI&= \frac{\text{NIR} - \text{Red}}{\text{NIR} + \text{Red}}\\ \end{split} \]

Predictive mapping is another interesting application of local raster operations. The response variable corresponds to measured or observed points in space, for example, species richness, the presence of landslides, tree disease or crop yield. Consequently, we can easily retrieve space- or airborne predictor variables from various rasters (elevation, pH, precipitation, temperature, landcover, soil class, etc.). Subsequently, we model our response as a function of our predictors using lm, glm, gam or a machine-learning technique. Spatial predictions on raster objects can therefore be made by applying estimated coefficients to the predictor raster values, and summing the output raster values (see Chapter 14).

4.3.4 Focal operations

While local functions operate on one cell, though possibly from multiple layers, focal operations take into account a central cell and its neighbors. The neighborhood (also named kernel, filter or moving window) under consideration is typically of size 3-by-3 cells (that is the central cell and its eight surrounding neighbors), but can take on any other (not necessarily rectangular) shape as defined by the user. A focal operation applies an aggregation function to all cells within the specified neighborhood, uses the corresponding output as the new value for the the central cell, and moves on to the next central cell (Figure 4.8). Other names for this operation are spatial filtering and convolution (Burrough, McDonnell, and Lloyd 2015).

In R, we can use the focal() function to perform spatial filtering. We define the shape of the moving window with a matrix whose values correspond to weights (see w parameter in the code chunk below). Secondly, the fun parameter lets us specify the function we wish to apply to this neighborhood. Here, we choose the minimum, but any other summary function, including sum(), mean(), or var() can be used.

r_focal = focal(elev, w = matrix(1, nrow = 3, ncol = 3), fun = min)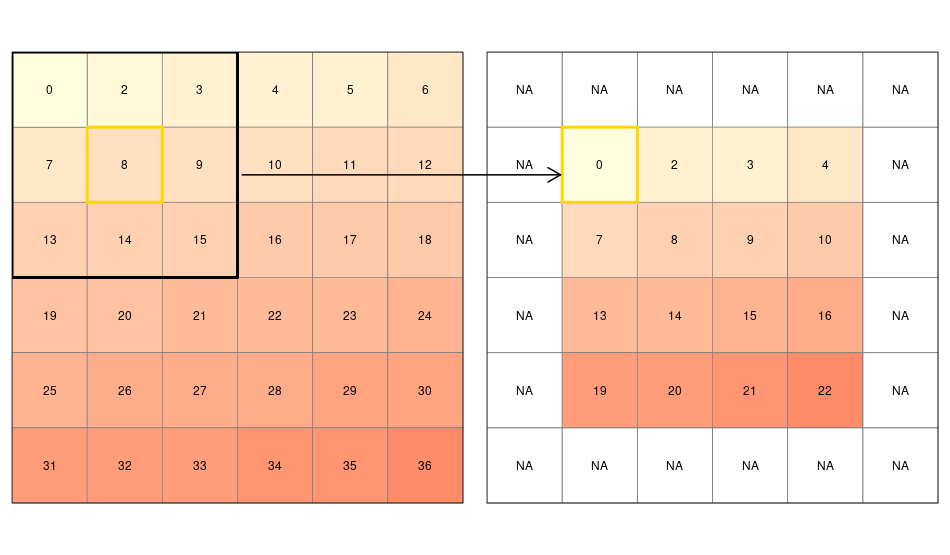

FIGURE 4.8: Input raster (left) and resulting output raster (right) due to a focal operation - finding the minimum value in 3-by-3 moving windows.

We can quickly check if the output meets our expectations. In our example, the minimum value has to be always the upper left corner of the moving window (remember we have created the input raster by row-wise incrementing the cell values by one starting at the upper left corner). In this example, the weighting matrix consists only of 1s, meaning each cell has the same weight on the output, but this can be changed.

Focal functions or filters play a dominant role in image processing. Low-pass or smoothing filters use the mean function to remove extremes. In the case of categorical data, we can replace the mean with the mode, which is the most common value. By contrast, high-pass filters accentuate features. The line detection Laplace and Sobel filters might serve as an example here. Check the focal() help page for how to use them in R (this will also be used in the exercises at the end of this chapter).

Terrain processing, the calculation of topographic characteristics such as slope, aspect and flow directions, relies on focal functions. terrain() can be used to calculate these metrics, although some terrain algorithms, including the Zevenbergen and Thorne method to compute slope, are not implemented in this raster function. Many other algorithms — including curvatures, contributing areas and wetness indices — are implemented in open source desktop geographic information system (GIS) software. Chapter 9 shows how to access such GIS functionality from within R.

4.3.5 Zonal operations

Just like focal operations, zonal operations apply an aggregation function to multiple raster cells. However, a second raster, usually a categorical raster, defines the zonal filters (or ‘zones’) in the case of zonal operations as opposed to a predefined neighborhood window in the case of focal operations (see previous Section). Consequently, the raster cells defining the zonal filter do not necessarily have to be neighbors. Our grain size raster is a good example (right panel of Figure 3.2) because the different grain sizes are spread in an irregular fashion throughout the raster. Finally, the result of a zonal operation is a summary table grouped by zone which is why this operation is also known as zonal statistics in the GIS world. This is in contrast to focal operations which return a raster object (see previous Section).

For example, to find the mean elevation for each grain size class (Figure 3.2), we use the zonal() function.

z = zonal(elev, grain, fun = "mean") %>%
  as.data.frame()
z
#>   zone mean
#> 1    1 17.8
#> 2    2 18.5
#> 3    3 19.2

This returns the statistics for each category, here the mean altitude for each grain size class, and can be added to the attribute table of the ratified raster (see previous chapter).

4.3.6 Global operations and distances

Global operations are a special case of zonal operations with the entire raster dataset representing a single zone. The most common global operations are descriptive statistics for the entire raster dataset such as the minimum or maximum (see Section 3.3.2). Aside from that, global operations are also useful for the computation of distance and weight rasters. In the first case, one can calculate the distance from each cell to a specific target cell. For example, one might want to compute the distance to the nearest coast (see also raster::distance()). We might also want to consider topography, that means, we are not only interested in the pure distance but would like also to avoid the crossing of mountain ranges when going to the coast. To do so, we can weight the distance with elevation so that each additional altitudinal meter ‘prolongs’ the Euclidean distance. Visibility and viewshed computations also belong to the family of global operations (in the exercises of Chapter 9, you will compute a viewshed raster).

4.3.7 Map algebra counterparts in vector processing

Many map algebra operations have a counterpart in vector processing (Liu and Mason 2009). Computing a distance raster (zonal operation) while only considering a maximum distance (logical focal operation) is the equivalent to a vector buffer operation (Section 5.2.5). Reclassifying raster data (either local or zonal function depending on the input) is equivalent to dissolving vector data (Section 4.2.3). Overlaying two rasters (local operation), where one contains NULL or NA values representing a mask, is similar to vector clipping (Section 5.2.5). Quite similar to spatial clipping is intersecting two layers (Section 4.2.1). The difference is that these two layers (vector or raster) simply share an overlapping area (see Figure 5.8 for an example). However, be careful with the wording. Sometimes the same words have slightly different meanings for raster and vector data models. Aggregating in the case of vector data refers to dissolving polygons, while it means increasing the resolution in the case of raster data. In fact, one could see dissolving or aggregating polygons as decreasing the resolution. However, zonal operations might be the better raster equivalent compared to changing the cell resolution. Zonal operations can dissolve the cells of one raster in accordance with the zones (categories) of another raster using an aggregation function (see above).

4.3.8 Merging rasters

Suppose we would like to compute the NDVI (see Section 4.3.3), and additionally want to compute terrain attributes from elevation data for observations within a study area. Such computations rely on remotely sensed information. The corresponding imagery is often divided into scenes covering a specific spatial extent. Frequently, a study area covers more than one scene. In these cases we would like to merge the scenes covered by our study area. In the easiest case, we can just merge these scenes, that is put them side by side. This is possible with digital elevation data (SRTM, ASTER). In the following code chunk we first download the SRTM elevation data for Austria and Switzerland (for the country codes, see the raster function ccodes()). In a second step, we merge the two rasters into one.

aut = getData("alt", country = "AUT", mask = TRUE)
ch = getData("alt", country = "CHE", mask = TRUE)
aut_ch = merge(aut, ch)

Raster’s merge() command combines two images, and in case they overlap, it uses the value of the first raster. You can do exactly the same with gdalUtils::mosaic_rasters() which is faster, and therefore recommended if you have to merge a multitude of large rasters stored on disk.

The merging approach is of little use when the overlapping values do not correspond to each other. This is frequently the case when you want to combine spectral imagery from scenes that were taken on different dates. The merge() command will still work but you will see a clear border in the resulting image. The mosaic() command lets you define a function for the overlapping area. For instance, we could compute the mean value. This might smooth the clear border in the merged result but it will most likely not make it disappear. To do so, we need a more advanced approach. Remote sensing scientists frequently apply histogram matching or use regression techniques to align the values of the first image with those of the second image. The packages landsat (histmatch(), relnorm(), PIF()), satellite (calcHistMatch()) and RStoolbox (histMatch(), pifMatch()) provide the corresponding functions. For a more detailed introduction on how to use R for remote sensing, we refer the reader to Wegmann, Leutner, and Dech (2016).

4.4 Exercises

1. It was established in Section 4.2 that Canterbury was the region of New Zealand containing most of the 100 highest points in the country. How many of these high points does the Canterbury region contain?

2. Which region has the second highest number of nz_height points in, and how many does it have?

3. Generalizing the question to all regions: how many of New Zealand’s 16 regions contain points which belong to the top 100 highest points in the country? Which regions?

   • Bonus: create a table listing these regions in order of the number of points and their name.

4. Use data(dem, package = "spDataLarge"), and reclassify the elevation in three classes: low, medium and high. Secondly, attach the NDVI raster (data(ndvi, package = "spDataLarge")) and compute the mean NDVI and the mean elevation for each altitudinal class.

5. Apply a line detection filter to raster(system.file("external/rlogo.grd", package = "raster")). Plot the result. Hint: Read ?raster::focal().

6. Calculate the NDVI of a Landsat image. Use the Landsat image provided by the spDataLarge package (system.file("raster/landsat.tif", package="spDataLarge")).

7. A StackOverflow post shows how to compute distances to the nearest coastline using raster::distance(). Retrieve a digital elevation model of Spain, and compute a raster which represents distances to the coast across the country (hint: use getData()). Second, use a simple approach to weight the distance raster with elevation (other weighting approaches are possible, include flow direction and steepness); every 100 altitudinal meters should increase the distance to the coast by 10 km. Finally, compute the difference between the raster using the Euclidean distance and the raster weighted by elevation. Note: it may be wise to increase the cell size of the input raster to reduce compute time during this operation.

References

Burrough, P. A., Rachael McDonnell, and Christopher D. Lloyd. 2015. Principles of Geographical Information Systems. Third. Oxford, New York: Oxford University Press.

Liu, Jian-Guo, and Philippa J. Mason. 2009. Essential Image Processing and GIS for Remote Sensing. Chichester, West Sussex, UK, Hoboken, NJ: Wiley-Blackwell.

Qiu, Fang, Caiyun Zhang, and Yuhong Zhou. 2012. “The Development of an Areal Interpolation ArcGIS Extension and a Comparative Study.” GIScience & Remote Sensing 49 (5): 644–63. https://doi.org/10.2747/1548-1603.49.5.644.

Tobler, Waldo R. 1979. “Smooth Pycnophylactic Interpolation for Geographical Regions.” Journal of the American Statistical Association 74 (367): 519–30. https://doi.org/10.1080/01621459.1979.10481647.

Tomlin, C. Dana. 1990. Geographic Information Systems and Cartographic Modeling. Englewood Cliffs, N.J: Prentice Hall.

Wegmann, Martin, Benjamin Leutner, and Stefan Dech, eds. 2016. Remote Sensing and GIS for Ecologists: Using Open Source Software. Data in the Wild. Exeter: Pelagic Publishing.

---

17. This can be verified with identical(st_geometry(nz), st_geometry(nz_avheight)).↩︎

18. Map algebra operations are also possible with headerless rasters; in this case the user has to make sure that in fact there exists a one-to-one locational correspondence. An example showing how to import a headerless raster into R is provided in a post at https://stat.ethz.ch/pipermail/r-sig-geo/2013-May/018278.html.↩︎