Chapter 2 Urban Form as Predictors
The concepts of ‘urban form,’ ‘built environment,’ and ‘land use’ are often exchangeable in literature. Adopted from some common usages, here, ‘urban form’ refers to the comprehensive physical expression of land use at the macro scale.
‘Built environment’ emphasizes the urban form attributes as a series of external factors with respect to travelers’ internal characteristics and is often used in disaggregated studies at mesoscale. When using ‘urban form’ and ‘built environment,’ one looks at them as the given conditions of travel decision. While ‘land use’ can represent either current status descriptions or designated future use at mesoscale and micro scales.
2.1 Influencing Direction
Before discussing the impact of land use on travel, the first question is whether land-use characteristics affect the outcome of travel behavior? Or the affecting direction is opposite? Technically, randomized control experiments can identify the causal relationship between them. But in real life, it is impossible to set up some experimental areas and randomly assign people to live in these areas.
Another way is to observe the dynamic of these factors to figure out the direction of influences. Muller (2004) reviews the evolution of the U.S. urban form and describe the four eras of intrametropolitan growth (Figure ) in U.S. history: the walking-horsecar era (1800s – 1890s), the electric streetcar or transit era (1890s – 1920s), the recreational automobile era (1930s – 1950s), and the freeway era (1950s – 2010s) (Rodrigue, Comtois, and Slack 2016). Each four-stage urban transportation development has its dominated spatial structure, which is hard represented by other socio-economic concepts. Each era has a distinctive travel mode, range of distance, and land-use patterns. People can see that the innovation of transportation technology is a determining constraint to other factors and a main driving force to launch the next era.
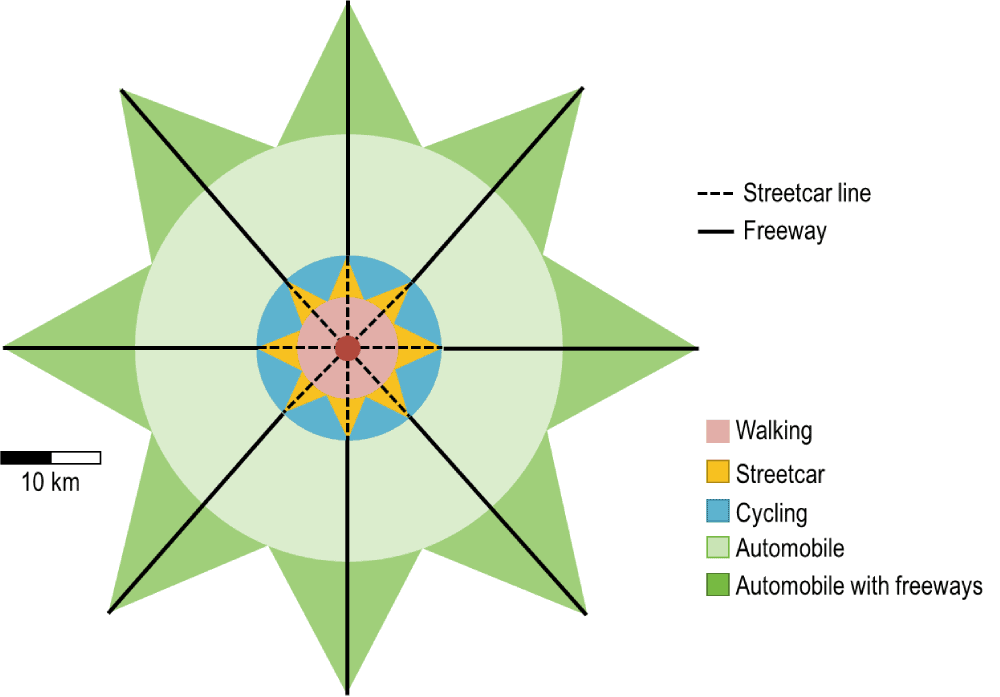
Figure 2.1: One Hour Commuting According to Different Urban Transportation Modes. Source: P.Hugill (1995), World Trade since 1431, p. 213.
New transportation tools shifted people’s travel modes, extended travel distance, and reshaped the urban form. In causal inference, the new tools are called confounder or common cause, affecting both treatment and outcome. But what is the relationship between travel and urban form? A simple way is to observe the sequence of events to happen. In each transition period, the new tools and new modes began ahead of the new urban development. Even today, multiple travel modes exist in the old town, but suburban seldom has the old way like the streetcar. Thus, urban form is more like an outcome rather than treatment.
However, the urban form remains relatively more stable than an individual’s travel behavior in each era. A family may be used to driving in Texas and turn to use the subway when they move to New York and vice versa. Given a period, VMT could be affected by density and other factors. It doesn’t make sense that VMT will change the density in the short term. Therefore, urban form can be treated as independent variables in the context of the current stage of urban development. The relationship of urban form with respect to travel can hold for a period of time.
Over the long term, the relationships among travel, urban form, and other physical, socio-economic, demographic factors were interactive and iterative. D. M. Levinson and Krizek (2018) emphasize transportation is a necessary but not a sufficient factor for any development. The change of eras is a comprehensive outcome of socio-economic and technological development. Which factor caused which effect does not have a simple answer. A conservative view is that land use and travel behavior are determined simultaneously by the transportation costs (Pickrell 1999).
Although randomized control experiments about travel and urban form are impossible, the regression model can still explore their associations once the simultaneous relationship holds.
2.2 Influencing Factors
For the complexity of travel behavior, many objective or subjective factors could change people’s travel decisions. They include but are not limited to physical, socio-demographic, individual, and policy determinants. It seems impossible to make an exhaustive list. Here briefly introduces several significant influencing factors.
A dichotomy of individual versus environmental factors is a common framework. All relevant factors involving personal or household characteristics can be categorized as internal factors. In comparison, the built environment and other environmental factors have external influences. Disaggregate analysis usually chooses this structure because the models can distinguish the different sources of variation from individual and environmental factors. For example, the VMT model is as follows.
\[\begin{aligned} \mathbf{Y}=\mathbf{X}_\mathrm{I}\boldsymbol{\beta}_\mathrm{I}+\mathbf{X}_\mathrm{E}\boldsymbol{\beta}_\mathrm{E}+\boldsymbol{\varepsilon} \end{aligned}\]
where \(\mathbf{X}_\mathrm{I}\) are travelers’ internal characteristics; \(\mathbf{X}_\mathrm{E}\) are built environment and other environment covariates.
2.2.1 Individual Factors
Previous research have identified many internal factors have strong impact on travel.
Vehicle ownership is a good indicator for choosing auto mode and longer travel distance (van der Waard, Jorritsma, and Immers 2013). Employment status or entry into the labor market often increases driving while retirement may have more walking or cycling for fewer time constraints. (Goodwin and Van Dender, 2013; Grimal, Collet, and Madre, 2013; Headicar, 2013)
Some factors shows significant impact on travel but give opposite directions. Sometimes, it implies some nonlinear features. For example, income usually has a positive relationship with car ownership and driving distance. But some studies find less-wealthy groups have more cars and longer driving distance (Goetzke and Weinberger 2012). Sometimes, it depends on the location and social background. Dargay and Hanly (2007) find the number of children in household has a positive relationship in the U.K. While Ding et al. (2017) find a negative effect in the U.S.
Larouche et al. (2020) make a scoping review of some major life events on travel behavior. They provide some explanation for the inconsistent results. Relocation provide windows of opportunity for travel behavior change, but the direction depend on people’s attitude. Psychological factors such as travelers’ habits and preferences are determinant. Similarly, the choice after school transitions depends on the new environmental factors. Marriage is not significant because couples may live together before marriage. In a similar way, parents may have more car use several years after childbirth for the purposes of childcare, school, recreation, etc.
Therefore, a well performed model should contain these influencing factors to increase models’ fitness. Controlling these independent variables, which can not be intervened by policy, can help to identify how large the effect sizes of adjustable factors are. These studies also notes that the range, location, and understanding of internal variables are critical for a proper model.
2.2.2 Environmental Factors
Environmental factors usually impact a large number of people. Three main categories are natural environment, socio-economic environment, and built environment. The natural terrain, temperature, and precipitation could change travelers’ choice. These factors can only be examined across cities and regions. They are also hard to change and are not included in many studies.
Socio-economic environment such as fuel price and crime rates also encourage/discourage people choosing driving for economic or safety reasons. Some of them, such as car culture are hard to measure and control as other psychological factors. Some factors could be related to the broader topics such as quality of life, or public security. In these cases car usage is not the core concerns.
Infrastructure supplement is also a set of strong explanatory variables. It has been proven that road capacity and parking space are two primary factors for driving. Chatman (2008) finds the effect of denser development on VMT is neutral after controlling the road service and parking demand. The problem is that reducing supply is painful for public and is subject to political pressure. Increasing and improving transit services are more attractive through providing a substitution of driving (Kuhnimhof, Zumkeller, and Chlond 2013).
Policy environment as treatment applied on a administrative region, such as restrictions on car use, can only be examined by comparing with the ‘control groups.’ Meanwhile, transportation policy is a context-dependent factor. The same policy in name may be implemented in very different ways across the country. Cross-sectional study is a challenge because existing the complex interaction effects between a policy and the characteristics of the ‘experimental group.’ Longitudinal study and Difference in Difference (DID) methods are more common in policy evaluations. There are also two types of policies. Travel Demand Management (TDM) heads directly toward change of travel behavior. For example, studies find parking management and low ticket fare by subsidies can attract more transit passengers (Grimal, Collet, and Madre 2013). While many urban development policies such as UBG, TOD, and rezoning have more comprehensive goals.
Built environment such as urban density and design is a primary focus of attention in urban studies because they are more changeable than natural environment. They are simple and measurable for implement. They are more acceptable for neutral meaning and can change people’s behavior inadvertently.
policy or planning might be able to intervene current and future land use, further achieve the goal of travel behavior change. “Attributes of the built environment influence travel by making travel to opportunities more or less convenient and attractive” (Domencich and McFadden 1975; D. M. Levinson, Marshall, and Axhausen 2017; Litman 2017). There are many complex unknown interaction effects between built-environment and other variables. Some research found that the habit discontinuity hypothesis, major life events may provide windows of opportunity during which individuals may reconsider their travel behaviors and be more sensitive to behavior change interventions (Verplanken et al. 2008). The changes in built-environment attributes may capture these windows of opportunity. Further introduction is placed in the next section.
2.2.3 Density
Density is the first built-environment factor added to the model. Early research of automobile trips and urban density can go back sixty years (Mitchell and Rapkin 1954). H. S. Levinson and Wynn (1963) suggest that the people who lived in high-density neighborhoods make fewer automobile trips. This argument stimulated an enormous volume of work. Although later studies construct more complex models, density factor stays in most of travel-urban form model even today.
The most influential aggregate studies start from Newman and Kenworthy. They published a series of studies to show a strong negative correlation between per capita fuel use and gross population density (GPD).3 Their sample covers from thirty-two to fifty-eight global cities (P. G. Newman and Kenworthy 1989a; P. Newman and Kenworthy 2015) and produced very convincing results. Their research points out the relationship rather than estimating the effect size. In this way, the denser cities have less fuel consumption, which implies less automobile dependence. This is a succinct argument and is widely accepted by planners and policy makers.
The criticisms include their ideological grounds, dataset, and model specification(Gordon and Richardson 1989; Dujardin et al. 2012; Perumal and Timmons 2017). A criticism is that, for aggregated data, the population variable on both sides of the equation artificially creates a hyperbolic function (Equation (2.1)). In many disaggregated studies, the effects of density are not significant and have a small magnitude (P. Zhao and Li 2021).
\[\begin{equation} \begin{split} & \text{VMT}_{average} =\beta\cdot \text{Density} +\cdots\\ \implies & \frac{\text{VMT}_{total}}{\text{Population}} = \beta\cdot \frac{\text{Population}}{\text{Area}} +\cdots\\ \implies & \text{VMT}_{total} = \beta\cdot \frac{(\text{Population})^2}{\text{Area}} +\cdots \end{split} \tag{2.1} \end{equation}\]Another criticism argues that the global comparisons are not valid, such as comparing Hong Kong and Houston. Reid Ewing et al. (2018) created a subset with only U.S. Metropolitan areas from Jeffrey R. Kenworthy and Laube (1999) ‘s original data set. They fit the same model but get a much lower \(R^2\) (0.096) than Kenworthy and Laube’s (0.72). A similar work by Fanis (2019) shows the low \(R^2\) for U.S. cities (0.1838) and European cities (0.2804) when deconstructing Newman and Kenworthy’s data by continent. Actually, any research question has its corresponding sampling design. Choosing a cutoff from the whole data often gets a different result. These criticisms are unfair for Kenworthy and Laube’s work. But it is true that U.S. cities have higher VMT and lower density than other countries’ cities. Recent evidence over a 20-year period from other cities and counties show that the status quo of the U.S. only represents a small window of the global trend(Jeffrey R. Kenworthy 2017).
Density as an explanatory variable have some advantages. Density is calculated by population size and area size from census data, which are widely available over the country. In contrast, some individual variables are not as measurable and accurate as density. Some studies found density might be an intermediate variable or proxy to other land use variables such as land use mix, street network, and transit services (Reid Ewing and Cervero 2010; Handy 2005a). The divisions of the statistical units in the U.S. are from an uniform criteria at multiple scales. Thus, density values is more objective, and comparable comparing other measurements.
Density is an informative factor. Except for the mean and variance, The moments function for Urban density such as skewness, kurtosis, or rank, all can be the predictor candidates. Scolar also explore more delicate measurements of density such as Propotional Weighted Density to replace overall density. “population-weighted density is equal to conventional density plus the variance of density across the subareas used for its calculation divided by the conventional density” (Ottensmann 2018). Some studies use a geographically weighted regression (GWR) (“Geographically Weighted Regression - an Overview | ScienceDirect Topics” n.d.) procedure to identify significant employment density peaks.
Urban density can be represented by many approximate variables – built-up density, residential density, employment density, destination density, or CBD density. Here this paper focus on population density – how many people live in a square mile of land - and involves others if possible.
2.2.4 D-variables
One trenchant criticism of Newman and Kenworthy’s work is that the univariate or bivariate models may leave some critical factors out. In a recent debate (Fanis 2019), Newman clarified that “All our work shows that there are multiple causes of car dependence and multiple implications.” Since travel behavior is a multi-dimensional issue, more socio-demographic and built-environment variables were added to the multivariate analysis. The work started from adding three ‘Ds’ variables, density, diversity, and design (Cervero and Kockelman 1997), extended to five ‘Ds,’ adding destination accessibility and distance to transit (Reid Ewing and Cervero 2001). It even grows to seven with the addition of demand management and demographics.
The idea of D-variables is from some urban planning and transportation theories such as “smart growth” and “new urbanism.” To address the urban sprawl, A “compact city” should be denser than a typical suburban development (Schimek 1996; Q. Zhang et al. 2019). Mixed land use could build a sense of community and allow more external trips being replaced by internal trips (Reid Ewing et al. 2011; Tian et al. 2015). The transit-oriented development (TOD) could reduce the distance to transit and encourage people drive less and choose active modes (McNeil and Dill 2020). Each variable may explain a part of travel behavior in some way.
Ds’ framework is a significance-centered mixed factor set and has become one of the most influential ideas in travel-built environment literature in the past decades. Using household-level or person-level data, these studies tried to disclose more complex relationships among the candidate factors by adding more relevant variables. This paper can not list all the studies of the vast travel-urban form literature. A highlight is the results from many studies are mixed. A factor may has significant impact on travel in some studies while not in others, or even has different influencing directions. For example, the effect of population density on bus trips is positive in the study by Brown et al. (2014), while it is negative in Alam, Nixon, and Zhang (2018) ’s study.
A criticism from Handy (2018) is that the D-variables may not be independent. A meta-analysis found that spatial multicollinearity is widespread in this field (Gim 2013). Although previous studies usually check multicollinearity issues, these variables still correlate with each other in some ways and may have strong interaction effects.
2.2.5 Synthesized Index
To address the multicollinearity and interactions issues, Clifton (2017) suggest to convert the various environmental characteristics to built environment indices. Some research try to use ‘compactness indices’ to replace the single density measurement (Reid Ewing et al. 2014; Hamidi and Ewing 2014; Hamidi et al. 2015; Reid Ewing, Hamidi, and Grace 2016). The primary method is principal components analysis (PCA) or principal components regression (PCR), which synthesizes many variables to four dimensions: development density, land use mix, activity centering, and street connectivity. The advantage of this method is to increase the elasticity value significantly. A recent study shows that the elasticity of VMT with respect to a county compactness index is -0.78. The disadvantage of this method is that the internal mechanisms of the indices are still not clear. Another disadvantage is that the various indices are not comparable. For example, Q. Zhang et al. (2019) use urban living infrastructure (ULI) as the local accessibility variable (ULI) and find ULI and household density have significant effects on household trip generation. Their ULI is the count number of retail, services, and social activities. Meanwhile, the Urban Liveability Index (ULI) by Higgs et al. (2019) are some indices supporting health and wellbeing. These indices include not only social infrastructure and transit service, but also walkability, public open space, housing, and employment. The two ULIs have different information and may not be comparable. Hence, the association between ULI and travel mode choice is a specific result unless an uniform measurement is widely applied on other studies and cities.
A smart application of synthesize method (common factor analysis) is to control the physiological effects in models. Hong, Shen, and Zhang (2014) convert eight attitudinal questions in the 2006 Household Activity Survey to three factors: Ease, Convenience, and Pro-transit. They fit the model using two geographic scales: 1-km buffer and traffic analysis zone (TAZ). After contolling the attitudinal effects, the nonresidential density and distance from CBD have significant effects on VMT at the TAZ level.
2.3 Meta-Aanalysis
This section introduces several influencing meta-analysis of travel-urban form studies. The relevant methods is in a separate chapter of Part II.
To get a general, comparable outcome, Reid Ewing and Cervero (2010) collected more than 200 related studies and summarized the elasticity values using meta-analysis. They exclude the aggregated studies to avoid “ecological fallacies.” The studies on specific groups such as aged people are also excluded. The selected studies must use multiple regression analysis with at least one response of VMT or travel modes, with at least one predictor from 5D variables. The studies using structural equation models are not included because these models will not give a single effects size of each 5D variables. The coefficients with respect to vary metrics of predictors are incomparable. Thus they convert all the estimates of coefficient to elasticities. Elasticity measures the percentage change in response with respect to a 1 percent increase in a predictor. Thus, it is a dimensionless parameter.
After screening, sixty-two studies were selected. This is a very small sample size because the research question involves five predictors (5D-variables) and three responses (VMT, walking, and transit use). Taking the VMT-density relationships for example, there are only nine selected studies in this meta-analysis. It is not large enough to get a sufficient inference. Looking at the distribution of elasticities, six of nine papers gave zero or insignificant elasticity. Three studies showed significant negative values (two are -0.04 and one is -0.12). Reid Ewing and Cervero (2010) use the nine observation to calculate the weighted-average elasticities of VMT with respect to population density. The result of -0.04 is mainly determined by the three observations.
Moreover, among the nine VMT-density studies, eight use single city/metro data. Only one nationwide study using NPTS data (Schimek 1996) finds logarithm of household VMT has a non-significant elasticity (-0.07).
Similarly, in this meta-analysis, the weighted-average elasticity of job density (sample size = 9) was zero. The largest elasticities of VMT are found be -0.20 with respect to job accessibility by auto (sample size = 5) and -0.22 with respect to distance to downtown (sample size = 3).
For the limitation of data quality, the standard error of elasticities are not included in this meta-analysis. When calculating the weighted-average values, Reid Ewing and Cervero (2010) use the sample size of each study as the weight factor. For the same reason, the confidence intervals are also not available.
| Study | Sites | Elasticity | note |
|---|---|---|---|
| R. Ewing et al. (2009) | Portland,OR | 0.00 | |
| Frank and Engelke (2005) | Seattle | 0.00 | |
| Greenwald (2009) | Sacramento | -0.07 | Non-peer-reviewed;Non-significant |
| Maria Kockelman (1997) | Bay Area | 0.00 | |
| Kuzmyak (2009b) | Los Angeles | -0.04 | Non-peer-reviewed |
| Kuzmyak (2009a) | Phoenix | 0.00 | Non-peer-reviewed |
| Zegras (2010) | Santiago de Chile | -0.04 | |
| B. (Brenda). Zhou and Kockelman (2008) | Austin | -0.12 | not log transform,\(R^2\)=0.097 |
| Schimek (1996) | U.S. | -0.07 | Non-significant |
This meta-analysis kindled researchers’ enthusiasm for this topic. After that, some studies try to cover multi-region data (Lei Zhang et al. 2012). Reid Ewing et al. (2015) accumulated a travel and built environmental dataset from 23 metropolitan regions in US (81,056 households and 815,204 people). They find that all of the 11 D-variables have statistically significant effects on VMT.
Stevens (2017a) extends this analysis and tries to explain the different outcomes using a meta-regression method. He focuses on the studies with VMT as the response and uses similar screening criteria. Based on the results from 37 studies, he finds the elasticity of population density is small (-0.10) and suggest that compacting development has a tiny influence on driving.
By adding a dummy variable, whether a study control residential self-selection or not, into the meta-regression, Stevens (2017a) shows that self-selection research design could impact the effect size significantly. For the studies with self-selection control, the estimated elasticity of population density becomes -0.22, which is much stronger than Reid Ewing and Cervero (2010) ’s result (-0.04). An advantage of meta-regression is the two groups with/without self-selection control can share the common errors, that fully utilizes the information and can overcome the small sample size issue to a certain extent. The number of studies with self-selection control is four, while the totoal selected studies is 19. This results is more reliable than the average value in self-selection control group.
Another improvement is that Stevens’ meta-regression uses weighted least squares (WLS) method. The weights are the precision (inverse of variance) of each observation. The same weights are applied on the weighted average and precision-effect estimate with standard error (PEESE) method in his ‘Technical Appendix for details.’ The estimated elasticities of population density with the three methods are -0.22, -0.13, and -0.20 respectively. Unfortunately, Stevens doesn’t share any information of standard error of coefficients in the article and technical appendix. It is not easy to check his data and results.
Note that one observation, the study by Chatman (2003) may twist Stevens’ result about density dramatically. In Chatman’s Tobit model, the average VMT is \(\bar y= 3.988\); the average household density is \(\bar x= 1.902\) (housing units per square mile, residential block group (1,000s)); the coefficient of household density is \(\beta=-0.082\). Then the elasticity should be
\[ \beta\cdot\frac{\bar x}{\bar y}=-0.082\cdot\frac{1.902}{3.988}=-0.0391 \]
This elasticity calculated by Reid Ewing and Cervero (2010) is -0.58. And it is not selected in meta-analysis because the response is VMT on commercial trips. Stevens (2017a) chooses this study and calculates a different elasticity -0.34. Whatever, -0.34 is the smallest elasticity and the second smallest one (Zahabi et al. 2015) is -0.22. While the rest studies give the range of elasticities from 0 to -0.20. Hence, these observations is highly skewed.
Chatman (2003) ‘s model is also the only one of four studies with self-selection control. If remove this case (-0.34), the estimated effect size will be much close to zero. Zahabi et al. (2015) has the largest sample size (147574). Steven finds the PEESE method for bias correction will change the weighted average elasticity from -0.13 to -0.20. He hesitates to remove this ’outlier’ because the outcome will become -0.09. At last, he choose to keep this observation and report the result without bias correction (-0.22). Changing the criteria after seeing the results is called post hoc analysis, or exploratory analysis.
Stevens’ work triggers a round of discussion. In Reid Ewing and Cervero (2017) ‘s reply, they don’t doubt Stevens’ results and criticize his conclusions. They agree with the values of elasticity but argue that Stevens’ results (-0.22 for density) are not small actually. They emphasize the extensive benefit of compacting development. They don’t think reporting bias is widely exist in built environment-travel studies. The difference results of meta-analysis is mainly duo to the studies selection, such as U.S. or international context. Keeping or removing the outlier is also make the difference.
Other scholars also contribute various insights. Manville (2017) supports the idea that compact development are related to less car use and look it as a “fundamental belief in urban planning.” Nelson (2017) agree that selective reporting bias does exist when some “interests or ideology dominate the discussion.” Clifton (2017) points out some weakness and potential sources of bias in current travel behavior studies. Heres and Niemeier (2017) support more application of meta-analysis on relevant studies. And they remind the substantial difference among the studies with vary methods, data sources of country, and metrics (e.g. commuting and noncommuting trips). They suggest to narrow the scope of studies down to get more specific conclusions for policymakers. Knaap, Avin, and Fang (2017) provide some suggestions for improving this approach from the perspective of sample size, model specification, and weighing. Among the discussion, a key issue is whether an universal effect of compact development with respect to driving distance exists, or the effect is totally context dependent. If the former is true, Stevens’ work should not be criticized for the cross-country scope. If the later is true, it still should be based on evidence rather than belief or experience. The complexity of urban issues makes it being an unsolved problem.
Handy (2017) agrees with the improvement by meta-regression but thinks that meta-analysis is not a direction worth to further investigation. In a later paper, Handy (2018) argues that the 5Ds framework should be replaced by accessibility-centered studies. In Stevens (2017b) ’s response to commentaries, he clarifies some research goals and important questions. He insists this meta-regression is currently “most accurate synthesis of the literature.”
Stevens’ study shows a uncommon direction of bias on elasticity of population density. An usual assumption of publication bias is small-studies tend to have greater standard errors and effect sizes. In contrast, among the 19 studies including density variable, the effect sizes in small-studies are closer to zero. An possible reason is the studies have high heterogeneity are answering different questions. In a highly heterogeneous field, researcher may not have too much pressure for small effect size. Another possible explanation is that most of recent studies include a bundle of predictors. Once one or more coefficients show significant, the paper will be treated equally. Publication bias only affects the nothing significant studies.
After the two milestones for meta-analysis of built environment and travel behavior, a recent update re-examines the post-2010 empirical literature. Aston et al. (2020) collected 146 studies containing 467 models and being recorded as 1662 data points. There are 15 predictors of research design, including the number of variables, aggregate/disaggregate data, general/commuter group, trip purposes, time periods, types of model, are used to examine how research design affects the built environment-mode choice studies. Instead of using elasticities as the response variable, they choose correlation, another dimensionless variable to measure the strength of the relationship between built environment and transit use. Their results shows that whether accounting residential self-selection and regional accessibility can account for 40% of variation of mode choice in the meta-regression.
Actually, this meta-regression use Stepwise selection method to remove the insignificant predictors. 40% is the coefficient of determination \(R^2\) in the four-predictor model for density and the five-predictor model for Diversity. In these meta-regression models, standard errors \(SE_r\) show the largest coefficient value. Control for covariance (which lack of explanation in this paper) contributes the second large one. Control for regional accessibility is a insignificant variable in both Density and Diversity models. How can get the conclusion of the 40% of variation are duo to the control of self-selection and regional accessibility? Aston et al. (2020) mention the asymmetry existed in the funnel plot for density and accessibility. It is an evidence of publication bias that could lead to overestimate the correlation. But the plot is not shown in the paper.
In a later paper, Aston et al. (2021) further improve the meta-analysis to examine the impacts of 5D variables on transit use. The number of studies are extended to 187. And 418 of 505 elasticities are used as valid response. They find that, using a random-effect model, the elasiticity of density on transit use (0.10) is close to Reid Ewing and Cervero (2010) ’s result (0.07). The standard error of estimate is also included \(SE=0.013\). Using this estimites, they re-examine the effects of control for self-selection and regional accessibility. The paired tests show that both of the two indicators have significant effects on elasticities of density. They also find the estimated elasticity of density in the studies after 2010 is significantly higher than the studies before 2010. The authors explain this change by more diverse study locations and more studies which control for regional accessibility after 2010.
2.4 Spatial Scales
2.4.1 Modifiable areal unit problem (MAUP)
Due to the various data sources or research interests, travel-urban form studies divide into two groups. One group uses aggregated travel and built-environment variables at the city, county, or metropolitan level. At the same time, the other group uses trip data at the individual or household level. The results of travel models at different scales are often inconsistent. Using the same data source, Reid Ewing et al. (2018) found that the elasticities of VMT with respect to population density is -0.164 in the aggregate models, which is a much higher value than disaggregate studies (-0.04 in the meta-analysis of Reid Ewing and Cervero (2010)). They suspect that this phenomenon is aggregation bias or ecological fallacy. They further explain that the two scales represent two different questions: The metropolitan-level density, which strongly affects the VMT, is not equivalent to the neighborhood density, which has much weaker effects on VMT.
Early in 1930, scholars noticed that, when a set of smaller areal units was aggregated into larger areal units, the variance structure will be changed and the estimated coefficients will be larger (Gehlke and Biehl 1934). This inconsistency/sensitivity of analysis results is called modifiable areal unit problem (MAUP) or ecological fallacy (Openshaw 1984). In spatial analysis, two kinds of MAUP often happen simultaneously (Wong 2004). The first one called ‘scale effect’ means that the correlation among variables depends on the size of areal units. Larger units usually lead to larger estimations. The second one, ‘zone effect’ describe the various results of correlation by choosing different areal shape or subset at the same scale.
Fotheringham and Wong (1991) found that multivariate analysis is unreliable when using the data from areal units. Both value and direction of estimated coefficients may change for different spatial configurations (G. Lee, Cho, and Kim 2016; P. Xu, Huang, and Dong 2018). The factors measured at a specific scale could only explain the variation generated at or above that level. Some factors such as density has cross scales. Their distributions in different units and scales are not identical. It is reasonable for them to have various meanings and influences on travel. A systematic comparison should be conducted among multi-scale studies. The inconsistent might not be about correct or wrong. As Reid Ewing et al. (2018) commented, the aggregate and disaggregate studies are asking the apples and oranges questions.
2.4.2 Aggregated Analysis
Aggregate data is more accessible and more convenient to combine with other data sources. Once a travel survey contains the attribute of geographic identifiers defined by Census, this information of travel can be integrated to other demographic, employment, and built environment data (e.g. American Community Survey (ACS)). Using the uniform coding, the data can further mapping to other levels (Table 2.2). For example, Reid Ewing et al. (2018) use the average per capita VMT of all urbanized areas across the U.S. from FHWA’s Highway Statistics. Then they join the 2010 census data in 157 urbanized areas (with populations of two hundred thousand or more) to FHWA’s VMT data.
| Area.Type | GEOID | Geographic.Area |
|---|---|---|
| Nested Entities | ||
| State | 41 | Oregon |
| County | 41051 | Multnomah County, OR |
| County Subdivision | 4105192520 | Portland West CCD, Multnomah County, OR |
| Tract | 410510056 | Census Tract 56, Multnomah County, OR |
| Block Group | 410510056002 | Block Group 2, Census Tract 56, Multnomah County, OR |
| Block | 410510056002014 | Block 2014, Census Tract 56, Multnomah County, OR |
| Other Entities | ||
| CSA | 440 | Portland-Vancouver-Salem, OR-WA |
| CMSA | 6442 | Portland-Salem, OR-WA |
| CBSA | 38900 | Portland-Vancouver-Hillsboro, OR-WA |
| UACE | 71317 | Portland, OR-WA |
| Places | 4159000 | Portland city, OR |
| PUMA | 4101314 | Portland City (Northwest & Southwest) |
Some aggregate studies shows that, using the simple averages of individual data, the estimations of coefficients in linear model are unbiased (Prais and Aitchison 1954). A condition is that the regression model must fix the omission error using proper specification (Amrhein 1995; Ye and Rogerson 2021). The check of unit consistency may help to examine the biases by MAUP on the estimations.
Tradition of aggregate analysis treat a city or metropolitan as an observation. Both dependent and independent variables are aggregated at macro level. The aggregate models confound the individual level’s variance. Urban form factors usually show significant effect. van de Coevering and Schwanen (2006) carry on Newman and Kenworthy’s work and consider four sets of potential explanatory variables: ten of urban form, six of transport service, five of housing and development history, and thirteen of socio-economic situations. They fit some linear regression models (all the variables keep the initial magnitude without taking logarithm or other transformation) and all of their adjusted \(R^2\) are higher than 0.7. Their models also show that the cities with higher population density drive less. They found the land use characteristics of the inner area are more important than metropolitan-wide population density.
In aggregate analysis the urban form factors measure the overall magnitude, such as population density, and can not reflect the land-use pattern or structure. A recent city-level study (Gim 2021) fits multiple regression models based on the data from 65 global cities. Using structural equation modeling, their results show that fuel price, household size, and congestion level have strong effects on travel time. In their model, the effect of overall population density becomes not significant while in the high-density built-up areas, the population density still has a larger effect on travel.
2.4.3 Disaggregated Analysis
For disaggregate studies, collecting complete personal travel records and the built environment information is difficult. A common way is to get travel survey data from the local department of transportation and combine it with census data and GIS data. Some scholars start their relevant research from individual data, then make a bottom-up aggregation to traffic zones (TAZ) or higher levels. (P. Zhao and Li 2021). In disaggregate analysis, the travel records by individual or household are the basic unit of dependent variables. Traveler’s socio-demographic characteristics such as income, working status, and vehicle ownership also keep this resolution. However, built environment factors technically have a minimum geographic unit as the measure scope. Census tract and block group are the most common unit in disaggregate analysis.
Scholars who choose disaggregate analysis believe that the internal difference of urban characteristics be neglected at region level. They are interested in the impact of meso-level built-environment factors like the population and employment distribution of intra-urban (Buchanan et al. 2006; Sultana and Weber 2007). Some study also confirm that individual-level data make the travel-land use model more reliable (M. Boarnet and Crane 2001). Using disaggregate data can disclose the neighborhood-level differences and eliminate aggregation bias. Using logarithms of VMTs per vehicle from National Personal Travel Survey (NPTS) data with 114 urban areas, Bento et al. (2005) fit the linear model with 19 variables. They found that, instead of population density, population centrality has a significant effect on VMT. The elasticity of annual VMT with respect to population centrality is 1.5.4
Aggregate and disaggregate are relative concepts. Literature usually treat the data at household level as disaggregated but it is aggregated by person or trip. Form Census Block to Tract, County, and Metropolitan Area, the data at these levels are all called aggregated but they have substantial difference. Schwanen, Dieleman, and Dijst (2004) explains that many urban form dimensions are tied to specific geographical scales. Recently, more studies import the spatial scales as an explanatory variable. In a report of travel and polycentic development, Reid Ewing et al. (2020) identify 589 centers in 28 U.S. regions. Then a categorical variable, ‘within/outside a center’ is added into the model. The results show that the household living within a center have more walk trips and fewer VMT than who living outside a center. S. Lee and Lee (2020) also conduct a study involving factors at three level: household, census tract, and urbanized area. They find that density and centrality affect VMT at urban level as well as the meso-scale jobs-housing mix. After controlling for factors, the effect of local factors the urban-level spatial structure moderates the effects size of local built environment on travel.
References
P. G. Newman and Kenworthy (1989a);P. G. Newman and Kenworthy (1989b);J. R. Kenworthy et al. (1999);P. Newman et al. (2006);P. Newman and Kenworthy (2011a);P. Newman and Kenworthy (2011b);P. Newman (2014);P. Newman and Kenworthy (2015);Jeffrey R. Kenworthy (2017)↩︎
“population centrality measure is computed by averaging the difference between the cumulative population in annulus n (expressed as a percentage of total population) and the cumulative distance-weighted population in annulus n (expressed as a percentage of total distance-weighted population).”↩︎