2.1 Probability functions for continuous random variables
For continuous random variables, the probability function is called a probability density function (PDF).
Example 2.1 (Probability density function) A rv \(X\) has the uniform continuous distribution defined from \(a\) to \(b\) if the PDF is \[ f_X(x) = \left\{ \begin{array}{ll} \displaystyle \frac{1}{b-a} & \text{if $a<x<b$};\\[6pt] 0 & \text{otherwise}. \end{array} \right. \] This is usually written, for convenience, as \[ f_X(x) = \displaystyle \frac{1}{b-a}\quad \text{for $a<x<b$}. \]
A PDF, say \(f_X(x)\) (or just \(f(x)\) when there is no ambiguity), has two properties:
- \(\displaystyle\int_{-\infty}^{\infty} f_X(x)\, dx = 1\); that is, the total probability is one (in other words, \(x\) certainly must take some value).
- \(f_X(x) \ge 0\) for all \(x\); that is, probabilities are non-negative.
Probabilities for continuous rvs are found by integrating over an appropriate area.
Example 2.2 (Uniform continuous distribution) A rv \(X\) has the uniform continuous distribution
defined from \(50\) to \(60\)
if the PDF is
\[
f_X(x) =
\displaystyle
\frac{1}{60-50} = \frac{1}{10}
\quad\text{for $50<x<60$};
\]
see Fig. 2.1 (left panel).
The probability that the \(X\) takes a value between \(50\) and \(55\) is
\[
\Pr(50<X<55) = \int_{50}^{55} f_X(x)\, dx = \int_{50}^{55} \frac{1}{10}\, dx = 0.5;
\]
see
Fig. 2.1 (right panel).
Note that the probability of observing
any value exactly is zero since \(X\) is continuous.
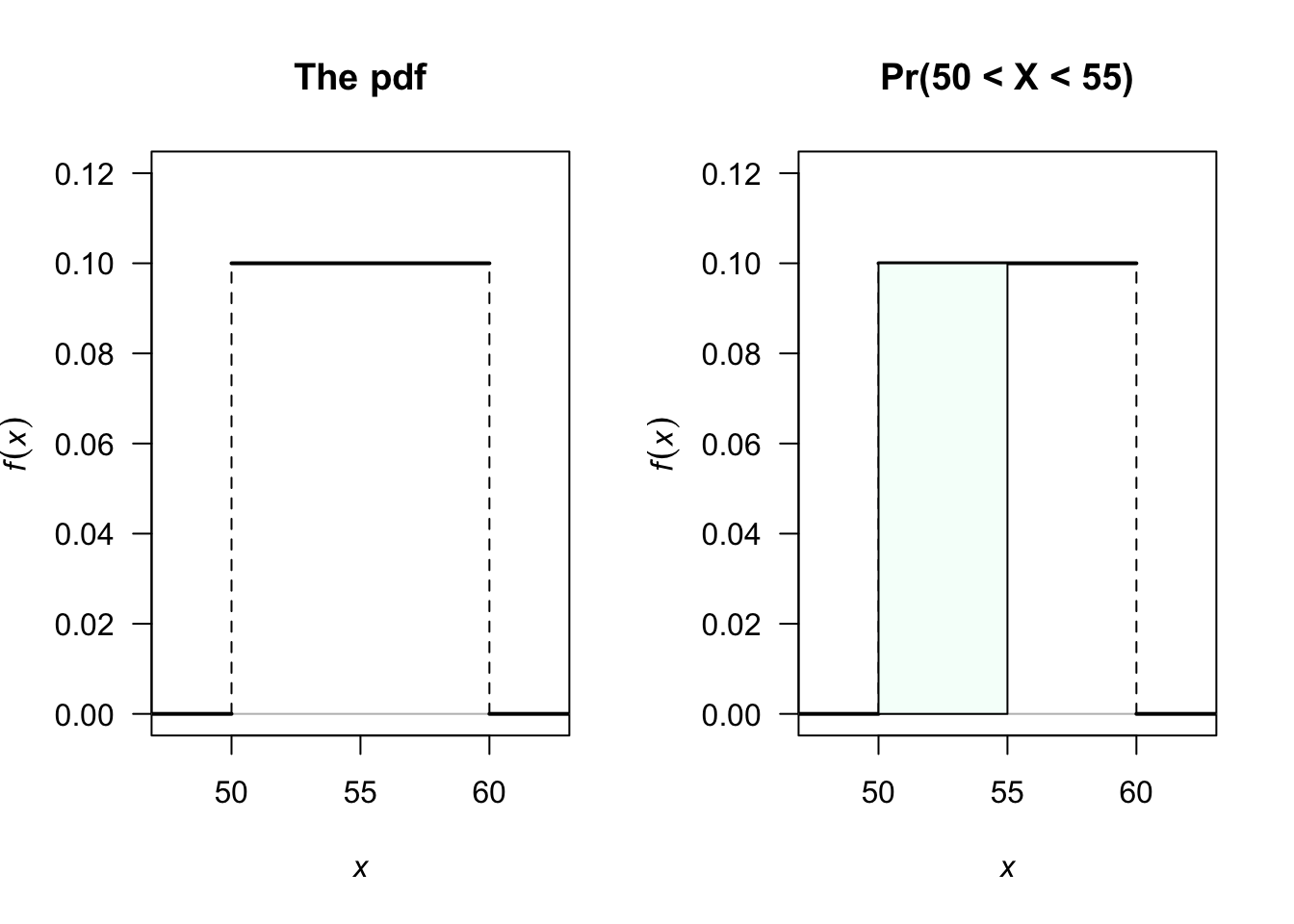
FIGURE 2.1: Left panel: A continuous uniform distribution defined for \(50<x<60\). Right panel: Displaying the probability that the value of \(X\) is between 50 and 55.
Example 2.3 (PDF: Continuous rv) Consider a rv \(Z\) with PDF \[ f_Z(z) = 3 z^2\quad\text{for $0<z<1$}. \] The probability that \(z>0.5\) is \[ \Pr(Z>0.5) = 3 \int_{1/2}^{1} z^2 \, dz = z^3 \bigg\rvert_{z=1/2}^{z=1} = 1 - \frac{1}{8} = \frac{7}{8}; \] see Fig.2.2.
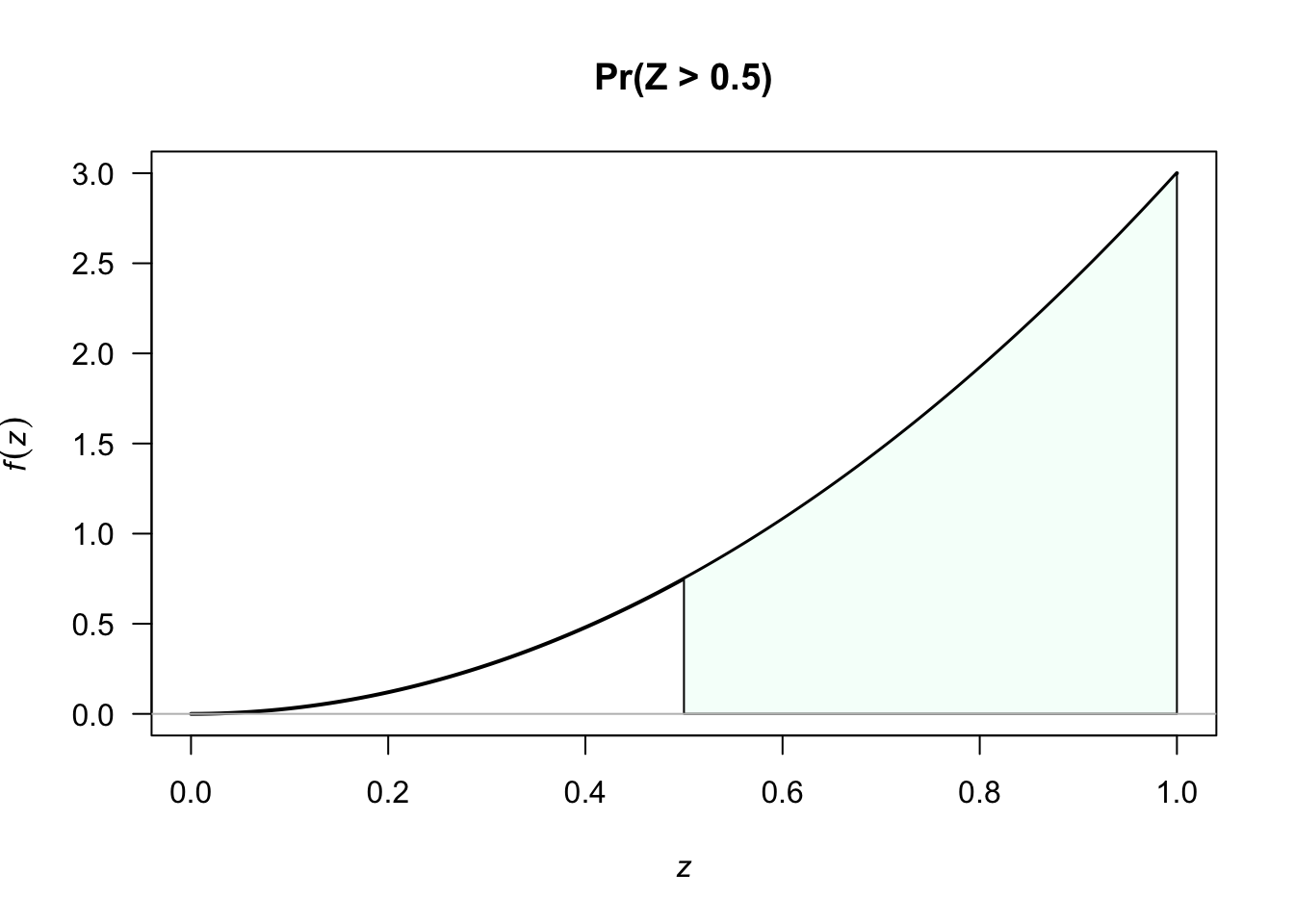
FIGURE 2.2: The PDF for the rv \(Z\)
Note that for \(X\) continuous:
- \(\Pr(X=x) = 0\) for all values of \(x\).
- Hence, \(\Pr(a < X < b) = \Pr( a \le X < b) = \Pr(a < X \le b) = \Pr(a\le X\le b)\).