3.1 CDF for continuous rvs

The CDF $F_X(x)$ for a continuous rv $X$ with PDF $f_X(x)$ is \[ F_X(x) = \Pr(T \le x) = \int_{-\infty}^x f(t)\,dt. \]

Example 3.1 (CDF: continuous rv) From Example 2.3, \[ f_Z(z) = 3 z^2\quad\text{for $0<z<1$}. \] The CDF is \[ F_Z(z) = \int_{-\infty}^z 3 t^2\, dt = \int_{0}^z 3 t^2\, dt = z^3. \] More completely and correctly, \[ F_Z(z) = \left\{ \begin{array}{ll} 0 & \text{for $z<0$}\\ z^3 & \text{for $0\le z \le 1$}\\ 1 & \text{for $z>1$} \end{array} \right.; \] see Fig. 3.1.

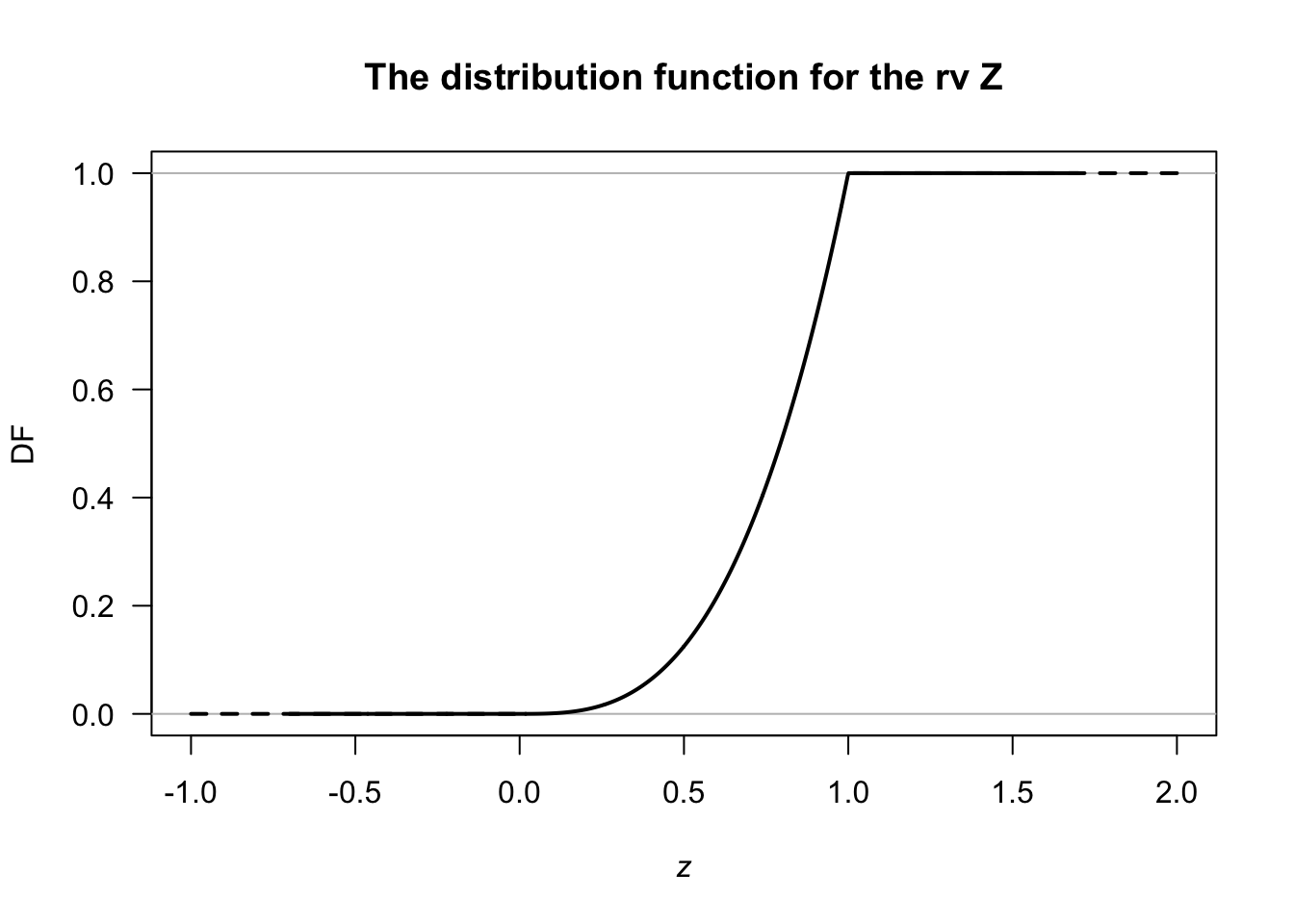
FIGURE 3.1: The distribution function for the variable $Z$