3.2 CDF for discrete rvs
The CDF \(F_X(x)\) for a discrete rv \(X\) with PMF \(f_X(x)\) is \[ F_X(x) = \Pr(T \le x) = \sum_{-\infty}^x f(t). \]
Example 3.2 (CDF: discrete rv) Consider the discrete rv \(Z\) from Example 2.6,
with PMF
\[
f_Z(z) = \frac{|z - 3|}{4} \quad\text{for $z=1, 2, 3, 4$}.
\]
The CDF is
\[
F_Z(z) =
\left\{
\begin{array}{ll}
0 & \text{for $z<1$}\\
1/2 & \text{for $1\le z < 2$}\\
3/4 & \text{for $2\le z < 4$}\\
1 & \text{for $z\ge4$}.
\end{array}
\right.
\]
See Fig. 3.2.
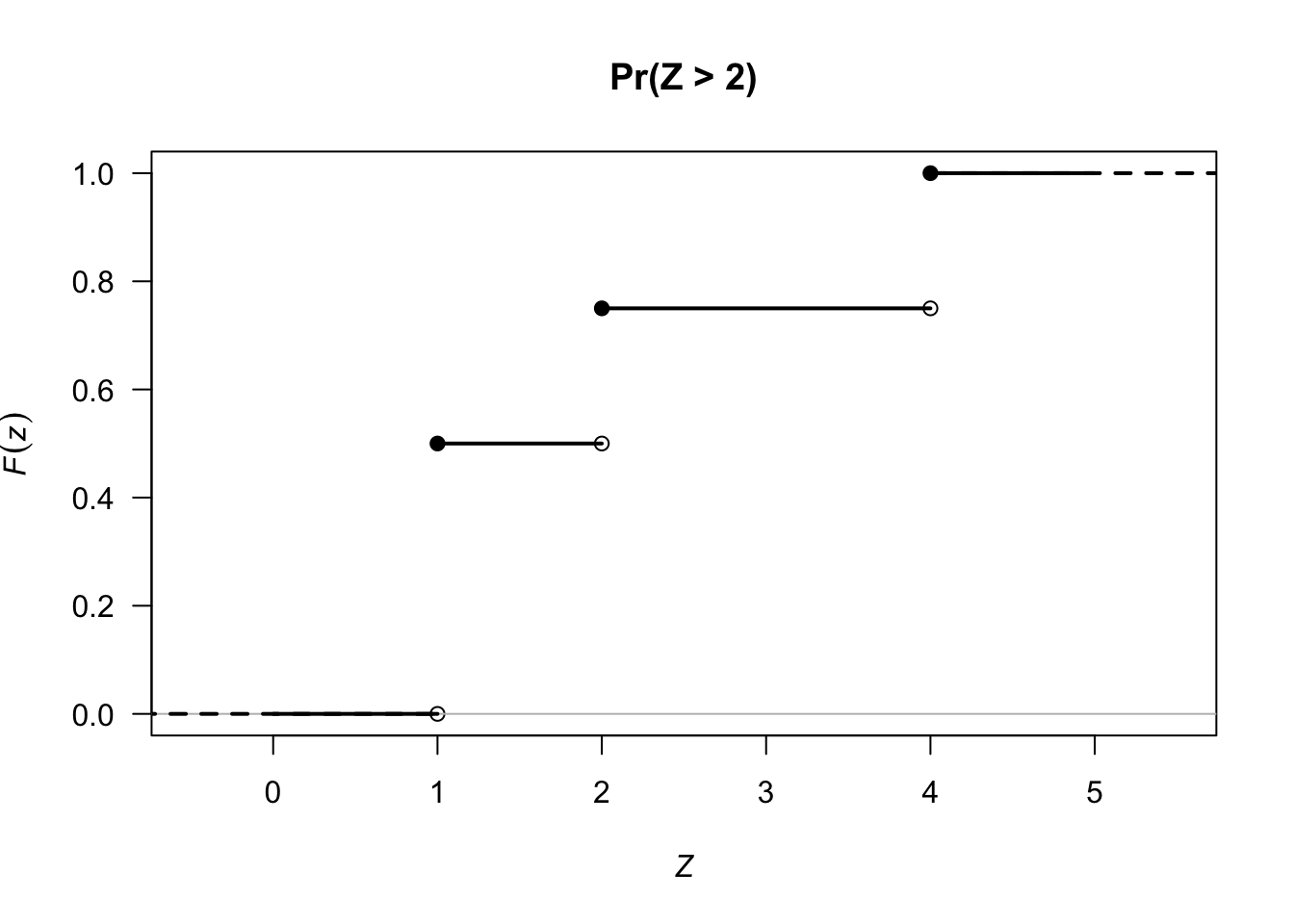
FIGURE 3.2: The cumulative distribution function (CDF) for \(Z\). Open dots mean that the point IS NOT included; solid dots mean the point IS included